GIS and the Social Sciences

4	GIS and network analysis

LEARNING OBJECTIVES

▪ Similarities and differences between geographical and social networks

▪ Network fundamentals

▪ Types of analysis relying on networks in a GIS setting

Introduction

If location is an intrinsic characteristic of geographic data, connection is not far behind. Connections between and across units – whether places, people, firms, water systems or streets – allow us to answer questions about relationships, flows, interactions or movements. In the case of these types of questions, knowledge about feature location is insufficient; we also need rules that capture the nature of the connections between each feature. In the case of a watershed, for example, we not only need to know whether a smaller stream joins a larger river, but also in which direction the water travels (since water travels uni-directionally in such a system). In a GIS environment, connections can be conceptualised through networks. By specifying which entities are linked to which, and what the rules of those connections are, networks are developed that can then be used in a range of social science applications.

Before delving further into the particulars of geographic networks (henceforth simply termed networks), it is important to distinguish between two different types of network analysis common across the social sciences. In this book, we are concerned with spatial aspects of networks, which could take the form of roads, public transportation lines or even shipping, air or rail routes. Other social science applications concern themselves with social network analysis: how a set of actors are connected to each other within a particular setting. Some aspects of both networks are similar. We might ask questions about information, for example, travelling through a spatial or a social network and the principles would be the same. Distance or routing in the case of a social network is not usually concerned with physical space, but rather how many people information travels through (like the child’s game of Chinese whispers telephone) before reaching the destination. Increasingly, there is interest in combining spatial and social network analysis. Here, however, we limit ourselves to coverage of spatial or geographical network analysis.

Spatial networks can be interesting in and of themselves – we can learn, for instance, how many streets meet at a particular intersection – but often they will be constructed in order to feed into subsequent analysis. A street network within a particular city or region provides information about which street segments are connected to other streets, but also how long the streets are and how long it takes to traverse them. Alone, this information is not especially useful. It becomes much more powerful when used for what is broadly termed network analysis. Network analysis, put simply, comprises a variety of analytical techniques that employ the network, along with other data, to answer questions about routes, shortest distances, coverage/accessibility or closest facilities. Sometimes, as with routes, the network is part of the solution: a ‘best’ path will be routed along the network. Other times, as with service areas, the network is being used to identify locations that meet a particular distance or cost criterion; the solution will not necessarily include the underlying network but will instead be a polygon or set of polygons. And occasionally, as with distance computation, there are multiple calculation alternatives. Other times, as in the case of most efficient route or service area, network analysis is required.

Part II of the book highlights specific applications of network analysis, and you work with network data sets in Practical D (Part I) and Practicals 5 and 6 (Part II). With an understanding of how to generate a network and what sorts of questions it can be used to answer, however, the potential range of uses of network analysis in the social sciences is enormous. The purpose of this chapter is to lay out the basics of networks, to give a general idea of the type of questions they can be used to answer and to provide an overview of the basic types of network analysis that a GIS can undertake.

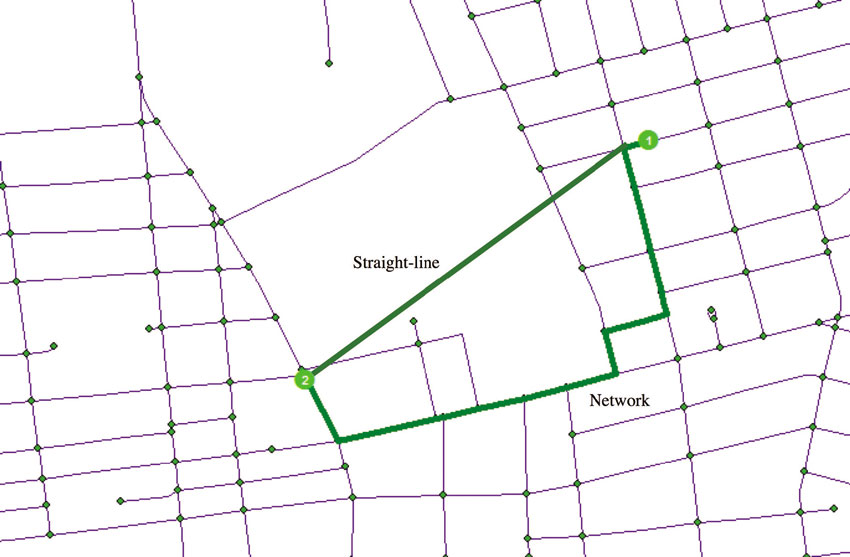
So what sorts of questions can networks help answer? One of their primary uses is simply to calculate distance from Point A to Point B – from household to grocery store, doctor to patient, or individual to hazardous waste site. The locations might be known, and we only seek to quantify their distance, or we might wish to find the distance to the closest facility, whether store, doctor, or park or school. Alternatively, we can use a network to find the distance to all facilities from some starting point or points. While straight-line, or ‘as the crow flies’, distance is easier to calculate in a GIS as it requires no network information, depending on the application it might fail to accurately capture the true distance an individual would cover when using existing streets, footpaths or other transportation networks. As Figure 4.1 shows, not only will straight-line distance be shorter (as it must: elementary geometry tells us that the shortest distance between two points is a straight line), it might also indicate a route that is not possible in the real world. When the goal is to replicate actual routes used, then incorporation of the underlying network is helpful. This type of use of a network, usually some sort of transportation network, is common throughout the social sciences – although, given the discussion above, one encounters straight-line distance more often than one might expect. Why is that? The simple explanation is that, although a network might be the ideal choice, it is not always achievable. For some parts of the world, accurate and reliable road data simply do not exist. And even in more developed areas, some types of network data, such as for roads, are more accessible than those for rail lines or bicycle paths. Where good data do not exist, the best solution is typically to fall back on straight-line distances.

Figure 4.1 Comparison of straight-line and network distances for identical origin and destination

Networks contribute to answering other sorts of questions as well. Research in health or retail that seeks to measure the share of an area covered by a particular set of facilities could use buffers (see Chapter 2) but might also use a transportation network for more realistic results. Networks can help identify locations for new schools or hospitals and can also help to develop routes – delivery or transportation, for instance – that meet certain criteria. In many cases, the research question or discipline might not obviously involve a network. As in the distance examples above, what sets network analysis apart is its incorporation of a network to investigate connections and distances.

When a network can help

As previous chapters have discussed, distance (or proximity) influences a wide range of social phenomena and a strength of GIS is the estimation of these spatial relationships. GIS offers many ways to conceptualise and capture distance; it is the researcher’s task to match measurement to application. Ideally, the way in which distance is measured should reflect how it matters in the real world. Because so much human interaction is governed by the constraints of transportation networks, streets in particular, it often makes sense to measure distance as traversed on these networks. Using a network can generate more accurate measurements, but also allows for considerations such as cost, time of day, intervening opportunities between origin and destination, and differences resulting from modal choice (e.g. if some patients take the bus to the doctor while others drive). Taken together, these aspects of distance can result in more realistic abstractions of reality.

We also use networks sometimes because we have to. In a GIS, many techniques, such as delineating service areas or locating new facilities, take place within a network environment because they rely on information about connectivity for computation. What this means, practically speaking, is that research using these techniques will require basic knowledge of network analysis and networks, even though the topic at hand might not appear network-dependent. We shall see, in Part II, that many applications of GIS involve knowledge of network analysis. This chapter provides introductory material that will assist in engaging more fully with those chapters.

That said, there are occasions in which networks are either overkill (too much data and work required for the result) or inappropriate to the subject at hand. Certainly, calculating straight-line distance will almost always be easier and faster. That means the decision to turn to network analysis depends on the sensitivity of the analytical results to accuracy of measurement, the availability of requisite data and a conviction that straight-line distance does not appropriately capture the spatial process under investigation. When considering distances between households and fire stations or routing ambulances from homes to hospitals, for example, accurate distance and routing is of prime importance. Longer distances – between cities in the United States – might give similar results for network or straight-line distance. Generating and then using a network for analysis requires data with certain charac-teristics. It also requires that these data be readily available and of good quality. Although many cities and regions in more developed countries possess good transportation data, this is often not the case for lesser-developed countries or, if the data exist, the area might be growing so quickly that data quickly become outdated. Finally, the best measurement of distance (or any other spatial variable) will depend on the research question: areas affected by a hazardous waste site might be best captured with a buffer or straight-line distance, whereas areas served by a hospital are best measured with network distance, or with travel time through that network.

Networks: the basics

A network is any representation of movement in directed space – so streets, but also utility networks or even river systems. Before performing network calculations, in general the network must be created in the GIS from raw data (the exception comes from cases in which the network was generated previously and is simply being reused or borrowed). Because networks are combinations of points and lines (or junctions and edges, Figure 4.2), the starting, input data are lines. Looking at the line features, whether streets or paths or bus routes, the researcher can often discern how movement would take place along those lines. The computer, however, needs to be explicitly told which line segments connect to which and what rules govern movement or flows along the network. The network creation process takes the input lines and develops the topological rules that need to be followed. Figure 4.3 shows the difference between a street layer and a street network.

Figure 4.2 A street network represented as combinations of junctions and edges

How does this work in practice? The most common input data are likely streets. The many line segments that combine to represent a city street system are used to generate the network. This process converts the line segments into edges – the streets carrying flows – and junctions, or intersection points. Depending on the data, the resulting street network will be of varying quality. Of paramount importance is that intersections and overpasses are accurately represented by junctions (or the lack thereof) and that connectivity in the network is complete. That is, there should be no line segments that are unreachable in the network, unless of course such a thing actually exists on the ground. We seek to be able to navigate the computer network in the same manner that we do the real network.

Figure 4.3 Converting streets to a street network

The network is more than its spatial component, however. Consider real-world movement on streets: this is controlled not only by where streets go and what they connect to but also by speed limits, distance and whether it is a one-way street, to name a few considerations. Traffic and toll costs might also be a factor. This is the information that lends verisimilitude to the spatial network. Some of this information – for example, distance – typically either comes with the data or can be easily calculated within a GIS. Other information such as directionality, traffic loads or speed limit must be present in the data in order to be incorporated into the network. If road type is available, it might be possible to estimate speed or traffic load based on average information for each type of road. Information about turns (and turn times) can also help provide more realistic analytical results for networks. In short, the best networks will be those containing information and variables that help it mimic real-world behaviour as closely as possible.

How does the GIS use the network to find the ‘best’ route? To define any sort of ‘best’ or ideal outcome using a network, the GIS needs decision rules and cost variables. The most common rules minimise a cost variable, such as time or distance. Rules can also maximise coverage. What rules have in common, though, is that they define best or optimal solutions. Analysis using the network – for instance, calculation of closest facility, distance or route – will also rely on one or more ‘cost’ or impedance variables. This cost is associated with travel along each link and summed to provide the total measure. In the case of closest facilities or best routes, but also other analytical tools, the GIS seeks the best of a set of options by minimising the cost variable. This is logical in the real world as well: the preferred route will generally be the shortest or quickest or cheapest. The computer is only as smart as the input data. If no measure of distance or cost (e.g. in terms of time or money) has been included, the GIS cannot pull this information from thin air. As noted above, distance is easily calculated by adding a line segment length variable in the street attribute table, if it is not already present. Other variables such as time and monetary cost must be estimated. It is normal for connectivity checking and estimation of cost or impedance variables to require a great deal of time.

Alone, the network, no matter how perfect, does very little. It is the combination of network plus other spatial information that allows analysis to be conducted. This additional spatial information is what tells the GIS where origins and destinations are, or which facilities are being used to compute service areas. This information usually comes in the form of geo-located point data – stores, hospitals or households – that might also contain additional attribute information. That is, any network analysis incorporates information about the underlying network and data about locations. Many GIS software applications allow the user to import existing point data, but also to search for addresses or manually locate them on a map.

In real-world networks, movement is occasionally disrupted, either cut off completely or slowed. Construction might close a length of street; a flood could impact an entire neighbourhood; or a malfunctioning traffic signal might render an intersection impassable. Once a network has been constructed in a GIS it is possible to assess the impacts that changes to the network, such as those listed above, will have on movement through it. Thus, it is possible to investigate connectivity in a street system and then measure the impacts that summer roadwork, for example, might have on traffic flows (see Figure 4.4). This ability to conduct a sort of impact analysis is another capability of network analysis in a GIS framework. Changes to the network can be implemented as barriers – either points, lines or polygons, depending on the type of disruption envisioned – that can be turned on and off to assess changes in routes and speeds.

Figure 4.4 Impact of an areal barrier (right) on route computation

A key element of networks is that movement is occurring along prescribed lines, whether streets or some other system. This is of course different from movement in continuous space – consider the difference between birds flying from place to place and cars driving from one location to another. Even within network space, however, we can distinguish between different sorts of networks. The type of network used in this book, and, in fact, most common across the social sciences, is what is termed an undirected network. Within these systems, the potential paths are predetermined. A car must travel on a street to get from one place to another. However, the car driver might choose to start the journey anywhere on the network and, similarly, the destination could be any other location reached via the street network. This is different from movement or flows taking place within, say, a city’s sewer system or a river system in the natural world. In those cases, flows originate at only certain locations (sources) and their subsequent route through the network is known. Imagine the confusion (and disgust) should the predictability of flows within a sewer system be upended. This type of network is called a directed network. The sorts of analysis done with directed networks are different from the material discussed above. Often, the main concern is with connectivity in a directed network. If water contamination occurs in a particular location of a city, for example, which households will be affected? If maintenance on one section of the electric grid is required, which portions of the system will become temporarily unavailable? Because directed networks are encountered so rarely in social science GIS applications, they are not further discussed here.

Common types of network analysis

As discussed in the introduction of this chapter, certain types of GIS analysis are usually associated with networks and are frequently termed ‘network analysis’. Some of the most common techniques are introduced below. Those seeking deeper information on any one method should see Part II of the book and also the suggestions for further reading below. It is worth noting that the algorithms and specifications for many of these methods are complex and are, in themselves, the subject of a great deal of research. This chapter provides only an introduction to the topic and is in no way meant to be exhaustive.

WHERE TO FIND ROAD DATA

▪ National or local governments. In some countries, such as the US, roads data are made freely available at a variety of administrative levels. This includes TIGER files at the national level but also data provided by states and cities. These data might require cleaning before being usable, however.

▪ OpenStreetMap (OSM, www.openstreetmap.org). This is open source, volunteered geographic information for the entire world, although data quality will vary by place and spatial scale.

▪ Proprietary or commercial data. ESRI, the ArcGIS software developer sells street data, as do HERE (formerly known as NAVTEQ) and Tele Atlas/TomTom.

Factors to consider in choosing data

▪ How old are the data? Particularly in rapidly expanding areas, data for streets can quickly become outdated as new roads are constructed.

▪ How complete are the data? Do you need information for smaller streets, as well as main thoroughfares? Do you need to model one-way streets? If so, your data must contain this information.

▪ How ‘good’ are the data? This includes completeness, but also accuracy – in terms of location, length of segments and even segment characteristics (e.g. number of lanes or paving type).

▪ Who or what is navigating your street network? Pedestrians? Cars? Bicycles or public transportation?

Routing is arguably the most frequently used network analysis tool and forms the basis of the practical accompanying this chapter. Routing in a GIS takes a set of at least two stops and finds the ‘best’ route, depending on the cost variable used and any barriers that might be included. Internet mapping tools that calculate directions and driving time from origin to destination use routing. A route is more than directions, though. Output is often visual (a map) and indicates which streets were used, but also includes the final cost calculation, which allows the routing option to be employed when the purpose is solely to derive a numerical result.

When more than two stops are included in a route, the GIS can be used to find not only the shortest route, but also the best ordering of stops. Figure 4.5 provides an example of a set of ten stops on a street network. In panel b, the shortest route is calculated for going to each stop as ordered in the list. Panel c shows the same stops: however, the GIS has ordered them in the most efficient way in order to minimise total distance travelled. The GIS will also allow the option to hold first and last stop constant or to allow all stops to be reordered.

Finding the best order for a given set of stops is known as the Travelling Salesperson Problem or TSP. The TSP is computationally intensive. Rather than the GIS having to find the shortest path for an ordered set of stops (which is already complex, given the number of routes that could be taken), it has to find the shortest path and find the best order of stops, given a specific cost variable (e.g. time or distance). Even with only five stops to make, ordering routes can quickly get out of hand. Should one do stop 1, 2, 3, 4 and then 5? Or 2, 1, 3, 4, 5? Or 2, 3, 4, 5, 1? Obviously, the number of options is vast (in fact, it is n2 – 1, or 24, if one assumes that direction of order matters). The result is that the computer does not necessarily find the optimal solution and instead often uses heuristics to arrive at nearly optimal solutions. On the other hand, this sort of spatial problem would be difficult if not impossible to calculate without computational assistance.

Service areas comprise those areas within a given distance of a set of facilities. In this case, the necessity for a network is not always apparent; one could also use buffers to identify locations close to facilities. The advantage of using the network, though, is that cost is calculated in terms of actual routes used. This advantage is made clear if time rather than distance is used as a cost variable. In that situation, ‘islands’ surrounding highway exits might fall into a service area, since travel time along a highway might be much faster than on smaller streets. Also the term ‘service area’ belies the utility of this tool: it can also be used to estimate market areas for retail and/or coverage for a set of public services, such as libraries, or accessibility in general.

Figure 4.5 Locations of (a) stops on a network; (b) a route for ordered stops; and (c) the shortest path for all stops

Figure 4.6 Using network analysis to compute service areas around facilities

The mechanics of service area computation are as follows: the GIS uses the cost variable to find all network locations that fall within the given cut-off or cut-offs. The output is either a set of polygons showing a service area or a set of lines showing all segments that meet the analytical criterion. Figure 4.6 gives a visual example of service area computation for three distances, a quarter mile, half mile and mile, for two facilities. The darkest shaded areas are those reachable within a quarter of a mile using the road network.

Service area polygons can be used in subsequent analysis to answer a range of questions, the most basic of which might be to assess the share of the population that has access to some type of facility within the given range. This coverage assessment might show whether the existing set of facilities provides coverage or access to the entire population. It might also indicate locations where additional facilities could be located, so as to increase overall coverage. The service area polygons also enable comparisons between areas inside different distance bandwidths of facilities. Perhaps the object of study is not access versus no access, but rather whether the characteristics of people or households differ according to accessibility. Service areas could thus be used to ascertain whether facilities are located equi-tably. Another use of service area analysis is to identify some set of locations that fall within identified polygons – for example, all the playgrounds located close to a set of schools.

Location-allocation refers to the inherently geographical challenge of locating facilities in such a way that some aspect of market or areal coverage is prioritised. The combination of location and allocation speaks to the process by which facilities are located and demand allocated to those facilities. As a tool, location-allocation is used most often in public sector GIS applications. It is harder to use these models in retail and commercial applications as the competitive nature of these sectors makes the location criteria of distance minimisation less relevant. In retail, for example, overlapping catchments are the norm whereas location-allocation catchment areas are unique to that facility. That is the reason why they work better for sectors that are not largely in competition, such as public facilities, for example libraries, fire stations, etc. That said, Goodchild (1984) offers an interesting modification of the models to better suit retail/business applications (see also the discussion in Chapter 8).

The goal of location-allocation might vary but the initial steps are similar. First, potential locations for facilities (whether schools, stores or public libraries, for example) are decided upon. The GIS will not propose site locations from nowhere; these should have been determined from previous analysis (available land, zoning, etc.). Potential sites might include prospective locations, existing locations or some combination of the two. It is also possible to specify whether certain sites must form part of the solution. The analysis also requires information about demand – locations of households, individuals or neighbourhood centroids – which will use the sites being located. These locations might be weighted by the number of people at the demand site. The two are then compared and locations are chosen that best fit the type of problem being solved. Within this framework, the analyst has a few choices, including:

1 Is the goal to maximise coverage? This option seeks to locate facilities such that the furthest distance travelled is minimised or falls within a particular cut-off. Coverage maximisation is used when it is important that even the longest distance travelled between demand point and facility meet a particular threshold. For example, the average distance between fire stations and housing units is less important than ensuring the fire engines can reach the furthest location within a set amount of time.

2 Is the goal to minimise total cost or impedance? This option can be used to locate just one facility or several. It is referred to as the 1-median problem in the former case and the p-median problem in the latter – with p referring to the number of facilities to be located. Here, the object of the analysis is to locate facilities such that the total, weighted aggregate travel is minimised. Because this point of Minimum Aggregate Travel (MAT) minimises the total burden on demand locations – whether households or businesses – it is often used in situations in which public services such as libraries are being located.

3 Is the goal to locate as few facilities as possible? Perhaps building the facilities will be expensive. If so, the goal might be to locate as few facilities as possible to still meet coverage requirements. With this option, the GIS will allocate as much demand as possible to the fewest potential locations.

4 Is the goal to secure a certain market share, given the locations of competitors? This choice chooses locations with regard to existing competitor locations and seeks to either maximise or ensure a certain market share. Depending on competitor and facility location, a larger or smaller share of the market will be allocated to the potential facilities; the aim of the analysis is to place them such that market share is maximised (or reaches some predetermined threshold).

Closest facility tools compare a set of facilities and incidents – really just two separate sets of spatial information – and identify the closest facility to a given incident, or vice versa. The terminology employed is the same one would use to find the closest hospital to a car accident (on the assumption that the closest hospital would be the best to go to in an emergency). Figure 4.7 shows a set of incidents and facilities and demonstrates that the process finds the closest facility for each incident, and there is no requirement that each facility be used. That is, one could also use the analysis to identify underused facilities. In spite of this language, closest facility analysis is actually applied in a range of situations. This is because it serves the dual purpose of calculating cost/distance between two points but also finds the closest from a larger set. So, given a set of communities and a set of doctors, closest facility could find the closest doctor and would also estimate the distance to reach her/him. Or given locations of children and a set of primary schools, children could be allocated to a school according to the shortest distance. As with other types of network analysis, the output is visual (see Figure 4.7) but a cost variable is also generated as part of the resulting attribute table. This variable can then be used for further analysis.

Figure 4.7 Finding the closest facility for a set of ‘incidents’

Origin–destination (O–D) matrix is exactly what it sounds like. Using the underlying network, the GIS calculates the lowest cost distance between a set of origins and destinations. These locations could be a set of cities, but also doctors and patients or neighbourhoods and schools. The result is a table with locations on the margins and distances in the cells. This table can then be joined back to an attribute table for either origins or destinations and then used in further analysis. For example, most calculations of accessibility (discussed in Chapter 1 and in most of our application chapters) require distances as inputs. The O–D matrix can be used to identify locations within a particular distance threshold or to calculate the most easily reachable locations in the data set. Unlike the closest facility option above, the O–D matrix provides distances from all (and to all) origins and destinations. You will work with O–D matrices in Practical 4a (retail) and Practical 10 (emergency planning).

Location-allocation models appear in a large number of applications of GIS. We shall explore them in various chapters in Part II, and you will be able to apply a location-allocation model to maximise coverage of health services in Practical 5. You can also apply network analysis in Practical 6 to assess the provision of fire stations serving an ‘at risk’ population.

Concluding comments

This book is designed to introduce basic GIS concepts and functionality in Part I and provide subject-specific information in Part II. Those who would like to learn more about network analysis in the social sciences can gain more insight in the applications that follow in Part II. In Practical D we examine how to create a network in ArcMap. This helps to address the question of how to work with a network data set for routing applications. In Part II we shall explore network analysis in relation to a number of key policy-relevant questions:

Chapter 7: Crime analysis

How can we estimate the ‘journey to crime’, or the distance between perpetrator and victim?

Chapter 8: Retail planning

Can we identify food deserts, areas far away from grocery stores, in a particular location?

Chapter 9: Health care

Do some residents lack proper access to health care? Does distance to a hospital or a doctor partly explain health outcomes?

Chapter 10: Emergency planning

If a natural disaster impacts an area, who will be affected and what is an appropriate evacuation plan?

Chapter 11: Education planning

How can school bus routing be optimised?

We hope the reader will use these application chapters to help understand the key concepts introduced in this chapter.

Accompanying practical

This introduction to networks in a GIS is accompanied by a practical activity that gives you the opportunity to work with a network data set (Practical D: Network analysis). The practical introduces a vector data set related to tram routes in the Australian city of Melbourne. We walk you through the process to create a network data set from these tram routes before exploring the tools provided by the software in order to carry out complex routing queries.