2
QUANTUM BEHAVIOR
“The theory of quantum electrodynamics describes Nature as absurd from the point of view of common sense. And it agrees fully with experiment. So I hope you can accept Nature as She is—absurd.”
RICHARD FEYNMAN, QED: THE STRANGE THEORY OF LIGHT AND MATTER (1985)
QUANTUM THEORY MATURES
In the 1920s, inspired work by Bohr, Heisenberg, and Schrödinger took quantum physics from a limited fix for a problem to a detailed description of quantum systems (anything from a single quantum particle to a whole collection of them). At this stage, however, quantum theory had limitations. Some physicists struggled with its probabilistic nature. When a particle was observed—for example, when a photon hit the screen in the double-slit experiment—it clearly had a specific location. There had to be some kind of mechanism to change the particle from a collection of probabilities to having an observed position. This mechanism, known as wave function collapse, was mysterious, and some felt there had to be a better interpretation. Physicists now prefer a concept known as decoherence, which describes the same process but avoids the need for a wave function to collapse.
As well as getting a better understanding of this mechanism, physicists were pushing the boundaries of application of quantum theory. Many quantum particles travel at high speeds, which made it necessary to bring in the special theory of relativity. Toward the end of the 1920s, English physicist Paul Dirac found a solution combining the original equations with relativity. But to make his new equation work, Dirac had to imagine an unlikely scenario featuring an infinite sea of electrons, all with negative amounts of energy. Strange though this seemed, the concept was testable, as it predicted the existence of a new kind of matter.
Antimatter and quantum fields
This “antimatter” consists of particles that are nearly identical to existing ones, but have opposite values of some properties, for example, electrical charge. A few years later, the first antimatter particles, positrons (also known as antielectrons), were discovered. In time, antimatter proved to be a fundamental player in the creation of the universe. With sufficient energy, photons can transform into a pair of particles—one matter, one antimatter. It is thought that it was from this process that the matter in the universe came into being. As often seems to be the case with quantum theory, the solution to one problem caused another. In this case, it is not yet fully answered: what happened to all the antimatter in the universe, as it now seems to be very rare?
At the same time as these developments, quantum physics was being transformed from a regime that primarily dealt with particles or waves to a field theory. Field theories had emerged in the late nineteenth century when trying to explain electricity and magnetism. The approach moves away from individual entities such as particles and waves, to a field, which is something that fills all of space and has a time-dependent value that could be different at each point in space. It’s easy to get hung up on worrying about whether light or an electron really is a particle or a wave or a disturbance in a quantum field. What we need to remember is that each of these is a model—a way of describing reality that allows us to make calculations and predictions. We are not saying that light, for example, is any of these, but each model is particularly useful in some circumstances, and the quantum field theory approach has tended to be particularly valuable for many calculations.
The intersection of light and matter
By the 1940s, the burgeoning quantum field theory had become quantum electrodynamics, or QED. This is an approach that describes not just the behavior of individual particles (or waves, or disturbances in quantum field—it can just be easier to say “particles”), but also of the interaction between them. Crucially, it covers all the circumstances where light interacts with matter, which occurs not only in the more obvious examples of a photon being absorbed or emitted by an electron in an atom, but also with any electromagnetic interaction between matter particles.
As physicists gained a better understanding of these kinds of quantum interaction, they were able to predict and explain the explicitly quantum phenomena that go on around us. They used the new quantum approach to show how, for example, a photon that hits a sheet of glass “decides” whether to reflect off it or pass through it. They also predicted and then demonstrated a process known as quantum tunneling, where a particle gets through an apparently unsurmountable barrier by simply appearing on the other side. This apparently highly unlikely process is essential for life on Earth. And tunneling even provides a mechanism by which a photon can apparently travel faster than the ultimate speed limit, the speed of light.
BIOGRAPHIES
ALBERT EINSTEIN (1879–1955)

The most famous scientist of modern times, Albert Einstein was born on March 14, 1879 in Ulm, Germany. From an early age, he struggled with authority—while he enjoyed some subjects at school, he couldn’t see the point of others, and by the age of fifteen, he had given up his German citizenship to avoid conscription. After gaining a mediocre degree at the Zurich Technical College, he could not get a position in academia, so became a patent clerk. In 1905, while working at the patent office, Einstein wrote four groundbreaking papers, including one establishing special relativity, one showing that E = mc2, and another showing the foundations of quantum physics, based on the photoelectric effect, which won him the Nobel Prize in Physics in 1922. After the publication of his masterpiece, the general theory of relativity, in 1915, which brings gravity into relativity, Einstein became a public figure. From this time onward, he spent considerable effort trying to undermine the quantum physics he had helped start, as he was unhappy with its dependence on probability. In the 1930s, Einstein left Germany as anti-Jewish sentiment grew, and worked at the Institute of Advanced Study in Princeton in the United States until his death in 1955 at the age of seventy-six.
WOLFGANG PAULI (1900–1958)

Born in Vienna, Austria, on April 25, 1900, Wolfgang Pauli has not achieved the same level of fame as some of the big names in quantum physics—but the principle named for him, the Pauli exclusion principle, won him the Nobel Prize in Physics in 1945. The exclusion principle is essential in providing a quantum explanation for everything from the chemical behavior of atoms to neutron stars and black holes. It was while lecturing at the University of Hamburg in the 1920s that Pauli made his most noteworthy contributions to quantum physics. However, his exclusion principle and his work on quantum spin would not be his only significant contributions to physical science—it was Pauli, for example, who predicted the existence of a new particle, later called the neutrino, which is important in understanding how nuclear reactions work. As a side interest, he worked with the psychiatrist Carl Jung, both as a patient and in helping Jung formulate his theories. Pauli moved to the United States in 1940, but returned after the war to Switzerland, which had been his home since the late 1920s. He died in Zurich in 1958, aged fifty-eight.
PAUL DIRAC (1902–1984)

Born in Bristol, England, on August 8, 1902, Paul Dirac is probably the most important physicist of the quantum age that hardly anyone has heard of. Dirac studied electrical engineering and mathematics at the University of Bristol before moving to Cambridge, England, which would be his academic home until his retirement. There, Dirac focused on relativity and quantum physics, combining the two by expanding Schrödinger’s equation to take in particles moving at high speeds. The equation Dirac produced required electrons to be able to have negative energies—which meant there should be no minimum energy level, but electrons could plunge lower and lower. As this wasn’t observed to be true, Dirac suggested instead that an infinite sea of negative-energy electrons filled all available spaces, so the only observed electrons had positive energy. This model predicted a different kind of particle—an antielectron, or positron, which was discovered experimentally a few years later. Dirac’s work won the Nobel Prize in Physics in 1933. He also made major steps forward in combining the main approaches to quantum physics and bringing electromagnetism into the fold. Apart from his work, he was best known for having limited social skills. Dirac died in Tallahassee, Florida, in 1984, aged eighty-two.
RICHARD FEYNMAN (1918–1988)

Richard Feynman, born on May 11, 1918, was anything but the stereotype of a socially inept physicist. Brash and an enthusiastic communicator, he was something of a showman throughout his career. During World War II, when working on the Manhattan Project, he was known as much for his spare-time activities of breaking into safes and secure filing cabinets to demonstrate the limitations of security as he was for his contributions to the physics of nuclear weapons. Shortly after the war, he made his breakthrough work in fundamental quantum physics—specifically, the quantum physics of the interaction of light with matter, and matter with matter. Along with Julian Schwinger and Sin’Itiro Tomonaga, he won the Nobel Prize in Physics in 1965 for his development of this quantum electrodynamics, or QED. One of Feynman’s most significant contributions was the development of Feynman diagrams, which help both to explain and to enable calculations on QED interactions. Feynman went on to become a popular physics communicator, and discovered the cause of the 1986 space shuttle Challenger crash as a member of the investigating commission, dramatically demonstrating his theory on live television. Feynman died in 1988, aged seventy.
TIMELINE
QUANTUM TUNNELING
Quantum tunneling, where a quantum particle’s probabilistic location enables it to pass through an otherwise unsurmountable barrier, is first observed by Friedrich Hund and is used in theoretical work the following year by George Gamow. Tunneling would prove essential in explaining the nuclear fusion process in stars.

THE DIRAC EQUATION
Paul Dirac produces an equation that describes the behavior of electrons at relativistic (near the speed of light) speeds. This is necessary to provide an effective quantum model of the atom. To make his equation work, Dirac has to postulate the existence of a sea of negative-energy electrons, which leads to the concept of antimatter.

ANTIMATTER
Carl Anderson discovers the first example of antimatter—an antielectron, also known as a positron, discovered in cosmic rays. This positively charged equivalent of an electron was predicted by Paul Dirac’s theory, but originally considered unlikely to exist. Antimatter equivalents of all matter particles were later discovered.

QED
Richard Feynman, Julian Schwinger, and Sin’Itiro Tomonaga build on Paul Dirac’s work to develop quantum electrodynamics (QED). QED describes how all electromagnetic quantum phenomena take place. As this covers all interactions between light and matter, and between matter and matter, it explains the majority of everyday experience.
FEYNMAN DIAGRAMS
Richard Feynman introduces Feynman diagrams, which both illustrate quantum interactions and are used in quantum physics calculations. Showing interactions over time, the diagrams feature straight lines for matter particles and wavy lines for photons. Although apparently simple, the diagrams make it practical to keep track of complex interactions and become universally used.

SENDING DATA
Günter Nimtz demonstrates the ability of quantum tunneling to carry information faster than light, using a recording of Mozart’s Fortieth Symphony, transmitted at over four times the speed of light. The demonstration at a conference in Snowbird, Utah, is in response to the suggestion that this quantum tunneling could be used to send only random data.
PROBABILITY REIGNS
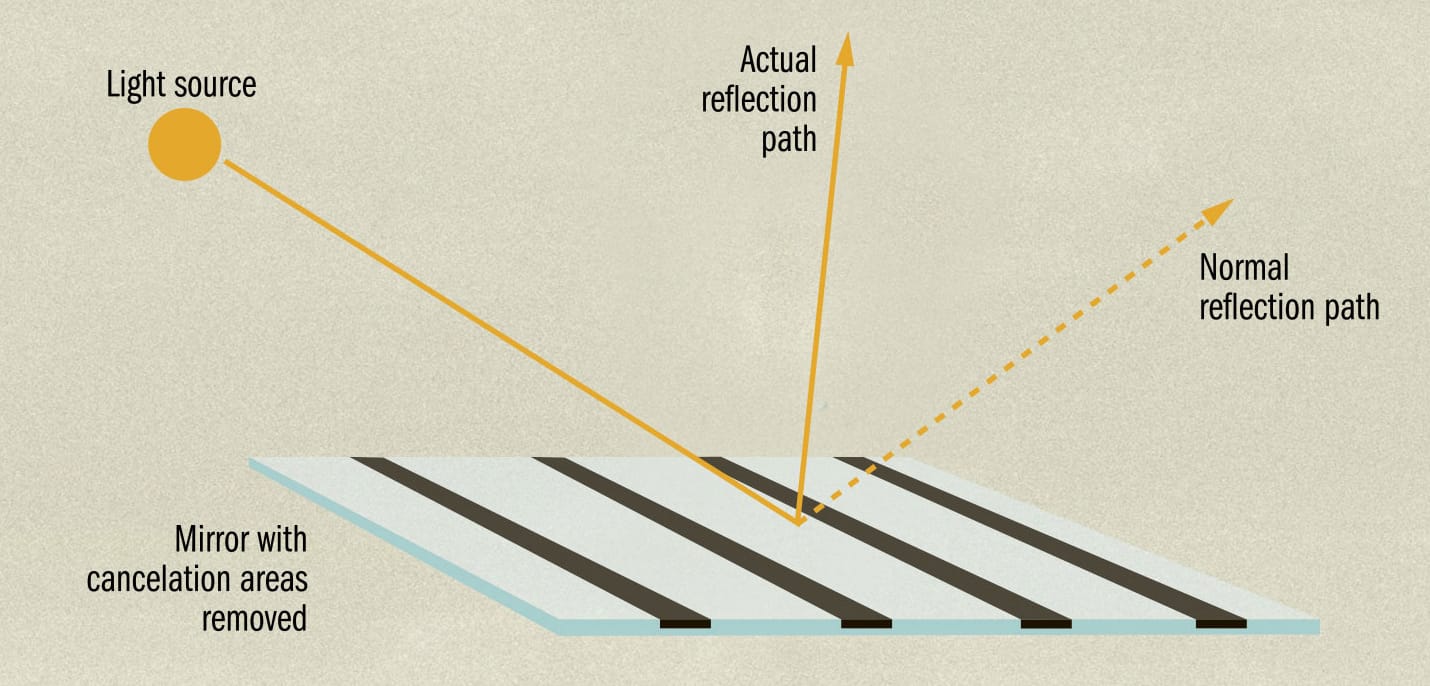
THE MAIN CONCEPT | Quantum physics is frequently described as mysterious. As US physicist Michio Kaku commented, “It is often stated that of all the theories proposed in [the twentieth] century, the silliest is quantum theory. Some say that the only thing that quantum theory has going for it, in fact, is that it is unquestionably correct.” The reason for this view is that quantum physics says that the components that make up the universe, such as atoms and electrons and photons of light, behave differently from the objects that are made from and interact with these components. If I put a ball somewhere, unless something moves it, it will stay there. If I throw a ball, it follows a predictable trajectory. And if I reflect light off a flat mirror, it will reflect at an angle equal to the angle at which it arrives. But quantum physics tells us that the particles making up the ball, the light, and the mirror are all subject to probability. When we look at a reflection in a mirror, for example, quantum theory tells us a photon has a probability of reflecting at every possible angle. Usually, most probabilities cancel out, but if we remove parts of the mirror that allow for this cancelation, light reflects at unexpected angles.
DRILL DOWN | The probabilistic nature of quantum particles is sometimes taken as meaning that quantum behavior is random and unpredictable, but physicists are quick to point out that the probabilities themselves are not random, but deterministic. So, for example, take the decaying particle used in the Schrödinger’s cat thought experiment. Probability enters into the situation because we don’t know—we cannot know—when the particle will decay. After a while without being observed, the particle will be in a superposition of decayed and nondecayed states. But we can specify exactly what the half-life of the particle is: a fixed period of time during which the particle has a 50/50 chance of decaying.
MATTER | Take a CD or DVD and tilt it at an angle. Rainbow patterns will appear on the surface. This is a direct result of the probabilistic nature of quantum physics. Optical disks store information as tiny pits in a reflective metal foil. The pits stop some of the possible routes for the light, producing reflections at unexpected angles, which vary by wavelength, causing the rainbow patterns.
COLLAPSING WAVE FUNCTIONS
THE MAIN CONCEPT | Perhaps the most controversial aspect of the original formulation of quantum theory among physicists themselves was the idea of collapsing wave functions. According to Schrödinger’s equation, the state of a quantum system was described by a wave function, which showed, for example, different probabilities of finding a particle at various locations. This wave function evolved over time, with the different probabilities spreading out to encompass wider areas. But if the particle were observed, the wave function was said to “collapse,” leaving the particle at the position where it was observed with one hundred percent probability. Some struggled with just what such a collapse meant; what was changing to represent this collapse? There was no mechanism provided—somehow the system went from a superposition of possible states (for example, locations) to occupying a single one—because that was what it did. But there was no suggestion as to how. Others dismissed wave function collapse as an issue (and still do)—their viewpoint, summed up as “shut up and calculate,” was that as long as the equations matched what was observed, it was pointless speculating about what was “really” happening. We would never be able to directly connect to reality, and so there was little point worrying about the nature of wave function collapse.
DRILL DOWN | Traditionally, we make a clear distinction between the observer and the experiment. But it is possible to consider them as forming a single system. Wave function collapse is arguably a relative term, dependent on isolating the quantum system being observed. However, whatever appears to cause the wave function to collapse—observing a particle, say—is part of a larger quantum system incorporating both the experiment and the cause. In this larger system, there is no collapse because, overall, the whole system of the experiment and its environment continues in principle to follow Schrödinger’s equation (in practice, the complete system is usually too complex to make a calculation of its evolution through time).
MATTER | We are unable to directly access reality, a problem that has plagued the philosophy of science ever since the time of Immanuel Kant. In the eighteenth century, Kant distinguished between the actual reality of nature—the “Ding an sich”—and our observations, which could only ever be interpretations of sensory inputs rather than a true description of “the thing itself.”

DECOHERENCE
THE MAIN CONCEPT | Those who were most uncomfortable with the notion of wave function collapse developed a new, subtle variant of the concept, known as decoherence. In effect, decoherence makes use of the approach where we take in the wider system, including more than the part of the system that is said to collapse, but without taking on the impossible complication of including everything in the universe that could influence the experiment in the calculation. Decoherence envisages that the experiment—for example, a quantum particle’s behavior—does not actually undergo wave function collapse, but that the interaction of the particle’s wave function and that of something causing the apparent collapse—for example, when it interacts with another particle—produces a combined effect that makes it look as if the wave function has collapsed. The practical explanation of this is called quantum entanglement—the particle becomes “entangled” with the other particle, their properties interacting, and ceases to act as a totally independent system. The advantage of decoherence over straight wave function collapse is that it does provide an explanation for apparent collapse occurring, rather than simply stating it as the way things are. Alternative explanations of quantum theory, notably the “many worlds” interpretation use decoherence rather than collapse.
DRILL DOWN | The more a piece of technology makes direct use of quantum states, the bigger the problem from decoherence. For example, the emerging field of spintronics makes use of an electron’s spin as well as its charge. And many teams are working on quantum computers, where the equivalent of the 0/1 values of a traditional computer bit are the superposed quantum states of a particle. If the particles used in these devices interact with their surroundings, decoherence occurs, and the quantum calculations fail. One of the main reasons it has taken forty years to get quantum computers from theory to practicality is the difficulty of avoiding decoherence over any practical timescale.
MATTER | The concept of decoherence depends on an aspect of quantum physics known as entanglement, a term that was introduced by Erwin Schrödinger when speaking at the Cambridge Philosophical Society in 1935. Because entanglement requires quantum particles to be able to interact at a distance, Einstein referred to it as “spükhafte Fernwirkungen,” literally spooky actions at a distance.

DIRAC’S EQUATION
THE MAIN CONCEPT | Schrödinger’s equation was a huge step forward for quantum physics, describing how a quantum system evolves with time. However, it did not include the influence of the special theory of relativity, where fast moving objects behave differently from expectation. British physicist Paul Dirac in the 1920s formulated a relativistic equivalent of Schrödinger’s equation. It built on Bohr’s model of the quantum atom, which had worked effectively only with a single electron, and only at low energies where relativistic effects could be ignored. Dirac’s equation made it possible to deal with fast moving electrons and more complex atoms, producing results that matched observation. Unfortunately, the Dirac equation only worked if it were possible for electrons to have both positive and negative energy—and no one was sure what a negative-energy electron would be like. If electrons could occupy negative-energy levels, electrons around atoms would continually leap down lower into the negative, giving off energy in the form of light. This should go on indefinitely—there is no bottom to this negative-energy “well.” Dirac fixed this by imagining that there was already an infinite sea of negative-energy electrons, which filled up all the spaces that were available. This meant that all observed electrons had to have positive energy, because there were available spaces only in the positive levels. Half of reality was totally occupied, with what was observed taking place in the other half.
DRILL DOWN | When an electron absorbs a photon, it undergoes a quantum leap, jumping up to a higher energy level. This process applies just as much to negative-energy electrons as positive-energy electrons. What remains is a gap, which could be filled by a positive-energy electron falling into it. The missing negative-energy electron proved mathematically identical to a present positive-energy particle, identical to an electron but positively charged. Such a particle—the positron or antielectron—was first observed a few years later. If positive-energy electrons dropped into gaps, they would disappear, producing photons. Again, this was observed to happen: when an electron and a positron collide, they annihilate, giving off energy.
MATTER | Conversations with Dirac were notoriously awkward, often involving remarks that were monosyllabic or strange. He tended to introduce his wife, for instance, as “Wigner’s sister” (referring to her brother, Hungarian physicist, Eugene Wigner). It perhaps didn’t help that at home, his mother spoke English, but his father only French. He once remarked that when young, he had thought men and women spoke different languages.
QUANTUM FIELD THEORY
THE MAIN CONCEPT | Although Schrödinger’s and Dirac’s equations proved immensely valuable in explaining the behavior of quantum particles, they could not provide a useful description of the wider interaction of quantum particles—for example, of light and matter. The classical description of light was based on field theory—started as a descriptive concept by Michael Faraday and given mathematical rigor by James Clerk Maxwell. The underlying concept of a field was a hypothetical “something” filling the universe, which could have a different value at every point in space and time. A two-dimensional equivalent would be a contour map, providing the two-dimensional space of the map with a value at each point. Fields made it possible to explain phenomena such as electricity and magnetism without resorting to action at a distance. Instead, for example, a magnet produced a traveling distortion in the field that was felt remotely. Light became an interaction between variations in the electrical and magnetic fields. Quantum field theory adds on the quantum nature of small-scale phenomena. It was first employed by Paul Dirac and required the values in the field to be quantized. In a quantum field description of reality, light, for example, was a traveling fluctuation in a field—and because it was a quantum field, those fluctuations were made up of photons.
DRILL DOWN | Some physicists consider reality to be nothing more than a collection of overlapping quantum fields, known as “the bulk.” In this picture, all phenomena are simply fluctuations in the various quantum fields. It certainly is one way of representing the universe, although it comes across as stark and mathematical, just as did Heisenberg’s matrix mechanics. Quantum fields are excellent ways of representing reality and performing mathematical manipulations to represent quantum actions, but it’s important that we do not forget that, as was the case with waves and particles, quantum fields are not reality—they are models that enable us to interpret what we can detect of reality better.
MATTER | The concept of a field strongly echoes the older idea of the ether, an invisible “something” filling all of space. When it was understood light sometimes behaved like a wave, it was difficult to explain what was doing the waving in empty space. The ether filled the gap. However, the ether was thought to be a substance, rather than a property of space itself.

ANTIMATTER
THE MAIN CONCEPT | The concept of antimatter emerged from Paul Dirac’s prediction that there should be negative-energy electrons, which he “fixed” by assuming there was an infinite sea of these electrons, filling all available negative-energy gaps. However, there was nothing to stop one of these electrons absorbing a photon and jumping up to a positive-energy level, leaving behind a hole in the negative-energy sea. This absence of a negatively charged, negative-energy electron proved to be identical to a positively charged, positive-energy positron, or antielectron. Within a few years of Dirac’s theory, the positron was discovered in cosmic rays—high-energy sprays of particles from space. The positron had the same mass as an electron, but the opposite charge. One of the predictions from the Dirac sea was that an ordinary, positive-energy electron could drop down into a negative-energy hole. If that happened, the electron would disappear, leaving only energy in the form of photons. This meant that if the matter and antimatter particles came together, they would annihilate each other, turning into pure energy. A few years later, an alternative approach to reaching Dirac’s equation meant that the infinite sea was no longer necessary—but the concept of antimatter it spawned is still going strong.
DRILL DOWN | Each matter particle has an equivalent antiparticle. The distinctions between particle and antiparticle are clearer with a charged particle—so, for example, an antiproton has the same mass as a proton, but a negative charge. The CERN laboratory has produced antihydrogen atoms, where a positron orbits an antiproton—but electrically neutral antiparticles such as antihydrogen are difficult to handle because they cannot be constrained by electromagnetic fields in the way charged particles can, so come into contact with ordinary matter and get annihilated. Neutral particles such as neutrons also have antiparticles that vary in other quantum numbers, while photons and similar particles are sometimes considered to be their own antiparticle.
MATTER | Photons can convert to matter (E = mc2), producing equal quantities of matter and antimatter. Since all the matter in the universe came from photons, it is strange that little antimatter is seen. It has been speculated that the antimatter is somehow separate from the rest of the universe or, more likely, an asymmetry between matter and antimatter resulted in more matter being created.

QUANTUM ELECTRODYNAMICS
THE MAIN CONCEPT | Quantum electrodynamics, or QED, describes the interaction of matter with matter, and matter with light, all dependent on electromagnetism. Three individuals developed QED independently just after World War II (winning the 1965 Nobel Prize for it)—Richard Feynman and Julian Schwinger in the United States and Sin’Itiro Tomonaga in Japan. Feynman loved to highlight how far removed QED was from everyday experience, with particles probabilistically taking every possible path. He said: “It is my task to persuade you not to turn away because you don’t understand it. You see, my physics students don’t understand it either. This is because I don’t understand it. Nobody does.” But strange though the theory was, it worked. Although QED is a quantum field theory, for practical purposes, Feynman’s approach treated the disturbances in the quantum field as particles, and was able to show that all the behavior of light and matter that seemed to imply the existence of waves could be handled using quantum particles that have a property called phase that changes direction with time. QED was immensely powerful, but it had one problem that would cause a significant challenge. Because of the way it added up possibilities over every possible outcome, it was easy to end up with an infinite result.
DRILL DOWN | QED explains many everyday interactions. There are the interactions of light and matter, where a photon pushes an electron to a higher energy level, or is given off when an electron jumps down. But there are also many more interactions between matter particles, often as a result of never-seen “virtual” photons, carrying the electromagnetic force. For example, when you sit on a chair, your atoms do not touch it. Instead, there is an electromagnetic interplay between the charged particles in your body and those of the chair, provided by an intense exchange of photons. This enables you to float above the chair—otherwise your atoms would pass straight through it.
MATTER | Scientific theories can make inaccurate predictions. The current calculation for a phenomenon called vacuum energy is many trillions of times bigger than reality. By comparison, QED makes accurate predictions—the agreement with tests measuring the strength of electromagnetic interaction between particles is within one ten billionth, equivalent to measuring the distance from New York to Los Angeles to a hair’s width.

RENORMALIZATION
THE MAIN CONCEPT | What do you do when you have a wonderfully effective theory that throws up infinite results? The power of QED is in the way it adds up all the possible ways of getting from the start to the end of a particle interaction. It might seem this will result in infinite outcomes because there are infinite possibilities. However, many options cancel each other out, or are so small that an infinite series of them converges. For example, the infinite series 1 + 1/2 + 1/4 + 1/8 + 1/16 . . . adds up to 2. But some series diverge—the total sum of 1 + 1/2 + 1/3 + 1/4 + 1/5 . . . is infinite. In QED’s particle interactions, there can be self-action, where a particle interacts with its own electromagnetic field and those around it to produce an infinite outcome. Clearly, in the real world, these infinities do not exist. The solution was renormalization. If, for example, QED predicted the mass of a particle should be infinite, it was replaced with the observed value. With this, the other results from QED worked perfectly. Renormalization was initially called a fudge, but was eventually considered to reflect a physical process—where something physical resets the value that would otherwise be infinite.
DRILL DOWN | Heisenberg’s uncertainty principle predicts that, because energy in a location in space could have any of a range of values over very short periods of time, pairs of “virtual” particles will constantly be popping into existence and disappearing again. Think of an electron sitting in apparently empty space—in QED, it is necessary to include any potential interaction with these virtual particles around the electron. Similarly, if an electron gives off a photon, there is a recoil effect—which results in the electron’s electromagnetic field acting on itself. The result of this combined assault on the electron is a prediction of values for mass, for example, that goes to infinity.
MATTER | Zeno’s paradox of Achilles and the tortoise shows an infinite series adding to a finite value. In a race, Achilles gives the tortoise a lead. By the time he reaches where the tortoise was, it has moved on. When he gets to its new destination, it is further ahead. And so on. But in reality, Achilles wins: the infinite set of distances adds to a finite value.
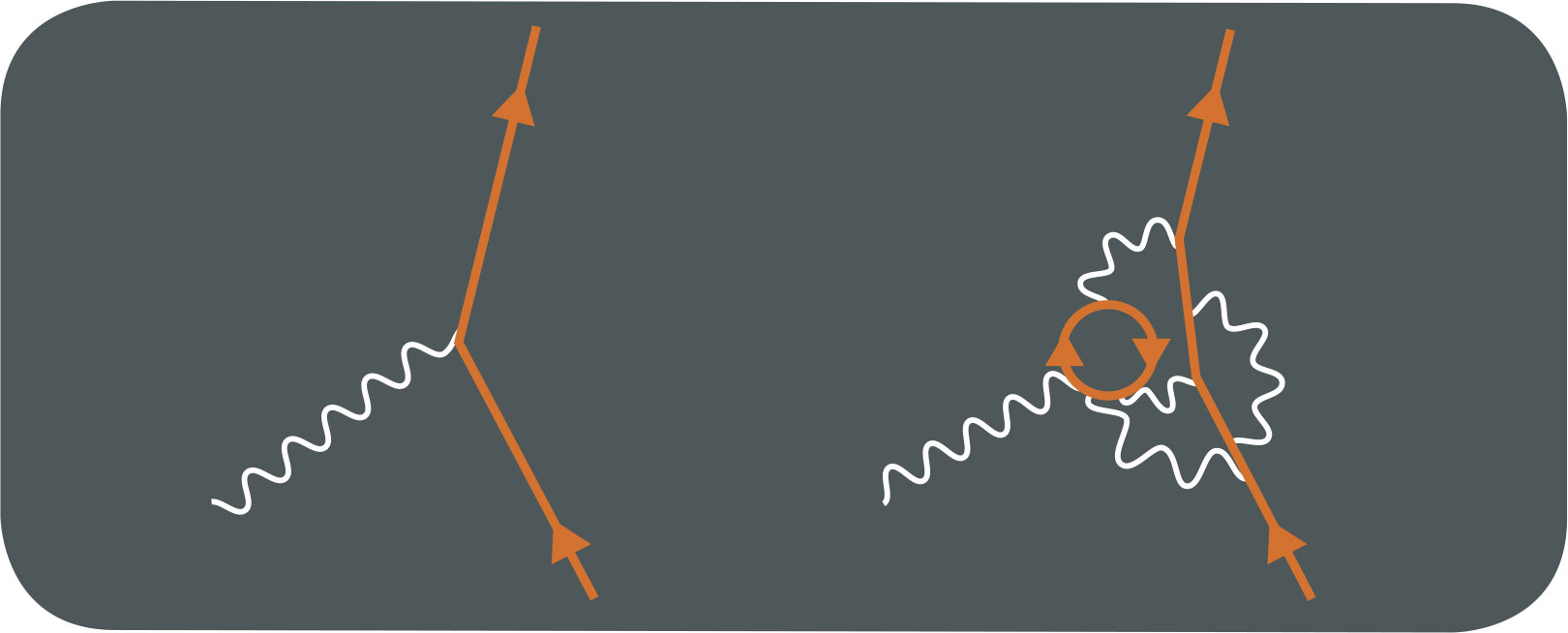
FEYNMAN DIAGRAMS
THE MAIN CONCEPT | Central to Richard Feynman’s approach to QED was the Feynman diagram, which has become a staple of quantum physics. The diagrams show how different quantum particles interact, providing a visual version of the mathematical description of an event. Time is shown on one axis of the diagram, while spatial position is shown on the other (there is no fixed standard for which is which)—so they display the progress of particles through time. Straight lines represent matter particles such as electrons, while wiggly lines stand in for photons—whenever two or more lines intersect, the particles are interacting. The diagrams have a dual benefit: they make it easier to see the different options for a particle interaction, but also each part of the diagram represents a part of the mathematical equations required to calculate the outcome. Because a quantum particle does not simply travel from A to B like a classical particle but has many probabilistic options, multiple diagrams are often required, with the overall outcome, known as the path integral, providing the sum across all possibilities. Feynman diagrams are still widely used today, and have been expanded beyond quantum electrodynamics to take in other quantum particle interactions such as quantum chromodynamics, which deals with strong nuclear-force interactions involving quarks and gluons.
DRILL DOWN | Antiparticles such as the positron, or antielectron, are treated differently from normal particles in Feynman diagrams. Antiparticles are shown as if they were the equivalent normal matter particle but going backward in time. So, for example, one of the simplest matter/antimatter interactions involves an electron and a positron coming together and annihilating to produce a pair of photons. This is shown with the direction in time arrow on the electron representing the positron running backward from the moment the two particles annihilate. Most physicists regard this “backward in time” direction to be a useful simplification for calculation (hence why it was introduced) rather than a statement of an actual particle’s behavior.
MATTER | Richard Feynman was so delighted with his diagrams that he had a new 1975 Dodge Tradesman Maxivan painted up with Feynman diagrams and was a popular sight, driving it around the Caltech campus. His license plates also reflected the theme, although because there was a limit of six letters on California plates at the time, he went for QANTUM.

ZERO-POINT ENERGY
THE MAIN CONCEPT | A remarkable implication of QED and Heisenberg’s uncertainty principle is that over short periods of time, the energy in a quantum system varies hugely. This is even true of empty space. Empty space has a positive energy value—known as zero-point energy. This has excited many, who feel it should be possible to make use of this energy. This is particularly appealing in space, as it would mean that spaceships would not need to carry fuel, and it would be possible to constantly apply a low acceleration, building up to immense speeds over time. Zero-point energy enthusiasts also suggest it could provide a limitless power source on Earth. However, there are two distinct problems to be faced. One is that the energy density is very low, so it would struggle to power anything significant. But more importantly, to make use of a certain level of energy, you need somewhere else with lower energy to produce work. But there is nowhere lower than zero-point energy, by definition. It’s like trying to make use of the potential energy in the middle of a mountain plateau. Yes, you are high above sea level—but you cannot roll something down and use the energy, because none of your surroundings are lower.
DRILL DOWN | Although it is unlikely zero-point energy could be harnessed, a phenomenon called the Casimir effect gives small-scale evidence of its presence. This is the impact of zero-point energy on two closely spaced metal plates. The two plates feel a force toward each other. One way of envisioning this is that the random fluctuations in energy will sometimes be enough for matter/antimatter pairs of particles to briefly pop into existence. When they do, they will cause pressure on the plates—but because the plates are so close together there isn’t enough room for this to occur to any significant extent between the plates, so they feel a net inward pressure.
MATTER | The EmDrive (“radio frequency resonant cavity thruster”), and the “Cannae Drive,” named for Star Trek’s Scotty’s habit of saying “I cannae change the laws of physics,” are controversial attempts to produce spaceship thrusters that do not emit propellants. Some suggest these make use of zero-point energy, but as yet there is no definitive evidence that they work at all.

WINDOWS & BEAM SPLITTERS
THE MAIN CONCEPT | It’s easy to consider quantum theory as something limited to the lab. But a glass window provides a demonstration of quantum physics in action, acting as a beam splitter. Stand in a lit room at night looking at the window, and you will see a reflection of the room. But go outside and you see into the room. So, despite some of the light from inside reflecting off the glass back into the room, the rest passes through the glass. This is classic quantum probabilistic behavior. Around five percent of the light reflects back into the room and ninety-five percent passes through. But how does a photon know whether to pass through or reflect? This was a puzzle to Isaac Newton, who believed light was made of particles. Newton thought the effect might be due to imperfections in the surface of the glass—but polishing the glass doesn’t make it go away. From a quantum viewpoint, we can see that there are no surface blemishes required to make the split. The photon exists merely as probabilities of passing through or reflecting, producing the statistical result. A sheet of glass isn’t a great beam splitter—for experiments, more sophisticated devices involving part-silvered mirrors or prisms, which split light 50/50, are used.
DRILL DOWN | When light reflects back off window glass, the probability of the photon reflecting from the inner surface depends on the thickness of the glass. Somehow, the photon “knows” how thick the glass is. With a wave-based approach, this is easy to explain as an interaction between waves that pass through the glass and reflect back from the outer surface and those that reflect off the inner surface. But with particles of light, it is only explainable if you take in the nonspecificity of a quantum particle’s location, which means it has a probability of already being at the far side of the glass and so can be influenced by its thickness.
MATTER | We only see the room reflected back from a window at night for the same reason we see stars at night. Stars are always there, but during the day, their weak light is washed out by sunlight. Similarly, we only see the outside view through a window during the day as there is far more light coming through than reflects back.

TUNNELING
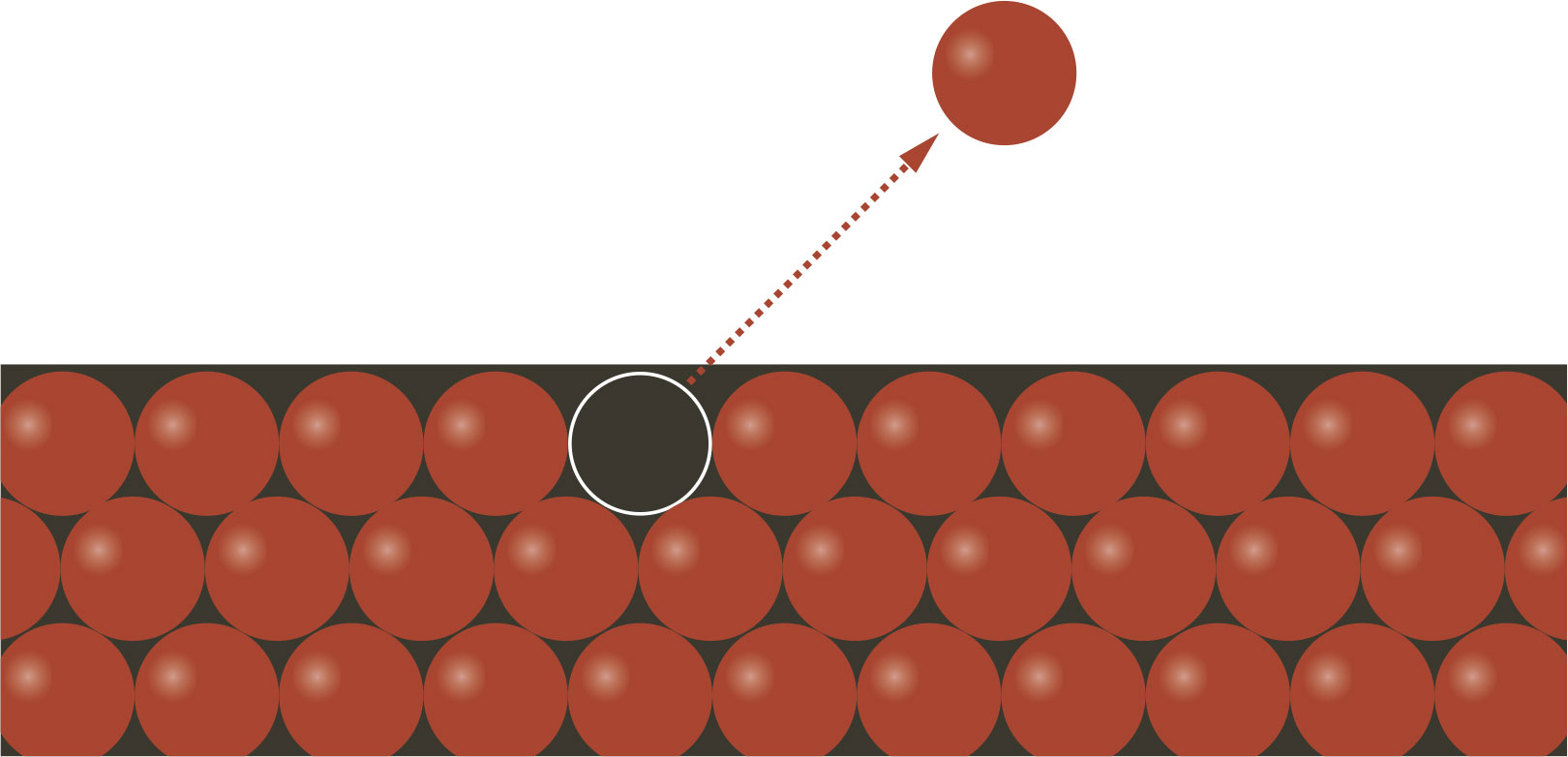
THE MAIN CONCEPT | A very significant quantum effect with an obvious impact on everyday life is quantum tunneling. This is directly linked to the indeterminate location of a quantum particle. If there is a barrier in the particle’s way that it does not have the energy to get over or through, a particle would usually be stopped. Think, for instance, of throwing a tennis ball at a wall, or trying to pitch one over a wall that is far higher than you can throw. But if the barrier is relatively thin, thanks to Schrödinger’s equation, we know that a quantum particle will have a probability of already being on the other side of the barrier. The wave equation shows the probability of its location spreading out over time—and is unaffected by barriers. It’s as if we put a car in a garage and came back to find it had jumped through the wall of the building and was out in the driveway. In a way, “tunneling” is a misnomer as it implies that the particle forces its way through the barrier; in reality, it is already on the other side. This means that the tunneling process is instantaneous—the particle does not take any time to get through the barrier.
DRILL DOWN | The existence of life on Earth is a dramatic demonstration of the power of quantum tunneling. The Earth would be uninhabitable without the Sun, which provides us with both light and warmth. And the process powering the Sun depends on tunneling. Inside a star, gravitational pressure forces positively charged protons together. They undergo nuclear fusion, where a number of protons combine to make helium, generating energy. But this process shouldn’t work. The electromagnetic repulsion between the positively charged protons is so strong, they cannot get close enough to fuse. It’s only because, as quantum particles, they can tunnel through the barrier of the repulsion that the Sun works and we’re alive.
MATTER | There is little danger of finding that your car has tunneled through the wall of your garage and appeared on the driveway. The chances of any particular particle tunneling are very small—and with the vast numbers of atoms in any normal object, you would have to wait far longer than the lifetime of the universe for tunneling to occur.

SUPERLUMINAL EXPERIMENTS
THE MAIN CONCEPT | One consequence of quantum tunneling is the ability—in a small way—to be able to break the generally accepted speed limit for information. Ever since Albert Einstein introduced the special theory of relativity, this speed limit has been the speed of light. In its simplest form, a superluminal experiment consists of a beam of light and a barrier that photons can tunnel through. As tunneling happens instantaneously, photons that tunnel will cover the total distance in the time they took to cover the section of the experiment outside the barrier. This results in a total speed that is faster than the speed of light. For example, imagine a simple setup where a photon covers one unit of distance ordinarily, then the same distance again tunneling through a barrier. It will take the amount of time that light takes to cover one unit of distance to cover a total of two units—so it traveled at twice the speed of light. There remains a dispute between physicists over whether the photons can truly be considered to break the light speed barrier, or whether the signal is distorted by the process, a little like a runner leaning forward to break the tape first and hence appearing to complete the distance of the run quicker.
DRILL DOWN | A kind of tunneling barrier that was discovered by Isaac Newton, known as frustrated total internal reflection, is often used by Austrian physicist and leading superluminal experimenter Günter Nimtz. When a beam of light enters a prism at a suitable angle, it bounces off the back of the glass rather than passing out of the prism, a process called total internal reflection. But Newton discovered that a second prism, placed close to but not touching the first, would enable part of the beam to flow through to the new prism instead of reflecting back. This happens because the photons tunnel through the barrier formed by the gap between the prisms.
MATTER | Mozart’s Fortieth Symphony has been transmitted at four times the speed of light. Physicists originally suggested that, while superluminal experiments apparently broke the speed of light barrier, they could only do so for random photons—the effect couldn’t be used to transmit ordered information. In 1995, Nimtz demonstrated that it could, by sending a Mozart recording through a superluminal setup.