3
INTERPRETATION & ENTANGLEMENT
“Quantum mechanics is certainly imposing. But an inner voice tells me that it is not yet the real thing . . . I, at any rate, am convinced that He is not playing at dice.”
ALBERT EINSTEIN LETTER OF EINSTEIN TO MAX BORN, 1926
INTERPRETATION GAME
Quantum physics is known for its “interpretations” such as the Copenhagen interpretation. These are attempts to provide an interface between the mathematical formalities of quantum theory and observation. No other branch of science feels the need for interpretations. No one provides interpretations for, say, evolutionary theory or the periodic table. Note that this is not merely explaining a complex theory in a way that is widely comprehensible. Popular science does this all the time. The interpretations of quantum physics are different beasts indeed.
The interpretations are not for communication to the public—they are designed for quantum physicists themselves. These theoretical approaches act as bridges between the mathematical structures of quantum physics and the practical observations made in experiments and everyday life. They seem to be required because of the surprisingly ad hoc nature of the development of quantum theory.
Theoretical leaps
Anyone telling the story of quantum theory tends to go straight from Albert Einstein’s assumption that photons were real to Niels Bohr’s theory of the quantum atom to Erwin Schrödinger and Werner Heisenberg developing mathematical representations of quantum systems, plus Max Born’s explanation of Schrödinger’s equation as representing the probability of finding a particle in a particular location.
What isn’t obvious in this story is how much the theoreticians were making things up as they went along. All the experimental evidence pointed to light being wave-like. Einstein’s assumption that particles of light (photons) were real entities went against every piece of experimental evidence, except for the photoelectric effect. It’s as if someone assumed popcorn is alive because, despite all the evidence to the contrary, it does one thing—jumping around when heated—that living things also do.
Then we come to Bohr’s atomic structure. It was at least partly inspired by New Zealand physicist Ernest Rutherford’s discovery of the atomic nucleus in 1911, and the need to put electrons in a stable configuration. There was a degree of experimental evidence that went into it. Even so, Bohr went out on a limb by postulating his strange “electrons on rails” that could not spiral into the nucleus. It was only when he discovered Johann Balmer’s work on the spectrum of hydrogen that there seemed to be some justification for making that leap.
As for Schrödinger, Heisenberg, and Born, there was no experimental starting point that inspired the approaches they took. Schrödinger’s wave equation and Heisenberg’s matrix mechanics were mathematical formulations that produced results that matched well with what had already been observed and, crucially with the many experiments that would come later—but no one could say why. Similarly, Born’s assertion on probability was not a result of anything that was observed, but rather a guess that made more sense than the original concept of predicting the locations of particles. Again, experimental evidence came later.
So quantum theory had a stack of mathematical procedures that matched observation well, but no reason for saying why they were appropriate. At the same time, quantum theory described quantum behavior that seemed strange—uncanny even—when set against the observable behavior of ordinary objects made up of quantum particles. How was it possible to get from “here”—a set of quantum behaviors predicted by the math—to “there”—the behavior of, say, a tennis ball or a container of gas?
A philosophy of reality
What the constructors of the interpretations were doing was more philosophy than physics. It is no surprise, then, that a major player in the Copenhagen interpretation was Bohr—the most philosophical of quantum physicists. Not everyone appreciated this. The third-generation quantum physicist John Bell called Bohr “an obscurantist.” Bohr’s approach seems to have been driven by philosopher Immanuel Kant’s realization that we can never know the reality of nature. All we can do is consider the phenomena we experience and use induction to suggest what lies beneath.
Bohr incorporated Kant’s philosophy into an interpretation that made it clear that all we can do with quantum theory is predict the outcomes of measurements. In this interpretation, there is nothing we can ever know lying behind these measurements. Before we measure a particle’s location, for example, it’s not that we don’t know its location. It doesn’t have one. Other interpretations attempted to make Bohr’s bleak assessment more approachable, or to replace it with a reality beneath. Arguably, no interpretation is entirely satisfactory.
BIOGRAPHIES
DAVID BOHM (1917–1992)

Born in Pennsylvania, United States, in 1917, David Bohm worked with Robert Oppenheimer during World War II and contributed to the Manhattan Project, developing nuclear weapons. When increasing anti-communist feeling in the United States led to Bohm being required to testify against Oppenheimer in 1949, Bohm refused and was charged with contempt of Congress. Although acquitted, he lost his job and worked for a number of years in Brazil and Israel before settling in the UK in 1957. There, he became Professor of Theoretical Physics at Birkbeck College, London, and a British citizen. He had considered an alternative to the existing interpretation of quantum physics since the early 1950s—now he fully developed his radically different interpretation. Influenced both by Albert Einstein’s concerns about the probabilistic aspects of quantum theory and the philosophy of Jiddu Krishnamurti, which stressed the oneness and connectedness of the universe, Bohm produced an interpretation of quantum physics where each particle is influenced by every other. Bohm’s approach mixed conventional physics with a mystical philosophical approach. Bohm died in London, England, in 1992, aged 74.
JOHN BELL (1928–1990)

Born in Belfast, Northern Ireland, in 1928, John Stewart Bell came from a working-class background—his siblings all left school age fourteen. After gaining a physics degree from Queen’s University Belfast, Bell went straight to work at the UK’s atomic research establishment at Harwell. While at Harwell, he completed a PhD at the University of Birmingham, and in 1960 moved with his wife Mary (also a Harwell physicist) to the European CERN laboratory near Geneva, Switzerland. His day job involved particle physics, but a sabbatical in 1963 enabled him to engage in his definitive work on quantum physics. Bell had some sympathy with Albert Einstein’s doubts. He once remarked: “I hesitated to think it might be wrong, but I knew that it was rotten.” In 1935, Einstein had come up with a thought experiment that showed either there was a flaw in quantum physics, and the properties of particles did have actual values, or the concept of “local reality,” that particles didn’t influence each other at a distance, was untrue. Bell came up with a hypothetical test that would distinguish between these two possibilities. Later experimenters, using Bell’s analysis, showed that quantum theory is not incorrect. Bell died in Geneva in 1990, aged sixty-two.
HUGH EVERETT (1930–1982)

Formally Hugh Everett III, this US physicist was born in Washington DC in 1930. He originally studied to be a chemical engineer, but moved via mathematics into physics. By now at Princeton, his PhD advisor was John Wheeler, previously Richard Feynman’s advisor. Everett’s PhD thesis expanded on a paper he had written entitled “Wave Mechanics Without Probability.” His primary idea was that the concept of wave function collapse was not necessary. If, rather than looking at individual particles, all interactions were taken into account, the picture transformed from one of two probabilities being selected to both possibilities taking place. His approach became known as the “many worlds” interpretation because one way of looking at it is that each time there is a quantum event, the universe splits into two versions, one for each possible outcome. Everett went on to work in defense on nuclear weapons, first for the government and then in industry. This saw yet another move in his interest from physics to computers; he spent much of his later career on computer programming, particularly for statistical applications. Everett died in McLean, Virginia, in 1982, aged fifty-one.
ALAIN ASPECT (1947–)

French physicist Alain Aspect was born in Agen, in the Bordeaux region, in 1947. After gaining a physics doctorate in Paris, he spent three years from 1971 in Cameroon as an aid worker. In the evenings, he took the opportunity to think through the areas of physics that fascinated him, notably quantum theory. He had come across both Albert Einstein’s EPR paper claiming quantum physics was flawed and John Bell’s work, and took the opportunity of unchallenged thinking to devise an experiment that could settle the dispute over the nature of quantum physics once and for all. There had been some attempts in the United States to explore the effects of quantum entanglement, which lay at the heart of the uncertainty over quantum physics, but they were inconclusive. By the time Aspect returned to Paris, he had the experiment set up in his mind. Here, Aspect undertook the entanglement test that Bell had envisaged. The result was a triumph—establishing that entanglement really did break the concept of local reality. Although future experiments would produce more detail, Aspect got there first. At the time of writing, Aspect is still working in the quantum field, specializing in materials known as Bose-Einstein condensates.
TIMELINE
QUANTUM BEHAVIOR
Niels Bohr and Werner Heisenberg finish developing their “Copenhagen interpretation” of quantum physics. Although never formally written down, this provides an explanation for quantum behavior in terms of probabilities and wave function collapse. Incorporating concepts such as wave/particle duality and complementarity, it remains the most widely supported interpretation.

EPR PAPER
Albert Einstein, assisted by Boris Podolsky and Nathan Rosen, writes a paper suggesting quantum physics incorporates a serious flaw. This “EPR” paper concludes that either it is possible for quantum particles to instantly interact at any distance, or quantum theory is wrong. But the quantum entanglement mechanism behind this prediction proves real.

BOHM INTERPRETATION
David Bohm starts work on his alternative interpretation of quantum physics based on pilot waves. Inspired by this idea of Louis de Broglie, Bohm takes a totally different view of reality, suggesting that it is impossible to separate a quantum system of particles from interaction with everything around it.
MULTIPLE UNIVERSES
Hugh Everett writes the paper “Wave Mechanics Without Probability,”” originating the “many worlds” interpretation of quantum physics. This moves away from the idea of wave function collapse and instead proposes that, effectively, all possible outcomes of quantum interactions occur, creating vast numbers of different universes.
ENTANGLED PARTICLES
John Bell writes his paper “On the Einstein—Podolsky—Rosen Paradox,”” establishing the Bell’s inequality measure. This is a way to practically test whether or not entangled particles truly can interact instantly at any distance, or whether there are “hidden variables” that predetermine the outcome.

DATA ENCRYPTION
Chinese researchers led by Pan Jian-Wei first send entangled photons from the satellite Micius to ground stations on Earth over 750 miles (1,200 km) apart. This makes it practical to use quantum entanglement to provide unbreakable encryption between widespread locations, essential to providing a “quantum internet.”
THE COPENHAGEN INTERPRETATION
THE MAIN CONCEPT | The behavior of quantum particles and systems is very different from what is observed in everyday objects made from those particles. By the late 1920s, Niels Bohr and Werner Heisenberg felt it necessary to answer the growing demand for an explanation that went beyond mathematical calculation. Their “Copenhagen interpretation” is arguably less of an explanation and more of a statement that there is nothing to explain. As it isn’t a document, it’s hard to be clear what makes up the Copenhagen interpretation. It certainly includes the idea that quantum systems don’t have parameters with fixed values, only probabilities until observed. The act of observation invokes “wave function collapse,” producing observed values. Rather than the separate concepts of waves and particles, the Copenhagen interpretation requires wave/particle duality and complementarity—the idea that a quantum object can behave as if it were a wave or a particle, but not both simultaneously. It incorporates the uncertainty principle. And it assumes it is possible to treat the laboratory and equipment in it as operating classically without quantum considerations. Opponents of the interpretation complain that it interprets what is observed without any attempt to reach an underlying reality. Supporters suggest that this is all that is possible, leading to the mantra “shut up and calculate.”
DRILL DOWN | A series of lectures given by Heisenberg in 1929 seem to have been the origin of the Copenhagen interpretation. In his book based on the lectures, The Physical Principles of the Quantum Theory, Heisenberg refers to the “Copenhagen spirit of quantum theory,” referring to the approach developed at Bohr’s Copenhagen-based institute. Bohr and Heisenberg never set out the interpretation in any detail, and would frequently contradict each other on minor details. The actual term “Copenhagen interpretation” seems to have been first used by Heisenberg in the 1950s, when alternative interpretations were being published and it seemed necessary to give this “Copenhagen spirit” a more technical-sounding title.
MATTER | The Institute of Theoretical Physics in Copenhagen (now the Niels Bohr Institute) was founded by Bohr in 1921. It became the de facto European center for quantum physics in the 1920s and 1930s. The institute was largely funded by the Carlsberg brewery, which also provided Bohr with use of its “House of Honor,” including an unlimited supply of free lager.

THE BOHM INTERPRETATION
THE MAIN CONCEPT | Not everyone was happy with Niels Bohr’s Copenhagen interpretation of quantum behavior. In the 1920s, French physicist Louis de Broglie, who had developed the idea that particles such as electrons could act as waves, developed the pilot wave theory, where each particle had an associated wave that guided it. When the double-slit experiment was performed with particles, he said it was the pilot waves that went through both slits, causing interference. US–British physicist David Bohm picked this idea up in the 1950s and developed it to provide a full interpretation of quantum physics (it is often known as the de Broglie–Bohm theory). Unlike the Copenhagen interpretation, Bohm’s version always has actual values for the positions of particles. However, each particle is constantly influenced by others around it—in principle, by every other particle in the universe—and this results in the observed quantum oddities. Initially, Bohm’s work was not taken seriously, but although few support the full interpretation, it has come to be considered an interesting alternative. Bohm’s theory takes a different approach to Max Born’s idea that the mathematical square of the wave function gives us probabilities of finding a particle in a certain location. If Bohm’s interpretation were true, Born’s idea should not always be the case—but as yet, there is no experimental evidence supporting Bohm’s interpretation.
DRILL DOWN | Bohm’s interpretation returns us to a deterministic universe—the clockwork universe that Newton’s laws predicted. As French scholar Pierre-Simon Laplace observed at the end of the eighteenth century, in such a universe an entity that could access perfect information about every object in the universe could map out the entire future. However, the big difference from the Newtonian universe is that Bohm’s is nonlocal—a particle on the far side of the universe could (and indeed would) influence a particle here, instantly. For many physicists, the lack of locality was a huge stumbling block because such a remote influence seemed impossible. However, quantum experiments involving entanglement do demonstrate nonlocal effects.
MATTER | Late in his career, and related to his interpretation, Bohm came up with the concept of “implicate and explicate order.” These are two different frameworks of reality, where the implicate order is where quantum phenomena takes place and is less dependent on time and space, more on connectedness, while the explicate order reflects what our perception of reality tells us.

THE OBSERVER EFFECT
THE MAIN CONCEPT | In the early days of quantum physics, the concept of wave function collapse when a “measurement” was made caused confusion and drove some scientists to the extreme viewpoint that the involvement of conscious observers impacted on quantum systems. It was suggested that the act of being observed by a conscious observer caused wave function collapse. So, in the case of the Schrödinger’s cat experiment, where we would now consider the measuring equipment monitoring the radioactive particle to be sufficient to cause decoherence and apparent collapse, the requirement for a conscious observer seemed to mean that the cat would indeed be both alive and dead until the box was opened and a conscious observer collapsed the wave function into one option. The (somewhat tenuous) argument behind the importance of the conscious observer is that they can see the world in only one particular state at a time, so they force collapse to occur. Hungarian–US physicist Eugene Wigner, probably the greatest supporter of such “consciousness collapse” of the wave function, suggested that if there was a variant of the Schrödinger’s cat experiment where a human was in the box as well (with a gas mask), then there would be no superposition as the observer would be constantly collapsing the wave function.
DRILL DOWN | If a conscious mind could influence a quantum system, could consciousness be a quantum phenomenon? This has been suggested by British physicist Roger Penrose, who proposes a link between the quantum wave function and the operations of the brain producing - consciousness. Many scientists are doubtful of Penrose’s suggestion, which is not supported by any experimental evidence. Ironically, Penrose also proposes an alternative to the Copenhagen interpretation where wave function collapse is a real process, not caused by observers (and certainly not conscious observers), but by an interaction between a quantum system and gravity, where too big a difference in the space-time curvature of the superposed quantum states brings on a collapse.
MATTER | Albert Einstein often discussed quantum theory with physicist Abraham Pais, who supported conventional quantum physics. In one conversation about Einstein’s idea that there was something real and nonprobabilistic behind what we observe, Einstein asked Pais if he “really believed that the Moon exists only when I look at it.” Einstein’s comment underlines the unlikely nature of the observer effect.

THE MANY WORLDS INTERPRETATION
THE MAIN CONCEPT | For physicists who do not accept the Copenhagen interpretation, where a collection of probabilities coalesce into distinct outcomes only when a quantum system interacts with another one, the “many worlds” interpretation provides a way out. Dreamed up by US physicist Hugh Everett and forming the basis of his PhD thesis, the many worlds approach totally removes the concept of wave function collapse. Instead, the suggestion is that we need to consider the total wave function covering the whole universe (or the part of it under observation). This never collapses, but each time a quantum system has the option of being in different states, all possible states actually occur. In effect (if not literally), the universe branches to incorporate one version of itself where, say, a particle is spin “up,” and one version where the particle is spin “down.” We cannot experience the whole many worlds universe because we inevitably take a single path through the universe where particular outcomes occur—but a different version of us could be said to experience each of the other possibilities. We no longer have the problem in a double-slit experiment of how a particle can appear to go through both slits—it goes through one slit in one set of the worlds and the other in a second set.
DRILL DOWN | Those who believe that the many worlds hypothesis reflects reality argue that it should be possible to play quantum Russian roulette. If you fire a gun at your head, they argue, in some of the many worlds outcomes, the gun will not fire. As the only versions of you that will remain aware of the experience will be those where the gun failed, you will always find that you survive. Apart from the obvious risk that the theory is wrong, some suggest that because the many worlds interpretation allows us to experience only one path through the various quantum options, the chances are that the path the current conscious “you” inhabits will not provide a happy ending.
MATTER | A natural reaction to the many worlds interpretation is that it falls foul of Occam’s razor. Occam’s razor is a simple mechanism for choosing between options where there is no evidence to support the choice, named for the fourteenth-century theologian William of Ockham. Although often now stated as making the choice with the fewest assumptions, the original “plurality must not be posited without necessity” seems particularly apt here.
EINSTEIN’S OPPOSITION
THE MAIN CONCEPT | Albert Einstein was one of the founders of quantum physics, showing it was necessary for light to come in the form of photons to explain the photoelectric effect. However, as a fuller picture of quantum theory developed in the 1920s, he became increasingly uncomfortable with its probabilistic nature. According to Niels Bohr, until a quantum system was observed, it would evolve through time as a set of probabilities without any “real” value for, say, the location of a quantum particle. It was only when the system interacted with another—for instance, when a measurement was made—that an actual value existed. Einstein instinctively felt that this had to be wrong. He believed there was a solid reality underlying what happened. We might not be able to discover the value of a property before measurement, but it still had one—an approach known as “hidden variables.” This requires that the value may be inaccessible, but it is still there in reality, unlike Bohr’s set, or “cloud,” of probabilities. Einstein began to challenge the accepted view, both by writing about his discomfort to his friend Max Born, who devised the probability aspect of quantum theory, and by challenging Niels Bohr with increasingly complex thought experiments that Einstein hoped would prove quantum theory wrong.
DRILL DOWN | In his letters to Born, Einstein came up with some of his best-known remarks. These include: “I find the idea quite intolerable that an electron exposed to radiation should choose of its own free will, not only its moment to jump off but its direction. In that case, I would rather be a cobbler, or even an employee in a gaming house, than a physicist” and “[Quantum] theory says a lot, but does not really bring us any closer to the secret of the ‘old one.’”
MATTER | Einstein presented Bohr with his best counterargument to quantum theory over breakfast at a conference. The experiment, which involved the change in weight and time when a photon left a box, seemed to challenge the uncertainty principle. It took Bohr until the following day’s breakfast to realize Einstein had forgotten to include the impact of general relativity, which wiped out the apparent paradox.

THE EPR PAPER
THE MAIN CONCEPT | In 1935, Albert Einstein along with Boris Podolsky and Nathan Rosen wrote a paper titled “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”, which is usually referred to by the initials of its authors, the “EPR” paper. The short work throws down a challenge to its readers. It shows that, if quantum physics is correct, then when two particles are produced in a state known as entanglement, observing a property such as the position or momentum of one particle instantly makes the other particle adopt a particular value for the equivalent property. But according to quantum theory, those properties are not established until the first particle is observed. Before then, all that exists is probability. The EPR paper suggests making measurements of both properties, then closes with a stark choice—either quantum theory is incorrect or entanglement makes it necessary to do away with a concept called local reality. The EPR paper comments: “No reasonable definition of reality could be expected to permit this.” Local reality has two components. “Local” means that it shouldn’t be possible to make something happen remotely without something traveling between the two locations. And “reality” means that particles should have properties such as location that have a real value, even if that value is not accessible.
DRILL DOWN | The original EPR paper described measuring both the position and momentum of a pair of entangled particles. In each case, the measurement of the property for one particle has an implication for the measurement on the other particle. The use of both momentum and position caused considerable confusion, as some thought that the intention of the paper was to challenge Heisenberg’s uncertainty principle, which relates momentum and position. Einstein wrote to Erwin Schrödinger that having the two properties “ist mir Wurst,” literally “is sausage to me”—meaning “I couldn’t care less about it.” Later versions of the EPR thought experiment avoided this confusion by using the single property of quantum spin.
MATTER | According to the physicist and biographer Abraham Pais, when Niels Bohr first heard of the EPR paper and its apparent challenge to quantum theory, he burst into a colleague’s room shouting “Podolsky, Opodolsky, Iopodolsky, Siopodolsky, Asiopodolsky, Basiopodolsky.” His explanation that this was meant to be a parody of a line in Ludvig Holberg’s play Ulysses von Ithaca did not particularly help.

BELL’S INEQUALITY
THE MAIN CONCEPT | The EPR paper described a thought experiment, but it was not a practical experiment to carry out. In 1964, Irish physicist John Bell, while on a sabbatical from his job at the CERN particle physics laboratory, thought up a measurement that would make it possible to distinguish between whether there were “hidden variables” and local reality was maintained, or the quantum physicists were right. Bell’s sympathies were with Albert Einstein. He too was uncomfortable with some aspects of quantum theory, although he was less sure than Einstein they were wrong. He once said: “I felt that Einstein’s intellectual superiority over [Niels] Bohr, in this instance, was enormous; a vast gulf between the man who saw clearly what was needed, and the obscurantist.” Bell imagined producing a pair of entangled particles from a single original particle (one of the simplest ways to generate entanglement), then using detectors to check the spins a distance away from each other. These detectors would be randomly oriented at different angles to each other. He proved that, were this the case, a reality with hidden variables would not produce the kind of linked behavior predicted by quantum theory. This “Bell’s inequality” would enable an experimenter to decide whether quantum theory was wrong or local reality was breached.
DRILL DOWN | Turning Bell’s idea into a working experiment took over ten years. US physicists Abner Shimony, Mike Horne, John Clauser, and Richard Holt did make a first attempt, but their results were inconclusive. The definitive demonstration of the long-range connection of entanglement (Einstein referred to it as “spooky action at a distance”) was made in Paris by the young French physicist Alain Aspect. The cleverest part of his approach was a way of ensuring the particles couldn’t communicate by conventional means. He did this by changing the direction of the measurement twenty-five million times a second, too fast for the information to reach the other particle in time to influence it.
MATTER | Bell used the example of physicist Reinhold Bertlmann’s socks to illustrate how hidden variables could give the impression of communication at a distance. Bertlmann always wore odd socks. If you saw one of his feet and it had a green sock on, you instantly knew the other sock wasn’t green, even if light hadn’t had time to reach you from the other foot.
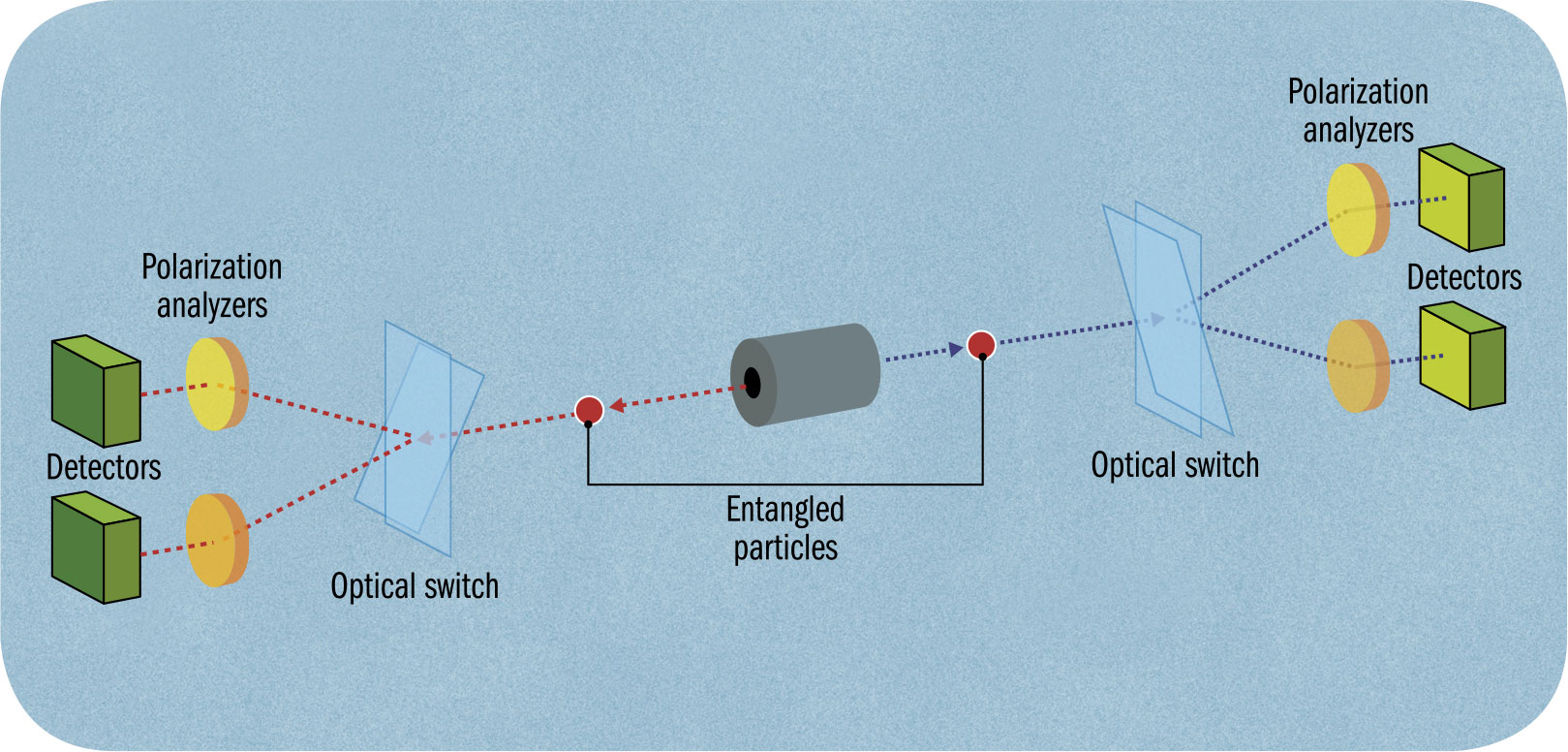
QUANTUM ENCRYPTION
THE MAIN CONCEPT | Throughout history, people have tried to keep messages secure. Since the early twentieth century, the unbreakable “one-time pad” method has been available. However, this relies on getting a key to both sender and receiver—a key that can be intercepted. What’s more, unless the key is random, there’s a chance it can be cracked. It was realized early on that the probabilistic nature of quantum physics means that a quantum source generates true random values—but it’s still necessary to get the key to both sender and receiver. Quantum entanglement provides a way both to generate a random key and to get that key to the receiver and sender before it’s generated. A stream of entangled particles is produced; each pair is split, one to the sender and one to the receiver. At this point, the key doesn’t exist. If the sender examines the spin of the particles, the equivalent receiver’s particles immediately adopt the opposite spin. The sequence of up or down spin is unpredictable, but the sender and receiver each get mirror-image versions of the key. The mechanism of quantum entanglement allows only random data to be sent, making it ideal to encrypt a conventional message, but it’s impossible to use the entangled particles themselves as a communication channel.
DRILL DOWN | It is possible to intercept entanglement-based quantum encryption. If someone captures one of the entangled stream of particles, they can read the values, then pass them onto their destination, leaving the particles in the form of the key. However, there is a way to test if pairs of particles are entangled. This takes a little longer, as an extra message has to be sent between receiver and sender, but is perfectly feasible. Any entanglement-based system has to regularly test the stream of particles, sampling every few particles to ensure that they still remain entangled. As long as the stream is known to be entangled, the communication link remains unbroken and secure.
MATTER | Encryption using quantum entanglement was first demonstrated in Vienna, Austria in 2004, by sending a quantum encrypted request to transfer 3,000 euros from City Hall to Bank of Austria in nearby Schottengasse. Setting up the link over a distance of 0.3 miles (500 m) involved threading optical cables through Vienna’s ancient sewers, previously best known as a setting for the Orson Welles movie The Third Man.
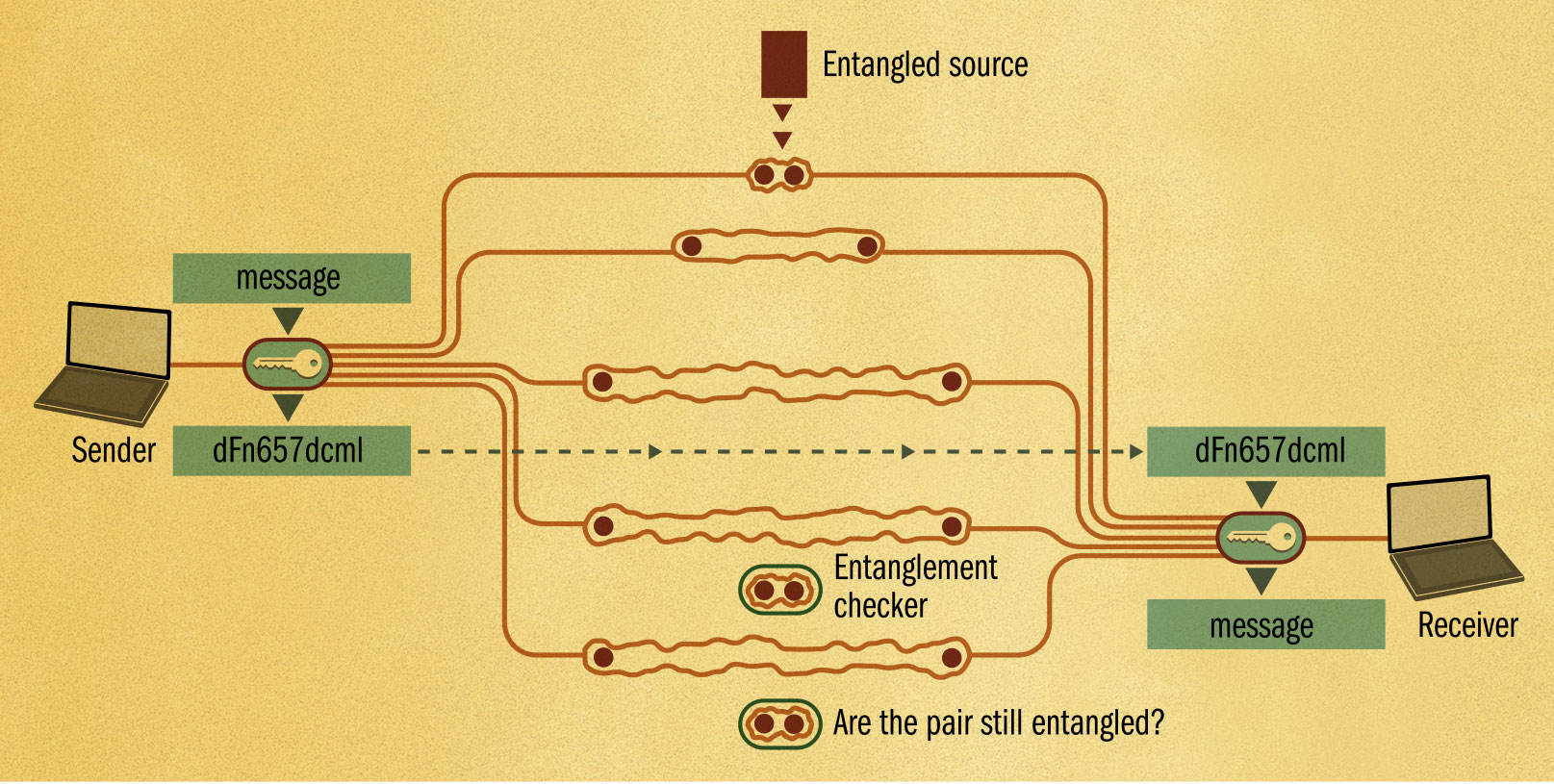
QUANTUM TELEPORTATION
THE MAIN CONCEPT | As well as providing unbreakable encryption, quantum entanglement has another trick up its sleeve—teleportation. In effect, this is a small-scale version of the Star Trek transporter. Some time before entanglement became practical, the “no cloning” theorem was proved. This shows that it’s impossible to make an exact copy of a quantum particle—the very act of discovering its properties changes them. However, with entanglement, something almost as good is possible. The process starts by providing both sender and receiver with one of a pair of entangled particles. The entangled particle is then used to interact with the particle to be teleported. Data from this interaction is sent by conventional communications to the receiver. The receiver then takes another particle of the same kind as the one to be teleported. This particle too undergoes a process along with the second entangled particle—the process is selected based on the conventional information transmitted. At the end of the process, one or more of the quantum properties will have been transferred from the sender’s particle to the receiver’s particle. The receiver’s particle becomes the same as the sender’s—in effect, it has been teleported. The process gets around the no-cloning theorem because the properties are never discovered—they are merely transferred by the entangled pair.
DRILL DOWN | Because of the Star Trek transporter, an immediate response to the idea of quantum teleportation is that this is a way to make the transporter a reality. However, there are three issues. First is the difficulty of examining the atoms in an object and then reconstructing the object from its component atoms. Then there is the timescale involved. There are so many atoms in a human, for example—around 7,000 trillion trillion—it would take thousands of years to scan them. Finally, it is worth remembering that with teleportation, you are not transmitted. Your body would be destroyed while an identical version is created—not a pleasant thought.
MATTER | Teleportation was first realized in 1997 by two teams in Europe: one under Anton Zeilinger (arguably Europe’s leading quantum entanglement experimenter) in Vienna, Austria, and the other led by Francesco de Martini in Rome, Italy. The original experiment was not a complete teleportation of all properties, but transferred the polarization of one photon to another.

ENTANGLED SATELLITES
THE MAIN CONCEPT | Whether your intention is encryption or teleportation, making use of entanglement requires a pair of entangled particles to be split, with one dispatched to each of sender and receiver. This is not trivial, because it’s easy for quantum particles to interact with the environment and lose their entanglement. The original entanglement experiments involved short distances in the laboratory, but two key individuals have driven experiments that have led to greater distances. In Vienna, Austria Anton Zeilinger was the first to start the long-distance trials, sending entangled particles 0.4 miles (600 m) in 2003. The next year, Pan Jian-Wei, in Heifei, China, achieved 8 miles (13 km), shortly before Zeilinger extended his range to 9.5 miles (15.2 km). These distances were selected because through sea-level atmosphere, they are roughly equivalent to the much greater distance to a satellite through increasingly thinning atmosphere. The goal of using a satellite was achieved by Pan in 2017. This makes it possible to send the two halves of an entangled pair to base stations 870 miles (1,400 km) apart. Such satellites are likely to form the backbone of a “quantum internet,” which would enable entangled communication to provide secure encrypted communication, or distributed quantum computing. Such a network would also require conventional connections, but we are likely to see many more entanglement generators on satellites.
DRILL DOWN | Ironically, one of the reasons we are likely to need a quantum entangled add-on to the internet is to keep our current internet connections secure from the attacks made possible by another quantum technology. Quantum computers, where each bit is a quantum particle, are far more powerful than conventional computers at certain processes. One of these is the ability to deduce the factors of a number produced by multiplying two very large prime numbers. Unfortunately, this is exactly the ability that is used in the RSA encryption used when a secure link is formed in the web (represented by a padlock in the browser). Quantum encryption may prove the only defense.
MATTER | The intention had been to provide the first quantum entangled particles from space via the International Space Station in 2014, but this experiment never materialized. Instead, the Micius satellite, named for the Latinized name of fifth-century BCE philosopher Mozi (or Mo Tzu), was launched in August 2016, orbiting around 320 miles (500 km) above the Earth, and achieved first transmission less than a year later.

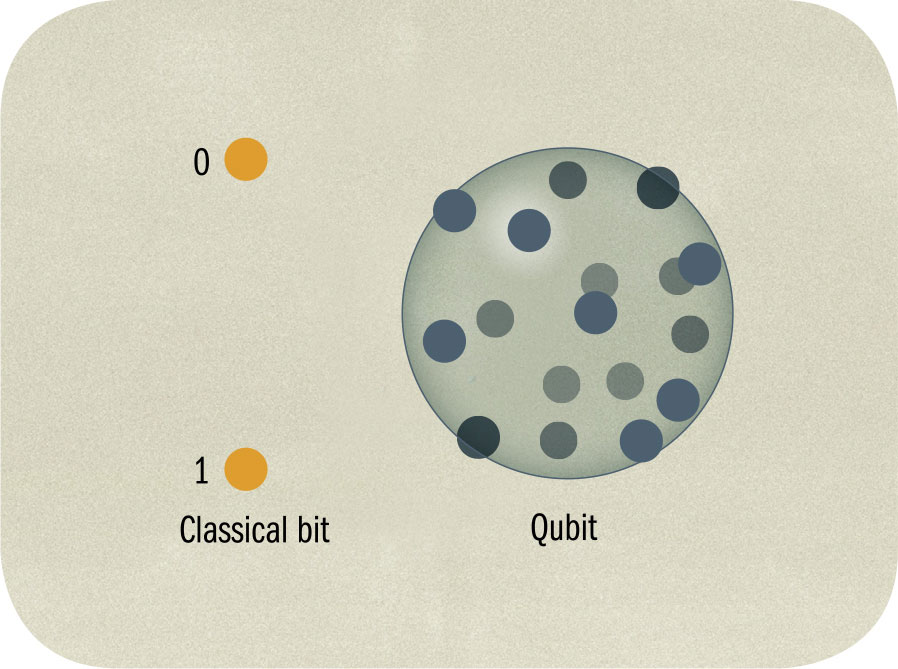
QUBITS
THE MAIN CONCEPT | Current computers are reaching their physical limits in terms of power, but many labs are working on a new generation of technology—quantum computers. To appreciate these devices needs an understanding of their fundamental unit, the “qubit.” A conventional computer uses bits, a contraction of “binary digit.” These are simply stores that hold an electrical charge. If a bit has a low charge, it is given the value 0—if it holds a higher charge, it becomes 1. This means a bit can be used to hold data in binary form—numbers to base two—and is employed in all current computers. A qubit—a quantum bit—stores data as a property of a quantum particle, typically its spin. When measured, spin will always come out “up” or “down” in the direction of measurement, but before measurement, it holds both values in superposition, with a specific probability of having one or other value. Probabilities can be 50/50, but can also be any other split such as 35.1117/64.8883. Multiple qubits can be considered as a system with more combined values than the equivalent bits. For example, three bits can hold eight values: 000, 001, 100, 101, 010, 011, 110, and 111. But three qubits can have 256 possible values.
DRILL DOWN | A wide range of options is being considered to implement qubits. In principle, any quantum particle could act as a qubit, but the most frequently used are photons and electrons. Electrons have the advantage of being easy to manipulate, but are more likely to interact with each other, so require more sophisticated traps. Photons are harder to handle, but ignore each other. Most early qubits came in forms suitable only for laboratories, often involving special cavities and devices that needed cooling to cryogenic temperatures. However, some success has now been made in producing solid-state qubits, which make it far more possible that a device based on them could become mainstream.
MATTER | The word “qubit,” which appears to be inspired by the ancient unit of measurement the cubit (based on the distance from elbow to fingertip), first appeared in the 1995 paper “Quantum Coding” by Benjamin Schumacher. In his acknowledgments, Schumacher says: “The term ‘qubit’ was coined in jest in one of the author’s many intriguing and valuable conversations with W. K. Wootters.”
QUANTUM COMPUTING
THE MAIN CONCEPT | As it has become practical to produce qubits—isolated quantum particles, using one of their quantum parameters as the equivalent of a bit—there has been furious activity attempting to make a working quantum computer. This would involve having sufficient qubits to produce effective calculation. Although modern conventional computers work on billions of bits at a time, because of the extra information involved in each qubit and the way they interact, it would be necessary to have only a few hundred or thousand qubits in a usable quantum computer. Because of the difficulties of protecting the qubits from decoherence and of getting data into, around, and out of a quantum computer, which uses entanglement, even such small numbers have proved immensely difficult. At the time of writing, IBM’s fifty-qubit machine is the best to be achieved. However, hundreds of labs are working on different approaches to quantum computing. Because keeping qubits from decoherence usually needs extremely low temperatures or specialist environments, quantum computers as currently envisaged are the equivalent of the original vacuum-tube-based electronic computers: unwieldy and suitable only for one-off construction. However, it may prove possible to put some quantum computing functions in variants of conventional electronic chips, making a widely available computer with quantum facilities a longer-term possibility.
DRILL DOWN | If a fully functional quantum computer were produced, we already have some algorithms to make them work, performing tasks that would take too long to complete on conventional computers. The earliest was Shor’s algorithm, developed by Peter Shor in 1994. This makes it possible to find integers multiplied together to form a larger number extremely quickly, putting the widely used RSA encryption method at risk. Another algorithm of great interest to search companies is Grover’s search algorithm, devised in 1996. Imagine you are searching one million locations for a particular piece of information. On average, a conventional search would require 500,000 tries. Grover’s algorithm would get there in just 1,000.
MATTER | A Canadian company, D-Wave, already sells a room-size quantum computer. However, this makes use of a specific process known as adiabatic quantum annealing. Instead of having logic gates like a conventional quantum computer, this makes use of a kind of analog quantum process. It has real benefits on certain applications such as image recognition, but isn’t a general-purpose quantum computer.
QUANTUM ZENO EFFECT
THE MAIN CONCEPT | One of the stranger effects associated with entanglement is the quantum Zeno effect. The “Zeno” part refers to ancient Greek philosopher Zeno, a student of Parmenides in the Eleatic school in the fifth century BCE. The school argued that all change was illusory, and Zeno came up with a series of paradoxes, attempting to demonstrate that there was something wrong with our understanding of movement and change. The quantum Zeno effect is supposedly based on Zeno’s arrow—in fact, it would have been better to have called it the quantum watched-pot effect. As we have seen, the properties of a quantum particle take on a fixed value only when measured and are otherwise in superpositions of values. The quantum Zeno effect involves making repeated interactions with a quantum particle, as a result of which the property never moves away from a fixed value, rather like the proverbial watched pot. Although there are few practical applications of the quantum Zeno effect as yet, it has been suggested that it may play a role in the ability of some birds to navigate using the Earth’s magnetic field. The suggested mechanism involves entanglement of electrons in the birds’ eyes and may use the Zeno effect to avoid other interactions of the electrons.
DRILL DOWN | Zeno’s arrow is a paradox exploring the nature of motion. Imagine an arrow flying through space. Let’s examine it at a moment in time; for comparison, let’s put alongside it another arrow that is not moving. How can we tell the difference between the two? In that moment, each sits at a fixed location in space. And this is true for every moment of time. Which means that the arrow is not moving. There are two issues here: one is that the two arrows are not identical—one has kinetic energy, for example. The other issue is that an infinite set of infinitesimally small values can sum to a nonzero total.
MATTER | Elea, the location of Parmenides’ school, now known as Velia, was on the west coast of Italy. The rejection of motion and change seems counterintuitive; it was based on the idea that the universe had an underlying unchanging unity that we cannot directly experience through our senses. None of Zeno’s writings survive, but we know of nine of his paradoxes via later writers.