Chapter 7
Fields, Matter and Morphic Resonance
In this chapter, I first consider how physicists conceive of the relationship of fields to matter. I then examine how the idea of morphic fields proposed by the hypothesis of formative causation relates to orthodox conceptions of fields, and go on to explore some of the consequences of this hypothesis at the levels of molecules and crystals, looking at some of the ways in which the theory could be tested experimentally. The chapter concludes with a discussion of the role of morphic resonance from a system’s own past in the development and maintenance of its structure.
Aether, fields and matter
Morphic fields, like the gravitational, electromagnetic, and quantum matter fields known to physicists, are intimately related to matter. They interact with it and organize it. At first sight, this idea seems to imply a duality of fields and matter. But matter is no longer conceived of as a passive, inert substance; it is no longer made up of the hard billiard-ball atoms of nineteenth-century physics. It is now thought to consist of rhythmic processes of activity, of energy bound and patterned within fields.
In order to obtain a clearer conception of the relationship of morphic fields to their associated organisms, it is helpful to trace the development of the field concept within physics and its relationship to the concept of matter.
Modern field theories are rooted in the work of Michael Faraday, who through his investigation of magnetism came to the conclusion that ‘lines of force’ extended around a magnet (Fig. 6.1). These were states of strain and were physically real.1 But they were not made of ordinary matter. So what sort of reality had they? He was not sure, and suggested alternative interpretations. Either they exist as states of a material medium ‘which we may call aether,’ or else they are states of ‘mere space.’ He preferred the idea that the lines of force were modifications of space because it was linked to his speculation that material particles were point centres of converging lines of force, an interpretation that broke down the distinction between matter and force.2 Indeed, he supposed that forces themselves were the sole physical substance, a substance filling all space, in which each point of the force field had a certain amount of force associated with it. Each point interacted with its neighbours, allowing for vibrations of force and for all kinds of patterns of force, including material bodies.3
However, these ideas of Faraday’s were not adopted by his successors, and it was not until Einstein that his favoured conception of the field as a state of ‘mere space’ was again taken seriously in physics. Maxwell adopted Faraday’s less favoured view and regarded the field as a state of a material medium, the aether. The aether had something of the nature of a fluid, within which were rotating tube-like vortices. If there was a difference between the speed of rotation of neighbouring vortices, then forces were exerted and states of stress arose. But Maxwell was very guarded in his use of the fluid analogy:
The substance here treated must not be assumed to possess any of the properties of ordinary fluids except those of freedom of motion and resistance to compression. It is not even a hypothetical fluid which is introduced to explain actual phenomena. It is merely a collection of imaginary properties which may be employed for establishing certain theorems in pure mathematics in a way more intelligible to many minds and more applicable to physical problems than that in which algebraic symbols are employed.4
But whatever its nature, the field was essential for Maxwell’s description of electromagnetic interactions at a distance because of the time delay in transmission. He took this delay to mean that physical processes must be taking place in the intervening space.5
In the late nineteenth century, Hendrik Lorentz abandoned the idea that the aether is a mechanical substance. He thought of it as immobile, and made a clear separation between aether and matter. He rejected contemporary attempts to conceive of the aether as subtle matter. Others took this process further; and by the end of the century, fields rather than matter were coming to be seen as primary. Instead of trying to explain fields in terms of matter, matter was being explained in terms of fields. For example, Joseph Larmor wrote in 1900 that ‘matter may be and likely is a structure in the aether but certainly aether is not a structure made of matter.’6
But then what was the aether? Lorentz continued to think of it as in some sense substantial. As late as 1916 he wrote: ‘I cannot but regard the aether, which can be the seat of an electromagnetic field with its energy and its vibration, as endowed with a certain degree of substantiality, however different it may be from all ordinary matter.’7 For Lorentz, the aether served as a medium and as an absolute reference frame, with a role similar to that of Newton’s absolute space.
But for Einstein the aether became ‘superfluous.’ In his special theory of relativity (1905), the electromagnetic field permeates the vacuum of empty space, and this space is no longer absolute. The field has no mechanical basis whatsoever; nevertheless, it is the seat of complex processes and, like matter, has energy and momentum. It can interact with matter and in so doing exchange energy and momentum with it. But the field is independent of matter. It is not a state of matter. It is a state of space.8
In his general theory of relativity, Einstein extended the field concept to gravitational phenomena. The gravitational field, a space-time continuum curved in the vicinity of matter, replaced gravitational force acting at a distance. Gravitation is a consequence of the geometrical properties of space-time itself. But Einstein failed to formulate a unified field theory in which electromagnetic effects could also result from these geometric properties. Many attempts have been made to define such a theory, and physicists are continuing these attempts in superstring and M-theories.9
The general theory of relativity deals with large-scale phenomena such as the movements of planets, and indeed embraces the very structure of the universe. The intimate interrelations of fields and matter in the realm of very small things such as atoms are the province of quantum theory.
Quantum theory started from the idea that atoms absorb and emit light in quanta, or units, of energy. Light waves have to be thought of in terms of ‘packets’, and these quanta give light a particulate aspect. The ‘particles’ of light are called photons.
A ‘quantum jump’ took place in quantum theory in 1924 when Louis de Broglie suggested that just as light waves have particulate properties, so should particles of matter display wavelike properties.10 This led to an entirely new conception of electrons and other subatomic particles, which had previously been pictured as tiny billiard balls. Experiments soon showed that electrons did indeed behave like waves. This is now a matter of practical engineering. For example, electron microscopes use electron waves instead of light waves. But de Broglie’s theory is not confined to subatomic particles: all matter has a wavelike aspect, even whole atoms and molecules.
This theory provides the basis for the idea of quantum matter fields. These fields are different in kind from electromagnetic fields, but are as real. The matter waves do not merely describe the behaviour of single particles such as electrons; they are taken to be aspects of a matter field in which the particles are quanta of excitation. Thus an electron is a particle in a matter field, just as a photon is a particle in the electromagnetic field.
There are many kinds of matter fields, one for each type of particle: an electron is a quantum of the electron-positron field, a proton is a quantum of the proton-antiproton field, and so on. Different kinds of matter fields can interact with each other, and they can also interact with electromagnetic fields. All these interactions are mediated by quanta.11
In these quantum matter fields, there is no duality of field and particle in the sense that the field is somehow external to the particle. Indeed, the essential physical reality has become a set of fields, and the fields specify the probabilities of finding quanta at particular points in space. The particles are manifestations of the underlying reality of the fields.
These fields are states of space, or of the vacuum. But the vacuum is not empty; rather, it is full of energy, and itself undergoes quantum fluctuations that create new quanta ‘from nothing’, which are then annihilated again. A particle and its antiparticle can spring into ‘virtual existence’ at a point in space and then immediately annihilate each other.12
Atoms and organisms: fields within fields
The result of all this is that particles of matter are quanta of energy in fields, which are states of space, or the vacuum. This is the modern foundation for the understanding of material reality. Yet this extraordinary theoretical vision has so far had very little effect on our understanding of living organisms. Biologists need know next to nothing about quantum matter fields, and molecular biologists deal with molecules that can for most purposes still be thought of as composed of ball-like atoms in ball and stick models. Quantum physics has dissolved atoms into a complex system of quantized fields, but the old atomistic way of thinking has persisted in other areas of science; atoms still seem to provide a reassuringly firm foundation for biology, and even for much of chemistry.
While physicists have felt free to introduce dozens of different kinds of matter fields in the context of subatomic particles, chemists have not introduced any comparable new fields at the molecular level. Certainly some of the properties of molecules have been interpreted in terms of the principles of quantum physics: chemical bonds, for example, can be partly understood in terms of shared electronic orbitals that embrace the bonded atoms.13 But this is an oversimplification. In 2011, Philip Ball summarized the situation as follows: ‘Describing the quantum chemical bond remains a matter of taste: all descriptions are, in effect, approximate ways of carving up the electron distribution … [A] molecule is ultimately a set of nuclei embedded in a continuous electron cloud that stabilizes a particular configuration, which balls and sticks can sometimes idealize and sometimes not.’14
Even in chemistry the reductionist approach does not fit the facts. The vibrating electron clouds of molecules are more than the sum of separate chemical bonds; they have an ‘emergent’ holistic quality. If we adopt an organismic rather than an atomistic perspective, there seems no good reason why organisms at all levels of complexity should not have characteristic fields. Indeed, de Broglie’s original idea of matter waves implied such a view: entire atoms and molecules were wave-like quanta, as indeed were all forms of matter. In this spirit we can think of an insulin molecule, say, as a quantum or unit in an insulin field; or of a swan as a quantum or unit in a swan field. But this may be just another way of thinking about morphic fields: any particular insulin molecule is a manifestation of the insulin morphic field; any particular swan is a manifestation of the swan morphic field.
Morphic fields as probability structures
An essential feature of morphic fields is that they are intrinsically probabilistic; in other words they are not sharply defined but are ‘structures of probability.’ There are at least three reasons for thinking that this is so.
First, individual organisms, or systems, or morphic units, or holons (see above) at every level of complexity show indeterminate or probabilistic features. In the biological realm, individual cells, tissues, organs, and organisms are never exactly the same, even if they are genetically identical and develop under practically identical conditions. No two leaves on an oak tree are identical, and even the two sides of a single leaf differ in detail. Their variability itself suggests that probabilistic processes play an important part in their development. Moreover, detailed studies of the functioning of cells have provided many examples of an intrinsic indeterminism or probabilism: for example, random fluctuations in the electrical potential across the membranes of nerve cells affect their tendency to ‘fire,’ and this has important consequences in the functioning of the nervous system.15 For these reasons alone, it seems natural to assume that morphic fields are probabilistic in nature;16 insofar as they interact with, or rather underlie, the material structures of organisms, the probabilistic behaviour of these structures seems likely to reflect an inherent probabilism of the associated fields.
The hypothesis of formative causation provides a second reason for thinking that these fields are probability structures. Morphic fields are built up and sustained by morphic resonance from innumerable previous similar organisms (see below). These organisms, although similar, are inherently variable. No two zebras, for example, are exactly the same. Morphic resonance from many past organisms gives rise to a morphic field that is a composite or average of the previous forms: it cannot therefore be sharply defined, but is a probability structure (cf. Fig. 6.4).
Thirdly, if morphic fields are akin to quantum matter fields, then this would also suggest that they are probabilistic in nature. The relationship of morphic fields to quantum matter fields is still obscure; but if they are similar in kind, not only would their interactions be easier to conceive, but a unified theory could ultimately embrace both.
The morphic field of an organism organizes the parts, or holons, within it; and the fields of these holons in turn organize the lower-level holons within them. For example, an organ field organizes tissues, and a tissue field organizes cells, and a cell field organizes subcellular holons such as the nucleus and the cell membranes. The holons and their associated fields are arranged in a nested hierarchy (Fig. 5.9).
At every level, the fields of the holons are probabilistic, and the material processes within the holon are somewhat random or indeterminate. Higher-level fields may act upon the fields of lower-level holons in such a way that their probability structures are modified. This can be thought of in terms of a restriction of their indeterminism: out of the many possible patterns of events that could have happened, some become more likely to happen as a result of the order imposed by the higher-level field. This field organizes and patterns the indeterminism that would be shown by the lower-level holons in isolation.
A provisional hypothesis
According to the hypothesis of formative causation, morphic fields are influenced by what has happened before. Their probability structures change, and such changes should be detectable experimentally. Thus it is possible to test this hypothesis even though much about the nature of the fields and the processes of morphic resonance remain unknown. Several possible experimental tests of the hypothesis are discussed in this and the following chapters.
Before Faraday’s investigations, magnetic effects were usually conceived of in terms of ‘effluvia’ or ‘subtle fluids.’ Though Faraday’s lines of force and Maxwell’s aetherial vortices were better defined, their nature remained obscure. The modern theory of the electromagnetic field represents a major advance in detailed understanding; but even so, the nature of the field and its quantized excitations are barely imaginable in terms of our direct experience. Theories of magnetism did not jump straight from the effluvia stage to the quantized electromagnetic field; the modern understanding took over a century to develop.
The concept of morphogenetic fields has already been developing for over 80 years, and if the present interpretation in terms of morphic resonance is supported by experimental evidence, it will enable researchers to understand these fields more deeply. Even so, a more detailed and adequate theory of these fields, including their relationship to the known fields of physics, could take years or even decades to evolve.
The hypothesis of formative causation is inevitably preliminary and provisional. But even in its present form, the concept of morphic resonance enables a large range of phenomena in chemistry, biology, and psychology to be seen in a new light, and it gives rise to many predictions. The remainder of this book explores these consequences and implications.
Molecular morphic resonance
If morphic fields are associated with holons at all levels of complexity, then we should expect each kind of chemical molecule to be associated with a characteristic morphic field.
At first sight this notion may seem unnecessary. It is usually assumed that molecular structures are in principle completely comprehensible in terms of quantum theory and electromagnetic fields. This means, in fact, that they are already conceived of in terms of fields. However, the assumption that the known kinds of fields are adequate to account for all chemical phenomena is supported by very little evidence.
Quantum mechanics is able to give a detailed account of the simplest of all chemical systems, the hydrogen atom. But with more complicated atoms and with simple molecules its methods are no longer so precise. The complexity of the calculations becomes formidable, and only approximate methods are feasible. Even the simplest of all molecular systems, the hydrogen molecule-ion, containing two protons and one electron, presents insuperable problems. Its properties can be calculated only by making a series of simplifying assumptions. In the words of John Maddox:
One distinctive feature of this simple system is that it is a three-body problem, which can no more be exactly solved in quantum than in classical mechanics … What the elementary textbooks on quantum chemistry fail to explain is that empirical spectroscopic evidence that might test these calculations is thin. Moreover, such tests as there may be tend to disappoint the calculators. But nobody need feel ashamed, for the complete calculation of the hydrogen molecule-ion, rotations as well as vibrations, depends on a succession of manifestly false assumptions.17
With the vast expansion of computing power and with new methods of approximation, it is now possible to calculate with a reasonable degree of accuracy some of the chemical properties of simple molecules such as carbon monoxide (CO).18 For more complex molecules and crystals, even more drastic approximations and simplifying assumptions have to be made in order to apply a mathematical analysis. These calculations have given an increased understanding of some of the properties of molecules and crystals; but this is a very different matter from predicting their forms and properties from first principles. Only if this were possible could we conclude that these known principles are capable of explaining the facts of chemistry. But this has never been demonstrated. The question is in fact quite open, even in relation to relatively simple molecules and crystals.19
The structure and morphogenesis of proteins
There is very little evidence that the known principles of physics can account for the structures and properties of complex molecules such as proteins. These are made up of chains of amino acids, called polypeptide chains, which spontaneously fold up into a characteristic three-dimensional conformation (Fig. 7.1). A protein can be denatured, in other words made to unfold into a flexible polypeptide chain that has lost its original conformation. If the denaturing treatment is gentle enough, it can usually be reversed. Unfolded polypeptide chains spontaneously refold into their original conformations; their normal shape is regenerated. Here is a textbook description:
This behaviour confirms that all the information determining the conformation must be contained in the amino acid sequence itself … Although all the information required for the folding of a protein chain is contained in its amino acid sequence, we have not yet learned to ‘read’ this information so as to predict the detailed three-dimensional structure of a protein whose sequence is known.20
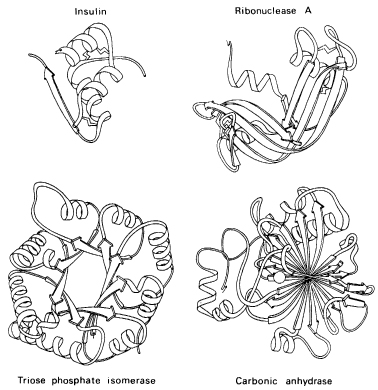
Figure 7.1 Diagrammatic representation of the three-dimensional structure of four kinds of protein molecules. (From Advances in Protein Chemistry 34 by J. S. Richardson, 1981. Reproduced by permission.)
A report in 2000 by the US National Institutes of Health summarized the situation succinctly: ‘For 50 years they’ve tried – and failed – to crack the code that governs protein folding.’21
The problem in understanding protein folding arises from the astronomical number of possible ways a polypeptide chain could fold up. Out of all the possible conformations, the protein adopts only one. Moreover, as the protein folds up, it cannot ‘explore’ at random these possible conformations until it ‘finds’ the one that is most stable energetically. Consider, for example, a chain of 100 amino acids such as might be found in a typical small protein. Such a chain could have up to 10100 possible conformations if each amino acid could adopt, on average, 10 conformations. ‘If all internal bond rotations interconverting these conformations occurred independently at the maximum rate of 1013 sec–1, the average time to sample all conformations would be 1085 seconds, or 1077 years. Another estimate is 1010 years. Since proteins are often observed to refold within seconds, the conclusion that the folding process is not random is perhaps inevitable.’22
Studies of protein structure have shown that the polypeptide chains (which are called the primary structure) arrange parts of themselves into helices or sheets (called α-helices and β-sheets). They are the proteins’ secondary structure. These ‘structural clichés’ in turn are often arranged in particular patterns, called domains, which are similar in many different proteins.23 A protein may have several different domains, which can be thought of as modular or structural units from which the protein as a whole is constructed. The conformation of the protein as a whole is called the tertiary structure. Finally, individual protein molecules often assemble with others to produce aggregates of characteristic form. This is the quaternary structure (Fig. 7.2).
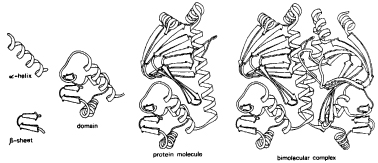
Figure 7.2 Hierarchical levels of protein structure. The bimolecular complex shown here is of the catabolite activator protein, which plays a role in the control of protein synthesis in the bacterium Escherischia coli by binding to DNA. (From Advances in Protein Chemistry 34 by J. S. Richardson, 1981. Reproduced by permission.)
Thus protein structure appears to consist of a hierarchy of levels. One theory proposes that protein folding occurs stepwise through these hierarchical levels. Another theory proposes that folding starts at ‘preferred points’ of the polypeptide chain and then propagates from these ‘nucleation centres.’24
Many attempts have been made to calculate the structure of proteins on the basis of the sequence of amino acids in their polypeptide chains. These models take into account known facts about protein structure and about the properties of different amino acids. On the basis of a variety of simplifying assumptions, these are then used to compute the conformations of the protein most likely to be stable from a thermodynamic point of view.25 But even so, they generate dozens or even hundreds of structures, all of which are equally stable, or in other words are ‘minimum-energy’ structures. In the literature on protein folding, this is known as the ‘multiple-minimum problem.’26 In successful calculations, one of the predicted conformations does in fact turn out to correspond to the known structure of the protein. But why should this conformation be adopted rather than the others? Even if more detailed calculations were able to show that this conformation was slightly more stable thermodynamically than the others, such a slight difference might not be able to stabilize the protein in this form, since the molecule is subject to relatively large energy fluctuations as a result of thermal vibration.
In any case, the assumption that the actual conformation of the protein is determined simply according to thermodynamic principles is not empirically testable. The protein will not fold into the other theoretically possible structures, and therefore their energetic stability cannot be compared experimentally.27
One suggested explanation for the unique conformations of protein molecules is an evolutionary speculation. Present-day proteins ‘are the rare survivors of a very long evolutionary process in which the vast majority of proteins had more random conformations, were less useful, and were therefore discarded through natural selection.’28 But natural selection cannot explain the rapidity of the folding process. In order to account for this, it has been suggested that the process of folding takes place in such a way that it leads only to one of the possible stable structures. Perhaps ‘the observed folded state is not the most stable thermodynamically of all those possible, but merely the most stable state of those which are kinetically accessible.’29
The hypothesis of formative causation provides an interpretation of protein folding that complements these interpretations. There are morphic fields for structural clichés such as a-helices; these are organized by higher-level fields into domains, and the overall field of the molecule organizes the domains into the characteristic structure of the protein. Still higher-level fields organize proteins into aggregates.
Fields at each of these levels canalize the folding process towards a characteristic end-point; the processes of folding follow chreodes (Fig. 6.2). Out of the many possible ways of folding and the many possible final forms, the fields stabilize particular folding pathways and final forms. In other words, the fields greatly increase the probability of these structures, rather than other possible ones, coming into being. Or, looking at this the other way round, they greatly reduce the randomness of the folding process.
The morphic fields are themselves stabilized by morphic resonance from innumerable past structures of the same kinds. The long evolutionary process has indeed stabilized those structures that have been useful and therefore favoured by natural selection; and the vast numbers of these past molecules have a powerful stabilizing effect on the fields by morphic resonance.
This interpretation means that not only the amino acid sequence but also the fields determine protein structure. This in turn means that ‘all the information required for the folding of a protein chain’ is not contained in its amino acid sequence (see above). Think again of the building analogy. The information for the structure of a house is not all contained in the building materials, even if they are supplied in modular units. The same materials can be used to build houses of different form; and, conversely, houses of identical design can be built from different materials: stone instead of brick, for example.
If morphic fields organize protein structure, these fields could give rise to similar structures even if the amino acid sequences were different. It is in fact known that domains of very similar structure occur in quite different proteins that contain different sequences of amino acids. Entire proteins may have a structure very similar to that of other proteins in spite of great differences in their amino acid composition. One example is provided by a family of protein-cleaving enzymes called serine proteases that include trypsin, a digestive enzyme, and thrombin, an enzyme involved in blood clotting. If any two of the enzymes in this family are compared, only about 40 per cent of the positions in their amino acid sequences are occupied by the same amino acid. Yet the similarity of their three-dimensional conformations, as determined by X-ray crystallography, is very striking. Most of the detailed twists and turns in these polypeptide chains, which are several hundred amino acids long, are identical.30
The haemoglobins provide an even more extreme example. These red proteins are responsible for the colour of blood and are found in a very wide range of animals, both vertebrate and invertebrate. Even peas and beans produce haemoglobin in their root nodules, which is why the nodules are pink inside. The three-dimensional structures of the various kinds of haemoglobin are extremely similar. However, their amino acid sequences are quite different. In all known haemoglobin sequences, only three out of a total of 140 to 150 amino acids are the same in the same positions.31
Such an extraordinary stability of structure in spite of differences in amino acid sequence is astonishing if we assume that all the information required for the folding of the protein chain is contained in the amino acid sequence. But it is much easier to understand on the basis of the morphic field hypothesis.
Experiments on protein folding
As we have just seen, protein structure is not fully explicable in terms of the sequence of amino acids in the protein chain and the known laws of physics and chemistry. From the orthodox point of view, this is just because the calculations are so complex that they cannot yet be carried out satisfactorily. From the point of view of the hypothesis of formative causation, morphic fields organize the structure of proteins under the influence of morphic resonance from protein molecules of the same kind in the past.
If this hypothesis could be applied to protein structure only speculatively, it would be of little value in molecular biology. But it should be testable if it is possible to make protein unfold into a denatured state that differs from any state in which the protein normally exists inside living organisms. The refolding of the chain will follow a different pathway from usual.32 If the refolding follows different chreodes from the normal folding process, the more often it is refolded in the laboratory, the more the previous refoldings will stabilize this chreode by morphic resonance. This chreode will become more probable, and the refolding process will take place quicker. This increased rate of folding should be measurable experimentally.
Consider the following experimental design. Several kinds of enzymes that have not already been used in folding experiments are selected. They are made to unfold, and then allowed to refold under standard conditions. The rate of refolding is measured for each of the enzymes in a laboratory in one place, say London.33
Then, in another laboratory, say in Berkeley, one of the enzymes is selected at random, and large quantities of it are made to unfold and refold under the same conditions as in London. The experimenters in London are not told which of the enzymes has been selected for this treatment in Berkeley.
Subsequently, the rate of refolding of all the enzymes is measured again in London under the same standard conditions. If the test enzyme now refolds significantly faster, and if there is no comparable increase in the rate of refolding of the other enzymes, which serve as controls, then this result would be in accordance with morphic resonance. Such a result would be unexpected from the point of view of all conventional theories.34
Morphic resonance in crystallization
Although the structures of many kinds of crystals have been described in detail, the ways in which these crystals take up their structures as they crystallize is very obscure. In the first place, just as in the case of protein structures, it is not possible to predict from first principles the way in which the molecules will pack themselves together in the crystal lattice. Even with quite simple molecules there are many possible lattice conformations that are equally stable thermodynamically, and there is no clear reason why one rather than any of the others is actually taken up during crystallization.35 For example, in 2004 researchers pointed out that ‘even for such a simple molecule as benzene, with only one known crystal structure at normal pressure, calculations yield at least 30 possible crystal structures’.36 Again, there is no way of empirically testing the assumption that the actual lattice structure is uniquely stable from an energetic point of view. The molecules simply will not crystallize into the other theoretically possible lattice structures, and therefore their energies cannot be measured and compared.
The second difficulty arises in trying to understand the way in which the crystal grows as a whole. Somehow, as molecules in solution come close to the growing surface of the crystal, they ‘snap’ into place in the growing aggregate. But the way in which they do this cannot be directly observed, and attempts to model the process mathematically are still very crude and have not been very successful so far.37 Such models take into account only local effects on the molecules joining the growing crystal. But crystals as a whole show patterns of symmetry that cannot possibly arise from a sum of local effects. Consider snowflakes. These crystals generally have a six-fold symmetry, but each snowflake is unique (Fig. 7.3). Within a snowflake, the intricate structure of the six arms is very similar, and these arms are themselves symmetrical. Although the differences among snowflakes can be explained in terms of random variations, the symmetrical development within each snowflake cannot be explained in this way.38 As John Maddox explained:
[This] must be the consequence of some co-operative phenomenon involving the growing crystal as a whole. What can that be? What can tell one growing face of a crystal … what the shape of the opposite face is like? Only the lattice vibrations which are exquisitely sensitive to the shape of the structure in which they occur (but which are almost incalculable if the shapes are not simply regular).39

Figure 7.3 Snowflakes. (From Snow Crystals by W. A. Bentley and W. J. Humphreys; Dover Publications, Inc., 1962. Reproduced by permission.)
From the point of view of the hypothesis of formative causation, the lattice structure is organized by a lattice morphic field, and a higher-level field organizes the structure of the crystal as a whole. The same lattice structure, for example that of water, can be organized into different types of crystal, as in sheets of ice, in snowflakes, and in various kinds of frost. The morphic field of the crystal as a whole is associated with ‘lattice vibrations which are exquisitely sensitive to the structure in which they occur’ and organizes the pattern in which the crystal grows.
Crystallization experiments
The fields of crystals that have already occurred many times in the past are highly stabilized by morphic resonance, and changes in these fields will not be experimentally detectable. But this is not the case with newly synthesized chemicals that have never existed before. Thousands of new kinds of molecules are made every year by synthetic chemists in universities and in industrial laboratories. Before such a substance crystallizes for the first time, there will be no morphic field for its lattice structure, or for the form of the crystal as a whole. There can be no morphic resonance from previous crystals of this type if none have existed. But when it crystallizes for the first time, the lattice and the crystal fields come into being. The second time, the fields will be influenced by morphic resonance from the first crystals; the third time, from the first and second crystals; and so on. There will be a cumulative build-up of morphic resonance stabilizing the fields of subsequent crystals, which will tend to render further crystallization of this type more probable. Consequently, the compound should tend to crystallize more and more readily as more of the crystals are made.
It is in fact well known to chemists that newly synthesized compounds are usually difficult to crystallize: weeks or even months may elapse before crystals appear in a supersaturated solution. Moreover, generally speaking, compounds become easier to crystallize all over the world the more often they are made. This happens in part because chemists tell each other of the appropriate techniques. But the most common conventional explanation for this phenomenon is that fragments of previous crystals are carried around the world from laboratory to laboratory, where they serve as ‘seeds’ for subsequent crystallizations. The folklore of chemistry has a rich store of anecdotes on this subject. The carriers of the seeds are often said to be migrant scientists, especially chemists with beards, which can ‘harbour nuclei for almost any crystallization process’.40 Or else seeds are thought to move around the world as microscopic dust particles in the atmosphere.
If morphic resonance plays a part in this phenomenon, the more often the new compounds are crystallized, the more readily they should tend to crystallize all over the world, even when migrant chemists are rigorously excluded and when dust particles are filtered out of the atmosphere. Experiments can easily be designed to test this prediction.41
Symmetry and internal resonance
According to the hypothesis of formative causation, crystal structures are stabilized by morphic resonance from other crystals of the same kind that existed in the past. But, in addition, the symmetry of crystals such as snowflakes seems explicable only in terms of some kind of resonance within the growing crystal: such an explanation seems necessary whether or not we take morphic fields into account. This raises a very general point about the morphogenesis of symmetrical structures: their symmetry seems to require some kind of resonant communication between the symmetrical parts. Consider, for example, your right and left hands. They are different from everyone else’s, both in the pattern of lines on the palms and the pattern of ridges on the finger tips. Yet they are very similar to each other,42 just as the arms of an individual snowflake are similar to each other. This suggests that within the developing organism morphic resonance takes place between similar structures, in this case between the fields of the embryonic hands. The same applies to other symmetrical structures such as the right and left sides of the face: again, although these are not exactly the same, they are very similar, and their development must have been correlated by some kind of resonant phenomenon.
We may conclude that in general within developing organisms there is an internal resonance between the fields of symmetrical structures, and this self-resonance is essential to their symmetry. Since symmetry is such an important feature of natural forms at every level of complexity, an internal resonance between symmetrical structures within the same organism is likely to be an important general feature of formative causation through morphic fields.
Such morphic resonance between spatially symmetrical structures that are developing at the same time within the same organism is, however, only one kind of self-resonance. Another aspect of self-resonance is just as fundamental: morphic resonance from an organism’s own past.
Self-resonance
The specificity of morphic resonance depends on the similarity of the patterns of activity that are resonating. The more similar the patterns of activity, the more specific and effective will the resonance be. In general, the most specific morphic resonance acting on a given organism will be that from its own past states, because it is more similar to itself in the past, especially in the immediate past, than to any other organism. This self-resonance will therefore tend to stabilize and maintain organisms in their own characteristic form, as well as harmonizing the development of symmetrical structures within the same organism. In living organisms, this self-stabilization of morphic fields may go a long way towards explaining how they are able to maintain their characteristic forms in spite of a continuous turnover of their chemical constituents.
If resonance from a holon’s own past states is of such importance, then how far in the past does a pattern of activity have to be to exert an influence by morphic resonance? The very notion of resonance implies a relationship between vibratory structures of activity, and the identity of such a structure cannot be defined instantaneously. Its ‘present’ must involve duration, since vibrations take time; and the frequency of vibration cannot be characterized until several similar vibrations have taken place. The ‘present’ must therefore consist of several cycles of vibration; hence the duration of the present depends on the characteristic vibratory frequencies of the organism. The slower these are, the longer the ‘present’ will be.
This general principle is, of course, apparent in quanta of radiation and of matter, which because of their wavelike nature cannot be considered to be sharply located: they are more like a ‘smear’ of probability. There is an inherent uncertainty in locating them at a particular point and assigning them a particular momentum.
In quantum matter fields, the vibration of the field itself underlies the quanta, or particles. The field, as the ground of the vibration, must endure or persist in time; indeed persistence in time, which implies a linkage of the present with the past, is inherent in the nature of the field. This linkage cannot take place through any kind of independently persisting material structure, since particles of matter are themselves manifestations of the field. So if a vibrating field is connected to its own past, which it must be if it is to persist, the linkage must be intrinsically temporal in nature. It must in fact depend on some kind of self-resonance.
Just as the position and momentum of a particle cannot be defined with certainty, neither can the exact duration of its present: it shades off into the past. These past patterns of activity become present again by morphic resonance, and by doing so maintain and stabilize the field as it persists in time.
From this point of view, the persistence of matter itself, and indeed of radiation, depends on a continuous process of resonance of the fields with their own past states. The continuity of any self-organizing pattern of activity at any level of complexity – from an electron to an elephant – results from this self-resonance. All organisms are dynamic structures that are continuously recreating themselves under the influence of their own past states.
These causal influences from an organism’s own past states must be capable of passing through or across not only time but space, or rather space-time. This requirement becomes obvious when we consider a moving organism, for example a galloping horse: its past patterns of activity with which it is in morphic resonance occurred in different places from the ones it now occupies. If it is in morphic resonance with its own past states, including those of only a few seconds ago, this causal influence must traverse the intervening space-time. Or, to look at it another way, its past patterns of activity, wherever and whenever they were, become present by morphic resonance.
Thus morphic resonance from the patterns of activity of similar past organisms, and self-resonance from an organism’s own past, are different aspects of the same process. Both involve formative causal connections across both space and time. Self-resonance, through its high specificity, stabilizes an organism’s own characteristic pattern of activity, and resonance with similar past organisms stabilizes the general probability structure of the field. This is what enables an organism to come into being and gives it its potentialities. As it actualizes itself, its own particular structure will tend to be maintained by self-resonance within the overall probability structure of the field.
This interpretation has much in common with Alfred North Whitehead’s idea that there is a ‘prehension’ from the ‘actual occasions’ of organisms to their immediate or more remote predecessors. The more often a pattern of activity has been repeated, the stronger its influence will be. In Whitehead’s words, ‘any likeness between the successive occasions of a historical route procures a corresponding identity between their contributions to the datum of any subsequent actual entity; and it therefore secures a corresponding intensification in the imposition of conformity.’43 However, Whitehead’s philosophy is rather obscure; and although he definitely envisaged a process similar to what is here called self-resonance, it is not clear to what extent he thought of a comparable influence from different organisms in the past.44
Quantum physics and morphic fields
Quantum physics provides a far more promising context for morphic fields and morphic resonance than anything in classical physics. Paradoxically, in the twentieth century, quantum theory revealed the limitations of a reductionist approach, while biology moved in the opposite direction, towards an extreme reductionism. As the quantum physicist Hans-Peter Dürr expressed it:
The original emphasis on the whole in consideration of living things, their shapes and Gestalts, has been replaced by a fragmenting, functionalist description, in which, for an explanation of the sequences of events, the focus is on the substances, matter, and its building blocks, the molecules and their interactions. The surprising thing about this development from holism and even vitalism to molecular biology is that it is occurring some decades after – and not before – a profound change in just the opposite direction took place at the foundations of natural science, in microphysics, during the first third of the century that has recently ended. There, fundamental limitations of the fragmenting, reductionist way of looking at things had become apparent. Divisible substance revealed in a strange way holistic aspects.45
Dürr suggested that ‘processes of quantum physics might in principle contain a fruitful potential for an explanation of Sheldrake’s morphic fields.’46
Another way in which morphic resonance and morphic fields might be related to modern physics is through extra dimensions of space-time. In the theory of General Relativity Einstein treated space-time as four-dimensional. In the 1920s, in the Kaluza-Klein theory, space-time was extended to five dimensions in an attempt to find a unified theory for gravitational and electromagnetic fields. Modern hopes of unifying the known fields of physics, including the strong and weak nuclear forces, are mainly centred on superstring theory, with 10 dimensions, or M-theory with 11.47
The value of superstring and M-theory is disputed, but their very existence shows that extra dimensions are no longer the preserve of esoteric speculations; they are mainstream in modern physics.48 But what do these extra dimensions do, and what difference do they make? Some physicists propose that they include ‘information fields’ that could help to explain the phenomena of life and mind.49
Another possible point of connection between morphic fields and modern physics is through the quantum vacuum field. According to standard quantum theory, all electrical and magnetic forces are mediated by virtual photons that appear from the quantum vacuum field and then disappear into it again. Thus all molecules within living organisms, all cell membranes, all nerve impulses, and indeed all electromagnetic and chemical processes depend on virtual photons appearing and disappearing within the all-pervading vacuum field of nature. Could morphic fields interact with regular physical and chemical processes through the vacuum field? Some theoreticians speculate that they can and do.50
Yet another possible meeting point between quantum physics and formative causation is quantum Darwinism, as developed by Wojciech Zurek and his colleagues. The focus of this theory is the transition of quantum systems from the vast potentiality of superposed states to simpler, particular states through a selection process that depends on the environment, and more particularly on the sea of photons in which the all quantum systems are immersed.51 Quantum Darwinism is primarily concerned with bridging the gap between the quantum level and the ‘classical’ world, and like the hypothesis of formative causation it emphasizes that there is a selective process whereby only some of the many quantum possibilities are realized, which then through a memory process are stabilized.
If a truly unified theory is ever to emerge, living organisms and conscious minds must be included within it along with the particles and fields of physics. There is a need for a new natural philosophy that goes further than physics alone can go but remains in harmony with it.
Perhaps the most profound of the new natural philosophies is the theory of the implicate order proposed by the physicist David Bohm. According to this theory, there are three major realms of existence: the explicate order, the implicate order, and a source or ground beyond both. The explicate order is the world of seemingly separate and isolated ‘thing-events’ in space and time. The implicate order is a realm in which all things and events are enfolded in a total wholeness and unity, which as it were underlies the explicate order of the world we experience through our senses.
The implicate order is not somehow inserted into material systems in space and time; rather, material systems and space and time themselves all ‘unfold’ from this underlying order. Any describable event, object, or entity in the ordinary, explicate world is ‘an abstraction from an unknown and undefinable totality of flowing movement.’ Bohm called this universal flux the holomovement: ‘The holomovement, which is ‘life implicit’, is the ground both of ‘life explicit’ and of ‘inanimate matter’, and this ground is what is primary, self-existent and universal.’52 The holomovement ‘carries’ the implicate order, and is an ‘unbroken and undivided totality’.53
Bohm argues that a conception of undivided wholeness is implicit in both relativity and quantum physics. Einstein proposed that reality be regarded from the very beginning as constituted of fields. Particles are regions of intense field that can move through space. The idea that they are separate and independently existent is, at best, ‘an abstraction furnishing a valid approximation only in a certain limited domain’.54
Quantum theory implies unbroken wholeness for three reasons. First, action is composed of indivisible quanta, and hence interactions between different entities (e.g. electrons) constitute ‘a single structure of indivisible links.’ Second, entities such as electrons can show differing properties (particle-like, wave-like or something in between) depending on their environmental context. Third, entities that have originally been combined show a peculiar non-local relationship or entanglement ‘which can best be described as a non-causal connection of things that are far apart’.55 (This is the Einstein-Podolsky-Rosen paradox.56)
One analogy for the implicate order is provided by holograms, in which the interference pattern in each region of the photographic plate is relevant to the whole structure, and each region of the structure is relevant to the whole of the interference pattern on the plate.57 However, this analogy has the obvious limitation of being static and does not capture the idea of holomovement.
Bohm emphasized the importance for physics, biology, and psychology of the notion of formative causation as ‘an ordered and structured inner movement that is essential to what things are.’ Any formative cause must evidently have an end or goal – what Aristotle called a final cause. Thus, for example, it is not possible to refer to the inner movement from the acorn giving rise to the oak tree without simultaneously referring to the oak tree that is going to result from this movement. Bohm pointed out that in the ancient view, ‘the notion of formative cause was considered to be of essentially the same nature for the mind as it was for life and for the cosmos as a whole.’58
Bohm related the idea of formative cause to the holomovement, and saw the organization of physical particles, living organisms, and minds in terms of the hierarchy of implicate orders in this undivided process of flux. We experience this forming activity of the mind in the flowing movement of our own awareness. Each moment of consciousness has a certain explicit content and an implicit context which is a corresponding background. The actual structure, function, and activity of thought are in the implicate order. ‘The distinction between implicit and explicit in thought is thus being taken. . . to be essentially equivalent to the distinction between implicate and explicate in matter in general.’59
Bohm’s theory of the implicate order is more fundamental than the hypothesis of formative causation, but the two approaches appear to be quite compatible. Bohm and I discussed their possible relationship,60 and he summarized his interpretation of morphic fields as follows:
The implicate order can be thought of as a ground beyond time, a totality, out of which each moment is projected into the explicate order. For every moment that is projected out into the explicate there would be another movement in which that moment would be injected or ‘introjected’ back into the implicate order. If you have a large number of repetitions of this process, you’ll start to build up a fairly constant component to this series of projection and injection. That is, a fixed disposition would become established. The point is that, via this process, past forms would tend to be repeated or replicated in the present, and that is very similar to what Sheldrake calls a morphogenetic field and morphic resonance. Moreover, such a field would not be located anywhere. When it projects back into the totality (the implicate order), since no space and time are relevant there, all things of a similar nature might get connected together or resonate in totality. When the explicate order enfolds into the implicate order, which does not have any space, all places and all times are, we might say, merged, so that what happens in one place will interpenetrate what happens in another place.61
Suggestive though Bohm’s ideas are, they go far beyond physics as it is currently practised, but together with theories of quantum Darwinism and other growing points of theoretical physics, they help point towards a science of the future in which formative causation will be integrated with physics, chemistry, biology and consciousness studies.
In Chapter 6 I considered the role of morphic fields in biological morphogenesis, and in this chapter their role in the morphogenesis of molecules and crystals. I also examined some of the general features of the hypothesis of formative causation: the idea of morphic fields as probability structures, and the importance of self-resonance in the development and maintenance of the form of individual organisms. I now turn to a discussion of the possible role of morphic resonance in biological heredity, and then in Chapter 9 consider the nature of animal memory and the light shed upon it by the idea of self-resonance from an animal’s own patterns of activity in the past.