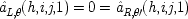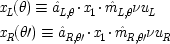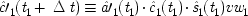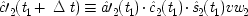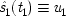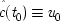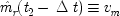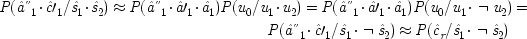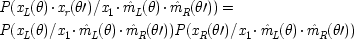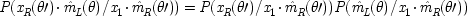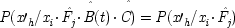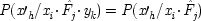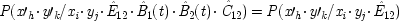Appendix I A More General Common-Cause Model for EPR
The aim is to construct a model for the EPR arrangement that explicitly includes the apparatuses. The critical assumption in considering the apparatuses and their states is that the two measurements are supposed to be made simultaneously. Thus the state of the apparatus in one wing at the time of measurement can have no effect on the outcome in the other. Indeed, in the experiments of Aspect et al.1 the choice of direction is made at the very last instant, to ensure that no causal connection is possible. Some other assumptions will make the notation easier. Suppose for simplicity that in any complete cause in which states of the apparatus figure as a part, it is always the same apparatus states. Designate the set of states positively relevant to spin-up outcomes along direction θ in the left-wing apparatus, m L,θ , those for the apparatus in the right wing, m R,θ . Allowing initially all combinations of possible partial causes, set
What kinds of causal connection are appropriate for an EPR experiment? The usual assumptions are
1.  
The state of the measuring apparatus on the right (left) does not influence the outcome on the left (right). This is expressed formally in the model by setting
2.  
The outcome on the right (left) does not affect the outcome on the left (right). So
3.  
x 1is not a complete cause of either the outcome on the left nor of the one on the right:
1 A. Aspect, J. Dalibard, and G. Roger, 'Experimental Tests of Bell's Inequalities Using Time Varying Analyzers', Physical Review Letters, 49 (1982), 1804-7.
end p.251
 
4.  
The state of the apparatus on the left (right) is not a complete cause of the outcome on the left (right):
5.  
x 1and m L, θare joint partial causes of x L, θ ; and x 1and m R,θ′ , of x R,θ′ :
Relabelling â L,θ(1, 1, 0, 0) as â L,θ ; and â R,θ′(1, 0, 1, 0) as â R,θ′ , the basic equations of the model will be:
end p.252
 
Appendix II Do Quantum Causes Propagate?
The arrangement for a two-slit experiment is described in section 6.7. There it was claimed that the quantum-mechanically predicted results show that the propagation requirement is not satisfied in the two-slit experiment. To see why, consider a region on the recording screen with low probability in the two-slit experiment, but high probability with only one slit open—say, slit one. Assume that some feature c operating at t 0in the source is partially responsible for a positive result, r, at t 2in the selected region of the screen. By the requirement for propagation, there must be some c roperating in the region of r, just before t 2 , which has been caused by c and which is part of the cause of r. As with EPR, suppose that the measuring apparatus state, m r , also contributes. Then
  • (1)
The causal influence c rmust propagate to r from c, and since it can appear only where the quantum state is non-zero, it—or some causal antecedent to it—must appear either at slit one at t 1when the beam passes the wall, or at slit two. Call the causal antecedent at slit one, c 1 , and at slit two, c 2 . Let s 1denote the state of the first slit when it is open at t 1 ; s 2 , the second. Allowing that s 1and s 2may themselves affect the propagating influence, and assuming for simplicity that there are no further internal contributions, gives the following structure:
  • (2)
  • (3)
  • (4)
  • (5)
  • (6)
  • (7)
Equation (3) contains an important and not yet noted assumption about the causal structure: s 2appears nowhere in the equation for c 1nor s 1in the equation for c 2 . This reflects the conventional assumption that the opening or closing of a distant slit has no effect at the other. If it were to do so, the
end p.253
 
general constraint on structural models that causes must precede their effects would require the distant opening or closing to occur earlier than its effect, and the demand for propagation requires that some capacity-bearing signal should move along a continuous path between.
What is the probability for r to occur, with both slits open? Dropping the time indices, and omitting all terms in which the errors figure:
Let the larger be P(â″ 1 · ĉ′ 1 /ŝ 1 · ŝ 2 ). With the usual assumptions that the operations are independent of the causes and the errors of each other
It follows that
Hence the probability for a particle to register at r with both slits open is at least as large as the larger of the probabilities with only one slit open. This is contrary to what happens.
end p.254
 
Appendix III Propagation, Effect Locality, and Completeness: A Comparison
In discussing the Bell inequalities, most authors do not separate questions of realism from questions of causality. Among the few who do address questions of causality separately, propagation is usually presupposed. Patrick Suppes is a good example. He produces some nice results on exchangeability that suggest that the requirement of conditional independence of the outcomes on the common-cause—i.e. factorizability—should be given up: 'The demand for conditional independence is too strong a causal demand.' The considerations in this chapter show why it is too strong. As 'a way of finding a new line of retreat', Suppes suggests making instead an 'independence of path assumption'. This assumption 'prohibits of course instantaneous action at a distance and depends upon assuming that the propagation of any action cannot be faster than that of the velocity of light'.1 In its most straightforward form, Suppes's suggestion amounts to the requirement for propagation.
A requirement for propagation also appears in the work of Jon Jarrett.2 Jarrett derives 'full factorizability' (recall section 6.5) from two simpler conditions. Completeness requires that the outcomes not cause each other; they are to depend on some prior state of the combined systems—say x 1 —and the states of the measuring apparatus. Jarrett puts the condition probabilistically. In the notation used here it reads thus:
Completeness (Jarrett)
Jarrett names his other condition locality. It is exactly the same as the first assumption of common-cause model No. 2 in section 6.5: the state of the measuring apparatus in one wing must have no effect on the outcome in the other. Again, Jarrett does not put the condition directly, but rather in terms of its probabilistic consequences:
1 P. Suppes, 'Causal Analysis of Hidden Variables', in P. Asquith and R. Gieve (eds.), PSA [proceedings of the biannual Philosophy of Science Association meetings] 1980, ii, (East Lansing, Mich.: Philosophy of Science Association, 1980), 529.
2 'On the Physical Significance of the Locality Condition in the Bell Arguments', Nous, 18 (1984), 569-89.
end p.255
 
Locality (Jarrett)
These, too, are factorization conditions, although superficially they may not seem so.3
The locality assumption is familiar from the discussion of full factorizability in section 6.5. It rests on the supposition that the two measurements are made simultaneously, and it may thus conceal a commitment to propagation. That depends on whether the distant apparatus is ruled out as a cause on the grounds of time-order alone—causes must precede their effects; or on the more complex grounds that the relativistic requirement that no signal can travel faster than the speed of light rules out any possibility of propagation (at the time of measurement) from the apparatus in one wing to the outcome in the other. But whatever is the case with Jarrett's locality assumption, his completeness requirement puts him squarely in favour of propagation.
In defending the completeness requirement, Jarrett sometimes talks about 'screening off'. This is language taken from discussions of the common-cause. But we have seen that this kind of factorizability condition is not an appropriate one for common causes in EPR. Nor does it really seem to be what Jarrett has in mind. For he does not in fact treat the hidden states as descriptions of the common cause at the source, but rather as features that the two systems possess separately at points between the source and the measurement. This is apparent in the example he gives to explain why he chooses the name 'completeness'. In the example, each of the two systems is supposed to have a genuine spin in some particular direction after it leaves the source, and that spin deterministically causes the measurement outcome in every other direction. Jarrett points out that in this case the measurement outcomes do not factor when information about the actual spins is omitted. Factorizability is restored when the description of the systems at the time of measurement is complete. This he claims to be generally true:
For a theory which assigns probabilities on the basis of the complete state description . . . any information about particle L (R) [the particle in the left wing (the particle in the right wing)] which may be inferred from the outcome of a measurement on particle R (L) [the particle in the right wing (the particle in the left wing)] is clearly redundant.4
3 They are equivalent to
and
4 Jarrett, op. cit., p. 580.
end p.256
 
Clearly the criticism only works for theories—like the one Jarrett proposes—which postulate that some intervening states exist. A theory can only be accused of incompleteness if there is something with respect to which it could be complete. So in calling his condition completeness, Jarrett already supposes that there are further states to be described, and that is the matter at issue. The completeness assumption presupposes both that there are spatially separated and numerically distinct states in each of the two systems between the time of interaction and the time of measurement, and also that these states contain all the information from the past histories of the systems which is causally relevant to the measurement results. Where do such states come from? They are no part of the common-cause models; but they are just what is needed for propagation.
Linda Wessels is more explicit in her assumptions than Jarrett. Her paper 'Locality, Factorability, and the Bell Inequalities'5 provides a long treatment of a concept she calls 'effect locality'. This paper is a unique contribution in the Bell literature, important because of the way it tries to get behind the factorizability condition to find out where it comes from. Wessels claims that the condition is a consequence of the demand that there is no action at a distance. This means that factorizability will turn out to be, for Wessels, a kind of propagation requirement.
Wessels describes effect locality 'very roughly and intuitively', thus:
the evolution of the characteristics associated with a body B 'in a moment', say (t,t + dt), depends only on the characteristics associated with B at t and the external influences felt by B during the moment. A slightly different but equally rough version of effect locality is the following two part claim: a) the past experience of B influences its own evolution at t only in so far as that past experience has either led to the characteristics associated wtih B at t or/and has influenced other systems (bodies, fields, whatever) which in turn exert external influences on B at t; and b) other systems influence the evolution of B at t only to the extent that they are the source of some external influence (force, field, whatever) acting on B in (t,t + dt)6 .
The bulk of Wessels' paper is devoted to presenting a more detailed and precise characterization from which a factorizability condition can be derived.
I will take up three topics in discussing Wessels' idea. The first will be a brief characterization of some of the features of her formalism that are missing from the more simplified accounts I have been presenting; the second will show why effect locality and propagation are the same; and the third will return to the basic naive assumptions with which worries about EPR correlations begin.
5 Nous, 19 (1985), 481-519.
6 Ibid. 489-90.
end p.257
 
(a) Wessels introduces a number of sophistications which I have omitted because they are not essential to the central ideas here. I have tried throughout to make as many simplifications as possible in order to keep the fundamental outlines clear. But there are a number of features present in Wessels' formalism that can be taken over to make my models more general. For a start, Wessels separates ' "influences" by which systems can affect one another . . . [which] might be characterized as forces, potentials, field strengths, or any other "felt influence" '7 from the conditions and states of other bodies which might affect the state of a body contiguous to them. (But in every case she requires that 'the quantitative properties involved are all empirically measurable': 'The morning tide is not explained merely by saying vaguely, "Ah, there is a force acting at a distance." A distance force has a quantitative measure.'8 ) In the kinds of simple structural equation considered here, this distinction is not drawn: all measurable quantities are represented in the same way by random variables.
Second, Wessels allows a variety of intervening states which can have different degrees of effect, whereas only the simplest case, where the propagating influence is of a single kind, is taken up here. Thirdly, she provides explicitly for the time evolution of the capacity-carrying states, and she allows for interactions along the path between the initial cause and the final effect (cf. her clause (EL4) and (EL2) respectively), something which is missing both from my account of propagation and from the at-at theory of Wesley Salmon on which it is modelled. Lastly, Wessels uses continuous densities and continuous time, which is a far more satisfactory way to treat questions of contiguity. In all these respects, Wessels provides a framework within which a more general formulation could be given of the basic models described in the earlier sections of this chapter. But I shall not do that here.
(b) A number of the conditions that define an effect-local theory serve to ensure the existence and law-like evolution of whatever states the systems may have. These conditions will be discussed below. Only three concern the causal connections among the states; and all three are formulated probabilistically by Wessels. The first is (EL3): 'EL3 says that the evolution of a body B over a period of time . . . depends only on the state of B at the beginning of the period and the influences at the positions of B during that period.'9 Specifically excluded are earlier states of the body, and any other circumstances that might surround it. Letting {x′ h } represent the set of states available at the end of the interval, {x i } the set of positively relevant states at the beginning, and {F j } the influences at the positions of B during the interval, the structural form for (EL3) is
7 Ibid. 490.
8 Ibid. 484.
9 Ibid. 491.
end p.258
 
Wessels does not put the condition structurally, but instead expresses it directly in terms of the probabilities. Representing the other circumstances by C and the set of earlier states by B(t), her probabilistic formulation, in the notation used here, reads thus:
  • (EL3′)
What matters for the EPR case is that the excluded circumstances 'include states of bodies other than B'.10 The set of states available to the distant system in the EPR experiment will be represented by {y k }. Referring to these states explicitly, (EL3) implies the familiar factorization condition
The second causal restriction in an effect-local theory is (EL6)
Effect locality requires that the way an interaction proceeds depends on nothing more than the states of the interacting systems just before the interaction (then regarded as bodies) and the influences external to the interaction at the location of and during the course of interaction. Other earlier states of the interacting systems, or of other systems, as well as influences evaluated at other places and/or at earlier times, are statistically irrelevant. This requirement is captured by Clause EL6.11
Letting E 12represent the external influences on the interacting bodies, B 1 (t) and B 2 (t), as before, the set of prior states of the two bodies, and C 12the circumstances:
  • (EL6)
Again, this is a familiar-looking factorization condition.
Thirdly, 'something like an assumption of sufficient cause for correlation is needed:
SC. If there has been nothing prior to or at a time t that causes a correlation of the states of two independent systems, then their states are uncorrelated at t.'12
In the application to EPR, (SC) is joined with the assumption usually made about the measuring apparatuses, that they have no causal history in common, to produce factorization of the outcomes on the apparatus states. This is the assumption that makes the theory 'local' in Jarrett's terminology. The real significance of Wessels' work comes from her characterization of
10 Ibid.
11 Ibid. 493.
12 Ibid. 508.
end p.259
 
effect locality, which provides the grounds for the condition that Jarrett calls 'completeness'.
Wessels gives the condition (SC) a new kind of name because she thinks that it is not part of the characterization of an effect-local theory. She says, 'SC is certainly in the spirit of effect-locality, but it does not follow from effect-locality as explicated above. It must be taken as an independent assumption.'13 On the contrary, I think there is more unity to be found in Wessels' conditions than she claims; for something like her assumption that a sufficient cause is required for correlation is already presupposed in her statistical characterizations (EL3) and (EL7). These are assumptions about causality: (EL3) is meant to assert that the state of the system in one wing is not causally relevant to the outcome in the other; and (EL7), that the only causes for the outcomes of an interaction between two bodies are the ingoing states of the bodies and the influences contiguous to them. Yet in both cases the formulation that Wessels gives to the conditions is probabilistic. (EL3) is supposed to say that F and x are the only causes of x′; earlier states play no causal role, nor do any of the states in the distant system. But what ensures that these states are statistically irrelevant? Something like Reichenbach's Principle of the common-cause is needed to bridge the gap; and (SC) is Wessels' version of it. This just confirms the point from earlier chapters that you cannot use probabilities to measure causality unless you build in some appropriate connection between causality and probability at the start.
A more substantial concern about the characterization of effect locality concerns factorizability. (EL3) is, after all, just the factorization condition that I have argued is unacceptable as a criterion in EPR. So when F j · x iis a common cause of both x h′and y k′ , (EL3′) will not generally be valid. But this is not a real problem in Wessels' derivation, because the use to which she puts (EL3) is more restricted than her general statement of it. In fact (EL3) is not used at any point where the antecedent state in question might be a common-cause. This is apparent from a brief review of Wessels' strategy, even without inspection of the details of her proof.
Wessels aims to produce an expression for the joint probability of the final outcome states in an EP R-type experiment. To do so, she starts at the end and works backwards. The probability for the outcomes is calculated by conditionalization from the probabilities just before, and those in turn by conditionalization on the states just before them, and so on in a chain backwards, each step employing (EL3). It is only at the first step, at the point of interaction, that (EL3) might fail, and that makes no difference; the last step is what matters. It is apparent both from the discussion of propagation in section 6.7 and from the discussion of Jarrett in this section, that factorizability is a trivial consequence once the individual systems have their own distinct states which are causally responsible for what happens to
13 Ibid.
end p.260
 
them thereafter. Indeed, Wessels' scheme satisfies all the requirements for propagation, since the travelling particles are each assigned states, localized along their trajectories, from the instant the interaction between them ceases.
This raises again the question: why assume that such states exist? Jarrett, we have seen, takes their existence as obvious. The propagation requirement of section 6.7 says that they are necessary if features of the interaction are going to make any difference to the outcomes. Wessels gives a different reason, and this is the point of most of the remaining conditions on effect-local theories; namely, once the interaction has ceased, the two separated systems should be treated as bodies, and bodies, in an effect-local theory, ought to have their own states.
(c) This notion of body is the third topic that I want to take up. I believe that Wessels is right in her characterization, and that it is just this notion of a body with localized states that lies at the core of the common refusal to attribute causal structures in quantum mechanics. This is in no way a novel view. The Einstein-Podolsky-Rosen paper was written partly in response to Niels Bohr's claims about the wholeness of quantum actions, and the paper precipitated Erwin Schroedinger's very clear statement of the entanglement of separated quantum systems.14
I will discuss wholeness versus separability of bodies briefly here to reinforce my conclusions about EPR and causality. There is a tendency to think that the distant correlations of an EPR-type experiment provide special obstacles to the postulation of causal structures in quantum mechanics. The general point of this chapter is that this is not so. The arrangement of probabilities is not a particular problem. What is a problem is the localizability of causal influence. Recall the discussion of the two-slit experiment in Appendix II. The derivation there of a wrong prediction for the pattern on the screen looks much like the standard derivation of that result. But it is not quite the same; for what is critical in Appendix II is not where the particle is, but where the causal influence is. The derivation requires that the influence be highly localized; this is the requirement that comes in Jarrett under the name 'completeness', in section 6.7 from the demand for propagation, and in Wessels from the treatment of the systems as bodies. If, by contrast, the causal influence is allowed to stretch across both slits—as the quantum state does—no problem arises. Under its old-fashioned name, this is the problem of wave-particle duality. The point I want to make here is that it is the very familiar problem of wave-particle duality that prevents a conventional causal story in EPR, and not its peculiar correlations.
14 This was the paper which introduced his famous cat paradox. Cf. A. Fine, Shakey Game (Chicago, Ill.: Chicago University Press, 1987).
end p.261
 
One quick way to see this is to consider an alternative to the quantum structure proposed in section 6.6. There the suggestion is to take the quantum state at the time of interaction as the common cause of the two measurement outcomes. The succeeding section shows that the influence from this cause cannot propagate along a trajectory. I think of it instead as operating across a gap in time. An alternative is to let it propagate, like the quantum state, as a 'wave'—or, finally, just to take the quantum state itself at the time of measurement as the immediate cause of both outcomes. That is really where the discussion of the EPR correlations starts, before any technicalities intervene. What is the idea of causation that prevents this picture? It is a good idea to rehearse the basic problem.
No one can quarrel with the assumption that a single cause existing throughout a region r can produce correlated effects in regions contiguous to r. That is a perfectly classical probabilistic process, illustrated by the example in section 6.3 and by a number of similar ones constructed by van Fraassen in his debate with Salmon. An extremely simplified version comes from Patrick Suppes. A coin is flipped onto a table. The probability for the coin to land head up is 1/2. But the probability for head up and tail down ≠ 1/2 × 1/2. The structure of the coin ensures that the two outcomes occur in perfect correlation. Similarly, if the quantum state for the composite at t 2− Δ t is allowed as a cause, then the EPR set-up has a conventional time-ordered common-cause structure with both propagation and a kind of effect locality. There is a state immediately preceding and spatially contiguous with the paired outcomes; the state is causally relevant to the outcomes; and this state, after the addition of whatever contiguous felt influences there are, is all that is relevant. But it does not produce factorization, and hence does not give rise to the Bell inequalities. What rules out this state as a cause?
Wessels rules it out by maintaining that the two separated systems are distinct bodies, with spatially separated surfaces. Her justification for this is her requirement (EL4): an effect-local theory will treat any system as a distinct body so long as it is not interacting with any other. It is the extent of the surface of the body that is the problem. There are three apparent choices: (1) something approximating to the classical diameter for the electron; (2) the spatial extent of the left-travelling half of the wave packet for the body in the left wing, and of the right-hand travelling half for the body in the right wing; or (3) the total extent of the wave packet. The first choice gives factorizability, but this is just the assumption that goes wrong in the two-slit experiment. The third is a choice that will not present the outcome probabilities as factors. The second is the one she needs, and that choice is hard to defend. It would be reasonable if one were willing to assume that the wave packet reduces when the two systems stop interacting; but that assumption will give the wrong predictions. Without reduction of the wave packet it is a strange blend, both taking quantum mechanics seriously and refusing to do so: the electrons are allowed to spread out in the peculiar way
end p.262
 
that quantum systems do, far enough to pass through both slits at once, for example; but the two electrons are kept firmly in the separate spread-out halves.
Imagine a single particle that strikes a half-silvered mirror. After a while the quantum state will have two almost non-overlapping humps, where each hump itself will be much wider than the classical dimensions of the particle, due to quantum dispersion. Where is the particle? Here is the problem of wave-particle duality. The 'surface' of the particle must spread like a wave across both humps. Quantum mechanics cannot locate it in either one hump or the other. In the spatial portion of the wave packet in EPR there are again two humps, although this time there are two particles. But nothing in quantum mechanics says that one particle is in one hump and the other in the other. If it is formulated correctly to express the assumptions of the problem, the theory will say that a measurement of charge or mass will give one positive answer on the right and one on the left, and never two on the same side; just as, with the half-silvered mirror, the theory should predict a positive reading on one side of the mirror or the other, but not on both sides at once. But that does not mean in either case that a particle can be localized in either of the two humps exclusively. There is good intuitive appeal in keeping particles inside their classical dimensions. But once they are spread out, what is the sense in trying to keep one very smeared particle on the left and the other on the right? It is just that assumption that makes EPR seem more problematic, causally, than older illustrations of wave-particle duality.
end p.263
 
end p.264