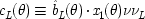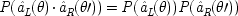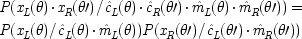6 What Econometrics Can Teach Quantum Physics: Causality and the Bell Inequality
Abstract: This chapter gives a concrete example of a question of current scientific interest where capacities matter: 'Do the Bell inequalities describingEinstein-Podolsky-Rosen (EPR) experiments show that causality is incompatible with quantum mechanics?' The question cannot be answered if we rely on probabilistic theories of causality and laws of associations alone. It takes the concept of capacity and related notions of how capacities operate even to formulate the problem correctly. Econometrics models with correlated errors, it is shown, can explain the EPR results when the correlations are given a capacity interpretation.
Nancy Cartwright
6.1. Introduction
At least since the 1870s social scientists have been prone to take physical theory as their model, and this has been no less true in economics than elsewhere. Adolphe Quételet's ideas for a social physics are one good example. A recent history
1 even claims that the probabilistic methods of econometrics emerged in an attempt by neo-classical economists to keep up with the indeterminism of the newly developed quantum theory. But there is at least one case in which the traditional order can be reversed, and in which the methods of econometrics can be used to disentangle a problem in quantum mechanics. This is the case of Bell's inequalities.
Bell's inequalities are supposed to show that no local hidden-variable theories are possible in quantum mechanics. But 'local' here is a peculiar term. It names a statistical condition that looks much like the common-cause conditions from Herbert Simon, described in section
1.2. The alternative name sometimes used, 'factorizability', is closer to what the statistical condition actually requires. The condition is essential to the derivation of the no-hidden-variables result, and therefore it is important to understand exactly what it means. This is where the structural models of econometrics help: the conclusions about structural models arrived at in Chapter
3 show that factorizability is not, as many assume, a criterion for the existence of a common cause.
Bits of this chapter are technically complicated. But the ideas are
end p.231
not. Readers who are not especially interested in the details should be able to follow the main arguments without attending to the equations. A review of section
3.3.3 should help as well.
6.2. Bell's Inequality
The inequalities were first derived by J. S. Bell in 1964. Since then there have been a number of different versions of them, based on Bell's methods, as well as a number of experiments confirming quantum mechanics at the expense of hidden variables. The setting is an experiment originally proposed by Einstein, Podolsky, and Rosen, in a paper which argues in favour of hidden variables and maintains that quantum mechanics is incomplete because it fails to describe them. I will call the experiment the EPR experiment, even though what I shall describe is a more modern version, more simple than the original proposal of Einstein, Podolsky, and Rosen and abstracted from any real experimental complications.
2
The experiment measures the spin components at two different angles, θ and θ′, of two spin − 1/2 particles widely separated and travelling in opposite directions. The particles might be electrons. To say that they are spin − 1/2 particles means that, regardless of the angle at which they are measured, they will be found to have a spin component of either + 1/2 (called 'spin-up') along that angle, or of − 1/2 ('spin-down'). The particles are supposed to have been emitted from a source with no angular momentum. Quantum mechanically they are said to be in 'the singlet state'. Since angular momentum is conserved in quantum mechanics, and spin is a kind of angular momentum, one particle will yield spin-up for a given angle if and only if the other yields spin-down. Quantum mechanics predicts that the outcomes will also be correlated for measurements along different angles. Let x
L (θ) represent the proposition, 'the outcome is + 1/2 in a measurement along angle θ on the particle in the left wing'; similarly for x
R (θ), in the right wing. The quantum mechanical predictions are that
end p.232
Here the dot (.) indicates logical 'and'.
These correlations between distant outcomes are the source of the puzzle. The simplest account of the correlations would be that each pair of particles was supplied at the source with a spin component in every direction, where the particle on the left got spin-up for a given angle just in case the right-hand particle got spin-down. This is the account urged by Einstein, Podolsky, and Rosen. But spins in different directions are incompatible quantities in quantum mechanics. That is typically taken to mean that they cannot have well-defined values at once (the more familiar case is position and momentum). Indeed, if a system can have well-defined values for spin along different directions, this is a fact that no state in quantum mechanics can express, and that is why Einstein, Podolsky, and Rosen accused the theory of incompleteness.
Bell is supposed to have shown that the ordinary understanding of quantum mechanics is right. The correlated outcomes cannot be accounted for by assuming that there are values there to be measured all along; even more strongly, no hidden or unknown variables at all can be postulated to account for the correlations without allowing mysterious collusion between the separated systems at the instant of measurement. The collusion would be mysterious because the two systems are supposed to be measured simultaneously, with no time to communicate to each other what response they will make to the apparatus they see. Hidden-variable theories without such collusion are called 'local' theories. What Bell did was to derive a set of inequalities that any local hidden-variable theory must satisfy in an EPR experiment. Quantum mechanics does not satisfy these inequalities, and it is quantum mechanics that has been subsequently experimentally confirmed.
Locality is expressed in a familiar-looking factorizability condition. Labelling the hidden variable
x
1 , Bell's derivation assumes
A superficial comparison with Simon's conditions may make factorizability appear the perfect way to express the fact that
x
Land
x
Rare not supposed to influence each other. For it is exactly
end p.233
analogous to the factorizability condition of section
1.2. But this is not the case. Section
3.3 showed what the general criterion for a common cause in a three-variable model is. Simon's is a special case and one not suited to EPR.
6.3. A General Common-Cause Criterion for the EPR Experiment
A simple example will illustrate how Simon's structure goes wrong. It is an example similar to ones proposed by Bas van Fraassen in criticisms he makes of Wesley Salmon's use of factorizability as a common-cause condition.
3 Suppose that a particle collides with an atom and the atom emits two new particles as a consequence. Particle 1 may be emitted either at angle θ or at angle θ′; and the probabilities are 50-50. Particle 2 may be emitted at − θ or at − θ′; and again the probabilities are 50-50. But momentum must be conserved. So particle 1 is emitted at θ if and only if particle 2 follows the path defined by − θ.
It is obvious in this situation that a cause may be at work: λ, when it is present in the atom, produces motions along θ, − θ; otherwise the atom emits the particles at angles θ′ and − θ′. In this example λ may be a deterministic cause: P(the angle of emission for particle 1 = θ/λ) = 1 = P(the angle of emission for particle 2 = − θ/λ), with P(λ) = .5. Or it may be a purely probabilistic cause: P(the angle of emission for particle 1 = θ/λ) = r = P(the angle of emission for particle 2 = − θ/λ); in which case, since 1/2 = P(θ .λ) + P(θ . − λ) = P(θ .λ), P(λ) = 1/(2r). If λ is totally deterministic in producing θ and − θ, the probabilities will factor: P(the angle of emission for particle 1 = θ and the angle of emission for particle 2 = − θ/λ) = 1 = P(the angle of emission for particle 1 = θ/λ) × P(the angle of emission for particle 2 = − θ/λ) = 1 × 1. But if the probabilities depart from 1 at all, factorizability will no longer obtain: P(the angle of emission for particle 1 = θ and the angle of emission for particle 2 = − θ/λ) = r ≠ P(the angle of emission for particle 1 = θ/λ) × P(the angle of emission for particle 2 = − θ/λ) = r2.
But in this case it is not reasonable to expect the probabilities to
end p.234
factor, conditional on the common cause. Momentum is to be conserved, so the cause produces its effects in pairs. This is just a special case of a cause which operates subject to constraints, a case familiar from section
3.3. In this example, whether one of the effects is produced or not has a bearing on whether the cause will produce the other effect. But factorizability is a criterion tailored to cases where the cause operates independently in producing each of its effects. Clearly it is not an appropriate condition for this example.
Before discussing the EPR experiment in more detail, it will be useful to translate the equations of Chapter
1, and the probabilistic criteria they give rise to, out of the language of random variables and into that of Boolean logic. This will provide immediate contact with the Bell literature, where it is customary to discuss the experiments using indicator functions; that is, functions which take the value 1 if the outcome in question—here, spin-up—occurs, and 0 if it does not. This demands modification in the shape of the equations, since no matter how many of the causes occur, the effect variable will never get larger than 1. One strategy to deal with this is to keep the random-variable format, but add terms to the equations. For illustration, the analogue to the three-variable equation of Chapter
1, for an effect
x
3whose causes are supposed to be
x
1and
x
2 , is
where
x
1 ,
x
2 ,
x
3 , and
u
3 , like â
31and â
32 , are allowed only the values 0 and 1.
The extension to more exogenous variables is straightforward. Alternatively, one can take the indicator functions to represent yes-no propositions, and use the notation of Boolean logic:
In that case the 'equation' will look just like those in Mackie's
inus account of causation discussed in section
1.3. The two strategies are equivalent. I shall use the second because it is notationally simpler.
Letting
x
1 ,
x
2 ,
x
3 , represent yes-no questions about events at
t
1<
t
2<
t
3which may be causally linked, the three-variable structure will look like this:
end p.235
The derivation of a common-cause condition proceeds in exact parallel with Chapter
1. The introduction of â, and
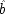
, and ĉ allows the structure to represent causes that work purely probabilistically: â represents the event of
x
1operating to produce
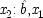
's operation to produce
x
3 ; and ĉ,
x
2 's operation to produce
x
3 . In keeping with this interpretation, it will be assumed that the operations of distinct causes are independent of each other and of everything that occurs previous to them. As in the random-variable structures, the
us may be necessary to ensure identifiability; but in general they are not, and can often be omitted.
So, dropping terms in the
us, it follows that
where

indicates 'zero' or logically false. This is true so long as
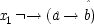
, i.e. so long as
x
2is indeed a cause of

, and sometimes
x
1produces
x
2without producing
x
3 . The condition says that
x
2plays no role in producing
x
3if and only if the joint occurrence of
x
2and
x
3is the same as the probability for
x
1to produce them jointly (plus, of course, any contributions from the omitted error terms).
To get from this general common-cause condition to factorizability, one sets
from which follows
Thus the factorizability condition does indeed depend on the assumption that the joint cause acts independently in producing its separate effects. This assumption does not fit the example above when the cause produces its outcomes in pairs. For that case the more general formula must be used. Clearly, one cannot just assume that factorizability is the right common-cause condition in EPR either.
6.4. Quantum Realism and the Factorizability Condition
There is a large literature discussing whether factorizability is an appropriate constraint to put on a hidden-variable theory for EPR,
end p.236
but before approaching that literature one needs to have a clear idea what purposes a hidden-variable theory is supposed to serve. Why want hidden variables? There are two distinct answers: to restore realism in quantum mechanics; and to restore causality. It turns out that factorizability is a very different condition in the two settings. This section will discuss the first answer.
Quantum systems notoriously are not supposed to have all the properties they should at any one time. Position and momentum are the classic examples; as already mentioned, spin components in different directions are also not simultaneously well defined. Quantum mechanics' failure to treat classic dynamic quantities, like position, momentum, energy, and angular momentum, as real all at once has been a major problem since the early days of the theory. It is well known that Einstein was deeply troubled by this aspect of quantum mechanics; his concern is reflected in the EPR paper. He thought that objects (at least macroscopic objects) do have all their dynamic properties at the same time. Quantum mechanics does not allow this; it is hence incomplete.
But is it true that realism of this kind is incompatible with quantum mechanics? J.S. Bell claims
4 that, until the time of his own work, Einstein might have been right. But the Bell inequalities, and their subsequent experimental tests, show that he was not. This claim of Bell's clearly relates the inequalities to the realism issue: the hidden variables are just the values that the spins really have, 'hidden' because they cannot all be measured at once.
In the context of quantum realism, factorizability is immediate:
Given the values for the spin, all the probabilities are one if the selected outcomes match the values; otherwise the joint probability is zero, and so too is at least one of the two marginal probabilities on the right. The rationale for the factorizability condition is thus entirely trivial. The same will not be true when the question is one of causality.
Even here, in the context of realism, there are problems with the condition, for the simple argument above about zero-one probabilities hides a number of non-trivial assumptions. One will do for illustration. The probabilities that matter in the Bell inequalities are probabilities for measurement outcomes. These are the probabilities
end p.237
that quantum mechanics predicts and that the various experiments can test. The argument for factorizability in the context of quantum realism assumes that, once all the normal corrections are made for experimental error, the measured values match the true values, and occur with the corresponding frequencies. This may not be the case. Of course, if the relation between the two is entirely unsystematic, the realism obtained would be vacuous. But Arthur Fine
5 has produced a number of models in which measured and possessed values do not match, and in which the assumption of such a match fails for specific reasons which are different in each model. In each case the factorizability condition is no longer appropriate. In a rigorous derivation of factorizability in the context of quantum realism, all the hidden assumptions, like those pointed out by Fine, would have to be laid out. But the point here is the converse: violations of the assumptions may provide reasons to reject factorizability; the reason to accept it as a requirement for quantum realism is just the trivial argument based on zero-one probabilities.
The second reason to look for hidden variables is to restore causality in quantum mechanics. Often the two reasons are not carefully distinguished. This is probably because, for many, an interest in causality is tantamount to an interest in determinism, and factorizability looks the same from a deterministic point of view as from a realistic one. Just partition the set of hidden states into classes:
x
1 (
x
L (θ),
x
R (θ′)) labels all the states that produce spin-up on the left in a measurement along θ and spin-up on the right along θ′;
x
1 (¬
x
L (θ),
x
R (θ′)) labels those that give spin-down on the left along θ and up on the right along θ′, and so forth. In that case, for the purposes of the Bell derivation the hidden states might as well represent the possessed spins themselves, for factorizability follows in exactly the same way:
6.5. A Common-Cause Model for EPR
When the hidden causes act stochastically, the situation is entirely changed. Where, then, does factorizability come from? It is usual,
end p.238
when applying a causal interpretation to the Bell results, to talk as if factorizability is a common-cause condition. But we have seen that this is not always appropriate. Different causal structures give rise to different common-cause conditions; the EPR set-up, it turns out, requires something other than factorizability. Indeed, the most primitive structure appropriate for EPR is similar to the one at the beginning of section
6.3. Conservation constraints apply. If there is a common cause in the source, it will not produce effects in the two wings independently. The operations for the two effects are correlated, and quantum mechanics tells us, essentially, what those correlations are.
Using the earlier example as a guide, it is easy to construct a simple common-cause model for EPR. A slightly more complicated model will be presented as well.
Common-Cause Model for EPR 1
- (1)
-

- (2)
-
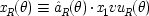
- (3)
-
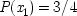
- (4)
-
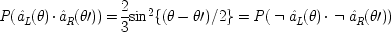
- (5)
-

The usual randomness assumptions on the
us makes them independent of each other and of
x
1and its operations, in all combinations:
- (6)
-
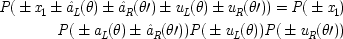
Equation (
6) might be viewed as a kind of locality constraint: the background production of 'up' outcomes in the left wing does not depend on the background in the right wing, and vice versa. It is not, however, the problematic assumption that usually goes by that name.
For symmetry, let
- (7)
-
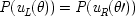
and assume
- (8)
-
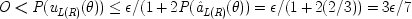
where ε is the amount of experimental error admitted. Obviously the model satisfies the appropriate common-cause condition.
end p.239
since the equations are constructed both to make
x
1a common cause of
x
Land
x
R , and to make these two causally irrelevant to each other. The omitted terms in the Common-Cause Condition 1 are all functions of
P(
u
L (θ)) and
P(
u
R (θ)); equation (
8) guarantees that the exact quantum prediction, which is on the right-hand side of (9), is within ε of the model prediction, on the left-hand side.
6
One important feature must be noted that distinguishes this quantum model from the more familiar models of the social sciences. In the usual construction of structural models, one begins with a field of propositions generated from elements like
x
1 ,
x
L (θ),
x
L (θ′),
x
L (θ″), . . . ,
x
R (θ),
x
R (θ′), . . . , and then prescribes a probability measure over this field. That is, one begins with a giant joint probability over the common cause and all its possible effects. But with EPR this will not be possible. A number of different proofs show that joint probabilities for incompatible outcomes like
x
L (θ) and
x
L (θ′) are not permitted in quantum mechanics. The most recent proof is due to Arthur Fine, and is of immediate relevance here. Fine has shown
7 that there is a function suitable to serve as a single joint distribution for all the observables of an EPR-type experiment if and only if there is a factorizable, stochastic hidden-variables model, and hence if and only if the Bell inequalities are satisfied. So a model compatible with quantum mechanics, like the common-cause models here, where factorizability fails, cannot be one where the probabilities sit in a common-probability space. Instead, the
end p.240
probabilities must be defined separately over each Boolean subfield generated by the external causes of the model plus their co-realizable effects. In model 1 this means {x
1 , x
L (θ), x
R (θ′), u
L (θ), u
R (θ′)} for any choice of θ and θ′. Similar care must be taken in defining the probability spaces for any model where the Bell inequality is violated; and the same applies in generalizing from yes-no propositions to random variables.
Model 1 is an especially simple structural model for EPR which includes a common cause. The simple model can be amended in a variety of ways to reflect a more complicated structure. It is now usual in the Bell literature to treat the influence of the measuring apparatuses explicitly, so it may serve as a useful illustration to construct a structural model that does this as well. Here I will just present the model. But in Appendix
I, I show how this model can be constructed, using the procedures of Chapter
1, from the natural assumptions that one wants to make about the relations in an EPR-type set-up—most notably that neither the state of the apparatus in one wing at the time of measurement, nor the outcome there, can affect the outcome of a simultaneous measurement in the distant wing.
The construction of Appendix I is entirely straightforward. Nevertheless, I want to lay it out explicitly in order to recall the advantages of using structural methods. It is usual in the Bell literature to present and defend factorizability in some intuitive fashion, often by use of commonsense examples. Even when the attempt is made to trace the condition to more basic assumptions (as in the work of Jon Jarrett or Linda Wessels, which is discussed in Appendix
II), the background assumptions about the causal structure of the EPR situation are still expressed directly as probabilistic conditions. Structural methods are more rigorous. All probabilistic conditions are derived from the structural equations, and the method provides a recipe for the exact expression of background causal information. The results of Chapter
1 then guarantee that the criteria derived provide a true representation of the hypothesized causal structure.
From Appendix
II, the enlarged model looks like this:
- (1′)
-
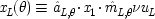
- (2′)
-
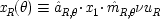
where

designates the set of left-wing apparatus states that are
end p.241
positively relevant to spin-up there; and similarly for
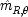
in the right wing. (Throughout, ŷ will designate the indicator function for
y, which takes value 1 when
y obtains, and 0 otherwise.) This structure is familiar from the discussion of Mackie in section
1.3:
x
1is a common partial cause of the outcomes in both the left wing and the right wing. The complete cause in a given wing also includes the state of the apparatus in that wing at the time of measurement. In this model there is no causal influence from one wing to the other, and that is apparent in the probabilities. The appropriate probabilistic condition to mark the absence of effects from
x
Lto
x
R , or the reverse, in a modified three-variable model of this sort can be readily derived:
The only new substantive assumption required in the derivation is that the operations of
x
1 , which occur at the source, are independent of the states the apparatuses take on somewhere else at a later time. This is a special case of the requirement from Chapter
3 that a causal theory should be 'local'. I return to this sense of locality below.
As already mentioned, a number of derivations of Bell-like results do take explicit account of the causal role of the measuring apparatuses. A necessary condition in these derivations is a requirement known as 'full factorizability':
It is apparent that full factorizability follows only if one adds to Model 2 the assumption that
P(â
L, θ · â
R, θ′ /
x
1 ) =
P(â
L, θ /
x
1 )
P(â
R, θ′ /
x
1 ), and that assumption, it has been seen, does not fit the EPR arrangement.
6.6. Quantum Mechanics and Its Causal Structure
The probabilities in equations (
4) and (
5) of the common-cause models for EPR should seem familiar; they are directly proportional to the quantum mechanical probabilities. Indeed, this particular model was chosen just to make that point. In fact, if
x
1is replaced by quantum mechanics' own description for the EPR systems at the end of the interaction, the singlet state (call it φ
EPR ),
end p.242
the quantum-mechanical predictions can be generated just by setting
P(φ
EPR ) = 1 and replacing the coefficient 2/3 by 1/2 wherever it appears. Assuming that
the predictions of the model and those of quantum mechanics will be the same, within the bounds of the experimental error ε. It seems that the quantum state itself can be a common-cause in EPR. Hidden variables are not needed to 'restore' a causal structure to quantum mechanics—the causal structure is there already.
It is important to be clear exactly what this means. Recall the two different motivations for introducing hidden variables: to restore realism, and to restore causality. Common-cause models like Nos. 1 and 2 have no bearing on the first issue. Rather, they are designed to answer the question, 'Is it possible, so far as EPR shows, to postulate a causal structure consistent with the probabilities that quantum mechanics sets out?' The answer is yes, and this means that quantum mechanics is a very special kind of probabilistic theory. From the point of view of the probabilities, what a causal structure does is to impose a complicated set of constraints: in a theory without causality, any set of consistent probabilistic laws is possible; with causality, the pattern of probabilities is drastically restricted. Contrary to what might have been assumed, quantum probabilities are restricted in just the right way. Simple common-cause models, such as those in the last section, show that the pattern of quantum probabilities in EPR is exactly the familiar pattern associated with a common-cause structure, and that it is indeed a structure of just the kind one wants: the quantum state consequent on the interaction operates, in conjunction with the separated apparatuses, as a joint cause of the results in each wing, with no direct causal connection between one wing and the other. So far as the probabilities go, the quantum mechanics of EPR is itself a perfectly acceptable causal theory. The conclusion that it is not acceptable comes from mistakenly taking factorizability as the way to identify a common-cause.
6.7. Factorizability and the Propagation of Causes
Probabilities are not all there is to causality. Hume put two different kinds of demand on a causal theory, and modern accounts usually
end p.243
agree: the cause and effect must not only be regularly associated; they must be contiguous in space and time as well. The statistical criteria discussed in Chapters
1 and
3 are the modern-day equivalent of Hume's demand for regular association. What about contiguity? It turns out that factorizability finds its proper role here. Though factorizability is not a universal criterion for common-causes, it is a necessary condition for causal propagation. But just on account of this, I shall argue, it is not an appropriate condition to apply in quantum mechanics.
The treatment of propagation that I shall follow is due to Wesley Salmon.
8 Salmon's is an instructive case because his recent book on causal processes falls naturally into two quite separate parts, matching Hume's two different demands. The first part deals with the requirement that causes and effects be regularly associated; it lays down a number of statistical measures like those described in Chapters
1 and
3. The second part deals with causal processes, and treats the question of how a causal influence propagates. It assumes that a cause never operates across a space-time gap, but instead must travel from the cause to the effect along some continuous path. The two conditions are quite distinct, though they are not always clearly separated, even in Salmon's work.
Salmon calls his theory 'the "At-At" theory' because it assumes that the influence propagates from the initial cause to its effect simply by being at every point on a continuous trajectory in between. One important sign of propagation for Salmon is that the sequence of events connecting the cause with the effect be capable of conveying some kind of signal, or 'mark': it should be possible to insert a mark into the process at its origin and to observe the same mark—or some appropriately evolved version of it—at the effect. But the mark itself is just a symptom. What is crucial is that the capacity to produce the effect, or some feature that carries this capacity, should propagate on a path from the cause across the space-time gap. Salmon's account is metaphysically extremely simple, yet it is rich enough to show the connection between factorizability and propagation, so it will be used here.
For the case of quantum mechanics, it seems reasonable to assume that the influence must propagate with the system; that is, that the capacity-carrying feature can occur only in regions and at times
end p.244
where the probability for the system to appear is non-negligible. The basic idea involved in the requirement of spatio-temporal contiguity can then be formulated quite simply. The notation introduced so far is not well suited to dealing with continuous quantities and their intervals. Rather than introducing a more cumbersome notation, I will instead make use of the convenient fiction that time is discrete, and that contiguity requires that a cause operating at t produce its effect at the very next instant, t + Δ t, and at the same place. In that case, following the lead of the at-at theory, Hume's second demand requires that a condition which I shall call 'propagation' be satisfied.
Propagation
|
x
cat
 causes (or is a partial cause of) x
eat
 only if either
|
(a) |
there is a c such that x
cat
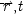 causes (or is a partial cause of) c at
 and c at r′, t′ − Δ t causes (or is a partial cause of) x
eat
 and c (or an appropriately time-evolved version of c) exists at every point on some continuous trajectory between
 and
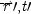 , where no region along the trajectory is quantum mechanically prohibited, or
|
(b) |
there is a chain of features beginning with x
cat
 and ending with x
eat
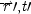 , where each causes (or is a partial cause of) the next later one and conditions like those in ( a) are satisfied in between.
|
One further assumption is needed to derive factorizability in the EPR situation, and it is an assumption that does not follow directly from the demand for contiguity of cause and effect. This is an assumption about how causes operate: distant causes cannot act in coincidence; once two causes are separated, their operations must be independent of each other. This is a special kind of locality condition, which can be formulated simply enough for the purposes at hand.
Locality of Operation
Let â
1represent the operation of
c
1at
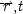
to produce an effect
e
1 , and â
2the operation of
c
2at
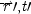
to produce
e
2 . Then
P(â
1 · â
2 ) =
P(â
1 )
P(â
2 ) unless
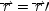
and
t =
t′.
The motivation for this kind of condition must be something like Reichenbach's Principle, which motivates the search for causal structure in EPR in the first place: there are no distant correlations without causal explanations. In EPR, as in the classical example in
end p.245
section
6.3, the causes act subject to the constraint that energy be conserved. But conservation of energy is not a kind of force or cause itself. As Linda Wessels argues,
Certainly there are conservation laws in classical theory that restrict the relations among properties of distant bodies. Conservation of energy and momentum are obvious examples. But the total energy of two spatially separated bodies (in the absence of any other influence) is conserved either because the bodies exert forces on one another or, if no mutual interaction is present, because the energy of each body is conserved separately. Conservation of energy does not put any constraints on the total energy of the two that is not already required by the laws governing the evolution and interaction of the bodies individually and pairwise respectively.
9 Hence there is the requirement for locality of operation.
Combining the requirements for propagation and locality of operation with those already assumed generates a variety of models for the EPR set-up. The simplest is one in which the capacity to produce spin-up propagates directly from the joint cause,
x
1 , to each wing of the experiment with no interactions along the way. The lessons for factorizability are the same whether the simplest model is assumed or a more complicated one. As before, the model is built with the assumption that the state and setting of the apparatus (
m
L (θ) or
m
R (θ′)) in one wing is not a cause of the outcome in the other; and also, in keeping with the requirement for spatio-temporal contiguity of cause and effect, with the assumption that the capacity propagated to one wing (
c
L (θ) or
c
R (θ′)) has no effect on the outcome in the other. The equations for the most simple common-cause model with propagation are then:
- (1)
-

- (2)
-

- (3)
-
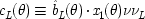
- (4)
-

where
c
Ris supposed to be produced at the time and place of emission and to appear at every point on some continuous trajectory to the right wing; and similarly for
c
L , to the left wing. Operation locality requires
- (5)
-
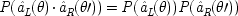
end p.246
Coupling (
5) with the normal randomness assumptions that the backgrounds, represented by
u
L(R) , ν
L(R) , are independent of each other and of the operation of the causes in all combinations, it is easy to derive that
This is exactly the requirement for full factorizability necessary for the Bell inequality and for other similar no-hidden-variable proofs. It follows immediately that any common-cause model with propagation and locality of operation will contradict quantum mechanics.
It is apparent from this discussion that factorizability is a consequence of conditioning on the hidden states c
L (θ) and c
R (θ′); but it is the propagation requirement that guarantees the existence of these states. Is propagation, then, a reasonable demand to put on a causal theory in quantum mechanics? Clearly one should be wary, since the difficulties of providing continuous space-time descriptions are arguably the oldest and most worrying in quantum mechanics. The two-slit experiment is the familiar philosopher's illustration of these difficulties, and it will serve here. If propagation is assumed, exactly the wrong predictions are made in the two-slit experiment.
In this experiment, a beam of particles emitted from a source passes through a wall, which contains two separated slits, and finally falls onto a recording screen which registers positions. Two different kinds of pattern are observed on the recording screen. With only one or the other of the two slits open, the particles tend to bunch around a point on the screen directly in line with the slit. But when both slits are open, something very different occurs—the interference pattern. This is exactly the kind of pattern that one would expect if the beam had been composed, not of particles, each of which must pass through one slit or the other, but rather of a wave, whose successive fronts pass through both slits at once. This suggests the conclusion that the particles do not have well-defined trajectories which pass through either slit exclusively.
What is important for the argument is that there are regions on the recording screen where the probability for a particle to register is high with either one slit or the other open, but is practically zero with both. That will be impossible in a causal structure that satisfies local
end p.247
operation and propagation. I will use the simplest model to highlight the essentials of the argument. Nevertheless, I put the discussion in an appendix (Appendix
II) because the details are of no special interest. The derivation in Appendix II is similar to the usual derivation that shows that the particles must be treated as waves at the slits. It differs in two respects: first, the quantum particles themselves are allowed to spread out like waves. It is only the causal influence that must follow a trajectory. Second, even when there is only one particle in the system at a time, the model allows that more than one chain of influences may be created in the source, and the trajectories of different influences may pass simultaneously through both slits.
The argument in Appendix
II shows that there can be no interference pattern on the screen if the propagation condition is satisfied. Any point on the screen must register at least as many counts with both slits open as with one. The model on which its conclusion is based is supplied with only the most primitive causal structure. Just two substantive causal claims are involved: first, that the production of particles at the source is partially responsible for their appearance at the screen; second, that the opening or closing of a distant slit has no causal influence on what happens simultaneously at the other slit. But even this primitive causal structure must be rejected if propagation is required.
6.8. Conclusion
Grant, for the sake of argument, that the realism issue has been settled by the Bell derivation: the separated systems do not have well-defined spins when they reach the measuring apparatuses. What causes the correlated outcomes, then? The natural answer would be, 'A common-cause in the source'. This chapter has argued that there is nothing wrong with this straightforward account. It is not even necessary to look for a hidden variable: the quantum state itself will serve as the joint cause. It is sometimes reported that the Bell derivation shows that the quantum probabilities are incompatible with any causal structure for the EPR set-up. But the models of section
6.5 show that this is a mistake. The probabilities are entirely consistent with a common-cause model appropriate to the situation.
Yet the models do have a peculiar feature. Although they get the
end p.248
probabilities right, they do not permit propagation between the cause and its effects. The common-cause, which exists in the combined systems at the time of interaction, must operate across a temporal gap. This is especially noticeable in experiments like those of A. Aspect, J. Dalibard, and G. Roger,
10 where the orientation of the measuring apparatus is not even set at the time the systems leave the source. In this case the common-cause is only a partial cause; it must combine with features that later obtain in the measuring devices to produce the measurement outcomes. But if the common-cause is to work in this way, it must operate at the time the particles leave the source, say
t
0 , to produce an effect at some later time,
t′, and with nothing to carry the causal influence between the two during the period in between. This is indeed a peculiar kind of causality, and probably most of us will find it just as objectionable as we would find a direct influence from one wing to the other. What distinguishes the two accounts?
Throughout this chapter, as throughout the book, my emphasis has been on the probabilities that follow from various specific structures. A crucial feature is built into all the structures: causes must precede their effects. It is for just this reason that outcomes in the two wings of the EPR experiment are not supposed to be able to influence one another directly. The relevant happenings in the separated wings are meant to occur simultaneously with each other; and much experimental effort must go into making that as true as possible. Of course, simultaneity is a relative concept. The proper past is past in any frame of reference, and it is in this sense that causes are meant to precede their effects. Sometimes one says that events in the proper past are events which are light-ray connectable; and this may somehow suggest that causes must be connected with their effects by something like a propagating light-ray. But this kind of propagation is well known not to work in quantum mechanics. It is true that the lessons of the two-slit experiment for quantum realism have not been altogether clear, and there have been a variety of proposals to save particle trajectories. But, in general, even theories which do provide the particles with a continuous path from the source to the recording screen do not propagate the causal influence along a trajectory as well. David Bohm's early hidden-variable models and the traditional pilot wave theory are good
end p.249
examples. In both cases the quantum state is a principal influence in determining where the particles will be, and the quantum state does not propagate along a trajectory. Whether or not the two-slit experiment refutes realism, it seems to rule out causal propagation, and that is the point of the simple model in Appendix
II.
What, then, of the bearing of the Bell inequalities on causality? It seems there are two attitudes one can take. EPR admits a familiar causal structure with proper time-order. It does not admit propagation of influence from cause to effect. Given the familiar lessons of the two-slit experiment, one may think that propagation is a crazy demand to put on a causal structure in quantum mechanics. In that case, the recent work of Bell will be irrelevant to questions of causality in quantum mechanics. Or one may wish for something firmer than the two-slit argument against propagation. The Bell inequalities provide that. But in any case it should be remembered that the connection between propagation and the inequalities is through factorizability; and although factorizability is a consequence of propagation in its most simple and natural form, more recondite assumptions may admit propagation without factorizability, just as the more elaborate models of Arthur Fine admit realism without factorizability. What follows most certainly from the arguments here is that, whatever the case with propagation, factorizability must not enter the argument as a common-cause condition.
end p.250
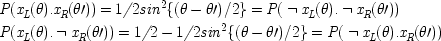
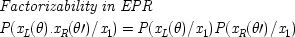
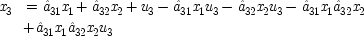
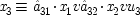
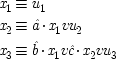
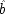 , and ĉ allows the structure to represent causes that work purely probabilistically: â represents the event of x
1operating to produce
, and ĉ allows the structure to represent causes that work purely probabilistically: â represents the event of x
1operating to produce
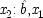 's operation to produce x
3 ; and ĉ, x
2 's operation to produce x
3 . In keeping with this interpretation, it will be assumed that the operations of distinct causes are independent of each other and of everything that occurs previous to them. As in the random-variable structures, the us may be necessary to ensure identifiability; but in general they are not, and can often be omitted.
's operation to produce x
3 ; and ĉ, x
2 's operation to produce x
3 . In keeping with this interpretation, it will be assumed that the operations of distinct causes are independent of each other and of everything that occurs previous to them. As in the random-variable structures, the us may be necessary to ensure identifiability; but in general they are not, and can often be omitted.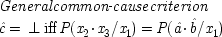
 indicates 'zero' or logically false. This is true so long as
indicates 'zero' or logically false. This is true so long as
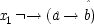 , i.e. so long as x
2is indeed a cause of
, i.e. so long as x
2is indeed a cause of
 , and sometimes x
1produces x
2without producing x
3 . The condition says that x
2plays no role in producing x
3if and only if the joint occurrence of x
2and x
3is the same as the probability for x
1to produce them jointly (plus, of course, any contributions from the omitted error terms).
, and sometimes x
1produces x
2without producing x
3 . The condition says that x
2plays no role in producing x
3if and only if the joint occurrence of x
2and x
3is the same as the probability for x
1to produce them jointly (plus, of course, any contributions from the omitted error terms).

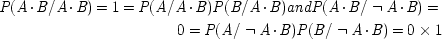
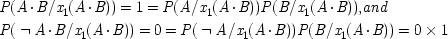

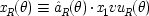
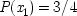
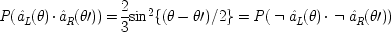

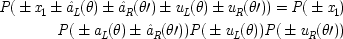
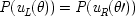
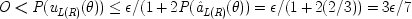

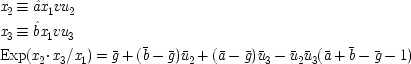
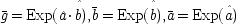 , and ūi = Exp(ui). Hence when ū2 = ū3 = ū and
, and ūi = Exp(ui). Hence when ū2 = ū3 = ū and  , as in EPR model No. 1,
, as in EPR model No. 1, 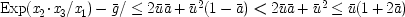 . Alternatively, the random backgrounds could be dropped throughout. The only case where this raises problems of identification is when θ′ = θ. In that case the quantum mechanical correlation between x2 and x3 is perfect; hence
. Alternatively, the random backgrounds could be dropped throughout. The only case where this raises problems of identification is when θ′ = θ. In that case the quantum mechanical correlation between x2 and x3 is perfect; hence 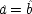 , so that ĉ =
, so that ĉ =  can no longer be identified or determined from the probabilities. (Recall the remark immediately following the general common-cause criterion in section
can no longer be identified or determined from the probabilities. (Recall the remark immediately following the general common-cause criterion in section 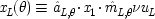
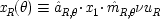
 designates the set of left-wing apparatus states that are
designates the set of left-wing apparatus states that are  in the right wing. (Throughout, ŷ will designate the indicator function for y, which takes value 1 when y obtains, and 0 otherwise.) This structure is familiar from the discussion of Mackie in section
in the right wing. (Throughout, ŷ will designate the indicator function for y, which takes value 1 when y obtains, and 0 otherwise.) This structure is familiar from the discussion of Mackie in section 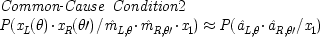
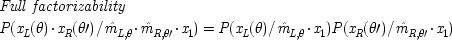
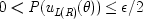
 causes (or is a partial cause of) x
eat
causes (or is a partial cause of) x
eat
 only if either
only if either
 causes (or is a partial cause of) c at
causes (or is a partial cause of) c at
 and c at r′, t′ − Δ t causes (or is a partial cause of) x
eat
and c at r′, t′ − Δ t causes (or is a partial cause of) x
eat
 and c (or an appropriately time-evolved version of c) exists at every point on some continuous trajectory between
and c (or an appropriately time-evolved version of c) exists at every point on some continuous trajectory between
 and
and
 , where no region along the trajectory is quantum mechanically prohibited, or
, where no region along the trajectory is quantum mechanically prohibited, or
 and ending with x
eat
and ending with x
eat
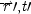 , where each causes (or is a partial cause of) the next later one and conditions like those in (a) are satisfied in between.
, where each causes (or is a partial cause of) the next later one and conditions like those in (a) are satisfied in between.
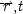 to produce an effect e
1 , and â
2the operation of c
2at
to produce an effect e
1 , and â
2the operation of c
2at
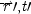 to produce e
2 . Then P(â
1 · â
2 ) = P(â
1 )P(â
2 ) unless
to produce e
2 . Then P(â
1 · â
2 ) = P(â
1 )P(â
2 ) unless
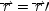 and t = t′.
and t = t′.