3 Singular Causes First
Abstract: 'Singular Causes First' rejects Hume's thesis that singular causal facts are reducible to generic ones, adopting a reverse position, taking singular causes as basic. Using idealized examples, Cartwright shows that strategies to establish causal claims without using singular causal facts as inputs all fail, including probabilistic theories of causality. Not only is singular causal input necessary if probabilities are to imply causal connections, the resulting causal output is also at base singular.
Nancy Cartwright
3.1. Introduction
How close can we come to a Humean account of causation? My answer is, not very close at all. For Hume's picture is exactly upside down. Hume began in the right place—with singular causes. But he imagined that he could not see these in his experience of the world around him. He looked for something besides contiguity to connect the cause with the effect, and when he failed to find it, he left singular causes behind and moved to the generic level. This move constitutes the first thesis of the Hume programme: the only thing singular about a singular causal fact is the space-time relationship between the cause and its subsequent effect. Beyond that, the generic fact is all there is. But the programme was far bolder than that, for at the generic level causation is to disappear altogether. It is to be replaced by mere regularity. That is the second thesis of the Hume programme: generic causal claims are true merely by virtue of regular associations.
Chapter
2 argued against the second of these theses: a regularity account of any particular generic causal truth—such as 'Aspirins relieve headaches'—must refer to other generic causal claims if the right regularities are to be picked out. Hence no reduction of generic causation to regularities is possible. This chapter will argue against the first thesis: to pick out the right regularities at the generic level requires not only other generic causal facts but singular facts as well. So singular causal facts are not reducible to generic ones. There is at best an inevitable mixing of the two levels.
I begin with a familiar puzzle. From Francis Bacon with his golden events onwards, philosophers and scientists alike have acclaimed the single instance. The classical probabilists like Bernoulli, Laplace, and Poisson are a striking case, for they are the theorists who developed the mathematical theory of association; already by the end of the eighteenth century their thinking had passed beyond Hume.
end p.91
Although Hume was much indebted to the early classical probabilists for his account of probability, they were always wary of the value of associations as an aid to finding causes in science, and certainly none of them ever believed that associations constituted causation. In the best case, we need no recourse to associations (or probabilities) at all. Buffon cited the familiar example of the interlocking gears and weights of a clock, where the causes are manifest. Laplace worried that associations born of convention would create illusory subjective probabilities about causes. Poisson was willing to revamp the mathematical theory of induction to bring it into line with the actual practice of first-rate scientists. It does not take a lifetime of associations to convince a reasonable person of electromagnetic induction; Oersted's single experiment was quite sufficient.
1 Poisson's point remains true in modern physics. The bulk of experiments that support the gigantic edifice of twentieth-century physics are never repeated, and they involve no statistics.
2The trick of the outstanding experimenter is to set the arrangements just right so that the observed outcome means just what it is intended to mean; and that takes repeated efforts, usually over months and sometimes over years. But once the genuine effect is achieved, that is enough. The physicist need not go on running the experiment again and again to lay bare a regularity before our eyes. A single case, if it is the right case, will do.
This point is a familiar one. Nevertheless, it is worth looking at an example to make vivid the experience of working scientific investigation, against the abstract background of the metaphysical and epistemological props that support Hume's position. I choose as an example a series of experiments by Einstein and W. J. de Haas, experiments that led to the wrong conclusion but where, quite clearly, repeatability was not the issue. Einstein and de Haas went wrong, not because they tried to establish a general truth from what they saw in the single case, but rather because they mis-identified what they actually saw.
In 1914 Einstein and de Haas set out to test the hypothesis that magnetism is caused by orbiting electrons. They tested it by suspending
end p.92
an iron bar in an oscillating magnetic field and measuring the gyrations induced when the bar was magnetized. They expected the bar to oscillate when the field was turned on and off because electrons have mass, and when they start to rotate they will produce an angular momentum. The ratio of this momentum to the magnetic moment—called the gyromagnetic ratio—should be 2m/e, where m and e are the mass and charge of the electron respectively. This is very close to the answer Einstein and de Haas found. But it is not the result they should have got. Later experiments finally settled on a gyromagnetic ratio about half that size, and nowadays—following the Dirac theory—the results are attributed, not to the orbiting electrons, but to a complex interaction of orbit and spin-orbit effects.
What went wrong with the Einstein-de Haas experiment? The answer is—a large number of things. I take this example from a paper by Peter Galison;
3the reader can see the complete details laid out there. Galison describes the work of ten different experimental groups producing dozens of different experimental constructions over a period of ten years to establish finally that the Einstein-de Haas hypothesis was mistaken. I will briefly discuss just one of the factors Galison describes.
Besides the effects of the hypothesized electron motion, it was clear that the magnetic field of the earth itself can also cause a rotation in the bar, so there had to be a shield against this field. 'At first [Einstein and de Haas] used hoops with a radius of one meter with coils wound around them to eliminate the earth's field.'
4In the next set of experiments de Haas wrapped the wire of the solenoid as well. He also arranged a compensating magnet near the centre of the bar, and two near the poles, as well as a neutralizing coil at right angles to the bar. In 1915 Samuel Barnett from Ohio State University performed similar experiments with a great number of improvements. In particular, he neutralized the earth's field with several large coils. As Galison reports, 'the outcome after his exhaustive preparations was a value [of the gyromagnetic ratio] less than half of that expected for orbiting electrons.'
5The story goes on, but this is
end p.93
enough to give a sense of the detail of thought and workmanship necessary to get the experiment right. The point is that we sometimes do get it right, and when we do, we can see the individual process that we are looking for, just as we see the process in Buffon's clock; and that is enough to tell whether the causal law is true or not.
The puzzle I raise about the lack of fit between the practical reliance on the single case versus the philosophical insistence on the primacy of the regularity is in no way new. Yet familiarity should not make us content with it; Hume's own view that we can lay our philosophy aside when we leave the study and enter the laboratory is ultimately unsatisfactory. In fact, he fatally failed to distinguish the laboratory from the rest of the world outside the study. Both the philosopher on one side and the experimentalist on the other must be concerned when epistemology and methodology diverge.
I realize that there are a number of ways in which the Humean can try to account for the schism between philosophy and practice. Admittedly, one-shot experiments, like those of Oersted, Einstein and de Haas, or Barnett, work in disciplines like physics where there is a gigantic amount of background information, precise enough to guarantee that the experiment isolates just the one sequence of events in question. The logic of these experiments involves a complex network of deductions from premisses antecedently accepted, and a good number of these premisses are already causal. Perhaps it is not surprising from the Humean point of view that singular confirmation is possible once one is operating within such a large set of assumptions.
But it must be surprising that no causal conclusions are possible outside such assumptions. Without antecedent information it is no more possible to establish a causal claim via a regularity than it is to demonstrate a singular cause directly; and in both cases the inputs must include causal information—not only information about general causal laws, but about singular facts as well. This is the argument on which I will concentrate in this chapter, because it attacks the regularity view directly. Arbitrary regularities do not amount to causal connections. Which regularities do? My basic claim is that figuring that out is a laborious job that must be undertaken anew in each new case, as the kinds of known causal structure in the background differ. In this chapter I will consider a few simple and idealized examples just to show that, in any case, information about singular causes is vital.
end p.94
The chapter ends with a more radical doctrine. Singular claims are not just input for inferring causal laws; they are the output as well. At the beginning of the introduction I said that the chapter would show how the generic and the singular are inextricably intertwined. But the ultimate conclusion is far stronger. Singular facts are not reducible to generic ones, but exactly the opposite: singular causal facts are basic. A generic claim, such as 'Aspirins relieve headaches', is best seen as a modalized singular claim: 'An aspirin can relieve a headache'; and the surest sign that an aspirin can do so is that sometimes one does do so. Hence my claim that Hume had it just upside down.
3.2. Where Singular Causes Enter
If the last chapter is correct, probabilities by themselves can say nothing about the truth of a general causal hypothesis. A good deal of information about other causal laws is needed as well. But that does not exhaust the information required: not only must other general causal claims be supposed, but information about singular causal facts must be assumed as well. To see why, return to formula
CC of Chapter
2. Formula
CC says that, for a generic causal claim to hold, the putative cause
C must increase the probability of the effect
E in every population that is homogeneous with respect to
E's other causes. But this condition is too strong, for it holds fixed too much. The other factors relevant to
E should be held fixed only in individuals for whom they are not caused by
C itself. The simplest examples have the structure of Fig.
3.1.
This is a case of a genuine cause
C, which always operates through some intermediate cause,
F. But
F can also occur on its own, and if it does so, it is still positively relevant for
E. Holding
F fixed leads to the mistaken conclusion that
C does not cause
E. For
end p.95
P(E/C ± F) = P(¬ C ± F). This is a familiar point: intermediate causes in a process (here F) screen off the initial cause (C) from the final outcome (E). If intermediates are held fixed, causes will not be identified as genuine even when they are. On the other hand, if factors like F are not held fixed when they occur for independent reasons, the opposite problem arises, and mere correlates may get counted as causes.
What is needed is a more complex characterization of the precise way in which a population must be homogeneous.
CC must be amended to ensure that
* Each test population of individuals for the law 'C causes E' must be homogeneous with respect to some complete set of E's causes (other than C). However, some individuals may have been causally influenced and altered by C itself; just these individuals should be reassigned to populations according to the value they would have had in the absence of C's influence.
This means that what counts as the right populations in which to test causal laws by probabilities will depend not only on what other causal laws are true, but on what singular causal processes obtain as well. One must know, in each individual where
F occurs, whether its occurrence was produced by
C, or whether it came about in some other way. Otherwise the probabilities do not say anything, one way or the other, about the hypothesis in question.
A very simple and concrete example with the problematic structure pictured above has been given by Ellery Eells and Elliot Sober.
6I expand it somewhat to illustrate how both holding
F fixed and failing to hold it fixed can equally lead to trouble. Your dialling me (
C), they suppose, causes my phone to ring (
F), and my phone's ringing causes me to lift the receiver (
E). 'So presumably your phoning me thus causes me to lift the receiver.'
7But this claim will not be supported by the probabilities if the ringing is held fixed, since
P(
E/
C ±
F) =
P(
E / ¬
C ±
F); that is, once it is given that the phone rings, additional information about how it came to ring will make no difference. To require the contrary 'would mean that your calling me at
t 1must have a way of affecting the probability of my picking up the phone at
t 3other than simply by producing the ringing
end p.96
at
t 2'.
8Holding fixed
F in this case would give a misleading causal picture.
On the other hand, not holding F fixed can be equally misleading, for reasons which are by now familiar. Imagine that you phone me in California every Monday from the east coast as soon as the phone rates go down. But on each Monday afternoon another friend, just a little closer, does the same at the same time, and you never succeed in getting through. In this case it is not your phoning that causes me to lift the receiver; though that may look to be the case from the probabilities, since now P(E / C) > P(E / ¬ C). But the causes and the probabilities do line up properly when F is held fixed in the way recommended by Principle*. Consider first the ¬ F population. This population should include all the Monday afternoons on which my phone would not otherwise ring. On these afternoons your dialling does cause me to lift the receiver, and that is reflected in the fact that (given ¬ F) P(E / C) > P(E / ¬ C) in this population. In the second population, of afternoons when my phone rings but because my other friend has called, your dialling does not cause me to lift the receiver, nor is that indicated by the probabilities, since here (given F) P(E / C) = P(E / ¬ C).
There are a number of ways in which one might try to avoid the intrusion of singular causes into a methodology aimed at establishing causal laws. I will discuss four promising attempts, to show why they do not succeed in eliminating the need for singular causes. The first tries to side-step the problem by looking at nothing that occurs after the cause; the second considers only probabilities collected in randomized experiments; the third holds fixed some node on each path that connects the cause and the effect; and the fourth works by chopping time into discrete chunks. The first two suffer from a common defect: in the end they are capable of determining only the 'net upshot' of the operation of a cause across a population, and will not pick out the separate laws by which the cause produces this result; the third falters when causes act under constraints; and the fourth fails because time, at least at the order of magnitude relevant in these problems, does not come already divided into chunks. The division must be imposed by the model, and how small a division is appropriate will depend on what singular processes actually occur. I will begin by discussing strategies (i) and (ii) in this section, then
end p.97
interrupt the analysis to develop some formalism in section
3.3. I return to strategies (iii) and (iv) in sections
3.4.1 and
3.4.2.
3.2.1. Strategy (i)
The first strategy is immediately suggested by the telephone example; and indeed it is a strategy endorsed by the authors of that example. Principle *, applied in this example, describes two rather complicated populations: in the first, every Monday afternoon which is included must be one in which my phone rings, but the cause of the ringing is something different from your dialling. By hypothesis, the only way your dialling can cause me to lift the receiver will be by causing my phone to ring. So in this population it never happens that your dialling causes me to lift the receiver; and that is reflected in the probabilities, since in this first population P(E / C) = P(E / ¬ C). But matters are different in the second population. That population includes the Monday afternoons on which my phone does not ring at all, and also those ones on which it does ring, but the ringing is caused by your dialling. In this population, your dialling does cause me to lift the receiver; and, moreover, that is also the conclusion dictated by the probabilities, since in the second population P(E / C) > P(E / ¬ C).
But in this case there is an altogether simpler way to get the same results. The ringing never needs to come into consideration; just hold fixed the dialling of the second friend. When the other friend does dial, since by hypothesis she gets connected first, your dialling plays no causal role in my answering the phone; nor does it increase the probability. When she does not dial, you do cause me to lift the phone, and that is reflected in an increase in the probability of my doing so. This is just the strategy that Eells and Sober propose to follow in general. Their rule for testing the law '
C causes
E' is to hold fixed all factors prior to or simultaneous with
C which either themselves directly cause (or prevent)
E, or which can initiate a chain of factors which can cause (or prevent)
E. Their picture looks like Fig.
3.2.
9It is not necessary to hold fixed causes of
E that occur after
C, argue Eells and Sober; holding fixed all the
causes of these causes will succeed in 'paying them their due'.
10end p.98
This is true in simple cases where causes operate in only one way to produce or prevent the effect. But often a factor has mixed capacities—it can both cause and prevent the same effect, or cause it in different ways with influences of different strengths. An example common in the philosophical literature comes from G. Hesslow.
11Hesslow argues that birth-control pills both inhibit and encourage thrombosis. Let
C represent the contraceptives;
T, thrombosis. He advocates then that not one but two causal laws are true: '
C causes
T' and '
C prevents
T'. The pills prevent thrombosis by preventing pregnancy (
P), which itself tends to produce thrombosis. On the other hand, they themselves frequently cause thrombosis. Hesslow does not specify any intermediate steps in the positive process, but one can imagine that the pills produce a certain chemical,
C′, that causes the blood to clot and thereby produces thrombosis. Hesslow's hypotheses are represented in Fig.
3.3. Fig.
3.3 follows the usual conventions and identities '
A prevents
B' with '
A causes ¬
B'.
For simplicity, imagine that pregnancy and the chemical C′ are the only factors relevant at t 2for producing or inhibiting thrombosis at t 3. It will help to keep the structure as simple as possible by
end p.99
assuming that the only way a factor at t 1bears on thrombosis at t 3is either via pregnancy or via C′; and also to treat all those factors that are relevant at t 1, other than the contraceptives themselves, together as a single general background which will be labelled B. In this case the Eells-Sober strategy for judging the effects of pills on thrombosis is to hold fixed B; and this is a sensible strategy from the point of view of the problems raised so far. For the familiar problems of joint effects, and of other related kinds of 'spurious correlations', arise when there are background correlations for some reason or another between the putative cause and other causal factors. In this case, by construction there are only two independent factors with which C might be correlated—C′ and P. But if all other causes of C′ and P are held fixed, there is no way for the contraceptives to be correlated with these, other than by their own causal actions. This is what Eells and Sober mean by 'paying them their due'.
Unfortunately, background correlations are not the only source of problems. The dual capacity of the contraceptives also makes trouble. Because the contraceptives can act in two different, opposed ways, their probabilistic behaviour will be different in different circumstances: in one kind of circumstance they push the probabilities up; in another they push them down. If these different circumstances are not kept distinct; but instead are lumped together, these opposing probabilistic tendencies can get averaged out, so that at best one, but possibly neither, of the opposing capacities will be revealed. This is easy to see in the four kinds of causally homogeneous populations produced by B: (1) C′ P, (2) C′ ¬ P, (3) ¬ C′ P, and (4) ¬ C′ ¬ P. The first population is one in which every woman is both pregnant and has the chemical C′ in her blood; in the second, no one is pregnant, but all have the chemical; and so forth. In the absence of C, it can be supposed that B produces these four populations in some fixed ratio, and the resulting level of thrombosis in the total group will be an average, with fixed weights, over its level in each of the four homogeneous populations taken separately.
What happens if
B does not act on its own, but
C occurs as well at
t 1? If the contraceptives do indeed affect both pregnancy and the amount of chemical in the blood, the ratios among these four populations will change.
12The second group, of women who have
C′ at
t 2and are not pregnant then, will stay at least as big as it was;
end p.100
since the contraceptives cause C′ and prevent pregnancy, they will not change the situation of anyone who would otherwise have had C′, or who would not have been pregnant in any case. Indeed, this group will grow larger; for it will receive additions from all the other groups. In the first group, the contraceptives will have no effect on the rate of C′, but they will prevent some pregnancies which would otherwise have occurred. Thus, some women who would have been in Group 1 under the action of B alone will move into Group 2 when C acts as well. Similar shifting occurs among the other groups. The group that has both effects already must necessarily grow bigger; and the group with neither effect will in the end be smaller; what happens in the other two depends on whether the tendency of the contraceptives to induce C′ is stronger or weaker than its tendency to inhibit pregnancy.
The net result for thrombosis of all these changes is unpredictable without the numbers. It depends not only on how effective C is, versus B, in producing the harmful chemical and preventing pregnancy, but also on how effective the chemical and pregnancy themselves are in producing thrombosis. Anything can happen to the overall probability. If the processes that operate through the prevention of pregnancy dominate, the number of cases of thrombosis will go down when contraceptives are taken; conversely, if the processes operating through the chemical dominate, the number will go up; and in cases where the two processes offset each other, the number will stay the same. But this does not in any way indicate that contraceptives have no power to cause or to prevent thrombosis, any more than the dominance of their good effects would show that they had no negative influence, or vice versa. No matter how the relative frequencies work out, the pills are both to be praised and blamed. In any case, they will have caused a number of women to get thrombosis who would otherwise have been healthy; and this fact is in no way diminished by the equally evident fact that they also prevent thrombosis in a number of women who would otherwise have suffered it. It is true that in either case the effect is achieved through some intermediary. The pills cause thrombosis by causing C′ where it would not otherwise occur; similarly, they prevent thrombosis by preventing pregnancies that would have occurred. But that is hardly an argument against their power. Since, at least at the macroscopic level, causal processes seem to be continuous, all causes achieve their effects only through intermediaries.
end p.101
The lesson to be learned from this case is that the strategy urged by Eells and Sober to avoid the mention of singular causes will not work when causes have mixed capacities. But will Principle *, which does rely on information about the single case, fare better? It should be apparent that the answer is yes. For this proposal involving singular causes retraces the argument that was just made. It says: to uncover the connection between contraceptives and thrombosis, assign individuals to groups on the basis of whether they would have C′ and P if C did not operate. Then consider, in each of these groups separately, how frequent thrombosis is among women who take contraceptives versus its frequency among women who do not. What the earlier argument showed is that both the positive capacity and the negative capacity of the contraceptives are bound to come out in this procedure, since in Group 4 the incidence of thrombosis will surely go up and in Group 1 it will surely go down.
This is, moreover, exactly the strategy that anyone would advocate, including Eells and Sober themselves, were it not for the awkward question of timing. Imagine, for instance, a slightly altered example in which
B operates exactly as before in producing
C′ and
P, but in which it operates a little earlier than
C, so that
C′ and
P are already in place before the pills are taken.
13In this case the need for the inconvenient singular counterfactual completely disappears. The action of the contraceptives moves women, not from groups they would have been in, but from groups they are in. By stopping pregnancies that would otherwise occur under the action of
B alone, they prevent thrombosis; and by producing the chemical
C when it did not exist before, they cause thrombosis. The results are apparent in the frequency of thrombosis in Group 1 (
C′
P) where the probability will be less with
C than without; and in Group 4 (¬
C′ ¬
P), where the converse holds. In Group 2 (
C′ ¬
P),
C can have no effect, and in Group 3 (¬
C′
P) the effects are mixed.
It is obvious in the case of the altered example that the four groups must be kept separate: C′ and P should be held fixed. When they are not, the consequent probability of the effect will be an average over its probability in each of the four groups separately; and when four
end p.102
different outcomes pointing in different directions are averaged, anything may result. Conventional wisdom teaches that averaging must be avoided in this case. Yet it is exactly this same averaging—with its untoward consequence—that results from the Eells and Sober strategy. Holding fixed only the factors that occur up to the time of the cause produces a population that mixes together the various different groups which need to be considered separately. It makes no difference whether the independently occurring causes take place before
C—as in the original example—or after
C—as in the altered example. They must not be averaged over in any case.
14 3.2.2. Strategy (ii)
The second strategy for eliminating the need for singular causes is to look only at the probabilities from randomized experiments and to see whether there is a higher frequency of the effect in the treatment group, where the cause has been introduced, than in the control group, where it has been withheld. Recall from Chapter
2 that randomized experiments go a long way toward eliminating the need for background causal knowledge. In particular, since the treatment is supposed to be introduced independently of any of the processes that normally occur, problems of spurious correlation can never arise. But the probabilities that show up in a randomized experiment, even in a model experiment where all the ideal specifications are met, will not reveal the true capacities which a cause may have. For conventional randomized experiments average over subsequently occurring causes in the way that has just been illustrated.
Consider the case of the birth-control pills. The standard randomization procedures are supposed to guarantee that the distribution of various arrangements of the background factors, summarized in B, will be identical in the treatment and the control group. This in turn should ensure that the relative frequencies of each of the effects of B are the same in both groups. But obviously neither the test nor the control group will be homogeneous with respect to these effects. Conceptually, each group could be segmented into the four sub-populations of the previous discussion, each homogeneous with respect to B's effects. But the separation is
end p.103
not made in the experiment; and the final probability for the effect inevitably averages over the probabilities in each of these four separate populations. What the experiment reveals is the net result of the operation of the cause across a population, disentangled from any confounding factors with which that cause might normally be correlated. This kind of information is extremely useful for social planning, and possibly even for personal decision-making. But it does not exhaust the causal structure. As has already been stressed, a cause whose net result across the population is entirely nil may nevertheless have made a profound difference, both in producing the effect where it would not otherwise have been and in preventing it where it otherwise might have been.
There remain two further strategies to be discussed. But it will help in proceeding in an orderly manner to balance the kind of intuitive argument I have been using so far, based on seeing what is at stake in various kinds of hypothetical example, with a tidier kind of argument that depends on a more formal structure. So the discussion of these remaining strategies will be delayed until section
3.4; before that, in section
3.3, a formal apparatus will be developed that will bring some system into my discussion of probabilistic causality.
3.3. When Causes Are Probabilistic
This section will show how to modify the conventional equations of a linear causal model to incorporate causes which act probabilistically. It will consist of three parts.
The first part will explain what notion of probabilistic causality is intended, and will show why the causes that are represented in the conventional linear equations are not probabilistic, despite the appearance of random error terms in those equations; and this section will finally suggest a simple way to amend the equations to make the causes probabilistic.
The second part uses the modified equations to get a clearer picture of what assumptions about causal structure are built into the original formalism. Using the new notation, it is easy to see that the conventional assumptions about the independence of the error terms in the standard equations presuppose that all causal processes operate independently of all others. This means that the standard
end p.104
representation has a quite restricted domain of application. A simple three-variable example will be given to show how much difference the independence assumption makes. The example involves a cause which produces two different effects, but subject to a conservation principle. As an illustration, at the end of the second part I will show how the familiar factorizability criterion for a common cause fails in this case, and what must be put in its place.
The third part looks ahead to see how this can make a difference to questions about causality in quantum mechanics.
3.3.1. A New Representation
In the usual equations of a causal model, the functional relation between a cause and its effect is exact. Whatever value the cause takes, it is bound to contribute its fixed portion to the total outcome. But often the operation of a cause is chancy: the cause occurs but the appropriate effect does not always follow, and sometimes there is no further feature that makes the difference. In the terminology of G. E. M. Anscombe,
15the cause is
enough to produce the effect, though it need not be sufficient to guarantee it.
It is possible for a chancy cause to operate entirely haphazardly. Sometimes it produces its effect and sometimes it does not, and there is no particular pattern or regularity to its doing so. I am going to ignore these cases and focus instead on causes that are better behaved—on purely probabilistic causes, causes which, when in place, operate with a fixed probability. Radioactive decay is a familiar example. A uranium nucleus may produce an alpha particle in the next second, and it may not; but the probability that it will do so is an enduring characteristic of the nucleus. Obviously more complicated cases are imaginable, cases in which not only is it a matter of chance whether the cause contributes its influence or not, but where the degree, or even the form, of the influence is only probabilistically fixed. I shall deal only with the simpler cases, where the form of the influence is fixed and only its occurrence is left to chance.
Before considering how best to deal with probabilistic causes, a short digression on adding influences will probably be of help. Econometricians sometimes say that the equations they study need not be linear in the variables, but only in the parameters. This means
end p.105
Common-cause Model With Constraint (I) |
| |
The last equation expresses the constraints in structural form; often weaker constraints, just involving probabilities, are used instead (for instance, Exp (
x 3x 2) /Exp (
x 22) = δ). The system is consistent only if ν = 1 − α δ / β + (α δ / β)
u, in which case ν and
u can be represented using a common factor,
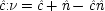
and
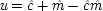
, where

. We may say that
u and ν
share a common factor since (recalling that
u and ν take only the values 0 and 1) in the notation of Boolean logic the expressions above for
u and ν are equivalent to
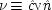
and
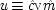
.
To make the connection with the notation in which the operations are represented directly, recall that a given cause operates if and only if its associated error term takes on the value zero. So, letting
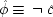
(or
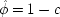
),
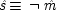
, and
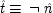
, the equations of structure I can be recast as a
local model:
| |
| |
| 2. 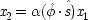 |
| 3.  |
To see why models of form II warrant the description 'local', compare structures of form I with structures of form II. By hypothesis
x 2precedes
x 3—that is assumed throughout. In general the events represented by these variables will be separated not only in time but in space as well. In neither model does
x 2cause
x 3. Yet values of the two are related. How do they come to be related? Structure I simply asserts the brute fact that the two variables are functionally related to each other. Structure II supposes that this functional relation is not just a brute fact, but has a simple causal account. It arises because the operation of
x 1to produce
x 2overlaps its operation to produce
x 3: the one event always shares some part with the other.
24The relationship between the separated occurrences
x 2and
x 3is due to facts about how two events that occur together at just the same
end p.116
time and place—viz. x 1's operation to produce x 2, and x 1's operation to produce x 3—relate to each other. That is the sense in which the model is local.
As a simple illustration, consider again the case of the shopper with a fixed budget: $10 to spend on both meat and vegetables, where the shopper's state of mind on entering the supermarket is supposed to be a probabilistic cause of the amounts spent. The meat is picked up first, the vegetables several minutes later. Yet the amounts are correlated. One may view the correlation along the lines of structure I as a brute fact: the separated events just are related to one another. Or, they can be modelled locally, by assuming that the decision to buy y dollars worth of meat is the very same event as the event of deciding to buy (10 − y) dollars worth of vegetables. In that case the model will look like structure II.
Does every probabilistic structure with consistent linear constraints have a local equivalent in the same variables? In general, no; but in some special cases, the answer is yes. In particular, if the constraint involves only variables which have all their causes in common, the model can always be recast as a local one. Structure I is a particularly simple example of this. So too is the structure of the Einstein-Podolsky-Rosen experiment.
The EPR experiment is concerned with correlations between the outcomes of measurements on separated systems, originally produced together at a common source. In modern-day versions, the measurements determine the spin along specific directions of two particles prepared at the source to be in a special state, called the single state. Let
x l(θ) represent the outcome for a measurement of spin in the direction θ in the left wing of the experiment;
x r(θ ′), the outcome for the (possibly different) direction θ ′ in the right wing; and designate the action function for the occurrence of the quantum singlet state by
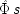
. Both
x l(θ) and
x r(θ ′) may take either the values 1 (for spin up in the direction θ or θ ′) or 0 (for spin down). Phenomenologically the experimental situation looks like this:
| |
| |
| |
| Exp (x l(Θ) x r(Θ ′)) = 1/2 sin 2 { (Θ − Θ ′) / 2} |
| |
| |
end p.117
I think the real lessons of the experiment concern quantum realism. But sometimes the results are taken to bear on causality. The question then is, can the correlations between the outcomes in this experiment be derived from a local common-cause model? Evidently, yes. As written here, the EPR structure is already a common-cause model, with consistent constraints, and any such model is trivially equivalent to a local one. This means that there is nothing in the probabilities to show that EPR cannot have a common-cause structure, and also a structure in which there are no correlations between the actions of separated causes.
Perhaps one wants more from a causal structure than just getting the probabilities right. It is usual, for instance, to demand some kind of spatio-temporal contiguity between the cause and the effect. Whether that is possible in the case of quantum mechanics will be discussed in Chapter
6. But with respect to the probabilities alone, there is no problem in assuming a common cause for the separated measurement outcomes. This structure only looks to be impossible if one uses the wrong criterion for a common cause; i.e. if one fallaciously uses condition 1, which is appropriate to models without constraints, rather than condition 2, which is the right one for the EPR experiment. Chapter
6 asks, 'What can econometrics teach quantum physics?' The answer lies in the straightforward reminder that equilibrium conditions put implicit restrictions on the error processes; and when the error processes are not independent, the causal structure cannot be determined in the ordinary way.
3.4. More in Favour of Singular Causes
With this apparatus in place, the intuitive arguments of section
3.2 can be recast more formally. I do so as a double-check. Each method of argument has its own internal weaknesses; together the two serve to balance each other. The reader who is not interested in the formulae can scan quickly for the principal philosophical claims.
Because the examples in section
3.2 follow recent philosophical literature in discussing qualitative causal relations, rather than quantitative ones, a Boolean representation will be more appropriate than one using linear equations. Mackie's treatment is the guide, except that his inus account requires that each complete cause be sufficient for its effect. Following the methods of the last section,
end p.118
Mackie's deterministic causes can be turned into probabilistic ones by introducing a proposition that indicates whether the cause operates or not. As in the last section, these propositions will be designated by 'hats':
A simple example like that of the birth-control pills, which involves one cause with dual capacities operating against a fixed background, will have the structure given in Model M.
Here
C is the dual cause (contraceptives) which can either promote
E (thrombosis) by producing a later cause
C ′ (chemical in blood) or inhibit
E by preventing a cause that might occur later, designated by
P (pregnancy).
B (for background) summarizes the effects of all other factors simultaneous with
C that can also produce
P or
C ′. In addition, it is assumed that nothing else is relevant.
The strategy that Eells and Sober take to eliminate singular causes is to control for
B. They then judge the causal role of
C by comparing the probability of
E with and without
C, when
B is fixed. The two probabilities in this case are given by formulae
X 1and
X 2:
| |
| 1. Given 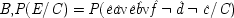 |
| 2. Given 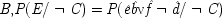 |
It is apparent from these formulae that the relation between
P(
E /
C) and
P (
E / ¬
C) will depend on exactly what values the probabilities take. There is nothing in the structure of the formulae that decides the matter. This result duplicates the conclusion of section
3.2. If only
B is held fixed, anything can happen: the probability of the effect may go either up or down in the presence of the dual cause; it may even stay the same.
In section
3.2 this was accounted for in a simple way: holding fixed
B produces a kind of averaging. It averages over populations in which some alternative causes—here
P and
C ′—would naturally occur and ones in which they would not. In Model M it is
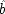
that tells whether
C ′ would naturally occur independently of
C; similarly,
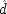
tells about the independent occurrence of
P. The averaging is apparent in formulae
X 1and
X 2, which condition on neither
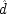
nor
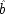
. As a
end p.119
consequence the populations picked out for examination are mixed ones, where

and

sometimes occur and sometimes do not, rather than the more homogeneous subgroups in which

and
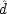
are fixed. It is evident that this will make a difference since, as the formulae show, both
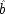
and
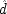
matter to
E.
My proposal here is to look instead at the frequency of
E by considering
four separate populations in turn, just as one would do if
B produced its effects on
C ′ and
P a little before
C acted. The populations, then, are segregated according to the values of

and

: two variables, each of which may be either
T or

, yield four populations. In each population the strategy is to assume that
B is given and then use formulae
X 1and
X 2to examine the influence of
C on
E.
The
first population is chosen so that every individual has
C ′ and would have
P from the action of
B alone unless
C acts to prevent it. That is, a population of those individuals for which

and

. In this population
C could only prevent
E; whether it has the power to do so or not depends on ĉ and
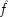
: it can do so if and only if ĉ and
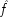
both occur sometimes, i.e. ĉ ≠

and

.
25But these are exactly the same conditions that guarantee that
P (
E / ¬
C) >
P (
E /
C), since in the case where
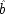
occurs and
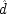
does not, formula
X 1and
X 2reduce to
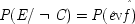
and
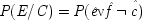
. So the probability of
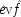
is bound to be bigger than that of
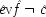
so long as
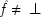
and ¬ ĉ ≠
T.
26Here matters are arranged as they should be; the probability for
E will decrease with
C if and only if occurrences of
C do prevent
Es in this situation.
In the
second population, where
B already acts both to produce
C ′ and to prevent
P, C will be causally irrelevant, and that too will be shown in the probabilities. For
P (
E /
C) =
P (ê â v ê) =
P (ê) =
P (
E / ¬
C), when
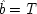
and
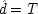
.
In the third population, C can both cause and prevent E, and the probabilities can go either way. This group provides no test of the powers of C. The fourth population, where B would by itself already prevent P but not cause C ′, is just the opposite of the first. The
end p.120
only possible influence
C could have is to cause
E, which it will do if ê â ≠

; and, as wanted, ê â ≠

if and only if
P(
E /
C) >
P(
E / ¬
C).
What does this imply about the possibility of testing causal claims? On the one hand the news is good. Although the analysis here is brief, and highly idealized, it should serve to show one way in which causal claims can be inferred from information about probabilities. A cause may have a number of different powers, which operate in different ways. In the simple example of the contraceptives, the cause has two routes to the effect—one positive and one negative. But this case can be generalized for cases of multiple capacities. The point is that, for each capacity the cause may have, there is a population in which this capacity will be revealed through the probabilities. But to pick out that population requires information not only about which of the other relevant factors were present and which were absent. It is also necessary to determine whether they acted or not. This is the discouraging part. It is discouraging for any investigator to realize that more fine-grained information is required. But the conclusion is a catastrophe for the Humean, who cannot even recognize the requisite distinction between the occurrence of the cause and its exercise.
Recall that the discussion in section
3.2 of how one might try to circumvent the need for this distinction and for singular causes was interrupted. It is time to return to it now, and to take up the two remaining proposals, one involving techniques of path analysis, the other the chopping of time into discrete chunks.
3.4.1. Strategy (iii)
Path analysis begins with graphs of causal structures, like Fig.
3.3 for the contraceptive example. Claims about any one path are to be tested by populations generated from information about all the other paths. The proposal is to hold fixed some factor from each of the other paths, then to look in that population to see how
C affects the probability of
E. If the probability increases, that shows that the remaining path exists and represents a positive influence of
C on
E; the influence is negative if the probability decreases; and it does not exist at all when the probability remains the same.
The idea is easy to see in the idealized contraceptive example, where only two paths are involved. In the population of women who
end p.121
have definitely become pregnant by time
t 2—or who have definitely failed to become pregnant—the power of the contraceptives to prevent thrombosis by preventing pregnancy at
t 2is no longer relevant. Thus the positive capacity, if it exists, will not be counter-balanced in its effects, and so it can be expected to exhibit itself in a net increase in the frequency of thrombosis. Similarly, holding fixed
C′ at
t 2should provide a population in which only the preventative power of the contraceptives is relevant, and hence could be expected to reveal itself in a drop in the number of cases of thrombosis. This is easy to see by looking at the formulae
| |
| 1. Given 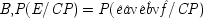 |
| 2. Given 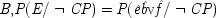 |
| |
| |
| 1. Given  |
| 2. Given 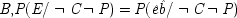 |
When
P is held fixed,
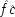
, which represents the track from
C to
E via
P, does not enter the formula at all. So long as all operations are independent of all others, it follows, both in the case of
P and in the case of ¬
P, that
P(
E /
C) >
P(
E / ¬
C) if and only if ê â ≠

; that is, if and only if there really is a path from
C to
E, through
C′.
When the operations are not independent, however, the situation is very different; and the conventional tactics of path analysis will not work. The practical importance of this should be evident from the last section. Some independence relations among the operations will be guaranteed by locality; and it may well be reasonable, in these typical macroscopic cases, to insist on only local models. But it is clearly unreasonable to insist that a single cause operating entirely locally should produce each of its effects independently of each of the others. Yet that is just what is necessary to make the procedures of the third strategy valid.
Consider what can happen in Model M when there is a correlation between the operation of C to prevent pregnancy and its operation to produce the harmful chemical. In particular, assume that if C fails in a given individual to prevent pregnancy, it will also fail to produce the chemical (i.e. ¬ ĉ → ¬ â). Behaviour like this is common in decay problems. For instance, consider the surprising case of
end p.122
protactinium, finally worked out by Lise Meitner and Otto Hahn. The case is surprising because the same mother element, protactinium, can by two different decay processes produce different final elements—in one case uranium, plus an electron, plus a photon; in the other thorium, plus a positron, plus a photon. The two processes are entirely distinct—the first has a half-life of 6.7 hours, the second of 1.12 minutes; and, as is typical in decay processes, the effects from each process are produced in tandem: the protactinium produces the uranium if and only if it produces an electron as well; similarly, thorium results if and only if a positron is produced.
Imagine, then, that the contraceptives produce their effects just as the decaying protactinium does. What happens to the probabilities? Consider first the +
P population. Expanding
Y 1and
Y 2gives
| Y 1′: Given 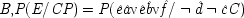 |
| Y 2′: Given 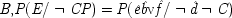 |
Given the other independence assumptions appropriate to a local model, it is apparent that
P (
E /
CP) =
P (
E / ¬
CP) when ¬ ĉ → ¬ â, and this despite the fact that ê â ≠

. In this case a probability difference may still show up in the ¬
P population; but that too can easily disappear if further correlations of a suitable kind occur.
27The point here is much the same as the one stressed in the last section. Many of the typical statistical relations used for identifying causes—like the path-analysis measure discussed here or the factorizability condition discussed in the last section—are appropriate only in local models, and then only when local operations are independent of each other. When causes with dual capacities produce their effects in tandem, steps must be taken to control for the exercise of the other capacities in order to test for the effects of any one. If you do not control for the operations, you do not get the right answers.
Besides these specific difficulties which arise when operations correlate to confound the probabilistic picture, there are other intrinsic problems that block the attempt to use causal paths as stand-ins for information about whether a power has been exercised
end p.123
or not. A detailed consideration of these problems is taken up in joint work by John Dupré and me.
28I here summarize the basic conclusions. The first thing to note about adopting causal paths as a general strategy is that there is some difficulty in formulating precisely what the strategy is. I have here really given only an example and not a general prescription for how to choose the correct test populations. It turns out that a general formulation is hard to achieve. Roughly, to look for a positive capacity one must hold fixed some factor from every possible negative path, and these factors must in addition be ones that do not appear in the positive paths. This means that to look for a positive capacity one has to know exactly how each negative capacity can be exercised, and also how the positive capacity, if it did exist, would be exercised; and vice versa for finding negative capacities.
This situation, evidently epistemologically grotesque, becomes metaphysically shaky as well when questions of complete versus partial causes are brought forward. For it then becomes unclear what are to count as alternative causal paths. It may seem that the question has a univocal answer so long as one considers only complete causes. But a formulation that includes only complete causes will not have very wide application. It is far more usual that the initial cause be only a partial cause. Together with its appropriate background, it in turn produces an effect which is itself only a partial cause of the succeeding effect relative to a new background of helping factors. To delineate a unique path, the background must be continually revised or refined as one passes down the nodes, and what counts as a path relative to one revision or refinement will not be a possible path relative to another.
Perhaps these problems are surmountable and an acceptable formulation is possible; but I am not very optimistic about the project on more general grounds. We are here considering cases where a single causal factor has associated with it different opposing capacities for the same effect. What are we trying to achieve in these cases by holding fixed intermediate factors on other causal paths? The general strategy is to isolate the statistical effects of a single capacity by finding populations in which, although the cause may be present, its alternative capacities are capable of no further exercise. Then any difference in frequency of effect must be due to the hypothesized
end p.124
residual capacity. The network of causal paths is a device that is introduced to provide a way to do this within the confines of the Humean programme. To serve this purpose the paths must satisfy two separate needs. On the one hand, they must be definable entirely in terms of causal laws, which can themselves be boot-strapped into existence from pure statistics. On the other hand, the paths are supposed to represent the canonical routes by which the capacities operate, so that one can tell just by looking at the empirical properties along the path whether the capacity has been exercised. I am sceptical that both these jobs can be done at once.
It should be noted that this scepticism about the use of causal paths is not meant to deny that capacities usually exercise themselves in certain regular ways. Nor do I claim that it is impossible to find out by empirical means whether a capacity has been exercised or not. On the contrary, I support the empiricist's insistence that hypotheses about nature should not be admitted until they have been tested, and confirmed. But the structure of the tests themselves will be highly dependent on the nature and functioning of the capacity hypothesized, and understanding why they are tests at all may depend on an irrevocably intertwined use of statistical and capacity concepts. This is very different from the Humean programme, a programme that distrusts the entire conceptual framework surrounding capacities and wants to find a general way to render talk about capacities and their exercise as an efficient, but imperspicuous, summary of facts about empirically distinguishable properties and their statistical associations. The arguments here are intended to show that the conventional methods of path analysis give no support to that programme.
Cases from quantum mechanics present another kind of problem for the methods of path analysis, problems which are less universal but still need to be mentioned, especially since they may help to illustrate the previous remarks. The path strategy works by pin-pointing some feature that occurs between the cause and the effect on each occasion when the cause operates. But can such features always be found? Common wisdom about quantum mechanics says the answer is no. Consider the Bohr model of the atom, say an atom in the first excited state. The atom has the capacity to de-excite, and thereby produce a photon. But it will not follow any path between the two states in so doing. At one instant it is in the excited state, at the next,
end p.125
3.5. Singular Causes in, Singular Causes out
Not all associations, however regular, can double for causal connections. That is surely apparent from the discussions in this chapter. But what makes the difference? What is it about some relations that makes them appropriate for identifying causes, whereas others are not? The answer I want to give parallels the account I sketched in the introduction of physics' one-shot experiments. The aim there, I claim, is to isolate a single successful case of the causal process in question. Einstein and de Haas thought they had designed their experiment so that when they found the gyromagnetic ratio that they expected, they could be assured that the orbiting electrons were causing the magnetic moment which appeared in their oscillating iron bar. They were mistaken about how successful their design was; but that does not affect the logic of the matter. Had they calculated correctly all the other contributions made to the oscillation on some particular occasion, they would have learned that, on that occasion at least, the magnetic moment was not caused by circulating electrons.
In discussing the connection between causes and probabilities in Chapters
1 and
2, I have used the language of measuring and testing. The language originates from these physics examples. What Einstein and de Haas measured directly was the gyromagnetic ratio. But in the context of the assumptions they made about the design of their experiment, the observation of the gyromagnetic ratio constituted a measurement for the causal process as well. What I will argue in this section is that exactly the same is true when probabilities are used to measure causes: the relevant probabilistic relations for establishing causal laws are the relations that guarantee that a single successful instance of the law in question has occurred. The probabilities work as a measurement, just like the observation of the gyromagnetic moment in the Einstein-de Haas bar: when you get the right answer, you know the process in question has really taken place. That means that the individual processes come first. These are the facts we uncover using our empirical methods. Obviously, it takes some kind of generalization to get from the single causal fact to a causal law; and that is the subject of the next two chapters. Before that, I turn again to the points made in the earlier sections of this chapter and the last to support two claims: first, that the probabilities reveal the single case; and second, that the kinds of general conclusions that
end p.131
can be drawn from what they reveal will not be facts about regularities, but must be something quite different.
The philosophical literature of the past twenty years has offered a number of different relations which are meant to pick out causes or, in some cases, to pick out explanatory factors in some more general sense. When Hempel moved from laws of universal association, and the concomitant deductive account of explanation, to cases where probabilistic laws were at work, he proposed that the cause (or the
explanans) should make the effect (the
explanandum) highly probable.
29Patrick Suppes amended that to a criterion closer to the social-science concept of correlation: the cause should make the effect more probable than it otherwise would be.
30Wesley Salmon
31argued that the requirement for increase in probability is too strong; a decrease will serve as well. Brian Skyrms
32reverted to the demand for an increase in probability, but added the requirement that the probabilities in question must be resilient under change in circumstance. There are other proposals as well, like the one called '
CC' in Chapter
2 here.
What all these suggestions have in common is that they are non-contextual. They offer a single criterion for identifying a cause regardless of its mode of operation.
33This makes it easier to overlook the question: what is so special about this particular probabilistic fact? One can take a kind of pragmatic view, perfectly congenial to the Humean, that causation is an empirical concept. We have discovered in our general experience of the world that this particular probabilistic relation is a quite useful one. It may, for instance, point to the kind of pattern in other probabilistic facts for other situations which is described in the next chapter. It turns out, one may argue, as a matter of fact, that this relation has a kind of predictive
end p.132
power beyond its own limited domain of applicability, and that others do not. This argument is harder to put forward once the context of operation is taken into account. One of the primary lessons of section
3.2 is that nature earmarks no single probabilistic relation as special. For instance, sometimes factorizability is a clue to the common cause, and sometimes it is not. This undermines the claim that it is the probabilities themselves that matter; and it makes it more evident that their importance depends instead on what they signify about something else—as I would have it, what they signify about the single occurrence of a given causal process.
Consider again the example of the birth-control pills. In section
3.3 I argued that the most general criteria for judging the causal efficacy of the pills would necessarily involve information about the degree of correlation between the occasions on which they operate to promote thrombosis and those on which they operate to inhibit it. The case where the operations are independent is a special one, but let us concentrate on it, since in that case the conventional methods of path analysis will be appropriate; and I want to make clear that even the conventional methods, when they work, do so because they guarantee that the appropriate singular process has occurred. The methods of path analysis are the surest of the usual non-experimental techniques for studying mixed capacities. Recall what these methods recommend for the birth-control example: to find the positive capacity of the pills to promote thrombosis, look in populations in which not only all the causal factors up to the time of the pills are held fixed, but so too is the subsequent state with respect to pregnancy; and conversely, to see whether they have a negative capacity to inhibit thrombosis, look in populations where, not
P, but
C′ is held fixed. Why is this a sensible thing to do?
First consider the inference in the direction from probability to cause. Suppose that in a population where every woman is pregnant at t 2regardless of whether she took the pills at t 1or not, the frequency of thrombosis is higher among those who took the contraceptives than among those who did not. Why does that show that contraceptives cause thrombosis? The reasoning is by a kind of elimination; and it is apparent that a good number of background assumptions are required to make it work. Most of these are built into the path-theoretical model. For instance, it must be assumed that the probability for a spontaneous occurrence of thrombosis is the same
end p.133
in both groups, and also that the fixed combination of background causes will have the same tendency to produce thrombosis with C as without C. In that case, should there be more cases of thrombosis among those with C than among those without, there is no alternative left but to suppose that some of these cases were produced by C.
The same kind of strategy is used in the converse reasoning, from causes to probabilities. Assume that occurrences of C sometimes do produce thrombosis. The trick is to find some population in which this is bound to result in an increase in the probability of thrombosis among those who take the pills. Again, the reasoning is by elimination of all the alternative possibilities; and again, the inference makes some rather strong assumptions, primarily about the background rates and their constancy. If birth-control pills do sometimes produce thrombosis, there must be more cases of thrombosis when the pills are taken than when they are not—so long as the pill-taking is not correlated with any negative tendencies. But normally it is, since the pills themselves carry the capacity to prevent thrombosis. This is why P is held fixed. A pregnant woman who has taken the contraceptives is no more likely to be the locus of a preventative action from the pills than is a pregnant woman who has not. So the individual cases in which the pills cause thrombosis are bound to make the total incidence of thrombosis higher among those who have taken the pills than among those who have not. The same is true among women who have not become pregnant by t 2as well. So holding fixed P is a good strategy for ensuring that the individual cases where the pills do cause thrombosis are not offset, when the numbers are totalled up, by cases in which they prevent it.
In both directions of inference the single case plays a key role: what is special about the population in which P is held fixed at t 2is that in this population an increase in probability guarantees that, at least in some cases, the pills have caused thrombosis; and conversely, if there are cases where the pills do cause thrombosis, that is sure to result in an increased probability.
This is just one example, and it is an especially simple one since it involves only two distinct causal paths. But the structure of the reasoning is the same for more complicated cases. The task is always to find a special kind of population, one where individual occurrences of the process in question will make a predictable difference to the probabilities, and, conversely, where that probabilistic
end p.134
difference will show up only if some instances of the process occur. The probabilities serve as a measure of the single case.
The argument need not be left to the considerations of intuition. The techniques of path analysis are, after all, not a haphazard collection of useful practices and rules of thumb; they are, rather, techniques with a ground. Like the statistical measures of econometrics described in Chapter
1, they are grounded in the linear equations of a causal model; and one needs only to look at how the equations and the probabilities connect to see the centrality of the single case. Return to the discussion of causal models in Chapter
1. There, questions of causal inference were segmented into three chunks: first, the problem of estimating probabilities from observed data; second, the problem of how to use the probabilities to identify the equations of the model; and third, the problem of how to ensure that the equations can legitimately be given a causal interpretation. Without a solution to the third problem the whole program will make no sense. But it is at the second stage where the fine details of the connection are established; and here we must remind ourselves what exactly the probabilities are supposed to signify.
The probabilities identify the fixed parameters; and what in turn do these represent? Superficially, they represent the size of the influence that the cause contributes on each occasion of its occurrence. But we have seen that this is a concept ill-suited to cases where causes can work indeterministically. Following the lessons of section
3.3, we can go behind this surface interpretation: the fixed parameter is itself just a statistical average. The more fundamental concept is the operation of the cause; and it is facts about these operations that the standard probabilistic measures are suited to uncover: is the operation of the cause impossible, or does the cause sometimes contribute at least partially to the effect? The qualitative measures, such as increase in probability, or factorizability, are designed to answer just that question, and no more. More quantitative measures work to find out, not just whether the cause sometimes produces its putative effect, but how often, or with what strength. But the central thrust of the method is to find out about the individual operation—does it occur sometimes, or does it not? When the answer is yes, the causal law is established.
Recall the derivation of the factorizability criterion in Chapter
1, or the generalization of that criterion proposed in section
3.3. In
end p.135
both cases the point of the derivation is to establish a criterion that will tell whether the one effect ever operates to contribute to the other. Or consider again the path-analytical population used for testing whether birth-control pills cause thrombosis. In this case pregnancy is to be held fixed at some time
t 2after the ingestion of the pills. And why? Because one can prove that the probabilities for thrombosis among pill-takers will go up in this population if and only if âê ≠

; that is, if and only if the operation of the pills to produce
C′ sometimes occurs in concatenation with the operation of
C′ to produce thrombosis. Put in plain English, that is just to say that the probability of thrombosis with pill-taking will go up in this population only if pills sometimes do produce thrombosis there; and conversely, if the pills do ever produce thrombosis there, the probability will go up. What the probabilities serve to establish is the occurrence of the single case.
3.6. Conclusion
The first section of this chapter argued that singular causal input is necessary if probabilities are to imply causal conclusions. The reflections of the last section show that the output is singular as well. Yet the initial aim was not to establish singular causal claims, but rather to determine what causal laws are true. How do these two projects bear on each other? The view I shall urge in the next two chapters fashions a very close fit between the single case and the generic claim. I will argue that the metaphysics that underpins both our experimental and our probabilistic methods for establishing causes is a metaphysics of capacities. One factor does not produce the other haphazardly, or by chance; it will do so only if it has the capacity to do so. Generic causal laws record these capacities. To assert the causal law that aspirins relieve headaches is to claim that aspirins, by virtue of being aspirins, have the capacity to make headaches disappear. A single successful case is significant, since that guarantees that the causal factor does indeed have the capacity it needs to bring about the effect. That is why the generic claim and the singular claim are so close. Once the capacity exhibits itself, its existence can no longer be doubted.
It may help to contrast this view with another which, more in
end p.136
agreement with Hume, tries to associate probabilities directly with generic claims, with no singular claims intermediate. It is apparent from the discussions in this chapter that, where mixed capacities are involved, if causes are to be determined from population probabilities, a different population must be involved for each different capacity. Return to the standard path-analysis procedure, where the test for the positive capacity of birth-control pills is made by looking for an increase in probability in a population where pregnancy is held fixed; the test for the negative capacity looks for a decrease in probability in the population where the chemical C′ is held fixed. This naturally suggests a simple device for associating generic claims directly with the probabilistic relations: relativize the generic claims to the populations.
Ellery Eells has recently argued in favour of a proposal like this.
34According to Eells, a causal law does not express a simple two-placed relation between the cause and its effect, but instead properly contains a third place as well, for the population. In the case of the birth-control pills, for instance, Eells says that contraceptives are causally positive for thrombosis 'in the subpopulation of women who become pregnant (a few despite taking oral contraceptives)'.
35They are also causally positive 'in the subpopulation of women who do not become pregnant (for whatever reason)'. In both these cases the probability of thrombosis with the pills is greater than the probability without. In the version of the example where the reverse is true in the total population of women, Eells concludes, 'in the whole population, [contraceptive-taking] is negative for [thrombosis]'.
36 Under this proposal, the generic causal claims, relativized to populations, come into one-to-one correspondence with the central fact about association—whether the effect is more probable given the cause, or less probable. It should be noted that this does not mean that for Eells causal laws are reducible to probabilities, for only certain populations are appropriate for filling in the third place in a given law, and the determination of which populations those are depends on what other causal laws obtain. Essentially, Eells favours a choice like that proposed in Principle CC. The point is that he does
end p.137
not use CC*. For Eells, there is neither any singular causal input nor any singular causal output.
An immediate problem for Eells's proposal is that the causal laws it endorses seem to be wrong. Consider again the population of women who have not become pregnant by time t 2. On the proposal that lines up correlations and causes, only one generic relation between pills and thrombosis is possible, depending on whether the pills increase the probability of thrombosis or decrease it. For this case that is the law that says: 'In this population, pills cause thrombosis.' That much I agree with. But it is equally a consequence of the proposal that the law 'In this population, pills prevent thrombosis' is false; and that is surely a mistake. For as the case has been constructed, in this population most of the women will have been saved from thrombosis by the pills' action in preventing their pregnancy. What is true in this population, as in the population at large, is that pills both cause and prevent thrombosis.
Eells in fact substantially agrees with this view in his most recent work. His forthcoming book
37provides a rich account of these singular processes and how they can be treated using single-case probabilities. The account is similar in many ways to that suggested in Principle
*. Eells now wants to consider populations which are defined by what singular counterfactuals are true in them, about what would happen to an individual if the cause were to occur and what would happen if it were not to. The cause 'interacts' with the different sub-populations which are homogeneous with respect to the relevant counterfactuals. His notion of interaction seems to be the usual statistical one described on page 164; basically, the cause has different probabilistic consequences in one group than in another. It looks, then, as if we are converging on similar views.
That is Eells himself. I want to return to the earlier work, for it represents a substantial and well-argued point of view that may still seem tempting, and I want to be clear about what kinds of problems it runs into. In the earlier work of Eells all that is relevant at the generic level are the total numbers—does the probability of thrombosis go up or down, or does it stay the same? But to concentrate on the net outcome is to miss the fine structure. I do not mean by fine structure just that Eells's account leaves out the ornateness of detail that would come with the recounting of individual histories; but
end p.138
rather that significant features of the nomological structure are omitted. For it is no accident that many individual tokens of taking contraceptives cause thrombosis; nor that many individual tokens prevent it. These facts are, in some way, a consequence or a manifestation of nature's causal laws.
Hume's own account has at least the advantage that it secures a connection between the individual process and the causal law which covers it, since the law is a part of what constitutes the individual process as a causal one. But this connection is hard to achieve once causes no longer necessitate their effects; and I think it will in fact be impossible so long as one is confined to some kind of a regularity view at the generic level, even a non-reductive one of the kind that Eells endorses. For regularity accounts cannot permit contrary laws in the same population. Whatever one picks as one's favourite statistic—be it a simple choice like Hempel's high probability, or a more complicated one like that proposed in Principle CC—either that statistic will be true of the population in question, or it will not; and the causal law will be decided one way or the other accordingly. This is just what we see happening in Eells's own account. Since in the total population the probability of thrombosis is supposed to be lower among those who take pills than among those who do not, Eells concludes, 'In the whole population [contraceptive-taking] is negative for [thrombosis]'; and it is not at the same time positive.
What, then, of the single cases? Some women in this population are saved from thrombosis by the pills; and those cases are all right. They occur in accord with a law that holds in that population. But what of the others? They are a sort of nomological dangler, with no law to cover them; and this despite the fact that we are convinced that these cases are no accident of circumstance, but occur systematically and predictably. Nor does it help to remark that there are other populations—like the sub-populations picked out by path analysis—where the favoured regularity is reversed and the contrary law obtains. For when the regularity is supposed to constitute the truth of a law, the regularity must obtain wherever the law does.
There are undoubtedly more complicated alternatives one can try. The point is that one needs an account of causal laws that simultaneously provides for a natural connection between the law and the individual case that it is supposed to cover, and also brings order into the methodology that we use to discover the laws. The account in terms of capacities does just that; and it
end p.139
does so by jettisoning regularities. The regularities are in no way ontologically fundamental. They are the consequence of the operation of capacities, and can be turned, when the circumstances are fortuitous, into a powerful epistemological tool. But a careful look at exactly how the tool works shows that it is fashioned to find out about the single case; and our account of what a law consists in must be tailored to make sense of that.
end p.140
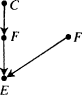

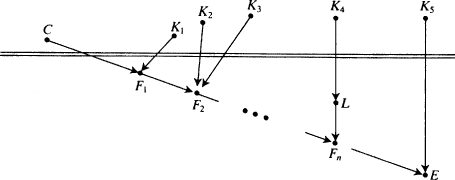
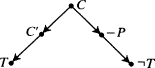
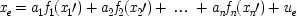
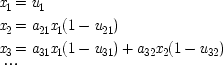
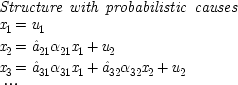
 ; if the operation is universally present when the cause is, the cause becomes deterministic. This will be expressed by â ji= T.
; if the operation is universally present when the cause is, the cause becomes deterministic. This will be expressed by â ji= T. , or, more accurately for the purposes of his proof, just in case C ¬ → ¬ Z, that is, if and only if C and Z can sometimes co-occur. But Z for him represents not the operation of the cause; instead it is supposed to represent some helping factors, factors that are necessary in order for the cause to operate. So his notation fails to distinguish the case in which C never brings about an E because it does not have the capacity to do so from cases where it indeed has the capacity but never has the opportunity because it is never present at the same time as its necessary helping factors. It is information about the former that we want to learn and to express, since in a good many cases we are in a position to rearrange the opportunities for the two factors to occur together.
, or, more accurately for the purposes of his proof, just in case C ¬ → ¬ Z, that is, if and only if C and Z can sometimes co-occur. But Z for him represents not the operation of the cause; instead it is supposed to represent some helping factors, factors that are necessary in order for the cause to operate. So his notation fails to distinguish the case in which C never brings about an E because it does not have the capacity to do so from cases where it indeed has the capacity but never has the opportunity because it is never present at the same time as its necessary helping factors. It is information about the former that we want to learn and to express, since in a good many cases we are in a position to rearrange the opportunities for the two factors to occur together.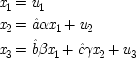
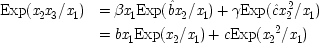
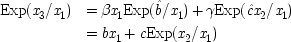
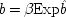 and c = γ Exp ĉ have been used. Given that u 2≠ 0 so that the factor in the denominator is not zero, and assuming that all multiplicative parameters are also non-zero, the result is familiar:
and c = γ Exp ĉ have been used. Given that u 2≠ 0 so that the factor in the denominator is not zero, and assuming that all multiplicative parameters are also non-zero, the result is familiar: 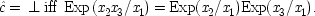
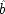 are independent of the level of x1 and similarly the expectation of ĉ is independent of x2.
are independent of the level of x1 and similarly the expectation of ĉ is independent of x2.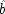 . Otherwise keep all the same assumptions as before. In this case Exp (
. Otherwise keep all the same assumptions as before. In this case Exp ( 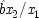 ) must be recalculated; for
) must be recalculated; for 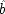 is no longer independent of x 2= â x 1+ u 2. By hypothesis
is no longer independent of x 2= â x 1+ u 2. By hypothesis 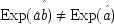 Exp (
Exp (  ), so factorizability fails, and the appropriate common cause condition becomes:
), so factorizability fails, and the appropriate common cause condition becomes: 
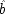 's occurrence guarantees â's (i.e.
's occurrence guarantees â's (i.e. 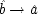 ). Otherwise the common-cause condition is valid.
). Otherwise the common-cause condition is valid.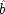 as well, and the method is easily generalized to more than three variables. The general lesson is that, even in the extended scheme where causes may be probabilistic, the causes may still be determined from the probabilities. But the probabilities are no longer just those for the occurrence of various measurable quantities; the operations must be treated as well. It is not enough to know how often the cause and effect co-occur, how often the joint effects co-occur, and the like. One must know how often the causes operate as well, and how often the operations coincide. Still, these are probabilities for genuine physical events, even though they are not ones favoured by the purest of Humeans.
as well, and the method is easily generalized to more than three variables. The general lesson is that, even in the extended scheme where causes may be probabilistic, the causes may still be determined from the probabilities. But the probabilities are no longer just those for the occurrence of various measurable quantities; the operations must be treated as well. It is not enough to know how often the cause and effect co-occur, how often the joint effects co-occur, and the like. One must know how often the causes operate as well, and how often the operations coincide. Still, these are probabilities for genuine physical events, even though they are not ones favoured by the purest of Humeans.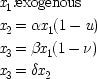
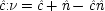 and
and 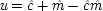 , where
, where  . We may say that u and ν share a common factor since (recalling that u and ν take only the values 0 and 1) in the notation of Boolean logic the expressions above for u and ν are equivalent to
. We may say that u and ν share a common factor since (recalling that u and ν take only the values 0 and 1) in the notation of Boolean logic the expressions above for u and ν are equivalent to 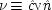 and
and 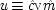 .
.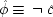 (or
(or 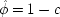 ),
), 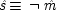 , and
, and 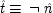 , the equations of structure I can be recast as a local model:
, the equations of structure I can be recast as a local model: 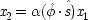

 . Both x l(θ) and x r(θ ′) may take either the values 1 (for spin up in the direction θ or θ ′) or 0 (for spin down). Phenomenologically the experimental situation looks like this:
. Both x l(θ) and x r(θ ′) may take either the values 1 (for spin up in the direction θ or θ ′) or 0 (for spin down). Phenomenologically the experimental situation looks like this: 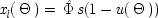
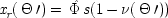
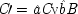
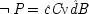
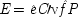
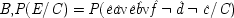
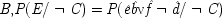
 that tells whether C ′ would naturally occur independently of C; similarly,
that tells whether C ′ would naturally occur independently of C; similarly, 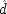 tells about the independent occurrence of P. The averaging is apparent in formulae X 1and X 2, which condition on neither
tells about the independent occurrence of P. The averaging is apparent in formulae X 1and X 2, which condition on neither 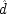 nor
nor 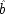 . As a
. As a  and
and  sometimes occur and sometimes do not, rather than the more homogeneous subgroups in which
sometimes occur and sometimes do not, rather than the more homogeneous subgroups in which  and
and 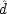 are fixed. It is evident that this will make a difference since, as the formulae show, both
are fixed. It is evident that this will make a difference since, as the formulae show, both 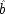 and
and 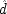 matter to E.
matter to E. and
and  : two variables, each of which may be either T or
: two variables, each of which may be either T or  and
and  . In this population C could only prevent E; whether it has the power to do so or not depends on ĉ and
. In this population C could only prevent E; whether it has the power to do so or not depends on ĉ and 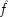 : it can do so if and only if ĉ and
: it can do so if and only if ĉ and 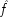 both occur sometimes, i.e. ĉ ≠
both occur sometimes, i.e. ĉ ≠  .
.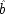 occurs and
occurs and 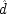 does not, formula X 1and X 2reduce to
does not, formula X 1and X 2reduce to 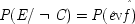 and
and 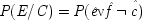 . So the probability of
. So the probability of 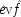 is bound to be bigger than that of
is bound to be bigger than that of 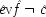 so long as
so long as 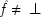 and ¬ ĉ ≠ T.
and ¬ ĉ ≠ T.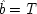 and
and 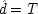 .
.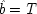 and
and 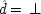 and
and 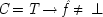 and ĉ ≠
and ĉ ≠  ; but this is precluded by the locality assumption. Since
; but this is precluded by the locality assumption. Since 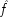 and ĉ represent actions of separated causes. In fact, it is required that
and ĉ represent actions of separated causes. In fact, it is required that  and
and  and
and 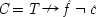 , and also that
, and also that  and
and 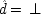 and
and 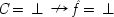 . But these are equivalent to the condition stated given the independence assumptions for local models. It is assumed throughout that all models are local.
. But these are equivalent to the condition stated given the independence assumptions for local models. It is assumed throughout that all models are local.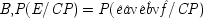
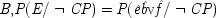

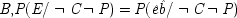
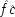 , which represents the track from C to E via P, does not enter the formula at all. So long as all operations are independent of all others, it follows, both in the case of P and in the case of ¬ P, that P(E / C) > P(E / ¬ C) if and only if ê â ≠
, which represents the track from C to E via P, does not enter the formula at all. So long as all operations are independent of all others, it follows, both in the case of P and in the case of ¬ P, that P(E / C) > P(E / ¬ C) if and only if ê â ≠ 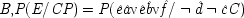
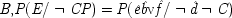
 so long as
so long as 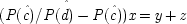 , where
, where 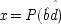 ,
, 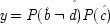 ,
,  .
.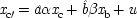
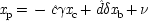
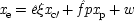
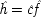 . The hope is to avoid the need to control for the operations by controlling instead for their intermediate consequences, x pand x c′. The earlier example showed how correlations and constraints can frustrate this hope. But the point here is different. It should be apparent that, even failing confounding correlations, the strategy will work only in domains where trajectories between the cause and effect are assured. More than that, it must be supposed that for each capacity there is some fixed and specifiable set of routes by which it exercises itself; and that is what I want to call into question. It seems to me that the plausibility of that suggestion depends on a thoroughgoing and antecedent commitment to the associationist view, that it must be the paths that are laid down by nature with capacities to serve as summarizing devices. But there is the converse picture in which the capacities are primary, and in which whatever paths occur, from occasion to occasion, are a consequence of the manner in which the capacities exercise themselves, in the quite different circumstances that arise from one occasion to another. Within this picture the paths are likely to be quite unstable and heterogeneous, taking on the regularity and system required by path analysis only in the highly ordered and felicitously arranged conditions of a laboratory experiment.
. The hope is to avoid the need to control for the operations by controlling instead for their intermediate consequences, x pand x c′. The earlier example showed how correlations and constraints can frustrate this hope. But the point here is different. It should be apparent that, even failing confounding correlations, the strategy will work only in domains where trajectories between the cause and effect are assured. More than that, it must be supposed that for each capacity there is some fixed and specifiable set of routes by which it exercises itself; and that is what I want to call into question. It seems to me that the plausibility of that suggestion depends on a thoroughgoing and antecedent commitment to the associationist view, that it must be the paths that are laid down by nature with capacities to serve as summarizing devices. But there is the converse picture in which the capacities are primary, and in which whatever paths occur, from occasion to occasion, are a consequence of the manner in which the capacities exercise themselves, in the quite different circumstances that arise from one occasion to another. Within this picture the paths are likely to be quite unstable and heterogeneous, taking on the regularity and system required by path analysis only in the highly ordered and felicitously arranged conditions of a laboratory experiment.