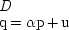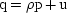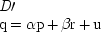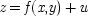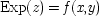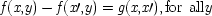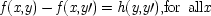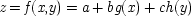4 Capacities
Abstract: In addition to the notion of causal law, the concept of capacity, modelled on Mill's notion of tendency, is required to make sense of standard methods in econometrics and standard accounts of probabilistic causality. General causal claims are shown to be ascriptions of capacities while causal laws are local causal claims, relative to a test population. Capacities are at a higher level of modality and are not reducible to causal laws, as causal laws are not reducible to laws of association that describe mere regularities; but unlike laws of association, capacities are real.
Nancy Cartwright
4.1. Introduction
This book begins with a defence of causal laws, which have received rough treatment at the hands of a number of empiricist philosophers. Hume would reduce them all to associations; Mach and Russell would cast them out of science. But in the last fifteen years in philosophy of science, causes have become more acceptable. A number of authors already discussed—Clark Glymour, Elliott Sober and Ellery Eells, or Wesley Salmon—maintain that Russell and Mach were wrong. In addition to the concept of a functional relation or a probabilistic law, science needs a separate notion of causal law as well. I want to argue in this chapter that they have not gone far enough: in addition to the notion of causal law, we also need the concept of capacity; and just as causal laws are not reducible to functional and statistical laws, so too ascriptions of capacity are not reducible to causal laws. Something more is required.
Perhaps, though, that is a misleading way to put the point. For the concept of causation that is employed in most of these authors is already a concept of capacity; and I am very glad to have recognized this, since it brings my views more into line with those of others. For I maintain that the most general causal claims—like 'aspirins relieve headaches' or 'electromagnetic forces cause motions perpendicular to the line of action'—are best rendered as ascriptions of capacity. For example, aspirins—because of being aspirins—can cure headaches. The troublesome phrase 'because of being aspirins' is put there to indicate that the claim is meant to express a fact about properties and not about individuals: the property of being an aspirin carries with it the capacity to cure headaches. What the capacities of individuals are is another, very complex, matter. For instance, must the relevant conditions for the exercise of the capacity be at least physically accessible to the individual before we are willing to ascribe the capacity to it? These are questions I will have nothing to say about.
end p.141
The claim I am going to develop in this chapter is that the concept of general sui generis causal truths—general causal truths not reducible to associations—separates naturally into two distinct concepts, one at a far higher level of generality than the other: at the lower we have the concept of a causal law; at the higher, the concept of capacity. I speak of levels of generality, but it would be more accurate to speak of levels of modality, and for all the conventional reasons: the claims at both levels are supposed to be universal in space and through time, they support counterfactuals, license inferences, and so forth. The level of capacities is 'higher' not only because the generalizations involved are broader in scope but also because the inferences that they allow are far stronger and, correlatively, the amount of metaphysics assumed in their use is far greater.
Part of my point is to make the metaphysics seem less noxious by making it seem more familiar. For I want to show that this higher-level concept is already implicit both in standard philosophical accounts of probabilistic causality and in the conventional methods for causal inference in medicine, agriculture, manufacturing, education, and the like—in short, anywhere that statistics are supposed to tell us about causes.
This point is important to the structure of my overall argument, for it ties together the work on causation at the beginning of the book with conclusions I draw here about capacities. I maintain that the crucial question for an empiricist must always be the question of testing. So we must ask: can capacities be measured? But that question has been answered, in Chapter
1 and in section
2.4. There I described how to use probabilities, treatment-and-control groups, and experiments constructed in the laboratory to test causal claims. What I want to show here is that these causal claims are claims about capacities, and that we already know how to test them.
4.2. Why Should Increases in Probability Recur?
If one looks in the recent philosophical literature on probabilistic causality, a number of works begin with roughly the same formula—the formula called Principle
CC in Chapter
2. The formula says that '
C causes
E' if and only if the probability of
E is greater with
C than without
C in every causality homogeneous background. It must be apparent from the discussions of Chapters
2 and
end p.142
3 that the exact formulation of the principle is a matter of controversy; and there has been a good deal of discussion of how the formula errs, what kinds of caveat need to be added, and so forth. I want to focus in this section on an aspect of the formula that has received little attention. The formula as I have written it in Chapter
2 appears with a strict inequality. Brian Skyrms
1writes it instead with the left-hand side 'greater than or equal to' the right-hand side. There has been discussion of that issue. But there has been little notice of what seems to me the most striking feature of this formula—the universal quantifier in front:
C is to increase (or at least not decrease) the probability of
E in
every homogeneous background. My central thesis here is that the concept of causality that uses such a universal quantifier is a strong one indeed; strong enough to double as a concept of capacity.
Some attention, of course, has been devoted to the matter of the universal quantifier in Principle CC. The last chapter was full of such discussion; and John Dupré, who has been deeply involved in the issues discussed there, even has a name for the phenomenon, which I shall use too: causes, he says, have contextual unanimity when they change the probability in the same direction in every homogeneous background. If the probability of the effect sometimes goes up with the presence of the cause, and sometimes goes down, then there is a lack of contextual unanimity. The reason I claim the quantifier is not much noticed, despite the discussions of the last chapter, is that the discussion there, like the discussion of Eells and Sober, already presupposes the conceptual framework of capacities. In Hesslow's example, birth-control pills have, I claimed, dual capacities; and their probabilities exhibit the same kind of systematic behaviour which, I will claim, is characteristic of situations where capacities are at work. In a sense, to start from failures of unanimity of the kind we see in the contraceptives example would be to beg the question. I would prefer, then, for the nonce, to disallow the possibility of dual capacities, and to ask the antecedent question: why expect any pattern of probability relations from one background setting to another, let alone the totally uniform pattern implied by the universal quantifier? By focusing only on examples where capacities are not dual, we will be able to sort out cases where the universal quantifier fails in a systematic way and for
end p.143
good reason—because an opposing capacity is at work—from cases where no pattern at all is to be expected, because no capacity exists.
It will help to return to the major conclusions of the last chapter. I of course endorse
CC*, and not the simpler
CC which Eells and Sober opt for, and probably Skyrms as well. In either case, one can ask: what is supposed to follow from an increase in probability of
E on
C in one of the specially selected populations (which I will henceforth call 'test situations')? According to Chapter
3, what follows is that, in those special test populations, it can be regularly relied on that some
Cs will produce
Es. The argument has two parts. One is already presupposed by the reference to probabilities rather than to actual frequencies. The use of the probability concept guarantees that there will be reliably (on average or in the long run) more
Es when
C is present than when
C is absent. The further conclusion that at least some of the
Es must be produced by
Cs depends on the specific features these test populations are supposed to have. Roughly, enough is supposed to be true about them to guarantee that if there is an increase in the number of
Es, there is no account possible except that
C produced the excess. The point I want to make about this argument is that it justifies a very local kind of causal claim: if in a given test population we see the increase in probability that we are looking for, that guarantees that
Cs cause
Es
there in that population. But it does not tell us any more. Since it is probabilities and not mere frequencies that are involved, it is assured that the causing of
Es by
Cs will happen regularly—but regularly in that kind of population. Who knows what happens elsewhere?
From now on I will call these very local kinds of causal claim 'causal laws', and I shall adopt the proposal of Ellery Eells, mentioned in the last chapter, that causal laws—in this sense—have, not two, but three places in them: causal laws are relative to a particular test population. My objection in the last chapter was not to the relativization itself. It seems to me that the kind of causal claim which is immediately supported by finding an increase in probability must be restricted to the population in which the increase occurs; even then it is only supported if that population has the very special characteristics that permit an inference from correlations to causes. What I objected to in the last chapter was the claim that the increase in probability in one of these special populations constitutes the truth of the causal law there. What makes the causal law true that C causes E in T is not the increase in probability of E with C in T, but
end p.144
rather the fact that in T some Cs do regularly cause Es. The increase in probability is only a sign of that; and, as I argued in the last chapter, there will generally be other causal laws true as well in the same population—laws which are not revealed in the probabilities.
If we adopt the convention of calling these local truths 'causal laws', we must look for another term to express the more usual concept of causation that philosophers have been grasping for in their various probabilistic theories of causality. For causal laws are now to be relativized to particular test situations. Yet the initial formula—either CC or CC*—quantifies over all test situations. What kind of a concept of causation does this universal quantification represent? Obviously a concept stronger and more general than the (relativized) causal laws just introduced. Of course one can de-relativize: do not consider 'Cs cause Es in T', but rather 'Cs cause Es', simpliciter. But what does this de-relativized claim say? There is a specific answer to that for the relativized version, an answer already apparent from the argument above. If the relativized law is true, then in T some Cs will produce Es, at least on average, or in the long run, or however one wants to read probability. What about the non-relative version? I think it reports that Cs—by virtue of being C—can cause E. In short, C carries the capacity to produce E. I think that in part because the universal quantifier involves just the kind of reasoning that is appropriate to capacities.
Consider why anyone would put that quantifier in. Recall that not many people note the quantifier. I do not know explicitly how it got there in other people's work. But I can explain why I have used it in introducing my version of either
CC or
CC*. I have always used it specifically because I think in terms of causal capacities. If
Cs do ever succeed in causing
Es (by virtue of being
C), it must be because they have the capacity to do so. That capacity is something they can be expected to carry with them from situation to situation. So if the probability goes up in one test situation, thus witnessing to the capacity, it will do the same in all the others. Hence the universal quantifier. Recall that the assumption that the probabilities will go the same direction in all test situations
2has a name: it is the assumption of contextual unanimity. So my thesis in short is this: to believe in contextual unanimity is to believe in capacities, or at least it is a good way along the road to that belief.
end p.145
It is important to remember that the use of this universal quantifier is widespread. That is, philosophers trying hard to characterize a concept of causal law commonly supposed that the concept they were aiming for guaranteed contextual unanimity. Yet most would eschew capacities on Humean grounds. There is more to capacities than contextual unanimity, I will agree. The more may be more palatable, though, if one only realizes how much has already been admitted in assuming that, where causes operate, there will be contextual unanimity. For contextual unanimity is a very peculiar concept for a Humean.
To see this, compare another now deeply entrenched concept, but one equally objectionable from an empiricist point of view—the concept of a law of nature. With all the work on possible-world semantics, philosophers seem to have become used to laws of nature, and the counterfactuals they license. So it is important to keep in mind how deeply this concept offends the basic tenets of a radical empiricist. Consider the very simple diagramatic example: all As, by law, are Bs. This law allows us to infer from one empirical fact, that something is an A, to another, that it is a B; we are able to know this second empirical fact without anybody ever having to look. This way of putting it can be misleading, though, for the matter is not just epistemological but metaphysical as well. When a law of nature is assumed, one empirical fact can constrain, or determine, the occurrence of another. But it is just these kinds of internal connection among empirical properties that empiricists set out to abolish.
The point of this short digression is that capacities are peculiar, from a radical empiricist point of view, in exactly the same way as laws, only one level up. Just as laws constrain relations between matters of fact, capacities constrain relations among laws. A property carries its capacities with it, from situation to situation. That means that, where capacities are at work, one can reason as above: one can infer from one causal law directly to another, without ever having to do more tests. In this way capacities are much like essences. If you are committed to the assumption that all the internal properties of electrons are essential, this makes science a lot easier for you. You can measure the charge or mass on one, and you know it on all the others. What I have been trying to show here is that it is a concept with just this peculiar kind of strength that is marked out by the universal quantifier in Principle CC.
In the next section, I want to show that it is a concept with exactly
end p.146
this same kind of peculiar modal strength that is presupposed by the conventional statistical methods used in the behavioural and life sciences. But first I summarize the three points that I hope have been established so far: first, that standard philosophical accounts of probabilistic causality employ a concept of causation stronger than the already troublesome concept of causal law; second, that the features that make it stronger are just those one would expect from a concept of capacity; and third, that if you are a radical empiricist, you should be very troubled by this concept, because the features that make it stronger introduce a peculiar modal force that no empiricist should countenance.
So far I have focused on modality as an inference licence. Yet in the Introduction I said that ascriptions of capacity are at a higher level of modality than causal laws not only because they license stronger inferences but also because they make stronger presuppositions about the stability and regularity of nature. The two are intimately connected, and both are closely related to my doctrines about testability and empiricism. Consider the question of induction and its scope. My arguments for a distinction between causal laws and ascriptions of capacity rest in part on claims about how general causal facts are established. Causal laws, which are relativized to certain given kinds of situation, can be inferred from the probabilities that obtain in those situations. To infer the stronger claim—what I call a capacity claim—one must suppose that the causal possibilities that are established in that situation continue to obtain in various different kinds of situation. It may seem that this makes for no great difference between the two kinds of causal claim: induction must be used in any case; what differentiates the two is just that an induction of wider scope is required for the stronger claim.
I think this suggestion is a mistake. On my view, induction never enters. The logic of testing is a bootstrap logic: the hypothesis under test is to be deduced from the data plus the background assumptions. Although inspired by Clark Glymour's account, this description is different from Glymour's own. I insist that in a reliable test the hypothesis itself should be derivable; Glymour asks only for an instance of the hypothesis. Then he still has to confront questions of the scope of the induction from the instance to the final hypothesis.
Of course there is ultimately no way to avoid these questions. In a sense, answers to them must already be built into the background assumptions if my version of bootstrapping is to succeed. But they
end p.147
are not always built in directly as explicit assumptions about scope. That is what much of this book has been about—how to deduce causal laws from probabilities—and no mention of scope has been made. If the generalized Reichenbach Principle is accepted, Chapter
1 shows how causal laws may be derived from facts about conditional probabilities—is the conditional probability of the effect with the putative cause present greater than, equal to, or less than the conditional probability with the cause absent? Scope enters only at the next stage. For the conditional probabilities are partial; other factors must be held fixed. The arguments of Chapter
1 allow causal laws to be established only one by one, population by population. Each different arrangement (or different level) of the other factors constitutes a new situation where the conditional probabilities must be assessed anew before a causal conclusion can be drawn.
One may of course be prepared to infer from the facts about conditional probabilities under one arrangement to facts about conditional probabilities in another. But that inference requires a different kind of licence, not yet issued; and in the bootstrap methodology that licence is provided by a correspondingly strong assumption in the background metaphysics—this time an assumption explicitly about the scope of induction, or the extent of regularity in nature. The same is true for the arguments earlier in this section, as well as in Chapter
2. Whether one follows the strategy of Chapter
1,
2, or
3, in no case can a causal law be admitted unless it has been tested. In all cases there must be a deductive argument that takes you from the data plus the background assumptions to the causal conclusion; and in all cases the arguments for the more specialized, lower-level claims, which I am now calling causal laws, require substantively weaker premisses than do the arguments for the more general claims usually made in science, which I render as ascriptions of capacity.
4.3. Forecasting and the Stability of Capacities
I turn now to the linear equations, common to causal modelling and to path analysis, that provide a rigorous ground for standard probabilistic measures of causality. I am going to discuss econometrics, and indeed very early econometrics, because my points are particularly patent there. But my conclusions should apply wherever
end p.148
these conventional probabilistic methods are put to use. Recall that econometrics got under way at the end of the 1930s and in the 1940s with the work of Jan Tinbergen, Ragnar Frisch, and Trygve Haavelmo. The work that these three began, along with Tjalling Koopmans, was carried out and developed at the Cowles Commission for Economic Research in Chicago. I give a quite distilled version of what Haavelmo and Frisch were doing. In order to keep the story all together, I will begin again at the beginning, and not rely too heavily on the various discussions of econometrics from earlier chapters.
Consider first a simple linear example familiar to everyone: a price-demand curve:
q represents quantity demanded, and
p, price;
u is supposed to represent some kind of random shock which turns the equation from a deterministic relationship into a probabilistic one. It is the fixed parameter α that is my focus of interest, and I will come to it in a moment.
First, though, it is important to note that this equation is supposed to represent a causal relationship, and not a mere functional relationship of the kind that Russell thinks typifies physics. Econometrics arises in an economic tradition that assumes that economic theory studies the relations between causes and effects. This assumption is so basic that, in a sense, it goes without mention. Few economists say, 'We are talking about causes'. Rather, this is a background that becomes apparent when topics which are more controversial or more original are discussed. I note just one example.
Jakob Marschak was head of the Cowles Commission during the important years (1943-8) when the basic ideas were worked out for what are now called Cowles Commission methods. In 1943, at the end of his first year as director of research, Marschak describes the fundamental ideas of three studies begun that year.
The method of the studies . . . is conditioned by the following four characteristics of economic data and economic theory: (a) the theory is a system of simultaneous equations, not a single equation; (b) some or all of these equations include 'random' terms, reflecting the influence of numerous erratic causes in addition to the few 'systematic' ones; (c) many data are given in
end p.149
the form of time series, subsequent events being dependent on preceding ones; (d) many published data refer to aggregates rather than to single individuals. The statistical tools developed for application in the older empirical sciences are not always adequate to meet all these conditions, and much new mathematical work is needed.
3 What I want to highlight is the language of the second characteristic: the random terms reflect the influences of erratic causes, which operate in addition to the few systematic ones. So, as I said, the methods aim to study the relationship between causes and effects; and the simple demand equation, D, follows the standard convention of writing causes on the right and effects on the left. Here the effect is quantity demanded, which is supposed to be determined simultaneously by the systematic influence of the price plus a number of other random erratic factors.
But there is more contained in this equation, more to displease Hume or Russell, than just the assumption of causality. The equation does not just assume that from one occasion to another the price causes, or is a contributing cause to, the demand, in some haphazard or unsystematic way. Rather, it assumes that the price has a stable tendency to influence demand, and that that tendency has a fixed and measurable strength. That is what is represented by the α, and by the way it is treated.
Consider α then: α represents the price elasticity of demand, a concept that was significant in the marginal revolution. But to my mind, α is treated very differently by the econometricians from the way it was treated, for example, by Alfred Marshall. When Marshall introduced the idea of demand elasticity in his
Principles of Economics, he immediately proceeded to consider 'the general law of the
variation of the elasticity of demand'. How does the elasticity
change? For instance, the price elasticity of demand will itself depend on the
level of the price: the elasticity of demand is great for high prices, and great, or at least considerable, for medium prices; but it declines as the price falls; and gradually fades away 'if the fall goes so far that the satiety level is reached'.
4In general, the econometricians by contrast treated the elasticity as if it did not vary: α
end p.150
measures an abiding or stable tendency of the system. Of course the two views are reconcilable, as is even suggested by the terminology. For the elasticity of a material is a characteristic of the material that remains fairly fixed over a wide range of conditions to which the material is normally subject; yet it can shift quite dramatically outside this range.
What I want to stress is that the assumption of stability is built into the demand equation. From the discussion of Marshall one would expect that α was a function of p, i.e. α = α(p), and of a number of other features as well: α = α(p, . . . ). But that is not how it is treated. It is treated as a constant—or fixed—parameter. Of course, econometricians do sometimes model price-dependent elasticities. I am using this simplified example to show what assumptions are hidden in the conventional methods. Let me give an example to illustrate the particular kind of stability assumption that I think is presupposed in these methods.
We have seen that, owing to the presence of the
u, the demand equation does not represent a deterministic relationship between
p and
q. Instead, there will be some probability distribution for the two. Assume, as is usual, that it is a bi-variate normal distribution. Recall from Chapter
2 that a bi-variate normal distribution can be completely identified by specifying five parameters: μ
p, μ
g, σ
p, σ
g, ρ, where it is conventional to scale the quantities so that both the means are zero (μ
p= 0 = μ
q) and both variances are 1 (σ
q= 1 = σ
p). Then the conditional distribution of
q for any fixed value of
p will again be normal, with mean ρ
p; and
q can always be written
which (so long as
u has mean 0 and variance 1 − ρ
2) is just the demand equation, if α is set equal to ρ.
The point of this is that you can go back and forth between the conditional distribution and the demand equation. The equation summarizes the same information as the distribution, and vice versa. So what is the point of the equation? This is an old question in causal-modelling theory; and there is a conventional answer. In the words of Marschak himself, 'the answer to this question involves . . . [a] discussion of the degree of permanence of economic laws.'
5end p.151
Or, as O. Duncan in his classic
Introduction to Structural Equation Models says,
there would not be much purpose in devising a model . . . if we did not have some hope that at least some features of our model would be invariant with respect to some changes in the circumstances. . . . If all the model is good for is to describe a particular set of data . . . then we might as well forego the effort of devising the model. . . .
6The point of the model, then, is that its equations express a commitment about what remains constant under change. In the case of the demand equation, that is supposed to be α. The point of expressing the information about a particular bi-variate normal distribution in the form of an equation is to signal the commitment that it is the ratio which stays fixed no matter how the variances shift. It follows from formula
D at the beginning of this section that α = Exp(
pq)/Exp(
p2) = ρ/σ
p2. What happens when the variance of
p changes? Now we will have a new distribution in
p and
q; even if we assume that it too is bi-variate normal, the parameters for the distribution will still be unsettled. Nature might, for instance, be very concerned with correlations, and fix it so that Exp(
pq) stays fixed no matter what the variance in
p is. Or it could be instead that Exp(
pq) is always varied in just the right way to keep α fixed. And so on.
Consider a different change. Imagine that we wish to adapt our study to more modern times, including the amount of television advertising as an independent cause that can also exert an influence on quantity demanded. Call this new variable
r. The natural way to modify the demand equation is this:
Just add
r as an additional influence, but assume that α stays the same. That is,
whether r
is there or not, we assume that the price elasticity stays the same.
It is important to see how peculiar this is. From the point of view of the new equation, the old equation expresses a relationship that holds in one particular circumstance: r = 0. When r is 0, p and q
end p.152
have a familiar distribution: a bi-variate normal. In principle, the distribution of p and q could be entirely different when r takes on some different value. But the way the equation is written denies that. The method of writing the equation assumes that, however p affects q, that is something that stays the same as the situation with respect to r changes, however it does so.
That, in general, is just what is reflected in econometric method. Parameters are estimated in one context, and those values are assumed to obtain in entirely different contexts. Couple that with the observation I made earlier that these parameters connect causes and effects, and you see why I talk here about stable causal tendencies. The methods presuppose that causes have stable tendencies of fixed strengths that they carry about with them from situation to situation. What p contributes to q—its total influence, α p—depends on p alone, and is the same no matter what goes on elsewhere. This is, in effect, the consequence of the commitment to the existence of a single linear theory that is supposed to hold across all different contexts and across all different statistical regimes.
Both the adjectives single and linear are important. It is not just the fact that one general theory is assumed across a variety of specific cases that brings in capacities, but rather the special form of that theory. Constraints on forms of theory are familiar, but the particular constraint that the theory be given in a set of linear equations, where the parameters are fixed, is an exceedingly strong one. Compare, for instance, the restriction that one might want to place on a modern quantum field theory, that it be renormalizable. Although this constraint is very limiting, it does not have the very peculiar feature that the assumption of the stability of the parameters produces for a linear model: namely that, given the constraint on the form, the theory itself can be inferred from the data. Of course, in econometrics the theory is not constructed from the 'raw' data, of observed frequencies in finite populations, but rather from the 'interpreted' data, or probabilities, that these frequencies are used to estimate. But this should not obscure the fact that the form allows us to discover in a single context the exact content of the theory that will cover all the rest.
It is partly because of this peculiarity that econometricians do not hold too uncritically to their commitment to a linear form with fixed parameters. In particular, they are always trying to determine, usually case by case, what kinds of variation in the parameters will
end p.153
provide better predictions. Indeed, the entire question is a matter of much discussion in econometrics at the moment, though the language used there is different from mine. Econometricians nowadays talk about targets, manipulations, and forecasting.
7Their fundamental concern is: will the parameters that have been estimated, under whatever conditions obtained in the past, continue to hold under various innovations? If not, their models will be of no help in forecasting the results that would occur should the economy be manipulated in various proposed ways.
One good example can be found in a well-known critique of the use of econometrics in policy evaluation, by Robert Lucas.
8Lucas argues that, in general, the parameters estimated in econometrics will not be stable across policy shifts, although they may be of use for forecasting where no policy change is envisioned. The primary reason is that the equations of econometrics, for which parameters are estimated, describe connections at the wrong level: they connect some 'forcing variables', which policy-makers might hope to influence, with macroscopic and observable states of the economy. The parameters are estimated from past observations. The policy-maker hopes to set the exogenous, or forcing, variables at some level, and expects that the resulting state of the economy will be that predicted by the equation. But that will not work, Lucas argues, because in general the parameters themselves will not be independent of the level at which policy sets the exogenous variables. That is because the macroscopic equations derive from some more fundamental equations which describe the decision procedures of individuals. But the structure of these more fundamental equations will be affected by the agents' expectations about policy shifts, and so the stability of the macroscopic parameters across policy changes is undermined: the macroscopic parameters are fixed by those at the micro-level; but these in turn respond to expectations about the level of the macroscopic forcing variables. So it is not likely that the parameters estimated under different policies will continue to be appropriate should policy be shifted. In Lucas's own words:
To assume stability of [the macroscopic equations and parameters] under alternative policy rules is thus to assume that agents' views about the
end p.154
behavior of shocks to the system are invariant under changes in the true behavior of these shocks. Without this extreme assumption, the kinds of policy simulations called for by the theory of economic policy are meaningless.
9Is Lucas's pessimism justified? This has been a matter of some debate. I bring up the example neither to endorse nor to reject his conclusions, but merely to stress how aware econometricians now are that the success of their methods depends on the kind of stability which I have been associating with the concept of capacity.
This was also a matter that was clear to the founders of econometrics, although it has not been much discussed between then and now. Lucas himself remarks that the criticisms he raises 'have, for the most part, been anticipated by the major original contributors'
10to econometrics. He cites Marschak and Tinbergen. I want instead to turn to Frisch and Haavelmo because of the richness of their philosophical views. A central concept behind their work, in both cases, was that of
autonomy. The difference between autonomous and non-autonomous laws is like the difference between fundamental laws, which hold by themselves, and derived or conditional laws, which hold on account of some particular (non-necessary) arrangement of circumstances. Haavelmo's own illustration explains it well:
Here is where the problem of
autonomy of an economic relation comes in. The meaning of this notion, and its importance, can, I think, be rather well illustrated by the following mechanical analogy:
If we should make a series of speed tests with an automobile, driving on a flat, dry road, we might be able to establish a very accurate functional relationship between the pressure on the gas throttle (or the distance of the gas pedal from the bottom of the car) and the corresponding maximum speed of the car. And the knowledge of this relationship might be sufficient to operate the car at a prescribed speed. But if a man did not know anything about automobiles, and he wanted to understand how they work, we should not advise him to spend time and effort in measuring a relationship like that. Why? Because (1) such a relation leaves the whole inner mechanism of a car in complete mystery, and (2) such a relation might break down at any time, as soon as there is some disorder or change in any working part of the car. . . . We say that such a relation has very little
autonomy, because its existence depends upon the simultaneous fulfillment of a great many other relations, some of which are of a transitory nature.
11end p.155
Both Haavelmo and Frisch agreed that in non-autonomous laws the parameters might not be independent of each other, or even of the level of the other variables. Imagine, say, two variables x 1and x 2in a long equation. If that equation derives from some others, then the parameters for these two variables could readily be functions of some more fundamental ones. So manipulations to change α 2may well result in variation in α 1. But what is more striking, and why these two econometricians are such good illustrations for me, is that both assumed that in the truly fundamental equations the parameters would be independent; that means that they really assumed that the fundamental structure of nature was one where causes could be assigned stable capacities of fixed strengths.
This was recognized by the opposition as well. As I have remarked before, one of the most notable critics of econometrics at its start was John Maynard Keynes. Keynes saw that econometrics did make just this assumption, and that was one of his principal objections to it. Nature, thought Keynes, did not work that way. According to Keynes, the methods of econometrics assumed that
The system of the material universe must consist . . . of bodies which we may term (without any implication as to their size being conveyed thereby)
legal atoms, such that each of them exercises its own separate, independent, and invariable effect, a change of the total state being compounded of a number of separate changes each of which is solely due to a separate portion of the preceding state. We do not have an invariable relation between particular bodies, but nevertheless each has on the others its own separate and invariable effect, which does not change with changing circumstances, although, of course, the total effect may be changed to almost any extent if all the other accompanying causes are different. Each atom can, according to this theory, be treated as a separate cause and does not enter into different organic combinations in each of which it is regulated by different laws.
12With respect to the central issue here—the question of capacities—it is worth noting that Keynes's criticism of econometrics is, not surprisingly, more radical than the Lucas critique. I say this is not surprising because Lucas's specific arguments are based on reflections on the relationship between the more autonomous laws that govern behaviour of individual firms and individual consumers, on the one hand, and the less autonomous, aggregative laws of macro-economics, on the other. Enduring capacities disappear from
end p.156
the macro-level, where parameters may drift in ways which seem unintelligible given the information available at that level, only to reappear at the micro-level. There they are not, of course, immutable, for they can at least be affected by expectations about future policies—that, after all, is the core of Lucas's argument. It is also an important feature of the philosophical story, for it fits the capacities into nature in a realistic way. They do indeed endure; on the other hand, their characteristics may evolve naturally through time, and they may be changed in systematic, even predictable, ways as a consequence of other factors in nature with which they interact. All this speaks in favour of their reality.
Keynes proposes a very different kind of world: not an atomistic but a wholistic world in which the behaviour of any particular feature—the very contribution it makes to the effect from one occasion to another—depends on the setting in which it is embedded. To return to the main theme of this chapter—the two levels of causality concept—this would not be a world in which capacities operate; but it might well be, and for Keynes probably would be, a world where causal laws are at work. For causal laws are allowed to be context-dependent. What is necessary for the truth of the law '
C causes
E in
T', as characterized in section
4.2, is that in
T, Cs can be regularly relied on to produce or contribute to the production of
Es. Sometimes this can be discovered by what might be characterized as the 'autopsy method'—i.e. tracing the process by which
C produces
E in specific individuals. But that is not a method easy to employ in economics, and I have not discussed it much here. More typical would be to use statistics. If
T is the right kind of situation—it has the characteristics of a 'test' situation—then a simple increase in probability of
E on
C will serve to establish the law. In the far more typical case where the situation of interest does not have the tidy properties that make for a test, one must consider how to construct some special test situation consistent with it. But, in any case, only the causal law will be established, and if the commitment to capacities is missing, no further inferences can be drawn. One could make an econometric model, but the enterprise would be otiose. For the model would offer no generalization over the facts already known. This is why I say, echoing Duncan, that the point of making the model is to endorse certain predictions and certain plans; and that endorsement only makes sense where an appropriate degree of autonomy can be presupposed.
end p.157
Econometrics is a notoriously uncertain science, with a spotty record for predictive success. Perhaps that is because Keynes is right; but perhaps it comes about for any number of less deeply metaphysical reasons. One principal claim I make here is, not that the phenomena of economic life are governed by capacities, but rather that the methods of econometrics presuppose this, at least if they are to be put to use for predicting and planning. But the claim is more far-reaching than that. I talk a great deal about econometrics, but econometrics serves just as an exemplar where the methods are laid out in a particularly rigorous way, and where the metaphysics that makes these methods reasonable is particularly transparent. What I claim for econometrics will be equally true in any field that uses conventional statistical methods to make inferences about causes. For it has been my thesis throughout that it takes something like the structural equations of econometrics (or path analysis) to secure a reliable connection between causes and probabilities; and it is just the feature of stability that I have pointed to in econometric structures that must be presupposed in any discipline if we are to infer from the statistics we observe in one set of conditions to the effects that might be achieved by varying these conditions. In the next chapter I will argue that the same is true of the methods of physics; and, whatever is the case in economics, in physics these methods work, and the capacities that justify them are scarcely to be rejected. Before that, I want to explain why capacity claims should not be thought of as just higher levels of modality, but instead must be taken as ascriptions of something real.
4.4. Beyond Modality
The last two sections argued that contemporary behavioural and life sciences, like sociology, medicine, and econometrics, do a variety of things that require a concept of causation far stronger than that of causal law; and that these are just the kinds of thing that one would expect to be able to do with a concept of capacity. The next chapter will argue that this is true of physics as well. Still, this does not force one to admit capacities as real. After all, the argument so far only shows that a level of modality, or of generalization, is required beyond the level already needed for causal laws. In a sense I have done a disservice to my own point of view. I aimed to defend capacities
end p.158
as real; what I have shown is how to modalize them away. But that is not the last word. For the concept of capacity involves more than just ascending levels of modality. This section will explain what more there is.
First, to understand what I mean by 'modalizing capacities away', consider how a logical positivist might respond to the arguments of the last two sections. I think that positivists should welcome them. Rudolf Carnap is a good case.
13Carnap assumed that causality is a concept used to say things in the material mode that would be more perspicuous if put in the formal mode. That is, when you use the concept of causality, you sound as though you are talking about the world, but in fact you are talking about linguistic representations of it. Bas van Fraassen
14has more recently argued the same view, but with a semantic idea of representation in contrast to Carnap's syntactic one. Sections
4.2 and
4.3 above are squarely in this positivist tradition: they fill in content for the structure that both van Fraassen and Carnap prescribe. In the picture provided so far, claims about capacities do not seem to report facts about powers, dispositions, or activities. Nor do they report causal laws. Rather, they function as metalinguistic summaries of facts about causal laws; and this is just like Carnap's original idea about causal laws themselves, only one modal level higher. To carry on the positivist program, the causal laws themselves must be recast in the formal mode as summaries of facts about (or sets of contraints on) non-causal laws—functional relations and probabilities. These laws too are to be eliminated in turn, in favour of merely occurrent regularities. One by one each level of modality is to be stripped from the material mode and relocated in the formal. The levels are pictured in Fig.
4.1.
Why won't this strategy work? Consider first the relation between the lowest modal level, that at which natural laws occur, but only laws of association, and the next level up, where causal laws are admitted as well. The answer to the question, for these two levels, is already implicit in Chapter
3. To see how it works, it is first necessary to reconstruct the earlier discussions of the connection between causal laws and probabilistic laws in order to highlight the modal aspect of this connection. Return to Principle
CC. Although it was not
end p.159
described this way in the original discussion in Chapter
2, when cast into the framework of Carnap or van Fraassen, Principle
CC functions as a modal principle, one rank above the level of the laws of association. It is one modal level higher for exactly the same reasons that capacity claims are modal relative to lower-level claims about causal laws. The claims at the higher level constrain what structure the total set of facts at the lower level can have, and thereby license inferences from one kind of fact at the lower level directly to another, without the need for any support from below.
Roughly the constraints work like this:
15a cause is supposed to increase the probability of its effect, holding fixed all the other causes. This will put a complicated restriction on the probability structure. Imagine, for example, that a new factor,
C n, raises the probability of
E when
C 1, . . . ,
C n − 1are held fixed. This means that
C nshould be admitted as a cause of
E, relative to
C 1, . . . ,
C n − 1. But now, what about each of these factors themselves? We may imagine that up until this point they have been correctly counted as causes, so that each raises the probability of
E relative to the others. But now that
C nhas been added, the judgement about each of
C 1, . . . ,
C n − 1must be re-evaluated. If
C nis to be a cause, then each of
C 1, . . . ,
C n − 1must increase the probability of
E when
C is held fixed as well. If one of these factors fails to do so, real complications follow. For in that case, it ought not to have been held fixed in the first place, in the evaluation of
C nitself. But what then about
C n? The process of evaluation must begin again; and sometimes, for some probabilities structures, there will be no choice of a set of causal factors possible for a given effect, consistent with Principle
CC.
This means that CC can be used to rule out some probability structures
end p.160
as possible; and that is what the positivist will take hold of. I see CC as a tool for getting new causal information out of old. But for the positivist there is no right or wrong about the old causal information. CC functions rather as an effective, but not very perspicuous, way of summarizing some very complicated facts about what the total pattern of purely associational laws is like. In this case, any set of so-called 'causal laws' that produces the right constraints on the laws of association is as good as any other. Correlatively, one should be able to tell whether a set of causal laws is acceptable or not just by looking at what relationships the probabilistic laws bear to one another.
Chapter
3 shows that one has to look further. One needs to know some fundamentally causal information as well—one needs to know facts about singular causes. It is indeed possible to see causal laws as inference tickets from one probabilistic law to another—but only if the individual causal histories are right. There is thus a concealed
ceteris paribus condition for the inference ticket to obtain; and that concealed condition brings in a notion of causality which is at the same modal level—or higher—than the one we are trying to eliminate. Exactly the same thing is true of capacities. So far we have not explored any of the caveats that need to be added to the schemes in the earlier sections of this chapter. When we do, we see that the constraints laid out there hold only
ceteris paribus; and the conditions that must be added use concepts, like interaction, that are already deeply infiltrated by the concept of capacity itself.
To see how the need for caveats affects the program for modalizing away both causes and capacities in turn, consider another central problem in philosophy of science where a similar strategy has been tried—the problem of the existence of theoretical entities. Positivists, once they had given up wanting to translate theoretical terms, tried instead to construe theories as summaries of laws about observables. The recent work by van Fraassen
16and Arthur Fine
17on empirical adequacy supplied the kind of modal force necessary to make this program plausible, and to give to positivist theories the same kind of power and applicability as can reasonably be assumed for their realist counterparts. Realists maintain that a belief in the truth of the theory and the existence of the
end p.161
entities it employs is the best way to justify our expectations that the predictions of the theory will obtain, and also the best way to explain why they do. Van Fraassen and Fine recommend a belief that stops just short of that, namely a belief in the complete empirical adequacy of the theory, with emphasis on complete. Briefly, the belief in the complete empirical adequacy of a theory commits one to an open-ended set of counterfactuals that follows from the theory, though not to the truth of the theory itself. It is this open-ended commitment that accounts for novel predictions, justifies applying the theory in untested domains, and yields empirical laws beyond those already known. The theory is thus for Fine and van Fraassen to be treated as a valid inference ticket—a totally valid inference ticket—but its claims are not to be taken seriously as descriptions of the world.
This is the same kind of programme as that outlined in this chapter, and it faces the same kind of objection. The objection is nicely put by Wilfrid Sellars.
18Theories are supposed to be summaries of laws about observables. But in fact there are no (or at least not enough) laws about observables to summarize. We do not need theoretical entities to explain the systematic behaviour of observables. Rather, they are necessary to systematize observable behaviour in the first place. Sellars's own example is of earthworm behaviouristics. There may well be certain regular things that earthworms do in response to different stimuli; and these will be accessible to a diligent behaviourist. But there is always a concealed
ceteris paribus assumption: this is what earthworms do
so long as they are neurologically sound. And neurological soundness is not something which can be behaviouristically defined. Sellars thinks the structure of this simplistic example is characteristic of the relationship between theory and observation. The point can be put quite generally. Theories do not have unlimited applicability; the domain and limitations on the domain can be constructed only by already using the theory and the concepts of the theory. Theories come before observables, or are at least born together with them. This forces us to give real content to the theoretical terms and not take them merely as part of a scheme, albeit a modal scheme, for summarizing laws about non-theoretical entities.
I do not here intend to start on a discussion of scientific realism in general, neither to defend nor to attack it. I introduce the subject
end p.162
purely for formal reasons. For Sellars's defence of realism about theoretical entities is exactly parallel in structure to the argument I want to give for interpreting capacities realistically. Difficulties for the purely modal view of capacities arise from two main sources: first from
ceteris paribus conditions involving interactions, and second from the need to control for multiple capacities associated with the same feature. I begin with interactions. Consider the argument in section
4.2, which carries one from causal laws true in one set of circumstances to those that must be true in others. That argument maintains that the first causal law gives evidence for a capacity, and that the capacity will exhibit itself in a new causal law in any new test situation. That assumes that the capacity remains intact. It is, of course, part of the point of taking capacities seriously as things in the world, and not just particularly strong modalities, that they should remain intact from one kind of situation to another. But that does not mean that there can be no exceptions; it means that any exception requires a reason. Probably the most common reason for a capacity to fail to obtain in the new situation is causal interaction. The property that carries the capacity interacts with some specific feature of the new situation, and the nature of the capacity is changed. It no longer has the power that it used to.
Causal interactions are a longstanding problem in philosophy of science. John Stuart Mill thought they were the principal reason why chemistry was far less successful than physics. When two forces in mechanics are present together, each retains its original capacity. They operate side by side, independently of one another. The resulting effect is a pure combination of the effect that each is trying to produce by itself. The law of vector addition gives precise content to this idea of pure combination. In chemistry, things are different. The acid and the base neutralize each other. Each destroys the chemical powers of the other, and the peculiar chemical effects of both are eliminated. This is not like the stationary particle, held in place by the tug of forces in opposite directions. When an acid and a base mix, their effects do not combine: neither can operate to produce any effects at all.
The generalizations, or inference tickets, of sections
4.2 and
4.3 need to be amended to allow for interactions. The principles should be prefixed, 'So long as there is no interfering causal interaction, then . . . '. But how is this to be done without admitting interactions into the descriptive content of the world? I think it cannot be done. I
end p.163
have argued already that, one modal layer down, the ceteris paribus conditions on the inference patterns licensed by causal laws cannot be specified without already invoking strong notions of causality. This same kind of problem arises here. Causal interactions are interactions of causal capacities, and they cannot be picked out unless capacities themselves can be recognized. The attempt to 'modalize away' the capacities requires some independent characterization of interactions; and there is no general non-circular account available to do the job.
Consider the usual statistical characterization of an interaction. For simplicity, I will discuss only the now familiar three-variable model. In this case the response variable
z is supposed to be dependent on two independent variables
x and
y, plus an error term whose expectation is taken to be zero. In the conventional structures of Chapter
1, the dependence was assumed to be additive; but here we allow more general forms of dependency, and assume only that
or
Then
x and
y have no interaction in their effect on
z if and only if
and
That is, the difference or contrast in the mean response for two different levels
x and
x′ of the first factor is independent of the level of the second, and conversely. Alternatively, instead of talking about the expectation of
z, one could talk about the influence which
x and
y jointly contribute. In that case, to say that
x and
y do not interact is to say that the level of
y does not affect the difference in contribution that comes from varying
x, and the other way around as well.
This is the standard characterization of interaction.
19Yet it is obviously of no help for the problem here. For we began with the commonsensical intuition that, at least in some special domains, one could determine the relationship between a cause and its effect with
end p.164
all the other causal factors fixed at some set levels; and then one could make a meaningful prediction: so long as no interactions occur, the relationship between x and z will be the same at new levels of y as at the level already studied. The idea behind the commonsense intuition is that an interaction is a special type of thing, with an identity of its own, a kind of process which—like any other real process—can be identified in a variety of different ways, depending on the concrete situation. Taking the statistical characterization above to give the essence of what an interaction is trivializes this intuition; and in particular it trivializes the prediction one wanted to express, and deprives it of content. The claim that one can expect the relationship between x and z to be the same no matter what the level of y is, except in cases where x and y interact, now says no more than this: you can expect the relationship to be the same except where it is different; and this is no proper expression of the methodology actually in use. In practice one looks for independent evidence that an interaction is occurring, and some account of why it should occur between these variables and not others, or at these levels and not others. The chemistry examples are a good case. One does not just say the acid and the base interact because they behave differently together from the way they behave separately; rather, we understand already a good deal about how the separate capacities work and why they should interfere with each other in just the way they do.
Besides the characterization in terms of levels, interactions are also sometimes defined in the modelling literature in terms of the linearity of the structural equations. As remarked earlier, it is not really linearity in the variables that matters, but rather linearity in the parameters. That means that the influences should add: the factors
x and
y are additive in their influences if there is a function
q (which is independent of
y) and a function
h (independent of
x) and real numbers
a, b, c such that
But this definition does not help with the problem at hand either, for it is equivalent to the first: that is, it is a theorem that the factors
x and
y have no interaction if and only if they are additive.
20 end p.165
What is needed for the positivist program to modalize away capacities is some separate, independent characterization of interaction, a characterization that employs no further problematic concepts like the concept of capacity itself. That is what we seem not to have, and for good reason, I have been arguing. For the concepts of capacity and interaction are genuine descriptive concepts, and are not in any way to be reduced to more primitive ideas. There are methods for determining when they obtain, but the methods cannot double as empirical reductions, for the two concepts are woven together in these methods and cannot be pried apart.
I describe only the interplay between these two concepts; but that is too simple. A large number of other equally non-reducible concepts are involved as well, concepts like those of enabling conditions, precipitating factors, triggers, inhibitors, preventatives, and the like. These are the kinds of concept that will have to go into a proper account of what capacities are and how they operate; that is, in some sequel to this book. I mention them just to make this point: given the rich fabric of all these interconnected concepts, we can make sense case by case of the methods we use to study any one of them and of the judgements we arrive at. But without them the whole enterprise of establishing and using any causal concepts at all will seem arbitrary, and even pernicious.
Rather than pursue these other concepts, the same point can be made by thinking again about an idea already discussed in a number of different places throughout this book—the concept of mixed capacities. Do you think the rain will result in more accidents or in fewer, this holiday weekend? The question is hard to answer, because the rain has different, opposing effects: by keeping people at home, it will tend to prevent accidents; but by worsening the conditions of the roads, it will tend to produce them. How, then, should one think about the question probabilistically? Principle
CC gives a preliminary version of the connection between causes and probabilities: a cause should increase the probability of its effect, and a preventative should lessen it, when all other causes are held fixed. But Chapter
3 teaches a more complicated lesson. It is not sufficient to hold fixed just the other causal factors; one must rather hold fixed the operation of all the other
capacities that may be at work as well, whether those capacities are attached to separate causal factors, or to the very one under investigation. Otherwise facts about capacities and facts about probabilities will have no systematic connection with
end p.166
each other. Again, the program to modalize away capacities founders. An ascription of a capacity cannot be taken merely as an inference ticket to get from one fact about probabilities to another, that is, as an efficient summary of complicated facts about the pattern of pure probabilities; for the pattern it summarizes is not a pattern involving just the probabilities themselves but a more variegated pattern, involving both probabilities and capacities in an essential way.
There is one sweeping reply to be made to this argument, the reply of what is often called 'the radical empiricist', and that is to reject the whole fabric of causal concepts, and all the layers of modality as well: there are just isolated empirical happenings, and nothing more. All the rest is talk. Applied to the case of theoretical entities and theoretical laws, this reply leads to the familiar doctrine of the radical underdetermination of theory by facts. The same is true for the fabric of causal concepts. Some interlocking sets of joint hypotheses about capacities, interactions, precipitating conditions, and the like will be ruled out; but always, it will be maintained, an infinity of equally satisfactory alternatives remains. In both cases, I think, the challenge to the radical empiricist is the same. What is so special about the elementary facts with which you are willing to begin? What characteristics do they have that singular causings or capacities lack? My own view is that once the foundational picture of knowledge and the infallibility of our sense experience have been renounced, there is no good answer to this question. It seems it must then be left to rest on some very implausible view of concept formation, and not to arise from any convincingly grounded strictures on how knowledge can be acquired or on what can count as justification. That is, radical empiricism is a doctrine either without ground, or grounded on mistaken premisses. The most stringent kind of empiricism that seems to me to make sense is the empiricism of practice that I advocate throughout; the empiricism that demands that each quantity be measured and each claim be tested. And the principal argument of this book is that causes and capacities are as empirical in that sense as it is possible to be.
There is one further point about radical empiricism that I should like to make, and that is to stress what a poor reconstruction of science it provides. There is now fairly widespread agreement that Carnap's project
21 to build the claims of science systematically from
end p.167
some acceptable empirical core upwards cannot work. Nothing remotely like the science that we have can be arrived at in this way. But there has recently been more optimism among empiricists for a strategy like van Fraassen's, which does not aim to reconstruct the claims of science from some data deemed acceptable as a starting-point, but rather takes the claims of science at face value, and aims only to fit the data into some single consistent model which exemplifies the laws and theories as well. Van Fraassen's book is after all called The Image of Science, and although he takes the name from a different source, this is commonly thought to be one of its chief advances: his semantic view of theories, together with his rejection of any empiricist doctrines of meaning, combine to give his programme the possibility of succeeding where Carnap's attempts at a logical construction of the world failed, in providing an image totally acceptable to an empiricist of much the same science that appears to everyone else.
That is the claim I quarrel with. It seems to me to contain far more illusion than fact. The most immediate thing to notice for the theses of this book is that there are no detailed examples that treat causal laws; so the programme of modalizing them away has not yet got any real attempts, let alone successes, to support it. Perhaps less apparent is the fact that the cases that have been studied, the cases that give content to the programme and make it seem plausible, are all essentially cases of fitting low-level theories into models of high-level theories, and not cases which handle the 'raw data' itself. That makes it easy to overlook two crucial problems. The first is the problem of how this 'raw data' is to be made to fit. There is perhaps the not fully articulated assumption that the data fit into low-level theory in exactly the same way that low-level theory fits into higher; and that the job of securing the fit must already have been carried out by the scientist in the process of justifying and accepting the theory. It remains to the philosopher just to reconstruct this work, to cast it into a form acceptable for a radical-empiricist image of science.
But that will not do, for even at the lowest level, science never treats of the kind of datum that the radical empiricist finds in the world. Scientific claims are tested, not against the empiricist's data (e.g. 'individual temperature readings from samples of lead, bubble chamber photographs') but rather against 'phenomena detected from them (e.g. the melting point of lead, the weak neutral current,
end p.168
changes in the rate of solar neutrino emission)'. The quotation is from a paper by James Bogen and James Woodward
22 which argues for just this claim. This is also one of the central theses of Ian Hacking's
Representing and Intervening.
23 I introduce it here to make the point that scientific practice itself cannot be relied on to have already, in outline, produced a model that contains both the raw data and the hypotheses which, according to the radical empiricist, are supposed to cover the data. One can, of course, continue to insist that only the kind of datum admissible for a radical empiricist is relevant. But to do so would make even our most sensible and trustworthy tests look crazy and unmotivated. The tests suppose that nature is full, not only of data, but of phenomena as well, phenomena which—relevant to the point here—include capacities, interactions, and the like; and I do not see why we need to start with the assumption that this is false.
The second problem with focusing on the connection between lower- and higher-level theories is that it is easy in doing so to lose sight of the
ceteris paribus conditions, some of which have played a central role in the arguments of this chapter. For the need for
ceteris paribus conditions is felt most acutely—and by many felt only at all—when the theory is brought to bear, not on a model, but on a real, concrete thing. For models are often constructed to fit the laws exactly, with no need for
ceteris paribus conditions.
24 Yet when one theory is related to another, it is usually by embedding the models of one in the models of another, and not by comparing the actual treatments the two would provide should they attempt to describe accurately the behaviour of concrete physical systems.
But here I do not want to dwell on these ceteris paribus conditions. Although I have devoted a lot of attention to them, I believe they are ultimately the wrong way to think about the problem. I used them as a kind of ladder to climb out of the modalization programme, a ladder to be kicked away at the end. They must be introduced if one is stuck with the project of reducing causings and capacities, or of modalizing them away. But I advocate giving up that programme
end p.169
entirely—especially since it seems not to work—and accepting that capacities and causings are real things in nature. There is, I think, no other view of nature that can give an adequate image of science. In this doctrine I follow John Stuart Mill, whom I will discuss in the next section. I turn to Mill because my views are almost an exact replication of his, and discussing his arguments may help to make my own more clear.
4.5. Mill in Defence of Capacities
Keynes, in the discussion cited at the end of section
4.3, maintained that economic phenomena were probably not atomistic—that is, in the terminology of this book, economic life is not governed by stable capacities. John Stuart Mill believed that it was. I want to review here Mill's ideas about method and theory in economics to see how he arrived at this conclusion. Briefly put, Mill believed that the laws of political economy and the laws of mechanics alike are laws, not about what things do, but about what tendencies they have. This thesis should be familiar. Substituting the word 'capacity' for Mill's word 'tendency', his claim is exactly what I aim to establish in this book. Indeed, the observations that brought me to this conclusion, although set in a different context, are almost identical to the arguments that moved Mill. For the remainder of this section and through most of Chapter
5, I suggest that the reader take my 'capacity' and Mill's 'tendency' to be synonymous. No distinction will be drawn until section
5.6.
Mill's ideas about the structure and method of political economy are most explicitly described in his essay 'On the Definition of Political Economy and on the Method of Philosophical Investigation in that Science', written in the 1830s,
25 and in the chapter 'On the Logic of the Moral Sciences' in his
System of Logic, which first appeared in 1843. Mill combined an original view on the structure of theories in political economy
26 with a well-known anti-inductivist view on method, which he shared with his father James Mill and other followers of Ricardo.
With respect to method it is important to note, as Samuel
end p.170
Hollander argues,
27 that for Mill the opposite of a pure inductive method was not a kind of 'a-priorism', but rather a 'mixed method of induction and ratiocination'. That means that the axioms from which scientific deductions begin are in no way arbitrary, but are rather to have two different kinds of support in experience: (1) there must be a 'direct induction as the basis of the whole', and (2) a kind of introspection or broad-based understanding of human nature, which is a source of information peculiar to the moral sciences. To illustrate:
Suppose, for example, that the question were, whether absolute kings were likely to employ the powers of governments for the welfare of or for the oppression of their subjects. The practicals would endeavour to determine this question by a direct induction from the conduct of particular despotic monarchs, as testified by history. The theorists would refer the question to be decided by the test not solely of our experience of kings, but of our experience of men. They would contend that an observation of the tendencies which nature has manifested in the variety of situations in which human beings have been placed, and especially observation of what passes in our own minds, warrants us in inferring that a human being in the situation of a despotic king will make a bad use of power; and that this conclusion would lose nothing of its certainty even if absolute kings had never existed or if history furnished us with no information of the manner in which they had conducted themselves.
28 Mention of axioms and deduction may make it appear as if Mill endorsed the hypothetico-deductive method, which today stands opposed to inductivism, with the difference just noted that modern empiricists look only to the deductive consequences of a hypothesis for its empirical support, whereas Mill allows extra input for hypotheses in the moral sciences from our more generalized knowledge of human nature. But this is not the case at all. To see that, we need to look at Mill's views on structure, which complement exactly his views on induction and empirical support. Although Mill described his theories as deductive in order to dissociate them from the inductivist critics of Ricardo, who backed both a different philosophy of science and a different theory of political economy, it is not a structure that I would call deductive. For one cannot deduce even in principle what will occur in any future circumstance. With that Mill agrees:
end p.171
When in every single instance, a multitude, often an unknown multitude, of agencies, are clashing and combining, what security have we that in our computation
a priori we have taken all these into our reckoning? How many must we not generally be ignorant of? Among those which we know, how probable that some have been overlooked; and even were all included, how vain the pretence of summing up the effects of many causes, unless we know the numerical law of each,—a condition in most cases not to be fulfilled; and even when it is fulfilled, to make the calculation transcends, in any but very simple cases, the utmost power of mathematical science with all its most modern improvements.
29 Mill recognizes the pure deductive structure that goes along with our modern picture of the hypothetico-deductive method. He calls it the 'geometrical, or abstract method', and he rejects it. It seems he came to reject the geometrical method by reflecting on the weaknesses in his father's views, and in particular on T. B. Macaulay's criticisms of James Mill's 'Essay on Government'. He explains in his autobiography:
On examining . . . what the mind does when it applies the principles of the Composition of Forces, I found that it performs a simple act of addition. It adds the separate effect of the one force to the separate effect of the other, and puts down the sum of these separate effects as the joint effect. But is this a legitimate process? In dynamics, and in all the mathematical branches of physics, it is; but in some other cases, as in chemistry, it is not; and I then recollected that something not unlike this was pointed out as one of the distinctions between chemical and mechanical phenomena, in the introduction to that favourite of my boyhood, Thomson's System of Chemistry. This distinction at once made my mind clear as to what was perplexing me in respect to the philosophy of politics. I now saw, that a science is either deductive or experimental, according as in the province it deals with, the effects of causes when conjoined, are or are not the sums of the effects which the same causes produce when separate. It followed that politics must be a deductive science. It thus appeared, that both Macaulay and my father were wrong; the one in assimilating the method of philosophizing in politics to the purely experimental method of chemistry; while the other, though right in adopting a deductive method, had made a wrong selection of one, having taken as the type of deduction, not the appropriate process, that of the deductive branches of natural philosophy, but the inappropriate one of pure geometry, which, not being a science of causation at all, does not require or admit of any summing-up of effects. A foundation was thus laid in my
end p.172
thoughts for the principal chapters of what I afterwards published on the Logic of the Moral Sciences; and my new position in respect to my old political creed, now became perfectly definite . . .
30 This apparently led Mill to write the essay discussed above.
The difference between geometry and natural philosophy, or mechanics, can be put this way. The axioms of geometry are mutually consistent, whereas those of mechanics are not. A conclusion which is derived from some proper subset of the principles of geometry will remain true when further premisses are added, but not so with conclusions in mechanics. The laws of mechanics interfere with each other:
Among the differences between geometry . . . and those physical Sciences of Causation which have been rendered deductive, the following is one of the most conspicuous: That geometry affords no room for what so constantly occurs in mechanics and its applications, the case of conflicting forces, of causes which counteract or modify one another. In mechanics we continually find two or more moving forces producing, not motion, but rest; or motion in a different direction from that which would have been produced by either of the generating forces . . . what the one force does, the other, partly or altogether, undoes. There is no similar state of things in geometry. The result which follows from one geometrical principle has nothing that conflicts with the result which follows from another. What is proved true from one geometrical theorem, what would be true if no other geometrical principles existed, cannot be altered and made no longer true by reason of some other geometrical principle.
31 Mill proposes, then, that political economy should be modelled on mechanics and not on geometry. But his view of mechanics is peculiar from the standpoint of a modern empiricist, who will construct mechanics itself on the model of geometry. This is implicit in Russell's remarks on causation, and it has been carefully and persuasively articulated in the standard American works of mid twentieth-century philosophy of science, notably by Ernest Nagel
32 and Carl Hempel.
33 To begin with, Mill takes the fundamental laws of nature (or more accurately, one major category of laws of nature, since he wants to allow different forms like conservation laws as
end p.173
well) to be laws about individual causes and their effects; and second, he thinks that individual causes in physics are atomic in the way Keynes described. Indeed, sometimes Mill even uses the same kind of language that I have used to describe the assumptions of econometrics: economics is lucky because it treats fixed capacities that are stable from one context to another.
Chemistry contrasts with physics in a second respect. Although the laws of chemistry are laws of cause and effect, the causes of chemistry are not governed by stable tendencies. Mill says:
A concurrence of two or more causes, not separately producing each its own effect, but interfering with or modifying the effects of one another, takes place, as has already been explained, in two different ways. In the one, which is exemplified by the joint operation of different forces in mechanics, the separate effects of all the causes continue to be produced, but are compounded with one another, and disappear in one total. In the other, illustrated by the case of chemical action, the separate effects cease entirely, and are succeeded by phenomena altogether different, and governed by different laws.
34 Talk about interference and tendencies was in no way new with Mill. On the contrary, these were common ideas in political economy, where none of the laws proposed ever seemed to obtain in reality. Mill's contribution comes from his analysis of how interference works. In the first place, he stresses that one must not try to deal with exceptions by allowing laws that hold only for the most part:
we might have cautioned inquirers against too extensive
generalization, and reminded them that there are
exceptions to all rules . . . We have avoided the use of these expressions purposely because we deem them superficial and inaccurate.
35 In another place he urges that it is a disservice to science to suggest that its laws have exceptions. The principal reason for this is that the fundamental laws (non-empirical laws, in Mill's terminology) do not hold for the most part, or even approximately for the most part; and conversely, those laws which are more or less true much of the time are not fundamental.
36
end p.174
The only laws that will be near to true for Mill are what he calls empirical laws. We are already familiar with the idea of an empirical law, as opposed to a fundamental one, from the discussion of Frisch and Haavelmo. The ideas translate fairly directly: what are empirical laws in Mill's terminology are laws which are low in autonomy for Frisch and Haavelmo. These laws hold because of some particular arrangement of background circumstances in a society through some period of time; and they remain true only so long as that particular arrangement persists. They thus have the limitation already noted when it comes to forecasting, for example, 'what would be the effect of imposing or of repealing corn laws, of abolishing monarchy or introducing suffrage, in the present condition of society and civilization in any European country'.
37 Mill says:
those immediate causes [in an empirical law] depend on remote causes; and the empirical law, obtained by this indirect mode of observation, can only be relied on as applicable to unobserved cases, so long as there is reason to think that no change has taken place in any of the remote causes on which the immediate causes depend. In making use, therefore, of even the best statistical generalizations for the purpose of inferring (though it be only conjecturally) that the same empirical laws will hold in any new case, it is necessary that we be well acquainted with the remoter causes, in order that we may avoid applying the empirical law to cases which differ in any of the circumstances on which the truth of the law ultimately depends.
38 More important for my thesis, however, is not the fact that laws which are nearly true, albeit for particular situations and finite periods, are not fundamental, but rather that fundamental laws are not true, nor nearly true, nor true for the most part. That is because fundamental laws are laws about distinct 'atomic' causes and their separate effects; but when causes occur in nature they occur, not separately, but in combination. Moreover, the combinations are irregular and changing, and even a single omission will usually make a big difference. The philosophers who followed the geometric method, Mill continues,
would have applied, and did apply their principles with innumerable allowances. But it is not allowances that are wanted. There is little chance of making due amends in the superstructure of a theory for the want of sufficient breadth in its foundations. . . . That the deductions should be from
end p.175
the whole and not from a part only of the laws of nature that are concerned, would be desirable even if those that were omitted were so insignificant in comparison with the others, that they might, for most purposes and on most occasions, be left out of the account. But this is far indeed from being true in the social sciences. The phenomena of society do not depend, in essentials, on some one agency or law of human nature, with only inconsiderable modifications from others. The whole of the qualities of human nature influence those phenomena, and there is not one which influences them in a small degree. There is not one, the removal or any great alteration of which would not materially affect the whole aspect of society, and change more or less the sequences of social phenomena generally.
39 This was one of the reasons why Mill was opposed to the statistical laws of Adolphe Quetelet's social physics. The statistics of social physics was modelled on astronomy, where the aim was to find the true orbit from a scatter of observations. The metaphysics was that of the major cause—either permanent or slowly evolving—like the arrangement of the other massive bodies in the heavens, and a myriad of minor, erratic, disturbing factors, which in a reasonable world would be independent and normally distributed around the true value so that their effects would average out. The Quetelet picture conceals a problem which Mill was deeply concerned about—a concern I share. Where in nature is the fundamental relation between a cause and its effect exhibited? In Quetelet's story of the major cause with its small, randomly distributed errors, it is easy to overlook the fact that the hypothesized relation never literally obtains for most causes. The cause is there, but some other different effect follows as a result of the interference of the minor causes. It is easier to overlook this problem from Quetelet's viewpoint than from Mill's: when the perturbing influences are small, at least the effect which occurs is close to the effect predicted, and although close is in no way good enough, it is somehow comforting. Mill could not indulge in this comfort. Society for Mill was nothing like the society of Quetelet. Causes did not divide themselves into major and minor, with the minor ones erratic and independent. All causes were subject to change, and the omission of even a single one from consideration could make a substantial difference.
This viewpoint of Mill is important to the question of capacities because it undermines a ready answer to my concerns. The question I pose is: what is stable in nature? Hume says that the association of
end p.176
events is regular (or at least that, where science is possible, the association of events must be regular). But Mill notices that this is not so, neither in mechanics nor in political economy. What actually happens is highly variable, because of the shifting mixture of causes. That is why simple induction will not work as a method of discovery in these sciences. Specific combinations of causes do not stay fixed long enough to produce the data necessary for a good induction. Even should they do so, and should we be able to identify the particular mixture that obtains, the resulting law would not be the kind we seek. For it would tell us only what happens in that very specific arrangement. That information provides no good basis for decision, nor for prediction.
Nowadays there is a conventional answer to this kind of problem, also I think too ready and too glib; and that is the resort to counterfactuals: the requisite regularities may not in fact hold, but they are true counterfactually. In the language of the debate about Ricardo's abstract methods and strong cases, a language common again today, they hold '
ceteris paribus'. That means they would hold
if all disturbing causes were absent. But that will not do. That was Mill's own view, and one that I support as well. Even if these regularities did hold
ceteris paribus—or, other things being
equal—that would have no bearing on the far more common case where other things are
not equal. Here are Mill's own words:
We might, indeed, guard our expression . . . by saying that the body moves in [the prescribed] manner unless prevented, or except in so far as prevented, by some counteracting cause, but the body does not only move in that manner unless counteracted, it
tends to move in that manner even when counteracted.
40 The solution that Mill offers is tendencies.
These facts are correctly indicated by the expression
tendency. All laws of causation, in consequence of their liability to be counteracted, require to be stated in words affirmative of tendencies only, and not of actual results.
41 This is a solution that Mill worries about. He is after all an empiricist, following in the tradition of those early British empiricists who in part defined themselves by their rejection of the mysterious and occult powers which they took to be typical of scholastic science.
end p.177
Nevertheless, he is ready to distinguish
laws about tendencies, i.e. fixed capacities, from the more common idea of
tendency laws, i.e. laws that say what tends to happen, or happens for the most part. These latter would describe at least partial regularities, or perhaps, counterfactual regularities, and hence be true to the philosophy of Hume. But we have seen that this is not what Mill is about. For Mill,
With regard to exceptions in any tolerably advanced science, there is properly no such thing as an exception. What is thought to be an exception to a principle is always some other and distinct principle cutting into the former, some other force which impinges against the first force and deflects it from its direction. There are not a
law and an
exception to that law—the law acting in ninety-nine cases, and the exception in one. There are two laws, each possibly acting in the whole hundred cases and bringing about a common effect by their conjunct operation.
42 This follows immediately after Mill's claim that the philosopher who makes a mistake by expecting the literal consequence of an observed cause to occur has generally not erred by generalizing too extensively, but by 'making the wrong
kind of assertion, he predicted an actual result when he should only have predicted a
tendency to that result—a power acting with a certain tendency in that direction'.
43
How seriously must we take this idea of powers? I have been arguing that modern science takes them very seriously indeed: that our methods and our use of science presuppose that tendencies, or 'capacities', are real. I think the same is true in Mill's work as well; given Mill's other assumptions, his talk about powers must be taken literally. One quick, final way to see this is to contrast Mill's endorsement of tendencies in the passages already cited with another silly suggestion that he makes to solve the same problem.
Peter Geach complains of Mill that he is not constant to his own arguments for tendencies. Geach refers to 'this doctrine of tendencies, which we have found in Mill mixed up with an entirely incompatible Humian invariable-succession theory. . . . '
44 That is because, on Geach's reading, 'Mill retreats into saying that physical laws do not state what
does happen, but what
would failing interference happen; but this is to abandon the Humian position.'
45 In
end p.178
contrast to Geach, it is not the introduction of counterfactuals that I complain of, but a completely unconvincing use of factuals that Mill resorts to in the
Logic. For sometimes Mill tries to avoid introducing tendencies by claiming that the laws of nature, read as exceptionless statements of pure regularities, are not false after all. Every time a particular cause occurs, so too does its effect, despite all appearances to the contrary. Each of the separate, atomic effects exists inside, or as part of, or somehow or other in connection with, the apparent resultant effect:
In this important class of cases of causation, one cause never, properly speaking, defeats or frustrates another; both have their full effect. If a body is propelled in two directions by two forces, one tending to drive it to the north, and the other to the east, it is caused to move in a given time exactly as far in
both directions as the two forces would separately have carried it . . .
46 This is an idea that seems to me to be silly. To claim that a motion exists in a body even when that body is at a standstill, and passes all the conventional empirical tests for being at a standstill, is to forsake empiricism, and to do so in a way that violates its fundamental tenets more seriously than the admission of powers or tendencies, for it severs the existence of the motion from all our standard methods of measuring motions. That is something that an empiricist should not allow. Given Mill's other views, that laws of nature are about causes and effects, that these laws allow the construction of forecasts, and so on, ultimately I think Mill's view has to be that the fundamental laws of nature are laws that assign stable tendencies to specific causes. Despite Hume and some of Mill's teachings in earlier sections of the Logic, laws are not uniformities or regularities in nature after all.
4.6. Conclusion
This chapter has argued for singular causal happenings and the capacities that make them possible, embedded in a rich fabric of other interrelated factors like interactions, or enabling and inhibiting conditions. Inevitably, because this book starts from a study of probabilistic causality, some elements of the fabric, like
end p.179
interactions, have received a good deal of attention, and others, like enabling conditions, have received virtually none at all. Still, I have tried to argue, all are equally necessary, all equally irreducible, and all equally objectionable to the radical empiricist. I have also maintained that this last does not matter: radical empiricism, without the accompanying doctrines of infallibility and foundationalism, is no longer a position to be reckoned with. But I have not argued for this last claim; and to do so would take an excursion into epistemology far from the more detailed issues of probability and method with which I began. Rather I offer, in its stead, another version of empiricism that I think can be taken seriously—and has been by large numbers of scientists since the seventeenth century—the empiricism of testing and measuring, an empiricism already too demanding to admit much of modern theoretical science, especially physics, which is prone to be driven more by the needs of mathematics than it is by the phenomena. Nevertheless, it does not exclude tendencies and causes.
Still, to say this is to side-step a crucial criticism. For the testing of causal claims at any level—whether claims about a single happening, about a more generic causal law, or about capacities and their operations—necessarily presupposes some metaphysical assumptions that cannot be tested by the same stringent logic. Yet this in no way distinguishes these claims from any other claims about the world. This is obvious in the case of laws of association. No regularity of pattern will tell us that a law obtains unless we know enough to ensure that the connections involved are law-like to begin with. Otherwise we are forced back to the hypothetico-deductive method, and that method provides no test at all. I think the same is universally true. Even what are supposed to be the 'purest' empirical assertions, like 'this facing surface is red', employ concepts which cannot be given ostensively but only make sense relative to an entire structure of other concepts in which they are embedded. Nor can they be tested, as many hoped, by pure inspection, without a rich background of assumptions, both physical and metaphysical, assumptions not much different in kind from those necessary to test causal claims.
But these are familiar views, and ones which are not very controversial at the moment. What I have wanted to do in this chapter is to attack a position that seems far more widespread nowadays than that of radical empiricism, a view that tries to let in just enough metaphysics, but not too much—the view that adopts laws, so long
end p.180