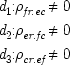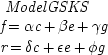'All the coins in my pocket are silver'. The difference between probabilities and frequencies is supposed to be like that.
The reason I am uneasy about taking probabilities as an empirical starting-point is that I do not believe in these nomological regularities, whether they are supposed to hold for 100 per cent of cases or for some other percentage. I do not see many around, and most of those I do see are constructions of the laboratory. The more general picture I have in view takes the capacities which I argue for in this book not just to stand alongside laws, to be equally necessary to our image of science, but rather to eliminate the need for laws altogether. Capacities are at work in nature, and if harnessed properly they can be used to produce regular patterns of events. But the patterns are tied to the capacities and consequent upon them: they do not exist everywhere and every when; they are not immutable; and they do not license counterfactuals, though certain assumptions about the arrangement of capacities may. They have none of the usual marks they are supposed to have in order to be counted as nomologicals; and there is no reason to count them among the governors of nature. What makes things happen in nature is the operation of capacities.
This is a strong overstatement of an undefended view, and does not really belong here. But I mention it because it helps put into perspective the arguments of this book. For the doctrines I am opposing here are not so much those of Hume, but doctrines like those of Russell and Mach or, more in our own time, of Hempel and Nagel. Their philosophies admit laws of nature, so long as they are laws of association and succession; but they eschew causes. That seems to me to be a crazy stopping-point. If you have laws you can get causes, as I argue in this chapter. And you might as well take them. They are not much worse than the laws themselves (as I argue in Chapter
3), and with them you can get a far more powerful picture of why science works, both why its methods for finding things out make sense and why its forecasts should ever prove reliable.
end p.36
Appendix: Back Paths and the Identification of Causes
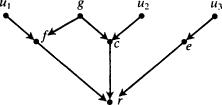
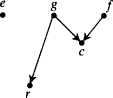
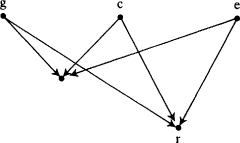
Suppose there is a set of factors
x i,
i = 1, . . . ,
m, each of which may, for all that is known, be a true cause of
x e, and such that
where each
x ihas an open back path. Assume transitivity of causality: if (
A →
B and
B →
C) then (
A →
C) ('
X →
Y' means here, '
X causes
Y'). Assume in addition a Reichenbach-type principle: given any linear equation in the form
z e= Σ
b iz i, which represents a true functional dependence, either (
a) every factor on the right-hand side is a true cause of the factor on the left-hand side, or (
b) the equation can be derived from a set of equations for each of which (
a) is true. Then each
x iis a true cause of x
e.
The argument is by
reductio ad absurdum. Assume there is some true causal equation for
x e:
and a set of true causal equations which allows
x e− Σ
b jy j= 0 to be transformed into
x e− Σ
a ix i= 0. Order the equations, including
T, by the time index of the effects. The matrix of coefficients will then form a triangular array. Designate the equation in which φ is the effect by
φ . Consider the
x iwith the last time index which is not a true cause of
x e, and designate it 'x
1'.
Claim. It is necessary to use x 1to transform T to S.
Argument. It is only possible to introduce x 1into T by using some equation in which x 1occurs. This requires using either x 1itself or else some other equation, φ , such that φ occurs after x 1and x 1→ φ. If x 1→ φ, then φ ≠ y jfor any j, otherwise by transitivity x 1is a true cause of x e. Thus φ introduces one new variable, φ, not already present in either T or S; and φ can only be eliminated by the use of a further equation for a variable with a later index. Only one of the y jcan eliminate φ without introducing yet another new variable needing to be eliminated. But φ can only be eliminated by y jif φ appears in y j. This means φ → y j—which is impossible by transitivity since x 1→ φ. Using an equation for a different variable φ′ cannot help, for the same reason. The only way to eliminate φ′ without introducing yet another variable itself in need of elimination is to use a y j. But if φ appears in φ ′, φ′ cannot appear in any y j, since then (x 1→ φ) implies (φ′ → y j). And so on. So the equation x 1itself must be used.
The equation x 1will introduce at least one factor—call it 'u 1'—that is part of an open back path. Hence u 1≠ x ifor all i, and also u 1≠ y jfor all j.
Claim. It is necessary to use u 1to transform T to S.
end p.37
Argument. Any equation for a variable after u 1in which u 1appears will introduce some new variable, φ, which must in turn be eliminated, since for all j, it is not possible that u 1→ y j, and also not possible for any i that u 1→ x i. This is because anything that u 1causes must be known not to cause x e. But φ itself cannot be eliminated without introducing yet another new variable, since φ cannot appear in any x ior y j, otherwise by transitivity u 1→ x ior u 1→ y j. And so on.
Now the conclusion follows immediately. For u 1introduces at least one variable, u 1′, which in turn can only be eliminated by using u 1′, and this equation introduces a u 1″ of which the same is true; and so on. Thus there will never be a finite set of equations by which S can be derived from T.
end p.38
2 No Causes in, No Causes out
Abstract: This chapter argues that one cannot get knowledge of causes from equations and associations alone, using critical analyses of theoretical examples in physics and of attempts in the philosophy of science and economics (e.g. Granger causality and various probabilistic theories of causality) to reduce causal claims to probabilities. Old causal knowledge must be supplied for new causal knowledge to be had. Analysis of experimental methods and actual experiments (Stanford Gravity Probe) show how this can be done.
Nancy Cartwright
2.1. Introduction
Chapter
1 showed how to get from probabilities to causes. It treated ideas that are primarily relevant to fields in the behavioural sciences and to quality control, and it tried to answer the question, 'How can we infer causes from data?' Section
2.2 of this chapter does the opposite. It starts with physics and asks instead the question, 'How can we infer causes from theory?' The principal thesis of section
2.2 is that we can do so only when we have a rich background of causal knowledge to begin with. There is no going from pure theory to causes, no matter how powerful the theory.
Section
2.3 will return to probabilities, to make the same point. It differs from Chapter
1, where the arguments borrowed some simple structures from causal modelling theory, especially the modelling theory of econometrics. Section
2.3 proceeds more intuitively, and its presentation is more reflective of the current discussion in philosophy of science. Its aim is to repeat the lesson of section
2.2, this time for the attempt to go from probabilities to causes. Its conclusion is one already implicit in Chapter
1: again, no causes in, no causes out.
This could be a source of despair, especially for the Humean who has no concept of causality to use as input. Section
2.4 reminds us that this is ridiculous. We regularly succeed in finding out new causes from old, and sometimes we do so with very little information in hand. Clever experimental design often substitutes for what we do not know. Section
2.5 returns to defend the thesis that some background causal knowledge is nevertheless necessary by showing why an alternative proposal to use the hypothetico-deductive method will not work. The chapter ends with a comparison of the informal arguments of section
2.2 with the more formally structured ones of Chapter
1.
end p.39
2.2. Causes at Work in Mathematical Physics
Any field in which the aim is to tell adequate stories about what happens in nature will inevitably include causal processes in its descriptions. Though philosophical accounts may suggest the opposite, modern physics is no exception. Philosophers have traditionally been concerned with space and time, infinity, symmetry, necessity; in modern physics they have tended to concentrate on questions surrounding the significance of relativity theory, or parity conservation and the algebraic structure of quantum mechanics, rather than how physics treats specific physical systems. The case treated in this section will illustrate one kind of causal reasoning in physics, reasoning that attempts to establish causes not by doing experiments but by using theory. Specifically, the example shows how a theoretical model for laser behaviour helped solve a puzzle about what produces a dip in intensity where it was not expected.
Once one begins to focus on studies where causality matters, all the questions of the last chapter intrude into physics. Physics is mathematical; yet its causal stories can be told in words. How does the mathematics bear on physics' causal claims? This is precisely the question asked in Chapter
1; and the answer is essentially the same: functional dependencies of the right kind are necessary for causation, though they are not by themselves sufficient. Yet in certain felicitous cases they may combine with other facts already well established to provide sufficient conditions as well.
Renaissance thought assumed that mathematics was the provenance of real science, and that in real science the steps of a derivation mirror the unfolding of nature. This is not true of modern physics. In contemporary physics, derivations need not provide maps of causal processes. A derivation may start with the basic equations that govern a phenomenon. It may be both accurate and realistic. Yet it may not pass through the causes. This is exactly what happens in the laser example of this section. The derivation provided is highly accurate, but it does not reflect the right causal story.
Nevertheless, it appears that a derivation is necessary if the theory is to support the causal story, although it is not the derivation itself that provides the support. What is needed is a kind of back-tracking through the derivation, following to their origins the features that are mathematically responsible for the effect. Still, this special kind of back-tracking is not sufficient for causal support. This is not
end p.40
surprising if the derivation through which one is tracing did not go via the causes in the first place. In the example here, two structurally similar trackings are apparent, one which leads back to the causes, and one which does not.
Why are the features targeted by one tracing correct, while those targeted by the other are not? The answer in this case is that one fitted nicely into a causal process already fairly well understood, and the other could find no place. Here, quite clearly, background causal knowledge combined with new theoretical developments to fix the cause of the unexpected dip. The example is a particularly nice one because it has a familiar structure: it is a case of spurious correlation in a deterministic setting, just like Mackie's example of the Manchester hooters, only in this case the example is real and the regularities are given by the equations of a sophisticated quantum-mechanical model. Let us turn now to the example itself.
1 The Lamb dip occurs in gas lasers. It is named after Willis Lamb, who first predicted its occurrence. Fig.
2.1, taken from Anthony Siegman's text
Lasers, shows the elements of a typical laser oscillator. There are three basic parts: the laser medium; the pumping process; and mirrors or other devices to produce optical feedback. At thermal equilibrium most atoms are in the ground state rather than in any of the excited states. A laser works by pumping the medium until there is a population inversion—more atoms in an upper state than in a lower. Light near the transition frequency between the upper and the lower states will be amplified as the atoms in the upper state de-excite, and if the mirrors at the end of the cavity are aligned properly, the signal will bounce back and forth, reamplifying each time. Eventually, laser oscillation may be produced. Later I shall use this as a prime example of a capacity ascription in physics: an inverted population has the capacity to lase.
The Lamb dip occurs in the graph of laser intensity versus cavity frequency, as illustrated in Fig.
2.2. The atoms in the cavity have a natural transition frequency, ω; the cavity also has a natural frequency, υ, depending on the placement of the mirrors. Prima facie it seems that the intensity should be greatest when the cavity frequency matches the atomic transition. Indeed, Lamb reports,
end p.41
end p.42
I naively expected that the laser intensity would reach a maximum value when the cavity resonance was tuned to the atomic transition frequency. To my surprise, it seemed that there were conditions under which this would not be the case. There could be a local minimum, or dip, when the cavity was tuned to resonance [
i.e. cavity frequency =
transition frequency]. I spent a lot of time checking and rechecking the algebra, and finally had to believe the results.
2Lamb did not know it at the time, but the Lamp dip is caused by a combination of
saturation, with its consequent
hole-burning, and
Doppler shifting, which occurs for the moving atoms in a gas laser such as helium-neon.
The concept of hole-burning comes from W.R. Bennett, and it was Bennett who first put hole-burning and the Lamb dip together in print; but both a footnote in the Bennett paper and remarks of Lamb (conversation, 1 October 1984) suggest that the connection was first seen by Gordon Gould. Bennett had been using hole-burning to explain unexpected beat frequencies he had been seeing in heliumneon lasers at the Bell Laboratories in 1961. But, Bennett explains, 'Ironically, a much more direct proof of the hole-burning process' is provided by the Lamb dip.
3 Bennett's paper appeared in
Applied Optics in 1962. Lamb's paper was circulating at the time but was not finally published until 1964. In fact, Lamb had been working on the calculations from the spring of 1961, and he says that he had already seen the dip (which Lamb calls 'the double peak' after the humps rather than the trough) by the fall of 1961.
4Lamb wrote both to Bennett and to A. Javan about the prediction. Bennett, who had been measuring intensity versus cavity-tuning frequency in the helium-neon laser, sent back a tracing of only a single peak. Javan answered more favourably, for he had been seeing frequency-pushing effects that could be easily reconciled with Lamb's general treatment. Javan then did a direct experiment to show the dip, which he published later with A. Szoke.
5end p.43
The first published report of the dip was by R.A. McFarlane,
6who attributed earlier failures to see the dip to the use of natural neon, whose two isotopes confound the effect. McFarlane used a single isotope instead, and got the results shown in Fig.
2.3.
Thus Lamb worked on the paper for three years before it was published. He is in general methodical and slow to publish. But there was special motivation in this case for holding back: he did not know what caused the dip. He could predict it, and he knew it existed; but he did not know what physical process produced it. This raises the first philosophical point of the example: the mathematical derivation of an effect may completely side-step the causal process which produces the effect; and this may be so even when the derivation is both (
a) faultless and (
b) realistic.
(a) | Lamb's mathematical treatment was accurate and careful. |
end p.44
| Bennett described it as 'an extremely detailed and rigorous development of the theory of optical laser oscillation', 7and that is still the opinion today. In fact, Lamb's study of gas lasers was the first full theoretical treatment of any kind of laser, despite the fact that Javan had produced a gas laser at the end of December 1960, and that ruby lasers had been operating since July 1960. The work of Schawlow and Townes, which was so important for the development of lasers, used bits of theory but gave no unified treatment. |
(b) | The calculations are based on a concrete, realistic model of the gas laser. This contrasts, for example, with an almost simultaneous theoretical treatment by Hermann Haken, which is highly formal and abstract. 8Lamb's calculations refer to the real entities of the laser—moving gas molecules and the electromagnetic field that they generate; and the equations govern their real physical characteristics, such as population differences in the atoms and the polarization from the field. Nevertheless, the derivation fails to pass through the causal process. Exactly how this happened will be described below. Here the point to notice is that the failure to reveal the causes of the Lamb dip did not arise because the derivation was unsound nor because it was unrealistic. |
Turn now to the concepts of hole-burning and saturation. For simplicity, consider two level atoms with a transition frequency ω. Once a population inversion occurs, a signal near the transition frequency will stimulate transitions in the atoms. The size of the response is proportional both to the applied signal and to the population difference. The stimulated emission in turn increases the signal, thereby stimulating an even stronger response. The response does not increase indefinitely because the signal depopulates the upper level, driving the population difference down, until a balance is achieved between the effects of the pumping and the signal. This is called saturation of the population difference. Oscillation begins when the gain of the beam in the cavity is enough to balance the losses due to things like leakage from the cavity. The intensity of the oscillations builds up until the oscillation saturates the gain, and brings it down. Steady-state oscillation occurs when the saturation brings the gain to a point where it just offsets the losses.
end p.45
Saturation produces unexpected effects when the laser medium is gas. In a gas laser the atoms are moving, and frequencies of the emitted light will be scattered around the natural transition frequency of the atoms, so that the observed spectral line will be much broader than the natural line for the atoms. That is because of Doppler-shifting. The moving atom sees a signal as having a different frequency from that of the stationary atom. The broadened line is actually made up of separate spectral packets with atoms of different velocities, where each packet itself has the natural line width, as in Fig.
2.4. This gives rise to the possibility of
hole-burning: an applied signal will stimulate moving atoms whose effective transition frequency approximates its own frequency, but it will have almost no effect on other atoms. So the chart of the population difference versus frequency across the Doppler-broadened line shows a 'hole' in the population difference of the atoms near the applied frequency (Fig.
2.5).
The discussion so far has involved the Doppler shift due to the interaction of a moving atom with a single travelling wave. In a laser cavity there are two travelling waves, oppositely directed, which superpose to form a single standing wave. So the standing wave interacts with two groups of atoms—those whose velocities produce the appropriate Doppler-shifted frequency to interact with the forward wave and those whose Doppler-shifted frequency will interact with the backward one. These atoms have equal and opposite velocities. The holes pictured in Fig.
2.6 result.
end p.46
end p.47
As Murray Sargent and Marian Scully explain, following Lamb's treatment in their
Laser Handbook article,
the holes, i.e., lack of population difference, represent atoms which have made induced transitions to the lower state. Hence the area of the hole gives a measure of the power [or intensity] in the laser. . . . For central tuning, the laser intensity is driven by a single hole because the two holes for the [velocities] ν and - ν coincide. The area of this single hole [
i.e. the power] can be less than that for the two contributing to detuned oscillation provided the Doppler width and excitation are sufficiently large.
9Hence there is a power or intensity dip at central tuning.
This is the qualitative account of what causes the Lamb dip. How does this account relate to Lamb's mathematical derivation? Here again the example is a particularly felicitous one, since this question is explicitly taken up in the advanced-level textbook by Sargent, Scully, and Lamb.
10They begin by considering the conditions that must be met for the amplified signal to oscillate. Steady-state oscillation occurs when the saturated gain equals the losses. The losses, we may recall, are due to structural features of the cavity, and thus, for a given cavity, the amount of saturated gain at steady state is fixed.
The saturated gain (α
g) is related to the intensity (
I) by a formula that integrates over the various velocities of the moving atoms. Under the conditions in which the Lamb dip appears, the formula for the saturated gain off resonance yields
But on resonance the formula is different:
Since α
gis fixed by the physical characteristics of the cavity α
gon = α
goff, which implies that
Ion = 1/2
Ioff, that is, the intensity on resonance is significantly smaller than the intensity off resonance. This is the Lamb dip.
The causes of the dip can be discovered by finding the source of the difference between the formulae for α gon and α goff. Most immediately the difference comes from the denominator of the full
end p.48
formula for α gbefore integration. The denominator is a function of two Lorentzian functions (the Lorentzian is defined by L γ(x) = (γ2/γ2 + ω2)). One Lorentzian has + ν in its ω argument; the other, − ν. When the integration over ν is carried out only one of the Lorentzians contributes off resonance, but both contribute on resonance.
This is just what Sargent, Scully, and Lamb note:
The Lorentzians . . . show that holes are burned in the plot of [the intensity curve]. Off resonance (υ ≠ ω), one of the Lorentzians is peaked at the detuning value ω − υ = Kv, and one at ω − υ = − Kν, thereby burning
two holes . . . On resonance (υ = ω), the peaks coincide and a
single hole is burned.
11The next step is to discover how the two different Lorentzians got there in the first place. The answer is found just where it is to be expected. Laser intensity is due to depopulating the excited level. Populations are depleted at two different velocities because there are two running waves with which the atoms interact. So the source of the Lorentzians should be in the running waves—as indeed it is. Sargent, Scully, and Lamb know this from comparing equations. The electromagnetic field in the cavity represented by a standing wave is really composed of two running waves. The Lorentzians first appear when the formula for the standing wave is written as a sum of the two running waves. Sargent, Scully, and Lamb report:
For υ > ω, an atom moving along the
z axis sees the first of the running waves . . . 'stretched' out or Doppler downshifted. . . . Comparison of the equation [
which writes the standing wave as a sum of the two running waves] with [
the equation used to generate the population difference] reveals that the Lorentzian in [
the saturation factor] results from this running wave. . . . Similarly, an atom moving with velocity − ν sees the second standing wave down-shifted, interacts strongly if the atom with velocity ν did, and produces the [
second] Lorentzian.
12Thus the story is complete. The Lamb dip has found its source in the combination of saturation and Doppler broadening, as promised.
In this exposition Sargent, Scully, and Lamb trace the mathematics and the causal story they want to tell in exact parallel. Fig.
2.7 summarizes the two, side by side. Notice exactly what Sargent, Scully, and Lamb do. They do not lay out a derivation; that has been
end p.49
done earlier. Rather, they take an intelligent backwards look through the derivation to pick out the cause. First, they isolate the mathematical feature that is responsible for the exact characteristic of the effect in question—in this case, the fact that two Lorentzians contribute off resonance and only one on resonance; second, they trace the genealogy of this feature back through the derivation to its origin—to the two terms for the oppositely directed running waves; third, they note, as they go, the precise mathematical consequences
end p.50
that the source terms force at each stage. The mathematics supports the causal story when these mathematical consequences traced back through the derivation match stage by stage the hypothesized steps of the causal story. This is the kind of support that causal stories need, and until it has been accomplished, their theoretical grounding is inadequate.
Although this is just one case, it is not an untypical case in physics. Just staying within this particular example, for instance, one could easily lay out a similar retrospective mathematical tracing for the causal claim that an applied beam saturates the population difference. For contrast, one might look at Bennett's own 'hole-burning model'
13which does not (so far as I can reconstruct) allow the kind of backwards causal matching that Lamb's does. I am not going to do that here, but simply summarize my conclusion: no matter how useful or insightful the more qualitative and piecemeal considerations of Bennett are, they do not provide rigorous theoretical support for the causal story connecting saturation and Doppler-broadening with the Lamb dip. Only matching back-tracking through the derivation in a realistic model can provide true theoretical support for a causal hypothesis.
Although this kind of back-tracking is necessary, it is not sufficient. For a derivation may well predict a phenomenon without mentioning its causes. This is just what happened in Lamb's original work. He predicted the dip, but missed its causes. When he went back to look for them, he found something in his derivation that was mathematically necessary for the dip, but which did not cause it. Just like the dip, the feature he focused on was the result of the Doppler-shifting that occurs in a gas laser, but it itself has no direct effect on the dip. For a while Lamb was misled by a spurious correlation.
To see this point, one needs to know something about the role of electric dipole moments, or atomic polarizations, in Lamb's theory. Lamb uses what he calls a 'self-consistency' treatment. He begins by modelling the radiating atoms of the laser medium as dipole oscillators; the amount of radiation is dependent on the dipole moment. The atoms start to radiate in response to the field in which they are located, and they in turn contribute to the field. The contribution can be calculated by summing the individual dipole moments, or
end p.51
atomic polarizations, to get a macroscopic polarization which then plays its normal role in Maxwell's equations. If the laser reaches steady-state oscillation, this process comes to a close. The field which results from Maxwell's equations must then be the same as the field which causes the atoms to radiate. As Lamb explains:
We understand the mechanism of laser oscillation as follows: an assumed electromagnetic field E(r,t) polarizes the atoms of the medium creating electric dipole moments P
i(r,t) which add up to produce a macroscopic polarization density P(r,t). This polarization acts further as the source of a reaction field E′ (r,t) according to Maxwell's equations. The condition for laser oscillation is then that the assumed field be just equal to the reaction field.
14Fig.
2.8 is Lamb's own diagram of the process.
Since the characteristics of laser oscillation that Lamb wanted to learn about depend on the macroscopic polarization, he was led to look at the atomic polarizations. In quantum mechanics the derivative for the atomic polarizations depends on the population differences, and vice versa. The two are yoked together: the rate of change of the population difference at a given time depends on the polarization at that time. But the polarization has been changing in a way dependent on the population difference at earlier times, which depends on the polarization at those times, and so on.
To solve the equations, Lamb used a perturbation analysis. Roughly, the perturbation analysis goes like this. To get the first-order approximation for the polarization, insert the initial value for the population difference, and integrate over time. Similarly, for the first-order approximation in the population difference, insert the initial value for the polarization. For the second-order approximations use, not the initial values in the time integrals, but the first-order values; and so on. It turns out that the contributions alternate through the orders, in just the way one naturally thinks about the problem. First, in zero order, the original inverted population difference interacts with the field, which produces a polarization contribution in first order; this in turn makes for a new population contribution in second order; which gives rise to a new polarization in third order. The first-order polarization, which has not yet taken into account any feedback from the stimulated atoms, is accurate enough to calculate the threshold of oscillation but not to study
end p.52
steady-state oscillation. Hence Lamb concentrated on the third-order polarization.
Calculating the intensity from the third-order polarization, one discovers the Lamb dip. But Lamb did not see the cause for the dip. Why? Because of an unfortunate shift in the order of integration.
15In calculating the third-order polarization one must integrate through time over the second-order population difference. Recall from the discussion of Doppler-shifting that the population difference varies significantly with the velocity of the atoms. Since the macroscopic polarization depends on the total contribution from all the atoms at all velocities, the calculation must integrate over velocity as well. For mathematical convenience, Lamb did the velocity integral first, then the time integral, and he thus wiped out the velocity information before solving for the population difference. He never saw the two holes at + ν and − ν that would account for the dip.
By 1963 Gould and Bennett had suggested the hole-burning explanation, and Lamb had inverted the integrals and derived the velocity dependence of the population difference. The calculation of the intensity, and back-tracking of the kind done by Sargent, Scully, and Lamb, is routine from that point on. But in 1961 and 1962 Lamb had not seen the true causal story, and he was very puzzled. What did he do? He did exactly the kind of mathematical back-tracking that we have seen from the text he wrote later with Sargent and Scully. He himself says, 'I tried very hard to find [the] origin [of the dip]
in my equations.'
16Lamb's back-tracking is just what one would expect: 'The dependence of a typical term . . . is . . . '; 'the physical consequence of the appearance of terms involving
Kν . . . is . . . '; 'only
end p.53
the first two possibilities are able to lead to non vanishing interference . . . ' Finally Lamb concludes,
Physically, one may say that a dominant type of process involves three interactions: first, one with a right (left) running wave at
t″′, then one with a left (right) running wave at
t″, and finally one with a left (right) running wave at
t′, with the time integrals obeying t − t′ = t″ − t″′ so that the accumulated Doppler phase angle . . . cancels out at time
t″′.
17Lamb spent a good deal of time trying to figure out the physical significance of these time interval terms but he could not find a causal role for them:
18'I never was able to get much insight from this kind of thing. The correct interpretation would have been obvious if I had held back the ν integration . . . '
19 So here is a clear case. The mathematical back-tracking that I claim is necessary to support a causal story is not sufficient to pick out the causal story. The velocity dependence of the population difference plays a significant role in the physical production of the dip, whereas facts about the time intervals are merely side-effects. Yet the mathematical dependencies are completely analogous. The first is singled out rather than the second, not by mathematical back-tracking, but by our antecedent causal knowledge, which in this case is highly detailed. Lamb starts with a sophisticated causal picture, outlined in Fig.
2.8—a picture of an applied field which polarizes the atoms and produces dipole moments. The dipole moments add up to a macroscopic polarization that produces a field which polarizes the atoms, and so on. The velocity dependence fits in a clear and precise way into this picture. But no role can be found for the time difference equalities. These find no place in the causal process that we already know to be taking place.
The lesson of this example for physics is that new causal knowledge can be built only from old causal knowledge. There is no way to get it from equations and associations by themselves. But there is nothing at all special about physics in this respect. I have gone into an example in physics in some detail just because this is one area in which the belief has been particularly entrenched that we can make do with equations alone. That is nowhere true. The last chapter argued that facts about associations can help us to find out about
end p.54
causes; but it must be apparent that the methods proposed there need causal information at the start. The next section will reinforce this point, this time setting the discussion of probabilities and causes in a more informal context than that of Chapter
1.
2.3. New Knowledge Requires Old Knowledge
It is an old and very natural idea that correlation is some kind of sign of causation, and most contemporary philosophical accounts take this idea as their starting-point: although causes may not be universally conjoined with their effects, at least they should increase their frequency. Formally,
P(
E/
C) >
P(
E/¬
C). But as Chapter
1 made clear, a correlation between two variables is not a reliable indicator that one causes the other, nor conversely. Two features
A and
B may be correlated, not because either one causes the other, but because they are joint effects of some shared cause
C. We have just seen an example of this in the last section, where the Lamb dip and the time-interval equalities owed their co-association to the combination of hole-burning and Doppler-shifting. The correlation described in Chapter
1 between Mackie's Manchester hooters and the stopping of work for the day in London is another good illustration. In these kinds of case, the frequency of
Bs among
As is greater than among not-
As for a somewhat complicated reason. A case in which
A occurs is more likely to have been preceded by
C than one in which
A does not occur, and once a
C has been selected, the effect
B will be more likely as well.
The conventional solution to this problem is to hold C fixed: that is, to look in populations where C occurs in every case, or else in which it occurs in no case at all. In either population, selecting an A will have no effect on the chance of selecting a C; so if A and B continue to be correlated in either of those populations, there must be some further reason. If all the other causes and preventatives of B have been held fixed as well, the only remaining account of the correlation is that A itself is a cause of B. So to test for a causal connection between a putative cause C and an effect E, it is not enough to compare P(E/C) with P(E/¬ C). Rather one must compare P(E/C ± F 1. . . ± F n) with P(E/¬ C ± F 1± . . . ± F n), for each of the possible arrangements of E's other causes, here designated by F 1, . . . , F n. The symbol ± F nindicates a definite choice of either F nor ¬ F n. This suggests the following criterion:
end p.55
| |
| P(E/C ± F 1± . . . ± Fn) > P(E/¬ C ± F 1. . . ± F n), where {F 1, . . . , F n, C} is a complete causal set for E. |
To be a complete causal set for
E means, roughly, to include all of
E's causes. The exact formulation is tricky; at this stage one should attend to more evident problems.
The practical difficulties with this criterion are conspicuous. The conditioning factors
F 1, . . . ,
F nmust include every single factor, other than
C itself, that either causes or prevents
E, otherwise the criterion is useless. Finding a correlation, or a lack of it, between
C and
E signifies nothing about their causal connection. A sequence of studies in econometrics will illustrate. The studies, published between 1972 and 1982 by Christopher Sims, used a criterion due to C.W.J. Granger to test the Keynesian hypothesis that money causes income.
20The Granger criterion is the exact analogue of condition
CC, extended to treat time-series data.
Sims began his discussion of causal ordering with the remark, 'It has long been known that money stock and current dollar measures of economic activity are positively correlated.' But which way, if any, does the causal influence run? Sims used a test based on the Granger definition to decide: 'The main empirical finding is that the hypothesis that causality is unidirectional from money to income agrees with the postwar U.S. data, whereas the hypothesis that causality is unidirectional from income to money is rejected.'
21 In this study no variables other than money stock and gross national product were considered. But in a four-variable model, containing not just money stock and GNP but also domestic prices and nominal interest rates, the conclusion no longer followed. Without interest rates, changes in money supply account for 37 per cent of the variance in production; with interest included, the money supply accounts for only 4 per cent of variance in production.
22When the model is expanded to include federal expenditures and federal
end p.56
revenues as well, the results are slightly different again. Production then seems to be influenced by both revenues and interest rates; and money supply by interest rates alone, with no direct influence from money to production. According to Sims, the 'simultaneous downward movements in [money] and [production] emerge as responses to interest rate disturbances in the larger system'.
23So the hypothesis that money causes income is not supported in this model. The well-known correlation between money stock and production appears to result from the action of a joint preventative. But the question remains, is a six-variable model large enough? Or will more variables reverse the findings, and show that money does cause activity in the economy after all?
The question of which variables to include is not only practical but of considerable philosophical importance as well. Followers of Hume would like to reduce causal claims to facts about association. Granger's definition is an attempt to do just that. But, like the related criterion
CC, it will not serve Hume's purposes. The definition is incomplete until the conditioning factors are specified. How are these factors to be selected? Roughly, every conditioning factor must be a genuine cause (or preventative) and together they must make up a complete set of causes. Nothing more, nor less, will do. So neither
CC nor the definition of Granger can provide a way to replace the concept of causality by pure association, a thesis already suggested by Chapter
1.
Granger's own solution to the problem is to include among the conditioning factors 'all the knowledge in the universe available at that time' except information about the putative cause.
24But this suggestion does not work. For it takes a strategy that is efficacious in the analysis of singular causal claims and tries to apply it to claims at the generic level, where it does not make sense. The question at issue is not one of singular causation: 'Did the occurrence of
C in a specific individual at a specific time (say 1000 hrs. on 3 March 1988) cause an occurrence of
E after a designated interval (say at 1100 hrs. on 3 March 1988)?'; but rather the general one: 'Is it a true law that
Cs occurring at some time
t cause
Es to occur at
t + δ
t?'
end p.57
The first claim refers to a specific individual at a specific time, and that individual will have some fixed history. One can at least imagine the question, 'For individuals with just that history, what is the probability for E to occur given that C does?' But in the second case, no specific individual and no specific time are picked out. No history is identified, so the suggestion to hold fixed everything that has happened to that individual up to that time does not make sense. What is needed is a list that tells what features are relevant at each time—not at each historical time but at each 'unit interval' before the occurrence of E. Indeed, this is probably the natural way to read Granger's suggestion: hold fixed the value of all variables from a designated set which have a time index earlier than that of the effect in question. But then the question cannot be avoided of what makes a factor relevant. If the correct sense of relevance is causal relevance, the problem of circularity remains.
A weaker, non-causal sense of relevance could evade the problem; but it is difficult to find a satisfactory one. The most immediate suggestion is to include everything which is statistically relevant, that is, everything which itself makes a difference to the probability of the effect. But this suggestion does not pick a unique set: F and F′ can both be irrelevant to E, simpliciter: P(E/F) = P(E/¬ F) and P(E/F′) = P(E/¬ F′); yet each is relevant relative to the other: P(E/F ± F′) ≠ P(E/¬ F ± F′) and P(E/F′ ± F) ≠ P(E/¬ F′ ± F). Are F and F′ both to be counted causes, or neither?
Sometimes it is maintained that probability arrangements like these will not really occur unless both
F and
F′ are indeed genuine causes. They may appear to be based on the evidence of finite data; but a frequency in a finite population is not the same as a true probability on almost anyone's view of probability. True probabilities do not behave that way.
25This seems an excellent proposal. But it does require some robust sense of 'true' probability; and one that does not itself depend on a prior causal notion, if it is to avoid the same circularity that besets principles like
CC.
One ready candidate is the concept of personal, or subjective, probability. But this concept will not serve as it is usually developed. Much work has been done to fill out the unfledged idea of personal
end p.58
degree of belief, to develop it into a rich and precise concept. Notably there is the proof that degrees of belief that are coherent (in the sense that, translated into betting rates, they do not allow a surewin strategy on the part of the betting opponent) will necessarily satisfy the probability calculus, as well as the identification of degrees of belief with betting rates; and the associated psychological experiments to determine, for instance, how fine-grained people's degrees of belief actually are. But nothing in this work tailors degrees of belief to match in the right way with the individual's causal beliefs. The concept of degree of belief must be narrowed before it will serve to rule out renegade probabilities that make trouble for the analysis of causation. Again, the question is, can this be done by using only concepts which are philosophically prior to causal notions? My own view, as an empiricist, is that probabilities are just frequencies that pass various favoured tests for stability. In that case it is quite evident that problematic cases occur regularly, and some stronger sense of relevance than statistical relevance will be needed to infer causes from probabilities.
An example of precisely the sort just described has shaken Clark Glymour's confidence in his own bootstrap method, which I advocate throughout this book. In Discovering Causal Structure, Glymour and co-authors Richard Scheines, Peter Spirtes, and Kevin Kelly describe an experiment in which newly released felons were given unemployment payments for up to six months after getting out of prison so long as they were not working. The rearrest rate was about the same in the test group, which received the unemployment payment, as in the control group, which did not. Did that mean that the payments were causally irrelevant to rearrest? The experimenters thought not. They hypothesized that the payments did indeed reduce recidivism, but that the effect was exactly offset by the influence of unemployment, which acts to increase recidivism. Glymour and co-authors favour the opposite hypothesis, that the payments are irrelevant; correlatively, they must endorse the claim that so too is unemployment.
It is clear from the tone of the discussion that the joint authors take this stand in part because of the bad arguments on the other side. Indeed, they introduce the example in order to undercut a lot of well-justified objections to the way in which causal modelling is put to use: 'In criticisms of causal modelling, judgements about issues of principle are often entangled with criticisms of particularly bad
end p.59
practices.'
26But the example also fits their central philosophical theses. They maintain that the relation between causal claims and statistics is hypothetico-deductive, so that there is never any way to infer from the statistics to the hypotheses. Nevertheless, among hypotheses that are all consistent with the same statistical data, some will be more probable than others.
The hypotheses that are more likely to be true for Glymour, Scheines, Kelly, and Spirtes are those that balance among three principles which 'interact and conflict'. One principle is called Thurstone's Principle: 'Other things being equal, a model should not imply constraints that are not supported by the sample data.'
27This principle matters for the realistic and difficult job that is undertaken in
Discovering Causal Structure—that of discovering the structures from actual data. In the language of Chapter
1 of this book, they simultaneously confront both Hume's problem—how do causes relate to probabilities?—and the problem of estimation—how can probabilities be inferred from very limited data? In the context of Hume's problem alone, Thurstone's Principle offers the relatively trivial advice to reject models that have false consequences; hence it will not be of special interest here.
The second of the three principles is very familiar—the Principle of Simplicity: simpler models are more likely to be true than complex ones, where 'In the special case of causal models, we understand simpler models to be those that posit fewer causal connections. In effect, we suppose an initial bias against causal connections, and require that a case be made for any causal claims.'
28This explains their preference for the model which has taken neither cash-in-pocket nor unemployment to influence recidivism, rather than both.
The remaining criterion is expressed in Spearman's Principle: 'Other things being equal, prefer those models that, for all values of their free parameters (the linear coefficients), entail the constraints judged to hold in the population.'
29To see how this principle works in the recidivism example, return to the methods of Chapter
1. Let
r represent recidivism,
c, cash-in-pocket, and
u, unemployment. It is clear from the situation that unemployment is one of the causes that
end p.60
produces the cash grant: so set
c =
u +
w. Adding the second hypothesis that neither
c nor
u acts as a cause of
r gives rise to Model 1:
Here
v and
w are error terms, assumed to be independent of the explicit causes in their respective equations. Coupling instead the hypothesis that both
c and
u are causes gives Model 2:
To produce the result in Model
2 that cash-in-pocket and unemployment exactly cancel each other in their influence on recidivism, set α γ = − β. In this case both models imply that there will be no correlation between cash-in-pocket and recidivism. But they differ in the degree to which they satisfy Spearman's Principle. Model 1 has no free parameters (excepting those for the distributions of the error terms); the structure itself implies the observed lack of correlation. Model 2 implies this result only when an additional constraint on the free parameters is added. So according to Spearman's Principle, Model 1 is more likely to be true than Model 2.
The kind of practical empiricism that I advocate looks at the matter entirely differently. If unemployment really does cause recidivism, then, given the lack of correlation, cash-in-pocket must inhibit it; and if unemployment does not cause recidivism, then cash-in-pocket is irrelevant as well. The statistics cannot be put to work without knowing what the facts are about the influence of unemployment; and there is no way to know short of looking. Glymour, Scheines, Kelly, and Spirtes advocate a short cut. For them, it is more likely that unemployment does not cause recidivism than that it does. That is in part because of their 'initial bias against causal connections'. But the hypothesis that unemployment does not cause recidivism is as much an empirical hypothesis as the contrary; and it should not be accepted, one way or the other, unless it has been reliably tested. Failing such evidence, how should one answer the question, 'Does cash-in-hand inhibit recidivism?' Glymour, Scheines, Kelly, and Spirtes are willing to claim, 'Probably not'. But
end p.61
the empiricist who insists on measurement will say, 'We don't know; and no matter how pressing the question, it is no good pretending one has (or probably has) an answer, when one doesn't.' For an empiricist, there is no alternative to evidence.
30 2.4. How Causal Reasoning Succeeds
The first main thesis of this book is that causal hypotheses pose no special problems for science. They can be as reliably tested as anything else. Chapter
1 showed one method that works; it explained how we can use probabilities as instruments to measure causes. But in the face of the discussion of sections
2.2 and
2.3, that claim seems disingenuous. Certainly we can measure causes with probabilities, but only if we have an impossible amount of information to begin with. It seems that a method that requires that you know all the other causes of a given effect before you can establish any one them is no method at all.
But that is not true. For the method does not literally require one to know all the other causes. Rather, what you must know are some facts about what the probabilities are in populations that are homogeneous with respect to all these other causes, and that you can sometimes find out without first having to know what all those causes are. That is the point of the randomized experiment which will be the first topic of this section. I will not spend long in discussing randomized experiments, however, for the theory is well known; and I want quickly to go on to an interesting example in physics where the experimenters claim they do know about all the other possible factors that might make a difference. That is the topic of the second section.
2.4.1. The Randomized Experiment
The classical discussion of randomization is R. A. Fisher's Design of
end p.62
Experiments,
31and his own example will illustrate. An experiment is conducted to test whether a particular person—let us call her
A—can tell whether it is the milk or the tea which has first been added to the cup.
A is to be given eight cups of tea to judge, four in which the tea came first, and four in which the milk came first. The null hypothesis in this case is that
A possesses no special talents at all, and her sorting is pure chance—that is, it has no cause. But obviously there is a great deal of room between having no special talent and sorting purely by chance. There is a near-infinity of other differences between cups of tea that may cause
A to sort them one way rather than another. What if all the cups with milk in first also had sugar in them? This is obviously an easy occurrence to prevent. But what about the others? Fisher says:
In practice it is probable that the cups will differ perceptibly in the thickness or smoothness of their material, that the quantities of milk added to the different cups will not be exactly equal, that the strength of the infusion of tea may change between pouring the first and the last cup, and that the temperature also at which the tea is tasted will change during the course of the experiment. These are only examples of the differences probably present; it would be impossible to present an exhaustive list of such possible differences appropriate to any one kind of experiment, because the uncontrolled causes which may influence the result are always strictly innumerable.
32 Fisher points here to just the problem discussed in section
2.3. The putative cause of
A's choices is the fact that the milk and not the tea was first added to the cup. But so long as this fact is correlated with any other possible influences on her choice, the probabilities in the experiment will signify nothing about the hypothesis in question. Formula
CC attacks this problem directly. The correlation between the putative cause and all other possible causes is broken by controlling for all these others. Fisher opposes this strategy, and for the obvious reason:
whatever degree of care and experimental skill is expended in equalizing the conditions, other than the one under test, which are liable to affect the result, this equalization must always be to a greater or less extent incomplete, and in many important practical cases will certainly be grossly defective.
33end p.63
The solution instead is to randomize.
An ideal randomized treatment-and-control group experiment must satisfy two related conditions. It will consist of two groups, the treatment group and the control group; in Fisher's experiment, the cups with milk in first and those with tea in first. The first requirement is that all other causes that bear on the effect in question should have the same probability distribution in both groups. Thick cups should not be more probable in one group than the other, nor strong infusions, nor any other possibly relevant factor. The second requirement is that the assignment of individuals to either the treatment or the control group should be statistically independent of all other causally relevant features that an individual has or will come to have. The random selection of individuals for one group or the other is supposed to be a help to both ends. But it is not the full story. Consider the placebo effect. How is the medicine to be introduced without also introducing some expectation for recovery, or perhaps, in the case of counter-suggestibility, some dread? This itself may be relevant to whether one gets better or not. There are a number of clever and well-known devices, for example blinds and double blinds, to deal with problems like these, and a vast amount of accompanying literature, both philosophical and practical, discussing their effectiveness.
I do not want to pursue this literature, but instead to return to my brief characterization of the ideal experiment. All of these procedures and devices are designed to ensure that the results of the real experiment will be as close as possible to the results of an ideal experiment. But one must still ask the prior question: what do the results of an ideal experiment signify? If the effect should have a higher probability in the treatment group than in the control group, what does that say about the causal powers of the treatment? In Chapter
3 I will describe an argument that starts with premisses about the nature of causality—like 'Every occurrence of the effect has a cause'—and ends with the conclusion that the kind of probability increases prescribed by Principle
CC will be sufficient to guarantee the truth of the corresponding causal law, and conversely. One could try a similar tactic with the ideal experiment: try to lay out just what assumptions must be made in order to justify the ideal experiment as an appropriate device for establishing causal laws. But this extra argument is not necessary. For it is not difficult to see that
end p.64
that experiment—that is, ideal experiment—and Principle CC are bound to agree.
To show this properly one needs to provide some formal framework where the ideal experiment can be defined precisely and a proof can be given. I think the gain is not sufficient to warrant doing that here. Intuitively the result is easy to see by considering a mental partitioning of both the control group and the test group into the kinds of homogeneous population that appear in CC. If, as CC requires, the probability of the effect occurring is greater with the treatment than without it in each of these sub-populations, then it will also be greater in the whole population where the treatment occurs than where it does not; and the converse as well. The point is that CC and the ideal experiment dovetail. We do not have the puzzle of two separate and independent methodologies that are both supposed to establish the same facts. Instead we can see why one works if and only if the other does.
In fact, matters are more complicated, for a number of caveats have to be added. These are taken up in Chapter
3. The convergence of the two methodologies is only assured in certain especially simple cases, where a given cause has no contrary capacities—that is, capacities both to produce and to inhibit the effect. When more complicated cases are taken into account, the randomized experiment, even in the ideal, is not capable of picking out the causal laws correctly, whereas an amended version of
CC is. That means that the methodology of
CC is more basic than that of the controlled experiment. One can derive from
CC why experiments allow us to draw some kinds of conclusion and not others; and also why they fail where they do.
In part it is because Principle CC is more fundamental that I concentrate so much on it in this book and on the more formal but analogous methods of causal modelling theories, rather than pursuing the study of randomized experiments. The point of discussing them here is to recall that the demand for total information that seems to follow from CC is not necessarily fatal. Sometimes we can find out what would happen were all the other causes held fixed without even knowing what the factors are that should be held fixed. It is important to keep in mind, however, that it takes an ideal experiment to do this, and not a real one. For, as with Principle CC itself, the connection between causality and regularity is drawn already
end p.65
homogeneous to 3 parts in 10−7 this will be no mere wishful thinking on his part. Rather, he will have measured and found it to be so, using Player's new precession interferometric techniques.
We return in the end, of course, full circle to the original question. Grant that the information about the connection between space-time curvature and precession can be secured, at least as well as any other information. Must it necessarily be given an ineliminably causal interpretation? Can this seemingly causal claim not be read in some more Humean way? That is another question, indeed the question that takes up the rest of this chapter and much of the book. The special case of physics has already been discussed in section
2.2.
I argued at the beginning of this chapter that the necessity for background causal knowledge could not be avoided. The problem has on each occasion to be faced, and to be solved. I have given a rough sketch of the most dominant kinds of solution: try to construct an experiment that gets the conclusions indirectly without learning the causes one by one, or try to figure out exactly what they are and control for them. In practice both kinds of experiments borrow a little of both methods. Usually social scientists first control for the causes they know about, and then randomize; and in the end the gravity-probe experiment is going to roll the spacecraft in the hope of averaging out any causes they did not know about. Now I want to turn back to the discussion of why this knowledge is necessary, to pursue further the program of Glymour, Scheines, Kelly, and Spirtes, which promises to make this kind of knowledge unnecessary.
2.5. Discovering Causal Structure: Can the Hypothetico-Deductive Method Work?
The bulk of this book is directed against the Humean empiricist, the empiricist who thinks that one cannot find out about causes, only about associations. But it is a subsidiary thesis that causes are, nevertheless, very difficult to discover; and our knowledge, once we have left the safe areas that we command in our practical life, is not very secure, except in a very few of the abstract sciences. The kinds of method endorsed by Glymour, Scheines, Kelly, and Spirtes in Discovering Causal Structure would make causal inference easier—too
end p.71
easy for an empiricist, argued section
2.2. Yet for an adherent of causality, methods like theirs are probably the most natural alternative to the stringent requirement of measurement that I insist on. So it is important to look at more of the details to see how effective their kind of programme can be. The story I will tell is one of systematic and interwoven differences. We disagree, not just on the central issue of measurement versus the hypothetico-deductive method, but on a large number of the supporting theses as well. They tell one story and I another; and it probably speaks in favour of at least the consistency of both that the stories disagree through and through.
This section will lay out some of the details of these systematic differences. The reader who wishes to proceed with the main arguments of this chapter should go directly to the next section. A good deal of the hard work and the original ideas that have gone into Discovering Causal Structure are concerned with how to implement the basic philosophical point of view in a computer program called 'Tetrad'. I will have little to say about Tetrad, but instead will focus on the more abstract issues that are relevant to the theses I want to defend in this book.
The first and most important difference between my point of view and that argued in Discovering Causal Structure has already been registered. I insist that scientific hypotheses be tested. Glymour, Scheines, Kelly, and Spirtes despair of ever having enough knowledge to execute a reliable test; still, they think they can tell which structures are more likely to be true. To do so, they will judge theories by a combination of a simplicity requirement and Spearman's Principle. I do not hold with either of these requirements.
With respect to the first, the debate is an old and familiar one. They assume that structures that are simple are more likely to be true than ones that are complex. I maintain just the opposite. In
How the Laws of Physics Lie37I have argued that nature is complex through and through: even at the level of fundamental theory, simplicity is gained only at the cost of misrepresentation. It is all the more so at the very concrete level at which the causal structures in question here are supposed to obtain. Matters are always likely to be more complicated than one thinks, rather than less. This view agrees exactly with that of Trygve Haavelmo in his early defence of the probability
end p.72
approach in econometrics. Haavelmo argued that the most acceptable structures in economics will generally be more complex than at first seems necessary:
Every research worker in the field of economics has, probably, had the following experience: When we try to apply relations established by economic theory to actually observed series for the variables involved, we frequently find that the theoretical relations are 'unnecessarily complicated'; we can do well with fewer variables than assumed a priori.
38What is the reason why it sometimes looks as if a simpler model will do? Haavelmo says that it is because, in some situations or over some periods of time, special conditions obtain. A large number of factors stay fixed, or average each other out. But these special conditions, he points out, cannot be relied on; so the original structures usually do not work when applied to different cases.
we also know that, when we try to make predictions by such simplified relations for a new set of data, the relations often break down, i.e., there appears to be a
break in the structure of the data. For the new set of data we might also find a simple relation, but a
different one.
39Glymour, Scheines, Kelly, and Spirtes believe that simpler models are better. But I agree with Haavelmo. Simplicity is an artefact of too narrow a focus.
The issues involved in Spearman's Principle are less familiar, and the differing philosophical positions less well rehearsed; so it needs a more detailed discussion. A first thing to note about this principle is how relative its application is. For what is and is not a free parameter in a theory depends on what form the theory is supposed to take. Recall from Chapter
1 that there is a close connection between the linear equations of a causal model and the probability distribution of the variables in the model. It may help to begin by focusing on the probability distributions. It is usually assumed that the distributions involved will be multi-variate normal ones. This is the kind of constraint on the form of theory that I have in mind when I say that what counts as a free parameter in a theory depends on a prior specification of what form the theory must have.
For simplicity, consider just two variables, x and y, whose
end p.73
distribution is bi-variate normal. That means that the distribution in each variable considered separately (the marginal distribution) is normal; so too is the distribution for
y in a cross-section at any point on the
x curve, and vice versa; i.e. the conditional distribution
f(
y/
x) is normal and so is
f(
x/
y). Making the usual simplification that
x and
y both have mean 0 and variance 1, and representing their covariance by ρ, it follows by a standard theorem that the mean of the conditional distribution of
y given a fixed value of
x is ρ
x; that the conditional variance is 1 − ρ
2; and that
(where μ has mean 0 and variance 1 − ρ
2).
Now consider the parameters, first for one variable, then for two. Given that a distribution in one variable is normal, the distribution is entirely specified by adding information about its mean and its variance; that is, the uni-variate normal distribution has just two free parameters. But this is not a necessary fact about a distribution. The exponential distribution has one; and for a totally arbitrary distribution one must specify not only the mean and the variance but an infinite sequence of higher-order moments as well. The point is a trivial one. The number of free parameters depends on how much information is antecedently specified about the distribution. In saying that the distribution in one variable is normal, one has already narrowed the choice from infinity to two; the fact that it is normal dictates what the higher-order moments will be once those two are fixed.
The bi-variate normal distribution has the five parameters described above: the mean and variance of each of the marginal distributions, plus the covariance of the two variables. But if one begins with the assumption that the distribution is a bi-variate normal with independent variables, then ρ must be equal to zero, and there are only four free parameters. Imagine, then, that one has (as in the example of cash-in-pocket and recidivism) data to show there is no correlation between x and y. Relative to one starting-point—the assumption that the distribution is bi-variate normal—the prediction of zero correlation is forthcoming only if one of the free parameters, ρ, takes on a certain specific value, in this case zero. Relative to the second starting-point the prediction follows, as in Model 1, no matter what values the free parameters take.
The same kind of point can be made by looking directly at the
end p.74
equations; and it is especially telling in the recidivism example. The most general set of consistent linear equations in
n-variables with error terms included looks like this
When these equations are supposed to represent causal structures, time-ordering can be used to bring the equations into a triangular array. The resulting form for a model in three variables is familiar from Chapter
1. Taking
r, u, c as the three variables involved, it looks like this:
This is the general form for any causal model that involves just these variables essentially, and in the prescribed temporal order.
This is the form that is usually presupposed. But relative to this form, Spearman's Principle does not favour Model 1 over Model 2 in the recidivism example; rather, it does the opposite. Altogether there are three free parameters in the general form (excepting those that describe the distribution of the error terms): α, β and γ. In order to produce the prediction of zero correlation between r and c, Model 1 sets both β = 0 and γ = 0. Model 2 obtains the same result by setting β = − α γ, where it is assumed that γ is negative and α and β are positive. In Model 1, just one parameter can still take arbitrary values; whereas in Model 2, two can. So Model 1 does not have the advantage by Spearman's Principle after all. Even if it did, it is not clear what that would signify. For the number of parameters necessary to account for the 'data' depends on what specific aspects of the data have been selected for attention. The correlation between r and c is just one aspect of the data. In principle one would want a model to account, not just for this or that correlation, but for the full probability distribution; and to do that, all the parameters would have to be fixed.
Glymour, Scheines, Kelly, and Spirtes avoid this problem by giving up the standard theory form. They proceed in a different order from what one might expect. They do not start with the usual sets of linear equations and then use Spearman's Principle to try to
end p.75
select among specific models. Rather, they use Spearman's Principle at the start to motivate a new general form for a causal theory. Here is how I would describe what they do. To get the new theory form, start with the old linear equations but replace all the usual continuous-valued parameters in the equations by parameters that take ony two values, zero and one. One can think of these new parameters as boxes, where the boxes are to be filled in with either a
yes or a
no; yes if the corresponding causal connection obtains and
no if it does not. A specific theory consists in a determination of which boxes contain
yes and which
no.
40This new theory form, they suppose, involves no free parameters (the two-valued ones do not seem to count). Here is where Spearman's Principle enters, to argue for the new theory form over the old.
The upshot of this implementation of Spearman's Principle is to reduce the information given in a causal theory from that implied by the full set of equations to just what is available from the corresponding causal pictures. The theory tells only about causal structures, that is, it tells qualitatively which features cause which others, with no information about the strengths of the influence involved. This move from the old theory form to the new one is total and irreversible in the Glymour, Scheines, Kelly, and Spirtes methodology, since the computer program they designed to rank causal theories chooses only among causal structures. It never looks at sets of equations, where numerical values need to be filled in. I think this is a mistake, for both tactical and philosophical reasons.
The philosophical reasons are the main theme of the remaining chapters of this book. The decision taken by Glymour, Scheines, Kelly, and Spirtes commits them to an unexpected view of causality. It makes sense to look exclusively at causal structures (i.e. the graphs) only if one assumes that (at least for the most part) any theory that implies the data from the causal structure alone is more likely to be true than one that uses the numbers as well. This makes causal laws fundamentally qualitative: it supposes that in nature only facts about what causes what are important; facts about strengths of influences are set by nature at best as an afterthought. I take it, by contrast, that the numbers matter, and that they can be relied on just as much as the presence or absence of the causal
end p.76
relations themselves—and that that is a fact of vital practical significance.
The assumption that causal relations are stable lies behind the efforts of Glymour, Scheines, Kelly, and Spirtes, as it does behind the arguments of Chapter
1. In both cases, causal hypotheses are inferred from probabilities that obtain in one particular kind of situation, most preferably the situation of either a randomized or of a controlled experiment. But the point is not just to determine what happens in the special conditions of the experiment itself. The assumption is that the same causal relations that are found in the experiment will continue to obtain when the circumstances shift to more natural environments. But the same is true for hypotheses about strength of causal capacities. They too can be exported from the special circumstances in which they are measured to the larger world around. These claims are developed in later chapters. They enter here because they stand opposed to the view of Glymour, Scheines, Kelly, and Spirtes, which puts causal relations first. I think, by contrast, that much of nature is quantitative and that causal capacities and their strengths go hand-in-hand.
The tactical objections to restricting the admissible theories to just the causal structures are a consequence of problems that this decision raises for the concept of evidence. If there are no numbers in the theory, the theory will not be able to account for numbers in the data. One certainly will not be able, even in principle, to derive the full distribution from the theory. What, then, should the theory account for? Obviously one must look to the qualitative relations that hold in the data. Which ones?
Glymour, Scheines, Kelly, and Spirtes focus on correlations, and they pick two specific kinds of constraint on the relations among correlations that must be satisfied. The first requirement is that any relation of the form ρ xz− ρ xyρ yz= 0 must be satisfied, where ρ abrepresents the correlation between a and b. This factor is just the numerator of ρ xz · y—i.e. the partial correlation between x and z controlling for y. Hence it is zero if and only if the partial correlation is zero. The partial correlation ρ xz · yis quite analogous to the conditional expectation Exp(xz/ y) that has been used throughout this book, and for purposes of the discussion here the reader can treat the two as identical. For Glymour, Scheines, Kelly, and Spirtes, then, the first constraint insists that the causal structure account for as many vanishing partial correlations in the data as possible.
end p.77
The second constraint concerns tetrad relations, from which their computer program takes its name. These relations involve products of correlations among a set of four measured variables. Glymour, Scheines, Kelly, and Spirtes explain them this way: 'Tetrad equations say that one product of correlations (or covariances) equals another product of correlations (or covariances).'
41For example, ρ
xyρ
zw= ρ
xzρ
wy.
The choice that Glymour, Scheines, Kelly, and Spirtes make about which qualitative relations matter is very different from the one dictated by a methodology of testing. This is clear as soon as one reflects on how the relevant relations must be selected by an empiricist who wishes to use statistics to measure causes. In general the empiricist's rule is this: the data that are relevant are the data that will fix the truth or falsity of the hypothesis, given the other known facts. That means, in the context of causal modelling, that the relevant relations among the probabilities are those that tell whether the appropriate parameter is zero or not (or, if more precise information about the strength of the capacities is required, those that identify the numerical value of the parameter). Other relations that may hold, or fail to hold, do not matter.
Because Glymour, Scheines, Kelly, and Spirtes employ the hypothetico-deductive method, they must proceed in the opposite order. Their basic strategy for judging among models is two-staged: first list all the relevant relations that hold in the data, then scan the structures to see which accounts for the greatest number of these relations in the simplest way. That means that they need to find some specific set of relations that will be relevant for every model. But, from the empiricist point of view, no such thing exists.
Consider Glymour, Scheines, Kelly, and Spirtes, own choice. They ask the models to predict, from their structure alone, all and only correlations (that is, not the numerical values of these correlations but whether they exist or not) that hold in the data between two variables, with a third held fixed, and also any remaining tetrad relations that are not already implied by the vanishing partial correlations. This is an apt choice if all the variables have two causes, but not otherwise. With three causes, the relevant correlation between a putative cause and its effect is the one that shows up—or fails
end p.78
to—with the other two held fixed; for four causes, three must be held fixed; and so forth; and when there is only one cause the correlation itself, with nothing held fixed, is what matters.
A better solution might be to include the higher-order (and lower-order) correlations as well: that is, to ask a structure to account for as many of the relations as might be relevant as it can. But that is bound to be wrong, since the very fact that makes an nth-order partial correlation the relevant one—that is, the fact that there are n other causes operating—also makes both higher- and lower-order ones irrelevant. Nor is there reason to think that some other choice will fare better. For what qualitative relations are relevant in the data depends on what causal structure is true; and each causal hypothesis must be judged against the data that are relevant for the structure they are, in fact, embedded in.
The difference in point of view about what data are relevant can be illustrated in the case that Glymour, Scheines, Kelly, and Spirtes themselves present to show what is wrong with methods, like those I have been defending, that try to infer causes from partial correlations. They discuss a study by Michael Timberlake and Kirk R. Williams that purports to show that 'foreign investment penetration [
f] increases government repression [
r] in non-core countries'. But, say Glymour, Scheines, Kelly, and Spirtes:
A straightforward embarrassment to the theory is that political exclusion is
negatively correlated with foreign investment penetration, and foreign investment penetration is
positively correlated with civil liberties and negatively correlated with government sanctions. Everything appears to be just the opposite of what the theory requires. The gravamen of the Timberlake and Williams argument is that these correlations are misleading, and when other appropriate variables are controlled for, the effects are reversed.
42The other variables Timberlake and Williams control for are energy development (
e) and civil liberties (
c). Controlling for these variables, they find that ρ
fr · ec≠ 0; that is, foreign investment and repression are indeed correlated.
To keep the algebra simple, I will assume that the original (non-partial) correlation between foreign investment (f) and political repression (r) is not negative, but zero, which would be equally
end p.79
damaging to Timberlake and Williams's hypothesis were no other causes at work.
43We begin, then, by supposing that the data supports
The model proposed by Timberlake and Williams then would be this:
where it is assumed that γ is negative. Since it is assumed throughout that the initial nodes of a graph are uncorrelated, a new factor
g has been introduced to produce the postulated correlation between
f and
c. The structure for Model TW is pictured in Fig.
2.12. The prediction that
f and
r are uncorrelated follows by setting α δ = − β γ.
Exactly the same thing is supposed to be happening in this structure as in the recidivism example: foreign investment causes political repression, but it is correlated with an equally powerful factor that prevents repression—civil liberties. Foreign investors tend to invest more in countries that already have a high level of civil liberties, and the two opposing factors exactly cancel each other, so that no positive correlation is observed between foreign investment and repression,
end p.80
despite the causal connection between the two. Is this a likely story? Just as in the recidivism example, it takes a lot more information before that question can be answered. In particular, independent evidence is necessary for the auxiliary assumptions connecting energy development and absence of civil liberties with political oppression. Otherwise the appearance of a correlation between
f and
r, when
e and
c are held fixed, is entirely irrelevant. Apparently that is a problem in this study: '
Absolutely nothing has been done to show that . . . [the] accompanying causal assumptions are correct.'
44But that is a case of bad practice, and, as Glymour Scheines, Kelly, and Spirtes stress in defending their own methods, bad practices do not necessarily imply bad principles.
To focus on the underlying principles, then, for the sake of argument assume that the other two causal assumptions are reasonably well established (along with the assumption that these exhaust the causes); and, correlatively, that the data support the corresponding probabilistic relations
These are the ones that matter for measuring the three causal influences.
Glymour, Scheines, Kelly, and Spirtes focus on different features from these three, since they look either for tetrad equations or vanishing three-variable partials. They find two relations in the data that are relevant under their criteria:
Looking at
d 4and
d 5, and ignoring
d 1,
d 2,
d 3, they favour a number of alternative structures, any one of which they take to be more likely than the one pictured in Fig.
2.12. Each of their structures reverses the causal order of
r and
c, making
c depend on
r, which is the easiest way to secure
d 5. Since the methods described in Chapter
1 assume that temporal order between causes and effects is fixed, a structure in which
f, c, and
e all precede
r, as they do in Model TW, will serve better for comparing the two approaches. Glymour, Scheines, Kelly,
end p.81
and Spirtes doubt that foreign investment really causes political repression. Fig.
2.13 will do as an example of a structure that implies
d 0,
d 4, and
d 5just from its causal relations alone, keeps the original time-ordering, and builds in the hypothesis favoured by Glymour, Scheines, Kelly, and Spirtes that investment does not produce repression. Again the model includes an extra, unknown, cause, represented by
g.
The example is an unfortunate one for Glymour, Scheines, Kelly, and Spirtes, however. For there is no way that this graph can account for the data
d 1,
d 2,
d 3, with or without numbers. Nor is it possible with any other graph, so long as the time precedence of
e, f, and
c over
r is maintained. If the original time-order is not to be violated, any model which accounts for
d 4and
d 5on the basis of its structure alone, and is consistent with
d 1,
d 2, and
d 3as well, must include the hypothesis that foreign investment causes repression.
45This raises a problem of implementation. The Tetrad program designed by Glymour, Scheines, Kelly, and Spirtes will never find this out, since it never goes back to the full models that have numbers in them, and it never looks at any further relations in the data beside tetrads and three-variable partial correlations. Should the relevant data be extended to include the four-variable partial correlations supposed to hold in this case, then the structure pictured in Fig.
2.13 would be ranked very high, despite the fact that it is inconsistent with the data, since it can account for four of the five qualitative relations (
d 3: ρ
cr.ef≠ 0 is the exception) on the basis of structures alone. One can, of course, check independently whether there is a corresponding
end p.82
model consistent with all the data available before finally accepting a graph recommended by Tetrad. But in the all too common cases, like this one, where no such model exists, the Tetrad programme has no more help to offer.
For completeness, I give Model GSKS, which includes Glymour, Scheines, Kelly, and Spirtes' favoured hypothesis, that foreign investment does not cause repression, and which does account for all the data, though of course not on the basis of structure alone:
where α δ = − γ φ. The corresponding causal structure is given in Fig.
2.14.
Which is preferable of Model TW and Model GSKS? Model GSKS contains Glymour, Scheines, Kelly, and Spirtes' favoured hypothesis, that investment does not cause repression; Model TW says that it does. It is clear by now that an empiricist cannot resolve the question without more evidence. But neither can Glymour, Scheines, Kelly, and Spirtes. Even if one were willing to accept that simplicity, conjoined with Spearman's and Thurstone's Principles, was likely to take one closer to the truth, rather than further away, the three principles are of no help in this particular decision.
It is apparent that the decision about which kinds of data are relevant matters here. If tetrads and three-variable partial correlations were replaced by four-variable partial correlations, both Model TW and Model GSKS would fare very well, since
d 1,
d 2, and
d 3follow, in both cases, just from the graphs (assuming Exp(
g2) ≠ 0). But the point of the examples is to make clear that that does not make the four-variable partials a better choice. Nor are they a worse choice. It
end p.83
is reasonable to demand that a model should account, from its structure alone, for just those relations in the data that hold because of the structure. But those relations cannot be identified in advance of any knowledge about what the structure is.
Given that they are, nevertheless, going to set out to choose some relations in advance, why do Glymour, Scheines, Kelly, and Spirtes opt for three-variable partials and tetrads? Practical problems of implementation provide a partial answer. But the choice is also based on principle. In the methodology of Chapter
1, three-variable partial correlations are significant because they identify causes in a three-variable model. That is not why Glymour, Scheines, Kelly, and Spirtes pick them. They pick them because of specific graph-theoretical results that show how three-variable partial correlations in the data generate constraints on the graph. In particular, their theorem (4.2) lays out some general conditions that any graph must satisfy if it is to account for vanishing correlations of this kind. Tetrad equations have a similar, though somewhat looser, motivation. Tetrad relations will occur when—though not only when—certain kinds of symmetry exist in the causal structure. What Glymour, Scheines, Kelly, and Spirtes themselves say about the vanishing three-variable correlations in the foreign investment example is this: 'These equations are interesting exactly
because they are the kind of relationship among correlations that can be explained by causal structure.'
46 This is an exciting attempt to secure universal relevance; but I do not think the connection is strong enough to do the job. The reason becomes clear by looking at a different kind of example, where problems of relevance arise regularly—say a scattering experiment. Consider an attempt to study the break-up of beryllium 9 by bombarding lithium 7 with deuterons. Two alpha particles and a neutron are produced. It is the alpha particles that will get detected. Since the final state involves three bodies, and not just two, the decay process may occur in a variety of different stages, so the model may be somewhat complicated. Imagine that the target is lithium sprayed on a carbon film, and that there are impurities in the target that produce irrelevant alpha peaks: the experimenters take measurements at a number of angles, and they find peaks at energies in the spectrum where they are not expected. In this case they do not use this data to build their model of beryllium 9; rather, they discard the
end p.84
data because it is an artefact of the experimental set-up. Good methodology insists that they should have independent reasons in order to declare the data irrelevant. But the converse is what is at stake here: what does it take to make the peaks relevant? It is true that if the peaks were produced by the process under study, they would constrain the model in important ways. But that fact does not argue that they are relevant.
The same should be true for causal structures as well. Theorems like Glymour, Scheines, Kelly, and Spirtes (4.2) may seem to provide a way to mark out certain relations as relevant: the vanishing three-variable partial correlation is relevant to judging every structure because it implies some facts about what any structure will look like that can account for it. But the original question is always looming: should a structure be required to account for it? The model should do so, of course; but should it do so on the basis of structure alone? The point is almost a logical one. Glymour, Scheines, Kelly, and Spirtes take an implication that holds conditionally, and use it as if it were categorical. The fact that a particular kind of datum would dictate constraints on the structure of the phenomena under study if it were relevant does not bear—one way or the other—on whether it is relevant.
So the argument has come full circle. Glymour, Scheines, Kelly, and Spirtes do a masterful job tailoring the pieces—Spearman's Principle, Thurstone's Principle, and the demand for simplicity—to fit together into a coherent and, equally importantly, a usable whole. They themselves mention the possibility of expanding the program, to seek out higher-order correlations in the data and to look for structures that would account for these correlations; and they are always willing to balance criteria against one another. But, as an empiricist, I want neither more correlations, nor different ones. I want just those in each case that will measure the causes there.
2.6. Conclusion
It will be apparent that the conclusions reached so far in this chapter are somewhat at odds with the conclusions of the preceding chapter. So too is the methodology. This chapter develops a connection between probabilities and causes outside of any formal framework. It begins with the hypothesis that the introduction of a cause should
end p.85
increase the level of the effect; and then considers what further conditions must obtain to ensure that this increase will reveal itself in the probabilities. The result is formula
CC, a formula that demands a lot in terms of background knowledge: what matters, according to this formula, is whether the cause increases the probability of the effect in populations where all other causally relevant features are held fixed. As section
2.4 argued, this does not necessarily mean that one has to know all the other causes in order to find out about any one of them. There are methods that circumvent the need for full information. Nevertheless, the justification for those methods rests on a formula that involves conditionalizing on a complete set of other causal factors.
Chapter
1 proceeded more formally; in the case of qualitative causes, by working with complete sets of inus conditions, and in the case of quantitative causes, by using sets of simultaneous linear equations. This means, in both cases, that very exact kinds of non-causal, or associational, information are presupposed: the truth of an equation, or the correctness of a set of conditions necessary and sufficient for the effect. It may seem that the use of these formal techniques avoids the need for conditioning on other causal factors. But that is not so. Before closing the chapter I want to point out exactly why. The reason lies in the open back-path-assumption. In order to draw causal conclusions from an equation, and thereby from the probabilities that identify the parameters of the equation, one must be assured that each factor in the equation has an open back path; and what that guarantees is that each of the factors is a genuine cause after all. So, in fact, the partial conditional probability that tells whether a particular parameter is zero or not—and thus tells whether a putative cause is genuine—is after all a probability that conditions on a complete set of other causal factors. The partial conditional probabilities that must be computed, either on the advice of Chapter
1 or on the advice of Chapter
2, are exactly the same. In a sense the open-back-path condition is doing the same kind of work that is done by the randomizations and controls of section
2.4: it side-steps the need for direct knowledge of the other causes by taking advantage of other knowledge that is more readily accessible.
There is a trade-off involved, however. For the open-back-path condition is quite cumbersome, and the accompanying proofs are bitty and inelegant. Both elegance and simplicity are restored if the condition is dropped and the devices of section
2.2 are resorted to:
end p.86
just demand that the enterprise begins with a knowledge of what all the other causes are. This same device will work in the linear structures of Chapter
1 as well, and it is a device that was used by many of the early econometricians, whose methods are mimicked in Chapter
1. The experience in econometrics is worth reflecting on. It is apparent in the fifty-year history of that field that the appeal of this strategy will depend on how confident one is about getting the necessary starting knowledge. Theory is the natural place to look for it; and much of the early work in econometrics was carried through in a more optimistic mood about economic theory than is now common. When theory was in fashion, it was possible to adopt the pretence that the set of factors under consideration includes a full set of genuine causes. The problem then was to eliminate the phonies; and the methods of multiple correlation which were emerging in econometrics—and which are copied in simpler form in Chapter
1—are well suited to just that task.
This is one of the features that Keynes stressed in his criticisms of the new uses of statistical techniques advocated by Tinbergen. The remark quoted in Chapter
1 continues:
If we already know what the causes are, then (provided all the other conditions given below are satisfied) Prof. Tinbergen, given the statistical facts, claims to be able to attribute to the causes their proper quantitative importance . . .
Am I right in thinking that the method of multiple correlation analysis essentially depends on the economist having furnished, not merely a list of the significant causes, which is correct so far as it goes, but a
complete list?
47As Keynes points out, the conventional methods are good for eliminating possibly relevant factors; but they are of no use unless the original set includes at least all the genuine causes. It is all right to start with too much, but not with too little. One can see this by returning to Fig.
1.5 (b). In that figure neither
y nor
x 1appears, along with
x 2, as a possible cause for
x e. Once both are included, the putative causes are no longer linearly independent (since
x 2=
ax 1+
y/
g). This means that the coefficients in the expanded equation,
x e=
ax 1+
bx 2+
cy +
u 3, are no longer identifiable and so cannot be determined from the data; the conventional methods will not tell which are zero and which are not.
end p.87
But linear independence bears only on identifiability, and it is clear from Chapter
1 that some additional argument is required to get from identifiability to causality. In this case the argument is easy—at least given something like Reichenbach's Principle, which is a necessary assumption in any attempt to forge a link between causes and probabilities. By hypothesis, the study is to begin with a set of variables {
x i} which includes at least all the causes of the effect variable
x e, and possibly other factors as well.
48The variables in this set must also satisfy a second condition: each is linearly independent of the others. Now an equation is given for
x e(
x e= Σ
a ix i). The equation is supposed to be true, but does it correctly represent the causal structure? If it does not, then by Reichenbach's Principle there must be another equation that does. By hypothesis this second equation will contain no new variables. But setting the two equations equal produces a linear relation among the members of {
x i}, which has been assumed impossible. So the original equation must give the true causal picture.
This is essentially the same line of argument as the one which guarantees identifiability; and, indeed, I am sure that this connection between the two ideas was intended by the early econometricians. Problems of identifiability, which were central to the work at the Cowles Commission, were for them problems of causality. This is discussed more fully in Chapter
4, but it is already apparent even in the piece by Herbert Simon described in Chapter
1. What Simon does is to solve a simple identification problem; what he says he does is to determine causal structure.
Why, then, are econometricians nowadays taught that identifiability and causality are distinct? One of the answers to this question illustrates the central thesis of this chapter: no causes in, no causes out. One has to start with causal concerns, and with causal information, to get causal answers. This is apparent in the comparison of Fig.
1.5 (a) and
(b).
The equations of Fig.
1.5 (b) are identifiable. One may suppose, moreover, that they are true, and adequate for prediction. Yet Fig.
1.5 (b) does not picture the real causal structure, which is supposed to be given in Fig.
1.5 (a). The link between identifiability
end p.88
and causality is missing because the equation for
x eassociated with Fig.
1.5 (b) does not include all the causes.
These are typical of the kinds of equation produced nowadays in econometrics—either the structures are not causal at all, or they are mixed structures, where some of the variables are causal and others are not. This is apparent from the form of the structures—almost none has the recursive or triangular form that is induced by the time-ordering of causes and effects. Even those that do often add phenomenological constraints, by setting one quantity equal to another, without any pretence of representing the causal processes that produce the constraints.
Consider, for example, the continuation of Malinvaud's discussion, cited in Chapter
1, of non-recursive systems. Malinvaud introduces a classic model of the competitive market, a non-recursive, non-causal model, which he describes as interdependent. The model sets quantity demanded at any price equal to quantity supplied at that price. The process which leads to this equilibrium was described by L. Walras as a continuing negotiation between buyers and sellers. I quote at length from Malinvaud, to give a detailed sense of how the structure of this causal process comes to be omitted. Malinvaud points out that, in the usual econometric models,
effective supply, effective demand and price are finally determined at the same time. This is expressed by the interdependent system.
However, it is true that the model does not describe the actual process of reaching equilibrium, and therefore it obscures the elementary relationships of cause and effect. A different model would give a better description of the tentative movements towards equilibrium. . . .
[This example] shows why we must often make do with the interdependent models in econometric investigations. For it is impossible for us to observe the process of reaching equilibrium at every moment of time. We must be content to record from actual transactions the prices which hold and the quantities which are exchanged. Only the interdependent models . . . will interpret such statistics correctly.
More generally, available statistics often relate to relatively long periods, for example to periods of a year, in which time lags are much less significant. Thus, periods of a month would no doubt reveal a causal chain among income, consumption and production. But this model could not be used directly to interpret annual data. It is then better to keep to an interdependent system like the elementary Keynesian model, than to introduce the
end p.89
blatantly false assumption that consumption in year
t depends solely on disposable income in year
t − 1, which depends solely on production during year
t − 2.
49 There are other, more theoretical reasons for thinking that some given set of variables in an econometric model does not represent the basic causes at work: perhaps the whole level of analysis is wrong. But Malinvaud presents one simple set of reasons. Like any science whose basic methods depend on the estimation of probabilities, econometrics needs data. That means that it must use variables that can be measured, and variables for which statistics can be gathered. What kinds of model can be constructed with variables like that? Models that can be relied on for forecasting and planning? That is a deep question; a question that divides the realist from the instrumentalist. For the answer depends on how closely the power of a model to forecast and predict is tied to its ability to replicate the actual causal processes. What Malinvaud's remarks show is why the models actually in use are not causal, though they may well be identifiable. The reason supports the central thesis of this chapter: you can only expect your structures to be causal if you begin with causal variables.
end p.90

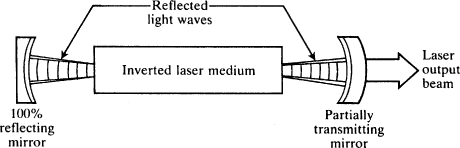

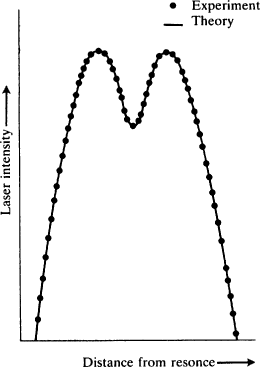
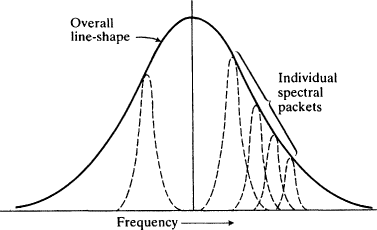
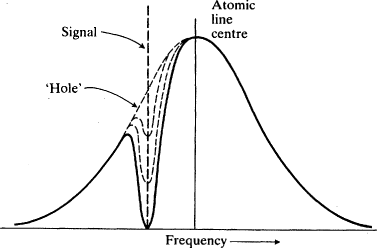
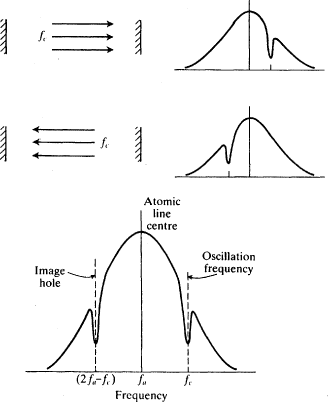
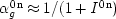



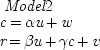
 2K), and that produces its own sequence of problems. The need for cryogenic temperatures is over-determined, however; for the star-tracking telescope must also operate at liquid helium temperatures to remove distortion due to temperature gradients. The entire experimental module is shown in Fig.
2K), and that produces its own sequence of problems. The need for cryogenic temperatures is over-determined, however; for the star-tracking telescope must also operate at liquid helium temperatures to remove distortion due to temperature gradients. The entire experimental module is shown in Fig.