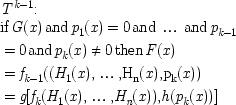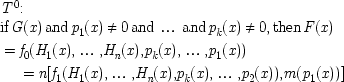as they are laws of pure association, but rejects causes and capacities. Usually the programme that goes with this view proposes to account for the systematic use of causal language in science by reconstructing it as an indirect way of describing facts about laws of association. The point of this chapter has been to argue that that project will not work. I want to conclude with my own account of why it will not work.
The chapter begins with a picture of layered modalities: first laws of association, then causal laws, then capacities. But section
4.4 argues that this picture is only half true. The capacities are more than modalities; they are something in the world. Where, then, does that leave the lower modal levels, and in particular the laws of association? The popular view, which I want to attack, takes these as nature's givens. It is by laying down laws that nature regulates the unfolding of events. But I want to urge a very different picture that is open to us once we admit capacities into our world. It is not the laws that are fundamental, but rather the capacities. Nature selects the capacities that different factors shall have and sets bounds on how they can interplay. Whatever associations occur in nature arise as a consequence of the actions of these more fundamental capacities. In a sense, there are no laws of association at all. They are epiphenomena.
This, it seems to me, will be the most powerful way to reconstruct a reasonable image of science; and it is this picture that I urge philosophers to take up and develop. Already there is one concrete exemplar available to show how it can work, in systems of simultaneous equations of the causal-modelling literature that have played a role throughout this book. There we see one way to represent capacities with precise quantitative strengths, and with a systematic pattern for their interplay: in general they are additive, with departures from additivity represented by interaction terms. What is important for the project of taking capacities as primary is that these models show how it is possible to begin with capacities and to end with probabilities which describe the associations in nature as a consequence.
One of the chief strengths of an ontology which takes capacities as fundamental and associations as secondary is the quite important one that it can hope to give a far more realistic picture than can the alternative. We all know that the regularity of nature so central to the more conventional picture is a pretence. It does not lie on
end p.181
nature's surface, but must be conceived, if there at all, to be somewhere in the deep structure. I, in general, advise against deep structures. John Stuart Mill gives an alternative account, and this account makes good sense of what we observe about regularities and the lack of regularities. Nature, as it usually occurs, is a changing mix of different causes, coming and going; a stable pattern of association can emerge only when the mix is pinned down over some period or in some place. Indeed, where is it that we really do see associations that have the kind of permanence that could entitle them to be called law-like? The ancient examples are in the heavens, where the perturbing causes are rare or small in their influence; and the modern examples are in the physics laboratory, where, as described in Chapter
2, our control is so precise that we ourselves can regulate the mix of causes at work. Otherwise, it seems to me, these vaunted laws of association are still very-long-outstanding promissory notes: laws of association are in fact quite uncommon in nature, and should not be seen as fundamental to how it operates. They are only fundamental to us, for they are one of the principal tools that we can use to learn about nature's capacities; and, in fact, most of the regularities that do obtain are ones constructed by us for just that purpose.
47
end p.182
5 Abstract and Concrete
Abstract: Modern science relies heavily on Galilean idealization, which establishes ceteris paribus laws—laws about what happens when a factor operates unimpeded. But these laws are of little direct use since factors seldom do operate unimpeded. The follow-up to Galilean idealization is abstraction—we talk simply of what the factor does. The best way to understand this abstraction is as an ascription of a capacity, not in terms of any kind of laws. Even the process of 'de-idealization' or of 'concretization' that results in a concrete phenomenological law inevitably involves further concepts in the capacity family.
Nancy Cartwright
5.1. Introduction
For John Stuart Mill the basic laws of economics are laws about enduring 'tendencies' and not laws about what happens; that is, laws about capacities and not just about the sequence of events. This is because the laws treat causes singly, but reality rarely isolates them from one another in this tidy way. Mill also maintains that the laws of economics are 'abstract', and by that he means something different. For the use of 'abstract' points, not to the content of the laws, but rather to the methods by which they can be established: inevitably an element of the a priori must be involved. But his claims about method and about content are driven by the same problems. Recall section
4.5. How could one establish a law about capacities by pure induction? The relevant instances of the isolated capacities never occur. We cannot do experiments in political economy which guarantee that each cause operates separately in order to observe its natural consequences. Worse, the mix of causes is continually changing, and it is almost always impossible to ascertain which are present. In a situation like this, the conventional methods of induction will be insufficient. For Mill, they must be augmented by principles we can glean from our general knowledge of human nature. This 'mixed method of induction and ratiocination' is what he calls 'a priori'.
1
The very same problems that force one to use a mixed method in 'going upwards' from experience to general principle reappear when one wants to turn about and 'argue
downwards from that general principle to a variety of specific conclusions'.
2 These problems are the focus of this chapter; and most of the themes are already present in Mill. First he argues that the route downwards involves adding
end p.183
corrections to allow for the effects of the disturbing causes that may be at work in any given situation. Following an analysis by Leszek Nowak, section
5.4 calls this the process of
concretization. It is important that the additions and corrections should not be arbitrary:
The disturbing causes are not to be handed over to be dealt with by mere conjecture . . . they may at first have been considered merely as a non-assignable deduction to be made by guess from the result given by the general principles of science; but in time many of them are brought within the pale of the abstract science itself. . . . The disturbing causes have their laws, as the causes which are thereby disturbed have theirs . . .
3 The passage contains in brief the answer to an important Humean question: why do we need to introduce capacities to serve as the subjects of our laws? Is it not sufficient to recognize that these laws are not literal descriptions of what happens in actual circumstances, but rather some kind of abstraction? The answer is, in a sense, yes: it is sufficient to recognize that the laws are abstractions of a certain sort. But that fact does not do the work a Humean needs. For capacities cannot be so readily decoupled from this notion of abstraction, since the converse processes of abstraction and concretization have no content unless a rich ontology of competing capacities and disturbances is presupposed. This mirrors the conclusions of section
4.4 that capacities cannot be modalized away, and is also one of the main theses of this chapter.
A second thesis which I share with Mill concerns the source of our information about the disturbing causes for any given case. Some are given by theory, but many are not:
The disturbing causes are sometimes circumstances which operate upon human conduct through the same principle of human nature with which political economy is conversant. . . . Of disturbances of this description every political economist can produce many examples. In other instances, the disturbing cause is some other law of human nature. In the latter case, it can never fall within the province of political economy; it belongs to some other science; and here the mere political economist, he who has studied no science but political economy, if he attempt to apply his science to practice, will fail.
4 The fact that a great many of the disturbing causes fall outside the domain of the science in question leads to serious problems when we
end p.184
try to tie our theories to reality. For it means there is never any recipe for how to get from the abstract theory to any of the concrete systems it is supposed to treat. We have only the trivial advice, 'Add back all the causes that have been left out and calculate the total effect by combining the capacities.' Is this the best we can do? If so, it highlights how ineliminable capacities are from our image of science; but it makes for a rather impoverished philosophy. I call this 'the problem of material abstraction'. Although I will have much more to say about it, I do not really have a complete analysis of the problem. I aim here to demonstrate its importance.
That indeed is the principal point of this chapter. I am going to describe a variety of different kinds of abstraction in science, and especially in physics. My central thesis is that modern science works by abstraction; and my central worry is that philosophers have no good account of how. In many cases the abstractions can be taken as claims about capacities; and hence this thesis supports my doctrine of the reality of capacities. But it has wider implications than that. I have wanted to argue, not just for capacities, but against laws; and where abstraction reigns, I will suggest, laws—in the conventional empiricist sense—have no fundamental role to play in scientific theory. In particular, scientific explanation seems to proceed entirely without them. They are the end-point of explanation and not the source.
5.2. Idealization and the Need for Capacities
The problem which drives Mill—and me—to tendencies is sometimes identified by philosophers of science with the problem of Galilean idealization. I begin with a characterization by Ernan McMullin of the specific aspect of Galileo's methods which is most relevant:
The really troublesome impediments, Galileo said more than once, are the causal ones. The unordered world of Nature is a tangle of causal lines; there is no hope of a 'firm science' unless one can somehow simplify the tangle by eliminating, or otherwise neutralizing, the causal lines which impede, or complicate, the action of the factors one is trying to sort out. . . . it is this sort of idealization that is most distinctively 'Galilean' in origin.
5 end p.185
The conceptual project of constructing ideal models along Galilean lines runs in exact parallel with the empirical project of designing a decisive experiment. The logic of such experiments was discussed in Chapter
2. McMullin describes them thus:
Experiment involves the setting up of an environment designed to answer a particular question about physical processes. The experimenter determines how Nature is to be observed, what factors will be varied, which will be held constant, which will be eliminated and so on. This sort of manipulation is not always possible; experimental method cannot be directly applied in palaeontology or in astrophysics, for instance. The move from the complexity of Nature to the specially contrived order of the experiment is a form of idealization. The diversity of causes found in Nature is reduced and made manageable. The influence of impediments, i.e. causal factors which affect the process under study in ways not at present of interest, is eliminated or lessened sufficiently that it may be ignored. Or the effect of the impediment is calculated by a specially designed experiment and then allowed for in order to determine what the 'pure case' would look like.
6 McMullin himself summarizes what the problem of Galilean idealization is:
In Galileo's dialogue,
The New Sciences, Simplicio, the spokesman for the Aristotelian tradition, objects strongly to the techniques of idealization that underlie the proposed 'new science' of mechanics. He urges that they tend to falsify the
real world which is not neat and regular, as the idealized laws would make it seem, but complicated and messy.
7 This problem is often thought to have a variety of fairly obvious solutions. McMullin's own paper is an attempt to lay these solutions out in a clear and persuasive way. I want to explain in this section why these solutions, good for the purposes for which they are intended, are nevertheless not solutions to the right problem. For they are solutions to an epistemological problem about how we know what happens in ideal circumstances, and not to the question which bears on capacities, the question of why one can extrapolate beyond the ideal cases.
First, a word about terminology. 'Idealization' is a common word to use in discussing Galilean methods, and also in many discussions about the connection between models and applications in contemporary science. But my problem, and Mill's—and also, I think,
end p.186
the principal problem in connecting models with reality—is not one of idealization, but rather one of abstraction; and that is indeed what the problem was called at the time of Mill and Ricardo. Briefly, I think we can distinguish two different processes of thought, the first of which I will call idealization, the second abstraction. What philosophers usually mean by 'idealization' nowadays is a blend of both. The conflation is not surprising, since the two are intimately linked. Usually, the point of constructing an ideal model is to establish an abstract law. But the law which is actually exemplified in the model is not the same as the abstract law which is thereby established. On the one hand, the abstract law seems to say more, since it is meant to cover a great variety of situations beyond those represented by the ideal model. On the other hand, as Mill pointed out, what it says seems to be literally true in not one of these situations, unless of course we take it to be a law about tendencies.
Here is how I want to distinguish idealization and abstraction for the purposes of this book: in idealization we start with a concrete object and we mentally rearrange some of its inconvenient features—some of its specific properties—before we try to write down a law for it. The paradigm is the frictionless plane. We start with a particular plane, or a whole class of planes. Since we are using these planes to study the inertial properties of matter, we ignore the small perturbations produced by friction. But in fact we cannot just delete factors. Instead we replace them by others which are easier to think about, or with which it is easier to calculate. The model may leave out some features altogether which do not matter to the motion, like the colour of the ball. But it must say something, albeit something idealizing, about all the factors which are relevant. In the end we arrive at a model of an 'ideal plane', ideal for purposes of studying inertial motion. Consider the ball rolling down the plane. To calculate its motion, you must know the forces in each of three orthogonal directions. The problem is undefined until all the forces are specified, so you cannot just omit them. You must set them to some value or other; otherwise you cannot study the actual motion.
By contrast, when we try to formulate Mill's laws of tendencies, we consider the causal factors out of context all together. It is not a matter of changing any particular features or properties, but rather of subtracting, not only the concrete circumstances but even the material in which the cause is embedded and all that follows from that. This means that the law we get by abstracting functions very
end p.187
differently from idealized laws. For example, it is typical in talking about idealizations to say (here I quote specifically from McMullin): the 'departure from truth' is often 'imperceptibly small', or 'if appreciably large' then often 'its effect on the associated model can be estimated and allowed for'.
8 But where relevant features have been genuinely subtracted, it makes no sense to talk about the departure of the remaining law from truth, about whether this departure is small or not, or about how to calculate it. These questions, which are so important when treating of idealizations, are nonsense when it comes to abstractions.
From the remarks of McMullin's that I just cited it will probably be clear why I want to make some distinction of this kind. When my problem of abstraction is assimilated to the problem of idealization, it is easy to think, erroneously, that one can solve the combined problem by developing some notion of approximate truth. But that does not work. That is why I stressed in the discussion of Mill the distinction between laws about tendencies or capacities, and tendency laws—laws that say what tends to happen, or laws that approximate to what happens. This distinction is particularly apparent in modern physics, where most of the effects we study now are very, very small. They make only a tiny contribution to the total behaviour of the system, so that the laws for these effects are very far from approximating to what really happens. Thus the laws in microphysics are results of extreme abstraction, not merely approximating idealizations, and therefore are best seen as laws about capacities and tendencies.
My thesis, then, is that idealization and abstraction are different, and that idealization would be useless if abstraction were not already possible. In the next section I will distinguish a couple of different senses of abstraction, one of which leads to what will be called 'symbolic representations'. The other leads to laws about tendencies. It is abstractions in the sense of tendency laws that concern me. My basic idea is that the method of Galilean idealization, which is at the heart of all modern physics, is a method that presupposes tendencies or capacities in nature. We can see at least what my thesis amounts to by considering typical discussions of idealization, and the questions they are designed to answer. First there is a familiar philosophical topic:
end p.188
(1) |
How can we know what would happen in ideal (i.e. not real) circumstances?
|
Most of McMullin's discussion addresses this question. A typical answer tries to extrapolate in some systematic way: you look at what happens as you get closer and closer to the ideal—for instance, you make the plane smoother and smoother—and then you try to take some kind of limit. What would happen if the plane were perfectly smooth? This raises a second question:
(2) |
Is the ideal some kind of limit of the real?
|
This question is the focus of the historian Amos Funkenstein, in a discussion I will describe below. My question is yet a third one:
(3) |
What difference does it make?
|
Imagine that what happens in some ideal circumstance is indeed a limiting case of what happens in a series of closer and closer approximations to it; assume, moreover, that we have some good idea of how to extrapolate the series to its limit. So now we know what would happen if the circumstances were ideal. What does that teach us? We think it teaches us a lot. But to think so is to believe in capacities.
I first came to see this point clearly in a historical setting by thinking about some claims that Amos Funkenstein makes about Galileo's work.
9 So that is the context in which I will try to explain it. Funkenstein thinks about what turns out to be my second question: is the ideal any kind of limit of the real? According to Funkenstein, herein lies the great advance of Galileo. In Aristotle and throughout the Middle Ages, ideal or counterfactual situations were thought to be incommensurable with reality. What happens in real cases, even as they get closer and closer to the ideal, has no bearing on what would happen were ideal circumstances to exist. I give the simplest of Funkenstein's examples, from Aristotle:
Aristotle shows that [motion in the void] is incommensurable, and hence incompatible, with any conceivable motion in the plenum. . . . Other things (force or weight) being equal, the velocity of a body moving (in analogy to forced motion) in the void must always be greater than the velocity of an equal body moving in a medium, however rare, since velocity increases in an
end p.189
inverse proportion to resistance, that is, in direct proportion to the rarity of the medium. Nowhere does Aristotle suggest, as do many of his interpreters to this day, that because of this, motion in the void would be instantaneous or with infinite speed, only that it would be 'beyond any ratio.' The temptation is strong to render his intentions with the equation lim
R → OF/R = ∞ (v = F/R), but it would be wrong. He argues only that velocities in the plenum are commensurable in the proportion of their media, i.e.,
v
1 /
v
2=
m
1 /
m
2 , and that this equation becomes meaningless when
m
2= 0 (void), since there is no proportion between zero and a finite magnitude. The movements of two equal bodies moved by equal forces in the void and in the plenum have no common measures.
10 Here is how Funkenstein summarizes his argument:
Counterfactual states were imagined in the Middle Ages—sometimes even, we saw, as limiting cases. But they were never conceived as commensurable to any of the factual states from which they were extrapolated. No number or magnitude
could be assigned to them. . . . For Galileo, the limiting case, even where it did not describe reality, was the constitutive element in its explanation. The inertial motion of a rolling body, the free fall of a body in a vacuum, and the path of a body projected had to be assigned a definite, normative value.
11 I want to focus on the middle sentence: 'For Galileo the limiting case, even where it did not describe reality, was the constitutive element in its explanation.' I focus on this because it is a glaring non sequitur. Funkenstein has been at pains to show that Galileo took the real and the ideal to be commensurable. Indeed, the section is titled 'Galileo: Idealization as Limiting Cases'. So now, post-Galileo, we think that there is some truth about what happens in ideal cases; we think that that truth is commensurable with what happens in real cases; and we think that we thereby can find out what happens in ideal cases. But what has that to do with explanation? We must not be misled by the 'ideal'. Ideal circumstances are just some circumstances among a great variety of others, with the peculiarly inconvenient characteristic that it is hard for us to figure out what happens in them. Why do we think that what happens in those circumstances will explain what happens elsewhere?
I hope by now it becomes apparent: the logic that uses what happens in ideal circumstances to explain what happens in real ones is the logic of tendencies or capacities. What is an ideal situation for
end p.190
studying a particular factor? It is a situation in which all other 'disturbing' factors are missing. And what is special about that? When all other disturbances are absent, the factor manifests its power explicitly in its behaviour. When nothing else is going on, you can see what tendencies a factor has by looking at what it does. This tells you something about what will happen in very different, mixed circumstances—but only if you assume that the factor has a fixed capacity that it carries with it from situation to situation.
The argument is structurally identical to my arguments in the last chapter that our standard ways of identifying, and then applying, causal models make sense only if one presupposes that there are capacities, stable capacities that remain the same even when they are removed from the context in which they are measured. I began with the econometricians because they are very explicit. But their methods are just a special case of the general method of Galilean idealization, which underlies all modern experimental enquiry. The fundamental idea of the Galilean method is to use what happens in special or ideal cases to explain very different kinds of thing that happen in very non-ideal cases. And John Stuart Mill has taught us that to reason in that way is to presuppose that there are stable tendencies, or capacities, at work in nature—as indeed is reflected in Galileo's own language. In
Two New Sciences, for instance, he explains that he is trying to discover 'the downward tendency which a body has from its own heaviness'.
12 This description of the project is not a happy one for followers of Hume; but it is, I think, a correct one where 'Galilean' method are employed.
5.3. Abstractions Versus Symbolic Representations
There is, according to the last section, an intimate connection between idealization and abstraction, as these ideas were characterized there: one looks for what is true in an ideal model in order to establish an abstract law. But there is a difference between what is true in the model and the abstract law itself. For the ideal model does not separate the factors under study from reality, but rather sets them into a concrete situation. The situation may be counterfactual; still it is realistic in one sense: all the other relevant factors appear as
end p.191
well, so that an actual effect can be calculated. What is ideal about the model is that these factors are assigned especially convenient values to make the calculation easy. Of course, the model is also to a great extent unrealistic. It is after all only a representation, and not the real thing, so necessarily much will be left out. In a scientific model the factors omitted altogether should be those deemed irrelevant to the effect under study. They do not need to be mentioned, because the values that they take will make no difference to the outcome.
But the difference between what is represented and what is not represented is not my main concern here. What I want to stress is the difference between the law which describes the happenings in the model and the abstract law which is thereby established. The first is a kind of ceteris paribus law: it tells what the factor does if circumstances are arranged in a particularly ideal way. In the abstract law the ceteris paribus conditions are dropped; and for good reason, since this law is meant to bear on what happens in the more frequent cases where conditions are not ideal. How are we to understand these abstract laws, laws that describe no real concrete situations not any counterfactual ones either? I have been maintaining that, in certain special cases where the composition of causes is at stake, those laws are best thought of as ascriptions of capacity. Will that serve as a general solution? We must start by distinguishing between two different kinds of abstraction that occur in the construction of theories. The problem of how to reconnect the abstract with the concrete is on a quite different scale in the two cases. Only one admits the tidy solution of tendencies or capacities, and that is the one that matters here. The other sense can be found in Pierre Duhem's well-known discussion of abstraction. This section will describe Duhem's ideas in order to make clear the difference between the two senses.
Duhem used the claim that physics' laws are abstract as a weapon to attack scientific realism. But Duhem was no anti-realist in general. Rather, he wanted to draw a distinction between everyday concepts and the very special concepts of science, especially of mathematical physics. According to Duhem, the concepts of common facts are concrete; those of physics, abstract and symbolic:
When a physicist does an experiment two very distinct kinds of representations of the instruments on which he is working fill his mind: one is the image of the concrete instrument that he manipulates in reality; the other is a
end p.192
schematic model of the same instrument, constructed with the aid of symbols supplied by theories; and it is on this ideal and symbolic instrument that he does his reasoning, and it is to it that he applies the laws and formulas of physics.
13 The two instruments can never collapse into one:
Between an abstract symbol and a concrete fact there may be a correspondence, but there cannot be complete parity; the abstract symbol cannot be the adequate representation of the concrete fact, and the concrete fact cannot be the exact representation of the abstract symbol.
14 For Duhem, a single theoretical fact may correspond to a variety of concrete facts. For example, 'The current is on' corresponds to a collection of concrete facts like the displacement of a spot in a galvanometer, the bubbling in a gas volt-meter, the glow of an incandescent lamp inserted in the wire, and so forth. Conversely:
The same group of concrete facts may be made to correspond in general not with a single symbolic judgment but with an infinity of judgments different from one another and logically in contradiction with one another.
15 In current philosophical jargon, the concrete facts underdetermine the theoretical. The simplest case has to do with the precision of measuring instruments: any of the incompatible values for a theoretical quantity that lie within the range 'of error' of the most precise instrument used correspond equally well to the facts available.
The abstractness of the objects that physicists reason about in contrast to the objects they manipulate comes from two sources. One is connected with issues of wholism, which philosophers nowadays commonly associate with Duhem. Theoretical concepts are abstract because they can only be applied to reality by presupposing an interconnected web of theoretical laws and rules of correction. The second source is connected with the methods modern physics uses to represent reality. Physics aims at simplicity of representation. But nature, as it comes, is complex and intricate. Hence there inevitably arises a mismatch between the abstract-theoretical representation and the concrete situations represented.
end p.193
The result is that the abstract formulae do not describe reality but imaginary constructions. They are best judged neither true nor false of reality itself.
An even more important problem than simplicity of representation, for Duhem, is the mathematical character of physics. The concepts of physics are precise, but reality itself does not exhibit this precise, quantitative nature:
Let us put ourselves in front of a real concrete gas to which we wish to apply Mariotte's (Boyle's) law; we shall not be dealing with a certain concrete temperature, but with some more or less warm gas; we shall not be facing a certain particular pressure embodying the general idea of pressure, but a certain pump on which a weight is brought to bear in a certain manner. No doubt, a certain temperature corresponds to this more or less warm gas, and a certain pressure corresponds to this effort exerted on the pump, but this correspondence is that of a sign to the thing signified and replaced by it, or of a reality to the symbol representing it.
16 Notice here that Duhem is talking about the theoretical concepts of a purely macroscopic physics, and is not concerning himself with the status of tiny, unobservable entities. A second example that Duhem uses is the sun. In order to find a 'precise law of the motion of the sun seen from Paris':
17
The real sun, despite the irregularities of its surface, the enormous protuberances it has, will be replaced by a geometrically perfect sphere, and it is the position of the center of this ideal sphere that these theories will try to determine. . . .
18 This kind of falsification is for Duhem an unavoidable consequence of the mathematical formulation of physics. He seems here to be echoing the earlier criticisms of Laplace and Poisson directed against Fourier's elevation of differential equations to first place in physics. Differential equations require sharp geometric boundaries.
19 So long as the differential equations are taken, as by Poisson especially, merely as convenient summaries of results that can be rigorously established by summing the interactions of molecules, the reality of these boundary conditions is irrelevant. But the
end p.194
issue can no longer be ignored if we drop the molecular basis and adopt the differential equations as primary. When we do so, we inevitably end up with a physics whose concepts no longer describe reality, but are irreducibly 'abstract and symbolic'.
There is a tendency nowadays to see Duhem's problem as one of approximation.
20 This, indeed, as McMullin points out, was Salviati's response to Simplicio: the geometrical configurations of the new world system may not be perfectly realized in nature; still, geometry provides the right way to describe nature. One must just be careful to allow for the impediments of matter when applying the theory to real cases: 'The errors lie then, not in the abstractness or concreteness, not in geometry or physics as such, but in a calculator who does not know how to keep proper accounts.'
21 McMullin acknowledges how controversial this view was. Mathematics itself was on trial as the language of physics. But in the end McMullin endorses the view that the problems are ones of approximation, which can be calculated away:
Mathematical idealization has worked well for the natural sciences. The extent to which it
is an idealization has steadily diminished as the mathematical language itself has become progressively more adapted to the purposes of these sciences. It would be hazardous today to argue . . . that there are causal factors at work in the natural world that are
inherently incapable of being grasped in mathematico-physical terms. The weight of the inductive argument is surely in the opposite direction. But it should be underlined once again that what has made this possible is not so much the reducibility of the physical as the almost unlimited plasticity of the mathematical.
22 Not all modern mathematical physicists have been as optimistic as McMullin. I have already mentioned Laplace and Poisson, who saw special problems in the mathematics of differential equations. Maxwell and Kelvin had even stronger views. They both despaired that any mathematics accessible to the human mind could represent nature even approximately as it is. I describe the barest outlines of their views to make clear the philosophical point. The reading I give of both Maxwell and Kelvin comes from Norton Wise, as does my reading of the debate between Laplace and Poisson, and Fourier; the
end p.195
full story can be found in Crosbie Smith and Norton Wise's biography of Kelvin.
23 The views of Kelvin and Maxwell, according to Wise, were rooted in the problem of free will, of how mind can act on nature without violating any law of nature. They saw a possible solution in a continuum theory of the physical world. Yet even an infinitesimal portion of a true continuum would require an infinite number of variables for a complete mechanical specification, which therefore lay outside human capacity. Furthermore, no portion of a continuum could be regarded as isolated from the remainder, so that only a physics that considered the behaviour of objects in physical connection to the infinity of their surroundings could be considered realistic. Finally, motion in the continuum would present essential instabilities and essential singular points, both incalculable and therefore beyond the scope of mechanical determination and of human knowledge.
In order to obtain a workable description of thermodynamic phenomena in this situation, Maxwell compounded idealizations to produce a statistical mechanics. A dedicated mechanical philosopher, Maxwell nevertheless thought statistics and probability theory a necessary addition. In
How the Laws of Physics Lie,
24 I described how the falsehoods inevitably introduced by the constraints of any given representational scheme can sometimes be mitigated by the introduction of still more falsehood. For example, imagine that one wants to stage a play about the signing of the Declaration of Independence and to make it as realistic as possible; that is, to try to reproduce the events of the signing, as far as one can, on the stage. Literal reproduction will be impossible because of the demands of the theatre. Two participants whisper, conspiring together over some strategy. But the whispering actors cannot be heard, so they stand up and leave the main table, to walk to the side of the stage and speak aloud to each other. I think this is just how Maxwell saw statistical mechanics. Although, considered in itself, the introduction of probabilistic laws was a significant misrepresentation of nature, it was nevertheless the best device to couple to the equally misrepresenting atomistic, or non-continuous, mechanics, in order to save the phenomena.
For Kelvin, too, matters came to a head over questions of thermodynamics
end p.196
and reversibility. He wanted to give up the ordinary
abstract dynamics of points and forces where, as Wise explains, 'total reversibility was conceivable in the idealized world of an isolated, finite system of discrete particles and conservative forces', and replace it by a
physical dynamics more suited to the infinite complexity of the real world, a dynamics where 'reversibility necessarily failed in the infinite real world of imperfectly isolated systems of friction and diffusion phenomena'.
25 But even physical dynamics would still get the essential description of nature wrong, for, as Kelvin said, 'The real phenomena of life infinitely transcend human science'.
26
Both Duhem and Kelvin used the word 'abstract' to describe a mathematical physics that they believed could not adequately picture the world, even by approximation. Duhem also uses the word 'symbolic'; and it is this label that I shall adopt. For I should like to reserve the word 'abstraction' to pick out a more Aristotelian notion, where 'abstraction' means 'taking away' or 'subtraction'. For Aristotle we begin with a concrete particular complete with all its properties. We then strip away—in our imagination—all that is irrelevant to the concerns of the moment to focus on some single property or set of properties, 'as if they were separate'. The important difference is that Aristotle's abstract properties are to be found in the real world whereas, in the view of Kelvin and Duhem, the symbols of physics do not correspond to anything in nature. For Aristotle, at least in principle, all the properties that science will study are there in the objects to begin with.
I say 'in principle' because this claim too is itself some kind of idealization. Consider a triangle, a real triangle drawn on a blackboard. Even when the chalk and the colour and all the other incidental features are subtracted, the shape that is left is never a real triangle. But let us pretend that it is, and use the label abstraction for the process of isolating an individual characteristic or set of characteristics in thought, for that will allow us to set aside one extremely difficult problem while we focus on another. The central question I want to pursue is: what do abstract or symbolic claims say about reality? However this question is to be interpreted, surely the answer must be easier for claims which are abstract in the narrower
end p.197
Aristotelian sense than for those which are symbolic. Since I assume that capacities are as much in the world as anything else, symbolic claims are not so immediately relevant to my project here. So I propose in the remainder of this chapter to concentrate just on the abstract in Aristotle's sense.
Even then the focus needs to be narrowed. For one can in the Aristotelian way abstract all sorts of different features and think about them in all sorts of different ways for different purposes. This is apparent in Aristotle, for the same property can be considered differently by different sciences. The triangular may be considered qua geometrical shape; for instance: are all triangles trilateral? But one may ask different questions and abstract for different purposes. Galileo, for example, speculated on its role in the substructure of matter: are the primitive parts of fire triangular in shape? If the triangles were sharply pointed, they could penetrate into other matter and thus account for why things expand on heating. For the purposes here I want to focus on the kinds of abstraction that end in laws of capacity, where the factor to be isolated is a causal factor and the question to be posed is, 'What does this factor produce by its own nature?' It should be clear by now that I have replaced the essentialism of Aristotle with its talk of natures by the more humdrum concept of capacity, and thereby translated the question into a new one: 'What capacities does this factor possess?' Much of this book has been dedicated to showing how we can answer that question, and in a way that should satisfy any reasonable empiricist. The problem of this chapter, and especially the next section, is almost converse to that one: Given a proposed answer, how is it to be understood? What does the abstract statement of capacity say about any concrete things?
5.4. What Do Abstract Laws Say?
What do abstract laws say about real things? There are two aspects to this question, which may or may not be the same depending on one's philosophical perspective:
(1) |
What facts in the world make abstract claims true?
|
(2) |
How do abstract laws bear on the more concrete and more descriptive laws that fall under them?
|
end p.198
To attack the first question directly is to become involved in ancient problems about the relations among universals or among abstract entities. Does the property of being a gravitational force have the second-level property of carrying a capacity? Or is this rather a way of categorizing the property of force? And in either case, what is the relation between the property itself and the fact which is supposed to be true of it? I want provisionally to set aside these traditional metaphysical issues and to focus instead on the second question, which bears more immediately on the day-to-day conduct of science.
I want to consider the relationship between the abstract capacity claim and the vast network of individual facts and concrete laws that fall under it. By concrete laws I mean ones which fill in, in their antecedent, all the relevant details; so that they can be read as literally true or false in the most straightforward sense. For short, I call this subordinate network of concrete laws the 'phenomenal content' of the abstract capacity law. The question I want to pose is: 'What determines the phenomenal content of an abstract law, and how does the phenomenal content bear on the truth of the law?'
The discussion has several parts. The first, 5.4.1, is a brief survey of some of the literature in semantics that treats of similar problems. But I think no help is to be found there. Essentially, the linguistics literature either reverts to a kind of simplified Platonism or wanders in the same quandaries and with the same kinds of question that I raise here. I include two specimens of recent discussions among philosophers of language to illustrate. The second section
5.4.2, describes the work of Leszek Nowak on abstraction which I think offers the best formulation available of how abstract and concrete laws relate. The last section,
5.4.3, raises a new problem that is not apparent from Nowak's scheme, one which opens new and difficult philosophical questions.
5.4.1. Semantics for Generics and Habituals
There is a new literature in semantics that might be of help, for abstract-tendency laws seem to work in much the same way as ordinary generic sentences, like 'Dogs bark', or habituals, like 'John smokes', and to create many of the same problems. In all three forms it is equally difficult to say what connection there is between individual cases and the more general truth they fall under. It is natural to
end p.199
suppose some kind of quantificational account, but it seems this is no more suitable for more general generic forms than it is for capacity laws. Should the quantifier be 'all' or 'most', or something weaker? None of these works for all of the following:
Dogs are mammals.
Dogs eat meat.
Dogs give milk to their young.
The list is taken from Greg Carlson's 'Generic Terms and Generic Sentences'.
27 One might try to solve the problem it presents by assuming that the meaning of generic sentences is to be given through a disjunction of different quantifiers. But, as Carlson argues, this strategy will not work, since 'the predicted ambiguity fails to materialize'. A conventional solution for capacity laws is to affix some restriction about normal conditions. But the solution fails, for, as sections
4.5 and
5.2 remark, the conditions in which capacities reveal themselves in their canonical behaviour are usually in no sense normal at all; it requires the highly artificial and contrived environment of a laboratory to manifest them. Nor does 'normalcy' seem any better for generics in general, for consider
Frenchmen eat horsemeat.
28 A typical strategy for linguists trying to construct a semantics for generics and habituals is to introduce abstract entities. Carlson is a good example.
29 Dogs in 'Dogs bark' is a kind-denoting term; and the John of 'John smokes' is some kind of abstract construction from the more primitive space-time instances of John which may get involved in specific episodes of smoking. This raises a technical problem. Once there are two different types of John there must equally be different types of smoking, since the enduring individual John is not a proper subject for smoking in the episodic sense, any more than the kind
dogs can bark in the same sense that an individual dog can. The trick, then, is to see that predicates too come in two types: gnomics and episodics; and that this distinction is grounded in a difference in reality:
One plausible answer is that our (conceptual) world consists of two very
end p.200
The cosy realm of mechanics may be an exception. But everywhere else there is no avoiding the problem of how to complete the process of concretization once theory gives out. I have labelled this 'the problem of material abstraction', with the laser example in mind. A physicist may preach the principles by which a laser should operate; but only the engineers know how to extend, correct, modify, or side-step those principles to suit the different materials they may weld together to produce an operating laser. The physics principles somehow abstract from all the different material manifestations of the laser, to provide a general description that is in some sense common to all, though not literally true of any.
But perhaps this focus on physics and how it attaches to the world is misleading. Mill saw the same kind of problem in political economy. There capacities are real, but abstract in just the sense I am trying to characterize: no amount of theory will ever allow us to complete the process of concretization. Each individual case sets its own criteria of relevance. This is the problem I just called 'the problem of material abstraction'. Yet, in political economy, talk about the material system, despite its familiarity, seems just a metaphor. Despite these reservations, I propose to keep to the idea that it is somehow the material that is subtracted in the first step up into theory, since this opens the possibility of using the traditional scheme of Aristotle's four causes to tie together a variety of different kinds of abstraction that occur in science. These are the topics of the next section.
Before that I should issue a warning. I realize that I have not here given a systematic or complete account of the problem that concerns me. What I have done, I hope, is to point to it clearly so that others can make out its importance and pursue it as well. My pointing has not been at all neutral. I chose deliberately the Aristotelian language of matter, form, and function because these terms are fundamental to a preliminary description of the phenomena that appear in my image of science. This language is a threat to the neo-Humean covering-law theorist, and it is meant as such. I think we cannot understand what theory says about the world nor how it bears on it until we have come to understand the various kinds of abstraction that occur in science, as well as the converse processes of concretization that tie these to real material objects. For the neo-Humean, the explanatory structure of nature consists in a set of natural laws which regulate the sequence of events. But I look for an explanatory
end p.211
structure that will make sense of the methods of abstraction and idealization which are at the heart of modern science, and mere laws are not enough for this difficult job. What kind of different explanatory structure is required? That is a question to pursue once the topics of this book are concluded. It is at least clear that a philosophy of science that uses in an essential way the language of 'underlying principles', 'capacities', 'causal structure', 'forms', and 'functions' is no philosophy of science for a neo-Humean world.
5.5. Concreteness and Causal Structure
Material abstraction, the subject of the last section, is crucial for the successful construction of a scientific theory, and it raises interesting and troubling questions about truth and realism in physics. But it is by no means the only kind of abstraction that occurs there. I want in this last section to discuss other kinds of abstraction that take place after the subtraction of matter, to see how they are to be understood. The discussion will centre around some examples that have long perplexed me. A laser is a more concrete object than a damping reservoir; a crystal diode rectifier is likewise more concrete than a reservoir. Why? Most obviously the laser is an object rich in properties, whereas the damping reservoir is practically bare; the crystal diode rectifier is far more fully specified than the reservoir. Certainly sheer number of features makes some difference, I shall argue, but it is not primarily what matters. A far more significant difference depends on the kinds of feature specified, and not on the number. Damping reservoirs (which I will describe in more detail below) are objects identified entirely in terms of their output: they are supposed to eliminate correlations in systems they interact with. But nothing is specified about how they produce this result. Similarly, a rectifier is supposed to turn alternating currents into direct ones. The crystal diode rectifier does the same job, but in a highly specific way. We not only know more about the crystal diode rectifier than about the reservoir; what we know is how it works. We know its causal structure. This, I shall argue, is why the crystal diode rectifier is significantly more concrete than the reservoir, and the laser than the reservoir.
The arguments and ideas of this section are taken from a paper
end p.212
written—and conceived—jointly by Henry Mendell and me.
47 Since there is no possibility of attributing the pieces separably to either of us, I shall follow the opposite strategy and reproduce the final joint product as closely as possible.
Scattered throughout the works of Aristotle we find expressions such as 'things in abstraction' or 'things from abstraction',
48 where, as described earlier in this chapter, 'abstraction' means 'taking away' or 'subtraction'. According to Aristotle, many sciences study objects which have properties subtracted. We begin with a particular substance and all its properties, both accidental and essential. For instance, if we examine a triangle in the context of a geometric discussion, we may begin with a triangular marking on a slate. We then subtract the stone and chalk, the colour, and other properties incidental to being a triangle. What is left when this psychological process is complete is the triangle which is to be treated as if it were substance. The subtracted properties may be conceived as incidental to what the object is treated as, namely a triangle. Of course, what the object actually is, a stone slab, will be among the accidents of the triangle. In other words, abstraction amounts to a psychological isolation of certain aspects of the slate.
Unfortunately, a direct application of Aristotle's concept to lasers and reservoirs would seem to involve us in awkward questions of counting. For Aristotle, the less abstract object is closer to substance than the more abstract. How are lasers closer to substance than reservoirs? By virtue of having fewer inessential properties stripped away? If we adopted this view, we would be faced with the unpleasant task of figuring out how to count properties. A simple example illustrates the difficulties. Suppose we examine two markings on the blackboard, one triangular, the other quadrilateral. We examine the first as a right triangle, the second as a rhombus. To examine the right triangle we must subtract lengths of the sides, and the two acute angles, except such properties as are necessary for the markings to be a right triangle. To examine the rhombus, we subtract lengths of the sides, except the relative lengths of opposite
end p.213
sides, and angles, except the relative size of opposite angles. Are rhombi more or less abstract than right triangles? The question, as would any answer to it, seems pedantic and baroque. For reasons such as this, it is not possible to develop a coherent total ordering for Aristotelian abstract objects. Some entities, such as rhombi and right triangles, are not ordered with respect to each other.
But there are natural ways of partially ordering the abstract. In his discussions of different sciences whose objects are known in abstraction, Aristotle suggests a simple criterion for ordering the relatively abstract and concrete. For example, the objects of geometry and mathematical astronomy are both known in abstraction. But the latter are nearer to substance, and hence are more concrete. Why? It is not because, if we count the properties subtracted in each case, we see that one set is smaller than the other. Rather, since geometry is used in mathematical astronomy, in doing mathematical astronomy we do not subtract geometric properties. But in doing geometry we subtract some properties which are in mathematical astronomy. For example, mathematical astronomy treats of the movement of stars. A geometric treatment of the same objects would not consider the movement, though it might treat the stars as fixed points, and the paths of the stars as circular lines. Hence, Aristotle claims, mathematical astronomy is nearer to substance. For it works with a more complete description of an object, and so comes closer to a description of what the object is.
Even within a science it is possible to see that certain objects are more abstract than others. Triangles are more abstract than right triangles, since the right angle of the right triangle is subtracted when it is treated just as a triangle. Yet all the properties of triangles apply to right triangles. We have, therefore, a means for partially ordering entities: A is a more abstract object than B if the essential properties, those in the description of A, are a proper subset of the essential properties of B.
In a similar way Aristotle orders sciences. Mathematical astronomy studies geometric properties of certain moving points. We can distinguish those properties which pertain to movement and those which pertain to geometric spaces. These constitute two different classes which are basic to human understanding. Thereby we can claim that the objects of science A are more abstract than those of science B if the set of kinds of property treated by A is a proper subset of the kinds of property treated by B. The basic insight is that,
end p.214
where there are two clear classes of properties, the entity with properties from one class will be more abstract than the entity with properties from both; that is, the entities can be ordered by looking at how their properties are nested.
The idea that we can partially order the abstract with reference to the nesting of kinds of property is intuitively reasonable, since the entity described by more kinds of property, in this very straightforward way, does seem to be more completely described. We cannot, however, literally apply these two Aristotelian orderings to the case of reservoirs and lasers: their properties are not nested, nor are they items in different sciences in a hierarchical ordering. Nevertheless, the Aristotelian notion gives us hints. Later in this section, this basic intuition will be deployed to develop a new notion of abstractness which fits the contrast in our paradigmatic case between lasers and reservoirs. But first it is necessary to isolate what the difference is that I have been trying to illustrate with my examples of lasers and reservoirs.
Section
5.4 described one obvious way in which the objects that physicists reason about may be abstract. They may lack stuff, and be made of no material. Contrast helium atoms, infra-red radiation, and electrons, on the one hand, with levers, oscillators, and reservoirs, on the other. The first are characterized in large part by what kinds of stuff they are made from; two electrons, two protons, and two neutrons; or electromagnetic waves between .75 and 1000 microns in length; or negatively charged matter. But its stuff is no part of what makes an oscillator an oscillator or a lever a lever. These objects are characterized in terms of what they do, and they may be made of any material that allows them to do what they are supposed to.
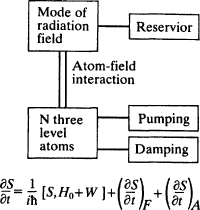
Reservoirs are another good example of this second kind. Reservoirs play a role in a variety of physical theories, especially thermodynamics and electromagnetics. Fundamentally, reservoirs are large objects, in one way or another, that swamp the systems they interact with. With respect to electricity, the earth is a reservoir that 'grounds' moving charge; in thermodynamics, a heat reservoir will give up heat until it finally brings the system it interacts with to its own temperature.
For specificity, the discussion here will concentrate on reservoirs in quantum optics, where the reservoir serves to erase the memory of systems with which it interacts. Correlatively, the reservoir is given
end p.215
only enough formal characteristics to justify this outcome mathematically. To erase the memory in a system, one wants circumstances that would justify introducing a Markov approximation there, and interaction with the reservoir licenses just this. The reservoir is assumed to have a very great number of degrees of freedom. Because it is large and chaotic, correlations among its own states persist for only a very short time, and it in turn destroys correlations in the systems to which it couples. Nothing else is necessary for an object to be a reservoir.
The reservoir is a paradigm 'black box'. We know only its final effects, but nothing of what goes on inside. Intuitively, it is a very abstract object. But what sense of abstractness expresses this intuition? Reservoirs undoubtedly lack stuff. Sometimes the electromagnetic field may serve as a reservoir (for oscillating atoms, for instance); sometimes the walls of a cavity; sometimes the environment in a room. But a large number of objects that physicists reason about lack stuff, and yet most are far more concrete than the reservoir. Consider a laser. Lasers are supposed to amplify light and produce a highly coherent beam of radiation. They too, like the reservoir, can come in a variety of substances. They may be made of rare earth ions floating in dissolved molecules, or from organic dye solutions, or from ruby rods, or numerous other materials. Yet certainly there is a sense in which the laser is a far more concrete object than a reservoir. It is that sense of concrete that I am trying to explain.
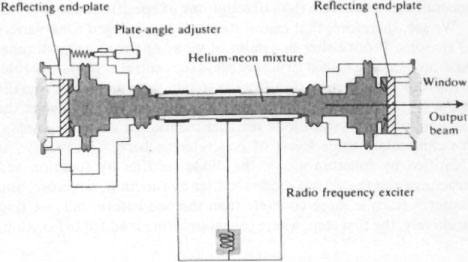
What is it that makes a laser a laser? The answer to this question will provide the key to my problem about the abstract and the concrete. The first operating laser was a ruby laser made in 1960 by T. H. Maimon. Any introductory discussion will point out that ruby is not essential. For instances:
Since 1960 many different kinds of lasers have been made. They do not all contain ruby, nor do they all use a flashtube [as Maimon's did]. But what they do have in common is an
active material (e.g. the ruby) to convert some of the energy into laser light; a
pumping source (e.g., the flashtube) to provide energy; and mirrors, one of which is semi-transparent, to make the beam traverse the active material many times and so become greatly amplified.
49 end p.216
We see that a laser consists of at least three distinct components: the active material, the pump, and the mirrors. A more theoretical treatment will also add the damping reservoir as another essential component in this list (see Fig.
5.2, p. 000). In one sense, then, the specific make-up of the laser is irrelevant: no particular material is required. But in another sense the make-up is essential. The components are a part of the characterization of a laser as a laser.
But the specification of the components is not sufficient. Lasers work in a very special way. Recall from section
2.2. that in normal circumstances far more atoms in a given population will be in the ground state than in the excited state. The trick in making a laser is to create a 'population inversion' in which the situation is reversed. Quantum theory then teaches that the radiation from an initial atom de-exciting will stimulate others to radiate as well, and the radiation that is produced in this way will be highly coherent, unlike light from ordinary sources. This method of production is even referred to in the name: 'laser' stands for '
light
amplification by
stimulated
emission of
radiation'.
It is, then, part of the concept of the laser that it consists of a specific set of components which produce highly coherent light by a specific causal process. The method of operation for a reservoir, by contrast, is completely unspecified. The relevant degrees of freedom that are represented mathematically are not identified with any concrete quantities, and no account is given of the process by which these quantities couple to the smaller system and destroy its correlations. This, we think, is why a reservoir is intuitively so much more abstract than a laser. Reservoirs are specified only in terms of their outputs, whereas lasers are specified, not just in terms of their output, but also in terms of the constituent parts and the causal processes by which the output is produced.
It should be noted that this variety of abstractness is independent of, in a sense orthogonal to, the concept of the abstract as symbolic attributed to Duhem in section
5.3. For Duhem, concepts in physics are abstract because they are not faithful to the objects they represent. But, as with any descriptions in physics, constitution and causal structure may be treated with more, or less, faithfulness. The real ruby laser that Maimon built had a particular concrete causal structure. But so too did the larger environment in which it ran that served as a reservoir to erase correlations in it. How realistically these structures can be copied in the physicist's model depends on the
end p.217
fit between reality and the mathematical needs of the theory; and even intricately detailed causal structures can be extremely symbolic in Duhem's sense. Nevertheless, in a different sense, even a highly symbolic object is more concrete with a causal structure than without one.
The conclusion reached so far about our specific example is this. A laser is characterized by its structure and its internal causal processes, as well as its output, unlike a reservoir, which is characterized only by its output. Mendell and I follow Ernan McMullin, to whom our joint paper is dedicated, in thinking this is a crucial difference. For causality is at the core of scientific explanation. That is obviously not a surprising thesis to find here, after the four earlier chapters of this book. For McMullin
50 the key to explanation is not subsumption, or derivability from law, as it is in the conventional deductive-nomological account. Laws, in his view, may play a role in helping to trace the causal processes, but what explains phenomena in typical theoretical explanations are the structures and processes that bring them about. As can be seen at the end of Chapter
4, my view is even stronger. The laws themselves are generally pieces of science fiction, and where they do exist they are usually the objects of human constructions, objects to be explained, and not ones to serve as the source of explanation. Causes and their capacities are not to play a role alongside laws in scientific explanation, but—at least in many domains—to replace them altogether.
Whether one wants to take the stronger view that I advocate, or the weaker view of McMullin—weaker, but still strong enough to offend the Humean—the crucial point is to establish the connection between causation and explanation, for that is essential to the story Mendell and I want to tell about abstraction. For we start from the assumption that to add to a scientific model a description of an object's structure and causal mechanisms is not just to add some information or other, but to add crucial explanatory information. In fact it is to add just the information that usually constitutes explanation in modern theoretical sciences.
There are two different intuitive ways that one object may be more concrete than another, which Mendell and I combine in our account.
end p.218
The first is the simple idea that an object is more concrete if it has more properties. Of course we do not know how to count properties. But we can still exploit this basic intuition by using the Aristotelian idea of nesting. If the properties used to describe one object are nested in those of another, the first description is less complete and, in that sense, more abstract than the other.
The second idea is that a description of an object is more concrete when we know, not just more about it, but more about what it really is under that description, that is, what is essential in that way of describing or treating the object. Again, we must face the problem of what counts as knowing more about what an object really is, and again we can take a solution from Aristotle. For Aristotle, the first and central role of a science is to provide explanatory accounts of the objects it studies and the facts about them. In each science the nature of the explanations may be different. In physics in particular, the basic objects, material substances, are to be explained in terms of the four causes. Julius Moravcsik
51 suggests that we regard the four causes of Aristotle as different factors in an account explaining what a substance or a system really is: source (efficient cause), constituent (matter), structure (form), and perfection or function (final cause).
The fullest explanation will give as many factors as may be appropriate. An account which specifies all four factors will give all the relevant information for identifying the material substance and for understanding what it truly is. For example, if the account is to be of a particular person, the fullest account will mention all four factors: parentage, flesh and bones, human soul, and what an active human soul does, in terms both of the growth of the person into a complete human and of the performance of a human soul. Other information is not relevant to understanding what this substance is as a person. Less information will be defective. Not all sciences, however, will use all explanatory factors. If we are to explain an Aristotelian unmoved mover, the constituent will be left out, because the unmoved mover is not encumbered with material constituents. Mathematics, on the other hand, is concerned with neither source nor function.
The four causes of Aristotle constitute a natural division of the sorts of property that figure in explanation, and they thus provide a way of measuring the amount of explanatory information given. We
end p.219
can combine this with the idea of nesting to formulate a general criterion of abstractness: (a) an object with explanatory factors specified is more concrete than one without explanatory features; and (b) if the kinds of explanatory factor specified for one object are a subset of the kinds specified for a second, the second is more concrete than the first. Notice that we are here nesting kinds of factor and not the individual factors themselves, and that, as with Aristotle's own hierarchy, the nesting provides only a partial ordering. For some pairs of objects this criterion yields no decision as to which is more abstract. If the description of one object employs both form and function and the second only function or only causal structure, the first is more concrete than the second. But if one object is given just a causal structure and the second just a function, the criterion gives no verdict.
Consider a simple example. We might describe a paper-cutter as an implement which rends paper. The definition refers just to the function of paper-cutters. How a paper-cutter rends paper is not a factor in the explanation. But the definition of scissors must give an account of the parts of scissors and how they cut, e.g. that they have at least two blades which operate by sliding past each other. We do not need to specify the material or constituents of scissors. Any material from which blades can be made will do. So too with the materials of lasers. Yet scissors are more concrete than paper-cutters because more is specified about how the object works and performs its function. Note that we could specify functions more finely. A smooth cutter will create smooth edges in rending paper. Smooth cutters are more abstract than scissors. For the variety of objects which can be scissors is restricted in a way in which smooth cutters are not. Their structural and material possibilities are still more diverse.
It might be objected that this notion of the abstract/concrete distinction is merely a variety of the general/specific distinction. But this is only partly the case. It is true that scissors are kinds of cutter, but it is not true that scissors are kinds of paper-cutter, and much less that they are kinds of smooth paper-cutter—some scissors cut meat. Yet we claim that paper-cutters are more abstract than scissors.
A second objection is that one could very vaguely indicate a structure and function for one item and specify a very specific function for another. For example, consider a mover where right and left are distinguished and an implement which cuts paper into
end p.220
frilled, square mats. Surely the cutter of frilled, square, paper mats is more concrete than the right-left mover, and surely this shows that we really ought to have given a general/specific distinction. What the example shows, rather, is that the general/specific distinction is relevant, and that our notion presupposes that the levels of description be not too divergent.
It is easy to see why this should be from the viewpoint of our distinction. As Aristotle observes about structure in the Physics, one cannot have just any matter with a given structure, but structure presupposes certain sorts of matter (one cannot make a laser of any material). So too a function presupposes certain structures (reservoirs have to be big). If the specification of structure is too general, as in the case of right-left movers, and we compare it with a function as specific as that of cutters of frilled, square, paper mats, we may get the impression that the very general structure and function is less specific than the highly specific function and structures presupposed by it. In other words, the class of structures presupposed by the functional description of cutters of frilled, square, paper mats may be more specific than the structure mentioned in the description of right-left movers.
Let us now apply this criterion to the example of the laser and the reservoir. It is one of the corollaries to my doctrines on capacities that covering-law accounts are only one special form of explanation offered in contemporary science. Both the laser and the reservoir are good examples. In both cases it is at least as important to the model to specify the capacities of the systems modelled as it is to give the equations which describe their behaviour. The two cases differ in how much detail is provided about how the capacities operate. As I argued above, in characterizing the laser we specify its complex causal structure and we specify what it does; in the case of a reservoir we specify only what it does. This is typical in modern science: explanatory models differ in what kinds of explanatory factor they fill in. The schema that Mendell and I suggest for categorizing the various kinds of explanatory factor that may be involved is taken very roughly from Aristotle's system of the four causes. Of course Aristotle's notion of perfection and function is in no way limited to what a system does, just as form is not precisely the causal structure. The perfection in Aristotle is sometimes the proper activity or state of a system, sometimes the proper result of a process; the form is usually the structure of the working system, which is sometimes
end p.221
identified with the activity itself. Here, inspired by Aristotle's distinction, we propose to treat form analogously as how the system operates and function as what it does. We may say, then, that lasers are more concrete than reservoirs because they are specified in terms of both form and function, whereas reservoirs are specified in terms of function alone.
It is easiest to illustrate our concept of abstraction in the context of Aristotle's division of explanatory factors into four kinds; but this particular division is not necessary. Our basic view is that one system is more concrete than a second when the kinds of explanatory feature used to identify the second are nested in those that identify the first. So the general strategy requires only that we have a way of sorting explanatory features from non-explanatory features, and of determining what kinds of explanatory feature there are. It is a common—though we think mistaken—assumption about modern physics, for example, that function is not an explanatory feature at all. If so, then structure and function is no more concrete than a structure alone.
Even when a number of different kinds of explanatory feature are admitted by a science, as with Aristotle's four causes, not all need be seen as equally central. McMullin, we have seen, argues that the causal structure is the primary explanatory feature in modern physics, and we agree. For Aristotle, too, structure plays a privileged role. It is the most important of the four explanatory factors in physics. The constituent is what a substance is made of; the function what it does or becomes; the source where it comes from. All these are a part of physical explanation. But structure is what the substance is. It is the essence of the substance, or what makes this material body what it really is. Structure, therefore, among all four of Aristotle's causes, gives most fundamentally what a thing is, and hence by our criterion contributes most to making it concrete. The one factor that may seem equally important is matter.
52 For there is a
end p.222
sense in which matter—as that which individuates structure—is more concrete: it serves more to isolate the individual. But this is a different sense from the one we have been considering. For designating or picking out the individual does not tell what it is. This is primarily the job of the structure.
In the case of lasers and reservoirs, the two relevant explanatory factors that we have isolated are function and structure. Between these two factors there is yet another reason for giving priority to causal structure in determining concreteness. For, given the causal structure, the function often comes along as a by-product, but not vice versa. One cannot usually infer from effects to a causal history. At best one can describe classes of structures which would have such effects, only one of which could be the structure of the particular system at hand. But one can, at least in principle, infer from a description of the causal structure to what that causal structure does. This is not to say that one may not also infer all sorts of side-effects. But all these effects are effects of that system as described. If a system is described in terms of causal structure, the addition of a description of certain effects of the system as essential serves merely to isolate those effects we are interested in from all the actual effects of the system. For this reason, descriptions of effects seem to add less to the descriptions of well-specified causal structures than do descriptions of causal structure to descriptions of well-specified causal effects. Hence, descriptions of specific causal structure are, in general, more concrete than descriptions of specific causal effects.
We see, therefore, that causal structure is privileged for a variety of reasons. From either our point of view, or the more traditional Aristotelian one, causal structure plays the central explanatory role. It thus contributes most significantly to removing an object from the realm of the abstract, and making it more concrete. Consider the example of the crystal diode rectifier mentioned at the beginning. We can isolate three levels of concreteness here. The rectifier is identified by function alone; the diode rectifier by function and structure; and the crystal diode rectifier by function, structure, and matter.
53 Each is more concrete than the one before; but, we find intuitively, the first step, where causal structure is added to function,
end p.223
is far greater for purposes of scientific understanding than the second, where the material is filled in. This mirrors the view of section
5.4.3 that material abstraction in science works by subtracting all those factors which are only locally relevant to the effect. What is left then is just factors which will be relevant independent of context, and these seem to be the proper subject of scientific understanding. This contrast between the rectifier and the diode rectifier parallels the case of the laser and the reservoir. Adding causal structure to functional description, as in a laser, produces a critical change in the degree of concreteness of the object. We have seen this critical difference in the contrast between the laser and the reservoir.
Aristotle did not treat his four kinds of explanatory factor on a par. Structure or form supplies the essence, what the substance most truly is. If Mendell and I are right, modern science also gives central place to structural factors. Given the Aristotelian ideal that the explanatory factors are what tell us what an object really is, an object without structure—like a reservoir—will be a shadow object indeed.
5.6. Conclusion
Mill used the term 'tendency' to refer to what the laws of nature are about. My views are almost identical to his and yet I use the term
end p.224
'capacity'. Why? The answer to this seemingly trivial terminological point provides a last argument in favour of capacities. The familiar example of lasers will illustrate. Consider Figs.
5.1 and
5.2. Fig.
5.1 is a schematic diagram of a laser constructed from specified materials in a specified way—it is a diagram of the first helium-neon gas laser. The diagram leaves out a large number of features, possibly even a large number that are relevant to its operation. Let us grant for the sake of argument that the concrete object pictured here operates under some law. I call the law a phenomenological law because, if we could write it down, it would literally describe the features of this concrete phenomenon and the nomological links within it. It would be a highly complex law, and would include a specific description of the physical structure and surroundings of the concrete device. Possibly it could not be written down; perhaps the features that are relevant to its operation make an open-ended list that cannot be completed. But because we are talking about a concrete object, it is at least conceivable that some such law is true of its operation.
Now look at Fig.
5.2 and its accompanying equation. Here we do not have a schematic diagram for a particular laser but rather a block diagram for any laser. In the block diagram we consider no particular medium, no specific way of pumping, no determinate arrangement of the parts. We abstract from the concrete details to focus, as we say, 'on the underlying principles'; the equation written beneath it records one of these principles. I will not explain the
end p.225
equation; it is not important to the philosophical point to know exactly what it says. The important question is: 'How do these two diagrams differ?' In the language of the last two sections, the second is a material abstraction whereas the first is not. The first diagram is a representation and not a real laser, so it will of necessity be incomplete; we have allowed that this may also be true of any equation we try to write down to describe its behaviour: no matter how long an equation we write for the laser of Fig.
5.1, it may not be literally true. But that does not make it abstract. The second equation is abstract; and that is why it is so short. It is not even an attempt to describe the actual behaviour of any material laser. Rather, it tells what a laser does by virtue of its function and the arrangement of its parts.
Here again I use the Aristotelian concepts which seem to me the natural way to describe the explanatory structures in physics. Again I will postpone past the end of this book the question of what this signifies about nature or about our image of it. The point I do want to make here is that no causality seems to be involved in either Fig.
5.1 or Fig.
5.2, nor in the equations appropriate to them. The example of an abstract law from laser theory in section
5.4 was different: 'An inverted population can lase.' That law tells what an inversion tends to cause. But the equation that accompanies the block diagram does not say what the laser tends to cause; rather, it says what the laser tends to do, or how it tends to behave. Here I think a difference in terminology is appropriate. Properties may carry a variety of different kinds of tendency—tendencies to behave in certain ways, to bear certain fixed relations to other properties, to evolve in a particular manner, or to produce certain kinds of effects. For all of these I use the general word 'tendency'; 'capacity' is reserved for a special subset of these—those tendencies which are tendencies to cause or to bring about something.
This book has been concerned with causation, and so has focused on capacities. But what about the broader category: are more general kinds of tendency real? My remarks in this conclusion are speculative and forward-looking, to projects yet to be undertaken; but it seems to me that a careful study will show that more general kinds of tendency are real; for not many of the arguments I have given in favour of capacities rely on their peculiarly causal nature. Following Mill, I have spoken of the composition of causes. But it seems fairly clear that, in giving scientific explanations and in
end p.226
making scientific predictions, we compose not only causes but behaviours.
This is transparent in physics, where equations and formulae are involved. The model Hamiltonians of section
5.4 are a good example. Although I introduced them into the middle of a discussion of capacities, there is nothing especially causal about them: to say, 'The Hamiltonian for a hydrogen atom is -' is not to say what the hydrogen atom produces but rather what energy configurations are possible for it. Yet Hamiltonians compose, just as capacities do; and if we do not think that the laws which describe the Hamiltonians for different kinds of situation are laws ascribing tendencies to these situations, how shall we interpret them to make them true? Read as pure statements of regularity, they are riddled with exceptions and seem to face all the same problems that led Mill to adopt tendencies. Indeed, although I put Mill to use to defend my doctrines in favour of stable causal tendencies, I think Mill himself had no special concerns with causality, and aptly used the more general term 'tendency' rather than my narrower conception of 'capacity'.
A second major argument for capacities concerned the exportability of information: we gather information in one set of circumstances but expect to use it in circumstances that are quite different. Again, there need be nothing especially causal about the information. Section
5.2 argued that this kind of stability and exportability is necessary to make sense of our use of what are called 'Galilean methods'. These methods are in no way confined to the study of causes, but are at work in almost every empirical enquiry in modern science. A third defence for capacities involved a counter-attack against the proposal to modalize them away. Again, the concepts of interaction and duality of capacity that played a central role in that counter-attack are just as relevant whether it is capacities in particular that are in question or some more general notion of tendency, though of course where probabilistic causes are not involved the statistical characterizations of these concepts will be irrelevant. Also, the same circle of irreducible concepts of enabling conditions, preventatives, precipitators, and the like will be just as important for the proper statement of general tendency claims as they are for claims about capacities.
From a crude first look, then, it seems that most of the arguments for capacities will double as arguments for more general kinds of tendency, and be equally compelling in both cases. That in itself
end p.227
turns into a powerful argument against the Humean and in favour of capacities. In Chapter
4 I argued that the most general kinds of causal claim in science are at base claims about capacities. This chapter has proposed a different but not incompatible way of looking at them: they are also material abstractions. But recall the block diagram of the laser (Fig.
5.2). If the arguments just sketched turn out to work, the accompanying equation ought to describe a general tendency, a tendency that lasers have by virtue of the abstract structure pictured in the diagram. Equally, both the diagram and the equation can be viewed as material abstractions. The equation is not some kind of regularity law with
ceteris paribus conditions repressed. The regularities appear in the phenomenal content, in the detailed equations that attempt to describe the behaviour of concrete lasers and of specific materials. Like capacity ascriptions, the abstract equation also has the troubling feature that there is no rule that takes you from the abstract law to the phenomenal content; the additions and corrections will depend in each instance on how the block structure is realized. But there is an important difference. In the case of a capacity claim, the realization-dependent laws that fall under it will be some complicated sort of causal law, whereas in general the content of an abstract claim in physics, like the equation for the block laser, may be entirely associational.
Return for a moment to my conclusions about causality. In the end I present a structure with three tiers. At the bottom we have individual singular causings. At the top we have general causal claims, which I render as statements associating capacities with properties—'Cash-in-pocket can inhibit recidivism', or 'Inversions have the capacity to amplify'. In between stands the phenomenal content of the capacity claim—a vast matrix of detailed, complicated, causal laws. These causal laws, which stand at level two, provide no new obstacles for the Humean beyond those that already appear at the bottom level. For these are just laws, universal or probabilistic, about what singular causings occur in what circumstances what percentage of the time. This claim was defended in Chapter
3.
Yet there is good reason for the Humean to be wary, at least the modern-day Humean who believes in laws but not in causes. For if the programme of section
4.6 succeeds, this treasured layer of laws will be eliminated altogether from our fundamental scientific
end p.228
picture. All that remains would be capacities and the causings for which they are responsible. The laws—even causal laws—would no longer play any basic role; and the pretence that nature is full of regularities could be dropped. This radical programme gets some support from the discussions of this chapter. For I hope it becomes clear that what are taken as the fundamental laws of, say, physics are not laws at all in the empiricist's sense, but abstractions. Section
5.5 proposes an Aristotelian scheme for treating the structure of abstractions in physics. This may not be the best way to do it. But whichever route is taken, it seems clear that the conventional idea of laws will not do at all. The abstract claims which physical theory consists of do not describe regularities, neither regularities about individual causal behaviour, nor regularities of association. What regularities there are occur at a far lower level in science, long, complicated, and local. They fit nobody's idea of a fundamental law.
But this is a programme. I hope to eliminate the middle level, but for the moment I have argued for a picture of science with three layers. The third is the most troubling of all for a conventional empiricist. It sounds doubly non-Humean. First we have causal connections in the single case; then we add some mysterious capacities, or occult powers. But the point of the block diagram is to show that the mystery concerning capacities is not isolated in the domain of causality, but spreads everywhere in physics. Sections
5.1-4 teach that a capacity claim, considered as an abstraction, has two distinct facets. First, it is a material abstraction, just like the equation for the block diagram and like most general claims in physics. Second, unlike the equation for the block diagram, the laws which make up the phenomenal content of the capacity claim are causal laws, not equations or other laws of association. The use of the term 'capacity law' rather than the more general 'tendency law' marks this special feature of the phenomenal content.
Yet neither facet introduces any new troubling ideas that are peculiar to causal discourse, beyond the already necessary notion of singular causation. What is especially causal about a capacity claim are the causal laws that make up its phenomenal content; these have just been discussed. Beyond that there is only the fact of what I have called 'material abstraction', and material abstraction cuts across the causal and the non-causal in science: whether causal or not, material abstractions cover a vast network of concrete laws which
end p.229
are both complex and detailed; and whether causal or not, the form of the concrete laws is highly realization-dependent. I have claimed that we have not even a good start on a philosophical account of how this realization-dependence works. But that is not any special problem to do with causality, since the process of material abstraction is fundamental throughout physics and probably to all of modern theoretical science. So the picture I draw of singular causings, causal laws, and capacities is at least not doubly non-Humean. Once we let in singular causation—as we must—we have no more special problems with capacity ascriptions than with any other abstract descriptions in physics. The most general claims of physics are indeed mysterious; but the causal claims are not more mysterious than others.
end p.230