Algebraic Logic

A monadic (Boolean) algebra is a Boolean algebra A together with an operator on A (called an existential quantifier, or, simply, a quantifier) such that , and whenever p and q are in A, Most of this note uses nothing more profound about monadic algebras than the definition. The reader interested in the motivation for and the basic facts in the theory of monadic algebras may, however, wish to consult [2].

Every Boolean algebra can be converted into a monadic algebra, usually in several ways. (One way is to write for all p; another is to write or 1 according as p=0 or p ≠ 0. These special operators are known as the discrete and the simple quantifier, respectively.) It follows, a fortiori, that every Boolean algebra can be embedded into a monadic algebra, and it is clear, on grounds of universal algebra, that among the monadic extensions of a Boolean algebra there is one that is “as free as possible.”

To be more precise, let us say that a monadic algebra A is a free monadic extension of a Boolean algebra B if

(i) B is a Boolean subalgebra of A,

(ii) A is (monadically) generated by B,

(iii) every Boolean homomorphism g that maps B into an arbitrary monadic algebra C has a (necessarily unique) extension to a monadic homomorphism f that maps A into C.

The statement that a monadic extension “as free as possible” always exists means that every Boolean algebra B has a free monadic extension A; the algebra A is uniquely determined to within a monadic isomorphism that is equal to the identity on B. The purpose of what follows is to give a “constructive” proof of this fact, i.e., a proof that exhibits A by means of certain set-theoretic constructions based on B (instead of a structurally not very informative proof via equivalence classes of strings of symbols). A by-product of the proof is a rather satisfying insight into the structure of the (Stone) dual space of the free monadic extension. The theorem can (and will) be formulated in such a way as to subsume the results of Hyman Bass [1] on the cardinal number of finitely generated free monadic algebras.

The idea of the construction is this. Step 1 : form a free Boolean algebra generated by a copy of B. Step 2 : adjoin the elements of that free algebra to those of B. Step 3: let be the mapping from B into the enlarged algebra that assigns to each element of B the corresponding free generator, and reduce the enlarged algebra by the relations that hold when is an increasing hemimorphism (i.e., , , and . Step 4: extend to the entire enlarged (and then reduced) algebra so as to ensure that the elements of the Boolean algebra generated by are invariant under (and hence that is indeed a quantifier). A little reflection on freedom (especially for Boolean algebras) suggests that the best approach is via duality. The desired algebra will be constructed as the dual of its dual space, and, in order to construct that dual space, the steps of the outline sketched above will be carried out in dualized form. The details go as follows.

STEP 1. Let W be the set of all 2-valued functions on B. (The symbol “2” here and throughout denotes the two-element Boolean algebra.) Endowed with the product-space topology, W is a Boolean space (i.e., a totally disconnected compact Hausdorff space).

STEP 2. Let Y be the (closed) subspace of W that consists of all 2-valued homomorphisms on B, and form the Cartesian product Y × W. The space Y is the dual of the algebra B.

STEP 3. Let V be the (closed) subspace of W that consists of all those 2-valued hemimorphisms on B that map 1 onto 1, and let X be the set of all those points (y, υ) of the product Y × V for which y is dominated by υ. A 2-valued function υ on B is a hemimorphism if

and

whenever p and q are in B. To say that υ dominates a 2-valued function y on B (notation: y v) means that

whenever p is in B. Since yp and υp vary continuously with (y, υ), the set X is a closed subset of Y × V, and, consequently, X is a Boolean space on its own right.

STEP 4. Let A be the dual algebra of the space X, and write

whenever p is in A. The supremum in (4) is extended over all those u in Y for which (u, υ) is in X (i.e., for which u and υ satisfy (1), (2), and (3)). To say that A is the dual of X means that A is the set of all 2-valued continuous functions on X.

The notation indicates, and it is in fact true, that the preceding construction produces the desired monadic algebra A ; it is, however, not yet clear how the given Boolean algebra B is to be embedded in A. This is achieved by means of the dual h of the natural projection c from X to Y The projection c is, of course, given by

The dual mapping h sends each element p of B onto the element hp of A defined by

The principal result of this note can now be stated as follows.

THEOREM. The mapping h defined by (5) is a monomorphism from the Boolean algebra B into the Boolean algebra A ; the operator defined by (4) is a quantifier on A; the monadic algebra A with the quantifier is a free monadic extension of its Boolean subalgebra hB.

Since the projection c is obviously continuous, and since h is indeed its dual (i.e., (hp)(x) = c(x)p whenever x is in X and p is in A), the mapping h is a homomorphism from B into A. To prove that h is one-to-one is the same as to prove that c maps X onto Y. This, in turn, is almost obvious; if y is in Y, then the point (y, y) belongs to X, and, of course, its image by c is exactly y.

A useful tool is the projection d from X to V defined by

An examination of the notation shows that

whenever x is in X and p is in A. In view of this connection between and d, it is an immediate consequence of §12 of [2] that is a quantifier on A if and only if d is a Boolean mapping on X, i.e., if and only if d is a continuous and open mapping of X onto V. The next part of the proof is devoted to showing that d does indeed have these properties. (The necessity for considering both the projections c and d emerged in the course of a conversation with F. B. Wright. The projection c is open also, but this fact is not needed below.)

The continuity of d is immediate. To prove that d is open, it is sufficient to prove that the image of each open set in a basis for X is open. A basis for X is obtained by forming a basis for Y × V and intersecting each set in that basis with X. This implies that as q varies over B and U varies over open subsets of V, the subset G of X, defined by

varies over a basis for X. It is therefore sufficient to prove that

for each such G; the openness of the right side is a consequence of the definition of the product-space topology in V.

If υ is in dG, so that in particular y υ, then yq′ υq′, so that υq′ = 1 (and, of course, υ is in U). Suppose now, conversely, that vq′ = 1 and v is in U. If a 2-valued function w on B is defined by

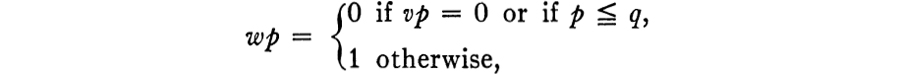
then w is a 2-valued hemimorphism on B and w v. The hemimorphism w is not identically zero (since wq′ = 1). Suppose now that there exists a 2-valued homomorphism y on B such that y w. Since wq = 0, this supposition implies that yq = 0 and hence that (y, v) is in G ; it follows that v is in dG, and (except for the unsupported supposition) this completes the proof of the openness of d. If the characterization of dG is applied to the case in which q = 0 and U = V, it follows that d maps X onto V.

The supposition of the preceding paragraph is a fact. To every 2-valued hemimorphism w on B there corresponds at least one 2-valued homomorphism y in B such that y w. It is even true that

where p is in B and the supremum is extended over all 2-valued homo-morphisms y on B that are dominated by w. This fact is a simple special case of the duality theorem for hemimorphisms [2, Theorem 8]; the special case has an easy independent proof also. (It would be of interest to know how far (6) can be generalized beyond the 2-valued case. In other words: when is a hemimorphism the supremum of the homomorphisms below it?)

For further progress it is convenient to digress to a brief study of functions of two variables that really depend on only one variable. A function p on a product space such as Y × V is independent of Y if P(y₁, v) = P(y₂, v) whenever y₁ and y₂ are in Y and v is in V; the definition of independence of V is similar. It is well known and easy to prove that the Boolean algebra generated by the set of all 2-valued continuous functions that are independent of either Y or V is equal to the algebra of all 2-valued continuous functions on Y × V. (Every clopen set in Y × V is a finite union of clopen rectangles.)

Consider now functions on a closed subspace of Y × V, such as, say, X. The definitions of independence of Y or of V still make sense; it is necessary only to insist that all the points of Y × V that are mentioned belong to the subspace X. Is it true that the algebra generated by all “one-variable” 2-valued continuous functions is equal to the algebra A of all 2-valued continuous functions on X? The answer is yes. Indeed, the process of restriction to X is a Boolean homomorphism from the algebra of all 2-valued continuous functions on Y × V onto the algebra of all 2-valued continuous functions on X; the asserted affirmative answer follows from the fact that the restriction of a one-variable function is a one-variable function.

One more auxiliary comment will be useful: every one-variable function on X is the restriction of some one-variable function on Y × V (2-valued and continuous understood throughout). The emphasis here (as opposed to the preceding paragraph) is that restriction, already known to be an onto map, maps a useful subset onto a useful subset. For the proof, suppose that p on X is independent of, say, Y. There exists a unique (necessarily 2-valued and necessarily continuous) function q on F such that p(y, v) = q(v) whenever (y, v) is in X. If r is defined on Y × V by r(y, v) = q(v), then r is independent of F and the restriction of r to X is exactly p.

In terms of the concepts just discussed it is possible to formulate a useful fact about the way h embeds B into A ; the assertion is that hB consists exactly of those functions in A that are independent of V. Inclusion one way is obvious: if p is in B, then hp is independent of V by the definition (5). If, conversely, q is in A and q is independent of V, then q is the restriction to X of some 2-valued continuous function r on Y × V that is independent of V. The elementary theory of Boolean duality implies that there exists an element p of B such that r(y, v) =yp identically in y and v, and hence q = hp.

Knowledge about hB can be exploited to get some knowledge about . The basic fact is that

whenever p is in B and (y, υ) is in X. For the proof, note first that

The fact that this upper bound is always attained follows from (6).

The preceding paragraph shows that every function in is independent of Y. (Caution: is not in general a Boolean algebra.) In the converse direction it is true that the Boolean algebra generated by includes all the functions in A that are independent of Y. The reason is that the coordinate functions on V generate the algebra of all 2-valued continuous functions on V; by (7), the restriction of the coordinate functions to X consists exactly of the functions in .

It is now clear that the monadic algebra generated by hB is A. Indeed, that generated monadic algebra includes the Boolean algebra generated by , hence it contains all one-variable functions in A, and, consequently, it coincides with A.

It remains to prove the third and crucial condition that makes A a free monadic extension of hB. Suppose, accordingly, that g is a Boolean homomorphism that maps hB into a monadic algebra C. Let Z be the dual space of C, i.e., the set of all 2-valued homomor-phisms on C. There are natural (and obviously continuous) mappings a and b from Z into Y and V, respectively. defined by

whenever p is in B. (Note that “” on the right side of the last equation denotes quantification in C.) It is easy to verify that (az, bz) is in X for all z in Z. The desired extension f of g associates with each element q of A that element fq of C for which

for all z in Z.

The verification that f is a Boolean homomorphism from A into C is straightforward. To prove that f is an extension of g, suppose that p is in B and q = hp. Since

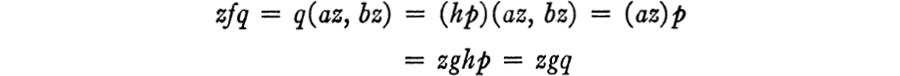
for every z in Z, it follows that fq is indeed equal to gq.

The last thing to prove is that f is a monadic homomorphism, i.e., that

whenever z is in Z and q is in A. Assume first that q = hp for some p in B ; then

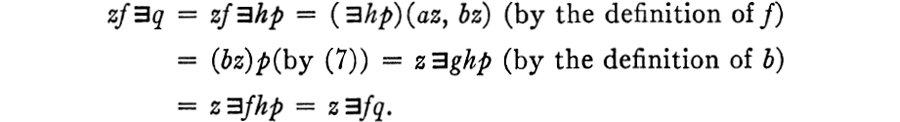
It is now tempting to argue as follows: agrees with on hB and hB generates the monadic algebra A, hence agrees with throughout A. This argument assumes that the set of elements on which agrees with is closed under the Boolean operations and under quantification. The assumption is not justified. The trouble is caused by infima and complements; the mappings and are not homomorphisms but merely hemimorphisms.

A minor refinement of the argument proposed above works. In its unrefined form the argument applies to every set of monadic generators of A (and fails) ; the refinement makes use of the fact that the particular generating set at hand (namely hB) is a Boolean subalgebra of A. This fact implies (and in any case it was proved above) that the Boolean algebra generated by is A. It follows that every element of A is a finite supremum of elements of the form

where p and all the q’s are in B and the ambiguous signs refer to possible complementations. Since both and preserve suprema, the desired end can be achieved by proving that and always coincide. The verification that this is so is a simple computation; the crucial step uses the fact that and do agree on hB.

The proof of the principal theorem is now complete. Since h may be regarded as an embedding of B into A, the subalgebra hB may be identified with B; the fact that A first presents itself as a free monadic extension of hB (and not of B) is merely a matter of notation.

The proof of uniqueness is an easy exercise in universal algebra. Suppose, indeed, that both A₁ and A₂ are free monadic extensions of B. If g₁ and g₂ are the natural injections of B into A₁ and A₂, respectively, then (by freedom) there exist monadic homomorphisms f₁ (from A₂ into A₁) and f₂ (from A₁ into A₂) that extend g₁ and g₂. Since f₁f₂ is a monadic endomorphism of A₁ that agrees with the identity on B, it must be equal to the identity throughout A₁, and, similarly, f₂f₁ is equal to the identity throughout A₂. This means that f₁ is a monadic isomorphism from A₂ onto A₁ with inverse f₂; the existence of such an isomorphism (equal to the identity on B) is what is meant by saying that the free monadic extension is essentially unique.

If S is an arbitrary set, the preceding results can be applied to the free Boolean algebra B generated by S. An arbitrary mapping from S into an arbitrary monadic algebra C has a (necessarily unique) extension to a Boolean homomorphism g that maps B into C The Boolean homomorphism g, in turn, has a (unique) extension f that maps A into C. Conclusion: the free monadic extension of a free Boolean algebra is a free monadic algebra.

If the number n of elements of S is finite, then, as is well known, B has 2ⁿ atoms; this says exactly that the dual space Y has 2ⁿ elements. How many elements are there in X? To find the answer, choose an arbitrary element y in Y (there are 2ⁿ ways of doing this), and ask for the number of elements υ in V that can be appended to it so as to yield an element of X. In order that a 2-valued mapping υ on B have this desired property, it is necessary and sufficient that υ be a 2-valued hemimorphism on B that dominates y. A hemimorphism on B is uniquely determined by its values on the atoms of B, and those values can be assigned arbitrarily; this implies that the number of 2-valued hemimorphisms on B is the number of sets of atoms, i.e., 2²ⁿ If p is the element of B that is mapped onto 1 by y and onto 0 by all other elements of Y, then a necessary and sufficient condition that a hemimorphism υ dominate y is that it send p onto 1 (recall that a hemimorphism is monotone). This observation finishes the enumeration ; the number of hemimorphisms υ for which υp = 1 is just half the total number, and, therefore, the number of elements in X is 2ⁿ·2²ⁿ⁻¹. Conclusion: the free monadic algebra with n generators has 2ⁿ·2²ⁿ⁻¹ atoms. This result was first obtained by Bass [1].

It is of some interest to observe that such enumeration results are of a strictly monadic character; the situation becomes completely different in the presence of two quantifiers. (This observation was made orally by Alfred Tarski.) The fact is that a single generator acted upon by the Boolean operations and two (commutative) quantifiers yields an infinite free algebra. The most efficient way of proving this is to exhibit one concrete (but not necessarily free) algebra of this kind that is generated by one element but has altogether infinitely many elements.

For this purpose, let K be the set of all pairs of natural numbers, and for each subset p of K let [or ] be the union of all horizontal [or vertical] lines that meet p. (Lines here consist, of course, of lattice points only.) The operators and are commutative quantifiers on the algebra 2^K. Let A be the least Boolean subalgebra of 2^K that contains the “triangle”

and is closed under the actions of both and . Assertion: A has infinitely many elements. For the proof, write and define the sequences {p_n} and {q_n} inductively by writing

A casual examination of either the geometry or the logic of the situation shows that the ranges of both these sequences are infinite; in fact

and

The construction of this example was inspired by a conversation with Dana Scott.

REFERENCES

1. Hymann Bass, Finite monadic algebras, Proc. Amer. Math. Soc. vol. 9 (1958) pp. 258–268.

2. Paul R. Halmos, Algebraic logic, I. Monadic Boolean algebras, Compositio Math. vol. 12 (1955) pp. 217–249

UNIVERSITY OF CHICAGO AND

INSTITUTE FOR ADVANCED STUDY

Received by the editors July 24, 1958.

¹ Research supported in part by a contract with the U. S. Air Force.