© Intel Corporation 2021

J. Reinders et al.Data Parallel C++https://doi.org/10.1007/978-1-4842-5574-2_9

9. Communication and Synchronization

James Reinders¹ , Ben Ashbaugh², James Brodman³, Michael Kinsner⁴, John Pennycook⁵ and Xinmin Tian⁶

(1)

Beaverton, OR, USA

(2)

Folsom, CA, USA

(3)

Marlborough, MA, USA

(4)

Halifax, NS, Canada

(5)

San Jose, CA, USA

(6)

Fremont, CA, USA

 

In Chapter 4, we discussed ways to express parallelism, either using basic data-parallel kernels, explicit ND-range kernels, or hierarchical parallel kernels. We discussed how basic data-parallel kernels apply the same operation to every piece of data independently. We also discussed how explicit ND-range kernels and hierarchical parallel kernels divide the execution range into work-groups of work-items.

In this chapter, we will revisit the question of how to break up a problem into bite-sized chunks in our continuing quest to Think Parallel. This chapter provides more detail regarding explicit ND-range kernels and hierarchical parallel kernels and describes how groupings of work-items may be used to improve the performance of some types of algorithms. We will describe how groups of work-items provide additional guarantees for how parallel work is executed, and we will introduce language features that support groupings of work-items. Many of these ideas and concepts will be important when optimizing programs for specific devices in Chapters 15, 16, and 17 and to describe common parallel patterns in Chapter 14.

Work-Groups and Work-Items

Recall from Chapter 4 that explicit ND-range and hierarchical parallel kernels organize work-items into work-groups and that the work-items in a work-group are guaranteed to execute concurrently. This property is important, because when work-items are guaranteed to execute concurrently, the work-items in a work-group can cooperate to solve a problem.

Figure 9-1 shows an ND-range divided into work-groups, where each work-group is represented by a different color. The work-items in each work-group are guaranteed to execute concurrently, so a work-item may communicate with other work-items that share the same color.

Figure 9-1

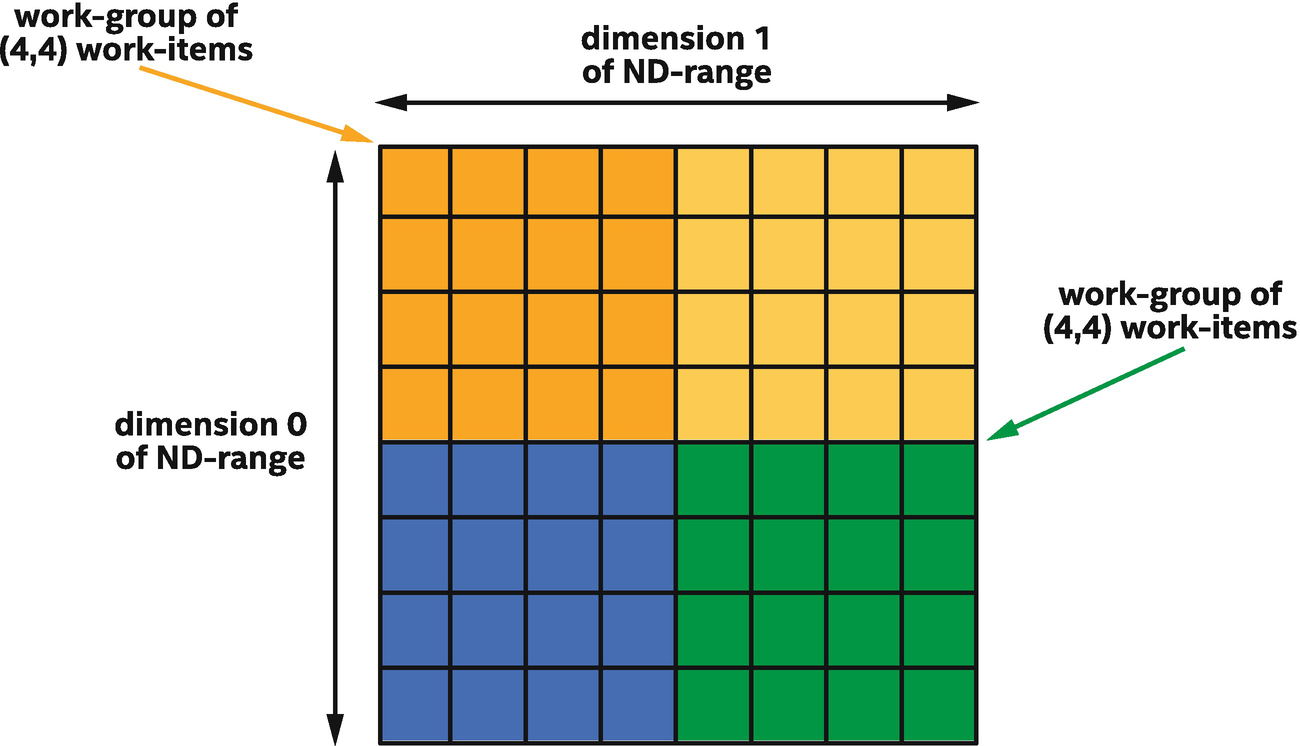
Two-dimensional ND-range of size (8, 8) divided into four work-groups of size (4,4)

Because the work-items in different work-groups are not guaranteed to execute concurrently, a work-item with one color cannot reliably communicate with a work-item with a different color, and a kernel may deadlock if one work-item attempts to communicate with another work-item that is not currently executing. Since we want our kernels to complete execution, we must ensure that when one work-item communicates with another work-item, they are in the same work-group.

Building Blocks for Efficient Communication

This section describes building blocks that support efficient communication between work-items in a group. Some are fundamental building blocks that enable construction of custom algorithms, whereas others are higher level and describe common operations used by many kernels.

Synchronization via Barriers

The most fundamental building block for communication is the barrier function. The barrier function serves two key purposes:

First, the barrier function synchronizes execution of work-items in a group. By synchronizing execution, one work-item can ensure that another work-item has completed an operation before using the result of that operation. Alternatively, one work-item is given time to complete its operation before another work-item uses the result of the operation.

Second, the barrier function synchronizes how each work-item views the state of memory. This type of synchronization operation is known as enforcing memory consistency or fencing memory (more details in Chapter 19). Memory consistency is at least as important as synchronizing execution since it ensures that the results of memory operations performed before the barrier are visible to other work-items after the barrier. Without memory consistency, an operation in one work-item is like a tree falling in a forest, where the sound may or may not be heard by other work-items!

Figure 9-2 shows four work-items in a group that synchronize at a barrier function. Even though the execution time for each work-item may differ, no work-items can execute past the barrier until all work-items execute the barrier. After executing the barrier function, all work-items have a consistent view of memory.

Figure 9-2

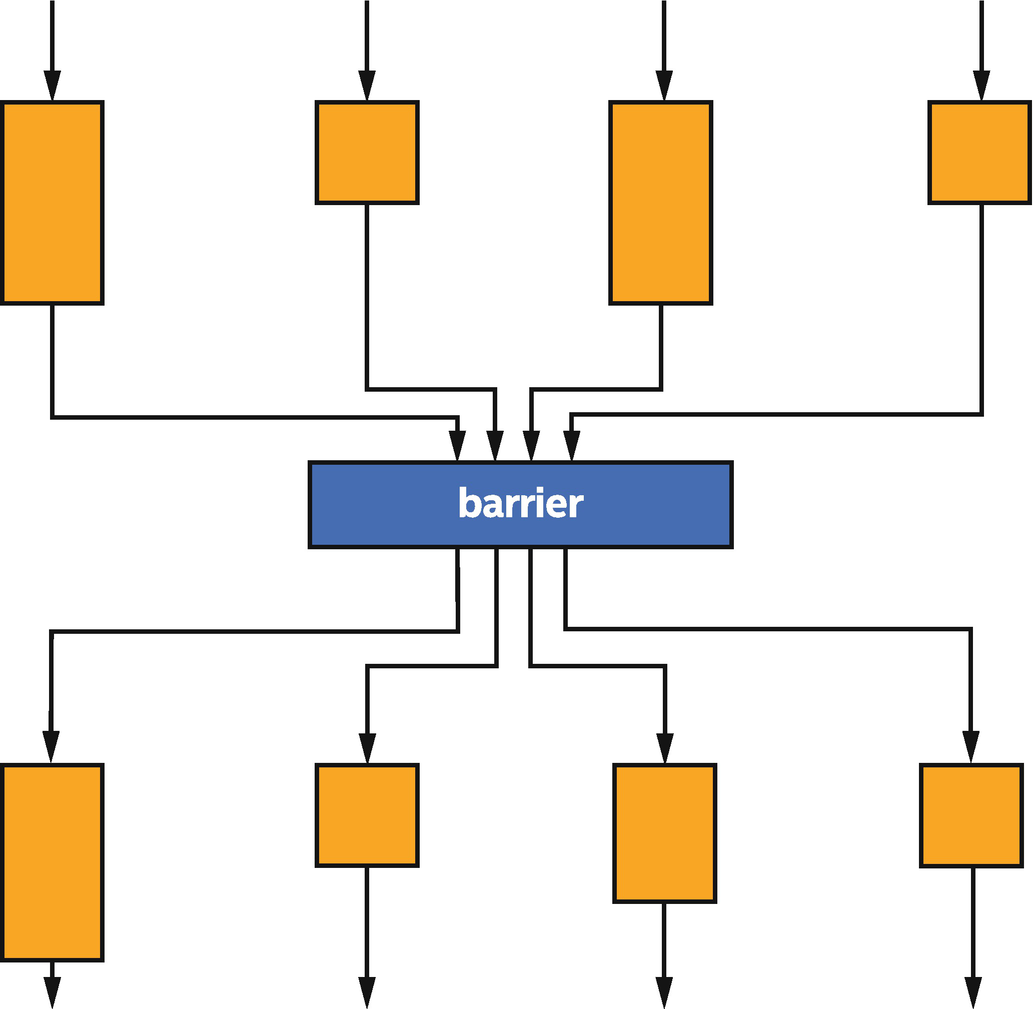
Four work-items in a group synchronize at a barrier function

WHY ISN’T MEMORY CONSISTENT BY DEFAULT?

For many programmers, the idea of memory consistency—and that different work-items can have different views of memory—can feel very strange. Wouldn’t it be easier if all memory was consistent for all work-items by default? The short answer is that it would, but it would also be very expensive to implement. By allowing work-items to have inconsistent views of memory and only requiring memory consistency at defined points during program execution, accelerator hardware may be cheaper, may perform better, or both.

Because barrier functions synchronize execution, it is critically important that either all work-items in the group execute the barrier or no work-items in the group execute the barrier. If some work-items in the group branch around any barrier function, the other work-items in the group may wait at the barrier forever—or at least until the user gives up and terminates the program!

COLLECTIVE FUNCTIONS

When a function is required to be executed by all work-items in a group, it may be called a collective function , since the operation is performed by the group and not by individual work-items in the group. Barrier functions are not the only collective functions available in SYCL. Other collective functions are described later in this chapter.

Work-Group Local Memory

The work-group barrier function is sufficient to coordinate communication among work-items in a work-group, but the communication itself must occur through memory. Communication may occur through either USM or buffers, but this can be inconvenient and inefficient: it requires a dedicated allocation for communication and requires partitioning the allocation among work-groups.

To simplify kernel development and accelerate communication between work-items in a work-group, SYCL defines a special local memory space specifically for communication between work-items in a work-group.

In Figure 9-3, two work-groups are shown. Both work-groups may access USM and buffers in the global memory space. Each work-group may access variables in its own local memory space, but cannot access variables in another work-group’s local memory.

Figure 9-3

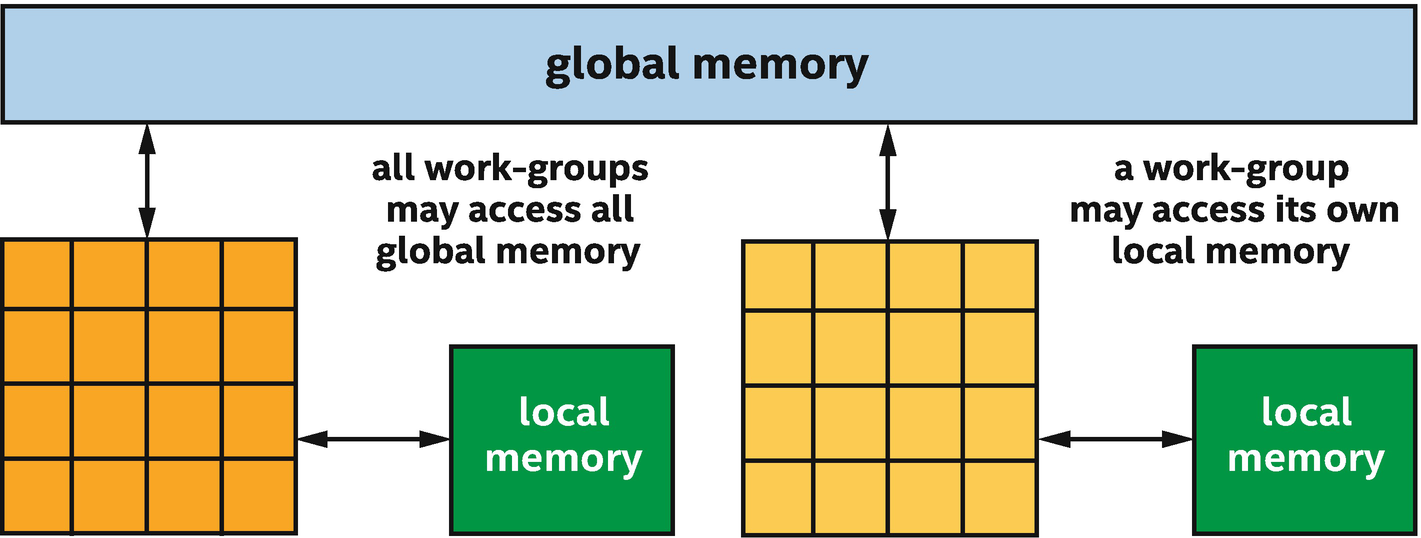
Each work-group may access all global memory, but only its own local memory

When a work-group begins, the contents of its local memory are uninitialized, and local memory does not persist after a work-group finishes executing. Because of these properties, local memory may only be used for temporary storage while a work-group is executing.

For some devices, such as for many CPU devices, local memory is a software abstraction and is implemented using the same memory subsystems as global memory. On these devices, using local memory is primarily a convenience mechanism for communication. Some compilers may use the memory space information for compiler optimizations, but otherwise using local memory for communication will not fundamentally perform better than communication via global memory on these devices.

For other devices though, such as many GPU devices, there are dedicated resources for local memory, and on these devices, communicating via local memory will perform better than communicating via global memory.

Communication between work-items in a work-group can be more convenient and faster when using local memory!

We can use the device query info::device::local_mem_type to determine whether an accelerator has dedicated resources for local memory or whether local memory is implemented as a software abstraction of global memory. Please refer to Chapter 12 for more information about querying properties of a device and to Chapters 15, 16, and 17 for more information about how local memory is typically implemented for CPUs, GPUs, and FPGAs.

Using Work-Group Barriers and Local Memory

Now that we have identified the basic building blocks for efficient communication between work-items, we can describe how to express work-group barriers and local memory in kernels. Remember that communication between work-items requires a notion of work-item grouping, so these concepts can only be expressed for ND-range kernels and hierarchical kernels and are not included in the execution model for basic data-parallel kernels.

This chapter will build upon the naïve matrix multiplication kernel examples introduced in Chapter 4 by introducing communication between the work-items in the work-groups executing the matrix multiplication. On many devices—but not necessarily all!—communicating through local memory will improve the performance of the matrix multiplication kernel.

A NOTE ABOUT MATRIX MULTIPLICATION

In this book, matrix multiplication kernels are used to demonstrate how changes in a kernel affect performance. Although matrix multiplication performance may be improved on some devices using the techniques described in this chapter, matrix multiplication is such an important and common operation that many vendors have implemented highly tuned versions of matrix multiplication. Vendors invest significant time and effort implementing and validating functions for specific devices and in some cases may use functionality or techniques that are difficult or impossible to use in standard parallel kernels.

USE VENDOR-PROVIDED LIBRARIES!

When a vendor provides a library implementation of a function, it is almost always beneficial to use it rather than re-implementing the function as a parallel kernel! For matrix multiplication, one can look to oneMKL as part of Intel’s oneAPI toolkits for solutions appropriate for DPC++ programmers.

Figure 9-4 shows the naïve matrix multiplication kernel we will be starting from, taken from Chapter 4.

Figure 9-4

The naïve matrix multiplication kernel from Chapter 4

In Chapter 4, we observed that the matrix multiplication algorithm has a high degree of reuse and that grouping work-items may improve locality of access which may improve cache hit rates. In this chapter, instead of relying on implicit cache behavior to improve performance, our modified matrix multiplication kernels will instead use local memory as an explicit cache, to guarantee locality of access.

For many algorithms, it is helpful to think of local memory as an explicit cache.

Figure 9-5 is a modified diagram from Chapter 4 showing a work-group consisting of a single row, which makes the algorithm using local memory easier to understand. Observe that for elements in a row of the result matrix, every result element is computed using a unique column of data from one of the input matrices, shown in blue and orange. Because there is no data sharing for this input matrix, it is not an ideal candidate for local memory. Observe, though, that every result element in the row accesses the exact same data in the other input matrix, shown in green. Because this data is reused, it is an excellent candidate to benefit from work-group local memory.

Figure 9-5

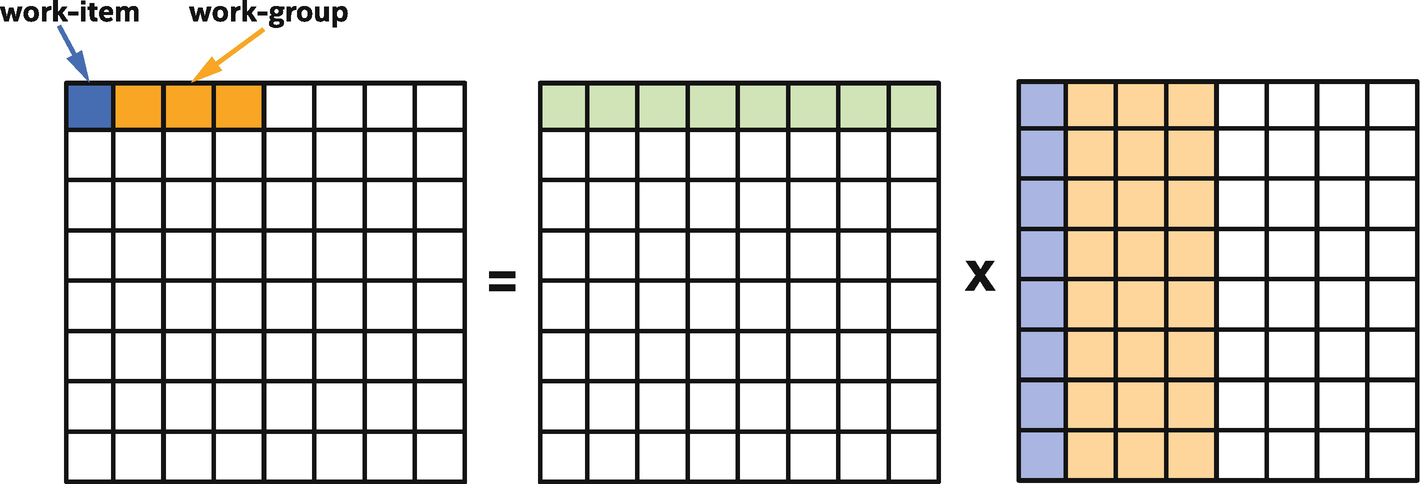
Mapping of matrix multiplication to work-groups and work-items

Because we want to multiply matrices that are potentially very large and because work-group local memory may be a limited resource, our modified kernels will process subsections of each matrix, which we will refer to as a matrix tile. For each tile, our modified kernel will load data for the tile into local memory , synchronize the work-items in the group, and then load the data from local memory rather than global memory. The data that is accessed for the first tile is shown in Figure 9-6.

Figure 9-6

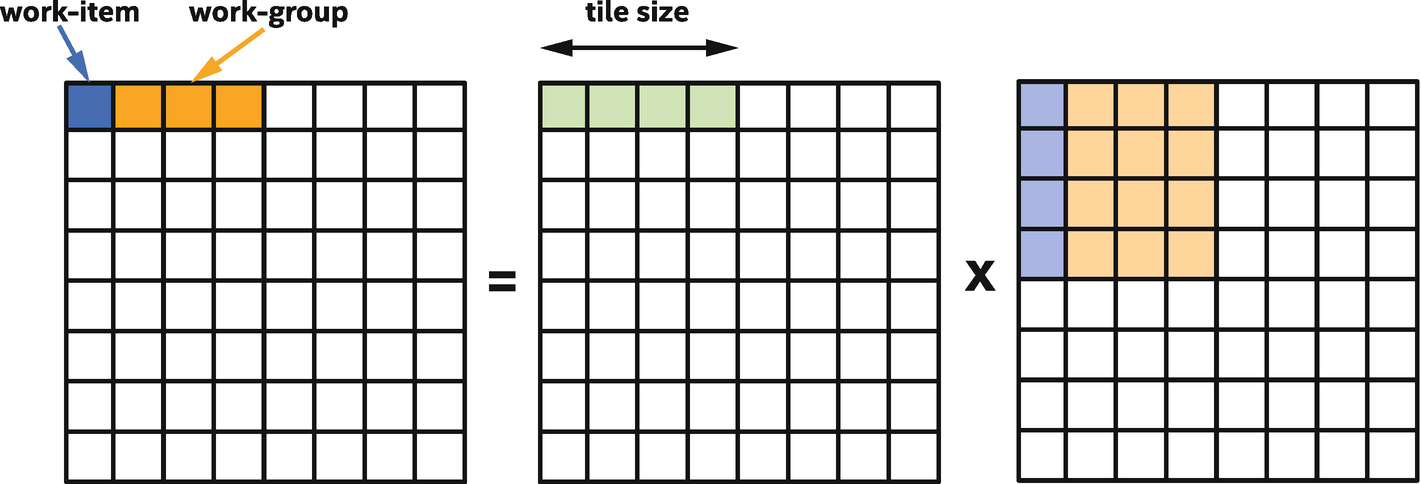
Processing the first tile: the green input data (left of X) is reused and is read from local memory, the blue and orange input data (right of X) is read from global memory

In our kernels, we have chosen the tile size to be equivalent to the work-group size. This is not required, but because it simplifies transfers into or out of local memory, it is common and convenient to choose a tile size that is a multiple of the work-group size.

Work-Group Barriers and Local Memory in ND-Range Kernels

This section describes how work-group barriers and local memory are expressed in ND-range kernels. For ND-range kernels, the representation is explicit: a kernel declares and operates on a local accessor representing an allocation in the local address space and calls a barrier function to synchronize the work-items in a work-group.

Local Accessors

To declare local memory for use in an ND-range kernel, use a local accessor. Like other accessor objects, a local accessor is constructed within a command group handler, but unlike the accessor objects discussed in Chapters 3 and 7, a local accessor is not created from a buffer object. Instead, a local accessor is created by specifying a type and a range describing the number of elements of that type. Like other accessors, local accessors may be one-dimensional, two-dimensional, or three-dimensional. Figure 9-7 demonstrates how to declare local accessors and use them in a kernel.

Figure 9-7

Declaring and using local accessors

Remember that local memory is uninitialized when each work-group begins and does not persist after each work-group completes. This means that a local accessor must always be read_write, since otherwise a kernel would have no way to assign the contents of local memory or view the results of an assignment. Local accessors may optionally be atomic though, in which case accesses to local memory via the accessor are performed atomically. Atomic accesses are discussed in more detail in Chapter 19.

Synchronization Functions

To synchronize the work-items in an ND-range kernel work-group, call the barrier function in the nd_item class. Because the barrier function is a member of the nd_item class, it is only available to ND-range kernels and is not available to basic data-parallel kernels or hierarchical kernels.

The barrier function currently accepts one argument to describe the memory spaces to synchronize or fence, but the arguments to the barrier function may change in the future as the memory model evolves in SYCL and DPC++. In all cases though, the arguments to the barrier function provide additional control regarding the memory spaces that are synchronized or the scope of the memory synchronization.

When no arguments are passed to the barrier function, the barrier function will use functionally correct and conservative defaults. The code examples in this chapter use this syntax for maximum portability and readability. For highly optimized kernels, it is recommended to precisely describe which memory spaces or which work-items must be synchronized, which may improve performance.

A Full ND-Range Kernel Example

Now that we know how to declare a local memory accessor and synchronize access to it using a barrier function, we can implement an ND-range kernel version of matrix multiplication that coordinates communication among work-items in the work-group to reduce traffic to global memory. The complete example is shown in Figure 9-8.

Figure 9-8

Expressing a tiled matrix multiplication kernel with an ND-range parallel_for and work-group local memory

The main loop in this kernel can be thought of as two distinct phases: in the first phase, the work-items in the work-group collaborate to load shared data from the A matrix into work-group local memory; and in the second, the work-items perform their own computations using the shared data. In order to ensure that all work-items have completed the first phase before moving onto the second phase, the two phases are separated by a call to barrier to synchronize all work-items and to provide a memory fence. This pattern is a common one, and the use of work-group local memory in a kernel almost always necessitates the use of work-group barriers.

Note that there must also be a call to barrier to synchronize execution between the computation phase for the current tile and the loading phase for the next matrix tile. Without this synchronization operation, part of the current matrix tile may be overwritten by one work-item in the work-group before another work-item is finished computing with it. In general, any time that one work-item is reading or writing data in local memory that was read or written by another work-item, synchronization is required. In Figure 9-8, the synchronization is done at the end of the loop, but it would be equally correct to synchronize at the beginning of each loop iteration instead.

Work-Group Barriers and Local Memory in Hierarchical Kernels

This section describes how work-group barriers and local memory are expressed in hierarchical kernels. Unlike ND-range kernels, local memory and barriers in hierarchical kernels are implicit, requiring no special syntax or function calls. Some programmers will find the hierarchical kernel representation more intuitive and easier to use, whereas other programmers will appreciate the direct control provided by ND-range kernels. In most cases, the same algorithms may be described using both representations, so we can choose the representation that we find easiest to develop and maintain.

Scopes for Local Memory and Barriers

Recall from Chapter 4 that hierarchical kernels express two levels of parallel execution through use of the parallel_for_work_group and parallel_for_work_item functions . These two levels, or scopes, of parallel execution are used to express whether a variable is in work-group local memory and shared across all work-items in the work-group or whether a variable is in per-work-item private memory that is not shared among work-items. The two scopes are also used to synchronize the work-items in a work-group and to enforce memory consistency.

Figure 9-9 shows an example hierarchical kernel that declares a variable at work-group scope in local memory, loads into it, and then uses that variable in work-item scope. There is an implicit barrier between the write into local memory at work-group scope and the read from local memory at work-item scope.

Figure 9-9

Hierarchical kernel with a local memory variable

The main advantage of the hierarchical kernel representation is that it looks very similar to standard C++ code, where some variables may be assigned in one scope and used in a nested scope. Of course, this also may be considered a disadvantage, since it is not immediately obvious which variables are in local memory and when barriers must be inserted by the hierarchical kernel compiler. This is especially true for devices where barriers are expensive!

A Full Hierarchical Kernel Example

Now that we know how to express local memory and barriers in hierarchical kernels, we can write a hierarchical kernel that implements the same algorithm as the ND-range kernel in Figure 9-7. This kernel is shown in Figure 9-10.

Figure 9-10

A tiled matrix multiplication kernel implemented as a hierarchical kernel

Although the hierarchical kernel is very similar to the ND-range kernel, there is one key difference: in the ND-range kernel, the results of the matrix multiplication are accumulated into the per-work-item variable sum before writing to the output matrix in memory, whereas the hierarchical kernel accumulates into memory. We could accumulate into a per-work-item variable in the hierarchical kernel as well, but this requires a special private_memory syntax to declare per-work-item data at work-group scope, and one of the reasons we chose to use the hierarchical kernel syntax was to avoid special syntax!

Hierarchical kernels do not require special syntax to declare variables in work-group local memory, but they require special syntax to declare some variables in work-item private memory!

To avoid the special per-work-item data syntax, it is a common pattern for work-item loops in hierarchical kernels to write intermediate results to either work-group local memory or global memory.

One final interesting property of the kernel in Figure 9-10 concerns the loop iteration variable kk: since the loop is at work-group scope, the loop iteration variable kk could be allocated out of work-group local memory, just like the tileA array. In this case though, since the value of kk is the same for all work-items in the work-group, a smart compiler may choose to allocate kk from per-work-item memory instead, especially for devices where work-group local memory is a scarce resource.

Sub-Groups

So far in this chapter, work-items have communicated with other work-items in the work-group by exchanging data through work-group local memory and by synchronizing via implicit or explicit barrier functions, depending on how the kernel is written.

In Chapter 4, we discussed another grouping of work-items. A sub-group is an implementation-defined subset of work-items in a work-group that execute together on the same hardware resources or with additional scheduling guarantees. Because the implementation decides how to group work-items into sub-groups, the work-items in a sub-group may be able to communicate or synchronize more efficiently than the work-items in an arbitrary work-group.

This section describes the building blocks for communication among work-items in a sub-group. Note that sub-groups are currently implemented only for ND-range kernels and sub-groups are not expressible through hierarchical kernels.

Synchronization via Sub-Group Barriers

Just like how the work-items in a work-group in an ND-range kernel may synchronize using a work-group barrier function, the work-items in a sub-group may synchronize using a sub-group barrier function. Whereas the work-items in a work-group synchronize by calling a group_barrier function or the barrier function in the nd_item class, the work-items in a sub-group synchronize by calling a group_barrier function or the barrier function in a special sub_group class that may be queried from the nd_item class, as shown in Figure 9-11.

Figure 9-11

Querying and using the sub_group class

Like the work-group barrier, the sub-group barrier may accept optional arguments to more precisely control the barrier operation. Regardless of whether the sub-group barrier function is synchronizing global memory or local memory, synchronizing only the work-items in the sub-group is likely cheaper than synchronizing all of the work-items in the work-group.

Exchanging Data Within a Sub-Group

Unlike work-groups, sub-groups do not have a dedicated memory space for exchanging data. Instead, work-items in the sub-group may exchange data through work-group local memory, through global memory, or more commonly by using sub-group collective functions.

As described previously, a collective function is a function that describes an operation performed by a group of work-items, not an individual work-item, and because a barrier synchronization function is an operation performed by a group of work-items, it is one example of a collective function.

Other collective functions express common communication patterns. We will describe the semantics for many collective functions in detail later in this chapter, but for now, we will briefly describe the broadcast collective function that we will use to implement matrix multiplication using sub-groups.

The broadcast collective function takes a value from one work-item in the group and communicates it to all other work-items in the group. An example is shown in Figure 9-12. Notice that the semantics of the broadcast function require that the local_id identifying which value in the group to communicate must be the same for all work-items in the group, ensuring that the result of the broadcast function is also the same for all work-items in the group.

Figure 9-12

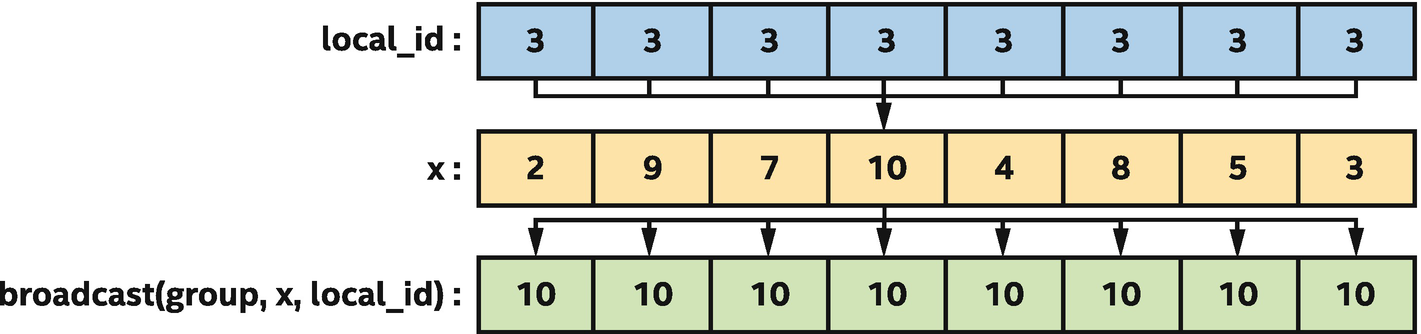
Processing by the broadcast function

If we look at the innermost loop of our local memory matrix multiplication kernel, shown in Figure 9-13, we can see that the access to the matrix tile is a broadcast, since each work-item in the group reads the same value out of the matrix tile.

Figure 9-13

Matrix multiplication kernel includes a broadcast operation

We will use the sub-group broadcast function to implement a matrix multiplication kernel that does not require work-group local memory or barriers. On many devices, sub-group broadcasts are faster than broadcasting with work-group local memory and barriers.

A Full Sub-Group ND-Range Kernel Example

Figure 9-14 is a complete example that implements matrix multiplication using sub-groups. Notice that this kernel requires no work-group local memory or explicit synchronization and instead uses a sub-group broadcast collective function to communicate the contents of the matrix tile among work-items.

Figure 9-14

Tiled matrix multiplication kernel expressed with ND-range parallel_for and sub-group collective functions

Collective Functions

In the “Sub-Groups” section of this chapter, we described collective functions and how collective functions express common communication patterns . We specifically discussed the broadcast collective function, which is used to communicate a value from one work-item in a group to the other work-items in the group. This section describes additional collective functions.

Although the collective functions described in this section can be implemented directly in our programs using features such as atomics, work-group local memory, and barriers, many devices include dedicated hardware to accelerate collective functions. Even when a device does not include specialized hardware, vendor-provided implementations of collective functions are likely tuned for the device they are running on, so calling a built-in collective function will usually perform better than a general-purpose implementation that we might write.

Use collective functions for common communication patterns to simplify code and increase performance!

Many collective functions are supported for both work-groups and sub-groups. Other collective functions are supported only for sub-groups.

Broadcast

The broadcast function enables one work-item in a group to share the value of a variable with all other work-items in the group. A diagram showing how the broadcast function works can be found in Figure 9-12. The broadcast function is supported for both work-groups and sub-groups.

Votes

The any_of and all_of functions (henceforth referred to collectively as “vote” functions) enable work-items to compare the result of a Boolean condition across their group: any_of returns true if the condition is true for at least one work-item in the group, and all_of returns true only if the condition is true for all work-items in the group. A comparison of these two functions for an example input is shown in Figure 9-15.

Figure 9-15

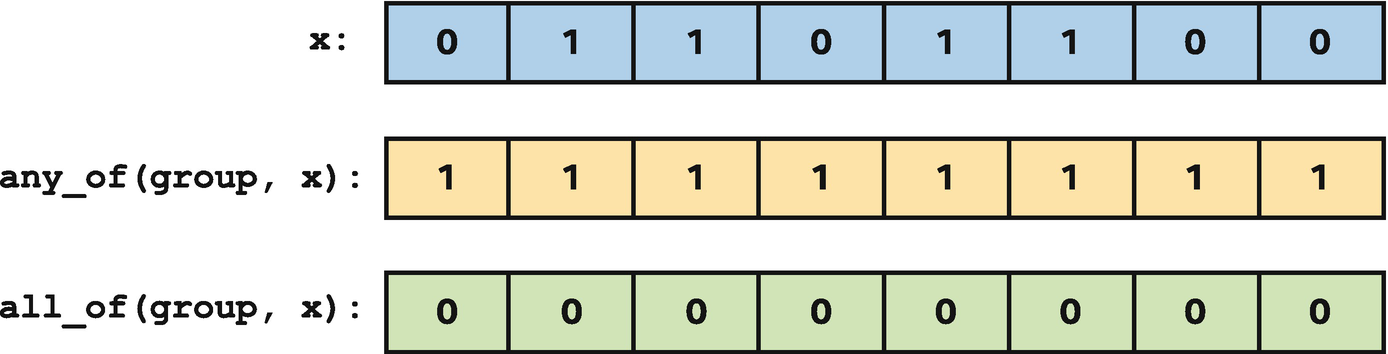
Comparison of the any_of and all_of functions

The any_of and all_of vote functions are supported for both work-groups and sub-groups.

Shuffles

One of the most useful features of sub-groups is the ability to communicate directly between individual work-items without explicit memory operations. In many cases, such as the sub-group matrix multiplication kernel, these shuffle operations enable us to remove work-group local memory usage from our kernels and/or to avoid unnecessary repeated accesses to global memory. There are several flavors of these shuffle functions available.

The most general of the shuffle functions is called shuffle, and as shown in Figure 9-16, it allows for arbitrary communication between any pair of work-items in the sub-group. This generality may come at a performance cost, however, and we strongly encourage making use of the more specialized shuffle functions wherever possible.

Figure 9-16

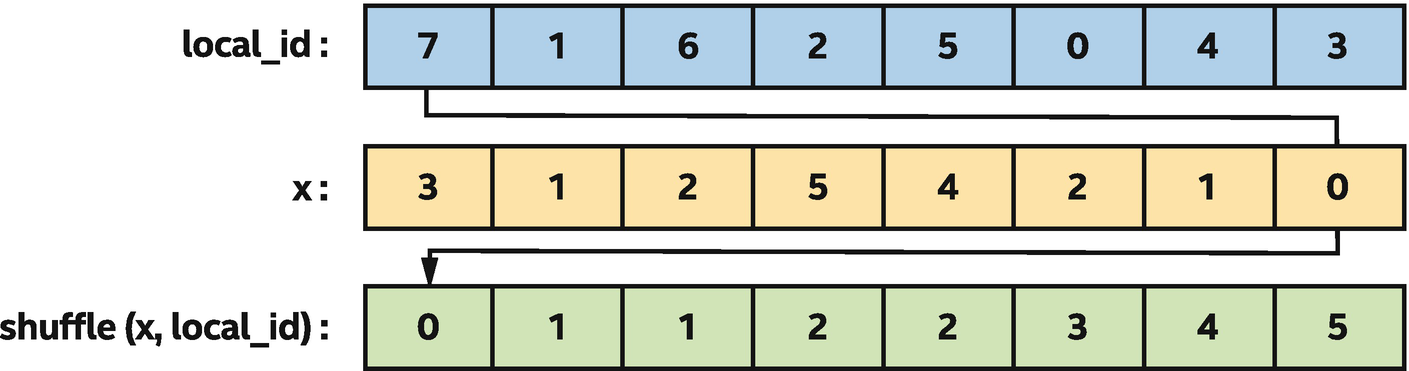
Using a generic shuffle to sort x values based on pre-computed permutation indices

In Figure 9-16, a generic shuffle is used to sort the x values of a sub-group using pre-computed permutation indices. Arrows are shown for one work-item in the sub-group, where the result of the shuffle is the value of x for the work-item with local_id equal to 7.

Note that the sub-group broadcast function can be thought of as a specialized version of the general-purpose shuffle function, where the shuffle index is the same for all work-items in the sub-group. When the shuffle index is known to be the same for all work-items in the sub-group, using broadcast instead of shuffle provides the compiler additional information and may increase performance on some implementations.

The shuffle_up and shuffle_down functions effectively shift the contents of a sub-group by a fixed number of elements in a given direction, as shown in Figure 9-17. Note that the values returned to the last five work-items in the sub-group are undefined and are shown as blank in Figure 9-17. Shifting can be useful for parallelizing loops with loop-carried dependences or when implementing common algorithms such as exclusive or inclusive scans.

Figure 9-17

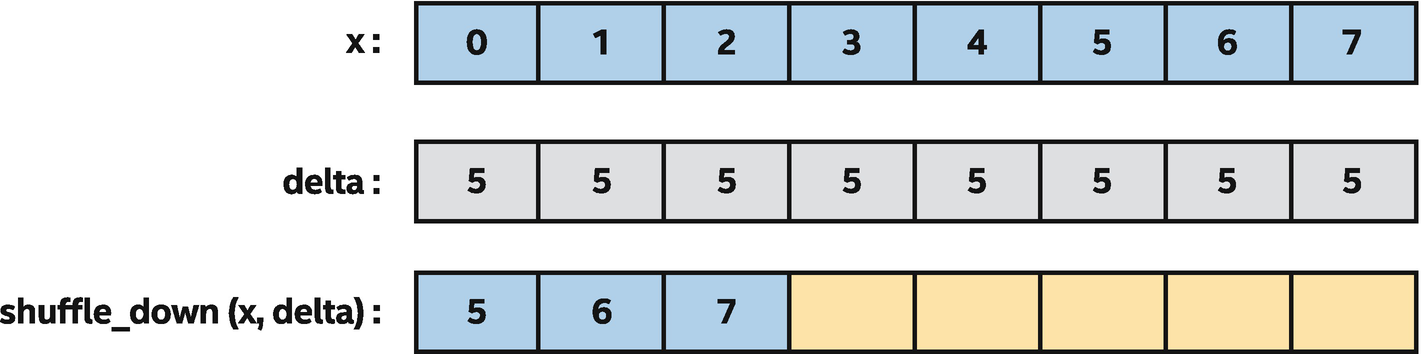
Using shuffle_down to shift x values of a sub-group by five items

The shuffle_xor function swaps the values of two work-items, as specified by the result of an XOR operation applied to the work-item's sub-group local id and a fixed constant. As shown in Figures 9-18 and 9-19, several common communication patterns can be expressed using an XOR: for example, swapping pairs of neighboring values

Figure 9-18

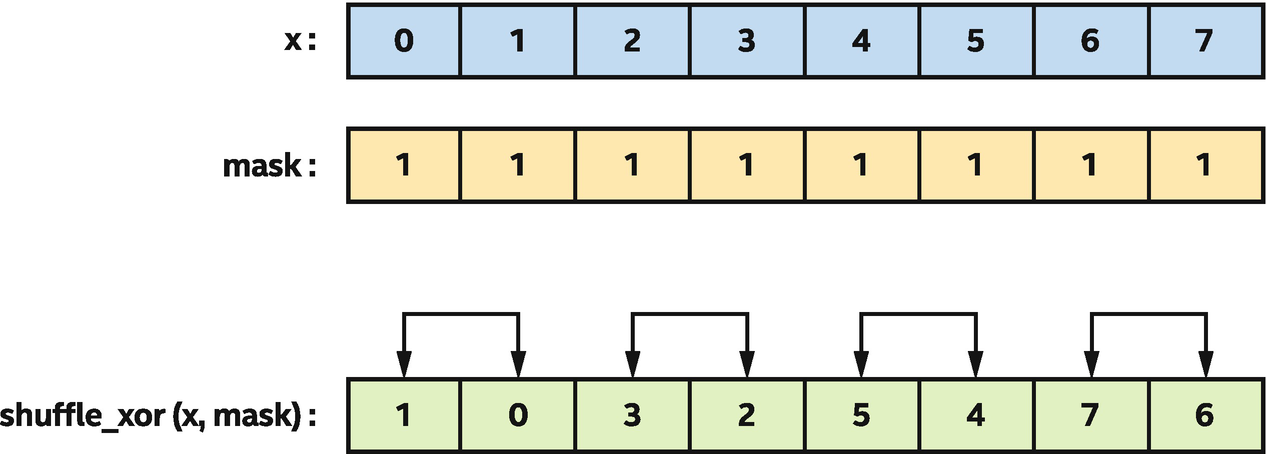
Swapping neighboring pairs of x using a shuffle_xor

Figure 9-19

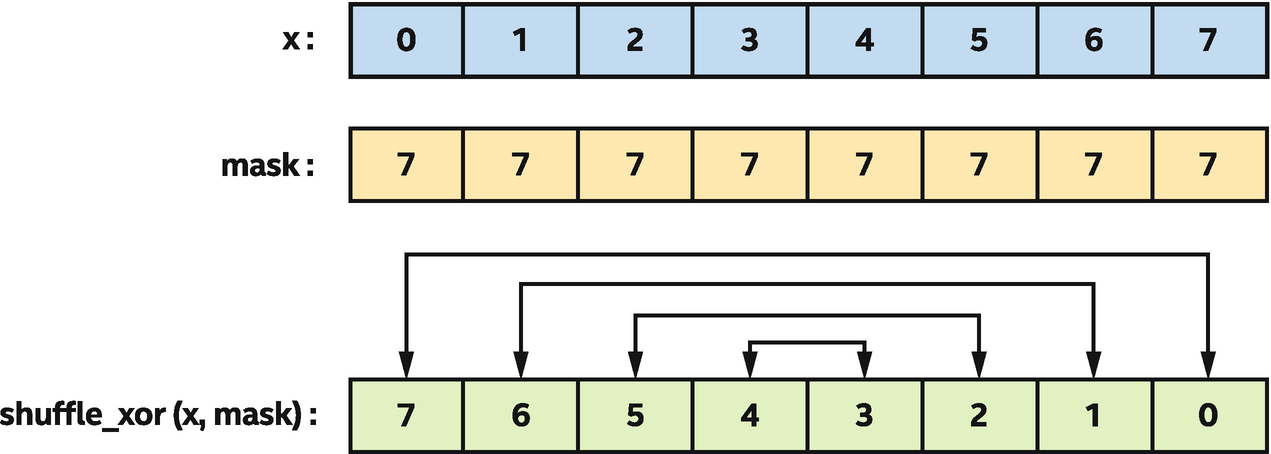
Reverse the values of x using a shuffle_xor

or reversing the sub-group values.

SUB-GROUP OPTIMIZATIONS USING BROADCAST, VOTE, AND COLLECTIVES

The behavior of broadcast, vote, and other collective functions applied to sub-groups is identical to when they are applied to work-groups, but they deserve additional attention because they may enable aggressive optimizations in certain compilers. For example, a compiler may be able to reduce register usage for variables that are broadcast to all work-items in a sub-group or may be able to reason about control flow divergence based on usage of the any_of and all_of functions.

Loads and Stores

The sub-group load and store functions serve two purposes: first, informing the compiler that all work-items in the sub-group are loading contiguous data starting from the same (uniform) location in memory and, second, enabling us to request optimized loads/stores of large amounts of contiguous data.

For an ND-range parallel_for, it may not be clear to the compiler how addresses computed by different work-items relate to one another. For example, as shown in Figure 9-20, accessing a contiguous block of memory from indices [0, 32) appears to have a strided access pattern from the perspective of each work-item.

Figure 9-20

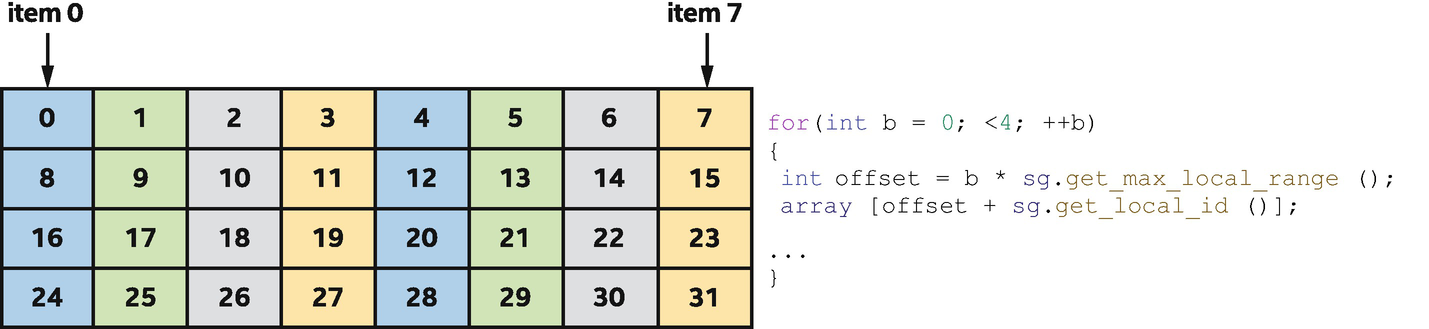
Memory access pattern of a sub-group accessing four contiguous blocks

Some architectures include dedicated hardware to detect when work-items in a sub-group access contiguous data and combine their memory requests, while other architectures require this to be known ahead of time and encoded in the load/store instruction. Sub-group loads and stores are not required for correctness on any platform, but may improve performance on some platforms and should therefore be considered as an optimization hint.

Summary

This chapter discussed how work-items in a group may communicate and cooperate to improve the performance of some types of kernels.

We first discussed how ND-range kernels and hierarchical kernels support grouping work-items into work-groups. We discussed how grouping work-items into work-groups changes the parallel execution model, guaranteeing that the work-items in a work-group execute concurrently and enabling communication and synchronization.

Next, we discussed how the work-items in a work-group may synchronize using barriers and how barriers are expressed explicitly for ND-range kernels or implicitly between work-group and work-item scopes for hierarchical kernels. We also discussed how communication between work-items in a work-group can be performed via work-group local memory, both to simplify kernels and to improve performance, and we discussed how work-group local memory is represented using local accessors for ND-range kernels or allocations at work-group scope for hierarchical kernels.

We discussed how work-groups in ND-range kernels may be further divided into sub-groupings of work-items, where the sub-groups of work-items may support additional communication patterns or scheduling guarantees.

For both work-groups and sub-groups, we discussed how common communication patterns may be expressed and accelerated through use of collective functions.

The concepts in this chapter are an important foundation for understanding the common parallel patterns described in Chapter 14 and for understanding how to optimize for specific devices in Chapters 15, 16, and 17.

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.