Notas
CAPÍTULO 1. LA HIPOTENUSA AL CUADRADO. TEOREMA DE PITÁGORAS
1. The Penguin Book of Curious and Interesting Mathematics de David Wells cita una forma breve del chiste. Un jefe indio tiene tres esposas que se preparan para dar a luz, una sobre la piel de un búfalo, otra sobre la piel de un oso y la otra sobre la piel de un hipopótamo. A su debido tiempo, la primera tuvo un niño, la segunda una niña y la tercera gemelos, un niño y una niña, de este modo ilustra el famoso teorema de que «the squaw on the hippopotamus is equal to the sum of the squaws on the other two hides» (la india del hipopótamo es igual a la suma de las indias de las otras pieles, el enunciado del teorema en inglés y el chiste suena muy parecido en inglés). El chiste se remonta al menos hasta mediados de la década de los cincuenta del siglo pasado cuando fue contado en un programa de radio de la BBC, «My Word», presentado por los guionistas de comedia Frank Muir y Denis Norden.
2. Citado sin referencia en: http://www-history.mcs.st- and.ac.uk/HistTopics/Babylonian_Pythagoras. html
3. A. Sachs, A. Goetze y O. Neugebauer. Mathematical Cuneiform Texts, American Oriental Society, New Haven 1945.
4. La figura se repite por comodidad en la figura 60.
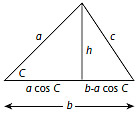
FIGURA 60. División de un triángulo en dos con ángulos rectos.
La perpendicular corta al lado b en dos. Usando trigonometría, una de las partes tiene una longitud de a cos C, de modo que la otra tiene una longitud de b – a cos C. Sea h la longitud de la perpendicular. Por el teorema de Pitágoras:
a2 = h2 + (a cos C)2
c2 = h2 + (b – a cos C)2
Esto es,
a2 – h2 = a2 cos2 C
c2 – h2 = b2 – 2ab cos C + a2 cos2 C
Restando la primera ecuación a la segunda, se elimina el superfluo h2. También desaparece a2 cos2 C, y queda:
c2 – a2 = b2 – 2ab cos C
que nos lleva a la fórmula indicada.
CAPÍTULO 2. ACORTANDO LOS PROCESOS. LOGARITMOS
1. http://www.17centurymaths.com/contents/napiercontents.html
2. Citado de una carta escrita por John Marr a William Lilly.
3. La prostaféresis estaba basada en una fórmula trigonométrica descubierta por François Viète, a saber:

Si tienes una tabla de senos, la fórmula te permite calcular cualquier producto usando solo sumas, restas y la división entre 2.
CAPÍTULO 3. FANTASMAS DE CANTIDADES DIFUNTAS. CÁLCULO
1. Keynes nunca dio la conferencia. La Royal Society planeaba conmemorar el tricentenario en 1942, pero la Segunda Guerra Mundial se interpuso, así que las celebraciones se pospusieron a 1946. Los conferenciantes eran los físicos Edward da Costa Andrade y Niels Bohr y los matemáticos Herbert Turnbull y Jacques Hadamard. La sociedad también invitó a Keynes, cuyos intereses incluían tanto los manuscritos de Newton como la economía. Keynes había escrito una conferencia con el título «Newton, the man» (Newton, el hombre), pero murió antes de que el evento tuviese lugar. Su hermano Geoffrey leyó la conferencia en su nombre.
2. Esta frase proviene de una carta que Newton escribió a Hooke en 1676. No era nueva, en 1159 John de Salisbury escribió que «Bernard de Chartres solía decir que somos como enanos a hombros de gigantes, de modo que podemos ver más que ellos». En el siglo XVII se había convertido en un cliché.
3. La división entre cero lleva a pruebas falaces. Por ejemplo, podemos «probar» que todos los números son cero. Sea a = b. Por lo tanto a2 = ab, así que a2 – b2 = ab – b2. Factorizamos para obtener (a + b)(a – b) = b(a – b). Dividimos por (a – b) para deducir que a + b = b. Por lo tanto a = 0. El error es la división por (a – b), que es 0 ya que consideramos a = b.
4. Richard Westfall. Never at Rest, Cambridge University Press, Cambridge 1980, p. 425.
5. Erik H. Hauri, Thomas Weinreich, Alberto E. Saal, Malcolm C. Rutherford y James A. Van Orman. «High pre-eruptive water contents preserved in lunar melt inclusions», Science Online (26 de mayo de 2011) 1204626. [DOI:10.1126/science.1204626]. Sus resultados resultan polémicos.
6. Sin embargo, no es una coincidencia. Funciona para cualquier función diferenciable: una con una derivada continua. Esto incluye todos los polinomios y todas las series de potencias convergentes, tales como las funciones logarítmicas, exponenciales y varias trigonométricas.
7. La definición moderna es: una función f(h) tiende al límite L a medida que h tiende a cero si para cualquier ε > 0 existe σ > 0 tal que |h| < σ implica que |f(h) – L| < ε. Usando cualquier ε > 0 se evita referirse a algo fluyendo o haciéndose más pequeño; aborda todos los posibles valores de una vez.
CAPÍTULO 4. EL SISTEMA DEL MUNDO. LEY DE GRAVITACIÓN UNIVERSAL
1. El libro del Génesis se refiere al «firmamento». La mayoría de los académicos creen que esto proviene de la antigua creencia hebrea de que las estrellas eran luces minúsculas fijadas a una bóveda del Cielo, con la forma de una semiesfera. Esto es lo que parece el cielo nocturno, el modo en que nuestros sentidos visuales responden a objetos distantes hace que las estrellas aparenten estar a más o menos la misma distancia de nosotros. Muchas culturas, especialmente en Oriente Medio y el lejano Oriente, pensaban en el cielo como un bol que giraba lentamente.
2. El Gran Cometa de 1577 no es el cometa Halley, sino otro de importancia histórica, ahora llamado C/1577 V1. Fue visible a la vista, sin necesidad de telescopio, en 1577 d.C. Brahe observó el cometa y dedujo que los cometas se encontraban fuera de la atmósfera terrestre. El cometa está actualmente a alrededor de 24.000 millones de kilómetros del Sol.
3. La cifra no se conoció hasta 1798, cuando Henry Cavendish obtuvo un valor razonablemente preciso en un experimento de laboratorio. Es sobre 6,67 × 10–11 newton metro cuadrado por kilogramo al cuadrado.
4. June Barrow-Green. Poincaré and the Three Body Problem, American Mathematical Society, Providence 1997.
CAPÍTULO 5. PRESAGIO DEL MUNDO IDEAL. RAÍZ CUADRADA DE MENOS UNO
1. En 1535, los matemáticos Antonio Fior y Niccolò Fontana (apodado Tartaglia, «el tartamudo») participaron en un concurso público. Se pusieron ecuaciones cúbicas para resolver el uno al otro, y Tartaglia venció a Fior rotundamente. En esa época, las ecuaciones cúbicas estaban clasificadas en tres tipos distintos, porque los números negativos no se reconocían. Fior sabía cómo resolver solo un tipo, inicialmente Tartaglia sabía cómo resolver un tipo diferente, pero poco antes del concurso averiguó cómo resolver los otros tipos. Entonces le puso a Fior solo los tipos que sabía que Fior no podría resolver. El concurso llegó a los oídos de Cardano, que estaba trabajando en su libro de texto de álgebra, y se dio cuenta de que Fior y Tartaglia sabían cómo resolver ecuaciones cúbicas. Este resultado mejoraría enormemente el libro, así que le pidió a Tartaglia que le revelase sus métodos.
Finalmente Tartaglia le reveló el secreto, más tarde afirmando que Cardano había prometido no hacerlo nunca público. Pero el método apareció en Ars Magna, así que Tartaglia acusó a Cardano de plagio. Sin embargo, Cardano tenía una excusa, y también tenía una buena razón para romper su promesa. Su estudiante Lodovico Ferrari había encontrado cómo solucionar ecuaciones de cuarto grado, un descubrimiento, igualmente, novedoso y espectacular, y Cardano lo quería también en su libro. Sin embargo, el método de Ferrari necesitaba la solución de una ecuación cúbica asociada, así que Cardano no podía publicar el trabajo de Ferrari sin publicar también el de Tartaglia.
Luego supo que Fior era un estudiante de Scipio del Ferro, de quien se rumoreaba que había solucionado los tres tipos de ecuaciones cúbicas, y le había contado a Fior solo la solución para un tipo. Los artículos no publicados de Del Ferro estaban en posesión de Annibale del Nave. De modo que Cardano y Ferrari fueron a Bolonia en 1543 a consultar a Del Nave y en los papeles encontraron las soluciones para los tres tipos. Así que Cardano podía, de manera honesta, decir que estaba publicando el método de Del Ferro, no el de Tartaglia. Tartaglia todavía se sintió traicionado y publicó una larga y amarga diatriba contra Cardano. Ferrare le retó a un debate público y le ganó sin despeinarse. Tartaglia nunca recuperó realmente su reputación después de eso.
CAPÍTULO 6. AGUJEROS, NUDOS Y MOVIMIENTOS. FÓRMULA DE EULER PARA LOS POLIEDROS
1. Resumido en el capítulo 12 de Las matemáticas de la vida de Ian Stewart, Crítica, Barcelona 2011.
CAPÍTULO 7. PATRONES DEL AZAR. DISTRIBUCIÓN NORMAL
1. Hay muchas falacias en la argumentación de Pascal. La principal es que se aplicaría a cualquier ser hipotético sobrenatural.
2. El teorema afirma que bajo ciertas (bastante comunes) condiciones, la suma de un número grande de variables aleatorias tendrá una distribución aproximadamente normal. Más precisamente, si (x1, ..., xn) es una secuencia de variables aleatorias independientes distribuidas de manera idéntica, cada una teniendo media μ y varianza σ2, entonces el teorema central del límite afirma que

Converge a la distribución normal con media 0 y desviación estándar σ a medida que n se hace arbitrariamente grande.
CAPÍTULO 8. BUENAS VIBRACIONES. ECUACIÓN DE ONDA
1. Observa estas tres masas consecutivas, numeradas n – 1, n, n + 1. Supongamos que en el tiempo t, se desplazan las distancias un – 1(t), un(t) y un + 1(t) desde sus posiciones iniciales en el eje horizontal. Por la segunda ley de Newton, la aceleración de cada masa es proporcional a las fuerzas que actúan sobre ella. Haz la suposición simplificada de que cada masa se mueve a través de una distancia muy pequeña solo en dirección vertical. Para una aproximación muy buena, la fuerza que la masa n – 1 ejerce sobre la masa n es entonces proporcional a la diferencia un – 1(t) – un(t), y de modo similar la fuerza que la masa n + 1 ejerce sobre la masa n es proporcional a la diferencia un + 1(t) – un(t). Sumándolas, la fuerza total ejercida en la masa n es proporcional a un – 1(t) – 2un(t) + un + 1(t). Esta es la diferencia entre un – 1(t) – un(t) y un(t) – un + 1(t), y cada una de estas expresiones es también la diferencia entre las posiciones de masas consecutivas. De modo que la fuerza ejercida en la masa n es una diferencia entre diferencias.
Ahora supongamos que las masas están muy cerca la una de la otra. En cálculo, una diferencia, dividida por una constante pequeña adecuada, es una aproximación a una derivada. Una diferencia entre diferencias es una aproximación a una derivada de una derivada, es decir, una segunda derivada. En el límite de infinidad de masas puntuales, infinitesimalmente juntas, la fuerza ejercida en un punto dado del muelle es por tanto proporcional a ∂2u/∂x2, donde x es la coordenada del espacio medida a lo largo de la longitud de la cuerda. Por la segunda ley de Newton esto es proporcional a la aceleración en ángulo recto de esa línea, que es la segunda derivada del tiempo ∂2u/∂t2. Escribiendo la constante de proporcionalidad como c2 obtenemos:

Donde u(x, t) es la posición vertical de la localización x en la cuerda en el momento t.
2. Para una animación véase: http://en.wikipedia.org/wiki/Wave_equation (o la versión española: http://es.wikipedia.org/wiki/Ecuaci%C3%B3n_ de_onda).
3. En símbolos, las soluciones son precisamente las expresiones:
u(x, t) = f(x – ct) + g(x + ct)
para cualquier función f y g.
4. Animaciones para los primeros pocos modos normales de un tambor circular se pueden encontrar en http://en.wikipedia.org/wiki/Vibrations_ of_a_circular_drum. Hay animaciones de tambores circulares y rectangulares en: http://www.mobiusilearn.com/viewcasestudies.aspx?id=2432
CAPÍTULO 9. ONDAS E INSTANTES. TRANSFORMADA DE FOURIER
1. Supón que u(x, t) = e–n2αt sen nx. Entonces:

Por lo tanto, u(x, t) satisface la ecuación del calor.
2. Esto es codificación JFIF, usada para la web. El código EXIF, para cámaras, también incluye «metadata» describiendo los ajustes de la cámara, como la fecha, la hora y la exposición.
CAPÍTULO 10. LA ASCENSIÓN DE LA HUMANIDAD. ECUACIÓN DE NAVIER-STOKES
1. http://www.nasa.gov/topics/earth/features/2010-warmest-year.html
CAPÍTULO 11. ONDAS EN EL ÉTER. ECUACIONES DE MAXWELL
1. Donald McDonald. «How does a cat fall on its feet?», New Scientist 7, n.º 189 (1960) 1647-1649. Véase también: http://en.wikipedia.org/wiki/Cat_ righting_reflex
2. El rotacional de ambos lados de la tercera ecuación da:

El cálculo vectorial nos dice que la parte izquierda de esta ecuación se simplifica a:

Donde también usamos la primera ecuación. Aquí ∇2 es el operador laplaciano. Usando la cuarta ecuación, la parte derecha se convierte en:

Cancelando un signo menos con el otro y multiplicando por c2 damos con la ecuación de onda para E:
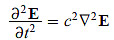
Un cálculo similar revela la ecuación de onda para H.
CAPÍTULO 12. LA LEY Y EL DESORDEN. SEGUNDA LEY DE LA TERMODINÁMICA
1. En concreto,

Donde SA y SB son las entropías en los estados A y B.
2. La segunda ley de la termodinámica es técnicamente una desigualdad, no una ecuación. He incluido la segunda ley en este libro porque su posición central en la ciencia demandaba su inclusión. Es, sin lugar a dudas, una fórmula matemática, una interpretación amplia de «ecuación» que se extiende más allá de la literatura científica técnica. La fórmula a la que se hace alusión en la nota 1 de este capítulo, usando una integral, es una ecuación genuina. Define el cambio de entropía, pero la segunda ley nos dice cuál es su característica más importante.
3. A Brown se le adelantó el fisiólogo holandés Jan Ingenhousz, quien vio el mismo fenómeno en el polvo de carbón flotando en la superficie del alcohol, pero no propuso ninguna teoría para explicar lo que había visto.
CAPÍTULO 13. UNA COSA ES ABSOLUTA. RELATIVIDAD
1. En el Laboratori Nazionali del Gran Sasso, en Italia, hay un detector de partículas de 1.300 toneladas llamado OPERA (acrónimo inglés para Oscillation Project with Emulsion-tRacking Apparatus). Durante más de dos años rastreó 16.000 neutrinos producidos en el CERN, el laboratorio europeo de física de partículas en Ginebra. Los neutrinos son partículas subatómicas eléctricamente neutras con una masa muy pequeña, y pueden pasar a través de materia ordinaria con facilidad. Los resultados fueron desconcertantes: de media los neutrinos completaban el viaje de 730 kilómetros en 60 nanosegundos (mil millonésimas de segundo) más rápido de lo que lo habrían hecho si hubiesen viajado a la velocidad de la luz. Las mediciones eran precisas con un margen de error de 10 nanosegundos, pero ahí se encuentra la posibilidad de algún error sistemático en el modo en que se calcularon e interpretaron los tiempos, que es sumamente complejo.
Los resultados han sido publicados online: «Measurement of the neutrino velocity with the OPERA detector in the CNGS beam» por OPERA Collaboration, http://arxiv.org/abs/1109.4897
Este artículo no reivindica haber refutado la relatividad, simplemente presenta sus observaciones como algo que el equipo no puede explicar con la física convencional. Un informe no técnico puede encontrarse en: http:// www.nature.com/news/2011/110922/full/news.2011.554.html
Una posible fuente de error sistemático, relacionado con las diferencias en las fuerzas de gravedad en los dos laboratorios, se propone en: http:// www.nature.com/news/2011/111005/full/news.2011.575.html, pero el equipo de OPERA cuestiona esta sugerencia.
La mayoría de los físicos creen que, a pesar del gran cuidado tenido por los investigadores, hay un error sistemático implicado. En concreto, observaciones de neutrinos anteriores de una supernova parecen entrar en conflicto con las nuevas. La resolución de la polémica necesitará experimentos independientes y estos requerirán varios años. Los físicos teóricos están ya analizando explicaciones en potencia que van de extensiones menores muy conocidas del modelo estándar de la física de partículas a una exótica nueva física en la cual el universo tiene más dimensiones que las cuatro habituales. En el momento en que leas esto, la historia ya habrá avanzado.
2. Una explicación rigurosa la da Terence Tao en su website: http:// terrytao.wordpress.com/2007/12/28/einsteins-derivation-of-emc2/
La obtención de la ecuación supone cinco pasos:
(a) Describir cómo las coordenadas del espacio y el tiempo se transforman cuando el marco de referencia se cambia.
(b) Usar esta descripción para calcular cómo la frecuencia de un fotón se transforma cuando el marco de referencia se cambia.
(c) Usar la ley de Planck para calcular cómo se transforman la energía y el momento de un fotón.
(d) Aplicar la conservación de la energía y el momento para calcular cómo la energía y el momento de un cuerpo en movimiento se transforman.
(e) Fijar el valor de una constante de lo contrario arbitraria en el cálculo comparando los resultados con la física newtoniana cuando la velocidad del cuerpo es pequeña.
3. Ian Stewart y Jack Cohen. Figments of Reality, Cambridge University Press, Cambridge 1997, p. 37.
4. http://en.wikipedia.org/wiki/Mass%E2%80%93energy_equivalence
5. Unos pocos no lo vieron de ese modo. Henry Courten, reanalizando las fotografías del eclipse solar de 1970, informó de la existencia de al menos siete cuerpos muy diminutos en órbitas rodeando al Sol muy cercanas a él, quizá la evidencia de un cinturón de asteroides interior poco poblado. No se ha encontrado ninguna prueba concluyente de su existencia, y habría sido de menos de 60 kilómetros de ancho. Los objetos vistos en las fotografías podrían tan solo haber sido pequeños cometas o asteroides pasando en órbitas excéntricas. Fuesen lo que fuesen, no eran Vulcano.
6. La energía del vacío en un centímetro cúbico de espacio libre se estima que es 10–15 julios. Según la electrodinámica cuántica debería ser en teoría 10107 julios, un error del orden de 10122. http://en.wikipedia.org/wiki/ Vacuum_energy
7. El trabajo de Penrose se presenta en Paul Davies. The Mind of God, Simon & Schuster, Nueva York 1992.
8. Joel Smoller y Blake Temple. «A one parameter family of expanding wave solutions of the Einstein equations that induces an anomalous acceleration into the standard model of cosmology», http://arxiv.org/abs/0901.1639
9. R.S. MacKay y C.P. Rourke. «A new paradigm for the universe, borrador», Universidad de Warwick, 2011. Para más detalles, véanse los artículos listados en http://msp.warwick.ac.uk/~cpr/paradigm/
CAPÍTULO 14. RAREZA CUÁNTICA. ECUACIÓN DE SCHRÖDINGER
1. La interpretación de Copenhague se dice habitualmente que surgió de las discusiones entre Niels Bohr, Werner Heisenberg, Max Born, y otros, en la mitad de la segunda década del siglo XX. Adquirió el nombre porque Bohr era danés, pero ninguno de los físicos involucrados usó el término en esa época. Don Howard ha sugerido que el nombre, y el punto de vista que engloba, aparece por primera vez a mediados de ese siglo, probablemente a través de Heisenberg. Véase D. Howard. «Who Invented the "Copenhagen Interpretation"? A Study in Mythology», Philosophy of Science 71(2004) 669-682.
2. Mi gato, Harlequin, puede con frecuencia observarse en una superposición de estados «dormido» y «roncando», pero esto probablemente no cuenta.
3. Dos novelas de ciencia ficción sobre esto son El hombre en el castillo de Philip K. Dick y El sueño de hierro de Norman Spinrad. SS-GB del escritor de misterio Len Deighton está también ambientado en una Inglaterra contrafactual regida por los nazis.
CAPÍTULO 15. CÓDIGOS, COMUNICACIONES Y ORDENADORES. TEORÍA DE LA INFORMACIÓN
1. Supón que tiro un dado y asigno los símbolos a, b, c de este modo:
a En el dado sale 1, 2, o 3
b En el dado sale 4 o 5
c En el dado sale 6
El símbolo a se da con una probabilidad de 1/2, el símbolo b tiene probabilidad 1/3, y el símbolo c tiene probabilidad 1/6. Entonces mi fórmula, cualquiera que esta sea, asignará un contenido de información H(1/2, 1/3, 1/6).
Sin embargo, podría pensar en este experimento de un modo diferente. Primero decido si en el dado sale algo menor o igual que 3, o algo mayor. Llama estas posibilidades q y r, de modo que:
q En el dado sale 1, 2 o 3
r En el dado sale 4, 5 o 6
Ahora q tiene probabilidad ½ y r tiene probabilidad ½. Cada uno transmite información H(1/2, 1/2). El caso q es mi a original, y el caso r son mi b y c originales. Puedo dividir el caso r en b y c, y sus probabilidades son 2/3 y 1/3 asumiendo que ha ocurrido r. Si ahora consideramos solo este caso, la información transmitida por cualquiera que resulte ser b y c es H(2/3, 1/3). Shannon ahora insiste en que la información original debería estar relacionada con la información en estos subcasos como sigue:
H(1/2, 1/3, 1/6) = H(1/2, 1/2) + ½ H(1/2, 1/3)
Véase la figura 61.

FIGURA 61. Elecciones combinadas de modos diferentes. La información debería ser la misma en cada caso.
El factor ½ delante de la H final está presente porque esta segunda elección se da solo la mitad de las veces, concretamente cuando se escoge r en la primera etapa. No existe este factor delante de H justo después del signo igual, porque esto se refiere a la elección que siempre se hace, entre q y r.
2. Véase el capítulo 2 de C.E. Shannon y W. Weaver. The Mathematical Theory of Communication, University of Illinois Press, Urbana, 1964.
CAPÍTULO 16. EL DESEQUILIBRIO DE LA NATURALEZA. TEORÍA DEL CAOS
1. Si la población xt es relativamente pequeña, de modo que es cercana a cero, entonces 1 – xt es cercano a 1. La siguiente generación tendrá, por lo tanto, un tamaño cercano a kxt, que es k veces tan grande como la actual. A medida que el tamaño de la población aumenta, el factor extra 1 – xt hace la tasa de crecimiento real más pequeña, y cae a cero a medida que la población se aproxima a su máximo teórico.
2. R.F. Costantino, R.A. Desharnais, J.M. Cushing y B. Dennis. «Chaotic dynamics in an insect population», Science 275 (1997) 389-391.
3. J. Huisman y F.J. Weissing. «Biodiversity of plankton by species oscillations and chaos», Nature 402 (1999) 407-410.
4. E. Benincà, J. Huisman, R. Heerkloss, K.D. Jöhnk, P. Branco, E.H. Van Nes, M. Scheffer y S.P. Ellner. «Chaos in a long-term experiment with a plankton community», Nature 451 (2008) 822-825.
CAPÍTULO 17. LA FÓRMULA DE MIDAS. ECUACIÓN DE BLACK-SCHOLES
1. El valor de una opción de compra es:
C(s, t) = N(d1)S – N(d2)Ke–r(T – t)
Donde

El precio de la opción de venta correspondiente es:
P(s, t) = [N(d1) – 1]S + [1 – N(d2)]Ke–r(T – t)
Donde N(dj) es la función de distribución acumulada de la distribución normal estándar para j = 1, 2, y T – t es el tiempo para el vencimiento.
2. En sentido estricto, el premio Sveriges Riksbank en Ciencias Económicas en memoria de Alfred Nobel.
3. M. Poovey. «Can numbers ensure honesty? Unrealistic expectations and the U.S. accounting scandal», Notices of the American Mathematical Society 50 (2003) 27-35.
4. A.G. Haldane y R.M. May. «Systemic risk in banking ecosystems», Nature 469 (2011) 351-355.