Information is the vital input into any active management strategy. Information separates active management from passive management. Information, properly applied, allows active managers to outperform their informationless benchmarks.
Information analysis is the science of evaluating information content and refining information to build portfolios. Information analysis works for managers who have a nonquantitative process and for managers who have a quantitative investment process— the only requirement is that there is a process.
Information is a rather fuzzy concept. Information analysis begins by transforming information into something concrete: investment portfolios. Then it analyzes the performance of those portfolios to determine the value of the information. Information analysis can work with something as simple as an analyst’s buy and sell recommendations. Or it can work with alpha forecasts for a broad universe of stocks. Information analysis is not concerned with the intuition or process used to generate stock recommendations, only with the recommendations themselves.
Information analysis can be precise. It can determine whether information is valuable on the upside, the downside, or both. It can determine whether information is valuable over short horizons or long horizons. It can determine whether information is adding value to your investment process.
Information analysis occurs before backtesting in the investment process. Information analysis looks at the unfettered value of signals. Backtesting then takes those signals that have been identified as containing information and develops investable strategies. Backtesting looks not only at information content, but also at turnover, tradability, and transactions costs.
This chapter will focus very explicitly on information analysis. It will present a unified treatment of information analysis, with both theoretical discussions and concrete examples. Information analysis is a broad subject. This chapter will cover the general approach, but will also recommend a specific approach to best analyze investment information. The key insights in the chapter are as follows:
■ Information analysis is a two-step process.
■ Step 1 is to turn information into portfolios.
■ Step 2 is to analyze the performance of those portfolios.
■ Event studies provide analysis when information arrives episodically.
The chapter will describe how and where information appears in the active management process, and then introduce and discuss in detail the two-step process of information analysis. We will include some discussion of performance analysis, but a more in-depth treatment of that subject will appear in Chap. 17. We will treat event studies of episodic information as a special topic. The chapter will end by describing the pitfalls of information analysis. Information analysis is a tool, and, as with a hammer, one must distinguish between thumb and nail.
Where and how does information arise in active management? Active managers, as opposed to passive managers, apply information to achieve superior returns relative to a benchmark. Passive managers simply try to replicate the performance of the benchmark. They have no information.
Active managers use information to predict the future exceptional return on a group of stocks. The emphasis is on predicting alpha, or residual return: beta-adjusted return relative to a benchmark. We want to know what stocks will do better than average and what stocks will do worse, on a risk-adjusted basis.
So, when we talk about information in the context of active management, we are really talking about alpha predictors. For any set of data pertaining to stocks, we can ask: Do these data help predict alphas? We will even call this set of data a predictor.
In general, any predictor is made up of signal plus noise. The signal is linked with future stock returns. The noise masks the signal and makes the task of information analysis both difficult and exciting. Random numbers contain no signal, only noise. Information analysis is an effort to find the signal-to-noise ratio.
A predictor will cover a number of time periods and a number of stocks in each time period. The information at the beginning of period t is a data item for each stock. The data item can be as simple as +1 for all stocks on a recommended buy list and −1 for all stocks on a sell list. On the other hand, the data item can be a precise alpha: 2.15 percent for one stock, −3.72 percent for another, etc. Other predictors might be scores. Crude scores can be a grouping of stocks into categories, a more refined version of the buy and sell idea. Other scores might be a ranking of the stocks along some dimension. Notice that it is possible to start with alphas and produce a ranking. It is also possible to start with a ranking and produce other scores, such as 4 for the stocks in the highest quartile, down to 1 for the stocks in the lowest quartile.
The predictors can be publicly available information, such as consensus earnings forecasts, or they can be derived data, such as a change in consensus earnings forecasts. Predictors are limited only by availability and imagination.
We can classify information along the following dimensions:
■ Primary or processed
■ Judgmental or impartial
■ Ordinal or cardinal
■ Historical, contemporary, or forecast
Primary information is information in its most basic form. Usually information is processed to some extent. An example would be a firm’s short-term liabilities as a primary piece of information, and the ratio of those liabilities to short-term assets as a processed piece of information. Just because information is processed doesn’t mean that it is necessarily better. It may be a poorer predictor of returns.
Judgmental information comes with significant human input. It is, by its nature, irreproducible. Expectations data from a single expert or a panel of experts is an example.
With ordinal data, assets are classified into groups and some indication of the order of preference of one group over the other is provided. The buy, sell, hold classification is an example of ordinal data. With cardinal information, a number is associated with each asset, with some importance associated with the numerical values.
We can categorize information as historical, contemporary, or forecast. Average earnings over the past three years is historical information; the most recent earnings is current information; and forecast future earnings is forecast information.
In this chapter, we will use the example of book-to-price data in the United States to generate return predictors according to various standard schemes. For instance, we can generate a buy list and a sell list by ranking all stocks according to book-to-price ratios and placing the top half on the buy list and the bottom half on the sell list. The purpose of this and other examples is not to suggest novel new strategies, but simply to illustrate information analysis techniques.
Underlying the book-to-price examples will be the hypothesis that book-to-price ratios contain information concerning future stock returns, and, in particular, that high-book-to-price stocks will outperform low-book-to-price stocks. Is this hypothesis true? How much information is contained in book-to-price ratios? We will apply information analysis and find out.
Information analysis is a two-step process:
Step 1: Turn predictions into portfolios.
Step 2: Evaluate the performance of those portfolios.
In step 1, the information is transformed into a concrete object: a portfolio. In step 2, the performance of the portfolio is then analyzed.
Information analysis is flexible. There are a great many ways to turn predictions into portfolios and a great many ways to evaluate performance. We will explore many of these alternatives below.
Let’s start with step 1, turning predictions into portfolios. Since we have predictions for each time period, we will generate portfolios for each time period.1 There are a great many ways to generate portfolios from predictions, and the procedure selected could depend on the type of prediction. Here are six possibilities. For each case, we have listed the general idea, and then discussed how to apply this to data concerning book-to-price ratios. Later we will analyze the performance of these portfolios.
■ Procedure 1. With buy and sell recommendations, we could equal- (or value-) weight the buy group and the sell group.
Using book-to-price ratios, we can generate the buy and sell lists, as described above, by first ranking stocks by book-to-price and then putting the top half on the buy list and the bottom half on the sell list.
■ Procedure 2. With scores, we can build a portfolio for each score by equal- (or value-) weighting within each score category.
We can generate scores from book-to-price ratios by ranking stocks by book-to-price ratio, as before, and then, for example, giving the top fifth of the list (by number or capitalization) a score of 5, the next fifth a score of 4, down to the bottom fifth, with a score of 1. This is simply dividing stocks into quintiles by book-to-price.
■ Procedure 3. With straight alphas, we can split the stocks into two groups, one group with higher than average alphas and one group with lower than average alphas. Then we can weight the stocks in each group by how far their alpha exceeds (or lies below) the average. This is an elaboration of procedure 1.
One way to generate alphas from book-to-price ratios is to assume that they are linearly related to the book-to-price ratios. So we can weight each asset in our buy and sell list by how far its book-to-price ratio lies above or below the average.
■ Procedure 4. With straight alphas, we can rank the assets according to alpha, then group the assets into quintiles (or deciles or quartiles or halves) and equal- (or value-) weight within each group. This is an elaboration of procedure 2.
For alphas linearly related to book-to-price ratios, this is a straightforward extension of procedure 3.
■ Procedure 5. With any numerical score, we can build a factor portfolio that bets on the prediction and does not make a market bet. The factor portfolio consists of a long portfolio and a short portfolio. The long and short portfolios have equal value and equal beta, but the long portfolio will have a unit bet on the prediction, relative to the short portfolio. Given these constraints, the long portfolio will track the short portfolio as closely as possible.
For book-to-price data, we can build long and short portfolios with equal value and beta, with the long portfolio exhibiting a book-to-price ratio one standard deviation above that of the short portfolio, and designed so that the long portfolio will track the short portfolio as closely as possible.
■ Procedure 6. With any numerical score, we can build a factor portfolio, consisting of a long and a short portfolio, designed so that the long and short portfolios are matched on a set of prespecified control variables. For example, we could make sure the long and short portfolios match on industry, sector, or small-capitalization stock exposures. This is a more elaborate form of procedure 5, where we controlled only for beta (asa measure of exposure to market risk). Using the book-to-price data, this is an extension of procedure 5.
The general idea should be clear. We are trying to establish some sort of relative performance. In each case, we will produce two or more portfolios. In the first, third, fifth and sixth procedures, we will have a long and a short portfolio. The long bets on the information; the short bets against it. In procedure 2, we have a portfolio for each score, and in procedure 4, we have a portfolio for each quintile.
Procedures 5 and 6 are more elaborate and “quantitative” than the first four procedures. They require more sophisticated technology, which we describe in detail in the technical appendix. However, the basic inputs—the information being analyzed— needn’t be based on a quantitative strategy. Numerical scores derived by any method will work.
While procedures 5 and 6 are more elaborate, they also isolate the information contained in the data more precisely. These procedures build portfolios based solely on new information in the data, controlling for other important factors in the market.
Because they set up a controlled experiment, we recommend procedure 5 or procedure 6 as the best approach for analyzing the information contained in any numerical scores.
To be explicit about step 1, let’s apply some of these procedures in two separate examples based on book-to-price ratios from January 1988 through December 1992.
For Example A, we will build portfolios according to procedure 2. Every month we will rank assets in the S&P 500 by book-to-price ratio, and then divide them into quintiles, defined so that each quintile has equal capitalization. We will turn these quintiles into portfolios by capitalization-weighting the assets in each quintile.
For Example B, we will build portfolios according to procedure 5. Every month we will build two portfolios, a long portfolio and a short portfolio. The two portfolios will have equal value and beta. The long portfolio will exhibit a book-to-price ratio one standard deviation above that of the short portfolio. And given these constraints, the long portfolio will track the short portfolio as closely as possible. What can these examples tell us about the investment information contained in book-to-price ratios?
We have turned the data into two or more portfolios. Now we must evaluate the performance of those portfolios.2 The general topic of performance analysis is a complicated one, and we will discuss it in detail in Chap. 17. Here we will simply present several approaches and summary statistics, including the information ratio and information coefficient.
The simplest form of performance analysis is just to calculate the cumulative returns on the portfolios and the benchmark, and plot them. Some summary statistics, like the means and standard deviations of the returns, can augment this analysis.
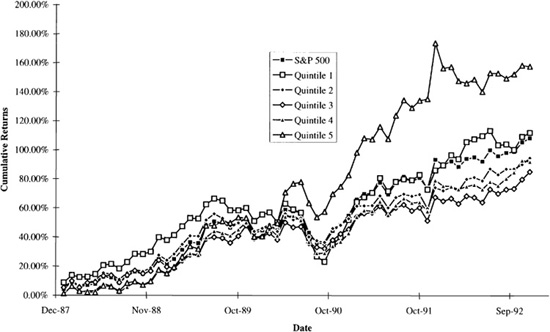
Figure 12.1 illustrates this basic analysis for Example A. It shows the cumulative active return on each of the five quintile portfolios. These results are interesting. From January 1988 through the beginning of 1989, the portfolios perform approximately in ranked order. The highest-book-to-price-quintile portfolio has the highest cumulative return, and the lowest-book-to-price-quintile portfolio has almost the lowest cumulative return. However, the situation changed dramatically in 1989 through 1990. Book-to-price ratios are standard “value” measures, and value stocks underperformed growth stocks in this period. And, over the entire five-year analysis period, the lowest-book-to-price-quintile portfolio has the highest cumulative return, with the highest-quintile portfolio in a distant second place. Still, we constructed the quintile portfolios based only on book-to-price ratios, without controlling for other factors. The quintiles may contain incidental bets that muddy the analysis.
Figure 12.2 shows the cumulative returns for the long, short, and net (long minus short) portfolios for Example B. It tells a slightly different story from Fig. 12.1. Here too the long portfolio, which bets on book-to-price, is the best performer over the early period, but the short portfolio, which bets against book-to-price, catches up by 1990. However, unlike the bottom-quintile portfolio from Example A, the short portfolio is not ultimately the best performer.
The net portfolio has a forecast beta of zero, and we can see that its returns appear uncorrelated with the market. The net bet on book-to-price works well until early 1989, and then disappears through 1990 and 1991. It begins to work again in 1992. Comparing Figs. 12.1 and 12.2, different approaches for constructing portfolios from the same basic information lead to different observed performance and different estimates of information content.
So far, we have discussed only the simplest form of performance analysis: looking at the returns. More sophisticated analyses go beyond this to investigate statistical significance, value added, and skill, as measured by t statistics, information ratios, and information coefficients. All are related.
Figure 12.1 Book-to-price quintile analysis.
Figure 12.2 Factor portfolio analysis.
We start with regression analysis on the portfolio returns, regressing the excess portfolio returns against the excess benchmark returns, to separate the portfolio return into two components, one benchmark-related and the other non-benchmark-related:
This regression will estimate the portfolio’s alpha and beta, and will evaluate, via the t statistic, whether the alpha is significantly different from zero.
The t statistic for the portfolio’s alpha is
simply the ratio of the estimated alpha to the standard error of the estimate. This statistic measures whether the alpha differs significantly from zero. Assuming that alphas are normally distributed, if the t statistic exceeds 2, then the probability that simple luck generated these returns is less than 5 percent.
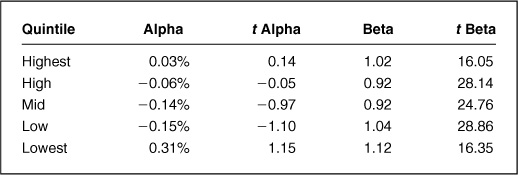
Applying regression analysis to Example A, we find the results shown in Table 12.1. This analysis corroborates the visual results from Fig. 12.1. Only the highest- and lowest-quintile portfolios outperformed the S&P 500, and only they exhibit positive alphas. Unfortunately, none of the alphas are significant at the 95 percent confidence level, according to the t statistics. The analysis of beta shows that the quintiles differed significantly in their exposure to the market.
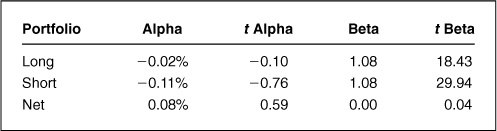
Applying regression analysis to Example B, we find the results shown in Table 12.2. This analysis is consistent with Fig. 12.2.* The alphas for both long and short portfolios are negative, with the net portfolio exhibiting zero beta and net positive alpha. None of the alphas are significant at the 95 percent confidence level.
So far, this analysis has focused only on t statistics. What about information ratios? As we have discussed in previous chapters, the information ratio is the best single statistic for capturing the potential for value added from active management. In Examples A and B, we observe the information ratios shown in Table 12.3.
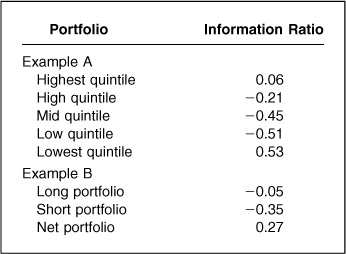
The highest information ratio appears for the lowest-quintile portfolio. The next best information ratio appears for the net portfolio, which explicitly hedges out any market bets.
The t statistic and the information ratio are closely related. The t statistic is the ratio of alpha to its standard error. The information ratio is the ratio of annual alpha to its annual risk. If we observe returns over a period of T years, the information ratio is approximately the t statistic divided by the square root of the number of years of observation:
This relationship becomes more exact as the number of observations increases.
Do not let this close mathematical relationship obscure the fundamental distinction between the two ratios. The t statistic measures the statistical significance of the return; the information ratio captures the risk-reward trade-off of the strategy and the manager’s value added. An information ratio of 0.5 observed over 5 years may be statistically more significant than an information ratio of 0.5 observed over 1 year, but their value added will be equal.3 The distinction between the t statistic and the information ratio arises because we define value added based on risk over a particular horizon, in this case 1 year.
The third statistic of interest is the information coefficient. This correlation between forecast and realized alphas is a critical component in determining the information ratio, according to the fundamental law of active management, and is a critical input for refining alphas and combining signals, as described in Chaps. 10 and 11.
In the context of information analysis, the information coefficient is the correlation between our data and realized alphas. If the data item is all noise and no signal, the information coefficient is 0. If the data item is all signal and no noise, the information coefficient is 1. If there is a perverse relationship between the data item and the subsequent alpha, the information coefficient can be negative. The information coefficient must lie between +1 and -1.
Going back to our example, the information coefficient of the book-to-price signals over the period January 1988 through December 1992 is 0.01.
As we saw in Chap. 6, the information coefficient is related to the information ratio by the fundamental law of active management:
where BR measures the breadth of the information, the number of independent bets per year which the information will allow. In our example, given an information ratio of 0.27 and an information coefficient of 0.01, we can back out that the book-to-price information allows a little over 700 independent bets per year. Since the information covers 500 assets 12 times per year, it generates 6000 information items per year. Evidently not all are independent. As a practical matter, the parameter BR is more difficult to measure than either the information ratio or the information coefficient.
The subject of performance analysis is quite broad, and we will cover it in detail in Chap. 17. Still, it is worth briefly mentioning some advanced topics that pertain to analyzing information.
The first topic concerns portfolio turnover. Our two-step process has been to turn information into portfolios and then analyze the performance of those portfolios. Since we have the portfolios, we can also investigate their turnover. In fact, given transactions costs, turnover will directly affect performance. Turnover becomes important as we move from information analysis to backtesting and development of investable strategies.
Other topics concern more detailed levels of analysis that our approach allows. For instance, when we build long and short portfolios to bet for and against the information, we can also observe whether our information better predicts upside or downside alphas.
Beyond upside and downside information, we can also investigate whether the data contain information pertaining to up markets or down markets. How well do the portfolios perform in periods when the market is rising and in periods when the market is falling?
Finally, some advanced topics involve the connection between performance analysis and the step of turning information into portfolios. We can investigate the importance of controlling for other variables: industries, size, etc. We can construct portfolios with different controls, and analyze the performance in each case.
So far, our analysis of information has assumed that our information arrives regularly—e.g., every month for every asset in our investment universe. This facilitates building monthly portfolios and then observing their performance. Some information doesn’t arrive in neat cross-sectional packages. Some information-laden events occur at different times for different assets. We need a methodology for analyzing these sources of information: the event study.
Where cross-sectional information analysis looks at all the information arriving at a date, event studies look at information arriving with a type of event. Only our imagination and the existence of relevant data will limit possible event studies. Examples of events we could analyze include
■ An earnings announcement
■ A new CEO
■ A change in dividend
■ A stock split
Three types of variables play a role in event studies: a description of the event, asset returns after the event, and conditioning variables from before the event. Often, the description of the event is a 0/1 variable: The event happened or it didn’t. This is the case, for example, if a company hires a new CEO. Other events warrant a more complicated description. For example, studies of earnings announcements use the “earnings surprise” as the relevant variable. This is the announced earnings less consensus forecasts, divided by the dispersion of analysts’ forecasts or some other measure of the uncertainty in earnings. As a second example, we could use the change in yield to describe a dividend change event.
Next, we need the asset’s return after the event. This requires special care, because event studies analyze events at different times. They must avoid confounding calendar time with the time measured relative to the event, by extracting the distortions that arise because the events occurred at separate calendar times. For example, stock ABC increased dividends from $1.65 to $1.70 on August 6, 1999, and stock XYZ reduced dividends from $0.95 to $0.80 on September 5, 1996. In both cases, we want to look at the performance of the stock in the month, quarter, and year subsequent to the event. But the market after September 5, 1996, might have differed radically from the market after August 6,1999. Hence, event studies typically use asset residual returns after the event.4
Finally, we may wish to use additional conditioning variables characterizing the firm at the time of the event. Starting with the above list of example events, here are some possible characterizations:
■ An earnings announcement
-Surprise in the previous quarter
■ A new CEO
-From the inside or outside
-Predecessor’s fate: retired, fired or departed?
■ A change in dividend
-Company leverage
■ A stock split
-Percent of institutional ownership
-Has there been a change in leadership?
In the generic case, we start with n = 1, 2,..., N events; residual returns cumulated from period 1 to period j following each event, θn(1,j); the residual risk estimate over the period, ωn(1,j); and conditioning variables Xnk, where k = 1, 2,...,K indexes the different conditioning variables for each event n.
Once we have compiled and organized all this information, the event study takes the form of a regression:
Once we have implemented the event study as a regression, we can apply the usual statistical analysis. We obviously care about the significance of the explanatory variables.
We will also be interested in how the coefficients change with distance from the event, even separating the future returns into segments. If we are counting trading days, we could look at performance by week: θn(1,5), θn(6,10), etc. To analyze performance in, e.g., the second week, run the regression
Note that in these event study regressions, the dependent variable (the left-hand side of the equation) has ex ante mean 0 and standard deviation 1, and the in-sample estimate of the IC of the signal is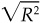 
from the regression.
Given the analysis above and an event that just occurred, the forecast alpha over the next j periods is
If the event occurred j1 periods earlier, the forecast alpha is
Equations (12.7) and (12.8) are consistent with the volatility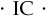 
score rule of thumb. The first term, ωn(1,j), is the volatility. The fitted part of the regression, 
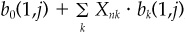, will be of the order of IC · score, since we made the dependent variable have ex ante mean 0 and standard deviation 1.
The results from an event study do not translate directly into an ex ante information ratio, as cross-sectional results do. We could, of course, calculate both an ex ante and an ex post information ratio using the alphas described above.
But we can also use a simple model to derive some insight into the relationship between our event study results and information ratios. Three factors are important to this relationship: the rate at which events occur, the ability to forecast future returns, and the decay rate of that forecasting ability.
Our simple model will first assume that the number of trading days between events has a geometric distribution. The probability that an event will occur in any given day is p. The probability that the next event occurs in j days is p · (1 − p)j-1. This just accounts for the probability that the event doesn’t occur for j − 1 days, and then occurs 1 day. The expected number of days between events is 1/p.
The model will then account for forecasting ability with the information coefficient. The information coefficient for the first day after the event is IC(1).
Finally, the model will account for the decay in forecasting ability as we move away from the event. This is the information horizon, which we treat in depth in Chap. 13. For now, we will simply assume that the information coefficient decays exponentially over time. For j days after the event,
Sometimes we have a better sense of a half-life than of a decay constant. We can easily convert from one to the other. The half-life in days is simply log{0.5}/log{γ}.
With this information, and assuming J trading days per year and an investment universe of N roughly similar assets, the model estimates the annual information coefficient,
and the information ratio,
The technical appendix provides the details. Note that combining Eq. (12.11) with the fundamental law of active management implies a measure of the breadth of the event information. Effectively, we are receiving fresh information on N* assets, where
Equation (12.12) captures the essence of the process. If p is large (close to 1), events happen every day and N* ≈ N. But what if p is small? If our event is the appointment of a new CEO, which might occur every 7 years or so, then p = 0.00056. For such rare events, the effective breadth is
Assuming an annual information coefficient of 0.04 and 1000 assets, Fig. 12.3 shows how the information ratio depends on the number of events per year and the half-life of the information.
Information analysis is a powerful tool. If we can use information analysis to evaluate the investment value of a set of raw data, we can also use it to refine those data. If this is done correctly, we are separating wheat from chaff. If it is done incorrectly, we are data mining.
Data mining can fool an analyst into believing that information exists when it does not. Data mining can lead managers to bet on information that doesn’t exist. Data mining is the bane of information analysis.
Figure 12.3 Sensitivity of information ratio to signal half-life.
Why is it that so many ideas look great in backtests and disappoint upon implementation? Backtesters always have 95 percent confidence in their results, so why are investors disappointed far more than 5 percent of the time? It turns out to be surprisingly easy to search through historical data and find patterns that don’t really exist.
To understand why data mining is easy, we must first understand the statistics of coincidence. Let’s begin with some noninvestment examples. Then we will move on to investment research.
Several years ago, Evelyn Adams won the New Jersey state lottery twice in 4 months. Newspapers put the odds of that happening at 17 trillion to 1, an incredibly improbable event. A few months later, two Harvard statisticians, Percy Diaconis and Frederick Mosteller, showed that a double win in the lottery is not a particularly improbable event. They estimated the odds at 30 to 1. What explains the enormous discrepancy in these two probabilities?
It turns out that the odds of Evelyn Adams’s winning the lottery twice are in fact 17 trillion to 1. But that result is presumably of interest only to her immediate family. The odds of someone, somewhere, winning two lotteries—given the millions of people entering lotteries every day—are only 30 to 1. If it wasn’t Evelyn Adams, it could have been someone else.
Coincidences appear improbable only when viewed from a narrow perspective. When viewed from the correct (broad) perspective, coincidences are no longer so improbable. Let’s consider another noninvestment example: Norman Bloom, arguably the world’s greatest data miner.
Norman Bloom died a few years ago in the midst of his quest to prove the existence of God through baseball statistics and the Dow Jones average. He argued that “BOTH INSTRUMENTS are in effect GREAT LABORATORY EXPERIMENTS wherein GREAT AMOUNTS OF RECORDED DATA ARE COLLECTED, AND PUBLISHED” (capitalization Bloom’s). As but one example of his thousands of analyses of baseball, he argued that the fact that George Brett, the Kansas City third baseman, hit his third home run in the third game of the playoffs, to tie the score 3-3, could not be a coincidence—it must prove the existence of God. In the investment arena, he argued that the Dow’s 13 crossings of the 1000 line in 1976 mirrored the 13 colonies which united in 1776—which also could not be a coincidence. (He pointed out, too, that the 12th crossing occurred on his birthday, deftly combining message and messenger.) He never took into account the enormous volume of data—in fact, the entire New York Public Library’s worth—he searched through to find these coincidences. His focus was narrow, not broad.
With Bloom’s passing, the title of world’s greatest living data miner has been left open. Recently, however, Michael Drosnin, author of The Bible Code, seems to have filled it.5
The importance of perspective for understanding the statistics of coincidence was perhaps best summarized by, of all people, Marcel Proust—who often showed keen mathematical intuition:
The number of pawns on the human chessboard being less than the number of combinations that they are capable of forming, in a theater from which all the people we know and might have expected to find are absent, there turns up one whom we never imagined that we should see again and who appears so opportunely that the coincidence seems to us providential, although, no doubt, some other coincidence would have occurred in its stead had we not been in that place but in some other, where other desires would have been born and another old acquaintance forthcoming to help us satisfy them.6
Investment research involves exactly the same statistics and the same issues of perspective. The typical investment data mining example involves t statistics gathered from backtesting strategies. The narrow perspective says, “After 19 false starts, this 20th investment strategy finally works. It has a t statistic of 2.”
But the broad perspective on this situation is quite different. In fact, given 20 informationless strategies, the probability of finding at least one with a t statistic of 2 is 64 percent. The narrow perspective substantially inflates our confidence in the results. When the situation is viewed from the proper perspective, confidence in the results decreases accordingly.7
Fortunately, four guidelines can help keep information analysis from turning into data mining: intuition, restraint, sensibleness, and out-of-sample testing.
First, intuition must guide the search for information before the backtest begins. Intuition should not be driven strictly by data. Ideally, it should arise from a general understanding of the forces governing investment returns and the economy as a whole. The book-to-price strategy satisfies the criterion of intuition. The information tells us which stocks provide book value cheaply. Of course, intuition is a necessary but not a sufficient criterion for finding valuable information. Some information is already widely known by market participants and fairly priced in the market. On the other hand, nonintuitive information that appears valuable in this analysis usually fails upon implementation. Sunspots, skirt lengths, and Super Bowl victories can appear valuable over carefully chosen historical periods, but are completely nonintuitive. Data mining can easily find such accidental correlations. They do not translate into successful implementations.
Second, restraint should govern the backtesting process. Statistical analysis shows that, given enough trials of valueless information, one incarnation (usually the last one analyzed) will look good. After 20 tests of worthless information, 1 should look significant at the 95 percent confidence level. In principle, researchers should map out possible information variations before the testing begins. There are many possible variations of the book-to-price information. We can use current price or price contemporaneous with the book value accounting information. We can try stock sectors, to find where the relationship works best. With each variation, the information drifts further from intuition, pushed along by the particular historical data.
Third, performance should be sensible. The information that deserves most scrutiny is that which appears to perform too well. Only about 10 percent of observed realized information ratios lie above 1. Carefully and skeptically examine information ratios above 2 that arise in information analysis. The book-to-price data in our example are straightforward, publicly available information. In the fairly efficient U.S. market, an information ratio above 2 for such information should not be believed. Information ratios far above 2 signal mistakes in the analysis, not phenomenal insight.
Fourth, out-of-sample testing can serve as a quantitative check on data mining. Valueless information honed to perfection on one set of historical data should reveal its true nature when tested on a second set of historical data. Book-to-price ratios tuned using 1980 to 1985 monthly returns must also outperform in 1986. Book-to-price ratios tuned using January, March, May, July, September, and November monthly returns must also outperform in February, April, June, August, October, and December. Out-of-sample testing helps ensure that the information not only describes historical returns, but predicts future returns.
This chapter has presented a thorough discussion of information analysis. Information analysis proceeds in two steps. First, information is transformed into investment portfolios. Second, the performance of those portfolios is analyzed. To quantify that performance—and the value of the information being analyzed—the information ratio most succinctly measures the potential investment value added contained in the information.
1. What problems can arise in using scores instead of alphas in information analysis? Where in the analysis would these problems show up?
2. What do you conclude from the information analysis presented concerning book-to-price ratios in the United States?
3. Why might we see misleading results if we looked only at the relative performance of top- and bottom-quintile portfolios instead of looking at factor portfolio performance?
4. The probability of observing a |t statistic| > 2, using random data, is only 5 percent. Hence our confidence in the estimate is 95 percent. Show that the probability of observing at least one |t statistic| > 2 with 20 regressions on independent sets of random data is 64 percent.
5. Show that the standard error of the information ratio is approximately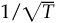 
, where T is the number of years of observation. Assume that you can measure the standard deviation of returns with perfect accuracy, so that all the error is in the estimate of the mean. Remember that the standard error of an estimated mean is 
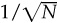, where N is the number of observations.
6. You wish to analyze the value of corporate insider stock transactions. Should you analyze these using the standard cross-sectional methodology or an event study? If you use an event study, what conditioning variables will you consider?
7. Haugen and Baker (1996) have proposed an APT model in which expected factor returns are simply based on past 12-month moving averages. Applying this idea to the BARRA U.S. Equity model from January 1974 through March 1996 leads to an information ratio of 1.79. Applying this idea only to the risk indices in the model (using consensus expected returns for industries) leads to an information ratio of 1.26. What information ratio would you expect to find from applying this model to industries only? If the full application exhibits an information coefficient of 0.05, what is the implied breadth of the strategy?
8. A current get-rich-quick Web site guarantees that over the next 3 months, at least three stocks mentioned on the site will exhibit annualized returns of at least 300 percent. Assuming that all stock returns are independent, normally distributed, and with expected annual returns of 12 percent and risk of 35 percent, (a) what is the probability that over one quarter at least 3 stocks out of 500 exhibit annualized returns of at least 300%? (b) How many stocks must the Web site include for this probability to be 50 percent? (c) Identify at least two real-world deviations from the above assumptions, and discuss how they would affect the calculated probabilities.
The science of information analysis began in the 1970s with work by Treynor and Black (1973), Hodges and Brealey (1973), Ambachtsheer (1974), Rosenberg (1976), and Ambachtsheer and Farrell (1979). These authors all investigated the role of active management in investing: Its ability to add value and measures for determining this. Treynor and Black and Hodges and Brealey were the first to examine the role of security analysis and active management within the context of the capital asset pricing model. They investigated what is required if active management is to outperform the market, and identified the importance of correlations between return forecasts and outcomes among these requirements. Ambachtsheer, alone and with Farrell, provided further insights into the active management process and turning information into investments. He also coined the term “information coefficient,” or IC, to describe this correlation between forecasts of residual returns (alphas) and subsequent realizations. Rosenberg investigated the active management process and measures of its performance as part of his analysis of the optimal amount of active management for institutional investors.
Ambachtsheer, Keith P. “Profit Potential in an ‘Almost Efficient’ Market.” Journal of Portfolio Management, vol. 1, no. 1, 1974, pp. 84-87.
______. “Where Are the Customers’ Alphas?” Journal of Portfolio Management, vol. 4, no. 1, 1977, pp. 52-56.
Ambachtsheer, Keith P., and James L. Farrell Jr. “Can Active Management Add Value?” Financial Analysts Journal, vol. 35, no. 6, 1979, pp. 39-47.
Drosnin, Michael. The Bible Code (New York: Simon & Schuster, 1997).
Frankfurter, George M., and Elton G. McGoun. “The Event Study: Is It Either?” Journal of Investing, vol. 4, no. 2, 1995, pp. 8-16.
Grinold, Richard C. “The Fundamental Law of Active Management.” Journal of Portfolio Management, vol. 15, no. 3, 1989, pp. 30-37.
Grinold, Richard C., and Ronald N. Kahn. “Information Analysis.” Journal of Portfolio Management, vol. 18, no. 3, 1992, pp. 14-21.
Haugen, Robert A., and Nardin L. Baker. “Commonality in the Determinants of Expected Stock Returns.” Journal of Financial Economics, vol. 41, no. 3, 1996, pp. 401-439.
Hodges, S. D., and R. A. Brealey. “Portfolio Selection in a Dynamic and Uncertain World.” Financial Analysts Journal, vol. 29, no. 2, 1973, pp. 50-65.
Kahn, Ronald N. “What Practitioners Need to Know about Backtesting.” Financial Analysts Journal, vol. 46, no. 4, 1990, pp. 17-20.
______. “Three Classic Errors in Statistics from Baseball to Investment Research.” Financial Analysts Journal, vol. 53, no. 5, 1997, pp. 6-8.
______. “Book Review: The Bible Code.” Horizon: The BARRA Newsletter, Winter 1998.
Kritzman, Mark P. “What Practitioners Need to Know about Event Studies.” Financial Analysts Journal, vol. 50, no. 6, 1994, pp. 17-20.
Proust, Marcel. The Guermantes Way, Cities of the Plain, vol. 2 of Remembrance of Things Past, translated by C.K. Scott Moncrieff and Terence Kilmartin (New York: Vintage Books, 1982), p. 178.
Rosenberg, Barr. “Security Appraisal and Unsystematic Risk in Institutional Investment.” Proceedings of the Seminar on the Analysis of Security Prices (Chicago: University of Chicago Press, 1976), pp. 171-237.
Salinger, Michael. “Standard Errors in Event Studies.” Journal of Financial and Quantitative Analysis, vol. 27, no. 1, 1992, pp. 39-53.
Treynor, Jack, and Fischer Black. “How to Use Security Analysis to Improve Portfolio Selection.” Journal of Business, vol. 46, no. 1, 1973, pp. 68-86.
This technical appendix will discuss mathematically the more controlled quantitative approaches to constructing portfolios to efficiently bet on a particular information item a, while controlling for risk. It will also detail the model used to connect event studies to cross-sectional studies.
Basically, this is just an optimization problem. We want to choose the minimum-risk portfolio ha subject to a set of constraints:
If we ignore the constraints, z, in Eq. (12A.3), then the solution to this problem is the characteristic portfolio for a. Constraints we could add include
■ hT · β = 0 (zero beta)
■ hT · e = 0 (zero net investment)
■ hT · X = 0 (zero exposure to risk model factors)
The portfolio ha will include long and short positions:
where haL and haS are defined such that their holdings are all nonnegative:
If we add the net zero investment constraint, then the long and short portfolios will exactly balance.
We see from Eq. (12A.4) that Var {ha} is identical to Var {haL - haS}, and so minimizing the variance of ha subject to constraints is the same as minimizing the tracking of haL versus haS subject to the same constraints.
We can separately monitor the performance of haL and haS to observe whether a contains upside and/or downside information, respectively.
This factor portfolio approach is related to the regression approach to estimating factor returns. Given excess returns r, information a, and exposures X, we can estimate factor returns:
where Y is an N × (J + 1) matrix whose first J columns contain X and whose last column contains a. Estimating b with weights W (stored as a diagonal N × N matrix) leads to
the estimates which minimize ∈T · W · ∈. These estimates are linear combinations of the asset returns; hence, we can rewrite this as
where
is the (J + 1) × N matrix of factor portfolio holdings. Note that
so each factor portfolio has unit exposure to its particular factor and zero exposure to all other factors.
The portfolio hJ+1, the last column of the matrix H, has return ba, the estimated return in Eq. (12A.9) corresponding to information a. Where ha is the minimum-risk portfolio with hT · a = 1 and subject to various constraints, hJ+1 is the portfolio with minimum ∈T · W · ∈ with hT · a = 1 and subject to various constraints.
The main text stated results [Eqs. (12.10) and (12.11)] connecting information coefficients from event studies, along with event rates and information horizons, to cross-sectional information ratios. We derive those results here.
First we derive the annual information coefficient IC(J), given the one-day information coefficient IC(1). (We assume J trading days in the year.) The one-day information coefficient states that the correlation between our signal and the one-day residual return is IC(1):
With no loss of generality, we can assume that our signal has standard deviation 1. Hence, the covariance of the signal with the one-day residual return is
We have assumed that our information coefficient decays with decay constant γ. Hence, the covariance of our signal with the residual return on day J is
To derive the annual information coefficient, we first need the covariance of our signal with the annual residual return, which is the sum of the J daily residual returns:
We can sum this geometric series to find
The annual information coefficient is simply the correlation associated with this covariance. We need only divide by the annual residual volatility:
This is Eq. (12.10) from the main text.
Next we need to derive the result for the information ratio. The annualized alpha, assuming that the event has just occurred, is
But if the information arrived j days ago, the alpha is
The information ratio for a given set of alphas is simply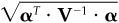 
. [See, for example, Eq. (5A.6).] We will calculate the square of the information ratio by taking the expectation of the square of this result over the distribution of possible signals z. We will assume uncorrelated residual returns. We must account for the fact that, cross-sectionally, different assets will have different event delays. So we must calculate
We can simplify this somewhat, to
We must make further assumptions to estimate the expectation in Eq. (12A.21). First, we assume the same expectation for each asset n:
Second, we assume that we can separate the two terms in the expectation. So effectively, for any value of j, we will take the expectation of z2, since the score shouldn’t depend on the value of j:
We must calculate one last expectation. Here we know the distribution of event arrival times. Hence
We can once again apply results concerning the summation of geometric series. We find
Combining Eqs. (12A.21) through (12A.23) and (12A.25) leads to the final result:
This is Eq. (12.11) from the main text.
