5

HOW STARS RADIATE
ENERGY (II)

NEIL DEGRASSE TYSON

I’d like to plug you into the rest of the universe. In chapter 4, we looked at curves showing the thermal emission of radiation from stars. Figure 5.1 is similar, except that we have added something. The vertical coordinate is intensity (power per unit surface area per unit wavelength), and the horizontal coordinate is wavelength—increasing to the right. The interval of wavelengths that we call “visible light” is identified with a rainbow-colored bar as before.

This figure shows thermal emission curves for the Sun at 5,800 K, a hot star at 15,000 K, a cooler one at 3,000 K, and a human at 310 K. The human emission curve peaks at about 0.001 centimeters. Way below this curve and off to the right is something new, an emission curve whose temperature is 2.7 K, which is the temperature of the whole universe! That’s the famous background radiation coming to us from all parts of the sky. Because it peaks in the microwave part of the spectrum, it is called the cosmic microwave background (CMB). It was discovered in New Jersey, at Bell Laboratories, in the mid-1960s. Arno Penzias and Robert Wilson used a radio telescope—they called it the “microwave horn antenna.” When they aimed it up at the sky, no matter which direction they pointed, they detected this microwave signal, from everywhere in the sky, which corresponds to something radiating at a temperature of about 3 K (the modern, more accurate, value is 2.725 K). And it’s the thermal radiation left over from the Big Bang. We will have much more to say about this in chapter 15.

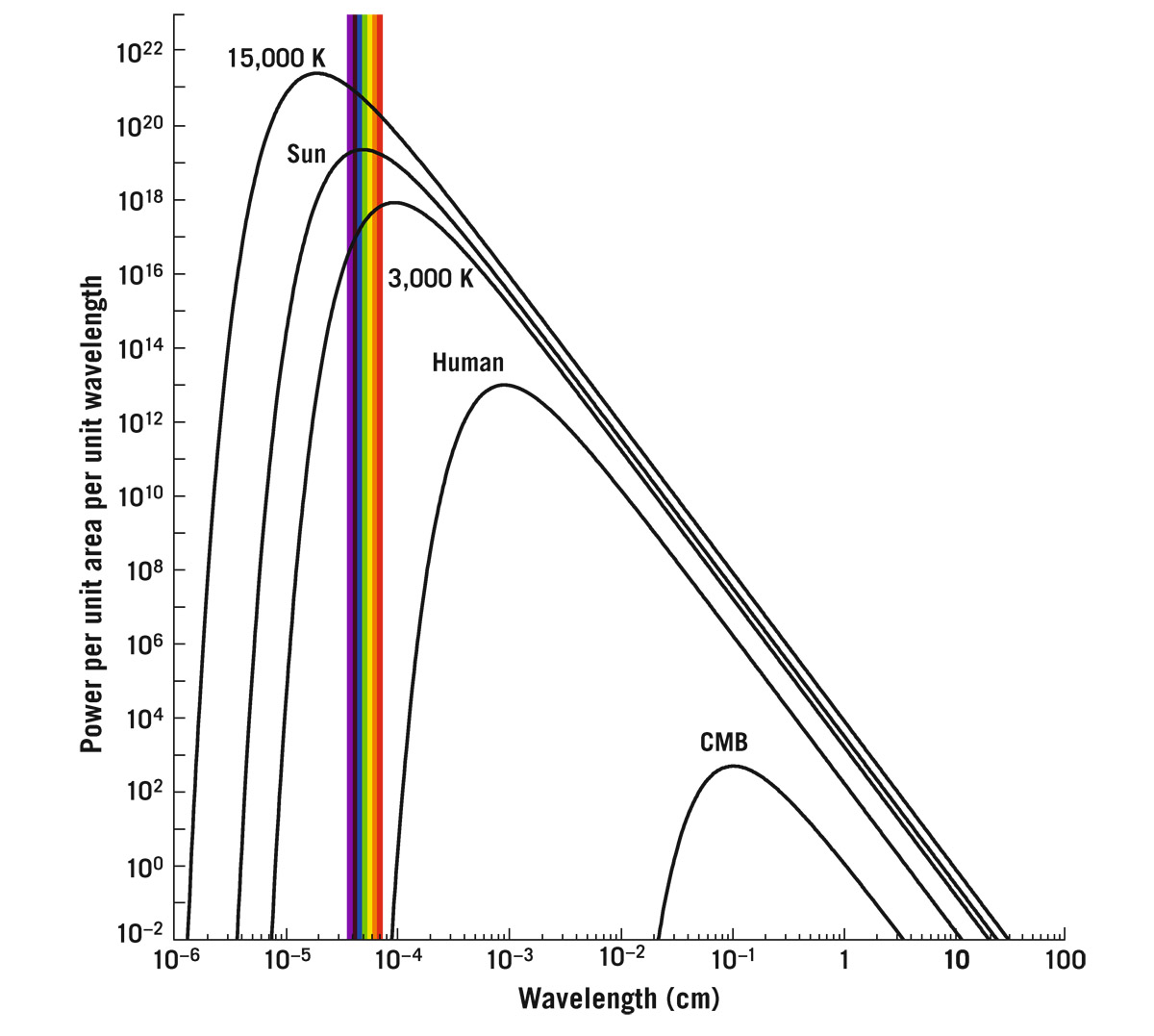
FIGURE 5.1. Thermal emission in the universe. The spectra of blackbodies of different temperatures, as a function of wavelength. The vertical coordinate plots energy per unit time (i.e., power), per unit wavelength, emitted per unit surface area of the object at the quoted temperature; the units are arbitrary. The curves correspond to stars of surface temperature 15,000 K (which will appear blue-white), 5,800 K (the Sun, which appears white), and 3,000 K (which will appear red). The visible part of the spectrum is shown as a colored bar; also shown is a human (310 K) and the cosmic microwave background (CMB, 2.7 K), about which we will learn much more in chapter 15.

Photo credit: Michael A. Strauss

As before, we can query these graphs in different ways. Where does each curve peak? They peak in different places. How much total energy is emitted per second? We need a way to add up the area under each curve to determine how much total energy is being emitted per second. First, we need to define some terms.

A blackbody is an object that absorbs all incident radiation. A blackbody that is at a certain temperature will emit what we call blackbody radiation, which follows the curves we’ve been showing. The term “blackbody” looks like a misnomer, but it is not. We agree that these stars aren’t black: one star glows blue, one star glows white, and one star glows red. Yet all qualify as blackbodies, as I’ve drawn them in the figure. A blackbody is quite simple; it eats any and all energy hitting it. I don’t care what you feed it—that doesn’t matter—it will eat it. You can feed it gamma rays or radio waves. Black things absorb all energy that falls on them. That’s why black clothing is not a common fashion option in the summer. Blackbodies then reradiate these curves—it is that simple. The curve’s shape and position depend only on the temperature of the blackbody.

You can heat something, increase its temperature, and all you need to do is ask, what is your new temperature? Then, return to your curves, and see where this new temperature fits in. I have a wonderful equation that describes these curves. They are distribution functions, called Planck functions, after Max Planck, whom we’ve met previously, and who was the first person to write down the equation for these curves. To the right of the equal sign, we have energy per unit time per unit area coming out per unit wavelength interval at a particular wavelength λ; we call this quantity intensity (I_λ), which depends only on the temperature T of the blackbody:

I_λ(T) = (2hc²/λ⁵)/(e^hc/λkT – 1)

Let’s understand the parts that make up this landmark equation. First of all, λ (lambda) is wavelength, no secrets there. The constant e is the base of the natural logarithms, and it has its own button on every scientific calculator, which is usually shown as e^x (“e to the x”). The value of e is 2.71828 . . . ; it’s a number like π whose digits go on forever. It’s just a number. The letter c is the speed of light, which we’ve seen before. The letter k is the Boltzmann constant. The letter T is simply temperature, and h (introduced in chapter 4) is Planck’s constant. If you assign a temperature T to an object, the only unknown in this equation is λ, the wavelength. So, as you run λ from very small values to very large values, you get a value for intensity I_λ as a function of wavelength that will precisely track these curves. Max Planck introduced this equation in 1900, and it revolutionized physics.

With his new constant, Planck gave birth to the quantum, which makes Max Planck the first parent of quantum mechanics. Look at just the first term in parenthesis, which is 2hc²/λ⁵. As wavelengths get longer, what happens to the energy being emitted? It drops. The 1/λ⁵ term goes to zero as λ becomes large. For large λ, the term hc/λkT becomes small. Mathematicians will tell you that e ^x becomes approximately 1 + x as x becomes small. So for large λ, the term hc/ λkT becomes small, and e^hc/λkT is approximately 1 + hc/λkT, and if we subtract 1 from that it makes the term (e^hc/λkT – 1) equal to hc/λkT . Thus, in the limit as λ becomes large, the whole expression becomes I_λ(T) = (2hc²/λ⁵)/(hc/λkT) = 2ckT/λ⁴. People were familiar with this relation before Planck. It is called the Raleigh-Jeans Law after its inventors Lord Raleigh and Sir James Jeans. As λ gets larger and larger the intensity I_λ starts dropping off, like 1/ λ⁴ in a very well-defined way. What happens when you move toward smaller and smaller wavelengths? As λ⁴ gets smaller and smaller, 1/λ⁴ gets bigger and bigger, making the equation blow up (and disagree with experiments). This was once called “the ultraviolet catastrophe.” Something was wrong. Wilhelm Wien figured out a law that had an exponential cutoff at small wavelengths that fit the data at small wavelengths but didn’t fit the data at large wavelengths. We had no real understanding of these blackbody curves until 1900, when Max Planck found a formula that fit at both the small and large wavelength limits and everywhere in between. The formula includes a constant h that quantizes energy, so that you only get energy in discrete packets. If you get it in discrete packets, then as you get to smaller and smaller wavelengths, the exponential in Planck’s formula kicks in and squashes the 1/λ⁵ term. When λ gets small, hc/λkT gets big, and e raised to that power (e^hc/λkT ) gets really big, really fast. It dominates the –1, so that you can forget about the –1 term, and with the e^hc/λkT in the denominator, the answer gets small. It’s a contest between these two parts of the equation: the 1/λ⁵ term and the 1/e^hc/λkT term. As λ goes to zero, the 1/e^hc/λkT goes to zero much faster than the 1/λ⁵ term is blowing up, making the whole curve go to zero. Without the exponential term, the formula would blow up to infinity as the wavelength went to zero, and we knew from experiments that this was not the way matter behaved. The quantum was needed to understand thermal radiation, and this equation captures how these curves work.

The formula’s got it all. It can tell you where the curve peaks. Isaac Newton invented math that allowed you to figure out where a function peaks: it’s where the slope of the curve goes to zero at the curve’s maximum. You can use Newton’s calculus to take the derivative of the function and determine this location. When we do that, we get a very simple answer: λ _peak = C/T, where C is a new constant, which we can find from the constants in the initial equation: C = 2.898 millimeters when T is expressed in kelvins. Where is the peak? If the temperature is T = 2.7 K, as in the CMB, then λ _peak is a little over 1 millimeter or 0.1 centimeter. We can confirm this by checking the CMB curve in figure 5.1. The human is about a hundred times hotter than that; the human emission peaks at about 0.001 centimeter (also shown in figure 5.1), in the infrared.

It’s beautiful. As temperature gets higher, the wavelength at which the curve peaks gets smaller and smaller. That is borne out just by looking at how this equation λ _peak = C/T behaves. With T in the denominator, it says that something twice as hot will peak at one-half the wavelength. (Wilhelm Wien figured this out—we call it “Wien’s Law.”)

How do I get the total energy per unit time per unit area coming out from under one of these curves? I want to add up the contributions from all the different wavelengths, the total area under a particular curve. I can use calculus again and integrate to find the area—once more, thank you, Isaac Newton. If we integrate the Planck function over all wavelengths, we get another beautiful equation:

Total energy radiated per second, per unit area = σT⁴, where σ = 2π ⁵k⁴/(15c²h³) = 5.67 × 10^–8 watts per square meter, with the temperature T given on the Kelvin scale. This law is called the Stefan–Boltzmann law. Josef Stefan and Ludwig Boltzmann were two towering figures in nineteenth-century physics. Sadly, Boltzmann committed suicide at age 62. But we have this law. If we integrate the Planck function, we get the value of the constant σ (Greek sigma). That’s profound. How did Stefan and Boltzmann figure out this law, when Planck had not yet derived his formula? Stefan found it experimentally, while Boltzmann derived it from a thermodynamic argument.

With total energy radiated per second per unit area = σT⁴, if I double the temperature, the energy flux being radiated increases by a factor of 2⁴ = 16. Triple the temperature and what do you get? 3⁴ = 81. Quadruple the temperature: 4⁴ = 256. And that trend is borne out in figure 5.1, which shows how much bigger these curves become as the temperature increases.

Here’s one way to remember why this formula works: Imagine taking some thermal radiation and putting it in a box. Now slowly squeeze the box until it has shrunk by a factor of 2. The number of photons in the box stays the same, but the volume of the box shrinks by a factor of 8, making the number of photons per cubic centimeter in the box go up by a factor of 8. But squeezing the box shrinks the wavelength of each photon by a factor of 2 as well. This makes the thermal radiation in the box hotter by a factor of 2, because its peak wavelength has shrunk by a factor of 2. It also doubles the energy of each photon, doubling the energy in the box. The increase in energy for each photon comes from the energy you invest in squeezing the box, pushing against the radiation pressure inside. That means that the energy density in the box is 8 × 2 = 16 times what it was before, and 16 equals 2⁴. Therefore, the energy density of thermal radiation is proportional to the fourth power of the temperature, or T⁴.

Let’s define some additional terms. Luminosity is the total energy emitted per unit time by a star. Luminosity is measured in watts, as in a light bulb. A 100-watt light bulb has a luminosity of 100 watts. The Sun has a luminosity of 3.8 × 10²⁶ watts. It’s a potent light bulb.

I propose a puzzle. Suppose the Sun has the same luminosity as another star that has a surface temperature of 2,000 K. How hot is the Sun? For this example, let’s just round the temperature to 6,000 K. The other star is only 2,000 K, so I know if it is that much cooler, it cannot be emitting nearly as much energy per unit area per unit time as the Sun, but then I declare that the Sun has the same luminosity as this star—how is that possible? I take that other star and I get a 1-square-inch patch of it, a 2,000 K patch, and I get a 1-square-inch patch from the Sun, at 6,000 K—three times hotter. How much more energy per unit time is being emitted by a 1-square-inch patch on the Sun than by a 1-square-inch patch on the other star? Eighty-one times more energy. How can this other star be emitting the same total energy per second as the Sun? Something else must be different about these two stars besides their temperatures for them to be equal at the end of the day. The other star, the cool star, must have much more surface area from which to radiate than does the Sun. In fact, it must have 81 times the surface area of the Sun. It must be a red giant star, with 81 times the surface area to make up for its deficiency in each little square-inch tile on its surface. Now let’s use our equations. What is the surface area of a sphere? It’s 4πr², where r is the radius of the sphere. You may have learned that equation in middle school. What comes next is so beautiful. If luminosity is energy emitted per unit time, and the energy emitted per unit time per unit area is equal to σT⁴, then I have an equation for the luminosity of the Sun:

L_Sun = σT_Sun⁴ × (4πr_Sun²).

I have a similar equation for the other star. Let’s denote the other star’s luminosity by an asterisk, L_*. The equation for its luminosity is L_* = σT_*⁴ × (4πr_*²). Now I have an equation for each of them. Furthermore, I have declared that L_Sun is equal to L_*. I have declared that, in posing the example, I don’t actually need to know the surface area of the Sun, because this problem is talking about the ratios of things. We can get tremendous insight into the universe simply by thinking about the ratios of things.

Let’s divide the two equations: L_Sun / L_* = σT_Sun⁴ × 4πr_Sun²/(σT_*⁴ × 4πr_*²). What do I do next? I cancel identical terms in the numerator and denominator of the fraction on the right side of the equation. First, I’ll cancel out the constant σ. I don’t even care what its particular value is, because when I’m comparing two objects and the constant shows up for both stars, I can cancel the constants out. The number 4 cancels, and π cancels too. Continuing, on the left of the equation, what is L_Sun/L_*? It is 1, because I stated that the two stars have equal luminosities; their ratio is 1. So, I am left with a simpler equation: 1 = T_Sun⁴r_Sun²/T_*⁴r_*². The temperature of the Sun is 6,000 K, and the temperature of the other star is 2,000 K. Of course, 6,000⁴ divided by 2000⁴ is the same thing as 3⁴, which is 81. Now I have 1 = 81r_Sun²/r_*². Let’s multiply both sides of the equation by r_*². Thus, r_*² = 81r_Sun² . Take the square root of both sides of the equation: r_* = 9r_Sun. The radius of the cooler star with the same luminosity as the Sun is 9 times that of the Sun! That’s our answer. If we are thinking in terms of area, this star has a surface area 81 times as large as that of the Sun, because the square of the radius is proportional to the area. These are immensely fertile equations.

I could have given a different example. I could have started with a star of the same temperature as the Sun, but 81 times as luminous. Both stars have the same amount of energy coming out per second per square inch of surface, so the other star must have 81 times the surface area of the Sun and 9 times the radius of the Sun. The equation has the same terms, but we’re putting different variables into different parts of the equation. That’s all we’re doing here.

Recall (from chapter 2) that the hottest part of the day on Earth is not at noon, but sometime after noon, because the ground absorbs visible light. That visible light slowly raises the temperature of the ground, and the ground then radiates infrared to the air. The ground is behaving as a blackbody—absorbing energy from the Sun, and then reradiating it according to the recipe given by the Planck function. The ground has a temperature of roughly 300 K. (That’s 273 K plus the ground temperature in Celsius—if it’s 27° C, that makes the ground an even 300 K.)

You can ask the question, what is your own body’s luminosity? Plug in your Kelvin body temperature, which is 310 K, take it to the fourth power, multiply by sigma—and you will get how much energy you emit per unit time, per unit area. If you multiply that by your total skin area (about 1.75 square meters for the average adult), you will get your luminosity—your wattage. It is not coming out in visible light. It is coming out mostly in infrared, but you for sure have a wattage. Let’s get the answer. The Stefan–Boltzmann constant σ is 5.67 × 10^–8 watts per square meter if the temperature is measured in K. Multiply by (310)⁴. The value of 310⁴ is 9.24 × 10⁹. Multiply that by 5.67 × 10^–8, giving 523 watts per square meter. Multiply by your area of 1.75 square meters, and you get 916 watts. That’s a lot. Remember, though, that if you are sitting in a room that is 300 K (80° F), your skin is absorbing about 803 watts of energy, by the same formula. Your body has to come up with about 100 watts of energy to keep yourself warm. You get that by eating and metabolizing food. Warmblooded animals that keep their body temperature higher than their surroundings need to eat more than coldblooded animals do. When you put air conditioning in a room, there are two major questions to ask: How big is the room? What other sorts of energy will be released in the room? This will include asking, for example, how many light bulbs will be on in the room and how many people will be in it, because every person is equivalent to a certain wattage light bulb that the air conditioning must fight against to maintain the temperature. To determine what air conditioning flow is required to keep the proper temperature, you have to account for how many people (with their watts) will gather in the room.

Let me toss in one more notion, called brightness. The brightness of a star you observe is the energy received per unit time per unit area hitting your telescope. Brightness tells you how bright the star looks to you. This depends on the star’s luminosity, as well as on its distance from you. Let’s think intuitively about brightness. How bright does an object appear to you? It should make sense to you that if you see an object shining with a particular brightness and then I move it farther away, its brightness will decrease. The luminosity, however, is energy emitted per unit of time by the object; it has nothing to do with its distance from you—it is simply what is emitted. It has nothing to do with your measuring it. A 100-watt light bulb has a luminosity of 100 watts, no matter where in the universe you put it. However, brightness will depend on an object’s distance from an observer.

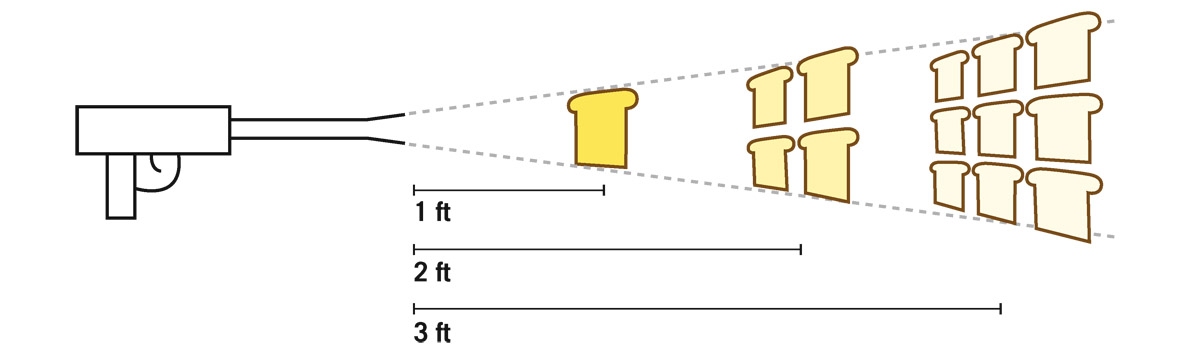
FIGURE 5.2. Butter gun. It can spray one slice of bread 1 foot away, four slices of bread 2 feet away, or nine slices of bread 3 feet away. Credit: J. Richard Gott

Brightness is simple, and I love it. Are you ready? Let me draw a contraption that I never built, but you can patent it if you like. It’s a butter gun: you load it with a stick of butter and it has a nozzle at the front where the butter sprays out (see figure 5.2).

Put a slice of bread 1 foot away from the butter gun. I have calibrated this butter gun such that, at a distance of 1 foot, I butter the entire slice of bread, exactly covering it. If you’re one of those people who like to butter up to the edge, this invention is for you. Now let’s say I want to save money, as any good businessperson wants to do: I’d like to take the same amount of butter and butter more slices of bread. But I still want to spread it evenly. The first slice of bread was 1 foot away—now let’s go 2 feet away. The spray of butter is spreading out. At twice the distance, the butter gun covers an area that is two slices of bread wide and two slices of bread tall. The spray covers a 2 × 2 array of slices, buttering 4 slices of bread. Just by doubling the distance, you can now spray 4 slices of bread. If I go three times the distance, you can bet that the spray will cover 3 × 3 = 9 slices of bread. One slice, four slices, nine slices. How much butter is one slice of bread 3 feet away getting compared to the single slice only 1 foot away? Only one ninth. It is still getting butter, but only a ninth as much. This is bad for the customer but good for my bottom line. I assert that there is a deep law of nature expressed in this butter gun. If, instead of this being butter, it were light, its intensity would drop off at exactly the same rate that this butter drops off in quantity. After all, light rays travel in straight lines just like the butter, and spread out in just the same way. At 2 feet away, the light from a light bulb would be 1/4 as intense as it was at 1 foot away. At 3 feet away, it would be 1/9 as intense; at 4 feet away, 1/16 as intense; and at 5 feet away, 1/25 as intense, and so on. It goes as one over the square of the distance—an inverse square. In fact, we have obtained an important law of physics, telling us how light falls off in intensity with distance, the inverse square law. Gravity behaves this way too. Do you remember Newton’s equation, Gm_am _b/r²? That r squared in the denominator shows it’s an inverse-square relation, because it is behaving like our butter gun. Gravity and butter are acting alike.

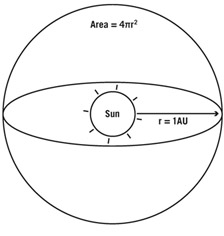
FIGURE 5.3. Sun in a sphere. The Sun’s rays spread out over an area of 4πr² as it passes through a sphere of radius r. Credit: J. Richard Gott

Imagine a light source like the Sun emitting light in every direction (figure 5.3). Let’s further imagine I surround the Sun with a big sphere having a radius r equal to the radius of Earth’s orbit (1 AU).

The Sun is emitting light in every direction, and I am intersecting some of the Sun’s light. I’m only getting a little piece of all the light that’s penetrating a Sun-centered sphere with a radius equal to the distance where I find myself. What is the area of that big sphere? It’s 4πr², where r is the radius of the sphere. Of all the light the Sun emits, the fraction hitting my detector is equal to the area of my detector divided by the area of that huge sphere (4πr²). If I move twice as far away, my detector stays the same size, but the radius of my sphere will be twice as big (2 AU), and the area the Sun’s rays are passing through will be four times as great. I will detect one quarter as many photons in my detector as I did when I was 1 AU away. Brightness is given in watts per square meter falling on my detector. To calculate the brightness that I observe at a radius r from the Sun, I start with the Sun’s luminosity (in watts) and divide by this spherical area—4πr². This gives the watts per square meter from the Sun falling on me. I multiply by the area of my detector (say, my telescope), and I get the energy per second falling on it. If L is the luminosity of the Sun, the brightness (B) of the Sun as seen by me is B = L/4πr², where r is my distance from the Sun. As my distance increases, the denominator (4πr²) gets larger, reducing the brightness. On Neptune, which is 30 times as far from the Sun as Earth is, the Sun appears only 1/900 as bright as it does here.

Suppose two stars have the same brightness in the sky, but I know that one is 10,000 times more luminous than the other. What must be true about these stars? The more luminous star must be farther away. How many times farther away? 100 times. How did I get 100? Yes, 100 squared is equal to 10,000.

You have just learned some of the most profound astrophysics of the late nineteenth and early twentieth centuries. Boltzmann and Planck, in particular, became scientific heroes for coming to the understanding that you have just gotten in this chapter and the previous one.