15

THE EARLY UNIVERSE

MICHAEL A. STRAUSS

The early universe just after the Big Bang was very hot and dense, but it was expanding and cooling. Our equations allow us to do detailed calculations of the expected state of matter in the early universe; it is a fertile area for physicists, because it involves the calculation of the properties of matter at extremely high temperatures and densities. Moreover, nuclear reactions in the early universe leave telltale traces in the chemical abundances of the elements we see in the universe today. We’ll see that these predictions of light-element abundances from Big Bang physics accord beautifully with observations, giving us confidence that we actually understand what happened in the first moments after the Big Bang. Let’s start the story about 1 second after the Big Bang. The universe was tremendously hot, about 10¹⁰ K (10 billion kelvins!) and terribly dense by human standards, about 450,000 times the density of water. Galaxies, stars, and planets didn’t exist yet. Indeed, it was much too hot for atoms or molecules, or even atomic nuclei to form. The ordinary material of the universe at this point consisted of electrons, positrons, protons, neutrons, neutrinos, and, of course, lots of blackbody radiation (i.e., photons). And if, as is currently thought, dark matter consists of as-yet undiscovered elementary particles, we would expect those particles to also exist in large numbers in the universe at this time.

But two and a half minutes later, the universe has cooled down to a temperature of “only” a billion kelvins; at this time, the photons have a blackbody spectrum peaking in gamma rays. A billion kelvins is cool enough to permit nuclear fusion reactions in which neutrons and protons are able to stick together. In the Sun, we found that under high temperatures and densities, protons fuse together to make helium nuclei (see chapter 7). In the center of stars like the Sun, it takes billions of years to turn 10% of the hydrogen into helium. The nuclear reactions taking place in the early universe go much faster, because free neutrons as well as protons are present. Proton–proton collisions require high energy, because both protons are positively charged and they repel each other, making actual collisions infrequent. Neutrons are electrically neutral (and thus are not repelled by protons), so neutron–proton collisions occur more often. Fusion can occur by adding neutrons to protons, on the way to producing helium. This allows the slow first steps of the solar fusion process (proton–proton collisions) to be skipped.

Protons and neutrons can transmute into each other. A neutron plus a positron can combine to give a proton plus an anti-electron neutrino, and vice versa. A neutron plus an electron neutrino can combine to give a proton plus an electron, and vice versa. And a neutron can decay into a proton by emitting an electron and an anti-electron neutrino. At 10 billion kelvins (the temperature when the Universe is 1 second old), these processes are in balance. Neutrons are slightly more massive than protons, meaning they take slightly more energy to make and so there are slightly fewer neutrons than protons 1 second after the Big Bang. But by the time the universe cools to a billion kelvins as it continues to expand, this balance changes so that more neutrons are converted into lighter protons, yielding seven protons for every neutron. At a temperature of a mere billion kelvins, less thermal energy is available to make up the (E = mc²) mass difference between protons and neutrons; neutrons, therefore, become rarer relative to protons. At this point, the universe has cooled enough for a neutron and a proton to collide and stick together to form a deuteron (the nucleus of heavy hydrogen—deuterium) without the deuteron immediately coming apart when it collides with the next particle. A deuteron can then participate in additional nuclear reactions to add an additional neutron and an additional proton to form a helium nucleus (two neutrons and two protons). After just a few minutes of nuclear burning, essentially every neutron is incorporated into a helium nucleus, and by that time, the universe has cooled and thinned enough that these nuclear reactions stop.

Let’s calculate how many helium nuclei result. There are two neutrons in each helium nucleus. With a ratio of one neutron for every seven protons, those two neutrons are paired with 14 protons. Two of those protons are also included in the helium nucleus, with 12 protons left over. This predicts that one helium nucleus forms for every 12 protons (these, of course, are hydrogen nuclei). After these first few minutes, the universe becomes too cool and thin for further nuclear reactions to take place. Thus, a significant number of helium nuclei are made in the Big Bang, along with trace amounts of leftover deuterons (the nuclei of deuterium), lithium and beryllium nuclei (which decay into lithium), and no heavier elements.

This basic calculation was first done by George Gamow and his student Ralph Alpher in the 1940s. They couldn’t resist the temptation to add Hans Bethe’s name as a co-author in their famous Alpher-Bethe-Gamow (“α-β-γ”) paper describing some of their results. One helium nucleus for every 12 hydrogen nuclei is excellent agreement with the results, dating back to the work of Cecilia Payne-Gaposchkin, that the stars are composed of about 90% hydrogen and 8% helium (see chapter 6). Thus, our predictions for the conditions in the universe just a few minutes after the Big Bang have given us a basic explanation of why hydrogen and helium are the two most abundant elements in the universe, and why they are found in the proportions we see! This is an astonishing success of the Big Bang model and gives us a strong justification for extrapolating the expansion of the universe to a time just a few minutes after the Big Bang, when temperatures were above a billion kelvins.

Gamow and Alpher hoped originally to explain the origin of all the elements from the Big Bang, but their calculations showed that the nuclear reactions proceeded only through the lightest elements. All the heavy elements (including the carbon, nitrogen, and oxygen in our bodies, and the nickel, iron, and silicon, which contribute to the makeup of Earth) were created later by nuclear processes taking place in the cores of stars, a process we have described in chapters 7 and 8. Fred Hoyle, a rival of Gamow’s, hoped to demonstrate just the opposite: that both the heavy and light elements could be created from hydrogen by nuclear cooking in the cores of stars without invoking an early hot dense phase in the universe’s history, and he spent much of his career trying to do so. He developed much of our modern understanding of the formation of the heavy elements in stars. But the quantity of helium that gets made in stars is not nearly enough to explain the amount that we observe.

The fact that we see some deuterium in the universe today points to a Big Bang origin. Deuterium (having one proton and one neutron) is fragile and is destroyed by being fused into helium in the cores of stars, rather than being manufactured there. Stars can’t make it. The only way we know how to make it is in the Big Bang, and calculation of the amount of deuterium created in the first few minutes after the Big Bang (one deuterium for every 40,000 ordinary hydrogen nuclei) is in excellent accord with the observed value. The nuclear burning after the Big Bang suddenly stops when the universe has thinned out sufficiently, leaving a small residual amount of deuterium that has not “finished” fusing into helium. The nonequilibrium nature of the burning, because things are changing so rapidly in the early universe, is the key to leaving a small residual amount of deuterium today. Gamow realized this. To Gamow, the observed cosmic abundance of deuterium was a smoking gun pointing to the Big Bang.

As the universe expands, space stretches, and the wavelengths of photons traveling through the cosmos stretch as well; this is just the redshift phenomenon we’ve already discussed. If space is expanding and we observe a distant galaxy, we will see photons from it redshifted, because it is moving away from us, and we can interpret this effect as a Doppler shift. But we could equally well interpret this as simply the stretching of space itself, stretching the distance between us and the distant galaxy, and stretching the wavelength of the photon traveling from the galaxy to us. Draw a wave on a thick rubber band and stretch the rubber band; the wavelength of the wave you have drawn will increase. Both interpretations of the redshift are equivalent: we can view the redshift as a Doppler shift from a distant object that is moving away because of the expansion of space, or we can interpret the redshift as the lengthening of the wavelength due to the stretching of space itself. Photons from the early universe retain their blackbody (Planck) spectrum, but as their wavelengths lengthen due to the expansion of space, the temperature of the photons drops. Gamow and his students, Alpher and Herman, conceived of the universe beginning with a hot Big Bang and then cooling off with time as it continued to expand.

Einstein, in thinking about the universe overall around 1917, hypothesized what we call the cosmological principle: on large scales, and at any given time, the universe looks more or less the same from any vantage point. If we step back far enough and look at large enough scales, the material in the universe should be smoothly distributed. We have seen one aspect of Einstein’s hypothesis already—the expansion of the universe looks the same from the perspective of any given galaxy—from which we inferred that the universe has no center. In the same way, an infinite plane has no point one can label the “center,” and the curved surface of a sphere has no point on its surface that can be labeled its “center,” as all points on the surface of a sphere are equivalent.

Of course, we look around the universe today, and it looks anything but smooth! The mass of our solar system is concentrated into planets and the Sun. Stars are separated by distances vast relative to their sizes. Stars are gathered into galaxies, which are separated from one another by distances of millions of light-years, and galaxies group together in clusters. Einstein’s cosmological principle suggests that we should step back even further, looking on scales of hundreds of thousands of galaxies, and we will see the universe as approximately uniform. Hubble’s observations showed that counts of faint galaxies in different directions were the same; the universe indeed looked uniform in space on the largest scales.

Fred Hoyle took this one step further: not only is the universe homogeneous in space, more or less the same wherever we look, he claimed, but also homogeneous in time. If you go back to the past, it should look the same as it does today, Hoyle figured. The laws of physics don’t change with time, so why should the universe? If you take this notion literally, then there can be no beginning or Big Bang to the universe; the universe has existed forever. Hoyle called this idea the perfect cosmological principle. Given that the distance between galaxies is growing with time due to the expansion of the universe, Hoyle had to hypothesize that new matter was being created in the space between galaxies, which would eventually form into new galaxies—a crazy idea, perhaps, but one that he thought was less crazy than forming the entire universe from a moment of infinite density and temperature, marking the beginning of time.

Which one of these pictures is right? As we continue to explore the predictions of the Big Bang model and compare them with what we observe, we will see that the empirical evidence for the Big Bang theory, in the form of agreement between its predictions and our observational data, is very strong indeed.

The first prediction the Big Bang model makes is that the universe should be expanding, as, of course, we observe. The model also predicts the age of the universe—13.8 billion years—in accord with the slightly smaller ages found for the oldest stars in the universe. This is an unambiguous success of the Big Bang model: if we had found stars that were a trillion years old, then we would have been forced to conclude that the Big Bang model couldn’t be right. Indeed, we’ve been through just such a crisis in the past: Hubble’s first estimate of his constant was H₀ = 500 (km/sec)/Mpc, corresponding to a time since the Big Bang (1/H₀) of only 2 billion years. It was clear by the 1930s from radioactive dating of rocks that Earth is older than that. This age was inconsistent with the Big Bang model: Earth can’t be older than the universe itself! This inconsistency was an argument in favor of Hoyle’s model, because in his model, the universe was infinitely old and ever-expanding, with new galaxies being formed in intergalactic space all the time. The discrepancy was resolved in the 1950s and 1960s with much-improved measurements of the distances to galaxies, greatly reducing the value of the Hubble constant and making (1/H₀) consistent with the ages of the oldest stars.

We also saw that the Big Bang predicts that there should be 12 hydrogen nuclei for every helium nucleus in the universe, and 40,000 hydrogen nuclei for every deuterium nucleus, exactly as is observed. It didn’t have to be this way; indeed, before the science of spectroscopy was fully mature, and Cecilia Payne-Gaposchkin and others had determined that the Sun is mostly hydrogen, people had little idea of the relative abundances of elements in the universe.

Let us take stock of the elements a few minutes after the Big Bang. Essentially all free neutrons have been incorporated into helium nuclei. Nuclear burning ceases, as the universe is too cool and too low density at this stage for any additional reactions to take place. In addition to these helium nuclei, and trace quantities of deuterium and lithium nuclei, we also have protons, electrons, neutrinos, and photons—the positrons present earlier have annihilated with electrons to produce additional photons, leaving behind just enough electrons to balance the charge of all the protons. It is very hot and, as we know, hot things emit photons, so there are plenty of photons around too. As the universe continues to cool and drop in density, its makeup does not change for about 380,000 years.

Up to this point, the material of the universe is a plasma (as in the interiors of stars): the atomic nuclei and the electrons are not bound together but move independently of one another. If an electron briefly is captured by a proton, forming an atom of neutral hydrogen, it will quickly be hit by one of the many high-energy photons present, kicking the electron free of the proton. Moreover, because photons interact so strongly with free electrons (i.e., those not bound up in an atom), a photon can’t travel very far before it collides with another electron and bounces (scatters is the technical term) off in a different direction. That is to say, the universe at that time was opaque; it was a bit like a thick fog in which you can’t see very far in front of you. This is analogous to what we found in the interior of stars: the interior of the star is opaque, and energy in the form of photons generated in the core takes a very long time, of order a couple of hundred thousand years, to diffuse outward to the surface.

The story changes drastically when the temperature has dropped to 3,000 K, at a time about 380,000 years after the Big Bang. At this point, the photons no longer have enough energy to ionize hydrogen, and the electrons and protons pair up to make neutral atoms. Neutral hydrogen does not scatter photons nearly as much as individual free electrons do, and the universe suddenly becomes transparent: the fog has lifted. The photons can now travel on straight trajectories.

This suggests that we, in the present-day universe, should be able to see those photons, which have been streaming freely toward us ever since that time when the universe became transparent, 380,000 years after the Big Bang. If the universe has no edge, we should expect to be receiving these photons from every direction in the sky. That is, in every direction we look, there is material at the appropriate distance such that the photons it emitted 380,000 years after the Big Bang are just reaching us today.

These photons are emitted by gas at a temperature of 3,000 K, and thus should have a blackbody spectrum appropriate to that temperature. Such a blackbody peaks at a wavelength of about 1 micron (10^–6 meter). However, we have to take one other important aspect of the story into account: the universe is expanding! This 3,000 K blackbody radiation is thus redshifted. The universe has expanded by a factor of about 1,000 from when it was 380,000 years old until today, 13.8 billion years later. The wavelength of the radiation is stretched by this same factor as the space expands. Thus the peak wavelength of the thermal radiation now is 1 millimeter rather than 1 micron. If the peak wavelength has increased by a factor of 1,000, the temperature has decreased by that same factor. That means today we should see this thermal radiation with a temperature of about 3 K coming to us from all directions in the sky. This radiation comes from a time when the universe was a mere 380,000 years old, 0.003% of its present age.

In 1948, Alpher and Robert Herman, another of Gamow’s students, predicted that the universe today should still be filled with this thermal radiation left over from the Big Bang, and calculated that by today its temperature should have dropped to about 5 K—close to the correct value.

But by the 1960s, the Herman and Alpher prediction was largely forgotten, and Bob Dicke, Jim Peebles, Dave Wilkinson, and Peter Roll of the Princeton University physics department went through a similar line of reasoning and came up with the same prediction. They took this one step further, realizing that blackbody radiation peaking at 1 millimeter could actually be detected with radio telescopes and sensors that Dicke had developed. (That meant they would be looking for microwaves, short-wavelength radio waves like those produced in a microwave oven.) They started building a microwave telescope on the rooftop of a building on the Princeton campus to see whether they could detect the blackbody radiation from the early universe that they had theorized must be there, if the Big Bang idea was correct.

In the end, they got scooped. This was 1964, very early in the Space Age, and Bell Laboratories was thinking about whether satellites could be used for long-distance communication. They had built a radio telescope in Holmdel, New Jersey, designed to detect radio emission bounced off a high-altitude balloon as a prototype for long-distance satellite communication. Two Bell scientists, Arno Penzias and Robert Wilson, decided to use the telescope to map the sky at microwave wavelengths. To their surprise, they found microwave radiation coming from every direction in the sky toward which they pointed the telescope. Once the Princeton folks heard about this, they realized that Penzias and Wilson had discovered the cosmic microwave background (CMB) radiation that they had predicted. Their two papers—the Princeton paper making the prediction, and the Penzias and Wilson paper, making the discovery—were published back-to-back in The Astrophysical Journal in May 1965.

With this result, another fundamental prediction of the Big Bang model was verified observationally. The CMB was emitted throughout the entire universe when it was 380,000 years old, and thus should be observable coming from all directions in the sky with the same intensity. This is exactly what is observed. Indeed, this observation reminds us that the Big Bang happened everywhere, with no well-defined center, and thus the leftover heat radiation from the Big Bang is coming to us equally from all directions. In 1967, Penzias and Wilson published a limit on variations in the strength of the emission over the sky of a few percent. As technology has improved, the measurements have gotten much better; as we’ll see below, the emission is actually uniform to an astonishing one part in 10⁵.

Alpher and Herman’s original paper in 1948 predicted that the temperature of the CMB blackbody spectrum should be about 5 K. Penzias and Wilson found a temperature of 3.5 K in their original paper (later refined with more precise measurements to be 2.725 K). This was astonishingly close to the original Alpher and Herman estimate. The discovery of the CMB convinced the astronomical community that the Big Bang model was correct. The unchanging universe model championed by Fred Hoyle, for example, has no natural way to explain the CMB, whereas it is an inevitable and direct prediction of the Big Bang model. This is how science proceeds. This process of continual testing is how scientists gain confidence in their ideas. Penzias and Wilson were awarded the 1978 Nobel Prize in Physics for their discovery.

Peebles and Wilkinson were just beginning their scientific careers in 1965. With the discovery of the CMB, they decided to devote their careers to cosmology, the study of the universe as a whole. Jim Peebles became one of the most important theorists working in the field. Dave Wilkinson made ever more sophisticated measurements of the CMB, first using radio telescopes here on Earth and eventually launching satellites to take data from space. (I should mention here that Wilkinson is my scientific grandfather. My PhD thesis advisor, Marc Davis, completed his PhD thesis under the aegis of Dave Wilkinson in 1974.)

The question Wilkinson wanted to address first was this: is the spectrum of the CMB really that of a blackbody? Wilkinson was one of the scientific leaders of the NASA satellite, the Cosmic Background Explorer (COBE), which was designed to measure the CMB spectrum to high accuracy. It succeeded spectacularly; the CMB spectrum that the COBE satellite measured follows the blackbody formula perfectly within the (very small) error bars. This experiment has been called the most accurate measurement of a blackbody in nature (figure 15.1).

FIGURE 15.1. Preliminary cosmic microwave background (CMB) spectrum from COBE. David Wilkinson showed this spectrum of the CMB from the COBE satellite in a 1990 talk at Princeton University, and the audience burst into applause. Its match to the theoretical Planck blackbody curve for thermal radiation is spectacular. (In the diagram, the Planck blackbody curve [solid line] is plotted on linear versus linear scales, with the data showing the observational error limits as little boxes. The Planck blackbody spectra shown in chapters 4 and 5 are on logarithmic versus logarithmic scales and thus appear a bit different.) Photo credit: Adapted from collection of J. Richard Gott

The next big question that Wilkinson tackled was: how uniform is the CMB—that is, does it have the same intensity (or equivalently, the same temperature) in all directions? The cosmological principle, whereby the universe is hypothesized to be smooth on very large scales, predicts that the CMB should be extremely uniform. Penzias and Wilson’s initial measurements could put only crude limits (of a few percent) on just how smooth it was, but by the late 1970s, Wilkinson and others discovered that the temperature of the CMB was not exactly the same in all directions, but varied smoothly across the sky, changing by about 0.006 K from one side of the sky to another. It quickly became apparent what was causing this variation. In addition to the relative motions of galaxies due to the overall expansion of the universe, galaxies can move individually because of the mutual gravitational attraction between them. In addition, the Sun is orbiting the center of our galaxy. These motions combine to give the Sun a velocity of about 300 km/sec relative to the bulk of the matter in the universe that is giving rise to the CMB. This causes a Doppler shift of about one part in a thousand (because 300 km/sec is 1/1,000 of the speed of light) in the CMB; the CMB is slightly blueshifted in the direction of our motion, slightly redshifted in the opposite direction, and varies smoothly in between—just as we observe.

We should pause at this moment to reiterate all the ways we are in motion, despite our perception of sitting still. Earth is rotating around its axis; at North American latitudes, this corresponds to a speed of about 270 m/sec. Earth orbits around the Sun at a speed of 30 km/sec. The Sun orbits around the center of the Milky Way at 220 km/sec, and the Milky Way and the Andromeda galaxy are falling toward each other at about 100 km/sec. Finally, the two galaxies together are moving at a speed of almost 600 km/sec with respect to the mean velocity of all the material in the observable universe. Add up all these different motions in different directions, and you get the Sun’s motion of 300 km/sec relative to the CMB. It is dizzying indeed to envision all this and is an illustration of Galileo’s dictum, refined in Einstein’s theories of relativity, that it is relative motions that are important. Without sophisticated astronomical measurements, we simply perceive ourselves as sitting still.

This Doppler shift induced by our motion with respect to the CMB gives a smooth deviation from uniformity in the CMB of one part in one thousand, which has now been observed to high accuracy. So subtract that effect out. The next question Wilkinson wanted to ask was whether there are any ripples in the CMB that are intrinsic and not just a consequence of our motion. If our understanding of the Big Bang is correct, the answer must be yes. Indeed, the early universe could not have been exactly smooth, without any deviations from perfect uniformity. A perfectly uniform universe will expand uniformly, and no structure will ever form: no galaxies, no stars, no planets, no humans to look up at the sky and wonder what it all means. The fact that we live in a Universe with structure, with real deviations from uniformity—that is, a universe in which we exist—tells us that the early universe, and thus the CMB, could not have been perfectly smooth.

How did structure form in the universe? Consider a region in the early universe in which the density of matter is slightly higher than in the neighboring regions. The mass associated with that region is also slightly higher, and thus it has a slightly higher gravitational pull than the material around it. A random hydrogen atom or particle of dark matter will be attracted toward that region, thereby increasing its density at the expense of the regions around it. Material thus falls into this region, increasing its mass, and in the gravitational tug-of-war, it will be even more effective in pulling extra matter toward it. As time goes on, this process will cause subtle fluctuations in the density of matter to grow with time—enough in principle to form the structures we find around us today. Jim Peebles has a wonderfully succinct way to describe this process of gravitational instability: “Gravity sucks!” he likes to say.

Given the amount of structure we observe in the universe today, and given the physics of gravity, how strong should the fluctuations in the early universe (and thus the observed undulations in the CMB) be? It’s a tricky calculation: the story is complicated by the fact that the universe is expanding at the same time matter is trying to clump because of gravity. You also have to understand all the components of matter, both dark matter and the ordinary stuff made of atoms. We mentioned earlier that while the universe was still completely ionized (before 380,000 years after the Big Bang), photons were continually scattering off the free electrons in the universe. The pressure from those photons kept fluctuations in the distribution of ordinary matter (electrons and protons) from growing under gravity. If this were the full story, the fluctuations could have been growing via gravity only since the time the universe became neutral, and the nonuniformities in the CMB would have to be larger than we observe.

However, as Jim Peebles realized in the 1980s, dark matter can explain the discrepancy. Dark matter is dark; that means it does not interact with photons, and therefore fluctuations in the dark matter can grow under gravity impervious to the pressure of photons. After the universe becomes neutral, ordinary matter can fall into the lumps of dark matter that had already been growing for some time. So, if there is dark matter, we can start off with fluctuations in the CMB that are smaller than if there were only ordinary matter present. By the 1980s, the limits on the fluctuations in the CMB were so stringent that models that didn’t invoke dark matter were ruled out.

So the dark matter we infer from the rotation of galaxies is also needed to understand the CMB. What is dark matter made of? Detailed comparison of the abundance of helium and especially deuterium with the predictions of the processes occurring in the early universe tell us that the average density of ordinary matter (i.e., that made from protons, neutrons and electrons) is a mere 4 × 10^–31 grams in each cubic centimeter. That’s equal to one proton in every four cubic meters! We’re reminded of the truly vast (and mostly empty) expanses between stars in galaxies, and from one galaxy to another. But measurements of the motions of galaxies, as well as the fluctuations in the CMB (which we’re about to describe), tell us that the total density of matter in the universe is roughly six times larger. The difference is the dark matter, but we conclude that dark matter cannot be made of ordinary protons, neutrons, and electrons. We suspect that dark matter is composed of unseen elementary particles of a yet-to-be-discovered type, which were presumably formed in the extreme heat and pressure of the early universe, just as protons, neutrons, and electrons were. There are a number of speculations as to what these elementary particles might be. The theory of supersymmetry predicts that each particle we observe should have a massive supersymmetric partner: the photino for the photon, the selectron for the electron, the gravitino for the graviton, and so forth. The search is on at the Large Hadron Collider for such particles. If one of them is discovered, it would prove the theory of supersymmetry. In 1982, Jim Peebles proposed that dark matter is composed of weakly interacting massive particles (and yes, astronomers actually call these “WIMPs”) considerably more massive than the proton. The lightest supersymmetric partner of a known particle might just fill the bill. George Blumenthal, Heinz Pagels, and Joel Primack proposed the gravitino as a candidate in 1982. It has to be the lightest, because the heavier ones are not stable in the theory; they decay to something lighter and so don’t stick around.

Another speculation is that dark matter could be made of elementary particles called axions. The Large Hadron Collider, the world’s most powerful particle physics experiment, which sits on the Swiss-French border, may be our best hope for finding and identifying any of these candidates. But if the mass of the Milky Way galaxy is mostly dark matter, we expect that there should be dark matter particles all around us. Dark matter particles should be passing through your body right now. But again, they are dark, which means that they don’t interact much with ordinary matter (except by gravity). However, the supersymmetric or axion models for dark matter predict that on rare occasions, a particle of dark matter may interact with an atomic nucleus and cause a reaction that we could hope to observe. Experiments are underway to look for such reactions. It’s a difficult game: one such experiment uses 100 kilograms of liquid xenon, looking for the flash of light expected if a dark matter particle scatters off one of the xenon nuclei. These experiments are placed in deep mines to minimize confusing interactions with normal particles. These experiments have not yet found convincing evidence of dark matter; but experimental limits on its properties are only now approaching the range the particle physics models predict. The search for the dark matter particles takes us to the forefront of particle physics.

Invoking the presence of dark matter, one predicts that the CMB should be smooth, with fluctuations at the level of one part in 100,000. The instruments on the COBE satellite had been designed with the required sensitivity. In 1992, I remember attending a presentation Dave Wilkinson gave for the Princeton astronomical community describing the satellite’s measurements. The fluctuations in the CMB that had to be there (according to our understanding of growth of structure in a hot Big Bang universe) had finally been detected by the satellite, at a level of one part in 100,000, just about the level that Peebles and others had predicted.

At that time, Wilkinson was already thinking about a next-generation satellite, with instruments capable of measuring these fluctuations (or anisotropies, in the jargon) with greater precision. Wilkinson put together a team, including many of the veterans from the COBE satellite, to build the Microwave Anisotropy Probe (MAP). MAP was launched in 2001, and mapped the sky for 9 years.

Sadly, Wilkinson was suffering from cancer through this period. He was able to see the early results from the satellite just before he passed away in September 2002. In February 2003, the team published the results from the first year’s data. NASA decided to rename the satellite after Wilkinson; it was henceforth known as the Wilkinson Microwave Anisotropy Probe, or WMAP.

Figure 15.2 shows the map of the fluctuations in the microwave background temperature as found by the WMAP satellite after 9 years of taking data (in 2010). The elliptical shape maps the full sphere of the sky. The north galactic pole is at the top, the south galactic pole is at the bottom, and the galactic equator, tracing the plane of the Milky Way galaxy, is the line passing horizontally across the middle of the map. Emission from the interstellar medium in the Milky Way, as well as the one-part-in-a-thousand deviation due to our motion relative to the CMB, have been subtracted.

FIGURE 15.2. WMAP satellite map of the cosmic microwave background. based on 9 years of data, 2010. This is a map of the entire sky, in the same projection as figure 11.1 and figure 12.2. Microwave emission from the Milky Way itself has been subtracted off as well as the Doppler shift due to Earth’s peculiar motion relative to the cosmic microwave background. Red denotes slightly above average temperature; blue, slightly below average temperature; and green, intermediate temperature. Photo credit: WMAP satellite, NASA

This is really a baby picture of the universe, our direct view of it when it was a tiny fraction of its present age. These photons have been traveling to us for all but 380,000 years of the 13.8-billion-year age of the universe. The contrast on this map has been cranked up so that the deepest reds and blues correspond to fluctuations of several times ±0.001%; the more typical values are ±0.001% (i.e., one part in 100,000).

Figure 15.3 shows the measured strength of these fluctuations as a function of the angular scale (note scale at the bottom). These measurements come from a successor satellite, called Planck, launched by the European Space Agency, as well as a variety of other telescopes on the ground.

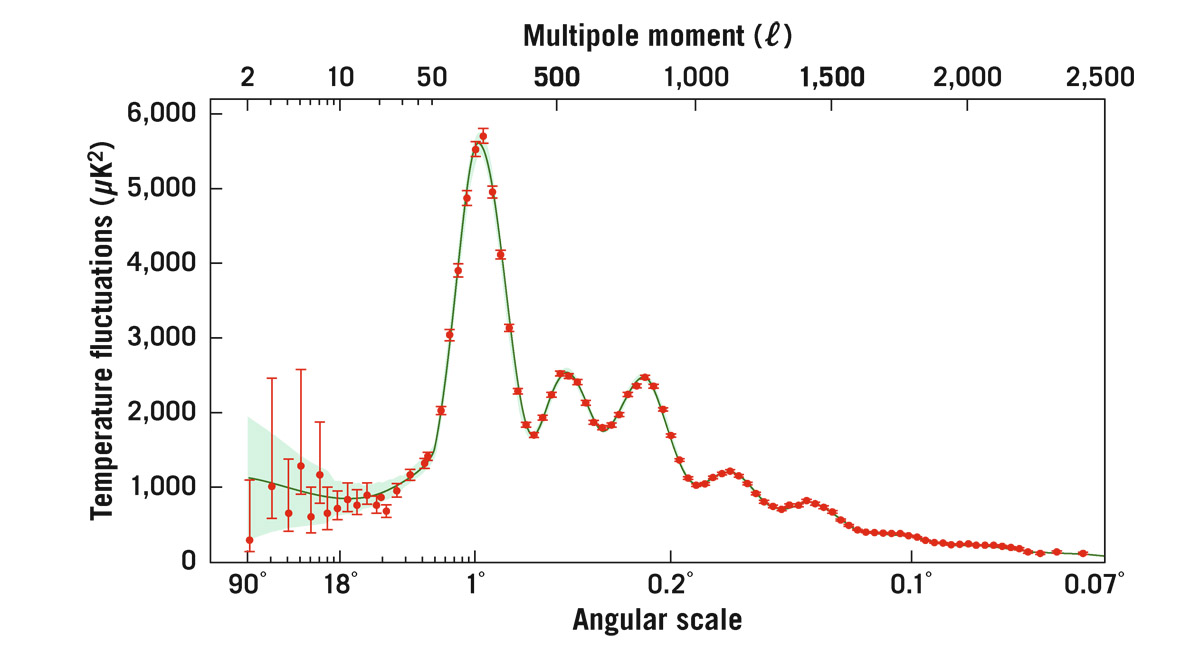
FIGURE 15.3. Strength of cosmic microwave background fluctuations as a function of angular scale (red dots) compared with theory (green curve), from the Planck Satellite Team 2013. The strength (power) in the variations of the temperature of the cosmic microwave background is plotted vertically, as a function of the scale of the fluctuations in degrees. The units on the vertical axis are micro-Kelvin squared, representing fluctuations from the uniform temperature of 2.7325 K of about one part in 100,000. The oscillations in the curve are due to sound waves traveling through the universe until the time of recombination. The solid curve going through the data points is the predicted curve given our model for the Big Bang, including the effects of dark matter, dark energy, and inflation (about which we learn much more in chapter 23); the essentially perfect agreement with the observations is stunning confirmation that the Big Bang model is correct. Data from NASA’s WMAP satellite earlier resulted in much the same conclusion. Credit: Courtesy ESA and the Planck Collaboration

There is a peak at an angular scale of 1°, corresponding to the typical size of the “bumps” you see in the WMAP image. The graph tells us, for example, that there are smaller variations from one 18°-wide patch to another than from one 1°-wide patch to another. Where no error bars are apparent, the observational errors are smaller than the size of the red dots.

The smooth green curve going through the points is the result of a theoretical calculation based on Big Bang theory, including the effects of dark matter, dark energy, and inflation (about which we learn much more in chapter 23). At large angular scales, the green line broadens to encompass the theoretically expected scatter in the predicted results. The agreement between the two is astonishing: the observations fall along the green theoretical curve within the observed errors. The Big Bang model has racked up another success: it predicts the detailed nature of the extremely subtle fluctuations seen in the CMB.

After recombination, material starts gathering into ever-denser lumps to make the first stars and galaxies. But given the angular size of structures we see in the CMB, we predict that there should be substantial structure in the universe on larger scales than just galaxies, which are a mere 100,000 light-years across. That is, the galaxies should not be randomly distributed in space but should be organized in larger structures. To map these structures, we return to Hubble’s law. Remember that when we look at an astronomical image, we see objects as if painted on the two-dimensional dome of the sky; we have no depth perception at all and cannot necessarily distinguish between a nearby galaxy and one lying at a much greater distance. But Hubble’s law gives us a method to explore the third dimension: by measuring the redshift of each galaxy, we can determine its distance and see how the galaxies are distributed in space.

Starting in earnest in the late 1970s, astronomers began measuring the redshifts of thousands of galaxies and were able to make three-dimensional maps of their distribution. They immediately noticed that the galaxies are not at all distributed randomly in space: they found clusters of galaxies (up to 3 million light-years across) containing thousands of galaxies, and empty regions (voids 300 million light-years across) almost completely devoid of galaxies. Indeed, these early maps caused people to question the cosmological principle; there was so much structure apparent in these maps that people wondered whether there was any scale on which the universe appeared smooth, or whether ever-larger surveys of the sky would show yet larger structures. The Sloan Digital Sky Survey was designed in part to address this question. It is a telescope dedicated to mapping the sky; it has measured redshifts now for more than 2 million galaxies. Figure 15.4 is a map of a small fraction of these galaxies, those in a 4°-wide slice in Earth’s equatorial plane; if we showed you all the data in one plot, the density of points in the figure would be so high that it would show solid ink, not allowing you to see any of the structure.

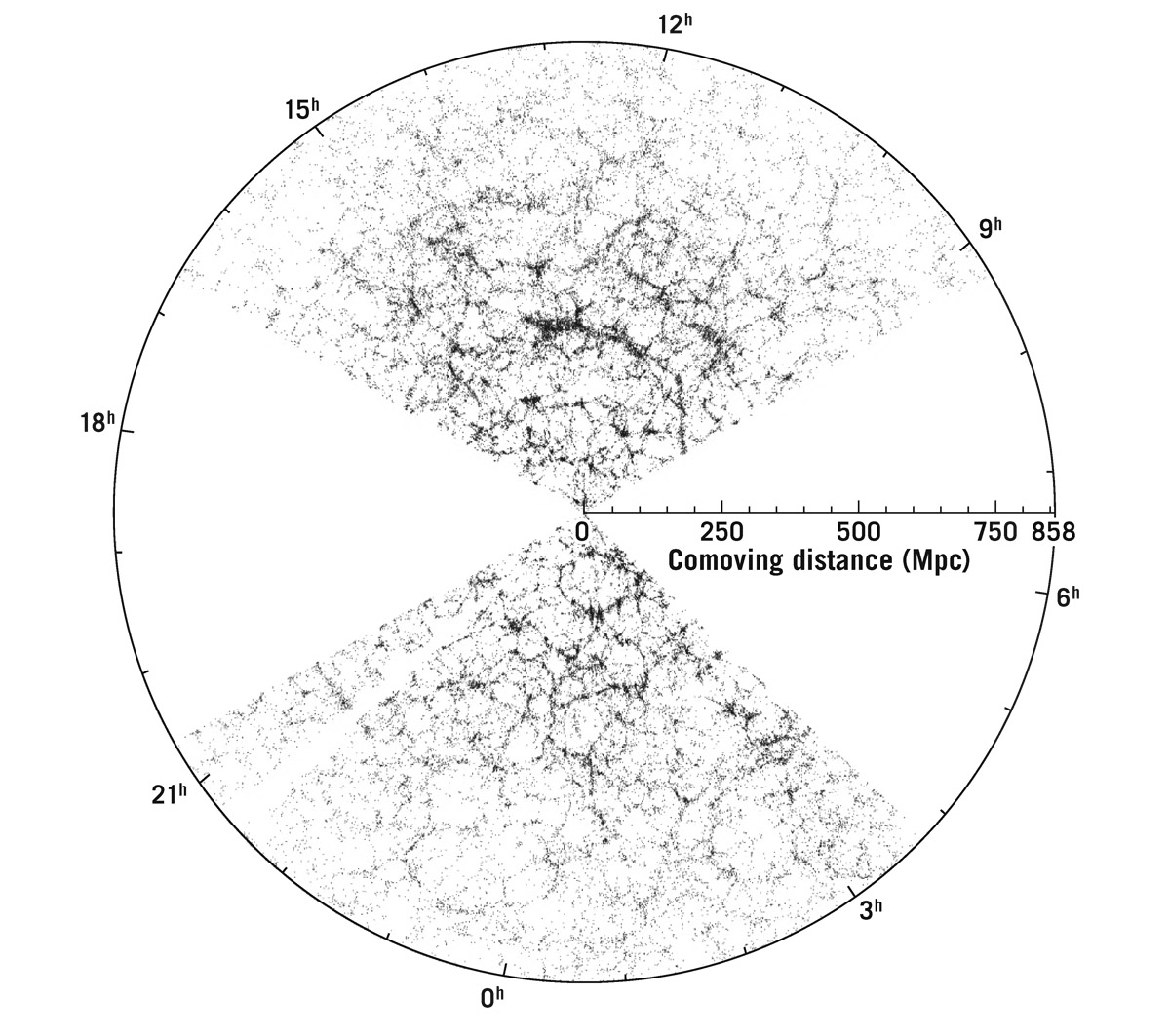
FIGURE 15.4. Distribution of galaxies in an equatorial slice from the Sloan Digital Sky Survey. The Milky Way is at the center. Each dot represents a galaxy. The two fans show galaxies in the survey region; the two blank regions are regions the survey did not cover. The radius of this diagram is about 2.8 billion light-years.

Credit: J. Richard Gott, M. Jurić, et al. 2005, Astrophysical Journal 624: 463–484

Each of the more than 50,000 dots in this figure represents a galaxy of 100 billion stars. It is worth taking a moment to appreciate the enormousness of these numbers.

We can see two big slices of the pie; the Milky Way galaxy sits at the center of the image. The empty regions on the left and the right have not been covered by the survey; this is the region obscured by dust from the Milky Way, making it difficult to pick out distant galaxies.

The radius of this figure is 860 Mpc, almost 3 billion light-years. Even a cluster of galaxies appears small in this picture; the majority of galaxies appear to lie along filaments, strings of galaxies hundreds of millions of light-years long. A particularly prominent filament, dubbed the Sloan Great Wall, appears somewhat above the center of the image. It has a length of 1.37 billion light-years. But no structures stretch across the entire width of either survey slice, indicating that on the very largest scales, Einstein’s cosmological principle holds.

Notice in the figure that the density of galaxies does drop off dramatically near the outer edges of the map. This is not evidence that the cosmological principle is wrong: it simply reflects the fact that galaxies in these regions are the most distant from us and are therefore the faintest. Only a small fraction of the most distant galaxies are luminous enough for the Sloan Digital Sky Survey to measure their spectra, and therefore for their redshifts to be included in this map.

If we compare this to our map of the CMB from WMAP, it is not obvious, even under the process of gravitational instability, that fluctuations at the level of one part in 100,000 can evolve into the incredibly structured universe we see today in the galaxy distribution. The equations of gravitational instability (which are based on Newton’s law of gravity, with the added complication of the expansion of the universe) can be solved approximately and tell us that the numbers are roughly right, but to do the calculation properly, and understand the gravitational tug of each parcel of matter in the universe on every other part, requires a large computer. One starts with a distribution of matter with subtle fluctuations at the level that we measure from the CMB map. Then one lets gravity, plus the expansion of the universe, take over and evolve the structure for 13.8 billion years on the computer. The resulting distribution of galaxies these computer simulations predict shows the same sort of structure we see in the galaxy maps: clusters, voids, and filaments, of just the right size and contrast to match observations.

Of course, we don’t expect the computer simulations to produce the exact structures of the present-day universe, just ones with the same statistical properties. Remember that the part of the universe we’re seeing in the CMB is very distant from us; we’re not seeing the matter that evolves into the galaxies that are near us. But we do assume that the general properties, including the fluctuations, of the material giving rise to the CMB, are statistically similar to that matter which gives rise to the galaxies around us. Overall, large computer simulations based on the Big Bang model have been remarkably successful in reproducing the filamentary weblike structure that we see in the observations.

This, then, is the final triumph of the Big Bang model. We have explored the predictions of the model and compared them with observations in every way that we could. We inferred that the universe was born 13.8 billion years ago, in excellent accord with (i.e., slightly older than) the ages of the oldest stars. We concluded that hydrogen and helium nuclei were formed in the first few minutes after the Big Bang, in a 12:1 ratio, which is exactly what is observed, and we are able to predict the quantity of deuterium produced, also in agreement with observations. We predicted the existence of the CMB, and its various properties: its spectrum, its temperature, and its incredible smoothness; all this is exactly as observed. Perhaps most impressively, we predicted that the CMB should not be perfectly smooth but should show fluctuations at one part in 100,000, with a predicted variation depending on the angular scale that should follow a complicated curve. The WMAP and Planck satellite measurements have confirmed this prediction as well. Finally, computer models of how these fluctuations should grow under gravitational instability predict a highly structured universe today, with galaxies arrayed along filaments hundreds of millions of light-years long, just as the maps from the Sloan Digital Sky Survey reveal. The Big Bang model is far more than “just a theory”: it is supported by a vast array of empirical, quantitative evidence and has passed every test we have given it with flying colors.