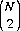Chapter Nine

Statistical Logic and Statistical Games

Strategic Selection

There are certain phenomena, such as weather and ocean wave movements, whose statistics are pseudostationary—in the sense that they would be statistically predictable if we possessed sufficient microscopic information regarding their nature. Since such data may never be practically available, they are treated as nonstationary. On the other hand, games whose outcomes depend to a large extent on human, animal, or psychological factors are truly nonstationary in nature. Statistics of horse-racing events, for example, change with improved training methods and breeding controls. Stock market activity, as another example, motivates different people to react differently, and the same person may well react differently to the same stimulus applied at different times. Eighty years ago, if J.P. Morgan advised, “Buy!,” almost everyone bought (while J.P. Morgan likely sold short). At present, no financier can influence investment behavior to the same extent.

Many of those professionally concerned with more serious games such as warfare, both military and economic, have long been accustomed to regard problems of strategy, where nonstationary statistics are involved, as too enigmatic to be subjected to intellectual analysis. Such problems were considered the exclusive province of men who had crystallized long experience into a set of heuristic rules of play. Mathematical models were viewed merely as exercises in fantasy; the usual approach was that precarious system of trial and error referred to by its adherents as pragmatism and by its opponents as willful bungling. Then, the rise in respectability of such disciplines as Operations Research instituted an incisive, analytic approach to such previously arcane domains as war strategy and weapons development. One consequence of the newer approach, on the national level, is a posture of greater political sophistication.

Yet, efforts to reduce human or animal behavior to precise mathematical formulae can prove less than convincing. We usually strive to determine a “best” decision constrained by the limitations of a practical model and its underlying assumptions.

The choice of a “probable best” course of action from two or more alternatives based on statistical inference as to their relative merits defines a process of strategic selection by weighted statistical logic. There are four basic steps leading to an ultimate decision:

1. Recognition and evaluation of the individual factors pertinent to the final decision.

2. Expression of the alternate courses of action in terms of the weighting assigned each of the individual pertinent factors.

3. Derivation of a composite ranking that represents the overall relative merit of each alternate course of action.

4. Identification and designation of the highest ranking alternative as the optimal course of action.

The key to this approach is the judicious choice and manipulation of the pertinent factors affecting the selective decision. In attempting to predict the outcome of a football contest, we might list such factors as weather, field conditions, home team, and the number of disabled players. To the extent that we include irrelevant parameters, our prediction rests on shaky foundations.

Each ingredient in our dialectical stew is examined for its likely level of contribution. The space of permissible outcomes is then described in a probabilistic sense. If our assessment of the relative importance of each factor is erroneous, our final ranking becomes questionable. Finally, our optimal prediction falls impotent in the face of a blocked kick, a fumble, or some other unforeseen catastrophic departure from planned behavior.

The Stock Market

A complex game comprising weighted subjective judgments and nonstationary statistics is that tendered by the stock market1 (or commodity markets). Constituting a gigantic decision-making phenomenon, the stock market—with its codified folklore and certified respectability—poses a broad appeal to the gambler (euphemistically referred to as a “speculator”). Like horserace handicappers, stock market analysts frequently attempt to predict the future on the basis of past performances, and, like horse racing, the market has successfully withstood all nostrums for financial success; the pot of gold exists, but the labyrinthine path to its den has not yet been charted.

Rigorous technical analysis of the stock market encounters a vertiginous array of factors, some real, some imagined, to which security prices respond with varying sensitivities. Treatment of the apparently whimsical fluctuations of the stock quotations as truly nonstationary processes requires a model of such complexity that its practical value is likely to be limited. An additional complication, not encompassed by most stock-market models, arises from the manifestation of the market as a non-zero-sum game.

The theory of games has shown that consideration of nonzero-sum games immediately injects questions of cooperation, bargaining, and other types of player interaction before and during the course of the game. Also, considerations of subjective utility functions arise—for non-zero-sum games we are generally concerned with equilibrium point-preserving vectors of utility functions. Even when treated as a zero-sum game, stock-market speculations imply utility functions that are non-strategy preserving (by definition, if a player’s strategy is independent of his fortune at the time of his play, his utility function is strategy preserving; it can be shown that such utility functions must be either linear or exponential).

A further peculiarity of the stock market arises from the time duration of a complete play (a buy-and-sell transaction, in either order). What constitutes a profit over an extended period of time is complicated by the time-varying purchasing power of money, taxation rates, availability of merchandise, inventions, war, government changes, political upheavals, and shifts in mass psychology influencing the mores of investors. Reflecting an amalgam of economic, monetary, and psychological factors, the stock market represents possibly the most subtly intricate game invented by man.

Descriptive Models

Tradition has it that the New York Stock Exchange (the “Big Board”)2 was established on Wall Street in 1792 under the sheltering limbs of a buttonwood tree. By 1815 it had moved indoors and was offering 24 issues for trade. Over 216 years it has grown into the world’s largest exchange with more than 2800 companies listed and a global capitalization of $22.6 trillion, five times the size of its nearest competitor (the Tokyo Stock Exchange). In 2005, the NYSE merged with the fully electronic exchange, Archipelago Holdings; accordingly, more than 50% of all orders are, at present, delivered to the floor electronically, a percentage that promises to increase.

In 1965, the NYSE Composite Index was created as a measure of the change in aggregate value of all common stocks traded on the Exchange (in contrast to the 30 stocks encompassed by the Dow Jones Industrial Average). Revised in 2003, the Index is weighted using free-float market capitalization and calculated on the basis of both price and total return (and is announced every half-hour). The four years from January 2003 to January 2007 witnessed a rise of 81% in the Index (from 5000 to 9069).

Throughout the more than two centuries of open stock auctions, multitudinous models have been proposed as descriptive of the behavior of security prices. Classically, efforts are directed toward relating the values of securities with industrial production levels or other measures of economic health. Yet industrial stocks and industrial production have moved together but 51% of the time since mid-19th century (36% of the time both have risen, while 15% of the time both have fallen; rising industrial production has seen a falling market 25% of the time, and stocks have risen despite falling production 24% of the time). The industrial cycle itself is exhibiting markedly changing characteristics. “boom” and “bust” periods are becoming less frequent and violent under the constraints of government controls. From 1854 through 1933, the United States experienced 21 economic depressions, an average of one every 45 months; between 1933 and 1965, six depressions resulted in an average of one every 64 months. From 1986 through 2006, economists have identified only five such cycles. (Depressions, now bowdlerized to “recessions,” are officially acknowledged by the National Bureau of Economic Research—NBER.)

Of those models that deal directly with security prices—short-circuiting economic and monetary analysis—the great majority are of an interpretive nature. The Dow theory and its host of relatives typify those models based on crude measurements with such ambiguous formulation as to require interpreters, most of whom disagree among themselves. We can only marvel at the contradictory conclusions that have evolved from a single collection of data.

Other models are predicated upon assumed (or imagined) correlations between stock price fluctuations and various fluctuating phenomena in and out of the world. Sunspot activity, astrological events, ionic content of the air, and Jovian radio signals are but some of the supposed correlated events; one enterprising individual ran, for a time, a fairly successful investment service based on his “readings” of comic strips in the New York Sun. Not surprising to the statistician, good correlations can be found over discretely chosen limited data samples in the past. Their failure to survive the transition from past to future can surprise only the irrepressible optimist.

Although the first serious study of a stock market (Vienna) was conducted prior to 1871 by Carl Menger (as a background for his theory of prices and the concept of marginal utility), it was not until 1900 that a competent mathematician began a scientific and empirical investigation into the nature of security prices. In that year, Louis Bachelier (Ref.), in his doctoral dissertation, developed an elaborate mathematical study of market prices that launched the theory of stochastic processes, established the probability law for diffusion in the presence of an absorbing barrier, and foreshadowed many other areas of interest to probability theorists.

Through the first half of the 20th century and beyond, several investigations into the ability of publicized forecasters to predict stock prices found that no success beyond that of chance could be attributed to their prognostications.

Subsequently, mathematicians and economists have combined efforts to understand the principles of trading securities. The University of Chicago, in 1960, established a Center for Research in Security Prices to investigate the behavior of stocks, individually and collectively. Monthly closing prices of all common stocks listed on the New York Exchange from 1926 through 1960 were recorded. It was determined that a “random” investor (the particular security and the buying and selling moments were selected at random) acquired a median gain of 10% per annum on his capital.

Virtually all academic investigators agree on one point: To a good approximation, price changes in speculative markets, such as commodities and securities, behave like independent, identically distributed random variables with finite variances. It then follows, according to the central limit theorem, that price changes over a small interval of time are normally distributed. (Actually, the log-normal distribution provides a better fit.) The model thus depicted is referred to by statisticians as a random walk and by physicists as Brownian motion. It asserts that a history of past prices alone is of no substantial value in the prediction of future prices. No gambling rule exists that can produce a profit (assuming truly independent price increments—see Theorem I, Chapter 3). Except for appreciation from earnings retention, the conditional expectation of tomorrow’s price, given today’s price, is today’s price.

The random-walk model is consistent with the postulate of stock exchanges as “perfect” markets. That is, if a substantial group of investors believed that prices were too low, they would enter buying bids, thereby forcing prices higher, and vice versa, quickly forcing prices into conformity with the “intrinsic value” of the securities.

Numerous studies have applied the technique of spectral analysis to time series of stock prices. A spectrum of a time series represents completely the autocorrelation function for any stationary stochastic process with finite variance and also determines the best linear predictor of that time series. This technique is resorted to with reservation in connection with economic data, since the basic phenomenon is nonstationary. However, if the underlying structure of the time series is not a fast-changing function of time, spectral analysis can prove useful. In virtually every case, the first differences of various stock aggregates exhibit a spectrum quite flat over the entire frequency range, thus providing additional support to the random-walk thesis.

Analyses of security prices are characterized by two distinct approaches. Fundamental analysis relies upon evaluation of economic and financial data to ascertain the intrinsic value of a corporate security—generally measured by the price-to-earnings ratio. It can be particularly difficult, however, to estimate earnings more than a year or two into the future.

Technical analysis, on the other hand, is concerned solely with market price trends and patterns—price histories are examined in search of patterns that portend future prices. The “technician” or “chartist” then speaks in terms of “head and shoulders,”“double tops,”“support levels,”“resistance points,” and the like, referring to structures delineated by a chart of price versus time. (In practice, most investment counselors combine fundamental and technical principles in appraising securities.) The random-walk model renders unavailing all technical analysis. Historical price patterns are merely statistical fossils (Ref. Thorp and Kassouf)—though their advocates, like astrologers, alchemists, psychics, and inventors of perpetual motion machines, refuse to give up the ghost.

Markets may be defined as strongly or weakly efficient. In the former category, all participants are afforded equality of opportunity but with average expectations. Only to the extent that a market deviates from strong efficiency can a participant exceed the average return on investment. (In a semistrongly efficient market, a favored few have gained access to “inside” information and can profit thereby. Government regulations militate against this type of market.)

In a weakly efficient market, pertinent information is made available to the investing public after a time lag (termed “relaxation time,” it describes the period for new information to be absorbed into the marketplace; relaxation time has grown ever shorter with greater and more rapid diffusion of knowledge). Essentially, all major stock exchanges constitute weakly efficient markets.

Burton P. Fabricand (Ref.) has demonstrated that strategic selection of stocks in a weakly efficient market can yield positive expectations. His suggested procedure arises from the fact that roughly 15% of listed companies will report quarterly earnings (RE) that exceed prior projections (PE) by 10% or more (while 7% of earnings reports will exceed projections by 20%). (Such projections are available from Value Line Investment Survey; actual earnings are promptly reported in the Wall Street Journal.) Fabricand’s strategy entails purchase of stocks (immediately upon the issuance of earnings reports) with RE to PE ratios > 1.1 and holding them so long and only so long as the ratio exceeds 1.1.

Clearly, the success of this procedure depends on the persistence of the weakly efficient nature of the stock market. To date, there is no evidence to suggest that this persistence has diminished; indeed, it seems likely that it is ingrained in the DNA of an auction market.

Sergei Maslov and Yi-Cheng Zhang (Ref.) have shown that processes similar to the Parrondo principle (Chapter 4) can be applied to the stock market to increase the value of a portfolio despite a long-term decline in each of its individual stocks. Specifically, the entire portfolio must be sold frequently (the “readjustment interval”), with the proceeds immediately reinvested in the same proportions as in the original portfolio. The net effect of such frequent rebalancing is to apply the gains from stocks temporarily performing better than average (and have therefore increased their relative proportions in the portfolio) to buy a higher percentage of those stocks that are temporarily performing below average. It has been demonstrated that the investor following this (counterintuitive) strategy improves his return over that of the investor who follows a static buy-and-sell strategy (Ref. Marsili, Maslov, and Zhang).

An interesting offshoot of the Maslov game is the “toy model” (impractical but possibly insightful) that exploits Parrondo’s principle by combining a stable stock (A), unlikely to engender significant gains or losses, with a highly volatile stock (B), the value of which equiprobably doubles or halves each day. An opposite strategy, proposed by D.G. Leunberger (Ref.) and termed volatility pumping, consists of selling both stocks each day and rebuying them in equal monetary proportions, thus rebalancing the portfolio. The result, quite remarkably, produces an exponential growth of the portfolio. Figure 9-1 (Ref. Abbott) illustrates a typical profile obtained by exercising the Parrondo principle on the two stocks, A and B. By the one-hundredth day, the initial portfolio has increased in value 10,000-fold.

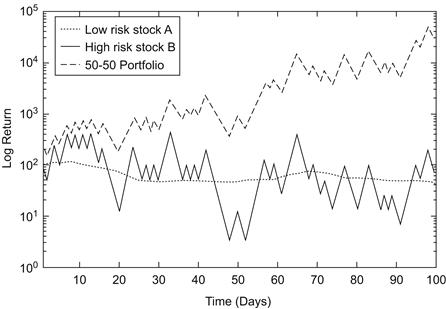
Figure 9-1 Volatility pumping a low-risk stock with a high-risk stock.

The principle can be equally adapted to two volatile stocks, each defined as stock B. For this case, the sell-and-rebalance procedure will have increased the value of the portfolio 1,000,000-fold after 100 days.

Transactions costs, for volatility pumping and for the Maslov strategy, would severely crimp the theoretical benefits.

Warrant Hedging

The practice of warrant hedging (simultaneously buying a security and shorting its associated warrant) has been recognized for several decades. Its effectiveness, its anatomy, and its operation, however, were not analyzed until the 1960s, when Edward O. Thorp and Sheen T. Kassouf (Ref.) performed a thorough autopsy.

A warrant is defined as an option to buy a share of common stock at a fixed price—referred to as the exercise price. Warrants themselves are bought and sold in essentially the same manner as common securities although, unlike stocks, they are (usually) issued with an expiration date, beyond which the warrant retains no value. Adroit hedging of the warrant against the stock largely cancels the risk attendant to each separately while still offering a substantial return on investment.

The specifics of a warrant-hedging transaction involve shorting m warrants at selling price w and exercise price e for every share of stock bought at price s (m is known as the mix). If, at or before the expiration date of the warrant, the stock is selling at price S and the warrant at price W, the percentage profit return R from concluding the transaction is

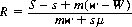(9-1)

where μ is the margin required for stock purchase and mw + sμ ≡ I is the initial investment capital.

As its expiration date approaches, the warrant will have a price approaching zero if the stock price is at or below the exercise price; if the stock price exceeds the exercise price, the warrant will sell for about the difference between the stock and exercise prices. That is,

Equation 9-1 can then be written in the form

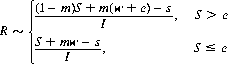(9-2)

R remains positive throughout the range

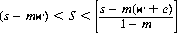
and assumes its maximum value when S = e (disregarding commissions). According to the random-walk model, the mean value of S is s; Eq. 9-2 for this case shows a profit of R = mw/I.

Thorp and Kassouf restrict the hedging system to those warrants whose expiration date is prior to four years from the transaction date and whose stock is selling at less than 120% of the exercise price. Further, they advance two “commonsensical rules” relating warrant prices to stock prices:

1. The price of a warrant should be less than the price of its associated common stock.

2. The price of a warrant plus its exercise price should be greater than the price of the stock.

For each transaction they select a mix that provides a conservative balance between potential risk and potential profit. Often the mix is chosen so that the zone of potential profit is distributed logarithmically equal above and below the stock price. Applying these guidelines, they report consistent profits of about 25% per year on invested capital.

As a numerical illustration, consider a stock selling at 20 with a warrant selling at 5 and an exercise price of 25. A mix of 2 provides equal logarithmic safety against stock fluctuations. Then, if we buy 100 shares of the stock and short 200 warrants, the invested capital with 50% margin is I = 200(5) + 100(20)(0.5) = $2000. The safety zone ranges throughout 10 < S < 40 with its maximum value at S = 25, whence (from Eq. 9-2)

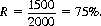
Examples of warrants suitable for hedging appear with decreasing frequency as the hedging system has become increasingly exercised in the marketplace. A different market with further profit potential was initiated in April 1973 when the Chicago Board of Options Exchange (CBOE) permitted public buying and selling of call options on selected stocks. Since a call can be treated identically to a warrant, a system of option-hedging (selling calls while buying the associated stock) is mathematically equivalent to warrant-hedging. The classic construct in this field is the Black–Scholes option model, which demonstrates that hedging options short and common stock long and continuously adjusting the mix lead to an essentially risk-free rate of profit return.

Horse Racing

Of the various games with formalized wagering, perhaps none so embodies the concept of subjective evaluation as horse racing, the “Sport of Kings.” Competitive racing can be traced back some 6500 years to the nomadic tribesmen of Central Asia. Wagering on the outcome of such races apparently originated among the Hittites in the second millennium B.C.; archaeologists have uncovered a lengthy treatise on the breeding and training of horses written for a Hittite king about 1500 B.C. The earliest full-length account of a chariot race appears in Book xxiii of the Iliad. Competitive rules for prescribed distances were instituted for the Thirty-third Olympiad of Greece, ca. 624 B.C. The Romans added handicapping and the concept of “betting against the House” for their chariot races. Thence, racing declined with the onset of the Middle Ages and was not renewed until early in the 17th century when James I sponsored its establishment at Epsom and Newmarket; his grandson Charles II was such an avid racing addict that he became known as the “father of the British turf.” In mid-18th century, the Jockey Club was formed as the governing board of racing in Great Britain. And, in 1894, the United States followed suit with the formation of the American Jockey Club, the “combined Congress and Supreme Court of American racing.”

Three major types of horse racing have held sway in the United States: Thoroughbred (by far the most popular), Standardbred, and Quarter-Horse racing (operating on 20-some major and hundreds of smaller tracks). By definition, a Thoroughbred is lineally descended from one of three Near East progenitors (the Byerly Turk, the Darley Arabian, and the Godolphin Barb) bred to English mares about the turn of the 18th century. Standardbred horses are descended from an English Thoroughbred named Messenger, brought to the United States in 1788. Quarter-horses (a mixture of Arabian, Spanish, and English stock with 11 different bloodlines) are bred for compact bodies appropriate to great speed at short distances (from 220 to 870 yards); they are also featured at horse shows and rodeo events. (The name derives from the practice of early 17th-century Virginia settlers to race them through quarter-mile clearings in a forest.)

Steeplechases (a remnant from the “sport” of fox hunting), more popular in the British Isles than elsewhere, are run over a 2- to 4-mile course that interposes obstacles such as hedges, stone walls, timber rails, and water jumps. England’s Grand National, held annually since 1839 at Aintree, is arguably the world’s most famous horserace.

Competition is generally staged among 6 to 12 horses and occurs over certain standard distances measured counterclockwise3 about an oval track: six furlongs, seven furlongs, one mile, 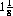miles, 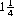miles, and 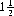miles. Races are also categorized according to prize, sex (three classes are recognized: stallions, mares, and geldings), age of the contending horses (all equine birthdays are celebrated on January 1 by decree of the Thoroughbred Racing Association), and the horse “rating” or quality. The general divisions are Handicap and Stakes races, Claiming and Optional Claiming races, Allowance and Classified Allowance races, and Maiden races.

For any and all data regarding the history, breeding, or racing of horses, the library on the grounds of the Keeneland (Kentucky) racetrack provides the most comprehensive source. Devoted exclusively to hippology, its volumes of racing literature and turf records date from the 18th century.

Predicting the outcome of a horse race is an activity that exerts a continuing appeal despite its complexity. A strategic selection by weighted statistical logic may entail numerous elements, many subjective in nature. An enumeration of the pertinent factors might include post position, track condition, weather, weight carried, previous performances, appearance or condition of the horse, earnings, jockey, owner, trainer, class of race, equipment changes, inter alia. No few of these factors comprise statistical phenomena of a nonstationary nature. For this reason, data samples gathered over a few seasons of racing at several tracks offer little predictive value, although copious records of past races have been sifted in the search for significant patterns. Any finite data sample, if analyzed persistently, will divulge patterns of regularity. A simple prediction, however, cannot sensibly be constructed on the shifting sands of nonstationary processes.

Pari-Mutuel Betting

Horse racing survives to this day as a major professional sport solely because of its venue for legalized gambling. The pari-mutuel betting system is based on the consensus of subjective probabilities assigned to the contending horses by the aggregation of bettors (thus constituting a weakly efficient market within a compressed time scale) and specifies payoff odds on each horse inversely proportional to the amount of money wagered on that horse. Invented in 1865 by a Parisian parfumeur, Pierre Oller, it essentially ensures a fixed profit to the track operator independent of the winning horses (pari-mutuel wagering is also applied for Greyhound racing and Jai Alai contests). In 1933, the first completely electronic totalizator, automatically computing odds and issuing tickets, was introduced at Arlington Park, Chicago, and subsequently installed at all major racing establishments.4

Generally (depending on the country or the state within the United States) track operators pocket from 15 to 25% of the total wagered on each race and redistribute the remainder among those bettors selecting the winning horses. Additionally, a 2.5% loss is sustained by each winner owing to the “breakage” rule—the payoff is quantized to the lower 10-cent level (based on the conventional minimum wager of $2.00). Standard bets include Win, Place (the horse to finish first or second), Show (the horse to finish first, second, or third), Across the Board (a minimum $6.00 wager divided equally among Win, Place, and Show), Daily Double (two horses in different races, usually the first and second, both to win), Quinella (two horses in the same race to finish first and second, without regard to order), Exacta or Perfecta (the first two finishers in exact order), Trifecta (the first three finishers in exact order), Superfecta (the first four finishers in exact order), Pick 3 (winning horses in three consecutive races), and Pick 6 (winners in six consecutive races). These last few bets obviously entail extravagant odds.

The legal minimum return on a $2.00 winning ticket is normally $2.10; when the totalizator indicates a smaller payoff (after deducting the House Take), the situation is termed a “minus pool,” and the difference to $2.10 is borne by the track operators.

To describe mathematically the pari-mutuel model, we postulate n bettors B₁, B₂, …, B_n concerned with a race involving m horses H₁, H₂, …, H_m. Each better B_i applies his weighted statistical logic to what he deems to be the pertinent factors and thereby achieves an estimate of the relative merits of each horse H_j expressed in quantitative terms—i.e., a subjective probability distribution over the m horses. Specifically, we have an n × m matrix {p_ij}, where p_ij designates the probability, in the judgment of B_i, that H_j will win the race. A sum b_i > 0 is then wagered by B_i in a manner that maximizes his subjective mathematical expectation. That is, B_i observes the pari-mutuel probabilities π₁, π₂, …, π_m, as indicated by the track tote board, that horses H₁, H₂, …, H_m, respectively, might win the race; he then follows a strategy of distributing the amount b_i among those horses H_j for which the ratio p_ij/π_j is a maximum.

We assume that the sum b_i is small with respect to the total amount wagered by the n bettors on the race and therefore does not appreciably influence the pari-mutuel probabilities. We further assume that each column of the matrix {p_ij} contains at least one entry; otherwise, if the jth column consists of all zeros, no bettor has selected horse H_j, and it can theoretically be eliminated from consideration.

The pari-mutuel system is described by three conditions. First, if β_ij is the sum wagered by B_i on H_j, we have

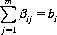(9-3)

Second, the pari-mutuel format imposes the relation

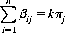(9-4)

where k is the constant of proportionality relating the amount bet on each horse to its pari-mutuel probability. Third, each B_i bets so as to maximize his subjective expectation E_i—that is, when

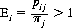(9-5)

and he bets only on horses for which the inequality holds. Nonnegative numbers π_j and B_ij that satisfy Eqs. 9-3, 9-4, and 9-5 are termed equilibrium probabilities and equilibrium bets, respectively. Their existence is readily proved by means of fixed-point theorems (a clever, elementary proof has been given by Eisenberg and Gale [Ref.]).

Pari-mutuel probabilities for the Win position are determined by the proportionality constant

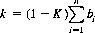
where K is the House Take, so that

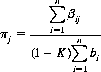(9-6)

The odds on each horse are quoted as (1 − π_j)/π_j to 1.

Pari-mutuel probabilities for Place are slightly more complicated. The total amount wagered for Place is decreased by the House Take and then divided into two halves, one half being distributed among bettors on the winning horse and the other among bettors on the placing horse. Similarly, pari-mutuel probabilities for Show are computed by dividing the total amount bet for Show less the House Take into three equal parts, which are distributed among bettors on the winning, placing, and showing horses. Thus, the payoff for a horse finishing Place or Show is a function of the other two horses sharing the mutuel pool. That payoff will be higher, the greater the odds on these two horses.

“Real” Probabilities for a Race

There are horse fanciers who profess the ability to determine the objective odds of each horse in a race. Such “dopesters,” can, presumably, assess the “real” probability ρ_j (as opposed to the subjective, pari-mutuel probability π_j) that horse H_j will finish first in a particular gymkhana. It is of interest to derive optimal betting strategy, given the distribution of real probabilities for the contenders.

Let the total capital bet on the jth horse, kπ_j (Eq. 9-4), be partitioned into the sum s_j wagered by the subjective “crowd” and the amount t_j contributed by our knowledgeable dopester. The dopester’s profit F(t₁, t₂, …, t_m) from an investment spread over the m horses is defined by

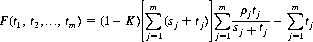
It is desired to select a value of t_j ≥ 0 so as to maximize F(t₁, t₂, …, t_m), where the maximal F possesses a positive magnitude.

Rufus Isaacs (Ref.), in his original statement of the problem, showed that F has a positive maximum if

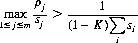
Consequently, for a solution 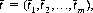we can write

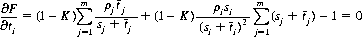
Then the quantity 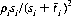exhibits the same value for all i such that 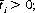defining this value by 1/λ², we have

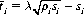
A maximal form of F never occurs for all 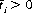(that is, the dopester never bets on all the horses). Rather, there may exist some number of horses k whose real expectation is greater than the subjective expectation realized from the actual capital wagered on them by the crowd. Then

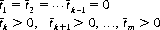
where 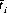is uniquely determined by k:

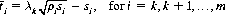(9-7)

and

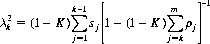(9-8)

As a numerical example, consider the horse-race data in Table 9-1. Horse H₇ offers the soundest investment, since it returns 75 times the wager less the House Take, yet possesses a win probability of 0.05. However, if the statistically minded dopester plunges heavily on H₇, the pari-mutuel reaction will alter the odds appreciably.⁵ To maximize his expected profit, the dopester should examine the subset (possibly null) of horses whose real expectation is greater than their subjective expectation. The subset for the race illustrated here is composed of horses H₂, H₅, and H₇. Thus, from Eq. 9-8 with K = 0.15 (15% House Take),

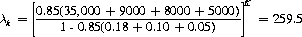
And, from Eq. 9-7, the optimal wager on horse H₂ is computed as

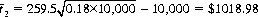
Table 9-1. Hypothetical Horse Race

Horse	“Real” Probability of Winning	Amount Wagered by the “Crowd”
H1	0.40	$35,000
H2	0.18	10,000
H3	0.12	9,000
H4	0.10	8,000
H5	0.10	7,000
H6	0.05	5,000
H7	0.05	1,000
		$75,000

No wager should be placed on horse H₅, since the House take of 15% leads to a negative value of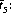

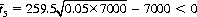
Horse H₇ should receive a bet of magnitude

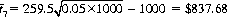
Herein, we have avoided pursuing the conceptual connotations of real probabilities as applied to horse races. However, it is intuitively apparent that any individual who can assess the probability of a given horse winning a race more accurately than the ensemble of other bettors can apply this profit maximization method.

The Equus Computer

Currently one of the most successful approaches to horse-race forecasting is the genetically programmed system EDDIE⁶ (Ref. Tsang, Butler, and Li). With this methodology (inspired by Darwinian evolution theory), a candidate solution is represented by a genetic decision tree (GDT) whose basic elements consist of rules and forecast values that correspond to the functions (relevant questions) and terminals (proposed actions) in genetic programming (GP). EDDIE applies GP to search the space of decision trees and to channel available “expert” knowledge into forecasting and the generation of pertinent rules.

Each function in a GDT consists of attributes (e.g., finishing positions in the horse’s previous races, weight carried in previous and forthcoming races, whether stepping up or down in class, etc.) and operators (various logical and relational operations that compare attributes). Processing these input data, EDDIE generates decision trees that rank the horses by ability.

As the functions are satisfied for each horse, the process is repeated—so as to evolve by way of natural selection a decision tree—and progressively moves down the tree until a terminal forecast value—an integer—is reached. This integer defines a confidence rating describing how well the specified horse is expected to perform in its impending race. That horse accruing the highest confidence rating is presumed the most probable winner.

EDDIE was put to the test with a database of 180 handicap races in the UK. A spectacular 88.2% return-on-investment resulted, an outcome that far outperformed other systems evaluating the same data.

This procedure is obviously analogous to financial forecasting, and genetic programs have also been adapted to financial markets with moderate if not dramatic success.

Psychological Betting Systems

Because of the inherently subjective nature of the pari-mutuel betting format, it may be feasible to devise methods of horse selection based solely on the psychological behavior of the bettors. For example, one “system” consists of wagering on the favorite (shortest odds) horse in the last race of a day’s program. While favorite horses are not more prone to win the last race than any other, the payoff is frequently greater than it would be in earlier races since there apparently exists a tendency to place a larger percentage of the total wagers on the longer-odds horses. This tendency possibly arises from the losers’ attempts to regain their losses and the winners’ inclinations to leave prior to the last race.

Another system advises wagering on the favorite horse if the previous two or more races have been won by favorites, and conversely. The rationale in this instance suggests that many bettors are susceptible to a “maturity of the chances” doctrine, and therefore tend to avoid wagering on a favorite horse when preceding races have produced winning favorites; thus the favorite offers higher odds than would arise from independent considerations. Both systems have been tested by examination of a limited data sample. The results indicate an increase in expectation of approximately 15% over a random selection of horses. Presumably, as bettors gain additional mathematical sophistication, this figure would decrease.

More cyclopedic means exist for utilizing the relatively invariant psychological behavior of bettors as reflected by the pari-mutuel probabilities. A logical method involves a statistical classification of races according to the subjective probability distribution of each horse’s winning chances and a comparison of the mathematical expectation with previous data. Each race can be distinguished by a distribution of the probabilities π_j, as specified by Eq. 9-6. One of several parameters might be chosen as a measure of this distribution; for simplicity, we select the natural and convenient measure of entropy. Thus, we categorize all races according to the entropy H of that race:

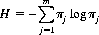
A maximum entropy race is one wherein all horses are accorded identical pari-mutuel probabilities (that is, identical sums are wagered on each horse). A uniform distribution of π_j over the interval 0 to 1 constitutes a minimum-entropy race. By examining records of past races, we can obtain a frequency distribution f(H) (actually a histogram) of pari-mutuel entropies.

For every race, we can then compute the frequency distribution g(π_j) of the pari-mutuel probabilities and therefore the distribution

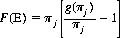
of expectations. Performing this computation over all possible entropies, we can construct a surface of expectation density as a function of entropy. To determine whether to bet on a particular race and on which horses, we first calculate the entropy of the race just prior to its running. For a particular entropy we have a pari-mutuel expectation density profile F₁(E) available from past data. A typical example is illustrated in Figure 9-2. The m pari-mutuel probabilities associated with the m horses are compared with this profile; if one or more values of π_j leads to a positive expectation, a wager on the corresponding horse(s) is advised.

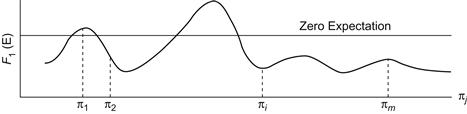
Figure 9-2 Expectation density profile of a particular entropy.

Compilation of data over a limited period of time at several tracks has revealed that a positive expectation usually occurs in races of relatively high entropy. For these situations, horses with odds of 6 to 1, 7 to 1, and 8 to 1 have more often exhibited a positive payoff probability.

Other than lotteries or football pools, horse racing constitutes one of the poorest forms of betting available to the average gambler, owing to the 15+% House Take plus breakage. Overcoming the highly negative mathematical expectation of horse racing poses virtually insurmountable obstacles in terms of acquiring the requisite knowledge, constructing an appropriate model, and performing the attendant computations. Records of the published handicappers indicate a lack of success for all methods based solely on subjective evaluations.

Horseplay

We inquire as to the number of ways, S(n, k), that n horses can cross the finishing line, allowing for all possible ties (Ref. qbyte.org). Here, k is the number of different blocks that describe the finishing order.

We can immediately write the recurrence relation

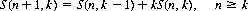
with initial conditions

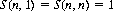
Thus the total number of ways, H_n, that n horses can finish is given by

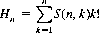
Table 9-2 lists the values of H_n for n ≤ 10.

Table 9-2. Number of Possible Finishes in an n-Horse Race

Duels and Truels

Dueling games, a subset of those games whose key element is timing, constitute another category with interesting ramifications; such games were first conceived and analyzed by Blackwell and Girschick (Ref.). Duels can be either noisy or silent. In the latter case, a player is unaware of the moment his opponent has fired. Duels can also be characterized by the number of bullets each player has at his disposal as well as his firing rate. Further, the bullets may exist only in a probabilistic sense.

In-Place, Noisy Duel, Unlimited Ammunition

One of the simplest forms of dueling constrains the two combatants A and B to remain in place, firing in turn with prescribed accuracies a and b, respectively. Firing continues indefinitely until only one duelist survives (Ref. Knuth).

Letf(a, b) denote the probability that A wins the duel, given that A fires first. Evidently,

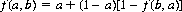
since A wins if his first shot is successful or if his opponent fails. Thus we have the linear equation

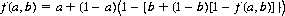
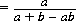
And, of course, A’s probability of winning increases as a increases and decreases as b increases. For equal accuracies, a = b, and f(a, a) = 1/(2 − a); this game is equitable for very low values of a and a certain win for A for values of a approaching 1 (since A fires first).

The probability that B wins the duel, given that A fires first, is

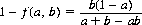
When B fires first, A’s probability of winning is

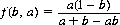
while B’s probability of winning, given that B fires first, is

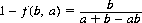
A Variant

In a somewhat more complex variant of the in-place duel, A may select any firing accuracy P. B’s accuracy is 0.5, and he fires first with that same probability P.

IfA selects 1.0, the game is equitable since B is given the first shot; however, A can improve his prospects. To complete A’s optimal value for P, we can express B’s probability of winning as

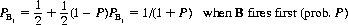
and

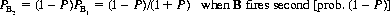
Thus B’s overall probability of winning, P_B, is

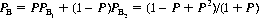
The derivative of P_B with respect to P determines the minimum value of P_B. To wit,

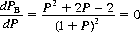
which yields

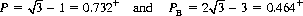
Thus A maximizes his probability of winning at 1 − 0.464⁻ = 0.536⁻ by selecting an accuracy of 0.732⁺. Note that A thereby gains an additional 7.2% over the strategy of selecting P = 1.0.

More generally, if B’s firing accuracy is q, we have

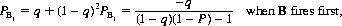
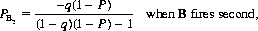
and

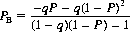
Setting the derivative of P_B with respect to P equal to zero and solving for P, we have

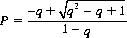
as A’s optimal firing accuracy. If, q = 0, A selects P = 1 (since allowing B to fire first does no harm). If, q = 1, P = 1/2, and the game is equitable.

Noisy Duel, Single Bullet Each

Here, A and B face each other at a distance X₀ at time t₀ and approach each other at a linear rate until X = 0 at time t_f. Each player possesses a single bullet and an accuracy p(t); that is, p_a(t) and p_b(t) are the probabilities that A and B, respectively, will succeed when firing at time t. It is presumed that p(t) is monotonically increasing to a value of unity at t_f. Thus, if one player fires at his opponent at time t < t_f and misses, the opponent’s obvious best course is then to await time t_f, thereby securing a sure kill. In general, if A fires at time t_a, t₀ ≤ t_a ≤ t_f, and B fires at time t_b, t₀ ≤ t_b ≤ t_f, the payoff to A, f(T), can be written in the form

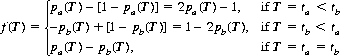(9-9)

where T = min(t_a, t_b). It is straightforward to show that the three forms of Eq. 9-9 take on equal values when

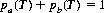(9-10)

Thus, Eq. 9-10 describes a minimax solution to the duel, and both players should fire simultaneously at this value of t (it is assumed that the value of killing an opponent is unity, while the value of being killed is −1). The value γ of the game is given by

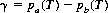
If the two duelists are equally skilled, they should fire when their accuracies reach 0.5; the value of such a game is, of course, zero.

Noisy Duel, Many Bullets, Probabilistic Bullets

If the two duelists possess equal accuracy functions p(t) but different numbers of bullets, their optimal strategies are immediately apparent. Specifically, if A is equipped with b_a(t) bullets, and B with b_b(t) ≤ b_a(t) bullets, an optimal strategy for A consists of firing a bullet when

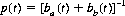(9-11)

If B is accorded fewer bullets, he should shoot only after A’s first firing time and then only if A has not fired. The value γ of this game is expressed by

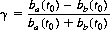(9-12)

where t₀ designates the starting time of the duel.

As an example, if A is initially furnished three bullets and B two bullets, then A should pull the trigger once when the accuracy function reaches the value p(t) = 1/5, as indicated by Eq. 9-11. If A misses, then both A and B fire one shot when p(t) = 1/4, and if both miss, the last bullets should be discharged simultaneously when p(t) = 1/2. Value of the game, from Eq. 9-12, is 1/5 to A.

Blackwell and Girschick (Ref.) considered the case of two duelists with equal accuracy, where each has only a probability of possessing a bullet—P₁ for A and P₂ < P₁ for B. Here A should fire with the density

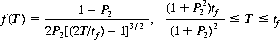
a fraction Γ of the time and should fire at time t_f the remaining fraction 1 − Γ of the time, where

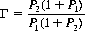
Evidently the moment at which A fires is a function only of his opponent’s probability of possessing a bullet, while the percentage of the time that he fires at that moment is a function of both P₁ and P₂. To obtain the optimal strategy for the case where P₂ > P₁, we simply interchange P₁ and P₂. The value of the game to A is

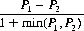
Alternate forms of dueling include silent duels (each gun equipped with a silencer) and duels where one combatant is supplied with both noisy and silent bullets that are fired in a prescribed order. An interesting variant is the machine gun duel, a game that introduces the notion of firing rate. Two players are planted a fixed distance apart and supplied with machine guns; the weapon assigned to A (B) possesses a single-shot hit-probability P_A (P_B) and a firing rate R_A (R_B) shots per unit time. Such a duel has been analyzed by A.D. Groves (Ref.).

Yet other variants of dueling games might include assigning a probability that a hit is not lethal but merely incapacitates the opponent so that his firing power is reduced; mixing live ammunition with blanks according to some probability distribution; multi-person duels, wherein m combatants on one side face n on the other; and handicapped duels—where one player, for example, is deaf (and thus compelled to play a silent duel), while his opponent plays a noisy duel. Further, we propose a “Fire and Flee” duel. In this version, each player is given n bullets and, after observing that some fraction of them have been discharged without felling his opponent, may exercise the option to flee the scene, thereby altering his opponent’s monotonic accuracy function and combining the duel with elements of a pursuit game.

Truels

Three-person games, or “truels,” are inherently more complex than duels and, sensibly, more consonant with real-world situations. The strongest of three players may not find himself in the most advantageous position—indeed, “survival of the weakest” is often a feature of truels, depending on the relative strength of the adversaries.

The format for truels posits three players, A, B, and C, with respective firing accuracies a ≥ b ≥ c, deployed on the vertices of an equilateral triangle, each firing at a player on another vertex or at no one. The firing order—a basic constituent of the game—may be sequential in fixed succession, sequential in random succession, simultaneous, or a function of the players’ firing accuracies (e.g., the least accurate player shoots first). Further, ammunition, and thus the number of rounds, may be limited or unlimited as well as noisy or silent. Pacts may be allowed and may be abrogated.

Consider the truel wherein each player simultaneously selects (and announces) his own accuracy function. A revolving order of firing is determined by an equitable random device. Each player, in designated turn, then fires a single bullet at either or neither of his two opponents (if two are yet alive). The game proceeds until either a single truelist remains or three successive shots are fired into the air. We assign a game value of +1, which is awarded to the survivor (if all three truelists survive, each receives 1/3).

Assuming that no player selects an accuracy less than 0.5, it is apparent that C (the least skilled player) never fires at either opponent if both remain (it is to C’s advantage to fire into the air until one adversary eliminates the other, thereby affording C first shot in the resulting duel). Thus, of the six possible firing echelons, only two are distinct: that in which A precedes B and that in which B precedes A. In either case, A fires at B (no one fires at C first, since he poses the lesser threat) if his mathematical expectation thereby produces a value of 1/3 or greater; otherwise, he fires into the air. Player B must inquire as to A’s expectation from firing (when A precedes B), and if it exceeds 1/3, B fires at A regardless of his own expectation. The winner of the A versus B duel, if it occurs, then engages C to resolve the truel.

The expectation of A, E(A), equals the probability P(A) of that player surviving, which equals the probability P(A → B) that A kills B times the probability P(A → C|A → B) that A kills C, given that A has first dispatched B. We can readily formulate these values. If A precedes B in the order of firing,

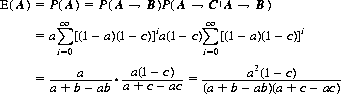(9-13)

Similarly,

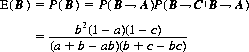(9-14)

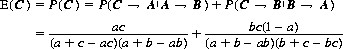(9-15)

If B precedes A in the order of firing,

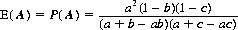(9-16)

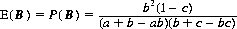(9-17)

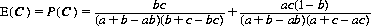(9-18)

Initially, A’s game expectation is given by the average of Eqs. 9-13 and 9-16, B’s expectation by the average of Eqs. 9-14 and 9-17, and C’s expectation by the average of Eqs. 9-15 and 9-18.

It is apparent that B finds himself in the most unenviable position. Each player strives to choose an accuracy function that is (1) the highest possible lowest value of the three accuracies, or (2) the highest accuracy—that is, 1.00. To be caught in the middle is anathema.

As an illustration, let the three players select accuracies a = 1.00, b = 0.75, and c = 0.50, respectively. If A wins a shooting position prior to B’s, he eliminates B with unity probability and then is shot at by C; if C misses (probability 1/2), A dispatches C on the next round. Hence P(A) = 0.50, P(B) = 0, and P(C) = 0.50. If B is selected to shoot first, he must fire at A although his expectation remains less than 1/3. If successful, he competes with C until either survives, with C shooting first; if he misses (probability 1/4), he is eliminated by A, who then engages C to resolve the truel. Player C, if awarded first shot, sends it skyward, thereby guaranteeing himself the first opportunity to eliminate the survivor of the A versus B contest. Equations 9-16, 9-17 and 9-18 yield P(A) = 1/8, P(B) = 9/28, and P(C) = 31/56. Thus, the a priori expectations of the three players with these accuracy functions are

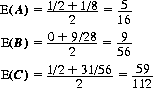
Note that the least effective marksman (C) is most likely to survive, and B the least likely.

Even for this elementary truel, computation of the optimal mixed strategies involves overwhelming arithmetical labor. Further, the definition of rational behavior is not immediately apparent in this type of three-sided competition; thus “optimal” strategy is not clearly defined. As with most multiperson, multimove games, this truel may not enjoy a unique, noncooperative equilibrium point (see Chapter 2).

We therefore introduce two simplifications that permit a complete description of the ensuing game: (1) each player is supplied with but a single bullet that he may fire at another player or into the air; and (2) the order of firing is announced before the accuracy functions are chosen. It is now more convenient to designate the notation A, B, and C as defining the players in their order of firing (rather than by accuracy functions). Evidently, if A fires at either adversary he selects as his target B or C, as b > c or c > b. Player B always shoots at C if the latter still survives or at A otherwise. Player C, if not eliminated before his turn, fires at A or B equiprobably if both remain (independent of their accuracy functions) or at A if B has been killed.

It is apparent that A always adopts the role of a perfect marksman (a = 1.00). By killing B or C, his expectation E_s(A) becomes

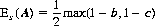
since his game value is 1/2 if the remaining player misses and 0 otherwise [probability min(b, c)]. By shooting into the air, A receives value 1/2 with probability b + (c/2)(1 − b), value 0 with probability (c/2)(1 − b), and value 1/3 with probability (1 − b)(1 − c). His expectation E_n(A) in this case is therefore given by

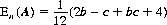
(We assume that C holds no grudges in deciding at whom he shoots.) Thus, A eliminates that opponent owning the higher accuracy function whenever E_s(A) > E_n(A). The values of b and c whereby this condition holds are indicated in Figure 9-3.

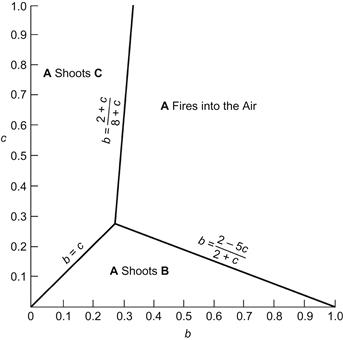
Figure 9-3 A truel firing diagram.

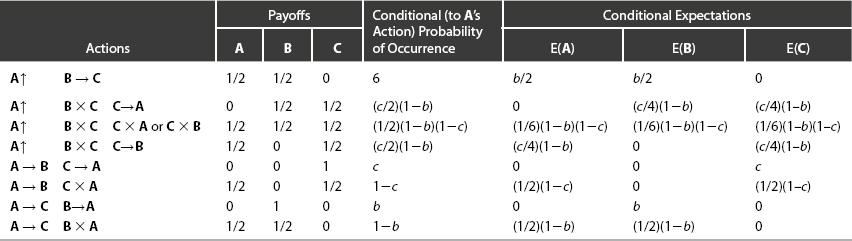
The overriding consideration for both B and C is that each wishes to select an accuracy function smaller than the other, thus diverting the fire of A if (b, c) lies within A’s firing region. From C’s viewpoint, lesser accuracies are even more attractive, since he must still worry over B’s shot if A fires into the air. Payoffs and conditional expectations for each action are shown in Table 9-3—the notation A↑ signifies that A fires into the air, and B × C denotes that B shoots at but misses C. From this table we can write for E(B|A↑), B’s expectation, given that A fires into the air,

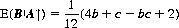(9-19)

Also

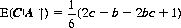(9-20)

Table 9-3. Truel Payoffs and Conditional Expectations

If collusion were permitted or were mutually advantageous between B and C, Eqs. 9-19 and 9-20 indicate that b = 1/3 and c = 1.00 result in an equitable game [E(A) = E(B) = E(C)]. However, the point (b, c) = (1/3, 1) does not represent an equilibrium point, since if either B or C deviates from this point by lowering his accuracy, the concomitant expectation increases (as A then fires at the other player). Consequently, the only “stable” point for B and C arises from the selection b = c = 0. Thus, B and C declare themselves totally impotent, and the value of the truel is 1/2 to A and 1/4 to B and C. This solution does not preclude the existence of other equilibrium points (e.g., those involving “bluffing” or “deterring”). Since it is possible here for two players to gain even by nonexplicit cooperation and lose by individual action, this truel constitutes a nonzero-sum game. The theory of games has yet to develop a completely satisfactory methodology for the solution of cooperative games.

Pacts (Ref. Kilgour and Brams)

Consider the truel defined by a = 0.8, b = 0.7, and c = 0.55. The respective survival probabilities for the players are P_A = 0.22, P_B = 0.16, and P_C = 0.62. Now suppose that A and B, dismayed by the supremacy of their weakest competitor, negotiate a pact obliging each of them to fire at C until C is eliminated (whence they will engage in their own duel). Under that circumstance,

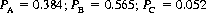
averaged over all six permutations of the firing order. C’s expectation has now declined precipitously, while B’s has risen from lowest to highest (since C, in accordance with the SASO [Shoot at the Stronger Opponent] strategy, will fire at A as long as both survive), and A has benefited considerably—confirming the wisdom of the pact.

Yet in the Hobbesian universe inhabited by game theorists, B calculates that he can improve his survival probability further (albeit marginally) by reneging on his agreement, assuming that A will initially adhere to the pact. Under this premise, B will fire at A at his first opportunity, and A, in all subsequent turns, will return fire at B (assuming that C has not dispatched A in the interim). Their respective survival probabilities now take on the values

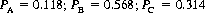
However, if A, anticipating that B will not honor the pact, reneges first (while B continues to fire initially at C), their respective survival probabilities are

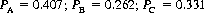
Only C, with no alternative, will steadfastly adhere to the SASO strategy. C’s survival probability will decrease drastically in the event of an honored pact between A and B, albeit to a lesser degree if either A or B violates the pact.

This particular example illustrates the general instability that can arise in multiperson games (as opposed to duels), an instability often reflected in the maneuvering of international relationships where a weak nation may gain the advantage over two more powerful competitors, each more fearful of the other.

Truels constitute a unique set of games in that all participants in the truel may maximize their expected payoffs by not firing. This situation does not pertain in duels—where one person’s gain is another’s loss—or in polyuels with four or more persons. In an N-uel game, it becomes yet more improbable for the player with the highest marksmanship to win out (since N − 1 guns will be trained on him). Usually, in an N-uel, combatants can be eliminated with advantage until the game is reduced to a truel.

Tournaments

Elimination

Of the various procedures for selecting a winner from among many contestants, perhaps the most common is the single elimination, or knockout, tournament. Players are matched pairwise for a single game, and the winners of each round advance to the succeeding round (such games cannot end in a tie). A particular configuration for matching the contestants is known as a draw. With 2ⁿ players in the tournament, there are 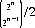ways of setting up the first round, and the total number of draws is, therefore,

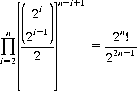
The tournament comprises 2ⁿ − 1 games with 2^{2 n−1} possible outcomes for each draw (the total number of outcomes for all draws is, of course, 2ⁿ!).

The probability that a given player wins the tournament following a random draw is simply his probability of winning n matches in succession averaged over all possible draws. Let p_ij be the pairwise win probability that the ith player defeats the jth player in a single trial, and as an example consider a tournament of eight players (n = 3) possessing the set of pairwise win probabilities shown in Table 9-4. Averaging over the 315 draws, we compute the probabilities P(i) that the ith player wins the tournament:

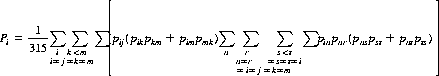(9-21)

Evaluating Eq. 9-21 for each i, using the sample pairwise win probabilities, the results are listed in the first column of Table 9-5.

Table 9-4. Illustrative Set of Pairwise Win Probabilities

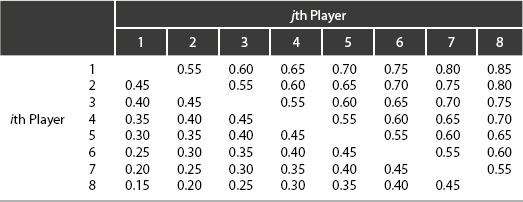
Table 9-5. Probability of a Tournament Win

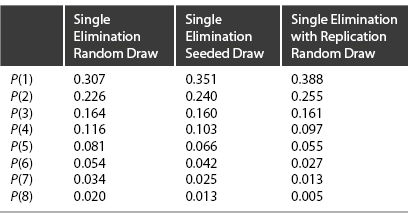
More often, the draw for a tournament is not selected at random but is designed to favor the better players. Such an arrangement, known as a seeded draw, is sketched in Figure 9-4. With the same set of pairwise win probabilities, the probabilities P(i) that the ith player emerges victorious become those shown in the second column of Table 9-5. As expected, the better players gain increased chances of winning, and the poorer players decreased chances.

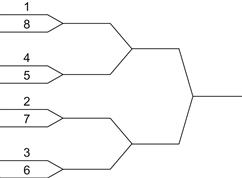
Figure 9-4 The seeded draw.

We can also compute the probability of the two best players entering the finals as 0.128 for a random draw and 0.258 for the seeded draw. This difference accounts for the attractiveness of the seeded draw in many professional sports (such as tennis).

If the number of players in a tournament is not exactly 2ⁿ, then one or more pseudo players are concocted and awarded win-probabilities of zero. A real player thus wins with probability one against a pseudo player and is said to have a “bye.” When i and j are both pseudo players, p_ij = p_ji = 0 (hence all byes are confined to the first round).

One method of improving the single elimination tournament (insofar as favoring the better players) consists of adding replication to each match. With this procedure each pair of players competes until one has won m games out of a possible 2m − 1. If p_ij is the probability that i defeats j in a single contest, the probability q_ij that i wins the best m out of a possible 2m − 1 is

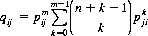
This type of tournament affords yet further advantage to the better players since we can show that, for p_ij ≥ 1/2, q_ij ≥ p_ij. Letting each competition be resolved by the best two out of three matches, and with our illustrative set of (single-trial) pairwise win probabilities (see Table 9-4), the distribution of final win probabilities for each player is that of the third column of Table 9-5. The extent to which superior players are favored by replication (or seeded draws) is, of course, strongly dependent upon the particular pairwise win-probabilities of the competing players.

Double elimination, or double knockout, tournaments also constitute a common format for handling a large number of competitors. Here, after the first round, the winning players are grouped in a W bracket, losing players in an L bracket. The W bracket is then conducted as a single-elimination tournament except that the losers of each round drop down to the L bracket. A loser in an L-bracket match is eliminated. Thus one-fourth of the contestants are eliminated at each round following the first. Ultimately, the W-bracket winner contends against the L-bracket winner, needing a single victory to win the tournament, while the L-bracket winner requires two wins to emerge victorious.

Double-elimination tournaments offer the advantage that the third and fourth places can be determined without recourse to a “consolation” match. Further, the higher-rated players (teams) are more likely to advance.

Another format is that of serial elimination—characterized as a single elimination tournament with 2ⁿ players followed by a second single elimination playoff among the winner and those n players beaten by the winner. If the winner does not also win the playoff, an additional game between the original winner and the playoff winner determines the ultimate victor. Serial elimination tournaments with replication can, of course, also be conducted. These tournaments have been investigated by D.T. Searls (Ref.) and by W.A. Glenn (Ref.).

Games Played

Since, in an N-player single-elimination tournament, there is a one-to-one correspondence between the number of games played and the number of losers, there are N − 1 games played to resolve a winner. Similarly, the number of games played in an N-player double-elimination tournament will be either 2(N − 1) or 2(N − 1) + 1, depending on whether the winner has no losses or one loss, respectively.

In general, for an N-person, M-tuple-loss tournament, (Ref. Bernander and Bernander) the number of games played is determined from the fact that all players except the winner will lose m games—for a total of M(N − 1) games. The winner will have experienced either 0, 1, …, or m − 1 losses. The number of games played, therefore, is

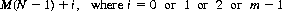(9-22)

The World Series of baseball constitutes a two-team, four-loss elimination tournament. Thus the total number of games played, as per Eq. 9-22, is 4, 5, 6, or 7 (see Chapter 5).

Round-Robin

Procedures (whereby each player vies against every other player a fixed number of times) are not generally efficient as elimination tournaments. However, the round-robin⁷ does exhibit some capability in this regard.

Mathematically, a round-robin tournament is a directed graph (digraph) obtained by choosing a direction for each edge in an undirected complete graph. The score of each node is its “outdegree”—i.e., the number of outward directed graph edges from a given vertex in the digraph. We define a score sequence, S₁, S₂, …, S_N, satisfying the following three conditions:

1. 0 ≤ S₁ ≤ S₂ ≤ … ≤ S_N

2. S₁ + S₂ + … + S₁ ≥ S_i for i = 1, 2, …, N − 1

3. S₁ + S₂ + … + S_N =

The number of different score sequences possible in an N-person round-robin tournament are, for N = 1, 2, …,

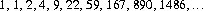
It should be noted that a score sequence does not uniquely resolve a tournament (Ref. Harary and Moser).

As one example, consider a round-robin tournament with N = 4 contestants. There are four possible outcomes (with six matches played):

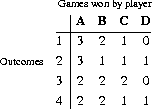
The first two outcomes declare A the winner; the third and fourth outcomes eliminate one and two players, respectively, and require further competition.

With five players, a single round-robin procedure may produce any of nine outcomes, five of which uniquely proclaim a winner; with six players, 13 of a possible 22 outcomes designate a winner; a round-robin of seven players admits of 59 possible outcomes, 35 of which specify a winner; and with eight players, there are 100 such outcomes of a possible 167.

Obviously the probability of each outcome is a function of the players’ pairwise win probabilities. If p_ij = p_ji = 1/2 for all i and j, the single round-robin tournament with four players has the following distribution of outcomes:

Hence the probability p of determining a winner in this four-player tournament is 0.5; with five players, p = 0.586; with six players, p = 0.627; a seven-player round-robin is uniquely resolved with probability p = 0.581; and with eight evenly matched players, p = 0.634. As the number of players increases indefinitely, the probability of obtaining a unique outcome approaches unity.

If one player has a high win probability against each of his adversaries, his probability of winning the tournament is generally greater from a round-robin than from a single elimination procedure.

Pairings

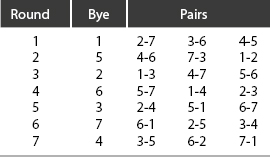
With 2n − 1 players (or teams) labeled 1, 2, …, 2n − 1 entered in a round-robin tournament, the general pairings are arranged as in Table 9-6.

Table 9-6. General Round-Robin Pairings

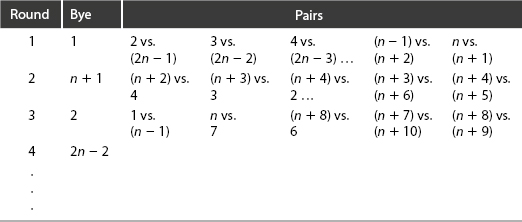
For n = 4, the seven players 1, 2, …, 7 are matched up as shown in Table 9-7.

Table 9-7. Seven-Player Round-Robin Pairings

Random Tic-Tac-Toe

An alternative to the pure-strategy forms of Tic-Tac-Toe (Chapter 10) was proposed by F.E. Clark (Ref.). From the set of nine numbers, 1, 2, … 9, A selects one at random and places an X in the corresponding square of the 3 × 3 Tic-Tac-Toe matrix (see Figure 10-1). B then randomly selects one of the eight remaining numbers and enters an O in the corresponding square, and so forth. The standard objective pertains: to configure three Xs (Os) in a straight line.

There are 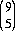= 126 possible configurations for A if the game is played through all nine moves (though rotational and mirror symmetries leave only 17 unique positions). Of the total number of configurations, only 16 will draw (probability 0.127)—since a draw requires B to have at least one O in a corner, and each corner placement leaves four combinations for his other three Os. Also, A will lose whenever B completes either of the two diagonals, there being six possibilities for each—i.e., 12 losses for A.

Further, there are 36 configurations with three Xs and three Os in a straight line. Six columns or rows can be completed by A, and two by B. Accordingly, of the 36 configurations, A will win

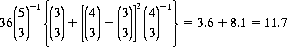
and will lose 36 − 11.7 = 24.3. A’s total losses, then, are 24.3 + 12 = 36.3, for a loss probability of 0.288; his wins total 126 − 16 − 36.3 = 73.7, for a win- probability of 0.585.

The game presents a value of 0.390 to A. He can offer B a 2-to-1 payoff and still retain a positive expectation.

The probability that A wins with his third, fourth, or fifth X is 2/21, 37/140, and 71/315, respectively. The probability that B wins with his third or fourth O is 37/420 and 1/5, respectively.

Inquizition

Solutions to the three following statistical problems are beyond the reach of all but the most agile game theorists. In each case, only partial analysis can be readily achieved.

1. The Harem-Staffing Problem. From a supply of n candidates, the Sultan wishes to select m maidens for his harem. The n aspirants are paraded one by one before the Sultan, each being either selected or rejected—and once rejected, cannot be recalled. Since m nymphs must be chosen, the final few may be forced upon the Sultan to complete the seraglio complement. A preference ordering of the candidates is assumed although not known a priori. What function of the girls’ desirability should the Sultan adopt as his objective, and what is his concomitant strategy?Note: For m = 1, assuming that the Sultan wishes to maximize his probability of engaging the “best” candidate, he assigns a utility of 1 to this girl and 0 to all others. Show that his optimal strategy consists of rejecting the first n/e candidates (for large n) and then selecting the first one who exceeds the best of that sample; if no better one appears, he is stuck with the final girl. Show also that his expected utility for this objective is approximately e⁻¹.

2. A Truel in the Sun. Each of three players, A, B, and C (with respective firing accuracies P_A, P_B, and P_C) fires in cyclical order (or abstains from firing) only at his successor in the order. After one truelist is eliminated, the remaining two duel until one is eliminated.Compute the players’ winning probabilities when P_A = P_B = P_C = p = 1/2. Determine the values of p for which the game degenerates into perpetual abstentions.

3. Martini Golf. The object of the game of golf is to impel a small white ball into a slightly larger hole with a minimum number of strokes delivered by means of a set of specialized clubs. We designate by p_a(n) and p_b(n) the probabilities that A and B, respectively, require n strokes for a given hole. Whenever a player wins a hole (by using fewer strokes than his opponent), he must consume one martini. After j martinis, A’s probability distribution p_a^j(n) of holing out in n strokes becomes

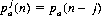
and, similarly,

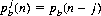
Compute the probability that A has taken fewer strokes after a round of 18 holes.If one player is permitted to add strokes deliberately, and the lower score on each hole wins one unit while the lower final score wins m units, what strategy should he follow to maximize his expected gain?

REFERENCES

Abbott Derek, (2009). Developments in Parrondo’s Paradox. In: In V, Longhini P, Palacios A, eds. Applications of Nonlinear Dynamics. Springer-Verlag: 307–321. .

Alexander SS, (1964). Price Movements in Speculative Markets: Trends or Random Walks. In: Cootner P, ed. The Random Character of Stock Market Prices. MIT Press: 338–372. .

Ali Mukhtar M, (1997). Probability and Utility Estimates for Racetrack Bettors. Journal of Political Economy.85:803–815.

Amengual Pau, Toral Raul, (2006). Truels or Survival of the Weakest. Computing in Science and Engineering.:88–95 [September–October].

Ancker CJ, (1964). Stochastic Duels With Limited Ammunition Supply. Operations Research.12(1):38–50.

Arvesen James N, Rosner Bernard, (1971). Optimal Pari-Mutuel Wagering. [Mimeograph Series #250] Department of Statistics, Purdue University [February].

Bachelier Louis, (1900). Théorie de la Spéculation. Gauthier-Villars.

Bauer RJ, (1994). Genetic Algorithms and Investment Strategies. Wiley.

Bernander Alan C, Bernander Barbara A, (1987). N-team, M-loss Elimination Tournaments. Journal of Recreational Mathematics.19(4):266–267.

Black F, Scholes M, (1973). The Pricing of Options and Corporate Liabilities. Journal of Political Economy.:637–654 [May–June].

Black F, Scholes M, (1972). The Valuation of Option Contracts and a Test of Market Efficiency. Journal of Finance.:399–417 [May].

Blackwell David, Girshick MA, (1949). A Loud Duel with Equal Accuracy Where Each Duellist Has Only a Probability of Possessing a Bullet. [Research Memorandum RM-219] The RAND Corporation.

Borel Emile, (1943). Les Probabilités et la Vie. Presses Universitaires de France.

Chen S-H, Yeh C-H, (1997). Speculative Trades and Financial Regulations: Simulations Based on Genetic Programming. Proceedings of the IEEE/IAFE 1997 Computational Intelligence for Financial Engineering (CIFEr).:123–129 [March].

Clark FE, (1959). Tic-Tac-Toe as a Game of Chance (Solution by T.M. Little). American Mathematics Monthly.66(2):144–145.

Clippenger, Don., ed., Thoroughbred Times Racing Almanac, Thoroughbred Times Co. Inc., Bow Tie Inc., 1985.

Cootner Paul H, (1962). Stock Prices: Random Versus Systematic Changes. Industrial Management Review.3:24–25.

Cootner Paul H, ed. The Random Character of Stock Market Prices. MIT Press.

Cowles Alfred, (1933). Can Stock Market Forecasters Forecast?. Econometrica.1:309–324.

David HA, (1959). Tournaments and Paired Comparisons. Biometrika.46:139–149.

Dresher Melvin, (1961). Games of Strategy—Theory and Applications. Prentice-Hall.

Eisenberg Edmund, Gale David, (1959). Consensus of Subjective Probabilities: The Pari-Mutuel Method. Annals of Mathematical Statistics.39(1):165–168.

Fabricand Burton P, (1979). The Science of Winning. Van Nostrand Reinhold.

Fama, E. F., “The Distribution of the Daily First Differences of Stock Prices: A Test of Mandelbrot’s Stable Paretian Hypothesis,” Doctoral Dissertation, University of Chicago, 1963.

Fisher Lawrence, (1965). Outcomes for ‘Random’ Investments In Common Stocks Listed on the New York Stock Exchange. The Journal of Business of the University of Chicago.38(2):149–161.

Glenn WA, (1960). A Comparison of the Effectiveness of Tournaments. Biometrika.47:253–262.

Godfrey MD, Granger CWJ, Morgenstern O, (1964). The Random Walk Hypothesis of Stock Market Behavior. Kylos.17:22–30.

Goldberg DE, (1989). Genetic Algorithms in Search Optimization and Machine Learning. Addison-Wesley.

Granger CWJ, Morgenstern Oskar, (1963). Spectral Analysis of New York Stock Exchange Prices. Kylos.16:1–27.

Groves, Arthur D., “The Mathematical Analysis of a Simple Duel,” Ballistic Research Laboratories, Report 1261, August 1964.

Harary Frank, Moser Leo, (1966). The Theory of Round-Robin Tournaments. American Mathematics Monthly.73(3):231–246.

Isaacs Rufus P, (1953). Optimal Horse Race Bets. American Mathematics Monthly.60(5):310–315.

Jackson, J. T. Ross., “Some Speculative Strategies in the Stock Market,” Doctoral Dissertation, Case Institute of Technology, 1964.

Kahn Herman, Mann Irwin, (1957). Game Theory. [RAND Report P-1166] The RAND Corporation [July].

Kassouf Sheen T, (1969). An Econometric Model for Option Price with Implications for Investors’ Expectations and Audacity. Econometrica.37(4):685–694.

Kemeny, John G., and Gerald L. Thompson, The Effect of Psychological Attitudes on the Outcomes of Games, Contributions to the Theory of Games, 3, in Annals of Mathematics Studies, No. 39, pp. 273–298, Princeton University Press, 1957.

Kilgour D Marc, Brams Steven, (1997). The Truel. Mathematics Magazine.70(5):315–326.

Knuth Donald F, (1973). The Truel: A New Solution. Journal Recreational Mathematics.6(1):1–7.

Koch, Alexander K., and Shing, Hui-Fai., Bookmaker and Pari-Mutuel Betting: Is a (Reverse) Favourite-Longest Bias Built In? Royal Holloway, University of London, Discussion paper No. 2007-4, November 2007.

Koza JR, (1992). Genetic Programming: On the Programming of Computers by Means of Natural Selection. MIT Press.

Leunberger DG, (1998). Investment Science. Oxford University Press.

Mandelbrot Benoit, (1963). The Variation of Certain Speculative Prices. Journal of Business.36(4):394–419.

Marsili Matteo, Maslov Sergei, Zhang Yi-Cheng, (1998). Dynamical Optimization Theory of a Diversified Portfolio. Physica A.253:403–418.

Maslov Sergei, Zhang Yi-Cheng, (1998). Optimal Investment Strategy for Risky Assets. International Journal of Theoretical and Applied Finance.1(3):377–387.

McLaughlin, Michael P., “A Tutorial on Mathematical Modeling,”www.causascientia.org/software/regress_plus.html.

Mosteller Frederick, (1952). The World Series Computer. Journal of American Statistical Association.47(259):355–380.

Narayana TV, Best DH, (1964). Computation of the Number of Score Sequences in Round Robin Tournaments. Canadian Mathematics Bull..7:133–136.

Nick’s Mathematical Puzzles, www.qbyte.org/puzzles/p131s.html.

Niederhoffer Victor, (1965). Clustering of Stock Prices. Operations Research.13(2):258–265.

Oussaidene Mouloud, Chopard B, Pictet O, Tomassini M, (1997). Parallel Genetic Programming and its Application to Trading Model Induction. Parallel Computing.23(8):1183–1198.

Pareto Vilfredo, (1927). Manuel d’Economie Politique. Giard et Brièie.

Parker, Mike., “The History of Horse Racing,” 1998, www.mrmike.com/explore/hrhist.htm.

Samuelson Paul A, (1965). Rational Theory of Warrant Pricing. Industrial Management Rev..6(2):13–31.

Samuelson Paul A, Merton Robert C, (1969). A Complete Model of Warrant Pricing that Maximizes Utility. Industrial Management Review.10(2):17–46.

Schwenk Allen J, (2000). What Is the Correct Way to Seed a Knockout Tournament?. The Mathematical Association of America.:pp. 140–150 [February].

Searls Donald T, (1963). On the Probability of Winning with Different Tournament Procedures. Journal of American Statistical Association.58:1064–1081 [December].

Shapley Lloyd S, (1963). Some Topics in Two-Person Games. [RAND Memorandum RM-3672–1-PR] The RAND Corporation [October].

Shapley Lloyd S, (1961). Values of Large Games, III: A Corporation With Two Large Stockholders. [RAND Memorandum RM-2650-PR] The RAND Corporation [December].

Shubik Martin, (1954). Does the Fittest Necessarily Survive?. In: Shubik Martin, ed. Readings in Game Theory and Political Behavior. Doubleday & Co.: 43–46. .

Smith Gerald, (1965). A Duel with Silent Noisy Gun versus Noisy Gun. University of California, Department of Mathematics [June].

Thorp, Edward O., and Sheen T. Kassouf, Beat the Market, Random House, 1967.

Thorp Edward O, (1973). Extensions of the Black-Scholes Option Model. Vienna: 39th Session of the International Statistical Institute; [August pp. 1029–1036].

Thorp Edward O, (1975). Portfolio Choice and the Kelly Criterion. In: Ziemba WT, Vickson RG, eds. Stochastic Optimization Models in Finance. Academic Press: 599–619. .

Tsang Edward PK, Butler James M, Li Jin, (1998). EDDIE Beats the Bookies.28(10):1033–1043.

Weisstein, Eric W., Score Sequence, http://mathworld.wolfram.com/ScoreSequence.html.

Windle David, (1993). Multiple Criteria Decision Making Applied to Horse Racing. Teaching Statistics.15(2):34–37.

Yu Philip, Cowan Richard, (1995). Statistical Models of Duplicate Tournaments in Games of Luck and Skill. Australian Journal of Statistics.37(1):1–17.

Bibliography

Ali Mukhtar M, (1998). Probability Models on Horse Race Outcomes. Journal of Applied Statistics.25(2):221–229.

Asch Peter, Malkiel Burton G, Quandt Richard E, (1984). Market Efficiency in Racetrack Betting. The Journal of Business.57(2):165–175.

Bedford, Julian., The World Atlas of Horse Racing, 1989.

Boulier Bryan L, Stekler HO, (38; Stekler (2003). Predicting the Outcomes of National Football League Games. International Journal of Forecasting.19(2):257–270.

Bueno de Mesquita Bruce, (2003). The Logic of Political Survival. MIT Press.

Bruss F Thomas, Ferguson Thomas S, (2002). High Risk and Competitive Investment Models. Annals of Applied Prob..12:1202–1226.

Crafts Nicholas FR, (1985). Some Evidence of Insider Knowledge in Horse Race Betting in Britain. Economica New Series.52(207):295–304.

Da Silva ER, Dorcus Roy M, (1961). Science in Betting. Harper.

Dorfman Robert, Samuelson Paul A, Solow Robert M, (1958). Linear Programming and Economic Analysis. McGraw-Hill.

Dowie Jack, (1976). On the Efficiency and Equity of Betting Markets. University of Kent Economica New Series.43(170):139–150.

Edelman David, (2007). Kalman-Filtered Radial Basis Function Networks for Horserace Odds Estimation. In: Ethier Stewart, Eadington William, eds. Optimal Play, Mathematical Studies of Games and Gambling. Institute for the Study of Gambling and Commercial Gaming, University of Nevada: 417–429. .

Fama Eugene F, Blume Marshall E, (1966). Filter Rules and Stock-Market Trading. The Journal of Business of the University of Chicago.39(1, Pt. 2):226–241.

Fisher Lawrence, Lorie James H, (1964). Rates of Return on Investments in Common Stocks. The Journal of Business of the University of Chicago.37(1):1–21.

Girshick MA, (1949). A Generalization of the Silent Duel, Two Opponents, One Bullet Each, Arbitrary Accuracy. [Research Memorandum RM-206] The RAND Corporation [August].

Goldberg DE, (1989). Genetic Algorithms in Search Optimization and Machine Learning. Addison-Wesley.

Golen, R. H., and W. Ziarko, “A Methodology of Stock Market Analyses Utilizing Rough Set Theory,” in Computational Intelligence for Financial Engineering, pp. 32–40, Proceedings of the IEEE/AAFE, 1995.

Green Donald P, Shapiro Ian, (1996). Pathologies of Rational Choice Theory. Yale University Press.

Harville David, (1977). The Use of Linear-Model Technology to Rate High School or College Football Teams. Journal of the American Statistical Association.72(358):278–289.

Huff Darrell, (1954). How to Lie with Statistics. W.W. Norton & Co.

Kelber Michael, (2005). Goldbug Variations. Mathematical Intelligencer.27(1):1–20.

Llorente Loreto, (2006). A Profitable Strategy in the Pelota Betting Market. In: Ethier Stewart, Eadington William, eds. Optimal Play, Mathematical Studies of Games and Gambling, Institute for the Study of Gambling and Commercial Gaming. University of Nevada: 399–415. .

Mandelbrot Benoit, Hudson Richard L, (2004). The (Mis)Behavior of Markets: A Fractal View of Risk, Ruin, and Reward. Basic Books.

Maher MJ, (1982). Modeling American Football Scores. Statistica Neerlandica.36(3):109–118.

Miller Steven J, (2007). The Pythagorean Won-Loss Formula in Baseball. Chance Magazine.20(1):40–48.

Moon JW, (1968). Topics on Tournaments. Holt.

Orrell David, (2007). Apollo’s Arrow: The Science of Prediction and the Future of Everything. HarperCollins.

Romer David, (2003). It’s Fourth Down and What Does the Bellman Equation Say? A Dynamic Analysis of Football Strategy. Econometrics Laboratory Software Archive, University of California-Berkeley [February].

Sahi Siddharta, Shubik Martin, (1988). A Model of a Sudden Death Field-Goal Football Game as a Sequential Duel. Mathematical Social Sciences.15:205–215 [June].

Samuelson Paul A, (1983). Foundations of Economic Analyses. [1947; enlarged edition, 1983] Harvard University Press.

Samuelson Paul A, (1957). International Price Equilibrium: A Prologue of the Theory of Speculation. Weltwirtschaftliches Archiv.79:181–221.

Schneweiss Thomas, Spurgin Richard, (1988). Multifactor Analysis of Hedge Fund, Managed Futures, and Mutual Fund Return and Risk Characteristics. The Journal of Alternative Investments.(Nos. 1 & 2):1–34.

Skierna Steven S, (2001). Calculated Bets: Computers, Gambling, and Mathematical Modeling to Win. Cambridge University Press.

Snyder Wayne W, (1978). Horse Racing: Testing the Efficient Markets Model. Journal of Finance.33(4):109–118.

Thaler RH, Ziemba WT, (38; Ziemba (1988). Parimutuel Betting Markets: Racetracks and Lotteries. Journal of Economic Perspectives.2(2):161–174.

Thorp Edward O, (1975). Options in Institutional Portfolios: Theory and Practice. Proceedings of the Seminar on the Analysis of Security Prices, Center for Research in Security Prices.:229–251 [May].

Van Huyck J, Battalio Raymond C, Beil Richard O, (1991). Strategic Uncertainty, Equilibrium Selection, and Coordination Failure in Average Opinion Games. The Quarterly Journal of Economics.106(3):885–910.

¹ So-called from the custom of English brokers of recording transactions by duplicating notches in two wooden stocks (the customer retained one stock and the broker the other; a matching of the notches presumably ensured honesty).

² In addition to the New York exchange, there are ten registered exchanges in the United States plus three Canadian exchanges.

³ English, Australian, and Japanese horses, among others, often race in clockwise fashion.

⁴ Totalizators are normally limited to the issuance of 12 different tickets. With 13 or more horses going to the post, two or more are coupled together as a betting unit, either because they share common ownership or because they are labeled as “field horses” (a group defined by their long odds).

⁵ An illustration of the sensitivity of the pari-mutuel system is supplied by the so-called builder play, a betting coup whereby some members of a gang obstruct the mutuel windows at a track, placing small wagers on unlikely winners, while confederates are placing large wagers with off-track bookmakers on the more probable winners. Notable builder plays include the 1964 coup at the Dagenham (East London) Greyhound Stadium and a 1932 feat staged at the Agua Caliente (Mexico) racetrack. In the latter instance, odds on the winning horse (Linden Tree) were increased from a logical 7 to 10 to almost 10 to 1. The Dagenham coup was better organized, allowing only a single on-track ticket to be sold on the winning combination (Buckwheat and Handsome Lass), yielding pari-mutuel payoff odds of 9872 to 1.

⁶ Evolutionary Dynamic Data Investment Evaluator.

⁷ From 17th-century French, ruban rond (round ribbon). Petitioners against authorities would append their names in a nonhierarchical circle—thus preventing identification of anyone as the ringleader.