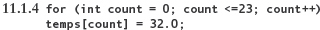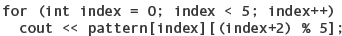11
Arrays
KNOWLEDGE GOALS
 To understand the structure of a one-dimensional array.
To understand the structure of a one-dimensional array.
 To know how to use a one-dimensional array in solving a problem.
To know how to use a one-dimensional array in solving a problem.
 To understand the structure of arrays of records.
To understand the structure of arrays of records.
 To know how index values can be chosen to have semantic content.
To know how index values can be chosen to have semantic content.
 To understand the structure of a two-dimensional array.
To understand the structure of a two-dimensional array.
 To understand the structure of a multidimensional array.
To understand the structure of a multidimensional array.
SKILL GOALS
To be able to:
 Declare a one-dimensional array, with and without initialization.
Declare a one-dimensional array, with and without initialization.
 Perform fundamental operations on one-dimensional arrays.
Perform fundamental operations on one-dimensional arrays.
 Apply subarray processing to a one-dimensional array.
Apply subarray processing to a one-dimensional array.
 Declare a two-dimensional array.
Declare a two-dimensional array.
 Perform fundamental operations on a two-dimensional array.
Perform fundamental operations on a two-dimensional array.
 Use arrays as parameters and arguments.
Use arrays as parameters and arguments.
 Declare and process a multidimensional array.
Declare and process a multidimensional array.
Data structures play an important role in the design process. The choice of data structure directly affects the design because it determines the algorithms used to process the data. In Chapter 10, we saw how the record (struct) gave us the ability to refer to an entire group of components by one name. This simplifies the design of many programs.
In many problems, however, a data structure has so many components that it is difficult to process them if each component must have a unique member name. For example, suppose we needed to represent a collection of 100 integer values, such as the male and female population figures for each state. If we used a struct to hold these values, we would have to invent 100 different member names. Then we would have to write 100 input statements to read the values and 100 output statements to display them—an incredibly tedious task! An array—the third of the structured data types supported by C++—allows us to program operations of this kind with ease.
11.1 One-Dimensional Arrays
If we want to input 1000 integer values and print them in reverse order, we could write a program of this form:

This program is more than 3000 lines long, and we have to use 1000 separate variables. Note that all the variables have the same name except for an appended number that distinguishes them. Wouldn’t it be convenient if we could put the number into a counter variable and use For loops to go from 0 through 999, and then from 999 back down to 0? For example, if the counter variable is number, we can replace the 2000 original input/output statements with the following four lines of code (where highlighted below, we enclose number in brackets to set it apart from value):

This code fragment is correct in C++ if we declare value to be a one-dimensional array. A one-dimensional array is a collection of variables—all of the same type—in which the first part of each variable name is the same, and the last part is an index value enclosed in square brackets. In our example, the value stored in number is called the index.
The declaration of a one-dimensional array is similar to the declaration of a simple variable (a variable of a simple data type), with one exception: You also declare the size of the array—that is, the number of values it can hold. To do so, you indicate within brackets the number of components in the array:
int value[1000];
This declaration creates an array with 1000 components, all of type int. The first component has index value 0, the second component has index value 1, and the last component has index value 999.
Here is the complete ReverseNumbers program, using array notation. It is certainly much shorter than our first version of the program.

Here is the input and the output for our program. We changed the array to be just 10 numbers long to keep from having to enter 1000 data values! Note that we show the input and output in two columns to save space.
Input |
Output |
1 |
10 |
2 |
9 |
3 |
8 |
4 |
7 |
5 |
6 |
6 |
5 |
7 |
4 |
8 |
3 |
9 |
2 |
10 |
1 |
As a data structure, an array differs from a struct in two fundamental ways:
1. An array is a homogeneous data structure (all of its components are of the same data type), whereas structs are heterogeneous types (their components may be of different types).
2. A component of an array is accessed by its position in the structure, whereas a component of a struct is accessed by an identifier (the member name).
Let’s now define arrays formally and look at the rules for accessing individual components.
Declaring Arrays
A one-dimensional array is a structured collection of components (often called array elements) that can be accessed individually by specifying the position of a component with a single index value. (Later in this chapter, we introduce multidimensional arrays, which are arrays that have more than one index value.)
One-dimensional array A structured collection of components, all of the same type, that is given a single name. Each component (array element) is accessed by an index that indicates the component’s position within the collection.
Here is a syntax template describing the simplest form of a one-dimensional array declaration:
ArrayDeclaration

In the syntax template, DataType describes what is stored in each component of the array. Array components may be of almost any type, but for now we limit our discussion to atomic components.
In the syntax template, ConstIntExpression is an integer expression composed only of literal or named constants. This expression, which specifies the number of components in the array, must have a value greater than 0. If the value is n, the range of index values is 0 through n – 1, not 1 through n. For example, the declarations

FIGURE 11.1 angle and testScore Arrays
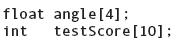
create the arrays shown in FIGURE 11.1. The angle array has four components, each capable of holding one float value. The testScore array has a total of ten components, all of type int.
Accessing Individual Components
Recall that to access an individual component of a struct or class, we use dot notation—the name of the struct variable or class object, followed by a period, followed by the member name. In contrast, to access an individual array component, we write the array name, followed by an expression enclosed in square brackets. The expression specifies which component to access.
ArrayComponentAccess

The index expression may be as simple as a constant or a variable name or as complex as a combination of variables, operators, and function calls. Whatever the form of the expression, it must result in an integer value. Index expressions can be of type char, short, int, long, or bool, because these are all integral types. Additionally, values of enumeration types can be used as index expressions, with an enumeration value implicitly being coerced to an integer.

FIGURE 11.2 angle Array with Values
The simplest form of index expression is a constant. Using our angle array, the sequence of assignment statements

fills the array components, one at a time (see FIGURE 11.2).
Each array component—angle[2], for instance—can be treated exactly the same way as any simple variable of type float. For example, we can do the following to the individual component angle[2]:
angle[2] = 9.6; |
Assign it a value. |
cin >> angle[2]; |
Read a value into it. |
cout << angle[2]; |
Write its contents. |
y = sqrt(angle[2]); |
Pass it as an argument. |
x = 6.8 * angle[2] + 7.5; |
Use it in an arithmetic expression. |
Now let’s look at index expressions that are more complicated than constants. Suppose we declare a 1000-element array of int values with the following statement:
int value[1000];
We then execute these two statements:

In the first statement, 5 is stored into an array component. If counter is 0, 5 is stored into the first component of the array. If counter is 1, 5 is stored into the second place in the array, and so forth.
In the second statement, the expression number+1 selects an array component. The specific array component accessed is divided by 10 and checked to see if the remainder is nonzero. If number+1 is 0, we are testing the value in the first component; if number+1 is 1, we are testing the second-place value; and so on. FIGURE 11.3 shows the index expression as a constant, a variable, and a more complex expression.
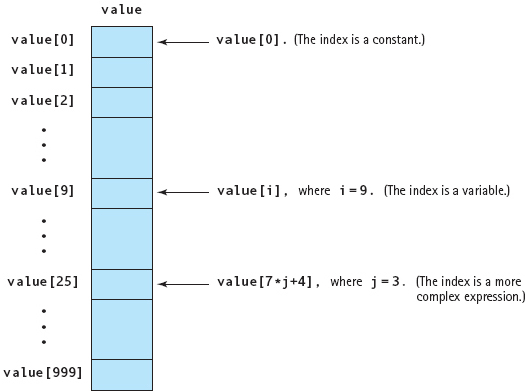
FIGURE 11.3 An Index as a Constant, a Variable, and an Arbitrary Expression
In earlier chapters, we saw how the string class allows us to access an individual character within a string:

Although string is a class (not an array), the string class was written using the advanced C++ technique of operator overloading to give the [ ] operator another meaning (string component selection) in addition to its standard meaning (array element selection).As a consequence, a string object is similar to an array of characters but has special properties. Thus we can write the last statement in the preceding example in an alternative manner:

Even though C++ supports this alternative syntax, we recommend using the at operation because it checks whether the requested position is within the valid range of positions for the given string. Accessing the string with array index notation doesn’t perform this check.
Out-of-Bounds Array Indexes
Given the declaration
float alpha[100];
the valid range of index values is 0 through 99. What happens if we execute the statement
alpha[i] = 62.4;
when i is less than 0 or when i is greater than 99? The result is that a memory location outside the array is accessed. C++ does not check for invalid (out-of-bounds) array indexes either at compile time or at run time. If i happens to be 100 in the preceding statement, the computer stores 62.4 into the next memory location past the end of the array, destroying whatever value was previously found there. It is entirely the programmer’s responsibility to make sure that an array index does not step off either end of the array.
Out-of-bounds array index An index value that, in C++, is either less than 0 or greater than the array size minus 1.
Array-processing algorithms often use For loops to step through the array elements one at a time. Here is a loop to zero out our 100-element alpha array (i is an int variable):
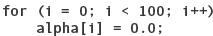
We could also write the first line as
for (i = 0; i <= 99; i++)
However, C++ programmers typically prefer to use the first version so that the number in the loop test (100) is the same as the array size. With this pattern, it is important to remember to test for less-than, not less-than-or-equal.
The following program shows what happens when you access places beyond the array bounds.
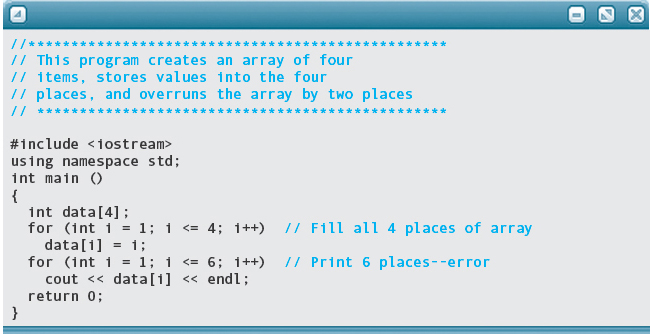
Output:
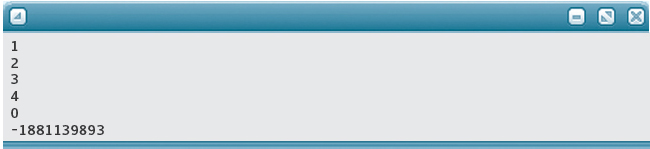
The first four values are the ones stored by the program. The next two are whatever happened to be in the two places in memory beyond the array.
Initializing Arrays in Declarations
You learned in Chapter 8 that C++ allows you to initialize a variable in its declaration:
int delta = 25;
The value 25 is called an initializer. You also can initialize an array in its declaration, using a special syntax for the initializer. To do so, you specify a list of initial values for the array elements, separate them with commas, and enclose the list within braces:
int age[5] = {23, 10, 16, 37, 12};
In this declaration, age[0] is initialized to 23, age[1] is initialized to 10, and so on. If you specify too many initial values, C++ generates a syntax error message. If you specify too few, the remaining array elements are initialized to zero.
Arrays follow the same rule as simple variables about the time(s) at which initialization occurs. A static array (one that is either global or declared as static within a block) is initialized once only, when control reaches its declaration. An automatic array (one that is local and not declared as static) is reinitialized each time control reaches its declaration.
An interesting feature of C++ is that you are allowed to omit the size of an array when you initialize it in a declaration:
float temperature[] = {0.0, 112.37, 98.6};
The compiler figures out the size of the array (here, 3) based on how many initial values are listed. In general, this feature is not particularly useful.
(Lack of) Aggregate Array Operations
In Chapter 10, we defined an aggregate operation as an operation on a data structure as a whole. Some programming languages allow aggregate operations on arrays, but C++ does not. In other words, if one and two are declared as
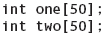
there is no aggregate assignment of two to one:

To copy array two into array one, you must do it yourself, element by element:
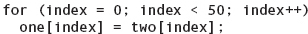
Similarly, there is no aggregate I/O of arrays:1

Nor is there aggregate arithmetic on arrays:
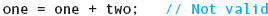
Comparison of arrays is possible, but it doesn’t do what you expect:

Rather than comparing the values stored in the two arrays, this statement checks whether the arrays are stored at the same address in memory. Similarly, attempting to return an array as the value of a value-returning function passes back the memory address of the first element of the array:

The only thing you can do to an array as a whole is to pass it as an argument to a function:
DoSomething(one);
Passing an array as an argument gives the function access to the entire array. The following table compares arrays and structs with respect to aggregate operations.
Aggregate Operation |
Arrays |
Structs |
I/O |
No (except C strings) |
No |
Assignment |
No |
Yes |
Arithmetic |
No |
No |
Comparison |
No |
No |
Argument passage |
By reference |
By value or by reference |
Return as a function’s return value |
No |
Yes |
Later in this chapter, we look in detail at the process of passing arrays as arguments.
Examples of Declaring and Accessing Arrays
Let’s look at some specific examples of declaring and accessing arrays. Here are some declarations that a program might use to analyze occupancy rates in an apartment building:

Here occupants is a 350-element array of integers (see FIGURE 11.4). occupants[0] = 3 if the first apartment has three occupants; occupants[1] = 5 if the second apartment has five occupants; and so on. If values have been stored into the array, then the following code totals the number of occupants in the building:


FIGURE 11.4 occupants Array
The first time through the loop, counter is 0. We add the contents of totalOccupants (that is, 0) to the contents of occupants[0], storing the result into totalOccupants. Next, the value of counter becomes 1 and the loop test occurs. The second loop iteration adds the contents of totalOccupants to the contents of occupants[1], storing the result into totalOccupants. Now the value of counter becomes 2 and the loop test is made. Eventually, the loop adds the contents of occupants[349] to the sum and increments counter to have the value to 350. At this point, the loop condition is false, and control exits the loop.
Note how we used the named constant BUILDING_SIZE in both the array declaration and the For loop. When constants are used in this manner, changes are easy to make. If the number of apartments changes from 350 to 400, we need to change only one line: the const declaration of BUILDING_SIZE. If we had used the literal value 350 in place of BUILDING_SIZE, we would need to update several of the statements in our previous code, and probably many more throughout the rest of the program.
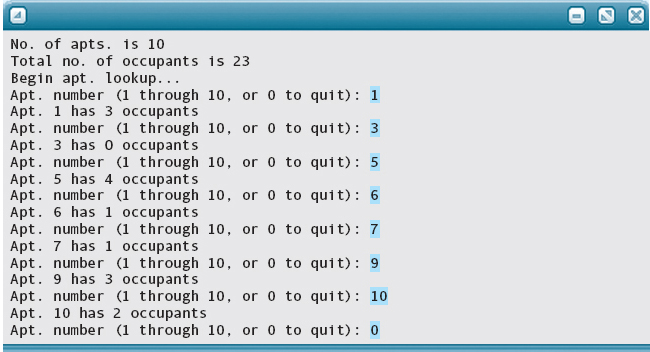
The following is a complete program that uses the occupants array. The program fills the array with occupant data read from an input file and then lets the user interactively look up the number of occupants in a specific apartment.
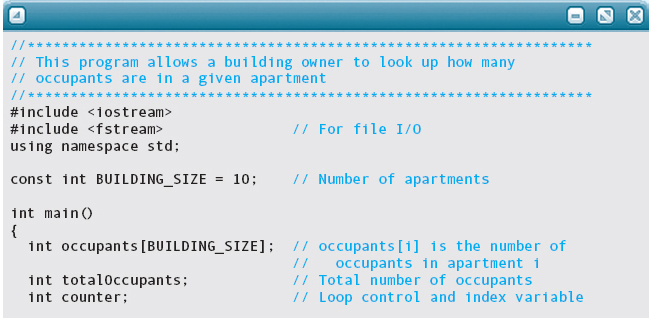
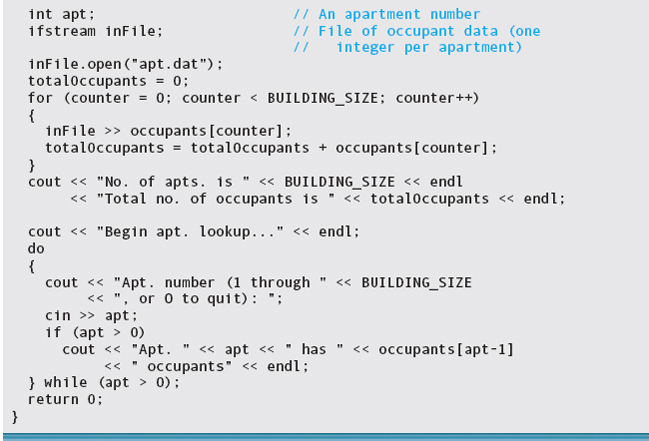
Look closely at the last output statement in this program. The user enters an apartment number (apt) in the range 1 through BUILDING_SIZE, but the array has indexes 0 through BUILDING_SIZE – 1. Therefore, we must subtract 1 from apt to ensure that the index refers to the proper place in the array.
The constant BUILDING_SIZE was changed to 10 for the following test run.
Input on apt.dat: 3 4 0 3 4 1 1 2 3 2
Output:
Because an array index is an integer value, we access the components based on their position in the array—that is, the first, the second, the third, and so on. Using an int index is the most common way of thinking about an array. C++, however, provides more flexibility by allowing an index to be of any integral type or enumeration type. (The index expression still must evaluate to an integer in the range from 0 through one less than the array size.)
The next example shows an array in which the indexes are values of an enumeration type:

Here Drink is an enumeration type in which the enumerators ORANGE, COLA, …, LEMON have internal representations 0 through 5, respectively. salesAmt is a group of six float components representing sales figures (in dollars) for each kind of drink (see FIGURE 11.5). The following code prints the values in the array:

Here is another example:

The grade array is pictured in FIGURE 11.6. Values are shown in the components, which implies that some processing of the array has already occurred. Following are some simple examples showing how the array might be used:
cin >> grade[2]; |
Reads the next nonwhitespace character from the input stream and stores it into the component in grade indexed by 2. |
grade[3] = 'A'; |
Assigns the character ‘A’ to the component in grade indexed by 3. |
idNumber = 5; |
Assigns 5 to the index variable idNumber. |

FIGURE 11.5 salesAmt Array

FIGURE 11.6 grade Array Filled with Values
grade[idNumber] = ‘C’; |
Assigns the character ‘C’ to the component of grade indexed by idNumber (that is, by 5). |
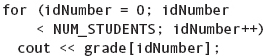
|
Loops through the grade array, printing each component. For this loop, the output would be FBCAFCAACB. |

|
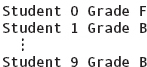
Loops through grade, printing each component in a more readable form. |
In the last example, idNumber is used as the index, but it also has semantic content—it is the student’s identification number. Here is the output of executing the code:
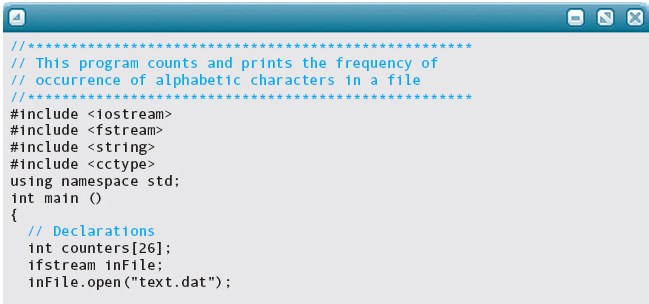
Here is one last example. Suppose we want to count the occurrences of characters within a text. We can set up an array of 26 positions in which each position serves as a counter for one letter in the alphabet (uppercase or lowercase). Because array indexes must be integral values, we can’t use a letter as an index, so how will we recognize a letter? Use an If statement with 25 tests? No, fortunately, there is a better way.
Recall that in ASCII (or Unicode) the uppercase letters are in order and the lowercase letters are in order. If we subtract ‘A’ from any uppercase letter, we get the letter’s position in the collating sequence. Likewise, if we subtract ‘a’ from any lowercase letter, we get its position in the collating sequence. That is,

FIGURE 11.7 counters Array
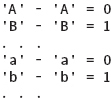
We can read a character and, if it is a letter, convert it to uppercase and use the result of subtracting 'A' from it as an index into the array of counters. See FIGURE 11.7.
Here is the program that uses the array to count the letters in text. The output is based on the same data that were used to test the Rich Uncle program in Chapter 7.
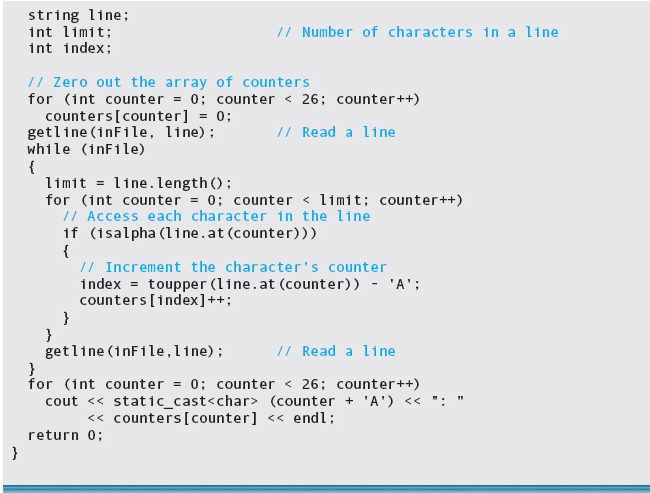
Output (in four columns to save space):
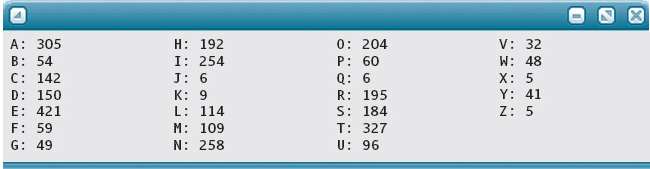
Notice that the index has to be converted back to a character before it is output. This conversion is the reverse of the original operation: The letter 'A' is added to the index and the result cast back to a character.
Passing Arrays as Arguments
In Chapter 8, we said that if a variable is passed to a function and it should not be changed by the function, then the variable should be passed by value instead of by reference. We specifically excluded stream variables (such as those representing data files) from this rule and noted that one more exception would be discussed later in the book. Now we can clarify this point: Arrays are the exception.
By default, C++ simple variables are always passed by value. To pass a simple variable by reference, you must append an ampersand (&) to the data type name in the function’s parameter list:

C++ doesn’t allow arrays to be passed by value; arrays are always passed by reference.2 Therefore, you should never use & when declaring an array as a parameter. When an array is passed as an argument, its base address—the memory address of the first element of the array—is sent to the function. The function then knows where the caller’s actual array is located and can access any element of the array.
Base address The memory address of the first element of an array.
Here is a C++ function that will zero out a one-dimensional int array of any size:

In the parameter list, the declaration of intArray does not include a size within the brackets. If you include a size, the compiler ignores it. The compiler wants to know only that it is an int array, not an int array of any particular size. Therefore, in the ZeroOut function you must include a second parameter—the number of array elements—if the For loop is to work correctly.
The calling code can invoke the ZeroOut function for an int array of any size. The following code fragment makes function calls to zero out two arrays of different sizes. Notice how an array parameter is declared in a function prototype.
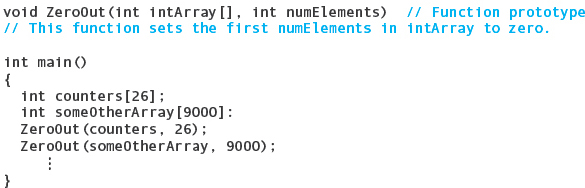
Keep in mind that within a function, an array parameter is simply a variable that is passed the address of the first element of the argument array. As mentioned earlier, C++ doesn’t support aggregate assignment of one array to another. However, you can assign a new address to an array parameter, causing it to refer to a different array. The assignment is not copying the array’s element values in this scenario, so it isn’t aggregate assignment. It’s a common mistake to forget this distinction.
With simple variables, passing by value prevents a function from modifying the caller’s argument. Although arrays are not passed by value in C++, you can still prevent the function from modifying the caller’s array. To do so, you use the reserved word const in the declaration of the parameter. Following is a function that copies one int array into another. The first parameter—the destination array—is expected to be modified; the second array is not.
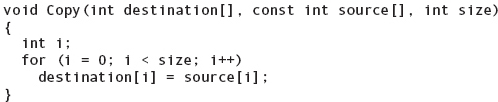
The word const guarantees that any attempt to modify the source array within the Copy function results in a compile-time error.
The following table summarizes argument passage for simple variables and one-dimensional arrays:
Argument |
Parameter Declaration for a Pass by Value |
Parameter Declaration for a Pass by Reference |
Simple variable |
int cost |
int& price |
Array |
Not allowed* |
int table[] |
* Prefixing the array declaration with the word const prevents the function from modifying the parameter.
One final remark about argument passage: It is a common mistake to pass an array element to a function when you actually intended to pass the entire array. For example, our ZeroOut function expects the base address of an int array to be sent as the first argument. In the following code fragment, the function call is an incorrect:

The error arises because counters[26] denotes a single array element—one int number—and not an entire array. Furthermore, there is no array element with an index of 26. The indexes for the counters array run from 0 through 25.
BACKGROUND INFORMATION
C, C++, and Arrays as Arguments

Some programming languages allow arrays to be passed either by value or by reference. Remember that when passing by value, a copy of the argument is sent to the function. When an array is passed by value, the entire array is copied. Not only is extra space required in the function to hold the copy, but the copying itself also takes time. Passing by reference requires only that the address of the argument be passed to the function; thus, when an array is passed by reference, just the address of the first array component is passed. Obviously, passing large arrays by reference saves both memory and time.
The C programming language—the direct predecessor of C++—was designed to be a system programming language. System programs, such as compilers, assemblers, linkers, and operating systems, must be both fast and economical with memory space. In the design of the C language, passing arrays by value was judged to be an unnecessary language feature. System programmers never use pass by value when working with arrays. Therefore, both C and C++ pass arrays by reference.
Of course, using a reference parameter can lead to inadvertent errors if the values are changed within the function. In early versions of the C language, there was no way to protect the caller’s array from being modified by the function.
C++ (and recent versions of C) added the ability to declare an array parameter as const. When the array is declared as const, a compile-time error will occur if the function attempts to modify the array. As a result, C++ supports the efficiency of passing arrays by reference yet also provides the protection (through const) of passing by value.
Whenever your design of a function’s interface identifies an array parameter as incoming only (to be inspected but not modified by the function), declare the array as const to obtain the same protection as passing by value.
Commenting Arrays
In comments, we often need to refer to a range of array elements:

To specify such ranges, it is more convenient to use an abbreviated notation consisting of two dots:

or more briefly:

Note that this dot-dot notation is not valid syntax in C++ language statements. we can use it only in comments within a program.
As an example of the use of this notation, here is how we would write the precondition and postcondition for our ZeroOut function:

SOFTWARE MAINTENANCE CASE STUDY: Modularizing a Program
MAINTENANCE TASK: The character counting program mentioned earlier in this chapter consisted of straight-line code. The task here is to modularize it using functions. Let’s examine the action part of the code.
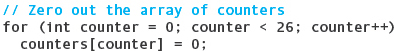
The comment says it all: We need a function to zero out the counters. In fact, we just discussed such a function as an example in the last section.
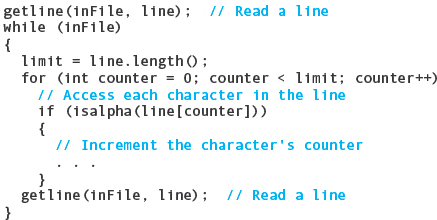
Again, the comments tell us what the loop body does: It accesses each character and increments its counter if it is a letter. Processing the text should be carried out through a function that takes the array of counters and the file name as parameters. The following section of code prints the output:

We can turn this code into a function that takes the array of counters as a parameter. Here is the character counting program reorganized using functions and proper documentation:

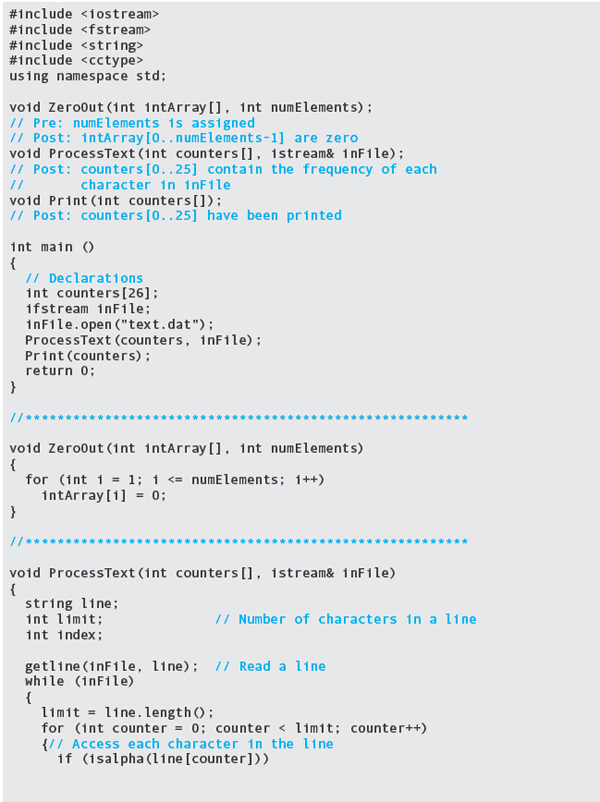
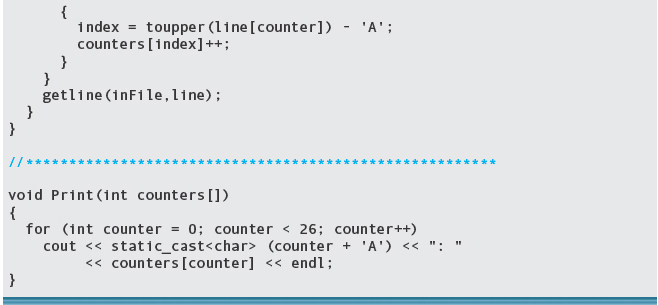
TESTING: The program was run with the same data, giving these results:
This makes no sense whatsoever! Some of the totals are correct, some are off slightly, some are way off, and some are negative. This looks like an initialization problem, but why are some right and others wrong? The ZeroOut function is correct: It sets each counter to 0—BUT it is never called. Whatever collection of bits that happened to be in a cell was just incremented.
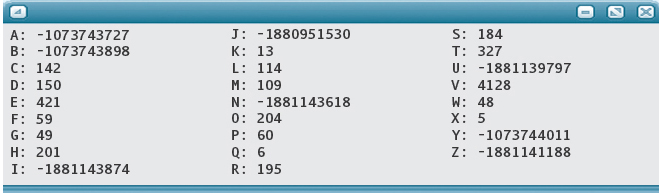
You add the call to ZeroOut and again run the program.
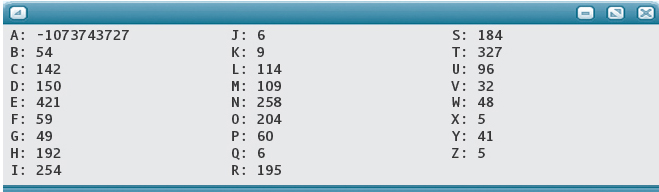
This is better, but the count for 'A' is still incorrect. Let’s look at the code for ZeroOut:

Of course! The loop should begin at 0 and stop when the counter is numElements. When this bug is corrected, the program gives the correct results.
Note that the location one beyond the array was set to 0. This did not affect the program because this location was not assigned to a variable.
Using Typedef with Arrays
In Chapter 10, we discussed the Typedef statement as a way of giving an additional name to an existing data type. We noted then that before bool became a built-in type in C++, programmers often used a Typedef statement such as the following:
typedef int Boolean;
We can also use Typedef to give a name to an array type. Here’s an example:
typedef float FloatArray[100];
This statement says that the type FloatArray is the same as the type “100-element array of float.” (Notice that the array size in brackets comes at the very end of the statement.) We can now declare variables to be of type FloatArray:

The compiler essentially translates these declarations into

In this book, we rarely use Typedefs to give names to one-dimensional array types. However, when we discuss multidimensional arrays later in the chapter, we’ll see that this technique can come in quite handy.
Pointer Expressions and Arrays
Although 0 is the only literal constant of the pointer type, another pointer expression is also considered to be a constant pointer expression: an array name without any index brackets. The value of this expression is the base address (the address of the first element) of the array. Given the declarations

the assignment statement
ptr = anArray;
has exactly the same effect as
ptr = &anArray[0];
Both of these statements store the base address of anArray into ptr. Because C++ allows us to assign an array to a pointer, it is a common misperception to think that the pointer variable and the array identifier are then effectively identical, but they are not. If you apply the sizeof operator to the pointer, it returns the number of bytes in the pointer. Applying it to the array identifier returns the number of bytes in the array.
Although we did not explain it at the time, you have already used the fact that an array name without brackets is a pointer expression. Consider the following code, which calls a ZeroOut function to zero out an array whose size is given as the second argument:

In the function call, the first argument—an array name without index brackets—is a pointer expression. The value of this expression is the base address of the velocity array; this base address is passed to the function. We can write the ZeroOut function heading in one of two ways. The first approach—one that you have seen many times—declares the first parameter to be an array of unspecified size:
void ZeroOut(float velocity[], int size)
Alternatively, we can declare the parameter to be of type float*, because the parameter simply holds the address of a float variable (the address of the first array element):
void ZeroOut(float* velocity, int size)
Whether we declare the parameter as float velocity[] or as float* velocity, the result is exactly the same from the perspective of the C++ compiler: Within the ZeroOut function, velocity is a simple variable that points to the beginning of the caller’s actual array. However, the first form is more self-documenting, because it tells the reader of the function definition that the parameter is meant to represent an array. Even though velocity is a pointer variable within the ZeroOut function, we are still allowed to attach an index expression to the name velocity:
velocity[i] = 0.0;
Indexing is valid for any pointer expression, not just an array name. (However, indexing a pointer makes sense only if the pointer points to an array.)
C-Style Strings
In Chapter 3, we introduced the C++ string data type and several of its associated functions, including length() and size(). In this section, we introduce an alternate string representation based on arrays and additional operations that are specific to this implementation.
Strings as Arrays
As we noted in Chapter 1, the C++ programming language is a superset of an older programming language named C, which was specifically designed for implementing the UNIX operating system. It focused on accessing low-level features of computer hardware and thus provided very little support for rich data types such as the C++ string. Even so, strings are very important for program input and output: they allow the user to interact with a program in a meaningful way. For this reason, C provides a primitive mechanism for representing strings, namely as an array of characters. Because C++ is a superset of the C programming language, it inherits all of C’s support for array-style string representation.
In previous sections, we discussed the declaration and use of arrays. A string can naturally be viewed as an array of characters. For example, the string “dogs” can be viewed as the sequence of characters ‘d’, ‘o’, ‘g’, ‘s’. This can easily be transcribed into the following C++ code segment:

In this case we are declaring an array of 4 chars and assigning to each entry in the array the characters that represent the string "dogs". We can then view the mystring variable as corresponding to the string "dogs". Although this works, it is cumbersome to declare strings this way, especially when they are longer. To ease the burden on the programmer, it is also possible to declare a C-style string using literal notation:
char mystring[] = "dogs";
This simplifies the effort for the programmer and lets the C++ compiler assign each character to individual locations in the array. In doing so, however, there is an important difference that results from this translation as compared with the previous manual approach. Instead of an array of length 4, it results in an array of length 5. The additional character is the null character, which is placed in the last element of the array to indicate the end of the string. The null character is represented by the special character '\0'. Thus, to truly declare a C-style string without the help of the string literal notation, we would write
char mystring[] = {'d', 'o', 'g', 's', '\0' };
using array initializer syntax. In this case, this char array declaration corresponds identically to the compiler-generated array using string literal notation.
C provides no built-in facilities for string manipulation (except using string literals to initialize a char array). In contrast, the C++ string data type provides a rich set of operations such as size(). The lack of built-in support will be important when we reference an array using pointers. For example, the same "dogs" string mentioned here can also be initialized using a pointer to char:
char* mystring = "dogs";
This is identical to using array notation and produces the same underlying array structure with the terminating null character. From understanding this representation, we can write functions for manipulating C-style strings such as the following length function that returns the length of the string given as an argument:
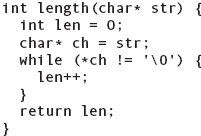
We could then use our length function to compute the length of the following C-style string:

C String Operations
Although the C-style string is not as rich as its C++ counterpart, there are a number of useful operations available in the string.h header file that can be used to achieve much the same effect. The following table shows samples of some of the functions provided:
Function |
Description |
size_t strlen(const char *s); |
Computes the length of the string s. |

|
Lexicographically compares strings s1 and s2 and returns an integer greater than, equal to, or less than 0. |
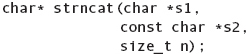
|
Appends a copy of n characters from the string s2 to the end of the string s1. The string s1 must be sufficiently long to hold the result. Returns a pointer to the new string. |
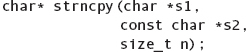
|
Copies n characters from the string s2 to the string s1. Returns a pointer to the new string. |
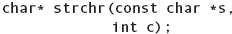
|
Locates the first occurrence of the character c in the string s. Returns a pointer to the location of the character in the string. |

|
Locates the first occurrence of the string s2 in the string s1 and returns a pointer to the start of that string. |
It is important to note that C-style strings are mutable. For example, assigning a character to any location in the string will overwrite that character with the one that you specify. Likewise, many of the string operations in the table overwrite their arguments. For instance, the strncpy function overwrites the string referenced by its first argument s1. In addition, because C-style strings are just pointers, you must be very careful in using functions such as strncat. The strncat function requires that its first argument must be sufficiently long to hold the result of appending the second argument. If it is not, it could lead to problems when the program is executing, possibly causing the program to crash. To this end you must program defensively and use these string functions properly. Thus, always make sure you know the length of a string.
Converting C Strings to C++ Strings
Programming in C++ will eventually lead to using a library that requires C-style strings. We may need to call a function that requires a C-style string argument or a function that returns a C-style string. You will then be required to convert between the C and C++ string abstractions. Converting from C-style strings to C++ strings is easy. The C++ string provides a constructor for creating C++ strings from C strings:
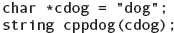
Likewise, we can convert the C++ string into a C-style string by using the c_str() function:
char *ccat = cppcat.c_str();
In this case the c_str() operation provided by the C++ string returns a C-style string, which can then be assigned to a variable of type char*.
Which String Representation to Use
Given that we have access to two different string representations, which string abstraction is best to use? In most cases, the programmer should choose the C++ string over the C-style string because it provides a safer abstraction. Although the C-style string enables representation of character data, it is still just an array of characters that can be accessed and changed in arbitrary ways. C++ provides a real-string data type with associated operations that work only for that data type. It captures the length of the string as part of its abstraction and alleviates the burden on the programmer to worry about how the string is implemented. When you must use functions that expect C-style strings, it is important to handle C-style strings appropriately or convert them into the C++ string data type.
QUICK CHECK

11.1.1 Why do we say that an array is a homogeneous data structure? (p. 518)
11.1.2 You are solving a problem that requires you to store 24 temperature readings. Which structure would be most appropriate for this problem: a record, a union, a class, or an array? (p. 518)
11.1.3 Write a declaration of an array variable called temps that holds 24 values of type float. (pp. 518–519)
11.1.4 Write a For loop that fills every element of the temps array declared in Exercise 11.1.3 with the value 32.0. (pp. 524–526)
11.1.5 How is a component of an array accessed? (p. 519)
11.1.6 A string in C++ can be treated like an array using the [ ] operator. Why is it preferred to use the at operation to access a character in a string? (p. 521)
11.2 Arrays of Records
Although arrays with atomic components are very common, many applications require a collection of records. For example, a business needs a list of parts records, and a teacher needs a list of students in a class. Arrays are ideal for these applications. We simply define an array whose components are records.
Arrays of Records
In Chapter 10, we defined a student record using a struct. We now need a collection of these student records. How do we implement a “collection”? By a file or an array. Because this chapter focuses on arrays, let’s declare an array of student records and look at how each field would be accessed. To make things a little more interesting, let’s add a user-defined type GradeType and an array of exam scores. As this is the beginning of a program, we show the structure as code.
This data structure can be visualized as shown in FIGURE 11.8.
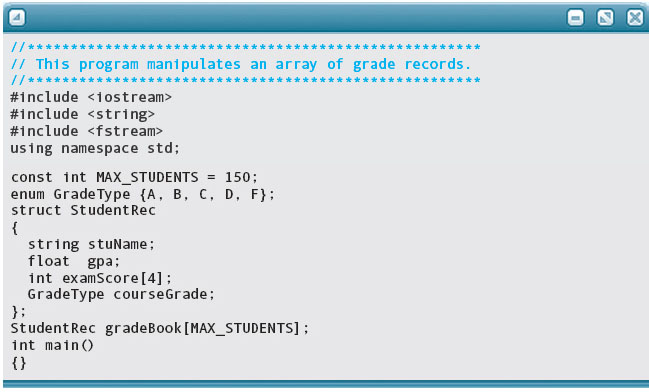
An element of gradeBook is selected by an index. For example, gradeBook[2] is the third component in the array gradeBook. Each component of gradeBook is a record of type StudentRec. To access the course grade of the third student, for example, we use the following expression:
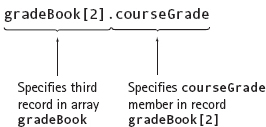
The record component gradeBook[2].examScore is an array. We can access the individual elements in this component just as we would access the elements of any other array: We give the name of the array followed by the index, which is enclosed in brackets.
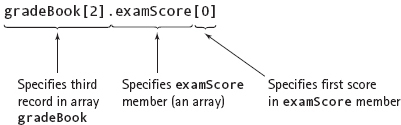
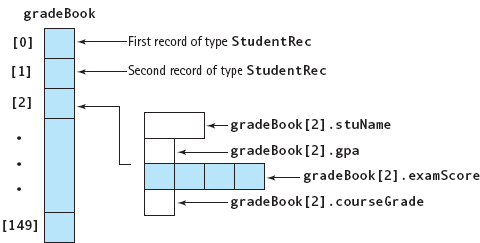
FIGURE 11.8 gradeBook Array with Records as Elements
The next step is to write a function that reads values from a file into the fields of the records. The file name and the record are parameters of the function. Both must be reference parameters: Files are always passed by reference, and we are sending back values to the calling code through the record.
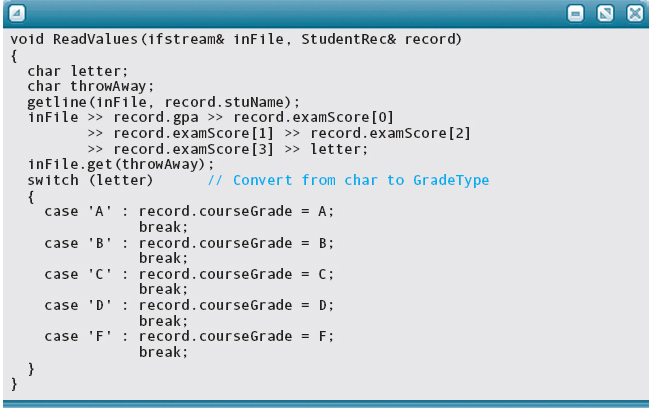
The only tricky part is getting past the eoln at the end of each student’s entry. This eoln follows the letter grade entered as a character. We can’t use a regular character read operation because it returns the first letter of the next student’s name. Instead, we must use inFile.get.
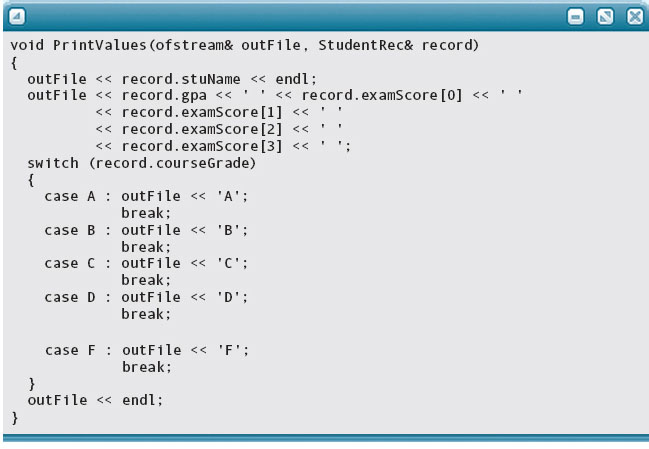
The function to write each student’s record is a mirror image of the input function.
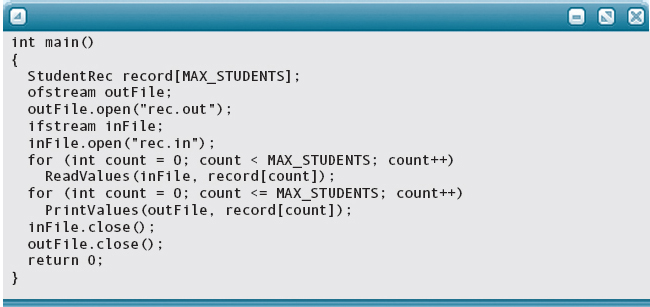
Now we must create a main program that uses these two functions to input the file of records, store them into an array, and print them on an output file.
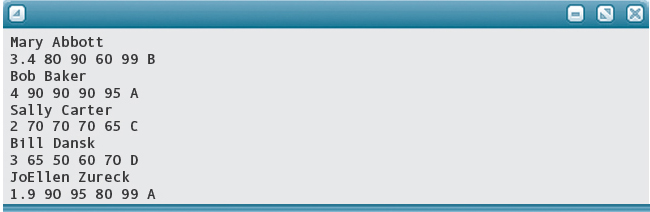
Here is an input file and the resulting output file. The constant for MAX_STUDENTS was changed to 5 for this run (for obvious reasons).
rec. in
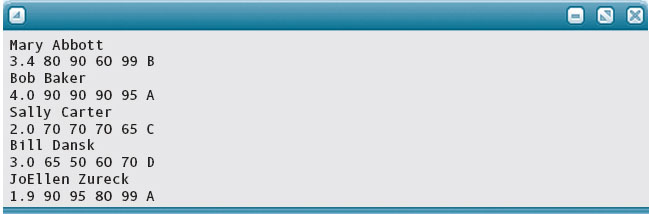
rec. out
QUICK CHECK

11.2.1 How would you access the third letter in a string data member (called street) of a struct variable that is the twelfth element of an array called mailList? (pp. 541–542)
11.2.2 Imagine we are extending a web browser with functionality that requires an array of records to maintain the coordinates for HTML elements in the browser window. How might you declare the struct representing coordinates and an array of 1000 elements for holding these records? (pp. 541–542)
11.3 Special Kinds of Array Processing
Two types of array processing occur especially often: using only part of the declared array (a subarray) and using index values that have specific meaning within the problem (indexes with semantic content). We describe both of these methods briefly here and give further examples in the remainder of the chapter.
Subarray Processing
The size of an array—the declared number of array components—is established at compile time. We have to declare an array to be as big as it will ever need to be. Because the exact number of values to be put into the array often depends on the data itself, however, we may not fill all of the array components with values. The problem is that to avoid processing empty positions in the array, we must keep track of how many components are actually filled.
As values are put into the array, we keep a count of how many components are filled. We then use this count to process only those components that have values stored in them; any remaining places are not processed. For example, if there were 250 students in a class, a program to analyze test grades would set aside 250 locations for the grades. However, some students might be absent on the day of the test. So the number of test grades must be counted, and that number—rather than 250—is used to control the processing of the array.
If the number of data items actually stored in an array is less than its declared size, functions that receive array parameters must also receive the number of data items as a parameter. We handled this task in the ZeroOut function by passing the array and the number of elements as two parameters. However, there is a better way: The array and the number of actual items in the array can be bound together in a record.
Consider, for example, the collection of student records. We could change the problem a little and say that the actual number of student records is not known. The reading loop would be an eof loop rather than a For loop. Let’s expand ReadValues and PrintValues to take the record containing the array and the number of items rather than just the array. Thus the loops would be found within the functions, not in main.
Here is the complete program with these changes. The definition of the data structure and the function prototypes are highlighted.


This program was run with the same data set used previously. It is always comforting to get the same results.
Indexes with Semantic Content
In some problems, an array index has meaning beyond simple position; that is, the index has semantic content. An example is the salesAmt array we showed earlier. This array is indexed by a value of enumeration type Drink. The index of a specific sales amount is the kind of soft drink sold; for example, salesAmt[ROOT_BEER] is the sales figure (in dollars) for root beer.
In the next section we will see some additional examples of indexes with semantic content.
QUICK CHECK

11.3.1 Explain how the index of an array of 24 hourly temperature readings has semantic content, if the index is an integer ranging from 0 through 23. (p. 548)
11.3.2 Write a loop that reads values from file indata into the temps array of Exercise 11.1.3, until either the end-of-file is reached or 24 values are input. The loop should keep track of the number of values in the array in an int variable called count. (pp. 545–546)
11.3.3 At what time is the size of an array established? (p. 545)
11.3.4 How might we avoid processing empty positions in an array? (p. 545)
11.4 Two-Dimensional Arrays
A one-dimensional array is used to represent items in a list or sequence of values. In many problems, however, the relationships between data items are more complex than can be depicted by a simple list. A two-dimensional array is used to represent items in a table with rows and columns, provided each item in the table is of the same data type. Two-dimensional arrays are useful for representing board games, such as chess, tic-tac-toe, or Scrabble, and in computer graphics, where the screen is thought of as a two-dimensional array.
Two-dimensional array A collection of components, all of the same type, structured in two dimensions. Each component is accessed by a pair of indexes that represent the component’s position in each dimension.
A component in a two-dimensional array is accessed by specifying the row and column indexes of the item in the array. This is a familiar task. For example, if you want to find a street on a map, you look up the street name on the back of the map to find the coordinates of the street, usually a letter and a number. The letter specifies a column to look at, and the number specifies a row. You find the street where the row and column meet.
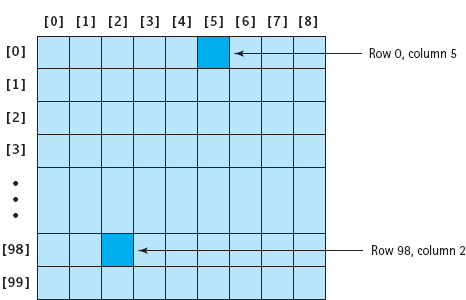
FIGURE 11.9 A Two-Dimensional Array
FIGURE 11.9 shows a two-dimensional array with 100 rows and 9 columns. The rows are accessed by an integer ranging from 0 through 99; the columns are accessed by an integer ranging from 0 through 8. Each component is accessed by a row–column pair—for example, 0, 5.
A two-dimensional array is declared in exactly the same way as a one-dimensional array, except that sizes must be specified for both of the two dimensions. Here is the syntax template for declaring an array with more than one dimension:
ArrayDeclaration

The following example declares alpha to be a two-dimensional array, all of whose components are float values. The declaration creates the array that is pictured in Figure 11.9.
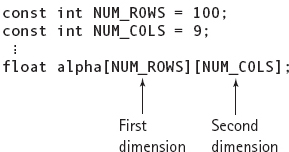
To access an individual component of the alpha array, two expressions (one for each dimension) are used to specify its position. Each expression appears in its own pair of brackets next to the name of the array:
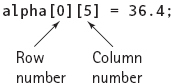
The syntax template for accessing an array component is
ArrayComponentAccess

As with one-dimensional arrays, each index expression must result in an integer value.
Now let’s look at some examples. Here is the declaration of a two-dimensional array with 364 integer components (52 × 7 = 364):
int hiTemp[52][7];
hiTemp is an array with 52 rows and 7 columns. Each place in the array (each component) can contain any int value. Our intention is that the array will hold high temperatures for each day in a year. Each row represents one of the 52 weeks in a year, and each column represents one of the 7 days in a week. (To keep the example simple, we ignore the fact that there are 365—and sometimes 366—days in a year.) The expression hiTemp[2][6] refers to the int value in the third row (row 2) and the seventh column (column 6). Semantically, hiTemp[2][6] is the temperature for the seventh day of the third week. The code fragment shown in FIGURE 11.10 would print the temperature values for the third week.

FIGURE 11.10 hiTemp Array
Another representation of the same data might be as follows:

Here hiTemp is declared the same as before, but now we can use an expression of type DayType for the column index. hiTemp[2][SUNDAY] corresponds to the same component as hiTemp[2][6] in the first example. (Recall that enumerators such as MONDAY, TUESDAY, … are represented internally as the integers 0, 1, 2, ….) If day is of type DayType and week is of type int, the code fragment shown in FIGURE 11.11 sets the entire array to 0. (Notice that by using DayType, the temperature values in the array begin with the first Monday of the year, which is not necessarily January 1.)
Another way of looking at a two-dimensional array is to see it as a structure in which each component has two features. Consider the following code:


FIGURE 11.11 hiTemp Array (Alternate Form)
This data structure uses one dimension to represent the color and the other dimension to represent the make of automobile. In other words, both indexes have semantic content—a concept we discussed in the previous section.
QUICK CHECK

11.4.1 How does a two-dimensional array differ syntactically from a one-dimensional array? (pp. 548–549)
11.4.2 Write the declaration for a two-dimensional array, called allTemps, that holds the 24 hourly readings for each day of a year (up to 366 days). (pp. 548–549)
11.4.3 What generic structure is a two-dimensional array typically used to represent? (p. 548)
11.4.4 Imagine we are using a two-dimensional array as the basis for creating the game battleship. In the game of battleship a ‘~’ character entry in the array represents ocean (i.e., not a ship), a ‘#’ character represents a place in the ocean where part of a ship is present, and an ‘H’ character represents a place in the ocean where part of a ship is present and has been hit by a torpedo. Thus, a ship with all ‘H’ characters means the ship has been sunk. Declare a two-dimensional array that is 25 × 25 that represents the entire ocean and an If statement that prints “HIT” if a torpedo hits a ship given the coordinates X and Y. (pp. 548–551)
11.5 Passing Two-Dimensional Arrays as Arguments
Earlier in the chapter, we said that when one-dimensional arrays are declared as parameters in a function, the size of the array usually is omitted from the square brackets:

If you include a size in the brackets, the compiler ignores it. As you learned, the base address of the caller’s argument (the memory address of the first array element) is passed to the function. The function works for an argument of any size. Because the function cannot know the size of the caller’s array, we either set the size as a constant, pass the size as an argument (as in SomeFunc), or, better still, bind the array and the number of elements together into a record and pass the record to the function.
When a two-dimensional array is passed as an argument, the base address of the caller’s array is sent to the function. You cannot leave off the sizes of both of the array dimensions, however. You can omit the size of the first dimension (the number of rows) but not the second (the number of columns). Here is the reason.
In the computer’s memory, C++ stores two-dimensional arrays in row order. If we think of memory as consisting of one long line of memory cells, the first row of the array is followed by the second row, which is followed by the third row, and so on (see FIGURE 11.12).
To locate beta[1][0] in Figure 11.12, a function that receives beta’s base address must be able to determine that there are four elements in each row—that is, that the array consists of four columns. Therefore, the declaration of a parameter must always state the number of columns:

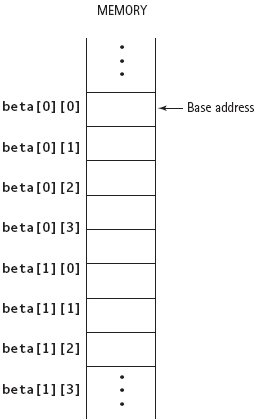
FIGURE 11.12 Memory Layout for a Two-Row by Four-Column Array
Furthermore, the number of columns declared for the parameter must be exactly the same as the number of columns in the caller’s array. As you can tell from Figure 11.12, if there is any discrepancy in the number of columns, the function will access the wrong array element in memory.
Our AnotherFunc function works for a two-dimensional array of any number of rows, as long as the array has exactly four columns. In practice, we seldom write programs that use arrays with a varying number of rows but the same number of columns. To avoid problems with mismatches in argument and parameter sizes, it’s practical to use a Typedef statement to define a two-dimensional array type and then declare both the argument and the parameter to be of that type. For example, we might make the declarations

and then write the following general-purpose function that initializes all elements of an array to a specified value:


The calling code could then declare and initialize one or more arrays of type ArrayType by making calls to the Initialize function. For example:

QUICK CHECK

11.5.1 Write the heading for a function that accepts the temps array of Exercise 11.1.3 and its length as parameters. Call the function Quick, and have it be a void function. (pp. 552–554)
11.5.2 What does the C++ compiler do if you provide the size of an array of one dimension in a parameter declaration? (p. 552)
11.5.3 Why can you omit the size of the first dimension but not the second dimension in a two-dimensional array? (p. 552)
11.5.4 What part of an array is passed as an argument to a function? (p. 552)
11.6 Processing Two-Dimensional Arrays
Processing data in a two-dimensional array generally means accessing the array in one of four patterns: randomly, along rows, along columns, or throughout the entire array. Each of these methods may also involve subarray processing.
The simplest way to access a component is to look directly in a given location. For example, a user might enter map coordinates that we use as indexes into an array of street names to access the desired name at those coordinates. This process is referred to as random access because the user may enter any set of coordinates at random.
In many cases, we might wish to perform an operation on all the elements of a particular row or column in an array. Consider the hiTemp array defined previously, in which the rows represent weeks of the year and the columns represent days of the week. If we wanted to find the average high temperature for a given week, we would sum the values in that row and divide by 7. If we wanted to find the average high temperature for a given day of the week, we would sum the values in that column and divide by 52. The former case is access by row; the latter case is access by column.
Now suppose that we wish to determine the average high temperature for the year. We must access every element in the array, sum their values, and divide by 364. In this case, the order of access—by row or by column—is not important. (The same is true when we initialize every element of an array to zero.) This is access throughout the array.
Sometimes we must access every array element in a particular order, either by rows or by columns. For example, if we wanted the average high temperature for every week, we would run through the entire array, taking each row in turn. However, if we wanted the average high temperature for each day of the week, we would run through the array one a column at a time.
Let’s take a closer look at these patterns of access by considering four common examples of array processing.
1. Sum the rows.
2. Sum the columns.
3. Initialize the array to all zeros (or some special value).
4. Print the array.
First, let’s define some constants and variables using general identifiers, such as row and col, rather than problem-dependent identifiers. Then, let’s look at each algorithm in terms of generalized two-dimensional array processing.

Sum the Rows
Suppose we want to sum row number 3 (the fourth row) in the array and print the result. We can do this easily with a For loop:
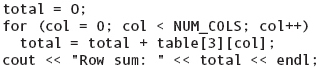
This For loop runs through each column of table, while keeping the row index fixed at 3. Every value in row 3 is added to total.
Now suppose we want to sum and print two rows—row 2 and row 3. We can use a nested loop and make the row index a variable:
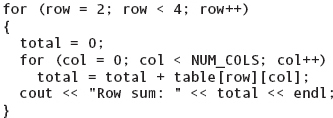
The outer loop controls the rows, and the inner loop controls the columns. For each value of row, every column is processed; then the outer loop moves to the next row. In the first iteration of the outer loop, row is held at 2 and col goes from 0 through NUM_COLS-1. Therefore, the array is accessed in the following order:
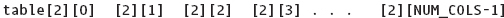
In the second iteration of the outer loop, row is incremented to 3, and the array is accessed as follows:
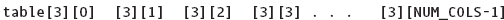

FIGURE 11.13 Partial Array Processing by Row
We can generalize this row processing to run through every row of the array by having the outer loop run from 0 through NUM_ROWS-1. However, if we want to access only part of the array (subarray processing), given variables declared as

then we write the code fragment as follows:
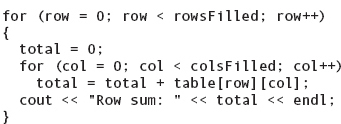
FIGURE 11.13 illustrates subarray processing by row.
Sum the Columns Revised
Before we look at different processing algorithms, let’s do what we did with our one-dimensional array: Let’s redesign our structure to be a record that contains the array and two variables, rowsFilled and colsFilled. Rather than look at the algorithms as code fragments, we look at them as functions.

The algorithm for summing a specific row in a two-dimensional array is encapsulated into the following function:

The following function uses function PrintRowSums to print the sums of each of the rows, calling SumRows to do the summing:

Why did we break the process of printing the sums of the rows of a two-dimensional array into two functions? Good style dictates that a function should accomplish only one task: The second function calls the first to return the row sum and then prints it.
Sum the Columns
Suppose we want to sum and print each column. The code to perform this task follows. Again, we have generalized the code to sum only the portion of the array that contains valid data.

In this case, the outer loop controls the column, and the inner loop controls the row. All of the components in the first column are accessed and summed before the outer loop index changes and the components in the second column are accessed. FIGURE 11.14 illustrates subarray processing by column.
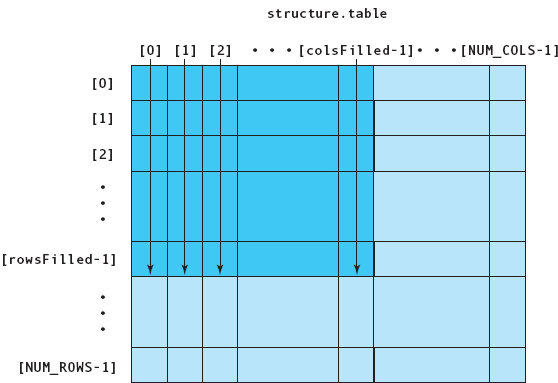
FIGURE 11.14 Partial Array Processing by Column
Initialize the Array
As with one-dimensional arrays, we can initialize a two-dimensional array either by initializing it in its declaration or by using assignment statements. If the array is small, it is simplest to initialize it in its declaration. To initialize a two-row by three-column array to look like this:
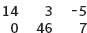
we can use the following declaration:

In this declaration, the initializer list consists of two items, each of which is itself an initializer list. The first inner initializer list stores 14, 3, and − 5 into row 0 of the array; the second stores 0, 46, and 7 into row 1. The use of two initializer lists makes sense if you think of each row of the two-dimensional array as being a one-dimensional array of three int values. The first initializer list initializes the first array (the first row), and the second list initializes the second array (the second row). Later in this chapter, we will revisit this notion of viewing a two-dimensional array as an array of arrays.
Initializing an array in its declaration is impractical if the array is large. For a 100-row by 100-column array, you don’t want to list 10,000 values. If the values are all different, you should store them into a file and input them into the array at run time. If the values are all the same, the usual approach is to use nested For loops and an assignment statement. Here is a function that zeros out an array of type TwoDArray:

In this case, we initialized the array one row at a time, but we could just as easily have run through each column instead. The order doesn’t matter so long as we access every element.
Print the Array
If we wish to print out an array with one row per line, then we have another case of row processing:

This code fragment prints the values of the array in columns that are 15 characters wide. As a matter of proper style, this fragment should be preceded by code that prints headings over the columns to identify their contents.
There’s no rule saying that we have to print each row on a line. If we liked, we could turn the array sideways and print each column on one line simply by exchanging the two For loops. When you are printing a two-dimensional array, you must consider which order of presentation makes the most sense and how the array fits on the page. For example, an array with 6 columns and 100 rows would be best printed as 6 columns, 100 lines long.
Almost all processing of data stored in a two-dimensional array involves either processing by row or processing by column. In most of our examples, the index type has been int; however, the pattern of operation of the loops is the same no matter what types the indexes are.
The looping patterns for row processing and column processing are so useful that we summarize them below. To make them more general, we use minRow for the first row number and minCol for the first column number. Remember that row processing places the row index in the outer loop, and column processing places the column index in the outer loop.
Row Processing

Column Processing

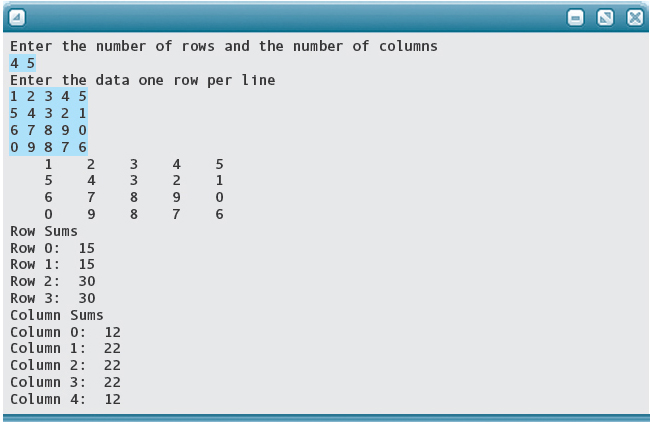
The following prototypes and main function use each of these functions to read the values into an array, print them, print the sum of the rows, and print the sum of the columns.
Output:
QUICK CHECK

11.6.1 Write a nested For loop that outputs the contents of the allTemps array declared in Exercise 11.4.2, with the 24 temperatures for a day on a line and 366 lines of days. (pp. 559–560)
11.6.2 What is the process called when a two-dimensional array is accessed by index? (p. 554)
11.6.3 What are the four patterns of accessing a two-dimensional array? (p. 554)
11.6.4 Write a nested For loop that outputs the average hourly temperature across 366 days of the allTemps array declared in Exercise 11.4.2, with the average hourly temperature on a line and 24 lines of hours. (pp. 559–560)
11.6.5 Write a declaration for a two-dimensional array for a tic-tac-toe board where we represent an empty square as O, a square with an X as 1, and a square with a O as 2, that is initialized without assignment statements with the following board state: (pp. 560–561)
X |
O |
O |
EMPTY |
X |
EMPTY |
X |
EMPTY |
O |
11.7 Another Way of Defining Two-Dimensional Arrays
We hinted earlier that a two-dimensional array can be viewed as an array of arrays. This view is supported by C++ in the sense that the components of a one-dimensional array do not have to be atomic. The components can themselves be structured—structs, class objects (which we introduce in Chapter 12), or even arrays. For example, our hiTemp array could be declared as follows:

With this declaration, the 52 components of the hiTemp array are one-dimensional arrays of type WeekType. In other words, hiTemp has two dimensions. We can refer to each row as an entity: For example, hiTemp[2] refers to the array of temperatures for week 2. We can also access each individual component of hiTemp by specifying both indexes: For example, hiTemp[2][0] accesses the temperature on the first day of week 2.
Does it matter which way we declare a two-dimensional array? Not to C++. The choice should be based on readability and understandability. Sometimes the features of the data are shown more clearly if both indexes are specified in a single declaration. At other times, the code is clearer if one dimension is defined first as a one-dimensional array type.
The following example shows a case when it is advantageous to define a two-dimensional array as an array of arrays. If the rows have been defined first as a one-dimensional array type, each row can be passed to a function whose parameter is a one-dimensional array of the same type. For example, the following function calculates and returns the maximum value in an array of type WeekType.

Our two-part declaration of hiTemp permits us to call Maximum using a component of hiTemp as follows:
highest = Maximum(hiTemp[20]);
Row 20 of hiTemp is passed to Maximum, which treats it like any other one-dimensional array of type WeekType (see FIGURE 11.15). It makes sense to pass the row as an argument because both it and the function parameter are of the same named type, WeekType.
With hiTemp declared as an array of arrays, we can output the maximum temperature of each week of the year with the following code:
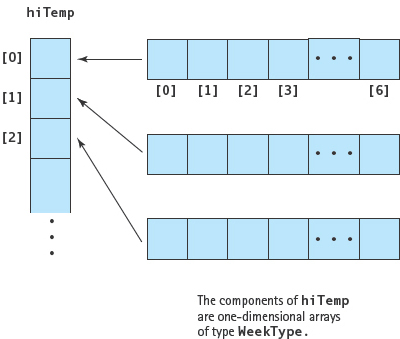
FIGURE 11.15 A One-Dimensional Array of One-Dimensional Arrays

11.8 Multidimensional Arrays
C++ does not place a limit on the number of dimensions that an array can have. We can generalize our definition of an array to cover all cases.
Array A collection of components, all of the same type, ordered on Ndimensions (N ≥ 1), Each component is accessed by N indexes, each of which represents the component’s position within that dimension.
You might have guessed from the syntax templates that you can have as many dimensions as you want. How many should you have in a particular case? Use as many as there are features that describe the components in the array.
Consider, for example, a chain of department stores. Monthly sales figures must be kept for each item by store. Three important pieces of information about each item are identified: the month in which it was sold, the store from which it was purchased, and the item number. We can define an array type to summarize this data as follows:

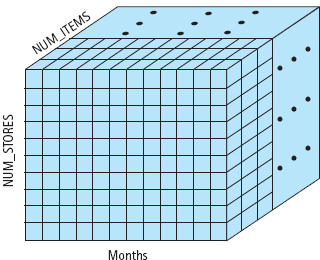
FIGURE 11.16 Graphical Representation of sales Array
FIGURE 11.16 provides a graphic representation of the sales array.
The number of components in sales is 12,000 (10 × 12 × 100). If sales figures are available only for January through June, then half of the array is empty. If we want to process the data in the array, we must use subarray processing. The following program fragment sums and prints the total number of each item sold this year to date by all stores:

Because item controls the outer For loop, we are summing each item’s sales by month and store. If we want to find the total sales for each store, we use store to control the outer For loop, summing its sales by month and item with the inner loops.

It takes two loops to access each component in a two-dimensional array; it takes three loops to access each component in a three-dimensional array. The task to be accomplished determines which index controls the outer loop, the middle loop, and the inner loop. If we want to calculate monthly sales by store, month controls the outer loop and store controls the middle loop. If we want to calculate monthly sales by item, month controls the outer loop and item controls the middle loop.
If we want to keep track of the departments that sell each item, we can add a fourth dimension to the array:

How would we visualize this new structure? Not very easily! Fortunately, we do not have to visualize a structure to use it. If we want the number of sales in store 1 during June for item number 4 in department C, we simply access the following array element:
sales[1][5][4][C]
When a multidimensional array is declared as a parameter in a function, C++ requires you to state the sizes of all dimensions except the first. For our four-dimensional version of SalesType, a function heading would look like this:
void DoSomething(int table[][12][NUM_ITEMS][NUM_DEPTS])
or, better yet, like this:
void DoSomething(SalesType arr)
The second version is the safest (and the most uncluttered for readers). It ensures that the sizes of all dimensions of the parameter match those of the argument exactly. With the first version, the reason that you must declare the sizes of all but the first dimension is the same as we discussed earlier for two-dimensional arrays: Because arrays are stored linearly in memory (one array element after another), the compiler must use this size information to locate correctly an element that lies within the array.
QUICK CHECK

11.8.1 Write a declaration for a multidimensional array for representing network access points in a building that has 15 floors, 10 rooms per floor, and up to 12 network access points per room. Each network access point is labeled with its state as being on or off and if it is on has the month it was turned on. (pp. 564–565)
11.8.2 Which aspect of a problem would lead you to consider using a multidimensional array as the representation of its data structure? (pp. 564–565)
11.8.3 Write a declaration for a multidimensional array that stores 24 hourly temperatures for each day of a year for a decade. Call the array decadeTemps. (pp. 564–565)
Problem-Solving Case Study
Calculating Exam Statistics
PROBLEM: You are the grader in your Government class. The teacher has asked you to prepare the following statistics for the last exam: average grade, maximum grade, minimum grade, number of grades above the average, and number of grades below the average. Because this is the first exam for the course, you decide to write a program to calculate these statistics so you can use the program for the remaining exams as well.
DISCUSSION: Let’s abstract this problem from the given context and look at the tasks in isolation. Three separate things must be done in this problem: compute an average of values on a file, find the minimum value and maximum value in a file, and compare each value to the average. There are several approaches to the solution to this problem. In the next chapter, we will look at an entirely different solution technique; however, here we base our solution on the fact that the values in the list are between 0 and 100. We use an array where the indexes have semantic content: Each index represents a grade.
The by-hand analogy is to mark off 101 lines on a sheet of paper and number (or label) the lines from 0 to 100. Each line number then represents a possible grade. As you read a grade, you make a hash mark on the line whose number is the same as the grade. When you have finished recording each grade in this fashion, you compute the sum of the grades by summing the products of each grade (line number) times the number of hash marks on that line. You can either count the number of grades as you read them or later, as you go through the list to sum them up.
To calculate the lowest grade, start at line 0 and look down the list; the number of the first line with a hash mark is the lowest grade. To calculate the highest grade, start looking backward from line 100; the line number where you find the first hash mark is the highest grade. To determine how many grades are above average, start at the line whose number is the average grade plus 1 and count the hash marks on the lines from there through line 100. To determine how many grades are below the average, sum the hash marks from the line whose number is the truncated average through line 0.
The data structure equivalent of your sheet of paper is an integer array declared to be of size 101. The index is the line number; the component corresponds to where you make hash marks (increment the component) each time the grade corresponding to the index occurs.
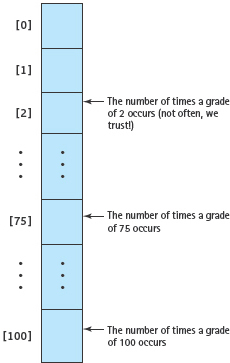
FIGURE 11.17
INPUT: A file, whose name is input from the keyboard, containing test grades.
OUTPUT: A file, whose name is input from the keyboard, showing the following statistics properly labeled:
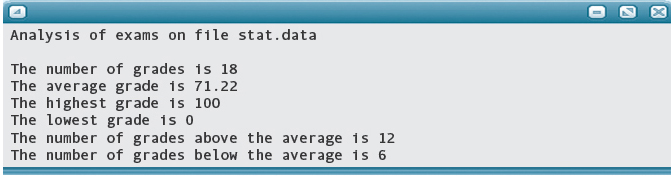
Number of grades
Average grade
Lowest grade
Highest grade
Number of grades above the average
Number of grades below the average
DATA STRUCTURE: The array of grades and the values to be calculated should be bound together into a record.

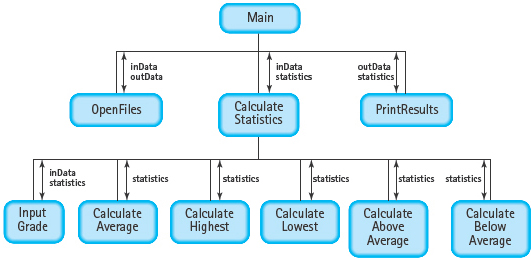
Main
Level 0
Open files
Calculate statistics
Print results
Close files
We can use the same “open files” function we have used in several other programs. However, the heading that is printed on the output needs to be changed.
Calculate Statistics
This function must input the grades and calculate the statistics. It needs the input file name and the record of type GradeStatistics. Let’s call this parameter statistics. We pass it to all of the modules, letting each module decide which of the values to access.
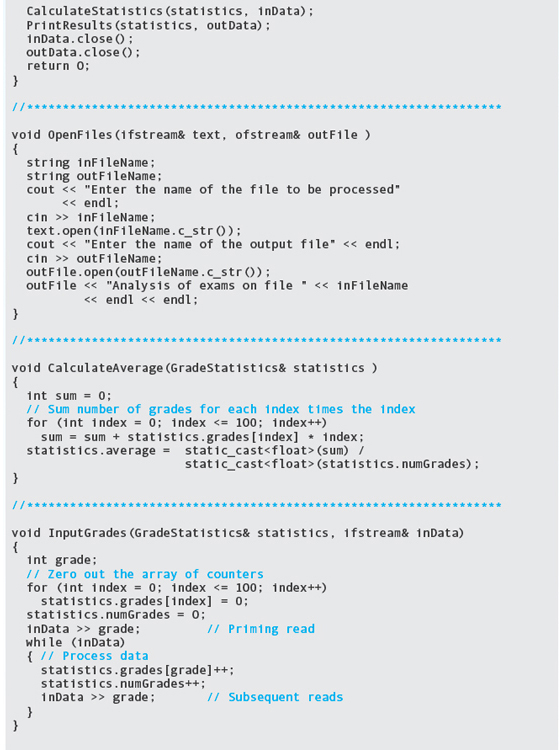
CalculateStatistics(In/out: inData, statistics)
Input grades
Calculate average
Calculate highest
Calculate lowest
Calculate number above average
Calculate number below average
Input Grades
Level 1
This function must have the file name and the array as parameters. The program needs to know the number of grades. As we said, this value can be calculated either as the grades are read or as the grades are summed to get the average. Let’s calculate it here and pass it as an argument to the function that computes the average.
lnputGrades(ln/out: statistics, inData:)
Set numGrades to 0
Read grade
WHILE NOT eof
Increment statistics.grades[grade]
Increment statistics.numGrades
Read grade
CalculateAverage(ln/out: statistics)
Set sum to 0
FOR index going from 0 through 100
Set sum to sum + statistics.grades[index] * index;
Set statisics.average to float(sum) / float(statistics.numGrades)
CalculateHighest(ln/out: statistics)
Set highGrade to 100;
WHILE statistics.grades[highGrade] equal to 0
Decrement highGrade
Set statistics.highest to highGrade
CalculateLowest(ln/out: statistics)
Set lowGrade to 0
WHILE statistics.grades[lowGrade] equal to 0
Increment lowGrade
Set statistics.lowest to lowGrade
CalculateAboveAverage(ln/out: statistics)
Set averagePlus to int(statistics.average) + 1
Set number to zero
FOR index going from averagePlus to 100
Set number to number + statistics.grades[index]
Set statistics.aboveAverage to number
CalculateBelowAverage(ln/out: statistics)
Set truncatedAverage to (int) statistics.average
Set number to zero
FOR index going from 0 to truncatedAverage
Set number to number + statistics.grades[index]
Set statistics.belowAverage to number
PrintResults(Inout: Outdata; In: statistics)
Print on outData “The average grade is” statistics.average
Print on outData “The highest grade is” statistics.highest
Print on outData “The lowest grade is” statistics.lowest
Print on outData “The number of grades above the average is” statistics.aboveAverage
Print on outData “The number of grades below the average is” statistics.belowAverage
MODULE STRUCTURE CHART




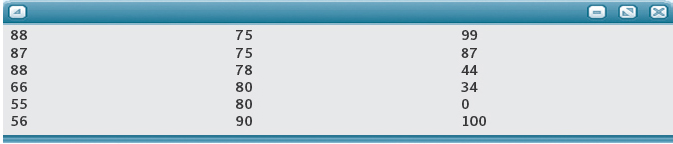
TESTING: When testing this program, it is the values of grades—not the size of the file—that determines the test cases. We must include values of MinGrade, MaxGrade, and values in between. The following data set meets this criterion. It is shown below in columns to save space.
Here is the output:
Problem-Solving Case Study
Favorite Rock Group
PROBLEM: At a small college, four campus rock groups have organized a fund-raising project, in which there will be a playoff among the groups. Each student gets to vote for his or her favorite group. Two prizes will be awarded: The best group gets a prize and the class with the best participation gets a prize.
INPUT: An arbitrary number of votes in a file voteFile, with each vote represented as a pair of numbers: a class number (1 through 4) and a rock group number (1 through 4); and group names, entered from the keyboard (to be used for printing the output).
OUTPUT: The following three items, written to a file reportFile: a tabular report showing how many votes each rock group received in each class, the total number of votes for each rock group, and the total number of votes cast by each class.
DISCUSSION: The data consists of a pair of numbers for each vote. The first number is the class number; the second number is the rock group number.
If we were doing the analysis by hand, our first task would be to go through the data, counting how many people in each class voted for each group. We would probably create a table with classes down the side and rock groups across the top. Each vote would be recorded as a hash mark in the appropriate row and column (see FIGURE 11.18).
When all of the votes have been recorded, a sum of each column tells us how many votes each group received. A sum of each row tells us how many people voted in each class.
As is so often the case, we can use this by-hand algorithm directly in our program. We can create a two-dimensional array in which each component is a counter for the number of votes for a particular group in each class; for example, the value indexed by [2][1] would be the counter for the votes in class 2 (sophomore) for group 1. Well, not quite. C++ arrays are indexed beginning at 0, so the correct array component would be indexed by [1][0]. When we input a class number and a group number, we must remember to subtract 1 from each value before using the values as an index into the array. Likewise, we must add 1 to an array index that represents a class number or group number before printing it out.
DATA STRUCTURES: A two-dimensional array named votes, where the rows represent classes and the columns represent groups. (2) A one-dimensional array of strings containing the names of the groups, to be used for printing (see FIGURE 11.19).
In our discussion we have used the word “class” to represent freshman, sophomore, junior, or senior. However, we need to be careful. We cannot use the word “class” in our program because it is a reserved word (as we will see in the next chapter). Let’s make the switch here and use the word “level” instead. In the design that follows, we use the named constants NUM_LEVELS and NUM_ROCK_GROUPS in place of the literal constants 4 and 4.
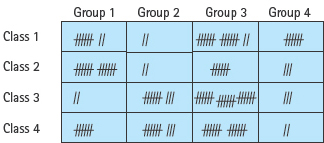
FIGURE 11.18 Vote-Counting Table

FIGURE 11.19 Data Structures for Favorite Rock Group Program
Main
Level 0
Get group names
Set votes array to 0
Read level, group from voteFile
WHILE NOT EOF on voteFile
Increment votes[level–1][group–1] by 1
Read level, rockGroup from voteFile
Write report to reportFile
Write totals per group to reportFile
Write totals per level to reportFile
Get RockGroup Names (Out: name)
Level 1
Print “Enter the names of the rock groups, one per line,
in the order they appear on the ballot.”
FOR rockGroup going from 0 through NUM_ROCK_GROUPS – 1
Read name[rockGroup]
Note that each rock group’s name is stored in the slot in the name array corresponding to its group’s number (minus 1). These names are useful when the totals are printed.
Set Votes to Zero (Out: votes)
FOR each level
FOR each group
Set votes[level][group] to 0
Write Report (In: votes, name; In/out: reportFile)
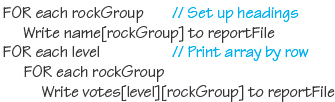
Write Totals per RockGroup (In: votes, name; Inout: reportFile)

Write Totals per Level (In: votes; In/out: reportFile)

MODULE STRUCTURE CHART
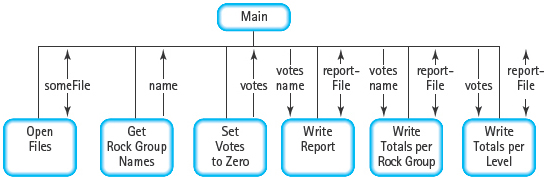



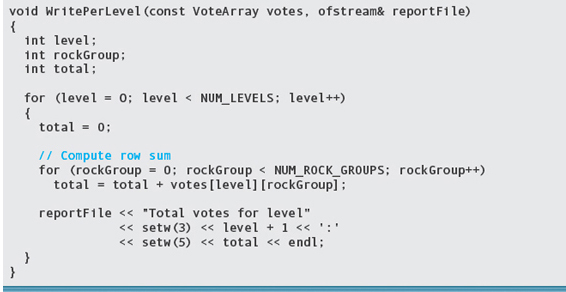
TESTING: This program was executed with the file data listed below. (We list the data in three columns to save space.) The keyboard I/O is shown below the file contents. In this data set, there is at least one vote for each group in each level. Case Study Follow-Up Exercise 7 asks you to outline a complete testing strategy for this program.
Input data on file Votes.dat:

Keyboard I/O:
Output on file Votes.out:

Testing and Debugging
One-Dimensional Arrays
The most common error in processing arrays is use of an out-of-bounds array index. That is, the program attempts to access a component using an index that is either less than 0 or greater than the array size minus 1. For example, given the declarations

the following For statement would print the 100 elements of the line array and then print a 101st value—the value that resides in memory immediately beyond the end of the array:

This error is easy to detect because 101 characters are printed instead of 100. The loop test should be counter < 100.
You won’t always use a simple For statement when accessing arrays, however. Suppose we read data into the line array in another part of the program. Let’s use a While statement that reads to the newline character:

This code seems reasonable enough, but what if the input line has more than 100 characters? After the hundredth character is read and stored into the array, the loop continues to execute with the array index out of bounds. Characters are stored into memory locations past the end of the array, wiping out other data values (or even machine language instructions in the program!).
The moral of the story is this: When processing arrays, pay special attention to the design of loop termination conditions. Always ask yourself if the loop could possibly keep running after the last array component has been processed.
Whenever an array index goes out of bounds, your first suspicion should be that a loop has failed to terminate properly. The second thing to check is any array access involving an index that is based on input data or a calculation. When an array index is input as data, a data validation check is an absolute necessity.
Complex Structures
As we have demonstrated in many examples in this chapter and the last, data structures may be combined in various ways: structs whose components are structs, structs whose components are arrays, arrays whose components are structs, arrays whose components are arrays (multidimensional arrays), and so forth. When arrays and structs are combined, confusion can arise about precisely where to place the operators for array element selection ([]) and struct member selection (.).
To summarize the correct placement of these operators, let’s use the StudentRec type we introduced earlier in this chapter:
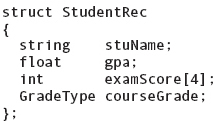
If we declare a variable of type StudentRec,
StudentRec student;
then what is the syntax for selecting the first exam score of the student (that is, for selecting element 0 of the examScore member of student)? The dot operator is a binary (two-operand) operator; its left operand denotes a struct variable, and its right operand is a member name:
StructVariable.MemberName
The [] operator is a unary (one-operand) operator; it comes immediately after an expression denoting an array:
Array[IndexExpression]
Therefore, the expression
student
denotes a struct variable; the expression
student.examScore
denotes an array; and the expression
student.examScore[0]
denotes an integer—the integer located in element 0 of the student.examScore array.
With arrays of structs or class objects, you must once again make sure that the [] and. operators are in the proper positions. Given the declaration
StudentRec gradeBook[150];
we can access the gpa member of the first element of the gradeBook array with the following expression:
gradeBook[0].gpa
The index [0] is correctly attached to the identifier gradeBook because gradeBook is the name of an array. Furthermore, the expression
gradeBook[0]
denotes a struct, so the dot operator selects the gpa member of this struct.
Multidimensional Arrays
Errors made while working with multidimensional arrays usually fall into two major categories: index expressions that are out of order and index range errors.
Suppose we were to expand the rock group program to accommodate ten rock groups and four levels. Let’s declare the votes array as
int votes[4][10];
The first dimension represents the levels, and the second represents the rock groups. An example of the first kind of error—incorrect order of the index expressions—would be to print out the votes array as follows:
If you look closely at the highlighted part of the code, you will see that the output statement specifies the array indexes in the wrong order. The loops march through the array with the first index ranging from 0 through 9 (instead of 0 through 3) and the second index ranging from 0 through 3 (instead of 0 through 9). The effect of executing this code may vary from system to system. The program may output the wrong array components and continue executing, or it may crash with a memory access error.
An example of the second kind of error—an incorrect index range in an otherwise correct loop—can be seen in this code:
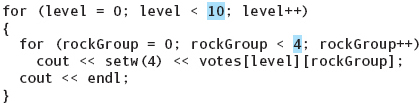
Here, the output statement correctly uses level for the first index and rockGroup for the second index. However, as the highlighting points out, the For statements use the opposite upper limits for the index variables—there are supposed to be four levels and ten groups. As with the preceding example, the effect of executing this code is undefined but is certainly wrong. A valuable way to prevent this kind of error is to use named constants instead of the literals 10 and 4. In the case study, we used NUM_LEVELS and NUM_ROCK_GROUPS. You are much more likely to spot an error (or to avoid making an error in the first place) if you write something like:
for (level = 0; level < NUM_LEVELS; level++)
than if you use a literal constant as the upper limit for the index variable.
Testing and Debugging Hints
1. When an individual component of a one-dimensional array is accessed, the index must be within the range 0 through the array size minus 1. Attempting to use an index value outside this range will cause the program to access memory locations outside the array.
2. The individual components of an array are themselves variables of the component type. When values are stored into an array, they should either be of the component type or be explicitly converted to the component type; otherwise, implicit type coercion occurs.
3. C++ does not allow aggregate operations on arrays; that is, it does not support aggregate assignment, aggregate comparison, aggregate I/O, or aggregate arithmetic. You must write code to do all of these operations, one array element at a time.
4. Omitting the size of a one-dimensional array in its declaration is permitted only in two cases: (1) when an array is declared as a parameter in a function heading and (2) when an array is initialized in its declaration. In all other declarations, you must specify the size of the array with a constant integer expression.
5. If an array parameter is incoming only, declare the parameter as const to prevent the function from accidentally modifying the caller’s argument.
6. Don’t pass an individual array component as an argument when the function expects to receive the base address of an entire array.
7. The size of an array is fixed at compile time, but the number of values actually stored there is determined at run time. Therefore, an array must be declared to be as large as it could ever be for the particular problem. Subarray processing is used to process only those components that contain data.
8. When functions perform subarray processing on a one-dimensional array, you must pass both the array and the number of items actually used or combine the array name and the number of items in a record.
9. With multidimensional arrays, you must use the proper number of indexes when referencing an array component. You should also make sure the indexes are in the correct order.
10. In loops that process multidimensional arrays, double-check the upper and lower bounds on each index variable to be sure they are correct for that dimension of the array.
11. When declaring a multidimensional array as a parameter, you must state the sizes of all but the first dimension. Also, these sizes must agree exactly with the sizes of the caller’s argument.
12. To eliminate the chance of a size mismatch (see item 11), use a Typedef statement to define a multidimensional array type.
13. If subarray processing is being used, combine the multidimensional array type and the number of actual values stored in each dimension into a record. Pass the record as a parameter.
14. In an expression, an array name without any index brackets is a pointer expression; its value is the base address of the array. The array name is considered a constant expression, so no assignment to it is possible. The following code shows correct and incorrect assignments.
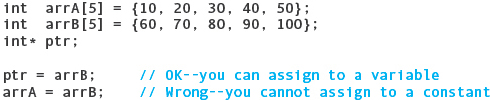
 Summary
Summary
The one-dimensional array is a homogeneous data structure that gives a name to a sequential group of like components. Each component is accessed by its relative position within the group (rather than by name, as in a struct), and each component is a variable of the component type. To access a particular component, we give the name of the array and an index that specifies which component of the group we want. The index can be an expression of any integral type, as long as it evaluates to an integer from 0 through the array size minus 1. Array components can be accessed in random order directly, or they can be accessed sequentially by stepping through the index values one at a time.
Two-dimensional arrays are useful for processing information that is represented naturally in tabular form. Processing data in two-dimensional arrays usually takes one of two forms: processing by row or processing by column. An array of arrays, which is useful if rows of the array must be passed as arguments, is an alternative way of defining a two-dimensional array.
A multidimensional array is a collection of like components that are ordered on more than one dimension. Each component is accessed by a set of indexes, one for each dimension, that represents the component’s position on the various dimensions. Each index may be thought of as describing a feature of a given array component.
If subarray processing is used, the array and the actual values stored in each dimension should be bound together into a record. This record should be passed as a parameter to functions.
 Quick Check Answers
Quick Check Answers
11.1.1 Because its elements are all of the same type.
11.1.2 An array.
11.1.3 float temps[24];
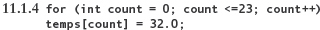
11.1.5 By its position. 11.1.6 The at operation checks the bounds of the array where as the [ ] operator does not.
11.2.1 mailList[12].street.at(2)

11.3.1 The index represents the hour during which the reading was taken, based on a 24-hour clock.

11.3.3 At compile time. 11.3.4 We need to keep track of how many entries are actually filled. 11.4.1 It is declared and accessed with two index values instead of one. 11.4.2 float allTemps[24][366];11.4.3 A table.
11.4.4 char board[25][25]; if (board[X][Y] == ‘#’) cout << “HIT” << endl;
11.5.1 void Quick (float table[], int numElements)
11.5.2 Nothing, it ignores it. 11.5.3 Because C++ stores a two-dimensional array in row order. Thus, you can leave off the number of rows, but not the number of columns. 11.5.4 The base address.

11.6.2 This process is referred to as random access. 11.6.3 randomly, along rows, along columns, and throughout the entire array.

11.6.5 int game[3][4] = { { 1, 2, 2 }, { 0, 1, 0 }, { 1, 0, 2 } };

11.8.2 If the problem has a homogeneous collection of data that is ordered by more than two indexes.
11.8.3 float decadeTemps[24][366][10]
 Exam Preparation Exercises
Exam Preparation Exercises
1. The components of an array can be of different types. True or false?
2. Arrays can have any type for their components. True or false?
3. Multidimensional arrays are limited to no more than four dimensions. True or false?
4. When you are declaring a one-dimensional array, its size must be specified with an integer. True or false?
5. The type of an index expression can be any of the integral types or an enumeration type. True or false?
6. What happens if a program tries to access an array using an index of − 1?
7. Which aggregate operations are allowed on arrays?
8. To what does the term “base address of an array” refer, and how is it used in a function call?
9. Which special type of array can be returned by a value-returning function?
10. If you want to use a nested loop to process a two-dimensional array row-by-row, which dimension’s index (row or column) would you increment in the inner loop, and which would you increment in the outer loop?
11. How many elements are there in each of the following arrays?
a. int x[27];
b. const int base = 10;
int y[base + 5];
c. int z[100][100][100][100];
12. What’s wrong with the following code segment?

13. What’s wrong with the following code segment?

14. What’s wrong with the following code segment?

15. What’s wrong with the following code segment?

16. What’s the potential danger in the following code segment?

17. What is the side effect of the following function?

18. What does the following code segment output?

19. Given the declaration of pattern in Exercise 18, what does the following loop output?
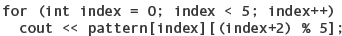
20. Given the declaration of pattern in Exercise 18, what does the following loop output?

21. Given the following declaration:
int examPrep [12][15];
a. Write a loop to print the first row of the array on one line on cout.
b. Write a loop to print the first column of the array on one line on cout.
c. Write a loop to print the first seven rows of the array, each on a single line.
d. Write a loop to print the entire array backward and upside down, so that the last line appears first, with the last column on the left.
22. An index expression (like those used with arrays) can be attached to any pointer variable, even if it doesn’t point to an array. True or false?
 Programming Warm-Up Exercises
Programming Warm-Up Exercises
1. Write the following declarations.
a. An array called topTenList, containing ten values of type string.
b. An enumeration type of the seven major colors of the spectrum, and a matching array declaration that can be indexed by the spectrum type. The array should be called colorMix, and should contain values of type float.
c. A two-dimensional array representing the days on a calendar page with up to 6 weeks. Call the array month, and declare an enumeration type consisting of the names of the days, which can be used to index the array columns. The weeks should be indexed by an int. For the component type of the array, declare a struct consisting of an int field called day, and a string field called activity.
2. Write a declaration of a named array type, and then declare three arrays of that type. The array type should be called DataSet, and the three arrays should be called input, output, and working. Each array should hold five float values.
3. Using the DataSet type declared in Exercise 2, declare an array of three data sets, called set.
4. Using the set array declared in Exercise 3, write a nested For loop that initializes all of the values of the three data sets to 0.0.
5. Write a function heading for a function called Equals that takes two arrays of the Data-Set type declared in Exercise 2 and returns a bool result. The array parameters should be const, as they are input-only parameters to the function.
6. Write the body of the Equals function described in Exercise 5. It should return true if each element of the first array is equal to its corresponding element in the second array.
7. A gallery needs to keep track of its paintings and photographs. It keeps at most 120 art works on its walls. Each one is described by the following information:
Artist (string)
Title (string)
Medium (oil, watercolor, pastel, acrylic, print, color photo, black-and-white photo)
Size (struct)
Height (int)
Width (int)
Room where it is hung (main, green, blue, north, south, entry, balcony)
Price (float)
Write a declaration for a struct that represents a piece of art. Declare struct and enumeration types as needed to make up the fields of the Artwork type. Write an additional declaration of a named array type that holds the list of all the artworks in the gallery. Lastly, declare an array of this type called currentList and an int variable numPieces. The numPieces variable contains the number of pieces represented in the array.
8. Write expressions that retrieve the following values from the array declared in Exercise 7.
a. The 37th work of art.
b. The title of the 12th work of art.
c. The width of the 85th work of art.
d. The room for the 120th work of art.
e. The first letter of the artist’s name for the 78th work of art.
9. Write a For loop that prints a list of the artist, title, and price for every artwork in the currentList array defined in Exercise 7.
10. Write a code segment that sums the prices of the artworks in the gallery described in Exercise 7.
11. Write a code segment that outputs the titles of the artworks in the blue room of the gallery described in Exercise 7.
12. Write a code segment that sums the prices of the oil paintings in the gallery described in Exercise 7 that are larger than 400 square inches in size.
13. A piano is tuned in a scale that is slightly unequal (called a “well-tempered scale”), rather than a perfectly scientific scale in which each note sounds at twice the frequency of the same note an octave below (called a “just scale”). For this reason, we can’t simply calculate the frequency of a note, but must keep it in a table. Declare a two-dimensional array (scale) to hold the frequencies of the well-tempered scale. A frequency is represented by a float value. The row dimension is indexed by an int value representing the octave (there are eight octaves, numbered 0 through 7), and the other should be indexed by an enumeration type (Notes) consisting of the names of the notes. When you write the declaration of the enumeration type, use only sharps (no flats). Thus the note names of an octave are C, CSHARP, D, DSHARP, E, F, FSHARP, G, GSHARP, A, ASHARP, and B, in that order.
14. Write a code segment that reads a table of frequencies into the scale array declared in Exercise 13 from a file called frequencies.dat. The frequency values are arranged one per line on the file.
15. Write a code segment that outputs the frequencies of the notes in the fourth octave of the scale array declared in Exercise 13.
16. Write a code segment that outputs the frequencies of all C notes in the scale array declared in Exercise 13.
17. Write a declaration for a four-dimensional array called humidity that is indexed by 10 years (0–9), 52 weeks (0–51), the 50 states (0–49), and an enumeration type consisting of MAX, MIN, and AVERAGE, called Type. The array holds humidity measurements (each component is a float).
18. Write a C++ function called Reset, which sets all of the components to zero in the humidity array declared in Exercise 17.
19. Write a declaration of a struct type called TimePlace that has three fields, one for each for the first three index values (year, week, state) in the humidity array declared in Exercise 17. TimePlace should have a fourth field called difference, which is a float. Then write a C++ function called MaxSpread that takes the humidity array as a parameter; scans through it to find the year, week, and state with the greatest difference in humidity over the course of a week; and returns these values as a TimePlace struct. If there is more than one week with the greatest difference, then the first one should be returned.
20. Write a code segment that outputs the AVERAGE component of the humidity array of Exercise 17, for all the weeks in the last 5 years for the 23rd state.
21. Declare a pointer variable charArrPointer and initialize it to point to the first element of a four-element char array named initials. Write assignment statements to indirectly store 'A', 'E', and 'W' into the first three elements of the array pointed to by charArrPointer.
 Programming Problems
Programming Problems
1. Imagine we are using a two-dimensional array as the basis for creating the game battleship. In the game of battleship a ‘~’ character entry in the array represents ocean (i.e., not a ship), a ‘#’ character represents a place in the ocean where part of a ship is present, and an ‘H’ character represents a place in the ocean where part of a ship is present and has been hit by a torpedo. Thus, a ship with all ‘H’ characters means the ship has been sunk. Declare a two-dimensional array that is 25 × 25 that represents the entire ocean and an If statement that prints “HIT” if a torpedo hits a ship given the coordinates X and Y. Write a C++ program that will read in a file representing a game board with 25 lines where each line has 25 characters corresponding to the description above. An example file might look like:

You should write a function called Fire that will take an X and Y coordinate and print “HIT” if a ship is hit and “MISS” if a ship is missed. If a ship is HIT you should update the array with an ‘H’ character to indicate the ship was hit. If a ship is hit that has already been hit at that location you should print “HIT AGAIN”. You should write a second function called FleetSunk that will determine if all the ships have been sunk. Your C++ program must then call these functions until all the ships have been sunk, at which point the program should display “The fleet was destroyed!”.
2. Write a program to play a game in which you try to sink a fleet of five navy vessels by guessing their locations on a grid. The program uses random numbers to position its ships on a 15 × 15 grid. The ships are of different lengths as follows:
Frigate: 2 locations
Tender: 2 locations
Destroyer: 3 locations
Cruiser: 3 locations
Carrier: 4 locations
The program must pick one square as the starting location, then pick the direction of the ship on the board, and mark off the number of squares in that direction to represent the size of the ship. It must not allow a ship to overlap with another ship or to run off the board.
The user enters coordinates in the range of 1 through 15 for the rows and A through O for the columns. The program checks this location, and reports whether it is a hit or a miss. If it is a hit, the program also checks whether the ship has been hit in every location that it occupies. If so, the ship is reported as sunk, and the program identifies which ship it is.
The user gets 60 shots to attempt to sink the fleet. If the user sinks all of the ships before using all 60 shots, then he or she wins the game. At the end of the game, the program should output the grid, so that the user can see where the ships are located.
3. Programming Warm-Up Exercises 7 to 12 deal with an array representing the inventory for an art gallery. Using the same representation, write a C++ program that reads the gallery’s inventory from a file called art.dat into the array. Then allow the user to look up the art by specifying any field in the record. As a reminder, here are the fields:
Artist (string)
Title (string)
Medium (oil, watercolor, pastel, acrylic, print, color photo, black-and-white photo)
Size (struct)
Height (int)
Width (int)
Room where it is hung (main, green, blue, north, south, entry, balcony)
Price (float)
The user should be able to specify a field, and a value for that field, and the program then returns all artworks that match those criteria. For example, the user may specify Artist and Smithely, and the program will output all of the information concerning every work in the gallery by that artist.
4. Programming Problem 1 in Chapter 7 asked you to write a program that takes a string as input and then outputs the corresponding words in the International Civil Aviation Organization (ICAO) alphabet that would be used to spell it out phonetically. For that program, you should have used a large Switch statement. Rewrite that program using an array of strings to hold the words of the alphabet, and index the array by the positions of the letters of the alphabet. By using an index with semantic content, you can avoid the need for the Switch statement. Be sure that you don’t try to index into the array using non-alphabetic characters, as that will result in an out-of-bounds access. For ease of reference, the ICAO alphabet is repeated here from Chapter 7:
A |
Alpha |
B |
Bravo |
C |
Charlie |
D |
Delta |
E |
Echo |
F |
Foxtrot |
G |
Golf |
H |
Hotel |
I |
India |
J |
Juliet |
K |
Kilo |
L |
Lima |
M |
Mike |
N |
November |
O |
Oscar |
P |
Papa |
Q |
Quebec |
R |
Romeo |
S |
Sierra |
T |
Tango |
U |
Uniform |
V |
Victor |
W |
Whiskey |
X |
X-ray |
Y |
Yankee |
Z |
Zulu |
Be sure to use proper formatting and appropriate comments in your code. Provide appropriate prompts to the user. The output should be clearly labeled and neatly formatted.
5. Programming Problem 6 in Chapter 6 asked you to write a program to check whether an input line is a palindrome (a word or phrase that is the same when read backward and forward). At that time, we needed to use the substring function to extract individual characters from a string. Because this is a cumbersome way to work with a string, we limited our definition of palindromes to just perfect palindromes—every letter and blank exactly the same in both forward and backward versions. Now that we know how to use arrays, we can expand the definition to ignore blanks, punctuation, and letter case. Thus
madam I’m adam
becomes
madamimadam
which is now a palindrome. Write a C++ program that reads a line of input and checks whether it is a palindrome on the basis of this less restrictive definition. Output the reversed line, with all blanks and punctuation removed, and all letters converted to lowercase along with the program’s decision.
6. Create a record representing a song on a CD or in an MP3 library. Write a C++ program that allows the user to specify the name of a data file containing songs (assume there are fewer than 200 songs on the file) and then reads the song data from the file into an array of songs. The user should then be allowed to enter the name of an artist, and the program will output all of the songs by that artist, along with any other information about the song that is in the array.
 Case Study Follow-Up
Case Study Follow-Up
1. There is no error checking in the Calculating Exam Statistics program. List at least two errors that could easily be checked.
2. All of the functions in the Calculating Exam Statistics program except OpenFiles, InputGrades, and PrintResults are value-returning functions. Rather than calculating and storing the values these functions calculate, could the values be calculated as they are being printed in PrintResults? If so, would it be a good idea to do it?
3. The solution to the exam statistics problem makes use of a technique called indexes with semantic content. Explain what this means in relation to this problem.
4. The heading for the output of the Calculating Exam Statistics program is coded directly in the OpenFiles function. Remove this statement, prompt the user to enter a heading, and write this heading on the output file.
5. Exercise 4 had the heading in the exam statistics program written in the OpenFiles function. Would it be better to have the PrintResults function prompt for the heading?
6. Rewrite the Favorite Rock Group program using an enumerated type for class (or level). Which code is more readable and self-documenting?
7. Design a complete testing strategy for the Favorite Rock Group program.
 To understand the structure of a one-dimensional array.
To understand the structure of a one-dimensional array. To know how to use a one-dimensional array in solving a problem.
To know how to use a one-dimensional array in solving a problem. To understand the structure of arrays of records.
To understand the structure of arrays of records. To know how index values can be chosen to have semantic content.
To know how index values can be chosen to have semantic content. To understand the structure of a two-dimensional array.
To understand the structure of a two-dimensional array. To understand the structure of a multidimensional array.
To understand the structure of a multidimensional array.




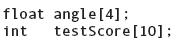







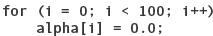


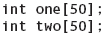

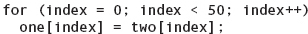

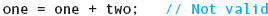













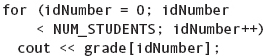



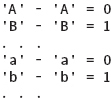













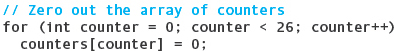
















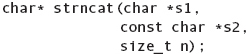
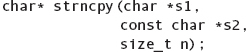
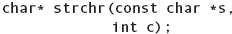

































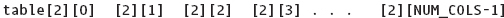
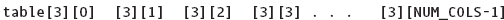








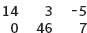





























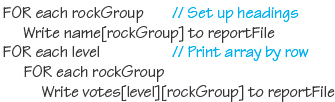


















 Summary
Summary