3
Numeric Types, Expressions, and Output
KNOWLEDGE GOALS
 To understand implicit type coercion and explicit type conversion.
To understand implicit type coercion and explicit type conversion.
 To recognize and understand the purpose of function arguments.
To recognize and understand the purpose of function arguments.
 To learn and use additional operations associated with the string type.
To learn and use additional operations associated with the string type.
 To learn how to format program statements in a clear and readable fashion.
To learn how to format program statements in a clear and readable fashion.
SKILL GOALS
To be able to:
 Declare named constants and variables of type int and float.
Declare named constants and variables of type int and float.
 Construct simple arithmetic expressions. Evaluate simple arithmetic expressions.
Construct simple arithmetic expressions. Evaluate simple arithmetic expressions.
 Construct and evaluate expressions that contain multiple arithmetic operations.
Construct and evaluate expressions that contain multiple arithmetic operations.
 Call (invoke) a value-returning function.
Call (invoke) a value-returning function.
 Use C++ library functions in expressions.
Use C++ library functions in expressions.
 Call (invoke) a void function (one that does not return a function value).
Call (invoke) a void function (one that does not return a function value).
 Use C++ manipulators to format output.
Use C++ manipulators to format output.
In Chapter 2, we examined enough C++ syntax to be able to construct simple programs using assignment and output. We focused on the char and string types and saw how to construct expressions using the concatenation operator. In this chapter, we continue to write programs that use assignment and output, but we concentrate on additional built-in data types: int and float. These numeric types are supported by numerous operators that allow us to construct complex arithmetic expressions. We show how to make expressions even more powerful by using library functions—prewritten functions that are part of every C++ system and are available for use by any program.
We also return to the subject of formatting output. In particular, we consider the special features that C++ provides for formatting numbers as they are output. We finish by looking at some additional operations on string data.
3.1 Overview of C++ Data Types
The C++ built-in data types are organized into simple types, structured types, and address types (see Figure 3.1). Do not feel overwhelmed by the quantity of data types shown in Figure 3.1. Our purpose is simply to give you an overall picture of what is available in C++. This chapter concentrates on the integral and floating types. Details of the other types come later in the book. First we look at the integral types (those used primarily to represent integers), and then we consider the floating types (used to represent real numbers containing decimal points).
3.2 Numeric Data Types
You already are familiar with the basic concepts of integer and real numbers in math. However, as used on a computer, the corresponding data types have certain limitations.
Integral Types
The data types char, short, int, and long are known as integral types (or integer types) because they refer to integer values—that is, whole numbers with no fractional part. (We postpone talking about the remaining integral type, bool, until Chapter 5.)
In C++, the simplest form of integer value is a sequence of one or more digits:
Commas are not allowed.
In most cases, a minus sign preceding an integer value makes the integer negative:

FIGURE 3.1 C++ Data Types
The exception is when you explicitly add the reserved word unsigned to the data type name:
unsigned int
An unsigned integer value is assumed to be only positive or zero. The unsigned types are used primarily in specialized situations. We rarely use unsigned in this book.
The data types char, short, int, and long are intended to represent different sizes of integers, from smaller (fewer bits) to larger (more bits). The sizes are machine dependent; that is, they may vary from machine to machine. The following table shows sample ranges:
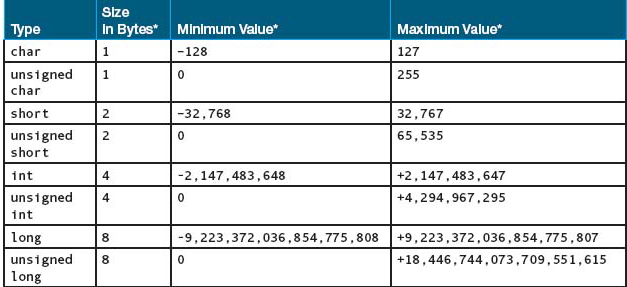
*These values are for one particular machine. Your machine’s values may be different.
On another machine, the size of an int might be the same as the size of a long. In general, the more bytes in the memory cell, the larger the integer value that can be stored there.
Although we used the char type in Chapter 2 to store character data such as 'A', C++ classifies char as an integral type because it also allows char to be used for storing integer values with a very limited range.
int is by far the most common data type for manipulating integer data. In the LeapYear program created in Chapter 1, the identifier, year, is of data type int. You nearly always use int for manipulating integer values, but sometimes you have to use long if your program requires values larger than the maximum int value. (On an embedded computer, such as the controller for a microwave oven, the range of int values might be from –32,768 through +32,767. More commonly, ints range from –2,147,483,648 through +2,147,483,647.) If your program tries to compute a value larger than your machine’s maximum value, the result is integer overflow. Some machines display an error message when overflow occurs, but others don’t. We talk more about overflow in later chapters.
One caution about integer values in C++: A literal constant beginning with a zero is taken to be an octal (base-8) number instead of a decimal (base-10) number. Thus, if you write
015
the C++ compiler takes this to mean the decimal number 13. If you aren’t familiar with the octal number system, don’t worry about why octal 15 is the same as decimal 13. The important thing to remember is that you should not start a decimal integer constant with a zero (unless you simply want the number 0, which is the same in both octal and decimal). In Chapter 10, we discuss the various integral types in more detail.
Floating-Point Types
Floating-point types (or floating types), the second major category of simple types in C++, are used to represent real numbers. Floating-point numbers have an integer part and a fractional part, with a decimal point in between. Either the integer part or the fractional part, but not both, may be missing. Here are some examples:

Starting 0.57 with a zero does not make it an octal number. It is only with integer values that a leading zero indicates an octal number.
Just as the integral types in C++ come in different sizes (char, short, int, and long), so do the floating-point types. In increasing order of size, the floating-point types are float, double (meaning double precision), and long double. Again, the exact sizes are machine dependent. Each larger size potentially gives us a wider range of values and more precision (the number of significant digits in the number), but at the expense of more memory space to hold the number.
Floating-point values also can have an exponent, as in scientific notation. (In scientific notation, a number is written as a value multiplied by 10 to some power.) Instead of writing 3.504 × 1012, in C++ we write 3.504E12. The E means exponent of base-10. The number preceding the letter E doesn’t need to include a decimal point. Here are some examples of floating-point numbers in scientific notation:
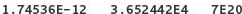
Most programs don’t need the double and long double types. The float type usually provides sufficient precision and range of values for floating-point numbers. Most personal computers provide float values with a precision of six or seven significant digits and a maximum value of about 3.4E+38. We use floating-point values to represent money and interest rate in the case study at the end of this chapter. The following table shows sample ranges for floating-point data types:

*These values are for one particular machine. Your machine’s values may be different.
There is one more thing you should know about floating-point numbers: Computers cannot always represent them exactly. You learned in Chapter 1 that the computer stores all data in binary (base-2) form. Many floating-point values can only be approximated in the binary number system. Don’t be surprised if your program prints out the number 4.8 as 4.7999998. In most cases, slight inaccuracies in the rightmost fractional digits are to be expected and are not the result of programmer error.
QUICK CHECK

3.2.1 What are the four integral types discussed in this section? (p. 92)
3.2.2 What does an integral type refer to? (p. 92)
3.2.3 What reserved word must be used for values that are only positive? (p. 93)
3.2.4 What is the smallest and largest integral types in terms of bytes studied in this section? (p. 93)
3.2.5 What is the smallest and largest integral types in terms of values? (p. 93)
3.2.6 What is the result if your program tries to compute a value larger than your machine’s maximum value? (p. 94)
3.2.7 What type is used to represent real numbers? (p. 94)
3.2.8 What are the floating-point types? (p. 94)
3.2.9 How do we write the real number 3.504 × 1012 as a C++ literal value? (p. 94)
3.3 Declarations for Numeric Types
Just as with the types char and string, we can declare named constants and variables of type int and float. Such declarations use the same syntax as before, except that the literals and the names of the data types are different.
Named Constant Declarations
In the case of named constant declarations, the literal values in the declarations are numeric instead of being characters in single or double quotes. Here are some example constant declarations that define values of type int and float. For comparison, declarations of char and string values are included.

Although character and string literals are put in quotes, literal integers and floating-point numbers are not, because there is no chance of confusing them with identifiers. Why? Because identifiers must start with a letter or underscore, and numbers must start with a
SOFTWARE ENGINEERING TIP
Using Named Constants Instead of Literals

It’s a good idea to use named constants instead of literals. In addition to making your program more readable, named constants can make your program easier to modify. Suppose you wrote a program last year to compute taxes. In several places you used the literal 0.05, which was the sales tax rate at the time. Now the rate has gone up to 0.06. To change your program, you must locate every literal 0.05 and change it to 0.06. If 0.05 is used for some other reason—to compute deductions, for example—you also need to look at each place where it is used, figure out what it is used for, and then decide whether to change it.
The process is much simpler if you use a named constant. Instead of using a literal constant, suppose you had declared a named constant, TAX_RATE, with a value of 0.05. To change your program, you would simply change the declaration, setting TAX_RATE equal to 0.06. This one modification automatically changes all of the tax rate computations without affecting the other places where 0.05 is used.
C++ allows us to declare constants with different names but the same value. If a value has different meanings in different parts of a program, it makes sense to declare and use a constant with an appropriate name for each meaning.
Named constants are also reliable—they protect us from mistakes. If you mistype the name PI as PO, for example, the C++ compiler tells you that the name PO has not been declared. At the same time, even though we recognize that the number 3.14149 is a mistyped version of pi (3.14159), the number is perfectly acceptable to the compiler. As a consequence, it won’t warn us that anything is wrong.
Variable Declarations
We declare numeric variables the same way in which we declare char and string variables, except that we use the names of numeric types. The following are valid variable declarations:

Given the declarations

the following are appropriate assignment statements:

In each of these assignment statements, the data type of the expression matches the data type of the variable to which it is assigned. Later in the chapter we see what happens if the data types do not match.
QUICK CHECK

3.3.1 Write a named constant declaration for the mathematical value of π = 3.14159. (p. 95)
3.3.2 Given the variable declarations:
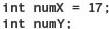
What is the type of the expression: (p. 96)
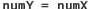
3.3.3 How does the declaration of named constants and variables of type int and float differ from declarations of named constants and variables of type string? (pp. 95–96)
3.4 Simple Arithmetic Expressions
Now that we have looked at declaration and assignment, let’s consider how to calculate with values of numeric types. Calculations are performed with expressions. Here, we look at simple expressions that involve at most one operator so that we may examine each operator in detail. Later, we move on to compound expressions that combine multiple operations.
Arithmetic Operators
Expressions are made up of constants, variables, and operators. The following are all valid expressions:
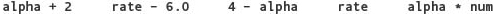
The operators allowed in an expression depend on the data types of the constants and variables in the expression. The arithmetic operators are

The first two operators are unary operators—they take just one operand. The remaining five are binary operators, taking two operands. Unary plus and minus are used as follows:
Unary operator An operator that has just one operand.
Binary operator An operator that has two operands.
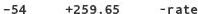
Programmers rarely use the unary plus. Without any sign, a numeric constant is assumed to be positive anyway.
You may not be familiar with integer division and modulus (%). Let’s look at these operations more closely. Note that % is used only with integers. When you divide one integer by another, you get an integer quotient and a remainder. Integer division gives only the integer quotient, and % gives only the remainder. (If either operand is negative, the sign of the remainder may vary from one C++ compiler to another.1)
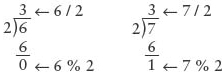
In contrast, floating-point division yields a floating-point result. For example, the expression
7.0 / 2.0
yields the value 3.5.
Here are some expressions using arithmetic operators and their values:
Expression |
Value |
3 + 6 |
9 |
3.4 - 6.1 |
–2.7 |
2 * 3 |
6 |
8 / 2 |
4 |
8.0 / 2.0 |
4.0 |
8 / 8 |
1 |
8 / 9 |
0 |
8 / 7 |
1 |
8 % 8 |
0 |
8 % 9 |
8 |
8 % 7 |
1 |
0 % 7 |
0 |
5 % 2.3 |
error (Both operands must be integers) |
Be careful with division and modulus. The expressions 7 / 0 and 7 % 0 both produce errors. With floating-point values, 7.0 / 0.0, produces a special infinity value that is displayed as “inf” when output. The computer cannot divide by zero.
Because variables are allowed in expressions, the following are valid assignments:
alpha = num + 6;
alpha = num / 2;
num = alpha * 2;
num = 6 % alpha;
alpha = alpha + 1;
num = num + alpha;
As we saw with assignment statements involving string expressions, the same variable can appear on both sides of the assignment operator. In the case of
num = num + alpha;
the value in num and the value in alpha are added together, and then the sum of the two values is stored back into num, replacing the previous value stored there. This example shows the difference between mathematical equality and assignment. The mathematical equality
num = num + alpha
is true only when alpha equals 0. The assignment statement
num = num + alpha;
is valid for any value of alpha.
Here’s a simple program that uses arithmetic expressions.
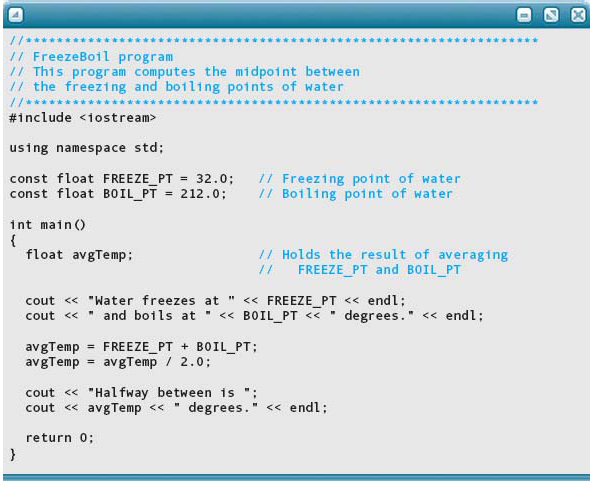
The program begins with a comment that explains what the program does. Next comes a declaration section where we define the constants FREEZE_PT and BOIL_PT. The body of the main function includes a declaration of the variable avgTemp and then a sequence of executable statements. These statements print a message, add FREEZE_PT and BOIL_PT, divide the sum by 2, and finally print the result. Here is the output:

Increment and Decrement Operators
In addition to the arithmetic operators, C++ provides increment and decrement operators:
++ |
Increment |
-- |
Decrement |
These unary operators take a single variable name as an operand. For integer and floatingpoint operands, the effect is to add 1 to (or subtract 1 from) the operand. If num currently contains the value 8, the statement
num++;
causes num to contain 9. You can achieve the same effect by writing the following assignment statement:
num = num + 1;
C++ programmers typically prefer the increment operator, however. (Recall from Chapter 1 how the C++ language got its name: C++ is an enhanced [“incremented”] version of the C language.)
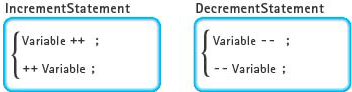
The ++ and -- operators can be either prefix operators:
++num;
or postfix operators:
num++;
Both of these statements behave in exactly the same way: They add 1 to whatever is in num. The choice between the two is a matter of personal preference.
C++ allows the use of ++ and -- in the middle of a larger expression:
alpha = num++ * 3;
In this case, the postfix form of ++ does not give the same result as the prefix form. In Chapter 7, we explain the ++ and -- operators in detail. In the meantime, you should use them only to increment or decrement a variable as a separate, standalone statement:
QUICK CHECK

3.4.1 If integer1 contains 37 and integer2 contains 7, what is the result of the expression 37 % 7? (pp. 97–98)
3.4.2 What does the expression 7 / 0 produce? (p. 98)
3.4.3 What value does the expression 7.0 / 0.0 produce? (p. 98)
3.4.4 What effect does the expression num++ produce? (p. 100)
3.5 Compound Arithmetic Expressions
The expressions we have used so far have contained at most a single arithmetic operator. We have also been careful not to mix integer and floating-point values in the same expression. Now we look at more complicated expressions—ones that are composed of several operators and ones that contain mixed data types.
Precedence Rules
Arithmetic expressions can be made up of many constants, variables, operators, and parentheses. In what order are the operations performed? For example, in the assignment statement
avgTemp = FREEZE_PT + BOIL_PT / 2.0;
is FREEZE_PT + BOIL_PT calculated first or is BOIL_PT / 2.0 calculated first?
The basic arithmetic operators (unary +, unary –, + for addition, – for subtraction, * for multiplication, / for division, and % for modulus) are ordered the same way mathematical operators are, according to precedence rules:
Precedence Level |
Operators |
Highest precedence level: |
Unary + Unary - |
Middle level: |
* / % |
Lowest level: |
+ - |
Because division has higher precedence than addition, the expression in the example given earlier is implicitly parenthesized as
FREEZE_PT + (BOIL_PT / 2.0)
That is, we first divide BOIL_PT by 2.0 and then add FREEZE_PT to the result.
You can change the order of evaluation by using parentheses. In the statement
avgTemp = (FREEZE_PT + BOIL_PT) / 2.0;
FREEZE_PT and BOIL_PT are added first, and then their sum is divided by 2.0. We evaluate subexpressions in parentheses first and then follow the precedence of the operators.
When an arithmetic expression has several binary operators with the same precedence, their grouping order (or associativity) is from left to right. The expression
int1 – int2 + int3
means (int1 – int2) + int3, not int1 – (int2 + int3). As another example, we would use the expression
(float1 + float2) / float1 * 3.0
to evaluate the expression in parentheses first, then divide the sum by float1, and finally multiply the result by 3.0. Following are some more examples.

In C++, all unary operators (such as unary + and unary -) have right-to-left associativity. Although this fact may seem strange at first, it turns out to be the natural grouping order. For example, − + × means − (+ ×) rather than the meaningless (− +) ×.
Type Coercion and Type Casting
Integer values and floating-point values are stored differently inside a computer’s memory. The pattern of bits that represents the constant 2 does not look at all like the pattern of bits that represents the constant 2.0. What happens if we mix integer and floating-point values together in an assignment statement or an arithmetic expression? Let’s look first at assignment statements.
Assignment Statements
If you make the declarations

then someInt can hold only integer values, and someFloat can hold only floating-point values. The assignment statement
someFloat = 12;
may seem to store the integer value 12 into someFloat, but this is not true. The computer refuses to store anything other than a float value into someFloat. The compiler inserts extra machine language instructions that first convert 12 into 12.0 and then store 12.0 into someFloat. This implicit (automatic) conversion of a value from one data type to another is known as type coercion.
Type coercion The implicit (automatic) conversion of a value from one data type to another.
The statement
someInt = 4.8;
also causes type coercion. When a floating-point value is assigned to an int variable, the fractional part is truncated (cut off). As a result, someInt is assigned the value 4.
With both of the previously given assignment statements, the program would be less confusing for someone to read if we avoided mixing data types:
someFloat = 12.0;
someInt = 4;
More often, it is not just constants but entire expressions that are involved in type coercion. Both of the assignments
someFloat = 3 * someInt + 2;
someInt = 5.2 / someFloat – anotherFloat;
lead to type coercion. Storing the result of an int expression into a float variable generally doesn’t cause loss of information; a whole number such as 24 can be represented in floating-point form as 24.0. However, storing the result of a floating-point expression into an int variable can cause loss of information because the fractional part is truncated. It is easy to overlook the assignment of a floating-point expression to an int variable when we try to discover why our program is producing the wrong answers.
To make our programs as clear (and error free) as possible, we can use explicit type casting (or type conversion). A C++ cast operation consists of a data type name and then, within parentheses, the expression to be converted:2
Type casting The explicit conversion of a value from one data type to another; also called type conversion.
someFloat = float(3 * someInt + 2);
someInt = int(5.2 / someFloat – anotherFloat);
Both of the statements
someInt = someFloat + 8.2;
someInt = int(someFloat + 8.2);
produce identical results. The only difference is in clarity. With the cast operation, it is perfectly clear to the programmer and to others reading the program that the mixing of types is intentional, not an oversight. Countless errors have resulted from unintentional mixing of types.
There is a nice way to round off rather than truncate a floating-point value before storing it into an int variable. Here is the way to do it:
someInt = int(someFloat + 0.5);
With pencil and paper, see for yourself what gets stored into someInt when someFloat contains 4.7. Now try it again, assuming someFloat contains 4.2. (This technique of rounding by adding 0.5 assumes that someFloat is a positive number.)
Arithmetic Expressions
So far we have been talking about mixing data types across the assignment operator (=). It’s also possible to mix data types within an expression:
someInt * someFloat
4.8 + someInt – 3
Such expressions are called mixed type (or mixed mode) expressions.
Mixed type expression An expression that contains operands of different data types; also called mixed mode expression
Whenever an integer value and a floating-point value are joined by an operator, implicit type coercion occurs:
1. The integer value is temporarily coerced to a floating-point value.
2. The operation is performed.
3. The result is a floating-point value.
Let’s examine how the machine evaluates the expression 4.8 + someInt – 3, where someInt contains the value 2. First, the operands of the + operator have mixed types, so the value of someInt is coerced to 2.0. (This conversion is only temporary; it does not affect the value that is stored in someInt.) The addition takes place, yielding a value of 6.8. Next, the subtraction (-) operator joins a floating-point value (6.8) and an integer value (3). The value 3 is coerced to 3.0, the subtraction takes place, and the result is the floating-point value 3.8.
Just as with assignment statements, you can use explicit type casts within expressions to lessen the risk of errors. Writing expressions such as
float(someInt) * someFloat
4.8 + float(someInt – 3)
makes it clear what your intentions are.
Explicit type casts are not only valuable for program clarity, but are also mandatory in some cases for correct programming. Given the declarations

suppose that sum and count currently contain 60 and 80, respectively. If sum represents the sum of a group of integer values and count represents the number of values, let’s find the average value:

Unfortunately, this statement stores the value 0.0 into average. Here’s why: The expression to the right of the assignment operator is not a mixed type expression. Both operands of the / operator are of type int, so integer division is performed. When 60 is divided by 80, it yields the integer value 0. Next, the machine implicitly coerces 0 to the value 0.0 before storing it into average.
Here is the way to find the average correctly, as well as clearly:
average = float(sum) / float(count);
This statement gives us floating-point division instead of integer division. As a result, the value 0.75 is stored into average.
As a final remark about type coercion and type conversion, you may have noticed that we have concentrated on the int and float types. It is also possible to stir char values, short values, and double values into the pot. The results can be confusing and unexpected. In Chapter 10, we return to this topic with a more detailed discussion. In the meantime, you should avoid mixing values of these types within an expression.
SOFTWARE MAINTENANCE CASE STUDY:
Precedence Error
PROBLEM: Numerous programming errors result from writing expressions that fail to take the precedence rules into account. For example, take a look at the following program, which is supposed to compute the radius of a circle from its circumference.

The problem is that, given a circumference of 10, for which the radius is approximately 1.59, the program outputs 15.707963265. What’s wrong? Because the circumference is stored as a constant, the only remaining potential source of error must be the expression that computes the radius.
We know that to get the radius from the circumference, we divide the circumference by 2 times pi, which is what the statement does. Or does it? Division and multiplication have the same precedence, so they are evaluated from left to right. The expression is really computing
radius = (circumference / 2) * 3.14159265;
In our test case, the application divides 10 by 2, giving 5, which is then multiplied by pi to get 15.707963265. What we really want is this:
radius = circumference / (2 * 3.14159265);
Whenever you face a debugging task, take the time first to narrow down your search for the bug by a process of elimination. Once you isolate the section of code that is the most likely source of the error, consider the common mistakes associated with those kinds of statements. Efficient debugging is not a hit-or-miss process. It takes careful thought and organization to zero in on a bug.
MAY WE INTRODUCE
Blaise Pascal

One of the great historical figures in the world of computing was the French mathematician and religious philosopher Blaise Pascal (1623–1662), the inventor of one of the earliest known mechanical calculators.
Pascal’s father, Etienne, was a noble in the French court, a tax collector, and a mathematician. Pascal’s mother died when Pascal was 3 years old. Five years later, the family moved to Paris and Etienne took over the education of the children. Pascal quickly showed a talent for mathematics. When he was only 17, he published a mathematical essay that earned the jealous envy of René Descartes, one of the founders of modern geometry. (Pascal’s work actually had been completed before he was 16.) It was based on a theorem, which he called the hexagrammum mysticum, or mystic hexagram, that described the inscription of hexagons in conic sections (parabolas, hyperbolas, and ellipses). In addition to the theorem (now called Pascal’s theorem), his essay included more than 400 corollaries.
When Pascal was about 20, he constructed a mechanical calculator that performed addition and subtraction of eight-digit numbers. The calculator required the user to dial in the numbers to be added or subtracted; the sum or difference then appeared in a set of windows. It is believed that his motivation for building this machine was to aid his father in collecting taxes. The earliest version of the machine did, indeed, split the numbers into six decimal digits and two fractional digits, as would be used for calculating sums of money. The machine was hailed by his contemporaries as a great advance in mathematics, and Pascal built several more in different forms. It achieved such popularity that many fake, nonfunctional copies were built by others and displayed as novelties. Several of Pascal’s calculators are now exhibited in various museums.
Pascal’s box, as it is called, was long believed to be the first mechanical calculator. However, in 1950, a letter from Wilhelm Shickard to Johannes Kepler, written in 1624, was discovered. This letter described an even more sophisticated calculator built by Shickard 20 years prior to Pascal’s box. Unfortunately, the machine was destroyed in a fire and never rebuilt.
During his twenties, Pascal solved several difficult problems related to the cycloid curve, indirectly contributing to the development of differential calculus. Working with Pierre de Fermat, he laid the foundation of the calculus of probabilities and combinatorial analysis. One of the results of this work came to be known as Pascal’s triangle, which simplifies the calculation of the coefficients of the expansion of (x + y)n, where n is a positive integer.
Pascal also published a treatise on air pressure and conducted experiments showing that barometric pressure decreases with altitude, which helped to confirm theories that had been proposed by Galileo and Torricelli. His work on fluid dynamics forms a significant part of the foundation of that field. Among the most famous of his contributions is Pascal’s law, which states that pressure applied to a fluid in a closed vessel is transmitted uniformly throughout the fluid.
When Pascal was 23, his father became ill, and the family was visited by two disciples of Jansenism, a reform movement in the Catholic Church that had begun six years earlier. The family converted, and five years later one of his sisters entered a convent. Initially, Pascal was not so taken with the new movement, but by the time he was 31, his sister had persuaded him to abandon the world and devote himself to religion.
Pascal’s religious works are considered no less brilliant than his mathematical and scientific writings. Some consider Provincial Letters, his series of 18 essays on various aspects of religion, to mark the beginning of modern French prose.
Pascal returned briefly to mathematics when he was 35. A year later his health, which had always been poor, took a turn for the worse. Unable to perform his usual work, he devoted himself to helping the less fortunate. Three years later, he died while staying with his sister, having given his own house to a poor family.
QUICK CHECK

3.5.1 What happens to the fractional portion of a floating-point number when it is converted to an integer type? (pp. 102–103)
3.5.2 What operators studied in this section have the highest precedence level? (p. 101)
3.5.3 What operators studied in this section have the lowest precedence level? (p. 101)
3.5.4 What must we use to force the evaluation of a subexpression outside of the regular precedence rules? (p. 101)
3.5.5 What must we use in order to mix integer and floating-point values in the same expression? (p. 101)
3.5.6 Assume we have a variable x declared as an int and a variable y declared as a float and the following expression: x = y + 1.25. What explicit type cast must be used to make this a valid expression? (p. 103)
3.5.7 How must the following expression be modified in order to correctly produce the correct percentage for a student’s score and the total points available in an assignment. Assume that score and total have type int: (p. 104)
float percentage = (score / total) * 100.0;
3.5.8 What is the result of the following expression? (p. 101)
27 + 8 * 6 – 44 % 5
3.6 Function Calls and Library Functions
Value-Returning Functions
At the beginning of Chapter 2, we showed a program consisting of three functions: main, Square, and Cube. Here is a listing of a portion of the program:

At the time we introduced the program, we said that all three functions are value-returning functions. Square returns to its caller a value—the square of the number sent to it. Cube returns a value—the cube of the number sent to it. Likewise, main returns to the operating system a value—the program’s exit status.
Let’s focus for a moment on the Cube function. The main function contains the following statement:
cout << " and the cube of 27 is " << Cube(27) << endl;
In this statement, the master (main) causes the servant (Cube) to compute the cube of 27 and give the result back to main. The sequence of symbols
Cube(27)
is a function call or function invocation. The computer temporarily puts the main function on hold and starts the Cube function running. When Cube has finished doing its work, the computer goes back to main and picks up where it left off.
Function call (function invocation) The mechanism that transfers control to a function.
In the preceding function call, the number 27 is known as an argument (or actual parameter). Arguments make it possible for the same function to work on many different values. For example, we can write statements like these:
cout << Cube(4);
cout << Cube(16);
Here’s the syntax template for a function call:
FunctionCall
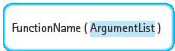
The argument list is a way for functions to communicate with one another. Some functions, such as Square and Cube, have a single argument in the argument list. Other functions, such as main, have no arguments. Finally, some other functions have two, three, or more arguments in the list, separated by commas.
Argument list A mechanism by which functions communicate with one another.
Value-returning functions are used in expressions in much the same way that variables and constants are. The value computed by a function simply takes its place in the expression. For example, the statement
someInt = Cube(2) * 10;
stores the value 80 into someInt. First the Cube function is executed to compute the cube of 2, which is 8. The value 8—now available for use in the rest of the expression—is then multiplied by 10. Note that a function call has higher precedence than multiplication, which makes sense if you consider that the function result must be available before the multiplication takes place.
Here are several facts about value-returning functions:
 The function call is used within an expression; it does not appear as a separate statement.
The function call is used within an expression; it does not appear as a separate statement.
 The function computes a value (result) that is then available for use in the expression.
The function computes a value (result) that is then available for use in the expression.
 The function returns exactly one result—no more, no less.
The function returns exactly one result—no more, no less.
The Cube function expects to be given (or passed) an argument of type int. What happens if the caller passes a float argument? The answer is that the compiler applies implicit type coercion. Thus the function call Cube(6.9) computes the cube of 6, not 6.9.
Although we have been using literal constants as arguments to Cube, the argument could just as easily be a variable or a named constant. In fact, the argument to this value-returning function can be any expression of the appropriate type. In the statement
alpha = Cube(int1 * int1 + int2 * int2);
the expression in the argument list is evaluated first, and only its result is passed to the function. For example, if int1 contains 3 and int2 contains 5, the preceding function call passes 34 as the argument to Cube.
An expression in a function’s argument list can even include calls to functions. For example, we could use the Square function to rewrite the earlier assignment statement as follows:
alpha = Cube(Square(int1) + Square(int2));
Library Functions
Certain computations, such as taking square roots or finding the absolute value of a number, are very common in programs. It would be an enormous waste of time if every programmer had to start from scratch and create functions to perform these tasks. To help make the programmer’s life easier, every C++ system includes a standard library—a large collection of prewritten functions, data types, and other items that any C++ programmer may use. The functions in the library are divided into separate files called header files. Here is a very small sample of some standard library functions:
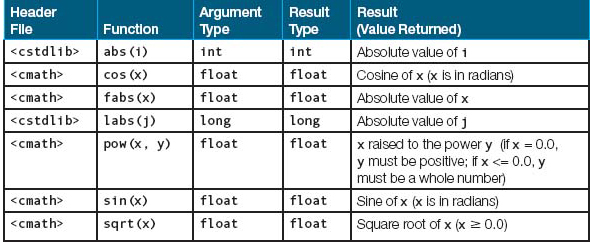
Technically, the entries in the table marked float should all say double. These library functions perform their work using double-precision floating-point values. Because of type coercion, however, the functions work just as you would like them to when you pass float values to them.
Using a library function is easy. First, you place an #include directive near the top of your program, specifying the appropriate header file. This directive ensures that the C++ preprocessor inserts declarations into your program that give the compiler some information about the function. Then, whenever you want to use the function, you just make a function call. Here’s a sample program that calls functions, along with its output:
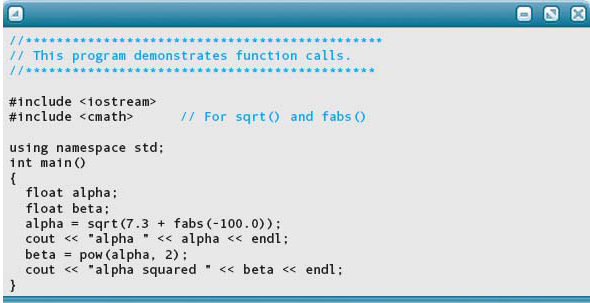
Output:

The C++ standard library provides dozens of functions for you to use. Appendix C lists a much larger selection than we have presented here. You should glance briefly at this appendix now, keeping in mind that much of the terminology and C++ language notation will make sense only after you have read more of this book.
Void Functions
Thus far, we have looked only at value-returning functions. In fact, C++ provides another kind of function. Look at the following definition for function CalcPay. Notice how it begins with the word void instead of a data type like int or float:

CalcPay is an example of a function that doesn’t return a value to its caller. Instead, it just performs some action and then quits. We refer to a function like this as a non-value-returning function, a void-returning function, or, most briefly, a void function. In some programming languages, a void function is known as a procedure.
Void function (procedure) A function that does not return a function value to its caller and is invoked as a separate statement.
Void functions are invoked differently from value-returning functions. With a value-returning function, the function call appears in an expression. With a void function, the function call is a separate, standalone statement. In the LeapYear program, main calls the IsLeapYear function using an expression like this:
Value-returning function A function that returns a single value to its caller and is invoked from within an expression.
if (IsLeapYear(year))
By comparison, a call to a void function has the flavor of a command or built-in instruction:
DoThis(x, y, z);
DoThat();
For the next few chapters, we won’t be writing our own functions (except main). Instead, we’ll be concentrating on how to use existing functions, including functions for performing stream input and output. Some of these functions are value-returning functions; others are void functions. Again, we emphasize the difference in how you invoke these two kinds of functions: A call to a value-returning function occurs in an expression, whereas a call to a void function occurs as a separate statement.
QUICK CHECK

3.6.1 Where do arguments appear, and what is their purpose? (pp. 107–108)
3.6.2 Write an expression that computes the square root of 17.5. (p. 109)
3.6.3 How does a call to a void function differ from a call to a value-returning function? (p. 110)
3.6.4 What does the computer do to main when a function is invoked? (p. 107)
3.6.5 What are in libraries and what are they used for? (p. 108)
3.6.6 How does a programmer use a library? (p. 109)
3.7 Formatting Output
To format a program’s output means to control how it appears visually on the screen or on a printout. In Chapter 2, we considered two kinds of output formatting: creating extra blank lines by using the endl manipulator and inserting blanks within a line by putting extra blanks into literal strings. In this section, we examine how to format the output values themselves.
Integers and Strings
By default, consecutive integer and string values are output with no spaces between them. If the variables i, j, and k contain the values 15, 2, and 6, respectively, the statement
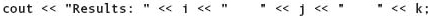
outputs the following stream of characters:
Results: 1526
Without spacing between the numbers, this output is difficult to interpret.
To separate the output values, you could print a single blank (as a char constant) between the numbers:
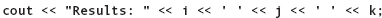
This statement produces the following output:
Results: 15 2 6
If you want even more spacing between items, you can use literal strings containing blanks, as we discussed in Chapter 2:
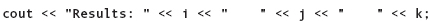
The resulting output is shown here:
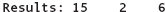
Another way to control the horizontal spacing of the output is to use manipulators. For some time now, we have been using the endl manipulator to terminate an output line. In C++, a manipulator is a rather curious thing that behaves like a function but travels in the disguise of a data object. Like a function, a manipulator causes some action to occur. But like a data object, a manipulator can appear in the midst of a series of insertion operations:
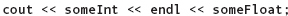
Manipulators are used only in input and output statements.
Here’s a revised syntax template for the output statement, showing that not only arithmetic and string expressions but also manipulators are allowed:
OutputStatement

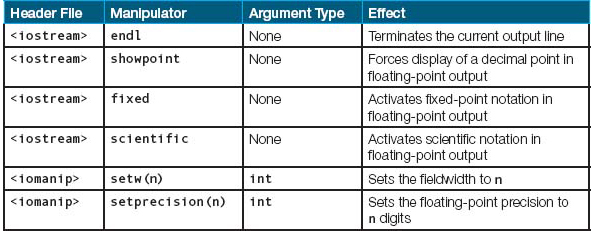
The C++ standard library supplies many manipulators, but for now we look at only five of them: endl, setw, fixed, showpoint, and setprecision. The endl, fixed, and showpoint manipulators come “for free” when we #include the header file iostream to perform I/O. The other two manipulators, setw and setprecision, require that we also #include the header file iomanip:
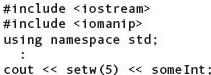
The manipulator setw—meaning “set width”—lets us control how many character positions the next data item should occupy when it is output (setw is typically used for formatting numbers and strings, rather than char data). The argument to setw is an integer expression called the fieldwidth specification; the group of character positions is called the field. The next data item to be output is printed right-justified (filled with blanks on the left to fill up the field).
Let’s look at an example. Suppose two int variables have been assigned values as follows:
ans = 33;
num = 7132;
Then the following output statements produce the output shown to their right:

In Example 1, each value is specified to occupy enough positions so that there is at least one space separating them. In Example 2, the values all run together because the fieldwidth specified for each value is just large enough to hold the value. This output obviously is not very readable. It’s better to make the fieldwidth larger than the minimum size required so that some space is left between values. Example 3 includes extra blanks for readability; Example 4 does not. In Example 5, the fieldwidth is not large enough for the value in ans, so it automatically expands to make room for all of the digits.
Setting the fieldwidth is a one-time action. This preference holds only for the very next item to be output. After this output, the fieldwidth resets to 0, meaning “extend the field to exactly as many positions as are needed.” For example, in the statement
cout << "Hi" << setw(5) << ans << num;
the fieldwidth resets to 0 after ans is output. As a result, we get the output
Hi 337132
Here is a short program that illustrates these manipulators, followed by the output.
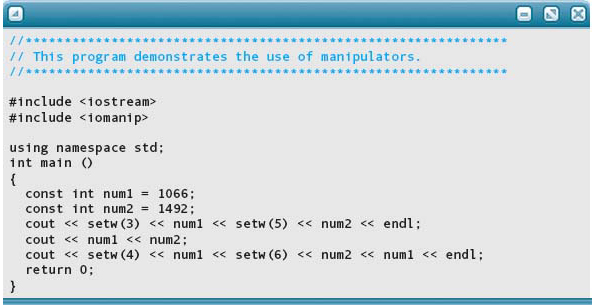
Output:

Floating-Point Numbers
You can specify a fieldwidth for floating-point values just as for integer values. When doing so, you must remember to allow for the decimal point when you specify the number of character positions. For example, the value 4.85 requires four output positions, not three. If x contains the value 4.85, the statement
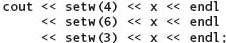
produces the following output:

In the third line, a fieldwidth of 3 isn’t sufficient, so the field automatically expands to accommodate the number.
Several other issues arise when we are working with the output of floating-point numbers. First, large floating-point values are printed in scientific (E) notation. The value 123456789.5 may print on some systems as
1.23457e+08
You can use the manipulator named fixed to force all subsequent floating-point output to appear in decimal form rather than scientific notation:
cout << fixed << 3.8 * x;
Second, if the number is a whole number, C++ doesn’t print a decimal point. Thus the value 95.0 is output as
95
To force decimal points to be displayed in subsequent floating-point output, even for whole numbers, you can use the manipulator showpoint:
cout << showpoint << floatVar;
Third, you often would like to control the number of decimal places (digits to the right of the decimal point) that are displayed. If your program is supposed to print the 5% sales tax on a certain amount, for example, the statement
cout << "Tax is $" << price * 0.05;
may produce the following output:
Tax is $17.7435
Obviously, you would prefer to display the result to two decimal places. To do so, use the setprecision manipulator as follows:
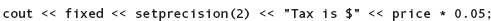
Provided that fixed has already been specified, the argument to setprecision specifies the desired number of decimal places. Unlike setw, which applies only to the very next item printed, the value sent to setprecision remains in effect for all subsequent output (until you change it with another call to setprecision). Here are some examples in which setprecision is used in conjunction with setw, given that x is 310.0 and y is 4.827:

Again, the total number of print positions is expanded if the fieldwidth specified by setw is too narrow. However, the number of positions for fractional digits is controlled entirely by the argument to setprecision.
For a scientific application, it may be desirable to force output values to be in scientific notation, which is accomplished using the scientific manipulator. When the output stream is in scientific mode, setprecision determines the number of digits displayed after the decimal point. We should also note that if neither fixed nor scientific mode has been set, then setprecision determines the number of digits displayed preceding the exponent. Here are two examples:

In the first case, scientific notation is output because the number is big enough to cause the output stream to automatically change to e notation. (If a smaller number is subsequently output, the stream switches back to normal formatting.) Because no manipulator for fixed or scientific formatting has previously been inserted into the stream, setprecision formats the number to have five digits preceding the e. In the second case, the scientific manipulator switches the stream into scientific mode. In this mode, setprecision formats the number with five digits between the decimal point and the e. Subsequent output will be in scientific notation until a fixed manipulator is used.
The following table summarizes the manipulators we have discussed in this section. Manipulators without arguments are available through the header file iostream. Those with arguments require the header file iomanip.
The following program and output demonstrates the use of these manipulators.
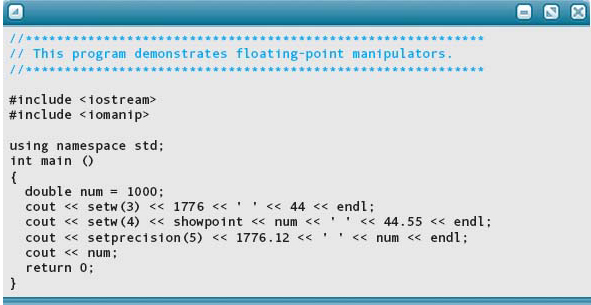
Output:

MATTERS OF STYLE
Program Formatting

As far as the compiler is concerned, C++ statements are free format: They can appear anywhere on a line, more than one can appear on a single line, and one statement can span several lines. The compiler needs blanks (or comments or new lines) only to separate important symbols, and it needs semicolons only to terminate statements. Of course, these restrictions are the bare minimum. In fact, it is extremely important that your programs be readable, both for your sake and for the sake of anyone else who has to examine them.
When you write an outline for an English paper, you follow certain rules of indentation to make it readable. These same kinds of rules can make your programs easier to read. It is much easier to spot a mistake in a neatly formatted program than in a messy one. Thus you should keep your program neatly formatted while you are working on it. If you’ve gotten lazy and let your program become messy while you were making a series of changes, take the time to straighten it up. Often the source of an error becomes obvious during the process of formatting the code.
Take a look at the following program for computing the cost per square foot of a house. Although it compiles and runs correctly, it does not conform to any formatting standards.
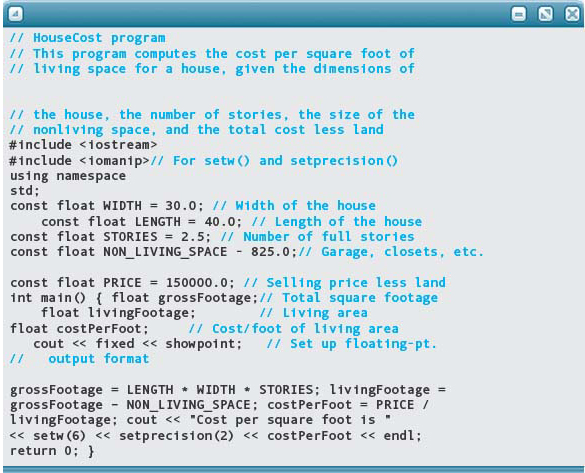
Now look at the same program with proper formatting:
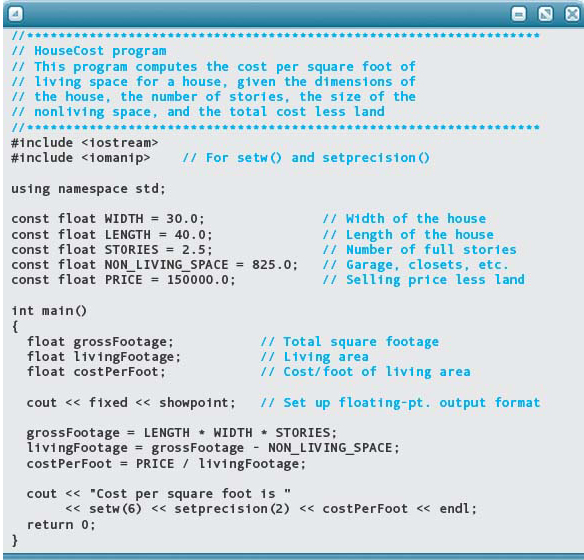
Need we say more?
Appendix F talks about programming style. Use it as a guide when you are writing programs.
QUICK CHECK

3.7.1 Neatly formatting a program makes it easier to find errors. True or false? (pp. 117–118)
3.7.2 Which stream manipulator would you use to set the output precision for floating-point values? (pp. 114–115)
3.7.3 What library must be included to set the output precision for floating-point values? (p. 116)
3.7.4 What does the setw manipulator do for us? (p. 112)
3.7.5 What does the showpoint manipulator do? (p. 114)
3.7.6 What manipulator is used to output scientific notation? (p. 115)
3.8 Additional string Operations
Now that we have introduced numeric types and function calls, we can take advantage of additional features of the string data type. In this section, we introduce four functions that operate on strings: length, size, find, and substr.
The length and size Functions
The length function, when applied to a string variable, returns an unsigned integer value that equals the number of characters currently in the string. If myName is a string variable, a call to the length function looks like this:
myName.length()
You specify the name of a string variable (here, myName), then a dot (period), and then the function name and argument list. The length function requires no arguments to be passed to it, but you still must use parentheses to signify an empty argument list. Also, length is a value-returning function, so the function call must appear within an expression:

Perhaps you are wondering about the syntax in a function call like
firstName.length()
This expression uses a C++ notation called dot notation. There is a dot (period) between the variable name firstName and the function name length. Certain programmer-defined data types, such as string, have functions that are tightly associated with them, and dot notation is required in the function calls. Suppose you forget to use dot notation, writing the function call as
length()
You will get a compile-time error message, something like UNDECLARED IDENTIFIER. The compiler thinks you are trying to call an ordinary function named length, not the length function associated with the string type. In Chapter 4, we discuss the meaning behind dot notation.
Some people refer to the length of a string as its size. To accommodate both terms, the string type provides a function named size. Both firstName.size() and firstName.length() return the same value.
The length and size functions return an unsigned integer value of type string::size_type. Most C++ compilers, however, allow you to declare the results to be of type int.3

Before leaving the length and size functions, we should remark on capitalization conventions for identifiers. In the guidelines given in Chapter 2, we said that in this book we begin the names of programmer-defined functions and data types with uppercase letters. We follow this convention when we write our own functions and data types in later chapters. However, we have no control over the capitalization of items supplied by the C++ standard library. Identifiers in the standard library generally use all lowercase letters.
The find Function
The find function searches a string to find the first occurrence of a particular substring and returns an unsigned integer value (of type string::size_type) giving the result of the search. The substring, passed as an argument to the function, can be a literal string or a string expression. If str1 and str2 are of type string, all of the following are valid function calls:

In each of the three cases, str1 is searched to see if the specified substring can be found within it. If so, the function returns the position in str1 where the match begins. (Positions are numbered starting at 0, so the first character in a string is in position 0, the second is in position 1, and so on.) For a successful search, the match must be exact, including identical capitalization. If the substring could not be found, the function returns the special value string::npos, a named constant meaning “not a position within the string.” (string::npos is the largest possible value of type string::size_type, a number like 4294967295 on many machines. This value is suitable for “not a valid position” because the string operations do not let any string become this long.)
Given the code segment

the statement
position = phrase.find("the");
assigns to position the value 12, whereas the statement
position = phrase.find("rat");
assigns to position the value string::npos, because there was no match.
The argument to the find function can also be a char value. In this case, find searches for the first occurrence of that character within the string and returns its position (or string::npos, if the character was not found). For example, the following program
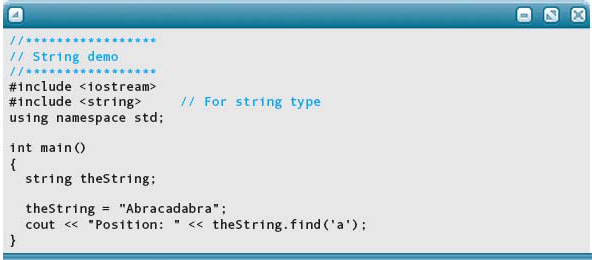
outputs

which is the position of the first occurrence of a lowercase a in theString.
Below are some more examples of calls to the find function, assuming the following code segment has been executed:

In the fourth example, there are two copies of the substring "Pro" in str1, but find returns only the position of the first copy. Also notice that the copies can be either separate words or parts of words—find merely tries to match the sequence of characters given in the argument list. The final example demonstrates that the argument can be as simple as a single character, even a single blank.
The substr Function
The substr function returns a particular substring of a string. Assuming myString is of type string, here is a sample function call:
myString.substr(5, 20)
The first argument is an unsigned integer that specifies a position within the string, and the second is an unsigned integer that specifies the length of the desired substring. The function returns the piece of the string that starts with the specified position and continues for the number of characters given by the second argument. Note that substr doesn’t change myString. Instead, it returns a new, temporary string value that is a copy of a portion of the string. Following are some examples, assuming the statement
myString = "Programming and Problem Solving";
has been executed.

In the third example, specifying a length of 0 produces the null string as the result. The fourth example shows what happens if the second argument specifies more characters than are present after the starting position: substr returns the characters from the starting position to the end of the string. The last example illustrates that the first argument, the position, must not be beyond the end of the string.
Because substr returns a value of type string, you can use it with the concatenation operator (+) to copy pieces of strings and join them together to form new strings. The find and length functions can be useful in determining the location and end of a piece of a string to be passed to substr as arguments.
Here is a program that uses find and substr to break a string into parts.
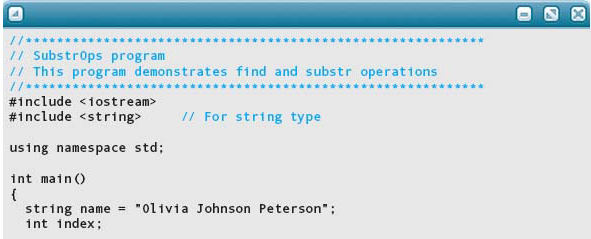
Output:

The program uses find to locate the first blank and substr to extract the substring beginning with the first character and extending to just before the first blank. This substring is stored in firstName. The original string is redefined to contain the string following the first blank through to the end. The process is repeated to extract the middle name. The remaining string is stored in lastName. Perhaps this process seems trivial—after all, we could have just created the three separate strings. However, in Chapter 4, when we examine how to read a string from the keyboard, this general algorithm will prove useful in breaking an input string into different parts.
Accessing Characters Within a String: The at Function
Sometimes it would be very useful to access characters directly by their position. C++ allows us to do so easily. You can access an individual character in a string by using the at function. Here is an example call to this function:
someCharVariable = someString.at(somePosition);
Within a string, the first character is at position 0, the second is at position 1, and so forth. Therefore, the value of somePosition must be greater than or equal to 0 and less than or equal to the string length minus 1. For example, if inputStr is a string object and letter is a char variable, the statement
letter = inputStr.at(2);
accesses the character at position 2 of the string (the third character) and copies it into letter. Calling at with a value that lies outside the allowable range will generate an error message.
Converting to Lowercase and Uppercase
When working with character data, you may sometimes find that you need to convert a lowercase letter to uppercase, or vice versa. Fortunately, the programming technique required to do these conversions is easy—a simple call to a library function is all it takes. Through the header file <cctype>, the standard library provides two value-returning functions named toupper and tolower. Here are their descriptions:

*Technically, both the argument and the return value are of type int. Conceptually, the functions operate on character data.
The value returned by each function is just the original character if the condition is not met. For example, tolower('M') returns the character 'm', whereas tolower('+') returns '+'.
The following program uses toupper to ensure that the first letter of a string is uppercase. The first letter is accessed and changed to uppercase. Then the string is concatenated with the original string with the first character removed.
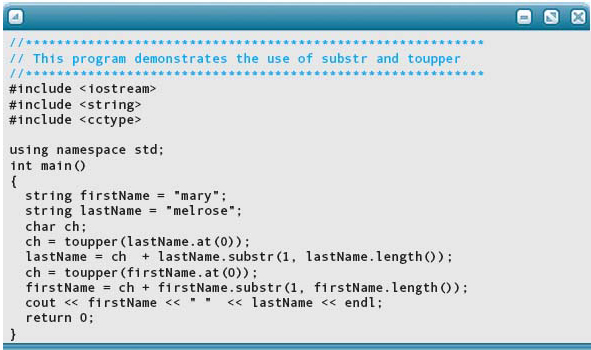
Output:

The following table summarizes the string and character operations we have looked at in this chapter.
*Technically, if pos is too large, the program generates what is called an out-of-range exception. Unless we write additional program code to deal explicitly with this exception, the program simply terminates with a message such as ABNORMAL PROGRAM TERMINATION. Using more advanced capabilities in C++, it is possible to catch such errors before the program halts and take corrective action.
SOFTWARE ENGINEERING TIP
Understanding Before Changing

When you are trying to get a program to run and you come across an error, it’s tempting to start changing parts of the program in an attempt to make it work. Don’t! You’ll nearly always make things worse. It’s essential that you understand what is causing the error and carefully think through the solution. The only thing you should try is running the program with different data to determine the pattern of the unexpected behavior.
There is no magic trick that can automatically fix a program. If the compiler tells you that a semicolon or a right brace is missing, you need to examine the program and determine precisely what the problem is. Perhaps you accidentally typed a colon instead of a semicolon. Or maybe there’s an extra left brace.
If the source of a problem isn’t immediately obvious, a good rule of thumb is to leave the computer and go somewhere else to quietly look over a printed copy of the program. Studies show that people who do all of their debugging away from the computer actually get their programs to work in less time and in the end produce better programs than those who continue to work on the machine—more proof that there is still no mechanical substitute for human thought.
Source: Basili, V. R., and Selby, R. W., “Comparing the Effectiveness of Software Testing Strategies,” IEEE Trans. on Software Engineering SE-13, no. 12 (1987): 1278–1296.
QUICK CHECK

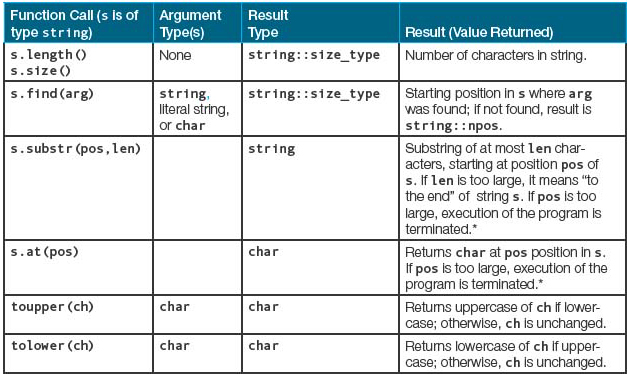
3.8.1 What is the value of the following expression, given that the string variable quickCheck contains the string "My friend I shall be pedagogic"? (p. 122)
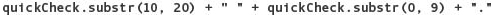
3.8.2 What is the result of the following expression if myString contains "Hello"? (p. 123)
myString.at(2)
3.8.3 What is the result of the following expression if myString contains "Hello"? (p. 120)
myString.find("H");
3.8.4 What library function can be used to make a character lowercase? (p. 124)
Problem-Solving Case Study
Mortgage Payment Calculator
PROBLEM: Your parents are thinking about refinancing their mortgage and have asked you to help them with the calculations. Now that you’re learning C++, you realize that you can save yourself a lot of calculator button-pressing by writing a program to do the calculations automatically.
DISCUSSION: In the case study in Chapter 1, we said that there are often three obvious steps in almost any problem of this type:
1. Get the data.
2. Compute the results.
3. Output the results.
The data we need in this case are the amount of money to borrow, the number of years for the loan, and the interest rate. From these three values, the monthly payment can be calculated. Although you could solve this problem for your parents using paper-and-pencil calculations, you might as well write a program to solve it. You can make the data values be constants now; later, when you learn how to input values, you can rewrite the program.
After a chat with your parents, you find that they still owe $50,000 on the house and have exactly 7 years worth of payments to go. The latest quote from their credit union is for an interest rate of 5.24% with no closing costs.
Define Constants
Set LOAN_AMOUNT = 50000.00
Set NUMBER_OF_YEARS = 7
Set INTEREST_RATE = 0.0524
You vaguely recall seeing the formula for determining payments, using compound interest, but you can’t remember it. You decide to go to the Internet and look it up.
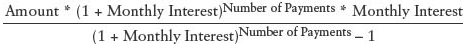
Hmmm. This may actually be easier to do on the computer than on a calculator. Two values taken to the number of payments power looks daunting. Fortunately, the C++ <cmath> header file, which we looked at earlier, contains a number of mathematical functions including the power function. Before you actually enter the values in the formula, two intermediate values need to be calculated: monthly interest rate and number of payments.
Calculate Values
Set monthlyInterest to YEARLY_INTEREST divided by 12
Set numberOfPayments to NUMBER_OF_YEARS times 12
Set payment to (LOAN_AMOUNT * pow(1+monthlyInterest,
numberOfPayments) * monthlyInterest) / (pow(1+monthlyInterest,
numberOfPayments) – 1)
Now all that is left is to print out the answer in a clear, concise format. Let’s use a precision of 2 for the floating-point values and a fixed format.
Output Results
Print “For a loan amount of “LOAN_AMOUNT” with an interest rate of
“YEARLY_INTEREST” and a “NUMBER_OF_YEARS “year mortgage,”
Print “your monthly payments are $“payment”.”
From the algorithm, we can create tables of constants and variables to help us write the declarations for the program.
CONSTANTS
Name |
Value |
Function |
LOAN_AMOUNT |
50000.00 |
Amount of the loan |
YEARLY_INTEREST |
0.0524 |
Yearly interest rate |
NUMBER_OF_YEARS |
7 |
Number of years |
VARIABLES
Name |
Data Type |
Description |
monthlyInterest |
float |
Monthly interest rate |
numberOfPayments |
int |
Total number of payments |
payment |
int |
Monthly payment |

Output:

Something looks strange about the output: The interest should be 0.0524, not 0.05. The decision to use a precision of 2 was correct for dollars and cents, but not for interest rates, which are rarely whole percentages. You are asked to make this correction in Case Study Follow-Up Exercise 1.
Testing and Debugging
1. An int constant other than 0 should not start with a zero. If it starts with a zero, it is an octal (base-8) number.
2. Watch out for integer division. The expression 47 / 100 yields 0, the integer quotient. This is one of the major sources of erroneous output in C++ programs.
3. When using the / and % operators, remember that division by zero is not allowed.
4. Double-check every expression against the precedence rules to be sure that the operations are performed in the desired order.
5. Avoid mixing integer and floating-point values in expressions. If you must mix them, consider using explicit type casts to reduce the chance of mistakes.
6. For each assignment statement, check that the expression result has the same data type as the variable to the left of the assignment operator (=). If not, consider using an explicit type cast for clarity and safety. Also, remember that storing a floating-point value into an int variable truncates the fractional part.
7. For every library function you use in your program, be sure to #include the appropriate header file.
8. Examine each call to a library function to confirm that you have the right number of arguments and that the data types of the arguments are correct.
9. With the string type, positions of characters within a string are numbered starting at 0, not 1.
10. If the cause of an error in a program is not obvious, leave the computer and study a printed listing. Change your program only after you understand the source of the error.
 Summary
Summary
C++ provides several built-in numeric data types, of which the most commonly used are int and float. The integral types are based on the mathematical integers, but the computer limits the range of integer values that can be represented. The floating-point types are based on the mathematical notion of real numbers. As with integers, the computer limits the range of floating-point numbers that can be represented. Also, it limits the number of digits of precision in floating-point values. We can write literals of type float in several forms, including scientific (E) notation.
Much of the computation of a program is performed in arithmetic expressions. Expressions can contain more than one operator. The order in which the operations are performed is determined by precedence rules. In arithmetic expressions, multiplication, division, and modulus are performed first, followed by addition and subtraction. Multiple binary (two-operand) operations of the same precedence are grouped from left to right. You can use parentheses to override the precedence rules.
Expressions may include function calls. C++ supports two kinds of functions: value-returning functions and void functions. A value-returning function is called by writing its name and argument list as part of an expression. A void function is called by writing its name and argument list as a complete C++ statement.
The C++ standard library is an integral part of every C++ system. It contains many prewritten data types, functions, and other items that any programmer can use. These items are accessed by using #include directives to the C++ preprocessor, which then inserts the appropriate header files into the program.
In output statements, the setw, showpoint, fixed, and setprecision manipulators can be used to control the appearance of values in the output. These manipulators do not affect the values actually stored in memory—only their appearance when displayed on the output device.
Not only should the output produced by a program be easy to read, but the format of the program itself should also be clear and readable. C++ is a free-format language. Using a consistent style that incorporates indentation, blank lines, and spaces within lines will help you (and other programmers) understand and work with your programs.
The string type provides a collection of useful functions that can be applied to strings: length and size return the number of characters in a string, find looks for a substring within a larger string, and substr returns a specified substring of a string. The char type provides two functions, toupper and tolower, that allow the user to force a character to be uppercase or lowercase, respectively. Characters within a string can be accessed by using the at function.
 Quick Check Answers
Quick Check Answers
3.2.1 char, short, int, and long 3.2.2 integer values (whole numbers without a fractional part). 3.2.3 unsigned 3.2.4 smallest: char or unsigned char; largest: long or unsigned long. 3.2.5 smallest: long; largest: unsigned long. 3.2.6 The result is integer overflow. 3.2.7 The floating-point type. 3.2.8 float, double, long double. 3.2.9 3.504E12 3.3.1 const float PI = 3.14159. 3.3.2 int 3.3.3 The declarations are exactly the same, except that we use the reserved word int or float instead of string, and we assign a numerical value to the constant rather than a string value. 3.4.1 37 % 7 = 2 3.4.2 An error. 3.4.3 A special infinity value displayed as “inf”. 3.4.4 It adds 1 to the value of the variable num. 3.5.1 The fractional part is truncated. 3.5.2 Unary + and -. 3.5.3 Binary + and -. 3.5.4 Parentheses ( ) 3.5.5 Type casting 3.5.6 x = int(y + 1.25). 3.5.7 float percentage = (float(score) / float(total)) * 100.0; 3.5.8 27 + (8 * 6) – (44 % 5) = 27 + 48 – 4 = 71 3.6.1 They appear in the call to a function, between parentheses, and are used to pass data to or from a function. 3.6.2 sqrt(17.5) 3.6.3 A void function call appears as a separate statement rather than being part of an expression. 3.6.4 It puts main temporarily on hold. 3.6.5 Libraries contain commonly used functions so programmers do not need to start from scratch. 3.6.6 They use the #include directive to get access to the library. 3.7.1 True. 3.7.2 setprecision 3.7.3 iomanip 3.7.4 It lets us control how many character positions the next data item should occupy when it is output. 3.7.5 It forces a decimal point to be displayed in subsequent floating-point output. 3.7.6 scientific 3.8.1 "I shall be pedagogic My friend." 3.8.2 'l' 3.8.3 0 3.8.4 tolower.
 Exam Preparation Exercises
Exam Preparation Exercises
1. The integer and floating-point types in C++ are considered (simple, address, structured) data types. (Circle one)
2. What are the four integral types in C++? List them in order of size, from smallest to largest.
3. What is the result if the computer tries to calculate a value that is larger than the maximum integer allowed for a given integral type?
4. In a floating-point value, what does it mean when the letter E appears as part of a number?
5. Label each of the following as an integer or floating-point declaration, and indicate whether it is a constant or a variable declaration.

6. What are the two meanings of the / operator?
7. What is the result of each of the following expressions?
a. 27 + 8 / 5 – 7
b. 27.0 + 8.0 / 5.0 – 7.0
c. 25 % 7 + 9.0
d. 17++
e. int(15.0 + 12.0 * 2.2 – 3 * 7)
f. 23--
g. 18 / 1.0
8. List the following operators in the order of highest precedence to lowest precedence. If a set of operators has the same precedence, write them enclosed in square brackets within the ordered list.
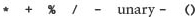
9. The increment and decrement operators can either precede or follow their operand. True or false?
10. Match the following terms to the definitions given below.
a. Unary operator
b. Binary operator
c. Type coercion
d. Type casting
e. Mixed type expression
f. Argument list
g. Void function
i. A computation involving both floating-point and integer values
ii. An operator with two operands
iii. A function that is called as a separate statement
iv. Explicitly changing a value of one type into another
v. The values that appear between the parentheses in a function call
vi. An operator with just one operand
vii. Implicitly changing a value of one type into another
11. The statement
count = count + 1;
is equivalent to which C++ operator?
12. How do you write a C++ cast operation?
13. Is main a value-returning function or a void function?
14. Show precisely what the following statement outputs:
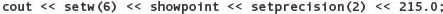
15. The prefix and postfix forms of the increment operator (++) always behave the same way. We can use them interchangeably anywhere in C++ code. True or false? Explain your answer.
16. Which data type do we use to declare a variable to hold the result of applying the length function to a string?
17. Given that the string variables str1 and str2 contain
"you ought to start with logic"
and
"ou"
respectively, what is the result of each of the following expressions?

18. What does the manipulator fixed do?
19. What does the function toupper do?
20. What does the function tolower do?
 Programming Warm-Up Exercises
Programming Warm-Up Exercises
1. Write an expression to convert a time stored in the int variables hours, minutes, and seconds into the number of seconds represented by the time. For example, if hours contains 2, minutes contains 20, and seconds contains 12, then the result of your expression should be 8412.
2. Given an int variable days that contains a number of days:
a. Write an expression that gives the number of whole weeks corresponding to days. For example, if days contains 23, then the number of whole weeks is 3.
b. Write an expression that gives the number of days remaining after taking the whole weeks out of the value in days. For example, if days contains 23, then the number of days remaining after 3 whole weeks is 2.
3. Given int variables called dollars, quarters, dimes, nickels, and pennies, write an expression that computes the total amount of the money represented in the variables. The result should be an integer value representing the number of pennies in the total.
4. Given the same variables as in Exercise 3, compute the total but store it in a floating-point variable so that the integral part is dollars and the fractional part is cents.
5. Write an assignment statement that adds 3 to the value in int variable count.
6. Write expressions that implement the following formulas.
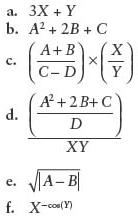
7. Write a series of assignment statements that find the first three positions of the string "and" in a string variable sentence. The positions should be stored in int variables called first, second, and third. You may declare additional variables if necessary. The contents of sentence should remain unchanged.
8. Write an assignment statement to find the first blank in a string variable called name. Store the result plus one in the int variable startOfMiddle.
9. Write an output statement that prints the value in float variable money in eight spaces on the line, with a leading dollar sign ($), and two digits of decimal precision.
10. Write an output statement that prints the value in double variable distance in 15 spaces on a line with 5 digits of decimal precision.
11. If you include the header file climits in a program, the constants INT_MAX and INT_MIN are provided, which give the highest and lowest int values that can be represented. Write the include statement for this file as well as an output statement that displays the two values, identified with appropriate labels.
12. Write the statement that accesses the third character in string variable myString.
13. Write the statement that changes the char variable letter to lowercase.
14. Write the statement that changes the char variable letter to uppercase.
15. Complete the following C++ program. The program should compute and output the Celsius value corresponding to the given Fahrenheit value.
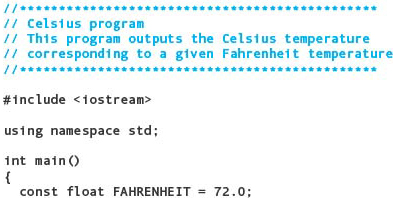
 Programming Problems
Programming Problems
1. Write a C++ program that computes and outputs the volume of a cone, given the diameter of its base and its height. The formula for computing the cone’s volume is:
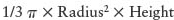
Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly.
2. Write a C++ program that computes the mean and standard deviation of a set of four integer values. The mean is the sum of the four values divided by 4, and the formula for the standard deviation is
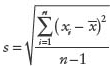
Where n = 4, xi refers to each of the four values, and 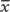 is the mean. Note that although the individual values are integers, the results are floating-point values. Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly and formatted neatly.
is the mean. Note that although the individual values are integers, the results are floating-point values. Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly and formatted neatly.
3. The factorial of a number n (written n!) is the number times the factorial of itself minus one. This self-referential definition is easiest to understand through an example: The factorial of 2 is 2 * 1; the factorial of 3 is 3 * 2 * 1; the factorial of 4 is 4 * 3 * 2 * 1; and so on. Factorials grow very large, very quickly. An approximation to the factorial for larger values is given by Stirling’s formula:
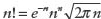
The exp function in the <cmath> header file gives the value of e raised to given power (see Appendix C.5). We’ve already discussed all of the other functions that are needed to write this formula. Write a C++ program that computes the factorial of 15 both directly and with Stirling’s formula, and outputs both results, together with their difference. You will need to use the double type for this computation. Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly and formatted neatly.
4. Write a C++ program that computes a student’s grade for an assignment as a percentage given the student’s score and the total points. The final score should be rounded up to the nearest whole value using the ceil function in the <cmath> header file. You should also display the floating-point result up to 5 decimal places.
5. Given the following string:
“Program testing can be used to show the presence of bugs, but never to show their absence”
Write a C++ program that will construct a new string in uppercase from the string above such that the new string is:
“I CAN WRITE CODE THAT RUNS”
6. The number of permutations of a set of n items taken r at a time is given by the following formula:
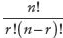
where n! is the factorial of n. (See Programming Problem 3 for a discussion of ways to compute the factorial.) If there are 18 people in your class and you want to divide the class into programming teams of 3 members, you can compute the number of different teams that can be arranged using this formula. Write a C++ program that determines the number of potential team arrangements. You will need to use the double type for this computation. Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly and formatted neatly.
7. Write a C++ program that takes a string containing a full name and outputs each part of the name separately. The name should be in the form of first, middle, and last name, separated from each other by a single space. For example, if the name string contains
"John Jacob Schmidt"
then the program would output
First name: John
Middle name: Jacob
Last name: Schmidt
8. Extend Programming Problem 7 to output the length of each name. This problem can be solved using a combination of the string operations presented in this chapter. Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly and formatted neatly.
 Case Study Follow-Up
Case Study Follow-Up
1. Change the output statements so that the interest rate is printed with four decimal places, but the dollar amounts continue to have two decimal places.
2. The program assumes that the number of months left on the old mortgage is an even multiple of 12. Change the program so that the constant is the number of months left, not the number of years.
3. We usually speak of interest rates as percentages. Rewrite the program so that the interest rate is set as a percentage—that is, as 5.24 rather than 0.0524.
4. The calculation of 1 + monthlyInterest is made twice. Rewrite the program so that it makes this calculation only once. In your judgment, which version of the program is better? Justify your answer.
 To understand implicit type coercion and explicit type conversion.
To understand implicit type coercion and explicit type conversion. To recognize and understand the purpose of function arguments.
To recognize and understand the purpose of function arguments. To learn and use additional operations associated with the string type.
To learn and use additional operations associated with the string type. To learn how to format program statements in a clear and readable fashion.
To learn how to format program statements in a clear and readable fashion.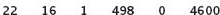



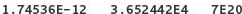







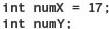
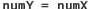
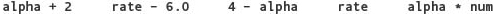

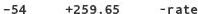
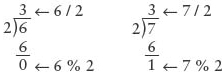











 The function call is used within an expression; it does not appear as a separate statement.
The function call is used within an expression; it does not appear as a separate statement.



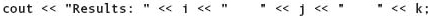
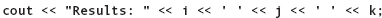
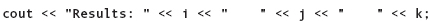
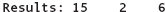
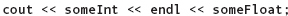





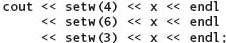

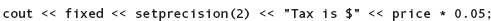






















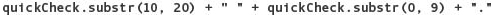
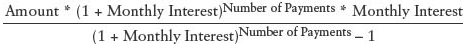


 Summary
Summary
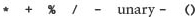
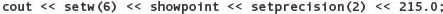

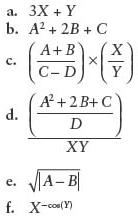

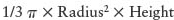
 is the mean. Note that although the individual values are integers, the results are floating-point values. Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly and formatted neatly.
is the mean. Note that although the individual values are integers, the results are floating-point values. Be sure to use proper formatting and appropriate comments in your code. The output should be labeled clearly and formatted neatly.