© Springer Nature Switzerland AG 2020
E. RosenbergFractal Dimensions of Networkshttps://doi.org/10.1007/978-3-030-43169-3_10

10. Computing the Correlation Dimension

Eric Rosenberg1 
(1)
AT&T Labs, Middletown, NJ, USA
 

Nothing makes the earth seem so spacious as to have friends at a distance; they make the latitudes and longitudes.

Henry David Thoreau (1817–1862) American author, poet, and philosopher, best known as the author of “Walden”.

In this chapter we investigate several practical issues related to the computation of d C.

10.1 How Many Points are Needed?

Several researchers have proposed a lower bound on the number of points needed to compute a “good” estimate of d C of a geometric object $$\varOmega \subset {\mathbb {R}}^E$$ . These bounds were summarized in [Theiler 90], who suggested that the minimal number N of points necessary to get a reasonable estimate of dimension for a d-dimensional fractal is given by a formula of the form N > ab d. Theiler also observed that although it is difficult to provide generically good values for a and b, limited experience indicated that b should be of the order of 10. For example, (9.​25) provided the upper bound d C ≤ 2log10N on d C, and this inequality also provides a lower bound on N, namely $$N \geq 10^{d_{{C}}/2}$$ . In this section we present other lower bounds, which differ markedly. Although this chapter concerns the computation of d C of a geometric object, in Chap. 11 we will study the “average slope” definition of d C of a network, and consider the question of how many nodes are required to compute a good estimate of d C of a rectilinear grid in E dimensions.

Smith’s Lower Bound: The lower bound
$$\displaystyle \begin{aligned} \begin{array}{rcl} N \geq 42^{E} {} \end{array} \end{aligned} $$
(10.1)
on the number of data points required to compute d C to within 5% was provided in [Smith 88]. To derive this bound, consider the ideal case where Ω is the E-dimensional unit hypercube [0, 1]E, so Ω contains an infinite number of uniformly distributed points, and d C = E. Recalling that with N points C(r) is the fraction of pairs of points separated by a distance at most r, assume that, in the limit of infinite N, the correlation integral C(r) is equal to the probability P(dist(x, y) ≤ r) that, for two points x and y randomly chosen from [0, 1]E and for r ∈ (0, 1), we have dist(x, y) ≤ r. Let x = (x 1, x 2, …, x E) and y = (y 1, y 2, …, y E) be two randomly chosen points in [0, 1]E. For E = 1 and r ∈ (0, 1) we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} C(r) = P( \vert x - y \vert \leq r ) = r (2-r) \, . {} \end{array} \end{aligned} $$
(10.2)
For example, if r = 1∕100, then C(r) = (1∕100)(199∕200) ≈ 1∕100. Assume that for x, y ∈ [0, 1]E we have dist(x, y) ≡max1≤i≤E|x i − y i|, i.e., distance is measured using the L ∞ norm. Then dist(x, y) ≤ r implies |x i − y i|≤ r for i = 1, 2, …, E. For the E-dimensional hypercube [0, 1]E we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} C(r) = P\big( \mathit{dist}(x,y) \leq r \big) = [P \big( \vert x_{{i}} - y_{{i}} \vert \leq r \big)]^E = [r(2-r)]^E \, . {} \end{array} \end{aligned} $$
(10.3)
For r ∈ (0, 1) the correlation dimension d C can be estimated by the derivative of the $$\log C(r)$$ versus $$\log r$$ curve at r. Denoting this derivative by d C(r),
$$\displaystyle \begin{aligned} {d_{{C}}}(r) &\equiv \frac{ \mathrm{d} } { \mathrm{d} \log r } \log C(r) = \left( \frac{ \mathrm{d} } { \mathrm{d} r } \log C(r) \right) \left( \frac{ \mathrm{d} r } { \mathrm{d} \log r }\right) \\ & = \left( \frac{ \mathrm{d} } { \mathrm{d} r } \log \big( [r(2-r)]^E \big) \right) \left( \frac{ \mathrm{d} \log r } { \mathrm{d} r }\right)^{-1} \\ &= E \left( 1 - \frac{r}{2-r} \right) \; . {} \end{aligned} $$
(10.4)
For r ∈ (0, 1) we have 0 < d C(r) < E. Suppose for a given α ∈ (0, 1) we want d C(r) to be at least αE. Since d C(r) is decreasing in r, let r max be the largest r such that d C(r) ≥ αE. From (10.4), r max is the value yielding equality in
$$\displaystyle \begin{aligned} E \left( 1 - \frac{r_{{max}}}{2-r_{{max}}} \right) \geq \alpha E \, , \end{aligned}$$
so r max = 2(1 − α)∕(2 − α). Let r min be the smallest usable r; this value must be greater than the mean nearest neighbor distance, and also large enough to overcome the effects of noisy data [Smith 88]. Define R ≡ r max∕r min. Then
$$\displaystyle \begin{aligned} \begin{array}{rcl} r_{{min}} = \frac{2(1-\alpha)}{R(2-\alpha)} \, . {} \end{array} \end{aligned} $$
(10.5)
If we partition the E-dimensional unit hypercube [0, 1]E into “small” E-dimen- sional hypercubes of side length r min, the required number of small hypercubes is (1∕r min)E. Since r min must be large enough so that each small hypercube contains at least one point, then (1∕r min)E is a lower bound on the number N of points required for the estimate of d C to be at least αd C. Finally, from (10.5)
$$\displaystyle \begin{aligned} \begin{array}{rcl} N \geq (1/r_{{min}})^E = \left( \frac{R(2-\alpha)}{2(1-\alpha)} \right) ^E \, . {} \end{array} \end{aligned} $$
(10.6)
Assuming α = 0.95 and R = 4, Smith obtained the bound (10.1). □

Exercise 10.1 Are the choices α = 0.95 and R = 4 in (10.6) good choices? □

Exercise 10.2 Referring to (10.2) above, prove the one-dimensional result that P(|x − y|≤ r) = r(2 − r). □

Theiler’s Lower Bound: It was shown in [Theiler 90] that at least 5E points are needed to estimate d C to within 5%. To derive this bound, much lower than the bound N ≥ 42E, consider again the E-dimensional unit hypercube [0, 1]E. By (10.4), for r ≪ 1 we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{C}}(r) = E \left( 1 - \frac{r}{2-r} \right) \approx \, E \left( 1 - \frac{r}{2} \right) \, , {} \end{array} \end{aligned} $$
(10.7)
so the relative error 𝜖(r) ≡|E − d C(r)| is given by 𝜖(r) ≈ r∕2. Since C(r) varies from a minimal value of 2∕[N(N − 1)] (if there is a single pair of points at distance r) to a maximal value of 1, a “natural choice” [Theiler 90] of r is the value $$\widetilde {r}$$ for which C(r) = 1∕N. From (10.3) and r ≪ 1 we have C(r) ≈ (2r)E, so setting C(r) = 1∕N yields
$$\displaystyle \begin{aligned} \begin{array}{rcl} \widetilde{r} \approx (1/2)N^{-1/E} {} \end{array} \end{aligned} $$
(10.8)
and $$\epsilon ({\widetilde {r}}) \approx \widetilde {r}/2 = (1/4)N^{-1/E}$$ is the relative error. Thus $$[4\epsilon ({\widetilde {r}})]^{-E}$$ points are required to achieve a relative error of $$\epsilon ({\widetilde {r}})$$ . Setting $$\epsilon ({\widetilde {r}}) = 5\%$$ yields N > 5E. □

Exercise 10.3 In the above derivation of Theiler’s bound N > 5E, why is choosing r to be the value at which C(r) = 1∕N a “natural choice”? □

Krakovská’s Lower Bound: Using the same model of the E-dimensional unit hypercube [0, 1]E, [Krakovska 95] showed that Smith’s lower bound of 42E is too high, and that Theiler’s lower bound of 5E is too low. For N points uniformly distributed in an E-dimensional cube with side length 1, the most probable distance between two points is r ⋆ = N −1∕E [Krakovska 95], and C(r) should not be computed for r < r ⋆, since that region yields poor statistics. Since d C(r), defined by (10.4), is a decreasing function of r, then for r ≥ r ⋆ we have
$$\displaystyle \begin{aligned} d_{{C}}(r) \leq d_{{C}}(r^{\star}) &amp;= E \left( 1 - \frac{r^{\star}}{2-r^{\star}} \right) = E \left( 1 - \frac{N^{-1/E}}{2-N^{-1/E}} \right)\\ &amp;= E \left( 1 - \frac{1}{2N^{1/E}-1} \right) \; . {} \end{aligned} $$
(10.9)
Assuming uniformly distributed random points in an E-dimensional unit hypercube, the bound (10.9) provides the N needed to achieve a given accuracy δ, as follows. From
$$\displaystyle \begin{aligned} E \left( 1 - \frac{1}{2N^{1/E}-1} \right) = \delta E \end{aligned}$$
we obtain
$$\displaystyle \begin{aligned} \begin{array}{rcl} N = \left( \frac{2 - \delta}{2 - 2 \, \delta} \right)^E \; . {} \end{array} \end{aligned} $$
(10.10)
From (10.10) we have N →∞ as δ → 1. For 95% accuracy we set δ = 0.95, and we require (10.5)E points; this estimate lies between Theiler’s estimate of 5E points and Smith’s estimate of 42E points. For the Lorenz attractor, for which E = 3 and d C ∈ (2.06, 2.08), for δ = 0.95 we have δd C ∈ (1.957, 1.976). Using Theiler’s formula, we need 5E = 125 points, and with 125 points the $$\bigl ( \log s, \log C(s) \bigr )$$ curve is very jagged and exhibits no plateau. Using Krakovská’s formula, we need 10.5E = 1158 points, and the $$\bigl ( \log s, \log C(s) \bigr )$$ curve provides the estimate d C ≈ 1.96. Using Smith’s formula, we need 42E = 74, 088 points, which provide a much better result than 95% of the true value of d C.

We can also use (10.9) to determine, with uniformly distributed random points in an E-dimensional hypercube, the amount by which d C is underestimated when using a finite number of points. For example, with N = 105 and E = 5, the estimated correlation exponent is the fraction $$1-\bigl (2 (10^5)^{1/5} -1 \bigr )^{-1} \approx 0.947$$ of the expected value of 5.

Having considered the issue of a finite rather than infinite number of points, [Krakovska 95] also considered the assumption of a uniform distribution of points. For deterministic systems, since the attractors are more “compressed” than a set of uniformly distributed random points, the same amount of data should, in most cases, yield a better estimate. Let r ⋆ be the most probable distance between a pair of points on the attractor and define ν ≡ d C(r ⋆). In practice ν is computed from the slope of the curve of $$\log C(r)$$ versus $$\log r$$ over the range of r values for which the slope is reasonably constant. Suppose the attractor is embedded in E-dimensional space, and E is the smallest such value; this implies E = ⌈d C⌉. Krakovská assumed that, for deterministic systems, corresponding to (10.9) we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \nu = d_{{C}} \left( 1 - \frac{1}{2N^{1/ d_{{C}} }-1} \right) \; , {} \end{array} \end{aligned} $$
(10.11)
so ν < d C. We approximate the term in parentheses by replacing d C by E. Since E > d C this yields
$$\displaystyle \begin{aligned} \begin{array}{rcl} \nu &gt; d_{{C}} \left( 1 - \frac{1}{2N^{1/E}-1} \right) \end{array} \end{aligned} $$
which we rewrite as
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{C}} &lt; \nu \left( 1 + \frac{1}{2 \bigl(N^{1/E}-1 \bigr)} \right) \, . {} \end{array} \end{aligned} $$
(10.12)
From ν < d C and (10.12) we obtain lower and upper bounds on d C:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \nu &lt; d_{{C}} &lt; \nu \left( 1 + \frac{1}{2 \bigl(N^{1/E}-1 \bigr)} \right) \, . \; \; \end{array} \end{aligned} $$
□
Eckmann and Ruelle’s Lower Bound: The lower bound
$$\displaystyle \begin{aligned} \begin{array}{rcl} N &gt; 10^{d_c/2} {} \end{array} \end{aligned} $$
(10.13)
was provided in [Eckmann 92]. To derive this bound, first define
$$\displaystyle \begin{aligned} F(r) = \sum_{i=1}^N \sum_{\substack{j=1 \\ j \neq i }}^N I_{{0}} \Big( r - \big( \mathit{dist}( x(i) , x(j) \big) \Big) \, . {} \end{aligned} $$
(10.14)
By definitions (9.​9) and (9.​11) we have
$$\displaystyle \begin{aligned} C(r) &amp;= \frac{1}{N(N-1)} \, \sum_{i=1}^N C\big( x(i), r \big) \\ &amp;= \frac{1}{N(N-1)} \, \sum_{i=1}^N \sum_{\substack{j=1 \\ j \neq i }}^N I_{{0}} \Big( r - \big( \mathit{dist}( x(i) , x(j) \big) \Big) \\ &amp;= \frac{F(r)}{N(N-1)} \, . {} \end{aligned} $$
(10.15)
Setting r = Δ, by definition (9.​7) of I 0, for all x(i) and x(j) we have
$$\displaystyle \begin{aligned} I_{{0}} \big( \varDelta - \mathit{dist} ( x(i) , x(j) ) \big) = 1 \, , \end{aligned}$$
so by (10.14) we have F(Δ) = N(N − 1) and by (10.15) we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} C(\varDelta) = \frac{F(\varDelta)}{N(N-1)} = 1 \, . \end{array} \end{aligned} $$
Assume $$C(r) \approx k r^{{d_{{C}}}}$$ for some constant k. Since C(Δ) = 1 then $$k ={\varDelta }^{-{d_{{C}}}}$$ , which with (10.15) yields
$$\displaystyle \begin{aligned} \begin{array}{rcl} F(r) = N(N-1) C(r) \approx N^2 \left( \frac{r}{\varDelta} \right)^{{d_{{C}}}} \, . {} \end{array} \end{aligned} $$
(10.16)
For statistical reasons we want F(r) ≫ 1, so by (10.16) we want
$$\displaystyle \begin{aligned} \begin{array}{rcl} N^2 \left( \frac{r}{\varDelta} \right)^{{d_{{C}}}} \gg 1 \, . {} \end{array} \end{aligned} $$
(10.17)
In determining the slope of the $$\log F(r)$$ versus $$\log r$$ curve, we want r ≪ Δ. Define ρ ≡ r∕Δ, where ρ ≪ 1. Taking the logarithm of both sides of (10.17), we obtain
$$\displaystyle \begin{aligned} \begin{array}{rcl} 2 \log N \gg - d_c \log \left( \frac{r}{\varDelta} \right) = - d_c \log \rho = d_c \log (1/\rho) \, . {} \end{array} \end{aligned} $$
(10.18)
Choosing the value ρ = 10−1, using base 10 logarithms, and replacing “≫” by “> ”, we obtain 2log10N > d clog10(10), which we rewrite as the desired result $$N &gt; 10^{{d_{{C}}}/2}$$ . So if d C = 6, we need at least 1000 points.

Values of ρ larger than 0.1 might be adequate but since d C is interesting mainly for highly nonlinear systems, such larger values would have to be justified. Rewriting (10.18), an upper bound on d C is d C ≤ 2log10N∕log10(1∕ρ). With N = 1000 and ρ = 0.1 we obtain d C ≤ 6. Thus, if the Grassberger–Procaccia method yields the estimate d C = 6 for N = 1000 points, this estimate is probably worthless, and a larger N is required [Eckmann 92].

The bound (10.13) was used in [Camastra 97] to study electric load forecasting. Using 4320 data points, they computed d C ≈ 3.9 using the Grassberger–Procaccia method. Since d C = 3.9 < 2log10N ≈ 7.2, then (10.13) holds. The impact of an insufficient number of points was illustrated in [Camastra 02], who used the Grassberger–Procaccia method to determine d C from a set of N points randomly distributed in the 10-dimensional hypercube [0, 1]10. Since we expect d C = 10, the lower bound on N is $$10^{ {d_{{C}}}/2} = 10^{ 5} $$ . The following table from [Camastra 02] provides the computed values of d C for different values of N (Table 10.1).
Table 10.1

Impact of N on computed d C

N

Computed d C

1000

7.83

2000

7.94

5000

8.30

10,000

8.56

30,000

9.11

100,000

9.73

Random sampling statistics were used in [Kember 92] to reduce the number of points required to accurately compute d C. They observed that the values I 0(r −dist(x(i), x(j))) form a population whose values are either 0 or 1. Hence the probability p that I 0(r −dist(x(i), x(j))) = 1 can be estimated by taking a random sample of the population: the fraction of terms equal to 1 in a random sample with replacement is an unbiased estimator for p. The savings in the number of points required are proportional to N δ(d C)2, where N δ is the number of points required to estimate d C to a relative accuracy of δ. Since the bounds of [Smith 88, Theiler 90, Eckmann 92, Krakovska 95] derived above are all of the form $$N_{\delta } \geq \exp ({O(d_{{C}})})$$ , then the savings using random sampling are dramatic for large d C.

Despite the theoretical bounds on the minimal number of points required for an accurate computation of d C, computational results in [Abraham 86] showed that d C can be successfully calculated even with as few as 500 data points. For example, for the much-studied Hénon attractor defined by
$$\displaystyle \begin{aligned} \big( x_{{{t+1}}}, y_{{{t+1}}} \big) = \big(y_{{t}} + 1 - a (x_{{t}})^2, b x_{{t}} \big) \end{aligned}$$

with a = 1.4 and b = 0.3, using N = 500, 1200, 4000, and 10, 000 points, for the range s ∈ [2.5, 5.5], they obtained d C = 1.28 ± 0.09, 1.20 ± 0.04, 1.24 ± 0.04, and 1.24 ± 0.02, respectively. Results in [Ramsey 89] found that for simple models, 5000 is a rough lower bound for the number of points needed to achieve reasonable results [Berthelsen 92].

10.2 Analysis of Time Series

A time series is a set of measurements of the same quantity, e.g., heart rate or the price of a stock, taken at regular time intervals. The correlation dimension has been used to analyze time series data in a wide variety of applications. The correlation dimension is the most widely used dimension in applied time series analysis [Martinerie 92, Boon 08], and can determine if the data follows a stochastic process or instead is generated by deterministic chaos.1 (For stochastic systems, the fractal dimension is equal to the phase-space dimension, while for purely chaotic systems, the fractal dimension is smaller and in general is not an integer [Badii 85].) The reasons for computing the dimension of a time series are [Martinerie 92]:

Estimating a signal’s dimension is often an important step in its dynamical characterization. In ideal cases when large sets of high-quality data are available, the dimension estimate can be used to infer something about the dynamical structure of the system generating the signal. However, even in circumstances where this is impossible, dimension estimates can be an important empirical characterization of a signal’s complexity.

To add to this list of reasons, in Sect. 11.​3 we will examine how the correlation dimension of a network can be estimated from the time series obtained from a random walk on the network.
We now consider the computation of d C of the time series, u t, t = 1, 2, …, N, where each u t is a scalar quantity measured at regular intervals. Let τ be the fixed time interval between measurements, e.g., every 3 min or hourly or every other day. Let E be a given positive integer, called the embedding dimension. We create a set of E-dimensional vectors x t as follows. For t = 1, 2, …, N − E + 1, define
$$\displaystyle \begin{aligned} \begin{array}{rcl} {x_{{t}}} = ({u_{{t}}}, {u_{{t+1}}}, \ldots, u_{\stackrel{}{t+E-1}}) \in {\mathbb{R}}^E \, . {} \end{array} \end{aligned} $$
(10.19)
For example, with E = 3, we have x 1 = (u 1, u 2, u 3), x 2 = (u 2, u 3, u 4), x 3 = (u 3, u 4, u 5), etc., so the components of the vectors x t overlap. Figure 10.1 illustrates an embedding with E = 3. The embedding of scalar times series data, where the measurements occur with time spacing τ, can be visualized as passing a comb along the data [Boon 08]. The number of teeth of the comb is the embedding dimension E, and the distance between the teeth of the comb is τ. When the comb is positioned at the first point in the data, the scalar points touched by the teeth of the comb define the E components of x 1. The coordinates of the next point x 2 are obtained by moving the comb τ time units to the right. The task is to estimate d C from these N − E + 1 vectors, where each vector is a point in $$\mathbb {R}^E$$ .2
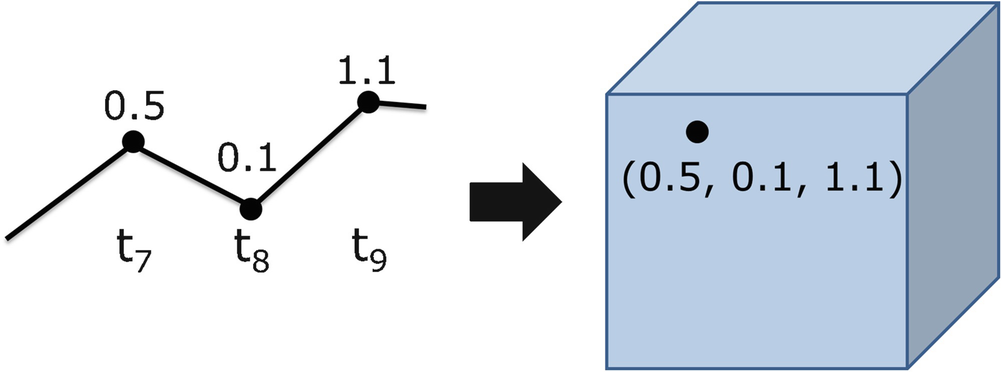
../images/487758_1_En_10_Chapter/487758_1_En_10_Fig1_HTML.png
Figure 10.1

Embedding dimension

Following [Barkoulas 98], let X be an open subset of $${\mathbb {R}}^K$$ , where K is a positive integer, and suppose that for some function $$F: X \rightarrow {\mathbb {R}}^K$$ the sequence x t defined by (10.19) satisfies x t = F(x t−1) for t = 1, 2, … . The sequence $$\{x_{{t}} \}_{t=1}^{\infty }$$ depends on the initial point x 1 but for simplicity of notation we write x t rather than x t(x 1). Let F 2(x t) denote $$F \bigl ( F({x_{{t}}}) \bigr )$$ , let F 3(x t) denote $$F \Bigl (F \bigl ( F({x_{{t}}}) \bigr ) \Bigr )$$ , and in general let F j(x t) denote the j-fold composition. A set Ω is invariant with respect to the trajectory $$\{x_{{t}} \}_{t=1}^{\infty }$$ if the following condition holds: if $$x_{{t_{{j}}}} \in \varOmega $$ for some time t j, then x t ∈ Ω for t > t j. A closed invariant set Ω ⊂ X is the attracting set for the system x t = F(x t−1) if there exists an open neighborhood Ω 𝜖 of Ω such that Ω = {limt→∞x t(x 1) | x 1 ∈ Ω 𝜖 }. We are interested in the dimension of the attracting set Ω.

In many financial studies, the data $${y_{{t}}} \in {\mathbb {R}}^K$$ represents the market over time. Suppose y t+1 = F(y t) for some function $$F: {\mathbb {R}}^K \rightarrow {\mathbb {R}}^K$$ . Suppose we observe, at equally spaced time increments, the univariate time series u t, e.g., u t might be the price of a single stock over time. Assume u t = g(y t), where $$g: {\mathbb {R}}^K \rightarrow R$$ , so the stock price u t is the output of a dynamical system. We want to recover the market dynamics by analyzing u t. To do this, let E be the embedding dimension and create, for t = 1, 2, …, the E-dimensional vector x t defined by (10.19). Since u t = g(y t) then
$$\displaystyle \begin{aligned} \begin{array}{rcl} {x_{{t}}} &amp;\displaystyle =&amp;\displaystyle ({u_{{t}}}, {u_{{t+1}}}, u_{{t+2}}, \ldots, u_{\stackrel{}{t+E-1}}) \\ &amp;\displaystyle =&amp;\displaystyle \Bigl( g(y_{{t}}), g(y_{{{t+1}}}), g(y_{{{t+2}}}), \ldots, g(y_{{{t+E-1}}}) \Bigr) \\ &amp;\displaystyle =&amp;\displaystyle \Bigl( g(y_{{t}}), g \big( F(y_{{t}}) \big), g\big( F^2(y_{{t}}) \big), \ldots , g\big( F^{E-1}(y_{{t}}) \big) \Bigr) \, . \\ &amp;\displaystyle \equiv&amp;\displaystyle \varPhi(y_{{t}}) \, . \end{array} \end{aligned} $$
The function $$\varPhi : {\mathbb {R}}^K \rightarrow {\mathbb {R}}^E$$ is called the delay coordinate map [Ding 93].

A theorem of [Takens 85] states that if F and g are smooth, then for E ≥ 2K + 1 the map Φ will be an embedding (a one to one and differentiable mapping [Ding 93]), and an analysis of the time series {x t} gives a correct picture of the underlying dynamics [Barkoulas 98], including the dimension of the attracting set. It actually suffices to choose E ≥ 2d B + 1 [Ding 93]. Moreover, it was proved in [Ding 93] that to estimate d C from a time series, it suffices to have E ≥ d C, and the condition E ≥ 2d B + 1, while necessary to ensure that the delay coordinate map is one to one, is not required to estimate d C. That is, choosing E ≥ d C, the correlation dimension d C can be estimated whether or not the delay coordinate map is one to one. Based on a random sample of papers published from 1987 to 1992, [Ding 93] found that the assumption that E ≥ 2d B + 1 is required to estimate d C is a widespread misconception.

In theory, if the points x t for t = 1, 2, ⋯ are independent and identically distributed, then the system has infinite dimension. With finite data sets, high dimensionality is indistinguishable from infinite dimensionality [Frank 89]. For a given E, let d C(E) be the correlation dimension for the series {x t} defined by (10.19). If the data are purely stochastic, then d C(E) = E for all E, i.e., the data “fills” E-dimensional space. In practice, if the computed values d C(E) grow linearly with E, then the system is deemed “high-dimensional” (i.e., stochastic). If the data are deterministic, then d C(E) increases with E until a “saturation” point is reached at which d C(E) no longer increases with E. In practice, if the computed values d C(E) stabilize at some value d C as E increases, then d C is the correlation dimension estimate.

The steps to estimate d C from a time series are summarized in [Ding 93] as follows:

(i) Construct the sequence {x t}, where $${x_{{t}}} \in {\mathbb {R}}^E$$ .

(ii) Compute the correlation sum C(r) for a set of values of r.

(iii) Locate a linear scaling region, for small r, on the $$\log C(r)$$ versus $$\log r$$ curve, and compute d C(E), the slope of the curve over that region.

(iv) Repeat this for an increasing range of E values, and if the estimates d C(E) appear to converge to some value, then this value is the estimate of d C.

To prevent a spurious estimate of d C, the following conditions are necessary [Martinerie 92]:

(i) The range of [r min, r max] over which d C is estimated must be sufficiently large; e.g., by requiring r max∕r min ≥ 5.

(ii) The $$\log C(r)$$ versus $$\log r$$ curve must be sufficiently linear over [r min, r max]; typically the requirement is that over [r min, r max] the derivative of the $$\log C(r)$$ versus $$\log r$$ curve should not exceed 15% of d C.

(iii) The estimate d C(E) should be stable as E increases; typically the requirement is that d C(E) not increase by more than 15% over the range [E − 4, E].

In computing d C from a time series, it is particularly important to exclude temporally correlated points from the sum (9.​11). Since successive elements of a time series are not usually independent, Theiler suggested removing each pair of points whose time indices differ by less than w, with the normalization factor $$1/\bigl (N (N-1) \bigr )$$ appropriately modified. The parameter w is known as the Theiler window [Hegger 99].

10.3 Constant Memory Implementation

The correlation dimension is based on computing the distance between each pair of points. While the distances need not be stored, each distance must be computed at least once, and the computational complexity of computing these distances is $${\mathcal {O}}(N^2)$$ [Wong 05]. This complexity is prohibitive for large data sets. An alternative to computing the distance between each pair of points is to use the results of Sect. 9.​5, where we showed that the number of pairs whose distance is less than s is approximated by the number of pairs which fall into any box of size s. Using (9.​29),
$$\displaystyle \begin{aligned} \begin{array}{rcl} \widetilde{C}(s) \approx \sum_{j=1}^{ B_{{D}} (s)} \left( \frac{N_j(s)}{N} \right)^2 \, . {} \end{array} \end{aligned} $$
(10.20)
We can approximate $$\widetilde {C}(s)$$ with only a single pass through the N points, so the complexity of computing $$\widetilde {C}(s)$$ is $${\mathcal {O}}(N)$$ . An $${\mathcal {O}}(N)$$ computational cost is acceptable, since each of the N points must be examined at least once, unless sampling is used. The memory required is also $${\mathcal {O}}(N)$$ since for sufficiently small s each point might end up in its own box.

Interestingly, there is a way to reduce the memory requirement without unduly sacrificing speed or accuracy. Drawing upon the results in [Alon 66], it was shown in [Wong 05] how for a given s we can estimate the “second moment” $$\sigma ^2(s) \equiv \sum _{j=1}^{B_{{D}} (s)} [N_j(s)]^2$$ in $${\mathcal {O}}(N)$$ time and $${\mathcal {O}}(1)$$ memory, i.e., a constant amount of memory independent of N. The accuracy of estimation is controlled by two user-specified integer parameters: α determines the level of approximation, and β determines the corresponding probability. For any positive integral values of α and β, the probability that the estimate of the second moment has a relative error greater than $$\sqrt {16/\alpha }$$ is less than e −β∕2.

For each s we generate αβ 4-tuples of random prime numbers, each of which defines a hash function. Estimating σ 2(s) requires one counter per hash function, so there are αβ counters. Assuming each of the N points lies in $${\mathbb {R}}^E$$ , each hash function, which is applied to each of the N points, returns a value of 1 or − 1, which is used to increment or decrement the counter associated with the hash function. For each s, the estimate of σ 2(s) is computed by first partitioning the αβ counters into β sets of α counters, squaring the α counter values in each of the β sets, computing the mean for each of the β sets, and finally computing the median of these means.

The method was tested in [Wong 05] using an accuracy parameter α = 30 and a confidence parameter β = 5. A linear regression of the $$\bigl ( \log s, \log \sigma ^s(s) \bigr )$$ values was used to estimate d C. The first test of the method considered points on a straight line, and the method estimated d C values of 1.045, 1.050, and 1.038 for E = 2, 3, 4, respectively. On the Sierpiński triangle with N = 5000, the method yielded d C = 1.520; the theoretical value is log23 ≈ 1.585. A Montgomery County, MD data set with N =  27,282 yielded d C = 1.557 compared with d B = 1.518, and a Long Beach County, CA data set with N =  36,548 yielded d C = 1.758 compared with d B = 1.732.

10.4 Applications of the Correlation Dimension

In this section we briefly describe some interesting applications of the correlation dimension. The literature on applications of d C is quite large, and the set of applications discussed below constitutes a very small sample. In the discussion below, a variety of approaches were used to compute d C, or some variant of d C. The first two applications we review also compare d C and d B. The discussion below on the hierarchical packing of powders, and on fractal growth phenomena, shows that d C has been applied to growing clusters of particles; this discussion also sets the stage for our presentation of the sandbox dimension in Sect. 10.5 below. Reading this range of applications will hopefully inspire researchers to find new applications of network models in, e.g., biology, engineering, or sociology, and to compute d C or related fractal dimensions of these networks.

Hyperspectral Image Analysis: In [Schlamm 10], d C and d B were compared on 37 hyperspectral images (they also considered the dimension obtained from principal component analysis [Jolliffe 86]).3 The 37 images were from 11 unique scenes (e.g., desert, forest, lake, urban) and 7 ground sample distances (GSDs). 4 Surprisingly, the d C estimates of the full images were consistently substantially larger (often by more than a factor of two) than the d B estimates. They concluded that, compared to the correlation method and principal component analysis, box counting is the best method for full image dimension estimation, as the results are the most reliable and consistent.

Root Systems of Legumes: In [Ketipearachchi 00], d C and d B were compared for the root system of six species of legumes (e.g., kidney beans and soybeans). Such analysis assists in understanding the functional differences and growth strategies of root systems among the species, and in screening for genetic improvement. For the d B calculation, they used box sizes from 2 to 256 pixels, and employed linear regression. For the d C calculation, they computed the average of 500 pointwise mass dimensions d(x) (Sect. 9.​3) centered at points x on the edge of the image. The pointwise dimensions were assumed to satisfy $$C(x,r) = k r^{ d_{{C}}}$$ for some constant k, where C(x, r) is the number of pixels in a box or disc of size r centered at x (see (11.​3)), and r varies from 3 to 257 pixels. Interestingly, for each species d C exceeded d B, as shown in Table 10.2; they noted that they are not the first to observe this relationship for a “natural fractal”. These results showed that the six species fall into two groups, with groundnut, kidney bean, and soybean in the group with the higher fractal dimension. They also observed that d C is less sensitive than d B to system size parameters such as root length, and thus d C is a “suitable alternative” to d B when evaluating root systems by focusing on branching patterns rather than system size parameters.
Table 10.2

Dimensions of legume root systems [Ketipearachchi 00]

Crop

d B

d C

Blackgram

1.45

1.52

Cowpea

1.45

1.54

Groundnut

1.61

1.76

Kidneybean

1.61

1.72

Pigeonpea

1.41

1.53

Soybean

1.57

1.68

Hierarchical Packing of Powders: The correlation dimension can be used to describe the packing of powders in hierarchical structures [Schroeder 91]. Suppose the primary powder particles tend to form clusters (in 3-dimensional space) with density ρ, where ρ < 1. Let γ be the ratio of the cluster radius to the primary powder particle radius, where γ > 1. These first-generation clusters then cluster together to form second-generation clusters, with the same or similar values of ρ and γ, the second-generation clusters form third-generation clusters, etc. This is illustrated in Fig. 10.2, which shows 7 primary particles in each first-generation cluster, 7 first-generation clusters in each second-generation clusters, and 7 second-generation clusters in the third-generation clusters. After t generations, the density of the power is ρ t and the radius R t of each generation t cluster is R t = γ t. The mass N t in each generation t cluster is the product of the cluster density and volume, and the volume is proportional to the cube of the radius, so $$N_t \propto \rho ^t R_t^3$$ . Using the identity $$\rho ^t = (\gamma ^t)^{\log \rho / \log \gamma }$$ , we have $$\rho ^t = (\gamma ^t)^{\log \rho / \log \gamma } = R_t^{\log \rho / \log \gamma } $$ . For t ≫ 1,
$$\displaystyle \begin{aligned} \begin{array}{rcl} N_t \propto \rho^t R_t^3 = R_t^{\log \rho / \log \gamma} R_t^3 = R_t^{3+ (\log \rho / \log \gamma)} \, , {} \end{array} \end{aligned} $$
(10.21)
so $$d_{{C}} = 3 + (\log \rho / \log \gamma )$$ and $$3 + (\log \rho / \log \gamma ) &lt; 3$$ , since ρ < 1 and γ > 1.
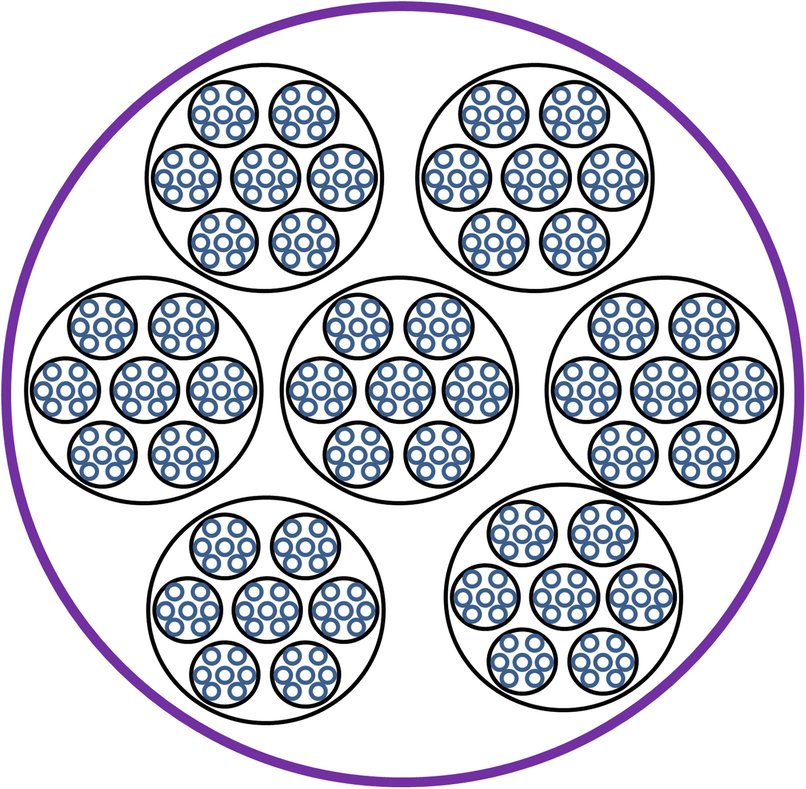
../images/487758_1_En_10_Chapter/487758_1_En_10_Fig2_HTML.png
Figure 10.2

Packing of powder particles

The β Model: Theoretical aspects of the use of small-angle X-ray scattering to compute the fractal dimension of colloidal aggregates were studied in [Jullien 92]. Derived theoretical results were compared to the results of the following 3-dimensional “random” fractal model, known as the β model. Pick a random positive integer k such that 1 < k < 8. At t = 0, start with the unit cube. At time t = 1, enlarge the cube by a factor of 2 in each of the three dimensions, and divide the enlarged cube into 23 = 8 unit cubes. Randomly select k of these 8 cubes and discard the unselected cubes; this completes the t = 1 construction. At time t = 2, expand the object by a factor of 2 in each of the three dimensions, and, for each of the k cubes selected in step t = 1, divide the cube into 8 unit cubes, from which k are randomly selected, and discard the unselected cubes. Each subsequent time t proceeds similarly. At the end of time t, the original unit cube now has side length 2t, and we have selected a total of k t unit cubes. The fractal dimension is $$\log (k^t) / \log (2^t) = \log k / \log 2$$ ; compare this to (10.21). As t →∞, the resulting fractal is not self-similar, since the selection of cubes is random; rather, the fractal is statistically self-similar. (Statistically self-similarity is also used in the randomized Sierpiński carpet construction described in Sect. 4.​3.) The object generated by the β model construction after some finite t differs from realistic aggregates since the cubes are not necessarily connected.

Brain Electroencephalogram: The d C of brain electroencephalogram (EEG) patterns produced by music of varying degree of complexity was studied in [Birbaumer 96]. Given a center point x and radius r, the number M(x, r) of points lying in a radius-based box of radius r was computed. Starting with a given r 1 such that M(x, r 1) = k, the sequence r i of radius values was chosen so that M(x, r i+1) − M(x, r i) = M(x, r i), yielding M(x, r i+1) = 2i−1k. This scheme reduced the problems associated with small radii. For a given x, as r increases, the plot of $$\log M(x,{r_{{i}}})$$ versus $$\log {r_{{i}}}$$ values starts out looking linear, and then levels off. A straight line was fitted to the $$\log M(x,{r_{{i}}})$$ versus $$\log {r_{{i}}}$$ curve for the 10 smallest values of r i. If the point $$\bigl (\log r_{{10}}, \log M(x,r_{{10}}) \bigr )$$ has the largest distance (comparing the 10 distances) to the straight line, then the linear fit was recalculated using only the smallest 9 points. If the point $$\bigl (\log r_{{9}}, \log M(x,r_{{9}}) \bigr )$$ has the largest distance (comparing the 9 distances) to the new straight line, then the linear fit was again recalculated using only the smallest 8 points. This procedure continues until for some r j, the distance from $$\bigl (\log r_{{j}}, \log M(x, r_{{j}}) \bigr )$$ to the line determined by the first j points is not the largest distance; the slope of this line is the pointwise dimension for this x. This typically occurred for when j is 5 or 6 or 7. Once the slope has been determined for each x, the correlation dimension was taken to be the median of these pointwise dimensions.

Fat Crystals: The d C of fat crystals (e.g., of milk fat, palm oil, or tallow) was computed in [Tang 06] by counting the number of particles in a square of size s centered on the image. The box size s ranged from 35% to 100% of the image size. The slope of the best linear fit to the $$\log M(s)$$ versus $$\log s$$ curve, obtained using regression, was taken as the estimate of d C.

Gels and Aerogels: The d C of gel and aerogel structures, for which the microstructure can be described as a fractal network with the length scale of 10−9 to 10−7 meters, was calculated in [Marliere 01]. However, this study only counted particles, and did not explicitly consider the network topology. The fractal structure results from an aggregation process in which silica beads form structures whose size is characterized by a fractal dimension of about 1.6. The addition of silica soot “aerosil” strongly modifies the aggregation process, and for sufficiently high concentrations of silica soot the resulting composite is non-fractal.

River Flows: As described in [Krasovskaia 99], river flows can exhibit roughly the same pattern year after year, or they can exhibit irregular behavior by alternating between a few regime types during individual years. In [Krasovskaia 99], d C was computed from a time series for different values of the embedding dimension. (Although rivers can be modelled as networks, this study did not utilize network models.) They determined that, for the more stable (regular) regimes, d C(E) quickly converges for small E, leading to a d C of just over 1. Irregular regimes require E > 4 and yield a d C of over 3.

Astronomy: In astronomy, the correlation sum provides the probability that another galaxy will be found within a given distance of a randomly selected galaxy. The transition to homogeneity, defined as the scale above which the fractal dimension of the underlying point distribution is equal to the ambient dimension of the space in which points are distributed, was studied in [Yadav 10], which provided this description of the role of d C in astronomy.

One of the primary aims of galaxy redshift surveys is to determine the distribution of luminous matter in the Universe. These surveys have revealed a large variety of structures starting from groups and clusters of galaxies, extending to superclusters and an interconnected network of filaments which appears to extend across very large scales. We expect the galaxy distribution to be homogeneous on large scales. In fact, the assumption of large-scale homogeneity and isotropy of the Universe is the basis of most cosmological models. In addition to determining the large-scale structures, the redshift surveys of galaxies can also be used to verify whether the galaxy distribution does indeed become homogeneous at some scale. Fractal dimensions of the galaxy matter distribution can be used to test the conjecture of homogeneity.

Medicine: The d C of the visual evoked potential (VEP), which is a brain electrical activity generated by a visual stimulus such as a checkerboard pattern, was studied in [Boon 08]. The d C may be a useful diagnostic tool and may find application in the screening and monitoring of acquired color vision deficiencies. In the study of Parkinson’s disease, the d C of the EEG is a sensitive way to discriminate brain electrical activity that is task and disease dependent.5 In the study of Alzheimer’s disease, d C can also discriminate the EEG arising from dementia from the EEG arising from vascular causes. For the treatment of glaucoma, the d C of the VEP of patients with glaucoma was lower than for healthy individuals. In the VEP study in [Boon 08], d C was estimated for the embedding dimensions E = 1, 2, 3, 4, 5, and 64 equally spaced values of the correlation distance r were used; practical aspects of applying least squares to determine d C were also considered.

Human Sleep: Crick and Mitchinson hypothesized that one of the functions of dreams is to erase faulty associations in the brain [Kobayashi 00]. Also, the human brain may have a nighttime mechanism to increase flexibility in order to respond to unexpected stimulations when awake. Much has been learned from computing d C of the EEG of human sleep patterns. For instance, d C decreases from the “awake” stage to sleep stages 1, 2, 3, and 4, and increases at REM sleep, and d C during sleep 2 and REM sleep in schizophrenia were significantly lower than in healthy people.6 Moreover, d C may relate to the speed of information processing in the brain. The sleep EEG over the entire night was studied in [Kobayashi 00]. The EEG on a tape was converted to 12 bit digital data, and the resulting time series was embedded in phase space, with a maximum embedding dimension of 19. When the change in the slope of $$\log C(r)$$ versus $$\log r$$ is less than 0.01 as the embedded dimension is increased, then d C was defined to be this slope. The mean d C of the sleep stages were 7.52 for awake, 6.31 for stage 1, 5.54 for stage 2, 3.45 for stage 3, and 6.69 for REM sleep.

Earthquakes: The San Andreas fault in California was studied in [Wyss 04]. They calculated a d C of 1.0 for the “asperity” region and a d C of 1.45–1.72 for the “creeping” region. They noted that r should vary by at least one order of magnitude for a meaningful fractal analysis. Their study established a positive correlation between the fractal dimension and the slope of the earthquake frequency-magnitude relationship.

The d C of earthquakes was also studied in [Kagan 07]. Defining C(r) to be the total number of earthquake pairs at a distance r, the correlation dimension was obtained by estimating $$\mathrm{d} \log C(r)/\mathrm{d} \log r$$ using a linear fit. Kagan derived formulae to account for various systematic effects, such as errors in earthquake location, the number of earthquakes in a sample, and boundary effects encountered when the size of the earthquake region being studied exceeds r. Without properly accounting for such effects, and also for data errors, practically any value for d C can be obtained.

Several reasons are provided in [Kagan 07] for utilizing d C rather than d B. The distances between earthquakes do not depend, as boxes do, on the system coordinates and grid selection. Distances can be calculated between points on the surface of a sphere, whereas it is not clear how to apply box counting to a large region on the surface of a sphere. Also, since seismic activity in southern California aligns with plate boundaries and the San Andreas fault, issues could arise when boxes are oriented along fault lines. For these reasons, box counting has been employed only in relatively limited seismic regions, like California.

The natural drainage systems in an earthquake-prone region provide clues to the underlying rock formations and geological structures such as fractures, faults, and folds. Analyzing earthquake related data for Northeast India, [Pal 08] computed the correlation dimension $${d^{ e}_{{C}}}$$ of earthquake epicenters, the correlation dimension $${d^{ f}_{{C}}}$$ of the drainage frequency (total stream segments per unit area, evaluated at the earthquake epicenters), and the correlation dimension $${d^{ d}_{{C}}}$$ of the drainage density (total length of stream segments per unit area, evaluated at the earthquake epicenters). They found that $${d^{ f}_{{C}}}$$ ranged from 1.10 to 1.64 for the various regions, $${d^{ d}_{{C}}}$$ ranged from 1.10 to 1.60, and $${d^{ e}_{{C}}}$$ ranged from 1.10 to 1.70, which indicated that $${d^{ f}_{{C}}}$$ and $${d^{ d}_{{C}}}$$ are very appropriate for earthquake risk evaluation.

Orbit of a Pendulum: The effect of noise in the computation of d C of a nonlinear pendulum was studied in [Franca 01]. Random noise was introduced to simulate experimental data sets. Their results illustrated the sensitivity of d C(E) to the embedding dimension E.

Aesthetics of Fractal Sheep: This study [Draves 08] was based on research by Sprott, beginning in 1993, which proposed d C as a measure of complexity of a fractal image, and examined the relationship of fractal dimension to aesthetic judgment (i.e., which images are more pleasing to the eye). “Fractal sheep” are animated images which are based on the attractors of two-dimensional iterated function systems. The images, used as computer screen-savers, are downloaded automatically (see https://​electricsheep.​org) and users may vote for their favorite sheep while the screen-saver is running. The aesthetic judgments of about 20,000 people on a set of 6400 fractal images were analyzed in [Draves 08], and d C was computed for each frame of a fractal sheep. Since the sheep are animated, d C varies over time, so an average fractal dimension, averaged over 20 frames, was computed. They found that the sheep most favored have an average fractal dimension between 1.5 and 1.8.

Complexity of Human Careers: In [Strunk 09], d C was used to compare the career trajectory of a cohort of people whose careers started in the 1970s versus a cohort whose careers started in the 1990s. There were 103 people in the 1970s cohort and 192 people in the 1990s cohort. In each of the first 12 career years of each cohort, twelve measurements were taken for each person; the measurements include, e.g., the number of subordinates, annual income, career satisfaction, and stability of professional relations. The time series of all people in each cohort were aggregated to create a single “quasi time series”, and 100 different variants of the time series for each of the two cohorts were generated and calculated separately. Strunk concluded that the first 12 career years of the 1970s cohort has a mean d C of 3.424, while the first 12 career years of the 1990s cohort has a mean d C of 4.704, supporting the hypothesis that careers that started later are more complex. Strunk observed that a limitation of d C is the lack of a test statistic for the accuracy of the estimated d C, and thus d C is not a statistically valid test for complexity.

Exercise 10.4 Using the techniques presented in the chapter, estimate the number of people in each cohort required to obtain a statistically significant estimate of d C. □

Pattern Recognition: The intrinsic dimension of a set of points $$\varOmega \subset {\mathbb {R}}^E$$ is the smallest integer M (where M ≤ E) such that Ω is contained in an M-dimensional subspace of $${\mathbb {R}}^E$$ . Knowing the intrinsic dimension is important in pattern recognition problems since if M < E both memory requirements and algorithm complexity can often be reduced. The intrinsic dimension can be estimated by d C, but the required number N of points, as determined by the bound (10.13), can be very large. The following method [Camastra 02] estimates the intrinsic dimension of any set Ω of N points, even if N is less than this lower bound.
  1. 1.

    Create a data set Ω ′ with N points whose intrinsic dimension is known. For example, if Ω ′ contains N points randomly generated in an E-dimensional hypercube, its intrinsic dimension is E.

     
  2. 2.

    Compute d C(E) for the data set Ω ′.

     
  3. 3.

    Repeat Steps 1 and 2, generating a new set Ω ′, for K different values of E, but always with the same value of N. This generates the set, with K points, $$\{ \bigl (E_1, {d_{{C}}}(E_1) \bigr ), \bigl (E_2, {d_{{C}}}(E_2) \bigr ), \ldots , \bigl (E_K, {d_{{C}}}(E_K) \bigr ) \}$$ . For example, [Camastra 02] used K = 18, with E 1 = 2 and E 18 = 50.

     
  4. 4.

    Let Γ be a curve providing a best fit to these K points. (In [Camastra 02], a multilayer-perceptron neural network was used to generate the curve.) For a point (x, y) on Γ, x is the intrinsic dimension, and y is the correlation dimension.

     
  5. 5.

    Compute the correlation dimension d C for the set Ω. If x is the unique value such that (x, d C) is on the curve Γ, then x is the estimated intrinsic dimension.

     

The validity of this method rests on two assumptions. First is the assumption that the curve Γ depends on N. Second, since different sets of size N with the same intrinsic dimension yield similar estimates of d C, the dependence of the curve Γ on the sets Ω ′ is assumed to be negligible.

Economic Applications: The correlation dimension has been of special interests to economists.

The correlation dimension, a measure of the relative rate of scaling of the density of points within a given space, permits a researcher to obtain topological information about the underlying system generating the observed data without requiring a prior commitment to a given structural model. If the time series is a realization of a random variable, the correlation dimension estimate should increase monotonically with the dimensionality of the space within which the points are contained. By contrast, if a low correlation dimension is obtained, this provides an indication that additional structures exists in the time series - structure that may be useful for forecasting purposes. In this way, the correlation dimension estimates may prove useful to economists … Furthermore, potentially the correlation dimension can provide an indication of the number of variables necessary to model a system accurately. [Ramsey 90]

Below are a few selected economic applications of the correlation dimension.

Greek Stock Market: In [Barkoulas 98], d C was used to investigate the possibility of a deterministic nonlinear structure in Greek stock returns. The data analyzed was the daily closing prices of a value-weighted index of the 30 most marketable stocks on the Athens Stock Exchange during the period 1988 to 1990. As E increased from 1 to 15, the computed d C(E) rose almost monotonically (with one exception) from 0.816 to 5.842, with some saturation underway by E = 14. Based on this and other analysis, [Barkoulas 98] concluded that there was not strong evidence in support of a chaotic structure in the Athens Stock Exchange.

London Metal Exchange: In [Panas 01], d C was used to study the prices of six metals on the London Metal Exchange. Each metal was studied individually, for E = 4, 5, …, 10. Panas observed that if the attractor has an integer d C, then it is not clear if the dynamical process is chaotic. Therefore, to determine if the system is chaotic, d C should be accompanied by computing other measures, e.g., the Kolmogorov K-entropy and the Lyapunov exponent [Chatterjee 92].

Thai Stock Exchange: In [Adrangi 04], d C was used to test for low-dimensional chaos in the Stock Exchange of Thailand. To estimate d C(E) for a given E and a given set {s j} of decreasing values of s, [Adrangi 04] computed the slopes
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{C}}(E, j) \equiv \frac{ \log C_E(s_{{j+1}}) - \log C_E(s_{{j}})} { \log s_{{j+1}} - \log s_{{j}} } \, , \end{array} \end{aligned} $$
where C E(s) is the correlation sum for a given E and s. For each value of E, the average of the three highest values of d C(E, j) was taken to be the estimate of d C(E).

Gold and Silver Prices: The correlation dimension of gold and silver prices, using daily prices from 1974 to 1986, was studied in [Frank 89]. The range of values for s was 0.933 ≈ 0.031 to 0.920 ≈ 0.121 (gold prices were in United States dollars per fine ounce, and silver prices were in British pence per troy ounce).7 The correlation dimension d C(E) was computed for E = 5, 10, 15, 20, 25; the results did not substantially change for E > 25. For gold, the computed d C(E) ranged from 1.11 for E = 5 to 6.31 for E = 25; for silver the range was 2.01 for E = 5 to 6.34 for E = 25. Using this and other analyses, [Frank 89] concluded that there appears to be some sort of nonlinear process, with dimension between 6 and 7, that generated the observed gold and silver prices.

U.S. Equity Market: In [Mayfield 92], d C was used to uncover evidence of complex dynamics in U.S. equity markets, using 20,000 observations of the Standard and Poor’s (S&P) 500 cash index, taken at 20-s samples. The correlation dimension d C(E) was computed for E = 2, 3, …, 10, 15, 20, and [Mayfield 92] concluded that the underlying market dynamics that determines these S&P index values is either of very high dimension, or of low dimension but with entropy8 so high that the index cannot be predicted beyond 5 min. 9

Fractal Growth Phenomena: The correlation dimension has been widely used in the study of fractal growth phenomena, a topic which received considerable attention by physicists starting in the 1980s [Vicsek 89]. Fractal growth phenomena generate such aggregation products as colloids, gels, soot, dust, and atmospheric and marine snowflakes [Block 91]. Fractal growth processes are readily simulated using diffusion limited aggregation (DLA), a model developed in 1981 in which a fractal aggregate of particles, sitting on an E-dimensional lattice, is grown in an iterative process. A walker, added at “infinity” (a faraway position), engages in a random walk until it arrives at a lattice site adjacent to an already occupied site. The walker stops, and this particle is added to the aggregate. The process starts again with another random walker added at infinity. The process is usually started with a seed set of stationary particles onto which a set of moving particle is released. The resulting aggregate is very tenuous, with long branches and considerable space between the branches. There is a large literature on DLA, in particular by Stanley and his students and colleagues; [Stanley 92] is a guide to early work on DLA.

A fractal generated by DLA is an example of one of the two fundamental classes of fractals [Grassberger 93]. For the class encompassing percolation or DLA clusters, the fractal is defined on a lattice, the finest grid used for box counting is this lattice, and each lattice site is either unoccupied or occupied by at most one particle. The other class describes fractals such as strange attractors (Sect. 9.​1) for which only a random sample of points on the fractal are known, and we need very many points per non-empty box to compute a fractal dimension.

In the DLA model of [Sorensen 97], one monomer is placed at the center of an E-dimensional sphere. Then other monomers are placed, one at a time, at a starting radius at a random angular position. The starting radius is five lattice units beyond the perimeter of the central cluster. Each monomer follows a random walk until it either joins the central cluster, or wanders past the stopping radius (set to three times the starting radius). Simulation was used to study the number N of monomer (i.e., primary) particles in a cluster formed by aggregation in colloidal or aerocolloidal systems, under the assumption $$N = k_0 ({r_{{g}}}/a)^{d_{{C}}}$$ , where r g is the root mean square of monomer positions relative to the center of mass, and the monomer radius a is used to normalize r g. The focus of [Sorensen 97] was to explore the dependence of the prefactor k 0 on d C.

A very similar definition of d C for DLA was given in [Feder 88]; this definition also mirrors (10.21). Let R 0 be the radius of the item (e.g., an atom or molecule) being packed, let R be the radius of the smallest sphere containing a cluster with N items, and let ρ be the density reflecting how densely the items are packed. If as N →∞ we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} N = \rho \left( \frac{R}{R_0} \right)^{d_{{C}}} {}, \end{array} \end{aligned} $$
(10.22)
then d C is the cluster dimension, also called the mass dimension [Feder 88].10 For a two-dimensional cluster formed by DLA we have d C = 1.71, and for a three-dimensional cluster we have d C = 2.50 [Feder 88].

To simulate diffusion limited cluster aggregation (DLCA), initialize the simulation with a list of monomers. To start the process, remove two monomers from the list. Position one of them at the center, and introduce the second at a random position on the starting radius, as with DLA. This second monomer then follows a random walk until it either joins the monomer at the center or wanders past the stopping radius. If the wandering monomer joins the one at the center, the resulting cluster is placed back into the list. Thus the list in general contains both monomers and clusters. In each successive iteration, two clusters are removed from the list; one is positioned at the center and the other wandered randomly. This process could be stopped after some number of iterations, in which case the list in general contains multiple clusters and monomers. Alternatively, the process could be allowed to continue until there is only a single cluster [Sorensen 97].

Diffusion Limited Deposition (DLP) is a process closely related to DLA. In DLP, particles do not form free-floating clusters, but rather fall onto a solid substrate. Techniques for simulating two-dimensional DLP were presented in [Hayes 94]. Consider a large checkerboard, in which the bottom (“south”) boundary (corresponding to y = 0) is the substrate, and represents the position of each particle by a cell in the checkerboard. In the simplest DLP, particles are released one at a time from a random x position at the top (“north”) boundary of the lattice. Once released, a particle P falls straight down (“south”, towards the x axis), stopping when either (i) P is adjacent to another particle (i.e., P and another particle share a common “east” or “south” or “west” boundary), or (ii) P hits the substrate. Once P stops, it never moves again. A variant of this above procedure makes particles move obliquely, as if they were driven by a steady wind.

In simulating DLP, instead of constraining each particle to only drop straight down, or obliquely, we can instead allow a particle to move in all four directions, with each of the four directions being equally likely at each point in time for each particle. A particle stops moving when it becomes adjacent to another particle or hits the substrate. The effect of the “east” and “west” boundary can be eliminated by joining the “east” edge of the checkerboard to the “west” edge, as if the checkerboard was wrapped around a cylinder. This “random walk” DLP generates a forest of fractal trees [Hayes 94]. A straightforward simulation of the “random walk” DEP can require excessive computation time, but two techniques can reduce the time. First, if a particle wanders too far from the growing cluster, pick it up and place it down again closer to the cluster, at a random x position. Second, if a particle is far from the growing cluster, allow it to move multiple squares (rather than just a single square) in the chosen direction. For 104 particles, these two techniques reduced the execution time from 30 h (on a 1994 vintage computer) to a few minutes [Hayes 94].

The geometry of the lattice makes a difference: simulations by Meakin on a square (checkerboard) lattice with several million particles generated clusters with diamond or cross shapes aligned with the axes of the lattice, and these shapes do not appear in simulations on a triangular or hexagonal lattice. Thus, as stated in [Hayes 94], “Simulations done with a lattice are more efficient than those without (largely because it is easier to detect collisions), but they are also one step further removed from reality.”

Example 10.1 The gyration dimension [Kinsner 07] is a variant of d C that characterizes an asymmetric growing geometric object, such as an object formed by diffusion limited aggregation (DLA). Consider a dynamical process described by $$\{ {\varOmega }_t \}_{t=1}^{\infty }$$ , where Ω t is a finite set of points in $${\mathbb {R}}^2$$ . Calling each point a “site”, the sequence $$\{ {\varOmega }_t \}_{t=1}^{\infty }$$ might describe a process in which the number of sites increases over time, but the sequence could also describe a cellular automata birth and death process. Defining N t ≡|Ω t|, the center of gravity $$x^{{cg}}_{{t}} \in {\mathbb {R}}^2$$ of the N t points in Ω t at time t is given by $$x^{{cg}}_{{t}} \equiv (1/N_t) \sum _{x \in {{\varOmega }_t}} x$$ . The center of gravity is also called the “center of mass” or the “centroid”. Define
$$\displaystyle \begin{aligned} \begin{array}{rcl} r_{{t}} \equiv \sqrt { \frac{1}{N_t} \sum_{x \in {\varOmega}_t} [ \mathit{dist}(x ,{x^{{cg}}_{{t}}})]^2 } {} \end{array} \end{aligned} $$
(10.23)
to be the radius of gyration at time t of the N t sites. The center of mass and radius of gyration are “ideally suited” to calculating a fractal dimension for asymmetric objects created by a fractal growth phenomenon such as DLA. For example, consider the asymmetric object (a tree, but treated as a geometric object and not as a network) illustrated in Fig. 10.3. The tree has a root node N 1 (colored green), but balls centered at N 1 do not tend to uniformly cover the tree. In contrast, balls centered at the center of gravity N 2 (colored red) tend to uniformly cover the tree. The center of gravity of the object need not be one of the N given points, as Fig. 10.3 illustrates. If
$$\displaystyle \begin{aligned} \lim_{t \rightarrow \infty} \frac{\log N_t}{\log r_{{t}}} \, \end{aligned}$$
exists, then this limit is the gyration dimension [Kinsner 07]. □
../images/487758_1_En_10_Chapter/487758_1_En_10_Fig3_HTML.png
Figure 10.3

Radius of gyration

10.5 The Sandbox Dimension

The sandbox method [Tél 89] is a popular method for approximating d C of a real-world geometric object Ω containing a finite number of points. Randomly choose N points x(n), n = 1, 2, …, N, from Ω. Let B(x(n), r) be the box containing each point y ∈ Ω such that dist(y, x(n)) ≤ r, and let M(x(n), r) be the number of points in B(x(n), r). Define
$$\displaystyle \begin{aligned} \begin{array}{rcl} M(r) \equiv (1/N ) \sum_{n=1}^N M\big( x(n), r \big) \, . {} \end{array} \end{aligned} $$
(10.24)
Definition 10.1 If for some exponent d sandbox and some range of r we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} M(r) \propto r^{d_{{{sandbox}}}} {}, \end{array} \end{aligned} $$
(10.25)
then d sandbox is the sandbox dimension of Ω. □

The sandbox dimension was designed for real-world systems of points, e.g., a finite number of points on a lattice, for which the distance between pairs of points does not become arbitrarily small. Thus, unlike the definition of d C, the definition of d sandbox is not in terms of a limit as r → 0. To see how the sandbox method can be applied to a pixelated image (e.g., of a blood vessel), randomly choose N occupied pixels (a pixel is occupied if it indicates part of the image, e.g., part of the blood vessel) from the full set of occupied pixels. Let x(n) be the coordinates of the center of the n-th occupied pixel. The points x(n) must not be too close to the edge of the image. Let B(x(n), s) be the box centered at x(n) whose side length is s pixels. The value s must be sufficiently small such that B(x(n), s) does not extend beyond the edge of the image. Let M(x(n), s) be the number of occupied pixels in the box B(x(n), s). Define $$M(s) = (1/N ) \sum _{n=1}^N M\big ( x(n), s \big )$$ . The scaling $$M(s) \propto s^{d_{{{sandbox}}}}$$ over some range of s defines d sandbox.

The sandbox method is sometimes presented (e.g., [Liu 15]) as an extension of the box-counting method. However, Definition 10.1 shows that d sandbox is an approximation of d C. Indeed, as discussed in Sect. 9.​3, in practice the correlation dimension d C of a geometric object Ω is computed by computing C(x, r) for only a subset of points in Ω, averaging C(x, r) over this finite set to obtain C(r), and finding the slope of the $$\log C(r)$$ versus $$\log r$$ curve over a finite range of r.

There are many applications of the sandbox method. It was used in [Hecht 14] to study protein detection. The mass M(x, r) was calculated for all center points x except for particles that were too close to the periphery of the system. It was used in [Daccord 86] to compute the fractal dimension of the highly branched structures (“fingers”) created by DLA on a lattice. In this application, each lattice point lying on a finger was chosen as the center of a box (as opposed to choosing only some of the lattice points lying on a finger). In [Jelinek 98], the box-counting method, the dilation method (Sect. 4.​5), and sandbox method (called the mass-radius method in [Jelinek 98]) were applied to 192 images of retinal neurons. Although different spatial orientations or different origins of the box mesh did yield slightly different results, the fractal dimensions computed using these three methods did not differ significantly.

In [Enculescu 02], both d B and d sandbox of silver nanocrystals were computed. To first calibrate their computer programs, they determined that for colloidal gold, both methods yielded 1.75, the same value determined by previous research. For silver nanoclusters in an alkali halide matrix, they computed d sandbox = 1.81 and d B = 1.775; for silver nanocrystals in NaCl they computed d sandbox = 1.758 and d B = 1.732; for silver nanocrystals in KBr they computed d sandbox = 1.769 and d B = 1.772. Though not mentioned in [Enculescu 02], since d sandbox is an approximation of d C, and since in theory we have d C ≤ d B (Theorem 9.1), it is interesting that in two cases (alkali halide and NaCl) they found d sandbox > d B.

As an example of a testimonial to the sandbox method, in an illuminating exchange of letters on the practical difficulties in computing fractal dimensions of geometric objects, Baish and Jain [Corr 01], in comparing the sandbox method to box counting, and to another variant of the Grassberger–Procaccia method for computing d C, reported that “the sandbox method has been the most robust method in terms of yielding accurate numbers for standard fractal objects and giving a clear plateau for the slope of the power-law plot.” The sandbox method also has been a popular alternative to box counting for computing the generalized dimensions of a geometric object (Sect. 16.​6) or of a network (Sects. 11.​3 and 17.​5).

In [Panico 95], a variant of the sandbox method was used to study retinal neurons. Let Ω be the set of N points x(n), n = 1, 2, …, N, where $$x(n) \in {\mathbb {R}}^E$$ . The center of gravity $$x_{{{cg}}} \in {\mathbb {R}}^E$$ is given by x cg ≡ (1∕N)∑x(n) ∈ Ωx(n). The radius of gyration r g was defined in [Panico 95] by
$$\displaystyle \begin{aligned} {r_{{g}}} \equiv (1/N) \sum_{x(n) \in \varOmega} {\mathit{dist}}\big( x(n), x_{{{cg}}} \big) \, , \end{aligned}$$
where dist(x(n), x cg) is the Euclidean distance from x(n) to x cg, so r g is the average distance to the center of gravity; this definition differs from (10.23) above. Define Ω I to be the set of points in Ω within distance r g of x cg, so Ω I is the “interior” of Ω. Define N I ≡|Ω I|. For example, suppose in one dimension (E = 1) we have Ω = {−3, −2, −1, 1, 2, 3}. Then x cg = 0 and r g = (3 + 2 + 1 + 1 + 2 + 3)∕6 = 2, so Ω I = {−2, −1, 1, 2}. For r ≤ r g and for x(n) ∈ Ω I, let M(x(n), r) be the number of points in Ω within Euclidean distance r of x(n). Define
$$\displaystyle \begin{aligned} M_I(r) \equiv \frac{1}{N_I} \sum_{x(n) \in {\varOmega}_I} M\big( x(n), r \big) \, . \end{aligned}$$
By choosing only centers x(n) in Ω I, the impact of “edge effects” is mitigated. Then Ω has the interior sandbox dimension d sandbox if $$M_I(r) \propto r^{d_{{{sandbox}}}}$$ over some range of r.

One conclusion of [Panico 95] was that this variant of the sandbox method is less sensitive than box counting at discriminating fractal from non-fractal images. For example, for a pixelated skeleton of a river, the linear region of the $$\log M_I(r)$$ versus $$\log r$$ plot was substantially smaller for the sandbox method than for box counting. The main result of [Panico 95] was that the calculated fractal dimension d of individual neurons and vascular patterns is not independent of scale, since d reflects the average of the dimension of the interior (this dimension is 2) and the dimension of the border (this dimension approaches 1). Moreover, “Thus, despite the common impression that retinal neurons and vessels are fractal, the objective measures applied here show they are not.” The general principle proposed in [Panico 95] is that to accurately determine a pattern’s fractal dimension, measurement must be confined to the interior of the pattern.