© Springer Nature Switzerland AG 2020
E. RosenbergFractal Dimensions of Networkshttps://doi.org/10.1007/978-3-030-43169-3_9

9. Correlation Dimension

Eric Rosenberg1 
(1)
AT&T Labs, Middletown, NJ, USA
 

Distance doesn’t exist, in fact, and neither does time. Vibrations from love or music can be felt everywhere, at all times.

Yoko Ono (1933- ) Japanese multimedia artist, singer, and peace activist, and widow of John Lennon of The Beatles.

Covering a hypercube in $${\mathbb {R}}^E$$ , with side length L, by boxes of side length s requires (L∕s)E boxes. This complexity, exponential in E, makes d B expensive to compute for sets in a high-dimensional space. The correlation dimension was introduced in 1983 by Grassberger and Procaccia [Grassberger 83a, Grassberger 83b] and by Hentschel and Procaccia [Hentschel 83] as a computationally attractive alternative to d B. The correlation dimension has been enormously important to physicists [Baker 90], and even by 1999 the literature on the computation of the correlation dimension was huge [Hegger 99, Lai 98]. The Grassberger and Procaccia papers introducing the correlation dimension were motivated by the study of strange attractors, a topic in dynamical systems. Although this book is not focused on chaos and dynamical systems, so much of the literature on the correlation dimension is motivated by these topics that a very short review, based on [Ruelle 80, Ruelle 90] will provide a foundation for our discussion of the correlation dimension of a geometric object (in this chapter and in the next chapter) and of a network (in Chap. 11).

9.1 Dynamical Systems

A dynamical system (e.g., a physical, chemical, or biological dynamical system) is a system that changes over time. A deterministic dynamical system models the evolution of x(t), where t is time and x(t) is a vector with finite or infinite dimension. A continuous time dynamical system has the form $$\mathrm{d} x(t)/\mathrm{d} t = F \bigl (x(t) \bigr )$$ , for some function F, while a discrete time dynamical system has the form $$x(t+1) = F \bigl (x(t) \bigr )$$ for some function F. A physical system can be described using its phase space, so that each point in phase space represents an instantaneous description of the system at a given point in time. We will be concerned only with finite dimensional systems for which the phase space is $${\mathbb {R}}^E$$ , and the state of the system is specified by x = (x 1, x 2, …, x E). For example, for a physical system the state might be the coordinates on a grid, and for a chemical system the state might be temperature, pressure, and concentration of the reactants. The E coordinates of x are assumed to vary with time, and their values at time t are x(t) = (x 1(t), x 2(t), …, x E(t)). We assume [Ruelle 80] the state at time t + 1 depends only on the state at time t:
$$\displaystyle \begin{aligned} \begin{array}{rcl} {x_{{1}}}(t+1) &\displaystyle =&\displaystyle F_1 \bigl(x(t) \bigr) \\ {x_{{2}}}(t+1) &\displaystyle =&\displaystyle F_2 \bigl(x(t) \bigr) \\ &\displaystyle \cdots &\displaystyle \\ {x_{{E}}}(t+1) &\displaystyle =&\displaystyle F_E \bigl(x(t) \bigr) \; . \end{array} \end{aligned} $$
Define F = (F 1, F 2, …, F E), so $$F: {\mathbb {R}}^E \rightarrow {\mathbb {R}}^E$$ . Given x(0), we can determine x(t) for each time t.

If an infinitesimal change δx(0) is made to the initial conditions (at time t = 0), there will be a corresponding change δx(t) at time t. If for some λ > 0 we have |δx(t)|∝|δx(0)|e λt (i.e., if δx(t) grows exponentially with t), then the system is said to exhibit sensitive dependence on initial conditions. This means that small changes in the initial state become magnified, eventually becoming distinct trajectories [Mizrach 92]. The exponent λ is called a Lyapunov exponent.

A dynamical system is said to be chaotic if for all (or almost all) initial conditions x(0) and almost all δx(0) the system exhibits sensitive dependence on initial conditions. The evolution of chaotic systems is complex and essentially random by standard statistical tests. Only short-term prediction of chaotic systems is possible, even if the model is known with certainty [Barkoulas 98]. Chaos was first observed by J. Hadamard in 1898, and H. Poincaré in 1908 realized the implications for weather predictability, a subject addressed by Edward Lorenz [Chang 08] in a famous 1963 paper that revitalized interest in chaos.1 Lorenz and others have shown that theoretically it is not possible to make reasonable weather forecasts more than one or 2 weeks ahead. An example of a continuous time chaotic dynamical system is the system studied by Lorenz in 1963:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{d} {x_{{1}}}/\mathrm{d} t &\displaystyle =&\displaystyle 10({x_{{2}}} - {x_{{1}}}) \\ \mathrm{d} {x_{{2}}}/\mathrm{d} t &\displaystyle =&\displaystyle {x_{{1}}} (28 - {x_{{3}}}) - {x_{{2}}} \\ \mathrm{d} {x_{{3}}}/\mathrm{d} t &\displaystyle =&\displaystyle {x_{{1}}} {x_{{2}}} - (8/3){x_{{3}}} \, . \end{array} \end{aligned} $$
These equations approximate the behavior of a horizontal fluid layer heated from below. As the fluid warms, it tends to rise, creating convection currents. If the heating is sufficiently intense, the convection currents become irregular and turbulent. Such behavior happens in the earth’s atmosphere, and since a sensitive dependence on initial conditions holds, this model provides some theoretical justification for the inability of meteorologists to make accurate long-range weather forecasts.2

There are two types of dynamical physical systems. When the system loses energy due to friction, as happens in most natural physical systems, the system is dissipative. If there is no loss of energy due to friction, the system is conservative. A dissipative system always approaches, as t →∞, an asymptotic state [Chatterjee 92]. Consider a dissipative dynamical system $$F: {\mathbb {R}}^E \rightarrow {\mathbb {R}}^E$$ , and suppose that at time 0, all possible states of the system lie in a set Ω 0 having positive volume (i.e., positive Lebesgue measure, as defined in Sect. 5.​1). Since the system is dissipative, Ω 0 must be compressed due to loss of energy, and Ω 0 converges to a compact set Ω as t →∞. The set Ω lives in a lower dimensional subspace of the phase space, and thus has Lebesgue measure zero in the phase space. The set Ω satisfies F(Ω) = Ω, and Ω can be extremely complicated, often possessing a fractal structure [Hegger 99]. Interestingly, Benford’s Law (Sect. 3.​2) has been shown to apply to one-dimensional dynamical systems [Fewster 09].

The term strange attractor was introduced by Ruelle and Takens in 1971. Informally, an attractor of a dynamical system is the subset of phase space to which the system evolves, and a strange attractor is an attractor that is a fractal [Theiler 90]. More formally, a bounded set $$\varOmega \subset {\mathbb {R}}^E$$ , with infinitely many points, is a strange attractor for the map $$F: {\mathbb {R}}^E \rightarrow {\mathbb {R}}^E$$ if there is a set U with the following four properties [Ruelle 80]:
  1. 1.

    U is an E-dimensional neighborhood of Ω, i.e., for each point x ∈ Ω, there is a ball centered at x and entirely contained in U. In particular, Ω ⊂ U.

     
  2. 2.

    For each initial point x(0) ∈ U, the point x(t) ∈ U for all t > 0, and x(t) is arbitrarily close to Ω for all sufficiently large t. (This means that Ω is attracting.)

     
  3. 3.

    There is a sensitive dependence on initial condition whenever x(0) ∈ U. (This makes Ω is strange attractor.)

     
  4. 4.

    One can choose a point x(0) in Ω such that, for each other point y in Ω, there is a point x(t) that is arbitrarily close to y for some positive t. (This indecomposability condition says that Ω cannot be split into two different attractors.)

     

To see how a strange attractor arises in dissipative systems, imagine we begin with a small sphere. After a small time increment, the sphere may evolve into an ellipsoid, such that the ellipsoid volume is less than the sphere volume. However, the length of longest principle axis of the ellipsoid can exceed the sphere diameter. Thus, over time, the sphere may compress in some directions and expand in other directions. For the system to remain bounded, expansion in a given direction cannot continue indefinitely, so folding occurs. If the pattern of compressing, expansion, and folding continues, trajectories that are initially close can diverge rapidly over time, thus creating the sensitive dependence on initial conditions. The amounts of compression or stretching in the various dimensions are quantified by the Lyapunov exponents [Chatterjee 92].

A well-known example of a discrete time dynamical system was introduced by Hénon. For this two-dimensional system, we have x 1(t + 1) = x 2(t) + 1 − ax 1(t)2 and x 2(t + 1) = bx 2(t). With a = 1.4 and b = 0.3, the first 104 points distribute themselves on a complex system of lines that are a strange attractor (see [Ruelle 80] for pictures); for a = 1.3 and b = 0.3 the lines disappear and instead we obtain 7 points of a periodic attractor.

Chaos in human physiology was studied in many papers by Goldberger, e.g., [Goldberger 90]. In the early 1980s, when investigators began to apply chaos theory to psychological systems, they expected that chaos would be most apparent in diseased or aging systems (e.g., [Ruelle 80] stated that the normal cardiac regime is periodic). Later research found instead that the phase-space representation of the normal heartbeat contains a strange attractor, suggesting that the dynamics of the normal heartbeat may be chaotic. There are advantages to such dynamics [Goldberger 90]: “Chaotic systems operate under a wide range of conditions and are therefore adaptable and flexible. This plasticity allows systems to cope with the exigencies of an unpredictable and changing environment.”

Several other examples of strange attractors were provided in [Ruelle 80]. Strange attractors arise in studies of the earth’s magnetic field, which reverses itself at irregular intervals, with at least 16 reversals in the last 4 million years. Geophysicists have developed dynamo equations, which possess chaotic solutions, to describe this behavior. The Belousov–Zhabotinski chemical reaction turns ferroin from blue to purple to red; simultaneously the cerium ion changes from pale yellow to colorless, so all kinds of hues are produced (this reaction caused astonishment and some disbelief when it was discovered). For a biological example, discrete dynamical models of the population of multiple species yield strange attractors. Even for a single species, the equation $$x(t+1) = R x(t) \bigl (1-x(t) \bigr )$$ , where R > 0, gives rise to non-periodic behavior. Ruelle observed that the non-periodic fluctuations of a dynamical system do not necessarily indicate an experiment that was spoiled by mysterious random forces, but rather may indicate the presence of a strange attractor. Chaos in ecology was studied in [Hastings 93].

Physicists studying dynamical systems want to distinguish behavior that is irregular, but low-dimensional, from behavior that is irregular because it is essentially stochastic, with many effective degrees of freedom [Theiler 90]. Calculating the fractal dimension of the attractor helps make this distinction, since the fractal dimension roughly estimates the number of independent variables involved in the process [Badii 85]. That is, the fractal dimension can be interpreted as the number of degrees of freedom of the system [Ruelle 90]. A finite non-integer fractal dimension indicates the presence of complex deterministic dynamics [Krakovska 95]. The connection between strange attractors and fractals was succinctly described in [Grassberger 83b]:

In a system with F degrees of freedom, an attractor is a subset of F-dimensional phase space toward which almost all sufficiently close trajectories get “attracted” asymptotically. Since volume is contracted in dissipative flows, the volume of an attractor is always zero, but this leaves still room for extremely complex structures.

Typically, a strange attractor arises when the flow does not contract a volume element in all directions, but stretches it in some. In order to remain confined to a bounded domain, the volume element gets folded at the same time, so that it has after some time a multisheeted structure. A closer study shows that it finally becomes (locally) Cantor-set like in some directions, and is accordingly a fractal in the sense of Mandelbrot [Mandelbrot 77].

We could determine the fractal dimension of an attractor by applying box counting. However, a major limitation of box counting is that it counts only the number of occupied boxes, and is insensitive to the number of points in an occupied box. Thus d B is more of a geometrical measure, and provides very limited information about the clumpiness of a distribution. Moreover, if the box size s is small enough to investigate the small-scale structure of a strange attractor, the relation $$B_{{D}} (s) \sim s^{-{d_{{B}}}}$$ (assuming diameter-based boxes) implies that the number B D(s) of occupied boxes becomes very large. The most interesting cases of dynamical systems occur when the dimension of the attractor exceeds 3. As observed in [Farmer 82], when d B = 3 and s = 10−2 from $$B_{{D}} (s) = s^{-{d_{{B}}}}$$ we obtain one million boxes, which in 1982 taxed the memory of a computer. While such a requirement would today be no burden, the point remains: box-counting methods in their basic form have time and space complexity exponential in d B. Moreover, for a dynamical system, some regions of the attractor have a very low probability, and it may be necessary to wait a very long time for a trajectory to visit all of the very low probability regions. These concerns were echoed in [Eckmann 85], who noted that the population of boxes is usually very uneven, so that it may take a long time for boxes that should be occupied to actually become occupied. For these reasons, box counting was not (as of 1985) used to study dynamical systems [Eckmann 85]. Nine years later, [Strogatz 94] also noted that d B is rarely used for studying high-dimensional dynamical processes.

An early (1981) alternative to box counting was proposed in [Froehling 81]. Given a set of points in $${\mathbb {R}}^E$$ , use regression to find the best hyperplane of dimension m that fits the data, where m is an integer in the range 1 ≤ m ≤ E − 1. The goodness of fit of a given hyperplane is measured by χ 2, the sum of deviations from the hyperplane divided by the number of degrees of freedom. If m is too small, the fit will typically be poor, and χ 2 will be large. As m is increased, χ 2 will drop sharply. The m for which χ 2 is lowest is the approximate fractal dimension. A better approach, proposed two years later in 1983, is the correlation dimension. Our discussion of the correlation dimension begins with the natural invariant measure and the pointwise mass dimension.

9.2 Pointwise Mass Dimension

The pointwise mass dimension is based upon the measure of a subset of $${\mathbb {R}}^E$$ . The study of measures of sizes of sets dates at least as far back as Borel (1885), and was continued by Lebesgue (1904), Carathéodory (1914), and Hausdorff (1919) [Chatterjee 92]. Recall that the Lebesgue measure μ L was defined in Chap. 5. Formalizing the qualitative definition of “dissipative” provided above, we say that a dynamical physical system g t, t = 1, 2, …, where $$g_{{\, t}} : {\mathbb {R}}^E \rightarrow {\mathbb {R}}^E$$ , is dissipative if the Lebesgue measure μ L of a bounded subset tends to 0 as t →∞, i.e., if for each bounded $$B \subset {\mathbb {R}}^E$$ we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{t \rightarrow \infty} \mu_{{\, L}} [g_t(B)] = 0 \, . {} \end{array} \end{aligned} $$
(9.1)
It can be shown that only dissipative systems have strange attractors [Theiler 90]. Suppose the dissipative system has the strange attractor Ω. Since by (9.1) we have μ L(Ω) = 0, then to study Ω we require a new measure defined on subsets of Ω; the measure of a subset should reflect how much of the subset is contained in Ω. The new measure μ of a subset B ⊂ Ω should count how often and for how long a typical trajectory visits B, and an appropriate definition is
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mu(B) \equiv \lim_{t \rightarrow \infty} \frac {1}{t} \int_0^t I_{B}[g_t(x_0)] \mathrm{d} t \, , {} \end{array} \end{aligned} $$
(9.2)
where $$x_{{0}} \in {\mathbb {R}}^E$$ is the starting point of the system g t, and I B[x] is the indicator function whose value is 1 if x ∈ B and 0 otherwise [Theiler 90]. The measure defined by (9.2) is the natural measure for almost all x 0. For a discrete dynamical system, the natural measure of B is [Peitgen 92]
$$\displaystyle \begin{aligned} \mu(B) = \lim_{t \rightarrow \infty} \frac{1}{t+1} \sum_{i = 0}^t I_{B}[x(t)] \, . \end{aligned}$$
The natural measure is an invariant measure, which means [Peitgen 92] that for the system x t+1 = f(x t) if f −1(B) is the set of points which after one iteration land in B, then μ(f −1(B)) = μ(B). For x ∈ Ω and r > 0, define
$$\displaystyle \begin{aligned} {\varOmega}(x,r) \equiv \{ y \in {\varOmega} : \, \mathit{dist}(x,y) \leq r \} \, , \end{aligned}$$
where the choice of norm determines the shape of Ω(x, r) (e.g., a hypersphere for the Euclidean norm, and a hypercube for the L ∞ norm). Then μ(Ω(x, r)) is the natural measure of the ball Ω(x, r).
Definition 9.1 The pointwise dimension of μ at x, denoted by d(x), is given by
$$\displaystyle \begin{aligned} \begin{array}{rcl} d(x) \equiv \lim_{r \rightarrow 0} \frac{\log \mu\big({\varOmega}(x,r)\big)} {\log r} \, . \; \; {} \end{array} \end{aligned} $$
(9.3)
□ Thus μ(Ω(x, r)) ∼ r d(x) as r → 0. The pointwise dimension at x is also called the local Hölder exponent at x. In contrast to the Hausdorff and box counting dimensions, which are global quantities whose computation requires covering all of Ω, the pointwise dimension is a local quantity, defined at a single point. If d(x) is independent of x, then the probability (i.e., “mass”) of Ω(x, r) depends only on r but not on x; this holds, e.g., when points in Ω are uniformly distributed. If d(x) is a non-constant function of x, then the mass of Ω(x, r) depends on x and r; this holds, e.g., for the Gaussian distribution. (See [Simpelaere 98] for additional theory of the pointwise dimension.) The average pointwise dimension, denoted by 〈d〉, is given by
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle d \rangle \equiv \int_{\varOmega} d(x) \mathrm{d} \mu(x) \, , {} \end{array} \end{aligned} $$
(9.4)
where dμ(x) is the differential of μ(x).

9.3 The Correlation Sum

Let $$\varOmega \subset {\mathbb {R}}^E$$ , and suppose we have determined N points in Ω. Denote these points by x(n) for n = 1, 2, …, N. Denote the E coordinates of x(n) by x 1(n), x 2(n), …, x E(n). We can approximate the average pointwise dimension 〈d〉 defined by (9.4) by averaging d(x) over these points, that is, by computing $$(1/N) \sum _{n=1}^N d\bigl (x(n) \bigr )$$ . Since by (9.3) each $$d\bigl (x(n) \bigr )$$ is a limit, then $$(1/N) \sum _{n=1}^N d\bigl (x(n) \bigr )$$ is an average of N limits. An alternative method of estimating (9.4) is to first compute, for each r, the average
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle \mu \big( {\varOmega}(r) \big) \rangle \equiv \frac{1}{N} \sum_{i=1}^N \mu \Big( {\varOmega}\big( x(i),r \big) \Big) {} \end{array} \end{aligned} $$
(9.5)
and then compute the limit
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{r \rightarrow 0} \frac{\log \langle \mu \big( {\varOmega}(r) \big) \rangle} {\log r} \, . {} \end{array} \end{aligned} $$
(9.6)
Thus, instead of taking the average of N limits, in (9.6) we take the limit of the average of N natural measures. Writing (9.6) in a computationally useful form will lead us to the correlation dimension.
Let $$I_{{0}}: {\mathbb {R}} \rightarrow {\mathbb {R}}$$ be the Heaviside step function, defined by
$$\displaystyle \begin{aligned} I_{{0}}(z) = \left\{ \begin{array}{ll} 1 & \mbox{if } z \geq 0 \\ 0 & \mbox{otherwise.} \end{array} \right. {} \end{aligned} $$
(9.7)
The subscript “0” in I 0 is used to distinguish this step function from one that will be defined in a later chapter. Note that I 0(0) = 1. Then
$$\displaystyle \begin{aligned} I_{{0}} \Big( r - \mathit{dist} \big( x(i) , x(j) \big) \Big) = \left\{ \begin{array}{ll} 1 & \mbox{if }\mathit{dist} \big( x(i), x(j) \big) \leq r \\ 0 & \mbox{otherwise.} \end{array} \right. {} \end{aligned} $$
(9.8)
Typically, dist(x, y) is the Euclidean distance; we could alternatively use the L ∞ (sup norm) and define $$\mathit {dist}(x,y) = \max _{i=1}^E {\vert x_{{i}} - y_{{i}} \vert }$$ [Frank 89]. Define
$$\displaystyle \begin{aligned} C \big( x(i), r \big) \equiv \sum_{\substack{j=1 \\ j \neq i }}^N I_{{0}} \Big( r - \big( \mathit{dist}( x(i) , x(j) \big) \Big) \, , {} \end{aligned} $$
(9.9)
so C(x(i), r) is the number of points, distinct from x(i), whose distance from x(i) does not exceed r.3 Although C(x(i), r) depends on N, for notational simplicity we write C(x(i), r) rather than, e.g., C N(x(i), r). We have 0 ≤ C(x(i), r) ≤ N − 1. We can approximate μ(Ω(x(i), r)) using
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mu \Big( {\varOmega} \big( x(i),r \big) \Big) \approx \frac{C\big( x(i), r \big)}{N-1} \, . {} \end{array} \end{aligned} $$
(9.10)
This is an approximation, and not an equality, since we only have a finite data set; the accuracy of the approximation increases as N →∞. Define the correlation sum C(r) by
$$\displaystyle \begin{aligned} \begin{array}{rcl} C(r) \equiv \frac{1}{N(N-1)} \, \sum_{i=1}^N C\big( x(i), r \big) \, . {} \end{array} \end{aligned} $$
(9.11)
Although C(r) depends on N, for notational simplicity we write C(r) rather than, e.g., C N(r). If 0 < dist(x(i), x(j)) ≤ r, then both (i, j) and (j, i) contribute to C(r).4 In words, C(r) is the ratio
$$\displaystyle \begin{aligned} \frac{\mbox{the number of nonzero distances not exceeding } r} {\mbox{the total number of nonzero distances}} \, . \end{aligned}$$
Equivalently, C(r) is the fraction of all pairs of distinct points for which the distance between the pair does not exceed r. An equivalent definition of C(r) that invokes the natural measure μ defines C(r) to be the probability that a pair of distinct points, chosen randomly on the attractor with respect to μ, is separated by a distance not exceeding r [Ding 93]. From (9.5), (9.10), and (9.11) we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle \mu \big( {\varOmega}(r) \big) \rangle \approx \frac{1}{N} \sum_{i=1}^N \mu \Big( {\varOmega}\big( x(i),r \big) \Big) = \frac{1}{N(N-1)} \sum_{i=1}^N C \big( x(i), r \big) = C(r) \, . {} \end{array} \end{aligned} $$
(9.12)

Grassberger stressed the importance of excluding i = j from the double sum defining C(r); see [Theiler 90]. However, taking the opposite viewpoint, [Smith 88] wrote that it is essential that the i = j terms be included in the correlation sum, “in order to distinguish the scaling of true noise at small r from fluctuations due to finite N”. The argument in [Smith 88] is that, when the i = j terms are omitted, $$\log C(r)$$ is not bounded as r → 0, and steep descents in $$\log C(r)$$ may result in large estimates of d C, which may exceed E. In this chapter, we will use definition (9.9).

Given the set of N points, for $$r \geq r_{\max } \equiv \max _{i, j} \mathit {dist} \big ( x(i) , x(j) \big )$$ , the distance between each pair of distinct points does not exceed $$r_{\max }$$ , so C(r) = 1. For $$r &lt; r_{\min } \equiv \min _{i \neq j} \mathit {dist} \big ( x(i) , x(j) \big )$$ , the distance between each pair of distinct points is less than $$r_{\min }$$ , so C(r) = 0. Hence the useful range of r is the interval $$[r_{\min }, r_{\max }]$$ . If there is a single pair of points at distance $$r_{\min }$$ , then $$C(r_{\min }) = 2/[N(N-1)]$$ , and $$\log C(r_{\min }) \approx -2 \log N$$ . Since $$\log C(r_{\max }) = 0$$ , the range of $$\log C(r)$$ over the interval $$[r_{\min }, r_{\max }]$$ is approximately $$2 \log N$$ . However, for box counting with N points, the number of non-empty boxes (i.e., B R(r) for radius-based boxes and B D(s) for diameter-based boxes) ranges from 1 to N, so the range of $$\log B_{{R}}(r)$$ or $$\log B_{{D}} (s)$$ is $$\log N$$ , which is only half the range of $$\log C(r)$$ . Similarly, for a single point x, over its useful range the pointwise mass dimension estimate (9.10) ranges from 1∕(N − 1) to 1, so the range of its logarithm is also approximately $$\log N$$ , half the range for $$\log C(r)$$ . The greater range, by a factor of 2, for $$\log C(r)$$ is “the one advantage” the correlation sum has over the average pointwise dimension [Theiler 90].

Consider an alternate definition $$\widetilde {C}(r)$$ of the correlation sum, now using the double summation $$\sum _{i=1}^N \sum _{i=j}^N$$ which does not exclude the case i = j. With this alternative definition, each of the N pairs (x(i), x(i)) contributes 1 to the double summation. Following [Yadav 10],
$$\displaystyle \begin{aligned} \begin{array}{rcl} \widetilde{C}(r) \equiv \frac{1}{N^2} \sum_{i=1}^N \sum_{j=1}^N I_{{0}} \Big( r - \mathit{dist} \big( x(i) , x(j) \big) \Big) = \frac{1}{N^2}\sum_{n \in {\mathbb{N}}} N_n(r) \, , {} \end{array} \end{aligned} $$
(9.13)
where N n(r) is the number of points whose distance from point n does not exceed r. For each n, since N n(r) always counts n itself, then N n(r) ≥ 1. For all sufficiently large r we have N n(r) = N for each n, in which case $$\widetilde {C}(r) = 1$$ . In (9.13), we can interpret N n(r)∕N as the expected fraction of points whose distance from n does not exceed r. Suppose this fraction is independent of n, and suppose we have a probability distribution P(k, r) providing the probability that k of N points are within a distance r from a random point. The expected value (with respect to k) of this probability distribution is the expected fraction of the N points within distance r of a random point, so
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{N_n(r)}{N} = \sum_{k=1}^N k P(k, r) \, , {} \end{array} \end{aligned} $$
(9.14)
which with (9.13) provides yet another way to write $$\widetilde {C}(r)$$ :
$$\displaystyle \begin{aligned} \begin{array}{rcl} \widetilde{C}(r) = \frac{1}{N} \sum_{k=1}^N k P(k, r) \, . {} \end{array} \end{aligned} $$
(9.15)
While (9.14) provides the mean (with respect to k) of the distribution P(k, r), to fully characterize the distribution we need its moments. So for $$q \in {\mathbb {R}}$$ define the generalized correlation sum
$$\displaystyle \begin{aligned} \begin{array}{rcl} {\widetilde{C}}_q(r) \equiv \frac{1}{N} \sum_{k=1}^N k^{q-1} P(k, r) \, , {} \end{array} \end{aligned} $$
(9.16)
which for q = 2 yields (9.15). For q ≫ 1 the terms dominating the sum in (9.16) are terms k q−1P(k, r) for which k is “large” (i.e., many points in the ball of radius r centered at a random point), whereas for q ≪ 0 the terms dominating the sum in (9.16) are terms k q−1P(k, r) for which k is “small” (i.e., few points in the ball of radius r). Thus studying the behavior of $${\widetilde {C}}_q(r)$$ for −∞ < q < ∞ provides information about regions containing many points as well as regions with few points. We will explore this further in Chap. 16 on multifractals.

9.4 The Correlation Dimension

Definition 9.2 [Grassberger 83a, Grassberger 83b, Hentschel 83] If the limit
$$\displaystyle \begin{aligned} \begin{array}{rcl} {d_{{C}}} \equiv \lim_{r \rightarrow 0} \lim_{N \rightarrow \infty} \frac {\log C(r)} {\log r} {} \end{array} \end{aligned} $$
(9.17)
exists, then d C is called the correlation dimension of Ω. □
Assume for the remainder of this section that d C exists. Then d C is independent of the norm used in (9.8) to define the distance between two points. Also, $$C(r) \sim r^{{d_{{C}}}}$$ as r → 0, where “∼” means “tends to be approximately proportional to” (see Sect. 1.​2 for a discussion of this symbol). However, the existence of d C does not imply that $$C(r) \propto r^{{d_{{C}}}}$$ , since this proportionality may fail to hold, even as r → 0. For r > 0, define the function $$\varPhi : {\mathbb {R}} \rightarrow {\mathbb {R}}$$ by
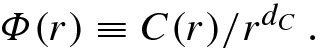
../images/487758_1_En_9_Chapter/487758_1_En_9_Equ20_HTML.png
(9.18)
We cannot conclude that Φ(r) approaches a constant value as r → 0, but the existence of d C does imply $$\lim _{r \rightarrow 0} \log \varPhi (r) / \log r = 0$$ [Theiler 88].

One great advantage of computing d C rather than d B is that memory requirements are greatly reduced, since there is no need to construct boxes covering Ω. With box counting it is also necessary to examine each box to determine if it contains any points; this may be impractical, particularly if r is very small. Another advantage, mentioned in Sect. 9.3 above, is that the range of $$\log C(r)$$ is twice the range of $$\log B_{{D}} (s)$$ or $$\log B_{{R}}(r)$$ . In [Eckmann 85], the correlation dimension was deemed a “quite sound” and “highly successful” means of determining the dimension of a strange attractor, and it was observed that the method “is not entirely justified mathematically, but nevertheless quite sound”.5 In [Ruelle 90] it was noted that “... this algorithm has played a very important role in allowing us to say something about systems that otherwise defied analysis”. The importance of d C was echoed in [Schroeder 91], which noted that the correlation dimension is one of the most widely used fractal dimensions, especially if the fractal comes as “dust”, meaning isolated points, sparsely distributed over some region. Lastly, [Mizrach 92] observed that, in the physical sciences, the correlation dimension has become the preferred dimension to use with experimental data.

There are several possible approaches to computing d C from the N points x(n), n = 1, 2, …, N. First, we could pick the smallest r available, call it r min, and estimate d C by $$\log C({r}_{{min}}) / \log {r}_{{min}}$$ . The problem with this approach is that the convergence of $$\log C(r) / \log r$$ to d C is very slow [Theiler 90]; this is the same problem identified in Sect. 4.​2 in picking the smallest s value available to estimate d B. A second possible approach [Theiler 88] is to take the local slope of the $$\log C(r)$$ versus $$\log r$$ curve, using
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\mathrm{d} \log C(r)}{\mathrm{d} \log r} = \frac{\left(\frac{\mathrm{d} C(r)}{\mathrm{d} r}\right)} {\left( \frac{C(r)}{r} \right)} \, . {} \end{array} \end{aligned} $$
(9.19)
A third possible approach [Theiler 88] is to pick two values r 1 and r 2, where r 1 < r 2, and use the two-point secant estimate
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{C}} \approx \frac{ \log C(r_{{2}}) - \log C(r_{{1}})} {\log r_{{2}} - \log r_{{1}} } \, . {} \end{array} \end{aligned} $$
(9.20)
While the third approach avoids the slow logarithmic convergence, it requires choosing r 1 and r 2, both of which should tend to zero. This approach was analyzed in [Theiler 93] and compared to other methods for estimating d C. (For a network, two-point secant estimates of fractal dimensions were utilized in [Rosenberg 16b, Rosenberg 17c, Wang 11].)

By far, the most popular method for estimating d C is the Grassberger–Procaccia method. The steps are (i) compute C(r) for a set of positive radii r m, m = 1, 2, …, M, (i) determine a subset of these M values of r m over which the $$\log C({r_{{m}}})$$ versus $$\log {r_{{m}}}$$ curve is roughly linear, and (iii) estimate d C as the slope of the best fit line through the points $$\bigl ( \log {r_{{m}}} , \log C({r_{{m}}}) \bigr )$$ over this subset of the M points. As observed in [Theiler 88], there is no clear criterion for how to determine the slope through the chosen subset of the M points. Finding the slope that minimizes the unweighted sum of squares has two drawbacks. First, the least squares model assumes a uniform error in the calculated $$\log C(r)$$ , which is incorrect since the statistics get worse as r decreases. Second, the least squares model assumes that errors in $$\log C(r)$$ are independent of each other, which is incorrect since C(r + 𝜖) is equal to C(r) plus the fraction of distances between r and 𝜖; hence for small 𝜖 the error at $$\log C(r+\epsilon )$$ is strongly correlated with the error at $$\log \, C(r)$$ .

Suppose C(r m) has been computed for m = 1, 2, …, M, where r m < r m+1. In studying the orbits of celestial bodies, [Freistetter 00] used the following iterative procedure to determine the range of r values over which the slope of the $$\log C({r_{{m}}})$$ versus $$\log {r_{{m}}}$$ curve should be computed. Since the $$\log C(r)$$ versus $$\log r$$ curve is not linear in the region of very small and very large r, we trim the ends of the interval as follows. In each iteration we first temporarily remove the leftmost r value (which in the first iteration is r 1) and use linear least squares to obtain d R, the slope corresponding to {r 2, r 3, …, r M}, and the associated correlation coefficient c R. (Here the correlation coefficient, not to be confused with the correlation dimension, is a byproduct of the regression indicating the goodness of fit.) Next we temporarily remove the rightmost r value (which in the first iteration is r M) and use linear least squares to obtain d L, the slope corresponding to {r 1, r 2, …, r M−1}, and the associated correlation coefficient c L. Since a higher correlation coefficient indicates a better fit (where c = 1 is a perfect linear relationship), if c R > c L we delete r L while if c L > c R we delete r M. We begin the next iteration with either {r 2, r 3, …, r M} or {r 1, r 2, …, r M−1}. The iterations stop when we obtain a correlation coefficient higher than a desired value.

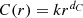An alternative to the Grassberger–Procaccia method is the method of [Takens 85], which is based on maximum likelihood estimation. Suppose we randomly select N points from Ω. Assume that d C exists and that the function Φ defined by (9.18) takes the constant value k, so ../images/487758_1_En_9_Chapter/487758_1_En_9_IEq77_HTML.gif. 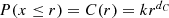Assume also that the distances between pairs of randomly selected points are independent and randomly distributed such that the probability P(x ≤ r) that the distance x between a random pair of points does not exceed r is given by ../images/487758_1_En_9_Chapter/487758_1_En_9_IEq78_HTML.gif. Let X(r) be the number of pairwise distances less than r, and denote these X(r) distance values by r i for 1 ≤ i ≤ X(r). The value of d C that maximizes the probability of finding the X(r) observed distances {r i} is given by the unbiased minimal variance Takens estimator $$\widetilde {T}(r)$$ , defined by Guerrero and Smith [Guerrero 03]
$$\displaystyle \begin{aligned} \begin{array}{rcl} \widetilde{T}(r) \equiv \biggl[ \frac{-1}{X(r)-1} \sum_{i=1}^{X(r)} \log \left( \frac{r_{{i}}}{r} \right) \biggr]^{-1} \, , {} \end{array} \end{aligned} $$
(9.21)
so $$\widetilde {T}(r)$$ uses all distances less than a specified upper bound r, but there is no lower bound on distances. As r → 0 and X(r) →∞ we have $$\widetilde {T}(r) \rightarrow d_{{C}}$$ . If we replace X(r) − 1 by X(r) (which introduces a slight bias [Guerrero 03]), we can write (9.21) more compactly as
$$\displaystyle \begin{aligned} \begin{array}{rcl} T(r) = -1/\langle \log(r_{{i}}/r) \rangle \, , \end{array} \end{aligned} $$
where 〈 〉 denotes the average over all distances (between pairs of points) not exceeding r. It can be shown that [Theiler 90]
$$\displaystyle \begin{aligned} \begin{array}{rcl} T(r) = \frac { C(r)}{ \int_{0}^r \left( \frac{C(x)}{x} \right) \mathrm{d} x} = \frac {\int_{0}^r \left( \frac{\mathrm{d} C(x)}{\mathrm{d} x} \right) \mathrm{d} x} {\int_{0}^r \left( \frac{C(x)}{x} \right) \mathrm{d} x} \; . {} \end{array} \end{aligned} $$
(9.22)
As in [Theiler 88], the slightly more unwieldy form of the right-hand side of (9.22) is shown for comparison with (9.19). The estimate
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac { C(r)}{ \int_{0}^r \left( \frac{C(x)}{x} \right) \mathrm{d} x} {} \end{array} \end{aligned} $$
(9.23)
(the middle term in (9.22) above) has been called the Takens-Theiler estimator [Hegger 99]. The advantage of this estimator is that, as r → 0, the Takens-Theiler estimate T(r) approaches d C much more rapidly than does $$\log C(r)/\log r$$ . However, for some fractal sets T(r) does not converge [Theiler 90]. The non-convergence is explained by considering the function Φ(r) defined by (9.18). A fractal has “periodic lacunarity” if for some positive number L we have Φ(r) = Φ(Lr). For example, the middle-thirds Cantor set exhibits periodic lacunarity with L = 1∕3. The Takens estimate T(r) does not converge for fractals with periodic lacunarity. Theiler also supplied a condition on Φ(r) under which T(r) does converge.

Exercise 9.1 Show that the middle-thirds Cantor set exhibits periodic lacunarity with L = 1∕3. □

To evaluate (9.23), the method of [Hegger 99] can be used. Since C(r) is only evaluated at the discrete points {r 1, r 2, r 3, …, r M}, we approximate $$\log C(r)$$ by the linear function $$a_{{i}} \log r + b_{{i}}$$ for r ∈ [r i−1, r i], which implies C(r) is approximated by the exponential function $$e^{b_{{i}}} r^{a_{{i}}}$$ for r ∈ [r i−1, r i]. The values a i and b i can be computed from the M points $$\bigl ( \log {r_{{i}}} , \log C({r_{{i}}}) \bigr )$$ . Assume r i ≤ r for 1 ≤ i ≤ M. Since the integral of a linear function is trivial,
$$\displaystyle \begin{aligned} \int_{x=0}^{r} \left( \frac {C(x)}{x} \right) \mathrm{d} x &amp; \approx \sum_{i=2}^M e^{ b_i} \int_{r_{{i-1}}}^{{r_{{i}}}} x^{\, (a_{{i}} -1)} \mathrm{d} x \\ &amp;= \sum_{i=2}^M \frac {e^{ b_{{i}}}}{a_{{i}}} ({r^{\, a_{{i}}}_{{i}}} - {r^{\, a_{{i}}}_{{i-1}}}) \, . {} \end{aligned} $$
(9.24)
Considering the M points $$\bigl ( \log {r_{{i}}} , \log C({r_{{i}}}) \bigr )$$ for i = 1, 2, …, M, suppose there are indices L and U, where 1 ≤ L < U ≤ M, such that a straight line is a good fit to the points $$\bigl ( \log {r_{{i}}} , \log C({r_{{i}}}) \bigr )$$ for L ≤ i ≤ U. Then, using (9.23) and (9.24), a reasonable estimate of d C is
$$\displaystyle \begin{aligned} \frac {C(r_{{H}})} {\sum_{i=L+1}^U \frac {e^{ b_{{i}}}}{a_{{i}}} ({r^{\, a_{{i}}}_{{i}}} - {r^{\, a_{{i}}}_{{i-1}}})} \end{aligned}$$
[Hegger 99]. Various other approaches to computing d C have also been proposed, e.g., [Shirer 97].

Exercise 9.2 Use (9.24) to estimate d C for the middle-thirds Cantor set for r ∈ [0.001, 1]. □

Whe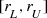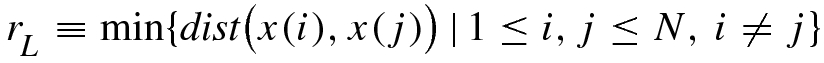n the Grassberger–Procaccia method is applied to a time series (Sect. 10.​2), as in the calculation of d C of a strange attractor of a dynamical system, the upper bound
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{C}} \leq 2 \log_{10} N {} \end{array} \end{aligned} $$
(9.25)
applies [Ruelle 90]. To derive this bound, define
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(r) \equiv \sum_{i=1}^N \sum_{j=i}^{N} I \big( r - \mathit{dist} ( x(i) , x(j) ) \big) \, . {} \end{array} \end{aligned} $$
(9.26)
The range of r over which f(r) can be computed is ../images/487758_1_En_9_Chapter/487758_1_En_9_IEq89_HTML.gif, where
../images/487758_1_En_9_Chapter/487758_1_En_9_Eque_HTML.png
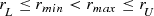and $$r_{\stackrel {}{U}} \equiv {\mathit {diam}}(\varOmega )$$ . For time series applications, only part of this range is usable, since the lower part of the range suffers from statistical fluctuations, and the upper part suffers from nonlinearities. Let r min be the smallest usable r for which we evaluate f(r), and let r max be the largest usable r, where ../images/487758_1_En_9_Chapter/487758_1_En_9_IEq91_HTML.gif. Suppose r max∕r min ≥ 10, so the range is at least one decade. The correlation dimension d C is approximately the slope m, where
$$\displaystyle \begin{aligned} m = \frac{ \log_{10} f({r_{{max}}}) - \log_{10} f({r_{{min}}}) } { \log_{10} {r_{{max}}} - \log_{10} {r_{{min}}} } \, . \end{aligned}$$
Since each point is within distance r of itself, then f(r) ≥ N for r > 0. Hence f(r min) ≥ N, so log10f(r min) ≥ 0. Also, f(r max) ≤ N 2. Since r max∕r min ≥ 10 then log10r max −log10r min ≥ 1. Hence
$$\displaystyle \begin{aligned} m = \frac{ \log_{10} f({r_{{max}}}) - \log_{10} f({r_{{min}}}) } { \log_{10} {r_{{max}}} - \log_{10} {r_{{min}}} } \leq \log_{10} f({r_{{max}}}) \leq \log_{10} N^2 = 2 \log_{10} N \, . \end{aligned}$$
Thus one should not believe a correlation dimension estimate that is not substantially less than 2log10N [Ruelle 90].

This bound was used in [Boon 08] to study the visual evoked potential. Unfortunately, numerous studies do violate this bound [Ruelle 90]. If the inequality r max∕r min ≥ 10 is replaced by the more general bound r max∕r min ≥ k, then we obtain d C ≤ 2logkN. Ruelle observed that it seems unreasonable to have the ratio r max∕r min be much less than 10.

To conclude this section, we quote these words of caution in [Hegger 99]:

… dimensions characterize a set or an invariant measure whose support is the set, whereas any data set contains only a finite number of points representing the set or the measure. By definition, the dimension of a finite set of points is zero. When we determine the dimension of an attractor numerically, we extrapolate from finite length scales … to the infinitesimal scales, where the concept of dimensions is defined. This extrapolation can fail for many reasons …

9.5 Comparison with the Box Counting Dimension

In this section we present the proof of [Grassberger 83a, Grassberger 83b] that d C ≤ d B for a geometric object Ω.6 We first discuss notation. The pointwise mass measure μ(Ω(r)) was defined in Sect. 9.2 in terms of the box radius r. The correlation sum C(r) given by (9.11), and the correlation dimension d C given by (9.17), were similarly defined using r. Since C(r) counts pairs of points whose distance is less than r, we could equally well have defined the correlation sum and d C using using the variable s, rather than r, to represent distance. The motivation for using s rather than r in this section is that we will compute d C by first covering Ω with diameter-based boxes, and we always denote the linear size of a diameter-based box by s. Therefore, in this section we will denote the correlation sum by C(s); its definition is unchanged.

For a given positive s ≪ 1, let $${\mathcal {B}}(s)$$ be a minimal covering of Ω by diameter-based boxes of size s, so the distance between any two points in a given box does not exceed s. Let N points be drawn randomly from Ω according to its natural measure and let N j be the number of points in box $$B_{{j}} \subset {\mathcal {B}}(s)$$ . Discard from $${\mathcal {B}}(s)$$ each box for which N j = 0, and, as usual, let B D(s) be the number of non-empty boxes in $${\mathcal {B}}(s)$$ .

Since diam(B j) ≤ s, then the N j points in B j yield N j(N j − 1) ordered pairs of points such that the distance between the two points does not exceed s. The sum $$\sum _{j = 1}^{{B_{{D}} (s)}} N_j (N_j -1)$$ counts all ordered pairs (x(i), x(j)) of points, separated by a distance not exceeding s, such that x(i) and x(j) lie in the same box. Since a given pair (x(i), x(j)) of points satisfying dist(x(i), x(j)) ≤ s may lie within some box B j, or x(i) and x(j) may lie in different boxes, from (9.9) and (9.11),
$$\displaystyle \begin{aligned} C(s) \geq \frac{1}{N(N-1)} \sum_{j = 1}^{{B_{{D}} (s)}} N_j (N_j -1) {} \end{aligned} $$
(9.27)
(recall that although C(s) depends on N, for notational simplicity we simply write C(s).) Let p j ≡ N j∕N be the probability of box B j, and define
$$\displaystyle \begin{aligned} \mu_{{\, j}} \equiv \lim_{N \rightarrow \infty} p_{{j}} \, . {} \end{aligned} $$
(9.28)
Although p j depends on both N and s, for notational simplicity we write p j; similarly, although μ j depends on s, for notational simplicity we write μ j. Following [Chatterjee 92, Grassberger 83a] and using (9.11) and (9.27),
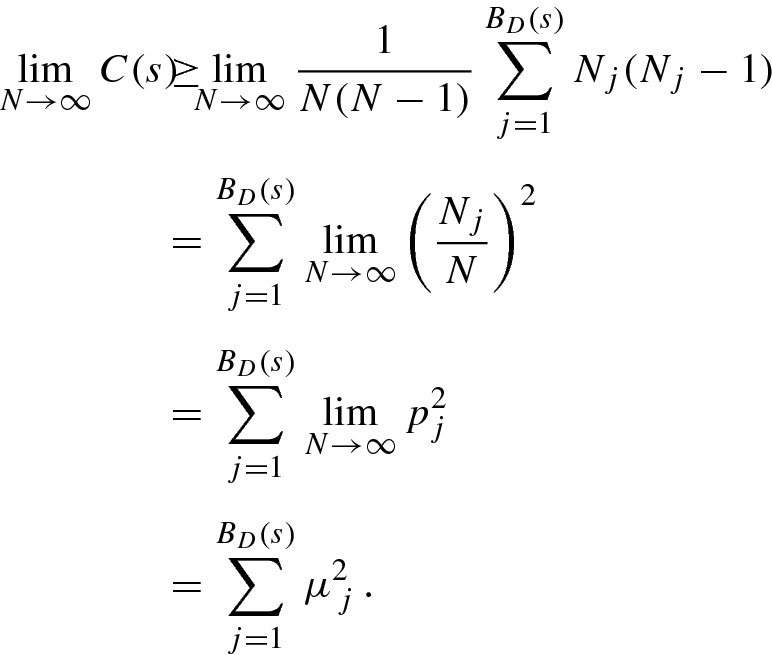
../images/487758_1_En_9_Chapter/487758_1_En_9_Equ32_HTML.png
(9.29)
Relation (9.29) says that for large N and small s, the correlation sum C(s) is no less than the probability that two points of Ω are contained in some box of size s [Krakovska 95].
A generalization [Peitgen 92] of the correlation sum considers q-tuples (x(1), x(2), …, x(q)) of distinct points, where q ≥ 2, such that the pairwise distance condition holds: for each pair of points x(i) and x(j) in the q-tuple we have dist(x(i), x(j)) ≤ s. With N, $${\mathcal {B}}(s)$$ , and B D(s) as defined as in the previous paragraph, let Q(N, s, q) be the number of q-tuples of the N points such that the pairwise distance condition holds. Then
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{N \rightarrow \infty} \frac{Q(N,s,q)}{N^q} \propto \sum_{j=1}^{{B_{{D}} (s)}} \mu_{{\, j}}^q \, . {} \end{array} \end{aligned} $$
(9.30)
The sum on the right-hand side of (9.30) is the probability that q points, randomly drawn from Ω according to its natural measure, fall into any box. From this generalized correlation sum we can define generalized dimensions, to be studied in Chap. 16.

Having shown that we can lower bound the correlation sum by covering Ω with boxes, we now present the proof [Grassberger 83a, Grassberger 83b] that d C ≤ d B. The proof in [Grassberger 83b] assumes $$B_{{D}} (s) \sim s^{-d_{{B}}}$$ and $$C(s) \sim s^{d_{{C}}}$$ . Since the symbol ∼ is ambiguous, we recast these assumptions as Assumptions 9.1 and 9.2 below.

Assumption 9.1 For some positive number d C and for some function $$\varPhi _{C}: {\mathbb {R}} \rightarrow {\mathbb {R}}$$ satisfying
$$\displaystyle \begin{aligned} \lim_{s \rightarrow 0} \log \varPhi_{C}(s)/ \log s = 0 \, , \end{aligned}$$
for all sufficiently small positive s we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{N \rightarrow \infty} C(s) = \varPhi_{C}(s) s^{{d_{{C}}}} \, , {} \end{array} \end{aligned} $$
(9.31)
where C(s) is defined by (9.11). □
Assumption 9.2. For some positive number d B and for some function $$\varPhi _B: {\mathbb {R}} \rightarrow {\mathbb {R}}$$ satisfying
$$\displaystyle \begin{aligned} \lim_{s \rightarrow 0} \log \varPhi_B(s)/ \log s = 0 \, , \end{aligned}$$
for all sufficiently small positive s we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} B_{{D}} (s) = \varPhi_B(s) s^{-{d_{{B}}}} \, , {} \end{array} \end{aligned} $$
(9.32)
where B D(s) is the minimal number of diameter-based boxes of size s needed to cover Ω. □
Jensen’s inequality says that if f is a convex function, $$\mathcal {X}$$ is a random variable, and $$\mathcal {E}$$ denotes expectation, then $${\mathcal {E}} \big (f({\mathcal {X}}) \big ) \geq f \big ( {\mathcal {E}}({\mathcal {X}}) \big )$$ . In particular, for a random variable taking a finite set of values, if $$\{ {\alpha }_{{j}} \}_{j=1}^J$$ are nonnegative weights summing to 1, if $$\{ x_{{j}} \}_{j=1}^J$$ are positive numbers, and if f(z) = z 2 then
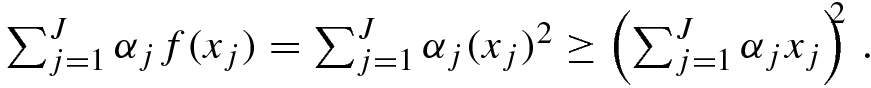
../images/487758_1_En_9_Chapter/487758_1_En_9_Equ36_HTML.png
(9.33)
Applying this to the covering of Ω, set J = B D(s) and x j = μ j and α j = 1∕J for 1 ≤ j ≤ J. From (9.33),
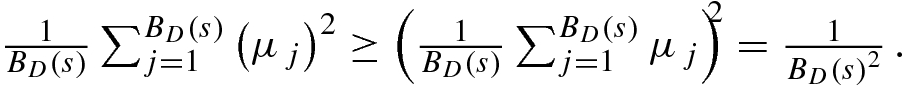
../images/487758_1_En_9_Chapter/487758_1_En_9_Equ37_HTML.png
(9.34)

Theorem 9.1 If Assumptions 9.1 and 9.2 hold then d C ≤ d B.

Proof For each s, let $${\mathcal {B}}(s)$$ be a minimal s-covering of Ω and let B D(s) be the number of boxes in $${\mathcal {B}}(s)$$ . Randomly select from Ω, according to its natural measure, the N points x(1), x(2), …, x(N). Let $$\mathbb {N}$$ be the set of these N points. For box $$B_{{j}} \in {\mathcal {B}}(s)$$ , let N j(s) be the number of points of $$\mathbb {N}$$ that are contained in B j, so $$\sum _{j=1}^{B_{{D}} (s)} N_j(s) = N$$ . From (9.29),
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{N \rightarrow \infty} {C}(s) {\kern-1pt}\geq{\kern-1pt} \sum_{j=1}^{B_{{D}} (s)} {\mu_{{\, j}}^2} {\kern-1pt}= {\kern-1pt}B_{{D}} (s) \left( \frac{1}{B_{{D}} (s)} \sum_{j=1}^{ B_{{D}} (s)} {\mu_{{\, j}}^2} \right) {\kern-1pt}\geq{\kern-1pt} B_{{D}} (s) \left( \frac{1}{[ B_{{D}} (s) ]^2} \right) {\kern-1pt}={\kern-1pt} \frac{1}{B_{{D}} (s)} \, , \quad {} \end{array} \end{aligned} $$
(9.35)
where the second inequality follows from (9.34).
By Assumption 9.1, for s ≪ 1 we have $$\lim _{N \rightarrow \infty } C(s) = \varPhi _C(s) s^{{d_{{C}}}}$$ . By Assumption 9.2, for s ≪ 1 we have $$B_{{D}} (s) = \varPhi _B(s) s^{-{d_{{B}}}}$$ , so $$1/B_{{D}} (s) = [\varPhi _B(s)]^{-1} s^{{d_{{B}}}}$$ . Hence, from (9.35) for s ≪ 1 we have
$$\displaystyle \begin{aligned} \lim_{N \rightarrow \infty} C(s) = \varPhi_C(s) s^{{d_{{C}}}} \geq 1/B_{{D}} (s) = [ \varPhi_B(s) ]^{-1} s^{{d_{{B}}}} \, . \end{aligned}$$
Taking logarithms yields
$$\displaystyle \begin{aligned} \log \varPhi_C(s) + {d_{{C}}} \log s \geq -\log \varPhi_B(s) + d_{{B}} \log s \, . \end{aligned}$$
Dividing both sides of the inequality by $$\log s$$ , which is negative, and letting s → 0 yields d C ≤ d B. □

For strictly self-similar fractals such as the Sierpiński gasket, the correlation dimension d C, the Hausdorff dimension d H, and the similarity dimension d S are all equal ( [Schroeder 91], p. 216).7