© Springer Nature Switzerland AG 2020
E. RosenbergFractal Dimensions of Networkshttps://doi.org/10.1007/978-3-030-43169-3_4

4. Topological and Box Counting Dimensions

Eric Rosenberg1 
(1)
AT&T Labs, Middletown, NJ, USA
 

A mind once stretched by a new idea never regains its original dimension.

Oliver Wendell Holmes, Jr. (1841–1935), American, U.S. Supreme Court justice from 1902 to 1932.

A fractal is often defined as a set whose fractal dimension differs from its topological dimension. To make sense of this definition, we start by defining the topological dimension of a set. After that, the remainder of this chapter is devoted to the box counting dimension, which is the first fractal dimension we will study.

4.1 Topological Dimension

The first dimension we will consider is the topological dimension of a set. This subject has a long history, with contributions as early as 1913 by the Dutch mathematician L. Brouwer (1881–1966). (The extensive historical notes in [Engelking 78] trace the history back to 1878 work of Georg Cantor.) Roughly speaking, the topological dimension is a nonnegative integer that defines the number of “distinct directions” within a set [Farmer 82]. There are actually several definitions of topological dimension. The usual definition encountered in the fractal literature is the small inductive dimension (also called the Urysohn–Menger dimension or the weak inductive dimension). Other topological dimensions [Edgar 08] are the large inductive dimension (also known as the C̆ech dimension or the strong inductive dimension), which is closely related to the small inductive dimension, and the covering dimension (also known as the Lebesgue dimension). 1

The notion of a topological dimension of a set Ω requires that $$\varOmega \subset {\mathcal {X}}$$ , where $$\big ({\mathcal {X}}, {\mathit {dist}}( \cdot , \cdot ) \big )$$ is a metric space. For example, if $$\mathcal {X}$$ is $${\mathbb {R}}^E$$ and $$x, y \in {\mathbb {R}}^E$$ , then dist(x, y) might be the L 1 distance $$\sum _{i=1}^E \vert {x_{{i}}} - {y_{{i}}} \vert $$ , the Euclidean distance $$\sqrt { \sum _{i=1}^E ({x_{{i}}} - {y_{{i}}})^2}$$ , the L ∞ distance $$\max _{i=1}^E \vert {x_{{i}}} - {y_{{i}}} \vert $$ , or the L p distance (3.​7). Our first definition of topological dimension is actually a definition of the small inductive dimension.

Definition 4.1 A set Ω has topological dimension d T if for each x ∈ Ω and for each sufficiently small positive number 𝜖, the set
$$\displaystyle \begin{aligned} \{ y \in \varOmega \; \vert \; dist(x,y) = \epsilon \} \end{aligned}$$
has topological dimension d T − 1, and d T is the smallest nonnegative integer for which this holds. The set Ω has topological dimension 0 if for each x ∈ Ω and each sufficiently small positive number 𝜖 we have
$$\displaystyle \begin{aligned} \{ y \in \varOmega \; \vert \; dist(x,y) = \epsilon \} = \emptyset \, . \; \; \end{aligned}$$
□

In words, this recursive definition says that Ω has topological dimension d T if the boundary of each sufficiently small neighborhood of a point in Ω intersects Ω in a set of dimension d T − 1, and d T is the smallest integer for which this holds; Ω has topological dimension 0 if the boundary of each sufficiently small neighborhood of a point in Ω is disjoint from Ω.

Example 4.1 Let Ω be the unit ball in $${\mathbb {R}}^3$$ defined by Ω = {x : ||x||≤ 1}. Choose $$\widetilde {x} \in \varOmega $$ such that $$\vert \vert \widetilde {x} \vert \vert < 1$$ . Then for all sufficiently small 𝜖 the set
$$\displaystyle \begin{aligned} \varOmega_1 \equiv \{ y \in \varOmega \; \vert \; dist(\widetilde{x}, y) = \epsilon \} \cap \varOmega \end{aligned}$$
is the surface of a ball centered at $$\widetilde {x}$$ with radius 𝜖. Now choose $$\widetilde {y} \in \varOmega _1$$ . The set
$$\displaystyle \begin{aligned} \varOmega_2 \equiv \{ y \in \varOmega_1 \; \vert \; \mathit{dist} (y, \widetilde{y}) = \epsilon \} \end{aligned}$$
is the set of points on this surface at a distance 𝜖 from $$\widetilde {y}$$ , so Ω 2 is a circle. Finally, choose $$\bar {z} \in \varOmega _2$$ . The set
$$\displaystyle \begin{aligned} \varOmega_3 \equiv \{ z \in \varOmega_2 \; \vert \; \mathit{dist} (z, \bar{z}) = \epsilon \} \end{aligned}$$
is the set of the two points {z 1, z 2} on the circle at a distance 𝜖 from $$\bar {z}$$ . The set Ω 3 has topological dimension 0 since for all sufficiently small positive 𝜖 we have
$$\displaystyle \begin{aligned} \{ z \in \varOmega_3 \; \vert \; \mathit{dist} (z, z_{{1}}) = \epsilon \} = \emptyset \;\; \mbox{ and } \{ z \in \varOmega_3 \; \vert \; \mathit{dist} (z, z_{{2}}) = \epsilon \} = \emptyset \, . \end{aligned}$$
Thus for Ω we have d T = 3, for Ω 1 we have d T = 2, for Ω 2 we have d T = 1, and for Ω 3 we have d T = 0. □ Exercise 4.1 What is the topological dimension of the set of rational numbers? □
Definition 4.2 Let $$\varOmega \subset {\mathcal {X}}$$ , where $$\big ({\mathcal {X}}, {\mathit {dist}}( \cdot , \cdot ) \big )$$ is a metric space, let x ∈ Ω, and let 𝜖 be a positive number. The 𝜖-neighborhood of x is the set
$$\displaystyle \begin{aligned} \{ y \; \vert \; y \in {\mathcal{X}} \mbox{ and } dist(x,y) < \epsilon \} \, . \end{aligned}$$
□

Definition 4.3 Let $$\big ({\mathcal {X}}, {\mathit {dist}}( \cdot , \cdot ) \big )$$ be a metric space, and let $$\varOmega \subset {\mathcal {X}}$$ . Then Ω is open if for each x ∈ Ω there is an 𝜖 > 0 such that the 𝜖-neighborhood of x is contained in Ω. □

For example, (0, 1) is open but [0, 1] is not open. The set $${\mathbb {R}}^E$$ is open. The set $$\{x \; \vert \; x \in {\mathbb {R}}^E \mbox{ and } \vert \vert x \vert \vert < \epsilon \}$$ is open but $$\{x \; \vert \; x \in {\mathbb {R}}^E \mbox{ and } \vert \vert x \vert \vert \leq \epsilon \}$$ is not open. Figure 4.1 illustrates the cases where Ω is open and where Ω is not open. In (ii), if x is on the boundary of Ω, then for each positive 𝜖 the 𝜖-neighborhood of x is not a subset of Ω. The notion of a covering of a set is a central concept in the study of fractal dimensions. A set is countably infinite if its members can be put in a 1:1 correspondence with the natural numbers 1, 2, 3, ⋯ .
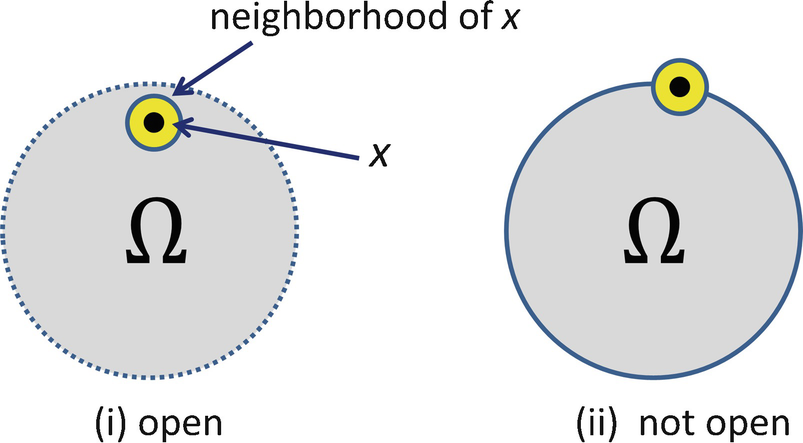
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig1_HTML.png
Figure 4.1

A set that is open, and a set that is not open

Definition 4.4 Let Ω be a subset of a metric space. A covering of Ω is a finite or countably infinite collection {S i} of open sets such that Ω ⊂⋃iS i. A finite covering is a cover containing a finite number of sets. □

For example, the interval [a, b] is covered by the single open set (a − 𝜖, b + 𝜖) for any 𝜖 > 0. Let $$\mathbb {Q}$$ be the set of rational numbers, and for 𝜖 > 0 and $$x \in {\mathbb {Q}}$$ let B(x, 𝜖) be the open ball with center x and radius 𝜖.

Then [a, b] is also covered by the countably infinite collection $$\bigcup _{x \in {\mathbb {Q}}} B(x,\epsilon )$$ .2 There is no requirement that the sets in the cover of Ω have identical shape or orientation, as illustrated in Fig. 4.2, which illustrates the covering of a square by six ovals, each of which is an open set.
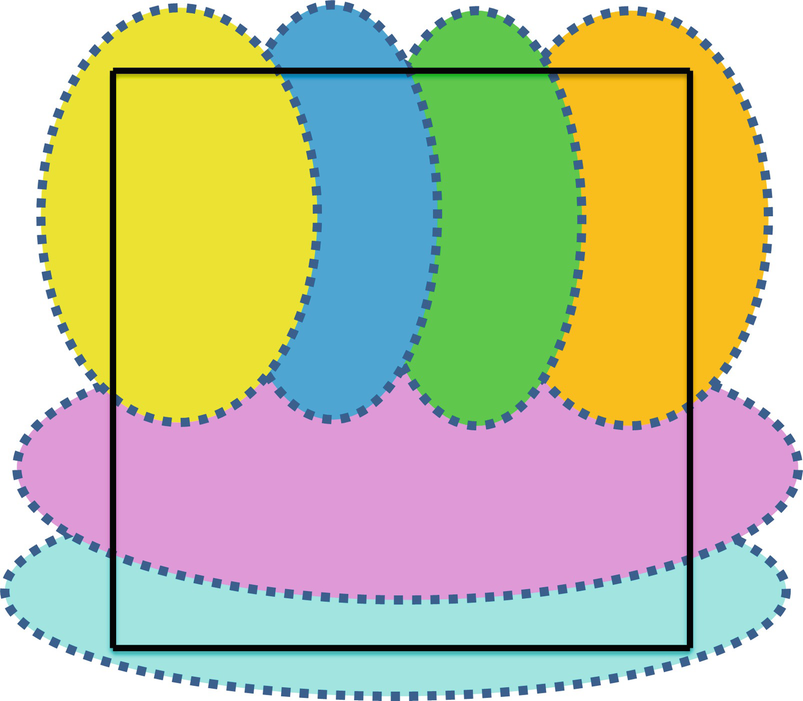
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig2_HTML.png
Figure 4.2

Covering of a square by six open sets

Our second definition of topological dimension, taken from [Eckmann 85], is actually a definition of the covering dimension.

Definition 4.5 The topological dimension d T of a subset Ω of a metric space is the smallest integer K (or ∞) for which the following is true: For every finite covering of Ω by open sets S 1, S 2, …, S J, one can find another covering $$S^{\prime }_1, S^{\prime }_2, \ldots , S^{\prime }_J$$ such that $$S^{\prime }_j \subset S_j$$ for j = 1, 2, …, J and any K + 2 of the $$S^{\prime }_j$$ will have an empty intersection:
$$\displaystyle \begin{aligned} S^{\prime}_{j_{{\, 1}}} \cap S^{\prime}_{j_{{\, 2}}} \cap \cdots \cap S^{\prime}_{j_{{\, K+2}}} = \emptyset \, . \; \; \end{aligned}$$
□

Another way of stating this definition, which perhaps is more intuitive, is the following. The topological dimension d T of a subset Ω of a metric space is the smallest integer K (or ∞) for which the following is true: For every finite covering of Ω by open sets S 1, S 2, …, S J, one can find another covering $$S^{\prime }_1, S^{\prime }_2, \ldots , S^{\prime }_J$$ such that $$S^{\prime }_j \subset S_j$$ for j = 1, 2, …, J and each point of Ω is contained in at most K + 1 of the sets $$S^{\prime }_j$$ .

Example 4.2 Figure 4.3 illustrates Definition 4.5 when Ω is a line segment (the bold black line in the figure). In (i), Ω is covered by five open sets: three ovals and two squares. These five sets are the S j, so J = 5. In (ii), we show the five sets $$S^{\prime }_j$$ , which have been chosen so that $$S^{\prime }_j \subset S_j$$ and each point of Ω lies in at most 2 of the sets $$S^{\prime }_j$$ . Since this can be done for each finite open cover S 1, S 2, …, S J, then d T = 1 for the line segment. □
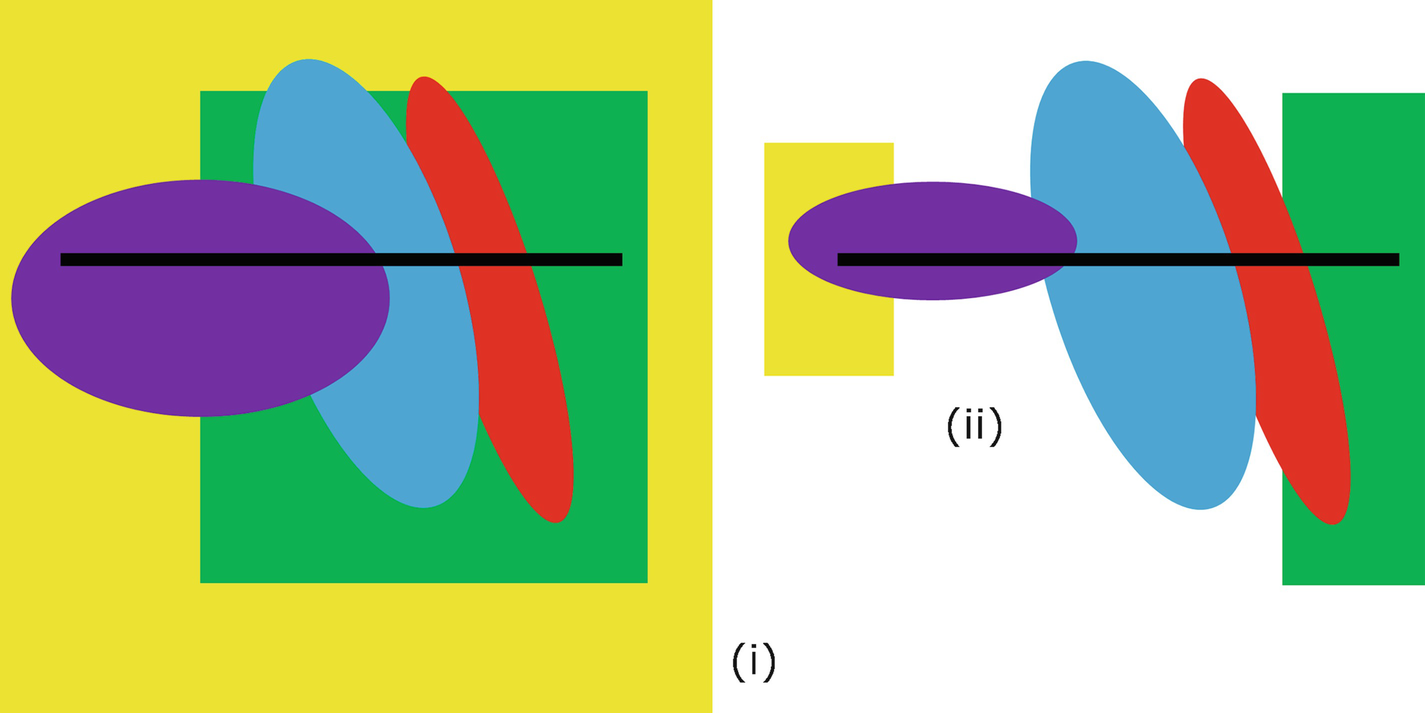
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig3_HTML.png
Figure 4.3

Line segment has d T = 1

Example 4.3 Let Ω be the square with a black border in Fig. 4.4.
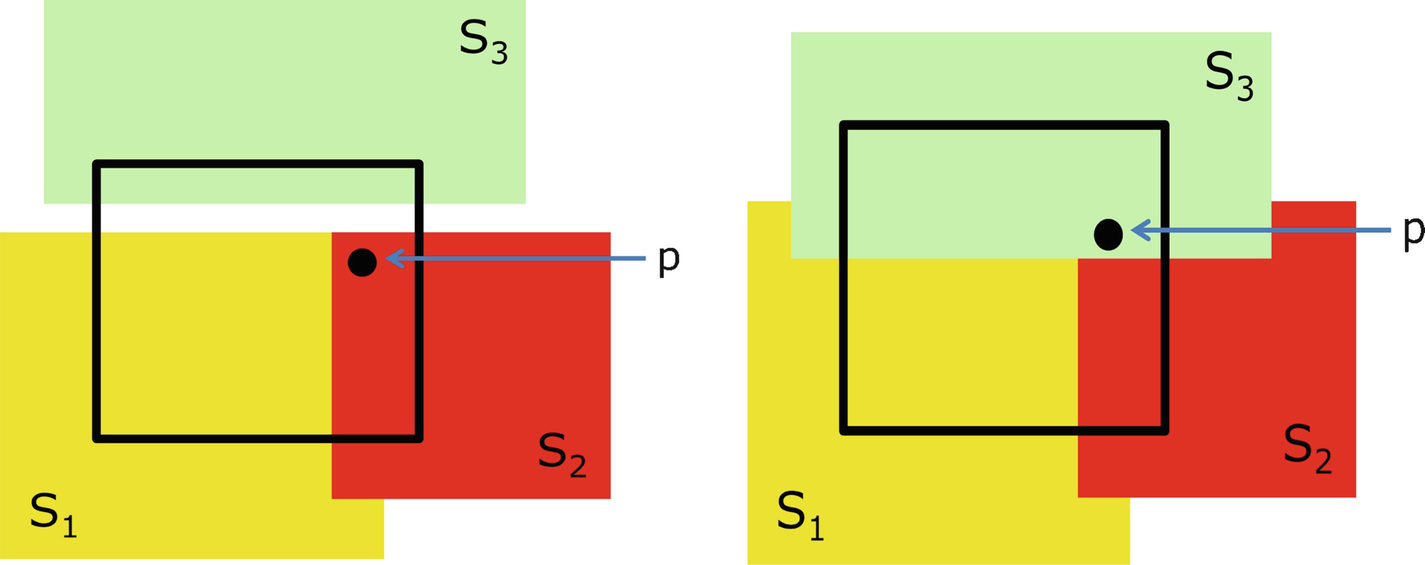
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig4_HTML.png
Figure 4.4

Topological dimension of a square

(for clarity, we have only shown the black border of Ω, but consider Ω to be the entire square, not just the displayed perimeter). Suppose we cover the lower part of Ω using S 1 and S 2, as illustrated in Fig. 4.4 (left). Since these are open sets, if they are to cover the bottom part of Ω, then they must overlap slightly, and hence we can always find a point p, indicated in the figure, such that p ∈ S 1 ∩ S 2. We intentionally choose p to be near the top of the intersection S 1 ∩ S 2, since we will now consider S 3, which currently does not cover that part of Ω not covered by S 1 ∪ S 2. Suppose we slide S 3 downwards so that it now covers Ω − (S 1 ∪ S 2), as illustrated in Fig. 4.4 (right). Then S 3 must overlap S 1 ∪ S 2, and hence if p is sufficiently close to the top of S 1 ∪ S 2, then p ∈ S 1 ∩ S 2 ∩ S 3. Moreover, for each covering $$S^{\prime }_1, S^{\prime }_2, S^{\prime }_3$$ satisfying $$S^{\prime }_j \subset S_j$$ we can always find a point p such that $$p \in S^{\prime }_1 \cap S^{\prime }_2 \cap S^{\prime }_3$$ . If we cover the square with the 4 sets shown in Fig. 4.5, then each point in the square is contained in at most 3 of the S j, and S 1 ∩ S 2 ∩ S 3 ∩ S 4 = ∅. □
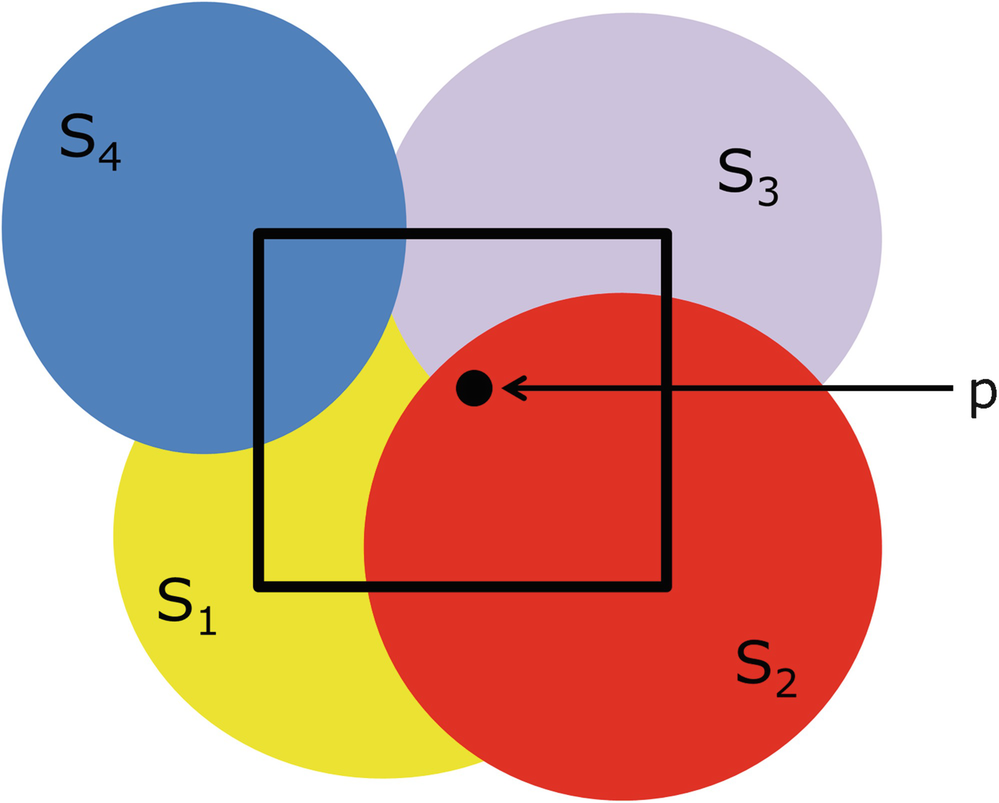
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig5_HTML.png
Figure 4.5

Covering a square by 4 sets

As a final example of Definition 4.5, a solid cube in $${\mathbb {R}}^3$$ has d T = 3 because in any covering of the cube by smaller cubes there always exists a point belonging to at most four of the smaller cubes. Clearly, Definition 4.5 of d T does not lend itself to numerical computation. Indeed, [Farmer 82] gave short shrift to topological dimension, noting that he knows of no general analytic or numerical methods to compute d T, which makes it difficult to apply d T to studies of dynamical systems.

Having presented the definitions of the small inductive dimension, and of the covering dimension, to place these definitions in a historical context we quote from [Engelking 78], who wrote

Dimension theory is a branch of topology devoted to the definition and study of of dimension in certain classes of topological spaces. It originated in the early [1920s] and rapidly developed during the next fifteen years. The investigations of that period were concentrated almost exclusively on separable metric spaces ⋯ .3 After the initial impetus, dimension theory was at a standstill for ten years or more. A fresh start was made at the beginning of the fifties, when it was discovered that many results obtained for separable metric spaces can be extended to larger classes of spaces, provided that the dimension is properly defined. ⋯ It is possible to define the dimension of a topological space $$\mathcal {X}$$ in three different ways, the small inductive dimension ind $$\mathcal {X}$$ , the large inductive dimension Ind $$\mathcal {X}$$ , and the covering dimension dim $$\mathcal {X}$$ . ⋯ The covering dimension dim was formally introduced in [a 1933 paper by Čech] and is related to a property of covers of the n-cube I n discovered by Lebesgue in 1911. The three-dimension functions coincide in the class of separable metric spaces, i.e., ind $$\mathcal {X}$$ = Ind $$\mathcal {X}$$ = dim $$\mathcal {X}$$ for every separable metric space $$\mathcal {X}$$ . In larger classes of spaces, the dimensions ind, Ind, and dim diverge. At first, the small inductive dimension ind was chiefly used; this notion has a great intuitive appeal and leads quickly and economically to an elegant theory. [It was later realized that] the dimension ind is practically of no importance outside of the class of separable metric spaces and that the dimension dim prevails over the dimension Ind. ⋯ The greatest achievement in dimension theory during the fifties was the discovery that Ind $$\mathcal {X}$$ = dim $$\mathcal {X}$$ for every metric space $$\mathcal {X}$$ .

To conclude this section, we note that some authors have used a very different definition of “topological dimension”. For example, [Mizrach 92] wrote that Ω has topological dimension d T if subsets of Ω of size s have a “mass” that is proportional to $$s^{{d_{{T}}}}$$ . Thus a square of side length s has a “mass” (i.e., area) of s 2 and a cube of side s has a “mass” (i.e., volume) of d 3, so the square has d T = 2 and the cube has d T = 3. We will use a definition of this form when we consider the correlation dimension d C (Chap. 9) and the network mass dimension d M (Chap. 12). It is not unusual to see different authors use different names to refer to the same definition of dimension; this is particularly true in the fractal dimension literature.

4.2 Box Counting Dimension

The simplest fractal dimension is the box counting dimension, which we introduced in the beginning of Chap. 3. This dimension is based on covering Ω by equal-sized “boxes”. Consider a line segment of length L. If we measure the line segment using a ruler of length s, where s ≪ L, as illustrated in Fig. 4.6(i), the number of rule lengths B(s) needed is given by B(s) = ⌈L∕s⌉≈ Ls −1 for s ≪ L. We call B(s) the “number of boxes” of size s needed to cover the segment. In this example, a “box” is a one-dimensional ruler of length s. Since the exponent of s in B(s) ≈ Ls −1 is − 1, we say that a line segment has a box counting dimension of 1.
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig6_HTML.png
Figure 4.6

Box counting for a line and for a square

Now consider a two-dimensional square with side length L. We cover the large square by squares of side length s, where s ≪ L, as illustrated in Fig. 4.6(ii). The number B(s) of small squares needed is given by B(s) = ⌈L 2∕s 2⌉≈ L 2s −2. Since the exponent of s in B(s) = Ls −2 is − 2, we say that the square has box counting dimension 2. Now consider an E-dimensional hypercube with side length L, where E is a positive integer. For s ≪ L, the number B(s) of hypercubes of side length s needed to cover the large hypercube is B(s) = ⌈L E∕s E⌉≈ L Es −E, so the E-dimensional hypercube has box counting dimension E.

We now provide a general definition of the box counting dimension of a geometric object $$\varOmega \subset {\mathbb {R}}^E$$ . By the term “box” we mean an E-dimensional hypercube. By the “linear size” of a box B we mean the diameter of B (i.e., the maximal distance between any two points of B), or the maximal variation in any coordinate of B, i.e., maxx,y ∈ Bmax1≤i≤E|x i − y i|. By a box of size s we mean a box of linear size s. A set of boxes is a covering of Ω (i.e., the set of boxes covers Ω) if each point in Ω belongs to at least one box.

Definition 4.6 [Falconer 03] Let B(s) be either (i) the minimal number of sets of diameter at most s needed to cover Ω, or (ii) the smallest number of closed balls of radius s needed to cover Ω. If
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{s \rightarrow 0} \frac{\log B(s)}{ \log (1/s)} {} \end{array} \end{aligned} $$
(4.1)
exists, then the limit is called the box counting dimension of Ω and is denoted by d B. □
The subscript B in d B denotes “box counting”. Although the limit (4.1) may not exist, the lower box counting dimension $$ \underline {{d_{{B}}}}$$ defined by
$$\displaystyle \begin{aligned} \begin{array}{rcl} \underline{{d_{{B}}}} \equiv \lim_{s \rightarrow 0} \inf \frac{\log \, B(s)}{ \log \, (1/s)} \; , {} \end{array} \end{aligned} $$
(4.2)
and the upper box counting dimension $$\overline {{d_{{B}}}}$$ defined by
$$\displaystyle \begin{aligned} \begin{array}{rcl} \overline{{d_{{B}}}} \equiv \lim_{s \rightarrow 0} \sup \frac{\log \, B(s)}{ \log \, (1/s)} \; {} \end{array} \end{aligned} $$
(4.3)
always exist. When $$ \underline {{d_{{B}}}} = \overline {{d_{{B}}}}$$ then d B exists, and $${d_{{B}}} = \underline {{d_{{B}}}} = \overline {{d_{{B}}}}$$ . In practice, e.g., when computing the box counting dimension of a digitized image, we need not concern ourselves with the possibility that $$ \underline {{d_{{B}}}} \neq \overline {{d_{{B}}}}$$ .

The fact that conditions (i) and (ii) of Definition 4.6 can both be used in (4.1) to define d B is established in [Falconer 03]. In practice, it is often impossible to verify that B(s) satisfies either condition (i) or (ii). The following result provides a computationally extremely useful alternative way to compute d B.

Theorem 4.1 If d B exists, then d B can also be computed using (4.1) where B(s) is the number of boxes that intersect Ω when Ω is covered by a grid of boxes of size s.

Proof [Falconer 03, Pearse] For $$\varOmega \subset {\mathbb {R}}^E$$ , let $$\widetilde {B}(s)$$ be the number of boxes of size s in some (not necessarily optimal) covering of Ω, and let B(s) be (as usual) the minimal number of boxes of size s required to cover Ω. For s > 0, a box of size s in the E-dimensional grid has the form
$$\displaystyle \begin{aligned}{}[ {x_{{1}}} s, ({x_{{1}}} + 1) s ] \times [ {x_{{2}}} s, ({x_{{2}}} + 1) s ] \times \cdots \times [ {x_{{E}}} s, ({x_{{E}}} + 1) s ] \; , \end{aligned}$$
where (x 1, x 2, …, x E) are integers. For example, if E = 2 and (x 1, x 2) = (2, −5), then one such box (a square, since E = 2) is [2s, 3s] × [−5s, −4s], which is the set {(x 1, x 2) | 2s ≤ x 1 ≤ 3s and − 5s ≤ x 2 ≤−4s}. Since the length of each of the E sides is s, the diameter of each box is $$( \sum _{i=1}^E s^2)^{1/2}= s \sqrt {E}$$ .
Since $$s \sqrt {E} \geq s$$ and the minimal number B(s) of boxes of size s needed to cover Ω is a non-increasing function of s, then
$$\displaystyle \begin{aligned} B(s \sqrt{E}) \leq B(s) \leq \widetilde{B}(s) \; , \end{aligned}$$
so $$B(s \sqrt {E}) \leq \widetilde {B}(s)$$ . For all sufficiently small positive s we have $$s \sqrt {E} < 1$$ and hence
$$\displaystyle \begin{aligned} \frac{ \log B(s \sqrt{E})}{- \log (s \sqrt{E})} = \frac{ \log B(s \sqrt{E})}{- \log s -\log \sqrt{E}} \leq \frac{\log \widetilde{B}(s)}{- \log s -\log \sqrt{E}} \; . \end{aligned}$$
Letting s → 0 yields
$$\displaystyle \begin{aligned} \begin{array}{rcl} {{d_{{B}}}} \leq {\lim\inf}_{s \rightarrow 0} \frac{ \log \widetilde{B}(s)}{- \log s} \; . {} \end{array} \end{aligned} $$
(4.4)
To prove the reverse inequality, the key observation is that any set of size s in $${\mathbb {R}}^E$$ is contained in at most 3E boxes of size s. To see this, choose an arbitrary point in the set, let B be the box containing that point, and then select the 3E − 1 boxes that are neighbors of B. This is illustrated for E = 2 in Fig. 4.7, which shows a set of size s contained in 32 = 9 boxes of size s; the arbitrarily chosen point is indicated by the small black circle. This yields the inequality $$\widetilde {B}(s) \leq 3^E B(s)$$ , from which we obtain
$$\displaystyle \begin{aligned} \frac{ \log \widetilde{B}(s)}{- \log s} \leq \frac{\log B(s)}{- \log s} + \frac{\log 3^E}{- \log s }\; . \end{aligned}$$
Letting s → 0, we obtain
$$\displaystyle \begin{aligned} \begin{array}{rcl} {\lim \sup}_{s \rightarrow 0} \frac{ \log \widetilde{B}(s)}{- \log s} \leq {{d_{{B}}}} \; . {} \end{array} \end{aligned} $$
(4.5)
From (4.4) and (4.5) we have
$$\displaystyle \begin{aligned} {{d_{{B}}}} \leq {\lim \inf}_{s \rightarrow 0} \frac{ \log \widetilde{B}(s)}{- \log s} \leq {\lim \sup}_{s \rightarrow 0} \frac{ \log \widetilde{B}(s)}{- \log s} \leq {{d_{{B}}}} \; , \end{aligned}$$
so $$\lim _{s \rightarrow 0} \log \widetilde {B}(s)/(-\log s)$$ exists and is equal to d B. □
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig7_HTML.png
Figure 4.7

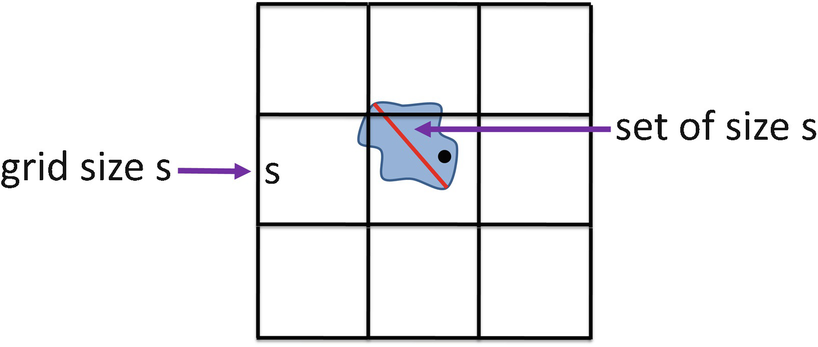
3E boxes cover the set

Thus we can compute d B by counting, for each chosen value of s, the number of boxes that intersect Ω when Ω is covered by a grid of boxes of size s. In practice, for a given s the value B(s) is often computed by picking the minimal B(s) over a set of runs, where each run uses a different offset of the grid (i.e., by shifting the entire grid by a small amount). However, this is time consuming, and usually does not reduce the error by more than 0.5% [Jelinek 98].

For a real-life example of box counting using a grid, 19 boxes are needed to cover the image of the starfish in Fig. 4.8.4 Actually, the image is not quite completely covered by these 19 boxes, since there are two starfish tips (pointed to by two arrows) that are not covered. So we could use two more boxes to cover these two tips. Or perhaps we could use only one additional box, if we translate each box by the same amount (i.e., if we shift the grid coordinates slightly). In general, it is computationally infeasible to find the minimal number of boxes required to cover Ω by a grid of boxes.
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig8_HTML.jpg
Figure 4.8

Starfish box counting

In the fractal literature (e.g., [Baker 90, Barnsley 12, Falconer 13, Feder 88, Schroeder 91]) d B is usually defined assuming that B(s) is either the smallest number of closed balls of radius s needed to cover Ω (i.e., condition (ii) of Definition 4.6), or that B(s) is the number of boxes that intersect Ω when Ω is covered by a grid of boxes of size s (as in Theorem 4.1); both of these choices assume that, for a given s, all boxes have the same size. The definitions of d B in several well-known books also assume that each box has the same size. All of the examples in this chapter illustrating d B employ equal-sized boxes. The reason for not defining d B only in terms of equal-sized boxes is that when we consider, in Chap. 7, the box counting dimension of a complex network $$\mathbb {G}$$ , the boxes that we use to “cover” $$\mathbb {G}$$ will in general not have the same linear size. Since we will base our definition of d B of $$\mathbb {G}$$ on Definition 4.6, we want the definition of d B for Ω to permit boxes to have different sizes.

In [Falconer 13], a 1928 paper by Georges Bouligand (1889–1979) is credited with introducing box counting; [Falconer 13] also noted that “the idea underlying an equivalent definition had been mentioned rather earlier” by Hermann Minkowski (1984–1909). 5 The “more usual definition” of d B was given by Pontryagin and Schnirelman in 1932 [Falconer 03]. A different historical view, in [Vassilicos 91], is that d B was first defined by Kolmogorov in 1958; indeed, [Vassilicos 91] called d B the Kolmogorov capacity, and observed that the Kolmogorov capacity is often referred to in the literature as the box dimension, similarity dimension, Kolmogorov entropy, or 𝜖-entropy. The use of the term “Kolmogorov capacity” was justified in [Vassilicos 91] by citing [Farmer 83] and a 1989 book by Ruelle.

Another view, in [Lauwerier 91], is that the definition of fractal dimension given by Mandelbrot is a simplification of Hausdorff’s and corresponds exactly with the 1958 definition of Kolmogorov (1903–1987) of the “capacity” of a geometrical figure; in [Lauwerier 91] the term “capacity” was used to refer to the box counting dimension. Further confusion arises since Mandelbrot observed [Mandelbrot 85] that the box counting dimension has been sometimes referred to as the “capacity”, and added that since “capacity” has at least two other quite distinct competing meanings, it should not be used to refer to the box counting dimension. Moreover, [Frigg 10] commented that the box counting dimension has also been called the entropy dimension, e.g., in [Mandelbrot 83b] (p. 359). Fortunately, this babel of terminology has subsided, and the vast majority of recent publications (since 1990 or so) have used the term “box counting dimension”, as we will.

Exercise 4.2 Let f(x) be defined on the positive integers, and let L be the length of the piecewise linear curve obtained by connecting the point (i, f(i)) to the point (i + 1, f(i + 1)) for i = 1, 2, …, N − 1. Show that d B of this curve can be approximated by $$1 + \big ( \log L / \log N \big )$$ . □

The existence of d B does not imply that B(s) is proportional to $$s^{-d_{{B}}}$$ . By (4.1), the existence of d B does imply that for each 𝜖 > 0 there is an $$\widetilde {s} < 1$$ such that for $$0 < s < {\widetilde {s}}$$ we have
$$\displaystyle \begin{aligned} & \Big \vert \frac{\log B(s)}{\log (1/s) } -d_{{B}} \Big \vert \leq \epsilon \\ &\quad \Leftrightarrow d_{{B}} - \epsilon \leq \frac{\log B(s)}{\log (1/s) } \leq d_{{B}} + \epsilon \\ &\quad \Leftrightarrow (d_{{B}} - \epsilon) {\log (1/s) } \leq {\log B(s)} \leq (d_{{B}} + \epsilon) {\log (1/s) } \\ &\quad \Leftrightarrow s^{- d_{{B}} + \epsilon } \leq B(s) \leq s^{ - d_{{B}} - \epsilon} \, . \end{aligned} $$
(4.6)
Following [Theiler 90], another way of interpreting d B is to define the function θ(⋅) by $$\theta (s) \equiv B(s) / s^{-d_{{B}}}$$ for s > 0. Then $$B(s) = \theta (s) s^{-d_{{B}}}$$ so
$$\displaystyle \begin{aligned} d_{{B}} = \lim_{s \rightarrow 0} \frac{\log B(s)}{\log (1/s)} = \lim_{s \rightarrow 0} \frac{ \log \theta(s) - d_{{B}} \log s}{\log (1/s)} = d_{{B}} - \lim_{s \rightarrow 0} \frac{ \log \theta(s)}{\log s} \, . \end{aligned}$$
Thus if d B exists, then
$$\displaystyle \begin{aligned} \lim_{s \rightarrow 0} \frac{ \log \theta(s)}{\log s} = 0 \, . \end{aligned}$$
Richardson’s empirical result on the length of the coast of Britain, presented in the beginning of Chap. 3, provided the box counting dimension of the coast. Recall that Richardson showed that L(s) ≈ L 0s 1−d, where d ≈ 1.25. Thus $$1-d = \lim _{s \rightarrow 0} \log \, L(s)/ \log \, s$$ . Since the minimal number B(s) of boxes of size s needed to cover the coast is given by B(s) ≈ L(s)∕s, then
$$\displaystyle \begin{aligned} \begin{array}{rcl} {d_{{B}}}&\displaystyle =&\displaystyle \lim_{s \rightarrow 0} \frac{\log B(s)} { \log( 1/s)} = \lim_{s \rightarrow 0} \frac{\log \bigl( L(s)/s \bigr) } { \log( 1/s)} = \lim_{s \rightarrow 0} \frac{\log L(s) - \log s } { - \log s} \\ &\displaystyle =&\displaystyle 1 - \lim_{s \rightarrow 0} \frac{\log L(s) } {\log s} = d \, , \end{array} \end{aligned} $$
so d B = d.

In the above application of box counting to a starfish, a box is counted if it has a non-empty intersection with the starfish. More generally, in applying Theorem 4.1 to compute d B of Ω, a box is counted if it has a non-empty intersection with Ω. The amount of intersection (e.g., the area of the intersection in the starfish example) is irrelevant. For other fractal dimensions such as the information dimension (Chap. 14) and the generalized dimensions (Chap. 16), the amount of intersection is significant, since “dense” regions of the object are weighted differently than “sparse” regions of the object. The adjective “morphological” is used in [Kinsner 07] to describe a dimension, such as the box counting dimension, which is a purely shape-related concept, concerned only with the geometry of an object, and which utilizes no information about the distribution of a measure over space, or the behavior of a dynamical system over time. Having now discussed both the topological dimension d T and the box counting dimension d B, we can present the definition of a fractal given in [Farmer 82]; he attributed this definition to [Mandelbrot 77].

Definition 4.7 A set is a fractal if its box counting dimension exceeds its topological dimension. □

Definition 4.7 is illustrated by Fig. 4.9, which shows the first six iterations of the Hilbert curve.6 This space-filling curve has topological dimension 1 (d T = 1). Since in generation t this curve consists of 22t − 1 segments, each of length 2−t, its box counting dimension is 2 (d B = 2) [Schroeder 91]. However, regarding Definition 4.7, [Falconer 03] wrote “This definition has proved to be unsatisfactory, in that it excluded a number of sets that clearly ought to be regarded as fractals. Various other definitions have been proposed, but they all seem to have this same drawback”.
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig9_HTML.png
Figure 4.9

Six iterations of the Hilbert curve

4.3 A Deeper Dive into Box Counting

In this section we provide more insight into the box counting dimension. A “natural and direct” approach to computing d B for a real-world object is to take the smallest s available, call it s min, and estimate d B by $$\log B(s_{{min}})/\log (1/s_{{min}})$$ . The problem with this approach is the very slow convergence of $$\log B(s) / \log (1/s)$$ to d B [Theiler 90]. To see this, assume $$B(s) = c s^{-{d_{{B}}}}$$ holds for some constant c. Then
$$\displaystyle \begin{aligned} \frac { \log B(s)}{ \log (1/s) } = \frac { \log (c s^{-{d_{{B}}}}) }{ \log (1/s) } = {d_{{B}}} - \frac { \log c }{ \log s }, \end{aligned}$$
which approaches d B with logarithmic slowness as s → 0, so this approach is not used in practice [Theiler 90]. Instead, to compute d B, typically B(s) is evaluated over some range of s values. Then a range [s min, s max] over which the $$\log B(s)$$ versus $$\log (1/s)$$ curve is approximately linear is identified. The slope of the curve over this range is an estimate of d B.
To illustrate how d B can be obtained by the slope of a line in $$\bigl (\log s, \log B(s) \bigr )$$ space, consider the Sierpiński carpet. The construction of this fractal starts with the filled-in unit square. Referring to Fig. 4.10, the first generation of the construction removes the center 1∕9 of the unit square. What remains is the shaded part of Fig. 4.10(i). This shaded area is covered by 8 of the small squares. Since the side length of the small squares is 1/3, then s = 1∕3 and B(1∕3) = 8. In generation 2, we consider each of the 8 small squares produced in generation 1. For each small square, we remove the center 1∕9 of the square. The result of the generation 2 construction is illustrated in (ii). The shaded area in (ii) is covered by 82 squares of side length 1∕9. Since each small square now has side length 1∕9, then s = 1∕9 and B(1∕9) = 82. In each subsequent iteration, we remove the center 1∕9 of each square sub-region. The slope of the line through $$(\log (1/9), \log 64)$$ and $$(\log (1/3), \log 8)$$ is
$$\displaystyle \begin{aligned} \frac{\log 64 - \log 8}{\log (1/9) - \log (1/3)} = \frac{\log 8}{\log (1/3)} = \frac{- \log 8}{\log 3}, \end{aligned}$$
so d B of the Sierpiński carpet is $${d_{{B}}} = \log 8/\log 3 \approx 1.893$$ .
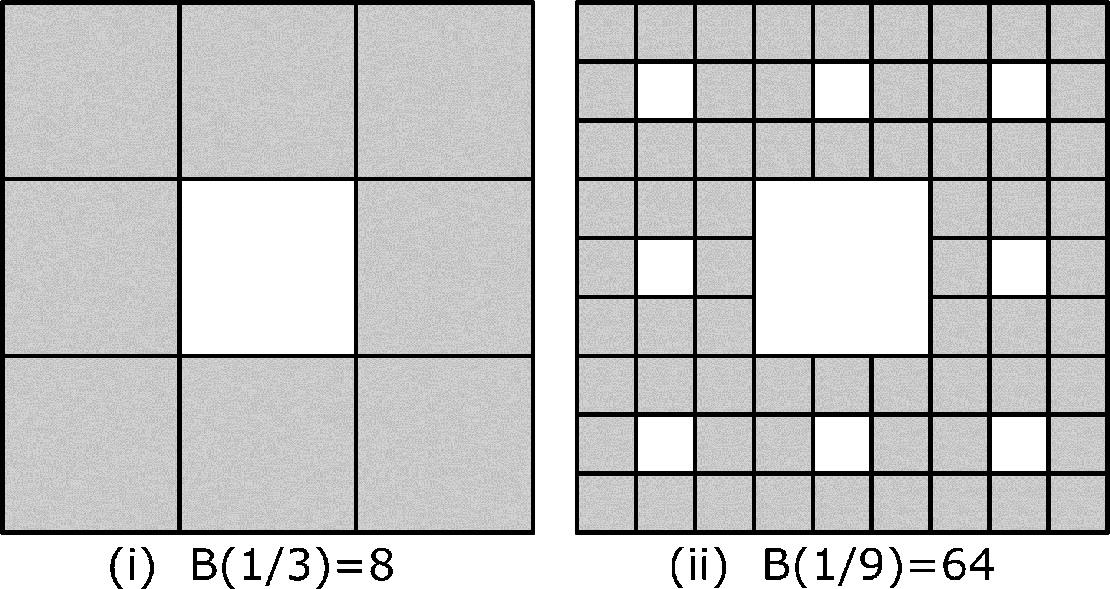
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig10_HTML.jpg
Figure 4.10

Two generations of the Sierpiński carpet

Exercise 4.3 The above calculation of d B just used the two box sizes s = 1∕3 and s = 1∕9. Show that $${d_{{B}}} = \log 8/\log 3$$ is obtained using any two powers of the box size 1∕3. □

Instead of always removing the center 1∕9 of each square region in the Sierpiński carpet, we can randomly choose, in each region, one of the nine sub-regions, and delete that randomly selected sub-region [Strogatz 94]. This randomized construction is illustrated in Fig. 4.11. In Ω 1, a random 1∕9 of the original solid square is deleted. In Ω 2, in each of the 8 remaining smaller squares, a random 1∕9 is deleted. Let Ω t be the pre-fractal object obtained after t generations of this construction. Each Ω t is not self-similar, since randomization was used to select the small squares to delete. Rather, each Ω t is statistically self-similar; a loosely defined term which expresses the fact that the object is “almost” self-similar, the “almost” referring to a randomization which does not change the dimension of the object.7 Indeed, we can apply box counting to find the box counting dimension d B of the randomized Sierpiński carpet, and the calculation is identical to the calculation of d B for the non-random Sierpiński carpet of Fig. 4.10; for the randomized Sierpiński carpet we also have $$d_{{B}} = \log 8/\log 3$$ .
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig11_HTML.png
Figure 4.11

Randomized Sierpiński carpet

Example 4.4 For another box counting example, consider the two-dimensional Cantor dust illustrated in Fig. 4.12. In each generation, each square is replaced by four squares, each 1∕3 the linear size of the previous generation. Each of the 4 second generations squares is 1∕3 the linear size of the first generation. Each of the 16 third generation squares is 1∕9 the linear size of the first generation. The slope of the line through the points $$\bigl ( \log (1/9), \log 16 \bigr )$$ and $$\bigl (\log (1/3), \log 4 \bigr )$$ is
$$\displaystyle \begin{aligned} \frac{\bigl(\log 16 - \log 4 \bigr)}{\bigl(\log (1/9) - \log (1/3) \bigr)} = \frac{\log 4}{\log (1/3)} = - \frac{ \log 4}{\log 3}, \end{aligned}$$
so for two-dimensional Cantor dust we have $${d_{{B}}} = \log 4/\log 3$$ . □
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig12_HTML.png
Figure 4.12

Cantor dust

Example 4.5 As an example of a set for which the box-counting method behaves badly [Falconer 03], consider the set $$\varOmega = \{ 0, 1, \frac {1}{2}, \frac {1}{3}, \ldots \}$$ . This is a bounded countably infinite set. Although we might expect the box counting dimension of Ω to be 0, in fact it is 1∕2. To see this, pick s < 1∕2 and let k be the integer such that $$\frac {1}{k(k+1)} \leq s &lt; \frac {1}{(k-1)k}$$ . Then $$\log \frac {1}{k(k+1)} \leq \log s$$ , so $$\log k(k+1) \geq - \log s$$ . Similarly $$\log s &lt; \frac {1}{(k-1)k}$$ implies $$- \log s &gt; \log k(k-1)$$ .

Suppose we cover Ω by boxes (i.e., line segments) of size s. Define $$\varOmega _k = \{ 1, \frac {1}{2}, \frac {1}{3}, \ldots , \frac {1}{k} \}$$ . For k ≥ 2, the distance between consecutive terms in Ω k is at least $$\frac {1}{k-1} - \frac {1}{k} = \frac {1}{k(k-1)} &gt; s$$ . Thus a box of size s can cover at most one point of Ω k, so k boxes are required to cover Ω k. This implies
$$\displaystyle \begin{aligned} \frac{ \log B(s)}{- \log s} \geq \frac{ \log k}{- \log s} \geq \frac{ \log k}{\log k(k+1)} = \frac{ \log k}{\log k + \log (k+1)} \; . \end{aligned}$$
Since k →∞ as s → 0, letting s → 0 yields $$ \underline {{d_{{B}}}} \geq 1/2$$ .
To prove the reverse inequality, first observe that since $$s \geq \frac {1}{k(k+1)}$$ then k + 1 boxes of size s cover the interval $$[0, \frac {1}{k}]$$ . These k + 1 boxes do not cover the k − 1 points $$1, \frac {1}{2}, \ldots , \frac {1}{k-1}$$ , but these k − 1 points can be covered by another k − 1 boxes. Hence B(s) ≤ (k + 1) + (k − 1) = 2k and
$$\displaystyle \begin{aligned} \frac{ \log B(s)}{- \log s} \leq \frac{ \log 2k}{- \log s} &lt; \frac{ \log 2k}{\log k(k-1)} \; . \end{aligned}$$
Letting s → 0 yields $$\overline {{d_{{B}}}} \leq 1/2$$ . Thus for $$\varOmega = \{ 0, 1, \frac {1}{2}, \frac {1}{3}, \cdots \}$$ we have $$1/2 \leq \underline {{d_{{B}}}} \leq \overline {{d_{{B}}}} \leq 1/2$$ , so the box counting dimension of this countably infinite set is 1/2. □

The fact that d B = 1∕2 for $$\varOmega = \{ 0, 1, \frac {1}{2}, \frac {1}{3}, \cdots \}$$ violates one of the properties that should be satisfied by any definition of dimension, namely the property that the dimension of any finite or countably infinite set should be zero. This violation does not occur for the Hausdorff dimension (Chap. 5). Such theoretical problems with the box counting dimension have spurred alternatives to the box counting dimension, as discussed in [Falconer 03]. In practice, these theoretical issues have not impeded the widespread application of box counting (Sect. 6.​5).

As observed in [Schroeder 91], the definition
$$\displaystyle \begin{aligned} \begin{array}{rcl} {d_{{B}}} = \lim_{s \rightarrow 0} \frac{\log B(s)}{- \log s} \end{array} \end{aligned} $$
of d B could alternatively be given by the implicit form
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{s \rightarrow 0} B(s) s^{d_{{B}}} = c {} \end{array} \end{aligned} $$
(4.7)
for some constant c satisfying −∞ < c < ∞. In (4.7), d B is the unique value of the exponent d that keeps the product B(s)s d finite and nonzero as s → 0. Any other value of d will result in the product B(s)s d approaching either 0 or ∞ as s → 0. This way of viewing the box counting dimension is fully developed when we explore the Hausdorff dimension in Chap. 5.

4.4 Fuzzy Fractal Dimension

If the box-counting method is applied to a 2-dimensional array of pixels, membership is binary: a pixel is either contained in a given box B, or it is not contained in B. The fuzzy box counting dimension is a variant of d B in which binary membership is replaced by fuzzy membership: a “membership function” assigns to a pixel a value in [0, 1] indicating the degree to which the pixel belongs to B. Similarly, for a 3-dimensional array of voxels, binary membership is replaced by assigning a value in [0, 1] indicating the degree to which the voxel belongs to B.8

Fuzzy box counting is useful for medical image processing, e.g., to determine the edges of heart images obtained from an echocardiogram [Zhuang 04]. Suppose that for pixel i in the 2-dimensional array we have the associated gray-scale level g i, which is between 0 and 256. Then we can choose g i∕256 as the membership function. Suppose the pixel array is covered by a set $${\mathcal {B}}(s)$$ of boxes of a given size s, and consider a given box B in the covering. Let $${\mathcal {I}}(B)$$ be the set of pixels covered by B. Whereas for “classical” box counting we count B if $${\mathcal {I}}(B)$$ is non-empty, for fuzzy box counting we compute
$$\displaystyle \begin{aligned} \begin{array}{ll} f(B) &amp; \equiv \max_{i \in {\mathcal{I}}(B)} \frac{g_{{{i}}}}{256} \\ f(s) &amp; \equiv \sum_{B \in {\mathcal{B}}(s)} f(B) \, . {} \end{array} \end{aligned} $$
(4.8)
If the plot of $$\log f(s)$$ versus $$\log (1/s)$$ is roughly linear over a range of s, the slope of the line is the estimate of the fuzzy box counting dimension.
The local fuzzy box counting dimension [Zhuang 04] restricts the computation of the fuzzy box counting dimension to the neighborhood $${\mathbb {N}}(j)$$ of all pixels within a given radius of a given pixel j, where we might define the distance between two pixels to be the distance between the pixel centers. Instead of (4.8), we calculate
$$\displaystyle \begin{aligned} \begin{array}{rcl} f \big({\mathbb{N}}(j), B \big) &amp;\displaystyle \equiv &amp;\displaystyle \max_{i \in {\mathcal{I}}(B) \cap {\mathbb{N}}(j)} \frac{g_{{{i}}}}{256} \\ f \big({\mathbb{N}}(j),s \big) &amp;\displaystyle \equiv &amp;\displaystyle \sum_{B \in {\mathcal{B}}(s)} f({\mathbb{N}}(j), B) \, . \end{array} \end{aligned} $$
If the plot of $$\log f \big ({\mathbb {N}}(j),s \big )$$ versus $$\log (1/s)$$ is roughly linear over a range of s, the slope of the line is the estimate of the local fuzzy box counting dimension in the neighborhood $${\mathbb {N}}(j)$$ of pixel j.

4.5 Minkowski Dimension

For $$\varOmega \subset {\mathbb {R}}^E$$ and $$x, y \in {\mathbb {R}}^E$$ , let dist(x, y) be the Euclidean distance between x and y. For r > 0, the set
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varOmega_r \equiv \{ y \in {\mathbb{R}}^E \, \vert \, {\mathit{dist}}(x,y) \leq r \mbox{ for some } x \in \varOmega \} \, \end{array} \end{aligned} $$
is the set of points within distance r of Ω. We call Ω r the r-neighborhood of Ω or simply a dilation of Ω. Let vol(Ω r) be the volume (in the usual geometric sense) of Ω r, and let d T be the topological dimension of Ω.

Example 4.6 Let E = 3 and let Ω be the single point x. Then d T = 0 and Ω r is the closed ball (in $$\mathbb {R}^3$$ ) of radius r centered at x. We have $$\textit {vol}(\varOmega _r) = (4/3) \pi r^3 = c_{{0}} r^{E-d_{{T}}}$$ for some constant c 0, so $$\textit {vol}(\varOmega _r)/r^{E-d_{{T}}} = c_{{0}}$$ . □

Example 4.7 Let E = 3 and let Ω be a line (straight or curved). Then Ω r is a “sausage” of diameter 2r (except at the ends) traced by the closed balls (in $$\mathbb {R}^3$$ ) whose centers follow the line. This construction is a standard method used by mathematicians to “tame” a wildly irregular curve [Mandelbrot 83b]. If Ω is a straight line segment of length L, then d T = 1 and $$\textit {vol}(\varOmega _r) \approx \pi r^2 L = c_{{1}} r^{E-d_{{T}}}$$ for come constant c 1, so $$\textit {vol}(\varOmega _r)/r^{E-d_{{T}}} \approx c_{{1}}$$ . □

Example 4.8 Let E = 3 and let Ω be a flat 2-dimensional sheet. Then Ω r is a “thickening” of Ω. If the area of Ω is A, then d T = 2 and $$\textit {vol}(\varOmega _r) \approx 2rA = c_{{2}} r^{E-d_{{T}}}$$ for some constant c 2, so $$\textit {vol}(\varOmega _r)/r^{E-d_{{T}}} \approx c_{{2}}$$ . □

Motivated by these examples, let Ω be an arbitrary subset of $${\mathbb {R}}^E$$ and consider vol(Ω r)∕r E−d as r → 0. Suppose for some nonnegative d the limit
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{r \rightarrow 0 } \frac{ \textit{vol}(\varOmega_r) } { r^{E-d} } {} \end{array} \end{aligned} $$
(4.9)
exists. Denote this limit, called the Minkowski content of Ω, by c; the Minkowski content is a measure of the length, area, or volume of Ω as appropriate [Falconer 03]. Pick 𝜖 > 0. For all sufficiently small r > 0 we have
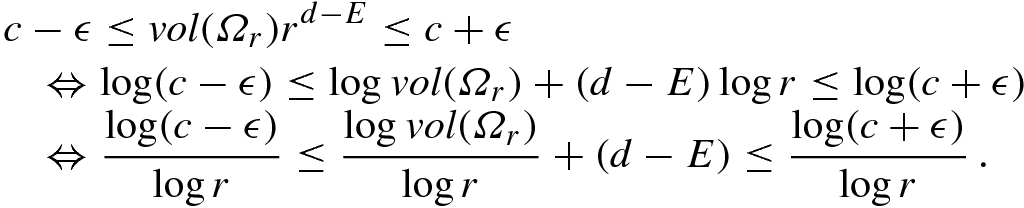
../images/487758_1_En_4_Chapter/487758_1_En_4_Equu_HTML.png
Letting r → 0 yields
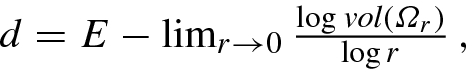
../images/487758_1_En_4_Chapter/487758_1_En_4_Equ14_HTML.png
(4.10)
and d is called the Minkowski dimension, or the Minkowski-Bouligand dimension, and is denoted by d K.9 Since Ω r is a dilation of Ω, the technique of using (4.10) to estimate d K is called the dilation method.

The three examples above considered the Minkowski dimension of a point, line segment, and flat region, viewed as subsets of $${\mathbb {R}}^3$$ . We can also consider their Minkowski dimensions as subsets of $${\mathbb {R}}^2$$ , in which case we replace “volume” with “area”.

Example 4.9 Figure 4.13 illustrates this dilation in $${\mathbb {R}}^2$$ for a curve and for a straight line of length L. Since now E = 2, the Minkowski dimension d K of a straight line of length L is
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{K}} &amp;\displaystyle =&amp;\displaystyle 2 - \lim_{r \rightarrow 0} \frac{\log \textit{area}(\varOmega_r)}{\log r} \; . \end{array} \end{aligned} $$
(4.11)
We have area(Ω r) = 2rL + 2(πr 2∕2) = 2rL + πr 2. Using L’Hôpital’s rule,
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{K}} &amp;\displaystyle =&amp;\displaystyle 2 - \lim_{r \rightarrow 0} \frac{\log (2r L+ \pi r^2)}{\log r} = 2- \lim_{r \rightarrow 0} \frac{(2L + 2 \pi r)/(2rL + \pi r^2)}{1/r} \\ &amp;\displaystyle =&amp;\displaystyle 2 - \lim_{r \rightarrow 0} \frac{2 r L + 2\pi r^2}{2rL + \pi r^2} = 1 \; . \; \; \end{array} \end{aligned} $$
□
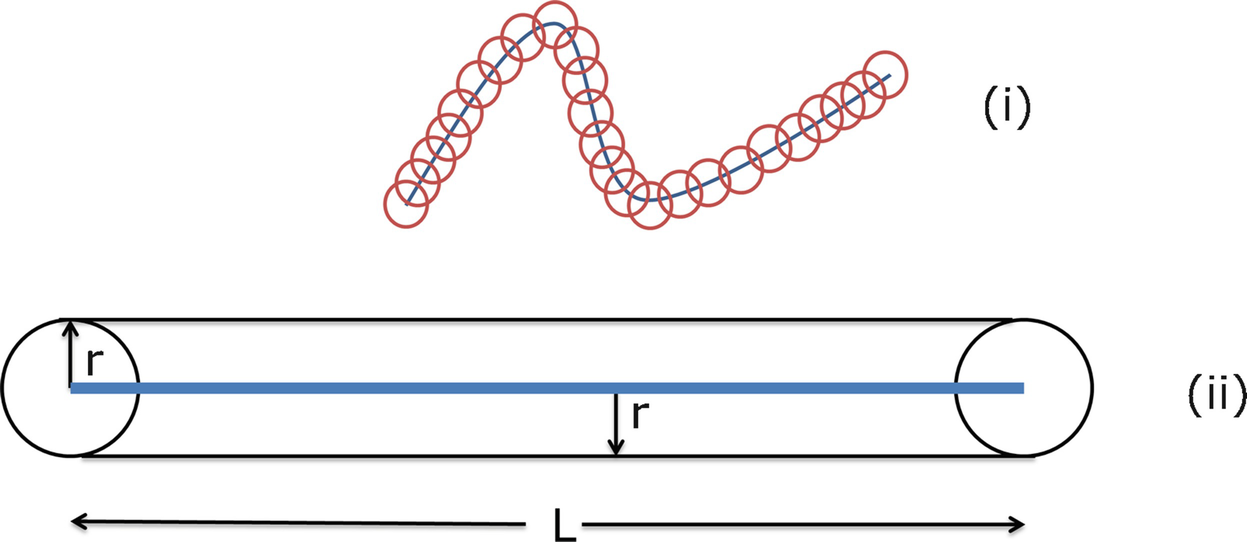
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig13_HTML.png
Figure 4.13

Minkowski sausage in two dimensions

If the limit (4.9) does not exist, we can still define
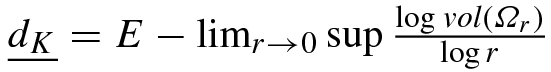
../images/487758_1_En_4_Chapter/487758_1_En_4_Equ17_HTML.png
(4.12)
and
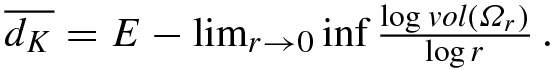
../images/487758_1_En_4_Chapter/487758_1_En_4_Equ18_HTML.png
(4.13)
It is proved in [Falconer 03] that the lower box counting dimension $$ \underline {{d_{{B}}}}$$ , defined by (4.2), is equal to $$ \underline {d_{{K}}}$$ , and that the upper box counting dimension $$\overline {{d_{{B}}}}$$ , defined by defined by (4.3), is equal to $$\overline {d_{{K}}}$$ . If $$ \underline {{d_{{B}}}} = \overline {{d_{{B}}}}$$ , then the box counting dimension d B and the Minkowski dimension d K both exist and d B = d K. Thus, while defined differently, the box counting dimension and the Minkowski dimensions, if they exist, are the same. For this reason, the box counting dimension is sometimes called the Minkowski dimension or the Minkowski-Bouligand dimension. In this book we will use d B when the dimension is computed using (4.1), and d K when the dimension is computed using (4.10). Although the Minkowski dimension is used much less frequently than the box counting dimension, there are many interesting applications, a few of which we describe below.

Estimating People Density: The Minkowski dimension was used in [Marana 99] to estimate the number of people in an area. This task is usually accomplished using closed-circuit television systems and human observers, and there is a need to automate this task, e.g., to provide real-time reports when the crowd density exceeds a safe level. To calculate d K, a circle of size r was swept continuously along the edges of the image (the edges outline the people). The total area A(r) swept by the circles of radius r was plotted against r on a log–log plot to estimate d K. This method was applied to nearly 300 images from a railway station in London, UK, to classify the crowd density as very low, low, moderate, high, or very high, and achieved about 75% correct classification. However, the method was not able to distinguish between the high and very high crowd densities. □

Texture Analysis of Pixelated Images: Fractal analysis was applied in [Florindo 13] to a color adjacency graph (CAG), which is a way to represent a pixelation of a colored image. They considered the adjacency matrix of the CAG as a geometric object, and computed its Minkowski dimension. □

Cell Biology: The dilation method was used in [Jelinek 98] to estimate the length of the border of a 2-dimensional image of a neuron. Each pixel on the border of the image was replaced by a circle of radius r centered on that pixel. Structures whose size is less than r were removed. Letting area(r) be the area of the resulting dilation of the border, area(r)∕(2r) is an estimate of the length of the border. A plot of 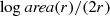../images/487758_1_En_4_Chapter/487758_1_En_4_IEq140_HTML.gif versus $$\log 2r$$ yields an estimate of d K. □

Acoustics: As described in [Schroeder 91], the Minkowski dimension has applications in acoustics. The story begins in 1910, when the Dutch physicist Hendrik Lorentz conjectured that the number of resonant modes of an acoustic resonator depends, up to some large frequency f, only on the volume V  of the resonator and not its shape. Although the mathematician David Hilbert predicted that this conjecture, which is important in thermodynamics, would not be proved in his lifetime, it was proved by Herman Weyl, who showed that for large f and for resonators with sufficiently smooth but otherwise arbitrary boundaries, the number of resonant modes is (4π∕3)V (f∕c)3, where c is the velocity of sound. For a two-dimensional resonator such as a drum head, the number of resonant modes is πA(f∕c)2, where A is the surface area of the resonator. These formulas were later improved by a correction term involving lower powers of f. If we drop Weyl’s assumption that the boundary of the resonator is smooth, the correction term turns out to be $$(Lf/c)^{d_{{K}}}$$ . The reason the Minkowski dimension governs the number of resonant modes of an acoustic resonator is that normal resonance modes need a certain area or volume associated with the boundary. □

Music Signal Analysis: The Minkowski dimension was used in [Zlatintsi 11] to analyze music signals for such applications as music retrieval, automatic music transcription, and indexing of multimedia databases. (The idea of using fractal dimension to discriminate different genres of music was proposed as early as 2000.) Suppose a window of size r (where the range of r corresponds to a time scale of up to about 50 ms.) is moved along the plot of the music signal, thus creating a dilation of the plot. For a given r, [Zlatintsi 11] computed
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(r) &amp;\displaystyle =&amp;\displaystyle \frac { \log [( \mathrm{area of graph dilated by disks of radius} r)/ {r^2}] } { \log (1/r) } \\ &amp;\displaystyle = &amp;\displaystyle 2 - \frac { \log ( \mathrm{area of graph dilated by disks of radius} r) } { \log r } \, . \end{array} \end{aligned} $$
The Minkowski dimension d K =limr→0f(r) was estimated by fitting a line to the f(r) values. □
As described in [Eins 95], Flook in 1978 noted that when computing d K for a figure containing “open ends” (i.e., end points of lines), using the dilation method can overestimate area; by (4.10) an overestimate of area causes an underestimate of d K. For example, an astrocyte, illustrated in Fig. 4.14, contains many open ends.10 The underestimate of d K arises since in [Eins 95] the length L(r) corresponding to a dilation was estimated from the dilated area A(r) using L(r) = A(r)∕(2r). Therefore, using the Richardson relation L(r) ≈ r 1−d (see (3.​1)), which we rewrite as $$d = 1 - \frac {\log L(r)}{\log r}$$ , an overestimate of L(r) yields an underestimate of d. The degree of underestimation depends on the number of end points and the image complexity. To eliminate the underestimation of d K, specially designed “anisotropic” shapes, to be used at the open ends of such figures, were proposed in [Eins 95].
../images/487758_1_En_4_Chapter/487758_1_En_4_Fig14_HTML.png
Figure 4.14

astrocytes

Statistical issues in estimating d K were considered in [Hall 93] for the curve X(t) over the interval 0 < t < 1, where X(t) is a stochastic process observed at N regularly spaced points. Group these N points into J contiguous blocks of width r. Let $${\mathbb {N}}_j$$ be the points in block j and define $$L_j \equiv \min _{j \in {\mathbb {N}}_j} X(j)$$ and $$U_j \equiv \max _{j \in {\mathbb {N}}_j} X(j)$$ . Then A =∑1≤j≤Jr (U j − L j) is an approximation to the area of the dilation Ω r, and $$2 - (\log A)/(\log r)$$ estimates d K. It was shown in [Hall 93] that this estimator suffers from excessive bias, and a regression-based estimator based on least squares was proposed.11