© Springer Nature Switzerland AG 2020
E. RosenbergFractal Dimensions of Networkshttps://doi.org/10.1007/978-3-030-43169-3_7

7. Network Box Counting Dimension

Eric Rosenberg1 
(1)
AT&T Labs, Middletown, NJ, USA
 

Little boxes on the hillside, little boxes made of ticky tacky,

Little boxes on the hillside, little boxes all the same.

There’s a green one and a pink one, and a blue one and a yellow one,

And they’re all made out of ticky tacky, and they all look just the same.

“Little Boxes” by Malvina Reynolds (1900–1978), American folk/blues singer-songwriter and political activist.

In this chapter we begin our detailed study of fractal dimensions of a network $$\mathbb {G}$$ . There are two approaches to calculating a fractal dimension of $$\mathbb {G}$$ . One approach, applicable if $$\mathbb {G}$$ is a spatially embedded network, is to treat $$\mathbb {G}$$ as a geometric object and apply techniques, such as box counting or modelling $$\mathbb {G}$$ by an IFS, applicable to geometric objects. For example, in Sect. 5.​3 we showed how to calculate the similarity dimension d S of a tree described by an IFS. Also, several studies have computed d B for networks embedded in $${\mathbb {R}}^2$$ by applying box counting to the geometric figure. This was the approach taken to calculate d B in [Benguigui 92] for four railroad networks, in [Arlt 03] for the microvascular network of chicks, in [Lu 04] for road networks in cities in Texas, and in [Hou 15] for electric power networks; later in this book we will consider those studies in more detail. These approaches to computing d B make no use of network properties. The focus of this chapter is how to compute a fractal dimension for $$\mathbb {G}$$ using methods that treat $$\mathbb {G}$$ as a network and not simply as a geometric object.

Just as there is no one definition of the “fractal dimension” of a geometric object, there is no one definition of “the fractal dimension” of $${\mathbb {G}}$$ . The network fractal dimensions we will consider include:

the box counting dimension (this chapter), based on the box-counting method for geometric fractals, describes how the number of boxes of size s needed to cover $${\mathbb {G}}$$ varies with s,

the correlation dimension (Chapter 11), which describes how the number of nodes within r hops of a random node varies with r, extends to networks the correlation dimension of geometric objects (Chapter 9),

the information dimension (Chapter 15) which extends to networks the information dimension of geometric objects (Chapter 14),

the generalized dimensions (Chapter 17) which extends to networks the generalized dimensions of geometric objects (Chapter 16).

As discussed in the beginning of Chap. 3 and in Sect. 5.​5, several definitions of “fractal” have been proposed for a geometric object Ω. None of them has proved entirely satisfactory. As we saw in Sect. 6.​5, applications of d B of Ω compare d B to the dimension of similar objects (e.g., healthy versus unhealthy lungs), or examine how d B changes over time. Although focusing on the definition of “fractality” for Ω does not concern us, in later chapters we will need to focus on the definition of “fractality” for $$\mathbb {G}$$ . The reason this is necessary for $$\mathbb {G}$$ is that, while the terms “fractality” and “self-similarity” are often used interchangeably for Ω, they have been given very different meanings for $$\mathbb {G}$$ . With this caveat on terminology, in this chapter and in the next chapter we study the box counting dimension of $${\mathbb {G}}$$ .

Analogous to computing d B of a geometric fractal, computing d B of $${\mathbb {G}}$$ requires covering $${\mathbb {G}}$$ by a set of “boxes”, where a box is a subnetwork of $${\mathbb {G}}$$ . The methods for computing a covering of $${\mathbb {G}}$$ are also called box counting methods, and several methods have been proposed. Most methods are for unweighted networks for which “distance” means chemical distance (i.e., hop count); a few methods are applicable to unweighted networks, e.g., spatially embedded networks for which “distance” means Euclidean distance. Most of this chapter will focus on unweighted networks, and we begin there. Recall that throughout this book, except where otherwise indicated, we assume that $${\mathbb {G}} = ({\mathbb {N}}, {\mathbb {A}})$$ is a connected, unweighted, and undirected network.

7.1 Node Coverings and Arc Coverings

In this section we consider what it means to cover a network $${\mathbb {G}} = ({\mathbb {N}},{\mathbb {A}} )$$ of N nodes and A arcs.

Definition 7.1 The network B is a subnetwork of $${\mathbb {G}}$$ if B can be obtained from $${\mathbb {G}}$$ by deleting nodes and arcs. A box is a subnetwork of $${\mathbb {G}}$$ . A box is disconnected if some nodes in the box cannot be connected by arcs in the box. □

Let $$\{ B_{{j}} \}_{j=1}^{J} \equiv \{ B_1, B_2, \ldots , B_{{J}} \}$$ be a collection of boxes. Two types of coverings of $${\mathbb {G}}$$ have been proposed: node coverings and arc coverings. Let s be a positive integer.

Definition 7.2 (i) The set $$\{ B_{{j}} \}_{j=1}^{J}$$ is a node s-covering of the network $${\mathbb {G}}$$ if for each j we have diam(B j) < s and if each node in $$\mathbb {N}$$ is contained in exactly one B j. (ii) The set $$\{B_{{j}}\}_{j=1}^{J}$$ is an arc s-covering of $${\mathbb {G}}$$ if for each j we have diam(B j) < s and if each arc in $$\mathbb {A}$$ is contained in exactly one B j. □

If B j is a box in a node or arc s-covering of $${\mathbb {G}}$$ , then the requirement diam(B j) < s in Definition 7.2 implies that B j is connected. However, as discussed in Sect. 8.​6, this requirement, which is a standard assumption in defining the box counting dimension of $${\mathbb {G}}$$ [Gallos 07b, Kim 07a, Kim 07b, Rosenberg 17b, Song 07], may for good reasons frequently be violated in some methods for determining the fractal dimensions of $${\mathbb {G}}$$ .

It is possible to define a node covering of $${\mathbb {G}}$$ to allow a node to be contained in more than one box; coverings with overlapping boxes are used in [Furuya 11, Sun 14]. The great advantage of non-overlapping boxes is that they immediately yield a probability distribution, as discussed in Chap. 15. The probability distribution obtained from a non-overlapping node covering of $${\mathbb {G}}$$ is the basis for computing the information dimension d I and the generalized dimensions D q of $${\mathbb {G}}$$ (Chap. 17). Therefore, in this book each covering of $${\mathbb {G}}$$ is assumed to use non-overlapping boxes, as specified in Definition 7.2.

Since a network of diameter 0 contains only a single node, a node 1-covering contains N boxes. Since a node 1-covering provides no useful information other than N itself, we consider node s-coverings only for s ≥ 2. Figure 7.1(i) illustrates a node 3-covering with J = 2; both boxes in this covering have diameter 2.
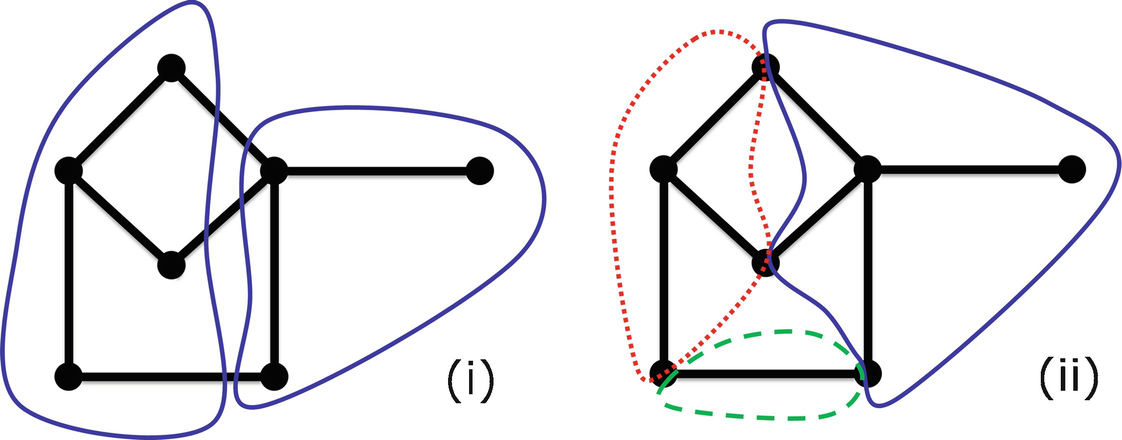
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig1_HTML.png
Figure 7.1

A node 3-covering (i) and an arc 3-covering (ii)

Figure 7.1(ii) illustrates an arc 3-covering of the same network using 3 boxes. The box indicated by the solid line contains 4 arcs and has diameter 2, the box indicated by the dotted line contains 3 arcs and has diameter 2, and the box indicated by the dashed line contains 1 arc and has diameter 1. Figure 7.2 illustrates arc s-coverings for s = 2, s = 3, and s = 4, using 6, 3, and 2 boxes, respectively.
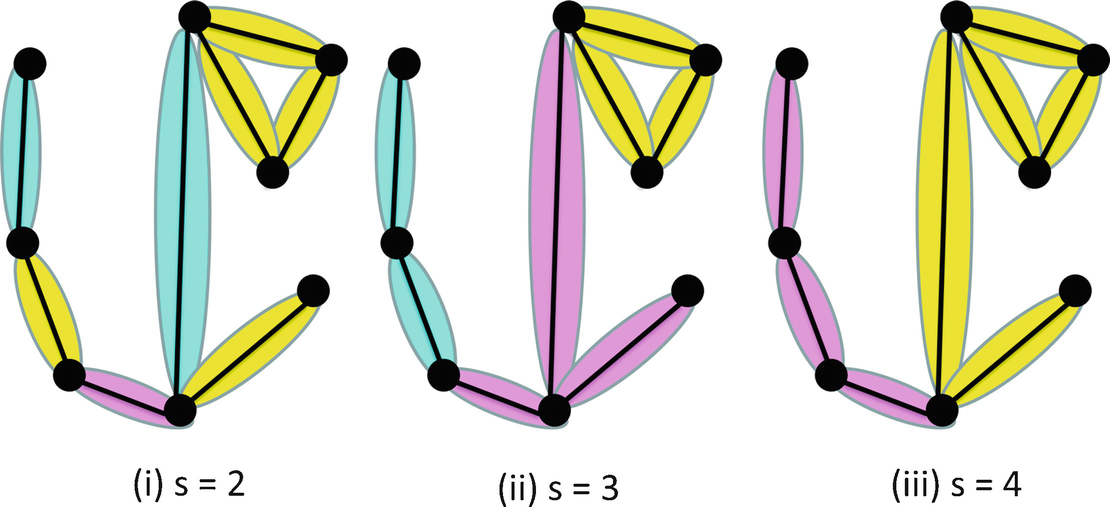
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig2_HTML.png
Figure 7.2

Arc s-coverings for s = 2, 3, 4

A node covering is not necessarily an arc covering, as illustrated by Fig. 7.3. The nodes are covered by B 1 and B 2, but the arc in the middle belongs to neither B 1 nor B 2.
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig3_HTML.png
Figure 7.3

A node covering which is not an arc covering

Also, an arc covering is not necessarily a node covering. For example, as shown in Fig. 7.4, an arc 2-covering of the 3 node chain network consists of the boxes B 1 and B 2; node n is contained in both B 1 and B 2, which violates Definition 7.2.
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig4_HTML.png
Figure 7.4

An arc covering which is not a node covering

Definition 7.3 (i) An arc s-covering $$\{B_{{j}}\}_{j=1}^{J}$$ is minimal if for any other arc s-covering $$\{B^{\prime }_j\}_{j=1}^{J^{\prime }}$$ , we have J ≤ J ′. Let B A(s) be the number of boxes in a minimal arc s-covering of $${\mathbb {G}}$$ . (ii) A node s-covering $$\{B_{{j}}\}_{j=1}^{J}$$ is minimal if for any other node s-covering $$\{B^{\prime }_j\}_{j=1}^{J^{\prime }}$$ , we have J ≤ J ′. Let B N(s) be the number of boxes in a minimal node s-covering of $${\mathbb {G}}$$ . □

That is, a covering is minimal if it uses the fewest possible number of boxes. For s > Δ, the minimal node or arc s-covering consists of a single box, which is $${\mathbb {G}}$$ itself. Thus B A(s) = B N(s) = 1 for s > Δ.

How large can the ratio B A(s)∕B N(s) be? For s = 2, the ratio can be arbitrarily large. For consider $${\mathcal {K}}_N$$ , the complete graph on N nodes, which has N(N − 1)∕2 arcs. For s = 2, we have B N(2) = ⌈N∕2⌉, since each box in the node 2-covering contains one arc, which covers two nodes. We have B A(2) = N(N − 1)∕2, since each box in the arc 2-covering contains one arc. Thus B A(2)∕B N(2) is $${\mathcal {O}}(N)$$ .

For s = 3, the ratio B A(s)∕B N(s) can also be arbitrarily large, as illustrated by Fig. 7.5.
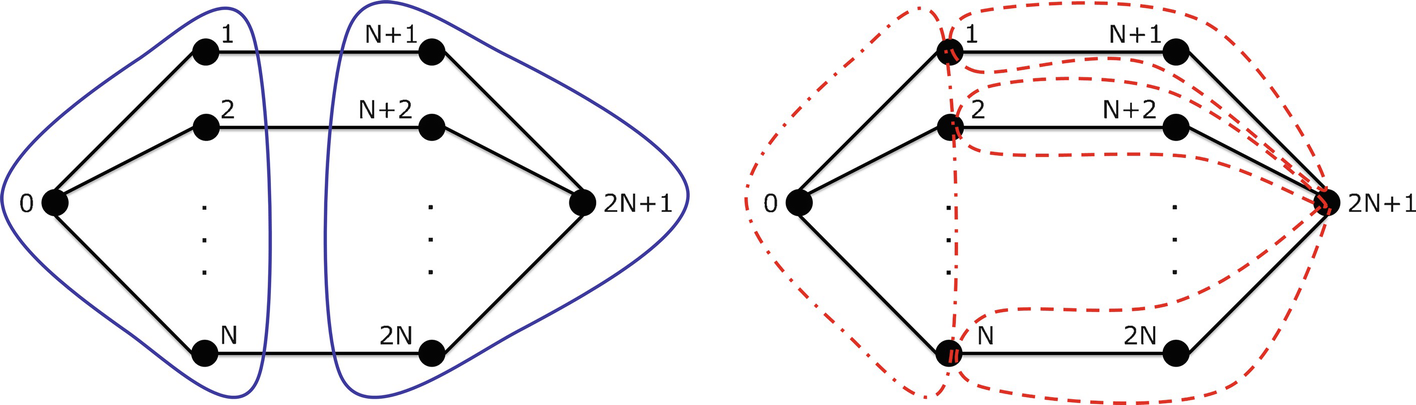
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig5_HTML.png
Figure 7.5

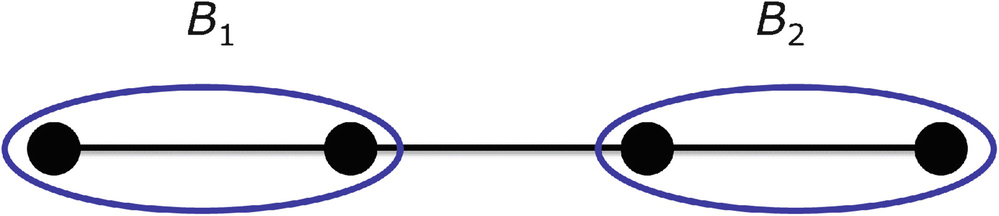
Comparing B N(2) and B A(2)

This network has 2N + 2 nodes and 3N arcs. We have B N(3) = 2; the two boxes in the minimal node cover are shown on the left. We have B A(3) = N + 1, as shown on the right. Thus B A(3)∕B N(3) is $${\mathcal {O}}(N)$$ .

Exercise 7.1 ⋆ For each integer s ≥ 2, is there a graph with N nodes such that B A(s)∕B N(s) is $${\mathcal {O}}(N)$$ ? □

Virtually all research on network coverings has considered node coverings; only a few studies, e.g., [Jalan 17, Zhou 07], use arc coverings. The arc covering approach of [Jalan 17] uses the N × N adjacency matrix M (Sect. 2.​1). For a given integer s between 2 and N∕2, the method partitions M into non-overlapping square s × s boxes, and then counts the number m(s) of boxes containing at least one arc. The network has fractal dimension d if m(s) ∼ s −d. Since m(s) depends in general on the order in which the nodes are labelled, m(s) is averaged over many shufflings of the node order.

The reason arc coverings are rarely used is that, in practice, computing a fractal dimension of a geometric object typically starts with a given set of points in $${\mathbb {R}}^E$$ (the points are then covered by boxes, or the distance between each pair of points is computed, as discussed in Chap. 9), and nodes in a network are analogous to points in $${\mathbb {R}}^E$$ . Having contrasted arc coverings and node coverings for a network, we now abandon arc coverings; henceforth, all coverings of $${\mathbb {G}}$$ are node coverings, and by covering $${\mathbb {G}}$$ we mean covering the nodes of $${\mathbb {G}}$$ . Also, henceforth by an s-covering we mean a node s-covering, and by a covering of size s we mean an s-covering.

7.2 Diameter-Based and Radius-Based Boxes

There are two main approaches used to define boxes for use in covering $${\mathbb {G}}$$ : diameter-based boxes and radius-based boxes.

Definition 7.4 (i) A radius-based box $${\mathbb {G}}(n, r)$$ with center node $$n \in {\mathbb {N}}$$ and radius r is the subnetwork of $${\mathbb {G}}$$ containing all nodes whose distance to n does not exceed r. Let B R(r) be the minimal number of radius-based boxes of radius at most r needed to cover $${\mathbb {G}}$$ . (ii) A diameter-based box $${\mathbb {G}}(s)$$ of size s is a subnetwork of $${\mathbb {G}}$$ of diameter s − 1. Let B D(s) denote the minimal number of diameter-based boxes of size at most s needed to cover $${\mathbb {G}}$$ . □

Example 7.1 For a rectilinear grid, the diameter-based box containing the largest number of nodes for s = 3 is shown in Fig. 7.6 (left); this box contains 5 nodes. The boxes containing the largest number of nodes for s = 5 and s = 7 are shown in Fig. 7.6 (right). □
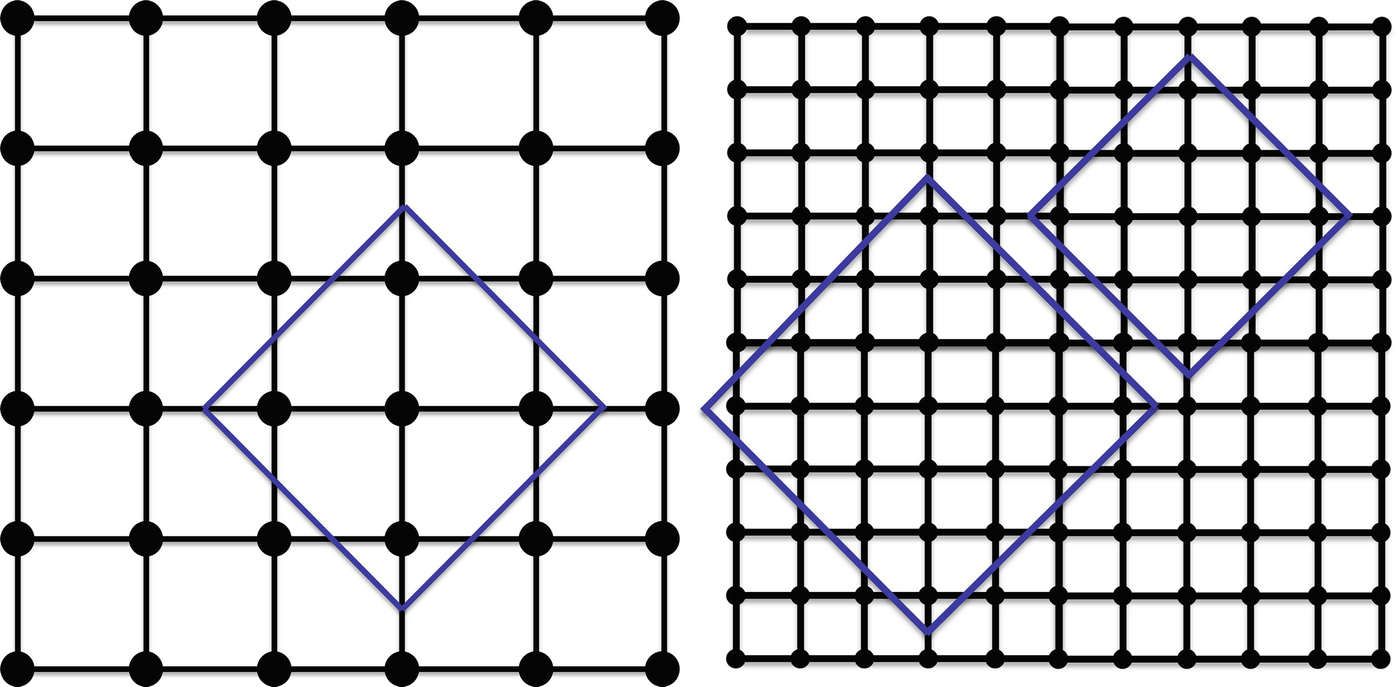
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig6_HTML.png
Figure 7.6

Optimal B D(3) box (left), and optimal B D(5) and B D(7) boxes (right)

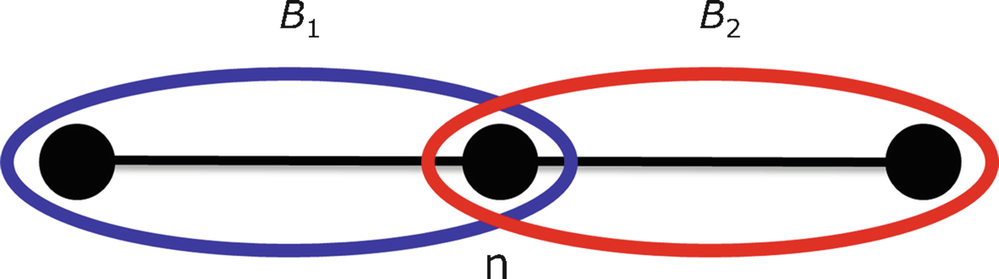
The subscript “R” in B R(n, r) denotes “radius”. Thus the node set of $${\mathbb {G}}(n,r)$$ is $$\{ x \in {\mathbb {N}} \, \vert \, {\mathit {dist}} (n,x) \leq r \}$$ . Radius-based boxes are used in the Maximum Excluded Mass Burning and Random Sequential Node Burning methods which we will study in Chap. 8. Interestingly, the above definition of a radius-based box may frequently be violated in the Maximum Excluded Mass Burning and Random Sequential Node Burning methods. In particular, some radius-based boxes created by those methods may be disconnected, or some boxes may contain only some of the nodes within distance r of the center node n.

For a given s there is in general not a unique $${\mathbb {G}}(s)$$ ; e.g., for a long chain network and s small, there are many diameter-based boxes of size s. A diameter-based box $${\mathbb {G}}(s)$$ is not defined in terms of a center node; instead, for nodes $$x, y \in {\mathbb {G}}(s)$$ we require dist(x, y) < s.1 Diameter-based boxes are used in the Greedy Node Coloring, Box Burning, and Compact Box Burning heuristics described in Chap. 8. The above definition of a diameter-based box also may frequently be violated in the Box Burning and Compact Box Burning methods. Also, since each node in $${\mathbb {G}}$$ must belong to exactly one B j in an s-covering $$\{B_{{j}}\}_{j=1}^{J}$$ using diameter-based boxes, then in general we will not have diam(B j) = s − 1 for all j. To see this, consider a chain of 3 nodes (call them x, y, and z), and let s = 2. The minimal 2-covering using diameter-based boxes requires two boxes, B 1 and B 2. If B 1 covers x and y, then B 2 covers only z, so the diameter of B 2 is 0.

The subscript “D” in B D(s) denotes “diameter”. The minimal number of diameter-based boxes of size at most 2r + 1 needed to cover $${\mathbb {G}}$$ is, by definition, B D(2r + 1). We have B D(2r + 1) ≤ B R(r) [Kim 07a]. To see this, let $${\mathbb {G}}({n_{{j}}},r_{{j}})$$ , j = 1, 2, …, B R(r) be the boxes in a minimal covering of $${\mathbb {G}}$$ using radius-based boxes of radius at most r. Then r j ≤ r for all j. Pick any j, and consider box $${\mathbb {G}}({n_{{j}}},r_{{j}})$$ . For any nodes x and y in $${\mathbb {G}}({n_{{j}}},r_{{j}})$$ we have
$$\displaystyle \begin{aligned} {\mathit{dist}} (x,y) \leq {\mathit{dist}} (x,n_{{j}}) + {\mathit{dist}} (n_{{j}}, y) \leq 2 r_{{j}} \leq 2r \, , \end{aligned}$$
so $${\mathbb {G}}({n_{{j}}},r_{{j}})$$ has diameter at most 2r. Thus these B R(r) boxes also serve as a covering of size 2r + 1 using diameter-based boxes. Therefore, the minimal number of diameter-based boxes of size at most 2r + 1 needed to cover $${\mathbb {G}}$$ cannot exceed B R(r); that is, B D(2r + 1) ≤ B R(r).
The reverse inequality does not in general hold, since a diameter-based box of size 2r + 1 can contain more nodes than a radius-based box of radius r. For example, consider the network $${\mathbb {G}}$$ of Fig. 7.7.
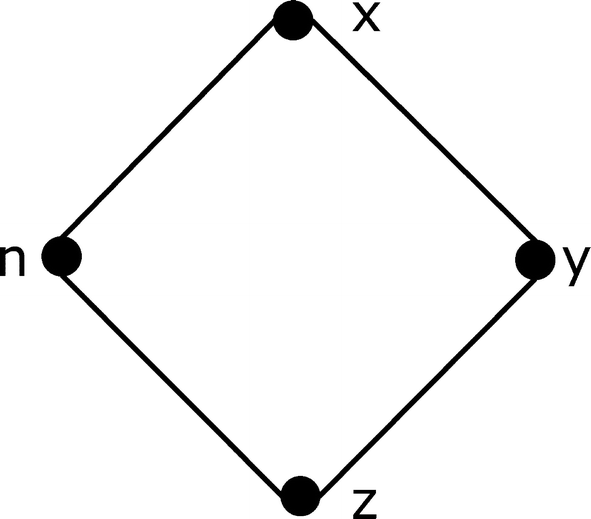
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig7_HTML.png
Figure 7.7

Diameter-based versus radius-based boxes

The only nodes adjacent to n are x and z, so $${\mathbb {G}}(n,1) = \{ n, x, z \}$$ and B R(1) = 2. Yet the diameter of $${\mathbb {G}}$$ is 2, so it can be covered by a single diameter-based box of size 3, namely $${\mathbb {G}}$$ itself, so B D(3) = 1. Thus B R(r) and B D(2r + 1) are not in general equal. Nonetheless, for the C. elegans and Internet backbone networks studied in [Song 07], the calculated fractal dimension was the same whether radius-based or diameter-based boxes were used. Similarly, both radius-based and diameter-based boxes yielded a fractal dimension of approximately 4.1 for the WWW (the World Wide Web) [Kim 07a].

As applied to a network $$\mathbb {G}$$ , the term box counting refers to computing a minimal s-covering of $${\mathbb {G}}$$ for a range of values of s, using either radius-based boxes or diameter-based boxes. Conceivably, other types of boxes might be used to cover $${\mathbb {G}}$$ . Once we have computed B D(s) for various values of s (or B R(r) for various values of r) we can try to compute d B.

Computing any fractal dimension for a finite network is necessarily open to the same criticism that can be directed to computing a fractal dimension of a real-world geometric object, namely that a fractal dimension is defined only for a fractal (a theoretical construct with structure at infinitely many levels), and is not defined for a pre-fractal. This criticism has not impeded the usefulness of d B of real-world geometric objects. Applying the same reasoning to networks, we can try to compute d B for a finite network, and even for a small finite network.

In the literature on fractal dimensions of networks, d B is often (e.g., [Song 07]) informally defined by the scaling $$B_{{D}} (s) \sim s^{-d_{{B}}}$$ . The drawback of this definition is that the scaling relation “∼” is not well defined, e.g., often in the statistical physics literature “∼” indicates a scaling as s → 0 (Sect. 1.​2), which is not meaningful for a network. In the context of network fractal dimensions, the symbol “∼”, is usually interpreted to mean “approximately behaves like”. Definition 7.5 below provides a more computationally useful definition of d B. Recall that Δ is the diameter of $$\mathbb {G}$$ .

Definition 7.5 [Rosenberg 17a] $${\mathbb {G}}$$ has box counting dimension d B if over some range of s and for some constant c we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \log B_{{D}} (s) \approx -{d_{{B}}} \log (s/\varDelta) + c \, . {} \end{array} \end{aligned} $$
(7.1)
If the box counting dimension of $${\mathbb {G}}$$ exists, then $${\mathbb {G}}$$ enjoys the fractal scaling property, or, more simply, $${\mathbb {G}}$$ is fractal. □

Alternatively and equivalently, sometimes (7.1) is written as $$\log B_{{D}} (s) \approx -{d_{{B}}} \log s + c$$ . If $${\mathbb {G}}$$ has box counting dimension d B, then over some range of s we have $$B_{{D}} (s) \approx \alpha s^{-d_{{B}}}$$ for some constant α. Since each box in the covering need not have the same size, it could be argued that this fractal dimension of $${\mathbb {G}}$$ should instead be called the Hausdorff dimension of $${\mathbb {G}}$$ ; a different definition of the Hausdorff dimension of $$\mathbb {G}$$ [Rosenberg 18b] is studied in Chap. 18. Calling $$\mathbb {G}$$ “fractal” if d B exists is the terminology used in [Gallos 07b].

Example 7.2 The dolphins network [Lusseau 03] is a social network describing frequent associations between 62 dolphins in a community living off Doubtful Sound, New Zealand. The network, which has 62 nodes, 159 arcs, and Δ = 8, is illustrated in Fig. 7.8.
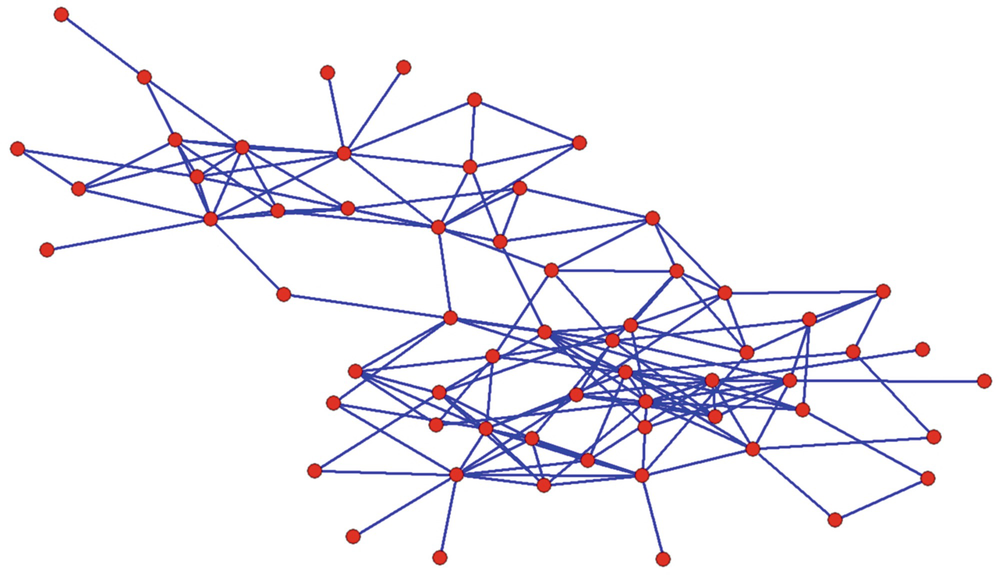
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig8_HTML.png
Figure 7.8

Frequent associations among 62 dolphins

Figure 7.9 provides the node degree histogram; clearly this is not a scale-free network.
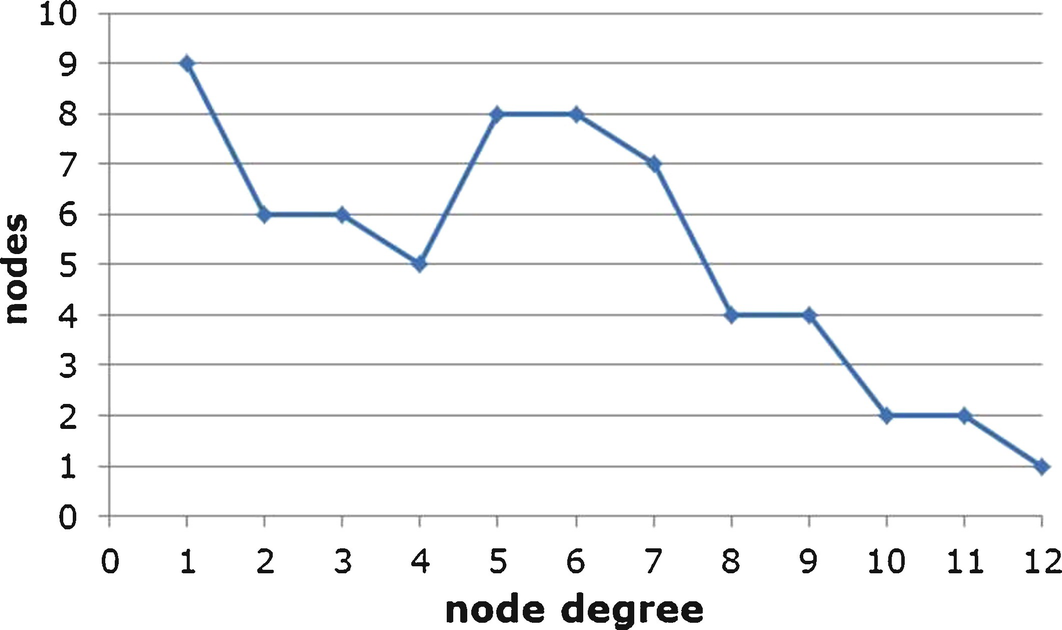
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig9_HTML.png
Figure 7.9

Node degrees for the dolphins network

The results from the Greedy Node Coloring box counting method (to be described in Sect. 8.​1), which uses diameter-based boxes, are shown in Fig. 7.10
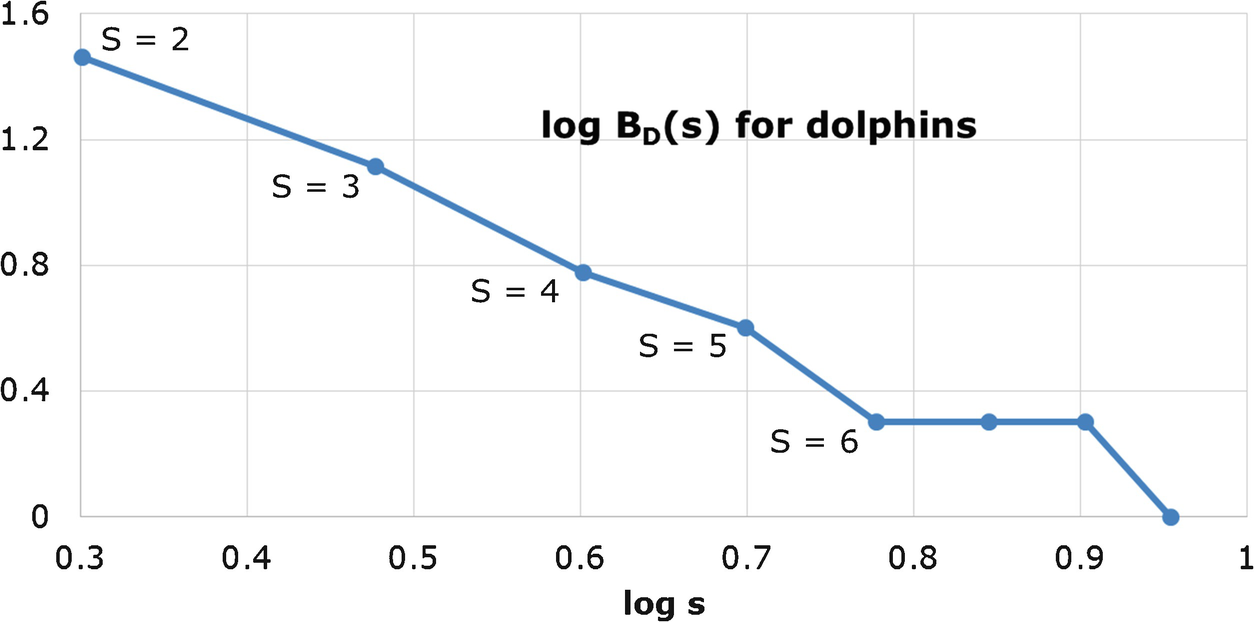
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig10_HTML.png
Figure 7.10

Diameter-based box counting results for the dolphins network

This figure suggests that d B should be estimated over the range 2 ≤ s ≤ 6. Applying regression to the $$\big ( \log s, \log B_{{D}} (s) \big )$$ values over this range of s yields the estimate d B = 2.38. □

Exercise 7.2 ⋆ In Sect. 5.​4 we defined the packing dimension of a geometric object. Can we define a packing dimension of a network? □

7.3 A Closer Look at Network Coverings

In describing their box counting method (which we present in Chap. 8), [Kim 07a] wrote “The particular definition of box size has proved to be inessential for fractal scaling.” On the contrary, it can make a great deal of difference which box definition is being used when computing d B. To see this, and recalling Definition 7.4, suppose we create two new definitions: (i) a wide box $$\widetilde {\mathbb {G}}(s)$$ of size s is a subnetwork of $${\mathbb {G}}$$ of diameter s, and (ii) let $$\widetilde {B}(s)$$ denote the minimal number of wide boxes of size at most s needed to cover $${\mathbb {G}}$$ . With these two new definitions, the difference between a wide box $$\widetilde {\mathbb {G}}(s)$$ of size s and a diameter-based box $${\mathbb {G}}(s)$$ of size s is that the diameter of $$\widetilde {\mathbb {G}}(s)$$ is s and the diameter of $${\mathbb {G}}(s)$$ is s − 1.

Consider a network of N nodes, arranged in a chain, as illustrated by Fig. 7.11 for N = 5.
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig11_HTML.png
Figure 7.11

Chain network

For N ≫ 1 we would expect such a 1-dimensional network to have d B = 1, or at least d B ≈ 1. Suppose we cover the chain of N nodes with wide boxes of size s. Since a wide box of size s contains s + 1 nodes, then $$\widetilde {B}(s) = \lceil N/(s+1) \rceil $$ . Let N = K! for some integer K. Then for 1 ≤ s ≤ K − 1, if we cover $${\mathbb {G}}$$ by wide boxes of size s, each box contains exactly s + 1 nodes, so there are no partially filled boxes in the covering. Figure 7.12
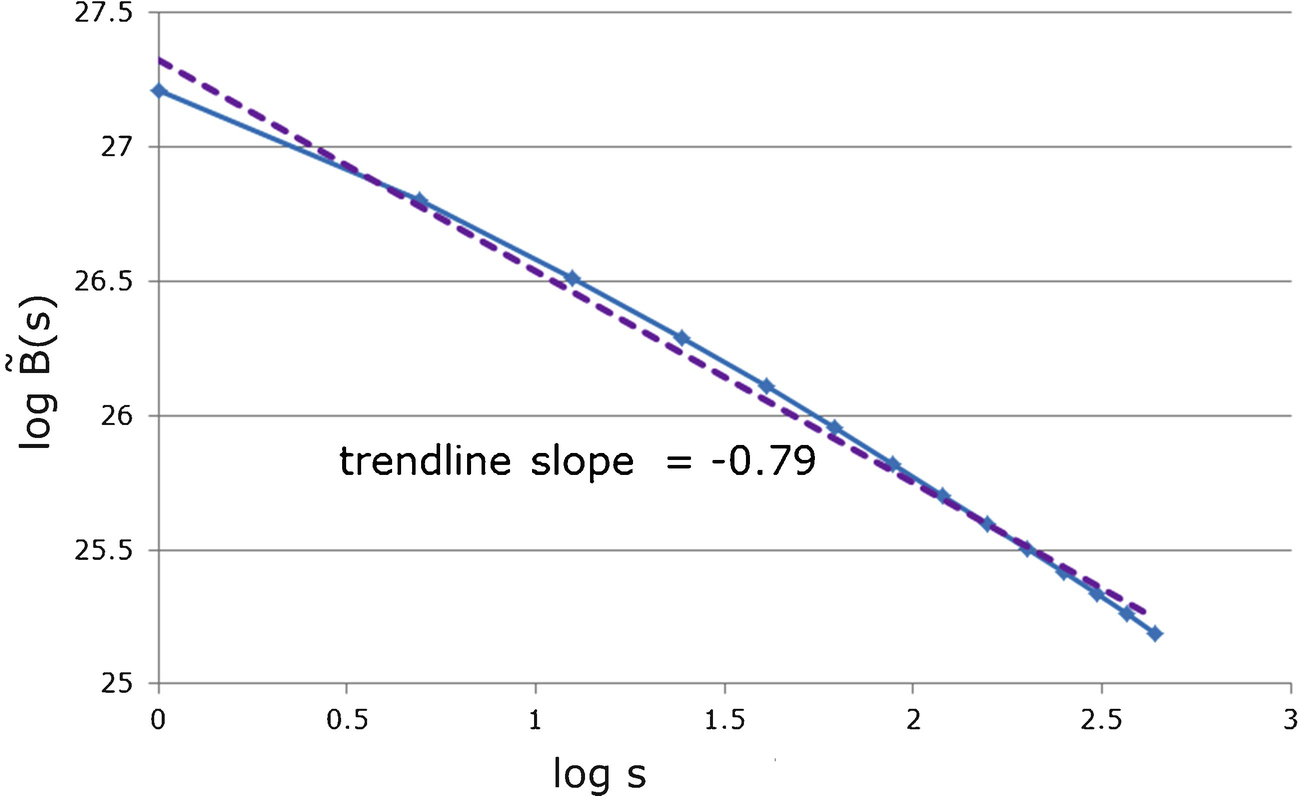
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig12_HTML.png
Figure 7.12

$$\log \widetilde {B}(s)$$ versus $$\log s$$ using wide boxes

plots $$\log \widetilde {B}(s)$$ versus $$\log s$$ for K = 15 and this range of s. The curve is concave, not linear, and a trend line for these points has a slope of − 0.79, rather than a straight line with a slope of − 1.

This example numerically illustrates that, for a chain network of N = K! nodes, when using wide boxes the relation $$\widetilde {B}(s) = \beta s^{-{d_{{B}}}}$$ cannot be satisfied, for some constant β, with d B = 1 for some range of s. To show analytically that for this chain network $$\widetilde {B}(s) = \beta s^{-{d_{{B}}}}$$ cannot be satisfied with d B = 1, suppose $$s \widetilde {B}(s) = \beta $$ for some range of s. For s ≤ K − 1 each wide box in the covering of the chain contains exactly s + 1 nodes, so $$\widetilde {B}(s) = K!/(s+1)$$ and
$$\displaystyle \begin{aligned} s \widetilde{B}(s) = K! \left( \frac{s}{s+1} \right) \end{aligned}$$
which is not independent of s. So $$\widetilde {B}(s) = \beta s^{-{d_{{B}}}}$$ with d B = 1 cannot hold, which provides the counterexample to the claim in [Kim 07a] that the particular definition of box size is inessential. However, if we use diameter-based boxes $${\mathbb {G}}(s)$$ as defined by Definition 7.4, then for a chain network of K! nodes the problem disappears, since then each box of size s contains s nodes, not s + 1. This leads to the following rule, applicable to any $${\mathbb {G}}$$ , not just to a chain network.

Rule 7.1 When using diameter-based boxes of size s, the box counting dimension d B of $${\mathbb {G}}$$ should be calculated using the ordered pairs $$\bigl ( \log s, \log B_{{D}} (s) \bigr )$$ . □

Now consider covering a chain network with radius-based boxes. By Definition 7.4, for a chain network a radius-based box $${\mathbb {G}}(n,r)$$ contains 2r + 1 nodes, assuming we are not close to either end of the chain. This is illustrated is Fig. 7.13, where for r = 2 the box covers 5 nodes.
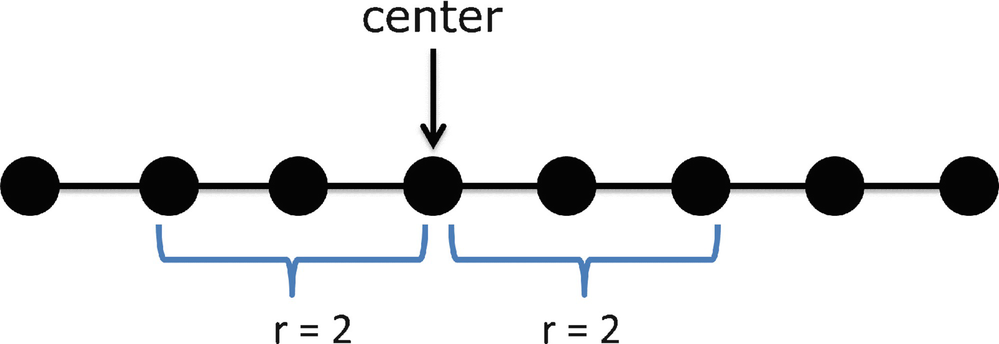
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig13_HTML.png
Figure 7.13

Radius-based box

Assume again that the chain network has N = K! nodes, for some K. Suppose we cover the nodes of this chain with radius-based boxes of radius r, where r ≤ (K − 1)∕2, so 2r + 1 ≤ K. By definition, B R(r) is the number of radius-based boxes of radius at most r needed to cover the chain. Since each box in the covering of the chain contains exactly 2r + 1 nodes, then for r ≤ (K − 1)∕2 we have B R(r) = N∕(2r + 1) = K!∕(2r + 1), which is an integer. Setting d B = 1 in $$B_{{R}}(r) = \beta r^{-{d_{{B}}}}$$ , where β is a constant, yields B R(r) = βr −1, which we rewrite as rB R(r) = β. Thus for r ≤ (K − 1)∕2,
$$\displaystyle \begin{aligned} r B(r) = K! \left( \frac{r}{2r+1} \right) = N \left( \frac{r}{2r+1} \right) \end{aligned}$$
which is not independent of r. The problem disappears when the scaling relation is written as B R(r) = β(2r + 1)−1, since then for r ≤ (K − 1)∕2 we obtain the desired identity
$$\displaystyle \begin{aligned} \beta = (2r+1) B_{{R}}(r) = (2r+1) \left( \frac{K!} {2r+1} \right) = N \, . \end{aligned}$$
This leads to the following rule, applicable to any $${\mathbb {G}}$$ , not just to a chain network.

Rule 7.2 When using radius-based boxes with radius r, the box counting dimension d B of $${\mathbb {G}}$$ should be calculated using the ordered pairs $$\bigl ( \log (2r+1), \log B_{{R}}(r) \bigr )$$ . □

Exercise 7.3 Since B D(s) = 1 when s > Δ, does it follow that B R(r) = 1 when 2r + 1 > Δ? □

Exercise 7.4 For a positive integer K, let G(K) denote a square K × K rectilinear grid. The diameter of G(K) is 2(K − 1). If K = K 1K 2, then we can cover G(K) using $$K_1^2$$ copies of G(K 2), or using $$K_2^2$$ copies of G(K 1). This is illustrated in Fig. 7.14 for K = 6, K 1 = 2, and K 2 = 3.
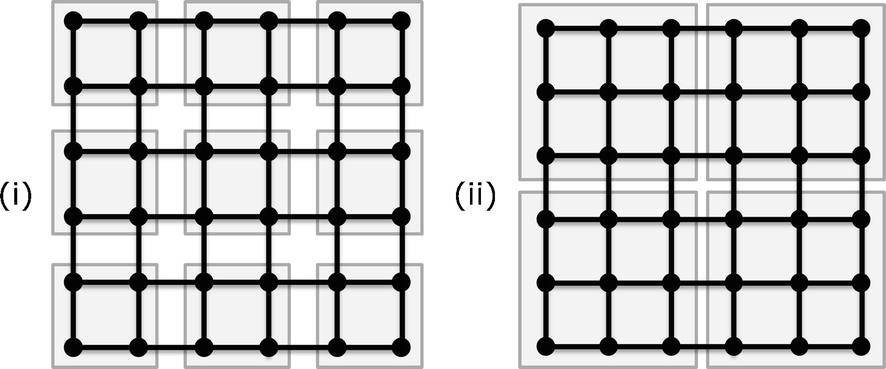
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig14_HTML.png
Figure 7.14

Covering a 6 × 6 grid

We can cover G(6) using 9 copies of G(2), or using 4 copies of G(3). Since diam(G(3)) = 4 and diam(G(2)) = 2, then the 4 copies of G(3) constitute a diameter-based covering of size 5, and the 9 copies of G(2) constitute a diameter-based covering of size 3. Estimating d B from these two coverings,
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{{B}} = \frac{ \log B_{{D}} (3) - B_{{D}} (5)}{\log 5 - \log 3} = \frac{\log (9/4) }{\log (5/3)} \, . {} \end{array} \end{aligned} $$
(7.2)
There is an error in the above analysis. What is the error? Why did we not obtain d B = 2? □

We will return to rectilinear networks in Sect. 11.​4, where we study the correlation dimension of a rectilinear grid.

Exercise 7.5 Consider an infinite rectilinear grid in $${\mathbb {R}}^2$$ . Show that, when s is odd, a box with the maximal number of nodes has a center node, and the maximal number of nodes in a box of size s is (s 2 + 1)∕2. □

Exercise 7.6 Let $$d_{{B}}({\mathbb {G}})$$ be the box counting dimension of network $${\mathbb {G}}$$ . Suppose $${\mathbb {G}}_1$$ is a subnetwork of $${\mathbb {G}}_2$$ . Does the strict inequality $$d_{{B}}({\mathbb {G}}_1) &lt; d_{{B}}({\mathbb {G}}_2)$$ hold? □

Exercise 7.7 As discussed in Sect. 5.​5, a geometric fractal is sometimes defined as an object whose dimension is not an integer. Is this a useful definition of a “fractal network”? □

Exercise 7.8 Consider an infinite rectilinear lattice in $${\mathbb {R}}^2$$ . What does a diameter-based box of size s look like when s is even? □

Exercise 7.9 Let $${\mathbb {G}}$$ be a 6 × 6 square rectilinear lattice in $${\mathbb {R}}^2$$ . Compute B D(s) for s = 2, 3, 4, 5. Compute B R(r) for r = 1, 2, 3. □

7.4 The Origin of Fractal Networks

Recall from Definition 7.5 that $$\mathbb {G}$$ is fractal if for some d B and some c we have $$\log B_{{D}} (s) \approx -{d_{{B}}} \log (s/\varDelta ) + c$$ over some range of s. The main feature apparently displayed by fractal networks is a repulsion between hubs, where a hub is a node with a significantly higher node degree than a non-hub node. That is, the highly connected nodes tend to be not directly connected [Song 06, Zhang 16]. This tendency can be quantified using the joint node degree distribution p(δ 1, δ 2) that a node with degree δ 1 and a node with degree δ 2 are neighbors. In contrast, for a non-fractal network $${\mathbb {G}}$$ , hubs are mostly connected to other hubs, which implies that $${\mathbb {G}}$$ enjoys the small-world property [Gallos 07b]. (Recall from Sect. 2.​2 that $${\mathbb {G}}$$ is a small-world network if $$\mathit {diam}(\mathbb {G})$$ grows as $$\log N$$ .) Also, the concepts of modularity and fractality for a network are closely related. Interconnections within a module (e.g., a biological subsystem) are more prevalent than interconnections between modules. Similarly, in a fractal network, interconnections between a hub and non-hub nodes are more prevalent than interconnections between hubs. Non-fractal networks are typically characterized by a sharp decay of B D(s) with s, which is better described by an exponential law B D(s) ∼ e −β s, where β > 0, rather than by a power law B D(s) ∼ s −β, with a similar statement holding if radius-based boxes are used [Gallos 07b]. These two cases are illustrated in Fig. 7.15, taken from [Gallos 07b],
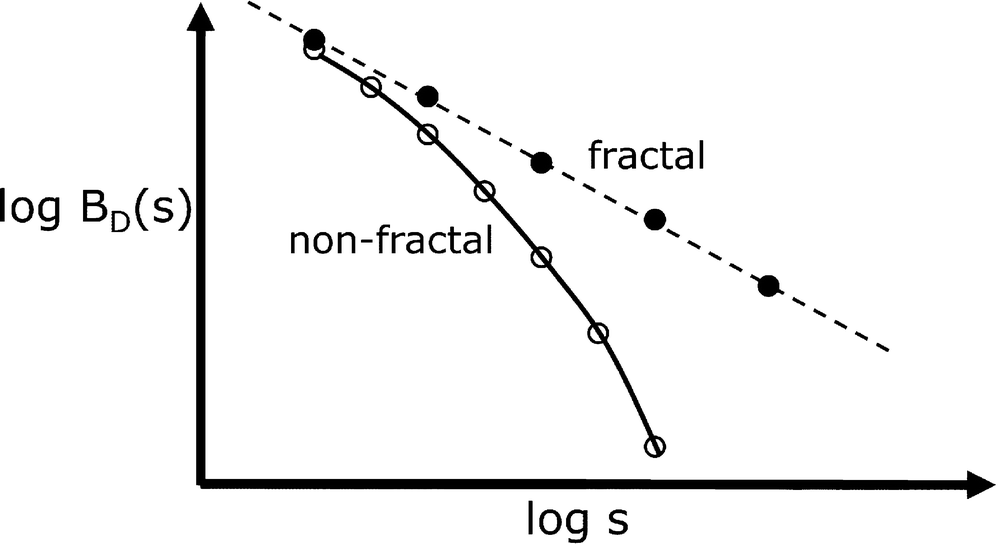
../images/487758_1_En_7_Chapter/487758_1_En_7_Fig15_HTML.png
Figure 7.15

Fractal versus non-fractal scaling

where the solid circles are measurements from a fractal network, and the hollow circles are from a non-fractal network.

Various researchers have proposed models to explain why networks exhibit fractal scaling. One proposed cause [Song 06] is the disassortative correlation between the degrees of neighboring nodes. A disassortative network is a network in which nodes of low degree are more likely to connect with nodes of high degree, and so there is a strong disassortativity (i.e., repulsion) between hubs. This can be modelled by Coulomb’s Law [Zhang 16].

A different explanation is based on the skeleton of $${\mathbb {G}}$$ (Sect. 2.​5). Recall that the skeleton $$skel({\mathbb {G}})$$ of $${\mathbb {G}}$$ is often defined to be the betweenness centrality or load-based spanning tree of $${\mathbb {G}}$$ . The skeleton of a scale-free network has been found [Kim 07b] to have the same topological properties as a random branching tree. Associated with a random branching tree is the parameter μ(r), the average number of children of a node whose distance from the root node is r. As r →∞, we have μ(r) → μ for some μ. The critical case for this branching process corresponds to μ = 1, and for this value the random branching tree is known to be fractal. Specifically, suppose $${\mathbb {G}}$$ is a scale-free random branching tree for which the probability p k that each branching event produces k offspring scales as p k ∼ k −γ and $$\langle k \rangle \equiv \sum _{k=0}^{\infty } k \, p_{{k}} =1$$ . Then the box counting dimension of $${\mathbb {G}}$$ is given by
$$\displaystyle \begin{aligned} {d_{{B}}} = \left\{ \begin{array}{c l} (\gamma-1)/(\gamma - 2) &amp; \mbox{for }2 &lt; \gamma &lt; 3 \\ 2 &amp; \mbox{for } \gamma &gt; 3 \, . \end{array} \right . \end{aligned}$$
Similar results have been found for supercritical branching trees, where supercritical means 〈k〉 > 1 [Kim 07b]. The significance of these results is that the original scale-free network can be modelled by first starting with a skeleton network with the properties of a critical or supercritical random branching tree, and then adding shortcuts, but not so many that fractality is destroyed. Since the number of boxes needed to cover $${\mathbb {G}}$$ and $$\mathit {skel}({\mathbb {G}})$$ have been found to be nearly equal [Kim 07b], then the fractal scaling enjoyed by $$\mathit {skel}({\mathbb {G}})$$ is also enjoyed by $${\mathbb {G}}$$ . For example, for the World Wide Web (WWW), the number of boxes needed to cover the WWW and its skeleton are nearly equal, and the same fractal dimension of 4.10 is obtained [Kim 07b]. The mean branching value μ(r) hits a plateau value μ ≈ 3.5 at r ≈ 20. In contrast, for non-fractal networks, the mean branching number of the skeleton decays to zero without forming a plateau.