© Springer Nature Switzerland AG 2020
E. RosenbergFractal Dimensions of Networkshttps://doi.org/10.1007/978-3-030-43169-3_18

18. Generalized Hausdorff Dimensions of Networks

Eric Rosenberg1 
(1)
AT&T Labs, Middletown, NJ, USA
 

Scientific research involves going beyond the well-trodden and well-tested ideas and theories that form the core of scientific knowledge. During the time scientists are working things out, some results will be right, and others will be wrong. Over time, the right results will emerge.

Lisa Randall (1962- ), American, theoretical physicist, professor at Harvard University, author of “Higgs Discovery: The Power of Empty Space” (2012)

The progression of topics in this book has been to first present a fractal dimension for a geometric object $$\varOmega \subset {\mathbb {R}}^E$$ , and then to show how the same dimension can be defined for a network $$\mathbb {G}$$ . Using this pattern, we defined, for example, the box counting dimension d B of Ω and then of $$\mathbb {G}$$ , the correlation dimension d C of Ω and then of $$\mathbb {G}$$ , and the information dimension d I of Ω and then of $$\mathbb {G}$$ . In this chapter we continue this pattern for two additional dimensions. First, the Hausdorff dimension d H of Ω was defined in Sect. 5.​1, and in this chapter we define d H of $$\mathbb {G}$$ . Second, the family $$\{D_q^H,{q \in {\mathbb {R}}} \}$$ of generalized dimensions of Ω was defined in Sect. 16.​9, and and in this chapter we define the generalized dimensions $$\{D_q^H,{q \in {\mathbb {R}}} \}$$ of $$\mathbb {G}$$ . The definition of d H of $$\mathbb {G}$$ , and the definition of $$\{D_q^H,{q \in {\mathbb {R}}} \}$$ of $$\mathbb {G}$$ , were introduced in [Rosenberg 18b].

18.1 Defining the Hausdorff Dimension of a Network

Computing the box counting dimension d B of a network $$\mathbb {G}$$ requires covering $$\mathbb {G}$$ by a minimal set $${\mathcal {B}}(s)$$ of boxes of diameter at most s, for a range of values of s. Then d B is typically computed from the slope of the $$\log B(s)$$ versus $$\log s$$ curve. Although, for a given s, the boxes in $${\mathcal {B}}(s)$$ do not in general have the same diameter or mass, this information is ignored in the computation of d B. However, the diameters of the boxes in $${\mathcal {B}}(s)$$ can be used to define the Hausdorff dimension d H of $$\mathbb {G}$$ . The reason for studying d H of $$\mathbb {G}$$ is that, for a geometric object, the Hausdorff dimension d H generalizes the box counting dimension d B, and d H is better behaved than d B. Thus it is of great interest to define and study d H of $$\mathbb {G}$$ .

To develop a definition of d H of $$\mathbb {G}$$ , first consider computing d B of a geometric object Ω. Recall that B(s) is the minimal number of boxes of linear size at most s required to cover Ω and that, as discussed in Sect. 4.​2, we can assume that, for each given s, all boxes in the minimal covering of Ω have the same diameter. From definitions (5.​1) and (5.​2), if each box has diameter s, then
$$\displaystyle \begin{aligned} v({\varOmega}, s , d) = {B({s}) {s}^{\, d}} \end{aligned}$$
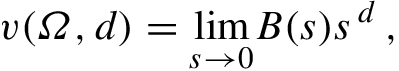
../images/487758_1_En_18_Chapter/487758_1_En_18_Equb_HTML.png
assuming the limit exists. The box counting dimension d B of Ω was characterized in ( [Schroeder 91], p. 201) as the unique value of d for which
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{s \rightarrow 0} B(s) s^{\, d} = c {} \end{array} \end{aligned} $$
(18.1)
for some c such that 0 < c < ∞. More precisely, the existence of d B does not imply (18.1) but rather, as noted in [Theiler 88] and discussed in Sect. 4.​2, only implies B(s)s d = Φ(s) for some function Φ(⋅) satisfying $$\lim _{\, s \rightarrow 0} { \log \varPhi (s) }/{ \log s} = 0$$ . We thus treat (18.1) as an approximation, rather than as an equality.
Now consider a network $$\mathbb {G}$$ . For integer s, where 2 ≤ s ≤ Δ, consider a minimal s-covering $${\mathcal {B}}(s)$$ of $$\mathbb {G}$$ . By Definition 7.5, the box counting dimension d B of $$\mathbb {G}$$ satisfies, over some range of s and for some constant c,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \log B(s) \approx -{d_{{B}}} \log (s/\varDelta) + c {} \, . \end{array} \end{aligned} $$
(18.2)
For reasons that will shortly become clear, it is useful to present a slightly different definition of d B.
Definition 18.1 $${\mathbb {G}}$$ has box counting dimension d B if, over some range of s and for some constant c,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \log B(s) \approx -{d_{{B}}} \log \big(s/(\varDelta+1) \big) + c \, . \; \; {} \end{array} \end{aligned} $$
(18.3)
□

Exercise 18.1 When using linear regression to estimate d B from a range of $$\big ( \log s, \log B(s) \big )$$ values, do both of the approximations (18.2) and (18.3), when treated as an equality, yield the same value of d B? □

Corresponding to (18.1) for Ω, and using Definition 18.1, if $$\mathbb {G}$$ has box counting dimension d B then for some constant c such that 0 < c < ∞ we have, over some range of s,
$$\displaystyle \begin{aligned} \begin{array}{rcl} B(s) [s/(\varDelta+1)]^{d_{{B}}} \approx c \, . {} \end{array} \end{aligned} $$
(18.4)
Hence one way to determine d B is to compute the value of d which minimizes, over d > 0, the standard deviation, over some range of s, of the values B(s)[s∕(Δ + 1)]d. We will later illustrate this approach for the dolphins network. We are not advocating this approach to computing the box counting dimension d B, but mention it to show the similarity between this approach to computing d B of $$\mathbb {G}$$ and the following approach to defining the Hausdorff dimension d H of $$\mathbb {G}$$ .
For a given box size s, where 2 ≤ s ≤ Δ, for box $$B_{{j}} \in {\mathcal {B}}(s)$$ let Δ j be the diameter of box B j, and define
$$\displaystyle \begin{aligned} \begin{array}{rcl} \delta_{{j}} \equiv (\varDelta_{{j}}+1) / (\varDelta + 1) \, , {} \end{array} \end{aligned} $$
(18.5)
so 0 < δ j < 1. If B j contains a single node, then δ j = 1∕(Δ + 1); if B j has diameter Δ − 1, then δ j = Δ∕(Δ + 1). Corresponding to definition (5.​1) of v(Ω, d, s) for Ω, define
$$\displaystyle \begin{aligned} \begin{array}{rcl} m({\mathbb{G}}, s, d) \equiv \sum_{B_{{j}} \in {\mathcal{B}}(s)} \delta_{{j}}^d \, . {} \end{array} \end{aligned} $$
(18.6)
Note that $$m({\mathbb {G}}, s, d)$$ is independent of the mass of (i.e., number of nodes in) each box. We can regard $$m({\mathbb {G}}, s, d)$$ as the “d-dimensional Hausdorff measure of $$\mathbb {G}$$ for box size s”. Just as d B is that value of d for which (18.4) holds for some c and some range of s, we can view d H as the value of d for which
$$\displaystyle \begin{aligned} \begin{array}{rcl} m({\mathbb{G}}, s, d) \approx c {} \end{array} \end{aligned} $$
(18.7)
holds for some c and some range of s. Expressed differently, d H is the value of d for which the Hausdorff measures $$m({\mathbb {G}}, s, d)$$ are nearly equal over some range of s. Note that, since $$m({\mathbb {G}}, s, d)$$ is not an explicit function of s, relation (18.7) does not yield a “traditional” fractal scaling law, similar to (1.​1), that relates s to some appropriately defined “bulk”.

We can now justify why we replaced the approximation (18.2) with (18.3) in the definition of d B. We want each term in the sum (18.6) to depend on d, so we want 0 < δ j < 1 for each j. Since a box in $${\mathcal {B}}(s)$$ containing only a single node has diameter 0, adding 1 to Δ j in (18.5) ensures that δ j > 0 for each j. On the other hand, if a box in $${\mathcal {B}}(s)$$ has diameter s − 1, then adding 1 to Δ in (18.5) ensures that δ j < 1 for each j.

Before we formalize the definition of d H, we must deal with non-uniqueness of $$m({\mathbb {G}}, s, d)$$ . For each s there are, in general, multiple minimal coverings $${\mathcal {B}}(s)$$ of $$\mathbb {G}$$ , all yielding the same minimal value B(s). As discussed in Sect. 17.​1, a definition of D q of $$\mathbb {G}$$ based on the partition function $$Z_q(s) \equiv \sum _{B_{{j}} \in {\mathcal {B}}(s)} [p_{{j}}(s)]^q$$ can be ambiguous, since different minimal s-coverings can yield different values of Z q(s), and hence different values of D q. The ambiguity was resolved by requiring each minimal s-covering used to compute Z q(s) to be lexicographically minimal. Similarly, as shown by Example 18.1 below, definition (18.6) does not in general unambiguously define $$m({\mathbb {G}}, s, d)$$ , since different minimal s-coverings can yield different values of $$m({\mathbb {G}}, s, d)$$ .

Example 18.1 Consider the 7 node chain network of Fig. 18.1, for which Δ = 6. From definitions (18.5) and (18.6), for the minimal 3-covering (i) we have
$$\displaystyle \begin{aligned} \widetilde{m}({\mathbb{G}}, 3, d) = 2 \left( \frac{2+1}{6+1} \right)^{\, d} + \left( \frac{0+1}{6+1} \right)^{\, d} = \frac{ 3^{\, d} + 3^{\, d} + 1^{\, d} }{7^{\, d}} \end{aligned}$$
while for the minimal 3-covering (ii) we have
$$\displaystyle \begin{aligned} \widehat{m}({\mathbb{G}}, 3, d) = \left( \frac{2+1}{6+1} \right)^{\, d} + 2 \left( \frac{1+1}{6+1} \right)^{\, d} = \frac{ 3^{\, d} + 2^{\, d} + 2^{\, d} }{7^{\, d}} \, . \end{aligned}$$
We have $$\widetilde {m}({\mathbb {G}}, 3, d) &gt; \widehat {m}({\mathbb {G}}, 3, d)$$ for d > 1, with equality when d = 1. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig1_HTML.png
Figure 18.1

Two minimal 3-coverings of a 7 node chain

The ambiguity in the definition of $$m({\mathbb {G}}, s, d)$$ can be eliminated by adapting the lexicographic approach of [Rosenberg 17b], described in Sect. 17.​1. Consider a minimal s-covering $${\mathcal {B}}(s)$$ and define J ≡ B(s). Recalling that Δ j is the diameter of box $$B_{{j}} \in {\mathcal {B}}(s)$$ , we associate with $${\mathcal {B}}(s)$$ the point
$$\displaystyle \begin{aligned} {\varDelta}(J) \equiv \big( \varDelta_{{1}}, \varDelta_{{2}}, \ldots, \varDelta_{{J}} \big) \in {\mathbb{R}}^J \, , \end{aligned}$$
where Δ 1 ≥ Δ 2 ≥⋯ ≥ Δ J. We call Δ(J) the “diameter vector” associated with $${\mathcal {B}}(s)$$ . An unambiguous choice of a minimal s-covering is to pick the minimal s-covering for which the associated diameter vector is lexicographically smallest. That is, suppose that, for a given s, there are two distinct minimal s-coverings $$\widetilde {\mathcal {B}}(s)$$ and $$\widehat {\mathcal {B}}(s)$$ . Let $$\widetilde {\varDelta }(J)$$ be the diameter vector associated with $$\widetilde {\mathcal {B}}(s)$$ , and let $$\widehat {\varDelta }(J)$$ be the diameter vector associated with $$\widehat {\mathcal {B}}(s)$$ . Then we choose $$\widetilde {\mathcal {B}}(s)$$ if $$\widehat {\varDelta }(J) \succeq \widetilde {\varDelta }(J)$$ , where “≽” denotes lexicographic ordering. Applying this to the two minimal 3-coverings of Fig. 18.1, the associated diameter vectors are (2, 2, 0) for (i) and (2, 1, 1) for (ii). Since (2, 2, 0) ≽ (2, 1, 1) we choose the covering (ii).
Having unambiguously defined $$m({\mathbb {G}}, s, d)$$ , we can now formalize the definition of d H of $$\mathbb {G}$$ as that value of d for which $$m({\mathbb {G}}, s, d)$$ is roughly constant over a range of s. Let $$\mathcal {S}$$ be a given set of integer values of s such that 2 ≤ s ≤ Δ for $$s \in {\mathcal {S}}$$ . For example, for integers L, U such that 2 ≤ L < U ≤ Δ we might set $${\mathcal {S}} = \{s \, \vert \, s \mbox{ is integer and } L \leq s \leq U \}$$ . For a given d > 0, define $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ to be the standard deviation (in the usual statistical sense) of the values $$m({\mathbb {G}}, s, d)$$ for $$s \in {\mathcal {S}}$$ as follows. Define
$$\displaystyle \begin{aligned} \begin{array}{rcl} m_{\textit{avg}}({\mathbb{G}}, {\mathcal{S}}, d) &amp;\displaystyle \equiv &amp;\displaystyle \frac{1}{\vert {\mathcal{S}} \vert} \sum_{s \in {\mathcal{S}}} m({\mathbb{G}}, s, d) {} \, . \end{array} \end{aligned} $$
(18.8)
We can regard $$m_{\textit {avg}}({\mathbb {G}}, {\mathcal {S}}, d)$$ as the “average d-dimensional Hausdorff measure of $$\mathbb {G}$$ for box sizes in $$\mathcal {S}$$ ”. Next we compute the standard deviation of the Hausdorff measures:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sigma({\mathbb{G}},{\mathcal{S}},d) &amp;\displaystyle \equiv &amp;\displaystyle \sqrt { \frac{1}{\vert {\mathcal{S}} \vert} \sum_{s \in {\mathcal{S}}} \big[ \, m({\mathbb{G}}, s, d) - m_{\textit{avg}}({\mathbb{G}}, {\mathcal{S}}, d) \, \big]^2 } \; . {} \end{array} \end{aligned} $$
(18.9)
We associate with $$\mathbb {G}$$ the Hausdorff dimension d H, defined as follows.

Definition 18.2 [Rosenberg 18b] (Part A.) If $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ has at least one local minimum over {d | d > 0}, then d H is the value of d satisfying (i) $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ has a local minimum at d H, and (ii) if $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ has another local minimum at $$\widetilde {d}$$ , then $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d_{{H}}) &lt; \sigma ({\mathbb {G}}, {\mathcal {S}}, \widetilde {d})$$ . (Part B.) If $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ does not have a local minimum over {d | d > 0}, then d H ≡∞. □

For all of the networks studied in [Rosenberg 18b], d H is finite. An interesting open question is whether there exists a network with a finite d B and infinite d H.

Definition 18.3 [Rosenberg 18b] If d H < ∞, then the Hausdorff measure of $$\mathbb {G}$$ is $$m_{\textit {avg}}({\mathbb {G}}, {\mathcal {S}}, d_{{H}})$$ . If d H = ∞, then the Hausdorff measure of $$\mathbb {G}$$ is 0. □

These definitions are with respect to a given set $$\mathcal {S}$$ . For a given $$\mathbb {G}$$ , choosing different $$\mathcal {S}$$ will in general yield different values of d H; this is not surprising, and a similar dependence was studied in Sect. 17.​2. The reason, in Part A of Definition 18.2, for requiring d H to yield a local minimum of $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ is that by definitions (18.5) and (18.6) for each s we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{d \rightarrow \infty} m({\mathbb{G}}, s, d) = 0 \, . {} \end{array} \end{aligned} $$
(18.10)
Suppose d H yields a local minimum of $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ . From (18.10), we know that $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ is not a convex function of d. Thus the possibility exists that $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ might have multiple local minima. To deal with that possibility, we require that $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d_{{H}})$$ be smaller than the standard deviation at any other local minimum. As for Part B, it may be possible that $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ has no local minimum. In this case, by virtue of (18.10) we define d H = ∞.

By Definition 18.2, the computation of d H of $$\mathbb {G}$$ requires a line search (i.e., a 1-dimensional minimization) to minimize $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ over d > 0. Since $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ might have multiple local minima, we cannot use line search methods such as bisection or golden search [Wilde 64] designed for minimizing a unimodal function. Instead, in [Rosenberg 18b] d H was computed by evaluating $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ from d = 0.1 to d = 6, in increments of 10−4, and testing for a local minimum (this computation took at most a few seconds on a laptop). For all of the networks studied, $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ had exactly one local minimum. While these computational results do not preclude the possibility of multiple local minima for some other network, a convenient working definition is that d H is the value of d yielding a local minimum of the standard deviation $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ .

In scientific applications of fractal analysis, it is well-established that the ability to calculate a fractal dimension of a geometric object does not convey information about the structure of the object. For example, box counting was used in [Karperien 13] to calculate d B of microglia (a type of cell occurring in the central nervous system of invertebrates and vertebrates). However, we were warned in [Karperien 13] that the fractal dimension of an object “does not tell us anything about what the underlying structure looks like, how it was constructed, or how it functions”. Moreover, the ability to calculate a fractal dimension of an object “does not mean the phenomenon from which it was gleaned is fractal; neither does a phenomenon have to be fractal to be investigated with box counting fractal analysis”.

Similarly, the ability to calculate d H of $${\mathbb {G}}$$ does not provide any information about the structure of $$\mathbb {G}$$ . Indeed, for a network $$\mathbb {G}$$ the definitions of fractality and self-similarity are quite different [Gallos 07b]; as discussed in Sect. 7.​2, the network $$\mathbb {G}$$ is fractal if $$B(s) \sim s^{-d_{{B}}}$$ for a finite exponent d B, while $$\mathbb {G}$$ is self-similar if the node degree distribution of $$\mathbb {G}$$ remains invariant over several generations of renormalization. (Renormalizing $$\mathbb {G}$$ , as discussed in Chap. 21, means computing an s-covering of $$\mathbb {G}$$ , merging all nodes in each box in the s-covering into a supernode, and connecting two supernodes if the corresponding boxes are connected by one or more arcs in the original network.) Moreover, “Surprisingly, this self-similarity under different length scales seems to be a more general feature that also applies in non-fractal networks such as the Internet. Although the traditional fractal theory does not distinguish between fractality and self-similarity, in networks these two properties can be considered to be distinct” [Gallos 07b]. With this caveat on the interpretation of a fractal dimension of $$\mathbb {G}$$ , in the next section we compute d H of several networks.

18.2 Computing the Hausdorff Dimension of a Network

The following examples from [Rosenberg 18b] illustrate the computation of d H of some networks, ranging from a small constructed example of 5 nodes to a real-world protein network of 1458 nodes. Since fractality and self-similarity of $$\mathbb {G}$$ are distinct characteristics, d H can be meaningfully computed even for small networks without any regular or self-similar structure.

Example 18.2 Consider the chair network of Fig. 18.2 (left), for which Δ = 3. We have B(3) = 2 and B(2) = 3. Using the two box sizes s = 2, 3 we have $$d_{{B}} = \big (\log B(2) - \log B(3) \big )/(\log 3 - \log 2) = 1$$ . For s = 2 the three boxes in $${\mathcal {B}}(2)$$ have diameter 1, and 1, and 0, so from definitions (18.5) and (18.6) we have $$m({\mathbb {G}}, 2, d) = (2/4)^d + (2/4)^d + (1/4)^d$$ . For s = 3 the two boxes in $${\mathcal {B}}(3)$$ have diameter 2 and 1, so $$m({\mathbb {G}}, 3, d) = (3/4)^d + (2/4)^d$$ . Figure 18.2 (right) plots $$m({\mathbb {G}}, 2, d)$$ and $$m({\mathbb {G}}, 3, d)$$ versus d. Set $${\mathcal {S}} = \{ 2, 3 \}$$ . Since for d = 1 we have $$m({\mathbb {G}}, 2, d) = m({\mathbb {G}}, 3, d) = 5/4$$ , then d H = 1 and $$\sigma ({\mathbb {G}}, {\mathcal {S}},d_{{H}}) = 0$$ . Moreover, d H = 1 is the unique point minimizing $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ . For this network we have d H = d B. By Definition 18.3, the Hausdorff measure $$m({\mathbb {G}}, {\mathcal {S}}, d_{{H}})$$ of $$\mathbb {G}$$ is 5∕4. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig2_HTML.png
Figure 18.2

chair network (left) and d H calculation (right)

Example 18.3 Consider the two networks in Fig. 18.3. The top network $${\mathbb {G}}_1$$ has Δ = 4; the bottom network $${\mathbb {G}}_2$$ has Δ = 5. Figure 18.4 shows box counting results, for s = 2 and s = 3, for the two networks. For s = 2 we have, for both networks, B(2) = 4, B(3) = 2, and B(4) = 2. Since B(3) = B(4), to compute d B we ignore the s = 4 results and choose $${\mathcal {S}} = \{ 2, 3 \}$$ . This yields, for both networks, $$d_{{B}} = \big ( \log B(2) - \log B(3) \big )/(\log 3 - \log 2) \approx 1.71$$ .
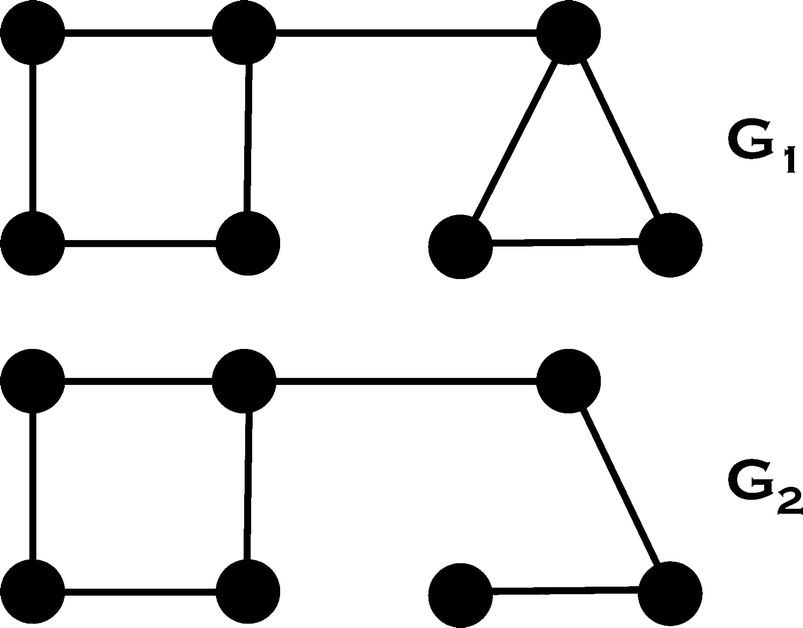
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig3_HTML.png
Figure 18.3

Two 7 node networks with the same d B but different d H

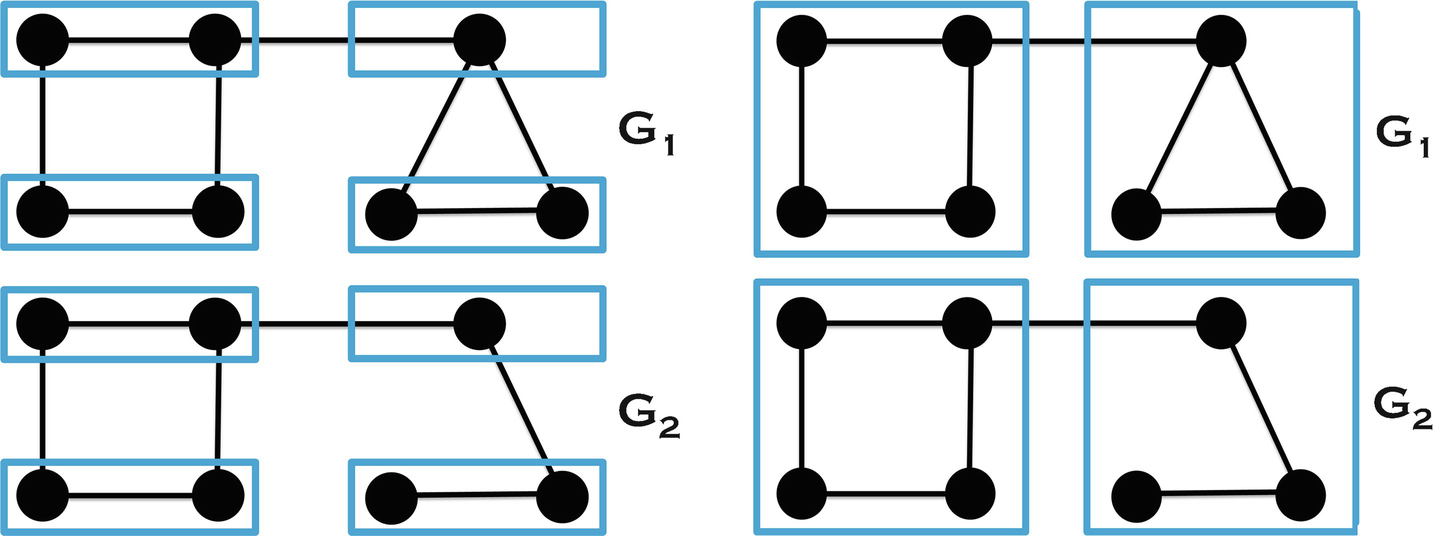
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig4_HTML.png
Figure 18.4

Box counting results for s = 2 (left) and s = 3 (right)

For $${\mathbb {G}}_1$$ , from (18.5) and (18.6) we have $$m({\mathbb {G}}_1, 2, d) = (3)(2/5)^d + (1/5)^d$$ and $$m({\mathbb {G}}_1, 3, d) = (3/5)^d + (2/5)^d$$ . For $${\mathbb {G}}_1$$ , the plots of $$m({\mathbb {G}}_1, 2, d)$$ versus d and $$m({\mathbb {G}}_1, 3, d)$$ versus d intersect at d H = 2, and $$m({\mathbb {G}}_1, 2, d_{{H}}) = m({\mathbb {G}}_1, 3, d_{{H}}) = 13/25$$ . Hence $$\sigma ({\mathbb {G}}_1, {\mathcal {S}},d_{{H}}) = 0$$ , and d H = 2 is the unique point minimizing $$\sigma ({\mathbb {G}}_1, {\mathcal {S}}, d)$$ . Thus for $${\mathbb {G}}_1$$ and $${\mathcal {S}} = \{ 2, 3 \}$$ we have d H = 2 > 1.71 ≈ d B, so the inequality d H ≤ d B, known to hold for a geometric object [Falconer 03], can fail to hold for a network. By Definition 18.3, the Hausdorff measure $$m({\mathbb {G}}_1, {\mathcal {S}}, d_{{H}})$$ of $${\mathbb {G}}_1$$ is 13∕25.

Turning now to $${\mathbb {G}}_2$$ , from (18.5) and (18.6) we have $$m({\mathbb {G}}_2, 2, d) = (3)(2/6)^d + (1/6)^d$$ and $$m({\mathbb {G}}_2, 3, d) = (2)(3/6)^d$$ . The plots of $$m({\mathbb {G}}_2, 2, d)$$ versus d and and $$m({\mathbb {G}}_2, 3, d)$$ versus d intersect at d H ≈ 1.31, and $$m({\mathbb {G}}_2, 2, d_{{H}}) = m({\mathbb {G}}_2, 3, d_{{H}}) \approx 0.81$$ . Thus for $${\mathbb {G}}_2$$ and $${\mathcal {S}} = \{2, 3\}$$ we have $$\sigma ({\mathbb {G}}_2, {\mathcal {S}}, d_{{H}}) = 0$$ , and $$m({\mathbb {G}}_2, {\mathcal {S}}, d_{{H}}) \approx 0.81$$ . The two networks $${\mathbb {G}}_1$$ and $${\mathbb {G}}_2$$ in Example 18.3 have the same number of nodes and the same d B, yet have different d H. □

Example 18.3 suggests that d H can be better than d B for comparing two networks, or for studying the evolution of a network over time. The reason d H provides a “finer” measure than d B is that d B considers only the variation in the number B(s) of boxes needed to cover the network, while d H recognizes that the different boxes in the covering $${\mathcal {B}}(s)$$ will in general have different diameters. The next two examples, from [Rosenberg 18b], show that the Hausdorff dimension of $$\mathbb {G}$$ produces expected “classical” results: for a large 1-dimensional chain we have d H = 1, and for a large 2-dimensional rectilinear grid we have d H = 2.

Example 18.4 Let $$\mathbb {G}$$ be a chain of N nodes, so Δ = N − 1. For s ≪ N, an s-covering of $$\mathbb {G}$$ consists of ⌊N∕s⌋ boxes, each containing s nodes and having diameter s − 1, and one box containing N − s⌊N∕s⌋ nodes and having diameter N − s⌊N∕s⌋− 1. By definitions (18.5) and (18.6), for s ≪ N we have
$$\displaystyle \begin{aligned} m({\mathbb{G}}, s, d) = \left \lfloor \frac{N}{s} \right \rfloor \left( \frac{s}{N} \right)^d + \left( \frac{N - s \lfloor N/s \rfloor}{N} \right)^d \approx \left( \frac{s}{N} \right)^{d-1} + \left( \frac{N - s \lfloor N/s \rfloor}{N} \right)^d \, . \end{aligned}$$
Setting d = 1 yields $$m({\mathbb {G}}, s, 1) \approx 1$$ . Now let $$\mathcal {S}$$ be a (finite) set of box sizes, such that s ≪ N for $$s \in {\mathcal {S}}$$ . By definitions (18.8) and (18.9), setting d = 1 yields $$\sigma ({\mathbb {G}}, {\mathcal {S}}, 1) \approx 0$$ , so d H = 1 for a long chain of N nodes. □
Example 18.5 Consider first an infinite two-dimensional rectilinear lattice such that each node has integer coordinates, and where node (i, j) is adjacent to (i − 1, j), (i + 1, j), (i, j − 1), and (i, j + 1). Let the distance between nodes (x, y) and (u, v) be |x − u| + |y − v| (i.e., the “Manhattan” distance). For r > 0, the number of nodes at a distance r from a given node z is 4r, so there are $$n(r) \equiv 1+ 4\sum _{i=1}^r = 2r^2 +2r+1$$ nodes within distance r of node z; the box containing these n(r) nodes has diameter 2r, and the box size s for this box is given by s = 2r + 1. Now consider a finite version of the infinite two-dimensional rectilinear lattice, defined as follows. For a positive integer K ≫ 1, let $${\mathbb {G}}$$ be a K × K two-dimensional rectilinear lattice such that each node has integer coordinates, where node (i, j) is adjacent to (i − 1, j), (i + 1, j), (i, j − 1), and (i, j + 1), and where each edge of the lattice contains K nodes. The diameter Δ of $$\mathbb {G}$$ is 2(K − 1). Figure 18.5 illustrates a box of radius r = 1 in the “interior” of a 6 × 6 lattice.
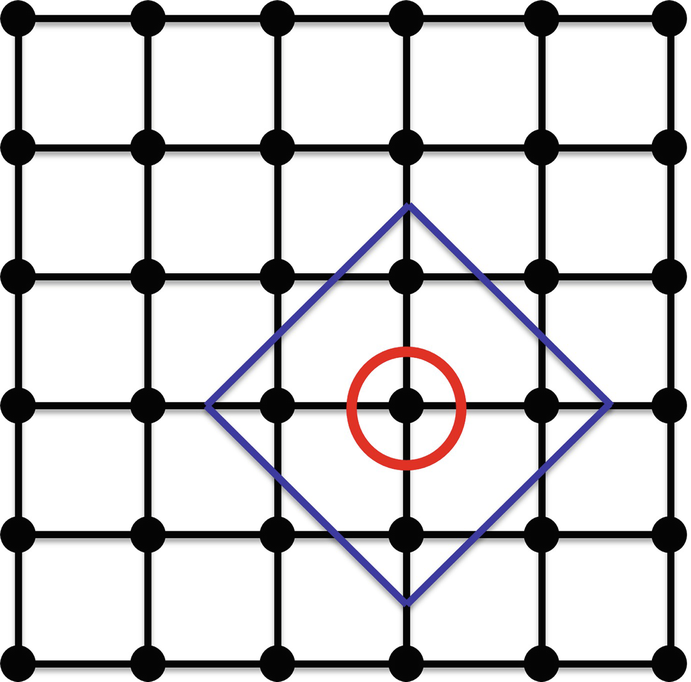
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig5_HTML.png
Figure 18.5

Box of radius r = 1 in a 6 × 6 rectilinear grid

For 1 ≪ r ≪ K, a (2r + 1)-covering of $$\mathbb {G}$$ using boxes of radius r consists of approximately K 2∕n(r) “totally full” boxes with n(r) nodes and diameter 2r, and $${\mathcal {O}}(K)$$ “partially full” boxes of diameter not exceeding 2r and containing fewer than n(r) nodes; these $${\mathcal {O}}(K)$$ partially full boxes are needed around the 4 edges of $$\mathbb {G}$$ . Since K ≫ 1, we ignore these $${\mathcal {O}}(K)$$ partially full boxes, and
$$\displaystyle \begin{aligned} m({\mathbb{G}}, s, d) \approx \left( \frac{K^2}{n(r)} \right) \left( \frac{2r+1}{2(K-1)+1} \right)^d \approx \left( \frac{K^2}{2r^2} \right) \left( \frac{2r}{2K} \right)^{d} = \left( \frac{1}{2} \right) \left( \frac{r}{K} \right)^{d-2} \, . \end{aligned}$$

Setting d = 2 yields $$\sigma ({\mathbb {G}}, {\mathcal {S}}, 2) \approx 0$$ , so d H = 2 for a large K × K rectilinear lattice. □

Example 18.6 Figure 18.6 plots box counting results for the dolphins network (introduced in Example 7.2), with 62 nodes, 159 arcs, and Δ = 8. For this network, and for all other networks described in this chapter, the minimal covering for each s was computed using the graph coloring heuristic described in [Rosenberg 17b]. Setting $${\mathcal {S}} = \{ 2, 3, 4, 5, 6 \}$$ , Fig. 18.6 shows that the $$\log B(s)$$ versus $$\log s$$ curve is approximately linear for $$s \in {\mathcal {S}}$$ . (In this example, as well as in subsequent examples, the determination of the set $$\mathcal {S}$$ was done by visual inspection.) Linear regression over this range yields d B ≈ 2.38. As discussed in Sect. 18.1, d B can also be viewed as the value of d minimizing, over {d | d > 0}, the standard deviation of the terms B(s)[s∕(Δ + 1)]d for $$s \in {\mathcal {S}}$$ . Figure 18.7 (left) plots B(s)[s∕(Δ + 1)]d versus d for $$s \in \mathcal {S}$$ for the dolphins network. The standard deviation is minimized at d ≈ 2.41, which is very close to d B ≈ 2.38.
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig6_HTML.png
Figure 18.6

$$\log B(s)$$ versus $$\log s$$ for the dolphins network

../images/487758_1_En_18_Chapter/487758_1_En_18_Fig7_HTML.png
Figure 18.7

B(s)[s∕(Δ + 1)]d versus d for $$s \in \mathcal {S}$$ (left) and $$m({ \mathbb {G}}, s, d)$$ versus d (right) for dolphins

The same $${\mathcal {S}}$$ was used to calculate d H of the dolphins network. Figure 18.7 (right) plots $$m({\mathbb {G}}, s, d)$$ for $$s \in {\mathcal {S}}$$ over the range d ∈ [1.6, 3]. Figure 18.8 (left), which plots $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ versus d over the range d ∈ [0, 3], shows that the location of d H is not immediately evident. Numerical calculation revealed that $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ has a unique local minimum at d H ≈ 2.34. Figure 18.8 (right) shows that $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ is quite “flat”1 in the vicinity of d H, since for d ∈ [2.26, 2.40] we have $$0.071 &lt; \sigma ({\mathbb {G}},{\mathcal {S}},d) &lt; 0.076$$ . □
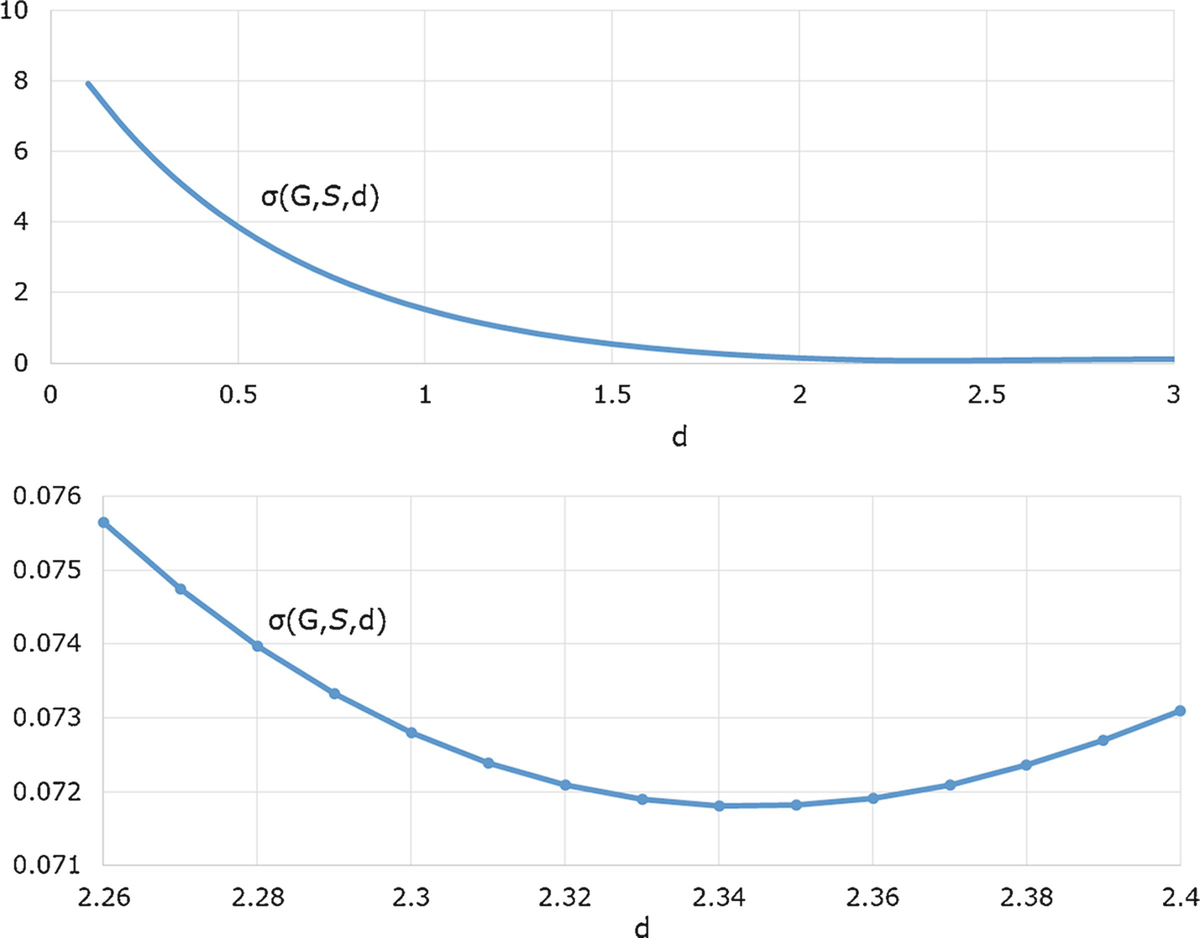
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig8_HTML.png
Figure 18.8

$$\sigma ({ \mathbb {G}}, {\mathcal {S}}, d)$$ versus d for dolphins for d ∈ [0, 3] (left) and d ∈ [2.26, 2.40] (right)

Example 18.7 Figure 18.9 plots box counting results for the USAir97 network [Batagelj 06], which has 332 nodes, 2126 arcs, and Δ = 6. Setting $${\mathcal {S}} = \{ 2, 3, 4, 5, 6 \}$$ , linear regression over this range yields d B ≈ 4.04. The shape of the $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ versus d plot for this network closely resembles the shape in Fig. 18.8 (left). There is a unique local minimum of $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ at d H ≈ 4.02. The standard deviation $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ is also quite flat in the vicinity of d H. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig9_HTML.png
Figure 18.9

$$\log B(s)$$ versus $$\log s$$ for the USAir97 network

Example 18.8 Figure 18.10 (left) provides box counting results for the jazz network (see Example 15.5), with 198 nodes, 2742 arcs, and Δ = 6. Setting $${\mathcal {S}} = \{ 2, 3, 4, 5, 6 \}$$ , linear regression over this range yields d B ≈ 2.66. Figure 18.10 (right) plots $$m({\mathbb {G}}, s, d)$$ for $$s \in {\mathcal {S}}$$ over the range d ∈ [1.6, 4]. There is a unique local minimum of $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ at d H ≈ 3.26. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig10_HTML.png
Figure 18.10

$$\log B(s)$$ versus $$\log s$$ (left) and $$m({ \mathbb {G}}, s, d)$$ versus d (right) for the jazz network

Example 18.9 Figure 18.11 (left) plots box counting results for s ∈ [2, 7] for the C. elegans network (see Example 17.4), with 453 nodes, 2040 arcs, and Δ = 7. Excluding the point $$\big (\log 2, \log B(2) \big )$$ , a linear fit is reasonable for the other five points, so we set $${\mathcal {S}} = \{ 3, 4, 5, 6, 7 \}$$ . Linear regression over this range yields d B ≈ 2.68. Figure 18.11 (right) plots $$m({\mathbb {G}},s, d)$$ for $$s \in {\mathcal {S}}$$ over the range d ∈ [1.5, 5]. Figure 18.12 (left) plots $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ versus d over the range d ∈ [0, 5]. There is a unique local minimum of $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d)$$ at d H ≈ 3.51.
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig11_HTML.png
Figure 18.11

$$\log B(s)$$ versus $$\log s$$ (left) and $$m({ \mathbb {G}}, s, d)$$ versus d (right) for the C. elegans network

../images/487758_1_En_18_Chapter/487758_1_En_18_Fig12_HTML.png
Figure 18.12

$$\sigma ({ \mathbb {G}}, {\mathcal {S}}, d)$$ versus d for C. elegans for d ∈ [0, 5] (left) and d ∈ [2.26, 2.40] (right)

Again, the $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ versus d plot is very flat in the vicinity of d H, as shown by Fig. 18.12 (right), since for d ∈ [3.45, 3.55] we have $$0.0560 &lt; \sigma ({\mathbb {G}},{\mathcal {S}},d) &lt; 0.0576$$ . □

Example 18.10 Figure 18.13 plots box counting results for the connected giant component of a protein network. 2 This component has 1458 nodes, 1948 arcs, and Δ = 19. Choosing the range $${\mathcal {S}} = \{ 4, 5, \ldots , 14 \}$$ , Fig. 18.13 shows that $$\log B(s)$$ is close to linear in $$\log s$$ for $$s \in {\mathcal {S}}$$ (the dotted line is the linear least squares fit), and d B = 2.44. The shape of the $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ versus d plot for protein has a shape similar to the plot for C. elegans, and for the protein network there is a unique local minimum of $$\sigma ({\mathbb {G}},{\mathcal {S}},d)$$ at d H = 3.08. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig13_HTML.png
Figure 18.13

$$\log B(s)$$ versus $$\log s$$ for s ∈ [4, 14] for the protein network

Figure 18.14, from [Rosenberg 18b], summarizes the above computational results. The proof that for geometric objects we have d H ≤ d B (Theorem 5.1) does not apply to networks with integer box sizes, and indeed Fig. 18.14 shows that for several networks d H exceeds d B, sometimes significantly so.
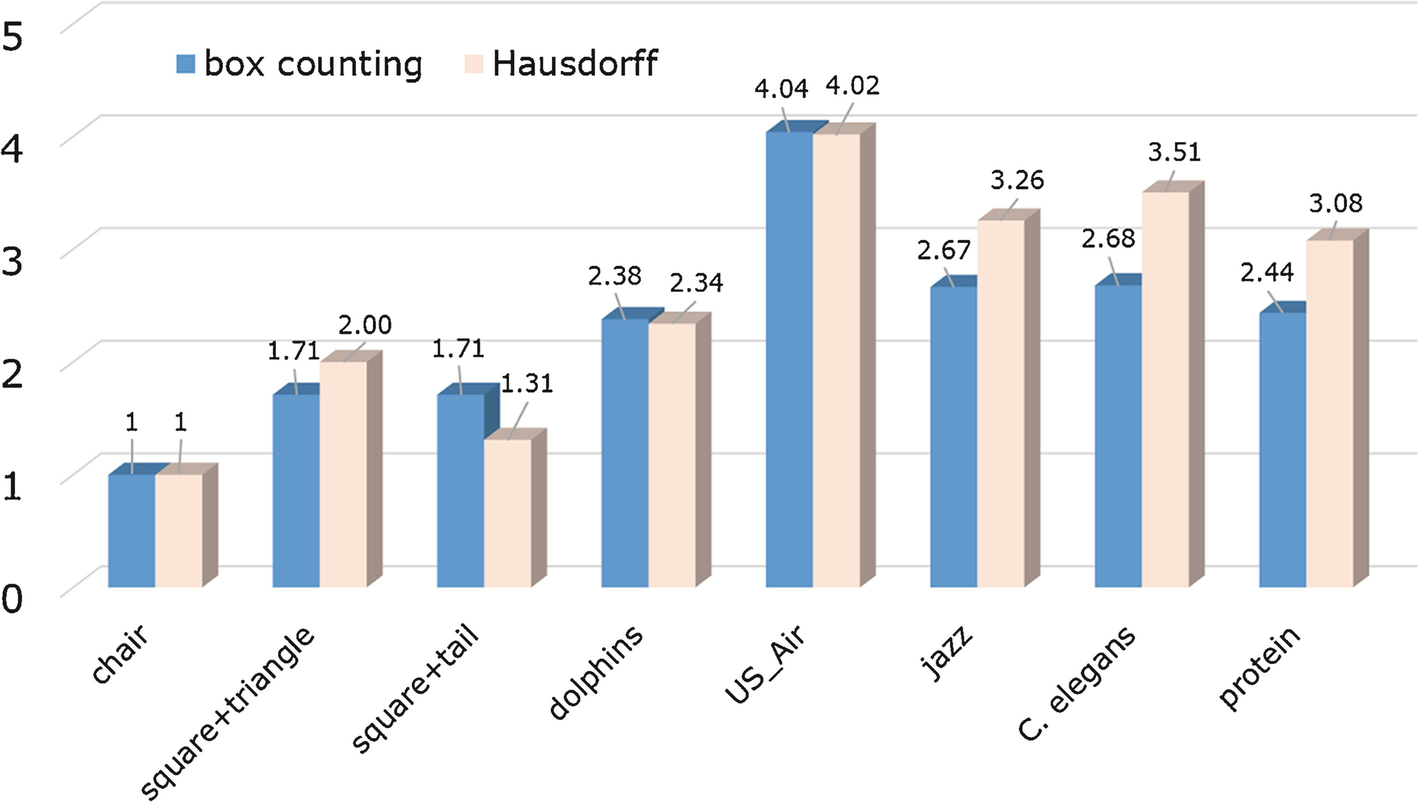
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig14_HTML.png
Figure 18.14

Summary of d B and d H computations

The above examples show that it is computationally feasible to compute d H of a network. The numerical value of d H depends not only on the minimal number B(s) of boxes for each box size s, but also on the diameters of the boxes in $${\mathcal {B}}(s)$$ . Any method for computing the box counting dimension d B of $$\mathbb {G}$$ suffers from the fact that in general we cannot verify that the computed B(s) is in fact minimal (although a lower bound on B(s) can be computed [Rosenberg 13]). Computing the Hausdorff dimension adds the further complication that there is currently no way to verify that a lexico minimal covering (Sect. 17.​1) has been found. Therefore, since for each box size s a randomized box-counting method is typically employed (e.g., the above results used the method described in [Rosenberg 17b]), it is necessary to run sufficiently many randomized iterations until we are reasonably confident that not only has a minimal covering of $$\mathbb {G}$$ been obtained, but also that a lexicographically minimal covering has been obtained. This extra computational burden is not unique to computing d H, since computing any fractal dimension of $$\mathbb {G}$$ other than the box counting dimension requires an unambiguous selection of a minimal covering, e.g., computing the information dimension d I of $$\mathbb {G}$$ requires finding a maximal entropy minimal covering (Sect. 15.​4), and computing the generalized dimensions D q of $$\mathbb {G}$$ requires finding a lexico minimal summary vector.

Example 18.11 [Rosenberg 18b] This example considers the impact on d B and d H of perturbing a network $$\mathbb {G}$$ . Let the arc set $$\mathbb {A}$$ of $$\mathbb {G}$$ be specified by a list $$\mathcal {L}$$ , so that $$\mathbb {G}$$ is built, arc by arc, by processing the list $$\mathcal {L}$$ . After each arc is processed, the node degree δ n of each node n in $$\mathbb {G}$$ is updated. To perturb $$\mathbb {G}$$ , choose P ∈ (0, 1). After reading arc a from $$\mathcal {L}$$ , pick two random probabilities p 1 ∈ (0, 1) and p 2 ∈ (0, 1). If p 1 < P, modify arc a as follows. Let i and j be the endpoints of arc a. If δ i > 1 and $$p_{{2}} &lt; \frac {1}{2}$$ , replace the endpoint i of arc a with a randomly chosen node distinct from i; otherwise, if δ j > 1, replace the endpoint j of arc a with a randomly chosen node distinct from j. (Requiring δ i > 1 ensures i will not become an isolated node.) This perturbation method was applied to the jazz network of Example 18.8 for P ranging from 0.01 to 0.08. The results, in Fig. 18.15, show that the d H versus P plot has roughly the same shape as the d B versus P plot. Although the range of d H over the interval 0 ≤ P ≤ 0.08 is smaller than the range of d B, sometimes d H magnifies the effect of a perturbation, e.g., d H changed much more than d B when P increased from 0.02 to 0.03. □
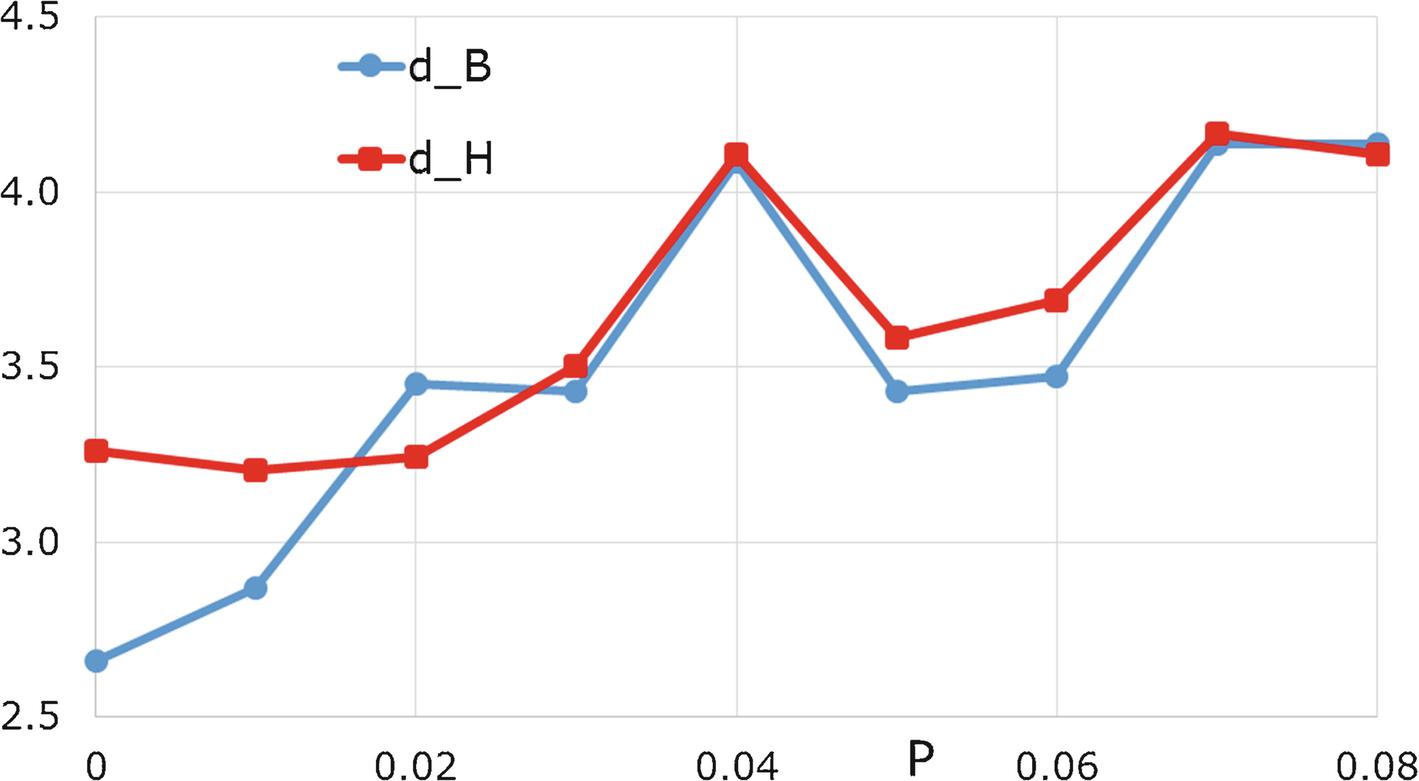
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig15_HTML.png
Figure 18.15

Perturbations of the jazz network

Example 18.12 [Rosenberg 18b] This example considers a Barábasi–Albert [Albert 02] preferential attachment model of a growing network. Assume that each new node n connects to a single existing node x, and the probability that x is chosen is proportional to the node degree of x. We start with an initial network of 3 nodes connected by 3 arcs, grow the network to 150 nodes, and compute d B and d H as the network grows. The diameter of the 150 node network is 11. Figure 18.16 plots the results. The 40 node network is an outlier due to its high d H. The range of d B (as the network grows from 10 to 150 nodes) is 0.48 and the range of d H is 1.15, so using the Hausdorff dimension, rather than the box counting dimension, magnifies, by a factor of 2.4, differences in the fractal dimensions of the growing network. In particular, the sharp increase in d H when the network size exceeds 110 nodes indicates that d H is sensitive to changes in the network topology that are not captured by the simpler measure d B. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig16_HTML.png
Figure 18.16

d B and d H of a network growing with preferential attachment

18.3 Generalized Hausdorff Dimensions of a Network

In Sect. 16.​9 we presented the definition in [Grassberger 85] of the generalized Hausdorff dimensions $$\{D_q^H \}_{q \in {\mathbb {R}}}$$ of a geometric object. Continuing our approach in this book of defining a fractal dimension for a geometric object and then extending it to a network, and having defined the Hausdorff dimension d H of a network $$\mathbb {G}$$ in Sect. 18.1 of this chapter, in this section we study the generalized Hausdorff dimensions $$\{D_q^H \}_{q \in {\mathbb {R}}}$$ of $$\mathbb {G}$$ , defined in [Rosenberg 18b]. These dimensions utilize both the diameter and mass of each box in the minimal covering $${\mathcal {B}}(s)$$ of $$\mathbb {G}$$ . Just as the computation of d H for $$\mathbb {G}$$ requires a line search, for each q the computation of the generalized Hausdorff dimension $$D_q^H$$ of $$\mathbb {G}$$ also requires a line search.

For a given box size s, let $${\mathcal {B}}(s)$$ be a minimal s-covering of $$\mathbb {G}$$ . The probability of box $$B_{{j}} \in {\mathcal {B}}(s)$$ is, as usual, p j(s) ≡ N j(s)∕N, where N j(s) is the number of nodes contained in box B j; for simplicity we write p j instead of p j(s). Recalling that δ j is defined by (18.5), we borrow from [Grassberger 85] and define
$$\displaystyle \begin{aligned} \begin{array}{l} m({\mathbb{G}}, s, q, d) \equiv \left\{ \begin{array}{ll} \left( \sum_{B_{{j}} \in {\mathcal{B}}(s)} p_{{j}} ({\delta_{{j}}^{\, d}} / p_{{j}} )^{1-q} \right)^{1/(1-q)} &amp; \mbox{if } \;q \neq 1 {} \\ \exp \left( \sum_{B_{{j}} \in {\mathcal{B}}(s)} p_{{j}} \log \big( \delta_{{j}}^{\, d}/p_{{j}} \big) \right) &amp; \mbox{if } \; q = 1 \, . \end{array} \right . \end{array} \end{aligned} $$
(18.11)
We can regard $$m({\mathbb {G}}, s, q, d)$$ as the “d-dimensional generalized Hausdorff measure of order q of $$\mathbb {G}$$ for box size s”.

Exercise 18.2 Prove that for q ≠ 1 the derivative with respect to d of $$m({\mathbb {G}}, s, q, d)$$ is negative. □

Extending the approach of Sect. 18.1, we define $$D^H_q$$ of $$\mathbb {G}$$ as that value of d for which $$m({\mathbb {G}}, s, q, d)$$ is roughly constant over a given range $$\mathcal {S}$$ of values of s. For d > 0, let $$\sigma ({\mathbb {G}},{\mathcal {S}},q, d)$$ be the standard deviation of the values $$m({\mathbb {G}}, s, q, d)$$ for $$s \in {\mathcal {S}}$$ :
$$\displaystyle \begin{aligned} m_{\textit{avg}}({\mathbb{G}}, {\mathcal{S}}, q, d) &amp; \equiv \frac{1}{\vert {\mathcal{S}} \vert} \sum_{s \in {\mathcal{S}}} m({\mathbb{G}}, s, q, d) \\ \sigma({\mathbb{G}},{\mathcal{S}}, q, d) &amp; \equiv \sqrt { \frac{1}{\vert {\mathcal{S}} \vert} \sum_{s \in {\mathcal{S}}} \big[ \, m({\mathbb{G}}, s, q, d) - m_{\textit{avg}}({\mathbb{G}}, {\mathcal{S}}, q, d) \, \big]^2. } \; \; {} \end{aligned} $$
(18.12)
We associate with $$\mathbb {G}$$ the generalized Hausdorff dimension of order q, denoted by $$D_q^H$$ , defined as follows.

Definition 18.4 [Rosenberg 18b] (Part A.) If $$\sigma ({\mathbb {G}}, {\mathcal {S}}, q, d)$$ has at least one local minimum over {d | d > 0}, then $$D_q^H$$ is the value of d satisfying (i) $$\sigma ({\mathbb {G}}, {\mathcal {S}}, q, d)$$ has a local minimum at $$D_q^H$$ , and (ii) if $$\sigma ({\mathbb {G}}, {\mathcal {S}}, q, d)$$ has another local minimum at $$\widetilde {d}$$ , then $$\sigma ({\mathbb {G}}, {\mathcal {S}}, q, D_q^H) &lt; \sigma ({\mathbb {G}}, {\mathcal {S}}, q, \widetilde {d})$$ . (Part B.) If $$\sigma ({\mathbb {G}}, {\mathcal {S}}, q, d)$$ does not have a local minimum over {d | d > 0}, then $$D_q^H \equiv \infty $$ . □

Definition 18.5 If $$D_q^H &lt; \infty $$ , then the generalized Hausdorff measure of order q of $$\mathbb {G}$$ is $$m_{\textit {avg}}({\mathbb {G}}, {\mathcal {S}}, q, D_q^H)$$ . If $$D_q^H = \infty $$ then the generalized Hausdorff measure of order q of $$\mathbb {G}$$ is 0. □

Setting q = 0, by (18.6) and (18.11) we have $$m({\mathbb {G}}, s, d) = m({\mathbb {G}}, s, 0, d)$$ . By (18.9) and (18.12) we have $$\sigma ({\mathbb {G}}, {\mathcal {S}}, d) = \sigma ({\mathbb {G}}, {\mathcal {S}}, 0, d)$$ . Hence, by Definitions 18.2 and 18.4 we have $$D_0^H = d_{{H}}$$ . In words, the generalized Hausdorff dimension of order 0 of $$\mathbb {G}$$ is equal to the Hausdorff dimension of $$\mathbb {G}$$ .

For a geometric object Ω, it was observed in [Grassberger 85] that if μ is the Hausdorff measure, then $$D_q^H = d_H$$ for all q, at least for strictly self-similar fractals. The following theorem, the analogue of Grassberger’s observation for a network $$\mathbb {G}$$ , says that if the mass of each box is proportional to δ j, then for q ≠ 1 we have $$D_q^H = 1$$ .

Theorem 18.1 [Rosenberg 18b] Suppose that for some constant α > 0 we have δ j = αp j for $$s \in {\mathcal {S}}$$ and for $$B_{{j}} \in {\mathcal {B}}(s)$$ . Then for q ≠ 1 we have $$D_q^H = 1$$ and the generalized Hausdorff measure of order q of $$\mathbb {G}$$ is α.

Proof Suppose δ j = αp j for $$s \in {\mathcal {S}}$$ and for $$B_{{j}} \in {\mathcal {B}}(s)$$ . Set d = 1 and pick q ≠ 1. From (18.11), for $$s \in {\mathcal {S}}$$ we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} m({\mathbb{G}}, s, q, 1)\!\!\!\! &amp;\displaystyle = &amp;\displaystyle \!\!\!\! \left[ \sum_{B_{{j}} \in {\mathcal{B}}(s)} p_{{j}} \left( \frac{\delta_{{j}}}{p_{{j}}} \right)^{1-q} \right]^{1/(1-q)} \; = \;\;\; \left[ \sum_{B_{{j}} \in {\mathcal{B}}(s)} p_{{j}} \left( \frac{\alpha p_{{j}}}{ p_{{j}}} \right)^{1-q} \right]^{1/(1-q)} \\ \!\!\!\!&amp;\displaystyle = &amp;\displaystyle \!\!\!\! \left[ \alpha^{1-q} \sum_{B_{{j}} \in {\mathcal{B}}(s)} p_{{j}} \right]^{1/(1-q)} \; = \;\;\; \alpha \, , \end{array} \end{aligned} $$
where the final equality follows as $$\sum _{B_{{j}} \in {\mathcal {B}}(s)} p_{{j}} = 1$$ . Since $$m({\mathbb {G}}, s, q, 1) = \alpha $$ , by (18.12) we have $$\sigma ({\mathbb {G}},{\mathcal {S}}, q, 1) = 0$$ . By Definition 18.4, we have $$D_q^H = 1$$ . By Definition 18.5, the generalized Hausdorff measure of order q of $$\mathbb {G}$$ is α. □

Exercise 18.3 Suppose that for some constant α > 0 we have δ j = αp j for $$s \in {\mathcal {S}}$$ and for $$B_{{j}} \in {\mathcal {B}}(s)$$ . What are the values of d I and $$D_1^H$$ ? □

Example 18.13 Consider again the chair network of Example 18.2. As shown in Fig. 18.2, the box with 1 node has p j = 1∕5 and δ j = 1∕4, each box with 2 nodes has p j = 2∕5 and δ j = 2∕4, and the box with 3 nodes has p j = 3∕5 and δ j = 3∕4. Since the conditions of Theorem 18.1 are satisfied with α = 5∕4, for q ≠ 1 we have $$D_q^H = 1$$ , and the generalized Hausdorff measure of order q of the chair network is 5∕4. □

Example 18.14 Consider again the network $${\mathbb {G}}_1$$ of Fig. 18.3. Figure 18.17 plots $$D_q^H$$ versus q for integer q ∈ [−10, 10]. Clearly $$D_q^H$$ is not monotonic decreasing in q, even over the range q ≥ 0, since $$D_0^H &lt; D_2^H$$ . Since for a geometric fractal $$D_q^H$$ is a non-increasing function of q [Grassberger 85], the non-monotonic behavior in Fig. 18.17 is perhaps surprising. However, the generalized dimensions D q of a network, computed using Definition 17.3, also can fail to be monotone decreasing in q (Sect. 17.​2). Thus it is not unexpected that the generalized Hausdorff dimensions of a network, computed using Definition 18.4, can also exhibit non-monotonic behavior. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig17_HTML.png
Figure 18.17

$$D_q^H$$ versus q for the network $${ \mathbb {G}}_1$$ of Fig. 18.3

Example 18.15 Consider again the dolphins network of Example 18.6, again with $${\mathcal {S}} = \{ 2, 3, 4, 5, 6 \}$$ . Figure 18.18 plots $$D_q^H$$ versus q. Remarkably, there is a “critical order” q c ≈−1.54 such that $$D_q^H$$ is finite for q > q c and $$D_q^H$$ is infinite for q < q c. □
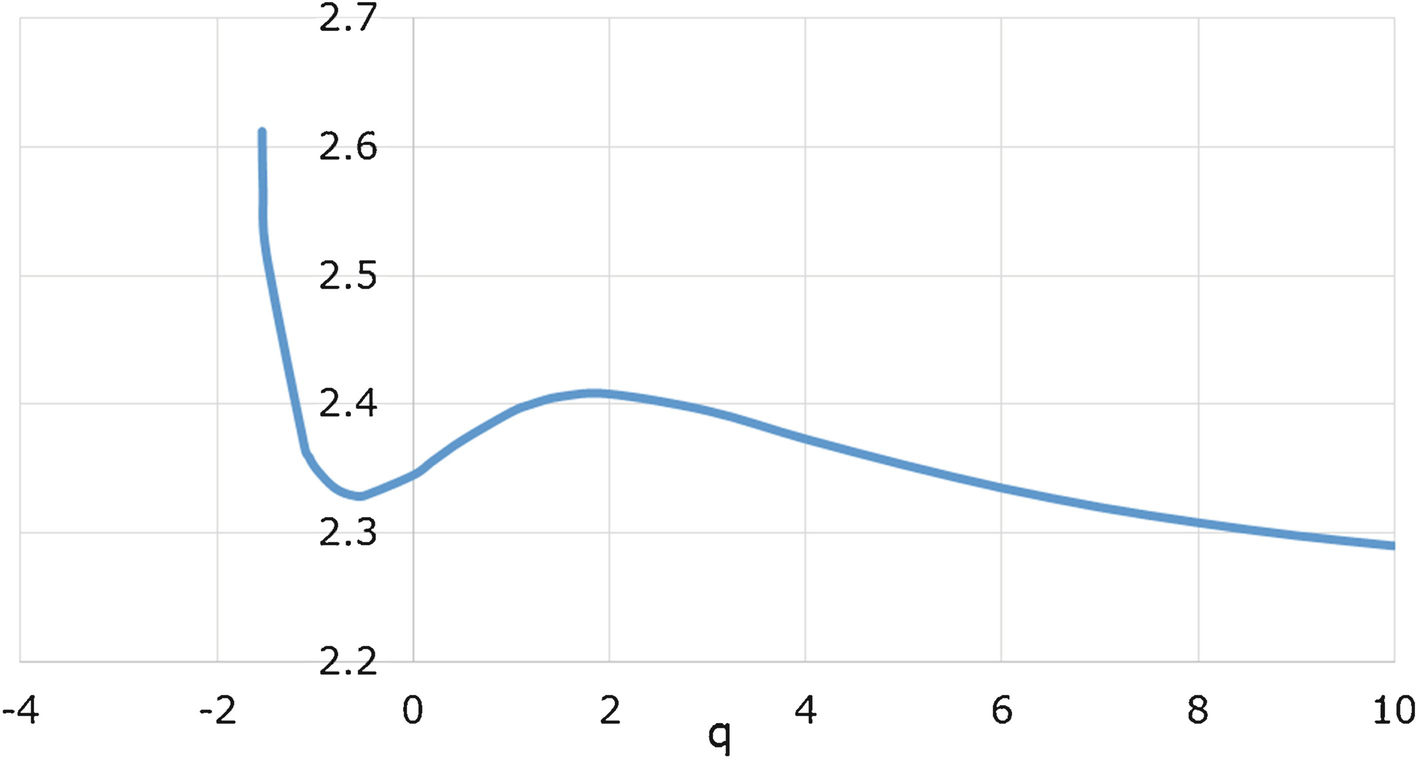
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig18_HTML.png
Figure 18.18

$$D_q^H$$ versus q for the dolphins network

Example 18.16 Consider again the jazz network of Example 18.8, again with $${\mathcal {S}} = \{ 2, 3, 4, 5, 6 \}$$ . Figure 18.19 plots $$D_q^H$$ versus q. There is a critical interval Q c ≈ [−3.9, −0.3] such that $$D_q^H$$ is infinite for q ∈ Q c and finite otherwise. □
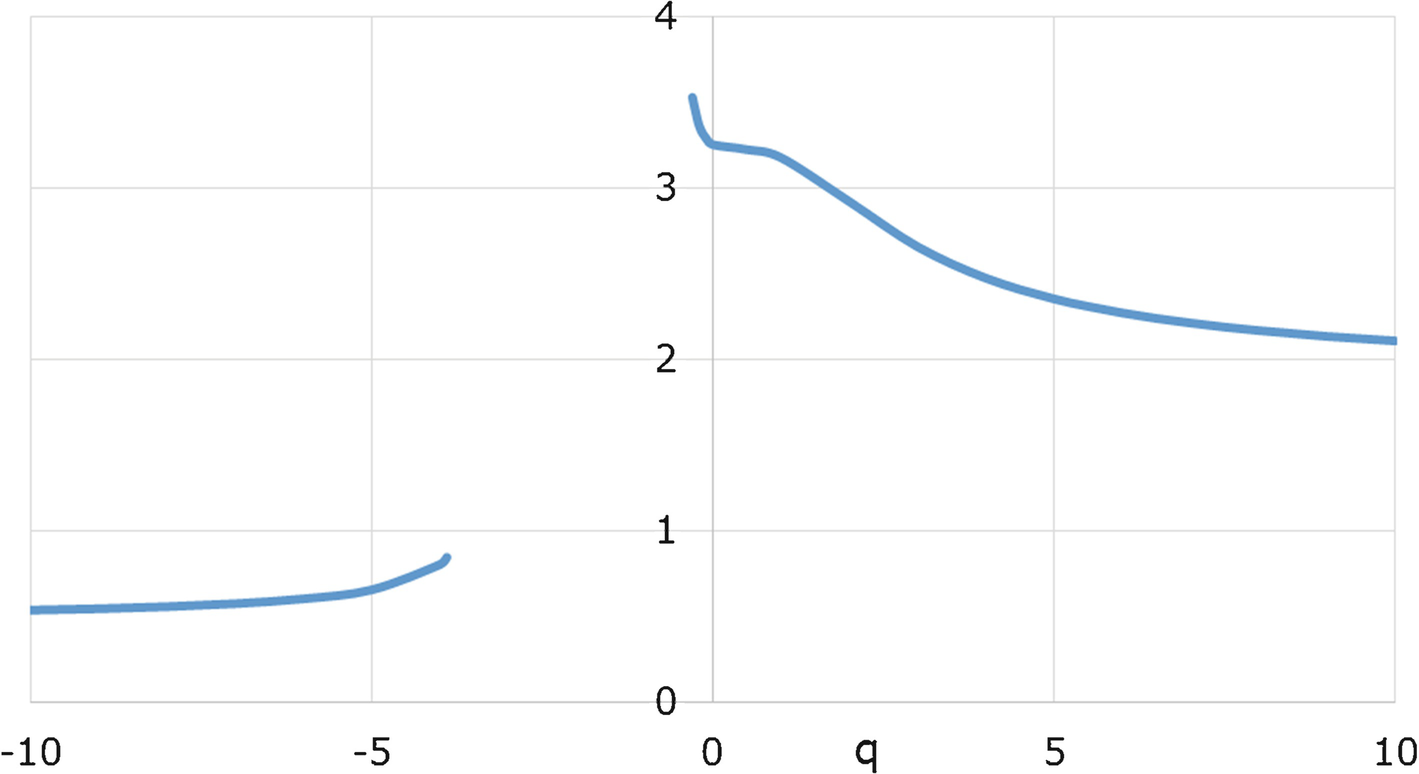
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig19_HTML.png
Figure 18.19

$$D_q^H$$ versus q for the jazz network

Example 18.17 Consider again the C. elegans network of Example 18.9, again with $${\mathcal {S}} = \{ 3, 4, 5, 6, 7 \}$$ . Figure 18.20 plots $$D_q^H$$ versus q. There is a critical interval Q c ≈ [−1.45, −0.25] such that $$D_q^H$$ is infinite for q ∈ Q c and finite otherwise. □
../images/487758_1_En_18_Chapter/487758_1_En_18_Fig20_HTML.png
Figure 18.20

$$D_q^H$$ versus q for the C. elegans network

The above examples show that $$D_q^H$$ can exhibit complicated behavior for q < 0. These findings align with several studies (e.g., [Block 91]) pointing to difficulties in computing and interpreting D q for a geometric object and the difficulties “imperceptibly hidden” in the negative q domain [Riedi 95]; see Sect. 16.​4. Thus, for a network, $$D_q^H$$ should probably be computed only for q ≥ 0. The existence of a critical interval in Examples 18.15–18.17 raises many questions, e.g., to characterize the class of networks possessing a critical interval.

To summarize the computational results presented in this chapter, d H can sometimes be more useful than d B in quantifying changes in the topology of a network. However, d H is harder to compute than d B, and $$D_q^H$$ is less well behaved than D q. We conclude that d H and $$D_q^H$$ should be added to the set of useful metrics for characterizing a network, but they cannot be expected to replace d B and D q.