When working with any normal distribution function, you have to let the function know which member of the normal distribution family you’re interested in. You do that by specifying the mean and the standard deviation.
Plotting a normal curve
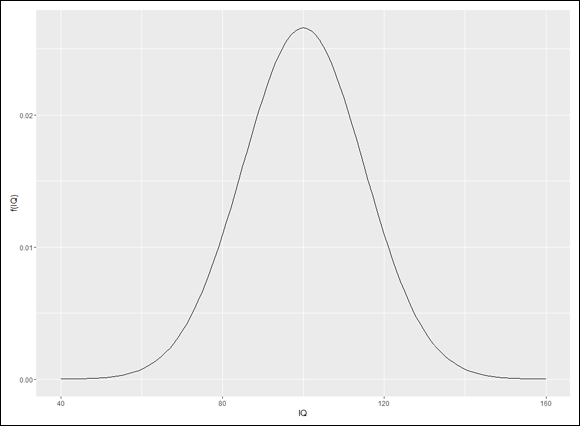
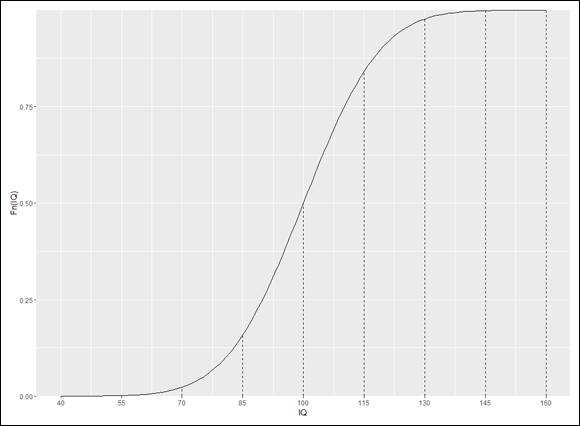
dnorm() is useful as a tool for plotting a normal distribution. I use it along with ggplot() to draw a graph for IQ that looks a lot like Figure 8-2.
Before I set up a ggplot() statement, I create three helpful vectors. The first
x.values <- seq(40,160,1)
is the vector I’ll give to ggplot() as an aesthetic mapping for the x-axis. This statement creates a sequence of 121 numbers, beginning with 40 (4 standard deviations below the mean) to 160 (4 standard deviations above the mean).
The second
sd.values <- seq(40,160,15)
is a vector of the nine standard deviation-values from 40 to 160. This figures into the creation of the vertical dashed lines at each standard deviation in Figure 8-2.
The third vector
zeros9 <- rep(0,9)
will also be part of creating the vertical dashed lines. It’s just a vector of nine zeros.
On to ggplot(). Because the data is a vector, the first argument is NULL. The aesthetic mapping for the x-axis is, as I mentioned earlier, the x.values vector. What about the mapping for the y-axis? Well, this is a plot of a normal density function for mean = 100 and sd =15, so you’d expect the y-axis mapping to be dnorm(x.values, m=100, s=15), wouldn’t you? And you’d be right! Here’s the ggplot() statement:
ggplot(NULL,aes(x=x.values,y=dnorm(x.values,m=100,s=15)))
Add a line geom function for the plot and labels for the axes, and here’s what I have:
ggplot(NULL,aes(x=x.values,y=dnorm(x.values,m=100,s=15))) +
geom_line() +
labs(x="IQ",y="f(IQ)")
And that draws Figure 8-3.
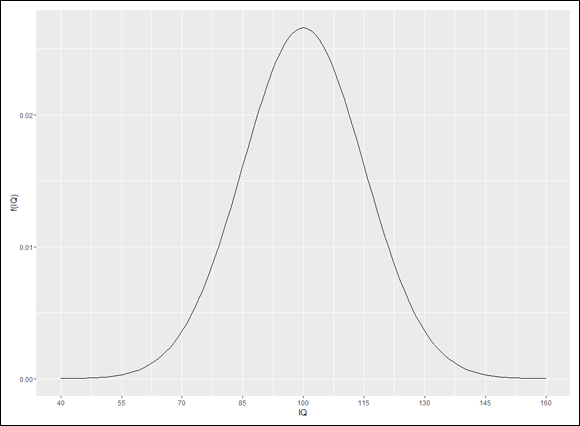
As you can see, ggplot() has its own ideas about the values to plot on the x-axis. Instead of sticking with the defaults, I want to place the sd.values on the x-axis. To change those values, I use scale_x_continuous() to rescale the x-axis. One of its arguments, breaks, sets the points on the x-axis for the values, and the other, labels, supplies the values. For each one, I supply sd.values:
scale_x_continuous(breaks=sd.values,labels = sd.values)
Now the code is
ggplot(NULL,aes(x=x.values,y=dnorm(x.values,m=100,s=15))) +
geom_line() +
labs(x="IQ",y="f(IQ)")+
scale_x_continuous(breaks=sd.values,labels = sd.values)
and the result is Figure 8-4.
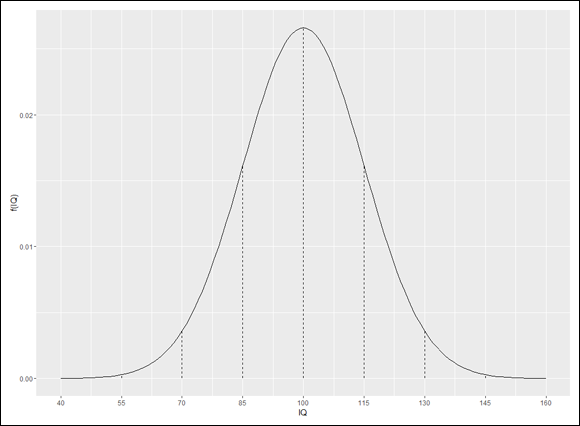
In ggplot world, vertical lines that start at the x-axis and end at the curve are called segments. So the appropriate geom function to draw them is geom_segment(). This function requires a starting point for each segment and an end point for each segment. I specify those points in an aesthetic mapping within the geom. The x-coordinates for the starting points for the nine segments are in sd.values. The segments start at the x-axis, so the nine y-coordinates are all zeros — which happens to be the contents of the zeros9 vector. The segments end at the curve, so the x-coordinates for the end-points are once again, sd.values. The y-coordinates? Those would be dnorm(sd.values, m=100,s=15). Adding a statement about dashed lines, the rather busy geom_segment() statement is
geom_segment((aes(x=sd.values,y=zeros9,xend =
sd.values,yend=dnorm(sd.values,m=100,s=15))),
linetype = "dashed")
The code now becomes
ggplot(NULL,aes(x=x.values,y=dnorm(x.values,m=100,s=15))) +
geom_line() +
labs(x="IQ",y="f(IQ)")+
scale_x_continuous(breaks=sd.values,labels = sd.values) +
geom_segment((aes(x=sd.values,y=zeros9,xend =
sd.values,yend=dnorm(sd.values,m=100,s=15))),
linetype = "dashed")
which produces Figure 8-5.
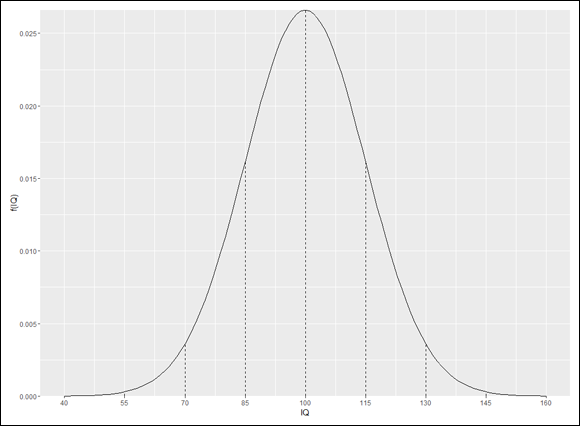
One more little touch and I’m done showing you how it’s done. I’m not all that crazy about the space between the x-values and the x-axis. I’d like to remove that little slice of the graph and move the values up closer to where (at least I think) they should be.
To do that, I use scale_y_continuous(), whose expand argument controls the space between the x-values and the x-axis. It’s a two-element vector with defaults that set the amount of space you see in Figure 8-5. Without going too deeply into it, setting that vector to c(0,0) removes the spacing.
These lines of code draw the aesthetically pleasing Figure 8-6:
ggplot(NULL,aes(x=x.values,y=dnorm(x.values,m=100,s=15))) +
geom_line() +
labs(x="IQ",y="f(IQ)")+
scale_x_continuous(breaks=sd.values,labels = sd.values) +
geom_segment((aes(x=sd.values,y=zeros9,xend =
sd.values,yend=dnorm(sd.values,m=100,s=15))),
linetype = "dashed")+
scale_y_continuous(expand = c(0,0))
 Meeting the normal distribution family
Meeting the normal distribution family Working with standard deviations and the normal distribution
Working with standard deviations and the normal distribution Understanding R's normal distribution functions
Understanding R's normal distribution functions
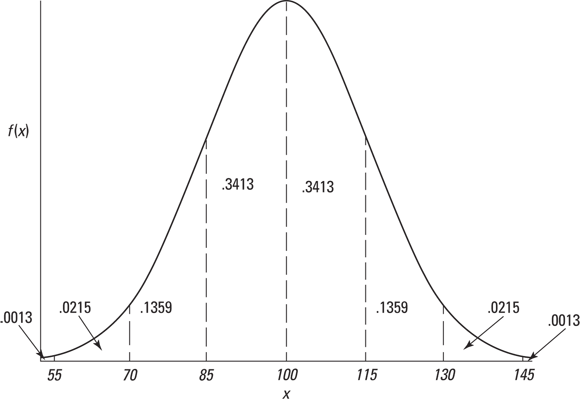
 You might have read elsewhere that the standard deviation for IQ is 16 rather than 15. That’s the case for the Stanford-Binet version of the IQ test. For other versions, the standard deviation is 15.
You might have read elsewhere that the standard deviation for IQ is 16 rather than 15. That’s the case for the Stanford-Binet version of the IQ test. For other versions, the standard deviation is 15. The proportions in
The proportions in 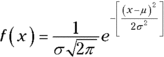
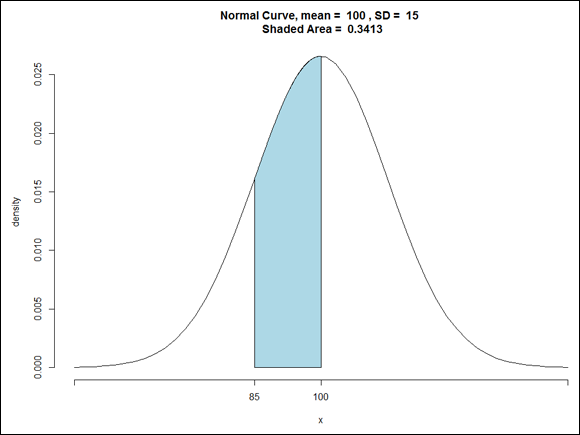
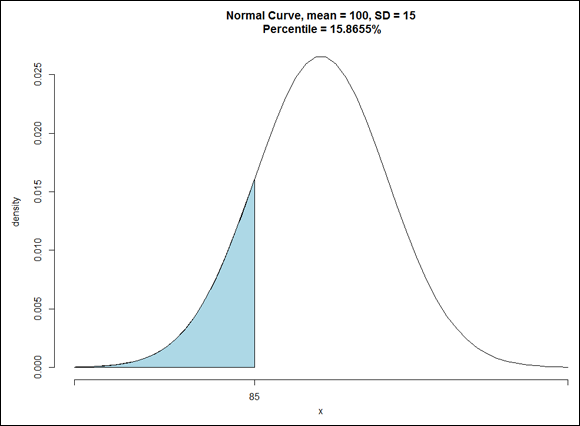
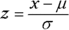
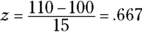
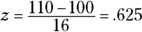
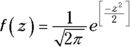
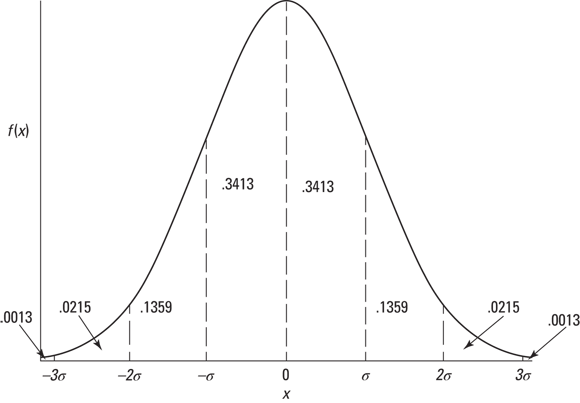
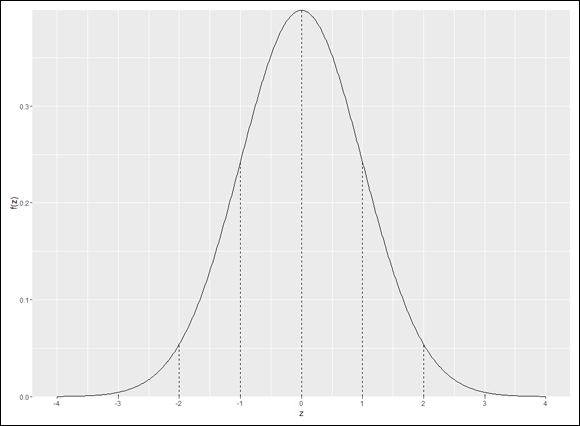
 This is the member of the normal distribution family that most people are familiar with. It's the one they remember most from statistics courses, and it's the one that most people have in mind when they (mistakenly) say the normal distribution. It's also what people think of when they hear about “z-scores.” This distribution leads many to the mistaken idea that converting to z-scores somehow transforms a set of scores into a normal distribution.
This is the member of the normal distribution family that most people are familiar with. It's the one they remember most from statistics courses, and it's the one that most people have in mind when they (mistakenly) say the normal distribution. It's also what people think of when they hear about “z-scores.” This distribution leads many to the mistaken idea that converting to z-scores somehow transforms a set of scores into a normal distribution.