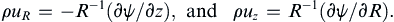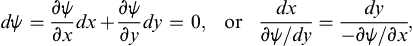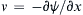4.3. Stream Functions

Consider the steady form of the continuity equation (4.7):

∇·(ρu)=0.

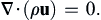(4.11)

The divergence of the curl of any vector field is identically zero (see Exercise 2.21), so ρu will satisfy (4.11) when written as the curl of a vector potential Ψ:

ρu=∇×Ψ,

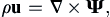(4.12)

which can be specified in terms of two scalar functions: Ψ = χ∇ψ. Putting this specification for Ψ into (4.12) produces ρu = ∇χ × ∇ψ, because the curl of any gradient is identically zero (see Exercise 2.22). Furthermore, ∇χ is perpendicular to surfaces of constant χ, and ∇ψ is perpendicular to surfaces of constant ψ, so the mass flux ρu = ∇χ × ∇ψ will be parallel to surfaces of constant χ and constant ψ. Therefore, three-dimensional streamlines are the intersections of the two stream surfaces, or stream functions in a three-dimensional flow.

The situation is illustrated in Figure 4.1. Consider two members of each of the families of the two stream functions χ = a, χ = b, ψ = c, ψ = d. The intersections shown as darkened lines in Figure 4.1 are the streamlines. The mass flux m˙ through the surface A bounded by the four stream surfaces (shown in gray in Figure 4.1) is calculated with area element dA, normal n (as shown), and Stokes’ theorem.

Defining the mass flux m˙ 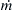through A, and using Stokes’ theorem produces:

m˙=∫Aρu·ndA=∫A(∇×Ψ)·ndA=∫CΨ·ds=∫Cχ∇ψ·ds=∫Cχdψ=b(d−c)+a(c−d)=(b−a)(d−c).

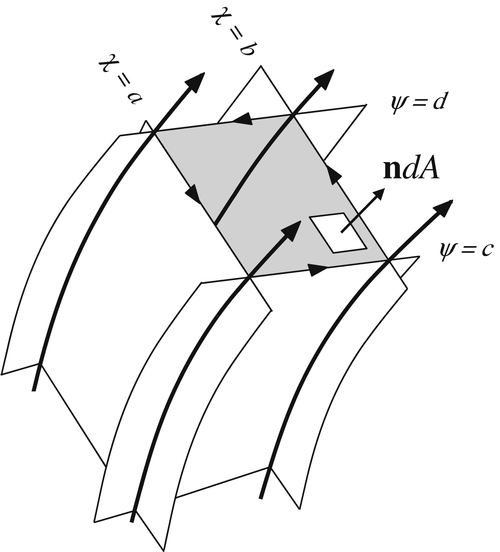
Figure 4.1 Isometric view of two members from each family of stream surfaces. The solid curves are streamlines and these lie at the intersections of the surfaces. The unit vector n points in the stream direction and is perpendicular to the gray surface that is bordered by the nearly rectangular curve C made up of segments defined by χ = a, χ = b, ψ = c, and ψ = d. The arrows on this boarder indicate the integration direction for Stokes’ theorem.

Here we have used the vector identity ∇ψ·ds = dψ. The mass flow rate of the stream tube defined by adjacent members of the two families of stream functions is just the product of the differences of the numerical values of the respective stream functions.

As a special case, consider two-dimensional flow in (x,y)-Cartesian coordinates where all the streamlines lie in z = constant planes. In this situation, z is one of the three-dimensional stream functions, so we can set χ = −z, where the sign is chosen to obey the usual convention. This produces ∇χ = –e_z, so ρu = –e_z × ∇ψ, or:

ρu=∂ψ/∂y,andρv=−∂ψ/∂x.

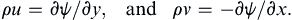
in conformity with Exercise 4.8.

Similarly, for axisymmetric three-dimensional flow in cylindrical polar coordinates (Figure 3.3c), all the streamlines lie in φ = constant planes that contain the z-axis so χ = −φ is one of the stream functions. This produces ∇χ = –R^–1e_φ and ρu = ρ(u_R, u_z) = –R^–1 e_φ × ∇ψ, or:

ρuR=−R−1(∂ψ/∂z),andρuz=R−1(∂ψ/∂R).

We note here that if the density is constant, mass conservation reduces to ∇·u=0 (steady or not) and the entire preceding discussion follows for u rather than ρu with the interpretation of stream function values in terms of volumetric flux rather than mass flux.

Example 4.3

In a planar constant-density flow, the stream function ψ is defined by u = (u,v) = –e_z × ∇ψ. Show that a curve of ψ(x,y) = const. satisfies the stream function tangency requirement, the first equality of (3.7).

Solution

On a curve of ψ(x,y) = const., the following will be true:

dψ=∂ψ∂xdx+∂ψ∂ydy=0,ordx∂ψ/dy=dy−∂ψ/∂x,

 

where the second equation is a rearrangement of the first. Evaluate the cross product in the problem statement to find u=∂ψ/∂y and v=−∂ψ/∂x, and substitute these into the second equality to reach: dx/u = dy/v, which is the first equality of (3.7).