Now that you have some knowledge of what goes on beyond the reaches of Earth’s atmosphere, you can more fully appreciate what you see when you look up after the Sun goes down. You don’t have to spend your life’s savings on hardware, but a few instruments can help you see a lot of interesting celestial objects.
As our cities swell, good places for astronomical viewing are becoming hard to find. We light up the darkness so that our streets are safe for driving powered vehicles, even as the exhaust from those machines thickens the veil between us and the Sun, Moon, planets, stars, nebulae, and galaxies. Tall buildings turn fields into canyons. Some children grow up without learning to recognize any celestial objects other than the Sun and Moon. It doesn’t have to be this way.
If you happen to live in a rural area, especially in one of the less populated parts of the country, consider yourself blessed.
Read this chapter before you start to shop for astronomical viewing aids. Then check out several stores; hobby shops are excellent. If there is a local astronomy club in your area, find out where and when it meets, and get some input from experienced amateur astronomers before spending any money. Your needs will depend on what you want to see “up there” and how important amateur astronomy really is to you.
Sky and Telescope magazine online has information about astronomy clubs all over the world. Go to the following Web site:
http://www.skypub.com
Click on “Site Map,” and then click on “Astronomical Directory.” As you know if you have used a computer online lately, the Web is always changing, and by the time you read this, the links may be different. In that case, go to this site:
http://www.google.com
Click on “Advanced Search,” and input the words astronomy clubs in the “exact phrase” box. Then take it from there!
Wherever you live, you need not travel far to get to a place where latter-day contrivances don’t interfere with your view of the nighttime sky. There are plenty of places, even near Boston, London, or Sydney, where the stars twinkle and the planets stand out like beacons. In this respect, ironically, some of the world’s poorest people are well-to-do. Have you ever wondered what folks in remote Afghanistan or Tibet see when they look at the sky on a clear and moonless night?
The next time the weather is favorable for sky watching, get out in a rural area, out on a big country lake, or offshore in the ocean in a small boat. Find a quiet place, a safe place, where human and animal pests will not disturb you. Bring along some insect repellent unless it’s winter. If it is winter, wear plenty of warm clothing! You’re not going to be jogging around or doing aerobics. Don’t trespass or put yourself in danger. Put at least 75 miles between yourself and the nearest big town.
Don’t expect to find a spot entirely without any human-made lights in view, but if they’re few in number and more than a city block away, it should be good enough. Give your eyes at least 15 minutes to adjust to the darkness. Then gaze upward. Better yet, lie flat on your back with an unobstructed half-sphere of sky above you.
Astronomers have always had a problem with night vision. Now you’ll find out first hand how they deal with it. On one side of the visibility equation, your eyes must adjust to the darkness, especially when the Moon is not above the horizon. On the other side of the equation, you’ll want to read star maps or consult other reference materials from time to time. You might have to check eyepiece specifications, make adjustments to a telescope, or otherwise fiddle around with “stuff.” You’ll need some sort of lamp to do this.
Get a flashlight and some red cloth or thin red tissue paper. This will serve as a color filter. Cover the business end of the flashlight with the filter. Secure it with a rubber band. The resulting light should be dim; you’ll have to experiment with various coverings to find out what works best. Use a flashlight with size D cells or, better yet, a lantern with one of those bulky 6-volt batteries. Be sure the cells or batteries are fresh, and carry a spare bulb. The light from the lamp should be bright enough so that you can read your star charts, eyepiece numbers, and other information after your eyes have fully adjusted to the darkness. But it shouldn’t be any brighter than that.
Red light has some special properties. It does not desensitize your eyes to the extent white light does. If you keep the filtered light source just bright enough so that you can read by it (but no brighter), it won’t interfere with your stargazing. Another plus: Red light attracts fewer insects than white light.
Once your eyes have adjusted to the darkness, it’s time to locate some stars, constellations, or planets. These vary depending on the time of year, the hour of the evening, and the latitude on the Earth at which you happen to live. You can refer back to Chapters 1, 2, and 3 to locate some of the major constellations and to figure out what point(s) of reference to use. The positions of the Moon and the planets, as you know, vary among the background of stars.
Current maps of the heavens can be viewed by going to Weather Underground at the following Web site:
http://www.wunderground.com
Click on the “Astronomy” link. You can input your location anywhere in the world, as well as the hour of the evening or night, and get a complete map of the sky. If this link isn’t available for some reason, Sky and Telescope online has excellent printable star maps. Go to:
If you can afford it, bring a notebook computer along on your stargazing expedition and have it equipped with wireless Internet access. In this way, you can check out the star maps on the fly. Turn down the display brightness to a low level so that it won’t degrade your night vision.
The circumpolar constellations are the best reference to begin with. This is so because they’re always above the horizon regardless of the time of year, unless you happen to live in the tropics (between approximately 20°N lat and 20°S latitude).
Your eyes alone can see a lot of interesting things in the sky once you know where to look. Mysterious fuzzy spots appear. Certain dim objects seem to pop out when you look slightly away from them, only to maddeningly vanish when you look straight at them. This is normal; it is a result of the anatomy of human eyes. The center of your field of vision is known as the fovea, representing the point on your retina where your gaze is directed precisely. This is where your eyes’ image resolution, also called resolving power, is greatest. However, this comes at the expense of sensitivity, which is better slightly off-center in your field of vision. Sensitivity and resolving power both can be improved dramatically, of course, with binoculars and telescopes. However, then you sacrifice absolute field of view.
Some amateur astronomers recommend that you obtain a pair of binoculars before you spend any money on a telescope. This is an individual choice. Binoculars are good for general star viewing at low magnification. Telescopes are a requirement for resolving detail in the planets, observing lunar terrain up close, or examining Sunspots.
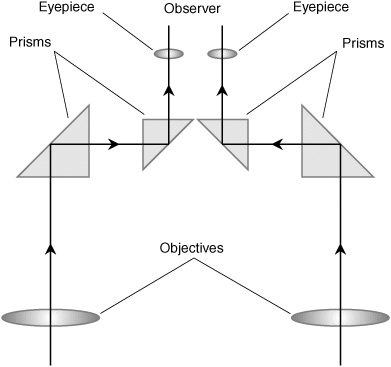
Figure 20-1 is a simplified functional diagram of a pair of binoculars. You can think of the assembly as two identical telescopes placed beside each other. The eyepieces are spaced to match the distance between the pupils of the observer’s eyes. This spacing is adjustable. In most types of binoculars, when the eyepiece spacing is adjusted, the spacing between the objectives also varies.
Figure 20-1. Functional diagram of a pair of binoculars.
The objectives are farther apart than the eyepieces. This exaggerates perspective for scenes within a few hundred meters but does not affect perspective for celestial objects, which are too far away for parallax to exist relative to any single observation point. The light enters the objectives, passes through a pair of prisms that bring the light beams closer together by means of internal reflection, and finally leaves the eyepieces to enter the observer’s eyes. The principle of operation of each half of a pair of binoculars is identical to that of a Keplerian refracting telescope. The prisms turn the image right-side up and also orient the view properly left to right.
Binoculars are rated in terms of the magnification (the number of times the apparent diameters of distant objects are increased), as well as in terms of the objective-lens diameter in millimeters (mm). You’ll see a pair of numbers separated by a multiplication symbol, for example 7 × 50, printed somewhere on the assembly. The first number is the magnification, and the second number is the objective-lens diameter.
In general, the light-gathering power of binoculars is proportional to the square of the objective-lens diameter. However, this holds true only when the binoculars are optimized for a particular observer. If you divide the objective-lens diameter by the magnification, you should get a number between approximately 4 and 8. This number is called the exit pupil of the instrument. For best viewing, the exit pupil of a pair of binoculars should be the same as the diameter of the pupils of the observer’s eyes (in millimeters) when adjusted to the darkness. In general, larger exit pupils (6 to 8 mm) are a good match for younger observers, and smaller exit pupils (4 to 6 mm) are better for older observers.
In terms of physical bulk and mass, binoculars range from tiny to huge. At least, this is the impression you’ll get. Some binoculars can fit in your pocket. (But always keep them in a carrying case when you’re not using them). Others are so large that you’ll want a tripod to support them. The most massive binoculars will make your arms tired if you have to hold them up for a long time. High-magnification binoculars, especially those greater than 8×, need the extrasteady support that a tripod can provide.
The biggest binoculars are more appropriately called binocular telescopes or stereoscopic telescopes. These are fabulous for viewing star clusters, galaxies, and nebulae. They also can deplete the average person’s bank account.
The prisms inside binoculars serve as mirrors to reflect the incoming light between the widely spaced objectives and the narrowly spaced eyepieces. Prisms provide better image resolution and contrast than mirrors. The best prisms are called porro prisms (Fig. 20-2A). They reflect the light entirely by total internal reflection, which you learned about in Chapter 17. Less effective but still superior to mirrors are roof prisms (see Fig. 20-2B), which have aluminized back surfaces that help reflect the light rays. Porro prisms are more expensive than roof prisms because a higher grade of glass must be used to get the highest amount of total internal reflection to occur without aluminized surfaces.
Another factor to consider in binoculars is whether or not the lenses are specially coated to minimize the amount of light they reflect. As you have seen if you’ve looked at the window of a darkened house from the outside during the daytime, all glass reflects light as well as transmitting it. Any light reflected is light that doesn’t pass through the glass. In binoculars or a telescope, you’ll want as much of the light as possible to reach your eyes and not be reflected back into space from the objective(s) or into the internal chamber of the instrument from the eyepiece(s). The best lenses have multiple coatings on both the inside surfaces and the outside surfaces. These binoculars will be specified as having fully multicoated optics.
Figure 20-2. The porro prism (A) provides better image quality than the roof prism (B).
When you look through a properly adjusted pair of binoculars, with the focus and barrel spacing optimized for your vision, you should see a single, large circular region. The absolute field of view is the angular diameter, in degrees of arc, of this region as measured against the background of distant stars. In some sets of binoculars, the absolute field of view is expressed in terms of feet at 1,000 yards instead of degrees.
The absolute field of view, which is defined in the same way as it is with telescopes (see Chapter 17), depends on the magnification and also on the apparent diameter of the circular region—the apparent field of view—as seen through the eyepiece. Binoculars with large apparent fields of view offer a more pleasant viewing experience than those with narrower apparent fields regardless of the absolute field of view.
Even if a pair of binoculars has a wide apparent field of view, the image quality won’t necessarily be good. How well do objects near the outer periphery of the field stay in focus compared with objects near the center? Are stars near the edge distorted or blurred? To what extent do “little rainbows” appear around stars, especially near the edge of the field? You can’t easily test these things in a hobby store when you are deciding which pair of binoculars to buy. Therefore, it’s a good idea to check out the return policy of any store with which you do business. If the binoculars prove unsatisfactory, you should be able to return them to exchange for a better pair or to get a full refund within a few days of purchase. Keep the sales receipt!
If you want to see planetary detail or intricate features on the Moon, you will need a telescope. The theory of telescope operation is discussed in Chapter 17. Here we’ll take a pragmatic view. If reading this chapter tempts you to go out and buy a telescope, that’s fine, but don’t spend more money than you can afford. Sleep on the idea before you act on it.
There are dozens of telescopes available for hobbyists. Some are inexpensive; others cost as much as a car. This chapter isn’t meant to be a shopping guide, but you should be aware of certain assets and limitations of the most popular hobby telescope designs. These include the Keplerian refractor, the Newtonian reflector, and a specialized form of Cassegrain reflector known as a Schmidt-Cassegrain telescope (SCT).
Before we compare the virtues and vices of the various telescope designs, there’s a specification you should know about. It is called the focal ratio, or f-ratio. This specification will appear as the letter f, followed by a slash, followed by a number.
If you’ve done much photography, you know about the f-ratio of a camera. In telescopes, the meaning is the same, but the dimensions are larger. The f-ratio is equal to the focal length of the objective divided by its diameter or aperture (Fig. 20-3). Thus, for example, an objective whose diameter is 20 cm with a focal length of 200 cm is an f/10 objective (as shown at A). If the focal length is cut to 100 cm, it is an f/5 objective (as shown at B).
Figure 20-3. The f-ratio of an objective is equal to the focal length divided by the diameter of the lens or mirror. At A, an f/10 objective; at B, an f/5 objective.
In general, objectives with smaller f-ratios make it possible to get larger absolute fields of view than is the case with large-f-ratio objectives. However, there is a tradeoff: The smaller the f-ratio, the more difficult it becomes to engineer the optics to provide quality images. This is especially true of refracting telescopes.
The Keplerian refractor, as you will remember from Chapter 17, uses a convex lens as the objective and a convex lens (actually, a set of two or more convex lenses) as the eyepiece. A well-made Keplerian refractor, mounted on a sturdy base, is a joy to use. The images are sharp, the viewing is stable, and the positioning of the telescope is intuitive. You can get great results without a lot of hassle. A poorly made refractor, however, can be, like anything shoddy, a source of frustration.
Refracting telescopes for amateur use range in diameter from about 50 mm (2 in) to 150 mm (6 in). The cost increases dramatically as the objective diameter increases. Another factor to consider is the manner in which the objective is made. Achromatic objectives are the most common; they consist of two different lenses, having different refractive indexes, glued together. This helps to reduce chromatic aberration, the tendency for focal length to vary with color, producing “rainbows” around stars and blurring planetary and lunar images. The greater the f-ratio, the less likely you are to have trouble with chromatic aberration in a refracting telescope if all other factors are constant. A typical value is f/10.
Apochromatic objectives provide the highest quality in refracting telescopes. As you should expect, telescopes that use this type of objective are expensive. Serious refracting-telescope lovers, to whom price is no object, seek apochromatic refractors. The f-ratios are generally smaller than those of the achromatic refractors, sometimes as low as f/5, and the image contrast is superior.
Overall, the Newtonian reflector can provide more light-gathering power for the money than any other hobby telescope. This is its chief advantage. The largest Newtonian reflectors in the amateur market have objective mirrors about 60 cm (2 ft) in diameter. Telescopes this large are heavy and bulky and are inconvenient to transport. But they’re fun to use, especially when looking at diffuse objects such as nebulae and galaxies.
Newtonian reflectors come in two types: normal-field and rich-field. Normal-field telescopes have large f-ratios; rich-field telescopes have small f-ratios. The cutoff between the two classifications is considered to be f/6. Normal-field telescopes produce crisper images for a given aperture, and they are also easier to collimate (adjust) than rich-field Newtonians. However, because the focal length is greater, the normal-field Newtonian’s tube is longer, and this makes it more difficult to carry around than a rich-field telescope of the same aperture. The rich-field telescope, as its name implies, can provide a larger absolute field of view than a normal-field telescope.
All Newtonian reflectors have part of their aperture blocked by the secondary mirror and its support. If you take a “star’s eye” view and look down the tube of a Newtonian reflector, you’ll see the obstruction (Fig. 20-4). This reduces the effective aperture slightly, although this is not significant in most designs. The bigger problem is that it reduces the image contrast. The light-gathering “hole” is not shaped like a perfect disk; the secondary mirror and its support put an irregular barrier there. Although you cannot notice it when you look through the telescope during normal use, this irregular barrier exacts a toll that refracting telescopes do not have to pay.
Figure 20-4. “Star’s-eye” view looking into the business end of a Newtonian reflector.
Some people dislike the fact that the Newtonian reflector’s eyepiece holder is in the side of the tube near the front. However, this is an asset in many, if not most, viewing situations, except with the largest normal-field designs. When looking at objects near the zenith using a modest-sized Newtonian, you don’t have to crouch or crane your neck. However, with larger Newtonians, you will need a stepladder to look through the eyepiece. A tall base support pedestal or tripod is also required for large-aperture, normal-field Newtonian reflectors. Otherwise, the mirror end will strike the ground when the instrument is aimed at objects high in the sky. Some people do not feel comfortable standing several rungs up on a stepladder in the dark.
All Newtonian reflectors, especially the rich-field types, exhibit a phenomenon called coma, in which objects near the edge of the field of view do not come to a perfect focus. Visually, this can be seen as a radial stretching out of stars near the periphery; in the most extreme cases, the stars near the edge of the apparent view field look like tiny, short-tailed comets. Coma can be overcome by a lens assembly called a coma corrector placed immediately on the objective side of the eyepiece.
In recent years, Schmidt-Cassegrain telescopes (SCTs) have become popular with amateur astronomers. Commercially manufactured SCTs are available with objectives ranging from about 13 cm (5 in) to more than 50 cm (20 in) in diameter.
The SCT has a physically short tube, even though its effective focal length is long. This is possible because of the convex secondary mirror. As a result, SCTs are more portable than Newtonian reflectors of comparable diameter. The eyepiece is located in the center of the objective mirror; this makes viewing more convenient for most people and eliminates the need for a tall tripod or pedestal to support large-diameter instruments. The secondary mirror is supported by a transparent corrector plate at or near the front of the telescope tube. This eliminates the need for side supports, so the secondary mirror produces less contrast reduction than is the case with Newtonian reflectors. The corrector plate seals the tube so that dust will not collect on the mirrors inside. Figure 20-5 is a “star’s-eye” view into a typical SCT.
Figure 20-5. View down the tube of a Schmidt-Cassegrain telescope. The transparent corrector plate serves to support the secondary mirror.
On the minus side, the SCT secondary mirror must be quite large to gather all the light from the primary mirror and direct it to the eyepiece. This means a greater reduction in the light-gathering area compared with the Newtonian design. An SCT is somewhat more expensive than a Newtonian of the same diameter. The corrector plate in an SCT has an annoying habit of developing condensation in humid environments.
The SCT is ideal for looking at nebulae and galaxies. If used in conjunction with a solid, heavy-duty, clock-driven equatorial mount (described later in this chapter), and if placed on level ground or pavement away from roads where trucks roll by and cause vibration, this type of telescope is exceptionally stable. It is preferred by many amateur astrophotographers for this reason.
You’ll need certain accessories with your telescope. You’ll want at least two good eyepieces. You will need some sort of finder scope or sighting device. A Barlow lens can provide extra magnification for your eyepieces. And, of course, there are optical filters of all kinds, some for looking at the Sun, others for the Moon, some for the planets, and others for more sophisticated purposes.
There are many different designs for telescope eyepieces. All make use of two or more lenses to optimize the apparent field of view, to provide good focus from the center of the view field to the edge, and to make it easy to look through the device. Most eyepieces have focal lengths between 4 and 40 mm.
In general, the longer the focal length of an eyepiece taken as a whole, the lower is the telescope magnification, all other things being equal. Remember how to calculate telescope magnification: Divide the focal length of the objective by the focal length of the eyepiece in the same units. If a telescope has a focal length of 2 m (or 2,000 mm), then a 4-mm eyepiece provides 500× and a 40-mm eyepiece provides 50×. The overall focal length of a telescope eyepiece is not necessarily the same as the focal length of any of its individual lenses.
Eye relief is an important specification of any telescope eyepiece. This is the maximum distance, in millimeters, that the surface of the eye can be away from the surface of the eyepiece lens on the observer side while still letting the observer see the entire apparent field of view. In general, the longer the focal length of an eyepiece, the greater is the eye relief. Larger eye relief numbers translate into easier viewing.
Some people find it difficult and unpleasant to look through short-focal-length eyepieces (6 mm or less) because the lens diameter is more or less proportional to the focal length. A few eyepieces have observer-side lens diameters smaller than the diameter of the pupil of the eye itself. This makes it necessary to bring the eye very close to the eyepiece. If the observer wears glasses, viewing through such eyepieces is compromised. People who don’t wear glasses will flinch away from the eyepiece if its surface comes into direct contact with the eyeball.
An eyepiece’s outside barrel diameter always should match the inside diameter of the telescope’s focusing mount. This is 31.75 mm (1¼ in) in most telescopes, but some instruments have focusing mounts that are 50.80 mm (2 in) across as measured through the inside. Adapters can be found to get small-diameter eyepieces into large-diameter mounts. However, if you want to use a large-diameter eyepiece in a small-diameter mount, you’ll have to improvise.
Here are four different types of eyepieces you are likely to find on the amateur market. Of these, the Ramsden and the Kellner are the simplest and therefore the cheapest. The orthoscopic and the Plossl are more sophisticated and expensive.
Figure 20-6A is a cross-sectional diagram of a Ramsden eyepiece. It consists of two planoconvex elements that have the same focal length. The larger lens is toward the telescope objective, and the shorter element is toward the observer. (This is true of virtually all telescope eyepieces.) The convex surfaces of the lenses face inward toward each other, and the flat surfaces face outward. This is an old design, dating all the way back to the 1700s. The Ramsden eyepiece is difficult to optimize because the spacing between the lenses is always a tradeoff between eye relief and the effects of lens aberration.
Figure 20-6B shows the Kellner design. It is similar to the Ramsden, except that the observer-side lens is a compound element consisting of a convex lens glued to a planoconcave lens. The compound element, when designed properly, eliminates the chromatic aberration inherent in the Ramsden design. The lenses must be coated to minimize reflection of light inside the eyepiece. Kellner eyepieces work best at the longer focal lengths, providing low to medium telescope magnification.
The orthoscopic eyepiece (see Fig. 20-6C) is among the most popular designs in use today. Image distortion and chromatic aberration are eliminated by the three-element compound lens on the objective side. This type of lens is noted for its excellent contrast and its ability to maintain focus from the center of the view field to the edge. In addition, the view field appears relatively flat as compared with some eyepiece designs that give the view field a concave (bowl-shaped) appearance. Orthoscopic lenses work well at all focal lengths.
Figure 20-6. Common telescope eyepiece designs: Ramsden (A), Kellner (B), orthoscopic (C), and Plossl (D). In each drawing, the observer’s eye is at left and the incoming light arrives from the right.
Figure 20-6D is a cross-sectional diagram of a Plossl eyepiece. This design first gained widespread acceptance among amateur astronomers in the 1980s. It has all the assets of the orthoscopic eyepiece. The eye relief of a well-made Plossl is adequate even at the shortest focal lengths. The observer-side lens has a relatively wide diameter. Plossls with long focal lengths (25 to 40 mm) are physically bulky, projecting some distance out from the telescope’s eyepiece tube, but they offer the ultimate in viewing comfort. Some have rubber eye guards to keep out external light.
Other eyepiece designs you might encounter are the Erfle, the zoom, the RKE, and the Huygens. The sheer variety of eyepieces can confuse the novice amateur astronomer. You can get on the Internet, enter eyepiece designs as keyword phrases (for example, Kellner eyepiece), and see what various folks have to say about the different designs. A salesperson at a hobby shop sometimes can help, but beware. A salesperson may be more motivated to get you to spend a lot of money than to sell you the best eyepieces for your needs.
With refractors and SCTs, the eyepieces are normally in line with the telescope tube. Viewing can be uncomfortable when such a telescope is aimed at objects high in the sky; you have to crouch down and crane your neck. However, there’s a simple and common solution to this problem: the star diagonal. This device bends the light path without introducing distortion, although it flips the image laterally, as a mirror flips your reflection.
A simple star diagonal employs a prism that causes the light to turn a 90-degree corner because of total internal reflection. The principle is the same as in binoculars. A cutaway view of a basic 90-degree star diagonal is shown in Fig. 20-7. More sophisticated star diagonals provide smaller angles, such as 45 degrees. Some star diagonals use two prisms rather than one, so the image is not laterally reversed.
Figure 20-7. A star diagonal uses a prism to bend the light, making it easier to view some celestial objects.
The lateral-reversal feature of basic star diagonals makes it rather inconvenient when you try to find objects in the sky using a star map. You have to imagine everything on the map backwards. With a little practice, however, most people can overcome this mental obstacle.
If you’ve ever used a telescope in an attempt to locate a planet or star and you didn’t have some sort of aiming or sighting device, you know how frustrating such an exercise can be. Except at the very lowest magnifications, you can end up searching for a long time. The simplest sighting devices are similar to gunsights. You aim the telescope as if it were a high-powered rifle. The more advanced type of sighting device has a small laser diode inside; it shines on a slanted glass to produce a variable-brightness red dot in the center of the view field. This dot is used to align the telescope with the object you want to observe.
Before you use it for celestial observations, the sighting device first must be aligned on a terrestrial target that is at least a couple of kilometers away. Find some object on the horizon that is large enough to see through the sighting device (that is, at 1×) yet small enough to fit into the view field of the telescope. Get the object centered in the view field of the telescope, fix the telescope in position, and then adjust the sighting device until the object lines up in it. Then check the view through the telescope again to be sure the object is still centered there. For good measure, go back and check the sighting device again too.
A more precise device for telescope aiming is a finder scope, often called simply a finder. This is a small Keplerian refractor. Most finders have objective diameters of 40 to 60 mm and magnify several times. The eyepiece has a pair of fine threads or wires, called cross hairs, placed at its focus. These produce a + or × pattern in the view field. The intersection point of the cross hairs is at the center of the view field. The finder position is adjusted until a star that falls at the cross-hair intersection point also shows up in the center of the view field of the main telescope at high magnification.
A finder can be aligned using the same technique as is used for a simple sighting device. The best finders are mounted in a pair of rings, both of which are attached to the main tube of the telescope near the eyepiece. Each ring has three or four adjustment screws. These should be fairly tight (but not so tight that the finder is damaged or the screw threads are stripped). A few finders have single-ring mountings. These are unstable. It is best to stay away from them.
A concave or planoconcave lens can be inserted in any telescope between the eyepiece and the objective, and the effect is to increase the apparent focal length of the objective. This type of lens is called a Barlow lens. It is placed close to the eyepiece. The lens is mounted inside a cylinder designed to fit into the eyepiece barrel of the telescope at one end and around the barrel of the eyepiece at the other end (Fig. 20-8).
Figure 20-8. A Barlow lens increases the magnification obtainable with a given eyepiece.
Because the Barlow lens increases the effective focal length of the objective, it provides increased magnification when a given eyepiece is used. Most Barlow lenses are rated at 2×. This means that they double the magnification for each eyepiece used. Some Barlow lenses are rated at 3×; these triple the magnification.
A Barlow lens can be useful in two situations. First, it eliminates the need for using eyepieces with extremely short focal lengths when high magnification is desired. An 8-mm eyepiece can be used in place of a 4-mm eyepiece, for example, when a 2× Barlow is inserted in the light path. Most people find an 8-mm eyepiece more viewer-friendly than a 4-mm eyepiece. Another asset of the Barlow lens is that it can double the number of obtainable levels of magnification, provided that you have chosen your eyepieces wisely. Suppose, for example, that you have a telescope whose objective has a focal length 1,000 mm and you have eyepieces whose focal lengths are 20 and 28 mm. This provides magnifications of 50× and 36×, respectively. If you obtain a 2× Barlow lens, you can obtain magnifications of 100× and 72× with the same two eyepieces. This gives you four well-spaced degrees of magnification.
A Barlow lens should not be used in an attempt to get extreme magnification. For example, if you have a telescope whose objective has a focal length of 2,000 mm and you use a 4-mm eyepiece with a 3× Barlow, you can theoretically obtain 1,500×. However, Earth’s atmosphere generally makes it futile to try for anything more than 500×, even with the largest telescopes. The slightest vibration will cause terrible wobbling of the image. In addition, the brightness of an observed image in any particular telescope decreases as the magnification increases. Remember the formula for the highest useful power you can get out of a telescope: approximately 20× per centimeter of objective diameter, or 50× per inch, with a maximum of 500× at sea level and most land-based locations.
Most hobby SCTs have f-ratios of around 10. This is all right for viewing planets, lunar surface features, and some star clusters. However, when looking at nebulae or galaxies, often you will want to reduce the magnification as much as possible. By so doing, you can concentrate the light so that dim, diffuse features show up more clearly against the background of the sky. Reducing the magnification with a given eyepiece also increases the absolute field of view.
A focal reducer/corrector is a convex lens that shortens the effective focal length of the SCT objective by a certain amount, usually 37 percent. This means that the effective focal length and the f-ratio are both cut to 63 percent of their values without the device installed. You might think of it as the opposite of a Barlow lens. With a 37 percent focal reducer/corrector, an f/10 telescope becomes an f/6.3 instrument. A focal reducer/corrector is larger in diameter than a Barlow lens and is equipped with a threaded mount that can be screwed into the opening in the objective mirror that passes light into the eyepiece holder.
Suppose that your SCT has an objective with a focal length of 2,000 mm. If you have a 40-mm eyepiece, a focal reducer/corrector shortens the effective focal length to 1,260 mm. This reduces the magnification from 50× to a little more than 30×. It also increases the absolute field of view by a factor of about 1.6. The corrector feature helps to ensure proper focus throughout the apparent field of view.
You can use a telescope to look at the Sun, but there are some precautions you must take to avoid damage to your telescope, your eyesight, or both. Before you point a telescope toward the Sun, get a solar filter that fits over the entire skyward opening of the telescope. The filter must be as large in diameter as the objective and is called a full-aperture solar filter. With such a filter, direct sunlight does not fall on any of the telescope optics. Only certain types of filters are acceptable; these block ultraviolet (UV) rays that otherwise could damage your eyes even if the image is not uncomfortably bright. The brand-name telescope manufacturers such as Celestron supply excellent solar filters. They’re not cheap, but neither are your telescope or your eyesight.
If you have a finder that uses lenses, such as a Keplerian refractor with cross hairs, cover it before aiming the telescope at the Sun. Otherwise, you risk damage to the finder’s eyepiece and cross hairs.
Never use a “sun filter” that screws into telescope eyepieces! Such a device is at the prime focus of the telescope objective, so it will heat up. Such filters have been known to melt or crack. If one of these “filters” fails while you’re looking at the Sun, you will remember the experience for the rest of your life. You’ll be lucky if your retina is not injured permanently.
Have you heard that you can aim a telescope at the Sun without a solar filter, with the eyepiece installed, and let the brilliant light shine onto a white piece of paper or a screen to see details of the Sun’s surface? In theory, this scheme works, and you can in fact get a decent image without risking damage to your eyes. Several people can view the image at the same time. But this is a bad idea. It subjects the eyepiece to direct focused sunlight, which can permanently damage the eyepiece. Besides this, as the Sun moves in the sky or as you move the telescope around while locating the Sun, the focused spot will strike and heat up interior components of the telescope.
Think of the focused, unfiltered rays of the Sun as the business end of a blowtorch. Would you turn a hot flame on anything you value? Of course not. So follow the universal rule: Always filter sunlight before it gets into a telescope (Fig. 20-9). Treat your telescope as kindly as you treat your own eyes.
If you have a telescope whose objective lens or mirror is larger than about 10 cm (4 in), the Moon will appear extremely bright at low magnification when it is near the full phase. In fact, at the lowest obtainable magnifications with SCTs using focal reducer/correctors, the full Moon can appear so brilliant that it hurts your eyes to look at it. A Moon filter, attached to the eyepiece, renders the Moon’s image tolerable under these conditions.
A Moon filter, also called a lunar filter, is tinted grayish, gray-green, or brownish, like the lenses in a high-quality pair of sunglasses. It is mounted in a threaded ring that screws into the objective side of the eyepiece. This placement is all right; the Moon’s light is not intense enough to cause damage to a telescope’s interior components or to an eyepiece. You’ll know when you need a lunar filter and when you don’t. At high magnification levels or when the Moon is a thin crescent, you won’t want one. At low magnification, after sundown, and when the Moon is gibbous or full, you will.
Figure 20-9. A solar filter should keep direct sunlight out of the interior of a telescope.
It is not easy for most people to find places where the nighttime sky is not polluted by airglow. Airglow doesn’t interfere very much with viewing of the Moon or the planets, although dust and particulate pollution, along with convection currents rising from the day-heated land that roil the evening air, can blur even these images and reduce their contrast. If you want to see nebulae, globular clusters, and galaxies, you will have trouble with airglow unless you take some measures to reduce it.
A light-pollution-reduction (LPR) filter reduces the effects of airglow at night. Most big outdoor lamps are sodium-vapor devices that emit most of their radiation at well-defined wavelengths in the yellow part of the visible spectrum. Mercury-vapor lamps are less common, but they too emit most of their light at certain discrete wavelengths. A line-type LPR filter is designed to transmit light at all visible wavelengths except specific ones. In this way, the airglow from sodium-vapor and mercury-vapor lamps can be attenuated, whereas light at other wavelengths passes through the filter unaffected. Other LPR filters include narrowband and broadband types. The particular filter that will work best in a given situation must be found by trial and error. The folks in your local astronomy club can give you advice based on their own experiences. All LPR filters, like Moon filters, are designed to be screwed into the objective side of an eyepiece.
Planetary filters are simple color filters that are screwed into eyepieces in the same manner as are Moon filters and LPR filters. They are available in almost any tint you can imagine. You can use an orange filter to look at Mars, a yellow-green filter to look at Jupiter, or a red filter to look at Venus. You can even use these filters (in addition to a full-aperture solar filter—never all by itself!) to look at the Sun. Experimentation is the key. Try all the filters you can find. Look at anything you want with them. See if you can borrow some from friends, so that you don’t spend a lot of money unnecessarily. You’re bound to see some interesting things.
Telescopes can be supported, mounted, and driven in various ways. Some systems are designed for simplicity and convenience; others are intended for ease of tracking once the telescope has been aimed. Any system can be driven by a motor that keeps it aimed at an object as the Earth rotates. The most sophisticated systems can locate objects using computer programs and can follow them so precisely that they remain in the field of view for an hour or so.
With the exception of the Dobsonian mount (described below), the most common amateur telescope support is the tripod. A telescope tripod resembles the tripods used for photography or video recording, but the telescope design is sturdier and more resistant to vibration. A typical telescope tripod can be adjusted in height from approximately 1 m (40 in) to 1.5 m (60 in). As its name implies, the tripod has three legs, the lengths of which are independently adjustable. This allows you to level the instrument even if the surface is somewhat irregular.
The pedestal support is preferred by some people for use with large telescopes, especially those using the German equatorial mount (described below). A pedestal consists of a single, massive, thick vertical post. The post can be supported on a flat base, or it can be driven and cemented into the ground. Pedestal supports are less portable than tripods (and of course, not portable at all if permanently secured to the surface). This type of support is sturdier than most tripods. Care must be exercised to ensure that the pedestal is perfectly plumb (vertical).
The simplest, and generally the cheapest, set of bearings you can get for a telescope is the azimuth-elevation (az-el) mount. It goes by other names too, such as altitude-azimuth, altazimuth, or alt-az. Figure 20-10 is a simplified drawing of a refractor employing this system. The azimuth bearing turns 360 degrees in the horizontal plane. The elevation bearing rotates in the vertical plane for as far as the telescope will allow. Theoretically, only 90 degrees of elevation range is necessary, from the horizon to the zenith. Using the bearings in combination, the telescope can be pointed to any object in the sky. Because of the construction of the particular az-el system shown in Fig. 20-10, it is sometimes called a fork mount.
Figure 20-10. The az-el mount makes it easy to aim a telescope at any point in the sky.
The az-el mount, while convenient for casual telescope users, has limitations. As Earth rotates, objects move across the sky in paths parallel to the celestial equator. Near the celestial equator, this motion is from east to west; near the celestial poles it is in circles, counterclockwise in the northern hemisphere and clockwise in the southern. In order to follow an object across the sky over a period of time, you’ll have to adjust both the azimuth and the elevation settings in an az-el mount (unless you happen to be at either the north or the south geographic pole). It would be much easier if you only had to move one of the bearings. This is possible with a simple modification of the az-el system.
If an az-el mount is tilted so that the plane of the “horizon” corresponds with the celestial equator rather than with the actual horizon, a telescope can track objects in the sky by continuous adjustment of only one bearing. The 360 degree azimuth bearing from the az-el system becomes a right-ascension (RA) bearing. When it is rotated, the telescope moves east and west in celestial longitude. The range of the elevation bearing from the az-el system must be extended to cover 180 degrees, and it becomes a declination bearing. When it is adjusted, the telescope moves north and south in celestial latitude.
The proper tilt for the converted az-el system is accomplished by means of a wedge, constructed or set at an angle that corresponds to the terrestrial latitude where the telescope is located. The fork mount, which gets its name from its shape, lends itself readily to this scheme (Fig. 20-11). This system is popular among SCT users.
The fork mount/wedge requires alignment to work properly. The RA axis (the axis of the right-ascension bearing) must point precisely at the north celestial pole. A slight misalignment will result in improper tracking, especially over long periods of time. To ensure that the alignment is correct, the wedge is adjustable. You should determine your latitude down to the minute of arc. (There are several Web sites that can provide you with this information if you live in a town of at least medium size. Because the Web page locations change constantly, the best way to find them is to enter the phrase latitude and longitude into a well-known search engine such as google.com.)
Large Newtonian telescopes—those over 25 cm (10 in) in diameter—present a special challenge when it comes to mounting them and viewing through them. The Dobsonian mount, named after its inventor, is an az-el system that sits directly on the ground or pavement (Fig. 20-12).
Figure 20-11. A wedge can be added to a fork mount for easy tracking of celestial objects.
Dobsonian mounts usually are constructed from plywood with Teflon bearings. The plywood helps to dampen vibrations transmitted through the ground, such as can be caused by heavy trucks on nearby streets. The Teflon bearings provide ease and smoothness of movement. Because the telescope sits lower to the surface than is the case with a tripod or pedestal mount, the eyepiece can be reached with less difficulty. However, with extremely large Newtonian reflectors (those over 40 cm across and/or with high f-ratios), a ladder is necessary for viewing objects near the zenith.
The limitations of the Dobsonian mount are similar to those of the az-el mount. Tracking can be inconvenient because both the azimuth and the elevation bearings must be moved. Special equatorial mounting tables are available for Dobsonian telescopes. The table is sloped, and the slope can be adjusted; it performs the same function as the wedge in the fork mount/wedge system. If you happen to live in the tropics, the slope of the table can interfere with the full range of movement of the Dobsonian mount. However, at higher latitudes, including most of Europe and North America, the equatorial table is a convenient option.
Figure 20-12. A Dobsonian mount is convenient for use with large Newtonian reflectors.
One of the best-known sets of telescope bearings is found in the German equatorial mount. It can be recognized by its unique configuration and counterweight (Fig. 20-13). It, like the fork mount/wedge, moves along RA and declination coordinates. The RA axis is adjustable and must be aimed at the north celestial pole. The most sophisticated German equatorial mounts are equipped with sighting scopes that make them fairly easy to align. Once the mount is adjusted properly and the telescope is aimed at an object in the sky, the object can be followed by moving only the RA bearing.
Some people find the German equatorial mount unnatural and awkward, especially when observing things in the circumpolar region. However, a well-made and well-adjusted system of this type is superior to any other for serious use with massive and bulky telescopes. Not surprisingly, the best German equatorial mounts are expensive. Some of the largest ones, including a heavy-duty pedestal base, cost more than $2,000.
Figure 20-13. Simplified drawing of a German equatorial mount.
If you want to gaze at celestial objects through a telescope for a long time, a clock drive is a great convenience. This is especially true if you have a group of people, each of whom must look through the telescope in turn and not all of whom are experts at aiming it. The higher the magnification, the more quickly a celestial object will “drift” out of the field of view unless some compensation is made. Objects near the celestial equator drift faster than objects near the celestial pole.
The heart of the clock drive is a slow motor that makes one complete 360-degree revolution per sidereal day, that is, every 23 hours and 56 minutes. This is accomplished by gearing-down and precise regulation of the actual motor speed. Clock drives are typically designed to work with either a fork mount/wedge or a German equatorial mount because only the RA bearing needs to be connected to the motor. Clock drives can function with az-el drive systems, but they are more complicated and more expensive because both bearings must be adjusted by the device as time passes.
With any clock drive, the quality of the gears is particularly important. If there is significant play in the gears, the telescope will wobble with the slightest disturbance. This effect is particularly annoying at higher magnification and takes away much of the advantage of the clock drive. If you plan to do any time-exposure astrophotography with your telescope, you will need a clock drive, an equatorial mount, and a guiding device that makes minute corrections based on a guide star that you select within the field of view. Under these circumstances, telescope vibration and gear play cannot be tolerated at all.
Clock drives require a source of electrical power. This can be a battery, or it can be the household utility current. Batteries tend to wear out fast in most clock drives, and they never go dead when it’s convenient. (No time is convenient for a power failure!) Use of the utility power requires an extension cord.
In recent years, a number of amateur telescopes, particularly SCTs, have been made available equipped with microcomputers that automatically guide the instrument to any of several thousand objects in the sky. These telescopes are manufactured by Celestron, Inc., among others. The most sophisticated models incorporate Global Positioning System (GPS) receivers so that the alignment process is automatic. You don’t even have to know where on Earth you are to set up such a telescope and use it.
A computerized drive, like the venerable videocassette recorder (VCR), requires the user to climb a learning curve. The system must be programmed and objects selected according to a certain sequence of entries. The information is entered on a keypad, and the system status is displayed on a screen. You also can locate objects manually using a set of up/down and left/right (or north/south and east/west) buttons. The slew rate (the speed at which the telescope turns as you hold down one of the buttons) can be selected over a range from slowest to fastest, for example, from 1 (very slow) to 9 (quite fast).
Once an object has been located in the sky, the telescope can be programmed to follow it. This scheme can work with az-el or equatorial systems, but if you have astrophotography in mind, the equatorial system is a must. Celestial objects rotate in the field of view over time when an az-el clock drive is used because an az-el–mounted telescope doesn’t maintain a constant attitude (orientation) with respect to celestial coordinates as the heavens sweep around the celestial pole. This will blur a time-exposure photograph, even if the bearings and the clock drive itself are aligned perfectly.
For a computerized drive to work correctly, the telescope must be aligned with great accuracy. If it doesn’t have the GPS feature, this means that it has to be set by using two or three reference stars. These stars must be far apart from one another in the sky, and they must all be above the horizon at the time of alignment. You will have to know your terrestrial latitude and longitude down to the minute of arc or better. In addition, you’ll have to know the exact time. This can be found at the following Web site (as of the time of this writing):
http://www.time.gov
It will take some practice to get good at aligning a computerized drive system unless it has GPS built in. You will have to learn to carry out the whole process within a few moments. With each tick of the clock, your reference stars move across the heavens by several seconds of arc. Once you have the telescope aligned accurately, you can select the object you want by navigating the computer menu, and the telescope will aim itself. It’s best to use the lowest available magnification initially because this gives your telescope the greatest margin for error. You can then fine-tune the position of the telescope if you want more magnification.
 Quiz
QuizRefer to the text if necessary. A good score is 8 correct. Answers are in the back of the book.
1. A telescope has an f-ratio of f/5. The magnification is 100×. What is the focal length?
(a) 500 mm
(b) 20 cm
(c) 100 mm
(d) It cannot be determined from this information.
2. A telescope has an objective focal length of 1,000 mm, and the eyepiece has a focal length of 25 mm. A 2× Barlow lens is used. What is the magnification?
(a) 20×
(b) 40×
(c) 80×
(d) It cannot be determined from this information.
3. Some telescopes have a tendency to produce blurring near the outer edge of the field of view, even when things are in perfect focus at the center. This is called
(a) coma.
(b) dispersion.
(c) chromatic aberration.
(d) depth of field.
4. The optimal position of a solar filter in an SCT is
(a) in front of the objective.
(b) between the objective and the secondary mirror.
(c) between secondary mirror and the eyepiece.
(d) between the eyepiece and the observer’s eye.
5. You see a pair of binoculars in a surplus store. You see “7 × 70” stamped on them. The diameter of the objective lenses is
(a) 10 cm.
(b) 70 cm.
(c) 0.1 m.
(d) 70 mm.
6. Suppose that an SCT has a magnification of 200× with a particular eyepiece. A focal reducer/corrector that cuts the f-ratio by 37 percent is installed. What is the resulting magnification if the same eyepiece is used?
(a) 63×
(b) 74×
(c) 126×
(d) 200×
7. The bearings of a properly adjusted fork mount/wedge move the telescope along coordinates of
(a) compass direction and elevation.
(b) celestial latitude and celestial longitude.
(c) azimuth and altitude.
(d) right ascension and elevation.
8. The light-gathering area of a refracting telescope is
(a) proportional to the objective diameter.
(b) proportional to the square of the objective diameter.
(c) proportional to the f-ratio.
(d) proportional to the magnification.
9. A filter that allows all light to pass through, with the exception of light at a single wavelength, is called
(a) broadband.
(b) line-type.
(c) planetary.
(d) lunar.
10. A prism that turns the path of the light rays entirely by means of total internal reflection is called
(a) a dispersive prism.
(b) a reflective prism.
(c) a flint prism.
(d) a porro prism.