Tests with High Direct Voltages

Abstract

HVDC test voltages represent the stress of insulations in HVDC transmission systems. Today, HVDC transmission systems are long point-to-point connections for the transmission of high power. These links are realized by HVDC overhead lines and HVDC cables, especially submarine cables. In the near future, it is expected that the application of the HVDC technology will increase and also HVDC networks will be established (Shu 2010). Therefore, also HV tests as well as PD and dielectric measurements under direct voltage are becoming of increasing importance. Design and testing of HVDC insulation has to be performed under a difficult understanding of the acting electric fields. The reason are space and surface charges which are generated even below the PD inception voltages and strongly influenced by thermal effects. There are many publications on these phenomena, e.g. (Hering et al. 2017; Ghorbani et al. 2017; Christen 2014). This chapter starts with the different circuits for HVDC test voltage generation. Then, the requirements for HVDC test voltages according to IEC 60060-1:2010 and the consequences for the components of test systems are considered. The interactions between test generator and test object are investigated for capacitive load—e.g. of submarine cables—and for resistive load in case of wet, pollution and corona tests. A short description of test procedures with HVDC test voltages follows. Finally, it is described how direct voltages can be measured by suitable measuring systems of resistive dividers and suited measuring instruments, and how measurements—e.g. PD measurements—at DC voltage are performed.

6.1 Circuits for the Generation of HVDC Test Voltages

Today, HVDC test voltages are generated by rectification of HVAC voltages of transformers (see Sect. 3.1.1). Modern solid state rectifier elements, in the following “diodes” (silicium diodes), enable the generation of all necessary test voltages and currents, but the limitations in the reverse voltage to few 1000 V require the series connection of these diodes for HV rectifiers with reverse voltages up to several 100 kV’s or even MV’s. When the circuits for HVDC test voltage generation are considered, all mentioned rectifiers are HV rectifiers assembled from many diodes (see Sect. 6.2.2).

6.1.1 Half-Wave Rectification (One-Phase, One-Pulse Circuit)

When a HV rectifier, a load capacitor C (e.g. capacitive test object or smoothing capacitor) and a resistive load R (e.g. resistive voltage divider or resistive test object) are connected to the output of a simple HVAC transformer circuit (Fig. 6.1a), a HVDC voltage is generated. The rectifier opens for half-waves of one polarity and closes for the opposite polarity. It opens only as long as the HVAC voltage at the “stiff” transformer output is higher than the voltage of the charged capacitor. As soon as the capacitor carries any charge, its discharging starts and becomes significant when the rectifier closes after the voltage has reached its maximum V_max (Fig. 6.1b). The capacitor is discharged to a minimum voltage V_min, until the rectifier opens again for a short time ΔT (also expressed by a phase angel α). This means the output voltage is not constant, and it shows a so-called “ripple” voltage δV which is defined by

$\partial V = \frac{{V_{ \hbox{max} } - V_{ \hbox{min} } }}{2}.$

(6.1)

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig1_HTML.gif — Fig. 6.1
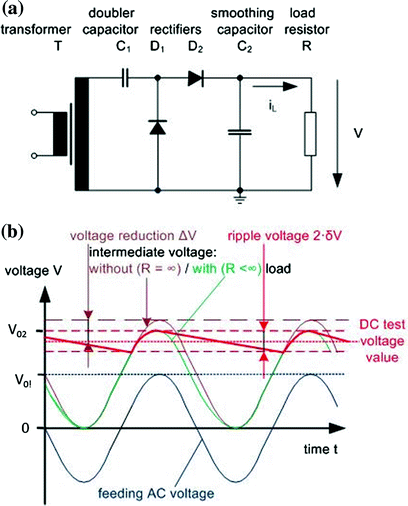
One-phase, one-pulse half-wave rectification, a equivalent circuit diagram, b feeding AC voltage and DC voltage with ripple, c modular test system for HVDC 135 kV/10 mA and HVAC 100 kV/11 kVA

The discharging current i_L(t) is connected with a charge Q which must be replaced within the short time ΔT by a current pulse i(t) from the transformer

$Q = \int\limits_{T} {i_{L} } (t){\text{d}}t = I \cdot T = 2 \cdot \partial V \cdot C = \int\limits_{{\Delta {\text{T}}}} {i(t){\text{d}}t} .$

(6.2)

The term “one-phase, one-pulse circuit” reflects that the feeding voltage is a single-phase one and the DC charging is performed by one current pulse per period. With the mean direct current

$I = \frac{{V_{ \hbox{max} } + V_{ \hbox{min} } }}{2 \cdot R}$

and the relation between the duration of period T and frequency f of the feeding AC voltage, one gets an important relation for the ripple

$\partial V = \frac{I \cdot T}{2 \cdot C} = \frac{I}{2 \cdot f \cdot C}.$

(6.3)

The lower the ripple, the smoother is the HVDC test voltage. The ripple decreases with increasing load resistance (This means with decreasing load!), increasing load capacitance and increasing frequency of the charging AC voltage. But, in case of half-wave rectification, the ripple remains quite large. Equation 6.2 shows additionally that the feeding HVAC transformer circuit must be able to supply a sufficient current i(t).

If the test object shows heavy pre discharges of relatively high pulse currents which may happen during wet and pollution tests, the voltage drops down as the transient energy demand cannot be supplied via the transformer, it must be taken from the smoothing capacitor C. To limit this voltage drop d_V, the smoothing capacitance should be large enough.

Note According to IEC 60060-1:2010, the voltage drop is the “instantaneous reduction of the test voltage for a short duration of up to few seconds”. Here, it will be used according to this definition. In literature, e.g. Kuffel et al. (2006) or Kind and Feser (1999), the term voltage drop is used for the continuous voltage reduction between the no-load case and the load case, especially of multi-stage cascades. The term “voltage reduction” will be used for this phenomenon in the following. The voltage reduction is caused due to the “forward voltage drop” and the internal resistance of the rectifiers.

HVDC sources with half-wave rectification are usually not powerful enough. They are used as HVDC attachments to HVAC test systems especially for demonstration circuits and for student’s training (Fig. 6.1c). The half-wave rectification causes a non-symmetric load of the HVAC power supply. This can even lead to saturation effects in the transformer. If a transformer with symmetric output—this means grounded midpoint—of the winding is available (Fig. 6.2), the opposite polarity of the AC voltage contributes to the charging of the smoothing capacitor C and avoids saturation effects, since each of the rectifiers opens for one half-wave. Consequently, two charging current pulses appear, and this one-phase, two-pulse circuit halves the ripple. The two-way half-wave rectifier circuits are also basic stages for HVDC cascade generators.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig2_HTML.gif — Fig. 6.2
One-phase two-pulse half-way rectification

6.1.2 Doubler and Multiplier Circuits (Greinacher/Cockcroft-Walton Cascades)

With the circuit of Fig. 6.3a, the output voltage can be doubled: The so-called doubler capacitor C₁ is charged to the voltage V_C1, and then, the voltage over the rectifier D₁ is oscillating around this value V_C1. Consequently, the smoothing capacitor is charged to a voltage which doubles the peak of the feeding AC voltage (Fig. 6.3b) if the losses in the circuit are neglected (R → ∞). With losses—this means with a load resistor R—the output voltage is reduced below the theoretical no-load value. For the usual design of a HVDC attachment with doubler circuit connected to a HVAC generator (Fig. 6.3c) of a rated direct current of few 10 mA and a ripple factor δV/V = δ ≤ 3%, this reduction might be in the order of 10%. Therefore, the smoothing capacitance should be selected large enough.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig3_HTML.gif — Fig. 6.3
One-phase, one-pulse doubler circuit with half-wave rectification, a equivalent circuit diagram, b AC feeding, oscillating intermediate and DC voltages (R → ∞), c modular test system with doubler circuit 270 kV/10 mA

The doubler circuit shall be understood as the basic stage of a multiplier circuit first proposed by Greinacher (1920) for HVDC power supply for nuclear physics and improved by Cockcroft and Walton later on in 1932. The principle shall be discussed for a cascade of three stages (Fig. 6.4): The left column of the capacitors contains the doubler capacitors [sometimes also called “blocking capacitors” (Kind and Feser 1999)], and the right column contains the smoothing capacitors (Fig. 6.4a). When voltage reduction and load resistance are neglected, the AC voltage V_AC(t) with a peak value of V_max is oscillating around a DC offset of $1 \cdot V_{\hbox{max} }$ at the first doubler capacitor and delivers a DC value of $V_{1} = 2 \cdot V_{\hbox{max} }$ at the output of the first stage of the smoothing column (Fig. 6.4b). At the second stage, the DC offset is $V_{12} = 3 \cdot V_{\hbox{max} }$ and the voltage at the smoothing column is $V_{2} = 4 \cdot V_{\hbox{max} }$ . Consequently, the DC offset at input of the third stage is $V_{13} = 5 \cdot V_{\hbox{max} }$ , and the output of the generator is a DC voltage of $V_{3} = 6 \cdot V_{\hbox{max} }$ .

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig4_HTML.gif — Fig. 6.4
Greinacher cascade (one-phase, one-pulse multiplier circuit), a equivalent circuit diagram, b potential at the three stages, c generator with 500 kV per stage for 1500 kV/30 mA

The direct voltage per stage is twice the peak voltage V_max of the feeding alternating voltage. In stationary operation and rated voltage, the necessary reverse voltage of the rectifiers is $2 \cdot V_{\hbox{max} }$ . Doubler capacitors (except that of the lowest stage) must be able to withstand a DC stress of $2 \cdot V_{\hbox{max} }$ plus the AC stress of the feeding voltage. Smoothing capacitors have to withstand a direct voltage of $2 \cdot V_{\hbox{max} }$ . The lowest doubler capacitor is only stressed with half of that voltage but causes the largest contribution to the ripple. Therefore, it should have the double value of the capacitance, this fits to the voltage distribution and reduces the ripple. The 1500 kV cascade with a stage voltage of 500 kV—shown in Fig. 6.4c—is fed for its rated voltage with an AC voltage of 250 kV/√2 = 177 kV (rms).

The ripple depends for this one-phase, one-pulse multiplier circuit also from the number of stages. The continuous current I through the test object is supplied from the smoothing capacitors. Usually, all capacitors in the smoothing column have the same capacitance, which is necessary for a linear voltage distribution in case of transient stresses, e.g. at breakdown of the test object. The ripple caused by the discharging of each smoothing capacitor could be calculated with Eq. (6.3) if no charge is transferred through the rectifiers to the oscillating doubler capacitors. But, in reality, the charge transfer causes a higher ripple δV and a voltage reduction ΔV for cascades with n stages which can be estimated (Elstner et al. 1983) by:

$\partial V = \frac{I}{f \cdot C} \cdot \frac{{n + n^{2} }}{4},$

(6.4)

$\Delta V = \frac{I}{f \cdot C} \cdot \frac{{2 \cdot n^{3} + n}}{3}.$

(6.5)

The relation between the real output voltage (V_Σ − ΔV) and the cumulative no-load charging voltage V_Σ = nV₁ of a HVDC multi-stage generator can be understood as an efficiency factor (as usual for impulse voltage generators)

$\eta_{\text{DC}} = \frac{{V_{\tiny{\sum}} - \Delta {\text{V}}}}{{V_{\tiny{\sum}} }}.$

(6.6)

For practical cases, the voltage reduction can be remarkably higher than expressed by Eq. (6.5) which considers only the parameters of the generator. Mainly, stray capacitances in the feeding circuit cause an additional voltage reduction (Spiegelberg 1984).

Greinacher cascades are the most applied generators in HVDC testing. The polarity can be reversed by turning the rectifiers inside the generator by hand or motor. They are well suited for capacitive test objects, but have limits in case of a resistive load. The ripple can be reduced and the efficiency factor improved when the smoothing capacitances C and the frequency f of the feeding voltage are increased. AC feeding voltages of higher frequencies are traditionally generated by motor-generator sets, but nowadays static frequency converters should be applied. Furthermore, the number of stages should be limited and the stage voltage increased as much as possible. For rated currents above 100 mA, more efficient circuits should be applied.

6.1.3 Multiplier Circuits for Higher Currents

Similar to the one-phase two-pulse circuit (Fig. 6.2), also doubler circuits can be designed. They are base stages of the so-called symmetric Greinacher cascade, a one-phase two-pulse multiplier circuit for currents of some 100 mA (Fig. 6.5). This principle can also be applied with three phases. Figure 6.6 shows a three-phase, six-pulse multiplier circuit with six charging pulses within one period of the feeding three-phase voltage. Therefore, this circuit is suited for high test currents in the order up to few amperes.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig5_HTML.gif — Fig. 6.5
Symmetric Greinacher cascade (one-phase, two-pulse multiplier circuit)

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig6_HTML.gif — Fig. 6.6
Three-phase, six-pulse multiplier circuit

Table 6.1 compares the ripple values and the voltage reductions for the conventional and the symmetric Greinacher cascades as well as for the three-phase, six-pulse multiplier circuit. They are related to the influence of the number of stages n on the voltage reduction and on the ripple. They are valid under the assumptions that all capacitors have the identical capacitance C, only the lowest doubling capacitor has 2C. Furthermore, in all cases, the current I required by a load R and the test frequency f are identical.

Table 6.1

Comparison of voltage reduction and ripple for multiplier circuits of n stages (The terms “x” and “y” are the factors according to lines 2 and 3 for the n = 5 stages.)

Type of circuit parameter	Greinacher cascade (one-phase, one-pulse multiplier circuit) (Fig. 6.4)	Symmetric Greinacher cascade (one phase, two pulse multiplier circuit) (Fig. 6.5)	Three-phase, six-pulse multiplier circuit (Fig. 6.6)
Voltage reduction ΔV	$\frac{\text{I}}{{{\text{f}} \cdot {\text{C}}}} \cdot \frac{{2{\text{n}}^{3} + {\text{n}}}}{3}$	$\frac{\text{I}}{{{\text{f}} \cdot {\text{C}}}} \cdot \frac{{2{\text{n}}^{3} - 3{\text{n}}^{2} + 4{\text{n}}}}{12}$	$\frac{\text{I}}{{{\text{f}} \cdot {\text{C}}}} \cdot \frac{{2{\text{n}}^{3} - 3{\text{n}}^{2} + 4{\text{n}}}}{36}$
Ripple voltage δV	$\tfrac{\text{I}}{{{\text{f}} \cdot {\text{C}}}} \cdot \tfrac{{({\text{n}}^{2} + {\text{n}})}}{4}$	$\frac{\text{I}}{{{\text{f}} \cdot {\text{C}}}} \cdot \tfrac{\text{n}}{4}$	$\frac{\text{I}}{{{\text{f}} \cdot {\text{C}}}} \cdot \tfrac{\text{n}}{12}$
Example n = 5: $\Delta V = \frac{I}{f \cdot C} \cdot x$	x = 85 (assumed to be 100%)	x = 16.25 (19%)	x = 5.4 (6.3%)
Example n = 5: $\updelta = \frac{\text{I}}{{{\text{f}} \cdot {\text{C}}}} \cdot {\text{y}}$	y = 7.5 (assumed to be 100%)	y = 1.25 (16.7%)	y = 0.42 (5.6%)

The conclusions are drawn from the comparison of multiplier circuits of n = 5 stages. They show that both, voltage reduction and ripple, are about five times lower when a symmetric Greinacher cascade is used instead of a conventional one. When the three-phase cascade is used, a further improvement by a factor of three appears. As mentioned before, the investigated circuits should be applied as follows:

for rated currents below 100 mA, the conventional Greinacher cascade (Fig. 6.4),
for rated currents of some 100 mA, the symmetric Greinacher cascade (Fig. 6.5),
for rated currents higher than 500 mA, the three-phase multiplier circuit (Fig. 6.6).

for rated currents below 100 mA, the conventional Greinacher cascade (Fig. 6.4),
for rated currents of some 100 mA, the symmetric Greinacher cascade (Fig. 6.5),
for rated currents higher than 500 mA, the three-phase multiplier circuit (Fig. 6.6).

6.1.4 Multiplier Circuits with Cascaded Transformers (Delon Circuits)

When a suited transformer cascade supplies the AC feeding voltage into each stage of a HVDC multiplier circuit (sometimes called “Delon circuit”), the influence of the stages is compensated, and ripple and voltage reduction are reduced to the case n = 1 according to Table 6.1. Figure 6.7 shows the simplest circuit with n = 2 stages. All of them are based on a one-phase, two-pulse rectifier circuit (Fig. 6.2). The transformers of the cascade are not grounded and have to be isolated against the HVDC stress. The secondary winding of the lowest transformer (Fig. 6.7) is connected to the lowest smoothing capacitor and must be isolated in minimum for its DC potential V₁. The transformer winding (also on V₁) is connected to the primary winding of the next transformer which is on the DC potential 3 · V₁. Therefore, the second and all further transformers have to be isolated for a DC potential of 2 · V₁. Usually, all transformers are of the same design with a DC isolation of 2 · V₁ each. This DC insulation might be subdivided for the primary and the transfer (tertiary) winding.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig7_HTML.gif — Fig. 6.7
Multiplier circuit with cascaded transformers

The multiplier circuits with cascaded transformers enable the design of HVDC sources of medium rated currents with relatively low ripple and low voltage reduction. This can also be modified by feeding, e.g. a Greinacher cascade not only into the lowest stage, but also in one of the higher stages. Even the single charging into upper stages improves ripple and voltage reduction. As an example, Fig. 6.8 shows a cascade for 2000 kV with seven stages and feeding into the first and the fifth stage.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig8_HTML.gif — Fig. 6.8
Greinacher cascade with feeding into the sixth stage, a simplified circuit diagram, b generator for 2000 kV and for very fast polarity reversal up to 700 kV

A second application of HVDC sources with cascaded transformers is that for modular DC test systems. One 400-kV oil-filled module may contain two 200-kV stages of a one-phase, one-pulse doubler circuit (Fig. 6.9), each equipped with its own stage of the transformer cascade (see Sect. 3.1.1.3), the elements of the rectifying circuit including smoothing capacitor. Also a voltage divider is arranged inside the module. Then, several modules can be arranged one above the next to a very space-saving HVDC test system. The polarity reversal is motor-driven. Figure 6.10a shows such a system including blocking impedance and coupling capacitor for PD measurement. After connection of the power supply and the control unit, the system is ready for voltage testing. Such HVDC test systems for currents up to few 10 mA can easily be assembled and used for on-site testing, too. For generators of higher voltages and reasonable currents, modules can be switched in parallel. A stationary 2200 kV HVDC generator with five stages and parallel modules of the two lower stages is shown in Fig. 6.10b.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig9_HTML.gif — Fig. 6.9
Simplified circuit diagram of a HVDC module with two internal stages

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig10_HTML.gif — Fig. 6.10
Modular HVDC generators, a 800 kV/30 mA of two modules, b 2200 kV/10 mA of 7 modules in parallel-series connection. Both generators with external blocking impedance and PD coupling capacitor (size of modules is identical in both pictures!)

6.2 Requirements to HVDC Test Voltages

According to IEC 60060-1:2010 (Fig. 6.11), some necessary features of the design of HVDC test systems are discussed. There is a strong interaction between the test system and the test object (load). Therefore, the role of capacitive and resistive test objects is described for the selection of the generation circuit and its parameters.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig11_HTML.gif — Fig. 6.11
Definitions to direct test voltages

6.2.1 Requirements to HVDC Test Voltages

According to IEC 60060-1:2010, the HVDC test voltage value is not—as for the other test voltages—the peak value (V_max), but the arithmetic mean value during one period T of the charging process:

$V_{m} = \frac{1}{T} \cdot \int\limits_{{t_{1} }}^{{t_{1} + T}} {v(t) \cdot dt} .$

(6.7)

The tolerance of the test voltage value is 1% for test durations up to 1 min, but for longer durations, 3% are acceptable. The definition of the mean value V_m results mainly from the voltage measurement with conventional voltmeters (moving-coil meters) which measure the mean value. One has to consider that the peak voltage V_max determines breakdown processes and must be applied for research work.

With the ripple voltage δV (Eq. 6.1), one gets the dimensionless ripple factor δ as a relation to the test voltage value

$\delta = \frac{{V_{\hbox{max} } - V_{\hbox{min} } }}{{2 \cdot V_{m} }} \cdot 100 \le 3\% .$

(6.8)

The requirement δ ≤ 3% accepts that a remarkable difference appears between the peak voltage—which determines discharge phenomena in the insulation—and the test voltage value. A high ripple reduces also the inception voltage of partial discharges. Therefore, for both sides of an acceptance test, it is useful to have a ripple factor as low as possible.

Heavy pre-discharges, especially during wet and pollution tests, cause remarkable current pulses which may reduce the test voltage value V_m to a lower value V_{m min}. The HVDC test system should be able to supply these transient discharge current pulses of up to few seconds without an instantaneous voltage drop higher than 10%:

${\text{d}}_{\text{v}} = \frac{{{\text{V}}_{\text{m}} - {\text{V}}_{{{\text{m}}\,{ \hbox{min} }}} }}{{{\text{V}}_{\text{m}} }} \le 10\% .$

(6.9)

Unfortunately, IEC 60060-1:2010 does not specify the current value and its duration, e.g. for an assumed rectangular pulse or any indication of the required charge. For more details, see Sect. 6.2.3.2. Some publications consider d_V ≤ 10% as a too high value, (e.g. Hylten-Cavallius 1988; Köhler and Feser 1987). See also Sect. 6.2.3.2 below.

The reference value of the parameters δ and d_V is always the measured test voltage value V_m. Therefore, the voltage reduction ΔV (Eq. 6.5) is not a parameter of the test voltage, but of the HVDC test system. It characterizes the utilization factor of the used test system and has to be considered when a new test system is required.

6.2.2 General Requirements to Components of HVDC Test Systems

The circuit diagrams discussed above are simplified because they consider ideal elements and stationary conditions. Additionally, a HVDC generator has to withstand also transient stresses, e.g. in cases of a breakdown of the test object or a fast polarity reversal. If no countermeasures are taken, the stray inductances and capacitances would influence the distribution of the stressing voltages inside the generator. Furthermore, high breakdown currents have to be taken into consideration.

6.2.2.1 Protection Against Transient Stresses

The fast breakdown of the test object may excite oscillations of the HV test circuit consisting of the generator capacitances and/or the unavoidable stray capacitances and inductances. Also the diodes and the feeding transformer are not ideal elements and have certain impedances. All this forms a quite complicate equivalent network which should not be considered here, only the most important practical consequences of related calculations are summarized. The oscillations may cause non-linear voltage distributions in the generator and over-stresses of the components. The only way to avoid damages of components is a protection scheme of the generator. This starts with an external damping resistor between the generator and the voltage divider or the test object (Fig. 6.8a). Furthermore, there should be an internal damping resistor in all capacitances. Also the rectifiers should be equipped with grading capacitors for a linear voltage distribution at transient stresses and with internal damping resistors for both, over-current and voltage limitation. A rectifier consists of many diodes in series. Figure 6.12 shows an example of the protection circuitry of diodes for both cases, stationary and transient stress of the rectifier (Kind and Feser 1999). The protection scheme should be completed by protection gaps or surge arresters on especially endangered parts of the generator, e.g. the uppermost rectifiers or the output of the feeding HVAC transformer.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig12_HTML.gif — Fig. 6.12
Example of a protection circuitry of the diodes in a rectifier

Note The protection scheme operates only if a breakdown occurs at the test object connected via the external damping resistor. A breakdown between any point of the generator and any grounded or energized object, e.g. due to wrong arrangements in the HV test hall, may change the relation between the single components of the protection scheme in such a way that rectifiers and/or capacitors of the generator are endangered.

6.2.2.2 Polarity Reversal and Switch-off

A reversal of the voltage is a very hard stress for HVDC insulation, mainly because of the space and/or surface charges existing during the steady-state condition before and acting after the polarity reversal, too. (e.g. Okubo 2012; Wang et al. 2017; Tanaka et al. 2017; Azizian, A.et al.). Therefore, several standards require a polarity reversal in type tests. The used HVDC test system must have a motor-driven polarity reversal as, e.g. indicated in Fig. 6.9. The principle of the polarity reversal for a column of three rectifiers is shown in Fig. 6.13a: It is presumed that the rectifiers are connected to a column of smoothing capacitors and a capacitive test object (Frank et al. 1983; Schufft and Gotanda 1997). The reversal cycle starts at t₁ with switching-off the feeding AC voltage and a turn of the rectifiers. The capacitors are slowly discharged via the resistive part of the voltage divider (compare Fig. 6.8a). When the rectifiers approach the opposite electrodes at t₂, spark overs between their electrodes and the related opposite fixed electrodes occur. Within a very short time of some milliseconds, the capacitances are rapidly discharged to zero via the rectifier column. Now, the AC voltage is switched on again, and the capacitances are charged into the opposite polarity (t₃). The charging time depends on the time constant determined by the capacitances to be charged (generator plus test object), the impedances of the charging circuit and the available power of the HVAC feeding circuit. It may range from few seconds to few 10 s which is sufficient for most test applications.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig13_HTML.gif — Fig. 6.13
Polarity reversal, a switching process of the rectifiers, b definition of the reversal time

Under certain conditions a much faster polarity reversal is required, e.g. within 200 ms. For that, the reversal time is defined as the interval between 90% of the outgoing voltage and the same 90% value of the opposite polarity (Fig. 6.13); whereas, the discharge phase is fast enough, the charging phase must be accelerated. This is realized by selecting a rated value for the charging much higher than necessary and interrupting the charging when 90% of the required voltage is reached (t₄). To avoid an overshoot of the opposite polarity, the feeding must be pulse-controlled to the exact voltage value.

A HVDC voltage cannot be simply switched off; the charged capacitance must be discharged via a resistor when the voltage shall be reduced. It is reduced when the feeding stops because the resistive divider and other resistances to ground cause a discharge process. The time constants are in a range of several seconds (see Sect. 6.2.3.1). The slow discharge can be accelerated by a discharging bar , consisting of a damping resistor, a hook (connected to the test field earth by a metal cord) and an isolating bar (Fig. 6.14). After the discharging, the same earthing bar is used for earthing by its grounding hook instead of its discharge contact (Fig. 6.14b).

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig14_HTML.gif — Fig. 6.14
Grounding of small HVDC generators

When the HVDC test system is designed for polarity reversals as described above, then the capacitors might be discharged via the turning rectifiers. After the feeding AC voltage is switched off, the grounding procedure starts with the discharge via the divider resistor down to about one-third of the rated voltage before the rectifiers are applied. They should not be applied for higher voltages to avoid an over-stress of the rectifiers. The permanent grounding of the capacitor columns shall only be used, after the generator is discharged. This can be done by earthing ropes or—for generators of rated currents up to several 10 mA by earthing switches (see Sect. 9.26 and Fig. 9.28). For discharging high capacitances see Sect. 6.2.3.1!

A new HVDC generator should be equipped with a well-established protection scheme and with a reliable discharge and grounding system. When the generator is not used, it shall be carefully grounded. For safety reasons, all capacitors of each stage of multi-stage generators must be directly grounded by a metal rope which can be moved through the generator by motor preferably. If protection scheme and grounding system of an older generator do not correspond to these requirements, an upgrade is urgently recommended.

6.2.2.3 Voltage Control, Selection of Smoothing Capacitances and Frequency

The output of the HVDC generator is controlled via the feeding AC voltage. This means that the control is one of the AC generation circuit. Traditionally, this is a regulating transformer and nowadays mainly a thyristor controller operating in a pulse-width mode. The wider the voltage pulse the higher is the output voltage. The shape of the AC voltage is not important for the output DC voltage because the HVDC generator can be understood as a filter which connects harmonics of the alternating voltage to ground. The DC output voltage is hardly influenced by conducted noise signals. The thyristor controller can be switched within less than a millisecond, what is necessary for the mentioned fast polarity reversals. When a very sensitive PD measurement shall be performed at direct voltage, the switching pulses of the thyristor controller could disturb. In such cases, the application of a regulating transformer can be recommended instead of or in addition to the thyristor controller.

With respect to voltage reduction and ripple, capacitance and frequency are interchangeable (Table 6.1). This means the system can be improved either by increasing the capacitances or by increasing the frequency of the feeding voltage. Of course, also both can be applied for improving a design. It must be taken into consideration that the frequency range of capacitors is limited. Capacitors for frequencies >300 Hz are remarkably more expensive than those for power frequency. Therefore, the selection of capacitances and frequencies of the feeding voltage should take the economic situation into account. There is no general rule for an optimum now. Each design and parameter combination has to be considered separately for a reasonable economic solution.

In the past, motor-generator sets have been applied for the generation of AC voltages of higher frequencies than 50/60 Hz for HVDC test systems. Today, static frequency converters are available (Figs. 3.26 and 3.35) and connect the selectable higher frequencies with the advantages of a thyristor controller. It can be assumed that in the next future, the power supply and control of HVDC test systems will be based on static frequency converters.

6.2.3 Interaction Between HVDC Test System and Test Object

HV testing requires the consideration of test circuits including test objects on the basis of the relevant standards. The standards of HVDC power systems are under a rapid development, a final survey cannot be given now. The IEC Technical Committee 115 on HVDC Power Transmission Systems is preparing the necessary basic standards. A survey on components of HVDC power transmission—including their HV testing—is e.g. given in the IEC Document 115/154/CD:2017. One should follow the related development of standards with the knowledge about the physical processes as tried to explain it in the following.

6.2.3.1 Capacitive Test Objects

Testing of HVDC cables : When a DC voltage is attached to an extruded cable, the externally applied voltage can be controlled, but the field strength distribution in the cable insulation depends additionally of material, time and temperature due to space charge formation (Maruyama et al. 2004; Pietsch 2012). This is well demonstrated by HVDC experiments with cable samples (Fig. 6.15):

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig15_HTML.gif — Fig. 6.15
Field strength distribution influence by space charges (explanations in the text), a sample made of “AC Polyethylene”, b sample made of “DC Polyethylene”

(a)
For “AC XLPE” as it is used in HVAC cables , one observes during and for a certain time after the HVDC charging of the cable sample a field strength distribution with the maximum at the inner electrode as expected for a coaxial system (Fig. 6.15a: Laplace field, blue). After 5 h due to space charges the maximum has shifted to the outer electrode (dotted, green), but when steady-state conditions are reached (e.g. after 2180 h, red) space charges of opposite polarity generate an extreme maximum of field strength near to the inner electrode. This would not be acceptable for real HVDC cables.
(b)
Therefore “DC XLPE” has been developed using special additives to the polyethylene, which prevent a high space charge field near the inner electrode (conductor) (Fig. 6.15b). This guarantees a quite uniform and very stable steady-state of the insulation (field strength distribution after 5 h (dotted, green) and 2180 h (red) are practically identical). Also depending on the applied DC voltage the characteristic of the distribution is not changed. “DC XLPE” is well suited for HVDC cables.

The selection of the test duration has to consider the space charge behavior of the insulation and is quite difficult. This includes also different charging and discharging processes.

For charging currents of usually 3–10 mA, the charging may take up to several minutes. For example, the controlled charging of a 10 km long HVDC cable system, (about 2 μF) to a test voltage of 250 kV with a constant current of 5 mA would take nearly 2 min. Even during that short time, the generation of space charges cannot be excluded. After the test voltage value is reached, the shift of the field strength distribution to the steady-state (Fig. 6.15b) takes place.

At a test object of very low leakage current, the highest voltage value can remain for hours after switching-off the feeding voltage. To avoid serious safety problems, all capacitances must be discharged and grounded immediately (see Sects. 6.2.2.2 and 9.2.6.2). The necessary discharge and grounding switch must be equipped with a carefully designed damping resistor R_d which can be adapted to different capacitances of the test object. It transfers the discharge energy into heat. At a test voltage V_t, the time-dependent discharge current i.e., the maximum discharge current I_{e max} and the discharge time constant τ_e are given by:

$i_{e} (t) = I_{{e{ \hbox{max} }}} \cdot e^{{\frac{ - t}{{\tau_{e} }}}} \;{\text{with}}\;I_{{e{ \hbox{max} }}} = \frac{{V_{\text{t}} }}{{R_{d} }}\;{\text{and}}\;\tau_{e} = R_{d} \cdot C_{c} .$

(6.10)

In the mentioned example of the 10-km cable and V_t = 250 kV the stored energy is 62.5 kJ which may be discharged within few seconds. The damping resistance must be able to absorb this energy. Therefore, a wire resistor needs a careful thermal design. With respect to the recovery voltage (see Chap. 5), it is necessary to guarantee a permanent grounding of the generator and the capacitive test object when not in use.

The CIGRE Working Group B1.32 summarized the state of the art on the behavior of DC XLPE insulation and published the Technical Report 496 (2012) on the testing of extruded HVDC cables which acts as a certain standard. The report comprises the electrical tests for transmission cables using the phase-to-ground voltage V₀ under operational conditions as the reference voltage:

Prequalification tests of cable systems shall demonstrate the satisfactory long term performance of all components in an about 100 m long cable system. It is made only once during the development and includes a long duration voltage test at V_t = 1.45 V₀ of different cycles with and without load current generated by a cable heating equipment (in total of 360 days). It is completed by polarity reversal $(2 \cdot 1.25 \cdot {\text{V}}_{0} )$ and composite voltage tests (superimposed voltage tests: DC/LI and DC/SI), Finally a detailed inspection shall be made.

Type tests are made before supplying cable systems on a general basis to demonstrate satisfactory performance characteristics. It is made at V_t = 1.85V₀ for 30 days on cable loops typical for the cable system. The type test include load cycles, polarity reversal $(2 \cdot 1.45 \cdot {\text{V}}_{0} )$ test, DC/LI and a DC/SI composite voltage test followed by a HVDC test.

Routine tests (factory acceptance tests) are made on each manufactured component (cable or accessories) to verify that they meet the specific requirement. Each delivery length of cable shall be submitted to a negative DC voltage ${\text{V}}_{\text{t}} = 1.45 \cdot {\text{V}}_{0}$ for one hour. The CIGRE WG expresses that in addition to the DC test voltage an AC voltage test, which enables PD measurement, can be considered, provided the cable design allows AC application. Also for the cable accessories PD-monitored AC voltage tests might be useful.

On-site acceptance test (after–installation tests) shall demonstrate the integrity of the cable system as installed. The installed cable system shall be subjected to a negative HVDC test of ${\text{V}}_{\text{t}} = 1.45 \cdot {\text{V}}_{0}$ , details must be agreed between supplier and user.

HVDC super-long cables : The charging and especially the discharging of the cable systems under test becomes really difficult if e.g. a large submarine cable (e.g. V_m = 550 kV, 200 km long, corresponding to 70 µF, e.g. see Fig. 1.3) is tested for commissioning (V_t = 1.45 ·V_m = 800 kV). The energy stored in the cable is about 22 MJ. The discharging of this example has been investigated by Felk et al. (2017):

The discharging due to the resistance of the cable insulation itself would take nearly 10 h. This means, the cable would be stressed much longer than during the test of e.g. 1 h. Furthermore no wire resistor has the necessary thermal capacity to overtake the energy. Therefore a HVDC discharge device based on an water filled vertical resistor is proposed. A water processing unit—as used for water end terminations for cable testing (see Fig. 3.44)—controls the value of the conductivity of the water. The processing unit increases the water conductivity by dosing salt into the water, and reduces it by a special resin bed for de-ionization. Because the water is heated due to its resistance, it is also cooled in the processing unit. The water circulates in the resistor, which consists of an inner tube (where the water goes up) and an outer tube (where the water goes down). The electric field between the two tubes as well as in vertical direction must be carefully designed. The thermal design should avoid dew on the outer surface of the resistor. The resistor can be connected of 400 kV modules with a water volume of about 70 litres each. For example, the 800 kV water resistor would consist of two modules and is always connected in parallel to the cable under test.

The water resistance is controlled so that it is very high during charging and testing the cable (which means with a very low influence on the HVDC voltage source) and low for discharging the cable. The thermal capacity of the water is so high that the energy of 22 MJ will increase the water temperature only by 40 K! For a new test the water must be cooled down and de-ionized.

Liquid-impregnated paper-insulated (LIP) HVAC cables : In some respect, HVDC testing of HVAC LIP cable systems is the classic example for direct voltage application to AC insulation, especially for testing on site (see Sect. 10.4.2). Therefore, the HVDC testing of HVDC cable systems does not cause new problems. Quite small HVDC test systems are able to charge the high capacitance of a LIP cable system. Also a certain relationship between the lifetime under AC operational stress and the results of suited HVDC tests has been found.

HVDC gas-insulated systems : For the connection of HVDC cables to HVDC power supplies, gas-insulated systems (GIS) are necessary to create safe disconnecter gaps, to measure the voltages and currents and to arrange arresters (Hering et al. 2017). The capacitance of such systems is not very high, but the insulation of the gas, preferably SF₆, in combination with solid spacers is quite sensitive. The reason is a change of the voltage distribution from a capacitive electrostatic field during the charging process, polarity reversals or over voltages to a resistive streaming field under steady-state DC conditions. Then the field is additionally influenced by the charge accumulation on the solid spacers as well as by thermal effects. Also the motion of particles may show the phenomenon of “firefly” , a hovering of sharp, PD-generating particles near to one of the electrodes. Partial discharges under HVDC conditions are very seldom, stochastic and difficult to measure (see Sect. 6.5). All these phenomena must be considered when test voltages are selected and test procedures are agreed (CIGRE JWG D.1/B.3.57, 2017). This CIGRE Joint Working Group recommends a very detailed electric type test consisting of

a DC voltage withstand test,
an AC voltage withstand test,
PD measurement at DC and AC voltage,
a polarity reversal DC test (see Sect. 6.2.2.2),
a DC/LI composite voltage test (see Sect 8.2.3),
a DC/SI composite voltage test (see Sect. 8.2.3),
load condition test (withstand tests at rated current),
an insulation system test on single components (withstand and PD ≤ 5 pC).

With respect to the high effort of the type test, the routine tests and the on-site acceptance tests shall be simple and time efficient. This cannot be reached with DC voltages. As an acceptable compromise, these tests shall be performed at AC voltages and completed by PD measurement.

Finally a prototype installation test , similar to the pre-qualification test of cable systems (see above) is being discussed (Neumann et al. (2017). This test shall demonstrate the long-time performance of the complete gas-insulated HVDC system (expected life time of 50 years). It is a long time test for 30 days containing load cycles and composite DC/LI and DC/SI voltage tests (see Sect. 8.2.3). For the load cycles a DC current corresponding to the rated current shall be injected. It requires a special current source for operating on HVDC potential (Neumann et al. (2017)).

6.2.3.2 Resistive Test Objects (Wet and Pollution Tests)

Wet and pollution tests require an active current due to a low surface resistance and/or to heavy predischarges. The limitation of the required current by the HVDC test system leads to a limitation of the test voltage (voltage reduction ΔV) in case of a permanent stress in stationary operation and to an instantaneous voltage drop (d_V) in case of transient stress. In both cases, the test cannot be performed correctly. Therefore, a lot of research work has been related to amplitude and shape of the required current (e.g. Reichel 1977; Rizk 1981; Matsumoto et al. 1983; Kawamura and Nagai 1984; Merkhalev and Vladimirsky 1985; Rizk and Nguyen 1987; Cigre TF 33.04.01, 2000). As a result, the IEC Technical Standard 61245:2015 gives hints for HVDC pollution testing, and the necessary specification of HVDC test systems (ripple factor ≤3%, voltage drop ≤10%, voltage overshoot ≤10%, voltage measurement for both, continuous and transient voltage components). The practice of HVDC pollution testing is described in several publications, e.g. Windmar et al. (2014).

Whereas the voltage reduction becomes only acceptable, when a HVDC test system of sufficient rated current is applied, the voltage drop d_V can be reduced to an acceptable value by a very large smoothing capacitor, possibly by an additional capacitor (Reichel 1977; Spiegelberg 1984) or by a feedback control with a higher feeding voltage (Köhler and Feser 1987).

According to the above references, the leakage current impulse (Fig. 6.17) increases with the surface conductivity from some 10 mA up to the order of 1–2 A, but its duration decreases from some 10 s with the increasing current amplitude down to the range of few 100 ms. The maximum charge of one-pulse might be in the order of 200–300 mC. The real pulse is replaced for calculations by triangular or rectangular current pulses (Fig. 6.16). The acceptable voltage drop at such an impulse is between 5% (Hylten-Cavallius 1988) and 8% (IEC 61245:1993; Köhler and Feser 1987). Merkhalev and Vladimirski (1985) estimated the relation of the measured flashover voltage (V_FL) of a polluted insulator when a current pulse with the charge q_p appears and an unregulated Greinacher generator with a limited smoothing capacitance C_sl, (charge Q_sL) has been used in comparison to a generator with values C_s0 (of a charge Q_s0) which do not influence the flashover voltage (V_F0):

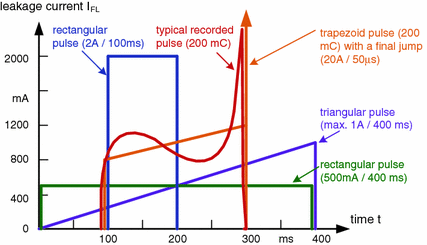
../images/214133_2_En_6_Chapter/214133_2_En_6_Fig16_HTML.gif — Fig. 6.16
Leakage current impulse (*red*) and its simplified replacements for calculations

$\frac{{V_{\text{FL}} }}{{V_{\text{F0}} }} = 1 + 0.5\left( {1 - \exp \left( {\frac{{ - q_{p} }}{{Q_{sL} }}} \right)} \right).$

(6.11)

The deviation between the measured, too high flashover voltage V_FL (caused by an insufficient generator) and the correct value V_F0 depends on the relation between the charge of the current pulse (q_p ≈ 200 mC) and that of the smoothing capacitor Q_sL. If the charge stored in the smoothing capacitor exceeds the charge of the current pulse by a factor of 10 (this means Q_sL ≈ 10 · q_p, = 2000 mC), then one gets the terms “exp(−q_p/Q_sL) ≈ 0.9” and “V_FL/V_F0 ≈ 1.05”. The influence of the generator on the flashover voltage is below 5%. That means, for the above-considered generator of V_r = 300 kV, a smoothing capacitor of

$C_{\text{s}} = \frac{{Q_{\text{sL}} }}{{V_{\text{r}} }} = \frac{{2\,{\text{As}}}}{{0.3\,{\text{MV}}}} \approx 6\, \upmu{\text{F}}$

would be necessary. This very high capacitance is too pessimistic (Hauschild et al. 1987; Mosch et al. 1988) when a powerful feeding and an optimized multiplier circuit (e.g. three-phase, six-pulse) are used. This shows that only the consideration of the required charge is too much simplified. A more detailed calculation shows that for q_p = 200 mC, a rectangular leakage current pulse of high peak and short duration causes a higher voltage drop than a lower current of longer duration (Fig. 6.17). This is related to the internal impedances of the test system. Consequently, the voltage drop—as also the above-mentioned voltage reduction—increases with the number of stages. The shape, maximum value and duration of leakage current pulses depend also from the height of the test voltage, the applied pollution test method and the parameters of the tested insulator.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig17_HTML.gif — Fig. 6.17
Output voltage of a HVDC generator (Fig. 6.19) depending on amplitude and duration of a rectangular leakage current impulse

For checking the suitability of a HVDC test system for pollution testing, a computer simulation of the behaviour of the whole test circuit under a leakage current pulse of, e.g. 200 mC, is recommended. Additionally, the assumed shape of that pulse must be selected (compare Fig. 6.16). This can be done using the results of earlier circuit simulations shown in Fig. 6.18 (Mosch et al. 1988): It compares the voltage drop caused by a trapezoid—recorded currents well describing—pulse of 200 mC including a very fast final jump—simulating the fast heating of the residual pollution layer and the immediate final leader discharge—with that of a short rectangular pulse (2 A, 100 ms). It has been shown, a rectangular pulse delivers an even larger voltage drop. The charge demand of the final jump is only few millicoulombs. Therefore, it is sufficient for the estimation of the voltage drop, to simulate the performance of a HVDC generator assuming short rectangular current pulses.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig18_HTML.gif — Fig. 6.18
Voltage drop for current pulses of rectangular and trapezoid shape

When the HVDC generator is fed by a thyristor controller with feedback control, the voltage drop can be limited to a preselected value by a suited regulator interval, e.g. to the required d_V ≤ 5% (Draft IEC 61245: 2013). Feedback control means that the test voltage and the leakage current are measured (Fig. 6.19 and used for the control of the feeding HVAC voltage. When a certain voltage drop is recorded, higher feeding AC pulses are applied for the duration of the leakage current pulse. Figure 6.20 shows that with increasing leakage current, the required frequency of the feeding pulses and, consequently, the ripple frequency of the output voltage increases. The regulating interval has to be selected in such a way that too high voltage drops and also overshoots (Draft IEC 61245:2013 requires ≤ 10%) are avoided. Today, most HVDC pollution tests are often performed with feedback—controlled HVDC test systems (Seifert et al. 2007; Jiang et al. 2010, 2011; Zhang et al. 2010a, b).

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig19_HTML.gif — Fig. 6.19
Circuit diagram of a HVDC test system with feedback control

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig20_HTML.gif — Fig. 6.20
Calculated output voltage of a feedback-controlled generator at different leakage currents, but identical pulse charge Q_p = 200 mC

HVDC pollution tests must not be performed at complete insulator chains; it is sufficient to test one insulator of a chain because a linear voltage distribution can be assumed within one chain of uniform pollution. Therefore, powerful HVDC test systems for pollution tests are usually limited to test voltages up to 600 kV.

In opposite to that, for insulators under artificial rain conditions, no uniform voltage distribution can be assumed, therefore wet tests must be performed up to the highest DC test voltages. This means HVDC test systems for rated voltages of 2000 kV are able to test open air insulations for 1000 kV HVDC transmission systems. Current pulses due to heavy streamer discharges in transition to leader discharges are characterized by charges up to 10 mC. These charges can be supplied by generators without feedback control and rated currents of few 100 mA. If it shall also be used for wet testing of contaminated insulators higher rated currents and feedback control might be useful (Su et al. 2005).

6.2.3.3 Corona Cages and HVDC Test Lines

A remarkable part of the active losses of an air insulated HVDC transmission system is caused by partial discharges which are usually designated “corona” discharges . The design of the bundle conductors of a HVDC transmission line is usually verified by tests in a corona cage and/or on a test line. A corona cage is a coaxial electrode system with an outer electrode up to few metres diameter, realized by metal rods, and the bundle conductor to be investigated forms the inner electrode on HVDC potential. The outer electrode is grounded via an impedance for measurement of corona current pulses or the average corona current. A HVDC test line is a one-to-one model of a future HVDC overhead line. It shall demonstrate the performance of all components under operational conditions. Both, corona cages and test lines are outdoor arrangements and require outdoor HVDC test systems (Elstner et al. 1983; Spiegelberg 1984).

Such test systems have to supply continuous currents of several 100 mA for avoiding a voltage reduction due to continuous corona discharges and short-term currents up to few amperes for avoiding voltage drops due to leakage current pulses. For a test line, both polarities must be supplied. This can be made by two separate HVDC test systems or by one system with bipolar output (Fig. 6.21). The shown system is a bipolar HVDC attachment to a 600 kV/3.3 A HVAC test system. It consists of two one-phase one-pulse doubler circuits, one for each polarity.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig21_HTML.gif — Fig. 6.21
Bipolar HVDC attachment of ±1000 kV/500 mA to a 600 kV/3.3 A HVAC test system.
Courtesy of KEPRI Korea

The test system itself must withstand its output voltage at all environmental conditions under which tests shall be performed. The details of those conditions (temperature range, atmospheric pressure range, humidity up to 100%, rain, natural contamination) must be carefully specified as well as a possible reduction of the rated voltage for certain test conditions. The external surface of all components shall be equipped with silicon rubber sheds (Fig. 6.21).

6.3 Procedures and Evaluation of HVDC Tests

Developed for all continuous voltages, the procedures and evaluations of HVAC tests (see Sect. 3.3 based on Sect. 2.4) can be applied for HVDC tests, too. Therefore, the described methods will not be repeated in this section, only few differences shall be mentioned.

The progressive stress test with continuously or step by step increasing direct voltage (Fig. 2.26) is used to determine a cumulative frequency distribution which can be approximated by a theoretical distribution function. The approximation can be performed according to the recommendations of Table 3.7. Also for life-time tests the remarks of Sect. 3.3.1 are applicable.

Compared with HVAC tests, it is more difficult to guarantee independence in HVDC tests. The reason is based on the phenomenon that partial discharges (and the trace of flashovers) at direct voltage cause surface and space charges of a long lifetime. Therefore, preceding stresses may influence the result of following stresses. It is absolutely necessary to check the independence of a test result before a further statistical evaluation will be made. The graphical check (Fig. 2.28) should be performed during the tests, and the test procedure should be modified if independence appears. Modifications are, e.g. the change of the rate of voltage rise, the careful cleaning of test objects after flashovers, the application of a new test object for each stress cycle or the application of a low alternating voltage between two stress cycles (“cleaning” by an alternating electric field). When a solid insulation is investigated, usually each test cycle requires a new sample.

In quality-acceptance testing, the procedure described in Sect. 2.4.6 and Fig. 2.39a is recommended also for direct voltages (IEC 60060-1:2010). The test should be performed at the polarity which delivers the lower breakdown voltages. If this is not clear testing at both polarities is necessary. Also PD-monitored withstand tests (Sect. 3.3.2) are applicable, but the randomness of partial discharges at direct voltage shall be considered (see Sect. 6.5). This may require longer durations on the different voltage levels (Fig. 2.39b). Other measurands than partial discharges, e.g. the leakage current or the insulation resistance, might be taken into consideration for diagnostic withstand testing.

6.4 HVDC Test Voltage Measurement

To measure high DC voltages up to some hundreds of kV originally sphere gaps have been used. As already pointed out in Sect. 2.3.5, based on experimentally determined breakdown curves of sphere gaps under clean laboratory conditions, a measuring uncertainty of about 3% is achievable for voltages ranging between 20 kV and about 2000 kV (Schumann 1923; Weicker 1927; Weicker and Hoercher 1938; IEC Publication 52:1960). However, the breakdown voltage of sphere gaps is not only affected by nearby earthed objects (Kuffel 1961) but also by the roughness of the electrodes as well as by dust and pollution deposited on the electrode surface, and as usual by the humidity and density of the ambient air. As charged particles are always attracted into direction of increasing electric field strength, which forces the deposition of dust particles on the electrode surface, the use of sphere gaps for measuring DC voltages above 200 kV is not recommended (see Table 2.7).

Based on experimental findings (Peschke 1968; Feser and Hughes 1988), DC voltages can also be measured at reasonable accuracy by means of rod– rod gaps in atmospheric air. Taking into account the correction factors for the humidity and density of air, a measuring uncertainty of about 2% is achievable for DC voltages ranging between approx. 20 and 1300 kV, as specified in the revised standard IEC 60052:2002 (see 2.3.5). However, the main drawback of air gaps used for measuring high voltages is the discontinuous measuring procedure, which is very time-consuming. Thus, since the 1920s spark gaps were increasingly replaced by electrostatic voltmeters (Starke and Schröder 1928), due to their capability to measure high voltages continuously. In the 1930s also measuring systems based on high-resistive converting devices have been introduced where the high voltage was indicated by either current or voltage meters, see Fig. 6.22 (Kuhlman and Mecklenburg 1935). Nowadays, the converting device provides commonly a resistive voltage divider, which is sometimes bridged by capacitances to record additional voltage changes superimposed on the stationary DC voltage, such as the ripple of DC voltages as well as the time-dependent voltage shape at polarity reversal.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig22_HTML.gif — Fig. 6.22
Basic principles commonly used for indirect HVDC measurements, a ammeter in series with a resistive converting device, b voltage measurement across the LV arm of a resistive voltage divider

An important design parameter of resistive voltage dividers used for DC measurements is the direct current flowing through the converting device. As dust and pollution deposited on the surface of the HV divider column may cause parasite leakage currents affecting the divider ratio, particularly at high air humidity, the direct current through the converting device should be chosen not lower than 0.5 mA (IEC 60060-2:2010). As already mentioned above, charged particles are always attracted into direction of increasing electric field strength, which forces thus the deposition of dust particles on the surface of the divider column. However, reducing the resistance of the HV arm to minimize the impact of dust and pollution is limited not only by the additional load acceptable for the HVDC test supply, but also by the permitted operation temperature which increases drastically at decreasing resistance of the HV divider column.

Example Consider the HV column of a 100 kV voltage divider having a total resistance of 10 MΩ, which is composed of 100 low-voltage resistors in series, each rated 100 kΩ and 1 kV. Applying a DC voltage of 100 kV, the current through the resistive converting device would attain 10 mA, so that the power dissipating in the HV divider column approaches 1,000 W. This leads not only to an increase of the operation temperature, which might change the divider ratio, but could also damage the HV arm. This is the reason why the current through the HV arm should be kept as low as possible, but not lower than 0.5 mA to prevent an impact of dust and pollution on the divider ratio, as mentioned above. Under this condition the voltage drop across each LV resistor forming the HV arm attains 0.5 kV, which is equivalent to a specific value of 1 MΩ/kV.
This example underlines that a divider current in the order of about 0.5 mA seems to be a reasonable choice, because from a thermal point of view the current should be as low as possible. However, a current below 0.5 mA would lead to an impact of parasite leakage currents on the measuring uncertainty, as mentioned above.

To limit the radial and tangential field gradients along the resistive HV arm, the LV resistors connected in series are commonly wounded around an insulating cylinder like a helix, as obvious from Fig. 6.23. The photograph shows a 300 kV DC divider designed by Peier and Greatsch (1979). The HV arm is composed of 300 pieces of LV resistors, each of 2 MΩ, where the bottom 2 MΩ resistor provides the LV arm, so that the divider ratio amounts 1:300. To accomplish a potential distribution along the resistor helix comparable to the electrostatic field distribution caused by the top electrode alone, i.e. without resistive divider column, the pitch of the resistor helix was varied accordingly, as originally proposed by Goosens and Provoost (1946) to design impulse voltage dividers, see Sect. 7.4.2. The HV resistor column is arranged in an oil-filled PMMA cylinder to improve the convection of the power dissipating in the HV column, which attains only 150 W at 300 kV. That means, the maximum current through the HV resistor attains 0.5 mA, which complies with the requirements discussed above, i.e. on one hand this minimizes the impact of dust and pollution on the parasite leakage current along the HV divider column and, on the other hand, the power dissipating in the HV divider resistor and prevents hence a significant change in the resistance. Using wire-wounded LV resistors, which were artificially aged by a temperature treatment, a measuring uncertainty of about 3 × 10⁻⁵ can be accomplished.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig23_HTML.gif — Fig. 6.23
Photograph of a high-precise DC voltage divider designed by Peier and Greatsch (rated voltage 300 kV, HV resistance 600 MΩ, total high 2.1 m)

In this context it should be mentioned that the above described resistive voltage divider, which is utilized by the German National Institute of Metrology (PTB Braunschweig) for high-precise reference measurements, is not applicable for DC voltage measurements in industrial test fields. This is because an unexpected breakdown of the test object is associated with fast changing over-voltages on account of the comparatively high self-inductance of the in series connected wire-wounded resistors. This causes a strong non-linear voltage distribution and would thus damage the HV arm. To enhance the energy capability, in principle metal-oxide film or carbon composition resistors could be used as alternative. However, the main obstacle is their comparatively high temperature coefficient, which would increase the measuring uncertainty, particularly under extended test duration causing a temperature rise in the HV arm. Even if this effect could be minimized by means of an artificial ageing, which is accomplished by a long-term temperature treatment, it has to be taken into account that such a conditioning is extremely time-consuming, which is thus applied only in very specific cases.

The best solution to avoid a possible damage of resistive dividers in case of unexpected breakdowns is the use of mixed voltage dividers, such as resistive–capacitive dividers or even capacitively graded dividers. An optimum performance is achieved by means of stacked capacitors connected to specific points of the resistive divider column, as obvious from the photograph shown in Fig. 6.24. As a rule of thumb, the capacitance of the HV column of such mixed voltage dividers should be chosen in the order of 200 pF. Moreover, shielding electrodes of comparatively large surface should be employed to prevent the occurrence of partial discharges, which could also affect the divider ratio.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig24_HTML.gif — Fig. 6.24
DC generator and a resistive–capacitive divider (2 MV, 1 mA) designed for the measurement of static and dynamic voltages

To measure the output voltage of HVDC dividers, in principle classical analogue instruments indicating the arithmetic mean value can be employed. However, the better approach is the use of oscilloscopes or even digital recorders to measure DC voltages under real test condition, i.e. besides the static DC voltage also typical dynamic voltages, such as the ripple and the voltage drop as well as the parameters characterizing the polarity reversal . The requirements for approved DC voltage measuring systems are specified in IEC 60060-2:2010. So, the arithmetic mean value shall be measured with an expanded uncertainty U_M ≤ 3%, which corresponds to a coverage probability of 95%. To determine the dynamic behaviour of the measuring system, it is subjected to a sinusoidal voltage at the input. Changing the frequency between 0.5 and 7 times of the fundamental ripple frequency f_r, the difference of the measured output voltage magnitude shall be within 3 dB.

The above-given uncertainty limits shall not be exceeded in the presence of the maximum ripple specified in IEC 60060-1:2010. The ripple magnitude shall be measured with an expanded uncertainty ≤1% of the arithmetic mean value of the DC test voltage or ≤10% of the ripple magnitude, whichever is greater (IEC 60060-2: 2010). To measure the mean value of the DC voltage and the ripple magnitude, either separate measuring systems or the same converting device in connection with two separate measuring modes for both DC and AC voltages may be used.

The scale factor of the ripple measuring system shall be determined at the fundamental ripple frequency f_r with an expanded uncertainty ≤3%. The scale factor may also be determined as the product of the scale factors of the various components. Measuring the amplitude/frequency response of the ripple measuring system in a frequency range between 0.5 and 5 f_r; the amplitude shall not be lower than 85% of that value occurring at the fundamental ripple frequency f_r.

To measure rising and falling DC test voltages as well as the ripple and the voltage shape at polarity reversal, the characteristic time constant of the DC measuring system shall be ≤0.25 s. In case of pollution tests, the time constant shall be ≤1/3 of the rise time typical for the appearing transients (voltage drop).

The results of the type and routine tests of HVDC measuring systems can be taken from the test protocol of the manufacturer, where routine test shall be performed on each component of the measuring system. Performance tests of the complete measuring system as well as performance checks must be performed under the responsibility of the user himself or by a calibration service. The performance test shall include the determination of the scale factor at the calibration as well as the dynamic behaviour for the ripple and shall be performed annually but at least every 5 years. Performance checks cover scale factor checks and should be performed at least annually or according to the stability of the measuring system; for more information on this issue see the Sects. 2.3.3 and 2.3.4.

6.5 PD Measurement at DC Test Voltages

The physics of gas discharges under direct voltage became especially of interest in the late 1930s when high DC voltage was increasingly used for physical, medical and military applications, for instance, to generate the operation voltage of X-ray equipment, cathode-ray tubes, electron-accelerators, image intensifiers, and radar facilities. At that time numerous technical papers and text-books have been published, mainly addressed to the fundamentals of discharges in various gases and even in vacuum (Trichel 1938; Loeb 1939; Raether 1939). An excellent survey on this subject can also be found in the textbook of Meek and Craggs (1978). In the 1960s, when the first long-distance HVDC transmission lines were put into operation, the measurement of partial discharges became also of interest, in particular to assess the insulation integrity of HVDC equipment after manufacturing, such as power cables and power capacitors (Rogers and Skipper 1960; Salvage 1962; Renne et al. 1963; Melville et al. 1965; Salvage and Sam 1967; Kutschinski 1968; Kind and Shihab 1969; Müller 1976; Densley 1979; Meek and Craggs 1978; Devins 1984).

The PD phenomena occurring in air gaps under DC voltage at both polarities are more or less comparable to those occurring under power frequency AC voltage. This applies in particular to so-called Trichel pulses (Trichel 1938) igniting under certain conditions at sharp negative electrodes in air, see Fig. 6.25. Due to their regular appearance in magnitude and repetition rate as well, Trichel pulses can advantageously be used for performance checks of PD measuring systems, for instance, to determine the actual pulse polarity, which appears often inverted when decoupled, transmitted and processed by a PD measuring system.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig25_HTML.gif — Fig. 6.25
Trichel pulses recorded for a point-to-plane air gap at test level close to the inception voltage, a under 50 Hz alternating voltage, b under direct voltage c shape of a single current pulse

To assess the insulation condition of HV apparatus and their components, however, the mechanism of internal discharges, such as cavity, interfacial and surface discharges, is especially of interest. To explain the PD occurrence as well as the charge transfer due to cavity discharges under direct voltage, the classical a-b-c model illustrated in Fig. 4.13 (see Sect. 4.2) has been modified accordingly (Fromm 1995). So the three characteristic capacitances were bridged by high-ohmic resistances to simulate the voltage distribution between the electrodes under constant DC stress as well as to assess the time elapsing between consecutive discharges, which is commonly referred to as recovery time , and dominated by the time constant deduced from the intuitively assumed cavity capacitance and the resistivity of the dielectric material (Fromm 1995; Beyer 2002; Morshuis and Smit 2005).

As an alternative, the dipole model according to Pedersen (1986) can also be used to explain the PD charge transfer as well as the recovery time (Lemke 2016), as will briefly be discussed in the following. For this purpose a PD event in a gaseous inclusion shall be considered, which is embedded in the bulk dielectric between plane-parallel electrodes. Basically, it can be distinguished between the following three stages (Fig. 6.26):

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig26_HTML.gif — Fig. 6.26
Basic stages typical for cavity discharges under DC stress

Stage I: Initializing the ionization processes

Rising the applied DC voltage very slowly, the potential distribution between the electrodes, and in particular the field strength in the gaseous cavity, is governed by the resistive elements shown in Fig. 6.26a. To assess the inception voltage, however, seems to be impossible due to the fact that the volume and surface resistivity of solid dielectrics decreases dramatically at increasing field strength and is furthermore strongly affected by the temperature.

Stage II: Establishment of the dipole moment

Assuming that a self-sustaining discharge ignites at static inception voltage, the number of electrons released from neutral gas molecules equals always that number of positive ions, as discussed in Sect. 4.2. As a result, a dipole moment is established because all positive ions are deposited at the cathode-side cavity wall, while the electrons and negative ions (formed by the attachment of electrons to neutral molecules) are deposited at the anode-side cavity wall. As the dipole moment opposes the electrostatic field resulting from the applied DC test voltage, the field strength inside the gaseous inclusion is diminished, so that the self-sustaining discharge processes will be quenched suddenly.

Stage III: Dissipation of the dipole moment

Even if the resistivity of insulating materials is extremely high, it is supposed that the positive ions deposited at the cathode-side dielectric boundary are slowly neutralized by the attachment of electrons de-trapped from the solid dielectric, which is forced by a strong field enhancement adjacent to the positive space charge. Simultaneously, the electrons, previously deposited at the dielectric wall, will enter this boundary and propagate further through the solid dielectric into anode direction. As the drift velocity of the electrons and thus the associated electron current is extremely low, the recovery time required to establish the initial field conditions and thus to ignite the next discharge becomes extremely long. Practical experience revealed that the time elapsing between two consecutive PD events may approach several minutes.

Example Consider a discharge in a gaseous inclusion embedded in the XLPE insulation of an extruded power cable. Assuming a field strength of E_p = 20 kV/mm, which appears in the XLPE insulation adjacent to the cavity, and a conductivity of the solid dielectric of $\kappa = 10^{ - 17} \left( {\varOmega \cdot {\text{mm}}} \right)^{ - 1}$ , the density of the current, which is exclusively carried by the electrons, would attain $G_{e} = E_{p} \cdot \kappa = \left( {2 \cdot 10^{4} \times \, 10^{ - 17} } \right)\;{\text{A}}/{\text{mm}}^{2} = 0.2\;{\text{pA}}/{\text{mm}}^{2}$ . Provided, a single PD event leads to the ionization of n_g = 10⁸ gas molecules, a positive space charge of $q_{ + } = e \cdot n_{g} = \left( {1.6 \times 10^{ - 19} \;{\text{C}}} \right) \cdot 10^{8} = 16\;{\text{pC}}$ would be deposited at the cathode-side dielectric boundary. This charge will slowly be neutralized by the electrons de-trapped from the solid dielectric adjacent to the cavity. Assuming this occurs over an area of A_c = 1 mm², the electron current crossing the dielectric boundary and neutralizing the positive space charge could be assessed by $I_{e} = G_{e} \cdot A_{c} = 0.2\;{\text{pA}}$ . Based on this the time span required to neutralize the positive space charge deposited at the cathode-side dielectric boundary gets $t_{r} \approx q_{ + } /I_{e} = \left( {16\;{\text{pC}}} \right)/\left( {0.2\;{\text{pA}}} \right) = 80\;{\text{s}}$ .
Considering now the negative space charge deposited at the anode-side dielectric boundaries, the current caused by the electrons when leaving the gaseous cavity can also be assessed as close to 0.2 pA, because this continues through the solid dielectric, i.e. from the anode-side dielectric boundary to the anode. Consequently, all electrons (including those attached to neutral gas molecules and thus forming negative ions) will leave the cavity within a time span of about 80 s. With other words: the initial space charge free field conditions will be accomplished after a relaxation time of about 80 s.

Performing PD tests under DC test voltage it has to be taken into account that only the following two PD quantities are measurable:

(i)
The pulse charge q_i of a single PD event appearing at instant t_i.
(ii)
The recovery time ∆t_i, which is inversely proportional to the PD pulse repetition rate.

To measure these both PD quantities, in principle the basic measuring circuits including the coupling units (Fig. 4.23) and measuring systems as well as the calibration procedures, as specified in IEC 60270:2000 for PD tests under power frequency AC voltage, are applicable. In this context it should be remembered that the pulse repetition rate under constant DC stress is extremely low, as discussed above and obvious from Figs. 6.27 and 6.28. Thus, appropriately long testing times have to be chosen. However, under this condition individual charge pulses received from the output of conventional PD measuring systems can hardly be visualized by means of classical digital oscilloscopes due to their short duration, which is usually below 100 µs. Thus this signal must either considerably be stretched, usually up to the second range, or even displayed as “accumulated pulse charge”, as illustrated in Figs. 6.27 and 6.28b. Another benefit of such a display mode is that the slope of the accumulated pulse charge is proportional to the mean PD current, which can be regarded as an additional valuable information (Lemke 1975). To prevent a saturation of the measuring device equipped with such a feature, a reset must be triggered just before an overload appears, as obvious from Fig. 6.27b.

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig27_HTML.gif — Fig. 6.27
Trains of charge pulses (CH1—pink trace) and accumulated pulse charge (CH2-green trace) recorded at direct voltage for discharges in a gaseous inclusion embedded in a PE cable sample, a recording time 20 s, test level slightly above PD inception voltage, b recording time 100 s, test level approx. 20% above PD inception voltage

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig28_HTML.gif — Fig. 6.28
Graphs recommended in the Amendment to IEC 60270 to display PD tests results under constant DC voltage level, a consecutive charge pulses appearing during a 30 min test period, b associated accumulated pulse charge

As the PD pulses are often scattering over an extremely wide range, which refers to both the magnitude and the repetition rate, a statistical analysis of the significant PD quantities is highly recommended. For this purpose, the PD measuring system should also be equipped with a unit, which enables to count the number of PD pulses exceeding preselected threshold levels (Fig. 6.29). In principle, such a pulse-high analyzer has already been employed earlier by Bartnikas and Levi in 1969. Practical experience revealed that PD tests of HVDC apparatus and their components should cover a minimum time period of 30 min. In this context the following definitions should be re-called, as specified in the Amendment to IEC 60270 (Ed. 3):2000, published in 2013:

../images/214133_2_En_6_Chapter/214133_2_En_6_Fig29_HTML.gif — Fig. 6.29
Graphs recommended in the Amendment to IEC 60270:2000 for a statistical analysis of the PD data. a Count of PD pulses exceeding the pulse charges 0, 1, 2, 3, 4 and 5 nC. b Count of PD pulses, occurring within the pulse charge classes (0–1) nC, (1–2) nC, (2–3) nC, (3–4) nC and (4–5) nC

Accumulated apparent charge qa

sum of the apparent charge q of all individual pulses exceeding a specified threshold level, and occurring during a specified time interval ∆t_i.

PD pulse count m

total number of PD pulses, which exceed a specified threshold level within a specified time interval ∆t_i.

Moreover it is recommended in the above mentioned Amendment to present the measured PD test results graphically, as exemplarily shown in the Figs. 6.28 and 6.29.

6. Tests with High Direct Voltages