Tests with High Lightning and Switching Impulse Voltages

Abstract

Lightning impulse (LI) over-voltages and switching impulse (SI) over-voltages are caused by direct or indirect lightning strokes or even by switching operations in electric power systems, respectively. They cause transient stresses to the insulations, much higher than the stresses due to the operational voltages. Therefore, insulations must be designed to withstand LI and SI over-voltages, and the correct design has to be verified by withstand testing using LI test voltages , respectively, SI test voltages . This chapter deals with the generation of aperiodic and oscillating LI and SI impulse voltages and the requirements for their application in HV tests. Special attention is given to the interactions between the LI/SI generator and the test object. The deviations from the standardized impulse shape, e.g. by an over-shoot on the LI peak, are analysed, and the evaluation of recorded pulses according to IEC 60060-1:2010 and IEEE St. 4 (Draft 2013) is described. This is completed by the description of components and of the procedures for the correct measurement of LI/SI test voltages. Also the measurement of the test currents in LI voltage tests and the PD measurement at SI, LI and VFT test voltages are included.

7.1 Generation of Impulse Test Voltages

7.1.1 Classification of Impulse Test Voltages

A lightning stroke may cause—e.g. on a transmission line—a travelling wave of a current pulse with a peak value ranging from few kiloamperes up to about 200 kA (in very rare cases, even up to 300 kA). Investigations of Okabe and Takami on UHV transmission systems (Takami 2007; Okabe and Takami 2009, 2011) considered peak currents up to 300 kA and a front duration in the range between 0.1 and 5 μs for the calculation of LI over-voltages (“external over-voltage”) based on the surge impedance of the overhead transmission line, the grounding resistance of a tower and the impedances of the involved components. Figure 7.1 shows the resulting over-voltages for a GIS and a power transformer. Whereas at the GIS, the shape and the peak of the over-voltage change with the front time of the current pulse, the over-voltage at the transformer is not influenced by the front time of the current impulse. In both cases, the front time of the over-voltage is in the order of 1 μs, but the over-voltage shows oscillations. IEC 60071-1:2006 and IEC 60060-1:2010 defines all impulse voltages with LI front times T₁ < 20 μs being LI voltages. Standard LI test voltages are aperiodic impulses. They are characterized by T₁ = 1.2 μs and an LI timetohalf-value of T₂ = 50 μs, abbreviation 1.2/50. In the case of Fig. 7.1 (Okabe and Takami 2011), the LI over-voltages are quite well represented by standard LI test voltages 1.2/50.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig1_HTML.gif — Fig. 7.1
LI over-voltage caused by 200 kA LI current pulse of different front times superimposed on the negative AC voltage peak at a GIS (*above*) and at a power transformer (*below*)

A switching process “on” or “off” in a power system causes an “internal over-voltage” due to the excitation of internal oscillation circuit(s) formed by the inductances and capacitances of the involved components of the system. The SI over-voltages are also oscillating with one or several frequencies which are remarkably lower than those of LI over-voltages (Fig. 7.2). All impulse voltages with front time T₁ > 20 μs are defined in IEC 60060-1:2010 being SI voltages. Shape and parameters of SI test voltages shall not only represent SI over-voltages, but should also be generated with the same test generator as LI test voltages (see Sect. 7.1.2). Their SI time-to-peak of about T_p = 250 μs should meet a minimum breakdown voltage of non-uniform air gaps with distances of about 5 m (Fig. 7.3, averaged characteristics according to Thione 1983). Therefore, standard SI test voltages are aperiodic impulses and characterized by T_p = 250 μs and a time to half-value of 2500 μs, abbreviation 250/2500. They shall represent all kinds of SI over-voltages.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig2_HTML.gif — Fig. 7.2
Example for an SI over-voltage

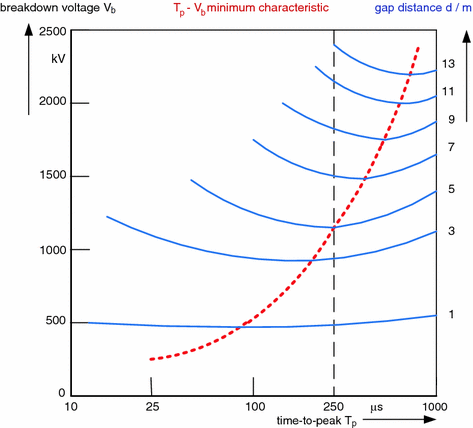
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig3_HTML.gif — Fig. 7.3
SI breakdown voltage of long air gaps depending on the time-to-peak

For on-site testing, also oscillating impulse voltages (OLI; OSI) are applied (IEC 60060-3:2006). OLI and OSI test voltages can be generated with a generator of efficiency factors about twice of those for LI and SI voltages (see Sect. 7.1.3). Even if this is made for easier transportation and handling of the test system, it should be mentioned that the used OLI and OSI test voltages represent quite well the related over-voltages (compare with Figs. 7.1 and 7.2). Also the so-called “damped alternating voltage” (IEC 60060-3:2006; DAC) used for PD testing of cable systems in the field—is an OSI voltage. OSI voltages can also be generated by test transformers (see Sect. 7.1.4).

Last but not least, it should be mentioned that in case of disconnector switching in SF₆-insulated systems (GIS), over-voltages faster than LI over-voltages are generated. They are represented by fast front test voltages (FFV) and generated by switching the disconnector in the GIS under test (see Sect. 7.1.5).

7.1.2 Basic and Multiplier Circuits for Standard LI/SI Test Voltages

7.1.2.1 Basic RC Circuit

The operation of the basic circuit for impulse voltages shall be explained by its equivalent circuit (Fig. 7.4a): When an impulse capacitor Ci is charged via a charging resistor R_c up to the DC breakdown voltage V₀ of the switching gap SG, the impulse voltage V_i is generated by the connected elements (Fig. 7.4b): Then, the load capacitor C_l is charged via the front resistor R_f which forms the front of the impulse voltage. At the same time, the impulse capacitor C_i is discharged via the tail resistor R_t and forms the tail of the impulse voltage. The superposition of both processes delivers a peak voltage V_ip which is lower than the breakdown voltage V₀ of the switching gap. The relation between the two voltages delivers the efficiency factor (also: utilization factor) of the “one-stage” (basic) impulse generator:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig4_HTML.gif — Fig. 7.4
Basic equivalent circuit for impulse voltage generation. a Equivalent circuit diagram. b Potential diagram

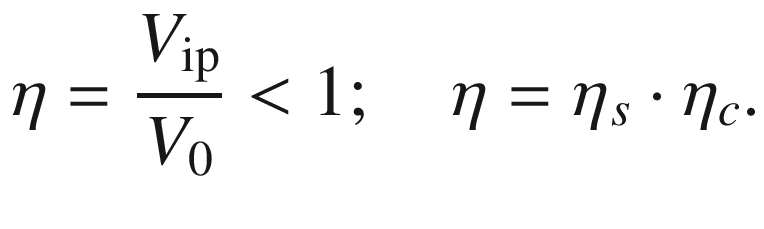
$\eta = \frac{{V_{\text{ip}} }}{{V_{0} }} < 1;\quad \eta = \eta_{s} \cdot \eta_{c} .$

(7.1)

The efficiency factor η can be understood as a product of the efficiency η_s depending on the impulse shape and the efficiency η_c depending on the circuit parameters (Hylten-Cavallius 1988). The shape efficiency η_s increases with the relation between tail and front time of the impulse to be generated. When an LI impulse voltage (1.2/50) shall be generated, the relation is, e.g. about 40, when an SI voltage (250/2500) is generated the relation is, e.g. 10 only. The circuit efficiency η_c depends mainly on the relation between impulse and load capacitor. The larger the impulse capacitance C_i in relation to the load capacitance C_l, the higher is the circuit efficiency η_c. The overall LI efficiency factor is relatively high (η ≈ 0.85…0.95) and the SI efficiency factor remarkably lower, η ≈ 0.70…0.80 only.

Note In addition of the circuit of Fig. 7.4a, a second basic circuit which has the tail resistor not before, but after the front resistor, is sometimes discussed in textbooks. This circuit has a lower efficiency factor. Therefore, it is not used practically and not discussed here.

The front of the impulse voltage is mainly determined by the time constant τ_f and its tail by τ_t

$\tau_{f} = R_{f} \cdot C_{l} ;\quad \tau_{t} = R_{t} \cdot C_{i} .$

(7.2)

Usually, an impulse voltage generator is equipped with an impulse capacitor C_i and a basic load capacitor C_l of fixed values. The front time can be adjusted by a correctly selected front resistor R_f and the time-to-half-value by an appropriate tail resistor R_t. With the fixed values of C_i and C_l, the maximum SI peak voltage is only about 80% of the maximum LI peak voltage.

Note The analytical calculation of the time parameters of impulse voltages and their efficiencies is given in older textbooks. Today, the analytical calculation is replaced by well-adaptable and commercially available software programs. This enables also the more detailed consideration of the characteristics of the test object and the stray capacitances in the test room and delivers more precise results.

The selection of the impulse capacitor C_i determines—together with the maximum charging voltage V_0max also the impulse energy of the generator:

$W_{i} = \frac{1}{2}C_{i} \cdot V_{{0{ \hbox{max} }}}^{2} .$

(7.3)

Whereas the maximum charging voltage of a generator depends on the required test voltages, the impulse capacitance must be selected according to the expected total load (basic generator load plus test object load), to guaranty C_i ≫ C_l.

7.1.2.2 Multiplier RC Circuit

The basic circuit (Fig. 7.4a) is usually applied for students training and demonstrations with voltages below 200 kV. For higher voltages, multiplier circuits proposed by E. Marx in 1923 are applied (Fig. 7.5a, without the red short-circuit bars).

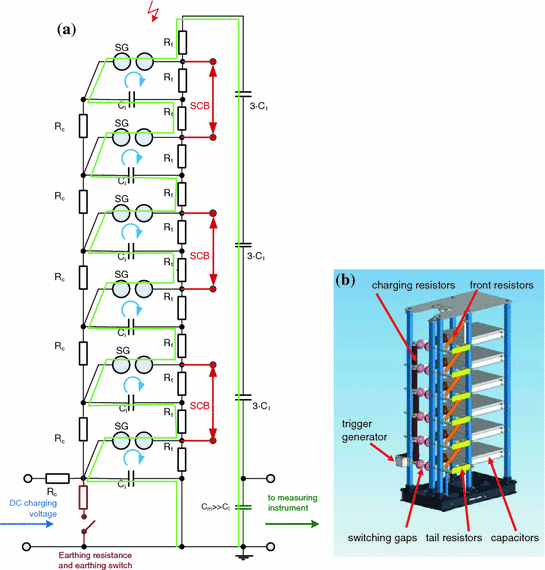
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig5_HTML.gif — Fig. 7.5
Multi-stage impulse generator of n = 6 stages. a Multiplier circuit (explanations in the text). b Impulse generator

The impulse capacitors C_i of all n stages are charged via the charging resistors R_c which are connected in series to one column. When the charging resistors are dimensioned correctly, it does not play any role that the charging resistance of the highest stage is n-times larger than that of the lowest one, because the charging time is selected long enough that all impulse capacitors are equally charged. Today, a thyristor-controlled charging with a constant current up to a pre-selected voltage V₀ is used, at which the switching gap is triggered for breakdown. Now, the impulse capacitors start to discharge via the tail resistors on each stage (Fig. 7.5a: blue path). At the same time, the external load capacitance C_l (basic load of a capacitive divider plus stray capacitances of the generator to ground plus test object) is charged from the series connection of all impulse capacitors and front resistors (green path). An impulse voltage generator of n stages (Fig. 7.5b) charged with a DC voltage V₀ delivers with the efficiency factor η the output impulse voltage

$V_{in} = n \cdot \eta \cdot V_{0}$

(7.4)

The term V_{0n max} = n · V_0max is called the cumulative charging voltage of the generator and usually used as the rated voltage of the impulse test system because V_{0n max} > V_{in max} one has to be careful with the valuation of rated voltages for impulse test systems. It is always necessary to know the efficiency factor for all impulse voltage shapes of interest for the calculation of the related output voltages additionally.

For calculation of its circuit elements, a multi-stage generator (n stages, elements R_f; R_t, C_i; C_l) is usually transferred into an equivalent basic circuit with the elements

$\begin{aligned} R_{f}^{*} & = n \cdot R_{f} \\ R_{t}^{*} & = n \cdot R_{t} \\ C_{i}^{*} & = C_{i} /n \\ C_{l}^{*} & = C_{l} . \\ \end{aligned}$

(7.5)

After the calculation of the circuit elements of the basic circuits, the above Eq. (7.5) are used for the determination of the multi-stage generator by re-transformation. The thermal design of the resistors—especially of the front resistors—determines the allowable impulse voltage repetition rate. The resistors are heated by the impulse current, which is flowing in case of the impulse voltage generation and should sufficiently cool down until the next impulse appears. A defined maximum temperature of the resistors must not be exceeded.

The controlled safe triggering characterizes a generator of high quality. Usually, only the lowest stage is equipped with a so-called “trigatron”, a three-electrode arrangement (Fig. 7.6a). A small, battery-operated trigger device generates a voltage pulse of several kilovolts which causes a small trigger discharge at a pilot gap. This discharge triggers the breakdown of the main gap of the lowest stage. The trigger discharge delivers charge carriers and photons for the immediate, fast breakdown process, if the field strength in the main gap is high enough. This requires a certain minimum voltage, the so-called lower trigger limit (Fig. 7.6b). If the voltage at the trigger gap is too high, a breakdown is caused without triggering. This self-ignition delivers the upper trigger limit of the charging voltage. The trigger range between the two limits (Fig. 7.6b) should be as wide as possible. Usually, its width is between 5 and 20% of the withstand voltage of the non-triggered gap (upper curve). It depends on the design of the trigatron, the energy of the trigger discharge and the height of the DC voltage at the main gap.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig6_HTML.gif — Fig. 7.6
Triggering of impulse voltage generators. a Trigatron spark gap. b Principle of the trigger range

The charging voltage and the trigger instant must be well controlled to guarantee safe triggering of the whole generator and to avoid “no-triggering” or self-ignition without triggering. As soon as the lowest switching gap breaks down, an over-voltage appears at the second stage, runs as a travelling wave through the generator (Pedersen 1967) and shall cause the breakdowns of all further gaps. The over-voltages must remain high enough to cause all necessary breakdowns. This depends on the impulse shape to be generated (e.g. damping front resistors) and on stray capacitances to ground which increase the over-voltages, whereas longitudinal stray capacitances reduce them (Rodewald 1969a, b). Based on such investigations, additional trigger measures (e.g. supporting gaps and ignition capacitors) have been introduced to maintain the height of over-voltages also for huge generators (Rodewald 1971; Feser 1973, 1974). Generators with symmetric charging (Sect. 7.1.2.4; Fig. 7.7) allow a save triggering without these additional measures (Schrader 1971).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig7_HTML.gif — Fig. 7.7
LI voltage generation circuit considering the inductance a Equivalent circuit diagram with inductances. b Over-shoot superimposed on LI voltages (schematically)

The modular design of multi-stage generators is helpful for later extension to higher voltages by additional stages. It enables also the parallel connection of stages for higher impulse energy at lower voltages [Fig. 7.5a, red short-circuit bars (SCB)] as they are, e.g. required for testing the low-voltage winding of power transformers or medium-voltage capacitors. Also impulse test currents can be generated by impulse voltage generators with parallel stages.

7.1.2.3 Consideration of the Inductance in the Circuit

Till to this Subsection, all explanations have not considered the inductance in the impulse test circuit which cannot be avoided. The inductance is not a property of a conductor carrying a current, but of the magnetic field besides of it: It is a property of the magnetic flux generated by the electric current in a closed circuit and influenced by the geometries of the conductor(s) and of the considered circuit as well as of the positions of the circuit elements to each other (Rodewald 2017). For practical application the inductance is represented by a “frequency-dependent resistor”, usually simply called “inductance” (symbol L). In an equivalent circuit diagram, these inductances L are switched in series to elements carrying the current and generating the magnetic flux according to the conditions of the circuit (e.g. the HV lead from a generator to the test object and the ground return). The strongest influence on the inductance is caused by the magnetic field in the vicinity of the conductor. Therefore, e.g. the inductance of HV leads of larger length (l ≥ 1 m, distance to ground >1 m) can be estimated from their cross sections and lengths (Table 7.1).

Table 7.1

Inductances to be assumed for HV leads

Length of HV lead (m)	Single wire, d = 2 mm (μH/m)	Metal foil, w = 10 cm (μH/m)	Metal tube, d = 10 cm (μH/m)	Metal foil, w = 50 cm or 2 foils with spacer in between (μH/m)
1	1.37	0.70	0.59	0.40
10	1.83	1.26	0.96	0.84

Inductances form oscillating circuits with the capacitances and cause damped oscillations superimposed on the aperiodic pulses. The damping depends on the front resistor. This is several 100′ Ω for SI voltages and suppresses the oscillations completely. The more or less damped oscillations and the “over-shoot” (only less than one period of the oscillation) are found at LI voltages only, because the LI generator is equipped with front resistances of few 10′ Ω (Fig. 7.7). There are internal inductances of the generator and external of the test object and its connections.

Internal inductances L_i are those of the capacitors, the resistors and the connections between them. For estimations, the inductance for 1 m of the loop (e.g. green path in Fig. 7.5a) is about 1 μH. The reduction in the internal inductance of a generator requires its compact design with a loop as short as possible. A good generator should have an internal inductance of L_i < 4 μH per stage. Usually, the user cannot influence the internal inductance of the generator easily. When only a part of the stages is sufficient to generate the necessary voltage (so-called “part operation”), the loop should be short and should exclude the not-used part of the generator and of the basic load (voltage divider). For very old generators, one should check the inductance of the front resistors: The front resistors must be designed with low inductance, which can be reached by a bifilar winding. This means that two isolated, close together arranged wires are wound on a fibreglass tube in opposite directions. The magnetic fields of the wires have opposite directions and compensate each other to a remaining inductance which corresponds to the length of the resistor tube. A second possibility is a resistor band where the insulated resistance wires are woven into a fabric as a meander. Resistor bands are commercially available. The inductance of resistors can also be reduced when, instead of a single resistor, two or more parallel resistors are applied resulting in the same resistance.

External inductances L_e are those of the test object (even if this mainly a capacitance), the HV lead to the test object and the voltage divider as well as those of the earth return. HV lead and earth return shall be especially very short and can often be influenced. With increasing LI test voltage, the distances between generator and test object become longer and oscillations and over-shoot cannot be controlled in testing UHV equipment (see Sect. 7.3). Up to a certain degree, also the inductance of the circuit can be reduced by an appropriate selection of the geometry of the HV lead. Table 7.1 gives some inductances depending on the shape and the length of the connection. Never a thin wire should be used for the HV lead or the ground return, because its inductance is higher than those of copper foil of a width w ≥ 10 cm or metallic tube of a diameter d ≥ 10 cm. A further reduction can be reached with a wider foil or two parallel foils and spacers with a distance d in between. Also quite useful is the application of the mentioned resistor bands as HV lead and external damping resistor to the test object. To maintain the impulse shape, the internal front resistor must be reduced, but the external resistor increases the damping efficiency including the efficiency factor.

Over-shoot compensations can be designed as low-pass filters of L/C/R combinations (serial or parallel compensation unit) arranged inside the generator or outside as separate components: Fig. 7.8 shows the principles of the two compensation units.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig8_HTML.gif — Fig. 7.8
Equivalent circuit diagrams of over-shoot compensation units. a Parallel compensation unit. b Series compensation unit

The series compensation unit (Fig. 7.8b; Wolf and Voigt 1997) prevents the penetration of higher-frequency contributions to the load capacitance which includes the test object. The series connection of compensation resistance R_c and compensation inductance L_c must be adjusted to that of the front resistor R_f and internal inductance L_i. Also the compensation capacitor C_c has to be related to the load capacitance C_l. The necessary adjustment covers a certain range of load cases, but if fine tuning is required, the compensation unit must be adapted. For larger impulse generators, the series compensation unit can be distributed to the different stages of the generator (with elements of the stage voltage, e.g. 200 kV) and without components of high-rated voltage (e.g. 3000 kV).

The parallel compensation unit (Fig. 7.8a, Schrader 2000; Hinow and Steiner 2009; Hinow 2011) is always a separate unit which might be combined with a chopping gap and a voltage divider to one compact unit (Fig. 7.9). Its adjustment has to consider the natural frequency range caused by internal and external inductances. The efficiency of the two principles is about the same. It seems that especially for LI testing of UHV equipment the handling of compensation units becomes too time-consuming and does not fit to the operation of an industrial test field. The problem can be easily solved by increased damping due to larger front resistors, but this requires larger tolerances for the front time of LI impulses (for details see Sect. 7.2.1)

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig9_HTML.gif — Fig. 7.9
Parallel compensation unit in combination with voltage divider and chopping gap

7.1.2.4 Some Details of the Design of Impulse Voltage Test Systems

The LI/ SI voltage test system (Fig. 7.10) includes the HV circuit consisting of the HV generator which is optionally completed by an over-shoot compensation unit, an HV chopping gap and a measuring system including an HV LI/SI divider (see Sect. 7.5). The test object is also a part of the HV circuit, but later considered under Sect. 7.3. Furthermore, it includes the control and measuring system, the switching cubicle with the thyristor controller and the DC voltage generator. In the following, some characteristics of the main elements are given. For the generator, see the above explanations.

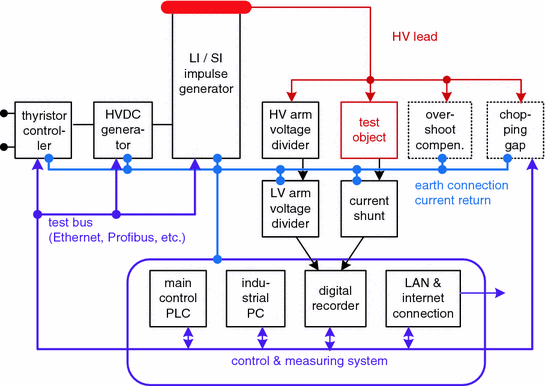
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig10_HTML.gif — Fig. 7.10
Components of an LI/SI test voltage system

Generator with symmetric charging: For larger impulse voltage generators, the charging voltage per stage is usually 200 kV. Because of the limited rated voltage of capacitors, usually two 100-kV capacitors are connected in series for 200 kV. To guarantee identical charging of both capacitors of a stage, potential resistors R_p must be arranged at the connection point of both capacitors (Figs. 7.11a and 7.12a). With a special circuit patented by Schrader (1971), a symmetric charging with ±100 kV is applicable (Figs. 7.11b and 7.12b). This requires a charging unit with symmetric output ±100 kV.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig11_HTML.gif — Fig. 7.11
Typical circuits for impulse voltage generators. a Unipolar charging (e.g. 200 kV). b Symmetric charging (e.g. ±100 kV)

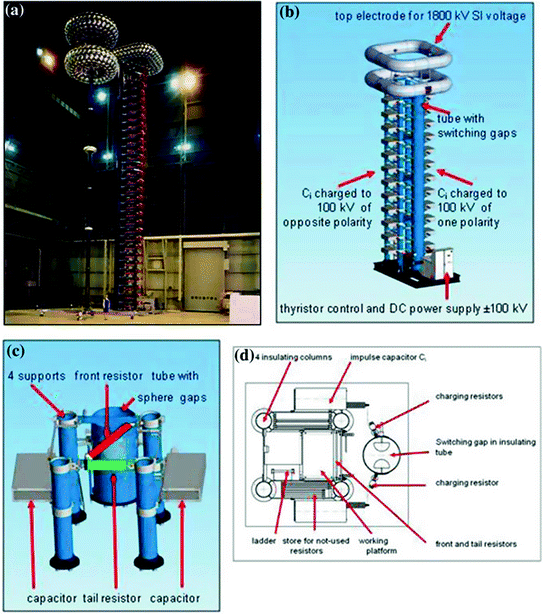
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig12_HTML.gif — Fig. 7.12
Impulse voltage generators for unipolar and symmetric charging. a Generator with unipolar charging (Courtesy of Haefely, Basel). b Generator with symmetric charging. c One-stage of a multi-stage generator (inside view). d Cross section of a generator with symmetric charging

For each polarity, a separate column of charging resistors R_c, but no potential resistors R_p are required. There are some advantages of the symmetric charging for larger impulse test systems with two capacitors in series per stage: In the first line, a stage with a short HV loop of low inductance can be designed (Fig. 7.12d). The safe triggering of large generators with symmetric charging does not require the additional measures mentioned above. As there are no voltage-dependent circuit elements, the impulse shape (described by the time parameters) is independent from the peak voltage (Fig. 7.13). Also the parallel connection of stages for the generation of impulses with a higher energy is very simple.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig13_HTML.gif — Fig. 7.13
Reproducibility of LI voltage shapes independent on peak voltage value

Chopped lightning impulse (LIC) voltages and chopping gap : An external over-voltage in the power system is limited to the protection level by a lightning arrester. This means the over-voltage is chopped and collapses to this protection level. The duration of the voltage collapse is very short, its steepness very high. Such steepness causes very non-linear stresses in equipment with windings (power, distribution and instrument transformers, reactors, rotating machines). The mainly stressed insulation at the HV terminals of the equipment must be designed accordingly and verified by a test with chopped lightning impulse (LIC; Fig. 7.14a) voltages.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig14_HTML.gif — Fig. 7.14
Chopped lightning impulse generation. a Chopped lightning impulse (LIC) voltage. b Circuit of two modules of a multiple chopping gap. c Multiple chopping gap for 1200 kV (six single gaps)

The LIC test voltage is generated as an LI test voltage described above and then chopped by a separate chopping gap. For LIC voltages up to about 600 kV, a usual sphere-to-sphere gap can be used; for higher voltages, multiple chopping gaps become technically mandatory (Fig. 7.14b, c). The voltage collapse of a multiple spark gap is much faster than that of a single large sphere gap. The chopping gap consists of in-series-connected sphere-to-sphere gaps, usually one gap for one stage of the generator. One sphere of each gap is fixed and arranged at a fixed insulating column. The other one—on suitable insulating support—is moveable by a motor drive and can be adjusted for the relevant voltage value. The parallel capacitor column controls the voltage distribution linearly (Rodewald 1972). This column might also be used as a damped capacitive voltage divider, which is usually a separate component (see Sect. 7.5). The instant of the chopping can be triggered as described above for the generator (Fig. 7.6). Also the combination with an over-shoot compensation unit is applied (Fig. 7.9).

Electrodes for the HV components: An impulse voltage generator and the other HV components require a sufficient clearance D from grounded or energized objects in an HV test laboratory (Fig. 7.15a) to avoid breakdowns of the air gap between the HV circuit and the surroundings. The necessary clearance depends on the kind of pre-discharges which determine the breakdown process. The optimum design of the electrodes of the HV components enables not only the correct operation of an LI/SI test system but ensures also their minimum space in the test laboratory.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig15_HTML.gif — Fig. 7.15
Electrodes for the HV components of LI/SI voltage test systems. a Necessary clearance D around a LI/SI generator. b Test system only for LI voltage generation (2000 kV), c Test system 1800 kV for LI/SI voltage generation at limited clearance to the ceiling. d Outdoor test system 4200 kV for SI and LI voltage generation.
Courtesy of KEPRI, Korea

Note This clearance should not be mixed up with the clearances for the test object according to Fig. 2.1. The clearances there consider that the voltage distribution at the test object is not influenced by the surroundings. Here, the operation of the generator shall not be disturbed by undesirable discharges or even breakdowns.

At LI test voltages, the streamer discharge determines the breakdown voltage of a non-uniform electric field in air. The electric field of an LI generator in an HV test room is such a non-uniform electric field. Consequently, the specific breakdown voltage is equal to the voltage demand of streamers of about 5 kV/cm for positive and about 10 kV/cm for negative polarity of the electrode with the larger curvature. This means that for a 3 MV LI generator, the minimum clearance should be 6 m (plus a certain safety margin of—say—20%). The curvature of the electrodes can be relatively small (Fig. 7.15b), because there is no need to avoid the streamer discharges.

Note The strong polarity effect is typical for streamer discharges in air. There is no remarkable polarity effect for internal insulation. If internal insulation, e.g. of a power transformer, shall be tested with LI voltage, a flashover of the air-part of the bushing is avoided when the test is performed at negative LI voltage.

At SI voltages, a combination of streamer and leader discharges determines the breakdown voltage between the generator and the surroundings. The electrodes of the HV components of the test system shall be designed in such a way that no leader discharge appears, this means with larger radii (Fig. 7.15c). The effect of enlargement of the distance to the surrounding is very week because of the low leader gradient (about 1 kV/cm). Therefore, it is recommended to optimize the electrodes of the HV components by a field calculation with the realistic conditions of the test room. As a rough hint, the distance must be in minimum 20% larger than for LI voltage, and the surface field strength of the electrodes at SI voltage should be below 20 kV/cm.

When a generator and related HV components are used for LI and SI voltage generation, the electrodes are determined by the maximum SI test voltages, even when they are about 25% lower than the maximum LI test voltages. An optimum utilization of a test area can be reached when a generator is moveable in the laboratory, e.g. by air cushions. The design principles for outdoor generators (Fig. 7.15d) are identical. They require also large electrodes for SI voltage generation, but under rainy conditions, the maximum output voltages must be remarkably reduced.

Control and measuring system : This—today usually computer-aided—sub-system of an LI/SI test system (Fig. 7.10; see also Sect. 2.2) of an LI/SI voltage test system enables the adjustment of the generator for the test voltage value and a certain test procedure (see Sect. 7.4), the measurement of LI/SI voltages and of related impulse currents (see Sects. 7.5 and 7.6). It is available for one, two or all three following modes:

1.
Manual operation with measurement and evaluation of LI/SI parameters: The operator has to control the test system including adjustment of the voltages and duration of the breaks between impulses, and the evaluation and presentation of the test result (test record). The charging and triggering process must be controlled. When control and measuring components are not connected to one system, this has to be done by the operator. This traditional mode is very seldom applied for industrial testing and research work, but applied for e.g. student’s training.
2.
Computer-supported operation and test result presentation: The test is performed manually, but the precise adjustment of test voltages—this means that of the distance of the switching gap as well as that of the charging DC voltage—and the test data presentation are overtaken by the system. Control and measuring components are connected. This mode is applied for larger and expensive test objects in industrial testing and for research work.
3.
Automatic testing according to a pre-given test procedure by a computer control: The PC software for the test procedure is configured by the operator before, the HV test itself is performed, evaluated and presented automatically. Intervention of the operator is not necessary, but the test can be interrupted or terminated at any time by the operator. This mode is applicable for testing of very similar or even identical test objects in a larger scale or for statistical investigations in research work.

The control system delivers the commands for switching the breakers on and off, for adjusting the switching gaps of the generator for the pre-selected voltage and for the appropriate charging voltage adjusted by a thyristor controller. Based on the voltage measurement, the computer control checks that the voltage values are within the pre-given sequence and tolerances. Based on the evaluation of the voltage shape, breakdowns are recorded for the evaluation of the test. Also the evaluation of the related currents might indicate whether a test has been successful or has failed. The style of the test record depends fully from the intention of the user.

Switching cubicle and DC rectifier unit : A LI/SI test system has a relatively low power demand of some 10 kW. The switching cubicle contains the power switch and the operation switch, the instrument transformers for supply voltage and current measurement and protective equipment. The built-in thyristor controller enables a constant-charging current output of the connected rectifier unit. This DC rectifier unit is usually a doubler circuit (see Sect. 6.1.2 and Fig. 6.3) or for symmetric charging, a half-wave rectifier with symmetric output (modification of Fig. 6.2). Depending on the rated power and energy of the impulse generator, the charging voltage corresponds to the stage voltages (100–200 kV) and the charging currents are between few 10 mA and some 100 mA. The duration of the charging which determines the impulse voltage repetition rate depends on the total energy of the generator and is usually between 10 and 60 s. For special application, also faster charging processes and higher repetition rates can be realized.

7.1.3 Circuits for Oscillating Impulse Voltages

For factory testing with aperiodic LI voltages according to IEC 60060-1:2010 or IEEE St.4:1995, the inductances in the circuit are disturbing elements, but a defined inductance L_s in the circuit establishes an oscillating circuit of this series inductance and the load capacitances C_l. This circuit is excited by the triggered discharging of the impulse capacitors of the generator (Fig. 7.16a). The output voltage is a damped oscillation around the discharge curve of the impulse capacitances of the generator. The oscillating frequency is the natural frequency

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig16_HTML.gif — Fig. 7.16
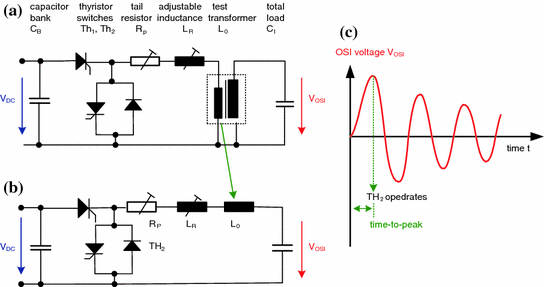
Oscillating lightning impulse voltages (OLI). a OLI test voltages. b Equivalent circuit for oscillating impulse voltage generation. c 900 kV impulse test system for 850 kV LI and 1600 kV OLI voltages.
Courtesy of Siemens Berlin

$f_{0} = \frac{1}{{2\pi \cdot \sqrt {L_{s} \cdot \frac{{C_{l} \cdot C_{i}^{*} }}{{C_{l} + C_{i}^{*} }}} }}.$

(7.6)

For a generator with n stages, one has to apply $C_{i}^{*} = C_{i} /n$ and $R_{t}^{*} = n \cdot R_{t}$ (Eq. 7.5). The total load C_l = C_lb + C_lt is the sum of the basic load and the test object load. The fixed series inductance L_s replaces the front (damping) resistors. According to IEC 60060-3:2006, impulse voltages with oscillations f₀ > 15 kHz are considered as “oscillating lightning impulse (OLI) voltages” (Fig. 7.16a), such with f₀ < 15 kHz as “oscillating switching impulse (OSI) voltages” (Fig. 7.17a). The damping is determined by the losses in the circuit, for pure capacitive test objects mainly by the tail resistors R_t of the aperiodic impulse. As these are higher for OSI than for OLI voltages, OSI voltages show not only a lower frequency, but also a larger damping (Fig. 7.17a).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig17_HTML.gif — Fig. 7.17
Oscillating switching impulse voltages (OSI). a OSI test voltages. b 1200 kV impulse test for 900 kV SI and 1600 kV OSI voltages

Theoretically, the oscillating impulse voltage (OLI or OSI) can reach a peak value which is twice the peak value of the relevant aperiodic impulse (LI or SI) voltage. In practice, it reaches about 90% of that value. The efficiency factors are

$\eta_{\text{OLI}} = \frac{{V_{\text{OLI}} }}{{V_{0\varSigma } }} \approx 1.7 \ldots 1.8\quad {\text{and}}\;\;\eta_{\text{OSI}} = \frac{{V_{\text{OSI}} }}{{V_{0\varSigma } }} \approx 1.3 \ldots 1.4.$

(7.7)

As an example, Fig. 7.18 shows the remarkable influence of the test object (load) capacitance on the efficiency factor and the time-to-peak. The high-efficiency factors compared with those of the aperiodic impulse voltages are especially important when mobile impulse test systems are required for the testing in the field. Therefore, OLI and OSI voltages have been proposed for on-site testing (Kind 1974; Feser 1981), and meanwhile, they are standardized in IEC 60060-3:2006. For more details, see Sect. 10.2.1.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig18_HTML.gif — Fig. 7.18
OLI characteristic of an impulse voltage test system (250 kV/5 kJ)

When the generator has to be designed for a maximum cumulative charging voltage V_0Σmax, the basic load capacitance and also the series inductance must be able to withstand the maximum oscillating impulse voltage which is much higher than the V_0Σmax (Eq. 7.7). The insulation design of the basic load capacitance for OLI and OSI voltages is practically identical, whereas that of the series inductance is very different (compare Figs. 7.16c with 7.17b). For OLI voltages, a low inductance is required which can be made easily. Contrary to that the OSI generation requires a much higher inductance. Now, stray capacitances must be taken into consideration which would cause a non-linear voltage distribution along the coil. To avoid that, a longitudinal voltage control by toroid electrodes is necessary. The coil for OSI voltage is much longer, thicker and heavier than the one for OLI voltage. Furthermore, it has been found that the benefit of OSI testing is low; therefore, mainly OLI testing is applied (see Sect. 10.3.1).

It should be mentioned that also bipolar oscillating impulse voltages can be generated based on impulse voltage circuits (Schuler and Liptak 1980). They arranged the inductance in parallel to the load capacitance and applied the bipolar OLI voltage for testing of rotating machines.

A special case of a bipolar OSI testing is applied for medium-voltage cables: The cable is charged with a DC voltage and then discharged via a suited switch (trigatron or semiconductor HV switch) in series with an inductance L_s and possibly a resistor R_d. The discharge causes a damped oscillation (Fig. 7.19). Under the term “damped alternating voltage” (DAC) (IEC 60060-3:2006), this bipolarly oscillating voltage is successfully used for diagnostic PD measurements on medium-voltage cable systems, but the whole test stress for the cable is a long DC ramp (duration in the order between 1 and 100 s) followed by the much shorter DAC voltage (duration in the order of few 100 ms). The duration of charging and the test frequency depends on the capacitance (length) of the cable, whereas the damping of the oscillation depends on the losses in the circuit. Therefore, the whole stress cannot be reproduced from cable test to cable tests. Occasionally, the voltage is used for withstand tests (Fig. 7.19c), but this cannot be recommended (for more details on DAC voltages, see Sect. 10.2.2.2).

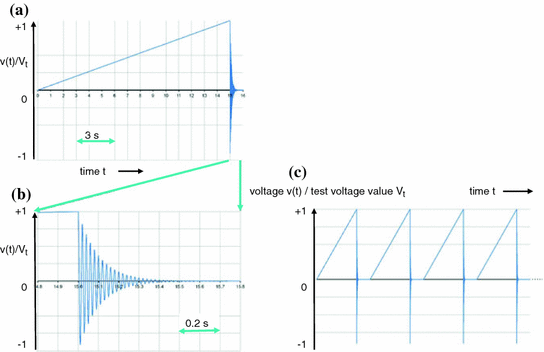
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig19_HTML.gif — Fig. 7.19
Damped alternating (DAC) voltage. a A full DAC impulse (including the DC ramp for charging). b The short oscillating part of the DAC impulse. c A sequence of DAC impulses as occasionally used for withstand tests

7.1.4 OSI Test Voltage Generation by Transformers

When an HV test transformer is excited by controlled discharging a capacitor bank into its low-voltage (LV) side, this impulse causes an oscillation, which is transformed to the HV side according to the transformer ratio (Kind and Salge 1965; Mosch 1969). The schematic circuit diagram (Fig. 7.20a) is transferred with the transformer ratio into an equivalent circuit (Fig. 7.20b), which is used for calculations of the shape and frequency of the OSI voltage (Schrader et al. 1989).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig20_HTML.gif — Fig. 7.20
Generation of unipolar OSI voltages by transformers (Schrader et al. 1989). a Schematic circuit diagram. b Equivalent circuit. c Unipolar OSI voltage

Shape and frequency are determined by the stray inductance of the transformer (L_o) and the series connection of the bank capacitance (C_B) with the transferred load capacitance $(C_{i}^{*} )$

$C = \frac{{C_{B} \cdot C_{l}^{*} }}{{C_{B} + C_{l}^{*} }}.$

(7.8)

The impulse parameters can be influenced by adjustable elements, an inductance L_R and a damping resistor R_p. With the total capacitance C and the total inductance L = L_o+ L_R one gets the frequency and the time-to-peak:

$f = \frac{1}{{2\pi \sqrt {L \cdot C} }}\quad {\text{and}}\;\;T_{p} \frac{1}{2f} = \pi \sqrt {L \cdot C} .$

(7.9)

The output (Fig. 7.20c) is a unipolar OSI voltage with frequencies of 100 up to 1000 Hz; this means with time-to-peak Tp > 500 μs.

Bipolar OSI voltages can be generated with a modified circuit (Fig. 5.21a, b) (Schrader et al. 1989). The load capacitance is charged in the same way as for unipolar OSI voltages, but when the first peak is reached, a short-circuit switching by a thyristor causes the bipolar OSI voltage at the HV output (Fig. 7.21c). The capacitor bank is not any longer involved in the oscillation.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig21_HTML.gif — Fig. 7.21
Generation of bipolar OSI voltages by transformers (Schrader et al. 1989). a Schematic circuit diagram. b Equivalent circuit. c Bipolar OSI voltage

Even under optimum conditions, shorter time-to-peak than mentioned above cannot be generated because of the value of stray inductances of test transformers. In many cases, these times are remarkably longer. When a transformer cascade of three stages shall be used for OSI generation, the stray capacitance depends on the kind of feeding (Fig. 7.22) (Schrader et al. 1989). Feeding into the primary side of the lowest transformer means highest stray inductance and lowest frequency, say 100 Hz. When feeding is applied to the middle of the cascade (tertiary winding of the second transformer), the frequency increases by a factor of two (200 Hz). When feeding is realized into the tertiary windings of all three transformers, the stray inductance decreases to 1/40 compared with case a), and consequently, the frequency increases to more than 600 Hz. This principle has been applied to the mentioned 3-MV cascade transformer (Frank et al. 1991), (Figs. 3.15 and 7.23). On each stage, there is a capacitor bank with a rectifier unit. The DC voltage is generated on the stages from a low-frequency AC voltage supplied via the windings of the transformer in a special mode. The three capacitor banks are discharged each into the tertiary winding of one transformer at the same time. This enables the generation of OSI voltages up to 4.2 MV. The leader discharges in air generated by this extremely high OSI voltage are very similar to natural lightning (Hauschild et al. 1991).

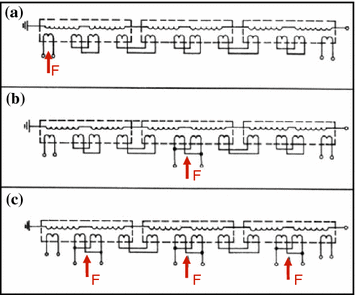
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig22_HTML.gif — Fig. 7.22
Feeding modes of a three-stage cascade transformer for OSI voltage generation. a Single feeding into the primary winding of the lowest transformer. b Single feeding into the tertiary winding of the middle transformer. c Triple feeding into the tertiary winding of each transformer

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig23_HTML.gif — Fig. 7.23
3-MV transformer cascade with OSI attachment and triple feeding mode

7.1.5 Circuits for Very Fast Front (VFF) Impulse Voltages and Solid-State Generators

VFF over-voltages are generated by switching GIS disconnectors and consecutive reflections in the GIS busbars, by steep LI voltage breakdowns of the insulation of overhead lines or by the operation of a lightning arrester. Similar voltages are expected in case of a nuclear explosion (EXO-EMP). They might be characterized by an oscillating impulse with a first front of some 10 ns up to few 100 ns and superimposed contributions of higher frequencies (Feser 1997). Figure 7.24 shows a typical example of a VFF voltage (CIGRE WG 33.03 1998). The development of UHV AC and especially UHV DC transmission systems strengthens the interest in VFF testing (Szewczyk et al. 2016; Rodrigues Filho et al. 2016).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig24_HTML.gif — Fig. 7.24
Time characteristic of a VFF voltage

VFF voltage testing of GIS is performed by defined switching of the disconnectors (IEC 61259:1994). There is no horizontal standard related to the requirements of VFF test voltages. For research and development of components which might be stressed by VFF over-voltages in service, VFF impulse voltages are usually generated by a Marx impulse voltage generator with a connected steeping circuit (Kind and Feser 1999) (Fig. 7.25), consisting mainly of a capacitor and a fast sphere gap with compressed-gas insulation and high breakdown field strength. This gap is connected in series with the test object and enables front times in the order of few 10 ns. An impulse voltage generator without steeping circuit, operating without front resistors, can generate impulse voltages with front times down to about 100 ns.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig25_HTML.gif — Fig. 7.25
Generation of VFF test voltages. a Equivalent circuit. b Potential diagram

The latest development of UHV equipment has directed the attention to the behaviour of compressed-gas insulation under VFF stress (Ueta et al. 2011; Wada et al. 2011). For VFF voltage generation, a metal enclosed, compressed-gas-insulated steeping circuit is applied (Fig. 7.26). In the field compartment before the series gap, an impedance (resistor or inductor) is arranged to generate different superimposed oscillations. When its position is changed related to the gap different superimposed oscillations appear (few MHz to 20 MHz). The test object is inside of the same metal enclosure.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig26_HTML.gif — Fig. 7.26
Principle circuit for VFF investigation of gas insulation

Solid state generators : For low output voltages and special applications, the progress of power electronics enables the development of impulse generators based on solid state elements instead of switching gaps [e.g. Shi et al. (2015), Elserougi et al. (2015), Kluge et al. (2015)]. They can also be recommended for HV testing e.g. of low voltage equipment (IEC 61180). This trend should deserve attention, even if it is not yet applicable for testing of high- and medium-voltage equipment.

7.2 Requirements to LI/SI Test Systems and Selection of Impulse Voltage Test Systems

The preceding subsections have shown that a wide variety of impulse voltage shapes can be generated. For research work, development and even diagnostic testing, this variety can be used. But for quality testing, impulse voltages shall be applied which represent external (lightning) and internal (switching) over-voltages being reproducible within certain tolerances. Requirements for these test voltages are given in standards like IEC 60060-1:2010 or IEEE Std. 4 (Draft 2013) and will be explained in the following.

7.2.1 LI Test Voltage and the Phenomenon of Over-Shoot

7.2.1.1 Requirements of IEC 60060-1 and IEEE Std. 4 to Standard LI Voltages 1.2/50

For a smooth LI impulse voltage, the direct parameter evaluation can be made according to the parameter definitions as described below. But when a LI test voltage shows oscillations or an overshoot, the parameters of a LI test voltage shall be evaluated using the so-called “k-factors” derived from “test voltage functions” (Fig. 7.27).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig27_HTML.gif — Fig. 7.27
Test voltage functions a According to IEC 60060-1:2010 with empirical data and limit value of IEC 60060-1:1989. b Comparison with proposal of CIGRE WG D1.36 (2017) for UHV LI tests

The k-factors used for equipment up to V_m ≤ 800 kV (Eq. 7.10a; Fig. 7.27a) respectively for testing UHV equipment (Eq. 7.10b; Fig. 7.27b) are empirically determined from the comparison of LI voltages with and without oscillations:

${k}\left( {f} \right) = 1/(1 + 2.2 \cdot {f}^{2} /{MHz}){for}\,{testing}\,{V}_{m} \le 800\;{kV}$

(7.10a)

${k}\left( {f} \right) = 1/(1 + 7.5 \cdot {f}^{2} /{MHz}){for}\,{UHV}\,{testing}$

(7.10b)

The k-factors express that an overshoot of long duration (low frequency) has a stronger influence on the breakdown voltage of an insulation than one of short duration (high frequency). This is the well-known breakdown voltage—breakdown time characteristic of insulations (Kind et al. 2016). As a first step of introduction of this new type of evaluation, IEC 60060-1:2010 recommends the application of Eq. 7.10a, b to all types of insulation with V_m ≤ 800 kV, for the necessary improvement of the method see Sect. 7.2.1.2. The determination of the test voltage curve V_t(t) from the recorded curve V_r(t) shall be made in the following steps (Fig. 7.28, for more details, see Annex B of IEC 60060-1:2010):

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig28_HTML.gif — Fig. 7.28
Determination and presentation of the test voltage curve. a Recorded curve, base curve and residual curve. b Test voltage function. c Base curve, filtered residual curve and test voltage curve. d Presentation of test voltage curve and recorded curve

1.
Determine the base curve V_b(t) as an estimate of the exponential function with the parameters V₀, τ₁ and τ₂:

$V_{b} (t) = V_{0} \cdot \left( {{\text{e}}^{{\left( {t/\tau_{1} } \right)}} - {\text{e}}^{{ - \left( {t/\tau_{2} } \right)}} } \right).$

(7.11)

The base curve (Eq. 7.11) represents the recorded curve without over-shoot and shall be characterized by its peak value V_B, whereas the full recorded curve is characterized by its extreme value V_E (Fig. 7.28a).
2.
Find the residual curve as the difference between the recorded curve and the base curve (Fig. 7.28a):

$V_{R} (t) = V_{r} (t) - V_{b} (t).$

(7.12)
3.
Use a digital filter with a transfer function (amplitude–frequency response) equal to the test voltage function H(f) = k(f) (7.10a, b, as described in detail in IEC 60060-1:2010, Annexes B and C) and use it for filtering the frequency spectrum V_R(F) of the residual curve. The result is the filtered residual curve in the frequency domain

$V_{\text{RF}} (f) = k(f) \cdot V_{R} (f),$

(7.13)
and—after re-transformation to the time domain—the filtered residual curve V_RF(t) (Fig. 7.28b).
4.
Superimpose the filtered residual curve on the base curve to get the test voltage curve (Fig. 7.28c):

$V_{t} (t) = V_{b} (t) + V_{\text{RF}} (t).$

(7.14)
5.
In a presentation of the result, both—the recorded curve and the test voltage curve—shall be shown (Fig. 7.28d).

Note It should be mentioned that the handling of the zero-level problem is not considered here. For the zero level and the details of the implementing the evaluation software, see IEC 60060-1:2010, Annexes B and C and IEC 61083-2:2013, see for the filter curve also Lewin et al. (2008).

It should be mentioned that in addition to the computer-aided evaluation, also a manual calculation of the test voltage value V_T is described in IEC 60060-1:2010 (Annex B.4) as well as by Berlijn et al. (2007). This procedure considers not the whole frequency spectrum of the residual curve, rather its corresponding value k(f_os) at the single main frequency f_os of the over-shoot which is simply multiplied with the maximum of the residual voltage V_Rmax(t). The result is superimposed on the estimated base curve to get the test voltage value V_T. In contrast, the filtering (Eq. 7.13) works also when the over-shoot is the result of a mixture of frequencies and when noise signals of higher frequencies are superimposed on the recorded curve. The manual evaluation cannot be recommended.

In case of a smooth recorded curve (Eq. 7.11) with V_E = V_B, one gets V_R(t) = V_RF(t) = 0 because of k(f) = 1. IEC 60060-1:2010 requires that all parameters of the LI test voltage are evaluated from the test voltage curve. When an LI test voltage fulfils the following requirements, it is a standard LI test voltage 1.2/50:

The test voltage value VT is the maximum value of the test voltage curve (Figs. 7.28c and 7.29). In an LI voltage test, the required test voltage value must be adjusted with a tolerance of ±3%.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig29_HTML.gif — Fig. 7.29
Parameter definition for full LI test voltages

The front time T₁ is a virtual parameter defined as 1.67 times the interval between the instants when the impulse voltage is 30 and 90% of the test voltage value (A and B in Fig. 7.29). The front time T₁ = 1.2 μs has a tolerance of ±30%, this means the real front time has to be within (0.84–1.56) μs.

Note For test objects of high capacitance as cables or capacitors, the upper tolerance limit might be significantly enlarged to 5 μs or even more. Also for UHV equipment, an upper tolerance limit in the order of 2.5 μs is under discussion.

The time-to-half-value T₂ is a virtual parameter as the time interval between the virtual origin which is the intersection between the time axis and the straight line drawn through the points A and B in Fig. 7.29, and the instant when the voltage crosses the half of the test voltage value (Fig. 7.29): It is required T₂ = 50 μs with a tolerance of ±20%, this means the real value has to be within (40–60) μs.

The relative over-shoot magnitude ß is the difference between the extreme value of the recorded curve and the maximum of the base curve related to the extreme value (IEC 60060-1:2010):

$\beta = \frac{{V_{E} - V_{B} }}{{V_{E} }} \le 10\%$

(7.15)

The latest edition of IEEE Std. 4 (2013) recommends an over-shoot up to 5%, but allows an increase to 10% for reasons “to allow waveforms accepted by the historical” smooth curve of the “over-shoot method” (IEEE Std. 4—1995 and IEC 60060-1:1989).

Quality tests require in addition to full LI test voltages also chopped LI test voltages (LIC) which represent the stress of the insulation after a protecting device (e.g. an arrester or a protection gap) has operated. An LIC voltage is also caused by any breakdown in the HV circuit, but in the following, only controlled breakdowns with a chopping gap will be considered (see Sect. 7.1.2.4).

The LI voltage can be chopped in the front (Fig. 7.30a) or on the tail (Fig. 7.30b). The instant of chopping is defined as the intersection of the line through the points C (0.7 V_CH) and D (0.1 V_CH) with the voltage level immediately before the collapse. The time to chopping T_C is the interval between the virtual origin O₁ and the instant of chopping. The duration of the voltage collapse T_CO is defined as 1.67 times the time interval between the points C and D. The virtual steepness S_C of the chopping is calculated with the voltage V_CH at the instant of chopping and the duration of the voltage collapse T_CO:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig30_HTML.gif — Fig. 7.30
Chopped lightning impulse voltages. a Front-chopped LIC voltage. b Tail-chopped LIC voltage. c Linearly rising front-chopped impulse

$S_{C} = \frac{{V_{\text{CH}} }}{{T_{\text{CO}} }}.$

(7.16)

Whereas IEC 60060-1:2010 specifies only a tail-chopped LIC voltage of T_C = 2–5 μs (Fig. 7.30b), the IEEE Std. 4 specifies also a standard front-chopped LIC voltage of T_C = 0.5–1.0 μs (Fig. 7.30a).

Note According to the IEC opinion, a front-chopped LIC voltage is not required for testing objects with windings, because the tail-chopped LIC voltage causes a higher steepness and consequently a more non-uniform voltage distribution in the test object. The traditional IEEE opinion considers more the representation of high over-voltages limited by protection devices. It seems that in a future version of IEEE Std. 4, the IEC practice will be applied, too.

A linearly rising front-chopped LIC voltage is a voltage rising with an approximately constant steepness until it is chopped at a voltage V_E. The linearly rising front-chopped LIC voltage is mainly applied in the test practice according to the IEEE standards. It is defined by the extreme value V_E, the front time T₁ and the steepness

$S_{F} = \frac{{V_{E} }}{{T_{1} }}$

(7.17)

The voltage increase is considered to be approximately linear from 30% up to the instant of chopping. The tolerance of the steepness is characterized by a band of ±0.05 · T₁ from the mean line through AB (Fig. 7.30c). The parameters of linearly rising LIC voltages are not specified in the horizontal standards, but in the relevant apparatus standards.

Voltage value : The evaluation of tail-chopped LIC voltages can be made with a method adapted to the k-factor calculation. For this, two records are needed, one of the tail-chopped LIC voltage from the performed test and one full reference LI voltage on lower voltage without changing the set-up of the HV test circuit (except of the switching gaps and the charging voltage of the generator) and the measuring system. The reference LI curve is used for the determination of the base curve. The recorded LIC curve is treated with that base curve similar as described above. For more details, see IEC 60060-1:2010 (Annex B.5). The problem of over-shoot does not appear for front-chopped impulses, they can be evaluated as shown in Fig. 7.30a.

7.2.1.2 Situation and Future of the Treatment of Over-Shoot

The evaluation method according to the IEC and IEEE standards as described above is an important first step into the direction of a physically correct evaluation of LI test voltages with overshoot, but it is also a compromise between new ideas and traditional thinking. Therefore, it shall be tried to explain in the following the possible directions of the further improvement of the k-factor method. Let us consider the new evaluation method in comparison with that of IEC 60-1:1989 (Fig. 7.27).

As considered in Sect. 7.1.2.3, the inductance and capacitances in the circuit may cause oscillations which are damped by the resistive losses in the circuit. The oscillations have remarkable influence on the breakdown behaviour when they appear in the region of the peak and increase the peak value of the LI test voltage. In case of a strong damping, the oscillation is reduced to a single half-wave, which is called “over-shoot”. In the following, the term “over-shoot” shall also include oscillations of lower damping.

The previous version of IEC 60-1:1989 tolerated oscillations and over-shoot up to 5% of the smooth peak. If their frequency “is not less than 0.5 MHz or the duration of the over-shoot not more than 1 μs, a mean curve should be drawn …for the purpose of measurement”. The test voltage value was the peak of the recorded curve for over-shoot frequencies f < 0.5 MHz; for f > 0.5 MHz, it is the maximum of the drawn mean curve. There was no rule how to estimate the mean curve. This abrupt change of the evaluation at 0.5 MHz (Fig. 7.27) is physically wrong, causes an error of up to 5% at that frequency, a certain arbitrariness for the operator or for provider of evaluation software. Therefore, a change had been urgent. On the mid of the 1990s, the CIGRE-Working Group 33.03 and a related European research project started experiments on the influence of the over-shoot (e.g. Garnacho et al. 1997, 2002; Berlijn 2000; Simon 2004). A combined voltage (see Sect. 8.1.1) of a smooth LI voltage and an oscillating short impulse were applied to insulation samples of air, SF₆, oil-impregnated paper and polyethylene. The test voltage values of test series were usually limited up to 200 kV. The experiments delivered 50% LI breakdown voltages for the breakdown of the impulse with over-shoot (extreme value V_E), for the smooth standard impulse (peak value V_LI) and enabled the determination of a well-defined base curve (Eq. 7.11; maximum V_B). For each sample, the results at different over-shoot frequencies have been combined as the frequency-depending test voltage factor (test voltage function)

$k(f) = \frac{{V_{\text{LI}} (f) - V_{B} (f)}}{{V_{E} (f) - V_{B} (f)}}.$

(7.18)

A clear decrease in the test voltage factor with increasing frequency has been found (Fig. 7.27, measuring points), but the dispersion of the results was so large, that no clear influence of the different types of insulations has been identified. Therefore, a common k-factor curve has been evaluated (Fig. 7.27 and Eq. 7.10a, b), which is overtaken into the standards (see Sect. 7.1.2.1).

The results of the LI parameter evaluation according to the valid IEC 60060-1:2010 differ from those according to IEC 60-1:1989. Even if the new evaluation delivers physically better results, the differences may have certain consequences for design and testing of equipment. The results of the evaluation of numerous LI voltages (e.g. of IEC 61083-2:2013) according to the old and the new procedure (Table 7.2) show the consequences. If there is an over-shoot with f < 0.5 MHz, an up to 3% higher LI test voltage would be necessary now. The front time would become shorter and the time to half-value longer. For f > 0.5 MHz, an up to 6% lower LI test voltage can be applied now, the front time increases and the time to half-value decreases. These results show the tendency, but they include not only the differences in the procedures, but also the uncertainties caused by the software. Further comparisons of the old and the new method are published by Pfeffer and Tenbohlen (2009).

Table 7.2

Differences of LI parameter evaluation according to IEC 60060-1:2010 and IEC 60-1:1989

Parameter	Over-shoot frequency f < 0.5 MHz	Over-shoot frequency f > 0.5 MHz
Test voltage value	0…−3%	+2%…+6%
(V₂₀₁₀ − V₁₉₈₉)/V₁₉₈₉	0…−3%	+2%…+6%
Front time	0…−6%	0…+15%
(T_{1 2010} − T_{1 1989})/T_{1 1989}	0…−6%	0…+15%
Time to half-value	0…+5%	−4%…7%
(T_{2 2010} −T_{2 1989})/T_{2 1989}	0…+5%	−4%…7%
Over-shoot	Independent on the frequency
(ß₂₀₁₀ − ß₁₉₈₉)/ß₁₉₈₉	−10%…+40%

An unexpected result was found for the values of the over-shoot which became usually higher according to IEC 60060-1:2010 than according to the old version. The reason is the missing rule for the old “mean curves” which got higher maxima by the old “user-friendly” software than the well-defined “base curves” (Eq. 7.11) by the new software. Also the definition of the over-shoot (Eq. 7.15) is physically not correct. It does not consider the duration of the over-shoot (Hinow et al. 2010), because the extreme value V_E of the recorded curve is the reference value. An over-shoot definition which considers the duration could follow a German proposal to TC 42 when the over-shoot magnitude would be defined from the test voltage curve—as the other parameters of LI voltage, too (Hinow et al. 2010):

$\beta^{*} = \frac{{V_{T} - V_{B} }}{{V_{T} }}$

(7.19)

The comparison of the two definitions (Fig. 7.31) shows that ß* delivers always lower values than ß. For an over-shoot frequency of f < 0.5 MHz, ß* is typically higher than for the case f > 0.5 MHz. With respect to the duration of the over-shoot, this is a plausible characteristic.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig31_HTML.gif — Fig. 7.31
Comparison of the over-shoot magnitudes of β (IEC definition Eq. 7.15) and ß* (Eq. 7.19)

A further point is the dependence on the frequency. The frequency is estimated from the duration of the over-shoot (Garnacho et al. 1997), but the breakdown process is influenced by the available time according to the well-known breakdown voltage—breakdown time characteristic (see Sect. 7.3). This characteristic can be described by a statistical time-lag followed by the formative time-lag. The latter can be described by the formative voltage– time area (Kind 1957; Kind et al. 2016). which might be also applied to the over-shoot treatment (Hauschild and Steiner 2009; Garnacho 2010; Ueta et al. 2011c). Then, the over-shoot will be characterized by the voltage–time area above a certain voltage value V_X (Fig. 7.32). This might be a certain percentage of the extreme value (Fig. 7.32a, b) or the test voltage value V_T (Fig. 7.32c). Then, for example, the relative over-shoot magnitude would be calculated by:

$\beta^{^\circ } = \frac{1}{{V_{T} \cdot T_{t} }} \cdot \int\limits_{{}}^{T} {\left( {V_{t} (t) - V_{T} } \right){\text{d}}t} ,$

(7.20)

with the over-shoot duration: $T_{t} = \sum\nolimits_{i = 1}^{n} {t_{i} \left( {V_{i} \ge V_{T} } \right)} .$

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig32_HTML.gif — Fig. 7.32
Definition of over-shoot in conjunction with the formative time model. a Example for an aperiodic over-shoot using a percentage of extreme value V_E. b Example for oscillating over-shoot using 0.9 · V_E. c Example for oscillating over-shoot using the test voltage value V_T

A limitation of ß° would mean a limitation of the formative voltage–time area which considers the really acting stress combination of voltage and time.

When an over-shoot definition related to the duration of the over-shoot is applied, it seems to be appropriate to apply also the test voltage function depending on the duration. The duration of an aperiodic over-shoot is related to the frequency by T_t ≈ 0.5/f, and one can derive from Eq. (7.10), the new test voltage function

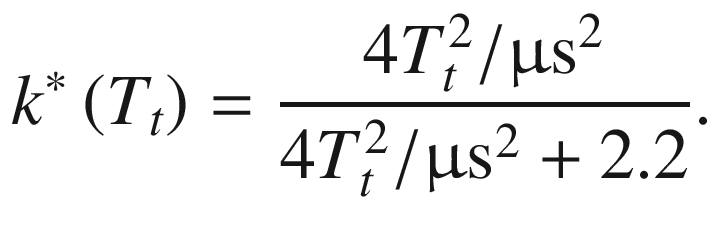
$k^{*} \left( {T_{t} } \right) = \frac{{4T_{t}^{2} /\upmu{\text{s}}^{2} }}{{4T_{t}^{2} /\upmu{\text{s}}^{2} + 2.2}}.$

(7.21)

This function (Fig. 7.33) would not only improve the physical understanding. It has a linear scale with a direct relation to the time parameters of the LI voltage. The case T_t = 0 means no over-shoot. The determination of the duration is even simpler than that of the frequency. It would also consider the case that the oscillations are only slightly damped (Fig. 7.32b), and the second peak contributes to the formative voltage–time area. Instead of using the test voltage function of IEC 60060-1:2010 (Eq. 7.10a, b), a different definition of the relative over-shoot magnitude can be used—e.g. as that of Eq. 7.20.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig33_HTML.gif — Fig. 7.33
Test voltage function depending on over-shoot duration (Eq. 7.21)

The test voltage function for higher voltages and different insulation samples is under investigation till now, e.g. by Garnacho (2010), Garnacho et al. (2014), Hinow with TU Cottbus (2011), Ueta et al. (2010, 2011b), Diaz and Segovia (2016) The present function (Eq. 7.10a, b) is based on experiments of small samples and voltages mainly V_T < 200 kV. Therefore, the breakdown is quite fast and the assumption to have a certain average characteristic seems to be not correct. It must be shifted (Fig. 7.34)—to the left (lower frequencies) for large insulation and/or relatively slow breakdown processes as for long air gaps or larger transformer insulation used for UHV transmission (Tsuboi et al. 2011, 2013; Ueta et al. 2012b) and only a bit to the right (higher frequencies) for small and compact insulation of very fast breakdown processes (SF₆; solids, vacuum, etc.), but till now, IEC TC42 has not yet drawn the final conclusion of that international research work.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig34_HTML.gif — Fig. 7.34
Expected modifications of the test voltage function

It can be assumed that different characteristics will be found for different electric fields, different insulation materials and possibly even for different over-shoot magnitudes. Also the evaluation algorithms and the remarkable uncertainty of the determination of the test voltage function (Okabe et al. 2015) must be taken into consideration. Possibly for a future standard IEC 60060-1, all available experimental results should be used to find one common test voltage function applicable within acceptable tolerances for parameter evaluations of all insulations.

The fitting method for extracting the base curve as described above (Eq. 7.11) is also subject of ongoing investigation, (e.g. Satish and Gururaj 2001; Kuan and Chen 2006; Ueta et al. 2011a, b, c, d, 2012a, b; Garnacho et al. 2013; Pattanadesh and Yutthagowith 2015). The introduction of a new evaluation method for the base curve could cause differences in the LI parameter evaluation. Contrary to the test voltage function, there seems to be no urgent need for the introduction of a new method for the determination of the mean curve. First, it must be shown that the present method is insufficient for practical cases.

Related to testing of UHV equipment , the CIGRE Working Group D1.36 (2017) has summarized the present knowledge: It has been shown that for UHV test objects the requirements T₁ ≤ 1.56 µs and ß ≤ 10% cannot be met, when the capacitance of the test objects reaches the order of 10 nF (see also the following Sect. 7.2.1.3). It is recommended to increase the upper tolerance limit to T₁ = 2.5 µs and the acceptable overshoot to ß ≤ 15% when testing UHV equipment with V_m > 800 kV. Furthermore the test voltage function for UHV LI testing is changed (Fig. 7.27b) to the above mentioned Eq. (7.10b) and an improved procedure for the base curve estimation is proposed. Hopefully IEC TC42 will provide on that basis the next edition of IEC 60060-1.

Last but not least, there are discussions to reduce the over-shoot in LI testing by the over-shoot compensation (see Sect. 7.1.2.3).

7.2.1.3 Interaction Between HVLI Test System and Test Object

Most test objects—like insulators, bushings, GIS, power transformers or cable samples—provide a capacitive load for the test system. In few cases, test objects have an inductive characteristic, like the low-voltage winding of power transformers. Resistive test objects do not play any role, because outdoor insulations are not tested under wet or polluted conditions with LI voltages. The influence of the test object shall be explained by the equivalent single-stage circuit (Fig. 7.4).

Capacitive test objects : The load capacitance C_l = C_b + C_i (usually consisting of the basic load C_b of the generator plus the test object capacitance C_to) determines the front time constant τ_f (together with the front resistor R_f, Eq. 7.2), the time constant for the tail τ_t (together with the impulse capacitor C_i and the tail resistor R_t) and the circuit efficiency factor η_c (together with the impulse capacitor C_i of the generator, Eq. 7.1):

$\tau_{f} = R_{f} \left( {\frac{{C_{i} \cdot \left( {C_{b} + C_{\text{to}} } \right)}}{{C_{b} + C_{\text{to}} + C_{i} }}} \right),$

(7.22a)

$\tau_{t} \approx R_{t} \left( {C_{i} + C_{b} + C_{\text{to}} } \right),$

(7.22b)

$\eta_{c} \approx \frac{{C_{i} }}{{C_{i} + C_{b} + C_{\text{to}} }}.$

(7.23)

The front time T₁ (characterized by τ_f, Eq. 7.22a) depends strongly from the test object capacitance because usually C_i ≫ C_b + C_to and consequently τ_f ≈ R_f · (C_b + C_to) with often C_to > C_b. In many cases, the front time is nearly doubled when the test object capacitance is doubled. Considering that the width of the front time tolerance (0.84–1.56 μs) is less than doubling its lower limit (Fig. 7.35), the front resistors R_f of a generator must be adapted accordingly. For a fixed value of τ_f—respectively, of the front time T₁—the necessary value of R_f for the upper, respectively, the lower tolerance limit of the front time can be calculated (Fig. 7.35a). A horizontal line through the resulting band corresponding to a certain range of load capacitance gives the range of load, for which one resistance R_f1 can be applied to deliver standard LI voltages. For higher load capacitance, a lower resistance R_f2 has to be applied and so on. If the front resistance becomes too low, an unacceptable over-shoot is generated which limits the generation of standard LI impulses. For the example of Fig. 7.35a, this is reached when the front resistance approaches about 100 Ω (This means e.g. 10 Ω per stage for a 10-stages generator).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig35_HTML.gif — Fig. 7.35
Influence of the load capacitance on selection of front and tail resistors of a generator 2000 kV/400 kJ of ten stages. a Principle of the selection of front resistance. b Situation of the tail resistance (Kind and Feser 1999)

The simplified consideration of Fig. 7.35 neglects the important influence of the circuit inductance which causes the overshoot (accepted by standards up to ß = 10%). The overshoot is damped by the front resistor which must exceed a minimum value. According to CIGRE WG D1.36 (2017), this minimum acceptable front resistor (in Ω) ${\text{R}}_{\text{fmin}}^{*}$ for T₁ ≤ 1.56 µs can roughly be estimated from the total capacitive load (in µF) (C_l = C_b + C_to) and the total circuit inductance (in µH) (L_s = L_generator + L_{HV lead} + L_{test object} + L_{current return}) by

${\text{R}}_{{{\text{f}}\hbox{min} }}^{*} = 1.45\sqrt {L_{s} /C_{l} }$

(7.24)

With the characteristic UHV load capacitances (up to more than 10 µF) it might be difficult to meet the limit of the overshoot β ≤ 10%. Therefore the test standards for UHV equipment (now under preparation) shall allow a higher LI overshoot (up to β = 15%) and/or longer LI front time (higher front resistors) for sufficient attenuation of the overshoot.

For the adaptation of the front resistance, each LI generator has several sets of resistors. Usually, these sets are designed in such a way that resistors can also be switched in parallel or even in series to vary the available values of front resistance by combinations for a wide range of capacitive load. For each single-resistance value, a certain load range is covered. Usually, a LI test system is equipped with three sets of front resistors enabling seven different resistance values by different parallel connections. For efficient handling of a larger LI test generator, the not-used resistors should be stored on the stages which should be easily reached by internal fixed ladders (Fig. 7.12d). Each impulse test system should be equipped with an instruction which resistors should be applied for which test object capacitance to cover a certain range of load capacitances (Fig. 7.36).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig36_HTML.gif — Fig. 7.36
Selection of front resistance depending on test object capacitance

The time to half-value T₂ (characterized by τ_t, Eq. 7.22b) is not strongly influenced by the test object capacitance because it is dominated by the impulse capacitance C_i (Fig. 7.35b). One tail resistance is sufficient to cover the whole tolerance band of the time to half-value between 40 and 60 μs.

The circuit efficiency factor can easily be estimated by Eq. 7.23. The generator with its basic load reaches usually a total efficiency factor η ≈ 0.95 for C_i ≫ C_to. It decreases slightly with increasing test object capacitance and values C_to > 0.2 C_i cannot be recommended.

An inductive test object combined with a capacitance is, e.g. found when the low-voltage side of a power transformer is tested (Fig. 7.37a). The inductance L_to forms an oscillating circuit especially with the impulse capacitance C_i and causes an impulse tail which is characterized by an oscillation instead by an exponential function. The oscillation shortens the time to half-value T₂, often outside the tolerance (T₂ < 40 μs), causes an undershoot to the opposite polarity as well as a reduction of the efficiency factor (Fig. 7.37c). The influence on T₂ is especially serious and increases with decreasing impulse capacitance C_i of the generator (Fig. 7.37c). As the LI test voltages of the low-voltage side of the transformer under test are relatively low, several stages of a multi-stage generator are connected in parallel to increase C_i. If this is not sufficient, the problem can be solved by a so-called “Glanninger attachment”: An inductance L_g is switched in parallel to the front resistor R_f and a resistor R_g in parallel to the test object inductance L_to (Fig. 7.37b). The Glanninger inductance L_g < L_to is correctly selected when it bridges the front resistor only for lower frequency (tail of the impulse) and when the time to half-value is sufficiently extended, but the voltage is divided between L_g//R_f and the test object (L_to//R_g) causing a further reduction of the efficiency factor. The “Glanninger” inductance shall be in the order of L_g = (0.01–0.1) L_to, and the “Glanninger” resistor is selected as R_g ≈ R_f · L_to/L_g. The Glanninger attachment is a separate unit switched to the parallel connected stages of the generator.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig37_HTML.gif — Fig. 7.37
Testing of objects with inductances. a Equivalent circuit. b Equivalent circuit with “Glanninger” attachment. c Comparison of the impulse shape

7.2.2 SI Test Voltages

7.2.2.1 Requirements of IEC 60060-1 and IEEE Std. 4

Over-shoot is not a problem for SI test voltages because a front resistor of quite high resistance is necessary to meet the front time parameter. The recorded curve has also a sharp beginning, the so-called “true origin”, and does not require a virtual origin (Fig. 7.38). Therefore, the parameters are evaluated from the recorded curve directly.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig38_HTML.gif — Fig. 7.38
Recorded curves of SI test voltages 250/2500 and their reproducibility for different peak values

When an SI voltage fulfils the following requirements, it is a standard SI test voltage:

The test voltage value Vt is the maximum value of the recorded voltage curve (Fig. 5.39). In a SI voltage test, the required test voltage value must be adjusted with a tolerance of ±3%.

The time-to-peak Tp is the time interval between the true origin and the maximum value of an SI voltage. It replaces the front time T₁ at LI voltages. The time-to-peak is determined also from the time of the intersection T_AB = t₉₀ − t₃₀ (Fig. 7.39a) according to

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig39_HTML.gif — Fig. 7.39
Definitions of SI test voltages. a Standard impulse 250/2500. b SI testing of equipment with saturation effects

$\begin{aligned} {\text{T}}_{\text{P}} & = {\text{K}} \cdot {\text{T}}_{\text{AB}} \quad {\text{with}}\quad K = 2.42 - 3.08 \cdot 10^{ - 3} \,T_{AB} + 1.51 \cdot T_{2} \cdot 10^{ - 4} \\ & \quad {\text{with}}\quad {\text{T}}_{\text{p}} ,T_{AB} \quad {\text{and}}\,{\text{T}}_{2} \,{\text{in}}\,\upmu{\text{s}} \\ \end{aligned}$

(7.25)

A standard SI test voltage requires T_p = 250 μs with a tolerance of ±20%. This means the real front time has to be within (200–300) μs.

Note When SI testing was introduced in the late 1960s, the evaluation of the time-to-peak has been made according to all appearances. This principle has not been suitable for computer evaluation, and therefore, the evaluation based on the intersection has been introduced with IEC 60060-1:2010.
The definition front time—which would be in the order of T₁ ≈ 170 μs—has not been introduced because the equivalent time-to-peak of T_p = 250 μs is used for decades, and for traditional reasons it should not be changed.

As shown by Sato et al. (2015) Eq. (7.25) is only valid for standard SI voltages, its application to non-standard SI voltages (e.g. 20/4000 µs as accepted for SI voltage tests on site, see Sect. 10.2.1.3) might lead to failures up to 25%. Sato et al. give an formula better adapted to the full range of SI voltages.

The time to half-value T₂ is a virtual parameter as the time interval between the true origin, and the instant when the voltage crosses the half of the test voltage value (Fig. 7.39a): It is required T₂ = 2500 μs with a tolerance of ±60%, this means the real value has to be within (1000–4000 μs).

Note The tremendous tolerance of T₂ is related to tests on equipment with saturation phenomena, e.g. caused by the iron cores of transformers and reactors. There the SI voltages cause a saturation of the magnetic core which leads to the immediate collapse of the voltage (Fig. 5.39b). For such tests additional parameters, the time above 90% and the time to zero have been introduced (see below). The wide tolerance interval is acceptable because the breakdown process in air—development of leader discharges (see Fig. 7.3)—is determined by the steepness of the front of the SI voltage and very few by development of its tail.

The time above 90% T₉₀ is the interval during which the SI voltage exceeds 90% of its maximum value (Fig. 7.39b).

The time to zero T_Z is the interval between the true origin and the instant when the SI voltage has its passage through zero (Fig. 7.39b).

The parameters shall not been mixed up, because a standard SI test voltage 250/2500 has to be characterized by the set (V_t; T_p; T₂) and for testing equipment with saturation effects the different SI set (V_t; T_p; T₉₀; T_Z) may be used.

7.2.2.2 Interaction Between HVSI Test System and Test Object

Consideration of polarity effects : Both, LI and SI voltage tests on internal insulation shall be performed at negative polarity to avoid flashovers at bushings or terminations in air. Whereas non-uniform air insulations have much lower breakdown voltages at positive polarity, there is approximately no, sometimes even a slight opposite polarity effect for internal insulation. Also the design of the control electrodes and of the insulation structures of the HV components of an LI/SI test system is determined by the maximum positive SI voltage to be generated. Positive specific SI breakdown voltages of non-uniform fields in air can go down to the order of 1 kV/cm, whereas at LI voltage one can assume a value of 5 kV/cm.

Capacitive test objects : It has been shown in Sect. 7.1.2 that the efficiency factor can be understood as the product of the shape efficiency and the circuit efficiency (Eq. 7.1). The shape efficiency factor η_s of SI voltage is much lower than of LI voltage. The circuit efficiency factor η_c can be estimated according to Eq. 7.24 as for LI voltages. For a load capacitance C_l = C_b + C_to = 0.2 · C_i, the circuit efficiency becomes ηc = 0.83. With a shape efficiency of η_s = 0.75 one gets a total efficiency factor of only η = 0.62 (Eq. 7.3). The time-to-peak is less sensitive to changes of the load capacitance than the front time of LI voltage. The tolerance of the time to half-value is so large that changes of the test object do not play any role for the selection of the tail resistors. When an LI/SI test system is ordered the maximum expected test object capacitance must taken into consideration for the selection of the impulse energy per stage (Eq. 7.3).

Resistive test objects : Wet and pollution tests of external insulation are also performed at SI test voltages, especially for EHV and UHV equipment. The influence of the resistance of a polluted test object to the total front resistance of an SI generator (up to some 10 k′ Ω) remains negligible. But during testing heavy discharges with currents of some Amperes may cause remarkable voltage drops. This is not only a problem for wet and pollution tests, but also when long air gaps with leader discharges are investigated. As described above for AC and DC voltage, the voltage drop can be calculated when the height and duration of the current pulse are known or assumed. Impulse currents of peak values above 10 A and duration of some 10 μs have been observed (Les Renardieres Group 1977). There is not yet any standard on the acceptable voltage drop at a pre-given current impulse. In any case for the mentioned tests, an impulse generator of high impulse energy should be applied.

Inductive test objects with saturation effects: For testing power transformers, the IEC 60076-3:2013 requires T_p > 100 μs; T₉₀ > 200 μs and T_Z > 1000 μs. For the prolongation of the time to zero, a pre-magnetization of the core with SI voltage of opposite polarity and lower maximum value (V_e > 0.7 · V_t) can be performed if necessary. Also after a SI voltage test, the core should be demagnetized by applying lower SI voltages of opposite polarity.

7.3 Procedures and Evaluation of LI/SI Voltage Tests

Breakdown and standardized withstand voltage tests as well as the statistical background are already described in Sect. 2.4. The following explanations are related to special LI/SI test procedures and refer to that section.

7.3.1 Breakdown Voltage Tests for Research and Development

The multiple-level method (MLM) is the most important and mainly used test method for the determination of the performance function of insulation samples (see Sect. 2.4.3 and Fig. 2.31). The performance function describes the relationship between stressing LI/SI voltages and breakdown probabilities completely. The MLM test can be easily performed on self-restoring insulation in air. The independence might be checked by independence tests. A procedure for that test is explained in Table 2.8. Usually the test results for air gaps are independent when the break between two LI/SI voltages is not shorter than several seconds.

For air or SF₆ insulation with surfaces to solid insulation (e.g. insulators), before the further evaluation of the test, a check of independence is more important than for gases alone. If dependence is indicated, the test procedure should be modified, e.g. by longer breaks between two impulses following each other. Also the short application of a lower impulse voltage of opposite polarity or of a low AC voltage during the break may help to get independent results.

For liquid impregnated and solid insulation the MLM application requires for each LI/SI voltage stress a new test sample. This is a remarkable effort and the limited reproducibility of the test samples causes an additional contribution to the dispersion of the measured performance function. For such test objects it can be checked to apply the progressive stress method (PSM; Fig. 2.26c). where one sample is applied to a series of impulses until breakdown. A single test sample delivers more information in a PSM test than in a MLM test.

The statistical evaluation should be made with a powerful software package based on the maximum-likelihood method (Speck et al. 2009). This delivers (Fig. 7.40) estimations of the breakdown probabilities including confidence regions for the used seven voltage levels, point estimations of the performance function (red line in the middle), its confidence limits (blue limits) and also confidence limits of the quantiles (pink lines). Figure 7.40 shows the evaluation based on the normal (Gauss) distribution. It can be repeated for a different distribution function to find the optimum adaptation. All possible conclusions can be drawn from a diagram like Fig. 7.40.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig40_HTML.gif — Fig. 7.40
Performance function of an air gap evaluated by the maximum-likelihood method based on a normal (Gauss) distribution

When instead of the whole performance function, the estimation of a certain quantile (e.g. V₅₀ or V₁₀) is sufficient, the up-and-down method can be applied (Sect. 2.4.4 and Figs. 2.38 and 2.39). Also for that test procedure a maximum-likelihood evaluation is possible and can be recommended.

7.3.2 LI/SI Quality Acceptance Tests

A passed quality acceptance LI/SI test verifies the insulation coordination (Sect. 1.2) by performing the test according to a standardized procedure, see Sect. 2.4.6; Fig. 2.43 and IEC 60060-1:2010.

For external, self-restoring insulation (mainly of atmospheric air), two procedures are acceptable (see also Sect. 2.4.6):

A1.
The LI/SI test voltage is lower than the 10%—breakdown voltage: V_t < V₁₀.
A2.
The LI/SI test voltage is 15-times applied and the number of breakdowns is k ≤ 2.

For internal, non-self-restoring insulation (all solid or liquid impregnated insulation) no breakdown may occur during the quality acceptance test; therefore, the following procedure is applied:

B.
The LI/SI test voltage is three times applied and no breakdown may occur (k = 0).

For insulation as that of a GIS consisting of a self-restoring (SF₆ gas) and a non-self-restoring (solid insulators) part, it has to be shown that the breakdown had happened in the self-restoring part. This can be indicated by a certain number of withstands at the LI/SI test voltage after the breakdown. A further indication can be a PD measurement which shows no increased PD level. The valid procedure is specified by the relevant apparatus committee of IEC or IEEE. In the following some examples for LI/SI acceptance test procedures are given:

Testing of external insulation (IEC 60071-1): The procedure A1 (V_t < V₁₀) requires the estimation of V₁₀ from a performance function measured down to this low breakdown probability or for known V₅₀ and standard deviation σ from V₁₀ = V₅₀–1.7 σ or from an up-and-down test with seven impulses per voltage level (see Sect. 2.4.4). The procedure A2 (n = 15/k = 2) is applicable for all other cases when the above necessary parameters are not available and the effort for their determination is assumed to be too high. It is necessary to mention that the LI voltage tests are applied to dry insulation (see Sect. 2.1.2), whereas the SI voltage tests are applied to wet insulation (see Sect. 2.1.3).

Testing of gas-insulated substation (GIS) (IEC 62271-203:2003): The GIS insulation is characterized by a self-restoring part, the SF₆ gas, and a non-self-restoring part, the surface and the epoxy resin of the spacer insulators. The LI/SI voltage tests are combined with numerous dielectric, thermal, power and mechanical measurements and tests. The standard waveforms are applied and the procedure A2 (15/2) shall be applied. It has to be guaranteed that no breakdown or flashover occurs in the non-self-restoring part. This is considered as verified, if the last five impulses are without such a disruptive discharge. If the first breakdown appears after the impulse no. 10, the number of total impulses has to be extended accordingly. In the worst case of a breakdown at no. 15, the total number of test impulses becomes 20.

Note It is important to state that the “horizontal” IEC 60071-1:1993 requires only three impulse voltages and in case of one breakdown nine additional voltage impulses during which no disruptive discharge is tolerated. This procedure is of higher uncertainty, and therefore, it had not been considered as sufficient when the “vertical” GIS standard was established in 2003.

Testing of power transformers (IEC 60076-3/FDIS:2013): The used impulse generator shall exceed a minimum impulse energy. The standard recommends an energy W_{i min} (in Joules) according to the empiric formula:

$W_{{i\,{ \hbox{min} }}} > \frac{{100 \cdot 2\pi f \cdot T_{2}^{2} \left( {V_{t}^{2} } \right) \cdot S_{r} }}{{Z \cdot V_{m}^{2} \cdot \eta^{2} }},$

(7.26)

with the parameters of the transformer under test:

V _m: rated phase-to-phase voltage in Volts;
f: rated frequency in Hertz;
Z: short-circuit impedance in % related to the test terminals;
S _r: three-phase power rating in Volt-Amperes;

and with the test parameters:

V _t: LI test voltage value in Volts;
T ₂: time to half-value of he LI voltage in μs;
η: efficiency factor in per unit.

The LI voltage test is a routine test for power transformers V_m > 72.5 kV, for lower rated voltages a type test. For transformers V_m > 170 kV, the test includes also chopped LI voltages (LIC). An SI voltage test is a routine test for transformers V_m > 170 kV and for lower rated voltage a special test. The impulse shall be of standard shape 1.2/50 within the usual tolerances. The evaluation according to the k-factor method is allowed, but alternatively IEC 60076-3:2013 defines some strange differences to IEC 60060-1:2010:

As long as the over-shoot does not exceed 5% (ß ≤ 5%), the extreme value may be taken as the test voltage value. If the over-shoot exceeds 5%, the front time might be extended up to T₁ = 2.5 μs and a test with chopped lightning impulses must be performed. Remains ß ≤ 5% also now, the test voltage value is the extreme value. Only for rare cases, when the over-shoot ß > 5% cannot be avoided, the evaluation according to IEC 60060-1:2010 shall be applied for transformers of rated voltage ≤800 kV. For UHV transformers, even longer front times can be agreed between the parties of an acceptance test. Also the lower tolerance limit of the time to half-value can be reduced up to T₂ = 20 μs by agreement. The test shall be performed in the following sequence:

one full LI reference voltage of (0.5–0.6) · V_t,
one full LI test voltage V_t,
two chopped (LIC) test voltages of 1.1 V_t,
two full LI test voltages V_t.

If an SI voltage test is performed, it follows after the LI/LIC test and before the tests with AC voltages (see Sect. 3.2.5). It consists of

one SI reference voltage (0.5–0.7) V_t and
three SI test voltages V_t.

Both tests are successful if no internal breakdown collapses the voltage. For the LI test, additionally, the normalized voltage shapes of the reference LI voltage and of the LI test voltage, as well as the normalized shapes of the measured impulse currents (see Sect. 7.5) at the two voltage levels should be identical.

LI/ SI testing of cables (IEC 62067:2006): The routine test of cables does not include an LI/SI test voltage. The AC withstand test and a sensitive PD measurement are considered to be sufficient for verifying a correct production, but in defined intervals, more detailed cable sample tests (which repeat parts of the type test) are performed to confirm the correct production.

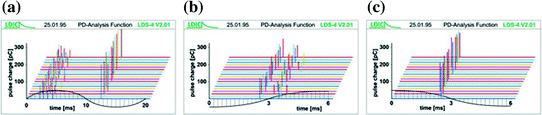
A cable type test includes a long set of single tests including LI/SI tests which are performed at warm cable samples after a heating cycle voltage test, which includes 20 single cycles of one day each, and a PD measurement. First, the SI test is performed with 10 positive and 10 negative SI voltages. If no breakdown occurs, the sample has passed and can be stressed with LI voltages according to the same procedure. The PD test is repeated after the LI/SI test.

Additionally, there are pre-qualification tests on complete cable systems of about 100 m length with joints and terminations. The total test duration is about one year with in minimum 180 heating cycles. The LI test voltage shall be applied to the whole test assembly or to samples with a length of in minimum 30 m after each heating cycle. The test temperature shall be in an interval between maximum conductor temperature and 5 K above. The test consists of 10 positive and 10 negative LI voltage applications again. It is passed if no breakdown occurs.

As the capacitances of the cable samples are between 0.15 and 0.3 nF/m, the test object capacitance for 30 m samples may reach 9 nF and for 100 m up to 30 nF. These are quite high capacitances, and therefore, the standard allows front times T₁ = 1…5 μs, T₂ is within the standard values T₂ = 40…60 μs. For SI test voltages, the usual tolerances shall be applied.

7.4 Measurement of LI and SI Test Voltages

To measure the peak value of high impulse voltages, originally sphere gaps have been employed, as already presented in Sect. 2.3.5. However, this direct measurement method is nowadays only recommended for performance checks including linearity tests. Occasionally, also field probes are applicable, as described in Sect. 2.3.6, particularly for measuring very fast transient voltages characterized by time parameters down to the nanosecond range (Feser and Pfaff 1984). This Section is addressed to indirect measuring methods using a HV converting device, which is connected to the LV measuring device via a transmission system, such as a BNC cable or even a fiber optic link. As the design of the converting device is the most challenging task, the following treatment focuses mainly on this issue. More details on this subject can also be found in the textbook of Schon published in 2013.

7.4.1 Dynamic Behaviour of Voltage Dividers

Lightning impulse voltages, particularly if chopped in the front, cover a frequency spectrum up to 10 MHz and even above. To prove whether the scale factor remains constant within such a wide frequency band, the dynamic behaviour of the entire HV measuring system must be known. As this is mainly governed by the voltage divider providing the converting device, only this component will be investigated in the following. Basically, the transfer function can be determined in either the frequency or the time domain. The set-up commonly used for the second method is sketched in Fig. 7.41.

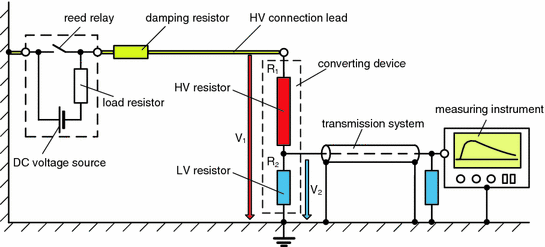
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig41_HTML.gif — Fig. 7.41
Set-up for measuring the step voltage response of LI voltage dividers

Usually, a step voltage of some 100 V in magnitude and a rise time in the nanosecond range is applied. To accomplish such a short rise time commonly a mercury-wetted relay is used, which is often referred to as Reed-Relay. If switching at repetition rate around 100 Hz, disturbing background noises can effectively be rejected by the so-called averaging mode. Due to the proximity effect, it has to be taken care that the voltage divider is arranged in agreement with real HV test conditions where neither the HV connection lead nor the measuring cable should be replaced after the performance test has been carried out.

Among others, the dynamic behaviour is mainly affected by the stray capacitances between divider column and earth as well as other grounded structures. For a better understanding, consider the equivalent circuit of a resistive voltage divider, as shown in Fig. 7.42a. Here, the HV arm is subdivided in n equal elements where the partial resistors as well as the associated earth capacitances are assumed as linearly distributed along the entire HV divider column:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig42_HTML.gif — Fig. 7.42
Equivalent circuits of unshielded resistive voltage dividers. a Distributed capacitances (transmission line). b Lumped capacitance connected to the HV arm. c Lumped capacitance integrated in the LV arm (low-pass filter) with R_s = R₁ and C_p= C_e/6

$R_{11} = R_{12} = \cdots = R_{1n} = R_{1} /n\quad C_{e1} = C_{e2} = \cdots = C_{en} = C_{e} /n$

Under this condition the potential distribution along the HV divider column can be approximated by a hyperbolical function, which is equivalent to that of a long transmission line (Raske 1937; Elsner 1939; Asner 1960). As the resistance R₁ providing the HV arm is much greater than the resistance R₂ providing the LV arm, the time-dependent voltage v₂ (t) appearing across R₂ can be deduced from the high voltage v₁ (t) applied to the top electrode using the classical Laplace transformation. For the here considered network, which is composed of distributed elements according to Fig. 7.42a, the following approximation applies:

$F\left( {j\omega } \right) = \frac{{V_{2} \left( {j\omega } \right)}}{{V_{1} \left( {j\omega } \right)}} \approx \frac{{R_{2} }}{{R_{1} }} \cdot \frac{\sin h\left( \gamma \right)}{{\sin h\left( {n \cdot \gamma } \right)}},$

(7.27)

with

$\left( {n \cdot \gamma } \right)^{2} = j\omega \cdot R_{1} \cdot C_{e} .$

(7.28)

To keep the measuring uncertainty as low as possible, the inequality (n ∙ γ)² ≪ 1 must be satisfied. Under this condition Eq. (7.27) can be simplified as follows:

$F\left( {j\omega } \right) \approx \frac{{R_{2} }}{{R_{1} }} \cdot \frac{1}{{1 + \left( {n \cdot \gamma } \right)^{2} /6}} = \frac{{R_{2} }}{{R_{1} }} \cdot \frac{1}{{1 + j\omega \cdot R_{1} \cdot C_{e} /6}} \approx \frac{{R_{2} }}{{R_{1} }} \cdot \frac{1}{{1 + j\omega \cdot \tau_{f} }}$

(7.29)

Based in this, the amplitude-frequency spectrum can be expressed as follows:

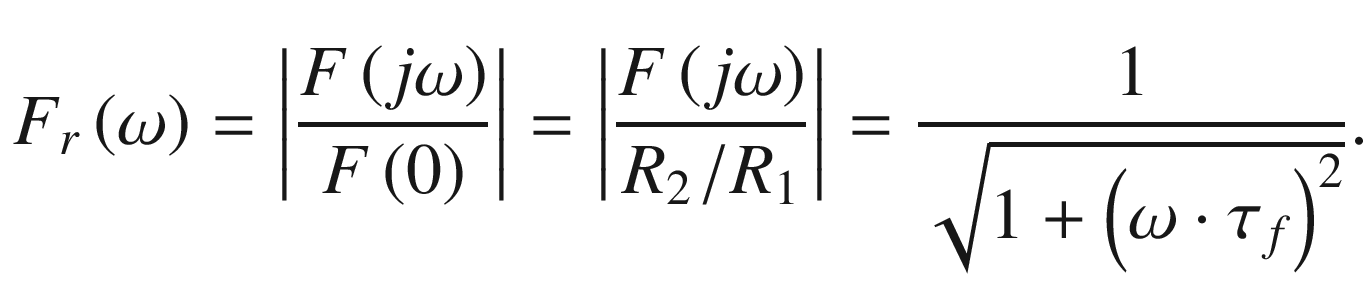
$F_{r} \left( \omega \right) = \left| {\frac{{F\left( {j\omega } \right)}}{F\left( 0 \right)}} \right| = \left| {\frac{{F\left( {j\omega } \right)}}{{{{R_{2} \, } \mathord{\left/ {\vphantom {{R_{2} \, } {R_{1} }}} \right. \kern-0pt} {R_{1} }}}}} \right| = \frac{1}{{\sqrt {1 + \left( {\omega \cdot \tau_{f} } \right)^{2} } }}.$

(7.30)

$F_{r} \left( f \right) = \frac{1}{{\sqrt {1 + \left( {2\pi f \cdot \tau_{f} } \right)^{2} } }} = \frac{1}{{\sqrt {1 + \left( {{f \mathord{\left/ {\vphantom {f {f_{2} }}} \right. \kern-0pt} {f_{2} }}} \right)^{2} } }}.$

(7.31)

Obviously, this is equivalent to the transfer function of a low-pass filter of first order, where the upper limit frequency is given by

$f_{2} = \frac{1}{{2\pi \cdot \tau_{f} }} = \frac{1}{{2\pi \cdot R_{1} \cdot C_{e} /6}}.$

(7.32)

In this context it should be noted that the network with distributed elements according to Fig. 7.42a can be replaced by an equivalent circuit, which contains only a single lumped capacitance, which is equal to 2/3 C_e, as illustrated in Fig. 7.42b. Even if this approach is commonly used in the relevant literature, it can further be simplified, as illustrated in Fig. 7.42c. Here, the series resistance of the low-pass filter is equal to the resistance R₁ of the HV arm, while the parallel capacitance amounts 1/6 of the total earth capacitance C_e of the HV divider column, which can roughly be estimated using the so-called antenna formula, as will be discussed below more in detail.

The amplitude-frequency response of a low-pass filter of first order given by Eq. (7.31) is plotted in Fig. 7.43a. For comparison purpose, the unit-step response in the time domain is drawn in Fig. 7.43b, which reads

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig43_HTML.gif — Fig. 7.43
Dynamic behavior of a low-pass filter of first order. a Amplitude–frequency response. b Unit-step response

$g\left( t \right) = 1 - \exp \left( { - t/\tau_{f} } \right).$

(7.33)

Example Consider the HV arm of an LI divider of resistance R₁ = 10 kΩ and stray capacitance of C_e = 30 pF, one gets the following values providing an equivalent low-pass filter of first order (Fig. 7.42c): R_s = R₁ = 10 kΩ and C_p = C_e/6 = 5 pF. Based on this the following values of the circuit elements are obtained:

• Response time constant	τ_f = R₁ · C_e/6 = 50 ns
• Rise time	t_r = 2.2 · τ_f = 110 ns
• Upper limit frequency	f₂ = 1/(2 · π · τ_f) = 3.2 MHz

To estimate the deviation from the real values of a front-chopped LI voltage, a linearly rising voltage ramp according to Fig. 7.44 (red curve) shall be considered. Under this condition, the recorded voltage (blue curve) follows nearly the applied voltage but delayed by the time constant τ_f = 50 ns. Thus, at chopping time T_c, the following peak value has to be expected:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig44_HTML.gif — Fig. 7.44
Voltage ramp v₁(t) chopped at time T_c = 500 ns and output signal v₂(t) after passing a low-pass filter of first order characterized by the time constant τ_f

$V_{p} = V_{c} \left( {1 - \tau_{f} /T_{c} } \right).$

Assuming the LI voltage is chopped at instant T_c = 500 ns, one gets the following relative deviation of the output voltage from the true value of the applied LI test voltage:

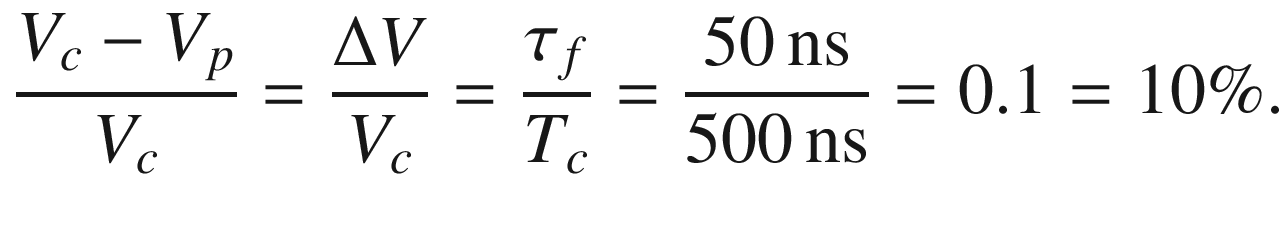
$\frac{{V_{c} - V_{p} }}{{V_{c} }} = \frac{\Delta V}{{V_{c} }} = \frac{{\tau_{f} }}{{T_{c} }} = \frac{{50\,{\text{ns}}}}{{500\,{\text{ns}}}} = 0.1 = 10\% .$

In this context it must be emphasized that under realistic condition instead of an exponential step response often an oscillating step response is encountered, as exemplarily shown in Fig. 7.45. This is mainly due to the interaction between the inherent inductance of the divider column with the earth capacitance. Thus, for comparison purposes, the so-called area time constant τ_a has been introduced. This approach is based on the fact that the area between the applied unit-step voltage and the related response function g(t) of a low-pass filter according to Eq. (7.33) is direct proportional to the characteristic time constant τ_f of the low-pass filter:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig45_HTML.gif — Fig. 7.45
Experimentally determined response (*red curves*) of a capacitive (a) and a resistive (b) divider subjected to a step voltage (*blue trace*)

$\tau_{a} = \int\limits_{0}^{\infty } {\left\{ {1 - \left[ {g(t)} \right]} \right\}} {\text{d}}t = \tau_{f} .$

(7.34)

The decisive unit-step response parameters recommended in IEC 60060-2, are illustrated in Fig. 7.46b and defined as follows:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig46_HTML.gif — Fig. 7.46
Unit-step response parameters of voltage dividers. a RC circuit (low-pass filter of first order). b RLC circuit

• Experimental response time	T_N = T_α − T_β + T_γ − T_δ + T_ε
• Partial response time	T _α
• Residual response time	T_R = T_β − T_γ + T_δ − T_ε …
• Over-shoot • Settling time • Origin of step response	β _rs t _s (definition see text below) O ₁ (definition see text below)

The unit-step response is usually recorded for a nominal epoch, which is defined as the range of values between the minimum (t_min) and the maximum (t_max) of the relevant time parameters of the impulse voltage for which the measuring system is to be approved, such as the front time T₁ for full and tail-chopped LI voltages, the time to chopping T_c for front-chopped LI voltages, and the time to peak T_p for SI voltages. Moreover, the so-called reference level epoch has to be considered, which is defined as the time interval in which the reference level of the step response is determined with its lower limit being equal to 0.5 times of the lower limit of the nominal epoch (0.5 t_min) and its upper limit being equal to 2 times the upper limit of the nominal epoch (2 t_max). The above listed parameters are determined for the time span, which elapses between the origin O₁ of the recorded unit step response and the settling time t_s, with O₁—the instant at which the recorded response curve starts a monotonic rise above the amplitude of the noise at the zero level of the unit step response, and t_s—the shortest time for which the relative contribution of the residual response time becomes and remains less than 2% of t_s, that means /T_N – T_R/ ≤ 0.02 t_s, which must be satisfied for t > t_s.

In the past, it was a common practice to estimate the measuring uncertainty of voltage dividers by the so-called convolution method, which is based on the characteristic unit-step response parameters. Results of international round robin tests revealed, however, that this method is not capable of determining the measuring uncertainty of technical HV impulse dividers within the limits specified in the relevant IEC standards. Among others (e.g. assumption of a low-pass filter) this is due to the fact that the origin of the recorded curve, which is denoted in IEC 60060-2010 as O_1, appears more or less delayed if compared with that instant t = 0 when the voltage step is applied, see Fig. 7.45. This signal delay is mainly governed by the travelling wave velocity, which is in the order of 30 cm/ns for HV connection leads and the divider column as well, and almost 20 cm/ns for measuring cables. Moreover, disturbing oscillations could be excited (Fig. 7.45), for instance, due to reflections at the ends of the HV connection leads, or even caused by a poor design of the ground return leads. Consequently, the above mentioned origin O₁ of the recorded response function cannot exactly be determined and leads thus inevitably to an erroneous determination of the characteristic response time parameters.

Despite the problems presented above, the determination of the unit-step response parameters has become a widely established procedure to optimize the dynamic behaviour of voltage dividers. Moreover, this method is recommended as a “finger print” for performance checks (see Sect. 2.3.2). To calibrate the scale factor as well as to prove the adequate dynamic behaviour, the standard IEC 60060-2:2010 recommends the comparison with reference measurement systems (RMS, see Sect. 2.3.3), which shall be capable of determining the expanded measuring uncertainty within the following limits:

≤1% for the peak values of full LI and SI voltages as well as tail-chopped LI voltages
≤3% for the peak values of front-chopped LI voltages
≤5% for the time parameters of LI and SI voltages, in its range of use.

To prove the appropriate performance of a HV measuring system, the calibration shall be based on comparison against such a RMS. Its calibration shall be traceable to the standards of a National Metrological Institute. For this purpose, LI voltages of various front times shall be applied covering the nominal epoch range. Alternatively, the scale factor of the reference measuring system shall be established for one impulse voltage shape by means of a higher-class reference measuring system at the relevant test voltage level. Additionally, the measured unit-step response parameters of a RMS shall satisfy the recommendations summarized in Table 7.3.

Table 7.3

Response parameters recommended for LI and SI voltage reference measuring systems

Parameter	Full and tail-chopped LI voltages (ns)	Front-chopped LI voltages (ns)	SI voltages (μs)
Experimental response time T_N	≤15	≤10
Partial response time T_α	≤30	≤20
Settling time t_s	≤200	≤150	≤10

Due to the fact that the measuring uncertainty of a HV measuring system is mainly governed by the voltage divider itself, the above recommendations can in principle also be adopted for reference voltage dividers alone either to be approved by a National Metrology Institute or even by a Calibration Laboratory accredited by the National Institute of Metrology.

7.4.2 Design of Voltage Dividers

To measure high impulse voltages, in principle resistive, capacitive or even mixed voltage dividers are applicable, see Fig. 2.10. As the design of LI voltage dividers is the most challenging task, the following treatment is addressed mainly to this subject. Generally, it has to be taken into account that LI dividers should always be arranged “after” the test object, as illustrated in Fig. 7.47, i.e. never “between” impulse generator and test object. Using the latter arrangement the transient current through the test object would cause an additional inductive voltage drop across the HV connection lead. Consequently, a peak voltage higher than that applied to the test object would be measured.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig47_HTML.gif — Fig. 7.47
Arrangement of a measuring system for LI test voltages

7.4.2.1 Resistive Voltage Dividers

To measure high LI voltages, in particular when chopped in the front, resistive voltage dividers should preferably be employed. Such dividers are in use since the beginning of the last century (Binder 1914; Peek 1915; Grünewald 1921; Marx 1926; Bellaschi 1933; Burawoy 1936; Finkelmann 1936; Hagenguth 1937; Raske 1937; Elsner 1939). As discussed previously, the dynamic behaviour and thus the measuring uncertainty of HV dividers are mainly governed by the stray capacitance C_e between the HV divider column and earth. This can roughly be assessed using the so-called antenna formula (Küpfmüller 1990), where the divider column is replaced by a vertical metallic cylinder of high h and diameter d. Under the generally satisfied condition d ≪ h one gets the following approximation:

$C_{e} \approx \frac{{2\pi \cdot \varepsilon_{0} \cdot h}}{{ln\left( {h/d} \right)}} \approx 56\left( {\text{pF/m}} \right) \cdot \frac{h}{{ln\left( {h/d} \right)}}.$

(7.35)

Example Consider a HV divider column of h = 4 m in high and d = 0.1 m in diameter. Inserting these values in Eq. (7.35), the earth capacitance attains C_e ≈ 58 pF. Provided, the resistance of the HV arm amounts R₁ = 10 kΩ, one gets the following characteristic time constant of the equivalent circuit according Fig. 7.42: τ_f = R₁ · C_e/6 ≈ 100 ns. Measuring a LIC voltage chopped at instant T_c = 0.5 μs, the measured peak value would be about 20% lower than the true value applied to the test object, see Fig. 7.44. Consequently, the here investigated voltage divider is not capable of measuring front-chopped LI voltages in compliance with in IEC 60060-2.

A photograph of a resistive divider designed for measuring LI voltages up to 2.2 MV is shown in Fig. 7.48. Despite of the comparatively high resistance being R₁ = 10 kΩ, an experimental response time as low as 15 ns was achieved, which is considerably lower than that gained for the above investigated divider of comparable geometric dimensions and equal resistance of the HV arm. Among others, this was accomplished by the use of a “shielding” electrode, as originally proposed by Davis in 1928 and Bellaschi in 1933, because this reduces the impact of the earth capacitance on the response time constant τ_f. So the partial currents I_e1, I_e2 … and I_e6 between divider column and earth are more or less compensated by the partial currents I_h1, I_h2 … and I_h6 between divider column and HV electrode, as schematically shown in Fig. 7.49.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig48_HTML.gif — Fig. 7.48
Photograph of a shielded resistive 2.2-MV LI voltage divider (Courtesy of TU Dresden)

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig49_HTML.gif — Fig. 7.49
Principle of the compensation of the partial currents between divider column and earth by the currents between HV electrode and divider column

Additionally, the field grading along the HV divider column was optimized, on one hand by the mentioned larger top electrode (Fig. 7.50) and, on the other hand, by modifications of the windings. For the latter purpose the pitch of the helix formed by the resistive wire wounded around an insulating core was varied accordingly, as originally proposed by Goosens and Provoost in 1946. Optimum conditions are accomplished when the field distribution along the divider column equals the field distribution between the top and earth electrodes alone, which would occur in absence of the divider column. Moreover, the inductance of the resistive HV arm was minimized by means of two bifilar windings wounded in opposite direction around a cylindrical core (Spiegelberg 1966). Another option earlier employed to minimize the inductance of the HV divider column is the use of meander-like resistors (Mahdjuri-Sabet 1977) known as Schniewind-band .

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig50_HTML.gif — Fig. 7.50
Distribution of equipotential lines along the HV column of resistive LI voltage dividers. a Without field grading. b With field grading using a large shielding electrode

Based on practical experiences it can be stated that shielded resistive dividers having a HV resistance in the order of 10 kΩ are the only one applicable for measuring front-chopped LI voltages in compliance with IEC 60060-2:2010 up to about 2 MV. For measuring higher LI voltages, the tall dividers must be equipped with excessively large and thus expensive shielding electrodes, which would reduce the mechanical stability. A carefully adapted shielding and potential grading is also limited under practical conditions due to the fact that the clearance to grounded and even energized structures must be chosen as large as possible to avoid any disturbances of the optimized field grading.

To improve the dynamic behavior, in principle the resistance of the HV arm could also be reduced significantly below 10 kΩ. However, this would substantially decrease the tail time and even the output voltage of the LI generator. Moreover, it has to be taken into account that the power dissipation in the HV divider column increases with the square of the applied voltage, which leads to a serious temperature rise. Based on practical experience it can be stated that an experimental response time below 15 ns can only be achieved when the resistance of the HV arm is reduced to few kΩ. Such voltage dividers, however, are only applicable for measuring LI voltages below 500 kV.

7.4.2.2 Damped Capacitive Dividers

To overcome the above discussed obstacles of pure resistive voltage dividers, the use of capacitive dividers seems to be a reasonable alternative because neither the output voltage of the LI generator nor the time parameters are adversely affected by a capacitive load. Moreover, the divider column will never be heated up, even if voltages up to several MV are applied. The main disadvantage of pure capacitive dividers is, however, that heavy oscillations might be excited, as exemplarily shown in Fig. 7.51a.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig51_HTML.gif — Fig. 7.51
Step-pulse response of a capacitive divider without and with a damping resistor

This is due to the fact that capacitive dividers act in the high-frequency range like an oscillating circuit, because under this condition the divider column composed of stacked capacitors can be simulated by a metallic cylinder and thus by an inductance, which interacts with the earth capacitances. To prevent such oscillations Zaengl (1964) and Spiegelberg (1964) proposed an interconnection of the stacked capacitors via serial resistors. The main benefit of this approach is not only that disturbing oscillations can drastically be attenuated, as exemplarily shown in Fig. 7.51b, but that the experimental response time constant can be reduced drastically, which is in contrast to the transfer characteristics of classical RC low-pass filters where the experimental response time constant increases proportional to the series resistance.

For a better understanding, the equivalent circuit shown in Fig. 7.52b shall be analysed in the higher frequency range. Under this condition the series capacitances act as short-circuited, so that only the following circuit elements must be considered:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig52_HTML.gif — Fig. 7.52
Equivalent circuit of a damped capacitive divider. a Damped C-divider with distributed elements. b Ideal R-divider connected to a RLC network

$\begin{aligned} R_{d} & = R_{11} + R_{12} + \cdots + R_{1n} = n \cdot R_{11} , \\ L_{d} & = L_{11} + L_{12} + \cdots + L_{1n} = n \cdot L_{11} , \\ C_{p} & = C_{e} / 6.\\ \end{aligned}$

To simplify the following treatment, the divider column shall be replaced by a metallic cylinder of high h and diameter d. Based on the classical antenna formula (Küpfmüller 1990) the equivalent inductance can roughly be assessed by

$L_{d} \approx \frac{{\mu_{0} \cdot h \cdot ln\left( {h/d} \right)}}{2\pi } \approx 0.2\left( {\upmu{\text{H/m}}} \right) \cdot \frac{h}{{ln\left( {h/d} \right)}}.$

(7.36)

Combining this with Eq. (7.35), the traveling wave impedance of the here considered rod antenna can be assessed as follows:

$Z_{a} \approx \sqrt {\frac{{L_{d} }}{{C_{p} }}} \approx \sqrt {\frac{{\mu_{0} }}{{\varepsilon_{0} }}} \cdot \frac{1}{2\pi } \cdot ln\left( {\frac{h}{d}} \right) = \frac{{Z_{0} }}{2\pi } \cdot ln\left( {\frac{h}{d}} \right).$

(7.37)

Inserting the characteristic wave impedance $Z_{0} = \sqrt {\mu_{0} /\varepsilon_{0} } \approx 377\,\Omega$ , it can also be written:

$Z_{a} \approx \frac{{377\,\Omega }}{2\pi } \cdot ln\left( {\frac{h}{d}} \right) \approx \left( {60\,\Omega } \right) \cdot ln\left( {\frac{h}{d}} \right).$

(7.38)

For further simplification it shall be assumed in compliance with the classical network theory that a transition from an oscillating response to a monotonic one is accomplished when the series resistance is chosen as

$R_{d} > 2\sqrt {\frac{{L_{d} }}{{C_{p} }}} .$

(7.39)

Replacing C_p by C_e/6 according to Fig. 7.42 and combining Eq. (7.39) with Eq. (7.38) one gets the following approach:

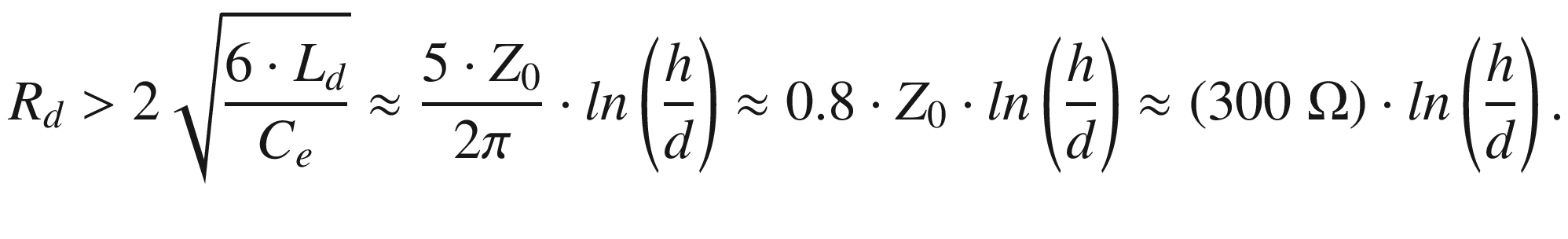
$R_{d} > 2\sqrt {\frac{{6 \cdot L_{d} }}{{C_{e} }}} \approx \frac{{5 \cdot Z_{0} }}{2\pi } \cdot ln\left( {\frac{h}{d}} \right) \approx 0.8 \cdot Z_{0} \cdot ln\left( {\frac{h}{d}} \right) \approx \left( {300\;\Omega } \right) \cdot ln\left( {\frac{h}{d}} \right).$

(7.40)

Even if this approach is the result of strong simplifications, it has successfully been proven as a fundamental design criterion for damped capacitive voltage dividers. In this context it has to be taken into account, however, that in addition to the “internal” damping resistor following from Eq. (7.40) also an “external” HV resistor of about 300 Ω has to be connected between test object and top electrode of the divider to prevent the occurrence of travelling waves.

Example Consider a 2 MV divider which is composed of five stacked capacitors, where the total divider column shall be h = 5 m in high and d = 0.25 m in diameter, i.e. h/d = 20. Based on Eq. (7.40) one gets R_d > (300 Ω) · ln (20) ≈ 900 Ω. Thus the five stacked capacitors should be connected by four series resistors, each of (900 /4) Ω ≈ 225 Ω. Using an additional external resistor of 300 Ω, the total series resistance of the HV divider arm attains (900 + 300) Ω = 1,200 Ω. This has to be taken into account to choose the resistance to be integrated in the LV arm.

In this context it should be emphasized that the design of the LV arm of damped capacitive dividers is a challenge because the ratio between the inductances of the HV and LV arm must comply with the divider ratio, which equals the resistance ratio and is inversely proportional to the capacitance ratio:

${{L_{2} } \mathord{\left/ {\vphantom {{L_{2} } {L_{1} }}} \right. \kern-0pt} {L_{1} }} \, = {{R_{2} } \mathord{\left/ {\vphantom {{R_{2} } {R_{1} }}} \right. \kern-0pt} {R_{1} }} = {{C_{1} } \mathord{\left/ {\vphantom {{C_{1} } {C_{2} }}} \right. \kern-0pt} {C_{2} }}.$

Example Applying Eq. (7.36) the effective inductance of the HV arm of the above considered 2 MV divider column of h = 5 m in high and d = 0.25 m in diameter gets L₁ = 0.2 (µH/m) · 5 m · ln (20) ≈ 3 μH. Assuming, for instance, a divider ratio R₂ /R₁ = C₁ /C₂ = 1 /1000, the inductance L₂ of the LV arm must be chosen as low as 3 nH.

The most effective way to minimize the inductance of the LV arm is to design this like a disc, i.e. to connect a great number of elements in parallel, as obvious from Fig. 7.53. Her each parallel connected element comprises a series connection of a capacitor with a resistor.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig53_HTML.gif — Fig. 7.53
LV arm of a damped capacitive divider comprising 60 parallel elements each composed of a resistor connected in series with a capacitor

Comparing the different divider types, it can be stated that damped capacitive dividers provide an excellent dynamic behaviour. Another benefit is that the power dissipating in the resistors inserted between the stacked capacitors is quite low due to the short duration of the transient current through the HV divider arm. Moreover, the effective capacitance of the HV arm provides a basic load for the LI generator. As the charging current is inversely proportional to the frequency, damped capacitive dividers are also well suited for measuring SI and AC voltages as well as composite voltages. If equipped with a high-ohmic resistor, which is connected in parallel to the HV arm, such an “universal” divider, as shown in Fig. 2.10, is also capable of measuring DC voltages including superimposed voltage ripples covering a frequency spectrum up to several kHz. Due to the wide field of application, the here presented damped capacitive divider is often also referred to as “multi-purpose divider”.

Due to the benefits mentioned above, most reference measuring systems (RMS) are nowadays equipped with damped capacitive dividers. In the following the general design principle of a 200 kV LIC divider shall briefly be described. The HV arm is composed of 10 ceramic capacitors in series each rated 25 kV/2 nF. The individual capacitors are connected in series via 9 resistor blocks, as illustrated in Fig. 7.54. Step pulse response measurements revealed that an optimum dynamic behaviour was achieved when the resistance of each resistor block is chosen to about 70 Ω. This was realized by means of low-inductive metal-oxide resistors rated 68 Ω. Four of them are connected in series and four of them in parallel, so that the resulting resistance of each resistor block attains also 68 Ω. Using the classical step-voltage response method the following time parameters according to Table 7.3 were determined:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig54_HTML.gif — Fig. 7.54
Section of a damped capacitive divider, rated voltage 200 kV

Experimental response time: T_N ≈ 2 ns
Partial response time: T_α ≈ 5 ns
Settling time: t_s ≈ 120 ns.

7.4.3 Digital Recorders

To measure fast transient signals in high-voltage technology, such as LI test voltages as well as travelling waves excited by lightning surges and propagating along HV transmission lines, originally cathode-ray oscilloscopes (CRO) have been employed (Binder1914; Gabor 1927; Krug 1927). Initially, the electromagnetic capability (EMC) was not a problem because the first available CRO were especially designed for HV measurements and thus not equipped with sensitive amplifiers, which have later been employed for the vertical and horizontal deflection of the electron beam. In the 1940s, peak voltmeters have been employed, using the first available vacuum tubes to rectify the fast LI signal. Digital recorders, originally referred to as “digitizers”, entered in HV measuring technique in the early 1980s (Malewski et al. 1982). After the initial EMC problems have successfully been solved (Strauss 1983 and 2003; Steiner 2011) digital recorders are nowadays almost exclusively used for recording and processing LI and SI test voltages (Fig. 7.55). Due to the recent achievements in digital signal processing (DSP), computerized digital recorders are also increasingly employed not only for LI and SI test voltage measurements but also for AC and DC voltage measurements as well as for measuring composite and combined test voltages.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig55_HTML.gif — Fig. 7.55
Recording and processing of LI test voltages (From the top: records of 50 and 100% test voltages; comparison of the normalized voltages; difference of the normalized voltages)

A photograph of a stand-alone device operating in connection with an industrial PC is shown in Fig. 7.56. As obvious from the simplified block diagram sketched in Fig. 7.57, the main units of a digital recorder are the attenuator at the input followed by a low-noise amplifier, an analogue–digital converter (ADC), a memory unit and an industrial computer (IPC). A micro-controller serves for the adjustment of the input sensitivity as well as for controlling the various units performing the digital signal processing, acquisition and data storage. The industrial computer runs with a specific software package, which enables the acquisition of the stored raw data and the visualization of the time-dependent input signal. Simultaneously, the relevant impulse parameters are indicated, such as the peak value of the measured LI/SI test voltage, the front and tail time and occasionally the chopping time.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig56_HTML.gif — Fig. 7.56
Photograph of a stand-alone digital recorder

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig57_HTML.gif — Fig. 7.57
Simplified block diagram of a digital recorder for HV measurements

The measuring uncertainty may be affected by both the hardware and the software. Due to the comparatively high quantization rate of nowadays available digital recorders, which attains usually 12 or 14 bits and even more, as well as the high sampling rate being in the order of 100 MS/s and above, the contribution of the hardware to the measuring uncertainty is much lower than that of voltage dividers. As the quantization error is given by 50% of the least significant bit (LSB), this is approx. 0.012% for a slow-rising signal at quantization rate of 14 bit. However, the deviation from the true value increases significantly when front-chopped LI voltage according to Fig. 7.58 are measured at a sample rate of 100 MS/s. This is because the voltage difference $\Delta V_{s}$ between each sample is inversely proportional to the sampling rate f_s. For an assumed chopping time of, for instance, T_c = 0.5 μs and a crest voltage V_c, the voltage difference between each sample can be approximated by $V_{s} = V_{c} /\left( {T_{c} \cdot f_{s} } \right) = V_{c} /50 = 0.02 \cdot V_{c} .$ Under this condition the maximum deviation of the measured value from the true value, which is given by 0.5 LSB, attains 1% of the crest value V_c.

Performing a digital signal processing, generally the classical Shannon theorem has to be taken into account (Shannon 1949; Stanley 1975; Robinson and Silvia 1978). Based on this it can be stated that the sampling rate should exceed twice the maximum frequency content of the signal to be measured, where the analogue bandwidth must substantially exceed this maximum frequency content. With reference to IEC 61083-1:2001 the analogue bandwidth should be not lower than 6 times the sampling rate.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig58_HTML.gif — Fig. 7.58
Quantization error of a front-chopped LI test voltage due to the analogue–digital conversion

To validate the measuring uncertainty, various calibration procedures are recommended in IEC 61083-1:2001, which refer to both the hardware and the software. To validate the uncertainty caused by the hardware, the differential non-linearity (DNL) as well as the integral non-linearity (INL) have to be determined using an “ideal” ADC as reference. The transfer function of such a reference ADC is characterized by a stepwise-increasing output code k = 1, 2 … 2^N, where the input voltage is increased stepwise by $w\left( r \right) = V_{\text{fsd}} /2^{N} .$ That means, for an output code $k = 2^{N} \cdot V_{in} /V_{\text{fsd}}$ one gets for the next step $k + 1 = 2^{N} \cdot \left( {V_{in} + w\left( r \right)} \right)/V_{\text{fsd}} .$ Here are V_in—the input voltage, V_fsd—the full-scale deflection voltage and N—the resolution in terms of bit.

According to Fig. 7.59, the DNL is given by the difference w(k) − w(r) for each possible value of the output code k, and the IDL presents the difference s(k) between the input voltage of both the investigated ADC and the reference ADC. As the determination of the DNL and IDL at stepwise increasing DC voltage is extremely time-consuming, particularly for ADCs of more than 8 bit resolution, the experimental results might strongly be affected by the long-term stability of the DC voltage source.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig59_HTML.gif — Fig. 7.59
Estimation of the differential non-linearity given by w(k) − w(r) and integral non-linearity s(k) given by the deviation of the actual input voltage from the reference voltage of an “ideal” ADC

Thus, as an alternative, the following method has been proposed by Steiner in 2011, see Fig. 7.60:

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig60_HTML.gif — Fig. 7.60
Comparison of a sin-shape input voltage with the output code of a non-linear 4-bit ADC

1.
Apply a precise sine wave of low frequency (e.g. 50 Hz) and adjust the amplitude close to the full-scale deflection (e.g. between −10 V and +10 V).
2.
Record in total ten periods of the applied AC voltage.
3.
Compare the count of occurrences of each code (code rate) with the ideal number of occurrences.
4.
Divide each code rate by the number of recorded periods, i.e. n = 10 for the here-considered case.
5.
Calculate the differential non-linearity (DNL) for each code:

$d\left( k \right) = \frac{{h\left( k \right)_{\text{nonlin}} }}{{h\left( k \right)_{\text{lin}} }} - 1.$

6.
Calculate the integral non-linearity (INL) for each code:

$s\left( k \right) = \sum\limits_{i = 0}^{k} {d\left( i \right)} .$

The test is passed if at full-scale deflection the requirements $d\left( k \right) = 10.81\%$ and $s\left( k \right) = 10.51\%$ are satisfied.

The software package is tested according to IEC 61083-2:2013. It recommends new rules for the calibration including the calculation of the k-factor relevant for LI test voltages of substantial over-shoot. To verify the performance of digital recorders intended for LI voltage measurements, in total 52 reference curves are recommended to be created by a computerized test data generator (TDG). These artificial curve shapes are available from either a compact disc (CD) or even an USB stick. Basically, the reference impulse wave-shapes applied should be representative for the test voltage shapes specified in IEC 60060-1:2010 and IEC 60060-3:2006, such as:

Full lightning impulse voltage (LI)
Front-chopped lightning impulse voltage (LIC)
Tail-chopped lightning impulse voltage (LIC)
Oscillating lightning impulse voltage (OLI)
Switching impulse voltage (SI)
Oscillating switching impulse voltages (OSI).

After digital signal processing of the data received from the TDG, the significant impulse parameters are determined by means of the implemented software. The procedures shall follow the evaluation principles given in IEC 60060-1:2010. These refer to the measurement of the peak value and the over-shoot as well as to the characteristic time parameters, such as the front and tail time and the chopping time for LIC, as well. The software is assumed as properly working when the results obtained are within a tolerance band specified in IEC 61083-2:2013, where any manipulation of the test data cannot be accepted.

Example Table 7.4 shows the comparison between the evaluated parameters of two reference LI wave shapes (wave shapes no. LI-A4 and LI-M7 of the test data generator (TDG)) and those required according to IEC 61083-2:2013. Whereas the evaluation of no. LI-A4 delivers results within the tolerance band required by the standard, not all parameters of no. LI-M7 are correctly determined. This means the software has to be improved before it can be applied for practical tests.
Table 7.4
Test of software with the test data generator (TDG) according to IEC 61083-2:2013
Reference number of IEC 61083-2
Parameter
IEC reference value
IEC acceptance limits
Example: evaluated values
Remarks

Test voltage value V_t
−856.01 kV
−(855.15…856.87) kV
−856.4 kV
Evaluation accepted
Front time T₁
0.841 μs
(0.824…0.858) μs
0.851 μs
Evaluation accepted
Time to half-value T₂
47. 80 μs
(47.32…48.28) μs
47.88 μs
Evaluation accepted
Relative over-shoot β
7.9%
(6.9…8.9) %
7.2%
Evaluation accepted

Test voltage value V_t
1272.3 kV
(1271.0…1273.5) kV
1272 kV
Evaluation accepted
Front time T₁
1.482 μs
(1.452…1.512) μs
1.390 μs
Evaluation rejected^a
Time to half-value T₂
50.03 μs
(49.53…50.53) μs
5 0.10 μs
Evaluation accepted
Relative over-shoot β
11.2%
(10.2…12.2) %
9.9%
Evaluation rejected^a
^aThe tested software must be improved with respect to the evaluation of reference LI—M7
Compared with IEC 61083-2, the polarity of the reference impulses is opposite

Reference number of IEC 61083-2	Parameter	IEC reference value	IEC acceptance limits	Example: evaluated values	Remarks
	Test voltage value V_t	−856.01 kV	−(855.15…856.87) kV	−856.4 kV	Evaluation accepted
Front time T₁	0.841 μs	(0.824…0.858) μs	0.851 μs	Evaluation accepted
Time to half-value T₂	47. 80 μs	(47.32…48.28) μs	47.88 μs	Evaluation accepted
Relative over-shoot β	7.9%	(6.9…8.9) %	7.2%	Evaluation accepted
	Test voltage value V_t	1272.3 kV	(1271.0…1273.5) kV	1272 kV	Evaluation accepted
Front time T₁	1.482 μs	(1.452…1.512) μs	1.390 μs	Evaluation rejected^a
Time to half-value T₂	50.03 μs	(49.53…50.53) μs	5 0.10 μs	Evaluation accepted
Relative over-shoot β	11.2%	(10.2…12.2) %	9.9%	Evaluation rejected^a

Generally, it can be stated that the measurement of the peak value of full LI test voltages at measuring uncertainty of 2% is accomplished when the amplitude resolution amounts 10 bits and the sampling rate attains 100 MS/s, where the analogue bandwidth should not be lower than 100 MHz. Moreover, the integral non-linearity should be below 0.5%, and the internal background noise level should not exceed 0.4% of the full-scale deflection. For more information in this respect see Hällström (2002), Hällström et al. (2003), Wakimoto et al. (2007) and Schon (2013).

7.5 Measurement of High Currents in LI Voltage Tests

Performing LI voltage tests, high impulse currents may occur not only as consequence of a breakdown but also when the test object passes the withstand test. This is due to the capacitive load current, which is direct proportional to the comparative high steepness of the applied LI voltage. Moreover it should be mentioned that the magnitude and shape of current pulses associated with LI voltage tests enables the identification of potential insulation failures. For this reason, impulse current measurements are mandatory for LI withstand voltage tests of power transformers. Performing such tests, just prior the specified (100%) LI test voltage level first a reference voltage level is applied, which is being 50–70% of the specified test level, see Fig. 7.61. To compare the shapes of both the LI voltage and the associated current pulse, the records are normalized to their respective extreme values.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig61_HTML.gif — Fig. 7.61
Voltage and current recorded during a LI withstand voltage test of a distribution transformer

The LI withstand test is passed when no significant differences are recognized between the normalized reference values and the normalized test values (IEC 60076-3:2013).

Circuits used for LI current measurement are composed of the following components (Fig. 7.62):

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig62_HTML.gif — Fig. 7.62
Basic components required for a LI current measuring system

Converting device, usually a shunt or even a fast current transformer to convert the transient current into a convenient measurable low voltage,
Transmission system, usually a BNC measuring cable or a fiber optic link,
Measuring instrument, usually a digital recorder.

The requirements for digital recorders comply in principle with those specified in IEC 61083-1:2006 for LI voltage measurements (see Sect. 7.4.3) and shall thus not be considered here. This Section is thus only addressed to the design principles of converting devices. For more information on this issue see also the textbooks of Schon (2010, 2013).

Note The classic application of high current measurements is addressed to performance tests of protecting devices, such as lightning arresters, where peak values up to some hundreds of kA have to be measured. Measuring such high currents, however, is not the subject of this book. For more details in this respect, see IEC 62475:2012 and the series of the IEC 60099 standards.

To measure high-current pulses associated with LI voltage tests various types of converting devices are in use, such as resistive shunts, Rogowski coils, current transformers, hall-sensors, and magneto-optic sensors. In the following, however, only some particularities of resistive and inductive converting devices will be reviewed, which are mostly used for measuring high transient currents associated with LI withstand and breakdown tests.

7.5.1 Resistive Converting Device (Shunt)

Even if the physical background of current measurements are based on Ohm’s law, which is hence easily understandable, it has to be taken into account that for measuring impulse currents in the kA range the resistance of the converting must be chosen extremely low, usually in the mΩ range, in order to attenuate the measurable voltage down to the Volt range. However, under this condition, the voltage collapsing across the shunt can substantially be affected by parasite inductances, as obvious from Fig. 7.63. Here, the left oscilloscopic record is obtained for a resistive shunt grounded via thin wire, whereas the right record is obtained for a shunt grounded via a Cu-foil. As the inductance of the thin wire is much greater than that of the Cu-foil, the left record shows a signal enhancement in the front region, which is the consequence of an inductive voltage component $v_{L} \left( t \right)$ superimposed on the resistive voltage signal $v_{R} (t)$ , as qualitatively illustrated in Fig. 7.64.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig63_HTML.gif — Fig. 7.63
Response of a current measuring system against an exponential rising current where the transducer was grounded via either a thin wire (left) or a low-inductive Cu foil (right)

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig64_HTML.gif — Fig. 7.64
Partial voltages v_R(t) and v_L(t) as well as the measurable voltage v_m(t) = v_R(t) + v_L(t) appearing across a resistive shunt in case of an exponential rising current pulse

Generally, the measurable voltage signal $v_{m} \left( t \right)$ following from the time-dependent current $i_{m} (t)$ can be expressed by

$v_{m} \left( t \right) = v_{R} \left( t \right) + v_{L} \left( t \right) = R_{m} \cdot i_{m} \left( t \right) + L_{m} \cdot \frac{{{\text{d}}i_{m} \left( t \right)}}{{{\text{d}}t}}.$

(7.41)

To prevent erroneous measurements, the inductive voltage component v_L(t) and thus the parasite inductance L_m of the measuring circuit must be kept as low as possible. For a better understanding consider Fig. 7.65, where the inductive measuring loop is indicated by the shaded area. For the here given geometric parameters a and b the parasite inductance L_c can simply be assessed using the following approach (Küpfmüller 1990):

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig65_HTML.gif — Fig. 7.65
Equivalent circuit used to estimate the inductive voltage component v_L(t) induced in the measuring loop between resistive shunt and BNC measuring cable

$L_{c} = \frac{{\mu_{0} \cdot b}}{2\pi } \cdot ln\left( {\frac{2a + d}{d}} \right)$

(7.42)

with µ₀ = 0.4π (nH/mm)—the permeability of air. Additionally, the self-inductance of the resistive transducer has also to be taken into account. Replacing this by a cylindrical conductor of diameter d and length b, the following approach can be adopted (Küpfmüller 1990):

$L_{s} \approx \frac{{\mu_{0} \cdot b}}{2\pi } \cdot ln\left( {\frac{b}{2d}} \right)$

(7.43)

Combining Eqs. (7.42) and (7.43) and inserting µ₀ = 0.4π (nH/mm) one gets the following resulting inductance of the measuring circuit:

$L_{m} = L_{c} + L_{s} \approx \frac{{\mu_{0} \cdot b}}{2\pi } \cdot ln\left( {\frac{a \cdot b}{{d^{2} }}} \right) = \frac{{0.4\pi \cdot b \cdot \left( {1\,{\text{nH}}} \right)}}{2\pi } \cdot ln\left( {\frac{a \cdot b}{{d^{2} }}} \right)$

(7.44)

Example Consider a resistive shunt characterized by the following parameters:

Shunt resistance	R_s = 10 mΩ
Shunt diameter	d = 10 mm
Measuring loop	a = b = 50 mm

Inserting these values in Eq. (7.44) one gets

$L_{m} \approx (0.2\;{\text{nH/mm}}) \cdot (50\,{\text{mm)}} \cdot ln\left( {\frac{{110 \cdot 50\,{\text{mm}}^{2} }}{{200\,{\text{mm}}^{2} }}} \right) = (10\,{\text{nH}}) \cdot ln(27.5) \approx 33\,{\text{nH}}.$

Provided, an exponential rising current pulse of time constant τ_c = 2 µs attains a crest value of 1 kA at instant t_p ≈ 3 · τ_c = 6 µs, the voltage appearing across an “ideal” shunt of 10 mΩ could be described by the following time function:

$v_{r} (t) = [(1\,{\text{kA}}) \cdot (10\,{\text{m}}\Omega )] \cdot [1 - exp (- t/\tau_{c} )] = (10\,{\text{V}}) \cdot [1 - exp( - t/\tau_{c} )]$

Due to the above estimated inductance of L_m = 33 nH an inductive voltage component would be induced (Fig. 7.64). As the steepness attains a maximum value of 1 kA/2 μs = 0.5 kA/μs at the very beginning of the current pulse, the superimposed inductive voltage component would approach a crest value of V_c = (33 nH) · (0.5 kA/μs) = 16.5 V. Obviously, this is almost 70% greater than the maximum value, which attains a peak value of V_p = (1 kA) ∙ (10 mΩ) = 10 V across a pure resistive shunt.

To minimize the measuring error, the parasite inductance and thus the shaded area shown in Fig. 7.65 must be kept as low as possible. In practice this is realized by means of coaxial or even disc-like designed shunts, see Fig. 7.66.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig66_HTML.gif — Fig. 7.66
Design principles of low-inductive shunts

7.5.2 Inductive Converting Device (Rogowski Coil)

Another way to eliminate the disturbing inductive voltage component is the use of pure inductive converting devices consisting of either a single turn (Fig. 7.67a) or even of numerous turns (Fig. 7.67b), as proposed by Rogowski in 1913. With reference to the geometric parameters obvious from Fig. 7.67, the output voltage of a Rogowski coil without load can roughly be assessed using the following approach (Küpfmüller 1990):

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig67_HTML.gif — Fig. 7.67
Principle of impulse current measurement using inductive converting devices. a Single-turn current transducer. b Multiple-turn current transducer (Rogowski coil)

$v_{l} \left( t \right) = M \cdot \frac{{{\text{d}}i}}{{{\text{d}}t}} = \left[ {\frac{{\mu_{0} \cdot n \cdot b}}{8} \cdot \ln \left( {\frac{2a + b}{2a - b}} \right)} \right] \cdot \frac{{{\text{d}}i}}{{{\text{d}}t}},$

(7.45)

with n—the turn number, a—the distance between the axis of the conductor carrying the time-dependent current i(t) to be measured and the axis of the perpendicular arranged Rogowski coil, and b—the core diameter.

As the output voltage v_l(t) is proportional to the derivate of the time-dependent current, an integration must be performed to get a signal, which is direct proportional to the time-dependent current (Fig. 7.68).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig68_HTML.gif — Fig. 7.68
Transfer characteristics of a Rogowski coil

In principle the dynamic behaviour of Rogowski coils is comparable to that of a high-pass filter, i.e. a stationary direct current is not measurable. Consequently, the measuring error increases at decreasing frequency content and thus at increasing length of the current pulse (Fig. 7.68). To reduce the lower-limit frequency, the coil inductance must be increased accordingly, which can effectively be achieved by winding the turns around a high-permeable core. Based on practical experience it can be stated that Rogowski coils are capable of measuring current pulses up to 100 kA/μs, where the pulse duration is limited below some tens of µs. Using classical current transformers, pulse lengths up to the ms range can be captured at reasonable measuring uncertainty, while the steepness is limited to approx 1 kA/μs.

As already discussed above, the output voltage of inductive converting devices without load is proportional to the derivate of the primary current to be measured. Therefore classical step response measurements are not recommended to investigate the dynamic behavior because under this condition the electronic device required to integrate the output signal of the transducer might be overloaded. Moreover it has to be taken into account that oscillations of the measuring signal could be excited due to the interaction between inductance and stray capacitances of the coil, which leads to erroneous measurements, as illustrated in Fig. 7.69. Thus, to investigate the dynamic behavior, it is recommended to use linearly rising and decaying current ramps, as shown in Fig. 7.70, where the rise and decay time should be comparable with those appearing under actual measuring conditions.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig69_HTML.gif — Fig. 7.69
Dynamic behavior of a current transformer at fast rising (left) and a slowly rising (right) primary current

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig70_HTML.gif — Fig. 7.70
Dynamic behavior of a current transformer subjected to linearly rising and decaying current ramps at repetition rates of 5.4 MHz (left) and 0.54 MHz (right)

7.6 PD Measurement at Impulse Voltages

From a physical point of view, PD measurements of HV equipment should be carried out under test voltages, which are representative for service conditions. This is the reason why the relevant standard IEC 60270:2000 is mainly addressed to the measurement of partial discharges under power frequency AC voltages, see Sect. 4.3. As known, under service condition the insulation of HV equipment is not only stressed by the continuously applied operation voltage but also by different kinds of over-voltages, such as switching impulse (SI) and lightning impulse (LI) voltages as well as very fast front (VFF) voltages. In the following specific aspects of PD measurements under such kinds of test voltages will briefly be highlighted.

7.6.1 SI Test Voltages

In the late 1980s, when paper-insulated lead-covered cables (PILC) were increasingly substituted by cross-linked polyethylene-insulated (XLPE) cables, the measurement of partial discharges became an inevitable tool for quality assurance tests of XLPE cables performed not only in laboratory after manufacturing but also in the field after installation. The reason for that was the fact that the high-polymeric insulation is very sensitive to partial discharges, because a PD activity in the pC range causes already irreversible degradation processes. However, energizing the comparatively high cable capacitance by the use of classical AC test transformers needs a high power and is thus very expensive, in particular if PD tests are performed under on-site condition. Therefore, to reduce the test expenditure, the feasibility of alternative test voltages have been extensively investigated (Dorison and Aucort 1984; Auclair et al. 1988; Lefèvre et al. 1989). Among others the use of switching impulse (SI) voltages has been found as a promising alternative due to the fact that the PD signatures of internal discharges are quite well comparable to those encountered under power frequency AC voltage (Lemke et al. 1987).

The major units of a single-stage SI generator originally used for on-site PD tests of medium voltage cables are shown Fig. 7.71. The most critical component is the spark gap because this emits heavy electromagnetic interferences and disturbs thus sensitive PD measurements, which has thus been replaced by a low-noise solid state switch. Basically it has to be taken into account that the entire charge required to energize the cable capacitance up to the desired test level must previously be stored in the surge capacitor shown in Fig. 7.71. Thus, for testing power cables of lengths up to some km this must be chosen in the µF range to accomplish a sufficient high utilization factor.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig71_HTML.gif — Fig. 7.71
SI voltage circuit for PD measurement. a Simplified block diagram of a single-stage SI generator. b Record of characteristic voltages with a 1 μF surge capacitor and a 0.22 μF cable capacitance. c Record gained for 1-μF cable capacitance

Example Fundamental PD studies under SI voltages revealed that potential PD defects in extruded power cables can be recognized at reasonable probability when the peak value of the applied SI voltage attains twice the phase-to-earth voltage, where the latter is expressed in terms of rms. Testing, for instance, a 12/20 kV XLPE cable of 1 km in length, a cable capacitance of nearly 0.2 µF must be charged up to a SI crest value of 24 kV. Using a single-stage SI generator according to Fig. 7.71, which is equipped with a 1 µF surge capacitor and a front resistor of 5.6 kΩ, the utilization factor attains 0.8, as obvious from the oscilloscopic screenshot shown in Fig. 7.71b. Consequently, the 1 μF surge capacitor must be charged up to a crest voltage of 31 kV to accomplish the desired SI crest voltage of 24 kV. Testing a cable of 5 km in length, a cable capacitance of approx. 1 μF must be charged. Under this condition, the utilization factor approaches 0.45, that means to accomplish the desired SI test voltage of 24 kV the 1 µF surge capacitor of the SI generator must be charged up to a crest voltage of 53 kV, see Fig. 7.71c.

Increasing the cable lengths leads not only to a reduction of the utilization factor, as discussed previously, but also to an increase of the time-to-crest of the SI voltage, which follows also from the oscilloscopic records displayed in Fig. 7.71b, c. Experimental studies revealed, however, that the characteristic PD signatures of typical PD defects in extruded power cables and their accessories are not significantly affected by the time to crest if increased from few hundreds up to some thousands of µs, as exemplarily shown in Fig. 7.72. Thus it is not necessary to change the front resistor of the SI generator when power cables lengths ranging between some hundreds and some thousands of meters are PD tested. In this context it should also be mentioned, that additional information on the PD activity is available when besides the main PD quantity “apparent charge” additionally the “accumulated pulse charge” is measured. Different to the apparent charge, this quantity is only marginally scattering and seems to be correlated to the applied SI test voltage, as obvious from Fig. 7.73b–f.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig72_HTML.gif — Fig. 7.72
PD signatures caused by an artificial cavity implemented in a cable sample at SI voltages of different steepness and almost identical peak values. a Rise time 400 μs, test voltage level 12 kV. b Rise time 1,600 µs, test voltage level 12.4 kV

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig73_HTML.gif — Fig. 7.73
Reproducibility of accumulated PD charges. a PD pulse train during the front time of an SI voltage. b–f Accumulated pulse charges recorded at identical front time and test voltage level (time scale: 200 μs/div, voltage scale: 4 kV/div, front time 1.6 ms, test voltage level 12.4 kV)

7.6.2 DAC Test Voltages

As discussed above, a main drawback of SI voltages used for PD tests of power cables is the strong reduction of the utilization factor at increasing cable length (Fig. 7.71). To overcome this crucial problem it seems to be very promising to use the cable capacitance itself as a surge capacitance because under this condition the utilization factor approaches 100%. This benefit has originally been utilized for after-laying tests of extra-high-voltage (EHV) XLPE cables (Dorison and Aucort 1984; Auclair et al. 1988; Lefèvre et al. 1989). Performing withstand tests, the cable capacitance was slowly charged by means of a DC test facility up to the desired test level and just thereafter discharged via an inductor in series with a spark gap (Fig. 7.74a). Under this condition the cable insulation is stressed by an oscillating switching impulse (OSI) voltage (see Sect. 7.3.1), later named “damped alternating (DAC) voltage” (IEC 60060-3:2006). The oscillations appearing in the kHz range are attenuated due to the dielectric losses dissipating in the cable insulation and additionally by the winding resistance as well as the magnetization losses in the iron core of the inductor. The reason behind the oscillating discharge of the cable capacitance was to avoid the accumulation of unipolar space charges on account of the pre-stressing DC voltage and thus to prevent local field enhancements in in the polymeric insulation, which could trigger an unexpected breakdown.

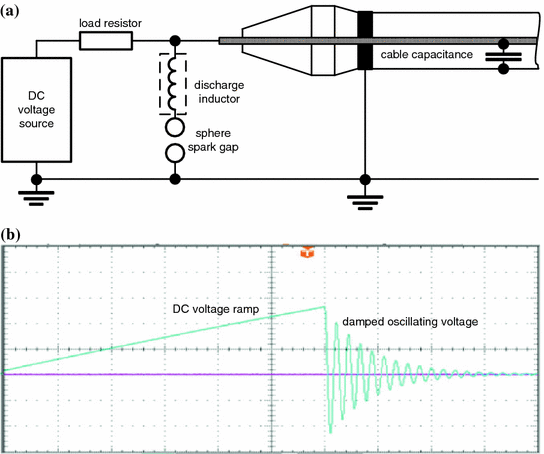
../images/214133_2_En_7_Chapter/214133_2_En_7_Fig74_HTML.gif — Fig. 7.74
Block diagram of a DAC test generator (a) and characteristic oscilloscopic record (b) showing the continuous rising DC stress and the damped AC voltage occurring just after the sphere spark gap has been triggered

Initially attempts were made to combine such withstand tests with PD measurements. However, these failed due to strong electromagnetic interferences radiated from the spark gap shown in Fig. 7.74a. Another obstacle was that the characteristic PD patterns as well as the apparent charge measured under DAC voltage were not comparable to PD test results gained under power frequency AC voltage. Without going into further details it can be stated that this is due to an enhancement of the PD inception voltage significantly above the static inception voltage as consequence of the statistical time-lag i.e. the time span which elapses between the instant when the static inception voltage is achieved and the instant at which an initiatory electron is available to initialize a self-sustaining discharge (Grey Morgan 1965). Experimental studies revealed that the impact of the time-lag on the PD inception voltage can substantially be reduced when the natural frequency of the applied DAC voltage is decreased from the originally used kHz range down to the power frequency (Lemke and Schmiegel 1995a, b). For this purpose the DAC test set was equipped with a 1 µF surge capacitor and a 4 H discharge inductor, as illustrated in Fig. 7.75. Under this condition the test frequency attained 80 Hz, where the PD signatures of typical imperfections in extruded power cables became quite well comparable with those gained under power frequency (50 Hz) AC voltage, as exemplarily shown in Fig. 7.76. The here displayed phase-resolved PD pulses, which refer to a defective MV cable termination, were recorded in a first test series under 50 Hz AC voltage adjusting the test level slightly above the inception voltage. To display the characteristic PD pattern like a waterfall diagram, the charge pulses occurring in only 18 AC voltage cycles were recorded in Fig. 7.76a. In a second test series, the cable termination was initially pre-stressed by a negative DC voltage ramp followed by a DAC voltage, where only those PD pulses occurring during at the first positive voltage sweep were displayed. This procedure has been repeated 18 times to create the waterfall diagram shown in Fig. 7.76b. In a third test series a positive DC voltage ramp (see Fig. 7.74b) was applied and the PD pulses occurring during the first negative DAC voltage sweep were displayed, see Fig. 7.76c.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig75_HTML.gif — Fig. 7.75
Block diagram of a DAC test facility used for fundamental PD studies

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig76_HTML.gif — Fig. 7.76
Phase-resolved PD patterns of void discharges in a cable sample. a Continuous 50-Hz AC voltage. b 80-Hz DAC voltage stress displayed for the first positive voltage sweep. c 80-Hz DAC voltage stress displayed for the first negative voltage sweep

The comparability of the characteristic PD patterns found for damped and continuous AC voltage was also confirmed by the PC screenshots shown in Fig. 7.77, which were also gained for a defective MV cable termination. Here the PD test was first performed under damped AC voltage of 80 Hz natural frequency, where the test level was again adjusted slightly above the inception voltage. The PD pulses displayed in Fig. 7.77a are the result of 180 DAC voltage applications. In a second test series, the cable termination was subjected to a continuous AC voltage of 50 Hz, where the test level was adjusted also slightly above the inception voltage. For comparison purpose only PD pulses occurring within 180 positive half-cycles were displayed in Fig. 7.76b. This was realized by means of a windowing unit, which was triggered once per 10 s, so that the entire test period covered 1800 s (90,000 AC cycles). Despite the large scattering of the PD pulse magnitudes (Fig. 7.77b) it can be stated that the PD test results gained under both damped and continuous AC voltage are reasonably comparable with each other.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig77_HTML.gif — Fig. 7.77
Pulse charge magnitudes measured for a MV cable termination. a Damped AC voltage of 80 Hz. b Continuous AC voltage of 50 Hz

As already discussed above, applying DAC voltages for PD diagnostic tests of XLPE cables, the high-polymeric insulation will be pre-stressed on account of the slowly rising DC voltage ramp (Fig. 7.74b). Depending on the cable length and thus the capacitance being charged, the pre-stressing period may vary between the second and minute range. Experimental studies revealed, however, that the PD signatures of PD defects representative for extruded medium-voltage power cables are not significantly affected by the duration of the DC pre-stress, as exemplarily shown in Fig. 7.78.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig78_HTML.gif — Fig. 7.78
PD signatures of a defective 20-kV cable termination at DAC test voltage using DC voltage ramps of 10, 50, and 250 μs rise time (from left to right)

7.6.3 Short Impulse Voltages (LI and VFF Test Voltages)

As known from the physics of gas discharges, the inception field strength of very fast changing test voltages, such as lightning impulse (LI) voltages and very fast transient (VFT) voltages may substantially be increased on account of the so-called statistical time-lag. This is the time span elapsing between the instant at which the static inception field strength is achieved and that one at which initiatory electrons liberated by natural processes are available to ionize gas molecules (Grey Morgan 1965). As a typical example compare the ignition of streamer discharges under both comparative slowly rising SI voltage and very fast rising impulse voltage according to Fig. 7.79, which refers to a rod-plane gap in ambient air of 20 cm in electrode spacing (Lemke 1967). Applying a negative impulse voltage of approx. 150 µs time-to-crest to the plane electrode, the first streamer discharge appeared at the positive cone electrode, where the inception voltage scattered around 10 kV. At rising voltage further streamer discharges of increasing length and pulse charge were recognized (Fig. 7.79a). However, applying a fast rising impulse voltage approaching an initial test level of 50 kV within less than one µs, only a single streamer discharge igniting at 50 kV was observed, i.e. the inception voltage was about 5-times greater than that measured under SI voltage. Despite the huge pulse charge of 180 nC created under the fast rising voltage, an ultimate breakdown was not encountered, even though the streamer filaments bridged the entire electrode spacing and the test voltage was additionally increased, at least up to 92 kV (Fig. 7.79b).

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig79_HTML.gif — Fig. 7.79
Lichtenberg figures (fotograms) of streamer filaments developing in a 20 cm cone-plane air gap under SI voltage (a) and steep front voltage (b) and associated oscilloscopic records (Lemke 1967), explanation in the text

Another measuring example, which underlines the impact of the statistical time-lag on the inception voltage and thus on the discharge mechanism, is shown in Fig. 7.80, which refers to interfacial discharges in a defective MV cable termination. Applying first an impulse voltage of about 8 µs time-to-crest (Fig. 7.80a), the inception voltage attained nearly 3 kV, and numerous PD pulses appeared thereafter. However, increasing now the steepness of the applied impulse voltage by decreasing the time-to-crest stepwise, at least down to about 3 µs (Fig. 7.80b), the inception voltage increased considerably, and only a single PD pulse of comparatively high charge was recognized, i.e. the previously observed PD pulse train disappeared completely.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig80_HTML.gif — Fig. 7.80
Impact of the front time of SI voltages on the PD signature of a cavity discharge. a 8 μs front time, 11.6 kV test voltage. b 3 μs front time, 11 kV test voltage

The above considered impact of the statistical time-lag on the inception voltage becomes especially dominant for discharges under very fast front transient (VFT) voltages, which might be excited by power electronic converters. This advanced technology was originally introduced to adjust the speed of industrial drives using square wave operating voltages. As the operation principle of such power converters is based on the fast chopping of inductive currents, high over-voltages may be excited associated with a severe PD activity as, for instance, in rotating machines, which is associated with an accelerated degradation of the exposed insulation (Stone et al. 1992; Kaufhold et al. 1996; IEC 61934:2006; IEC 60034-18-41:2014; IEC 60034-18-42:2008; IEC 60034-25:2007; IEC 61934:2006). Nowadays this problem became also an issue for other industrial networks and even smart grids due to the increasing use of power electronic systems, for instance, to convert the variable frequency of wind farm turbines into power frequency AC voltage, as well as to convert the low DC voltage of photo-voltaic plants into high AC or DC voltage required for long-distance power transmission links.

As known from the classical network theory, chopping an inductive current is associated with a transfer of the “inductive” energy into the parallel connected load. In case of a pure capacitive load, the peak value of the excited voltage surge becomes often considerably higher than the operation voltage, as exemplarily shown in Fig. 7.81.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig81_HTML.gif — Fig. 7.81
Commutating voltage surges (pink trace) excited by repetitive chopping of inductive currents (blue trace) recorded at time scales of 10 ms/div (a) and 1 ms/div (b), explanation in the text

Example The oscilloscopic screenshots displayed in Fig. 7.81 refer to a stator of a low voltage motor having a coil inductance of L_c = 0.17 H. One coil termination was connected to a constant direct voltage of V₁ = 210 V, while the other coil termination was periodically (about 150-times per second, see Fig. 7.81a) connected for a time span of T_d = 2.2 ms to ground potential. Just thereafter the inductive current was chopped by means of a fast solid state switch realized by an insulated gate bipolar transistor (IGTB). At time period when the stator coil is connected to ground potential, the inductive current rises almost linearly and attains finally a crest value of I_c = 2.7 A, which follows also from Faraday´s induction law:

$V_{1} = L_{c} \cdot {\text{d}}i/{\text{d}}t \approx L_{c} \cdot I_{c} / T_{d} ,$

$I_{C} = V_{1} \cdot T_{d} / L_{c} = \left( {210\,{\text{V}}} \right) \cdot \left( {2.2\,{\text{ms}}} \right)/0.17 \,{\text{H}} \approx 2.75\,{\text{A}}$

At instant T_d = 2.3 ms when the inductive current through the stator coil is chopped, the entire inductive energy is transferred to the capacitive load, which was chosen as C_p = 0.1 µF. Under this condition the peak value V₂ of the voltage appearing across the parallel connected elements L_c and C_p can be calculated for using the following known relation:

$\frac{1}{2} \cdot L_{c} \cdot I_{c}^{2} = \frac{1}{2} \cdot C_{p} \cdot V_{2}^{2} ;$

$V_{2} = I_{c} \cdot \sqrt {L_{c} /C_{p} } \approx \left( {2.7\,{\text{A}}} \right) \cdot \sqrt {\left( {0.17\,{\text{H}}} \right)/\left( {0.1\,\upmu{\text{F}}} \right)} \approx 3.52\,{\text{kV}}.$

This exceeds the applied direct voltage by more than one order and is in well agreement with the measured peak voltage, as indicated in Fig. 7.81b.

Very fast transient voltages excited by power electronics, sometimes also referred to as commutating surges, are characterized by rise and decay times in the µs range as well as repetition frequencies up to some tens of kHz. These are especially harmful for the winding insulation of rotating machines, because under this condition the inception field strength may be enhanced substantially and thus the PD activity, too, as discussed previously. This is underlined by the measuring example shown in Fig. 7.82, which refers to discharges between two circular-shaped magnet wires, each of 1.2 mm in diameter and coated by an insulating film of approx. 30 µm in thickness.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig82_HTML.gif — Fig. 7.82
Charge pulses (pink trace) of discharges between two circular shaped magnetic wires under repetitive commutating surges (green trace), recorded at time scale of 100 µs/div (a) and 10 µs/div (b), (explanation in the text)

Applying repetitive voltage surges of 3.4 kV in magnitude (green trace), which was measured by means of a low-capacitive field probe (Lemke 2016), the maximum pulse charge scattered around 10 nC (pink trace). This comparatively high magnitude is due to the fact that most of the PD events ignited in the crest region of the applied voltage surges, where the actual inception voltage exceeded considerably the static inception voltage. Further experimental studies revealed that the shape of the captured current pulses as well as the peak values were randomly distributed over an extremely wide range, often between some tens and some thousands of mA, see Fig. 7.83.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig83_HTML.gif — Fig. 7.83
Current pulses (pink trace) of discharges igniting in a 60 µm air gap between two circular shaped magnetic wires under commutating surges (green trace), recorded at time scale of 20 ns/div (a) and 4 ns/div (b), explanation in the text

In this context it is noteworthy that usually so-called twisted pairs are employed to qualify the turn/turn insulation of random wound rotating machines under commutating surges. For this purpose a pair of film-insulated magnet wires is twisted together over a length of about 120 mm (IEEE Std. 522:2004). Using such test samples for apparent charge measurements according to IEC 60270:2000 it has to be taken into account that only a low measuring sensitivity is achievable due to the comparatively high capacitive load current, as exemplarily shown in Fig. 7.84a. To enhance the signal-to-noise (S/N) ratio, one option would be an increase of the lower cut-off frequency, which should be chosen significantly above the frequency spectrum representative for the commutating surges. This is underlined by the measuring example shown in Fig. 7.84b, where the lower cut-off frequency of the measuring system was adjusted to f₁ ≈ 1.8 MHz. Of course, this is in conflict with IEC 60270:2000, which recommends measuring frequencies below 1 MHz to measure the PD quantity apparent charge. Thus, as an alternative non-conventional methods could also be used, such as the PD detection in the UHF range or to evaluate the associated acoustic and optic signals. However, under this condition the PD activity can only be evaluated qualitatively but not quantitatively, as has already been pointed out in Sects. 4.7 and 4.8. Generally it can be stated that PD testing of inductive components stressed by commutating surges requires new approaches. For more information on this issue see also the Technical Brochure TB 703 published by Cigre WG D1.43 in 2017.

../images/214133_2_En_7_Chapter/214133_2_En_7_Fig84_HTML.gif — Fig. 7.84
Charge pulses (pink trace) superimposed on the capacitive load current caused by the high frequency commutating surges (green trace). Test conditions: 60 µm air gap between twisted pairs of magnetic wires; the current was integrated by means of a wide-band PD measuring system where the lower cut-off frequency was adjusted to 20 kHz (a) and to 1.8 MHz (b), explanation in the text

7. Tests with High Lightning and Switching Impulse Voltages