 |
|
In this chapter, we introduce the foundations of thermodynamics. A major goal is to establish what is meant by the concept of equilibrium, described informally in the context of the party example in chapter 1. The idea of equilibrium is an outgrowth of our understanding of three laws of nature, which describe the relationship between heat and work and identify a sense of direction for change in natural systems. These laws are the heart of the subject of thermodynamics, which we apply to a variety of geochemical problems in later chapters.
To reach our goal, we need to examine some familiar concepts like temperature, heat, and work more closely. It is also necessary to introduce new quantities such as entropy, enthalpy, and chemical potential. The search for a definition of equilibrium also reveals a set of four fundamental equations that describe potential changes in the energy of a system in terms of temperature, pressure, volume, entropy, and composition.
TEMPERATURE AND EQUATIONS OF STATE
It is part of our everyday experience to arrange items on the basis of how hot they are. In a colloquial sense, our notion of temperature is associated with this ordered arrangement, so that we speak of items having higher or lower temperatures than other items, depending on how “hot” or “cool” they feel to our senses. In the more rigorous terms we must use as geochemists, though, this casual definition of temperature is inadequate for two reasons. First of all, a practical temperature scale should have some mathematical basis, so that changes in temperature can be related to other continuous changes in system properties. It is hard to use the concept of temperature in a predictive way if we have to rely on disjoint, subjective observations. Second, and more important, it is hard to separate this common perception of temperature from the more elusive notion of “heat,” the quantity that is transferred from one body to another to cause changes in temperature. It would be helpful to develop a definition of temperature that does not depend on our understanding of heat, but instead relies on more familiar thermodynamic properties.
Imagine two closed systems, each of which is homogeneous; that is, each system consists of a single substance with continuous physical properties—from now on, we will call this kind of substance a phase—that is not undergoing any chemical reactions. If this condition is met, the thermodynamic state of either system can be completely described by defining the values of any two of its intensive properties. These might be pressure and viscosity, for example, or acoustic velocity and molar volume. To study the concept of temperature, let’s examine the relationship between pressure and molar volume, using the symbols p and  in one system, and P and
in one system, and P and  in the other. (Refer back to chapter 1 to confirm that molar volume, the ratio of volume to the number of moles in the system, is indeed an intensive property. Notice, also, that we are now beginning to use the convention of an overscore to identify molar quantities, as described in chapter 1.)
in the other. (Refer back to chapter 1 to confirm that molar volume, the ratio of volume to the number of moles in the system, is indeed an intensive property. Notice, also, that we are now beginning to use the convention of an overscore to identify molar quantities, as described in chapter 1.)
If we place the two containers in contact, changes of pressure and molar volume will take place spontaneously in each system until, if we wait long enough, no further changes occur. When the two systems reach that point, they are in thermal equilibrium. Let’s now measure their pressures and molar volumes and label them P1,  1 and p1,
1 and p1,  1. There is no reason to expect that P1 will necessarily be the same as p1 or that
1. There is no reason to expect that P1 will necessarily be the same as p1 or that  1 will be equal to
1 will be equal to  1. In general, the systems will not have identical properties.
1. In general, the systems will not have identical properties.
If we separate the systems for a moment, we will find it possible to change one of them so that it is described by new values P2 and  2 that still lead to thermal equilibrium with the system at p1 and
2 that still lead to thermal equilibrium with the system at p1 and  1. There are, in fact, an infinite number of possible combinations of P and
1. There are, in fact, an infinite number of possible combinations of P and  that satisfy this condition. These combinations define a curve on a graph of P versus
that satisfy this condition. These combinations define a curve on a graph of P versus  (fig. 3.1a). Each combination of P and
(fig. 3.1a). Each combination of P and  describes a state of the system in thermal equilibrium with p1 and
describes a state of the system in thermal equilibrium with p1 and 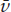 1. All points on the curve are, therefore, also in equilibrium with each other. This observation has been called the zeroth law of thermodynamics: “If A is in equilibrium with B and B is in equilibrium with C, then A is in equilibrium with C.” Notice—this is important—that figure 3.1a could describe either system. We could just as well have varied pressure and molar volume in the other system and found an infinite number of values of p and
1. All points on the curve are, therefore, also in equilibrium with each other. This observation has been called the zeroth law of thermodynamics: “If A is in equilibrium with B and B is in equilibrium with C, then A is in equilibrium with C.” Notice—this is important—that figure 3.1a could describe either system. We could just as well have varied pressure and molar volume in the other system and found an infinite number of values of p and  that lead to thermal equilibrium with the system at P1,
that lead to thermal equilibrium with the system at P1,  1. These values would define a curve on a graph of p versus
1. These values would define a curve on a graph of p versus  , shown in figure 3.1b.
, shown in figure 3.1b.
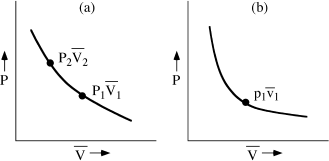
FIG. 3.1. (a) ALL states of a system for which f (P, V) = T are said to be in thermal equilibrium. A Line connecting all such states is called an isothermal. (b) If another system contains a set of states Lying on the isothermal f (p, v) = t, and if t = T, then the two systems are in thermal equilibrium.
Curves like these are called isothermals. What we have just demonstrated is that states of a system have the same temperature if they lie on an isothermal. Furthermore, two systems have the same temperature if their states on their respective isothermals are in thermal equilibrium. These two statements, together, define what we mean by “temperature.” You could express these two statements algebraically by saying that the each of isotherms in our example can be described by a function:
f(p, 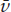 ) = t or F(P,
) = t or F(P,  ) = T,
) = T,
and that the systems are in thermal equilibrium if t = T. Functions like these, which define the interrelationships among intensive properties of a system, are called equations or functions of state.
Because many real systems behave in roughly similar ways, several standard forms of the equation of state have been developed. We find, for example, that many gases at low pressure can be described adequately by the ideal gas law:
P = RT,
= RT,
in which R is the gas constant, equal to 1.987 cal mol−1K−1. Other gases, particularly those containing many atoms per molecule or those at high pressure, are characterized more appropriately by expressions like the Van der Waals equation:
(P + a/ 2)(
2)( − b) = RT,
− b) = RT,
in which a and b are empirical constants. We apply these and other equations of state in chapter 4.
Our notion of temperature, therefore, depends on the conventions we choose to follow in writing equations of state. A practical temperature scale can be devised simply by choosing a well-studied reference system (a thermometer), writing an arbitrary function that remains constant (that is, generates isothermals) for various states of the system in thermal equilibrium, and agreeing on a convenient way to number selected isothermals.
In general terms, work is performed whenever an object is moved by the application of a force. An infinitesimal amount of work dw, is therefore described by writing:
dw = F dx,
in which F is a generalized force and dx is an infinitesimal displacement. By convention, we define dw so that it is positive if work is performed by a system on its surroundings, and negative if the environment performs work on the system. We know from experience that an object may be influenced simultaneously by several forces, however, so it is more useful to write this equation as:
dw =  Fidxi.
Fidxi.
The forces may be hydrostatic pressure, P, or may be directed pressure, surface tension, or electrical or magnetic potential gradients. All forms of work, though, are equivalent, so the total work performed on or by a system can be calculated by including all possible force terms in the equation for dw. The thermodynamic relationships that build on the equation do not depend on the identity of the forces involved.
This description of work is broader than it often needs to be in practice. Work is performed in most geochemical systems when a volume change dV is generated by application of a hydrostatic pressure:
dw = PdV.
This is the equation we most often encounter, and geochemists commonly speak as if the only work that matters is pressure-volume work. Usually, the errors introduced by this simplification are small. It is always wise, however, to examine each new problem to see whether work due to other forces is significant. Later chapters of this book discuss some conditions in which it is necessary to consider other forces.
Note that we have defined work with a differential equation. The total amount of work performed in a process is the integral of that equation between the initial and final states of the system. Because forces in geologic environments rarely remain constant as a system evolves, the integral becomes extremely difficult to evaluate if we do not specify that the process is a slow one. The work performed by a gas expanding violently, as in a volcanic eruption, is hard to estimate, because pressure is not the same at all places in the gas and the gas is not expanding in mechanical equilibrium with its surroundings.
THE FIRST LAW OF THERMODYNAMICS
During the 1840s, a series of fundamental experiments were performed in England by the chemist James Joule. In each of them, a volume of water was placed in an insulated container, and work was performed on it from the outside. Some of these experiments are illustrated in figure 3.2. The paddle wheel, iron blocks, and other mechanical devices are considered to be parts of the insulated container. The temperature of the water was monitored during the experiments, and Joule reported the surprising result that a specific amount of work performed on an insulated system, by any process, always results in the same change of temperature in the system.
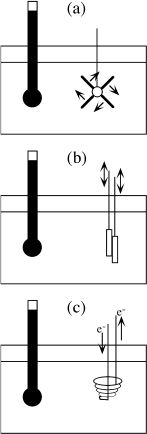
FIG. 3.2. English chemist James Joule performed experiments to relate mechanical work to heat. (a) A paddlewheel is rotated and a measurable amount of work is performed on an enclosed water bath. (b) Two blocks of iron are rubbed together. (c) Electrical work is performed through an immersion heater.
What changed inside the container, and how do we explain Joule’s results? In physics, work is often introduced in the context of a potential energy function. For example, a block of lead may be lifted from the floor to a tabletop by applying an appropriate force to it. When this happens, we recognize not only that an amount of work has been expended on the block, but also that its potential energy has increased. Usually, problems of this type assume that no change takes place in the internal state of the block (that is, its temperature, pressure, and composition remain the same as the block is lifted), so the change in potential energy is just a measure of the change in the block’s position. When Joule performed work on the insulated containers of water, however, it was not the position of the water that changed, but its internal state, as measured by a change in its temperature. The energy function used to describe this situation is called the internal energy (symbolized by E) of the system, and Joule’s results can be expressed by writing
dE = −dw.
Thus, there are two ways to change the internal energy of a system. First, as we implied when considering the meaning of temperature, energy can pass directly through system walls if those walls are noninsulating. Energy transferred by this first mode is called heat. If Joule’s containers had been noninsulators, he could have produced temperature changes without performing any work, simply by lighting a fire under them. Second, as Joule demonstrated, the system and its surroundings can perform work on each other.
To investigate these two modes of energy transfer, we need to distinguish between two types of walls that can surround a closed system. What we have spoken of loosely as an “insulated” wall is more properly called an adiabatic wall. (The Greek roots of the word adiabatic mean, appropriately, “not able to go through.”) Adiabatic processes, like those in Joule’s experiments, do not involve any transfer of heat between a system and its surroundings. Perfect adiabatic processes are seldom seen in the real world, but geochemists often simplify natural environments by assuming that they are adiabatic. A nonadiabatic wall, however, allows the passage of heat. It is possible to perform work on a system that is bounded by either type of wall.
Equation 3.1 is an extremely useful statement, referred to as the First Law of Thermodynamics. In words, it tells us that the work done on a system by an adiabatic process is equal to the increase in its internal energy, a function of the state of the system. We may conclude further that if a system is isolated, rather than simply closed behind an adiabatic wall, no work can be performed on it from the outside, and its internal energy must remain constant.
Equation 3.1 can be expanded to say that for any system, a change in internal energy is equal to the sum of the heat gained (dq) and the work performed on the system (−dw):
dE = dq − dw.
Notice that dE is a small addition to the amount of internal energy already in the system. Because this is so, the total change in internal energy during a geochemical process is equal to the sum of all increments dE:
dE = Efinal − Einitial = ΔE.
The value of ΔE, in other words, does not depend on how the system evolves between its end states. In fact, if the system were to evolve along a path that eventually returns it to its initial state, there would be no net change whatever in its internal energy. This is an important property of functions of state, described in more mathematical detail in appendix A.
In contrast, the values of dq and dw describe the amount of heat or work expended across system boundaries, rather than increments in the amount of heat or work “already in the system.” When we talk about heat or work, in other words, the emphasis is on the process of energy transfer, not the state of the system. For this reason, the integral of dq or dw depends on which path the system follows from its initial to its final state. Heat and work, therefore, are not functions of state.
Consider the system illustrated in figure 3.3, whose initial state is described by a pressure P1 and a temperature T1. This might be, for example, a portion of the atmosphere. Recall that the equation of state that we use to define isothermals for this system tells us what the molar volume,  1 under these conditions is. For ease of calculation, assume that the equation of state for this system is the ideal gas law,
1 under these conditions is. For ease of calculation, assume that the equation of state for this system is the ideal gas law,  = RT/P. Compare two ways in which the system might slowly evolve to a new state in which P = P2 and T = T2. In the first process, let pressure increase slowly from P1 to P2 while the temperature remains constant, then let temperature increase from T1 to T2 at constant pressure P2. In the second process, let temperature increase first at constant pressure P1, and then let pressure increase from P1 to P2. (If this were, in fact, an atmospheric problem, the isobaric segments of these two paths might correspond to rapid surface warming on a sunny day, and the isothermal segments might reflect the passage of a frontal system.) Is the amount of work done on these two paths the same?
= RT/P. Compare two ways in which the system might slowly evolve to a new state in which P = P2 and T = T2. In the first process, let pressure increase slowly from P1 to P2 while the temperature remains constant, then let temperature increase from T1 to T2 at constant pressure P2. In the second process, let temperature increase first at constant pressure P1, and then let pressure increase from P1 to P2. (If this were, in fact, an atmospheric problem, the isobaric segments of these two paths might correspond to rapid surface warming on a sunny day, and the isothermal segments might reflect the passage of a frontal system.) Is the amount of work done on these two paths the same?
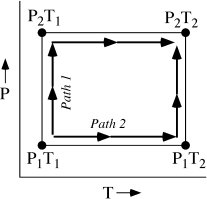
FIG. 3.3. As a system’s pressure and temperature are adjusted from P1T1 to P2T2, the work performed depends on the path that the system follows.
This problem is similar to problem 1.8 at the end of chapter 1. If the only work performed on the system is due to pressure-volume changes, then the work along each of the paths is defined by the integral of Pd . For path 1,
. For path 1,

Along path 2,
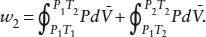
To evaluate these four integrals, find an expression for d by expressing the equation of state as a total differential of
by expressing the equation of state as a total differential of  (T,P):
(T,P):
d  = (∂
= (∂ /∂T)PdT + (∂
/∂T)PdT + (∂ /∂P)TdP = (R/P)dT − (RT/P2)dP,
/∂P)TdP = (R/P)dT − (RT/P2)dP,
and substitute the result into w1 and w2 above. The result, after integration, is that the work performed on path 1 is:
w1 = R[(T2 − T1) + T1ln(P1/P2)]
but the work performed on path 2 is:
w2 = R[(T2 − T1) + T2 ln(P1/P2)],
which is clearly different. Similarly, if we had a function for dq, the heat gained, we could integrate it to show that q1 and q2, the amounts of heat expended along these paths, must also be different. We are about to do just that.
ENTROPY AND THE SECOND LAW OF THERMODYNAMICS
Taken by itself, equation 3.2 tells us that heat and work are equivalent means for changing the internal energy of a system. In developing that expression, however, we have engaged in a little sleight-of-hand that may have led you, quite incorrectly, to another conclusion as well. By stating that heat and work are equivalent modes of energy transfer, the First Law may have left you with the impression that heat and work can be freely exchanged for one another. This is not the case, as a few commonplace examples will show.
A glass of ice water left on the kitchen counter gradually gains heat from its surroundings, so that the water warms up and the room temperature drops ever so slightly. In the process, there has been an exchange of heat from the warm room to the relatively cool water. As Joule showed, the same transfer could have been accomplished by having the room perform work on the ice water. It is clearly impossible, however, for a glass of water at room temperature to cool spontaneously and begin to freeze, although we can certainly remove heat by transferring it first from the water to a refrigeration system. In a similar way, a lava flow gradually solidifies by transferring heat to the atmosphere, but this natural process cannot reverse itself either. It is impossible to melt rock by transferring heat to it directly from cold air.
If we were shown films of either of these events, we would have no trouble recognizing whether they were being run forwards or backwards. Equation 3.2, however, does not provide us with a means of making this determination of direction theoretically. On the basis of experience with natural processes, therefore, we are driven to formulate a Second Law of Thermodynamics. In its simplest form, first stated by Rudolf Clausius in the middle of the nineteenth century, the Second Law says that heat cannot spontaneously pass from a cool body to a hotter one. Another way of stating this, which may also be useful, is that any natural process involving a transfer of energy is inefficient, with the result that a certain amount is irreversibly converted into heat that cannot be involved in further exchanges. The Second Law, therefore, is a recognition that natural processes have a sense of direction.
Two difficult concepts are embedded in what we have just said. One is spontaneity and the other is reversibility. A spontaneous change is one that, under the right conditions, can be made to perform work. The heavy weight in figure 3.4 can perform the work of raising the lighter weight as it falls, so that this change is spontaneous. If the lighter weight raised the heavier one, we would recognize the change as nonspontaneous and we would assume that some change outside the system had probably caused it. When we face a conceptual challenge in telling whether a change is spontaneous, it is usually because we haven’t defined the bounds of the system clearly. Notice also that a spontaneous change doesn’t have to perform work; it just has to be capable of it. The heavy weight will fall spontaneously whether it lifts the lighter weight or not.
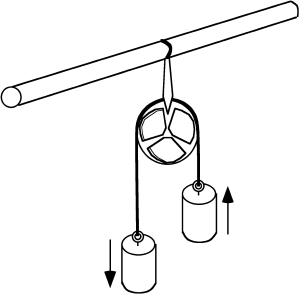
FIG. 3.4. Two weights are connected by a rope that passes over a frictionless pulley. If one weight is infinitesimally heavier than the other, then it will perform the maximum possible amount of work (the work of lifting the other weight) as it falls. The smaller the weight difference between them is, the greater the amount of work and the more nearly reversible it is.
This leads us to consider reversibility. A change is reversible if it does the maximum amount of possible work. The falling weight in figure 3.4, for example, will be undergoing a reversible change if it lifts an identical weight and loses no energy to friction in the pulley and rope that connects it to the other weight. Experience tells us that reversibility is an unattainable ideal, of course, but that doesn’t stop engineers from designing counter-weighted elevators to use as little extra energy as possible. It also doesn’t stop geochemists from considering gradual changes in systems that are never far from equilibrium as if they were reversible. The conceptual challenge arises because true reversibility is beyond our experience with the natural world.
Another perspective on the Second Law, then, is that it tells us that nature favors spontaneous change, and that maximum work is never performed in real-world processes. Just as the internal energy function was introduced to present the First Law in a quantitative fashion, we need to define a thermodynamic function that quantifies the sense of direction and systematic inefficiency that the Second Law identifies in natural processes. This new function, known as entropy and given the symbol S, is defined in differential form by:
dS = (dq/T)rev,
in which dq is an infinitesimal amount of heat gained by a body at temperature T in a reversible process. It is a measure of the degree to which a system has lost heat and therefore some of its capacity to do work. Many people find entropy an elusive concept to master, so it is best to become familiar with the idea by discussing examples of its use and properties.
Figure 3.5 illustrates a potentially reversible path for a system enclosed in a nonadiabatic wall. Suppose that the system expands isothermally from state A to state B. In doing so, it performs an amount of work on its surroundings that can be calculated by the integral of PdV. Graphically, this integral is represented by the area AA′B′B. Because this is an isothermal process, state A and state B must be in equilibrium with each other, which is another way of saying that the internal energy of the system must remain constant along the path between them. Therefore, the work performed by the system must be balanced by an equivalent amount of heat gained, according to equation 3.2. Suppose, now, that it were possible to compress the system isothermally, thus reversing along the path B → A without any interference due to friction or other real-world forces. We would find that the work performed on the system (the heat lost by the system) would be numerically equal to the work on the forward path, but with a negative sign. That is, the net change in entropy around the closed path is:
dS = dq/T − dq/T = 0.

FIG. 3.5. The work performed by isothermal compression from state A to state B is equal to the area AA’B’B. Because dE = 0, an equivalent negative amount of heat is gained by the system. If this change could be reversed precisely, the net change in entropy dS would be zero.
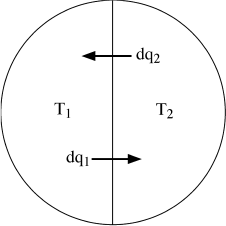
FIG. 3.6. Two bodies in an isolated system are separated by a nonadiabatic wall and may, therefore, exchange quantities of heat dq1 and dq2 as they approach thermal equilibrium.
The entropy function for a system following a reversible pathway, therefore, is a function of state, just like the internal energy function.
Next, consider an isolated system in which there are two bodies separated by a nonadiabatic wall (fig. 3.6). Let the two bodies initially be at different temperatures T1 and T2. If we allow them to approach thermal equilibrium, there must be a transfer of heat dq2 from the body at temperature T2. Because the total system is isolated, an equal amount of heat dq1 must be gained by the body at temperature T1. The net change in entropy for the system is:
dSsys = dS1 + dS2,
or
dSsys = dq1 ([1/T1] − [1/T2]).
Remember, though, that the Second Law tells us that heat can only pass spontaneously from a hot body to a cooler one, so this result is only valid if T2 > T1. Therefore, the entropy of an isolated system can only increase as it approaches internal equilibrium:
dSsys > 0.
Finally, look at the closed system illustrated in figure 3.7. It is similar to the previous system in all respects, except that is bounded by a nonadiabatic wall, so that the two bodies can exchange amounts of heat 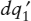 and
and 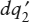 with the world outside. As they approach thermal equilibrium, the heat exchanged by each is given by:
with the world outside. As they approach thermal equilibrium, the heat exchanged by each is given by:
(dq1)total = dq1 + 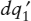 ,
,
and
(dq2)total = dq2 + 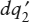 .
.
Any heat exchanged internally must still show up either in one body or the other, so as before:
dq1 = −dq2.
The net change in system entropy is, therefore,
| dSsys | = (dq1)total + (dq2)total |
= (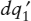 /T1) + ( /T1) + (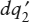 /T2) + dq1([1/T1] − [1/T2]). /T2) + dq1([1/T1] − [1/T2]). |
It has already been shown that the Second Law requires the last term of this expression to be positive. Therefore,
dSsys > (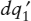 /T1) + (
/T1) + (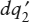 /T2).
/T2).
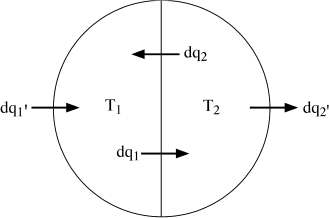
FIG. 3.7. The system in figure 3.6 is allowed to exchange heat with its surroundings. The net change in internal entropy depends on the values of 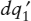 and
and 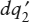 .
.
This result is more open ended than the previous one. Although the entropy change due to internal heat exchanges in any system will always be positive, it says that we have no way of predicting whether the overall dSsys of a nonisolated system will be positive unless we also have information about 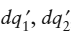 , and the temperature in the world outside the system.
, and the temperature in the world outside the system.
To appreciate this ambiguity, think back to the difference between placing a glass of ice water on the kitchen counter and placing it in the freezer. In both cases, internal heat exchange results in an increase in system entropy. When the glass is refrigerated, however, 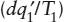 and
and 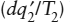 become potentially large negative quantities, with the result that the change due to internal processes is overwhelmed and the entropy within the glass decreases. The Second Law, therefore, does not rule out the possibility that thermodynamic processes can reverse direction. It does tell us, though, that a spontaneous change can only reverse direction if heat is lost to some external system. A local decrease in entropy must be accompanied by an even larger increase in entropy in the world at large. When we have difficulty with this notion, as we commented earlier, it is usually because we have not been clear about defining the size and boundaries of the system. Therefore, except for those cases in which a system evolves sufficiently slowly that we are justified in approximating its path as a reversible one, its change in entropy must be defined not by equation 3.3, but by:
become potentially large negative quantities, with the result that the change due to internal processes is overwhelmed and the entropy within the glass decreases. The Second Law, therefore, does not rule out the possibility that thermodynamic processes can reverse direction. It does tell us, though, that a spontaneous change can only reverse direction if heat is lost to some external system. A local decrease in entropy must be accompanied by an even larger increase in entropy in the world at large. When we have difficulty with this notion, as we commented earlier, it is usually because we have not been clear about defining the size and boundaries of the system. Therefore, except for those cases in which a system evolves sufficiently slowly that we are justified in approximating its path as a reversible one, its change in entropy must be defined not by equation 3.3, but by:
dS > (dq/T)irrev.
Entropy is commonly described in elementary texts as a measure of the “disorder” in a system. For those who learned about entropy through statistical mechanics, following the approach pioneered by Nobel physicist Max Planck in the early 1900s, this may make sense. This is sometimes less than satisfying for people who address thermodynamics as we have, because the mathematical definition in equations 3.3 and 3.4 doesn’t seem to address entropy in those terms. To see why it is valid to think of entropy as an expression of disorder, consider this problem.
Two adjacent containers are separated by a removable wall. Into one of them, we introduce 1 mole of nitrogen gas. We fill the other with 1 mole of argon. If the wall is removed, we expect that the two gases will mix spontaneously rather than remaining in their separate ends of the system. It would require considerable work to separate the nitrogen and argon again. (See problem 3.5 at the end of this chapter.) By randomizing the positions of gas molecules and contributing to a loss of order in the system, we have caused an increase in entropy.
Suppose that the mixing takes place isothermally, and that the only work involved is mechanical. Assume also, for the sake of simplicity, that both argon and nitrogen are ideal gases. How much does the entropy increase in the mixing process? First, write equation 3.2 as:
dq = dE + PdV.
Because we agreed to carry out the experiment at constant temperature, dE must be equal to zero. Using the equation of state for an ideal gas, we can see that dq now becomes:
dq = (nRT/V)dV,
from which:
dS = dq/T = (nR/V)dV.
(Notice that this problem is cast in terms of volume, rather than molar volume, because we need to keep track of the number of moles, n.) We can think of the current problem as one in which each of the two gases has been allowed to expand from its initial volume (V1 or V2 into the larger volume V1 + V2. For each, then, the entropy change due to isothermal expansion is:
ΔSi = ΔniR ln([V1 + V2]/Vi),
and the combined entropy change is:
ΔS1 + ΔS2 = n1R ln([V1 + V2]/V1) + n2R ln([V1 + V2]/V2).
This can be simplified by defining the mole fraction, Xi, of either gas as Xi = ni/(n1 + n2) = Vi/(V1 + V2); thus,
Δ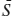 = −R(X1 ln X1 + X2 ln X2),
= −R(X1 ln X1 + X2 ln X2),
where the bar over Δ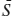 is our standard indication that it has been normalized by n1 + n2 and is now a molar quantity. The entropy of mixing will always be a positive quantity, because X1 and X2 are always <1.0. The answer to our question, therefore, is that entropy increases by:
is our standard indication that it has been normalized by n1 + n2 and is now a molar quantity. The entropy of mixing will always be a positive quantity, because X1 and X2 are always <1.0. The answer to our question, therefore, is that entropy increases by:
2 × Δ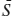 |
= 2 × −(1.987)(0.5 ln 0.5 + 0.5 ln 0.5) |
| = 2.76 cal K−1 or 11.55 J K−1. |
REPRISE: THE INTERNAL ENERGY FUNCTION MADE USEFUL
With the First and Second laws in hand, we can now return to the subject of equilibrium, which was defined informally at the beginning of this chapter as a state in which no change is taking place. The First Law restates this condition as one in which dE is equal to zero. From the Second Law, we find that entropy is always maximized during the approach to equilibrium, and that dS becomes equal to zero once equilibrium is reached.
ENTROPY AND DISORDER: WORDS OF CAUTION
The description of entropy as a measure of disorder is probably the most often used and abused concept in thermodynamics. In many applications, the idea of “disorder” is coupled with the inference from the Second Law that entropy should increase through time. Like all brief descriptions of complex ideas, though, the statement that “entropy measures system disorder” must be treated with some care. It is common practice among chemical physicists to estimate the entropy of a system by calculating its statistical degrees of freedom—computing, in effect, the number of different ways that atoms can be configured in the system, given its bulk conditions of temperature, pressure, and other intensive parameters. A less rigorous description of disorder, however, can lead to very misleading conclusions about the entropy of a system and thus the course of its evolution.
Creationists, for example, have grasped at the idea of entropy as disorder as a vindication of their belief that biologic evolution is impossible. In their view, “higher” organisms are more ordered than the more primitive organisms from which biologists presume that they evolved. Because this interpretation presents evolution as a historical progression from a less ordered to a more ordered state, it describes an apparent violation of the Second Law. There are so many flaws in this argument that it is difficult to know where to begin to discuss it, and we will mention only a few.
The first is the question of the meaning of “order” as applied to organisms or families of organisms. This is far from a semantic problem, because it is by no means clear that higher organisms are more ordered than primitive ones, from the point of view of thermodynamics. The biologic concept of order, although potentially connected to thermodynamics in the realm of biochemistry, is based largely on functional complexity, not equations for energy utilization. The situation becomes even murkier when applied to groups of organisms, rather than to individuals.
Furthermore, from a thermodynamic perspective, living organisms cannot be viewed as isolated systems, separated from their inorganic surroundings. As we have tried to emphasize, the definition of system boundaries is crucial if we are to interpret system changes by the Second Law. A refrigerator, for example, might be mistakenly seen to violate the Second Law if we failed to recognize that entropy in the kitchen around it increases even as the contents of the refrigerator become more ordered.
Finally, we note that there may be instances in which entropy and disorder in the macroscopic sense can be decoupled, even in a properly defined isolated system. For example, if two liquids are mixed in an adiabatic container, we might expect that they will mix to a random state at equilibrium. We know, however, that other system properties may commonly preclude a random mixture. Oil and vinegar in a salad dressing unmix readily, as a manifestation of differences in their bonding properties. If the attractive force between similar ions or molecules is greater than that between dissimilar ones, then complete random mixing would imply an increase, rather than a decrease, in both internal energy and entropy. A macroscopically ordered system, in other words, can easily be more stable than a disordered one without shaking our faith in the Second Law of Thermodynamics.
The results expressed in equations 3.3 and 3.4 can be used to recast equation 3.2 as:
dE ≤ TdS − dw.
Under most geologic conditions, mechanical (pressure-volume) work is the only significant contribution to dw, and it is reasonable to substitute PdV for dw:
dE ≤ TdS − PdV.
This is a practical form of equation 3.2, although only correct under the conditions just discussed. In most geologic environments, we assume that change takes place very slowly, so that systems can be regarded as following nearly reversible paths. Generally, therefore, the inequality in equation 3.5 can be disregarded, even though it is strictly necessary.
Because much of the remaining discussion of thermodynamics in this book derives from equation 3.5, we should recognize three other relationships that follow directly from it and from the fact that the internal energy function is a function of state. First, equation 3.5 is a differential form of E = E(S, V). Assuming that changes take place reversibly, it can be written as a total differential:
dE(S, V) = (∂E/∂S)V dS + (∂E/∂V)S dV.
Comparison with equation 3.5 yields the two statements:
T = (∂E/∂S)V,
and
P = −(∂E/∂V)S.
In other words, the familiar variables temperature and pressure can be seen as expressions of the manner in which the internal energy of a system responds to changes in entropy (under constant volume conditions) or volume (under adiabatic conditions). Second, because E(S, V) is a function of state, dE(S, V) is a perfect differential (perfect differentials are reviewed in appendix A). That is,
(∂2E/∂S∂V) = (∂2E/∂V∂S),
or
(∂T/∂V)S = −(∂P/∂S)V.
This last equation is known as one of the Maxwell relationships. These and other similar expressions to be developed shortly can be used to investigate the interactions of S, P, V, and T. Some of these will be discussed more fully in chapter 9, when we look in more detail at the effects of changing temperature or pressure in the geologic environment.
Equation 3.5 is adequate for solving most thermodynamic problems. In many situations, however, it is possible to use equations of greater practical interest, which can be derived by imposing environmental constraints on the problem.
The first of these equations can be derived by writing equation 3.5 as:
dE + PdV ≤ TdS.
If we restrict ourselves by looking only at processes that take place at constant pressure, this is the same as writing:
d(E + PV) ≤ TdS,
because d(PV) = PdV + VdP, which equals PdV if dP = 0.
The quantity E + PV is a new function, called enthalpy and commonly given the symbol H. It is useful as a measure of heat exchanged under isobaric conditions, where dH = dq. Reactions that evolve heat, and therefore have a negative change in enthalpy, are exothermic. Those that result in an increase in enthalpy are endothermic.
The left side of this last equation can be expanded to reveal a differential form for dH:
dH = d(E + PV) = dE + PdV + VdP,
or
dH ≤ TdS + VdP.
As we did with equation 3.5, we can compare the total differential dH(S, P) and equation 3.7 under reversible conditions to recognize that:
T = (∂H/∂S)P,
and
V = (∂H/∂P)S.
Enthalpy, like internal energy and entropy, can be shown to be a function of state, because it experiences no net change during a reversible cycle of reaction paths. This makes it possible, among other things, to determine the amount of heat that would be exchanged in geologically important reactions, even when those reactions may be too sluggish to be studied directly at the low temperatures at which they take place in nature. The careful determination of such values is the business of calorimetry.
Because H is a function of state, it is also possible to extract one more Maxwell relation like equation 3.6 from its cross-partial derivatives (also reviewed in appendix A):
(∂T/∂P)S = (∂V/∂S)P.
By analogy with the way we introduced enthalpy, we can discover another useful function by writing equation 3.5 as:
dE − TdS ≤ −PdV.
Under isothermal conditions, this expression is equivalent to:
d(E − TS) ≤ −PdV.
The function F = E − TS is best referred to as the Helmholtz function, although you may see it referred to elsewhere as Helmholtz free energy or the work function.
Unfortunately, a variety of symbols have been used for the internal energy, enthalpy, and Helmholtz functions, as well as Gibbs free energy, which is discussed shortly. This has led to some confusion in the literature. In the United States, F is commonly used to designate Gibbs free energy (for example, in publications of the National Bureau of Standards). The International Union of Pure and Applied Chemistry, however, has recommended that G be the standard symbol for Gibbs free energy. This usage, if not yet standard, is at least widespread. In the United States, those who use F for Gibbs free energy generally use the symbol A for the Helmholtz function. To complete the confusion, internal energy, which we have identified with the symbol E, is frequently referred to as U, to avoid confusing it with total (internal plus potential plus kinetic) energy. Always be sure you know which symbols you are using. Nicolas Vanserg has written an excellent article on the subject, which is listed among the references at the end of this chapter (Vanserg 1958).
Because it might be mistaken for Gibbs free energy, which is ultimately a more useful function in geochemistry, it is best to avoid the term Helmholtz free energy. The name work function, however, is fairly informative. The integral of dF at constant temperature is equal to the work performed on a system. This expression has its greatest application in mechanical engineering.
It is easy to derive the differential form dF:
dF = d(E − TS) = dE − TdS −SdT,
or
dF ≤ −SdT − PdV.
The total differential dF(T, V), when compared with equation 3.9, yields the useful expressions:
S = −(∂F/∂T)V,
and
P = −(∂F/∂V)T.
Because F is a function of state and dF(T, V) is therefore a perfect differential, we also gain another Maxwell relation:
(∂S/∂V)T = (∂P/∂T)V.
Although the Helmholtz function is rarely used in geochemistry, the Maxwell relationship equation 3.10 is quite widely used. When we return for a second look at thermodynamics in chapter 9, equation 3.10 will be discussed as the basis of the Clapeyron equation, a means for describing pressure-temperature relationships in geochemistry.
The most frequently used thermodynamic quantity in geochemistry can be derived by writing equation 3.5 in the form:
dE − TdS + PdV < 0.
Under conditions in which both temperature and pressure are held constant, this expression becomes:
d(E − TS + PV) < 0.
In the now familiar fashion in which we have already defined H and F, we designate the quantity E − TS + PV with the symbol G and call it the Gibbs free energy, in honor of the Josiah Willard Gibbs, a chemistry professor at Yale University, who wrote a classic series of papers in the 1870s in which virtually all of the fundamental equations of modern thermodynamics appeared for the first time. Colloquially, among geochemists, it is common to speak simply of “free energy.”
The differential dG can be written:
dG = d(E − TS + PV) = dE − TdS − SdT + PdV + VdP,
or
dG ≤ −SdT + VdP.
As with the previous fundamental equations, we can apply our knowledge of the total differential dG(T, P) of this state function to find that:
−S = (∂G/∂T)P, V = (∂G/∂P)T,
and
−(∂S/∂P)T = (∂V/∂T)P.
It can be seen from equation 3.11 that the Gibbs free energy is the first of our fundamental equations written solely in terms of the differentials of intensive parameters. This and the ease with which both temperature and pressure are usually measured contributes to the great practical utility of this function.
However, what is “free” about the Gibbs free energy? Consider the intermediate step in equation 3.11. At constant temperature and pressure, this reduces to:
dG = dE − TdS + PdV.
Substituting dE = dq − dw, we have:
dG = dq − dw − TdS + PdV.
If the quantity of heat dq is transferred to the system isothermally and any changes are reversible, then dq = TdS and dw = dwrev, so we can rewrite this last expression as:
−dG = dwrev − PdV.
The decrease in free energy of a system undergoing a reversible change at constant temperature and pressure, therefore, is equal to the nonmechanical (i.e., not pressure-volume) work that can be done by the system. If the condition of reversibility is relaxed, then:
−dG > dwirrev − PdV.
In either case, the change in G during a process is a measure of the portion of the system’s internal energy that is “free” to perform nonmechanical work.
The free energy function provides a valuable practical criterion for equilibrium. At constant temperature, the net change in free energy associated with a change from state 1 to state 2 of a system can be calculated by integrating dG:
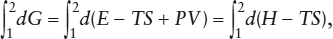
from which:
ΔG = ΔH − TΔS,
where ΔG = G2 − G1, ΔH = H2 − H1, and ΔS = S2 − S1.
Energy is available to produce a spontaneous change in a system as long as ΔG is negative. According to equation 3.13, this can be accomplished under any circumstances in which ΔH − TΔS is negative. Most exothermic changes, therefore, are spontaneous. Endothermic processes (those in which ΔH is positive) can also be spontaneous, but only if they are associated with a large positive change in entropy. This possibility was not appreciated at first by chemists. In fact, in 1879 the French thermodynamicist Marcelin Berthelot used the term affinity, defined by A = −ΔH, as a measure of the direction of positive change. According to his reasoning, a spontaneous chemical reaction could only occur if A > 0. If an endothermic reaction turned out to be spontaneous, he assumed that some unobserved mechanical work must have been done on the system. As chemists became familiar with Gibbs’s papers on thermodynamics, however, it became clear that Berthelot and others had misunderstood the concept of entropy. Affinity was a theoretical blind alley.
In summary, a thermodynamic change proceeds as long as there can be a further decrease in free energy. Once free energy has been minimized (that is, when dG = 0), the system has attained equilibrium.
Worked Problem 3.3
To illustrate how enthalpy, entropy, and temperature are related to G, consider what happens when ice or snow sublimates at constant temperature. Those who live in northern climates will recognize this as a common midwinter phenomenon. Figure 3.8 is a schematic representation of the way in which various energy functions change as functions of the proportions of water vapor and ice in a closed system. (Strictly speaking, snow does not sublimate into a closed system, but into the open atmosphere. On a still night, close to the ground, however, this is not a bad approximation.) Notice that the enthalpy of the system increases linearly as vaporization takes place. This can be rationalized by noting we have to add heat to the system to break molecular bonds in the ice. If enthalpy were the only factor involved in the process, therefore, the system would be most stable when it is 100% solid, because that is where H is minimized. Entropy, however, is maximized if the system is 100% water vapor, because the degree of system randomness is greatest there. It can be shown from statistical arguments, however, that entropy is a logarithmic function of the proportion of vapor, rising most rapidly when the vapor fraction in the system is low. Therefore the free energy of the system, G = H − TS, is less than the free energy of the pure solid until a substantial amount of vapor has been produced. Sublimation occurs spontaneously. At some intermediate vapor fraction, H − TS reaches a minimum, and solid and vapor are in equilibrium at Gmin. If the vapor fraction is increased further, the difference H − TS exceeds Gmin again, and condensation occurs spontaneously. This is the source of the beautiful hoar frost that develops on tree branches and other exposed surfaces on still winter mornings.
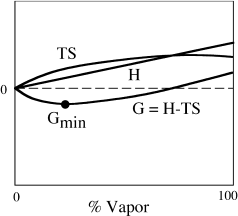
FIG. 3.8. The quantity G = H − TS varies with the amount of vapor as sublimation takes place in an enclosed container. The free energy when vapor and solid are in equilibrium is Gmin. (Modified from Denbigh 1968.)
CLEANING UP THE ACT: CONVENTIONS FOR E, H, F, G, AND S
Except in the abstract sense that we have just used G in worked problem 3.3, there is no way we can talk about absolute amounts of energy in a system. To say that a beaker of reagents contains 100 kJ of enthalpy or 55 kcal of free energy is meaningless. Instead, we compare the value of each of the energy functions to its value in a mixture of pure elements under specified temperature and pressure conditions (a standard state). For example, we would measure the enthalpy of a quantity of NaCl at 298 K relative to the enthalpies of pure sodium and pure chlorine at the same temperature and at one atmosphere of pressure, using the symbol 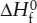 . The superscript 0 indicates that this is a standard state value and the subscript f indicates that the reference standard is a mixture of pure elements. By convention, the
. The superscript 0 indicates that this is a standard state value and the subscript f indicates that the reference standard is a mixture of pure elements. By convention, the 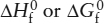 for a pure element at any temperature is equal to zero. The same notation is used for internal energy and the Helmholtz function as well, although they are less frequently encountered in geochemistry.
for a pure element at any temperature is equal to zero. The same notation is used for internal energy and the Helmholtz function as well, although they are less frequently encountered in geochemistry.
In our discussions so far, we have perhaps given the impression that whatever thermodynamic data we might need to solve a particular problem will be readily available. The references in appendix B do, in fact, include data for a large number of geologic materials. We have largely ignored the thorny problem of where they come from, however, and where we turn for data on materials that have not yet appeared in the tables. As an example of how thermodynamic data are acquired, we now show how solution calorimetry is used to measure enthalpy of formation. In chapter 10, we show how to extract thermodynamic data from phase diagrams.
It is not necessary (or even possible) to make a direct determination of 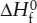 for most individual phases, because we can rarely generate the phases from their constituent elements. Instead, we measure the heat evolved or absorbed as the substance we are interested in is produced by a specific reaction between other phases for which we already have enthalpy data. Because most reactions of geologic interest are abysmally slow at low temperatures, even this enthalpy change may be almost impossible to measure directly. However, because enthalpy is an extensive variable, we can employ some sleight-of-hand: we can measure the heat lost or gained when the products and reactants are each dissolved in separate experiments in some solvent at low temperature, and then add the heats of solution for the various products and reactants to obtain an equivalent value for the heat of reaction.
for most individual phases, because we can rarely generate the phases from their constituent elements. Instead, we measure the heat evolved or absorbed as the substance we are interested in is produced by a specific reaction between other phases for which we already have enthalpy data. Because most reactions of geologic interest are abysmally slow at low temperatures, even this enthalpy change may be almost impossible to measure directly. However, because enthalpy is an extensive variable, we can employ some sleight-of-hand: we can measure the heat lost or gained when the products and reactants are each dissolved in separate experiments in some solvent at low temperature, and then add the heats of solution for the various products and reactants to obtain an equivalent value for the heat of reaction.
Worked Problem 3.4
Consider the following laboratory exercise. We wish to determine the molar enthalpy for the reaction:
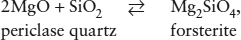
to which we assign the value Δ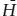 1. This can be determined by measuring the heats of solution for periclase, quartz, and forsterite in HF at some modest temperature:
1. This can be determined by measuring the heats of solution for periclase, quartz, and forsterite in HF at some modest temperature:
2MgO + SiO2 + HF ⇄ (2MgO SiO2)solution,
which gives Δ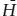 2, and:
2, and:
Mg2SiO4 + HF ⇄ (2MgO, SiO2)Solution,
which gives Δ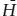 3. If the solutions are identical, we can see that the first of these equations is mathematically equivalent to the second minus the third, so that:
3. If the solutions are identical, we can see that the first of these equations is mathematically equivalent to the second minus the third, so that:
Δ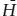 1 = Δ
1 = Δ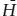 2 − Δ
2 − Δ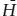 3.
3.
In this way, solution calorimetry can be used to determine the enthalpy of formation for forsterite from its constituent oxides at low temperature. As you might expect, however, solvents suitable for silicate minerals (such as hydrofluoric acid or molten lead borate) are generally corrosive and hazardous to handle. Consequently, these experiments require considerable skill and specialized equipment. Most geochemists refer to published collections of calorimetric data rather than making the measurements themselves.
What we have just described is not a measurement of 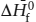 , because the reference comparison was to constituent oxides, not pure elements. If we wanted to determine
, because the reference comparison was to constituent oxides, not pure elements. If we wanted to determine 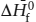 , we would search for tabulated data for reactions forming the oxides from pure elements (typically measured by some method other than solution calorimetry). Again, recalling that enthalpies are additive, we could recognize that
, we would search for tabulated data for reactions forming the oxides from pure elements (typically measured by some method other than solution calorimetry). Again, recalling that enthalpies are additive, we could recognize that 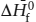 for MgO is defined by the reaction:
for MgO is defined by the reaction:
2Mg + O2 ⇄ 2MgO,
and 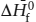 for SiO2 is defined by:
for SiO2 is defined by:
Si + O2 ⇄ SiO2.
Label these two values Δ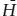 4 and Δ
4 and Δ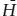 5. Therefore, for the enthalpy Δ
5. Therefore, for the enthalpy Δ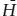 6 of the net reaction:
6 of the net reaction:
2Mg + 2 O2 + Si ⇄ Mg2SiO4,
we obtain:
Δ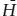 6 = Δ
6 = Δ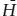 2 − Δ
2 − Δ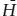 3 + Δ
3 + Δ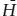 4 + Δ
4 + Δ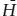 5.
5.
The value Δ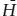 6 in this case is the enthalpy of formation for forsterite derived from those for the elements,
6 in this case is the enthalpy of formation for forsterite derived from those for the elements, 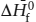 .
.
Although most thermodynamic functions are best defined as relative quantities like 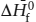 , entropy is a major exception. The convention observed most commonly is an outgrowth of the Third Law of Thermodynamics, which can be stated, in paraphrase from Lewis and Randall (1961): If the entropy of each element in a perfect crystalline state is defined as zero at the absolute zero of temperature, then every substance has a nonnegative entropy; at absolute zero, the entropy of all perfect crystalline substances becomes zero. This statement, which has been tested in a very large number of experiments, provides the rationale for choosing the absolute temperature scale (i.e., temperature in Kelvins) as our standard for scientific use. For now, the significance of the Third Law is that it defines a state in which the absolute or third law entropy is zero. Because this state is the same for all materials, it makes sense to speak of S0, rather than
, entropy is a major exception. The convention observed most commonly is an outgrowth of the Third Law of Thermodynamics, which can be stated, in paraphrase from Lewis and Randall (1961): If the entropy of each element in a perfect crystalline state is defined as zero at the absolute zero of temperature, then every substance has a nonnegative entropy; at absolute zero, the entropy of all perfect crystalline substances becomes zero. This statement, which has been tested in a very large number of experiments, provides the rationale for choosing the absolute temperature scale (i.e., temperature in Kelvins) as our standard for scientific use. For now, the significance of the Third Law is that it defines a state in which the absolute or third law entropy is zero. Because this state is the same for all materials, it makes sense to speak of S0, rather than 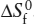 .
.
With this new perspective, return for a moment to equation 3.13. It should now be clear that the symbol Δ has a different meaning in this context. In fact, although it is rarely done, it would be less confusing to write equation 3.13 as:
Δ(ΔG) = Δ(ΔH) − TΔS,
in which the deltas outside the parentheses and on S refer to a change in state (that is, a change in these values during some reaction), and the deltas inside the parentheses refer to values of G or H relative to some reference state. We examine this concept more fully in later chapters.
Although we have not felt it necessary to prove, it should be apparent that each of the functions E, H, F, G, and S is an extensive property of a system. The amount of energy or entropy in a system, therefore, depends on the size of the system. In most cases, this is an unfortunate restriction, because we either don’t know or don’t care how large a natural system may be. For this reason, it is customary to normalize each of the functions by dividing them by the total number of moles of material in the system, thus making each of them an intensive property.
Up to now, the functions we have considered all assume that a system is chemically homogeneous. Most systems of geochemical interest, however, consist of more than one phase. The problem most commonly faced by geochemists is that the bulk composition of a system can be packaged in a very large number of ways, so that it is generally impossible to tell by inspection whether the assemblage of phases actually found in a system is the most likely one. To answer questions dealing with the stability of multiphase systems, we need to write a separate set of equations for E, H, F, and G for each phase and apply criteria for solving them simultaneously. We will do this job in two steps.
To describe the possible variations in the compositions and proportions of phases, it is necessary to define a set of thermodynamic components that satisfy the following rules:
As long as these criteria are met, the specific set of components chosen to describe a system is arbitrary, although there may often be practical reasons for choosing one set rather than another.
These rules set very stringent restrictions on the way components can be chosen, so it is a good idea to spend time examining them carefully. First, notice that the solid phases we encounter most often in geochemical situations have compositions that are either fixed or are variable only within bounds allowed by stoichiometry and crystal structure. This means that if we are asked to find components for a single mineral, they must be defined in such a way that they can be added to or subtracted from the mineral without destroying its identity. A system consisting only of rhombohedral Ca-Mg carbonates, for example, cannot be described by entities such as Ca2+, MgO, or CO2, because none of them can be independently added to or subtracted from the system without violating its crystal chemistry. The most obvious, although not unique, choice of components in this case would be CaCO3 and MgCO3.
When a system consists of more than one phase, it is common to find that some components selected for individual phases are redundant in the system as a whole. This occurs because it is possible to write stoichiometric relationships that express a component in one phase as some combination of those in other phases. For each stoichiometric equation, therefore, it is possible to remove one phase component from the list of system components and thus to arrive at the independent variables required by rule 2. It is also possible, and often desirable, to choose system components that cannot serve as components for any of the individual phases in isolation. Such a choice is compatible with the selection rules if the amount of the component in the system as a whole can be varied by changing proportions of individual phases. Petrologists usually refer to nonaluminous pyroxenes, for example, in terms of the components MgSiO3, FeSiO3, and CaSiO3, even though CaSiO3 cannot serve as a component for any pyroxene considered by itself.
Worked Problem 3.5
Olivine and orthopyroxene are both common minerals in basic igneous rocks. For the purposes of this problem, assume that olivine’s composition varies only between Mg2SiO4 (Fo) and Fe2SiO4 (Fa), and that orthopyroxene is a solid solution between MgSiO3 (En) and FeSiO3 (Fs). What components might be used to describe olivine and orthopyroxene individually, and how might we select components for an ultramafic rock consisting of both minerals?

FIG. 3.9. Olivine and pyroxene solid solutions can each be represented by two end-member components.
The simplest mineral components are the end-member compositions themselves. The end-member compositions are completely independent of one another in each mineral and, as can be seen at a glance in figure 3.9, any mineral composition in either solid solution can be formed by some linear combination of the end members. Compositions corresponding to Fo, Fa, En, and Fs, therefore, satisfy our selection rules.
A choice of FeO or MgO would not be valid, because neither one can be added to or subtracted from olivine or orthopyroxene unless we also add or subtract a stoichiometric amount of SiO2. Changing FeO or MgO alone would produce system compositions that lie off of the solid solution lines in figure 3.9.
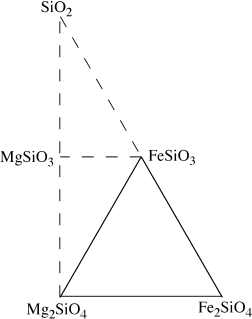
FIG. 3.10. If we choose to describe a system containing olivines and pyroxenes, we need three components. Phase compositions lying outside the triangle of system components require negative amounts of one or more components.
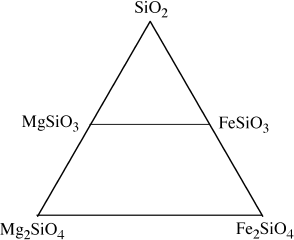
FIG. 3.11. An alternative selection of components for the system in figure 3.10. All olivine and pyroxene compositions now lie within the triangle.
If olivine and orthopyroxene are not isolated phases but are constituents of a rock, however, we need to choose a different set of components. The mineral components are still appropriate, but one of them is now redundant. We can eliminate it by writing a stoichiometric relationship involving the other three. For example:
MgSiO3 = 0.5Mg2SiO4 + FeSiO3 − 0.5Fe2SiO4.
Notice that this is only a mathematical relationship among abstract quantities, not necessarily a chemical reaction among phases. We have tried to emphasize this by using an equal sign rather than an arrow. The solid triangle in figure 3.10 illustrates the system as defined by the components on the right side.
As required by the negative amount of Fe2SiO4 in the equation above, magnesium-bearing orthopyroxenes have compositions outside of the triangle defined by the system components. There is nothing wrong with this representation, but it is awkward for most petrologic applications. A more conventional selection of components is shown in figure 3.11. The mineral compositions at the ends of the olivine solid solution are still retained as system components, but the third component, SiO2, does not correspond to either mineral in the system.
It is very important to recognize that components are an abstract means of characterizing a system. They do not need to correspond to substances that can be found in nature or manufactured in a laboratory. Orthopyroxenes, for example, are frequently described by the components MgSiO3 and FeSiO3, even though there is no natural phase with the composition FeSiO3. Monatomic components such as F, S, or O are also legitimate, even though fluorine, sulfur, and oxygen invariably occur as molecules containing two or more atoms. For some petrological applications, it makes sense to use such components as CaMg−1 which clearly do not exist as real substances. In fact, the carbonates discussed above can be characterized quite well by MgCO3 and CaMg−1, as can be seen from the stoichiometric relationship:
MgCO3 + CaMg−1 = CaCO3.
Components of this type, known as exchange operators, have been used to great advantage in describing many metamorphic rocks (Thompson et al. 1982; Ferry 1982). Because components are abstract constructions, we are not required to use them in positive amounts. Fe2O3, for example, can be described by the components Fe3O4 and Fe, even though we need to add a negative amount of Fe to Fe3O4 to do the job:
3Fe3O4 − Fe = 4Fe2O3.
Worked Problem 3.6
The ratio K/Na in coexisting pairs of alkali feldspars and alkali dioctahedral micas can be used to infer pressure and temperature conditions for rocks in which they were formed. We see how this is done in chapter 9. For now, let’s ask what selection of components might be most helpful if we were interested in K ⇄ Na exchange reactions between these two minerals.
The exchange operator KNa−1 is a good choice for a system component in this case. Feldspar compositions can be generated from:
NaAlSi3O8 + x KNa−1 = KxNa1−x AlSi3O8,
for any value of x between 0 and 1. Similarly, mica compositions can be derived from:
NaAl3Si3O10(OH)2 + yKNa−1 = Ky Na1−yAl3Si3O10(OH)2.
If we also select the two sodium end-member compositions as components, then all possible compositional variations in the system can be described. Figure 3.12a shows one way of illustrating this selection. A more subtle diagram, using the same set of components, is presented in figure 3.12b.
This is not a contrived example. We have selected it to emphasize that chemical components are abstract mathematical entities, but it is also meant to illustrate how a very common class of geochemical problems can be reconceived and simplified by choosing components creatively.
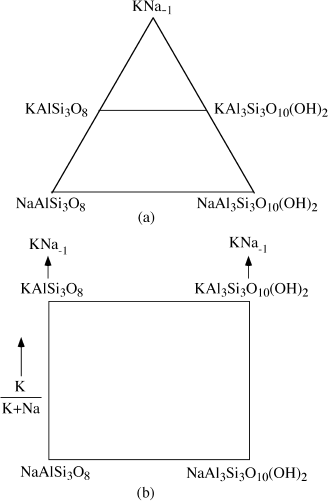
FIG. 3.12. (a) Alkali micas and feldspars can be described by a component set that includes KNa−1. (b) An orthogonal version of the diagram in (a). Its vertical edges both point to KNa−1.
CHANGES IN E, H, F, AND G DUE TO COMPOSITION
Consider an open system containing only magnesian olivine, a pure phase. The internal energy of the system is equal to E =  FonFo, where
FonFo, where  Fo is the molar internal energy for pure forsterite and nFo is the number of moles of the forsterite component in the system. Suppose that it were possible to add a certain number of moles of the fayalite component, nFa, to the one-phase system without causing any increase in energy as a result of the mixing itself. Because E is an extensive property, the internal energy of the phase would then be equal to:
Fo is the molar internal energy for pure forsterite and nFo is the number of moles of the forsterite component in the system. Suppose that it were possible to add a certain number of moles of the fayalite component, nFa, to the one-phase system without causing any increase in energy as a result of the mixing itself. Because E is an extensive property, the internal energy of the phase would then be equal to:
E = 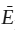 Fo nFo +
Fo nFo + 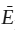 Fa nFa.
Fa nFa.
Further infinitesimal changes in the amounts of forsterite or fayalite in the system would result in a small change in E:
dE = 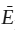 Fo dnFo +
Fo dnFo + 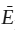 Fa dnFa.
Fa dnFa.
This differential equation can be written in the form of a total differential, from which it can be seen that:
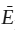 Fo = (∂E/∂nFo)nFa,
Fo = (∂E/∂nFo)nFa,
and
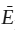 Fa = (∂E/∂nFa)nFo.
Fa = (∂E/∂nFa)nFo.
This is an idealized process, of course, chosen to demonstrate that the internal energy of a phase can be changed—in addition to the ways we have already discussed—by varying its composition. It is more realistic to recognize that the mixing process as described involves increases in both entropy and volume. Notice also that the total internal energy of the phase, E, is not a molar quantity, because it has not been divided by the total number of moles in the system. The relationships dEolivine = 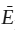 Fodn or dEolivine =
Fodn or dEolivine = 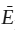 Fa dn can only be valid if the olivine is either pure forsterite or pure fayalite. In between, as we see in later chapters, dE takes a nonlinear and generally complicated form. The quantities labeled
Fa dn can only be valid if the olivine is either pure forsterite or pure fayalite. In between, as we see in later chapters, dE takes a nonlinear and generally complicated form. The quantities labeled 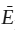 Fo and
Fo and 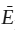 Fa above are more useful if written with these restrictions in mind:
Fa above are more useful if written with these restrictions in mind:
Ei = (∂E/∂ni)S,V,nj ≠ i.
We have now identified a new thermodynamic quantity, the partial molar internal energy, which describes the way in which total internal energy for a phase responds to a change in the amount of component i in the phase, all other quantities being equal. You may think of it, if you like, as a chemical “pressure” or a force for energy change in response to composition, in the same way that pressure is a force for energy change in response to volume. To emphasize the importance of this new function, it has been given the symbol μi and is called the chemical potential of component i in the phase.
The internal energy of a phase, then, is:
E = E(S, V, n1, n2. . ., nj).
We can rewrite equation 3.5 to include the newfound chemical potential terms:
dE ≤ TdS − PdV + μ1dn1 + μ2dn2 + . . . + μjdnj ≤ TdS − PdV +  μidni.
μidni.
In the same way, it can be shown that the auxiliary functions H, F, and G are also functions of composition:
dH ≤ TdS + VdP + μ1dn1 + μ2 + . . . + μjdnj ≤ TdS + VdP +  μidni,
μidni,
dF ≤ −SdT − PdV + μ1dn1 + μ2dn2 + . . . + μjdnj ≤ −SdT − PdV +  μidni,
μidni,
dG ≤ −SdT + VdP + μ1dn1 + μ2dn2 + . . . + μjdnj ≤ −SdT + VdP +  μidni.
μidni.
Chemical potential, therefore, can be defined in several equivalent ways:
| μi | = (∂E/∂ni)S,V,n j ≠ i (3.16a) |
| = (∂H/∂ni)S,P,n j ≠ i (3.16c) |
|
| = (∂F/∂ni)T,V,n j ≠ i (3.16b) |
|
| = (∂G/∂ni)T,P,n j ≠ i (3.16d) |
and can be correctly described as the partial molar enthalpy, the partial molar Helmholtz function, or the partial molar free energy, provided that the proper variables are held constant, as indicated in equations 3.16a–d.
CONDITIONS FOR HETEROGENEOUS EQUILIBRIUM
We are now within reach of a fundamental goal for this chapter. Having examined the various ways in which internal energy is affected by changes in temperature, pressure, or composition, we may now ask: what conditions must be met if a system containing several phases is in internal equilibrium? This is a circumstance usually referred to as heterogeneous equilibrium.
A system consisting of several phases can be characterized by writing an equation in the form of equation 3.15a for each individual phase:
dEΦ ≤ TΦdSΦ − PΦdVΦ +  (μiΦdniΦ),
(μiΦdniΦ),
where we are using the subscript Φ to identify properties with the individual phase. For example, if the system contained phases A, B, and C, we would write an equation for dEA, another for dEB, and a third for dEC. The final term of each equation is the sum of the products μidni for each system component (1 through i) for the individual phase.
It is easiest to examine the equilibrium condition among phases if we consider only the simple (and geochemically unlikely) situation in which system components correspond one-for-one with components of the individual phases. We also consider only the equilibrium conditions for an isolated system. We are doing this only for the sake of simplicity, however. We would arrive at the same conclusions if we took on the more difficult challenge of a closed or open system, or if we considered a set of system components that differ from the set of all phase components.
Because the system is isolated, we know that its extensive parameters must be fixed. That is,
| dEsys | =  dEΦ = 0 dEΦ = 0 |
| dSsys | =  dSΦ = 0 dSΦ = 0 |
| dVsys | =  dVΦ = 0 dVΦ = 0 |
| dn1,sys | =  dn1,Φ = 0 dn1,Φ = 0 |
| dn2,sys | =  dn2,Φ = 0 dn2,Φ = 0 |
 |
|
| dni,sys | =  dni,Φ = 0. dni,Φ = 0. |
There is one dni,sys equation for each component in the system. Despite these equations, there is no constraint that prevents the relative values of E, S, V, or the various n’s from readjusting themselves, as long as their totals remain zero. That is, the various individual values of EΦ, VΦ, and the ni,Φ are not independent. Whatever leaves one phase in the system must show up in at least one of the others. On the other hand, there are constraints on the intensive parameters in the system. To see what they are, let’s write an equation for the total internal energy change for the system, dEsys:

The only way to guarantee that  dEsys = 0 is for each of the terms on the right side of this equation to equal zero. We have already agreed that dS, dV, and each of the dni might differ from phase to phase. It would be a remarkable coincidence if TΦ, PΦ, and each of the μiΦ could also vary among phases in such a way that
dEsys = 0 is for each of the terms on the right side of this equation to equal zero. We have already agreed that dS, dV, and each of the dni might differ from phase to phase. It would be a remarkable coincidence if TΦ, PΦ, and each of the μiΦ could also vary among phases in such a way that  (TΦdSΦ),
(TΦdSΦ),  (PΦdVΦ), and
(PΦdVΦ), and  (
( (μiΦdniΦ)) were always equal to zero. Fortunately, we do not need to rely on coincidence. Unlike extensive properties, intensive properties are not free to vary among phases in equilibrium. We showed earlier in this chapter that this is true for temperature and pressure; at equilibrium
(μiΦdniΦ)) were always equal to zero. Fortunately, we do not need to rely on coincidence. Unlike extensive properties, intensive properties are not free to vary among phases in equilibrium. We showed earlier in this chapter that this is true for temperature and pressure; at equilibrium
TA = TB = . . . = TΦ
PA = PB = . . . = PΦ.
It should be evident now that the same is true for chemical potentials; at equilibrium
μ1A = μ1B = . . . = μ1Φ
μ2A = μ2B = . . . = μ2Φ

μiA = μiB = . . . = μiΦ.
Because this conclusion is so crucial in geochemistry, we emphasize it again: At equilibrium, the chemical potential of any component must be the same in all phases in a system. To be sure that these general results are clear, let’s examine heterogeneous equilibrium in a specific system.
Worked Problem 3.7
An experimental igneous petrologist, working in the laboratory, has produced a run product which consists of quartz (qz) and a pyroxene (cpx) intermediate in composition between FeSiO3 and MgSiO3. Assuming that the two minerals were formed in equilibrium, what conditions must have been satisfied?
To answer this question, first choose a set of components for the system. Several selections are possible, some of which we considered in an earlier problem. This time, let’s choose the end-member mineral compositions FeSiO3, MgSiO3, and SiO2. Heterogeneous equilibrium then requires that the intensive parameters be:
Tqz = Tcpx = T
Pqz = Pcpx = P
μSiO2,qz = μSiO2,cpx = μSiO2
μFeSiO3,qz = μFeSiO3,cpx = μFeSiO3
μMgSiO3,qz = μMgSiO3,cpx = μMgSiO3.
Notice that the chemical potentials of FeSiO3 and MgSiO3 are defined in quartz, despite the fact that they are not components of the mineral quartz itself, and μSiO2 is defined in pyroxene, although SiO2 is not a component of pyroxene. All three are system components. The chemical potential of any component is a measure of the way in which the energy of a phase changes if we change the amount of that component in the phase. For example, if chemical potentials are defined by equation 3.16d, the constraint on FeSiO3 should be read to mean that at constant temperature and pressure, the derivative of free energy with respect to the mole fraction of FeSiO3 is identical in pyroxene and in quartz. If it were possible to add the same infinitesimal amount of FeSiO3 to each, the free energies of the two phases would each change by the same amount:
dG = μFeSiO3 dnFeSiO3.
One final, very useful relationship can be derived from this discussion of chemical potentials. Consider equation 3.15a for a phase that is in equilibrium with other phases around it. It is possible to write an integrated form of equation 3.15a:
E = TS − PV+ μini.
μini.
Therefore, the differential energy change, dE, that takes place if the system is allowed to leave its equilibrium state by making small changes in any intensive or extensive properties is:
| dE = | TdS + SdT − PdV − VdP +  μidni μidni |
+  nidμi. nidμi. |
To see how the intensive properties alone are interrelated, subtract equation 3.15a, which was written in terms of variations in extensive parameters alone, from this equation to get:
0 = SdT − VdP +  nidμi.
nidμi.
This expression is known as the Gibbs-Duhem equation. It tells us that there can be no net gradients in intensive parameters at equilibrium. Of more specific interest in geochemical problems, at constant temperature and pressure, there can be no net gradient in internal energy as a result of composition in a phase in internal equilibrium. This can be seen, in a way, as another way of stating the conclusions from our discussion of heterogeneous equilibrium.
What is equilibrium? Our discussion of the three laws of thermodynamics has led us to discover several characteristics that answer this question. First, systems in equilibrium must be at the same temperature: this is the condition of thermal equilibrium. Second, provided that work is exclusively defined as the integral of PdV, there can be no pressure gradient between systems in equilibrium: this is the condition of mechanical equilibrium. Finally, the chemical potential of each component must be the same in all phases at equilibrium. This is the least obvious of the conditions we have discussed, and is the focus of many discussions in subsequent chapters.
We have also repackaged the internal energy function in several ways and examined the role of entropy, which will always be maximized during the approach to equilibrium. To demonstrate that each of the equilibrium criteria is a direct consequence of the three laws, we used the internal energy function, E(S, V, n), as the basis of our discussion. As we progress, though, we will quickly abandon E in favor of the Gibbs free energy. Any of the energy functions, however, can be used to clarify the conditions of equilibrium.
With the ideas we have introduced in this chapter, we are now ready to begin exploring geologic environments. This has only been a first look at thermodynamics, however. We return to the topic many times.
There are many good introductory texts in thermodynamics, although most are written for chemists rather than for geochemists. Among the best, or at least most widely used, texts for geochemists are listed here, along with excellent but challenging articles and historical accounts.
Denbigh, K. 1968. The Principles of Chemical Equilibrium. London: Cambridge University Press. (Heavy going, but almost anything you want to know is in here somewhere.)
Ferry, J. M., ed. 1982. Characterization of Metamorphism through Mineral Equilibria. Reviews in Mineralogy 10. Washington, D.C.: Mineralogical Society of America. (An enlightening selection of articles designed for classroom use. Chapters 1–4 are particularly relevant to our first discussion of thermodynamics. Be prepared to stretch.)
Fraser, D. G., ed. 1977 Thermodynamics in Geology. Dordrecht, Holland: D. Reidel. (Topical chapters showing both fundamentals and applications of thermodynamics.)
Goldstein, M., and I. F. Goldstein. 1978. How We Know: An Exploration of the Scientific Process. New York: Plenum. (The historical development of our notions of heat and temperature is discussed in chapter 4 of this thought-provoking book.)
Greenwood, H. J., ed. 1977. Short Course in Application of Thermodynamics to Petrology and Ore Deposits. Mineralogical Association of Canada. (A very readable book, with many sections of interest to economic geologists.)
Kern, R., and A. Weisbrod. 1967. Thermodynamics for Geologists. San Francisco: Freeman, Cooper. (Perhaps the simplest treatment of thermodynamics available for the geologist, although now a bit dated.)
Lewis, G. N., and M. Randall. 1961. Thermodynamics, revised by K. S. Pitzer and L. Brewer. New York: McGraw-Hill. (A classic text still in widespread use.)
Nordstrom, D. K., and J. Munoz. 1985. Geochemical Thermodynamics. Menlo Park: Benjamin Cummings. (An excellent text for the serious student.)
Smith, E. B. 1982. Basic Chemical Thermodynamics, 3rd ed. New York: Oxford University Press. (A remarkably clear text for the serious beginner.)
Thompson, J. B., J. Laird, and A. B. Thompson. 1982. Reactions in amphibolite, greenschist, and blueschist. Journal of Petrology 23:1–27. (A good study for the motivated student. Reactions in amphibole-bearing assemblages are discussed in terms of exchange operators.)
Vanserg, N. 1958. Mathmanship. The American Scientist 46: 94A–98A. (This article does not deal with thermodynamics directly, but is a commentary on the use of symbols. Its author was better known by his real name, Hugh McKinstry, professor of geology at Harvard for many years.)
(3.1) Refer to figures 3.9 and 3.10. Notice that by adding or subtracting SiO2, we change the proportions of olivine and pyroxene in a rock, but not their compositions. Changing the amount of any other system component in figure 3.9 or 3.10, however, alters both the compositions and the proportions of minerals. Can you find another set of components that includes one which, when varied, changes the compositions but not the proportions of olivine and pyroxene?
(3.2) Show that the work done by 1 mole of a gas obeying the Van der Waals equation during isothermal expansion from V1 to V2 is equal to w = RT ln([ 2 − b]/[
2 − b]/[ 1 − b] + a([1/
1 − b] + a([1/ 2] − [1/
2] − [1/ 1]).
1]).
(3.3) How much work can be obtained from the isothermal, reversible expansion of one mole of chlorine gas from 1 to 50 liters at 0°C, assuming ideal gas behavior? What if chlorine behaves as a Van der Waals gas? Use the result of problem 3.2; a = 6.493 l2 atm mol−2, b = 0.05622 l mol−1.
(3.4) What is the maximum work that can be obtained by expanding 10 grams of helium, an ideal gas, from 10 to 50 liters at 25°C? Express your answer in (a) calories, (b) joules.
(3.5) Suppose that a mixture of two inert gases is divided into two containers separated by a wall. Imagine a microscopic valve placed in the wall that allows molecules of one gas to move into container A and molecules of the other gas to move into container B, but does not allow either gas to move in the opposite direction. Such an imaginary device is called Maxwell’s demon. How would such a device violate the Second Law of Thermodynamics?
(3.6) What conditions must be satisfied if hematite, magnetite, and pyrite are in equilibrium in an ore assemblage?
(3.7) Construct a triangular diagram for the alkali feldspar-mica system similar to figure 3.12a, but in which you swap the positions of NaAl3Si3O10(OH)2 and KAlSi3O8. What component must now take the place of KNa−1 at the top corner of the diagram? Where would this component have been plotted on figure 3.12a? Where does KNa−1 plot on your diagram?
(3.8) Using the Maxwell relations, verify that −(∂V/∂T)P/(∂P/∂T)V = (∂V/∂P)T.