
 |
|
This is a chapter about solutions, important to us because most geological materials have variable compositions. They are, in fact, mixtures at the submicroscopic scale between idealized end-member substances such as albite, water, grossular, dolomite, or carbon dioxide, which lose their molecular identities in the mixture. To see how thermodynamics can be used to predict the equilibrium state in a system dominated by phases with variable compositions, we examine first the structure of solutions of solids, liquids, and gases, and discuss ways in which this architecture is reflected in mole fractions of end-member components.
At the end of chapter 3, we developed thermodynamic equations that describe the state of equilibrium for a heterogeneous system. Among these equations are constraints implying that the compositions of phases in equilibrium are controlled by the system’s overall drive toward a minimum ΔG. As we study the structure of solutions in this chapter, we look explicitly at the compositions of phases in equilibrium and apply the thermodynamic principles from chapter 3. Specifically, we begin to develop equations that relate mole fractions and other mixing parameters (which we introduce) to ΔG.
The results of this investigation can be applied to many problems in the realm of geochemistry. We begin applying them in this chapter by studying aqueous fluids and the phenomenon of solubility. This study not only presents an opportunity to use the equations we develop, but also prepares the way for our later discussions of the oceans, diagenesis, and weathering reactions.
Most phases of geochemical interest do not have fixed compositions. With the conspicuous exception of quartz, each of the major rock-forming minerals is a solid solution between two or more end-member molecules. The range of allowable compositions in any solution is dictated by rules of structural chemistry that consider both crystal architecture and the size and electronic configuration of ions. For many minerals, these rules permit liberal replacement of iron by magnesium or calcium, sodium by potassium, or silicon by aluminum. At first glance, the degree of flexibility that we observe in mineral compositions looks random. It seems to spoil any hope that we might be able to apply thermodynamic principles to geologic materials. Liquids and gases follow even fewer structural guidelines and have even more variable compositions. Can the principles of equilibrium thermodynamics we have just explored in chapter 3 make sense in the more complicated world of these real phases? To answer, we first need to know more about solutions.
Most geologically important materials are crystalline solids; that is, solids in which atoms are arranged in a periodic three-dimensional array that maintains its gross structural identity over fairly large distances. A “fairly large” distance is not easily defined, however. If we see a mineral grain in thin section that has continuous optical properties, it is clearly large enough. Even submicroscopic grains are judged to be crystalline if their structures are continuous over distances sufficient to yield an X-ray diffraction pattern. We can get reliable results from thermodynamic calculations for most geochemical purposes if the materials we study are crystalline at this scale. We can still apply principles of thermodynamics at smaller scales, but the rules become more complex. In very fine-grained crystalline aggregates, for example, surface properties make a major contribution to free energy. In highly stressed materials, too, dislocations or defects constitute a significant volume fraction of the material and call for special methods. Finally, intimately intergrown materials, such as those in figure 4.1, in which two or more phases are structurally compatible and randomly intermixed, are difficult to model. We take a look at some of these special cases in chapter 10, but for now we stick with crystalline materials that have uniform properties over distances of thousands of unit cell repeats.

FIG. 4.1. High-resolution transmission electron microscope (HRTEM) image of an intergrowth of ortho- and clinopyroxenes. This material is crystalline, but the identity of the structural unit changes after a random, rather small number of repeats (arrows). Thermodynamic characterization of such material is very difficult.
The rules that dictate where atoms sit in a crystalline substance are quite flexible. Two major factors govern which atoms may occupy a given site: their ionic charges and their sizes. Charge is important because of the need to obtain electrical neutrality over the structure. Size is important because it influences the degree of “overlap” between the orbitals of valence electrons of the ion and those that surround it. Recall our discussion of these principles in chapter 2 and scrutinize figure 2.11 again. You will find that several ions available to a growing crystal will satisfy these constraints. In addition, the charge balance requirement can be satisfied by the formation of randomly distributed vacancies or by inserting ions into defects or into positions that are normally unoccupied. Local charge imbalances caused when an inappropriately charged ion occupies a site, therefore, can be averaged out over the structure as a whole. As a result, minerals are most properly viewed as crystalline solutions in which many competing ions substitute freely for one another. We must consider both the bulk composition of a solution and the way in which it is mixed as we describe it with thermodynamics.
To illustrate, let us compare two possible mixing schemes, using the clinopyroxene solid solution CaMg-Si2O6 (diopside)-NaAlSi2O6 (jadeite) as an example. First, take a look at figure 4.2 as we do a quick overview of pyroxene structural chemistry. The atoms in silicates are arranged so that each silicon is surrounded by four oxygens to form a tetrahedral unit with a net electrical charge of −4. These are connected to each other and to other atoms by bonds that are largely ionic in nature. The manner in which the units are linked together, and the identity of other atoms that occupy sites between them, determine the mineral’s structure and establish its bulk chemical identity. (Review our discussion of coordination polyhedra in chapter 2.) In a pyroxene, SiO4 tetrahedra are linked by corners to form long single chains. Diopside and jadeite are C2/c pyroxenes, in which cations occupy two other types of sites, designated M1 and M2, between these chains. M1 is surrounded by six oxygens and is nearly a regular octahedron. It is occupied by the relatively small cations Mg2+ and Al3+. The M2 site is eight-coordinated, 20–25% larger, and irregular in shape. Ca2+ and Na+, relatively large cations, prefer this site. For a detailed but very readable description of pyroxene crystal chemistry, see the articles by Cameron and Papike (1980, 1981).

FIG. 4.2. The crystal structure of C2/c pyroxene, showing the geometry of M1 and M2 cation sites, each of which is surrounded by six oxygen atoms, and their relationship to tetrahedral (T) sites, which are largely occupied by silicon atoms. This diagram, a projection onto the (100) crystallographic plane, is drawn to emphasize the geometry of cation sites. (Modified from Cameron and Papike 1981.)
So much for the general context. Now, if we consider only the pure end-member pyroxenes, we should have no trouble figuring out how sites are occupied, because there is only one type of cation available for each site. Once we investigate intermediate compositions, however, two possible cation arrangements suggest themselves. The first, called molecular mixing, assumes that charge balance is always maintained over very short distances. That is, calcium and magnesium ions substitute for sodium and aluminum ions as a coupled pair: each time we find a Ca2+ in an M2 site, there is a Mg2+ in an adjacent M1 site. The end-member pyroxenes mix as discrete molecules and complete short-range order results. In this case, the mole fraction of CaMgSi2O6 in the solid solution (XCaMgSi2O6,cpx) is equal to the proportion of the diopside molecule present. Until recently, molecular mixing was widely assumed by petrologists.
The other possibility, known as mixing on sites, assumes that Ca2+ and Na+ are randomly distributed on M2 sites, unaffected by whether adjacent M1 sites are filled with Mg2+ or Al3+ ions. This style of mixing may produce local charge imbalances, but the average stoichiometry is satisfied over long distances even in the absence of short-range order. Because each of the sites, according to this model, behaves independently of the others, we must now calculate the mole fraction XCaMgSi2O6,cpx as the product of XCa,M2,cpx and XMg,M1,cpx. This follows from a basic principle of statistics: if the probability of finding a Mg2+ ion in M1 is some value x and the probability of finding a Ca2+ in M2 is y, then the combined probability of finding both ions in the structure is xy. Thus, if 80% of the ions in the M1 site are Mg2+ and 80% of the M2 atoms are Ca2+, XCaMgSi2O6,cpx is equal to 0.64. If the tetrahedral site were partially occupied by something other than silicon, we would have to multiply by XSi,T,cpx as well.
How can we tell which of these two mixing models is the correct one? It is logical to infer that the degree of randomness among atoms distributed on M1 and M2 affects the molar entropy of a phase, and therefore each of the energy functions E, H, F, and G. In theory, then, it should be possible to use these two extreme models to calculate the relative stabilities of clinopyroxene solutions and see which one matches what we see in the natural world. To do this requires calculating bond energies from electrostatic equations and detailed crystallographic data. Large-scale computer models exist for this purpose, but are successful only with very simple structures. Ronald Cohen (1986), however, has done the next best thing. By evaluating a large body of calorimetric data and phase equilibrium studies for aluminous clinopyroxenes, he concluded that the macroscopic behavior of pyroxene solid solutions provides no observational justification for molecular mixing. His conclusions suggest that other common silicate solutions (feldspars, micas, amphiboles) behave similarly. Unless crystallographic evidence suggests otherwise, therefore, we may assume that mixing takes place on sites.
This is a significant finding. It is not the end of the discussion about how to model clinopyroxenes, however. We have assumed that each of the cations occupies only one type of site, for example. In fact, this is not the case. Although Mg2+ prefers the smaller M1 site, it may also be present in M2. Fe2+ and Mn2+ may also be found in either M1 or M2. Other possible complications include the stabilizing effect felt by certain transition metal cations as a result of site distortions (more about this in chapter 12) and the degree of covalency of bonds in the structure (refer again to chapter 2). Because we generally have no way of testing each of these effects directly, thermodynamic interpretation of crystalline solutions is an empirical process, based largely on the macroscopic behavior of materials. Models of site occupancy rely strongly on observations made by spectroscopic and X-ray diffraction methods, and on our understanding of the rules of crystal chemistry that govern element partitioning. These still leave considerable uncertainty, so most calculations can only be performed by making simplifying assumptions.
Worked Problem 4.1
To illustrate how we can calculate mole fractions in a disordered mineral structure, consider the following analysis of a C2/c omphacite (pyroxene), which was first reported by Clark et al. (1969). The abundances are recorded as numbers of cations per six oxygens in the clinopyroxene unit cell. (The analysis in Clark et al. [1969] also includes 0.002 Ti3+, which we have omitted for simplicity. Including Ti3+ would change the contents of the M1 site slightly.)
| Atom | Abundance |
|---|---|
| Si | 1.995 |
| Al | 0.238 |
| Fe3+ | 0.123 |
| Fe2+ | 0.116 |
| Mg | 0.582 |
| Ca | 0.583 |
| Na | 0.325 |
To estimate the site occupancy, we first assume that all tetrahedral sites are filled with either Si or Al (the only two atoms in the analysis that regularly occupy tetrahedral sites). Because the ratio of tetrahedral cations to oxygens in a stoichiometric pyroxene should be 2/6, we see that 0.005 Al must be added to the 1.995 Si to fill the site. An alternative, which might also be justifiable, is to assume that Si is the only tetrahedral cation, and simply normalize the Si in the analysis to 2.00.
Of the remaining cations, we may assume that Ca and Na (both of which are large) are restricted to the M2 site, whereas Al and Fe3+ (both relatively small) prefer the more compact M1 site. X-ray structure refinement by Clark et al. indicates, further, that the ratio Fe/Mg in M1 is 0.40 and in M2 is 0.54. Using these pieces of information, we proceed as follows:
 M1) is, therefore,
M1) is, therefore,
 M1 = (Al) + (Fe3+) + x + y = 0.233 + 0.123 + 0.092 + 0.538 = 0.986.
M1 = (Al) + (Fe3+) + x + y = 0.233 + 0.123 + 0.092 + 0.538 = 0.986.
The total cation abundance in M2  M2), similarly, is:
M2), similarly, is:
 M2 = (Ca) + (Na) + (0.116 − x) + (0.582 − y) = 0.583 + 0.325 + 0.024 + 0.044 = 0.976.
M2 = (Ca) + (Na) + (0.116 − x) + (0.582 − y) = 0.583 + 0.325 + 0.024 + 0.044 = 0.976.
 M1 or 1/
M1 or 1/ M2 to get:
M2 to get:
One way to model this pyroxene is to choose likely molecular end members such as NaAlSi2O6 (jadeite), CaMgSi2O6 (diopside), NaFe3+Si2O6 (aegirine), among others. We might then calculate mole fractions of each on the assumption that an M1 site occupied by Al is always adjacent to an M2 site containing Na, an M2 occupied by Na is either adjacent to an Al or an Fe3+ in M1, and so forth. We have just argued that molecular mixing is generally a poor way to proceed, however. Instead, if we wish to consider a reaction in which the NaAlSi2O6 component of this pyroxene is involved, we calculate its mole fraction as the cumulative probability of finding both Al and Na at random on their respective sites:
XAl,M1,cpxXNa,M2,cpx = (.236)(.333) = 0.079.
Likewise,
XAeg,cpx = XFe3+,M1,cpxXNa,M2,cpx = (.125)(.333) = 0.042,
and
XDi,cpx = XMg,M1,cpxXCa,M2,cpx = (.546)(.598) = 0.327.
Glasses and other amorphous geological materials have structures that differ from crystalline materials only in their degree of coherency. An amorphous solid has no long-range structural continuity but may still consist of numerous very small-scale ordered domains. Many of the concerns we had about mixing in crystalline solids are therefore also valid for amorphous materials. Their greatest importance for geochemists, however, is that they provide a conceptual bridge toward our understanding of liquids.
The only geologically significant melt systems that we understand in any detail are silicate magmas. Our knowledge of silicate melt structures has been acquired primarily since the late 1970s, with the help of improved X-ray diffraction and spectroscopic methods. Geochemists now understand that silicon and oxygen atoms continue to associate in SiO4 tetrahedral units beyond the melting point, and that the units tend to form polymers. Depending on the composition of the melt, these units may be chain polymers similar to the ones found in pyroxenes, or they may be branched structures of various sizes—the remnants (or precursors) of sheet and framework crystalline structures.
The degree of polymerization depends on temperature, but is most strongly influenced by the proportion of network-formers such as silicon and aluminum and network-modifiers such as Fe2+, Mg2+, Ca2+, K+, and Na+. In silica-rich melts, the highly covalent nature of the Si-O bond tends to stabilize structures in which a large number of oxygen atoms are shared between SiO4 units. As a result, these melts are highly viscous and have low electrical conductivities. Adding even a small proportion of Na2O or another network modifier, however, reduces viscosity drastically and increases melt conductivity. As in crystalline silicates, the bonds between oxygen and the larger cations are ionic. These break more easily than the Si-O bonds, thus reducing the melt’s overall tendency to form large, tenacious polymeric structures. Water also acts as a network modifier in silicarich melts, apparently by reacting with the bridging oxygens in a polymer. This reaction may be described generically by:
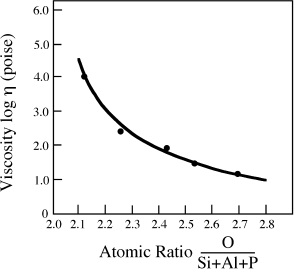
FIG. 4.3. Relationship between melt viscosity and composition at 1150°C. The variable on the horizontal axis is the atomic ratio of oxygen atoms to network-formers (Si + Al + P). The filled circles represent compositions of natural magmas.

Figure 4.3 illustrates the degree to which melt structure influences thermodynamic properties by showing the qualitative relationship between viscosity and composition.
Worked Problem 4.2
Before much of the modern experimental work to examine to relationship between melt structure and viscosity was begun, Jan Bottinga and Daniel Weill (1972) developed a simple empirical method for predicting melt viscosity. They noted that the natural logarithm of viscosity (η) may be approximated by a function of composition that is linear within restricted intervals of SiO2 content. Specifically, they showed that the empirical coefficients Di in the equation:
ln η= XiDi
XiDi
are constants at a given temperature and a given value of XSiO2.
In the table below are values of Di at 1400°C for melts with two different silica contents, calculated statistically by Bottinga and Weill from the measured viscosities of a large number of silicate melts. Notice from the arithmetic signs on Di that some melt components tend to increase viscosity (that is, they act as network-formers), whereas others tend to decrease it (by acting as network-modifiers). Notice also that some components, such as FeO, behave differently in silica-rich melts than in silicapoor ones.

To illustrate this method, we consider two different melt compositions, a granite and a diabase. For each, we have tabulated a bulk analysis in weight percentage of oxides and a recalculated analysis in mole percentage. In the recalculation, all iron has been converted to FeO, phosphorus has been added to SiO2, water has been omitted (a serious omission, but at least we can compare anhydrous melt viscosities this way), and the total has been adjusted to 100 mole percent.

For the granite,
| ln η = |  XiDi = (.8013)(10.5) + (.0038)(−3.61) XiDi = (.8013)(10.5) + (.0038)(−3.61) |
| + (.0183)(6.17) + (.0011)(−6.41) | |
| + (.0102)(−2.23) + (.0047)(−4.82) | |
| + (.0241)(−1.74) + (.0768)(15.1) | |
| + (.0597)(15.1) = 10.48 |
η = 3.56 × 104 poise = 3.56 × 103 kg m−1 sec−1.
For the diabase,
| ln η = |  XiDi = (.5845)(9.25) + (.0126)(−4.26) XiDi = (.5845)(9.25) + (.0126)(−4.26) |
| + (.1083)(−6.64) + (.0019)(−5.41) | |
| + (.0995)(−4.27) + (.0476)(−5.54) | |
| + (.0628)(−0.22) + (.0685)(7.48) | |
| + (.0143)(7.48) = 4.54 |
η = 9.37 × 101 poise = 9.37 kg m−1 sec−1.
To an even greater extent than is true for crystalline solids, our limited understanding of melt structures makes it impossible to calculate thermodynamic quantities from models that consider the potential energy contributions of individual atoms. Enthalpies and free energies of formation for melts are determined on macroscopic systems, and therefore represent an average of the contributions from an extremely large number of local structures. Thermodynamic models that make simple assumptions about how mixing takes place between melts of different end-member compositions are surprisingly successful, but tend to be more descriptive than predictive. We discuss these more fully in chapter 9.
An electrolyte solution is one in which the dissolved species (the solute) are present in the form of ions in a host fluid that consists primarily of molecular species (the solvent). In the geological world, these are usually aqueous fluids, although CO2-rich solvents may be increasingly important with increasing depth in the crust and upper mantle. Electrolyte solutions do not exhibit the large-scale periodic structures found in either melts or solids. The ions and solvent molecules, however, cannot generally be treated as a mechanical mixture of independent species. Electrostatic interactions among solute and solvent species place limits on the concentration of free solute ions and can produce complexes that influence the thermodynamic behavior of a solution. These effects are most obvious as the concentration of dissolved species increases and require a rather complicated mathematical treatment. Many of the later sections of this chapter are devoted to understanding the behavior of aqueous electrolyte solutions.
Gases at low pressure mix nearly as independent molecules. In this way, they are perhaps the simplest of geologic materials and therefore the best to study initially. Except for transient species in high-energy environments, most gas species are electrically neutral. Their neutrality and the relatively large distances between molecules at low pressure allow us to treat atmospheric and most volcanic gases as mechanical mixtures. As such gas mixtures interact with other geological materials (say, in weathering reactions), the thermodynamic influence of each of the individual gas species is directly proportional to its abundance in the mixture. Only at elevated pressures do gas molecules interfere with each other and begin to alter the thermodynamic behavior of the mixture.
For each type of solution we have considered in this brief discussion, there is some range of composition, pressure, and temperature over which the end-members mix as nearly independent species. For many, this range is distressingly narrow, but it provides us with a simplified system from which we can extrapolate to examine the behavior of “real” solutions. When the end-member constituents of solutions act nearly as if they were independent, we refer to their behavior as ideal.
In this section and the following one on nonideal solutions, we begin with a discussion of gases. This is done partly because gases are found in every geological environment, but largely because their behavior is the easiest to model.
We have already seen (equation 3.11) that the Gibbs free energy for a one-component system can be written as G(T, P). In differential form:
dG = − SdT + VdP.
Furthermore, dG can be recognized as dG = ndḠ = ndμ. Suppose we are interested in the difference in chemical potential between some reference state for the system (for which we will continue to use the superscript 0) and another state in which temperature or pressure is different. To extract this information, we must integrate dG between the two states:

The integration, unfortunately, is harder than it looks. We can move the variable n outside of the integrals for Ḡ and μ because the amount of material in a system is not a function of its molar free energy. We could not do the same with S or V, however, because they are, respectively, functions of T and P. To make the problem solvable, we need to supply S(T) and V(P). The first of these is difficult enough to define that we will avoid it for now by declaring that we are only interested in isothermal processes. In this chapter, therefore, the integral of SdT is equal to zero. Later, in chapter 9, we consider temperature variations.
The pressure-volume integral is easier to handle. The function V(P) is obtained from an equation of state, the most familiar of which is the ideal gas equation: V = nRT/P. The integral equation for an isothermal ideal gas, therefore, reduces to:

If we do the integration, we see that:
μ −μ0 = RT ln(P/P0).
It is standard practice to choose the reference pressure as unity, so that this equation takes the form
μ = μ0 + RT ln P.
Notice that because P in equation 4.1 really stands for P/P0, it is a dimensionless number. We have now derived an expression for the chemical potential of a single component in a one-component ideal gas at a specified temperature and pressure.
Next, consider a phase that is a multicomponent mixture of ideal gases. There must be a stoichiometric equation that describes all of the potential interactions between gas species in the mixture:
vj+1Aj+1 + . . . + vi−1Ai−1 + viAi = v1A1 + v2A2 + . . . + vjAj.
This is a standard equation that you have seen many times, but the notation may look a little strange, so let’s pause to explain it. We keep track of each gas species by associating it with a unique subscript. Subscripts 1 through j refer to product species and j + 1 through i refer to reactants. The quantities v1 through vi are stoichiometric coefficients and A1, A2, A3, . . ., Ai are the individual gases. If the gas were a two-component system of carbon and oxygen species, for example, and if we were to ignore all possible species except for CO2, CO, and O2, then the stoichiometric equation would be

The species CO, O2, and CO2 here are A1, A2, and A3, and the stoichiometric coefficients are ν1 = ν2 = 1 and ν3 = 0.5. We use this notation in stoichiometric equations throughout the rest of this book.
Returning now to the gas mixture, we find that the expanded form of equation 3.11 to describe variations in free energy looks like:
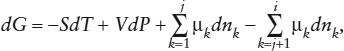
in which the chemical potentials are properly defined as partial molar free energies (equation 3.16d):
μi = (∂G/δni)T,P,nj≠i = Ḡi.
The summation terms in equation 4.2 do not contradict equation 3.15d, where positive and negative compositional effects on free energy were combined implicitly in a single term. Here, we separate them explicitly merely to emphasize that quantities associated with product species (1 through j) are meant to be added to the free energy of the system; those associated with reactant species (j + 1 through i) are subtracted.
If you have been following this discussion closely, it might bother you that we said we would use the subscript i in stoichiometric equations to identify real chemical species and have now reverted to the convention of using i to identify components. As we have emphasized before, the relationship between species and components is one of the hardest concepts in this book to understand, so we encourage you to re-examine the final sections of chapter 3 if you are confused. The practice of using i in equation 4.2 to count species implies that there are stoichiometric equations that relate species compositions to system components. For example, if we were describing the two-component system of carbon and oxygen species it would be fair to incorporate μCO, μO2, and μCO2 in equation 4.2, even though only two of the quantities CO, O2, and CO2 can be system components. The parallel to the stoichiometic equation 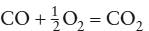 is a Gibbs-Duhem equation (3.17), which assures us that at equilibrium μCO + 0.5μO2 = μCO2. The individual quantities dni in equation 4.2, in other words, are not independent, but are tied to the stoichiometric coefficients vi and related to each other by:
is a Gibbs-Duhem equation (3.17), which assures us that at equilibrium μCO + 0.5μO2 = μCO2. The individual quantities dni in equation 4.2, in other words, are not independent, but are tied to the stoichiometric coefficients vi and related to each other by:
| (dn1/ν1) | = (dn2/ν2) = . . . = (dnj/νj.) = −(dnj+1/νj+1) |
| = . . . = −(dni−1/νi−1) = − (dni/νi) = dζ. |
The important point here is that changes in the amount of each species in the system are proportional by a common factor to their stoichiometric coefficients in the reaction. That factor, dζ, is a convenient measure of how far a reaction among species has proceeded.
With the insight that vi = dni/dζ, we can rewrite equation 4.2 at constant T and P as:

We have just derived a very useful quantity,
ΔḠr = dG/dζ,
known as the free energy of reaction or the chemical reaction potential. At equilibrium, it has the value zero. If ΔḠr < 0, then the reaction proceeds to favor the product species; if ΔḠr > 0, then the reaction is reversed to favor reactant species. This is a quantitative explanation of LeChatlier’s Principle, which states that an excess of species involved on one side of a reaction causes the reaction to proceed toward the opposite side.
Because this is still a discussion of ideal gas mixtures, the equation of state for the gas phase remains V = nRT/P, but the total amount of material in the system, n, is now equal to the sum of the amounts of species, ni. The pressure exerted by any individual species in the mixture is, therefore, a partial pressure, defined by:
Pi = niRT/V = Pni/n = PXi.
For each species in a gas mixture, then, we can write an expression like equation 4.1:
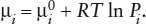
For the mixture as a whole, equations 4.3 and 4.4 tell us that the free energy of reaction can be divided into two parts, one of which refers to the free energy in some standard state (often one in which solutions with variable compositions consist of a limiting end member) and the other of which tells us how free energy changes as a result of compositional deviations from the standard state.
In summary, the free energy of reaction is written as:

If the gas phase is in internal (homogeneous) equilibrium, then ΔḠr = 0 and:

or
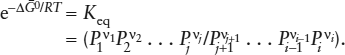
The new term, Keq, is called the equilibrium constant, and equation 4.6 is the first answer to our question: “What controls the compositions of phases at equilibrium?”
It is time to apply what we have discussed to a specific example.
Worked Problem 4.3
The Soviet Venera 7 planetary probe measured the surface temperature on Venus to be 748 K and determined that the total pressure of the atmosphere is 90 bar. The Pioneer Venus mission, which parachuted four probes to the surface in 1978, determined that the lower atmosphere consists of 96% CO2 and contains 20 ppm of CO. Other gases in the atmosphere (primarily N2) have a marginal effect on chemical equilibria in the C-O system. Given these data and assuming that CO2, CO, and O2 behave as ideal gases, what should be the partial pressure of O2 at the surface of Venus?
The first step is to write a balanced chemical reaction among the species:

Equation 4.6 for this example, then, should be written:

We can calculate the value of Δ(Ḡ0 from the standard molar free energies of formation of each of the reactant and product species from the elements at 475°C (748 K):

The value of Keq, therefore, is:
Keq = exp[52.022 kcal mol−1/(0.001987 kcal deg−1 mol−1) (748 K)] = 1.59 × 1015.
From this and the expression for Keq, we calculate that:
PO2 = (PCO2/Keq PCO)2 = (86.4 bar/(1.59 × 1015)(.00002)(90 bar))2 = 9.11 × 10−22 bar.
This quick “back of the envelope” answer is consistent with what we know from observations: the amount of free oxygen in Venus’s atmosphere is below the detection limits of our planetary probes. Except as an example of how to use Keq, however, you should not take this numerical result very seriously. Several other factors would need to be considered if we were to attempt a rigorous calculation, including equilibria involving solid silicate and carbonate minerals in the Venusian crust.
With only small modifications, this derivation for gaseous systems can yield a similar expression that can be used for ideal liquid or solid solutions. If we stipulate that both pressure and temperature are constant for these solutions, then:
dPi = d(PXi) = P dXi.
The equation analogous to 4.4 is therefore:

and the free energy of reaction is:

The superscript * on both μ* and ΔḠ* is a reminder that each is a function of temperature and pressure, unlike μ0 and Δ(Ḡ0, which depend only on temperature. When we discuss the effects of pressure on mineral equilibria in chapter 9, we will see that it is necessary to add an extra term to the free energy equations for solid and liquid phases to allow for compressibility. For gases, that adjustment is made in the RT ln Keq term.
Because equations 4.5 and 4.8 are similar in form, they can be combined to formulate a general equation relating the compositions of several ideal solutions or gas mixtures in a geochemical system to their molar free energies:

Each of the free energies, mole fractions, and partial pressures should be understood to carry a subscript to identify the phase to which they refer. For example, the mole fraction of CaAl2Si2O8 in plagioclase should be shown as XCaAl2Si2O8,Pl. Except where they are necessary to avoid ambiguity, however, we usually follow standard practice and omit phase subscripts. Let’s try a problem involving both a gas phase and condensed phases to see how equation 4.9 works in practice.
Worked Problem 4.4
During greenschist facies metamorphism (∼400°C), rocks containing crysotile, calcite, and quartz commonly react to form tremolite, releasing both CO2 and water. Assume, for the moment, that calcite is pure CaCO3, that the other two solids are pure magnesian end members of crystalline solutions, and that water and CO2 mix as an ideal gas phase. This reaction is strongly affected by total pressure, and we have not yet discussed adjustments for pressure. Suppose, however, that you tried to simulate this reaction by heating crysotile, calcite, and quartz to 400°C in an open crucible. What would ΔḠr be under these circumstances?
The balanced reaction for this example is:
5 Mg3Si2O5(OH)4 + 6 CaCO3 + 14 SiO2 ⇄ 3 Ca2Mg5Si8O22(OH)2 + 6 CO2 + 7 H2O.
Data relevant to this problem are available in Helgeson (1969):

The partial pressure of CO2 in the atmosphere is ∼3.2 × 10−4 atm, and the partial pressure of H2O, although variable, is ∼1 × 10−2 atm. If the crucible is open to the atmosphere and mixing is rapid, then these partial pressures should remain roughly constant.
The molar free energy of reaction can be calculated from:
ΔḠr = Δ 0 − TΔ
0 − TΔ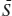 0 + RT ln Keq,
0 + RT ln Keq,
in which:
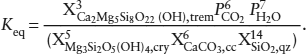
From the data above, we calculate:
Δ 0 = 0 = |
3(−2894140) + 6(−87451) + 7(−54610) |
| − 5(−1012150) − 6(−279267) − 14(−212480) | |
| = 121256 cal mol−1 |
Δ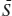 0 0 |
= 3(258.8) + 6(65.91) + 7(51.97) − 5(118.55) |
| − 6(41.65) − 14(20.87) = 399.32 cal deg−1 mol−1. |
Because we assumed that the solid phases have end-member compositions, each of the mole fractions is equal to one. To reach the final answer, then, we calculate:
ΔḠr = 121256 − 673(399.32) + 1.987(673)[6 ln(3.2 × 10−4) + 7 ln(1 × 10−2)] = −255161 cal mol−1.
The reaction, therefore, favors the products under the conditions specified. We should expect CO2 and water vapor to be released from our open crucible.
Suppose that we performed the same experiment, but used an impure calcite with a composition (Ca0.8Mn0.2CO3). How would you expect the free energy of reaction to change, assuming that Ca-Mn-calcite behaves as an ideal solid solution?
The expressions for ΔḠr and Keq remain the same, as do the values for Δ 0 and Δ
0 and Δ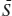 0. The mole fraction of CaCO3 in calcite is no longer 1.0, however, so the value of (−6 ln XCaCO3) is no longer zero. We find, now, that:
0. The mole fraction of CaCO3 in calcite is no longer 1.0, however, so the value of (−6 ln XCaCO3) is no longer zero. We find, now, that:
| ΔḠr | = 121256 − 673(399.32) + 1.987(673) |
| (6 ln(3.2 × 10−4) + 7 ln(1 × 10−2) − 6 ln(0.8) | |
| = −253371 cal mol−1. |
The reaction still favors the products, but ΔḠr has increased by 1790 cal mol−1.
SOLUTIONS THAT BEHAVE NONIDEALLY
In many cases, it is appropriate to assume that real gases follow the ideal gas equation of state. More generally, however, interactions between molecules force us to modify the ideal gas law by adding correction terms to adjust for nonideality. Before we worry about the precise nature of these adjustments, let us illustrate how nonideality complicates matters by writing the corrected equation of state as a generic power function:
PV = RT + BP + CP2 + DP3 + EP4 + . . .,
in which the coefficients B, C, D, and so forth are empirical functions of T alone. Assuming isothermal conditions and following the procedure by which we derived equation 4.1, we now get:
μ = μ0 + RT ln P + B(P − 1) + C(P2 − 1)/2 + . . . .
This is a clumsy equation to handle, particularly if we are headed for a generalized form of equation 4.9, and it is only valid for the empirical equation of state we chose. The way we avoid this problem is to repackage all the terms containing P and introduce a new variable, f, so that:
μ = μ0 + RT ln(f /f0).
This new quantity is known as fugacity, and it will serve in each of the equations as a “corrected” pressure; that is, as a pressure which has been adjusted for the effects of nonideality. Notice that equation 4.10 is identical in form to equation 4.1. The reference fugacity, f0, used for comparison is usually taken to be the fugacity of the pure substance at 1 atmosphere total pressure and at a specified temperature. (A variety of standard states are possible. For any given problem, the one we choose is partly governed by convenience and partly by convention. In chapter 9, we discuss a number of alternate standard states.) For a pure (one-component) gas, f0 = P0 = 1 atm. The ratio f/f0 is given the special name activity, for which we use the symbol a. The activity of a gas is, therefore, a dimensionless value, numerically equal to its fugacity.
We have certainly made the integrated power function look simpler, but this is an illusion because we have only redefined variables. We have not improved our understanding of nonideal gases unless we can evaluate fugacity. To do this, we differentiate equation 4.10 with respect to P at constant temperature:
(∂μ/∂P)T = RT (∂ ln a/∂P)T.
(Remember that μ0 is a function of T only, so that (∂μ0/∂P)T is equal to zero.) This can be recast another way by recalling from equation 3.11 that (∂μ/∂P)T = (∂Ḡ/∂P)T=  , so that:
, so that:
RT d ln a =  dP.
dP.
Subtract the quantity RT d ln P from both sides to get:
| RTd ln(a/P) | =  dP − RT d ln P dP − RT d ln P |
= ( − [RT/P])dP, − [RT/P])dP, |
and then integrate the result between the limits zero and P. This procedure yields the expression:
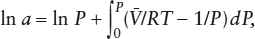
which is just what we were looking for. The adjustment for nonideality is expressed as an integral that can be evaluated by replacing  with an appropriate equation of state,
with an appropriate equation of state,  (P). Notice that if
(P). Notice that if  (P) = RT/P (the ideal gas equation), then the integral has the value zero at any pressure. The quantity:
(P) = RT/P (the ideal gas equation), then the integral has the value zero at any pressure. The quantity:

defines the activity coefficient, γ, which is equal to the ratio a/P.
Activities of species in nonideal gas mixtures are defined the same way we followed in deriving equation 4.5, except that all partial pressures Pi must now be multiplied by appropriate activity coefficients γi. The resulting equilibrium constant is given by:
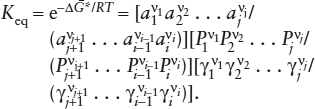
ACTIVITY COEFFICIENTS AND EQUATIONS OF STATE
One good way to illustrate the nonideal behavior of real gases with increasing pressure is to plot values of pressure against the experimentally-determined quantity P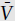 /RT, which serves as a measure of compressibility. For an ideal gas, P
/RT, which serves as a measure of compressibility. For an ideal gas, P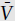 /RT will, of course, be equal to 1 at all pressures; values >1 indicate that a gas is more compressible than an ideal gas; values >1 indicate that it is less compressible. In figure 4.4, we show the behavior of molecular hydrogen and oxygen on this type of plot.
/RT will, of course, be equal to 1 at all pressures; values >1 indicate that a gas is more compressible than an ideal gas; values >1 indicate that it is less compressible. In figure 4.4, we show the behavior of molecular hydrogen and oxygen on this type of plot.
At low pressures, most gases occupy less volume than we would expect from the ideal gas equation of state, suggesting that attractive forces between gas molecules reduce the effective mean distance between them. In 1879, the Dutch physicist Van der Waals recognized this phenomenon and adjusted the equation of state by adding a term a/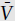 2 to the observed pressure, where a is an empirically determined constant for the gas. This modification correctly describes the deviation shown in figure 4.4 at very low pressures, although research has shown that a is not a constant, in fact, but depends on both pressure and temperature.
2 to the observed pressure, where a is an empirically determined constant for the gas. This modification correctly describes the deviation shown in figure 4.4 at very low pressures, although research has shown that a is not a constant, in fact, but depends on both pressure and temperature.
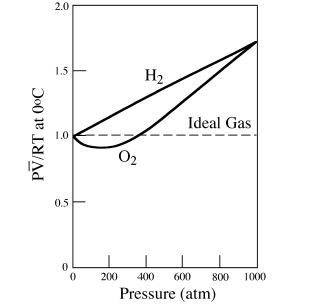
FIG. 4.4. Total pressure versus P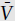 /RT for H2 and O2. A gas for which P
/RT for H2 and O2. A gas for which P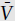 /RT < 1 is more compressible than an ideal gas; if P
/RT < 1 is more compressible than an ideal gas; if P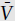 /RT > 1, the gas is less compressible.
/RT > 1, the gas is less compressible.
This correction for intermolecular attractions, however, predicts that real gases will become even more compressible as pressure is increased. This is clearly not the case. Consequently, the full form of Van der Waals’ equation includes a second empirical adjustment on the molar volume:
(P + [a/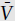 2])(
2])(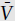 − b) = RT.
− b) = RT.
As pressure increases, an increasingly significant volume in the gas is occupied by the molecules themselves. The factor b, therefore, can be thought of as a measure of the excluded volume that already contains molecules. The remaining volume, in which molecules are free to move, is much less than the total volume, and pressure is higher than it would be for an ideal gas. The full equation, therefore, reflects a balance between attractive and repulsive intermolecular forces that affect the molar volume of a real gas.
To calculate an activity coefficient using the Van der Waals equation of state, we need to rearrange it in terms of 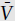 :
:
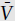 3 −
3 − 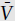 2(b + RT/P) +
2(b + RT/P) + 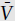 (a/P) − ab/P = 0.
(a/P) − ab/P = 0.
This cubic equation can be shown to have three real roots at temperatures and pressures below the critical point, of which the largest root is the true molar volume for the gas. (We do not define the critical point until chapter 10. For now, think of it as a condition in temperature and pressure beyond which there is no physical distinction between liquid and vapor states. Virtually all near-surface environments are below the critical point.) It is this solution that should replace 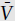 in equation 4.11. In practice, equation 4.11 is solved numerically by computing molar volumes iteratively over the range of pressures from zero to P as part of the algorithm that solves the integral. This is a reasonably straightforward and reliable procedure at moderate temperatures and pressures.
in equation 4.11. In practice, equation 4.11 is solved numerically by computing molar volumes iteratively over the range of pressures from zero to P as part of the algorithm that solves the integral. This is a reasonably straightforward and reliable procedure at moderate temperatures and pressures.
At the more elevated pressures at which many igneous or metamorphic reactions may involve gas phases, the Van der Waals equation of state is less successful. Redlich and Kwong (1949) found that they could only predict the nonideal behavior of gases at very high pressures by modifying the attractive force term. Their equation,

has been widely used in petrology, and has been modified further in many studies. Good reviews of these modifications, and of the use of Redlich-Kwong type equations of state in calculating activity coefficients, can be found in Holloway (1977) and Kerrick and Jacobs (1981).
In a similar way, nonideal liquid or crystalline solutions can be treated by modifying equation 4.9. As with gases, activity is defined as the ratio f/f0. Most species in liquid or solid solution, however, have negligible vapor pressures at 1 atmosphere total pressure, so that f0 is rarely equal to one. Furthermore, because fugacities in solution are so small, it is impractical to use the fugacity ratio to measure quantities like the activity of Fe2SiO4 in a magma. Instead, it is common to write:

in which we declare that ai = γiXi. In practice, it is common to specify, further, that ai is equal to 1 for a pure substance at any chosen temperature. More specifically,
ai → Xi as Xi → 1.
Following this convention and applying equation 4.13, the activity of MgSiO3, for example, would be equal to 1 in pure enstatite (XMgSiO3 = 1). Other conventions are also common, however. Aqueous geochemists are more comfortable with compositions expressed in molal units (moles per kilogram of solution), rather than in mole fractions. Therefore, in very dilute aqueous solutions, we usually define the activity of solute species by the relation ai = γimi, in which mi is the molality of species i. This produces an equation like equation 4.13 in which the Xi quantities are replaced by mi. We generally apply this expression by specifying a standard state in which mi = 1 and then extrapolating to infinite dilution, where:
ai → mi as mi → 0.
We discuss this standard state more fully in chapter 9.
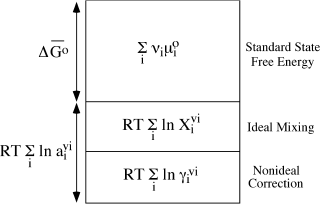
FIG. 4.5. Schematic representation of the various contributions to the free energy of a nonideal solution.
According to either of these conventions and others that we have not mentioned, solutions approach ideal behavior (γi → 1) as their compositions approach a single-component end member. The greatest difficulty arises when we have to consider nonideal solutions that are far from a pure end-member composition. We consider that problem for nonelectrolyte solutions and examine standard states for activity more fully in chapter 9. Figure 4.5 summarizes graphically the various contributions to ΔGr we have discussed so far.
ACTIVITY IN ELECTROLYTE SOLUTIONS
Species in aqueous solutions such as seawater or hydrothermal fluids present an unusual challenge. Although natural fluids commonly contain some associated (that is, uncharged) species, it is much more common to find free ions. In a typical problem, for example, we may be asked to evaluate the solubility of sodium sulfate in seawater. Ignoring the fact that crystalline sodium sulfate usually takes the form of a hydrate, Na2SO4⋅H2O, the relevant chemical reaction is:

which we always write with the solid phase as a reactant and fully dissociated ions as products. For this type of reaction, we refer to the equilibrium constant as an equilibrium solubility product constant, Ksp:
Ksp = (aNa+)2aSO42/aNa2SO4.
(The activity of Na2SO4 is unity, because it is a pure solid phase.)
In general, ionic species in solution do not behave ideally unless they are very dilute, because ions tend to interact electrostatically. They also generally associate with water molecules to produce “hydration spheres” in which the chemical potential of H2O is different from that in pure water. (Look again at figure 2.17 and accompanying discussion.) The result is that the free energies of both the solvent (H2O) and the solute (dissolved ions) differ from their standard states, and their activities differ from their concentrations.
Unfortunately, there is no way to measure the activity of a dissolved ion independently. Because charge balance must always be maintained, we cannot vary the concentration of a cation such as Na+ without also adjusting the anions in solution. It is impossible, for example, to determine how much of the potential free energy change during evaporation of seawater is due to increasing aNa+ and how much is the result of parallel increases in aCl−, aSO42−, and other anion activities.
Several approaches have been taken to solve this problem. One is to define the mean ionic activity, given by:
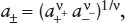
in which a+ and a− are the individual activities of cations and anions, respectively, and the stoichiometric coefficients ν = ν+ + ν− count the number of ions formed per dissociated molecule of solute. For example, the dissociation reaction for Mgcl2 is:
MgCl2 ⇄ Mg2+ + 2Cl−,
so ν+ = 1, ν− = 2, and ν = 3. The mean ionic activity of MgCl2 in aqueous solution is therefore equal to:
a± (MgCl2 = (aMg2+aCl−2)1/3.
Mean activities, unlike the activities of charged ions, are readily measurable. From these, it is possible to calculate mean ion activity coefficients by using the relationship:
γ± = a±/m±.
The quantity m± is the mean ionic molality, which is related to the molal concentration of total (nondissociated solute), m, by:

Again, for MgCl2 in aqueous solution,
m±(MgCl2) = mMgCl2([1]1[2]2)1/3.
It is customary to calculate individual ion activity coefficients, γ+ and γ−, by referring to a standard univalent electrolyte in a solution of the same effective concentration as the one we are studying. Potassium chloride is a common standard electrolyte for this purpose because it has been determined experimentally that γK+ = γCl−, so that:
γ±(KCl) = (γK+γCl−)1/2 = γK+ = γCl−.
If we wanted to calculate an individual ion activity coefficient for Mg2+ by this mean salt method, then, we would assume that the value of γCl− in an MgCl2 solution is the same as the value of γ± (KCl) that we measured in a KCl solution. In other words,
γ±(MgCl2) = (γMg2+[γCl−]2)1/3 = (γMg2+γ±(KCl)2)1/3,
and, therefore:
γMg2+ = γ±(MgCl2)3/γ±(KCl)2.
Geochemists use the mean salt method to estimate activity coefficients for anions as well as cations. Because the basis for the method is an empirical comparison to a well studied electrolyte such as KCl, and because the comparison is always done between solutions with the same effective concentration, the method is reliable over a very wide range of conditions.
Because the mean salt method relies on the use of γ± from simple electrolyte solutions, you need access to measurements on a large number of electrolytes over a wide range of concentrations. Fortunately, there are extensive tables and graphs of experimentally derived activity coefficients in the chemical literature (see the highlighted discussion of nonideality in natural waters for one example). For those who prefer to generate their own values, an alternative nonempirical method for calculating ion activity coefficients in dilute solutions is provided by Debye-Hückel theory, which attempts to calculate the effect of electrostatic interactions among ions on their free energies of formation. The disadvantage of the theory is that it is only reliable in dilute solutions. Nevertheless, because very many solutions of geologic interest fall within its range of reliability, geochemists find the Debye-Hückel method extremely useful.
To evaluate the cumulative effect of attractive and repulsive forces, we define first a charge-weighted function of species concentration known as ionic strength (I):

In this way, we recognize that ions in solution are influenced by the total electrostatic field around them and that polyvalent ions (|z| > 1) exert more electrostatic force on their neighbors that monovalent ions. A 1 m solution of MgSO4, for example, has an ionic strength of 4, whereas a 1 m solution of NaCl has an ionic strength of only 1.
In its most commonly used form, the Debye-Hückel equation takes into account not only the ionic strength of the electrolyte solution, but also the effective size of the hydrated ion of interest, thus estimating the number of neighboring ions with which it can come into contact. Values of the size parameter, å, for representative ionic species, are given in table 4.1, along with values of empirical parameters A and B, which are functions only of pressure and temperature. We calculate the activity coefficient for ion i from:

Pytkowicz (1983) has discussed the theoretical justification for this equation and a critique of its use in aqueous geochemistry.
TABLE 4.1. Values of Constants for Use in the Debye-Hückel Equation

Data from Garrels and Christ (1982).
Worked Problem 4.5
What is the activity coefficient for Ca2+ in a 0.05 m aqueous solution of CaCl2 at 25°C? How closely do answers obtained by the mean salt method and the Debye-Hückel equation agree?
To calculate γCa2+ by the Debye-Hückel method, we first determine the ionic strength of the solution:
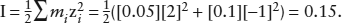
Then, using the data in table 4.1, we find that:

So,
γCa2+ = 0.357.
How does this compare with γCa2+ calculated by the mean salt method? The mean ionic activity coefficient γ±CaCl2 in 0.05 m aqueous solution has been reported by Goldberg and Nuttall (1978) to be 0.5773. To use the mean salt method, we need to know the mean ion activity coefficient for KCl at the same effective concentration as the CaCl2 solution; that is, at the same ionic strength. A KCl solution of ionic strength 0.15 is 0.15 molal. Robinson and Stokes (1949) report that γ±KCl = 0.744 in 0.15 m aqueous KCl. You can verify this, although with less precision, from the graph in figure 4.6. From this value, we calculate that:
γ±CaCl2 = (γCa2+ [γCl−]2)1/3 = (γCa2+ [γ ±KCl]2)1/3.
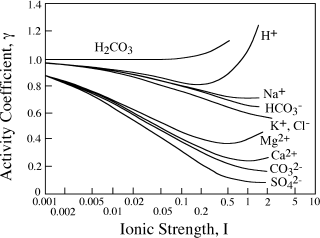
FIG. 4.6. Activity coefficients for common aqueous species as a function of ionic strength.
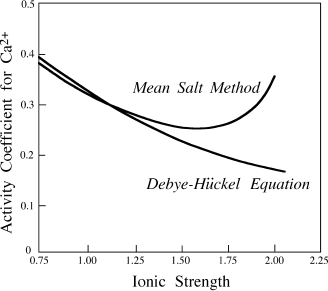
FIG. 4.7. Ion activity coefficient for Ca2+ as a function of ionic strength, calculated from the Debye-Hückel equation and by the mean salt method. Notice the deviations at higher ionic strengths.
Therefore,
γCa2+= (γ±CaCl2)3/[γ± KCl]2) = (0.577)3/(0.649)2 = 0.347.
This is very close to the 0.357 value calculated by Debye-Hückel theory. In figure 4.7, we have repeated this pair of calculations for a range of ionic strengths from 0.05 to 3.0. It is apparent that the methods agree at ionic strengths less than ∼0.3, but diverge strongly in more concentrated solutions, as Debye-Hückel theory fails to model changes in the structure of the solute adequately. Other calculation schemes have been used to model highly concentrated solutions, particularly at elevated temperatures (see, for example, Harvie et al. [1984], or the Helgeson references in appendix B), but most researchers continue to use values obtained by some variant of the mean salt method in those situations.
Many of the interesting questions facing aqueous geochemists have to do with mineral solubility. How much sulfate is in groundwater that is in equilibrium with gypsum beds? How much fluoride can be carried by an ore-forming hydrothermal fluid? What sequence of minerals should be expected to form during evaporation of seawater? What processes can cause deposition of ore minerals from migrating fluids? How are the compositions of residual (zonal) soils affected by the chemistry of soil water? How might a chemical leak from a waste disposal site affect the stability of surrounding rocks and soils? To address these questions and others like them in coming chapters, we must first look at broad conditions that affect solubility.
In worked problems 4.6–4.10, we will make successive refinements in our approach to a typical problem, illustrating by stages the major thermodynamic factors influencing solubility.
Worked Problem 4.6
What is the solubility of barite in water at 25°C? The simplest answer can be calculated from data for the molar free energies of formation of species in the reaction:
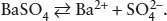
We find the following values in Parker et al. (1971):

The standard molar free energy of reaction is calculated by:
| ΔḠr | = −134.02 + (−177.97) − (−325.6) |
| = 13.61 kcal mol−1. |
If the fluid is saturated with respect to BaSO4, then the reaction above is perfectly balanced and ΔḠr = 0. Therefore,

If we assume that the solution behaves ideally, then the solubility of barite can be calculated by recognizing that charge balance in the fluid requires that 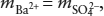 , and that:
, and that:

From this, we get:
mBa2+ = m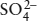 = 1.02 × 10−5 mol kg−1.
= 1.02 × 10−5 mol kg−1.
NONIDEALITY IN NATURAL WATERS
The water in streams and the aquifers that we typically draw on for irrigation and public water supplies is in fact a dilute electrolyte solution. People and plants are sensitive to small variations in composition. Some electrolytes affect cosmetic qualities of water such as taste and smell, and others can have profound effects on health. Inorganic solutes can also interact with pipes and machinery, producing corrosion or scale. For this reason, the composition of natural water in most parts of the world is monitored quite closely.
As we discuss in greater detail in chapters 5 and 7, the composition of natural waters is controlled largely by weathering reactions. The dominant cations in surface and ground waters (Ca2+, Mg2+, Na+, and K+) and the dominant anions  are derived from silicate and carbonate minerals and the oxidation of metal sulfides. Hydrogeologists commonly trace the chemical history of water from an aquifer or reservoir by studying the relative abundances of these ions, expressed as concentration ratios in either molalities (moles/kg) or equivalencies (moles × charge/liter). Using diagrams such as those in figure 4.8, for example, we can distinguish between waters that have equilibrated with limestone (relatively Ca2+, Mg2+, and
are derived from silicate and carbonate minerals and the oxidation of metal sulfides. Hydrogeologists commonly trace the chemical history of water from an aquifer or reservoir by studying the relative abundances of these ions, expressed as concentration ratios in either molalities (moles/kg) or equivalencies (moles × charge/liter). Using diagrams such as those in figure 4.8, for example, we can distinguish between waters that have equilibrated with limestone (relatively Ca2+, Mg2+, and  rich) and those that are more likely to have equilibrated with shale (relatively Na+, and K+ rich). These are useful qualitative indicators of where a water sample has been.
rich) and those that are more likely to have equilibrated with shale (relatively Na+, and K+ rich). These are useful qualitative indicators of where a water sample has been.
The more quantitative thermodynamic and kinetic analyses that we introduce in chapters 5 and 7 will require ion activities, rather than concentrations. You can use either the mean salt method or the Debye-Hückel method to calculate ion activity coefficients. To decide which method is most likely to give a reliable result for a given water sample, calculate its ionic strength. Except when some other ion is present in significant amounts, this is equal to:


FIG. 4.8. Classification diagram for anion and cation facies in terms of major ion percentages. Groundwater types are designated according to the domain in which they occur on diagram segments. (After Freeze and Cherry 1979.)
As table 4.2 suggests, the ionic strengths of natural waters range from about 1.0 × 10−3 in rivers and lakes to as much as 1 × 10−1 in groundwater. Oilfield brines and saline lakes have significantly higher ionic strengths. The ionic strength of seawater is 7 × 10−1. Because the Debye-Hückel method is unreliable above ionic strengths of 1.0 × 10−1 (see figure 4.7), therefore, you should use the mean salt method for any solution more saline than groundwater.
TABLE 4.2. Analyses of Groundwater and River Waters
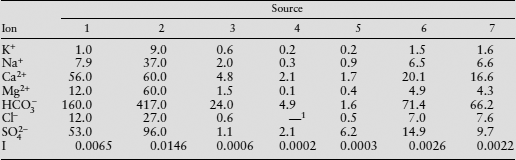
Values in mg/l. Sources are: 1, limestone aquifer, Florida (Goff 1971); 2, dolomite aquifer, Manitoba (Langmuir 1971); 3, granitic glacial sand aquifer, Northwest Ontario (Bottomley 1974); 4, streams draining greenstone, South Cascade Mountains, Oregon (Reynolds and Johnson 1972); 5, streams draining granite, metamorphics, and glacial till, Hubbard Brook watershed, New Hampshire (Likens et al. 1977), analysis also contains trace amounts of  ; 6, average river waters, corrected for pollution, North America (Meybeck 1979); 7, average river waters, corrected for pollution, Asia (Meybeck 1979).
; 6, average river waters, corrected for pollution, North America (Meybeck 1979); 7, average river waters, corrected for pollution, Asia (Meybeck 1979).
1No measurement.
The result in worked problem 4.6 is quite close to the value of 1.06 × 10−5 mol kg−1 measured in experiments by Blount (1977), even though we assumed the fluid was ideal. This agreement may be fortuitous, however, because we should anticipate some nonideal behavior. Let’s do the problem again.
Worked Problem 4.7
What are the activity coefficients for Ba2+ and 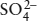 in a solution saturated with respect to barite, and how much does the calculated solubility change if we allow for nonideal behavior?
in a solution saturated with respect to barite, and how much does the calculated solubility change if we allow for nonideal behavior?
The easiest way to solve this problem is to design a numerical algorithm and iterate toward a solution by computer. In outline form, the procedure looks like this:
 from the Debye-Hückel equation, using constants in table 4.1.
from the Debye-Hückel equation, using constants in table 4.1.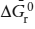 , calculate improved values of mBa2+ and
, calculate improved values of mBa2+ and  .
. do not change in successive iterations by more than some acceptably small amount.
do not change in successive iterations by more than some acceptably small amount.When we did this calculation, it took four cycles to satisfy the condition |mBa2+ (old) − mBa2+ (new) | < 10−9, which is a calculation error of less than one part in 104 (much better than is justified by the uncertainties in 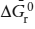 . Notice that charge balance constraints require that mBa2+ = mSO42−.
. Notice that charge balance constraints require that mBa2+ = mSO42−.

As we suspected in worked problem 4.6, a solution saturated with BaSO4 is nearly ideal. By taking the slight nonideality into account, however, the computed solubility increased to within 1% error of the value measured by Blount (1977).
The reason that there is progressive improvement with each iteration in worked problem 4.7 is that each cycle calculates the ionic strength with an improved set of activity coefficients. Suppose, however, that there were other ions in solution as well as Ba2+ and 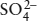 . Natural fluids, in fact, rarely contain only a single electrolyte in solution. Most hydrothermal fluids or formation waters are dominated by NaCl. To calculate the ionic strength correctly, we must consider not only the amount of Ba2+ and
. Natural fluids, in fact, rarely contain only a single electrolyte in solution. Most hydrothermal fluids or formation waters are dominated by NaCl. To calculate the ionic strength correctly, we must consider not only the amount of Ba2+ and 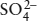 but also include the concentrations of all other ions in solution. This, in turn, leads to an adjustment in the solubility of BaSO4.
but also include the concentrations of all other ions in solution. This, in turn, leads to an adjustment in the solubility of BaSO4.
Worked Problem 4.8
What effect do other solutes have on the solubility of barite? In particular, what would be the solubility of barite in a solution at 25°C that is already 0.2 m in NaCl? Assuming that there is little tendency for Ba2+ to associate with Cl− (Sucha et al. 1975) or for Na+ to associate with 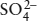 (Elgquist and Wedborg 1978), we should expect that barite solubility changes only as the result of increased ionic strength. To verify this, we repeat the calculation of worked problem 4.7, this time calculating ionic strength in each iteration by
(Elgquist and Wedborg 1978), we should expect that barite solubility changes only as the result of increased ionic strength. To verify this, we repeat the calculation of worked problem 4.7, this time calculating ionic strength in each iteration by 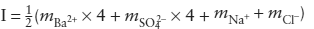 .
.

These values, once again, compare favorably with Blount (1977), who measured barite solubility in 0.2-m NaCl-H2O at 25°C and found mBa2+ = 3.7 × 10−5 mol kg−1 and γ± = 0.2754.
In many natural fluids, the solubility of minerals like barite increases with ionic strength, as we saw in worked problem 4.8. This is not the case, however, if ions produced by dissociation of the solute are also present from some other source in solution. For example, if barite is in equilibrium with a solution that contains both NaCl and Na2SO4, the charge balance constraint on the fluid becomes:
2mBa2+ + mNa+ = 2m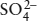 + mCl−.
+ mCl−.
Sulfate is a common ion in BaSO4 and Na2SO4. Extra 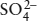 ions in solution, whether they come from Na2SO4 or some other source, force the reaction:
ions in solution, whether they come from Na2SO4 or some other source, force the reaction:

toward the left (remember equation 4.3?), decreasing the solubility of barite. To demonstrate this common ion effect, we offer the following problem.
Worked Problem 4.9
How does the addition of successive amounts of Na2SO4 to an aqueous fluid affect the solubility of barite?
The molal concentration of Ba2+ can be calculated from this expression and the equilibrium constant, K:
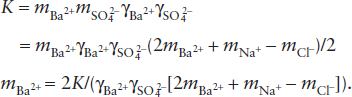
This equation can be solved by the same numerical procedure we applied in worked problems 4.7 and 4.8. We can simplify the calculation in this case, because the solubility of barite has been shown to be quite low. We can assume that all 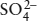 in solution is due to dissociation of Na2SO4, as long as we examine only solutions of moderately high m
in solution is due to dissociation of Na2SO4, as long as we examine only solutions of moderately high m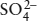 . The charge balance constraint, in other words, is approximately:
. The charge balance constraint, in other words, is approximately:
mNa+ = 2m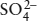 + mCl−.
+ mCl−.
The ionic strength calculated with this simplification will differ only very slightly from the “true” ionic strength.
To illustrate the effect of a common ion (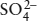 in this case), we have calculated mBa2+ in a variety of NaCl-Na2SO4-H2O solutions with ionic strength equal to 0.2.
in this case), we have calculated mBa2+ in a variety of NaCl-Na2SO4-H2O solutions with ionic strength equal to 0.2.

As expected, the addition of sulfate, even in very small amounts, dramatically lowers the solubility. Barite will precipitate if the product  equals or exceeds Keq (1.31 × 10−9 at ionic strength 0.2). With increasing amounts of sulfate in solution, this condition is met with vanishingly small amounts of dissolved Ba2+. The same effect would be observed if we were to provide barium ions from some source other than barite (for example, from barium chloride).
equals or exceeds Keq (1.31 × 10−9 at ionic strength 0.2). With increasing amounts of sulfate in solution, this condition is met with vanishingly small amounts of dissolved Ba2+. The same effect would be observed if we were to provide barium ions from some source other than barite (for example, from barium chloride).
In stream waters (ionic strength < 0.01 on average) and in most surficial environments on the continents, dissolved species are highly dissociated. As ionic strength increases, however, electrical interactions between ions also increase. The result is that many ions in concentrated solutions exist in groups or clusters known as complexes. For ease of discussion, these may be divided into three broad classes: ion pairs, coordination complexes, and chelates. By convention (not universally observed, unfortunately), the stability of any complex is expressed by a stability constant, Kstab, which is written for the reaction forming a complex species from simpler dissolved species. Thus, for example, Mg2+ and 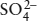 ions can associate to form the neutral ion pair
ions can associate to form the neutral ion pair  by the reaction
by the reaction

for which  at 25°C. The larger a stability constant, the more stable the complex it describes.
at 25°C. The larger a stability constant, the more stable the complex it describes.
The distinctions among different types of complexes are not easy to define and, for thermodynamic purposes, not very important. Ion pairs are characterized by weak bonding; hence, small stability constants. The dominant complex species in seawater and most brines fall into this category. In chapter 8, we examine the effect of ion pair formation on the chemistry of the oceans.
Coordination complexes involve a more rigid structure of ligands (usually anions or neutral species) around a central atom. This well-defined structure contributes to greater stability. Transition metals, such as copper, vanadium, and uranium have been shown to exist in aqueous solution primarily as coordination complexes like  , in which the negatively charged ends of several polar water molecules are attracted to the metal cation to form a “hydration sphere” like the one we illustrated in figure 2.17. Other polar molecules also commonly form coordination complexes with metal cations. One that may be familiar to you from analytical chemistry is ammonia, which combines readily with Cu2+ in solution to form the bright blue complex
, in which the negatively charged ends of several polar water molecules are attracted to the metal cation to form a “hydration sphere” like the one we illustrated in figure 2.17. Other polar molecules also commonly form coordination complexes with metal cations. One that may be familiar to you from analytical chemistry is ammonia, which combines readily with Cu2+ in solution to form the bright blue complex  . The stability constant for this species is 2.13 × 1014.
. The stability constant for this species is 2.13 × 1014.
Molecules like water, ammonia, Cl−, and OH−, which form simple coordination complexes because they can only attach to one metal cation at a time, are called unidentate ligands. Other species, usually organic molecules or ions, are called multidentate or polydentate ligands. Chelates, which form around these, have larger, more complicated structures that include several metal cations. Chelates differ from coordination complexes only in their degree of structure. Some, like the hexadentate anion of ethylenediaminetetraacetic acid (mercifully known as EDTA) are widely used by analytical chemists to scavenge metals from very dilute aqueous solutions.
In nature, the vast number of humic and fulvic acids and other dissolved organic species also serve as chelating agents. In general, the larger and more complicated these are, the more stable the complexes they form. Because they have very high stability constants and can coordinate several cations at once, chelating agents can contribute significantly to the chemistry of transition metals and of cations such as Al3+ in natural waters, even if both they and the metal cations are in very low concentration.
The formation of complex species increases the solubility of electrolytes by reducing the effective concentration of free ions in solution. In a sense, we can think of ions bound up in complexes as having become electrostatically shielded from oppositely charged ions and therefore unable to combine with them. Because the activity product of free ions is lowered, equilibria that involve those ions favor the further dissolution of solid material. Thus, although the activity product of free ions at saturation will still be equal to Ksp, the total concentration of species in solution will be much higher than in a solution without complexing.
Worked Problem 4.10
Calcium and sulfate ions can associate in aqueous solution to form a neutral ion pair,  . This is one of several ion pairs that affect the concentration of species in seawater, as we shall see in chapter 8. How does it affect the solubility of gypsum?
. This is one of several ion pairs that affect the concentration of species in seawater, as we shall see in chapter 8. How does it affect the solubility of gypsum?
The solubility product constant, Ksp, for gypsum is calculated from the free energy of the reaction:

In reasonably dilute solutions, the activity of water can be assumed to be unity. Gypsum, a pure solid, is in its standard state and also has unit activity. Ksp, then, is equal to  . At 25°C, it has the value 2.45 × 10−5.
. At 25°C, it has the value 2.45 × 10−5.
The stability constant, Kstab, for  is derived by experiment for the reaction:
is derived by experiment for the reaction:

at 25°C. By combining the two expressions for Ksp and Kstab and rearranging terms, we can calculate:
a = KstabKsp = 5.09 × 10−3.
= KstabKsp = 5.09 × 10−3.
Because  is a neutral species, its concentration in solution will be nearly the same as its activity. The concentration of the ion pair, therefore, is ∼5 mmol kg−1. It can be shown, using the iterative procedure in worked problem 4.7, that the concentration of Ca2+ in the absence of complexing is ∼10 mmol kg−1. The total calcium concentration in solution is thus ∼15 mmol kg−1, or ∼50% higher than the concentration of Ca2+ alone.
is a neutral species, its concentration in solution will be nearly the same as its activity. The concentration of the ion pair, therefore, is ∼5 mmol kg−1. It can be shown, using the iterative procedure in worked problem 4.7, that the concentration of Ca2+ in the absence of complexing is ∼10 mmol kg−1. The total calcium concentration in solution is thus ∼15 mmol kg−1, or ∼50% higher than the concentration of Ca2+ alone.
We see now that the structure and stoichiometry of solutions play a key role in determining how they act in chemical reactions. The free energy of any reaction can be expressed in terms of a standard state free energy and a contribution due to mixing of end-member species in solutions. Relatively few solutions of geochemical interest are ideal; in most, interactions among dissolved species or among atoms on different structural sites produce significant departures from ideality. In many cases, however, we gain valuable first impressions of a system by assuming ideal mixing and then adding successive corrections to describe its actual behavior.
We discuss solution models more fully in chapters 9 and 10, where, in particular, we address the problem of calculating activity coefficients for nonideal systems of petrologic interest. In the next few chapters, however, we make use of the Debye-Hückel equation and the mean salt method, which yield the activity coefficients we need to explore dilute aqueous solutions. Solubility equilibria will dominate our discussion of the oceans, of chemical weathering, and of diagenesis.
Several excellent textbooks are available for the student interested in the thermodynamic treatment of solutions. The ones listed here are a selection of some that the authors have found particularly useful.
Drever, J. I. 1997. The Geochemistry of Natural Waters. New York: Simon and Schuster. (This is a very good book for the student who is new to aqueous geochemistry. There are quite a few carefully written case studies to show the use of geochemistry in the real world.)
Garrels, R. M., and C. L. Christ. 1982. Solutions, Minerals, and Equilibria. San Francisco: Freeman, Cooper. (Perhaps the most often used text in its field.)
Powell, R. 1978. Equilibrium Thermodynamics in Petrology. London: Harper and Row. (A good text for classroom use. Chapters 4 and 5 consider the calculation of mole fractions in crystalline and liquid solutions.)
Pytkowicz, R. M. 1983. Equilibria, Nonequilibria, and Natural Waters, vol. I. New York: Wiley. (An exhaustive treatment of the theoretical basis for the thermodynamics of aqueous solutions. Chapter 5 has more than 100 pages devoted to the determination of activity coefficients.)
Robinson, R. A., and R. H. Stokes. 1968. Electrolyte Solutions. London: Butterworths. (A reference for chemists rather than geologists, but widely quoted by aqueous geochemists. Highly theoretical, but not difficult to follow.)
Stumm, W., and J. J. Morgan. 1995. Aquatic Chemistry. New York: Wiley. (A detailed, yet highly readable text with an emphasis on the chemical behavior of natural waters. Chapter 6, dealing with complexes, is particularly well written.)
The following articles were referenced in this chapter. An interested student may wish to explore them more thoroughly.
Blount, C. W. 1977. Barite solubilities and thermodynamic quantities up to 300°C and 1400 bars. American Mineralogist 62:942–957.
Bottinga, J., and D. F. Weill. 1972. The viscosity of magmatic silicate liquids: a model for calculation. American Journal of Science 272:438–475.
Bottomley, D. 1974. Influence of Hydrology and Weathering on the Water Chemistry of a Small Precambrian Shield Watershed. Unpublished MSc. Thesis, University of Waterloo.
Cameron, M., and J. J. Papike. 1980. Crystal chemistry of silicate pyroxenes. Mineralogical Society of America Reviews in Mineralogy 7:5–92.
Cameron, M., and J. J. Papike. 1981. Structural and chemical variations in pyroxenes. American Mineralogist 66:1–50.
Clark, J., D. E. Appleman, and J. J. Papike. 1969. Crystal-chemical characterization of clinopyroxenes based on eight new structure refinements. Mineralogical Society of America Special Paper 2:31–50.
Cohen, R. E. 1986. Thermodynamic solution properties of aluminous clinopyroxenes: Non-linear least-squares refinements. Geochimica et Cosmochimica Acta 50:563–576.
Elgquist, B., and M. Wedborg. 1978. Stability constants of Na , MgSO4, MgF+, MgCl+ ion pairs at the ionic strength of seawater by potentiometry. Marine Chemistry 6:243–252.
, MgSO4, MgF+, MgCl+ ion pairs at the ionic strength of seawater by potentiometry. Marine Chemistry 6:243–252.
Freeze, R. A., and J. A. Cherry. 1979. Groundwater. Englewood Cliffs: Prentice-Hall.
Goff, K.J. 1971. Hydrology and Chemistry of the Shoal Lakes Basin, Interlake Area, Manitoba. Unpublished Master’s thesis, University of Manitoba.
Goldberg, R. N., and R. L. Nuttall. 1978. Evaluated activity and osmotic coefficients for aqueous solutions: The alkaline earth halides. Journal of Physical and Chemical Reference Data 7:263.
Harvie, C. E., N. Moller, and J. H. Weare. 1984. The prediction of mineral solubilities in natural waters: The Na-K-Mg-Ca-H-Cl-SO4-OH-HCO3-CO3-CO2-H2O system to high ionic strengths at 25°C. Geochimica et Cosmochimica Acta 48: 723–752.
Helgeson, H. C. 1969. Thermodynamics of hydrothermal systems at elevated temperatures and pressures. American Journal of Science 267:729–804.
Holloway, J. R. 1977. Fugacity and activity of molecular species in supercritical fluids. In D. G. Fraser, ed. Thermodynamics in Geology, pp. 161–180. Boston: D. Reidel.
Kerrick, D. M., and G. K. Jacobs. 1981. A modified Redlich-Kwong equation for H2O, CO2, and H2O-CO2 mixtures at elevated pressures and temperatures. American Journal of Science 281:735–767.
Langmuir, D. 1971 The chemistry of some carbonate groundwaters in Central Pennsylvania. Geochimica et Cosmochimica Acta 35:1023–1045.
Likens, G. E., F. H. Bormann, R. S. Pierce, J. S. Eaton, and N. M. Johnson. 1977. Biogeochemistry of a Forested Ecosystem. New York: Springer-Verlag.
Livingstone, D. A. 1963. Chemical Composition of Rivers and Lakes. U.S. Geological Survey Professional Paper 440G.
Meybeck, M. 1979. Concentrations des eaux fluviales en éléments majeurs et apports en solution aux océans. Revues de Géologie Dynamique et de Géographie Physique 23: 215–246.
Parker, V. B., D. D. Wagman, and W. H. Evans. 1971. Selected Values of Chemical Thermodynamic Properties: Tables for the Alkaline Earth Elements (Elements 92 through 97 in the Standard Order of Arrangement). Technical Note 270–6. Washington, D.C.: U.S. National Bureau of Standards.
Redlich, O., and J.N.S. Kwong. 1949. An equation of state: Fugacities of gaseous solutions. Chemical Review 44: 233–244.
Reynolds, R. C., and N. M. Johnson. 1972. Chemical weathering in the temperate glacial environment of the Northern Cascade Mountains. Geochimica et Cosmochimica Acta 36: 537–544.
Robinson, R. A., and R. H. Stokes. 1949. Tables of osmotic and activity coefficients of electrolytes in aqueous solutions at 25°C. Transactions of the Faraday Society 45:612.
Sucha, L., J. Cadek, K. Hrabek, and J. Vesely. 1975. The stability of the chloro complexes of magnesium and of the alkaline earth metals at elevated temperatures. Collected Czechoslovakian Chemical Communications 40:2020–2024.
(4.1) Use the Debye-Hückel equation to calculate values for the ion activity coefficients for Cl− and Al3+ at 25°C in aqueous solutions with ionic strengths ranging from 0.01 to 0.2. Plot these on a graph of γ versus log I. What physical differences between these two ions account for the differences in their activity coefficients?
(4.2) Using the procedure introduced in worked problem 4.5, calculate the solubility of gypsum in water at 25°C.
(4.3) To produce a solution that is saturated with respect to fluorite at 25°C, you need to dissolve 6.8 × 10−3 g of CaF2 per 0.25 liter of pure water. Assuming that CaF2 is 100% dissociated, and that the solution behaves ideally, calculate the Ksp for fluorite. What is the free energy for the dissociation reaction?
(4.4) The Ksp for celestite is 7.6 × 10−7 at 25°C. How many grams of SrSO4 can you dissolve in a liter of 0.1 m Sr(NO3)2? Assume that the activity coefficients for all dissolved species are unity, and that no complex species are formed in solution.
(4.5) Repeat the calculation in problem 4.4, again assuming that complex species are absent, but correcting for the ionic strength effect by calculating activity coefficients with the Debye-Hückel equation.
(4.6) The following analysis of water from Lake Nipissing in Ontario was reported by Livingstone (1963):

What is the ionic strength of this water? (Recall that concentrations in ppm are equal to concentrations in mmol kg−1 multiplied by formula weight.)
(4.7) Calculate the mole fractions of forsterite and fayalite in an olivine with the composition Mg0.7Fe1.3SiO4.
(4.8) A garnet has been analyzed by electron microprobe and found to have the following composition:
| SiO2 | 39.08 wt % |
| Al2O3 | 22.66 |
| FeO | 29.98 |
| MnO | 1.61 |
| MgO | 6.67 |
Calculate the mole fractions of almandine, pyrope, and spessartine in this garnet.
(4.9) Calculate the mole fractions of enstatite, ferrosilite, diopside, CaCrAlSiO6 (Cr-CATS), and Mg1.5AlSi1.5O6 (pyrope) in the orthopyroxene analysis below. Assume complete mixing on sites in such a way that all tetrahedral sites are filled by either Si or Al; M1 sites by Al, Cr, Fe3+, Fe2+, or Mg; and M2 sites by Ca, Fe2+, or Mg. Assume also that the ratio of XFe to XMg is that same in M1 and M2 sites. (This problem, modified from Powell 1978, requires a fair amount of effort.)
