 |
|
This chapter expands on the thermodynamic principles introduced in chapter 3 and provides the preparation for the next chapter on phase diagrams. We first give a thermodynamic definition for equilibrium. We also derive the phase rule and explore its use as a test for equilibrium. The effects of changing temperature and pressure on the free energy of a system at equilibrium are analyzed, and a general equation for dḠ at P and T is formulated. P-T and Ḡ-T diagrams for one-component systems are introduced. The utility of the Clapeyron equation in constructing or interpreting phase diagrams is explored. We then introduce concepts that are necessary for understanding systems with more than one component. Raoult’s law and Henry’s law are defined, and expressions for the chemical potentials of components that obey these laws are derived. The concept of standard states is introduced, and we examine how activity coefficients are defined in mixing models. The usefulness of these concepts is illustrated by discussing formulation of a geothermometer and a geobarometer.
WHAT DOES EQUILIBRIUM REALLY MEAN?
In previous chapters, we have introduced and made use of the concept of thermodynamic equilibrium. By this time, you should be comfortable with the idea that the observable properties of a system at equilibrium will undergo no change with time, as long as physical conditions imposed on the system remain constant. Although this statement is commonly used to define equilibrium, it is actually a consequence of equilibrium rather than a strict definition of it. A more rigorous definition of the equilibrium state that we have not seen before is: a condition of minimum energy for that portion of the universe under consideration.
We have also learned that Gibbs free energy is a convenient way of describing the energy of a system. The relationship of this thermodynamic quantity to temperature, pressure, and the amounts of the constituent components of a system is given by the following:
| dG = | (∂G/∂T)P,ni dT + (∂G/∂P)T,ni dP |
| + (∂G/∂ni)P,T,nj≠i dni, (9.1) |
where ni represents the number of moles of component i. The quantities (∂G/∂ni)P,T,nj≠i are chemical potentials, symbolized by μi and defined in chapter 3. The goal of this chapter is to learn how to evaluate all of the quantities in this equation.
DETERMINING WHEN A SYSTEM IS IN EQUILIBRIUM
How can we determine whether a geologic system is in a state of equilibrium? Although we can never be completely sure, we can at least argue for equilibrium on the basis of our experience with reactions in the laboratory and the absence of any observational evidence for disequilibrium. Consider, for example, a metamorphic rock consisting of biotite, garnet, plagioclase, sillimanite, and quartz. We know from experiments that these minerals can constitute a stable assemblage under conditions of high temperature and pressure. Let’s assume that textural observations of this rock provide no indication of arrested reactions between any of the constituent minerals. Furthermore, grains of all five minerals are observed to be touching each other, and no zoning or other kind of chemical heterogeneity within grains is present. In this case, we might infer that the rock system is in a state of equilibrium, but this indirect evidence may be less than convincing. Is there another way to test for equilibrium?
Let’s describe the equilibrium configuration of a system in more quantitative terms. The general relationships among phases, components, and physical conditions are given by the phase rule, first formulated by J. Willard Gibbs more than a century ago. The phase rule describes the maximum number of phases that can exist in an equilibrium system of any complexity. As we will see, this provides an additional test for equilibrium.
The variance (f), also called the degrees of freedom, of a system at equilibrium is the number of independent parameters that must be fixed or determined to specify the state of the system. The number of independent parameters equals the number of unknown variables minus the number of known (dependent) relationships between them. Assume that there are p phases and every phase contains one or more of the c chemical components that constitute the system. For each phase p in the system, we can write a Gibbs-Duhem equation:
0 = 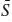 dT −
dT −  dP +
dP +  ncdμc,
ncdμc,
where μc is the chemical potential of each component in the phase. Recall also some of the major conclusions of chapter 3; namely, that at equilibrium, the temperatures and pressures in all phases must be the same, and μc must be the same in all phases that contain component c. The total number of potentially unknown variables, therefore, is c (the number of components) plus two (for temperature and pressure, whatever their values). The number of known relationships among them is p (the number of Gibbs-Duhem equations). The variance, therefore, is the difference:
f = (c + 2) − p.
Equation 9.2 is a mathematical statement of the phase rule. To illustrate its use, consider an ordinary glass of water at room temperature and atmospheric pressure. The number of components c necessary to describe the compositions of all the phases in this system is one (H2O), and the number of phases p is also one (liquid water). Thus, from equation 9.2, the variance of the system is two. This means that two variables (in this case, temperature and pressure) can be changed independently with no resulting effect on the system. Our everyday experience tells us that this is true—it would still be a glass of water if transported from sea level to a mountain top, where the temperature is cooler and atmospheric pressure is less—but there is some finite limit to the permissible variation. For example, the phase in this system (liquid water) would certainly change if we were to lower the temperature drastically by putting the glass of water in a freezer. However, in the case of a frozen glass of water, the variance would still be two, because there is still only one component (H2O) and one phase (ice in this case). Are there situations in which the variance of this system is other than two?
The phase diagram for water, illustrated in figure 9.1, summarizes how this simple system reacts to changing conditions of temperature and pressure. The diagram consists of fields in which only one phase is stable, separated by boundary curves along which combinations of phases coexist in equilibrium. The three boundary lines intersect at a point, called the triple point, at which three phases occur. The boundary between the liquid water and water vapor fields terminates in a critical point, above which there is no distinction between liquid and vapor. From inspection of this figure, it is obvious that a single phase is stable under most combinations of temperature and pressure. Within these one-phase fields, the variance is two, and the fields are said to be divariant.
However, there are certain special combinations of temperature and pressure at which several phases coexist at equilibrium. For example, because two phases coexist along the boundary curves in this diagram, the variance at any point along the boundary curves is one. (Prove this yourself using the phase rule.) These boundary curves are thus univariant. Coexistence of three phases at the triple point produces a variance of zero, forming an invariant point.

FIG. 9.1. Schematic phase diagram for the system H2O. Most of the area of the diagram consists of regions in which only one phase is stable at equilibrium. Boundary curves are combinations of pressure and temperature along which two phases are stable, and three phases occur at the triple point. The boundary between liquid water and water vapor terminates in a critical point, above which the distinction between these phases is meaningless.
For a more complex system, such as a rock, of course, more components are required to describe the system, and there will probably be more phases. In an assemblage of minerals, it is unlikely that every component will occur in every phase. However, the phase rule is a general result and is valid for systems in which some components do not occur in all phases.
Worked Problem 9.1
What is the variance for the metamorphic rock described at the beginning of this section? There are five phases, and the eight components that describe the compositional variation of each phase are listed beside each mineral below. From our discussion of components in chapter 3, you should recognize that the components listed below are not unique, and you might try devising your own set of components to replace the ones given here. Note that it would be necessary to choose additional components if some of these minerals were more complex solid solutions:
biotite: KMg3AlSi3O10(OH)2, KFe3AlSi3O10(OH)2
garnet: Fe3Al2Si3O12, Ca3Al2Si3O12
sillimanite: Al2SiO5
plagioclase: NaAlSi3O8, CaAl2Si2O8
quartz: SiO2
As we learned in chapter 3, not all of these components may be necessary to define the rock system, if they are not all independent. For example, we can write a mathematical expression between the Ca3Al2Si3O12 component of garnet, Al2SiO5, SiO2, and the CaAl2Si2O8 component of plagioclase (it does not matter that such a reaction might never take place in nature):
Ca3Al2Si3O12 + 2Al2SiO5 + SiO2 = 3CaAl2Si2O8.
Thus we can express anorthite in terms of the other three components. In fact, any one of these four components can be expressed in terms of the other three by rearranging the equation, and so we can delete one of these (take your choice) as a system component. We then are left with five phases and seven components, which give a variance of four. This means that temperature and pressure can be varied independently (within some reasonable limits), as well as the compositions of two phases (for example, biotite and garnet, or garnet and plagioclase), without changing the number of phases in the system at equilibrium.
The discussion so far assumes that the system is closed. However, there are examples of geologic systems in which some components are free to migrate into and out of the system. A common example of such a mobile component is the fluid that is present during the metamorphism of some rocks. We may describe this situation using the same Gibbs-Duhem equations that we formulated before, but in this case, we have an additional restriction. In a closed system, the chemical potentials of all components are the same in every phase, but in an open system, the chemical potentials of mobile components are controlled by phases or other parameters outside of the system. Consequently, we have an additional constraining equation for each mobile component. These additional chemical restrictions r are reflected in the phase rule as additional known relationships. The number of known relationships therefore becomes p + r. Substitution of this value into equation 9.2 produces the relation:
f = (c + 2) − (p + r).
This open-system modification provides an alternative form of the phase rule for systems in which mobile components can be handled.
Worked Problem 9.2
Consider a rock containing calcite, quartz, and wollastonite, which is undergoing metamorphism in equilibrium with a fluid of H2O and CO2. Does the variance of this assemblage change if the system is closed or open to fluid migration?
The system has four phases (H2O and CO2 in the fluid are miscible in all proportions under these conditions). The components of each of the phases can be expressed as:
calcite: CaCO3
quartz: SiO2
wollastonite: CaSiO3
fluid: H2O, CO2
But we can reduce the number of system components from the five listed above to four, because of the following relationship:
CaCO3 = CaSiO3 + CO2 − SiO2.
Under closed-system conditions, the variance of this system is then given by equation 9.2:
f = (4 + 2) − 4 = 2.
Now let’s suppose that this rock is metamorphosed in an open system with a mobile fluid, whose composition is controlled from outside the rock itself. (If this is hard to visualize, consider a situation in which there is a vast reservoir of fluid and only a thin layer of carbonate rock, so that the reaction in the rock exerts virtually no influence on the composition of the fluid that passes through.) As before, we again have four phases and four system components. However, we also have the additional restriction r that the proportions of CO2 and H2O in the fluid are fixed. Solving equation 9.3, we find that the variance is:
f = (4 + 2) − (4 + 1) = 1.
Therefore, metamorphism of this rock under closed-system conditions is divariant, but the system becomes univariant if the mobile fluid composition is controlled from outside the system.
Now let’s return to our discussion of the utility of the phase rule as a test for equilibrium. We still cannot demonstrate equilibrium with certainty, but by examining the variance the system, we can now cite an additional observation that is consistent with equilibrium. In the phase diagram for water (fig. 9.1), it is apparent that most of the area of the diagram is occupied by divariant fields, and those parts of the diagram with lower variance comprise only a tiny fraction of the total area. The same holds true for complex systems such as rocks. Although univariant and invariant mineral assemblages surely are formed under just the right combinations of temperature and pressure, the probability of finding such assemblages in the field is slight compared with the likelihood of sampling divariant assemblages that are stable over a range of temperatures and pressures. For example, locating univariant mineral reactions precisely in a metamorphic terrain may be difficult, because most outcrops will contain either reactants or products, but not both. Some isograds may mark the locations of univariant reactions, but most are probably the first outcrops to be found on the other side of the reaction. We can therefore conclude that most rocks should have variances of two or higher if they have equilibrium mineral assemblages. Those assemblages that appear to be univariant or invariant probably represent disequilibrium in most cases, unless it can be shown by field mapping that these rocks lie between appropriate divariant assemblages.
CHANGING TEMPERATURE AND PRESSURE
You are probably aware that water boils at different temperatures at the seashore and in the mountains. The boundary curve between liquid water and water vapor in figure 9.1 defines the boiling point of water at any given pressure, and its slope explains this phenomenon. Changing conditions of temperature and pressure obviously influence more complex geological systems as well.
It is most convenient to describe modifications in the state of a geochemical system in terms of changes in free energy (ΔG), because differentials of ΔG with respect to T and P are easily evaluated. Recall that the concept of free energy was developed in chapter 3 for fixed T and P conditions. In the following sections, we see how to evaluate ΔG under different sets of temperature and pressure conditions.
Temperature Changes and Heat Capacity
First we examine the effect of changing only temperature on a system at equilibrium. Differentiating the expression dΔḠ = Δ dP − Δ
dP − Δ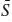 dT with respect to temperature at constant pressure gives:
dT with respect to temperature at constant pressure gives:
(∂ΔḠ/∂T)P = −Δ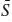 .
.
Because it is often not easy to evaluate the entropy change Δ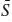 directly, we must resort to using another more readily measurable quantity, enthalpy (Δ
directly, we must resort to using another more readily measurable quantity, enthalpy (Δ ). Since ΔḠ = Δ
). Since ΔḠ = Δ − TΔ
− TΔ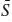 (equation 3.13), equation 9.4 is equivalent to:
(equation 3.13), equation 9.4 is equivalent to:
(∂ΔḠ/∂T)P = (ΔḠ − Δ )/T.
)/T.
Because we are holding pressure is constant in this example, we can rewrite this as:
dΔḠ = (ΔḠ − Δ )dT/T.
)dT/T.
Dividing both sides of this expression by T and rearranging yields:
dΔḠ/T − (ΔḠ)dT/T2 = −(Δ )dT/T2.
)dT/T2.
The left side of this equation is equivalent to d(ΔḠ/T), so that:
d(ΔḠ/T) = −(Δ )dT/T2.
)dT/T2.
If we consider the expression above at standard conditions, then ΔḠ0 and Δ become ΔḠ0 and Δ
become ΔḠ0 and Δ 0, respectively. For a system at equilibrium, ΔḠ0 = −RT ln Keq, so that:
0, respectively. For a system at equilibrium, ΔḠ0 = −RT ln Keq, so that:
d ln Keq/dT = Δ 0/RT2,
0/RT2,
−d ln Keq = [Δ 0/R]d(1/T).
0/R]d(1/T).
Equations 9.5a,b, known in either form as the van’t Hoff equation, provide a useful way to determine enthalpy changes.
Worked Problem 9.3
Determine Δ for the breakdown of annite (the Fe end-member component of biotite) by the reaction:
for the breakdown of annite (the Fe end-member component of biotite) by the reaction:

From equation 9.5b, we can see that Δ 0 can be obtained from a plot of ln Keq versus 1/T. The slope of this line is equivalent to −Δ
0 can be obtained from a plot of ln Keq versus 1/T. The slope of this line is equivalent to −Δ 0/R.
0/R.
Hans Eugster and David Wones (1962) found experimentally that the equilibrium constant for this reaction could be expressed by:
log Keq = −(9215/T) + 10.99.
In other words, a plot of log Keq versus 1/T gave a straight line of slope −9215K. Therefore,

and
Δ 0 = 0 = |
2.303(1.987 cal K−1mol−1)(9215K) |
| = | 42.2 kcal mol−1. |
The van’t Hoff equation works well for standard conditions, but how can we determine enthalpy differences under nonstandard conditions? First let us define a new variable, the heat capacity at constant pressure,  P:
P:
 P = (dq/dT)p = (∂
P = (dq/dT)p = (∂ /∂T)P.
/∂T)P.
If a material is heated at constant pressure, then its molar enthalpy increases with temperature, according to the relationship
dΔ = Δ
= Δ PdT,
PdT,
where Δ is the increase in enthalpy through a temperature interval dT. Tabulations of thermodynamic data for minerals normally give enthalpy at 298 K, and it is necessary to integrate equation 9.6 to obtain enthalpy at any other temperature. Thus, we have:
is the increase in enthalpy through a temperature interval dT. Tabulations of thermodynamic data for minerals normally give enthalpy at 298 K, and it is necessary to integrate equation 9.6 to obtain enthalpy at any other temperature. Thus, we have:

However, heat capacities are not generally independent of temperature, so the integrated form of the expression for Δ P is somewhat complex. The experimental data from which integrated
P is somewhat complex. The experimental data from which integrated  P values are determined are commonly given in the form of a power series:
P values are determined are commonly given in the form of a power series:
 P = a + bT + c/T2,
P = a + bT + c/T2,
where a, b, and c are experimentally determined constants.
Coincident with a change in enthalpy with temperature (equation 9.6), the system will also experience a change in entropy, because
dΔ = T dΔ
= T dΔ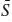
at constant pressure. Consequently, entropy can also be expressed in terms of the heat capacity:
dΔ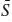 = (Δ
= (Δ P dT)/T.
P dT)/T.
We can obtain the entropy at any temperature by integrating this equation:

We now have all the necessary tools to determine the effect of a change in temperature on the free energy of a system. ΔḠ at any temperature can be evaluated by substituting enthalpy (equation 9.7) and entropy (equation 9.9) values at the appropriate temperature into the familiar equation ΔḠ = Δ − TΔ
− TΔ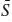 :
:

Worked Problem 9.4
As an example of the use of equation 9.10, determine the free energy change for the following reaction at 800°C and atmospheric pressure:

The thermodynamic data for these phases are given in table 9.1.
After confirming that the reaction is balanced, we calculate Δ values for products (Di + CO2) minus reactants (En + Cc + Qz):

Substitution of these values, along with T = 1073K, into equation 9.10 gives:
| ΔḠ1073 = | 14,720 − 6.38 − 1073(37.01 − .0059) |
| = | −23,304 cal mol−1. |
An interesting variation on this problem is to specify the value of PCO2, say, at 0.1 bar. To solve this problem now, we must first write an expression for the equilibrium constant Keq, which in this case is:
Keq = PCO2 = 0.1 bar.
From the relationship:
ΔḠ = ΔḠ0 + RT ln Keq,
we obtain a value of ΔḠ = −28,833.65 cal mol−1.
Pressure Changes and Compressibility
The effect of changing pressure on a system at equilibrium can be determined by differentiating dΔḠ = Δ dP − Δ
dP − Δ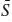 dT with respect to pressure at constant temperature:
dT with respect to pressure at constant temperature:
(∂ΔḠ/∂P)T = Δ .
.
Consequently, the change in free energy of a reaction with respect to pressure alone is equal to the change in the molar volume of products and reactants. Molar volume changes can be determined from simple physical measurements of product and reactant molar volumes. For reactions involving only solid phases under most geologic conditions, the effects of temperature and pressure on Δ are small and can be ignored. In this case, integration of equation 9.10 gives:
are small and can be ignored. In this case, integration of equation 9.10 gives:
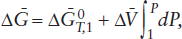
where  is the free energy for the reaction at 1 bar and temperature T.
is the free energy for the reaction at 1 bar and temperature T.
TABLE 9.1. Thermodynamic Data for Worked Problems 9.4 and 9.7

From Helgeson et al. (1978).
Worked Problem 9.5
Consider the polymorphic transformation of aragonite to calcite. Use equation 9.12 to calculate the pressure at which these two minerals coexist stably at 298 K.
At equilibrium, ΔḠ = 0, so:

or
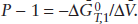
Appropriate thermodynamic data are: 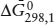 (kJ mol−1) = −1127.793 for aragonite and −1128.842 for calcite;
(kJ mol−1) = −1127.793 for aragonite and −1128.842 for calcite;  (J bar−1) = 3.415 for aragonite and 3.693 for calcite. For the reaction aragonite → calcite, ΔḠ0 = −1049 J mol−1 and Δ
(J bar−1) = 3.415 for aragonite and 3.693 for calcite. For the reaction aragonite → calcite, ΔḠ0 = −1049 J mol−1 and Δ = 0.278 J bar−1. By substituting these values into the equation above, we calculate that P = 3773 bars.
= 0.278 J bar−1. By substituting these values into the equation above, we calculate that P = 3773 bars.
Aragonite has the lower molar volume and is thus the phase that is stable on the high-pressure side of this reaction. Therefore, at 298 K, calcite is the stable polymorph to ∼3.7 kbar pressure. From this computation, we can readily see why aragonite precipitated by shelled organisms at low pressure is metastable.
Equation 9.12 is an extremely useful relationship for determining the effect of pressure on many equilibria of geologic interest. For any reactions involving fluids (such as many metamorphic reactions), however, or for solid phase reactions at very high pressures and temperatures (such as those under mantle conditions), we cannot assume that Δ is independent of temperature and pressure. In these cases, we must take into account the expansion or contraction of a fluid or crystal lattice as temperature changes and the compression or relaxation due to changing pressure. For gases, it is permissible to use an equation of state, such as the ideal gas law
is independent of temperature and pressure. In these cases, we must take into account the expansion or contraction of a fluid or crystal lattice as temperature changes and the compression or relaxation due to changing pressure. For gases, it is permissible to use an equation of state, such as the ideal gas law  = RT/P, to describe the effects of changing temperature or pressure:
= RT/P, to describe the effects of changing temperature or pressure:
(∂ /∂P)T = −RT/P,
/∂P)T = −RT/P,
and
(∂ /∂T)P = R/P.
/∂T)P = R/P.
More complex equations of state for fluids have already been introduced in chapter 3.
For solid phases, we can correct Δ for changing temperature using the thermal expansion, αp, defined as:
for changing temperature using the thermal expansion, αp, defined as:
αP = 1/ (Δ
(Δ /ΔT)P,
/ΔT)P,
where  is the molar volume of the phase at the temperature at which αP is measured. The temperature dependence of αP is large near absolute zero, but becomes small at the temperatures at which most geologic processes operate. If we ignore this small variation, this expression can be rearranged to give:
is the molar volume of the phase at the temperature at which αP is measured. The temperature dependence of αP is large near absolute zero, but becomes small at the temperatures at which most geologic processes operate. If we ignore this small variation, this expression can be rearranged to give:

where  0 is the molar volume at 298 K and 1 bar, and ΔT = T − 298.
0 is the molar volume at 298 K and 1 bar, and ΔT = T − 298.
The effect of changing pressure on Δ is corrected by using the compressibility βT, defined by:
is corrected by using the compressibility βT, defined by:
βT = −1/ (Δ
(Δ /ΔP)T,
/ΔP)T,
where  is the molar volume of the phase at the pressure at which βT is measured and ΔP = P − 1. The effect of pressure on βT can as a first approximation be neglected at pressures < 2 or 3 GPa, although it is very important in interpreting mantle seismic data. If we regard βT as constant in the pressure range where most observable geologic processes operate, this expression becomes
is the molar volume of the phase at the pressure at which βT is measured and ΔP = P − 1. The effect of pressure on βT can as a first approximation be neglected at pressures < 2 or 3 GPa, although it is very important in interpreting mantle seismic data. If we regard βT as constant in the pressure range where most observable geologic processes operate, this expression becomes
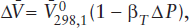
where  0 is the molar volume at l bar and 298°C. By combining the definitions of αP and βT in a total differential expression for
0 is the molar volume at l bar and 298°C. By combining the definitions of αP and βT in a total differential expression for  , we obtain
, we obtain
d = = |
(∂ /∂T)P dT + (∂ /∂T)P dT + (∂ /∂P)T dP /∂P)T dP |
| = | αP dT − βT dT − βT dP dP |
or

This produces the result:
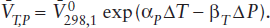
Because the term in parentheses is very small, we can use the approximation exp x ≈ 1 + x to yield:

This last expression allows us to gauge the effect of changing thermal expansion and compressibility on the volume change for a reaction occurring under high-temperature and high-pressure conditions.
Worked Problem 9.6
What is the change in molar volume of forsterite in going from 25 to 800°C and from 1 bar to 5 kbar? To answer this question, we need the following data for forsterite:

Inserting these values into equation 9.13 gives the following result:
 800,5000 = 4.379[1 + (41 × 10−6)(1073 − 298) − (0.8 × 10−6)(5000 − 1)] = 4.501 cm3.
800,5000 = 4.379[1 + (41 × 10−6)(1073 − 298) − (0.8 × 10−6)(5000 − 1)] = 4.501 cm3.
The change in molar volume is thus:
Δ = 4.501 − 4.379 = 0.122 cm3 mol−1.
= 4.501 − 4.379 = 0.122 cm3 mol−1.
Temperature and Pressure Changes Combined
A general equation for the effect of both temperature and pressure on free energy can be obtained by simply combining the equations we have already derived for the effects of temperature alone (equation 9.10) or pressure alone (equation 9.12), as follows:

In using this equation, remember that care must be exercised in obtaining the integrated form of ΔCP, normally done by employing the relationship in equation 9.8. As written, equation 9.14 assumes that thermal expansion and compressibility do not need to be taken into account. However, evaluating Δ the last term for reactions at very high temperatures and pressures or when a fluid phase is present may require equation 9.13.
the last term for reactions at very high temperatures and pressures or when a fluid phase is present may require equation 9.13.
Worked Problem 9.7
Consider again the reaction enstatite + calcite + quartz → diopside + CO2. In worked problem 9.4, we calculated the free energy of this reaction at 800°C and 1 bar. Now calculate the value of ΔḠ at 800°C and 2000 bars pressure, assuming that PCO2 = 0.1 bar.
To do this, we need to make some assumption about (∂ /∂P)T. It is clear that Δ
/∂P)T. It is clear that Δ is not constant, because CO2 is quite compressible. Let’s assume instead that all of the compressibility is due to CO2, and pretend that it is an ideal gas, so that Δ
is not constant, because CO2 is quite compressible. Let’s assume instead that all of the compressibility is due to CO2, and pretend that it is an ideal gas, so that Δ = RT/ΔP. Which is stable under these conditions, reactants or products?
= RT/ΔP. Which is stable under these conditions, reactants or products?
From the data in table 9.1, we can calculate  , ΔCP, and
, ΔCP, and  . (In fact, we have already done this in worked problem 9.4). The change in molar volume Δ
. (In fact, we have already done this in worked problem 9.4). The change in molar volume Δ of CO2 between 1 bar and 2000 bar pressure is (1.987 cal K−1 mol−1)(1073K)/2000 bar = 1.066 cal bar−1. Substituting these values into equation 9.14 gives:
of CO2 between 1 bar and 2000 bar pressure is (1.987 cal K−1 mol−1)(1073K)/2000 bar = 1.066 cal bar−1. Substituting these values into equation 9.14 gives:
ΔḠ800,200 = −30,027.05 cal mol−1
Because ΔḠ is negative, the reaction proceeds as written and diopside + CO2 is stable under these conditions.
A GRAPHICAL LOOK AT CHANGING CONDITIONS: THE CLAPEYRON EQUATION
A phase diagram of temperature versus pressure summarizes a large quantity of data on the stabilities of various phases and combinations of phases in a system. It is important to recognize, however, that such a diagram gives information about the thermodynamic properties of these phases as well. Let’s see how.
The phase diagram for the Al2SiO5 system is illustrated in figure 9.2. Like the phase diagram for water, this is a one-component system containing three possible phases: the polymorphs kyanite, andalusite, and sillimanite. Ignore, for the moment, the dashed horizontal lines. At the beginning of this chapter, we noted that equilibrium is defined as a condition of minimum energy for a system. Therefore, the divariant fields in figure 9.2 represent regions of P-T space where the free energy of the system is minimized by the occurrence of only one phase, and the univariant curves and the invariant point define special combinations of pressure and temperature at which two or more coexisting phases provide the lowest free energy.
To illustrate this relationship between free energy and phase diagrams graphically, we construct qualitative Ḡ-T diagrams at constant pressure for the aluminosilicate system. The traces of such isobaric sections are represented by the horizontal dashed lines in figure 9.2. At pressure P1 and any temperature below T1, kyanite is the stable phase, so it must have a lower free energy than the other Al2SiO5 polymorphs. This is shown in figure 9.3a. Because (∂Ḡ/∂T)P = −Δ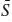 and the entropy of any phase must be greater than zero, free energy decreases in all phases as temperature increases. At temperature T1, the Ḡ-T lines for kyanite and sillimanite intersect, and the coexistence of both phases provides the lowest free energy configuration. At temperatures above T1 sillimanite has the lowest free energy and is the stable phase. Andalusite never appears at this pressure because its free energy is higher than those of the other polymorphs. The Ḡ-T diagram at pressure P2, shown in figure 9.3b, is similar to the P1 case except that the Ḡ-T line for andalusite is depressed so that it intersects those of kyanite and sillimanite at temperature T2, the aluminosilicate triple point. At temperatures other than T2, however, the other polymorphs still offer lower free energy configurations.
and the entropy of any phase must be greater than zero, free energy decreases in all phases as temperature increases. At temperature T1, the Ḡ-T lines for kyanite and sillimanite intersect, and the coexistence of both phases provides the lowest free energy configuration. At temperatures above T1 sillimanite has the lowest free energy and is the stable phase. Andalusite never appears at this pressure because its free energy is higher than those of the other polymorphs. The Ḡ-T diagram at pressure P2, shown in figure 9.3b, is similar to the P1 case except that the Ḡ-T line for andalusite is depressed so that it intersects those of kyanite and sillimanite at temperature T2, the aluminosilicate triple point. At temperatures other than T2, however, the other polymorphs still offer lower free energy configurations.
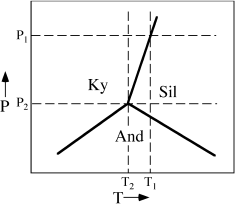
FIG. 9.2. Schematic phase diagram for the system Al2SiO5. Dashed lines represent the traces of isobaric sections used to construct Ḡ-T diagrams.

FIG. 9.3. Ḡ-T diagrams for the system Al2SiO5 at constant pressure: (a) corresponds to pressure P1 in figure 9.2, and (b) corresponds to P2. At any temperature, the stable phase or combination of phases is that with the lowest free energy.
There are other, even more useful relationships between phase diagrams and thermodynamic quantities. In chapter 3, we derived a Maxwell relationship from d (equation 3.8):
(equation 3.8):
(∂P/∂T) = (Δ
= (Δ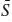 /Δ
/Δ )T,
)T,
which is equivalent to:
dP/dT = Δ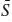 /Δ
/Δ = Δ
= Δ /TΔ
/TΔ .
.
This expression, known as the Clapeyron equation, is extremely useful in constructing and interpreting phase diagrams. Notice that the left side of the Clapeyron equation is the slope of any line in a P-T phase diagram. Thus, this relationship enables us to calculate phase boundaries from thermodynamic data, provided that one point on the boundary is known. Alternatively, ratios of thermodynamic quantities can be obtained from experimentally determined reactions.
Worked Problem 9.8
To illustrate how the Clapeyron equation is used, calculate the approximate slope of the kyanite-andalusite boundary curve in figure 9.2. The data we need are:  (J bar−1) = 4.409 for kyanite, 5.153 for andalusite, and 4.990 for sillimanite;
(J bar−1) = 4.409 for kyanite, 5.153 for andalusite, and 4.990 for sillimanite; 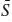 800 (J mol−1 K−1) = 242.42 for kyanite, 251.31 for andalusite, and 252.94 for sillimanite. Inspection of these data indicates the relative positions of the phase fields for the three polymorphs. Kyanite, which has the smallest molar volume, should be stable at the highest pressures, and sillimanite should be stable at the highest temperatures because of its high molar entropy. Substituting values of
800 (J mol−1 K−1) = 242.42 for kyanite, 251.31 for andalusite, and 252.94 for sillimanite. Inspection of these data indicates the relative positions of the phase fields for the three polymorphs. Kyanite, which has the smallest molar volume, should be stable at the highest pressures, and sillimanite should be stable at the highest temperatures because of its high molar entropy. Substituting values of 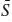 and
and  for kyanite and andalusite into equation 9.15, we obtain:
for kyanite and andalusite into equation 9.15, we obtain:
dP/dT = (251.37 − 242.42 J mol−1 K−1)/(5.153 − 4.409 J bar−1) = 12.03 bar K−1
for the slope of the kyanite-andalusite boundary curve.
To complete the construction of this line, we must fix its position by determining the location of some point along it. The triple point has been located by experiment, although not without controversy (see the accompanying box), and its position can be used to locate this boundary in P-T space. There is a considerable amount of potential error in most calculated P-T slopes because of uncertainties in thermodynamic data. For this reason, it is preferable to determine phase diagrams experimentally. However, calculations such as these can be valuable in estimating how systems behave under conditions other than those under which experiments have been carried out. Calculations also enable the geochemist to limit experimental runs to the probable location of a line or point, thus saving time and money.
Many geochemical reactions involve production of a fluid phase; that is, they are dehydration or decarbonation reactions. At low pressures and high temperatures, H2O and CO2 are not very dense, so reactions that liberate these fluids have large, positive Δ . Consequently, the slopes of the reaction lines on P-T diagrams, dP/dT = Δ
. Consequently, the slopes of the reaction lines on P-T diagrams, dP/dT = Δ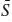 /Δ
/Δ , are small. If the same reactions occur at higher pressures, fluids are more compressed, so that Δ
, are small. If the same reactions occur at higher pressures, fluids are more compressed, so that Δ is smaller and the slopes of the reaction lines are steeper. For this reason, dehydration or decarbonation reactions on P-T diagrams typically are curved upward. Because fluids are more compressible than solids, high pressures may ultimately so compress the fluid that Δ
is smaller and the slopes of the reaction lines are steeper. For this reason, dehydration or decarbonation reactions on P-T diagrams typically are curved upward. Because fluids are more compressible than solids, high pressures may ultimately so compress the fluid that Δ for these reactions becomes negative. However, Δ
for these reactions becomes negative. However, Δ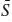 is still positive, so the reaction curves bend back on themselves with negative slopes. This phenomenon is nicely illustrated by the reaction:
is still positive, so the reaction curves bend back on themselves with negative slopes. This phenomenon is nicely illustrated by the reaction:
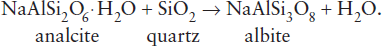
PHASE EQUILIBRIA IN THE ALUMINOSILICATE SYSTEM
The tortuous history of attempts to determine phase equilibria in the aluminosilicate system illustrates the difficulties that can be encountered in this kind of work. E-An Zen summarized the state of affairs in 1969, after decades of experiments, in the diagram shown as figure 9.4. Because of the constant shifting of the position of the aluminosilicate phase boundaries with each new experimental determination, this situation came to be known popularly as the “flying triple point.” Zen discussed a number of causes for this experimental difficulty. One possibility was experimental error, such as incorrect pressure calibration. This might be due to failure to take into account the strength of the material, friction, and other factors in converting the gauge pressure to actual pressure in the sample. He also observed that most of the experiments to that time were synthesis experiments; that is, they were based only on the first appearance of a phase and either failed to demonstrate reversibility or represented some synthesis reaction that did not occur in metamorphic rocks. For example, in one set of experiments, sillimanite was synthesized from gels or kaolinite. Another potential source of error was that some of the polymorphs were synthesized in the presence of water. If they contained small quantities of H2O, the polymorphs would not be true one-component phases.
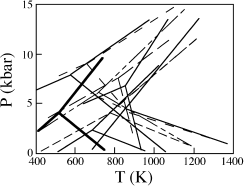
FIG. 9.4. Experimental determinations of phase equilibria in the system Al2SiO5. These data, summarized by Zen (1969), illustrate the difficulties in these measurements. The phase relationships determined by Holdaway and Mukhopadhyay (1993), shown in heavy lines, provide the most commonly accepted value for the aluminosilicate triple point.
The problem has been evaluated more recently by Daniel Kerrick (1990), who summarized data obtained since Zen’s review and critically evaluated potential problems with each experimental determination. Kerrick also considered constraints on the position of the triple point from consistency with thermodynamic data and field calibrations from metamorphic mineral assemblages.
Many metamorphic petrologists now accept the experimental determination of Michael Holdaway and Biswajit Mukhopadhyay (1993) as the best available phase equilibria for this system. The phase diagram of Holdaway and Mukhopadhyay is shown in heavy lines in figure 9.4. Its triple point is located at 504 ± 20°C and 3.75 ± 0.25 kbar. Discrepancies between previous data and Holdaway’s experiments may be explained by the difficulty in measuring small amounts of reaction, the occurrence of fibrolite (a rapidly grown, fine-grained sillimanite often intergrown with quartz), and the presence of Fe2O3 in sillimanite.
For most fluid-release reactions, the slope reversal occurs at very high pressures, but the analcite dehydration reaction, common in low-pressure metamorphic rocks, exhibits a bend-back at very modest pressures (fig. 9.5). The reaction has a small slope at very low pressure, which rapidly becomes negative as pressure increases.

FIG. 9.5. The dehydration reaction for analcite changes slope (dP/dT) and finally bends back on itself with increasing pressure, reflecting the large change in volume of the fluid phase.
RAOULT’S AND HENRY’S LAWS: MIXING OF SEVERAL COMPONENTS
So far in this chapter, we have focused mostly on the effects of changing temperature and pressure on systems with one component. In systems with several components, it is necessary to understand how the various components interact. For example, if we define our system as a grain of olivine, we must determine the behavior of the components Mg2SiO4 and Fe2SiO4 when mixed together. The mixing characteristics of these two components may be very different from the mixing behavior of some trace olivine component such as Ni2SiO4. The interaction of various components in combinations of coexisting minerals, magmatic liquid, or hydrous fluid is in some cases nonideal, resulting in their selective concentration in one phase or another. We now examine the thermodynamic basis for various kinds of mixing behavior.
In an ideal solution, mixing of components with similar volumes and molecular forces occurs without any change in the energy states or total volume of the system. Under these conditions, mixing is neither endothermic nor exothermic, that is, Δ mixing = 0. The activities of components (ai) mixing on ideal sites are thus equal to their concentrations:
mixing = 0. The activities of components (ai) mixing on ideal sites are thus equal to their concentrations:
ai = Xi,
which is a statement of Raoult’s Law.
Interactions between molecules or ions, however, may cause the chemical potentials of individual species to increase or decrease on a certain site, resulting in nonideal mixing. In this case, Δ mixing is not equal to zero, and the activities will deviate from ideal behavior, as illustrated in figure 9.6. However, as the nonideal component becomes increasingly diluted (as Xi becomes much less than one), the component becomes so dispersed that eventually it is surrounded by a uniform environment of other ions or molecules. Therefore, at high dilution, its activity becomes directly proportional (but not equal) to its concentration, as shown by the straight dashed line in figure 9.6. In other words,
mixing is not equal to zero, and the activities will deviate from ideal behavior, as illustrated in figure 9.6. However, as the nonideal component becomes increasingly diluted (as Xi becomes much less than one), the component becomes so dispersed that eventually it is surrounded by a uniform environment of other ions or molecules. Therefore, at high dilution, its activity becomes directly proportional (but not equal) to its concentration, as shown by the straight dashed line in figure 9.6. In other words,
ai = hiXi,
where hi is a proportionality constant. This is a statement of Henry’s Law.
These two laws can be used to explain the mixing behavior of the components of many minerals. Raoult’s Law behavior is a common assumption for many major components of solid solution series, as in the case of the Mg2SiO4 (forsterite) and Fe2SiO4 (fayalite) components of olivine. Henry’s Law is commonly used to describe the behavior of many trace components, such as nickel in olivine.
STANDARD STATES AND ACTIVITY COEFFICIENTS
Chemical potentials are functions of temperature, pressure, and composition. It is common practice to define the chemical potential relative to a chemical potential at some reference value of temperature and pressure (called the standard state), adding a term that corrects this value for deviations in temperature, pressure, and composition:

where μi is the chemical potential of component i at T and P in the phase of interest,  is its value at some standard set of conditions, and ai is the activity of the component. Note that when the component of interest is in its standard state, its activity ai must equal one, so that its logarithm is zero and the second term drops out.
is its value at some standard set of conditions, and ai is the activity of the component. Note that when the component of interest is in its standard state, its activity ai must equal one, so that its logarithm is zero and the second term drops out.
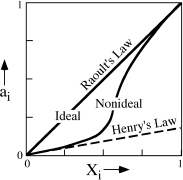
FIG. 9.6. Relations between activity and mole fraction for solutions obeying Raoult’s Law and Henry’s Law. Raoult’s Law may be a good approximation for nonideal solutions in which Xi. is large, and Henry’s Law is applicable to highly diluted components.
The standard state can be chosen arbitrarily, because it has no effect on the final result as long as we are consistent in its use. It might seem most logical to choose the standard state as a pure end-member component at 298 K and 1 bar. However, because of the availability of tabulated thermodynamic data, it is often more convenient to select the standard state as a pure component at the temperature and/or pressure of interest.
The relationships between chemical potential and the activity term in equation 9.16 can be most readily seen in graphical form. Figure 9.7a shows μi versus ln Xi. The line illustrated is not straight (because it is for a real substance that does not mix ideally at all concentrations): it has two linear segments (shown extended with dashed lines). In the straight line segment extending from pure component i (Xi = 1, so that ln Xi = 0) to slight dilution with another component, component i obeys Raoult’s Law (ai = Xi). The slope of this segment is RT and its intercept on the μi axis is  . In the region where Raoult’s Law holds, chemical potential can be expressed as:
. In the region where Raoult’s Law holds, chemical potential can be expressed as:
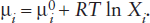
The Henry’s Law region extends from infinite dilution of component i to some modest value and, because ai = hiXi, it is also represented by a straight line in figure 9.7a. Its slope is also RT, but its intercept on the μi. axis is not  . Instead, this intercept is now
. Instead, this intercept is now  plus the added term RT ln hi, which is a function of temperature, pressure, and the composition of the component with which i is diluted, but is not a function of Xi. The expression for chemical potential in the Henry’s Law region, therefore, is:
plus the added term RT ln hi, which is a function of temperature, pressure, and the composition of the component with which i is diluted, but is not a function of Xi. The expression for chemical potential in the Henry’s Law region, therefore, is:

where hi is the Henry’s Law constant for component i in this phase. Combining the two logarithmic terms in this equation gives:


FIG. 9.7. (a) Plot of μi versus ln Xi showing the dependence of chemical potential on composition. In the Raoult’s Law region,  ; in the Henry’s Law region,
; in the Henry’s Law region,  ln hi. The slope of the Raoult’s and Henry’s Law regions is RT. The normal standard state for component i in a pure substance at P and T is
ln hi. The slope of the Raoult’s and Henry’s Law regions is RT. The normal standard state for component i in a pure substance at P and T is  . (b) Plot of μi versus ln Xi showing how the intermediate region changes with activity coefficient. With ideal mixing (γi = 1), the Raoult’s and Henry’s Law regions lie along the same trend. As γi becomes larger, the inflection appears and the intermediate region becomes larger.
. (b) Plot of μi versus ln Xi showing how the intermediate region changes with activity coefficient. With ideal mixing (γi = 1), the Raoult’s and Henry’s Law regions lie along the same trend. As γi becomes larger, the inflection appears and the intermediate region becomes larger.
The intermediate region between Henry’s and Raoult’s Law behavior is characterized by a curved segment that connects the two straight line segments (fig. 9.7a). This region is thus expressed by an equation that is intermediate between equations 9.17 and 9.18. To formulate such an equation, we can describe the degree of nonideality by using γi, the activity coefficient, introduced in chapter 4. The activity coefficient is a function of composition, such that in the Raoult’s Law region,
γi → 1, so that ai → Xi,
and in the Henry’s Law region,
γi → hi, so that ai → hiXi.
Thus we can formulate a general equation for chemical potential of a pure component i in any phase at any temperature and pressure:
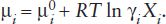
We can see that as component i becomes more similar to the other component with which it is mixing, hi → 1. Moreover, greater similarities in these components will increase the size of the Raoult’s and Henry’s Law regions in figure 9.7a, to the point where the intermediate region disappears and the Raoult’s and Henry’s Law regions connect. In such a case, we would then have one straight mixing line in this diagram (equivalent to the line that extrapolates to  ), and the mixing would be ideal. The effects of changing activity coefficients on the various mixing regions are illustrated in figure 9.7b.
), and the mixing would be ideal. The effects of changing activity coefficients on the various mixing regions are illustrated in figure 9.7b.
Besides the standard state we have just considered, there are others that could be used, and in fact, it is advantageous to do so under certain conditions. Obviously, we must use another standard state if it is not possible to make the phase of interest out of pure component i. For example, we cannot synthesize a garnet of lanthanum silicate, so  in garnet based on the pure phase cannot be determined directly. In this case, the standard state could be a hypothetical garnet with properties obtained by extrapolating the Henry’s Law region to the pressure and temperature of interest. Such a situation is illustrated in figure 9.8a. This is the standard state we assumed without any explanation in chapter 4. In fluids, it is not possible to measure the activity of pure Na+ ions, for example, so we must extrapolate from the dilute salt solution.
in garnet based on the pure phase cannot be determined directly. In this case, the standard state could be a hypothetical garnet with properties obtained by extrapolating the Henry’s Law region to the pressure and temperature of interest. Such a situation is illustrated in figure 9.8a. This is the standard state we assumed without any explanation in chapter 4. In fluids, it is not possible to measure the activity of pure Na+ ions, for example, so we must extrapolate from the dilute salt solution.
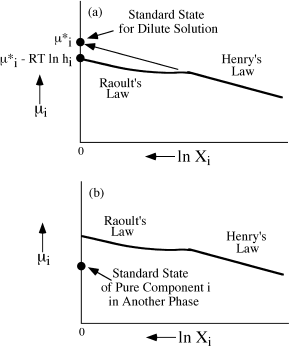
FIG. 9.8. Diagrams of μi versus ln Xi illustrating (a) the standard state for component i in a dilute solution extrapolated from the Henry’s Law region, and (b) the standard state for component i taken as the activity of i in another phase at P and T.
We might also envision a case where component i cannot be studied directly in the phase of interest, but its chemical potential can be analyzed in another phase. This could occur, for example, if we were interested in determining the chemical potential of Al2O3 in a magma but found it easier to study glass quenched from the magma. We could use the activity of Al2O3 in a glass of pure Al2O3 composition to define the standard state. Such a standard state is illustrated in figure 9.8b. The expressions for chemical potentials using other standard states can be derived from equation 9.19.
SOLUTION MODELS: ACTIVITIES OF COMPLEX MIXTURES
Activity coefficients are functions of temperature, pressure, and composition. They can be greater or less than one. The values for activity coefficients cannot be determined from thermodynamic properties but must be obtained experimentally from measurements of ai and Xi or estimated empirically from mineral data. Many different expressions for activity coefficients as a function of composition—often called solution models—have been formulated. The only restrictions on them are that they must obey the constraints given above for the Raoult’s and Henry’s Law regions; that is, they must explain mixing at the extreme ends of the compositional spectrum, where Xi → 1 and Xi → 0.
One solution model that is often used in solving geochemical problems assumes ideal mixing. This is a trivial model, because the expression for γi = 1. From figure 9.7, we can see that the assumption will be correct in the Raoult’s Law region, but will become increasingly less accurate in moving toward the intermediate and Henry’s Law regions. Thus, this solution model works best in cases for which Xi is large.
Another solution model that is commonly used is that for a symmetric regular solution. For this model,

where W is an interaction parameter that is a function of temperature and pressure but not composition, and Xi. Worked Problem 9.9 is the mole fraction of the other component with which component i is mixing. Substitution of this expression in equation 9.20 gives the chemical potential for component i using a symmetric regular solution model:
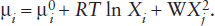
Note that this equation obeys the necessary restrictions in the Raoult’s and Henry’s Law regions. In the case of Raoult’s Law, as  and γi → 1. For Henry’s Law, as
and γi → 1. For Henry’s Law, as 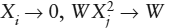 and γi → hi.
and γi → hi.
In the regular solution model, the inflection point in the intermediate region on the μi-ln Xi plot is flanked by symmetric limbs, as illustrated in figure 9.9. However, in real systems, mixing behavior need not be this regular. The asymmetric regular solution model is a somewhat more complex formulation that is also very useful in some situations. This model involves two interaction parameters, Wi and Wj, rather than one as in the regular solution model. For the asymmetric regular solution model,
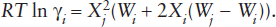
This model can be used in situations in which mixing is not symmetric, as illustrated in figure 9.9. Note that when Wi = Wj, the asymmetric regular solution model reduces to the symmetric regular solution model. This mixing model also obeys the necessary restriction in the Raoult’s and Henry’s Law regions. However, in the Henry’s Law region, RT ln γi → Wi and RT ln γj → Wj.

FIG. 9.9. The difference in mixing behavior for the symmetric and asymmetric regular solution models is illustrated by the shapes of the intermediate regions. The symmetric solution model produces symmetrical limbs flanking the inflection point, and the asymmetric model does not.
Worked Problem 9.9
Calculate the relationship between activity and mole fraction of Fe3Al2Si3O12 (almandine) in a garnet solid solution. Although some geochemists have argued that almandine mixes nearly ideally with Mg3Al2Si3O12 (pyrope), others have advocated a symmetric regular solution model with a temperature-dependent interaction parameter of the form:
WFe-Mg = 3480 − 1.2T,
where T is the temperature in °C and W has units of cal g−1 atom−1. Strictly speaking, regular solution models do not allow for variation of W with temperature, but let’s ignore this minor problem and use this solution model to illustrate how interaction parameters work.
The garnet we consider has the following composition: XFe = 0.710 and XMg = 0.088, along with minor amounts of Ca and Mn. Let’s calculate the activity of Fe in garnet at 827 K or 554°C (the reason this temperature was chosen will become clear shortly). The value of the interaction parameter is therefore:
WFe-Mg = 3480 − 1.2(554) = 2815 cal g−1 atom−1.
Applying this value to equation 9.20, we have:
RT ln γFe = 2815(1 − XFe)2,
or
ln γFe = (2815)(1 − 0.710)2/(1.987)(827) = 0.144
and
γFe = 1.155.
Fe mixes on three crystallographic sites in garnet, so aFe =  . Therefore, the activity of Fe in this garnet is:
. Therefore, the activity of Fe in this garnet is:
aFe = 1.155(0.710)3 = 0.413.
For comparison, for an ideal solution (γFe = 1), the activity of Fe in this garnet would be:
aFe = 1(0.710)3 = 0.446.
THERMOBAROMETRY: APPLYING WHAT WE HAVE LEARNED
The formulation and application of geothermometers and geobarometers involves many of the concepts just introduced. We use one rather simple example of each of these techniques to illustrate how useful the concepts can be in solving geologic problems. For a particular reaction to be used as a geothermometer, it must be a strong function of temperature but be nearly independent of pressure. Conversely, a geobarometer should be sensitive to pressure but not to temperature. We have already seen that at equilibrium:
ΔG0 = − RT ln Keq = Δ − TΔ
− TΔ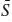 + PΔ
+ PΔ .
.
This equation assumes that Δ is independent of temperature and pressure; otherwise we would have to include expressions for thermal expansion and isothermal compressibility. The form of this equation indicates that if Keq is constant, there is only one equilibrium pressure at any given temperature, and fixing Keq determines the position of the equilibrium reaction curve in P-T space. The factors that control the slopes of equilibrium curves in P-T space can be evaluated by differentiating the above equation with respect to temperature at constant pressure and with respect to pressure at constant temperature:
is independent of temperature and pressure; otherwise we would have to include expressions for thermal expansion and isothermal compressibility. The form of this equation indicates that if Keq is constant, there is only one equilibrium pressure at any given temperature, and fixing Keq determines the position of the equilibrium reaction curve in P-T space. The factors that control the slopes of equilibrium curves in P-T space can be evaluated by differentiating the above equation with respect to temperature at constant pressure and with respect to pressure at constant temperature:
(∂ ln Keq/∂T)P = Δ /RT2
/RT2
and
(∂ ln Keq/∂P)T = −Δ /RT.
/RT.
If the right side of equation 9.23 is larger than that of 9.24, then the equilibrium depends more on temperature than pressure and would be a suitable geothermometer. Thus, we can see that geothermometer reactions should have large values of Δ and, conversely, that geobarometer reactions should be characterized by large Δ
and, conversely, that geobarometer reactions should be characterized by large Δ values. It will also be necessary to have accurate standard-state thermodynamic data for the reaction available, as well as formulations for activity coefficients.
values. It will also be necessary to have accurate standard-state thermodynamic data for the reaction available, as well as formulations for activity coefficients.
Worked Problem 9.10
The partitioning of Fe and Mg between coexisting biotite and garnet serves as a very useful geothermometer. The exchange reaction is:

The enthalpy change for this reaction is large but Δ is quite small, as appropriate for a geothermometer. Available data suggest that Fe and Mg mix almost ideally in biotite and garnet, so we assume that they obey Raoult’s Law and ai = Xi. The Fe-Mg partitioning between these phases is for the most part only a function of T (and, to a lesser extent, P) so long as we assume ideal mixing in both garnet and biotite. No formulation for their activity coefficients is necessary in this case. (Recall that some workers have suggested that a symmetric regular solution model provides a better expression for garnet mixing, as we explored in worked problem 9.9.)
is quite small, as appropriate for a geothermometer. Available data suggest that Fe and Mg mix almost ideally in biotite and garnet, so we assume that they obey Raoult’s Law and ai = Xi. The Fe-Mg partitioning between these phases is for the most part only a function of T (and, to a lesser extent, P) so long as we assume ideal mixing in both garnet and biotite. No formulation for their activity coefficients is necessary in this case. (Recall that some workers have suggested that a symmetric regular solution model provides a better expression for garnet mixing, as we explored in worked problem 9.9.)
There are quite a few expressions for the garnet-biotite geothermometer; we will consider the experimental calibration of John Ferry and Frank Spear (1978). They measured the progress of this exchange reaction at a series of temperatures, and obtained the following expression for T (in kelvins):
ln KD = −2109/T + 0.782,
where KD equals (XMg/XFe)garnet/(XMg/XFe)biotite. (For equilibria in which the same phase or phases appear on both sides of the equation, Keq is commonly called KD, the distribution coefficient.) The coefficients were determined by a linear least-squares fit of the experimental values of ln KD versus 1/T, determined at a pressure of ∼2 kbar. (To see how this is done, refer to appendix A.) Using the Clapeyron equation, Ferry and Spear were also able to calculate dP/dT and, therefore, to estimate the dependence of the reaction on pressure. Their expression for this Fe-Mg exchange reaction at any pressure and temperature is:
ln KD = −(2089 + 0.0096P)/T + 0.782
where P is in bars and T is in kelvins. From this equation, we can see that the effect of pressure on this exchange equilibrium is small, and it can be ignored if no pressure estimate is available. To verify that the error generated by ignoring pressure is small, let’s solve for temperature in two ways.
First, we use this geothermometer to calculate the temperature of equilibration for a metamorphic rock containing garnet and biotite with these compositions:
garnet: XFe = 0.710, XMg = 0.088
biotite: XFe = 0.457, XMg = 0.323
The value of KD is then:
KD = (0.088/0.710)/(0.323/0.457) = 0.1743
Since we do not know the pressure, we can use equation 9.25 to obtain T:
ln 0.1743 = −2089/T + 0.782;
T = 827 K = 554°C.
Let’s now say that we have an independent measure of pressure, determined to be 5 kbar. What effect does including the pressure term have on the calculated temperature? Applying equation 9.26:
−1.743 = −(2089 + 0.0096[5000])/T + 0.782.
Solving this expression for T (our second temperature estimate), we obtain:
T = 846 K = 573°C,
a difference of only 11°C, or about 2°C per kbar of pressure.
Worked Problem 9.11
A useful geobarometer is based on the reaction:
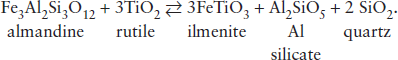
This reaction is almost independent of temperature, but has a large Δ that varies slightly depending on which aluminosilicate polymorph (kyanite, andalusite, or sillimanite) is produced by the reaction. The equilibrium constant for this reaction is:
that varies slightly depending on which aluminosilicate polymorph (kyanite, andalusite, or sillimanite) is produced by the reaction. The equilibrium constant for this reaction is:
Keq = [(ailm)3(aAl2SiO5)(aqz)2]/[(aFe gar)(aru)3].
The great advantage of this particular geobarometer is that so many of the activity terms in equation 9.27 are equal to unity (rutile, quartz, and the aluminosilicate polymorphs form essentially pure phases). Ilmenite forms a solid solution with hematite, but it rarely contains more than 15 mol % Fe2O3 and can be treated as an ideal solution or, in some cases, a pure phase. Fe in garnet can be treated as an ideal solution or as a symmetrical regular solution, as we saw in worked problem 9.8. Consequently, the activity terms for garnet and ilmenite depend on their compositions.
The end-member reaction (involving pure almandine garnet) was calibrated experimentally by Steven Bohlen and coworkers (1983). They then calculated the relationship between P, T, and Keq, which of course takes into account other compositions of garnet and ilmenite. To do this, Bohlen and his collaborators used available data on molar volumes, thermal expansion, and compressibility, and the relationships we have already derived in this chapter. They presented their results in graphical form, contouring log Keq for the reaction on a P-T diagram, as shown in figure 9.10. You can see that the slopes of the log Keq contours in this diagram are very shallow, demonstrating that the reaction is very sensitive to pressure but almost independent of temperature. Also note that the slopes change slightly when contours move from the kyanite field into the sillimanite field or when they cross the α-quartz–β-quartz transition, reflecting changes in Δ of the reaction.
of the reaction.
Let’s use this diagram to determine the equilibration pressure of a metamorphic rock containing rutile, kyanite, ilmenite, and quartz, as well as garnet and biotite with the compositions as in worked problem 9.10. Note that we have already used this same garnet-biotite pair to calculate the temperature (554°C). To keep the problem simple, when calculating Keq, we stipulate that ilmenite is a pure phase. Bohlen and coworkers recommended a symmetric regular mixing model for Fe in garnet, and we have conveniently already used this model (and a temperature of 554°C) to determine aFe in worked problem 9.9. Substituting this value into equation 9.27 gives:
Keq = 1/0.413 = 2.421.
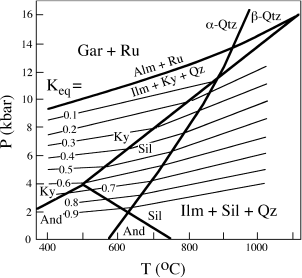
FIG. 9.10. P-T diagram showing the experimentally determined reaction almandine + rutile ⇄ ilmenite + Al2SiO5 + quartz, and contours of log Keq for the reaction with impure garnet and ilmenite compositions, after Bohlen et al. (1983). The slopes of the contours show that the reaction is strongly dependent on pressure but not on temperature (as appropriate for a geobarometer). Boundary curves for the polymorphic transformation of andalusite, kyanite, and sillimanite, and of α-and β-quartz are also shown.
Therefore,
log Keq = 0.384.
Applying this value and a temperature of 554°C to figure 9.10, we obtain a pressure of ∼6 kbar.
Before leaving this problem, let’s see how much difference it would make if instead we had used an ideal solution model for Fe in garnet. From equation 9.27, the value of Keq becomes:
Keq = 1/(0.710)3 = 2.793,
and
log Keq = 0.446.
The log Keq value corresponds to a pressure of about 5 kbar, a difference of 1 kbar.
We have reaffirmed that equilibrium is a condition of minimum free energy for a system. The phase rule provides a useful test for equilibrium. Most geologic systems at equilibrium have variances of two or higher (reflecting the fact that most rocks are stable over a range of temperatures and pressures). The effects of changing temperature and pressure on the free energy of a system can be determined, and the direction of a particular reaction under different conditions can be predicted from appropriate thermodynamic data. The Clapeyron equation illustrates the usefulness of thermodynamic data in assessing the slopes of reactions on P-T diagrams.
Systems containing more than one component require analysis of the way such components interact in the phases that constitute the system. Components that mix ideally obey Raoult’s Law; that is, their activities equal their concentrations. Components at high dilution obey Henry’s Law; that is, their activities are directly proportional to (but not equal to) their concentrations. The chemical potentials of components are generally expressed in the form  ln γiXi (the chemical potential at some standard state plus an activity term that corrects this value for deviations in conditions and composition). Activity coefficients are equal to one for Raoult’s Law behavior and hi for Henry’s Law behavior. Various solution models have been formulated for activity coefficients for components exhibiting intermediate (nonideal) behavior. Solution models find practical application in the formulation of geothermometers and geobarometers.
ln γiXi (the chemical potential at some standard state plus an activity term that corrects this value for deviations in conditions and composition). Activity coefficients are equal to one for Raoult’s Law behavior and hi for Henry’s Law behavior. Various solution models have been formulated for activity coefficients for components exhibiting intermediate (nonideal) behavior. Solution models find practical application in the formulation of geothermometers and geobarometers.
With this thermodynamic background, we are now ready to consider phase diagrams for multicomponent systems. These are introduced in chapter 10.
There are a number of excellent textbooks that provide an introduction to thermodynamics, as well as various geological applications. These generally contain significantly more detail than has been presented here, and are highly recommended for the serious student.
Denbigh, K. 1971. The Principles of Chemical Equilibrium. London: Cambridge University Press. (A classic thermodynamic text containing rigorous derivations but no examples of geologic interest; a superb reference, but not for the fainthearted.)
Ernst, W. G. l976. Petrologic Phase Equilibria. San Francisco: Freeman. (A very readable introductory text; chapter 3 illustrates the computational approach to phase diagrams, and chapter 4 contains descriptions of Ḡ-T diagrams.)
Essene, E. J. 1982. Geologic thermometry and barometry. In J. M. Ferry, ed. Characterization of Metamorphism through Mineral Equilibria. Reviews of Mineralogy 10. Washington, D.C.: Mineralogical Society of America, pp. 153–206. (An excellent review of the calibration, assumptions, and precautions in determining metamorphic temperatures and pressures.)
Kretz, R. 1994. Metamorphic Crystallization. New York: Wiley. (Chapter 2 provides a good description of relations between thermodynamic properties and metamorphic equilibria.)
Philpotts, A. R. 1990. Principles of Igneous and Metamorphic Rocks. Englewood Cliffs: Prentice-Hall. (Chapter 9 of this comprehensive textbook gives an especially good section on solution models.)
Powell, R. 1978. Equilibrium Thermodynamics in Petrology. London: Harper and Row. (An excellent introductory text that dispenses with proofs; chapter 2 describes Ḡ-T diagrams, and chapter 3 gives useful formulations for various standard states not presented in the present book.)
Saxena, S. K. 1973. Thermodynamics of Rock-Forming Crystalline Solutions. New York: Springer-Verlag. (A more advanced book that provides a wealth of information on mixing models and solution behavior for real mineral systems.)
Wood, B. J., and D. G. Fraser. 1977. Elementary Thermodynamics for Geologists. Oxford: Oxford University Press. (A clear and concise introduction to thermodynamics, with numerous worked examples of geologic interest; chapter 3 treats regular solution models, and chapter 4 provides a much more detailed look at geothermometers and geobarometers than is given in the present book.)
These papers were also referenced in this chapter.
Bohlen, S. R., V. J. Wall, and A. L. Boettcher. 1983. Experimental investigations and geological applications of equilibria in the system FeO-TiO2-Al2O3-SiO2-H2O. American Mineralogist 68:1049–1058.
Eugster, H. P., and D. R. Wones. 1962. Stability relations of the ferruginous biotite, annite. Journal of Petrology 3:82–125.
Ferry, J. M., and F. S. Spear. l978. Experimental calibration of the partitioning of Fe and Mg between biotite and garnet. Contributions to Mineralogy and Petrology 66:113–117.
Helgeson, H. C., J. M. Delany, H. W. Nesbitt, and D. K. Bird. 1978. Summary and critique of the thermodynamic properties of the rock forming minerals. American Journal of Science 278A:1–229.
Holdaway, M. J., and B. Mukhopadhyay. 1993. A reevaluation of the stability relations of andalusite: Thermochemical data and phase diagram for the aluminum silicates. American Mineralogist 78:298–315.
Kerrick, D. M., ed. 1990. The Al2SiO5 polymorphs. Reviews of Mineralogy 22. Washington, D.C.: Mineralogical Society of America.
Zen, E. 1969. The stability relations of the polymorphs of aluminum silicates: A survey and some comments. American Journal of Science 267:297–309.
(9.1) Using figure 9.2, construct qualitative Ḡ-P diagrams for the Al2SiO5 system at temperatures T1 and T2.
(9.2) From the understanding that (∂ΔḠ/∂T)P = −Δ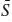 and (∂ΔḠ/∂P)T = Δ
and (∂ΔḠ/∂P)T = Δ , construct a schematic
, construct a schematic 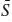 -T diagram at pressure P1 and a
-T diagram at pressure P1 and a  -P diagram at temperature T2 for the Al2SiO5 system (fig. 9.2).
-P diagram at temperature T2 for the Al2SiO5 system (fig. 9.2).
(9.3) Consider an isolated system containing the following phases at equilibrium: (K,Na)Cl, (Na,K)AlSi3O8, and aqueous fluid. (a) Choose a set of components for this system. (b) State the conditions necessary for the system to be in complete equilibrium.
(9.4) Clinoenstatite (MgSiO3) melts incongruently to forsterite (Mg2SiO4) plus liquid at 1557°C at atmospheric pressure. (a) Using thermodynamic data from some reliable source, calculate the chemical potential of SiO2 in the liquid, when these three phases coexist at equilibrium. (b) What will happen to the system if μSiO2 is increased while T and P are held constant?
(9.5) Using the data provided,
(a) Calculate 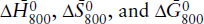 for the following reaction:
for the following reaction:
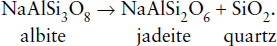
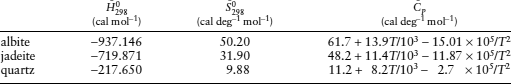
(b) Calculate 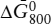 for the reaction assuming Δ
for the reaction assuming Δ P = 0. Compare the two values and comment.
P = 0. Compare the two values and comment.
(9.6) In worked problem 9.8, we calculated the slope of the andalusite-kyanite boundary in P-T space. Its location was fixed using the experimentally determined triple point of Holdaway and Mukhopadhyay discussed in a highlighted box. Using the Clapeyron equation and data in worked problem 9.8, construct the remainder of the aluminosilicate phase diagram. Assume that Δ P = 0 and that
P = 0 and that  is independent of P and T.
is independent of P and T.
(9.7) For the reaction:

(a) Calculate the equilibrium temperature for the reaction at 1000 bars pressure using thermodynamic data from some appropriate source. Assume that Δ P = 0, Δ
P = 0, Δ solids = constant, and that H2O behaves as an ideal gas.
solids = constant, and that H2O behaves as an ideal gas.
(b) Calculate the equilibrium temperature under the same conditions as before, but this time with PH2O = 0.5.
(9.8) Using the values for molar volume, thermal expansion, and isothermal compressibility given below, calculate  for each of these phases at 800°C and 3 kbar.
for each of these phases at 800°C and 3 kbar.
(a) Almandine:
 298,1 = 118.2 cm3 mol−1;
298,1 = 118.2 cm3 mol−1;
αP = 25 × 10−6 deg−1;
βT = 1.27 × 10−6 bar−1.
(b) Quartz:
 298,1 = 22.69 cm3 mol−1;
298,1 = 22.69 cm3 mol−1;
αP = 69 × 10−6 deg−1;
βT = 26.71 × 10−6 bar−1.
(9.9) Calculate ai as Xi increases, using Raoult’s Law and a symmetric regular solution model with W = 10 kJ, and determine how small Xi can become before Raoult’s Law is no longer a good approximation.
(9.10) Given the reactions below, discuss what standard states you would choose for the chemical potentials:
(a) leucite + SiO2 (melt) → orthoclase, at 1 bar and 1170°C;
(b) EuAl2Si2O8 (melt) → EuAl2Si2O8 (plagioclase), at 1300°C and 1 bar;
(c) gypsum → anhydrite + water, at 100°C and 1 kbar.