8
Geostatic Equilibrium: the K₀ Effect

Chapters 3 to 7 were focused on solutions of dissipation relations near the minimum dissipation allowed by selected boundary conditions. This chapter now explores a situation of maximal dissipation, constrained by specific boundary conditions: the geostatic equilibrium of earth pressure “at rest”.

First, some insight is provided into the main features of solutions set by the basic relations for such situations, and the corresponding micromechanical solutions for the statistical distributions of contact internal actions. Then, a simple model is elaborated for the development of this geostatic equilibrium, through composite local micromechanical motions, resulting in bulk mono-dimensional settlement (oedometer-like motion). The main consequence for this composite motion is that global motion stops when the main movement enters the domain of dilatancy because the secondary movement should bear intense volume contraction, which is not sustainable.

The resulting principal stress ratio condition is shown to be close to the classical Jaky formula for dense or medium dense granular materials.

8.1. Background and framework of the analysis

Within a horizontal indefinite soil mass in equilibrium with gravity, global analysis of normal equilibrium conditions and symmetries points to the fact that the principal stresses are vertical and horizontal, and that the ratio between horizontal and vertical stresses is constant. However, this ratio is not statically determined and further assumptions on the buildup of equilibrium stress system in the soil mass, or on the “stress history” leading to this equilibrium, are necessary to reach its evaluation.

This ratio σ_h/σ_v, named “coefficient of earth pressure at rest” or “coefficient K₀”, appears frequently in the design of civil infrastructures (definition of thrusts to be supported), particularly when the works avoid perturbations of the surrounding soil mass equilibrium. This is the case of civil infrastructures in urban areas: roadway trenches in “cut and cover” and other retaining works for deep excavations, underground works [PEC 69, 72], etc., such as access shafts for underground works shown in Figure 8.1 (note the highway and railway nearby the works, requiring special care).

Figure 8.1. Principles of design thrusts for underground works in soft ground. For a color version of the figure, please see www.iste.co.uk/frossard/geomaterials.zip

This coefficient K₀ appears also in the design of tunnel boring machines for soft grounds [MAI 96].

To assess this ratio in granular soils, professionals commonly use the empirical Jaky formula, initially published for the design of silos [JAK 48], linked to the shear strength of the considered soil by its “internal friction,” as measured in common laboratory tests (“triaxial” or shear tests)

[8.1]

This formula is renowned for providing a reasonable assessment of this earth pressure “at rest” stress ratio (see [MES 93, LEE 13]), although the rational basis of this formula has been recently revisited in detail – and shown to not be so clear – by Michalowski [MIC 05].

8.2. The micromechanical process of geostatic stress-building in the soil mass

The present approach also provides an answer, based on the following considerations:

• – The process, which leads to this internal equilibrium, is a sequence of local irreversible internal movements, which occur during the deposition and progressive consolidation of the soil mass, triggered by the evolution of internal forces distribution.
• – This evolution is helped by small fluctuations or small perturbations in external forces, such as seasonal underground water table fluctuations, vibrations and earth tremors.
• – These local elementary internal movements are sets of elementary contact sliding which interfere by an internal feedback effect in such a way that globally there is no global resultant “output power.”
• – The resultant of these local movements is a global motion of uniaxial vertical settlement, belonging to the maximum dissipation motions in the granular mass (Chapter 1, sections 1.2.6 and 1.2.7).
• – The energy dissipated in the process is provided by gravity.
• – The equilibrium is reached when the conditions are such that a significant part of these movements is no longer sustainable.

Let us consider a mass of granular soils constituted by horizontal layers, e.g. by a process of transportation and deposition (streams, wind, etc.). At the moment of its placement, the superficial layer seems to be in an initial equilibrium:

• – near the limit between transportation and deposition, hence near the limit of horizontal shear;
• – in which the principal stresses are neither vertical nor horizontal.

During the building up of the soil mass, a soil layer, which was superficial when deposited, is submitted to a process of burying by increasing vertical stress and rotation of principal stress directions, the major principal stress becoming progressively vertical. This adjustment of the stress system is associated with adjustment in inter-granular forces, which produce local shear movements with local volume variations, whose resultant is globally a maximum dissipation uniaxial motion, globally axisymmetric, with the vertical axis.

8.3. The solutions provided by the multi-scale approach

The previous chapters show that movements in granular materials, once started, tend quickly toward the neighborhood of minimal dissipation motions compatible with boundary conditions (e.g. section 6.1.1, Figure 6.1).

So, in our situation, we assume that the global motion is sufficiently developed (indeed the settlements reach commonly various % in the vertical direction) to display this trend toward the neighborhood of minimal dissipation motions, within the boundary conditions. In other words, the globally monoaxial motion is assumed sufficiently developed toward the combination/juxtaposition of local movements separately near the minimal dissipation.

Such motions have been investigated in [FRO 01]: the global motion, detailed in Appendix A.8.1, results from the juxtaposition of local main movements distributed on the following two components:

• – the main component resulting from a distribution of plane strain direct motions, which receive the energy of gravity, the resultant being a Mode I Direct motion with a vertical axis;
• – a secondary component resulting from another distribution of plane strain reverse motions, which receive the output energy transmitted by the main component, the resultant being a Mode II Reverse motion, also with the vertical axis;
• – the respective participation in the total dissipation is approximately 75% for the main component in Mode I Direct, and 25% for the secondary component in Mode II Reverse, for a typical value of (see Appendix A.8.1);
• – in the equilibrium build-up process within a large soil mass, these two components of motion do not necessarily occur simultaneously and at the same points; they are better considered as distributed within a sufficiently large material domain, over a certain time lapse.

A visualization of these internal movements is shown in Figure 8.2: main movements of the main component in Mode I Direct may be schematized by local motion in plane strain (vertical contraction and horizontal dilatation) whose output energy is absorbed by small secondary local movements of secondary components in Mode II Reverse, also in plane strain (but here with vertical dilatation and horizontal contraction) distributed in a certain influence area, around the place of main motion.

Figure 8.2. Normal geostatic equilibrium – stress adjustment process. (a) Stress adjustment process and associated elementary shear movements. (b) Resultant granular mass tensor P and micro-scale polarization patterns

Figure 8.2 also shows the micro-scale polarization patterns associated with this composite motion, each lobe being scaled according to the corresponding participation in global energy dissipation.

8.4. The resulting K₀ formula based on micromechanics

If there were no movement to ease the adjustment of stresses, an increase in vertical load would increase the ratio . The local shear movements, whose global resultant is uniaxial, attenuate this increase of the ratio because local shear movements with horizontal dilatations locally produce an increase of horizontal normal stress; moreover, these local movements in horizontal dilatations remain constrained by internal compatibility of motion inside the material.

The analysis of composite movement, Appendix A.8.1, shows that under increasing ratio , the particular value (i.e. the characteristic state, see section 5.7) marks the border between two kinds of motions:

• – below this value, the two components (in Mode I and in Mode II) are both contracting in volume;
• – above this value, the main component in Mode I becomes dilatant in volume.

In a situation where the stress state comes outside the characteristic state, as the global motion remains a settlement with volume reduction, the eventual evolution of the main movements in Mode I Direct (otherwise widely predominant) toward dilatancy requires high volume contraction rates in the secondary movements in Mode II Reverse (otherwise widely in the minority) in order to maintain the global motion with volume reduction.

However, high volumetric contraction rates are not sustainable at large extents in granular materials: the jamming resulting between particles quickly blocks the motion and, furthermore, motions in reverse modes are associated with a rapid decrease in the principal stress ratio (see Figures 6.3 and 6.5), making the surrounding stress state restored within the characteristic state limit.

Hence, the above elements lead to the conclusion that the global motion stops:

• – when the ratio falls close to this value , or slightly above;
• – i.e. when the specific volume tends to become stationary, or even slightly dilatant in the main movements;
• – i.e. when the material reaches the characteristic state.

Thus, the present approach leads to the following formula:

[8.2]

8.5. Comparison with empirical Jaky formula

The internal friction Φ displayed in the Jaky formula can be connected to our apparent inter-granular friction 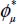, as detailed in Chapter 6 and Appendix A.6.1; however, this relation depends on the degree of compacity of the material, as it involves the dilatancy rate at peak shear resistance (see Appendix A.8.2).

The comparison between the results given by relation [8.1] or [8.2], for dense to medium dense materials (dilatancy rates between 2 and 1.5) is shown in Figure 8.3.

Figure 8.3. Earth pressure coefficient at rest. For a color version of the figure, please see www.iste.co.uk/frossard/geomaterials.zip

The new approach proposed here with an original micro-mechanism for the movements within the material, based on the admissible solution of granular mass mechanics, provides quantitative results in fairly good agreement with commonly used values, in trend and in order of magnitude.

The difference between the results of relations [8.1] and [8.2], shown in Figure 8.3, remains in the range of uncertainties, which affect the existing measured data of this coefficient K₀.

8.6. The two limits of geostatic equilibrium

Now, consider a granular soil mass, initially in normal geostatic equilibrium, which happens to be progressively unloaded by the removal of horizontal layers (effect of erosion or large-scale excavations) (Figure 8.4):

• – in the upper part of the soil mass, the vertical stress decreases, and unless horizontal stresses are adjusted, the ratio decreases;
• – adjustment movements do indeed take place, attenuating this decrease of ratio .

Such movements, in the present approach, are again of the kind of monoaxial vertical movement, associated with the settlement (global contraction in volume), fed by the force of gravity at work.

By a reasoning similar to the preceding one, but here with a decreasing ratio , the ratio of principal stresses at equilibrium obtained is the reciprocal value of the previously calculated K₀, at least in the upper part of the soil mass:

The stress states displayed in this pattern include “trapped” horizontal stresses. In the long term, the relaxation (under small perturbations, such as seasonal underground water table fluctuations, vibrations, and earth tremors) disappears progressively, and the equilibrium falls back to the geostatic “normal” equilibrium.

Figure 8.4. The other limit of the geostatic equilibrium

8.7. Limit of geostatic equilibriums when apparent inter-granular friction vanishes

When apparent inter-granular friction 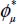vanishes, the two equilibrium coefficients K₀ and K₁ defined above tend toward the value of 1: hence, both equilibrium stress states tend toward isotropy, such as hydrostatic equilibrium.

We have noted that when apparent inter-granular friction vanishes, the features of granular mass mechanics provided by the present approach tend toward the mechanics of “perfect incompressible fluid” (Chapter 5, section 5.5).

The result found here on equilibrium coefficients K₀ and K₁ is consistent with this trend: both geostatic equilibriums tend actually toward the hydrostatic equilibrium (Figure 8.5). A similar effect would also be noted on active and passive thrust coefficients.

Figure 8.5. Geostatic coefficients and hydrostatic equilibrium