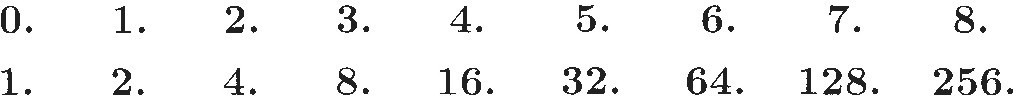
| 27 | Counting Ratios Logarithms |
Put aside your calculator, take out a large sheet of paper, dip your quill pen into your inkwell, and divide 1867392650183 by 496321087, correct to 10 significant digits. When you're done — perhaps after dinner — you might have some idea of the time-consuming drudgery of arithmetic in the late 16th century. That was a time when European astronomy, impelled by such sharp-eyed observers as Tycho Brahe and Johannes Kepler, required more and more exact calculations to distinguish among competing theories of our planetary system and its relationship to more distant parts of the universe.
Astronomers of that time had extensive tables of sines and cosines, some of which were based on a radius of 10,000,000,000 to avoid dealing with fractions. As a result, the typical sine was a nine-digit number. (Decimals were not yet in use.) Since many uses of plane and spherical trigonometry require multiplying and dividing sines and cosines, astronomers had to do a lot of tedious arithmetic. Several tricks were used to make the work easier, but they didn't always work well.
Enter the Scottish "laird" John Napier, a landowning gentleman of leisure. In the 1590s, Napier developed an interest in finding ways to simplify computing with large numbers. He was probably inspired by the double sequence that had appeared in Michael Stifel's Arithmetica Integra of 1544:
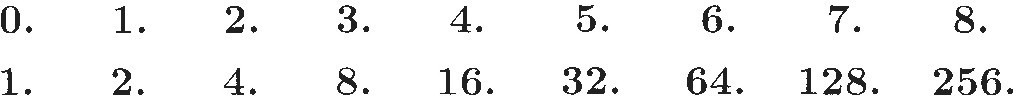
The first of these two sequences is arithmetic — each term differs from its predecessor by the same amount. The second sequence is geometric — each term differs from its predecessor by the same ratio. Mathematicians of the 16th century did not have exponential notation, but they knew how to calculate with numbers in a geometric sequence by "counting" the number of ratio factors for each one. In Stifel's second sequence, for instance, the ratio is 2. and the number of 2s in each term is counted by the first sequence. To multiply two numbers in that sequence (say 8 and 16), it suffices to add the total number of 2s used for each one (3 + 4 = 7) and the product will be the number corresponding to that many factors (128). Similarly, division within the sequence can be done by subtracting numbers of 2s. Of course, many numbers we might want to multiply or divide are not powers of 2.
Initially, Napier's goal was to extend this computational simplicity to the astronomers' table of sines. For clarity and brevity, we use here some present-day algebraic language and notation to describe his work. Most of that, however, was not part of Napier's toolkit. Working at a time before calculus and coordinate geometry, when even the symbols of algebra were not standardized (see Sketch 8), he described his remarkable insights almost entirely in words.
Napier began with the "total sine," which is sin (90°), the radius of the implied circle. He visualized it as a segment TS of length 10,000,000. He envisioned a point g moving from T to S with velocity decreasing so that "in equal times, [it] cutteth off parts continually of the same proportion to the lines [segments] from which they are cut off." For instance, if g moves from T to g1 and from g1 to g2 in equal times, then
For example, g might move a fifth of the way in the first minute, then a fifth of the remaining segment in the next minute, then a fifth of what was left, and so on. (Napier used 1/1000 for his computations.) Clearly, g never arrives at S.
Now, here's the brilliant step. Napier envisioned a corresponding point a on an infinite half-line moving with constant velocity in such a way that, as g passed through each gi point, a passed through the point i. The corresponding positions of a and g at each instant associated each sine with a unique number (generally not an integer) on the half-line. In particular, as a moves through an arithmetic sequence of equally spaced points, the corresponding g-points form a geometric sequence of sines!
At first Napier called those a-numbers "artificial"; then he decided to dub them "ratio numbers" by putting together the Greek words logos (ratio) and arithmos (number) to form logarithm. Napier defined the logarithm of the segment gi S to be i multiplied by a large power of 10 (in order to avoid decimals). This makes the logarithm of the total sine 0. Since the point g never arrives at S, Napier said the logarithm of zero was infinite.
In effect, Napier's geometric intuition had extended the idea of exponents from the counting numbers to the entire real line, even though non-integral exponents were not understood at that time. (Napier seems never to have thought about his logarithms as exponents.)
Napier's logarithms had some very nice properties. The key fact was expressed in terms of ratios: if w x, y, and z are sines such that 
then log(x) – log(w) = log(z) – log(y).1 This was perfect for applications to trigonometry.
The problem was that this elegant dynamic model did not provide a method for calculating the logarithms of specific sines. Napier tackled this problem with ingenuity and doggedness over a period of many years, and finally published Mirifici logarithmorum canonis descriptio ("Description of the marvelous table of logarithms") in 1614. This small book contained 90 pages of logarithmic tables. About 50 more pages described their uses and relations to various geometric theorems, but gave no explanation of how they were constructed. It quickly became a popular tool for astronomers and other scientists. Of course, mathematicians wanted to know how and why it worked. The explanation appeared in Mirifici logarithmorum canonis constructio, which only appeared two years after Napier's death in 1617.
In 1615 a copy of the Descriptio found its way into the hands of Henry Briggs, professor of geometry at Gresham College in London. Briggs was so impressed that he journeyed to Scotland to visit Napier at Merchiston Tower, his home near Edinburgh. He stayed for a month or so, working with Napier to remedy some difficulties in the system. Two critical changes deserve mention. The first was the choice of "starting point." Both men saw a great advantage in modifying the definition so that log(l) = 0. This, coupled with Napier's result about proportions cited above, leads easily to computing products and quotients via sums and differences of logs. The second, less obvious but equally useful, change was the choice of ratio. Briggs made log(l0) = 1014, which allowed his logarithms to work well with our decimal notation for numbers. Once people were more comfortable with decimals, this was simplified to log(10) = 1.
As before, the hard part is computing the actual logarithms, which takes a lot of time. Briggs began by computing (by hand) the square root of 10 to find that 0.5 = log(3.16227766016837933199 889354). He computed square roots 53 more times, ending up with a number very close to 1 whose logarithm is
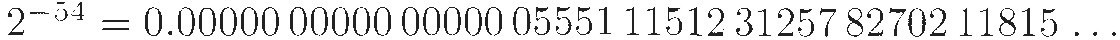
From that he built back up, using the fact that the logarithm of a product is the sum of the logarithms. In 1624 Briggs published Arithmetica logarithmica, a table of the logarithms for the integers 1 to 20,000 and 90.000 to 100,000, accurate to 14 digits. He struggled for the next several years to calculate values for the numbers between 20,000 and 90,000, until a Dutch publisher produced a second edition of Briggs's work (without his knowledge) in which the accuracy was reduced to a mere 10 digits and the missing values were included.
As Napier and Briggs worked in Scotland, the Thirty Years' War was spreading misery on the European continent. One of its side effects was the loss of most copies of a 1620 publication by Joost Bürgi, a Swiss clockmaker. Bürgi had discovered the basic principles of logarithms while assisting the astronomer Johannes Kepler in Prague in 1588, some years before Napier, but his book of tables was not published until six years after Napier's Descriptio appeared. When most of the copies disappeared, Bürgi's work faded into obscurity.
While Briggs was calculating, Grégoire de Saint Vincent, a Belgian Jesuit living in Prague, was studying properties of the area under a hyperbola. One of his results, published in 1647, had major implications for logarithms: If A, B, C, D,... is a sequence of points on the x-axis such that the lengths AB. AC, AD,... increase geometrically, then the areas over these segments and under the hyperbola increase arithmetically. As one of Saint Vincent's students observed in 1648, this implies that the areas between the hyperbola and the x-axis segments are logarithms of some sort. Following the terminology of [70], if the hyperbola is the graph of y = 
we will call the area under it from 1 to some x ≥ 1 the hyperbolic logarithm of x and write it as Hlog(x).
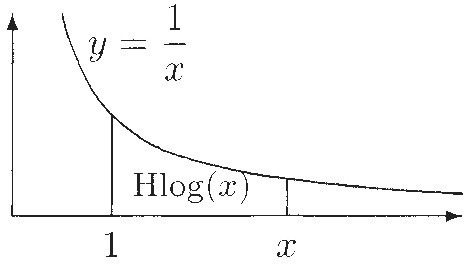
In the 1660s James Gregory, a Scottish mathematician living in Padua in northern Italy, investigated hyperbolic logarithms. Like others of his time, he used large numbers to avoid decimal fractions, which were still relatively unfamiliar despite Napier's extensive use of them. In particular, he used successive approximation with inscribed and circumscribed polygons to calculate Hlog(10). Adjusted by appropriate powers of 10, his result was
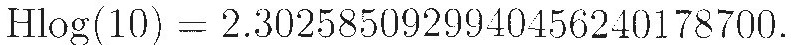
This made it clear that hyperbolic logarithms were not the same as the ones developed by Napier and Briggs. It also showed that a logarithmic relationship may appear "naturally" when computing areas.
As Gregory was working on Hlog in Italy, Isaac Newton in England was investigating area under the hyperbola 
Between 1664 and 1665, Newton determined that the area under this hyperbola from 0 to some 0 < x < 1 can be calculated by the infinite series
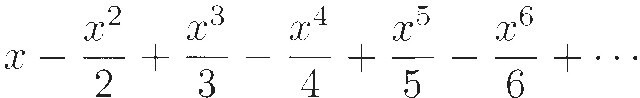
Since this hyperbola is just a translation of y =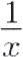 
one unit to the left, this series represents Hlog(l + x) — in our notation, but not in his.
About ten years later, Newton provided one more piece in the Hlog puzzle, albeit indirectly. By that time, integral exponents had been in general use for awhile, as a shorthand for repeated multiplication. Fractional powers, on the other hand, were not commonly used, and this kept Napier and others from thinking of their logarithms in terms of exponents. Around 1675, Newton sent a letter to the Royal Society of London explaining some of his work on infinite series, including his binomial theorem, which gave a series for powers of (1 + x). Because this worked for fractional powers too, Newton described what they meant. This unlocked the door to a more general understanding of the exponentiation process, a door opened wide in the following century.
A systematic description of logarithms as exponents was published in 1742 by William Gardiner, citing William Jones as a source of his work. But what really established this point of view was the authority of the eminent Swiss mathematician Leonhard Euler. His two-volume Introductio in Analysin Infinitorum, the most influential mathematics text of its time, was published in 1748. In it he describes exponentiation as a function y = az for any real number z, presuming without explicit definition that the idea of fractional exponents can be extended to all real numbers. He then says:
'"[C]onversely, given any positive value of y, there is a convenient value of z that makes az = y; this value of z ... is usually called LOGARITHM of y."
But which logarithm? In Euler's approach there is a log function for each positive base a ≠ 1. Euler showed that all logarithms of a number y are multiples of each other. Specifically (in modern terms), for any two bases a and b, there exists a number K (depending on a and b, of course) such that
So which log function is "best"? Is it the base-10 logarithm of Briggs, or Hlog, or something else? To a certain extent, the answer depends on what you're doing. Certainly, Briggsian logarithms are very convenient for making tables and for calculating with our decimal numeration system. But is that the most convenient base for the mathematical theory? Euler resolved that question using infinite series. The main idea works like this.2
For any logarithm, the base is the number whose log is 1. Now consider y = az for some a > 1. Euler used Newton's binomial theorem to expand az in an infinite series involving a constant k whose value depended on the value of a:
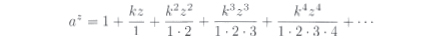
If we choose a "nice" value for a. say a = 2, the constant k turns out to be a very ugly number. Euler decided that it would be best to choose the constant a so that the annoying k would turn out to be equal to 1, making the formula very simple. Euler dubbed this base e (the first letter of "exponential"); so we get
When Euler computed the logarithm function for his carefully chosen base e, he got
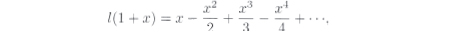
which is the series that Newton had found for Hlog! Thus, the simplest member of the family of log functions is actually the hyperbolic log, known now by Euler's name for it, natural logarithm, and sometimes written "ln(x)".
Finally, using his series expansion, Euler calculated the derivative of f(x) = ln(x), and saw that f'(x) = 
Of all the log functions, this one has the simplest derivative, making it truly deserving of the name "natural."
For a Closer Look: The information for this Sketch was drawn primarily from Chapter 2 of [70] (pp. 68–147). A shorter and very clear account of Napier's work can be found in section 13.2 of [99]. Many sourcebooks provide extracts from the relevant texts.
1 This generalizes the idea that, if two pairs of terms in a geometric sequence are in proportion, then they must be the same number of steps apart.