THE GEOBIOSPHERE builds and maintains structural storages with productive work. Some structural storages are nonliving, such as those of a mountain or a thunderstorm. When inputs decrease, nonliving structures dissipate, and later if energy inputs are again available, self-organization has to start over. With information the products of self-organization carry over from one episode of growth to another, making life, progress, and evolution possible (see chapter 4). The configurations of structural storage are extracted, copied, duplicated, and tested in new applications. This chapter considers structure, information, evolution, and their energy basis.
ENERGY AND STRUCTURE
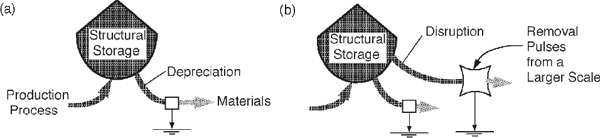
The storage tank symbol (fig. 8.1) represents accumulations of energy and emergy above the surroundings.1 To be sustained, structure has to be continually supplied by processes of productive buildup. As already described with the second energy law, there is spontaneous loss of structure that is called depreciation.

FIGURE 8.1 Energy support and loss from a structural storage (a) with depreciation from small-scale fluctuations; (b) including the disruption losses from large-scale pulses.
The Perpetual Shakedown
The jumping motions of warm molecules in all matter, plus the many kinds of frictions in the world of larger systems, invariably shake structure into disorder. The higher the temperature, the faster the little structures shake apart; and the more weathering processes, mechanical wind processes, destructive radiations, and earth movements there are, the more the large structural patterns become disrupted. The loss of structure is another manifestation of the principle of energy degradation.2 When some of the small molecular structures shake apart as the molecules wander and vibrate, the effects may be very large energetically because there are so many molecules in a small volume.
The classical concept of the second law is too simple because it concerns only one small scale. The destructive pulses from higher levels in the energy hierarchy involve less energy, but they have higher transformity and large effects (fig. 8.1b). There is a second law action at every scale in which the oscillations of the next lower scale wear away structures while the infrequent pulses of the larger scale dismantle structure in bursts. Thermodynamic teaching will remain incomplete until the energetics of different scales is recognized with the fifth law of energy hierarchy (chapter 4).
Self-organization of Nonliving Structure
As explained in chapter 3 (fig. 3.6), productive processes recycle materials and accelerate output with autocatalytic feedback reinforcement (fig. 8.2). Nonliving examples of structural storage include the cold ice in a glacier, a heated house in winter, the elevated rocks of a mountain, the accumulations of water in a lake, or the clouds in the sky (fig. 5.3). Figure 8.2 shows depreciation losses driven by the available energy of the structural storage and energy-aided decrease caused by infrequent actions of larger units. Destruction or consumption by larger-scale units on longer time scales may seem catastrophic to those on a smaller scale. There is net gain and growth when there is a positive balance of inputs and outflows between episodic removal pulses.
Structure and Operation
Structures exist because of the necessary part they play in operations useful to other units and processes. Clouds may be part of operations that generate rain. Mountain storages facilitate the earth cycles; leaf structures are necessary to photosynthetic operations. As drawn in fig. 8.2, the building of structure and the contribution to other operations are mutually reinforcing outputs from the same production process. Whether we are discussing nonliving or living structures, where autocatalytic processes are involved, units may be represented in overview with the hexagonal symbol of fig. 2.10i.
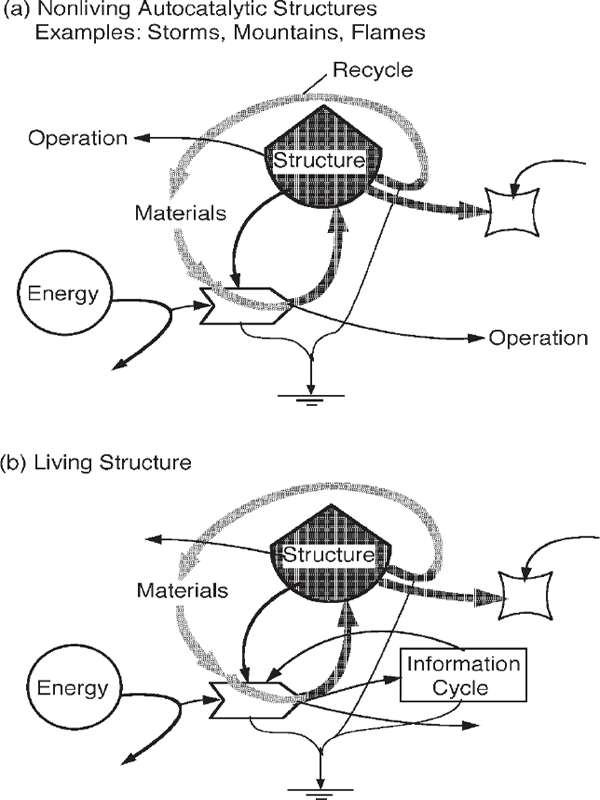
FIGURE 8.2 Comparison of nonliving and living structures, including the main features of self-organizing processes: a renewable energy source, energy transforming interaction, autocatalytic reinforcement, recycling of materials, depreciation, input of disruptive pulses from a larger scale, and contributions to operations upscale and downscale. (a) Nonliving structure; (b) living structure containing an information maintenance loop (see fig. 4.15).
Selection by Reinforcement in Nonliving Systems
Whenever substantial power supplies are available, a selection from among variable energy flows3 rewards and reinforces the pathways that draw the greater power. A familiar example is cumulus cloud formation on sunny summer days (fig. 5.3). The heating of the ground develops variation in many small rising currents that form small competing cumuli that draw on the energy of the stored moisture. The ones that receive the most loop reinforcement draw more air flow and thus more energies, causing the demise of the others. The process of selection may develop a few large-scale thunderstorms by the end of the day. The rising columns are parts of loops of air that pass in downcurrents back to the ground, constituting a mechanism that reinforces the cloud over the rising column and helps it move higher and increase in volume. This is a natural selection process that builds structure by selecting from a variety of contributors the pattern that reinforces energy input.
Another example is the development of branching stream networks (Leopold and Langbein 1962) driven by the potential energy of rain. At first, choice is generated by random development of many small tributary branches. Later, as these varied developing drainage patterns join each other, some are reinforced and others pirated. The cutting of the ground allows the big ones to be reinforced and takes energy away from the smaller ones. The drainage pattern in the land represents structure that is carried to the future as landscape memory.
Many features of fluid dynamics may be explainable in these general systems terms. The ratio of forces required to start eddies is described by Reynolds’s number for two adjacent flows at different speeds and by Richardson’s number for one flow rising from a heat surface relative to another fluid. These numbers indicate energy thresholds for autocatalytic reinforcement for maximum empower.4
INFORMATION AND IMMORTALITY
Apparently missing on many other planets, information developed on earth in the evolution of life and is now operating with the social learning systems of humans and their computers. The development of information vastly improved the ways of building and sustaining structure. As plans are copied, duplicate structures and operations are made and widely shared. By means of information, systems structures could be made, improved, and replaced indefinitely.
In chapter 4, information was introduced as the description of components, configurations, and programmed sequences of functional systems that is sustained by extracting, copying, and reapplication to operations (fig. 4.15). Life is made possible by its information maintenance cycle (fig. 4.15), which is shown as a box in the structural unit in fig. 8.2b.
An item is useful information if using it to reconstruct a system is easier than generating the system from scratch. For example, the electrical system of a radio is a network of parts, connections, and adjusted temporal responses. The essence of the system can be written on paper, including specifications and wiring diagrams. These plans are information, which can be copied, distributed, and shared. With the plan, the radio can be reconstructed without being reinvented.
Thus to repair and replace we can use templates and plans, just as is done in the building industry and in biological reproduction. But even the templates and plans shake apart and develop errors according to the second law.
Carrier Depreciation, Information Loss, and the Correction of Error
Even the information written as ink on paper carries a small content of potential energy. The ink pattern is a chemical concentration capable of depreciation and dispersal (Brillouin 1962), and the paper carrying the information has enough potential energy to drive its own depreciation. If the paper and its ink depreciate, potential energy disperses. Although the potential energy content is tiny, the quality of this information may be great (high transformity) and the loss important.
Figure 8.3 illustrates how error accumulates in structural damage over time. First there are damages that can be repaired, but later there are irreparable errors, and the unit fails (fig. 8.3a). To continue the function, errors have to be repaired by replacement of the structure using the information template (fig. 8.3b). But later, after errors develop in the information template, replacements don’t work, and the function is lost. To sustain the structures and functions indefinitely requires making many copies, using them to make many structures, selecting and keeping those that function best.
Readers will recognize the concepts of natural selection introduced by Darwin to explain the maintenance and evolution of species. The making of more offspring than can survive provides the opportunity for those most suited to surrounding conditions to last and in turn produce more offspring. If all the offspring survive, there is no selection; a choice must be provided by excess creation and mechanisms of selection. The simplest is self-selection by the best adapted.
The concept of natural selection involves the choice by nature from among alternatives provided. In energetic terms, reproducing excess offspring is a power-demanding process that can be measured in terms of the energy flow required for the reproductive process and the offspring.
Thus on one hand we have the shaking and other disordering forces, and on the other hand we have the process of proffering more duplicates than are needed and selecting the best to serve as the templates for the next round. As fast as errors develop in the templates, the selective process takes them out. If too little power is put into super-duplicating and selection, the errors will exceed the repair, and the stock will lose structure and fail.
Information Cycle
To sustain information without error requires continual processing in a circle (figs. 4.15 and 8.4). The plans (information) for successful systems are extracted, copied, distributed, and used to make more structure to operate systems. To be sustained, a system must maintain enough copies without errors, shared widely enough and tested continuously enough to keep the structures functional and competitive. Large-scale patterns of society reproduce and maintain their information with education one generation after another, a process of copying and selecting.
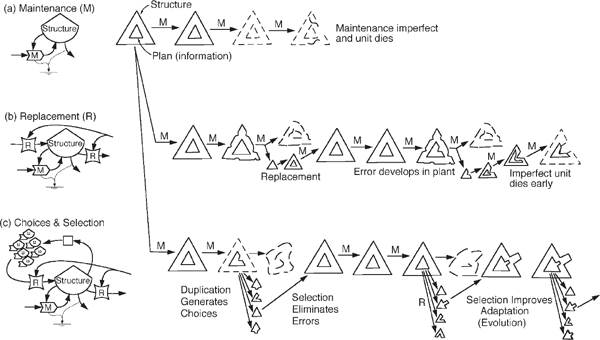
FIGURE 8.3 Sustaining structure, (a) Maintenance work: Structure is maintained, but imperfectly, so that eventually the unit fails, (b) Maintenance and replacement: Structure is maintained, and one unit is reproduced to replace the one that wears out, but eventually errors develop in the plan used for reproduction, and the unit becomes imperfect and dies, (c) Maintenance, replacement, and loop selection of extra choices: Structure is maintained and also has reproductive replacement. There is the additional work of maintaining an error-free plan or generating an improved plan by combining extra reproduction, generating choices and selection that benefits them.
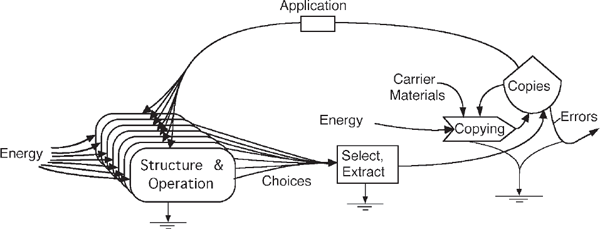
FIGURE 8.4 Cycle of information and operational testing. The cycle includes selection of operations, extraction of information, duplication of plan, distribution for sharing, and reapplication to operations.
Biological examples of the cycle of information and operational testing are the life cycles of species reproduction and dispersal. Thousands and thousands of reproductive life cycles are known to biological science; all are examples of the cycle that maintains genetic integrity. There is a timely need to put all these diagrams on a common basis, arranging the stages from left to right in order of transformity. The empower of a closed loop is the sum of the contributing inputs, which is a constant for the entire loop in any given averaging interval (i.e., one life cycle). Transformities are obtained by dividing the loop empower by the energy flow in each stage.
An example is the salmon life cycle in fig. 8.5, calculated for the Umpqua River in Oregon.5 In the course of one cycle, part of the empower is supplied by the mountain river and part by the oceanic food chain. Transformity is highest in the eggs, which is the stage of extracted information before its dispersal and reapplication to form juvenile fish.
To sustain the system of structure and information, the cycle has to generate and test template copies faster than errors develop. In the rapid evolution of computer software, as in biological evolution, there are many examples where designs were eliminated because the population of users sharing the information was too small or the energy of support too little.
Whatever the scale, fluctuations on a smaller scale generate variations and errors during copying and operation. These variations provide the choices for selection according to the performance of operations. When this process develops an improvement in functions, the progressive change is called evolution.
Structural Life Cycles
To sustain structures indefinitely requires a system of life cycle replacement, whether it is cars, microbes, or landscapes. Main pathways are shown in fig. 8.6.
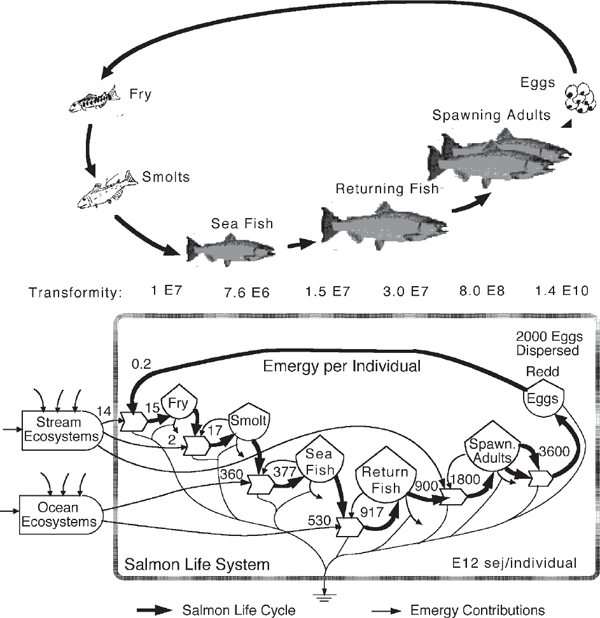
FIGURE 8.5 Life cycle and transformities of salmon, illustrating the cycle of copying, application, selection, extraction, and recycle that sustains a species. NOTE: Emergy units are solar emjoules.
The life cycle of structure includes construction, depreciation, repair, and removal for replacement with new construction. A self-maintaining population pumps in flows of materials and potential energy; combines materials to form parts; throws old parts out, sometimes reusing them as materials; rearranges new parts and disarranged situations; and transforms fuel energies into structural storages of potential energy with the form needed to operate the system.
Figure 8.6 shows the system for sustaining and testing information and structure. In populations of living organisms the system is tightly packaged, whereas the same functions are separate and more flexibly combined in society’s structures. Living structures with capacity for self-repair hold their form and function using a continuous cold fire (biochemical reactions with the energies coupled to do work). Living maintenance is continuous. When an animal or plant tissue is doing nothing except resisting the shakedown, its rate of burning fuel and using oxygen is called basal metabolism. The more structure there is, the more metabolism is required for its support (Mayumi 1991). However, the metabolism per unit structure decreases with size and scale, as explained with fig. 6.6.
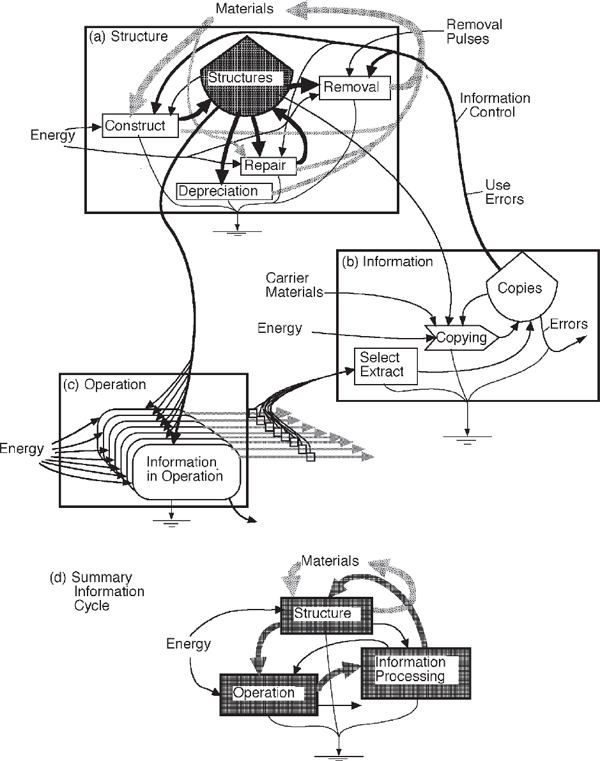
FIGURE 8.6 System of structure, operation, and information necessary to sustain and evolve structure. (a) Structural life cycle with pathways of repair and replacement; (b) information process with selection, extraction, copying, and reapplication for error correction and evolution; (c) set of parallel operations, each organized with a copy of the structural and operational information; (d) summary of the system of structure, information, and operation, with the information circle darkly shaded.
Repair, Senescence, and Replacement
Among higher organisms, the pattern of survival includes some temporary repairs (fig. 8.3a), but generally, a deterioration of structure is allowed, followed by a discard at death, with the new individuals being made with mass production processes (fig. 8.3b). What is repair and what is replacement is a matter of scale. A structure often is repaired by replacing a smaller part. What is replacement on one scale is a part of repair of the next larger scale.
As a structure of connected parts gets older, accumulating damages, making a new one becomes energetically cheaper than repairing the old one. For organisms and cars, the parts are attached and intricately connected so that repair by rearrangement, or by removal and replacement of a part, is difficult. Repair is not a mass production procedure. However, a set of separate unconnected units does not show such collective senescence, and units can be replaced as needed. The pattern is similar in this respect for people, oaks, and automobiles. In the open ecological system the parts are not intimately connected geometrically; therefore, they may be separated and repaired one at a time easily.
Thus senescence and replacement of the whole may be economical when the parts are intimately connected, whereas repair by part replacement and potential immortality may be the pattern when the parts are not intimately connected. Senescence apparently occurs only in physically attached units of such complexity that the requirements of disengaging parts for replacement becomes too high. Senescence is a property of the compact and complex.
Loose associations of mobile organisms are found in lower levels of the energy hierarchy, whereas concentrated, intricately connected, monolithic rigid structures tend to develop where power flows are highly concentrated in hierarchical centers. Examples of unconnected associations are the organisms in plankton of the sea, the scattered plants in a new field, or the houses in suburbs. Examples of connected associations are the reefs of oysters (Copeland and Hoese 1967), heavy root networks of some tropical forests, or the continuous apartment complexes of cities. It is the latter group that develops senescence at the group level as well as in its parts. We are used to the idea in urban renewal that some high-density, continuous structures are more cheaply replaced than repaired. An example in a simpler ecosystem is the senescence of barnacle associations illustrated by Barnes and Powell (1950) and shown in fig. 8.7. When old and top-heavy, they break off or are broken off by animals that serve an urban renewal role in the animal city. New growth and succession refill the gaps.

FIGURE 8.7 Associations that have monolithic structure and develop senescence. (a) Cross-section through crowded barnacle growths from Barnes and Powell (1950); (b) urban ghetto where houses have common walls.
Little Shaking in a Big Corral
To maintain order of a tiny structure, we must repair it more often, for the molecular shaking can break it apart readily if the structure is only slightly larger than the molecules doing the shaking. Many readers may remember seeing demonstrations of Brownian movement through the microscope. Visible particles smaller than bacteria can be seen to shake because of the bombarding and wiggling of the invisible molecules around them.
A structural form can be built on a larger scale and maintained with less if it is made up of large blocks (fig. 8.8). The molecules may wander and disorganize within the small blocks without ruining the desired structure, which is on a larger scale or is in the relationship of the big blocks. Thus, we see such different structures as buildings of bricks or bodies of elephants, with less maintenance required per pound than those of microscopic structures such as electrode metal surfaces and microorganismal bodies. The energy hierarchy (chapter 4) explains why energy transformations and dispersal at microscopic levels can maintain structures of greater dimension but less energy.
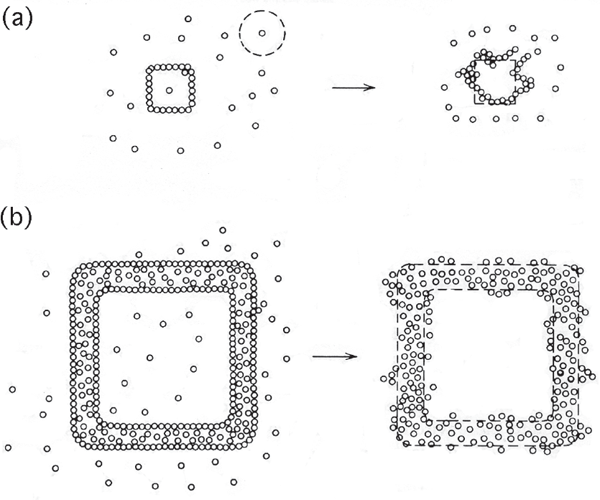
FIGURE 8.8 Comparison of the relative loss of form of large and small squares through random molecular motion. (a) Small square in which the action of one molecule constitutes a large proportion of the form; (b) large square in which the random motions of single molecules are less important, and the form lasts longer without repair.
Levels of Selective Reinforcement in the Energy Hierarchy
As explained by the energy hierarchy in chapter 4, units of each size support and are controlled by units of a larger size. The larger units can select the smaller structures and operations that maximize power contribution, as in fig. 8.9. Rapid processes and pulses on the smaller scale generate variations and choices that are available for selection by larger-scale units to the right. The energy used performs the work of generating the choices and supporting the chosen. Duplicates not chosen may be consumed for energy and materials.
The classification of organisms is a hierarchy with many individuals in a species, many species in a genus, many genera in family, many families in an order, many orders in a class, and many classes in a phylum. Territory and turnover time increase along this scale. The information in the higher categories spreads and distributes the smaller categories while accumulating the products that result from the more successful.6
In plant succession, multiple seeding and initial colonization constitute the choice generator, whereas mineral cycles and developing food chains provide choice machines for rewarding the plants by developing feedback loops.
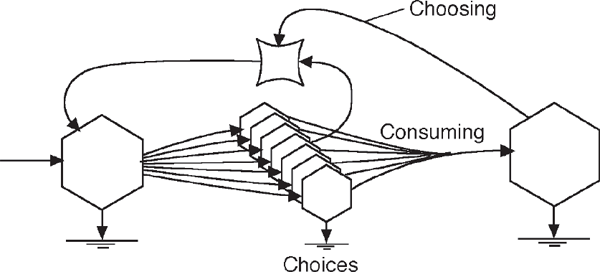
FIGURE 8.9 Information maintenance using 2 levels of the energy hierarchy. For an ecological example, high-level consumers provide choosing services that reinforce maximum power of the prey and predator.
In the embryological development of blood vessels or enzyme systems, the initial proliferation of many possible connections, largely at random, constitutes choice generation; the reward of those that manage to find a reinforcement loop by establishing successful circular flow provides the selection that draws resources from the others and reinforces the chosen. Much evidence of adaptive growth within organisms is given by Goss (1964).
In animal populations, the choice generator is excess reproduction, and the choice machine may be the carnivores selecting the best adapted by eating those less adapted (fig. 8.9). In organized reproductive systems, the mutations and reassortments of genetic mechanisms are the choice generator. In development and progress in industry, the choice generator is the research division, and management serves as the selector.
In higher organisms, selection may be programmed into the behavior of managerial species such as carnivores. In humans, the introduction of will, consciousness, and group-favoring motivations (e.g., religious, economic, egoistic) further specializes the selection of subsystems. These mechanisms help maximize empower.
Reinforcement in Information Networks
Even within the networks of information processing there is organization, with choice generating and selective reinforcement. For example, creative thinking often consists of hours of mental testing and trials that constitute the choice generator. Most of the ideas fail to receive the encouragement of striking a rewarding sensation of truth, but a few are reinforced. Creative thinking therefore relies on an effectively motivated thought generator and a well-developed truth-reward response. People who are not creative may be impatient with the necessary unrewarded probing, may lack a random thought generator, or may not have enough pleasure sensation when the ideas ring true. Creative children, with their half-organized thought generators, often devastate the teacher’s desired classroom order and are disapproved, and their potential for innovation may be discouraged.
Creative special-purpose learning computers have been made, each with a varying device followed by a selection process that fixes the pathways that match some outside criteria (Nilsson 1965).
Figure 8.9 also illustrates the normal process of science. Many kinds of trials called hypotheses are attempted, but the choosing system is empirical measurement that makes certain the concept is loop rewarded by some agreement with nature. In this way, the network of theory grows, joining empirical facts. It is the empirical choosing system that sets science apart from philosophy. Ideas by themselves that do not receive loop reinforcement from real measurement wander off into interesting but unreal patterns. Both working units are required: the idea generator and the chooser.
Coon (1954) describes humans as connectors who transform potential energy into social structure. The shared information of social structure is an emergent property at a higher level based on the contributions of people.
INFORMATION BITS AND ENTROPY
There is a large body of quantitative knowledge concerned with the complexity of information, which is called information theory.
Information Bits
To most people information is a broad term covering words, data, messages, codes, and other inputs to the human mind that are stored in the memory or in libraries and are the basis for effective actions. Shannon and Weaver (1949) provided a quantitative measure of complexity intended to define information. This information index is the logarithm of the number of possibilities. The number of combinations increases as the product of added possibilities. Because logarithms are exponents, adding exponents multiplies the possibilities. In other words, this logarithmic information index is an additive measure of the complexity of possibilities.
This index of information measures the number of possible combinations of components or interconnections, expressing the result in bits. A bit is defined as the amount of uncertainty in the situation of one decision between two possibilities. For example, there is one information bit in flipping a coin, which has two possibilities, heads or tails, requiring one decision to make a choice.7
In any system, some of the possible organization may exist, some may not exist, and some may be unknown. In the following equation, total information bits are the sum of that defined and recorded, that uncertain, and that not organized.
I = Iorganized and known + Iuncertain + Iknown to be unorganized·
For example, consider that there are 16 possible pathways in the system in fig. 2.8, including a path from each unit to itself. A count of these is a measure of the uncertainty inherent in a situation with 16 pathway possibilities. But fig. 2.8 only has eight known pathways. The other possible connections are either missing or unknown.
In networks with one interconnection between each unit, the number of connections increases as the square of the number of units. The energy required for organizing and maintaining the network may be proportional to the number of pathways and increase similarly. The information bit measure indicates the decisions and work necessary to arrange a system, to keep it organized, or to transmit the message to another place or to the future using memory (fig. 8.10).
The information bits in a system are not only in the connections but also in the number of functional units. These information bits are the number of decisions necessary to specify the units.8 Most systems have different kinds of units with different numbers of each kind. There is uncertainty, and thus information bits, in the opportunity for various ratios in different species quite apart from pathway organization, which we have already discussed. The information bit content associated with species composition was introduced by Margalef (1957) and widely used in ecology. Species information is calculated as if the species were letters in a message, which they actually are in the message of inheritance by which ecosystems are maintained and developed. Along with graphic expressions of species diversity, the information bits in species counts are used as a diversity index.9 See chapter 10.
Information Content of Molecular Patterns
At the molecular level with billions and billions of molecules, the information content becomes very large. A gram of water, for example, has about 3 E22 molecules, with an immense number of possible configurations. The information bit content is huge.
Traditionally it is assumed that the molecules are disordered, distributed at random as they move and shake. The heat energy (which is molecular motion energy) keeps the molecules vibrating and shuffling.10 The information bits are regarded as measuring the disorder. However, fig. 4.13 suggests there is a hierarchical organization in the distribution of energized molecules. Let us not assume that molecular complexity is all disorder.
Earlier and independently from the Shannon-Weaver use of information, the logarithm of the number of molecular configurations was found to be a measure of the complexity of chemical substances and, if multiplied by Boltzmann’s constant, identical with entropy.11 Entropy is the information content (uncertainty) of the complexity of the molecular states.
When water evaporates, the molecules move about more freely as vapor, producing even more complexity than before, with more combinations of states possible. The entropy has increased and, in this sense, so has the complexity. After transport to other areas there may be potential energy in the relationships of the water vapor to the surroundings. The energy in the vapor state is called latent heat and is the main fuel of atmospheric storms, where the vapor condenses into cloud droplets (liquid phase), releasing the latent energy, heating the air, and causing winds (fig. 5.6).
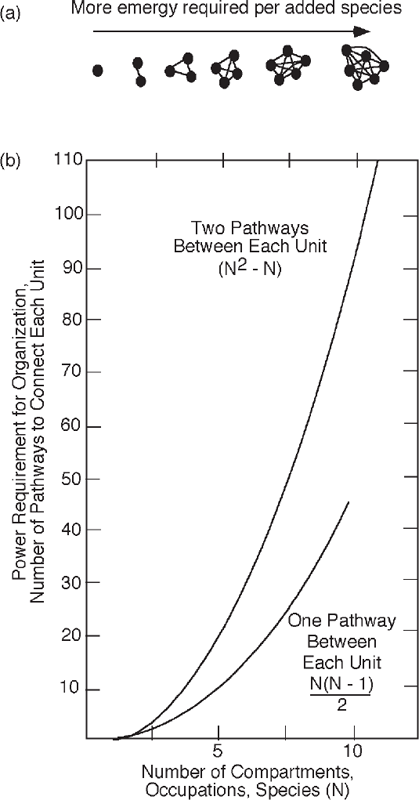
FIGURE 8.10 Emergy required to organize diversity. (a) Emergy and the number of possible connections increasing with number of kinds; (b) power required to connect different populations.
Entropy and Life
Maintaining living structure can be compared to maintaining ice because both have structure that tends to be dispersed by heat. Refrigerators work by removing the disordering heat from the box while storing potential energy in the process. While the refrigerant fluid circulates, the refrigerators store ice at low temperature with available energy relative to surroundings (fig. 8.1a). The entropy is less in the cold ice. As required by the second law, the cooling is possible because much more available energy from the power source is degraded into heat of the environment, an entropy increase. That there has to be an overall increase in molecular entropy is one way of stating the second law.
Using entropy, Schrödinger (1944) put basal metabolism of living organisms into similar language. He said that the high degree of ordered structure (low entropy) in biological tissue is maintained by removing disorder with processes that degrade into environmental heat (high entropy). For example, there is much more available energy in food than is stored as biological, ordered structure. Refrigerators, crystals, tissues, and societies have an ordered structure (improbably low entropy content), which is maintained by continually pumping out into the environment large quantities of dispersing heat so that the overall entropy (storage and environment) always increases. In the nonliving refrigerator system, we maintain a low-temperature, low-entropy storage with less shaking (crystalline ice). In the living system, nonrandom structure is maintained at normal temperature by pumping out the shaking actions that would disrupt it.
However, the Schrödinger description is only half the story because not everything useful has low entropy. Useful storages are maintained at higher temperature than their surroundings, as in the warmth of mammals or heated houses in winter. At high temperatures, the molecular complexity (entropy) is higher than that of the surroundings. Whereas some biological structures such as bone crystals have low entropy, some aspects of living structure have higher complexity than their surroundings. Energy transformations support structural storages that are a mix of low-entropy materials and high-information networks, both maintained away from equilibrium.12 R. E. Ulanowicz and S. Jorgensen initiated other approaches for relating the energy used to the entropy and information supported.13
EVOLUTION
In evolution, not only are the structures and patterns of the system maintained against the disordering influences, but, by definition of the term, novel changes are made, which may be progressive. The origin of life was the start of an information cycle.
The Ecological System Precedes the Origin of Life
Many have wondered how the great complexity of present life could have started from a nonliving world of unorganized chemical substances. The energetic history of the earth suggests that a long time is required to achieve the present complexity of life through step-by-step additions of information. Natural selection organizes by its choices a few bits at a time. As already explained, natural selection operates on nonliving, self-organization as well as on living systems.
Earth energy flows circulate matter and hold ordered patterns of structure by pumping their potential energy budgets down the energetic drain. These flows include those in the world’s wind systems, hurricanes, the water systems of rivers and oceans, and the cycle of erosion, deposition, and mountain building (chapter 5). As long as there is a steady power inflow of potential energy such as sunlight, and as long as there are closed circuits of minerals, a system has the ingredients necessary for duplication, selection, and reinforcement. As shown in fig. 8.11, the circulation of seas provided a route for materials to pass from an upper photochemical zone where sunlight energy is received to a dark zone where chemical reactions can reorganize using stored energy and activated molecules energized by the light. Figure 8.11 suggests some steps in the chemical evolution toward life.
Differences in solar heating circulate waters (fig. 5.1b), which contain mineral elements and organic molecules generated by ultraviolet radiation. At the surface photons cause oxidation–reduction separations, which drive dark reactions. Thus the first part of the modern system of P and R existed before life. While circulating between light and dark zones, the molecules persist that grow longer polymer strands. Natural selection chooses the strands that break, in a kind of primitive reproduction. Thereafter selection favors those that last longer and develop more complex structures. There probably never was an exact moment life started to exist, for the energetics and cycles were already there. The specialization, capsulization, and subdivisions into living units occurred step by step. Information was increased in small increments one choice at a time, bit by bit.
The scheme to explain the origin of life shown in fig. 8.11 is like the production–consumption pattern of the modern biosphere (figs. 1.3f and 2.2) and like the model of choice–loop selection in fig. 8.9. The photochemical action was a choice generator; the circulating fluid provided a reinforcing loop, and competition in the dark selected the units capable of evolutionary change.
Power and Evolution
The rate of evolutionary change depends on the available power. More energy flow generates more choices and selections. Innovation can occur if outside conditions have changed and more power is available than is required to maintain and replace structures and information. For example, more food resource generates extra offspring and more of the larger organisms that select. Without power excess, not much change of structure and information is possible, and losses of structure may occur.
When the environment is changing, the allocation of power may go toward mechanisms of adaptation. Conversely, in times of stability more power goes to make smaller-scale processes efficient. Examples are plants and animals that reproduce asexually when conditions are uniform but apply energy to sexual processes when the environment is changing.
The energy control of evolution applies to any reproducing system on any scale, including primitive organisms and our complex society. The evolutionary changes on a large scale may require emergy inputs of high transformity such as those from the deep earth, astronomical impact, or innovative information.
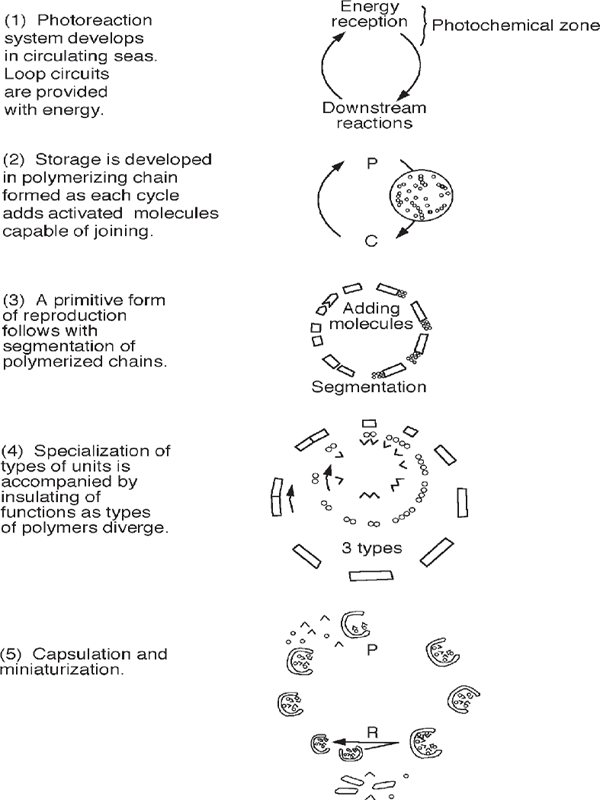
FIGURE 8.11 Diagram of the step-by-step origin of life with the choice–loop–selector mechanisms acting on circulating molecules energized daily with photochemical reactions.
Miniaturization
Many mechanical and electronic systems that are initially large and clumsy later evolve into miniaturized, economical systems. Engines, radios, and computers have gone through such stages of development. Miniaturization provides more function for less power and less space, ultimately allowing more function and complexity for the same resources.
We may suspect a similar history in biological evolution. Many groups of animals and plants first appear in the fossil record as large simple structures and later are replaced by smaller, possibly more efficient species. For example, at first there were large armored fishes, ferns, trees, birds, dinosaurs, giant foraminifers, insects, and so on.
If the origin of life was a step-by-step capsulation of the loose circulations of molecules in the sea, as suggested in fig. 8.11, the earliest forms must have been so large and had so little structure that they left little in the fossil record. Gradually, with miniaturization, some component structures must have become recognizable after millions of years of chemical production and consumption. Such a history would help explain the sudden appearance of advanced fossils in Paleozoic rocks. Life from earlier periods may have been too large and loose to be recognized.
If early life formed in this way, with large loops preceding the small capsules, some of our best-miniaturized modern world dominants such as the bacteria may not have been the earliest forms.
Speciation and Insulation
In chapter 3 we introduced the concept of species as functional and specialized energy flows out of which complex networks were self-designed. The formation of species has been called microevolution, and an extensive literature shows examples of species generation. As summarized by Mayr (1963), a population that becomes divided by space or other factors generates genetic differences by mutations and genetic recombination phenomena. Differences in stocks are then exposed to differences in natural selection so that populations develop dissimilarities. In the language of the previous paragraphs, speciation, like other creative work, involves a variety-generating process followed by a choosing mechanism. However, each species depends on the rest of the ecosystem and its support. Speciation is best considered as the process of adapting parts (populations) to evolving ecosystems.
The development of specific behavioral and chemical means for keeping the species functions separate constitutes insulation of the circuits and is expensive in work drains on the available energy budget. If insulating mechanisms are absent, energies are lost through leaks between circuits. The energy reinforcement for developing species-insulating mechanisms is greater when networks are complex. See, for example, the energy network diagram for a section of a rainforest (fig. 6.18).
In human affairs, the evolution of complex industries with specialized occupations is an equivalent process. Each industry receives selective reinforcement and economic rewards for contribution to the larger economy. Whereas maximizing expansion takes precedence during times of growth on excess resources, contributing to the rest of the system takes priority at other times. See chapter 9 on economic systems for more on macroeconomic designs for maximum empower.
Emergy of Information and Its Hierarchy
Information has the emergy content of developing the first copy, the emergy of making and distributing copies, and the emergy of the users involved. Widely shared information has high transformities and broad influence. Like other series of energy transformations (chapter 4), information networks form hierarchical series in which information entities have increasing transformities, territory, and turnover times. Figure 8.12 shows the transformity of information increasing with increasing territory and replacement time to the right. These bars were calculated by dividing the emergy of formation by the energy carrying the information (DNA for the genetic examples and paper for the book examples).
The emergy per book copy is smaller when there are 1,000 copies but much larger when there is only one copy left. The emergy to make duplicate leaves is small compared with the emergy required to maintain a sustainable population of that tree species. The whole emergy required to evolve a species from its precursor species is assigned to a few copies when a species is endangered. The “Species DNA” on the right assigns the whole emergy of biological evolution to the estimated number of species that have ever existed. The highest transformity in fig. 8.12 is the emergy of life assigned to a culture of algae as if it was the last life in existence.
Apparently greater differences in genetic information require more evolutionary time for development. Thus, the emergy content increases along the scale of biological classification from individual to species to genus to family to order to class and phylum.
INFORMATION SUPPORT
Information Storing and Memory
The development of computers has shown how large quantities of information can be stored as memory by putting it in small, microscopic form on tiny computer chips. The entire set of coded genes for a human being is stored in the microscopic genetic strands in each biological cell. Brains also have a huge capacity for learned information, which is stored in nerve connections, also in microscopic form. But the ability to retrieve and use information is rapidly diluted as the number of stored information items increases. To accumulate information without selection is to lose its use.
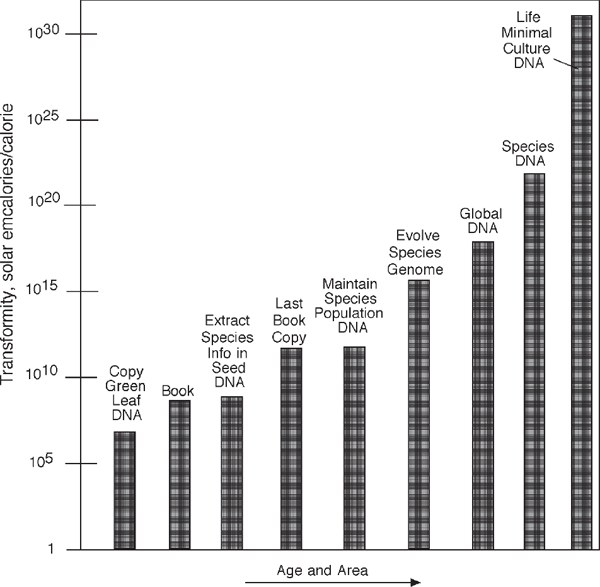
FIGURE 8.12 Transformity of categories of information arranged according to increasing scale of territory and replacement time. Duplicating a leaf, maintaining a forest tree species population, extracting information into a seed, and evolving a tree species were from table 12.1 in Odum (1996). Data are given in joules (J) and solar emjoules (sej).
Emergy of global DNA:
(9.44 E24 sej/yr)(2 E9 years evolution) = 1.9 E34 sej.
Energy of the world’s genes:
(1 g dry live biomass/m2)(5.1 E14 m2/earth)(2 E-3 g DNA/g bio) = 1.0 E12 g DNA/earth;
(1.0 E12 g DNA/earth)(5 kcal/g DNA)(4,186 J/kcal) = 2.1 E16 J DNA.
Transformity = (1.9 E34 sej)/(2.1 E16 DNA/earth) = 9 E17 sej/J.
Emergy of the minimal DNA to sustain the essence of life in a minimal culture was estimated from the time to evolve divided by the minimum sustainable DNA, such as that of a microcosm culture of (1,000 g/m3)(1 E-3 g DNA/g) = 1 g DNA;
(1 g DNA)(5 kcal/g)(4,186 J/kcal) = 2.1 E4 J DNA in minimum life.
Transformity: 1.9 E34 sej to form life/2.1 E4 J DNA min life = 9 E30 sej/J.
Assume size of one individual of a species is about 100g and DNA 0.001 of that, or (0.1 g)(5 kcal/g)(4,186 J/kcal) = 2.1 E3 J;
(1.26 E25 sej/spec)/(2.1 E3 J DNA) = 6 E21 sej/J.
Emergy of a book that took 2 years to write: (2,500 kcal/person/day)(365 d/yr)(2 yr)(4,186 J/kcal)(500 E6 sej/J) = 3.8 E18 sej/book 1st copy manuscript.
1,000 copies and $20 each to produce each copy: ($20,000 service)(1 E12 sej/$) = 2 E16 sej/1,000 books.
If book is (500 g)(4 kcal/g)(4,186 J/kcal) = 8.4 E6 J/book copy.
Transformity per book: (3.82 E18 sej)/(1,000 books) = 3.82 E15 sej/copy; (3.82 E15 sej/copy)/(8.4 E6 J/book copy) = 4.54 E8 sej/J.
If a book is the last copy: (3.82 E18 sej)/1 book=3.82 E18 sej/last copy and (3.82 E18 sej/copy)/(8.4 E6 J/book copy) = 4.54 E11 sej/J.
Brains deal with excess information by processing it through short-term and long-term memory. Items worth saving from the short-term memory are selected and stored in the long-term memory, while the rest is dumped. A good student learns how to learn by training his or her mind to save the right information. The information society is developing an analogous process in which the huge amount of information on the Internet seems to be society’s short-term memory. Heretofore, libraries and scholars have been society’s long-term memory. But books decay and have to be replaced. Storage with air conditioning to reduce the silverfish and dry rot is expensive. A challenge for new technology is to find a better long-term memory for the world’s information explosion.
Although putting information on a microscopic scale increases memory capacity, it also makes the bits more vulnerable to the errors of molecular shaking, as explained with fig. 8.8. Making many copies and distributing them widely protects information (fig. 8.4). Apparently the long-term information in the brain is not local but distributed over the whole. Information shared over the global society also becomes long-term memory with a long replacement time. But the items globally shared are few, and maintaining such broad status requires continuous expensive recopying and replacement. The Bible, the Koran, and the textbooks of elementary education are examples.
Information Transmission and Power
In the transfer of information, there must be some kind of power flow to carry the information, such as the electricity in the telephone line, the sound waves from the radio, or the energy of a flying bird carrying seeds. Although small, information pathways are energy flows and should be shown on the energy diagrams, usually from right to left. For example, see figs. 8.4 and 8.6. In our society, human thoughts are transmitted, stored, restated, and used to control.
Because potential energy self-organizes autocatalytic circuits and energy-dispersing eddies, noise, and short circuits, the amount of byproduct complexity increases with the power. Power lines, highways, factories, jet planes, and fast rivers are noisy. The word noise often is used not only for sound but for all kinds of variations and losses in energy flows.
Because high-power flows are noisy and full of complex variations, they are not the best media for sending information messages. A power administrator does not put a telegraph key on a 100,000-volt power line transmission to the next city. Instead, she might send a message over a low-voltage telephone line. Similarly, we observe that power circuits and information circuits are separated in ecosystems, although both are energy transmissions.
The transmission of information is an important part of any complex system. A plant manager makes his company respond on the basis of a stock market report. A cell makes its biochemical machinery respond on the basis of codes received from its genes. An ecosystem makes its power flows respond on the basis of its memory storages, some of which are biological and some of which may be physical or in libraries, records, rocks, or wood structure. Although there is vastly more energy flow in a power line, a phone message may have very high transformity and be capable of controlling the power line. Items of higher transformity are more easily transmitted and often provide a means to send flows of large empower. Birds flock together before migration, increasing their empower concentration, transformity, and information transmission.
Historical Information and Archaeology
In the earlier history of human evolution little emergy was available for transmitting information to the future. In our current emergy-rich society, we have the luxury of seeking clues in the material remnants of the past for information about early humans. These studies are the field of archaeology. Figure 8.13a shows how the number of these “artifacts” of the past decreases over time with the disordering influences described in this chapter. The emergy of a fossil or pottery remnant is that of its original formation, plus the annual empower of the deposit that protected it, multiplied by the time of preservation, plus the emergy used by archaeologists in collecting it (fig. 8.13b). The information it carries is the emergy of the original number of items (i.e., pottery items) divided by the copies remaining. As time passes, the emergy increases, and the number of copies decrease, so that the transformity and scarcity increase.
Irvin (2000) placed an emergy value of about 100 million emdollars on the Old Spanish Fort Matanzas in Florida by summing the emergy of the coquina rock used, the empower of the builders multiplied by the years required for construction, plus the annual empower of the land times the years since its construction.
Information Limits
Communication engineers describe limits in transmitting messages by the capacity of the channel and the ratio of signal to noise. We have a noisy channel of information transfer from the past to the future. Can we put too many messages in it? What happens when the fuel base of our society decreases and less information can be maintained?
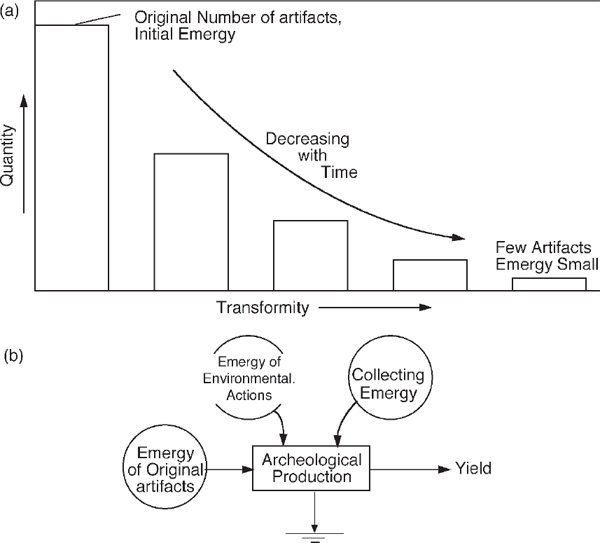
FIGURE 8.13 Emergy of fossils and archeological artifacts. (a) Survival curve of past objects with increasing transformity of its information; (b) emergy inputs to surviving evidence.
The information explosion is a perplexing property of our public decision processes, for energy requirements are large, and great costs are involved. Information development on the west coast of the United States helped create an electrical power shortage in the year 2001. Society is so concerned with the electronic web and information processing that it may be neglecting long-term information storage. Even libraries are using their resources to foster retrieval of Internet information on servers that may not be there in 10 years. Faculty in universities are pressured to do contract research to support students, whereas their traditional role and the long-term need is to consolidate knowledge and develop simplifying principles.
Particularly as resources decline, tough decisions are required as to what books and disks should be saved. What information is most important? There is a limit to what can be supported because access to information decreases as it becomes more complex. Perhaps decisions can be made on what information to save according to its transformity.
SUMMARY
Energy transformations sustain the structures of environment and society through repair and replacement and by sustaining a linked system of controlling information. Similar patterns and processes of organization are found from the molecules to the global scale of society and the economy. On each scale, the energy hierarchy adaptations for maximum power are sustained by generating choices that are selected by the next level. Integrity of information is maintained by a circle of selecting, extracting, copying, and reapplication to operational use, where performance is the basis for further selection and maximum empower. Some structural storages are in the form of high and low complexity, as measured in entropy units, but the emergy per bit increases with scale. A plausible gradual scenario for the origin of life is stepwise selection of emergent chemical structures in circulating fluids energized by pulses of solar energy over geological time. Emergy values are largest in globally shared genetic and learned information. Rates of biological and cultural evolution and the development of structural storages are greatest in times of high power and are expected to decline with the rising scarcity of concentrated fossil fuels.
BIBLIOGRAPHY
Barnes, H. and H. T. Powell. 1950. The development, general morphology and subsequent elimination of barnacle populations Balanus crenatus and B. balanoides, after a heavy initial settlement. Journal of Animal Ecology, 19: 178–179. Sketch of original photograph from Kendigh, S. C. 1961. Animal Ecology. Englewood Cliffs, NJ: Prentice Hall.
Brillouin, L. 1962. Science and Information Theory, 2nd ed. New York: Academic Press.
Coon, C. S. 1954. The Story of Man. New York: Knopf.
Copeland, B. J. and H. D. Hoese. 1967. Growth and mortality of the American oyster Crassostrea virginica in high salinity shallow bays. Publications of the Institute of Marine Sciences, 11: 149–158.
Goss, R. J. 1964. Adaptive Growth. New York: Logos Press, Academic Press.
Irvin, C. 2000. Emergy Evaluation of an Estuarine Reserve in Florida. M.S. research paper, University of Florida, Gainesville.
Jorgensen, S. E., H. Mejer, and S. N. Nielsen. 1998. Ecosystem as self-organizing critical systems. Ecological Modelling, 111: 261–268.
Leopold, L. B. and W. B. Langbein. 1962. The Concept of Entropy in Landscape Evolution. Washington, DC: U.S. Geological Survey Paper 500A.
Margalef, R. 1957. La teoria de la informacion en ecologia. Memorias de la Real Academia de Ciencias y Artes de Barcelona, 32(13): 373–449. Translation in Society of General Systems Yearbook, 3: 360–371.
Mayr, E. 1963. Animal Species and Evolution. Cambridge, MA: Harvard University Press.
Mayumi, K. 1991. A critical appraisal of two entropy theoretical approaches to resources and environmental problems, and a search for an alternative. In C. Rossi and E. Tiezzi, eds., Ecological Physical Chemistry, 109–130. Amsterdam: Elsevier.
Nilsson, N. J. 1965. Learning Machines. New York: McGraw-Hill.
Odum, H. T. 1970. In H. T. Odum and R. F. Pigeon, eds., A Tropical Rainforest. Division of Technical Information TID 24270, U.S. Atomic Energy Commission. Springfield, VA: Clearinghouse for Federal and Technical Information.
———. 1989. Emergy and evolution. In S. C. Holberg and K. Samuelson, eds., Preprints of 33rd Annual Meeting of International Society for the Systems Sciences, Vol. 1, 211–218. Ostersund, Sweden: International Society for the Systems Sciences.
———. 1996. Environmental Accounting, Emergy and Decision Making. New York: Wiley.
———. 2000. Emergy of Global Processes. Folio #2, Handbook of Emergy Evaluation. Gainesville: Center for Environmental Policy, Environmental Engineering Sciences, University of Florida.
Rossi, C and E. Tiezzi, eds. 1991. Ecological Physical Chemistry. Proceedings of an International Workshop Held in Sienna, Italy, November 8–12, 1990. New York: Elsevier.
Schrödinger, E. 1944. What Is Life? Cambridge, MA: Cambridge University Press.
Shannon, C. E. and W. Weaver. 1949. Mathematical Theory of Communication. Urbana: University of Illinois Press.
Ulanowicz, R. E. 1986. Growth and Development, Ecosystems Phenomenology. New York: Springer-Verlag.
NOTES
1. In Environment, Power, and Society, the word order was used for accumulations away from equilibrium. However, that word is ambiguous because it may be used to refer to such regular structures as atoms in a crystal and to very irregular patterns, such as the gases in a hot flame. Nor is entropy a good word for storage with potential. A cold crystal is a low-entropy state, and a hot flame is a high-entropy state, but both may have potential energy relative to the surroundings.
2. This principle is also stated as follows: The universe tends to run down; molecular patterns trend from the less probable to the more probable. In dispersion of energy as discussed in chapter 1, the wandering of molecules from some less probable situation to one more probable is a heat dispersion. The ratio of heat dispersed (Q) to the temperature (T) is called the change of entropy. The molecules wander so as to even up the intensity of their motion (temperature), and the ratio in the section from which the molecules wander goes down more than the ratio goes up in the section into which the molecules wander. Consequently, the overall ratio always increases, counting the whole process of wandering. Thus, this entropy ratio is often said to measure the amount of degradation going on.
3. In Environment, Power, and Society, the source of variation was attributed to randomness. However, small-scale variation was explained in chapter 3 as the normal pulses of smaller scale phenomena rather than inherent randomness. On each size there is a smaller scale that generates choices for the next larger scale to selectively reinforce.
4. The Reynolds number is a dimensionless number in fluid dynamics providing a criterion for dynamic similarity. It is named after Osbourne Reynolds (1842–1912). Typically it is given as follows:
Re = ρνsL/η,
where
νs = mean fluid velocity,
L = characteristic length,
η = (absolute) dynamic fluid viscosity,
ρ = fluid density.
The Reynolds number is used for determining whether a flow is laminar or turbulent.
Richardson’s number (Ri) is used to predict the instability of air. It is the ratio of the static stability (N2) to the square of the wind shear (dU/dz):
Ri = N2/(dU dz)2,
where N2 = (g/q)(dq/dz).
Here U is the wind speed, g the gravitational acceleration (about 9.8 m/s2), q the potential temperature, and z the height.
5. The following are notes on the emergy evaluation of salmon in the Umpqua River, Oregon. Data are based on joules, and emergy is expressed in solar emjoules (sej). There are 4.187 joules per calorie and 4,187 joules per kilocalorie.
Emergy of headwater streams from rain, 32.7 E20 sej/yr; and from geologic emergy of the mountains, 32.0 E20 sej/yr; therefore,
(64.7 E20 sej/yr)/(1.10 E10 m3/yr runoff) = 5.9 E11 sej/m3 H2O.
Emergy of rain at the surface = 2.9 E4 sej/J from table 4 in Folio #2; for
1,000 m, 25.1 E4 sej/g; for 500 m, 19.8 E4 sej/g.
For each cubic meter of rain per year on 1 square meter at average elevation 500 m, emergy from rain is (1.98 E5 sej/g)(1 E6 g/yr) = 2 E11 sej/m3 water/yr.
Emergy from the mountain into that water from a square meter is
(1 m2 area/m3 rain)(32 E20 sej/yr/3.1 E10 m2) = 1 E11 sej/m2/yr.
Sum of rain and geologic input = 2.0 + 1.1 = 3.1 E11 sej/m3 rain on land;
(3.1 E11 sej/m3 rain on land)/(1 E6 g/m3) = 3.1 E5 sej/g rain on land;
(350 m3/sec)(3.15 E7 sec/yr)(1 E3 kg/m3) = 1.10 E13 kg/yr discharge;
(64.7 E20 sej/yr)/(1.10 E16 g/yr) = 5.9 E5 sej/g;
(1.10 E10 m3/yr)/(1.3 E10 m3 rain) = 84.6 % runoff.
Emergy in headwater streams is concentrated from 3.1 E10 g/yr rain to 1.1 E10 g/yr of runoff:
(3.1/1.1)(3.1 E5 sej/g water) = 8.7 E5 sej/g.
Emergy added per redd from share of stream water times its transformity:
(1 m width)(0.1 m depth)(0.1 m/sec)(60 days)(8.64 E4 sec/day)(5.9 E11 sej/m3) = 3.1 E16 m3;
(3.1 E16 m3)/(2,000 eggs/redd) = 1.5 E13 sej/egg emerging;
(1.5 E13 sej/fry)/(1,000 J/ind) = 1.5 E10 sej/J.
Emerging fry:
2 months egg developing in gravels = 20% of eggs (0.2)(2 E8) = 4 E7 eggs remaining.
Smolts = 10% of eggs: (0.1)(4 E7) = 4 E6 individuals; 40 g each.
Energy in individual:
(40 g)(0.2 dry)(5 kcal/g)(4,186 J/kcal) = 1.67 E5 J each; emergy of the added growth:
10% conversion of food energy with transformity: 1 E6 sej/J; energy input used;
(1.67 E5 J/ind)(10)(1 E6 sej/J) = 1.7 E12 sej/ind;
(1.7 E12 sej/ind)/(1.67 E5 J/ind) = 1.0 E7 sej/J.
Emergy of global ocean area:
15.83 E24 sej/yr from Folio #2 (Odum 2000), table 1 divided by area of ocean: (15.83
E24 sej/yr)/(3.61 E14 m2) = 4.38 E10 sej/m2/yr.
Fish at sea = 1% of eggs: (0.01)(2 E8) = 2 E6 fish.
Energy per fish:
(12,000 g/fish)(0.20 dry)(5 kcal/g)(4,186 J/kcal) = 5.0 E7 J/fish.
Fish food per square meter of ocean as 1% of the net primary production:
(4 kcal/m2/day)(365 days)(4,186 J/kcaI)(0.01 efficiency) = 61,116 J/m2/yr.
Transformity: Emergy flow/area divided by the food energy flow:
(4.38 E10 sej/m2/yr)/(61,116 j/m2/yr) = 7.16 E5 sej/J.
Emergy per fish based on 10% efficiency and transformity of food:
(10)(5.0 E7 J/fish)(7.16 E5 sej/J) = 3.6 E14 sej/fish;
(3.6 E14 sej/fish)/(5.0 E7 J/fish) = 7.2 E6 sej/J for sea fish;
Emergy of returning fish, 7.2 E20 sej/yr.
For Umpqua watershed: (408,000 returning fish/yr)/(1.3 E4 km2) = 31.4 fish/km2;
(4.1 E5 ind/yr)(15,000 g/ind)(0.20 dry)(5 kcal/g)(4,186 J/kcal) = 2.57 E 13 J/yr or 6.3 E7 J/fish.
Emergy of sea fish to generate returning fish:
(3.6 E14 sej/ind)(2 E6 fish)/4.1 E5 fish = 1.76 E15 sej/fish, an increment of
(17.6 – 3.8 = 13.8 E14 sej/fish); (1.76 E15 sej/fish)/(6.3 E7 J/fish) = 2.8 E7 sej/J.
Spawning adults=0.1% of eggs; (15,000 g)(0.20 dry)(5 kcal/g)(4,186 J/kcal) = 6.3 E7 J stored.
(4.1 E5 returning)(1.76 E15 sej/ind)/(2 E5 spawning) = 3.6 E15 sej/ind, increment (3.6 E15 sej/ind – 0.9 E15 sej/ind = 2.7 E15 sej/ind); (3.6 E15 sej/ind)/(6.3 E7 J/ind) = 5.7 E7 sej/J.
Eggs from spawning adults: Half females; eggs half of body weight:
(2,000 eggs/adult/yr)(1 E5 female spawning fish) = 2 E8 eggs.
Egg volume:
(0.1)(15,000 g/fish)(1 ml/g)/(2,000 eggs) = 0.75 ml/egg.
Egg energy:
(0.75 ml/egg)(0.10 g dry/ml)(7 kcal/g)(4,186 J/kcal) = 2,197 J/egg.
Emergy:
(3.6 E15 sej/spawning adult)(2 adults)/(2,000 eggs) = 3.6 E12 sej/egg before release.
(3.6 E12 sej/egg)/(2.2 E3 J/egg) = 1.6 E9 sej/J (a value of the isolated information of an egg).
6. A computer simulation model of taxonomic evolution, based on 10,000 years to evolve a species, was used to estimate the emergy of higher categories of systematics (Odum 1989, 1996).
7. Information complexity (I) is defined as the logarithm to the base 2 of the possible combinations (C). Thus, I=log 2 C. A logarithm to the base 2 is the exponent one applies to 2 to get C. When one combines two parts of a system, one may compute the total possible combinations in the new complex by multiplying together the possible combinations in each part. Because logarithms are exponents, one accomplishes this by adding them. Information is thus an additive measure of complexity.
8. The number of decisions needed to specify one unit depends on the number of possible choices. Having defined one unit among a number of units leaves one less possibility for the next decision, two less for the next decision, etc. Therefore, the number of decisions to define the set of units is the factorial of the number. The information bit content is the logarithm of the factorial. To define the four units in fig. 2.8, the number of yes–no choices is 4 × 3 × 2 × 1 = 24. Its logarithm to the base 2 is 3.32log1024 = 4.6 bits.
9. Where a system has many kinds of items, each present in different ratios, such as letters of the alphabet in a message or species in a forest, there is a form of the information formula that gives the bits per individual (H) due to the composition in the system or in information messages used to describe and transmit it. Thus,
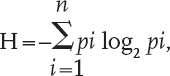
where pi is the probability of each type of item in the system and n is the number of kinds.
10. Heat is the molecular shaking motion; the level of molecular shaking is called temperature. When a person feels hot, his molecules have energy, are shaking more, and indicate this to the person’s conscious self through a sensory system. As the shaking decreases, we say the temperature goes down. At a certain temperature, which is almost reached in some laboratory work, the shaking is zero and the thermometer reads –273°C; temperature cannot go below this point, called absolute zero. The molecules are still and are said to be ordered. The absolute temperature scale starts at absolute zero and thus is at +273°K when water freezes.
If we start adding some of the shaking energy (heat) to material initially at absolute zero, the temperature rises. If we sum up little by little the heat calories added and divide each amount by the temperature at which it was added, according to the entropy quotient formula described earlier, we obtain a gradually increasing quantity that measures how much shaking would have to be removed again to restore the complete order of absolute zero. Thus, the final quantity determined by such calculations is the entropy content of the structure.
11. The Boltzmann–Planck formula is S=k log m, where m is the number of unorganized molecular states, k is Boltzmann’s constant, 33 E-27 kcal/(°C)(molecule). A mole is 6.02 E23 molecules. Here log to the natural base e is used (2.718). To convert units, use the following:
1 cal/degree = 8 E23 bits. There is about 1 bit per molecule for each cal/(°C)(mole).
12. The Schrödinger booklet implied that there is some law about the amount of power flow that has to go into the drain (increasing external disorder and entropy) to sustain each unit of structure and storage against its thermal shaking and other disorganizing tendencies. An appropriate Schrödinger ratio is the ratio of entropy increase required per unit of entropy maintained. This ratio was calculated for the tropical rainforest at El Verde, Puerto Rico, by expressing the energy of metabolism and the potential energy of forest storage in entropy units by dividing each by the environmental temperature (Odum 1970). Where temperatures are similar and constant, the ratio is the replacement rate. Recognizing the concepts of energy hierarchy, Tiezzi suggested that entropy of different scales should be put on a common basis with the concept emptropy, in which each of the heat changes is expressed on a common basis as emergy divided by the Kelvin temperature (Rossi and Tiezzi 1991). In some articles the definition of information and the definition that was independently made for molecules so as to yield entropy were done with different algebraic signs. Either is correct if used consistently. We can talk about positive and negative information bits and positive and negative entropy without really changing anything except the agreed-upon convention. As disordering proceeds, negative entropy increases in magnitude, as does positive entropy. They both would become zero when all disorder is converted into crystalline order at absolute zero.
13. Ulanowicz (1986) developed the concept of ascendency, in which the logarithm of the complexity of pathways (macroscopic entropy) was calculated after the pathways were weighted according to their energy flow. This is an index of the complexity of power circuits. Jorgensen et al. (1998) assigned exergy values to genes by estimating Gibbs free energy weighted according to the probabilities of formation of complex molecules.