Mathematics for the Nonmathematician

CHAPTER 11 PROJECTIVE GEOMETRY

The gods did not reveal all things to men at the start; but as time goes on, by searching, they discover more and more.

XENOPHANES

11–1 THE PROBLEM SUGGESTED BY PROJECTION AND SECTION

The origins of mathematical ideas are far more novel and surprising than is commonly believed. Practical and scientific problems no doubt most frequently suggest new areas of exploration. However, not only are there other sources, but these often give rise to major branches of mathematics, some of which become valuable tools in scientific and practical endeavors. The questions raised by the painters during their work on the mathematics of perspective caused them and, later, professional mathematicians to develop the subject known as projective geometry. This subject, the most original creation of the seventeenth century, is now one of the principal branches of mathematics.

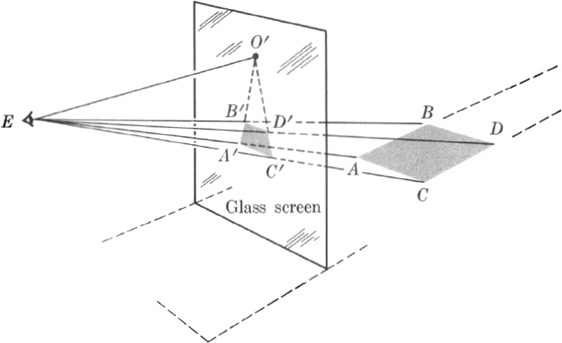
Let us see just what problems led to this development. The basic mathematical concepts in the system of focused perspective are projection and section. A projection we may recall, is a set of lines of light from the eye to the points of an object or scene; a section is the pattern formed by the intersection of these lines with a glass screen placed between the eye and the object viewed.

Fig. 11–1.
The section of the projection of a horizontal square.

Let us consider, as an example, the section of the projection of a square. Suppose that the square is horizontal (Fig. 11–1) and is viewed from a point somewhere above the level of the plane in which it lies. Furthermore, let us suppose that a vertical glass screen is placed parallel to the front and back edges of the square. We know from our work on perspective that the section on the screen of the two sides of the square which are perpendicular to the glass screen will consist of two line segments which tend to meet in the principal vanishing point. That is, the extensions of A′B′ and C′D′ meet at O′. Since the sides AC and BD of the square are parallel to the screen, they give rise to the parallel sections A′C′ and B′D′.

The section A′B′D′C′ is not a square because the sides A′B′ and C′D′ are not parallel. Nor is it a rectangle. The angles, then, of the section do not equal the corresponding angles of the original figure. The size of the section clearly depends upon where the glass screen is placed. Hence neither the lengths of the sides of the section nor the area equals the corresponding quantities in the original figure. In the language of Euclidean geometry, we may say that the section is neither congruent, similar, nor equivalent to the original figure. But the section does create the same impression on the eye as the original figure does. Hence it should possess some properties in common with the original. The question then becomes, What geometrical properties do the section and original figure have in common?

It is a natural step from this question to the next one. If two observers view the same scene from different positions, two different projections are formed (Fig. 11–2). If a section of each of these projections is made, then, in view of the fact that the sections are determined by and suggest the same scene, the sections should possess common geometrical properties. What are they?

Fig. 11–2.
The different sections of two different projections of a square.

These questions, which were originally raised by the artists, could occur to anybody who thinks about what he sees. Suppose that an observer looks at a rectangular picture frame from various positions. The figure he actually perceives varies with his position. Thus he would be led to ask the same question that we raised above, What properties do these various shapes have in common? Again, as a man walks along a street and near a street lamp, his shadow changes in size and shape. The projection here consists of the lines of light from the street lamp, which takes the place of the eye, extending to the outlines of the man’s body and then continuing to the ground. The section made by the plane of the ground is the shadow, although in this case the lamp and the section are on opposite sides of the actual object. The mathematical question raised by this example is, What properties do the various shadows have in common?

Another familiar, contemporary example illustrating projection and section is the photograph. In this case, the eye is the lens of the camera, and rays of light proceed from the scene through the lens to the film. The section is made by the film. We know that different sections can be obtained by placing the camera closer or farther from the scene being photographed or by tilting the camera. Yet all photographs of the same scene should contain some common geometrical properties.

The study of properties common to a figure and a section of a projection of that figure, or to two sections of the same projection, or to two sections of two different projections of the same figure has led to new concepts and theorems which today comprise a whole new branch of geometry, namely projective geometry. We shall attempt in this chapter to gain some understanding of the nature of this subject.

11–2 THE WORK OF DESARGUES

If we study any section of the projection of a figure and consider its relation to the original figure, then a few facts are readily noted. Mathematically the eye is a point, and this point and any line in the actual figure determine a plane, which is the projection determined by the line. The glass screen which cuts the projection is also a plane, and since two nonparallel planes meet in a line, the section is a line. Hence corresponding to a line in the actual scene there is a line in the section. We may therefore say that the property of linearity is common to an actual line and any section of a projection of that line. Similarly, it is easy to visualize that two intersecting lines of the actual figure will generate two intersecting lines in the section. This, then, is another minor mathematical property which is common to actual object and section. It follows that a triangle will give rise to a triangular section, although the shape of the triangle in the section will not necessarily be the same as that of the original triangle. Likewise a quadrilateral will correspond to a quadrilateral.

But the discovery of these few properties which a figure and its section or two sections of the same projection have in common hardly elates one nor does it give us any significant answers to the question of what properties figures and sections or various sections have in common. The first man to explore the problem and come up with nontrivial answers was Girard Desargues (1593–1662). Desargues was not a professional mathematician; he was a self-educated architect and engineer. His motive in tackling the subject was to help his colleagues. He believed that he could compile in compact form the many theorems on perspective that were useful to architects, engineers, painters, and stone-cutters. He even invented a special terminology which he thought would be more comprehensible to craftsmen and artists than the usual mathematical language. Of his motives Desargues writes:

I freely confess that I never had taste for study or research either in physics or geometry except in so far as they could serve as a means of arriving at some sort of knowledge of the proximate causes . . . for the good and convenience of life, in maintaining health, in the practice of some art, . . . having observed that a good part of the arts is based on geometry, among others the cutting of stone in architecture, that of sundials, that of perspective in particular.

Desargues began by organizing numerous theorems and published one book on the construction of sundials and another on the application of his own geometric theories to stone-cutting and masonry. He lectured in Paris about 1626, and wrote a pamphlet on perspective ten years later. Desargues’ chief contribution, a book on projective geometry, appeared in 1639.

The basic theorem of projective geometry, a theorem now fundamental in the entire field of mathematics, was formulated and proved by Desargues and is named after him. It illustrates how mathematicians responded to the questions raised by perspective.

Suppose the eye at point O (Fig. 11–3) looks at a triangle ABC. The lines from O to the various points on the sides of the triangle constitute, as we know, a projection. A section of this projection will then contain a triangle, A′B′C′, where A′ corresponds to A, B′ to B, and C′ to C. Alternatively, we may regard both triangles as sections of a projection of a third triangle. The two triangles, ABC and A′B′C′, are said to be perspective from the point O. Desargues’ theorem states an important geometrical fact which relates triangles ABC and A′B′C′. If we prolong the corresponding sides AC and A′C′, they will meet in a point P; the sides AB and A′B′ extended will meet in a point Q; and the extensions of BC and B′C′ will meet in a point R. Then, the theorem asserts, P, Q, and R will lie on a straight line. In more compact language, the theorem says:

If two triangles in different planes are perspective from a point, the three pairs of corresponding sides meet in three points which lie on one straight line.

The proof of this theorem is simple. The lines AC and A′C′ lie in one plane because OAA′ and OCC′ are two intersecting lines and, as such, determine a plane. Then AC and A′C′ will meet in a point because any two lines in one plane meet in a point.* Let us denote this point by P. The same argument shows that AB and A′B′ meet in a point Q, and that BC and B′C′ meet in a point R.

Fig. 11–3.
Desargues′ theorem.

We now wish to show that P, Q, and R lie on one line. Now P, Q, and R lie in the plane of triangle ABC because P lies on AC, Q on AB, and R on BC. Likewise P, Q, and R lie in the plane of triangle A′B′C′. Now the points common to two planes must lie on one line, the line of intersection of the two planes. Hence, P, Q, and R lie on one line.

The reader may be troubled about the assertion in Desargues’ theorem that each pair of corresponding sides of the two triangles must meet in a point. He may ask, If these sides happen to be parallel, does the theorem fail? Desargues had taken account of this possibility. We observed in the preceding chapter that a set of lines which are parallel in a particular scene being painted may have to be drawn on the canvas so as to meet in a point. In this case, there is a point in the section which does not correspond to any point in the scene itself. This breakdown of the correspondence between points in the scene and points in the section can be repaired by agreeing that any set of parallel lines is to be regarded as having a point in common. Where is this point? The answer is that it cannot be visualized, although the student is often advised to think of it as being at infinity, a bit of advice which essentially amounts to answering a question by not answering it. However, whether or not one can visualize the point common to parallel lines, a point distinct from the usual, finitely located points of the lines, it is convenient to say that they have a point in common. In addition, it is agreed that two or more parallel lines are to have just one point in common as do nonparallel lines. Hence we say of any two lines in projective geometry that they meet in one and only one point. This agreement is further recommended by the argument that projective geometry is concerned with problems which arise from the phenomenon of vision, and we never see parallel lines, as the familiar example of apparently converging railroad tracks illustrates.

One more agreement must be made about these new points introduced in projective geometry. We just agreed that any set of parallel lines has one point in common. Since there are many sets of parallel lines in one plane, each set having its own direction, there are many such new points in the plane of projective geometry. It is agreed that all these new points lie on one new line, sometimes called the line at infinity.

Let us now turn back to Desargues’ theorem. If each of the three pairs of corresponding sides of the triangles presented in Desargues’ theorem consisted of parallel lines, it would follow from our agreements that the two lines of each pair intersect in one point and that the three points of intersection lie on one line, the line at infinity. These conventions or agreements about points and a line at infinity obviate the necessity for making special statements when parallel lines happen to be involved in the theorems. This is as it should be, because the property of parallelism plays no role in projective geometry as opposed to Euclidean geometry. The reader who balks at accepting the agreements about parallel lines may nevertheless accept the theorems of projective geometry, with the mental reservation that they fail to state the truth when parallel lines are involved.

Fig. 11–4.
A section of a projection of four points on a line.

Desargues discovered another fundamental property which is common to a figure and to a section of a projection of that figure. Let us consider the figure consisting of the line l on which any four points are selected and designated A, B, C, and D (Fig. 11–4). We may form a projection of this figure from an arbitrary point O and cut this projection with the usual glass screen to obtain a section. The original figure and the point O determine a plane. Then the section consists of the line l′ on which A′ corresponds to A, B′ to B, and so on. Since length in the figure differs from length in a section or, to use more technical phraseology, length is not invariant under projection and section, we should not expect that A′B′ would equal AB, or that any segment on l would equal the corresponding segment on l′. One might next consider the ratio CA/CB and venture that perhaps this ratio would equal the corresponding ratio C′A′/C′B′. This conjecture is not correct. However, one can prove the surprising fact, namely that

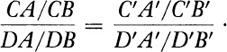
Thus this ratio of ratios, or cross ratio as it is called, is a projective invariant. This is a very surprising fact. It does not matter where the points A, B, C, and D lie on the line l or which points are labeled A, B, C, or D. The cross ratio of the lengths they determine and the cross ratio of the corresponding lengths in the section will be the same.

Incidentally the fact that the cross ratio of four points on a line is the same in the section as in the original figure permits us to check the correctness of a painting executed in accordance with the system of focused perspective. If four points A′, B′, C′, D′ in the painting correspond to four points A, B, C, D which lie on one line in the original scene, then the cross ratio of the first set must equal the cross ratio of the second set. This fact, however, is not too useful in constructing the painting itself.

EXERCISES

1. What fact or facts may you assert about:

a) a section of a projection of an equilateral triangle;

b) a section of a projection of a square?

2. Why should one expect that a figure and a section of a projection of that figure should possess some geometrical properties in common?

Fig. 11–5

3. Figure 11-5 shows two triangles lying in the same plane, the plane of the paper. Moreover, these two triangles are perspective from the point O.

a) What is the difference between this figure and the one considered in the text?

b) Verify by actually drawing lines that the pairs of corresponding sides of the two triangles in Fig. 11–5 meet in three points which lie on one straight line.

c) What generalization of Desargues’ theorem is suggested by the result in (b)?

Fig. 11–6

4. Given the points and lengths in Fig. 11–6, what is the cross ratio of the lengths determined by A, B, C, and D?

5. What is the meaning of the statement that a geometrical property is invariant under projection and section?

Fig. 11–7

6. In projective geometry, lengths are sometimes regarded as directed. For the positions shown in Fig. 11–7, CA would be taken to be negative, whereas CB is positive because it is in the opposite direction. Then the cross ratio

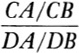
in the present case is negative. When the cross ratio is −1, the four points A, B, C, D are said to form a harmonic set. Suppose now that D is moved indefinitely far to the right and C is moved so as to keep the cross ratio −1. Can you discover any special property of the point C in relation to A and B?

11–3 THE WORK OF PASCAL

In the domain of projective geometry, Desargues’ ideas were further advanced by Blaise Pascal (1623–1662). This man of many contradictory qualities, beset by deep emotional conflicts, is commended to us also by his superb original work in other branches of mathematics, physics, literature, and theology. His father, a judge and tax commissioner, recognized that his son was bright and guided his education. He decided that Blaise should not tackle mathematics until he was 16 years old, but somehow the boy got started on his own and learned a good deal quickly.

When Pascal was still a youth in Paris his father took him to the weekly sessions of a group of noted intellectuals, Roberval, Mersenne, Mydorge, and others. There Blaise met Desargues and as a result became interested in studying properties of geometric figures which remain invariant under projection and section. At the age of 16 he proved a famous theorem, still called Pascal’s theorem, which we shall examine shortly. He then wrote the Essay on Conic Sections, which contains many original results. Mathematics became his great passion. To aid his father he conceived the idea of having a machine perform arithmetic operations, and he constructed the first successful computing machine. He also was one of the notable precursors of Newton and Leibniz in the creation of the calculus and, together with Pierre de Fermat, another great French mathematician whom we shall meet later, founded the theory of probability.*

Pascal made some famous physical experiments which confirmed the discovery by Evangelista Torricelli, a pupil of Galileo, that the air presses down upon us, or that the air has weight, and he also clarified and furthered the study of pressure in liquids, a study which, in technical parlance, is known as hydrostatics.

It was clear to Pascal that the data of experience are the starting points of knowledge and he respected and superbly exercised the power of reason. His Spirit of Geometry, an essay on method and rules of thought, may well be classed with Descartes’ Discourse on Method, another landmark on the role of reason. But as he grew older, he became more and more dissatisfied with the limited results attained by reason. About ten years before he died, he began to find emptiness in the knowledge of nature and acquired some distaste for it. “Don’t overrate science,” he cautioned. He became convinced that the truths of mathematics were not broad enough to encompass all of man’s world. He would frequently say that all the sciences could not comfort one in days of affliction, but that the doctrines of Christian truth would comfort one at all times both in affliction and in one’s ignorance of these sciences. Famous are his epigrams, “The heart has its reasons which the reason knows nothing of” and “Nothing that has to do with faith can be the concern of reason.” More and more he turned to religion. He had been brought up as a Catholic, but he would not accept the strict dogmatic theology of the powerful Jesuits. He became a Jansenist and his Provincial Letters, one of his famous literary works, is filled with anti-Jesuitical polemics. In his Pensées, another literary classic, he penned many more of his thoughts on religion. The conflict between science and faith ended with a victory for religion. Ironically, Pascal, the defender of faith, helped immensely to found the ensuing Age of Reason.

Typical of theorems in projective geometry is the one conceived and proved by Pascal. This theorem, like Desargues’, states the property of a geometrical figure which is common to the figure and to any section of any projection of that figure; that is, it states a property of a geometrical figure which is invariant under projection and section.

Pascal has this to say: Draw any six-sided polygon (hexagon) inscribed in a circle and letter the vertices A, B, C, D, E, F (Fig. 11–8). Prolong a pair of opposite sides, AB and DE say, until they meet in a point, P. Extend another pair of opposite sides, AF and CD say, until they meet in a point, Q. Finally, prolong the third pair until they meet in a point, R. Then, Pascal asserts, P, Q, and R will always lie on one straight line. The mathematician, with his usual passion for brevity, says:

If a hexagon is inscribed in a circle, the pairs of opposite sides intersect in three points which lie on one straight line.

We shall not give the proof of this theorem because it would require more time than we should devote to the subject. The statement, however, offers another illustration of the type of theorem investigated in projective geometry.

Fig. 11–8.
Pascal’s theorem.

Fig. 11–9.
A section of a projection of a hexagon inscribed in a circle.

As stated, Pascal’s theorem seems to have little to do with properties common to all sections of a projection. However, let us visualize (Fig. 11–9) a projection of the figure involved in Pascal’s theorem and a section of this projection. The projection of the circle is a cone, and a section of this cone will not necessarily be a circle, but, as we know from the work of the Greeks, it may be an ellipse, a parabola, or a hyperbola, that is, a conic section. To each side of the hexagon inscribed in the circle there corresponds a side of the hexagon inscribed in this conic section, and to each intersection of lines in the original figure there belongs an intersection of the corresponding lines in the section. Finally, since the points P, Q, R lie on one line in the original figure, the corresponding points will be on one line in the section. Hence Pascal’s theorem states a property of a circle which continues to hold in any section of any projection of that circle.

EXERCISES

1. Draw a circle, choose any six points on it as the vertices of a hexagon, find the points of intersection of the three pairs of opposite sides, and see whether they lie on a straight line.

2. Draw any two straight lines. Choose three points on one and label them A, B, C. Choose three points on the second line and label them A′, B′, C′. Find the point of intersection of AB′ and A′B; do the same for AC and A′C, and for BC′ and B′C. Do you observe any interesting fact about these three points of intersection?

11–4 THE PRINCIPLE OF DUALITY

It would be pleasant to relate that the innovations of Desargues and Pascal were immediately appreciated by their fellow mathematicians and that the potentialities in their methods and ideas were eagerly seized upon and further developed. Actually this pleasure is denied to us. Perhaps Desargues’ novel terminology baffled his contemporaries just as many people today are baffled and repulsed by the language of mathematics. At any rate, except for Descartes, Pascal, and Fermat, Desargues’ colleagues exhibited the usual reactions to radical ideas: they dismissed them, called Desargues crazy, and forgot projective geometry. Desargues himself became discouraged and returned to the practice of architecture and engineering. Every printed copy of Desargues’ book, originally published in 1639, was lost. Pascal’s work on conics and his other studies on projective geometry, though published in 1640, also remained unknown until almost 1800. Fortunately, a pupil of Desargues, Philippe de La Hire, made a manuscript copy of Desargues’ book which was accidentally picked up in a bookshop by the nineteenth-century geometer Michel Chasles, and thus the world finally learned the full extent of Desargues’ major work. Apart from some results which La Hire used and which were incorrectly credited to him for 150 years, Desargues’ and Pascal’s discoveries had to be remade one by one by the nineteenth-century geometers.

Another reason for the neglect of projective geometry during the seventeenth and eighteenth centuries was that analytic geometry, created by Desargues’ contemporaries, Descartes and Fermat (see Chapter 12), and the calculus, developed chiefly by Newton and Leibniz during the latter half of the seventeenth century (see Chapters 16 and 17), proved to be so useful in the rapidly expanding branches of physical science that mathematicians concentrated on these subjects.

The study of projective geometry was revived through a series of accidents and events almost as striking as those which had first stimulated interest in this discipline. The problem of designing fortifications attracted the geometrical talents of Gaspard Monge (1746–1818), the inventor of descriptive geometry. It is relevant that this subject, though distinct from projective geometry, uses projection and section. Monge was a most inspiring teacher, and there gathered about him a host of bright pupils, among them Charles J. Brianchon (1785–1864), L. N. M. Carnot (1753–1823), and Jean Victor Poncelet (1788–1867). These men were so impressed by Monge’s geometry that they sought to show that geometric methods could accomplish as much and more than the algebraic or analytical methods of treating geometry introduced by Descartes. Carnot in particular wished “to free geometry from the hieroglyphics of analysis.” As if to take revenge on Descartes whose creation had caused the abandonment of pure geometry, the early nineteenth-century geometers made it their objective to outdo Descartes.

The revival of projective geometry was launched dramatically by Poncelet. While serving as an officer in Napoleon’s army, he was captured during the campaign in Russia and spent the year 1813–1814 in a Russian prison. There Poncelet reconstructed without the aid of any books all he had learned from Monge and Carnot and then proceeded to create new results in projective geometry. He was the first mathematician to appreciate fully that this subject was indeed a totally new branch of mathematics, and he consciously sought properties of geometrical figures which were common to all sections of any projection of a given figure. A group of French and, later, a group of German mathematicians continued Poncelet’s work and developed intensively the subject of projective geometry.

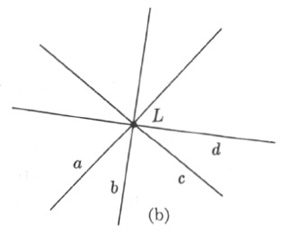
Fig. 11–10.
(a) A set of points on a line;
(b) a set of lines on a point.

The many accomplishments of this period were capped by the discovery of one of the most beautiful principles in all mathematics—the principle of duality. It is true in projective geometry, as in Euclidean geometry, that any two points determine one line or, as we now prefer to put it, any two points lie on one line. But in projective geometry it is also true that any two lines determine, or lie on, one point. (The reader who has refused to accept the convention that parallel lines in Euclid’s sense are also to be regarded as having a point in common will have to forego the next few paragraphs and pay for his stubbornness.) It will be noted that the second italicized statement can be obtained from the first one by merely interchanging the words point and line. We say in projective geometry that we have dualized the original statement or that one is the dual of the other. If we are discussing a set of points on a line and interchange “point” and “line,” we obtain the phrase a set of lines on a point. Figure 11–10 illustrates the two dual statements.

A triangle consists of three points not all on the same line and the lines joining them. We could speak of three lines not all on the same point and the points joining them. We usually do not speak of a point as joining two lines; rather, we refer to such a point as the point of intersection of the lines. But the meaning is clear either way. The figure described by the rephrased or dualized statement is again a triangle. Because the dual figure of the triangle is a triangle, the triangle is called self-dual.

In projective geometry the quadrilateral is defined as a figure consistng of four lines and the six points in which the lines join in pairs. This use of the term “quadrilateral” differs slightly from the one common in Euclidean geometry. A picture of a quadrilateral is shown in Fig. 11–11(a). We can equally well speak of a figure consisting of four points and the six lines which join the points in pairs (Fig. 11–11b). This new figure is called a quadrangle. Hence quadrilateral and quadrangle are dual figures.

Fig. 11–11.
(a) A quadrilateral;
(b) a quadrangle.

We seem to be able to take the statement describing any figure and by dualizing the statement obtain a new figure. Let us try next something more ambitious. We shall dualize Desargues’ theorem. We shall consider the case where the two triangles and the point O from which the triangles are perspective all lie in one plane, and see what results when we interchange point and line. We shall use the fact already noted that the dual of a triangle is a triangle.

Desargues’ Theorem	Dual of Desargues’ Theorem
If we have two triangles	If we have two triangles
such that lines joining	such that points which join
corresponding vertices	corresponding sides
lie on one point, O,	lie on one line, o,
then corresponding sides	then corresponding vertices
join in three points	are joined by three lines
which lie on one straight line.	which lie on one point.

If we examine the new statement we see that it is actually the converse of Desargues’ theorem; that is, the hypothesis and the conclusion in Desargues’ theorem are now interchanged. Hence by interchanging point and line we have discovered a possible theorem. It would be too much to ask that the proof of the new statement should be obtainable from the proof of the original theorem by interchanging point and line. Although it is too much to ask, the gods have been generous beyond our merits, for the new proof can indeed be obtained in this way.

The principle of duality, as thus far described, tells us how to obtain a new statement or theorem from a given one involving points and lines. But projective geometry also deals with curves. How should one dualize statements describing curves? The clue lies in the fact that a curve is after all but a collection of points satisfying some condition. For example, the circle is the set of all points at a fixed distance from a given point. The principle of duality suggests, then, that the figure dual to a given curve might be a collection of lines satisfying the condition dual to the condition defining the given curve. (However the definition given for the circle is not in the form which can be dualized.) This collection of lines may also be called a curve, for a collection of lines suggests a curve as well as does a collection of points (Fig. 11–12). It is called a line curve.

Fig. 11–12.
(a) A point curve; (b) a line curve.

Fig. 11–13.
Brianchon’s theorem, the dual of Pascal’s theorem.

For conic sections, the figure dual to a point conic, that is, a conic regarded as a collection of points, turns out to be the collection of tangents to that point conic. Thus if the conic section is a circle, the dual figure is the collection of tangents to that circle. This collection of tangents suggests the circle as well as does the usual collection of points, and we shall call this collection of tangents the line circle.

We have dualized statements about simple figures with suggestive results. Let us now see whether the application of the principle of duality to theorems on curves is equally productive. As a test we shall dualize Pascal’s theorem. Figure 11–13 illustrates the content of the dual statement.

Pascal’s theorem	Dual of Pascal’s theorem
If we take six points, A, B, C, D, E, and F on the point circle, then the lines which join A and B and D and E join in the point P; the lines which join B and C and E and F join in the point Q; the lines which join C and D and F and A join in the point R. The three points P, Q, and R lie on one line, l.	If we take six lines a, b, c, d, e, and f on the line circle, then the points which join a and b and d and e are joined by the line p; the points which join b and c and e and f are joined by the line q; the points which join c and d and f and a are joined by the line r. The three lines p, q, and r lie on one point, L.

Geometrically the dual statement has the following meaning: Since the line circle is the collection of tangents to the point circle, the six lines on the line circle are any six tangents to the point circle, and these six tangents form a hexagon circumscribed about the point circle. Hence the dual statement tells us that if we circumscribe a hexagon about a point circle, the lines joining opposite vertices of the hexagon, lines p, q, and r in the dual statement, meet in one point. This dual statement is indeed a theorem of projective geometry. It is called Brianchon’s theorem after the man who discovered it by applying the principle of duality to Pascal’s theorem.

The principle of duality in projective geometry says that we can interchange point and line in a theorem about figures lying in one plane and obtain a meaningful statement. Moreover—although nothing said so far justifies the assertion—the new, or dual, statement will itself be a theorem; that is, it can be proved. However, it is possible to show by one proof that every rephrasing of a theorem of projective geometry in accordance with the principle of duality must lead to a theorem. The principle of duality is a remarkable property of projective geometry. It reveals the symmetry in the roles which point and line play in the structure of that geometry, and this symmetry in turn reveals that line and point are equally fundamental concepts.

The principle of duality also gives us some insight into the process of creating mathematics. Whereas the discovery of this principle as well as of theorems such as Desargues’ and Pascal’s calls for imagination and genius, the discovery of new theorems by means of the principle is an almost mechanical procedure.

EXERCISES

1. Given the figure consisting of four points no three of which are on the same line, what is the dual figure?

2. State the principle of duality.

3. Given the figure consisting of four points all on one line, what is the dual figure?

4. Given the figure consisting of three points on one line, a fourth point not on that line, and the lines joining any two of these points, what is the dual figure?

5. In what way is the principle of duality a means of discovering new theorems?

11–5 THE RELATIONSHIP BETWEEN PROJECTIVE AND EUCLIDEAN GEOMETRIES

Projective geometry offers many more exciting concepts than we can hope to survey. Let us see rather what the broader features of the subject are. The basic concept is projection and section and the main goal is to find properties of geometric figures which hold for any section of any projection of those figures. A careful examination of the properties which prove to be invariant under projection and section shows that these properties deal with the collinearity of points, that is, with points lying on the same line; with the concurrence of lines, that is with a set of lines meeting in one point; with cross ratio; and with the fundamental roles of point and line as exhibited by the principle of duality. On the other hand, Euclidean geometry, which, of course, was well known to the nineteenth-century projective geometers, deals, for example, with the equality of lengths, angles, and areas. A comparison of these two classes of properties suggests that the projective properties are simpler than those treated in Euclidean geometry. One might say that projective geometry deals with the very formation of the geometrical figures whose congruence, similarity, and equivalence (equal area) are discussed in Euclidean geometry.

With hindsight to aid us, we can see that there should be a geometry more fundamental than Euclidean geometry. Anybody first perceives the position in space of trees, houses, roads, and other objects and only then thinks of distances and sizes. When traveling, one must first choose a particular road to follow before being concerned with how far to move along the road. That is, position and relative position precede distance in importance both practically and logically.

Hence one might suspect that logically projective geometry is the more fundamental and encompassing subject and that Euclidean geometry is in some sense a specialization. This conjecture is correct. The clue to the relationship between the two geometries may be obtained by again examining projection and section. Consider a geometric figure, a rectangle say (Fig. 11–14). Let a projection of this figure be formed from an arbitrary point O, and then let a section of this projection be made by a plane parallel to the plane of the rectangle. By applying some theorems of Euclidean geometry one can prove that the section will be a rectangle similar to the original one. Hence the relationship of similarity is a special type of projective relationship in which the plane of the section and the plane of the original figure are parallel.

If, now, the point O moves indefinitely far to the left, the lines of the projection come closer and closer to being parallel to each other. When the center of the projection is the “point at infinity”(!), these lines are parallel; then the section made by a plane parallel to the rectangle is a rectangle congruent to the original one (Fig. 11–15). This last type of projection, called parallel projection, thus yields congruent sections. In other words, from the standpoint of projective geometry, the relationships of congruence and similarity which are so intensively studied in Euclidean geometry can be studied through projection and section for special projections. We see therefore that Euclidean geometry is not only a logical subdivision of projective geometry, but we can now look upon it in a new light, namely, as a study of properties of geometric figures which are invariant under special projections.

Fig. 11–14.
Similar figures related by projection and section.

Fig. 11–15.
Congruent figures related by projection and section.

Although projective geometry was initiated by Desargues for the very practical purpose of extending and systematizing theorems which might help the artists, it is not highly significant from the standpoint of applications to art or science. The subject has been developed and cultivated by mathematicians who sought and found pleasure in its ideas. The Renaissance artists and geometers opened up new themes which the Greek world did not grasp, the investigation of the properties of intersections of lines, cross ratio, duality, projection and section, and, above all, the theme of properties invariant under projection and section. Projective geometry is now a vast branch of mathematics because it does offer latitude to intuition, new methods of proof, elegant results, and aesthetically satisfying ideas. This subject born of art makes its primary contribution to mathematics as an art.

EXERCISES

1. What major mathematical problem was suggested by the artists’ use of projection and section?

2. How would you distinguish projective geometry from Euclidean geometry with respect to the properties of geometrical figures?

3. Write a short essay on how the rise of realistic painting in the Renaissance stimulated a new mathematical development.