Chapter 12. Operator Overloading

One of the goals of C# is to allow you to create new classes that have all the functionality of built-in types such as integer (int) and Boolean (bool). (See Chapter 3 for a discussion of these intrinsic types.) For example, suppose you define a type (Fraction) to represent fractional numbers. The following constructors establish two Fraction objects, the first representing 1/2 and the second representing 3/4:

    Fraction firstFraction = new Fraction(1,2); // create 1/2
    Fraction secondFraction = new Fraction(3,4); // create 3/4

The assumption here, of course, is that the first parameter will represent the numerator, and the second parameter will represent the denominator.

Ensuring that the Fraction class has all the functionality of the built-in types means that you must be able to perform arithmetic on instances of your fractions (add two fractions, multiply, and so on) and to convert fractions to and from built-in types such as int.

Hypothetically, you could implement methods for each of these operations. For example, for your Fraction type, you might create an Add( ) method and invoke it by writing a statement such as:

    // add 1/2 and 3/4
    Fraction theSum = firstFraction.Add(secondFraction);

Although this will work, it is ugly and not how the built-in types are used. It would be much better to be able to write:

    // add 1/2 and 3/4 using + operator
    Fraction theSum = firstFraction + secondFraction;

Statements that use operators (in this case, the plus sign) are intuitive and easy to use. Equally important, this use of operators is consistent with how built-in types are added, multiplied, and so forth.

In this chapter, you will learn techniques for adding standard operators to be used with your user-defined types. When you create an operator for a class, you say you have “overloaded” that operator, much as you might overload a member method (discussed in Chapter 8). The C# syntax for overloading an operator is to write the keyword operator followed by the operator to overload. The next section demonstrates how you might do this for the Fraction class.

The chapter also discusses the special case of overloading the equals operator, which is used to test whether two objects are equal. Overriding this operator also requires you to override the class’s Equals( ) method.

Later in the chapter, you will learn how to add conversion operators to your user-defined types so that they can be implicitly and explicitly converted to other types.

Using the operator Keyword

In C#, operators are static methods. The return value of an operator represents the result of an operation. The operator’s parameters are the operands.

Thus, to create an addition operator for a Fraction class, you use the C# syntax of combining the operator keyword with the plus sign (+) operator combined with the keyword static. For example, the overloaded addition operator (the operator+ method) takes two Fraction objects (the fractions you want to add) as parameters and returns a reference to another Fraction object representing the sum of the two parameters. Here is its signature:

    public static Fraction operator+(Fraction lhs, Fraction rhs)

And here’s what you can do with it. Assume, for instance, you’ve defined two fractions representing the portion of a pie you’ve eaten for breakfast and lunch, respectively. (You love pie.)

    Fraction pieIAteForBreakfast = new Fraction(1,2); // 1/2 of a pie
    Fraction pieIAteForLunch = new Fraction(1,3);     // 1/3 of a pie

The overloaded operator+ allows you to figure out how much pie you’ve eaten in total. (And there’s still 1/6 of a pie left over for dinner!) You write:

    Fraction totalPigOut = pieIAteForBreakfast + pieIAteForLunch;

The compiler takes the first operand (pieIAteForBreakfast) and passes it to operator+ as the parameter lhs; it passes the second operand (pieIAteForLunch) as rhs. These two Fractions are then added, and the result is returned and assigned to the Fraction object named totalPigOut.

Tip

It is my convention to name the parameters to a binary operator lhs and rhs. A binary operator is an operator that takes two operands. The parameter name lhs stands for “lefthand side” and reminds me that the first parameter represents the lefthand side of the operation. Similarly, rhs stands for “righthand side.”

To see how this works, you’ll create a Fraction class, as described previously. The complete listing is shown in Example 12-1, followed by a detailed analysis.

Example 12-1. Implementing operator+ for Fraction
using System;

public class Fraction
{
   private int numerator;
   private int denominator;

   // create a fraction by passing in the numerator
   // and denominator
   public Fraction( int numerator, int denominator )
   {
      this.numerator = numerator;
      this.denominator = denominator;
   }

   // overloaded operator + takes two fractions
   // and returns their sum
   public static Fraction operator+( Fraction lhs, Fraction rhs )
   {
      // like fractions (shared denominator) can be added
      // by adding their numerators
      if ( lhs.denominator == rhs.denominator )
      {
         return new Fraction( lhs.numerator + rhs.numerator,
         lhs.denominator );
      }

      // simplistic solution for unlike fractions
      // 1/2 + 3/4 == (1*4) + (3*2) / (2*4) == 10/8
      // this method does not reduce.
      int firstProduct = lhs.numerator * rhs.denominator;
      int secondProduct = rhs.numerator * lhs.denominator;
      return new Fraction(
      firstProduct + secondProduct,
      lhs.denominator * rhs.denominator
      );
   }

   // return a string representation of the fraction
   public override string ToString(  )
   {
      String s = numerator.ToString(  ) + "/" +
      denominator.ToString(  );
      return s;
   }
}


public class Tester
{
   public void Run(  )
   {
      Fraction firstFraction = new Fraction( 3, 4 );
      Console.WriteLine( "firstFraction: {0}", firstFraction.ToString(  ) );

      Fraction secondFraction = new Fraction( 2, 4 );
      Console.WriteLine( "secondFraction: {0}", secondFraction.ToString(  ) );

      Fraction sumOfTwoFractions = firstFraction + secondFraction;
      Console.WriteLine(
         "firstFraction + secondFraction = sumOfTwoFractions: {0}",
         sumOfTwoFractions.ToString(  ) );

   }
   static void Main(  )
   {
      Tester t = new Tester(  );
      t.Run(  );
   }
}

The output looks like this:

    firstFraction: 3/4
    secondFraction: 2/4
    firstFraction + secondFraction = sumOfTwoFractions: 5/4

In Example 12-1, you start by creating a Fraction class. The private member data is the numerator and denominator, stored as integers:

    public class Fraction
    {
     private int numerator;
     private int denominator;

The constructor just initializes these values. The overloaded addition operator takes two Fraction objects, returns a Fraction, and is marked static:

    public static Fraction operator+(Fraction lhs, Fraction rhs)
    {

If the denominators for the fractions are the same, you add the numerators and return a new Fraction object created by passing in the sum of the numerators as the new numerator and the shared denominator as the new denominator:

    if (lhs.denominator == rhs.denominator)
    {
         return new Fraction(lhs.numerator+rhs.numerator,
         lhs.denominator);
    }

The Fraction objects firstFraction and secondFraction are passed in to the overloaded addition operator as lhs and rhs, respectively. The new Fraction is created on the heap, and a reference is returned to the calling method, Run( ), where it is assigned to sumOfTwoFractions:

    Fraction sumOfTwoFractions = firstFraction + secondFraction;
    Console.WriteLine( "firstFraction + secondFraction = sumOfTwoFractions: {0}",
       sumOfTwoFractions.ToString(  ) );

Back in the implementation of the operator, if the denominators are different, you cross-multiply before adding. This allows you to add like Fractions.

        int firstProduct = lhs.numerator * rhs.denominator;
        int secondProduct = rhs.numerator * lhs.denominator;
        return new Fraction(
         firstProduct + secondProduct,
         lhs.denominator * rhs.denominator
     );

The two local variables, firstProduct and secondProduct, are temporary; they are destroyed when the method returns. The new Fraction created, however, is not temporary; it is created on the heap, and a reference is returned as previously.

Tip

A good Fraction class would, no doubt, implement all the arithmetic operators (addition, subtraction, multiplication, division). To overload the multiplication operator, you would write operator*; to overload the division operator, you would write operator/.

The Fraction class overrides the ToString( ) method (inherited from Object) to allow you to display the fractions by passing them to Console.WriteLine( ). (For more information about overloading methods, see Chapter 8.)

Creating Useful Operators

Operator overloading can make your code more intuitive and enable it to act more like the built-in types. However, if you break the common idiom for the use of operators, operator overloading can make your code unmanageably complex and obtuse. Therefore you should always resist the temptation to use operators in new and idiosyncratic ways.

For example, although it might be tempting to overload the increment operator (++) on an employee class to invoke a method incrementing the employee’s pay level, this can create tremendous confusion. The increment operator normally means “increase this scalar value by one.” Giving it the new meaning of “increase this employee’s pay level” will be obvious to the person implementing the operator, but may be very confusing to you or other programmers who have to maintain the code. It is best to use operator overloading sparingly, and only when its meaning is clear and consistent with how the built-in classes operate.

The Equals Operator

The Object class (which is the root of every class in C#) offers a virtual method called Equals( ). (Virtual methods are discussed in Chapter 11.) If you overload the equals operator (==), it is recommended that you also override the Equals( ) method.

Overriding the Equals( ) method allows your class to be compatible with other .NET languages that do not overload operators (but do support method overloading).

The Object class implements the Equals( ) method with this signature:

    public virtual bool Equals(object o)

From this signature, you can see that your override of this method will take an object as a parameter, and return a bool (true if the two objects are equal, where “equality” is defined by the creator of the class).

By overriding this method, you allow your Fraction class to act polymorphically with all other objects. For example, anywhere you can call Equals( ) on two Objects, you can call Equals( ) on two Fractions.

Inside the body of Equals( ), you need to ensure that you are comparing one Fraction object with another Fraction object. If the other object is not a fraction, they cannot be equal, and you’ll return false.

    public override bool Equals(object o)
    {if ( ! (o is Fraction) )
         {
            return false;
         }
         return this == (Fraction) o;
    }

The is operator is used to check whether the runtime type of an object is compatible with the operand (in this case, Fraction). Thus o is Fraction evaluates true if o is, in fact, a Fraction or a type derived from Fraction.

If you are comparing two Fractions, you can delegate the decision as to their equality to the overloaded operator (operator==) that you’ve already written. This allows you to avoid duplicate code.

    public override bool Equals(object o)
    {
         if (! (o is Fraction) )
         {
            return false;
         }return this == (Fraction) o;
    }

In this way, the Equals( ) method determines only that you do in fact have two fractions. If so, it delegates deciding if the two fractions are truly equal to the already implemented operator ==.

The complete modification of the Fraction class is shown in Example 12-2, followed by the analysis.

Example 12-2. Implementing equality operators
using System;

public class Fraction
{
   private int numerator;
   private int denominator;

   // create a fraction by passing in the numerator
   // and denominator
   public Fraction( int numerator, int denominator )
   {
      this.numerator = numerator;
      this.denominator = denominator;
   }

   // overloaded operator+ takes two fractions
   // and returns their sum
   public static Fraction operator +( Fraction lhs, Fraction rhs )
   {
      // like fractions (shared denominator) can be added
      // by adding thier numerators
      if ( lhs.denominator == rhs.denominator )
      {
         return new Fraction( lhs.numerator + rhs.numerator,
         lhs.denominator );
      }

      // simplistic solution for unlike fractions
      // 1/2 + 3/4 == (1*4) + (3*2) / (2*4) == 10/8
      // this method does not reduce.
      int firstProduct = lhs.numerator * rhs.denominator;
      int secondProduct = rhs.numerator * lhs.denominator;
      return new Fraction(
      firstProduct + secondProduct,
      lhs.denominator * rhs.denominator
      );
   }// test whether two Fractions are equal
   public static bool operator ==( Fraction lhs, Fraction rhs )
   {
      if ( lhs.denominator == rhs.denominator &&
      lhs.numerator == rhs.numerator )
      {
         return true;
      }
      // code here to handle unlike fractions
      return false;
   }
   // delegates to operator ==
   public static bool operator !=( Fraction lhs, Fraction rhs )
   {
      return !( lhs == rhs );
   }
   // tests for same types, then delegates
   public override bool Equals( object o )
   {
      if ( !( o is Fraction ) )
      {
         return false;
      }
      return this == (Fraction)o;
   }
   // return a string representation of the fraction
   public override string ToString(  )
   {
      String s = numerator.ToString(  ) + "/" +
      denominator.ToString(  );
      return s;
   }
}


public class Tester
{
   public void Run(  )
   {
      Fraction f1 = new Fraction( 3, 4 );
      Console.WriteLine( "f1: {0}", f1.ToString(  ) );

      Fraction f2 = new Fraction( 2, 4 );
      Console.WriteLine( "f2: {0}", f2.ToString(  ) );

      Fraction f3 = f1 + f2;
      Console.WriteLine( "f1 + f2 = f3: {0}", f3.ToString(  ) );

      Fraction f4 = new Fraction( 5, 4 );
      if ( f4 == f3 )
      {
         Console.WriteLine( "f4: {0} == F3: {1}",
         f4.ToString(  ),
         f3.ToString(  ) );
      }

      if ( f4 != f2 )
      {
         Console.WriteLine( "f4: {0} != F2: {1}",
         f4.ToString(  ),
         f2.ToString(  ) );
      }


      if ( f4.Equals( f3 ) )
      {
         Console.WriteLine( "{0}.Equals({1})",
         f4.ToString(  ),
         f3.ToString(  ) );
      }


   }
   static void Main(  )
   {
      Tester t = new Tester(  );
      t.Run(  );
   }
}

The output looks like this:

    f1: 3/4
    f2: 2/4
    f1 + f2 = f3: 5/4
    f4: 5/4 == F3: 5/4
    f4: 5/4 != F2: 2/4
    5/4.Equals(5/4)

Example 12-2 starts by implementing the overloaded equals operator, operator==. If the fractions have the same denominator, you test whether the numerators are equal. If they are, you return true; otherwise, you return false.

Tip

This is a mathematical simplification to keep the example readable. Testing for true equality (such as 3/4 = 6/8) is left as an exercise for the reader.

    public static bool operator ==( Fraction lhs, Fraction rhs )
    {
       if ( lhs.denominator == rhs.denominator &&
       lhs.numerator == rhs.numerator )
       {
          return true;
       }
       // code here to handle unlike fractions
       return false;
    }

This method is invoked in the Run( ) method when you write:

    if (f4 == f3)

The if statement expects a Boolean value, which is what operator== returns.

It is quite common to overload the equals operator (==) to test whether two objects are equal. C# insists that if you overload the equals operator, you must also overload the not-equals operator (!=). Similarly, the less than (<) and greater than (>) operators must be paired, as must the less than or equal to (<=) and greater than or equal to (>=) operators.

It is good programming practice to have the inequality operator delegate its work to the equality operator, so that if you change the definition of equality, you are assured that the inequality operator will use the new definition.

    public static bool operator !=(Fraction lhs, Fraction rhs)
    {
       return !(lhs==rhs);
    }

This operator is invoked in Run( ) when you write:

    if (f4 != f2)

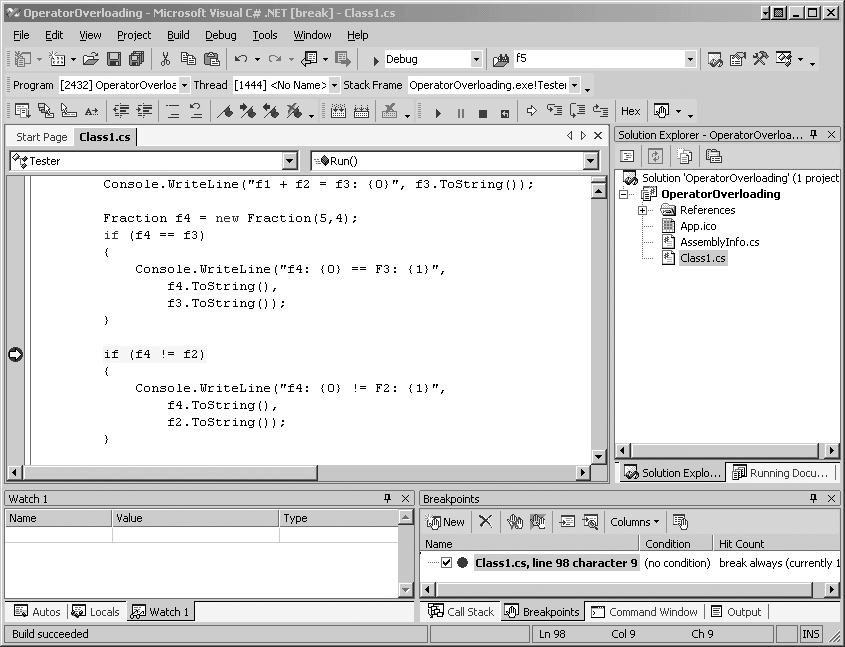
Put a breakpoint on this line of code and run to this line in Visual Studio .NET, as shown in Figure 12-1. (For more about breakpoints, see Chapter 9.)

Running to the breakpoint
Figure 12-1. Running to the breakpoint

Press F11 to step into the method call—you’ll step into the != operator at the return statement. Press F11 again and step into the == operator. Whatever value is returned by the == operator is negated when it is returned by the != operator. If false is returned by ==, then true is returned by !=.

You can make the reversal of equality explicit by adding a temporary Boolean variable named “equality.” Rewrite the != operator as follows:

    public static bool operator !=(Fraction lhs, Fraction rhs)
    {
         bool equality = lhs == rhs;
         return !(equality);
    }

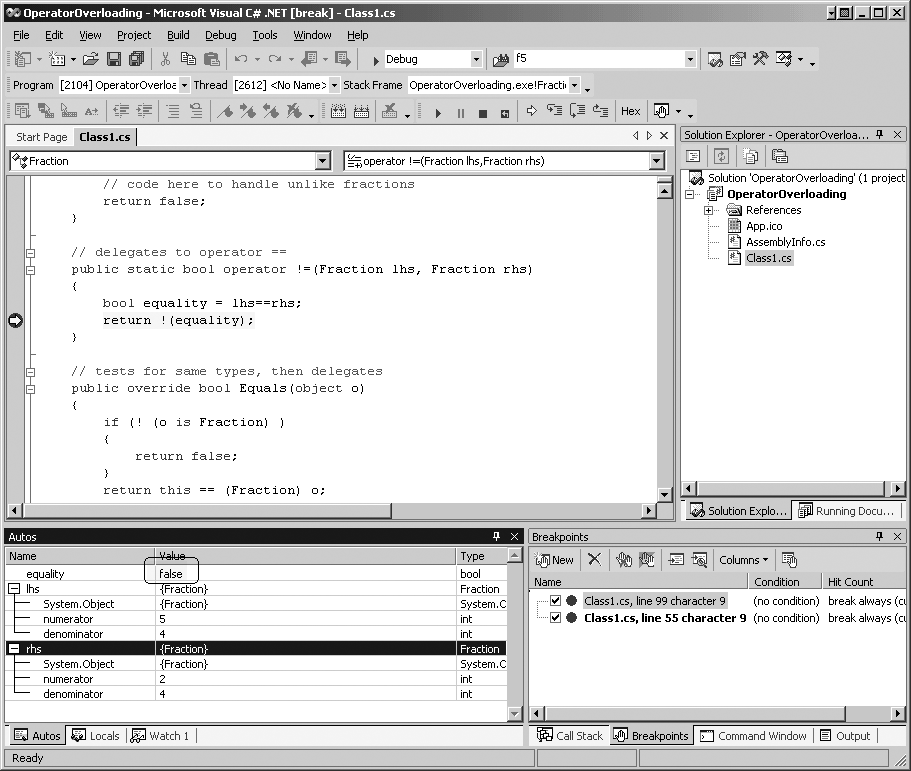
You can now put a breakpoint on the second line of this method and examine the value returned by operator==, as shown in Figure 12-2.

Examining the interim value
Figure 12-2. Examining the interim value

You can see in the Autos window that the value of equality (shown circled and highlighted) is false. The fractions have been expanded to show their values (5/4 and 2/4), and they are not equal. The value returned by the != operator is the opposite of false; that is, true.

In addition to implementing the == and != operator, you implement the Equals( ) method, for the reasons explained previously.

    public override bool Equals( object o )
    {
       if ( !( o is Fraction ) )
       {
          return false;
       }
       return this == (Fraction)o;
    }

If the two objects are not both Fractions, you return false; otherwise, you delegate to the == operator, casting o to a Fraction type. Put a breakpoint on the return line, and you’ll find that you step back into operator==. The value returned by operator== is the value returned by the Equals( ) method if both objects are fractions.

The Meaning of Equality

It is up to you, as the class designer, to decide what it means for two instances of your class to be equal. Two employees might be equal if they have the same name, or you might decide they are only equal if they have the same Employee ID.

Conversion Operators

C# will convert (for example) an int to a long implicitly but will only allow you to convert a long to an int explicitly. The conversion from int to long is implicit because you know that any int will fit into the memory representation of a long without losing any information. The reverse operation, from long to int, must be explicit (using a cast) because it is possible to lose information in the conversion:

    int myInt = 5;
    long myLong;
    myLong = myInt;        // implicit
    myInt = (int) myLong;  // explicit

You want to be able to convert your Fraction objects to intrinsic types (such as int) and back. Given an int, you can support an implicit conversion to a fraction because any whole value is equal to that value over 1 (15 == 15/1).

Given a fraction, you might want to provide an explicit conversion back to an integer, understanding that some information might be lost. Thus, you might convert 9/4 to the integer value 2 (truncating to the nearest whole number).

Tip

A more sophisticated Fraction class might not truncate, but rather round to the nearest whole number. This idea is left, as they say, as an exercise for the reader, to keep this example simple.

You use the keyword implicit when the conversion is guaranteed to succeed and no information will be lost; otherwise, you use explicit. implicit and explicit are actually operators, often called cast or casting operators because their job is to cast from one type to another (int to Fraction or Fraction to int).

Example 12-3 illustrates how you might implement implicit and explicit conversions; detailed analysis follows.

Example 12-3. Conversion operators
using System;

public class Fraction
{
   private int numerator;
   private int denominator;

   // create a fraction by passing in the numerator
   // and denominator
   public Fraction( int numerator, int denominator )
   {
      this.numerator = numerator;
      this.denominator = denominator;
   }

   // overload the constructor to create a
   // fraction from a whole number
   public Fraction( int wholeNumber )
   {
      Console.WriteLine( "In constructor taking a whole number" );
      numerator = wholeNumber;
      denominator = 1;
   }// convert ints to Fractions implicitly
   public static implicit operator Fraction( int theInt )
   {
      Console.WriteLine( "Implicitly converting int to Fraction" );
      return new Fraction( theInt );
   }

   // convert Fractions to ints explicitly
   public static explicit operator int( Fraction theFraction )
   {
      Console.WriteLine( "Explicitly converting Fraction to int" );
      return theFraction.numerator / theFraction.denominator;
   }


   // overloaded operator + takes two fractions
   // and returns their sum
   public static Fraction operator +( Fraction lhs, Fraction rhs )
   {
      // like fractions (shared denominator) can be added
      // by adding their numerators
      if ( lhs.denominator == rhs.denominator )
      {
         return new Fraction( lhs.numerator + rhs.numerator,
         lhs.denominator );
      }

      // simplistic solution for unlike fractions
      // 1/2 + 3/4 == (1*4) + (3*2) / (2*4) == 10/8
      // this method does not reduce.
      int firstProduct = lhs.numerator * rhs.denominator;
      int secondProduct = rhs.numerator * lhs.denominator;
      return new Fraction(
      firstProduct + secondProduct,
      lhs.denominator * rhs.denominator
      );
   }

   // test whether two Fractions are equal
   public static bool operator ==( Fraction lhs, Fraction rhs )
   {
      if ( lhs.denominator == rhs.denominator &&
      lhs.numerator == rhs.numerator )
      {
         return true;
      }
      // code here to handle unlike fractions
      return false;
   }

   // delegates to operator ==
   public static bool operator !=( Fraction lhs, Fraction rhs )
   {
      bool equality = lhs == rhs;
      return !( equality );
   }

   // tests for same types, then delegates
   public override bool Equals( object o )
   {
      if ( !( o is Fraction ) )
      {
         return false;
      }
      return this == (Fraction)o;
   }

   // return a string representation of the fraction
   public override string ToString(  )
   {
      String s = numerator.ToString(  ) + "/" +
      denominator.ToString(  );
      return s;
   }
}


public class Tester
{
   public void Run(  )
   {
      Fraction f1 = new Fraction( 3, 4 );
      Fraction f2 = new Fraction( 2, 4 );
      Fraction f3 = f1 + f2;

      Console.WriteLine( "adding f3 + 5..." );
      Fraction f4 = f3 + 5;
      Console.WriteLine( "f3 + 5 = f4: {0}", f4.ToString(  ) );

      Console.WriteLine( "\nAssigning f4 to an int..." );
      int truncated = (int)f4;
      Console.WriteLine( "When you truncate f4 you get {0}",
      truncated );
   }
   static void Main(  )
   {
      Tester t = new Tester(  );
      t.Run(  );
   }
}

Output:
adding f3 + 5...
Implicitly converting int to Fraction
In constructor taking a whole number
f3 + 5 = f4: 25/4

Assigning f4 to an int...
Explicitly converting Fraction to int
When you truncate f4 you get 6

In Example 12-3, you add a second constructor that takes a whole number and creates a Fraction:

    public Fraction(int wholeNumber)
    {
         Console.WriteLine("In constructor taking a whole number");
         numerator = wholeNumber;
         denominator = 1;
    }

Tip

Notice that in this and the following code samples, you add WriteLine( ) statements to indicate when you’ve entered the method. This is an alternative to stepping through in a debugger. While using the debugger is usually more effective, this kind of output can help you trace the execution of your program for review at a later time.

You want to be able to convert Fractions to and from ints. To do so, create the conversion operators. As discussed previously, converting from a Fraction to an int requires truncating the value, and so must be explicit :

    public staticexplicit operator int(Fraction theFraction)
    {
         Console.WriteLine("Explicitly converting Fraction to int");
         return theFraction.numerator /
         theFraction.denominator;
    }

Note the use of the explicit keyword, indicating that this requires an explicit cast from a Fraction to an int. You see the cast in the Run( ) method:

    int truncated = (int) f4;

The cast from an int to a Fraction, on the other hand, is perfectly safe, so it can be implicit:

    Fraction f4 = f3 + 5;

Notice that there is no explicit cast (in parentheses). When you add the int to the Fraction, the int is implicitly cast to a Fraction. The implementation of this is to create a new Fraction object and to return it:

    public staticimplicit operator Fraction(int theInt)
    {
         Console.WriteLine("Implicitly converting int to Fraction");
         return new Fraction(theInt);
    }

Calling the implicit cast operator causes the constructor to be invoked:

    public Fraction(int wholeNumber)
    {
         Console.WriteLine("In constructor taking a whole number");
         numerator = wholeNumber;
         denominator = 1;
    }

You see this sequence of events represented in the output:

    Implicitly converting int to Fraction
    In constructor taking a whole number

Summary

Quiz

Question 12–1

What is operator overloading?

Question 12–2

Are operators implemented as properties, static methods, or instance methods?

Question 12–3

How does the compiler translate:

    Fraction f3 = f2 + f1;

assuming that f2 and f1 are Fraction objects and you have overloaded the + operator for the Fraction class?

Question 12–4

What should you also do if you overload the == operator?

Question 12–5

What is the difference between implicit and explicit conversion?

Exercises

Exercise 12-1

Create a class Invoice, that has a string property vendor and a double property amount. Overload the addition operator so that if the vendor properties match, the amount properties of the two invoices are added together in a new invoice. If the vendor properties do not match, the new invoice is blank.

Exercise 12-2

Modify the Invoice class so that two invoices are considered equal if the vendor and amount properties match. Test your methods.