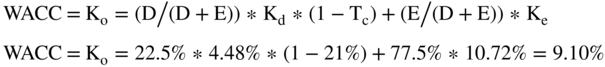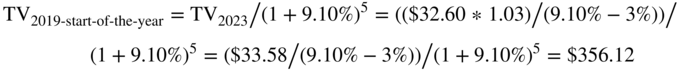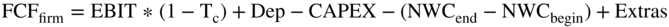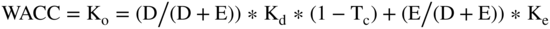CHAPTER 16
Valuation (Sungreen B)

In the last chapter, we introduced valuation and explained how to value a firm or project by using the discounted cash flow technique and free cash flows to the firm. In this chapter, we will complete the valuation of Sungreen's Kingsport mill and plant that we started in Chapter 15. We will use the projected cash flows as estimated in Chapter 15. Then we will calculate the cost of capital and terminal value for this project and demonstrate how the projected cash flows, terminal value, and cost of capital are used to value a project or firm. In keeping with our theme of repetition, we will do this in future chapters as well.

SUNGREEN'S PROJECTED CASH FLOWS

Table 16.1 presents the forecast free cash flows to the firm for Sungreen's Kingsport mill and plant, which we derived in Table 15.8 of Chapter 15.

TABLE 16.1 Sungreen's Pro Forma Free Cash Flows to the Firm Kingsport

($ millions)	2019	2020	2021	2022	2023
Earnings before interest and taxes	34.66	36.96	39.33	41.31	43.37
(1 − Tc)= 1 − 0.21	0.79	0.79	0.79	0.79	0.79
EBIT*(1 − Tc)	27.38	29.19	31.07	32.64	34.26
Plus depreciation	9.38	9.28	9.21	9.17	9.14
Less CAPEX	(5.63)	(6.50)	(7.37)	(8.25)	(9.14)
Less increase in working capital	(1.26)	(1.81)	(1.91)	(1.60)	(1.66)
Free cash flow to the firm	29.87	30.16	31.00	31.96	32.60

As we presented in Chapter 15, the formula for free cash flows to the firm is:

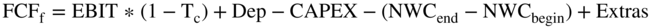
The cash flow formula above is dutifully memorized by most finance students without understanding how it is derived. The formula is somewhat unusual for several reasons. One is that it starts with the term 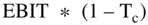. This term never appears on an Income Statement, because taxes are not deducted from EBIT. Taxes are deducted from EBIT minus interest (also called “profit before taxes”). In other words, on Income Statements, taxes are not computed using earnings before interest and taxes. Taxes on Income Statements are computed using profit before tax (which is EBIT after deducting interest expense).

In contrast, the FCF formula uses 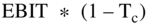, where taxes are calculated on all of EBIT. The formula thus seemingly overstates the amount of taxes the firm is actually paying. Why does the FCF formula do this? It is because of how we calculate the discount rate, which is the WACC in the case of the free cash flows to the firm.

THE WEIGHTED AVERAGE COST OF CAPITAL (WACC)

As noted in the last chapter, the formula for the weighted average cost of capital is as follows:

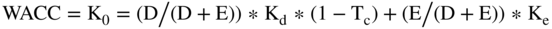
where:

• D = interest-bearing debt
• E = equity
• (D/(D + E)) = the percentage of debt in the capital structure
• (E/(D + E)) = the percentage of equity in the capital structure
• K_d = cost of debt
• T_c = the marginal tax rate
• K_e = cost of equity

As shown in the formula, WACC is the percentage of debt times 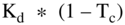plus the percentage of equity times K_e.

Why is the cost of debt (K_d) reduced by the tax rate? To account for the interest tax shield associated with debt. This means the value of the tax shield of debt is included in the WACC. Since the tax shield is already included in the WACC, we do not want to double count it in the FCF. The tax shield should only be counted in one place, either in the cash flows or in the discount rate. Since WACC is computed with the after-tax cost of debt, this means the tax shield is included in the WACC and should not also be included in the cash flows. This is why we use 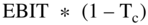in the FCF formula even though 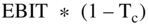is never seen on an Income Statements.¹

We also explained in the last chapter that since the free cash flows to the firm are for the Kingsport plant, they must be discounted at the cost of capital for the Kingsport plant and mill using the Kingsport plant's expected capital structure. Thus, the WACC reflects the cost of capital and the capital structure for the Kingsport plant.

To calculate the WACC for the Kingsport plant, we need to determine its components. That is, we have to define the “weights and rates.”

The Weights

What are the weights (i.e., the percentage of total financing) for debt and equity? For debt, we include interest-bearing debt and use market values if they are available. Unfortunately, market values are usually not easily available for debt, and this leads us to use the book value for debt. It is not perfect, but the book value of debt is normally a close proxy for the market value of debt.² For equity, we use the market capitalization (the market price per share times the number of shares outstanding). If the market capitalization is not available, can we turn to the book value for equity? Yes and no. It is done, but the book value for equity is generally not a reasonable proxy for the market value of equity. In practice, it is most often book debt and market equity, but theoretically it should be market debt and market equity.

To determine the percentages of debt and equity in the project's capital structure, we will begin with the capital structure of Sungreen as a whole to show how it is done. We do this because we have the data for Sungreen (of course we do, as we mentioned before, this is an “armchair” case, i.e., made up by your authors sitting in an armchair) and can demonstrate how capital structure is measured. We will address the capital structure of the Kingsport plant and mill shortly.

For Sungreen, we turn to Table 15.2 in Chapter 15. From the Balance Sheet, we find the 2017 book value of Sungreen's total interest-bearing debt was $1,628 million (this is equal to $10 million of short-term debt plus $95 million of the current portion of long-term debt plus $1,523 million of long-term debt). The book value of its equity was $2,242 million, but the market value of the equity was $3,775 million (Table 15.3 in Chapter 15). The share price was $37.75 per share, and there were 100 million shares outstanding. Using the book or accounting number for equity calculates that Sungreen was financed with 42.1% debt ($1,628/($1,628 + $2,242)) compared to the more accurate 30.1% debt using the market value of equity ($1,628/($1,628 + $3,775)).

If the Kingsport plant and mill were going to be run with the same capital structure as Sungreen, then the 30.1% would be our estimated debt level for the project. However, as will be explained below, the Kingsport plant and mill are assumed to have a lower target debt level.

Use the Project's Capital Structure

Why is a firm's (i.e., Sungreen's) total capital structure not used as the relative weights when estimating one of its project's cost of capital? Alternatively, how should risk be treated in a company with different projects in different divisions?

Imagine you own shares in two firms. One drills for oil while the other builds oil pipelines. Assume the market charges a 20% cost of capital for the oil drilling business (which is considered high risk) and a 10% cost of capital for the pipeline business (which is considered low risk since we don't build a pipeline until oil is found).

Further, imagine the oil drilling firm has four potential oil drilling projects with returns of 16%, 18%, 22%, and 25%, respectively. Which of these projects should the firm undertake? Only the projects returning 22% and 25%. Why? Because only those two have returns above the oil drilling firm's hurdle rate, which is its 20% cost of capital.

Now, imagine the pipeline firm has four potential pipeline projects with returns of 8%, 9%, 12% and 14%, respectively. Which of these projects should the pipeline firm undertake? Only the projects returning 12% and 14%, because only those two are above the pipeline firm's 10% cost of capital.

Now let's change the scenario slightly. Suppose instead of two separate firms you have one integrated oil company that does both oil drilling (50% of its business) and pipelines (50% of its business). What is the firm's weighted average cost of capital? It is the weighted average of the cost of capital for each of the firm's two divisions: 15% (calculated from 50% * 20% + 50% * 10%). Let this firm have the same eight projects listed above (the four drilling projects with returns of 16%, 18%, 22%, and 25% as well as the four pipeline projects with returns of 8%, 9%, 12%, and 14%). Which projects should the firm do? The firm should do the same projects it did before (the oil drilling projects with returns of 22% and 25% plus the pipeline projects with returns of 12% and 14%).

Why? Shouldn't the integrated firm accept all projects with a return over 15% and none with a return below 15% (which would be all the oil drilling projects and none of the pipeline projects)? Think about what would happen if the firm applies the 15% hurdle rate to all its projects. All oil drilling projects above a return of 15% will be accepted, and no pipeline projects below a return of 15% will be accepted. This means some bad drilling projects will be accepted, and some good pipeline projects will be rejected. (A project is considered “bad” if a project's return is less than its cost of capital, and a project is considered “good” if its return is greater than its cost of capital.)

Furthermore, the firm will very quickly move away from being balanced (50% in oil drilling and 50% in pipelines) but will instead be increasingly focused on the oil drilling business. And, as the firm increasingly becomes an oil drilling firm, what happens to its cost of capital? Well, the lenders may initially lend money at 15%, but they should soon realize that they are lending money at 15% to drill oil projects, which have a risk of 20%. In our example where only oil projects are done, lenders should charge 20% for the new projects. Thus, the firm won't remain 50/50 (drilling and pipelines) with a 15% cost of capital. It will eventually become primarily an oil drilling company with a cost of capital of 20% and several oil drilling projects that return less than 20%.

This simple illustration shows why each division, business, or project must use a discount (hurdle) rate that reflects the risk of the project and not the average risk of the firm. The concept is called multiple hurdle rates. Managers who want to justify a project may often argue the firm should charge the average rate that the firm pays. The flaw in this argument is that the firm's overall cost of capital is based on the firm's portfolio of all its projects, and no individual project should be subsidized by any other.

You might think all firms would understand this and act accordingly, but in reality they don't. Some years ago, one of your authors consulted for a major U.S. bank that used a single cost of capital across the whole firm. The bank was lending overnight to investment banks (which was low risk) at the same rate at which they were lending to less developed countries (LDCs), which had higher risk. Not surprisingly, over time the bank's portfolio of loans was increasingly made up of loans to LDCs, while the safer loans became a smaller portion of the bank's lending. Why? Because they were overcharging for the safe loans (and losing that business) while undercharging for the risky loans (and winning all that business). You would think a bank would be sophisticated in finance, but this is a common and often costly mistake for all types of firms.

Because this is such an important concept, let's think about this another way. Find the firm on the NYSE with the lowest cost of capital, call it LOWCOST. Now assume this firm, with its lowest cost of capital, seeks to acquire any other firm on the exchange. If LOWCOST applies its cost of capital to any other firm, call it ANYOTHER, it will look like the merger has a positive NPV. Why? You are valuing ANYOTHER's cash flows using LOWCOST's lower cost of capital.

If LOWCOST sets out to acquire all firms with a positive NPV, when using its discount rate, which firms would LOWCOST seek to acquire? All the firms in the world. However, as LOWCOST starts to acquire the world, its cost of capital would go up and would cease being the lowest in the world. This is why when valuing a project, you must use the project's cost of capital and not the firm's cost of capital.

The bottom line is that if you use the wrong cost of capital, you won't get an accurate idea of whether the project should be undertaken. Remember to think, “project, project, project.” Project cash flows, project discount rate, project capital structure.

Execution Financing

Another important point: Do not confuse execution financing with the target debt level. What does that mean? At the time a firm purchases a business or acquires another firm, it may do so primarily with debt. This is execution financing—the amount of financing at the time of the purchase or acquisition. However, if this level of debt is not how the firm plans to run the project over the long run, then this is not the debt level to use in projections. The debt level may change because the debt may be reduced after an equity issue or be allocated elsewhere in the firm. The capital structure must be calculated using the project's target debt level, meaning the way the project is expected to be run. This will be discussed further in the next chapter.

The Rates: Beta and the Risk Return Spectrum

Before choosing which debt and equity rates to use, let us consider a risk return spectrum going from the lowest risk to the highest risk. What is the lowest-risk asset in which people or companies can invest? U.S. government bonds have the lowest risk, which is why they have the lowest rate. What type of investment would have the next-lowest risk? AAA corporate bonds. Other grades of bonds would extend along our risk spectrum. Soon, equities would make an appearance. The lowest-risk equities would include public utilities. Next would probably be supermarkets. At some point, the risk for the market as a whole would appear on the risk spectrum. Individual equities would continue to the right of the spectrum. For example, to the right of the market as a whole (i.e., riskier than the market as a whole) would be chemical companies, airlines, and going up perhaps to bio-tech firms.

One way to place a firm's debt and equity on a risk spectrum is to borrow the concept of beta from capital market theory. Beta is the measure of market risk used in the capital asset pricing model (CAPM). It is defined as how the return on a particular investment moves with the general market return.³

Returning to our risk profile, we can measure the risk along the profile by betas. What is the beta of a Treasury bond? Zero. Why? Because it is a riskless security, and its return does not change regardless of what happens in the market.⁴ Using a beta of zero in our CAPM formula (introduced in Chapter 7 as 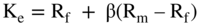), makes the return 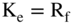(where R_f is defined as the risk-free rate).

What is the beta of a AAA corporate bond? It is very low, about 0.15. This means, its return does not change much with changes in the overall market. Thus, its beta is close to that of government bonds, consistent with AAA corporate bonds being just to the right of government bonds on a risk spectrum. Next, what is the beta of a public utility stock? Somewhere between 0.6 and 0.75. What is the beta of a supermarket chain? It is about 0.85.

What is the beta of the market as a whole (e.g., the S&P 500)? It is 1.00 by definition. When deriving the CAPM, the return on the market moves up and down with itself. Using a beta of 1.00 in our CAPM formula 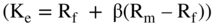, results in 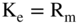_, which is the return to the market as a whole.

To finish our example, what are the betas of a chemical company, an airline, and a biotech firm? They are about 1.2, 1.6, and 2.1, respectively, since these firms are riskier than the market as a whole. Thus, beta correlates with our concept of a risk spectrum.

How do most people actually calculate beta? Well, most people don't do the calculation. Most people simply look it up online or ask a broker. Okay, but how do those who provide you with the beta make the calculation? It is normally calculated as the coefficient of the regression of the returns on an asset (usually a firm's stock) on the returns to the market. The returns can be regressed against the New York Stock Exchange or any market benchmark. How long a period is used for the regression? It used to be five years. Why five years? Because in the past, monthly data was used and five years provided 60 data points (5 years * 12 months per year), which is usually large enough to obtain statistical significance. Today the regressions are normally done with one year's daily stock returns against one year's daily stock market returns (with about 240 trading days in a year).⁵

So, what is the beta for Sungreen's Kingsport project? We don't know. This is because the Kingsport plant and mill do not yet exist, and even when they do, it will be part of a larger company. As such, there are no returns or stock prices to run a regression on. So, is Sungreen's beta of 1.1 (given in Table 15.3 in Chapter 15) the correct beta to use to compute the cost of capital for the Kingsport facility?⁶ No, since wrapping paper is riskier than Sungreen's current product line and we know from our earlier discussion that we should use project cash flows, project cost of capital, project capital structure.

How can we find the beta of the project? The usual method is to find a comparable “twin” firm, and use that comparison firm's beta as a proxy for the project's beta.

TWIN FIRMS

The twin-firm technique is a concept used in finance all the time. For example, in trying to price a new 20-year bond that will be rated BBB, investment bankers look at the current market yields for similar BBB bonds. Not surprisingly, to estimate the beta for a privately held firm, or a specific project, we start with the betas of publicly held firms in the same industry. And that is what we will do for Sungreen's Kingsport plant and mill.

To do this properly takes several steps. We want to match not only the firm's product market risk, but also its financial risk. This means we must take into account its product line and its financial leverage. We do this with the following four steps.

1. Find a public firm (or firms) in businesses that are comparable to the project being valued.
2. Find the comparison firm's beta and then remove the effect that the firm's current debt level (i.e., leverage) has on its beta (called “unlevering the beta”).
3. Use the comparison firm's unlevered beta as a proxy for the project's unlevered beta.
4. Relever the project's unlevered beta found in step 3 to take into account the project's target debt level (i.e., the debt level it will be operated at). The end result will be a beta for the project that takes into account the project's product market and financial risk.

Step 1: Ms. Summers' team at Sungreen finds two public firms, Cyperus Paper and Standard Paper, whose businesses are similar to the type of paper mill and plant that Sungreen management is thinking of creating. Both primarily sell wrapping paper. Using the cost of capital of these two firms in valuing the Kingsport project will be more accurate than using the cost of capital of Sungreen as a whole. As shown in Table 16.2 below, Cyperus and Standard have betas of 1.38 and 1.55, respectively.

TABLE 16.2 Financial Information on Kingsport Project's Twin Firms

	Cyperus Paper	Standard Paper
Sales	$1,688 million	$2,755 million
Net profit	$  133 million	$  193 million
Wrapping paper as a percentage of total sales	88.4%	93.6%
Earnings per share	$2.95	$4.75
Year-end stock price	$70.98	$73.83
Book value of debt	$  800 million	$1,000 million
Market value of equity	$3,200 million	$3,000 million
Leverage (debtbv/(debtbv + equitymv))	20.0%	25.0%
Bond rating	A	A
Equity beta	1.38	1.55

Step 2: The current betas reflect the twin firms' product market and financial risk at their current debt levels. Estimating the beta for the Kingsport project requires adjusting the financial risk for the leverage of the project (which may be different from the leverage of the twin firms). This is done by “unlevering” the betas of the twin firms and then “relevering” them to the project's expected debt level. This is done using the following formulas:

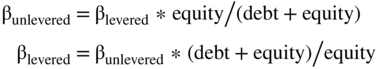
There are numerous formulas that can be used to unlever beta. Many firms and schools have their own particular versions of the formula, each with a particular adjustment. For example, if you meet someone using a formula with tax shields in the beta unlevering formula, it probably means she went to the University of Chicago. Why? Because Bob Hamada, a former professor and dean at the University of Chicago, developed a model with tax shields and that is the formula taught at the University of Chicago. If you study at MIT, you will learn the model we give above, because this is the model used in the Brealy and Myers textbook (both Stewart Myers and one of your authors are professors at MIT). Your authors believe it is the best formula to use: it is the most common formula and contains the simplest assumptions, while the more complex formulas don't significantly change the result.⁷

Using the formula above to unlever the betas for Cyperus Paper and Standard Paper requires knowing each firm's debt and equity. From Table 16.2 we see that Cyperus Paper has book value of debt of $0.8 billion and market value of equity of $3.2 billion while Standard Paper has book value of debt of $1.0 billion and market value of equity of $3.0 billion. This means Cyperus has a capital structure with 20% debt ($0.8/(0.8 + $3.2)) while Standard Paper has a capital structure with 25% debt ($1.0/($1.0 + 3.0)). We can compute the unlevered betas as follows:

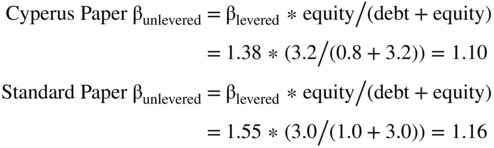
Not surprisingly, given the similarity of the two businesses, the two unlevered betas are very close to each other. Unlevered betas measure basic business risk (BBR), and since the two firms are in the same industry, we expect its BBR to be similar. Unlevered betas are sometimes called asset betas because they represent the risk of the asset without any financial risk. Given the similarity of the twin firms' unlevered betas, we can pick one or the other or an average. Let's choose the average of 1.13 ((1.10 + 1.16) / 2). This is step three.

Step 4: So, do we use the beta of 1.13 to determine the cost of equity for Sungreen's Kingsport plant and mill? Not unless Sungreen plans to operate the plant and mill with no debt. Remember, we have just computed the asset beta for the business risk of the project, but what we need is an equity beta that represents both the risk of the business and the financial risk. Our next step is to relever the beta using the project's target debt level. Which is what? Let's assume the Kingsport plant and mill will be run at a debt level of 22.5% (this is the average of the Cyperus and Standard debt levels. In other situations, there may be additional information about a firm's planned capital structure which we would use instead).

We relever the beta by reversing the unlevered formula to get:

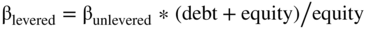
Thus, for the Kingsport plant and mill:

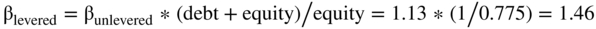
Note that the relevered beta is basically the average of Cyperus's and Standard's levered betas since we have taken the unlevered betas and relevered at their average capital structure. If we unlever and relever at the same rate, we really don't need to do this step. (We did it here primarily to demonstrate the mechanics involved, but also to remind you to relever the plant at the plant's target debt ratio, not at the firm's debt ratio.)

Now, it is important to note that these formulas are approximations with two big assumptions: first, they assume that the relationship between the beta and the amount of debt is linear. This means that if the debt goes up from 10% of capital structure to 20% or from 50% to 60%, the impact on beta (the increase in risk) is the same (increases linearly). However, we know this is not true. We know from Chapter 6 that as risk increases, the cost of K_e grows slowly at first and then increases at increasing rates. So, in fact, beta will increase in a curvilinear, not linear, line.

Second, the formula assumes the beta of the debt is zero. In fact, the beta of the debt is usually not zero but it is pretty low (remember, it is zero for government debt, 0.15 for AAA debt, etc.). We will show in the next chapter that relaxing this assumption (done in another more detailed formula) will normally not change the final result. For now, just remember that for this formula to work, it assumes the beta of debt is zero.

THE COST OF EQUITY

We now ask: What is the cost of equity for Sungreen's Kingsport project? In theory, the cost of equity is the return that stockholders require for investing in a firm. The most commonly used method today to determine the cost of equity (K_e) is the capital asset pricing model (CAPM), which states:

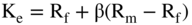
where

• R_m = the market rate
• R_f = the risk-free rate
• β = a measure of risk

The value for beta is 1.46 as derived in the previous section. This leaves R_f and 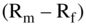to be estimated. R_f is the risk-free rate and 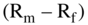is the market risk premium.

How do we estimate R_f, the risk-free rate? The rate on U.S. government bonds is the best proxy of a risk-free rate. Why U.S. government bonds? As we noted in Chapter 7, U.S. government bonds are the safest investment available. The next question is: Which U.S. government bond rate (since the U.S. government issues many bonds with many different maturities)? Typically, most finance professionals use the long-term (i.e., 20- or 30-year) U.S. government rate. However, many people in finance (and those teaching finance) argue that the rate should be matched to the maturity of the project. So that a 10-year project will use the 10-year rate, while a longer project will use the 20- or 30-year rate.

A few people (including your authors) make an additional adjustment to the risk-free rate. For longer-time projects (i.e., 20 or 30 years) your authors calculate R_f using the U.S. long-term government bond rate minus 1%. Why? The “minus 1%” adjustment is because the theory for the capital asset pricing model assumes the formula prices the cost of equity at an instant in time. This means that the R_f should be the short-term rate. However, if the K_e is to be used for longer time periods, the R_f needs to be the short-term rate estimated over the long time period.

To make this adjustment, we need to understand that investors require a risk premium to hold long-term debt rather than short-term debt.⁸ This risk premium is often called the “liquidity premium” or the “term premium.” It is the additional yield an investor must receive for the risk of making a longer-term investment.⁹

Roger Ibbotson¹⁰ calculates the liquidity premium of long-term government bonds over T-bill rates as approximately 0.8% (80 basis points).¹¹ For simplicity, it is often rounded up to 1%. Thus, our calculation for the risk-free rate in our CAPM takes the long-term government bond rate less a liquidity premium of 1% since that is the best estimate of the long-term T-bill rate.¹²

For Sungreen's Kingsport plant, using the 20-year government bond rate of 2.96% less a 1% liquidity premium gives a risk-free rate (R_f) of 1.96%.

We have one last piece left to estimate before we calculate the cost of equity (K_e): the market risk premium, or R_m – R_f. The market risk premium is the expected return to the market minus the expected return on a riskless asset. It is the additional return received for holding the risk of the market. The market risk premium is generally calculated as the average return to the market minus the T-bill rate.

Just like the beta, which is usually taken from other sources, the market risk premium is as well.¹³ The estimates use the average (mean) of the difference between R_m – R_f over time. How is the mean calculated? There are two ways to calculate the mean: an arithmetic mean (add up all the numbers and divide by the number of numbers) or a geometric mean (the compound rate of return, or the nth root of the product of the n values).

Which method of calculating the mean is correct? First, let's use a simple illustration. Imagine you have the following returns for six periods, 10%, 10%, 10%, 10%, 10%, and 10%. The arithmetic average is 10%, and the geometric average is 10%. But now imagine the returns fluctuate between positive 30% and negative 10% (+30%, –10%, +30%, –10%, +30%, –10%). The arithmetic average is still 10% (60%/6). The geometric mean, however, is now less than 10% (8.17%, as shown below).

To explain: imagine an investor starts with $100, makes 30%, and then loses 10%. How much does the investor have in the end? The answer is $117. (The math is: $100 * (1 + 30%) = $130, next $130 * (1 – 10%) = $117). The arithmetic (or average) mean return is 10% ((30% – 10%)/2). The compound return (or geometric mean) is 8.17% ($117/(1 + r)²). In fact, the compound rate of return (geometric mean) is always less than or equal to the arithmetic average return (and it is only equal when all individual returns are the same).¹⁴ (We won't delve into this in great detail because it is a mathematical concept, not a finance one.)

So, should we use the arithmetic or geometric mean? The arithmetic mean. Why? Because our best estimate of the return going out one year is the arithmetic mean (in this case 10%). This is the expected return each and every year given the time series of returns. The fact that the returns are variable year to year does not change what our expected return is. Unfortunately, not everyone understands this concept, and many textbooks and articles used to argue for the geometric mean, which is incorrect.¹⁵

Over what time period do we estimate the market risk premium? It is usually estimated from 1926 to the present. Why do we start in 1926? We go back to 1926 because it is the earliest year for which we have machine readable data. It is when the Center for Research into Security Prices (CRSP) began its time series of stock returns. If the Center's data had started in 1946, we would go back to 1946. Others have argued that estimates should start in the 1960s. Using a different estimation period is not necessarily wrong, but you have to consider if the estimation period is long enough to provide a good forecast for the future. For example, if you only look at a period that had an up market, this might bias the estimate.

For Sugnreen's Kingsport plant and mill's cost of equity, we will use an estimated market premium, 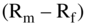, of 6%. We take this from Ibbotson & Associates' estimate of the arithmetic mean of the market premium for the period 1926–2016.¹⁶

Now, putting all the inputs together we can calculate a K_e as follows:

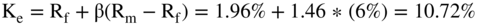
Since R_f = 1.96% (the government bond rate of 2.96% less our 1% liquidity adjustment), β = 1.46 (using the twin firm approach), and 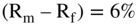(the market premium or the difference in the market return less U.S. T-bills).

THE COST OF DEBT

We now estimate the cost of debt for the Kingsport plant and mill. The easiest way to determine the cost of debt is to look at the market rate for debt: How much would it cost to issue the additional debt needed for the new project? We do not use what the firm paid in the past to finance past projects because it has nothing to do with what it will cost a firm to finance a project now. Imagine friends are thinking about buying a house and ask you about mortgage rates. Would you tell your friends what the mortgage rates were when you borrowed at some point in the past? No, you would tell them what the mortgage rate is today because that is the rate at which they will borrow.

While the financial markets had been quite volatile a decade ago, the situation in January 2019 was relatively calm. Yields on investment-grade bonds had increased somewhat in recent months but were still below their historical averages. Capital markets data is given in Table 16.3.

TABLE 16.3 Capital Markets Data as of June 11, 2018¹⁷

Market rates:
	U.S. 20 Year	U.S. 5 Year	U.S. T-Bills (6 month)	Bank Prime Rate
	2.96%	2.80%	2.06%	4.75%
Corporate bond rates:
	AAA	AA	A	BBB	BB
	4.00%	4.35%	4.48%	4.85%	6.10%
Leverage for different bond ratings (debt % total capital at equity market values):
	AAA	AA	A	BBB	BB
Industrials	18%	25%	30%	37%	47%
Paper industry		18%	23%	30%	40%

From Table 16.3, since Sungreen's debt level is 30.1%, its debt would likely be rated A, and its interest rate would be 4.48%. The Kingsport plant and mill are expected to have a debt level of 22.5% (the average of their twin firms). This means the Kingsport's project debt would also be probably rated A.¹⁸ Lahey's staff, after considering debt ratios for the paper industry and the fact that the Kingsport project will be run at a lower debt level of 22.5%, estimated the cost of debt for the plant at 4.48%.

Adjusting for the Tax Shield

When we calculate the weighted average cost of capital (WACC), we use the after-tax cost of debt, K_d * (1 – T_c). We must next estimate the T_c, which is the marginal tax rate that Sungreen expects to pay on the income from the Kingsport plant and mill. From 2015 through 2017, Sungreen's actual tax rate was 30%, 34%, and 35%, respectively. However, the U.S. corporate tax rate, as noted earlier, dropped in 2018 to 21% due to the Tax Cuts and Jobs Act. For our calculations we will use 21%.

The K_o or WACC for the Plant

So now we have all the elements to calculate the overall cost of capital for the Kingsport plant and mill. From above the:

¹⁹

THE FINAL VALUATION

We can now calculate the net present value of the Kingsport plant and mill. We recommend valuing it in three pieces as follows:

1. The initial investment (or purchase price). This is $410 million (as given in Chapter 15).
2. The present value of the cash flows. This is the present value of the cash flows from the pro formas for 2019 to 2023 (as given in Table 15.8 from Chapter 15), discounted at a WACC of 9.10%. This value is shown in Table 16.4 to equal $120.24 million.
3. The terminal value. This is the value of the future cash flows at the end of 2023. Chapter 15 discussed briefly how to estimate terminal values. Chapter 17 will examine terminal values in much more detail. Here we simply use the perpetuity formula with a growth rate of 3% (as forecast by Lahey's staff as mentioned in Chapter 15) and the cost of capital of 9.10% (as computed above). The terminal value must be then discounted back to the present (in this case the start of 2019). This gives us a terminal value of $356.12 million as follows:
   • 

TABLE 16.4 Net Present Value of Free Cash Flows to the Kingsport Plant

($ millions)	2019	2020	2021	2022	2023
Free cash flow to the firm	29.87	30.16	31.00	31.96	32.60
Discount factor/(1+r)n	1.09	1.19	1.30	1.42	1.55
Present value FCF/(1+r)n	27.38	25.34	23.87	22.56	21.09
Net present value (5-year sum)	120.24
Net present value of 2019–2023 free cash flows is	$120.24 million
Net present value of the terminal value is	$356.12 million
This give a total net present value of Kingsport is	$476.36 million
The purchase price of Kingsport is	$410.00 million
Thus, the Kingsport project has a positive NPV of	$  66.36 million

The net present value of the Kingsport project is the sum of the three elements above: the $120.24 million present value of the cash flows plus the $356.12 million present value of the terminal value less the $410 million purchase price, for a total of $66.36 million.

The reason to list the terminal value separately from the NPV of the cash flows is to consider the relative importance of the terminal value on the project's NPV. For example, assume two projects, each with an initial investment of $10 million and an NPV of $20 million. Further, assume the first project has the following three values: an initial investment of $10 million, a present value of $18 million for five years of cash flows, and a present value of $12 million for the terminal value. NPV therefore equals $20 million (or –$10 + 18 + 12). Now, assume the second project has the following three values: an initial investment of $10 million, a present value of $8 million for five years of cash flows, and a present value of $22 million for the terminal value. The NPV of this second project also equals $20 million (or –10 + 8 + 22). The NPVs are identical, so we should be indifferent between the two projects if we are looking purely at NPV. However, it is useful to know that the first project gives us a positive NPV after five years while the second has a negative NPV after five years. If the projects are mutually exclusive, this may cause the first project to be preferred. (This is why the payback method still has some value.)

For the Kingsport plant and mill, separating out the present value of the terminal value from the present value of the cash flows also provides additional insight. In this case, it is clear the terminal value is the key to making the project have a positive NPV (the Terminal Value is 3.0 times the five-year cash flows, or 74.8% of the total of all cash flows). The greater the percentage of total value coming from the terminal value, the less comfortable we feel. Why? Because more of the value occurs farther in the future, making it less certain.

So now we have an NPV of the Kingsport project, but we are clearly not done. At the beginning, we emphasized that each investment has three pieces: strategy, valuation, and execution. We also mentioned that we would do this out of order and do valuation first. That is only because this is a finance text. In practice, we would do the strategic analysis first and see if the investment fits the firm's product market strategy. Let's say a few words about strategic analysis here and defer a deeper discussion until Chapter 19.

STRATEGIC ANALYSIS

What do we mean by strategic analysis? Essentially, we are trying to answer the question: Should Sungreen buy the mill and plant? The finance valuation answer is “Yes, because it has a positive NPV.” Why it has a positive NPV is the answer to our strategic analysis. For this project to be a positive NPV for Sungreen means the firm will receive a rate of return on the Kingsport project that is higher than the competitive rate. The reason for this is that the Kingsport plant and mill must either have higher cash flows or a lower cost of capital than a competitive mill and plant.

If a firm acquires or builds a new plant, one question is: Do we expect it to have lower costs than its competitors in the industry? If we expect the costs to be higher (e.g., it is a poor location and has higher transport fees), then it is probably not a good strategic decision. If the costs are lower (e.g., it is in a location with significantly lower shipping costs to customers, below that of competitors), then it is probably a good strategic decision.

So, will our pro forma estimates come true? The answer is ultimately decided in the product market. For example, if we assume a sales growth of 10% per year, there must be a product market reason for the assumption. Assume industry sales are projected to grow at 2% and all the competitors are investing in new capacity. Why would this firm grow at 10%? It probably won't. This is why strategic analysis provides the economic underpinnings and rationale for the pro formas.

What will cause the Kingsport project to have a positive NPV? Any of the following factors: it can extract higher prices, sell more units, and/or have lower costs. There are a number of ways each of these can occur. Perhaps the firm gains monopoly power by building or acquiring the new plant. If so, the firm can raise prices and receive more revenue for the same number of units and the same cost of production. Perhaps the firm adopts a new technology with lower costs. Perhaps the current management is not effective and is being replaced with a more effective one. Perhaps the firm achieves lower labor costs than its competitors with a new contract. Finally, perhaps Sungreen achieves economies of scale from the new plant.

There are clearly many other possibilities, and we are only noting a few here. A positive NPV after an acquisition or new investment means that the new management achieves higher revenues and/or lower costs than the old management or its competitors. Remember, Sungreen is a fictitious firm used to demonstrate valuation. For this reason, we have not included too much product market information, which is required to do a true strategic analysis. This will be done in more depth in Chapter 19 using a real-life company.

Strategic analysis is a large part of an entrepreneurial finance or venture capital course. The valuation piece is the same as shown here: pro forma cash flows discounted at the cost of capital. The difference is in the strategic analysis and in contracting for all contingencies and options. For example, if a buyer calls the selling firm six months after the purchase and asks for help in solving a technical problem, the seller is likely to hang up. However, if there is still a large outstanding payment based on some final result, the seller is motivated to ensure the final result occurs. In this latter situation, the seller has the same incentive as the buyer to ensure the project works as promised and is much more likely to cooperate with the buyer. Although important, this type of analysis is beyond the scope of this book. Our emphasis here is on valuation.

SUMMARY

1. This chapter values Sungreen's Kingsport plant and mill using the discounted cash flows to the firm technique. DCF is one of our five techniques for valuation; free cash flows to the firm is the most commonly used variant of the DCF technique.
2. The DCF technique using free cash flows to the firm requires projecting a firm's cash flows (as covered in Chapter 15), determining the cost of capital (in the case of free cash flows to the firm, the cost of capital is the WACC), and calculating a terminal value.
3. Free cash flows to the firm are defined as:
   • 
4. WACC is defined as:
   • 
5. The relative weights of debt and equity in the WACC formula are usually calculated using the book value for debt and the market value for equity. The K_d used is the market rate at which the project can currently borrow debt (which is not necessarily the rate at which the whole firm can borrow). The K_e is calculated using the one-factor CAPM model, which requires the beta of the project, a risk-free rate as well as a market risk premium. The risk-free rate is the rate on U.S. government bonds for the same time horizon as the project (minus 1% if the time horizon is long). The market risk premium is the arithmetic mean of the projected premium of the stock market over the T-bill rate. The tax rate used, or T_c, is the marginal expected tax rate.
6. Importantly, projects are always valued using the mantra “project, project, project.” That is, use the project's cash flows, the project's capital structure, and the project's cost of capital.
7. Valuation should be calculated with three elements: the initial investment (or purchase price), the present value of the cash flows, and the present value of the terminal value. This allows us to see the relative importance of each piece.
8. Finally, this chapter introduced the strategic analysis underlying investments. More specifically, we examined how/whether the economics of the project will achieve the projected pro forma cash flows. In particular, pro formas can't be developed without a sound economic underpinning.

Coming Attractions

This chapter covered the basics of how to do a discounted cash flow valuation. The next chapter covers some of the finer points or nuances of valuation.

NOTES

  1 As we will explain in a later chapter, this is also why free cash flows to the firm is not equal to free cash flows to equity plus the free cash flows to debt.

  2 As long as market interest rates and the credit quality of the debt have not changed a great deal since the debt was issued, the market value should be close to the issue value.

  3 This is a very cursory explanation of beta, which is generally covered in capital markets finance textbooks and is used as a measure of an asset's risk. Literally speaking, beta is the co-variance between the return to an asset and the return to the market divided by the variance of the market's return.

  4 Prior to the U.S. financial crisis of 2008, most thought U.S. government bonds were riskless. Today we understand there is always some risk involved, even with U.S. government bonds. However, if the U.S. government ever defaults, the risk on the government's debt will be the least of our worries.

  5 If a firm is undergoing a merger (e.g., just acquired another firm) or for some other reason has radically changed its business risk from the prior year, then using the beta calculated over the prior year may not accurately reflect the firm's current risk.

  6 A beta of 1.1 for Sungreen makes intuitive sense because a paper company's stock price probably moves closely with the overall market and has less risk than airline or biotech stocks.

  7 Alternative formulas for levering and unlevering beta, as well as the derivation of these formulas, are discussed in Chapter 17.

  8 As an illustration, if the short-term expected U.S. T-bill rates are flat at 10% for the next five periods (10%, 10%, 10%, 10%, and 10%), the five-year interest rate is often above 10%. The amount above 10% is the liquidity premium.

  9 Note that outside the context of the term structure of interest rates, liquidity premium can mean something else.

10 Professor Ibbotson of Yale University founded Ibbotson Associates (now owned by Morningstar), which provides financial research.

11 U.S. government-issued securities with a maturity of less than a year are called “bills” and often abbreviated as T-bills (the T stands for Treasury).

12 An important caveat: If the reader ever has a job interview and states that the correct rate is the long-term government bond rate minus 1%, the person interviewing you may not be familiar with this practice. Many people have not learned it this way. Regardless, subtracting a liquidity premium from the long-term government bond rate is, in fact, a better estimate (in our opinion).

13 Unlike betas, which are available almost everywhere for U.S. stocks (e.g., Google Finance, Yahoo! Finance, Value Line, etc.), the market premium is not as easily found. The principle source is Ibbotson Associates. The estimate used for the market risk premium differs across banks and other financial institutions. Our readers should understand that many of the differences in valuation across different banks originate from different estimates of the inputs used in a WACC including the market risk premium.

14 An even simpler example: The return is +10% then –10%. The arithmetic average is 0 (from (10 – 10)/2). The geometric mean is negative. Again, it starts with $100, goes up 10% or $10 to $110, then goes down 10% or $11 to $99. The return is a loss of $1, which is less than zero.

15 An early edition of Brealy and Myers noted in a footnote that the reason to use the arithmetic mean “is obvious” with no further explanation. Our apologies if this was obvious to you.

16 For an in-depth discussion of estimates for the market risk premium, see Pablo Fernandez, “Equity Premium in Finance and Valuation Textbooks,” IESE Business School–University of Navarra, 2008.

17 Some of the numbers in this table were obtained from www.federalreserve.gov on January 10, 2014. Others were estimated by your authors.

18 Bond ratings are meant to measure the risk associated with investing in a particular bond. While the percentage of debt is a large component of the rating process, it is by no means the only factor. Other factors include the size of the firm, the quality of management, the number of years of operation, and the like.

19 As a comparison, the WACC for Sungreen as a whole would be 30.1% * 4.48% * (1 – 21%) + 69.9% * 8.7% = 7.105%.