CHAPTER 17
Valuation Nuances
In the previous two chapters, we valued Sungreen Corporation using the free cash flow to the firm approach. That is, we estimated future cash flows to the firm and discounted them using an average weighted cost of capital (WACC). This chapter will extend the analysis and provide some nuances about valuation.
This chapter is organized around providing more detail about each of the pieces of valuation: cash flows, cost of capital, and terminal value. For each piece, we will extend the analysis from Chapters 15 and 16. At the end, we will examine alternative valuation techniques (APV and APT) as well as other topics.
CASH FLOW NUANCES
When doing valuations, it is important to remember that cash is king. Cash flows, not earnings, are what make or break a firm. A firm can survive for a time with negative earnings but doesn't last long after experiencing negative cash flows. Remember the quote from the first chapter: “Cash is like air, profits are like food. You need both to survive, but you die much quicker without air.”
For example, start-ups (like the dot-coms) worry mostly about something called the burn rate. That is, how fast a firm “burns” (spends) its cash. Many never have positive earnings, but their survival time is actually about how long the cash will last.
This is not to say earnings don't matter; earnings matter because they are usually a large part of a firm's cash flow. However, we don't value a firm merely on earnings, and it is ultimately the total cash flow that is critical. In Chapter 1, we also noted an old saying: “You buy champagne with earnings, but you buy your beer with cash.” So remember that cash, not earnings, is number one in valuation.
Cash Flows: What Is and Is Not Included
Next let's discuss what is and what is not included in cash flows. As used in investment valuations, cash flows ignore noncash items (e.g., accounting accruals and allocations) and sunk costs. For example, corporate overhead is considered a sunk cost in project valuations because it is not an incremental cash flow. If an item doesn't change with the addition of the investment being valued, then it is excluded.
What are sunk costs? They reflect cash that was spent in the past. As an example, an engineering feasibility study that has already been completed is a sunk cost—the funds have already been spent. Sunk costs are not included in project valuations (cash flows generated from previous investments in the project are included but not the cash spent on the previous investments). Investment analysis is always forward-looking.
If we're valuing a project as opposed to an entire firm, we also ignore the cash flows of unrelated projects or unrelated parts of the firm if they do not change with the project. That is, if it is not part of the project being evaluated, it is not a relevant cash flow and is therefore ignored in the project valuation.
One way to identify relevant project cash flows is to find those that change with the introduction of the project. That is, we include any cash flow changes related to the project regardless of where they occur in the firm. This may seem contradictory to our emphasis on “project, project, project,” but it is not. What matters are the total cash flows from the project, not where they occur. At the same time, we exclude cash flows that occur regardless of the project (those that are not affected by or part of the project).
The timing of a cash flow is also important. We said earlier that one way to identify a relevant cash flow is to examine whether it changes with the project. This change can either be in the amount or timing. That is, if the project causes the same cash flows to occur earlier or later than they otherwise would have, then these changes in cash flows must be included in the valuation because the time value of cash flows matter (the time value of cash flows is covered in detail in Chapter 14).
The U.S. Tax Cuts and Jobs Act of 2018 offers an example of a change in the timing of cash flows. The new law allows the acceleration of depreciation. Many capital expenditures are allowed to be fully expensed immediately instead of depreciated over time. These accelerated depreciation cash flows will increase the value of the firm due to the time value of money.
What about the cash flows for an asset that has potentially multiple purposes, some of which are unrelated to the project we're evaluating? Consider, for example, a new project that requires a train line. If the right-of-way necessary for the train line can't be used for any other purpose, then its entire cost must be picked up by the project using it. However, if the right-of-way will be used for other purposes regardless of whether the new project is done (if power lines, pipelines, telecommunication cables, etc., will also use its right-of-way), then the cost of the right-of-way can be ignored. It is the changes in the cash flows caused by the new project that matter.
Should you charge a project for using excess capacity in another division? That is, if there is excess capacity in the firm that you now use for the project, how does it impact the valuation of the project? If the excess capacity would never be used by the firm without the project, then there is no charge to the new project. If the excess capacity would eventually be used, then it has a cash flow impact and should be charged to the new project. The charge would be the future cost of any additional capacity required.
What other relevant items should be considered when evaluating a project's cash flows? Cash flow analyses often overlook the opportunity costs generated by the project. Adding a new project often causes a disruption to current operations and thus to other cash flows in the firm. For example, in its simplest form, a new product may impact the sales of current products (e.g., an addition to the firm's product line may cannibalize sales from other products). The full impact should be carried through to the cash flows that are used in the project's valuation (i.e., the loss in output creates a loss in revenue, which creates a loss in EBIT, etc.).
Abandonment costs are another example of a relevant cash flow that is often ignored. These are the cash flows associated with ending a project, and they must be included in project valuation.1 Abandonment costs include net working capital. In particular, accounts receivable or inventory that are written off must be included.
To summarize: Valuation must consider all relevant cash flows, whether they are the new ones from the project or any changes in existing cash flows caused by the project. Valuation is also all about cash—real cash—and not accounting earnings. Furthermore, anything done in the past is gone and forgotten (i.e., it is a sunk cost). We care about the amount and timing of future cash coming in and going out from the new project.
What about Inflation and Cash Flows?
As discussed in Chapter 15, it is important to use either real cash flows (which exclude inflation) with real discount rates or nominal cash flows (which include inflation) and nominal discount rates (which include inflation and are market discount rates).
Most practitioners use nominal cash flows with nominal discount rates. Why? They do this primarily because the nominal versions are easier to obtain. The nominal cash flows are the ones actually received, and accounting statements use nominal numbers. The nominal discount rates are the ones charged by the market. So the usual method is nominal-nominal. This has an additional advantage if the different elements of the cash flows grow at different rates. For example, a firm's labor costs may be subject to a union contract with a fixed rate of increase, while material costs may increase at a different rate with inflation. Using nominal cash flows allows us to adjust for the different rates easily.
COST OF CAPITAL NUANCES
When we calculated the cost of capital for the free cash flows to the firm in Chapter 16, we used the weighted average cost of capital (WACC). The formula for WACC is:
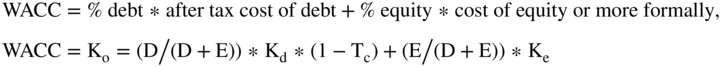
where:
- D = interest-bearing debt
- E = equity
- (D/(D + E)) = the percentage of debt in the capital structure
- (E/(D+ E)) = the percentage of equity in the capital structure
- Kd = cost of debt
- Tc = the marginal tax rate2
- Ke = cost of equity
The formula for the WACC requires us to determine the percentages of debt and equity, the cost of debt, the cost of equity, and the tax rate. Furthermore, the cost of equity requires us to determine a beta, a risk-free rate, and the market premium of Rm – Rf. The formula for cost of equity (Ke) is:
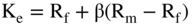
where:
- Rm = the market rate
- Rf = the risk-free rate
- β = a measure of risk
The WACC we calculated in Chapter 16 was straightforward. Below, we add some nuances to that calculation.
An important point when calculating the percentage of debt and equity is to not confuse execution financing with the target debt level. What does that mean? At the time a firm invests in a project or acquires another firm, it may use a type of financing that is not meant to be permanent.
For example, a firm may initially finance the assets being purchased entirely with debt (or entirely with equity). This is the execution financing: the amount and form of financing at the time of the investment or purchase. However, if the financial structure (i.e., the level of debt and equity) used to finance the project is not how the firm plans to run the project over the long run, then this is not the debt level to use in the cost of capital. The execution debt level may temporarily use the debt capacity of the entire firm, and it may be reduced after equity is increased (either through retained earnings or a new equity issue). Alternatively, the initial percentage of equity used in a stock transaction may also change over time (through new debt issues). To repeat, the cost of capital for the project needs to reflect the capital structure from the project's target debt level, which is the way the project is expected to be run.
Assumptions Behind the WACC
The WACC formula estimated in Chapter 16 contains some important assumptions that should be considered. One underlying assumption behind the formula is that WACC assumes a constant debt ratio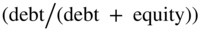 
. WACC doesn't assume that a set amount of debt is issued at one time and that this then remains constant. Rather, the WACC assumes the debt remains at a constant percentage to the value of the firm. Thus, as the value of the firm goes up or down, so does the amount of debt outstanding. For example, if the debt starts out at 22.5% and the value of the firm doubles, then the amount of debt doubles so that the percentage remains the same.
This is a very strong assumption, and it is not always followed in practice. The reason that WACC should assume a constant debt ratio is that the value of the tax shield is generated from a perpetuity formula. Thus, WACC assumes the debt is perpetual. In practice, the capital structure varies a bit even in pro formas, and a WACC estimated on the average capital structure is often used. This is particularly true as a firm switches from execution financing to permanent financing. In Table 15.5 we made the capital structure a constant 22.5%.
Another feature of the WACC is that the free cash flows to the firm do not change with changes in capital structure (as we will show in Chapter 20). Also, finance is an art, not a science, so any proper valuation will include a sensitivity analysis with different costs of capital.
When is the assumption that the debt ratio is constant most important? Consider the valuation of LBOs or private equity deals (which we will cover in detail in Chapter 18). In either case, the firm is typically levered up at first (to a very high debt ratio), and then the debt is paid down over time. As the value of the firm is (hopefully) increasing, the amount of debt is decreasing. Thus, the percentage of debt is not constant as a function of the value of the firm but rather decreases over time. In this situation, the valuation can't be done using a WACC because the tax shields are clearly not perpetual. Instead, the valuation should use the free cash flows to equity discounted at Ke (we will cover this in Chapter 21).
Cost of Debt
The cost of debt used in determining the WACC assumes the cost of debt is at the market rate. This means there are no subsidies that would cause interest rates to be lower than the market rate (e.g., no industrial revenue bonds or special tax rebates from the government).3 Exceptions to the assumption of the market rate are easily managed. The benefits from any reduction in interest rates are calculated separately and then added to the net present value of the project. However, it is important to remember that when there is a subsidy, the WACC still uses the market rate, not the subsidized rate.
How should subsidized interest rates be treated? Let's consider an armchair example (an armchair example is one made up for illustrative purposes). Assume that the current market rate on long-term debt is 10.0% but an industrial revenue bond is offered for the first three years of a project at 7.0%. What is the correct discount rate for the project if the project is getting a lower-than-market rate? The project's discount rate should still be the 10.0% long-term market rate. Why is the project's discount rate not the 7.0% rate for the industrial bond being given to the project? First, the industrial bond rate doesn't reflect the risk of the project in the market—it is a subsidized rate. The discount rate used must reflect the same risk for the project that the market rate for the project does. Second, it is unlikely the firm can borrow all the funds it needs at the subsidized rate. So, do you ignore the subsidized rate on the industrial bond? No, the value of the subsidy must be considered separately and added to the value of the project.
Let's use an example that may be of use to you personally. Imagine you decide to buy yourself a car when you finish reading this book, to celebrate your understanding of finance. When you go to the car dealership, they offer you a deal. If you pay cash, they will give you $3,000 cash back (i.e., $3,000 off) the $23,000 purchase price (for a net of $20,000). Alternatively, they offer to finance the car at 1%, although the current rate at your bank for a car loan is 6%. What should you do, take the cash back or the low-interest loan? Well, how much is the 1% financing worth? You have to calculate the present value of the lower-rate financing, compare it to the $3,000 cash back, and then choose the one with the higher present value.
How would you do it? Since every reader of this book should know more than a car salesman about what that number is, let us walk you through how you would do this.
One way is to figure out the monthly savings from financing a $23,000 car at 1% instead of at 6% (we will assume a three-year car loan with monthly payments, with the first payment occurring at the date of sale).
- Finance $23,000 at 6% and the monthly payments are $696.22.4
- Finance $23,000 at 1% and the monthly payments are $648.25.
- The difference is $47.97 per month.
Discounting this monthly difference of $47.97 at 6% (the market rate that the bank charges and the risk of the cash flows) results in a present value of $1,584.71.
This is then compared to the cash back at the time of purchase, which is worth exactly $3,000 on the date of purchase.
It is clearly preferable to take the $3,000 cash back (providing an NPV of $1,415.29).
Another way to do the comparison is to compare the actual payments you have to make under each alternative. If you finance the car at the dealer, you have to finance the full purchase price of $23,000. However, if you finance the purchase at the bank and pay the dealer with cash, you only need $20,000 ($23,000 less the $3,000 cash back).
- Finance $23,000 at 1% and the monthly payments are $648.25.
- Finance $20,000 at 6% and the monthly payments are $605.41.5
You save $42.84 per month by paying the dealer cash after borrowing $20,000 from your bank at 6%. Discounting $42.84 per month at 6% provides an NPV of $1,415.23—the difference between the two methods results in a very small $0.06 rounding error.
This is exactly the same method you use to value what a subsidized (below-market) rate is worth for any project. The lower rate is a subsidy that has value and must be included as added value to the project. But the subsidized rate is not the cost of capital for the project, because the firm can't obtain the subsidized rate on the entire project (e.g., you can't get the car loan's subsidized rate on your other purchases either). Furthermore, the subsidized rate is generally only for a limited time, not for the life of the project, so the project's market rate is the correct discount rate to use.
Interest Tax Shields Now Limited in the U.S.
The U.S. Tax Cuts and Jobs Act of 2018 has an important impact on how WACC should be used. Until this tax law, all corporate interest was fully deductible from corporate income in all countries (as we discussed in Chapter 6). The new U.S. tax law now limits the deductibility of interest in the U.S. to 30% of EBITDA until 2022 and then to 30% of EBIT thereafter.
How should the 30% cap on interest deductibility be accounted for? As discussed above, WACC assumes tax shields are perpetual and unlimited. Since the current corporate tax law caps the tax shield at 30% of EBITDA, this means using WACC in its present form overvalues the project (by the amount of the disallowed tax shields). When using the WACC, properly valuing this reduction in tax shields requires treating the disallowed interest similarly to the subsidized interest rates discussed above. However, instead of adding value, there will be a reduction in value from the WACC amount.
Valuing the disallowed portion of the tax shield and subtracting it from the WACC valuation will give us the correct NPV. The tax shields that have been disallowed should be discounted at the cost of debt since we assume that measures the risk of achieving the tax shields.
Note that the disallowed portion of the tax shield can be carried forward and used in the future at a time when the 30% cap is no longer binding. Properly allocating for the timing of these tax shields adds further complexity to the calculations but should be conceptually understandable. We expect in practice that if the cap is binding for the first few years, most practitioners will ignore the value of the deferred tax shields since the PV of the future tax shields are likely to be small compared to the total NPV.
Table 17.1 (also shown in Chapter 6) shows that this change in the new U.S. tax law is important. The table provides percentages of NYSE firms by industry that would have been affected by these two 30% ceilings in 2017 (i.e., had the law been in effect in 2017).
TABLE 17.1 Percent of NYSE companies that have interest expense greater than 30% of EBIT and EBITDA in 2017
Source: Compustat
| Industry | EBITDA | EBIT |
| Paper, rubber, and plastics | 3.4% | 27.6% |
| Pharmaceuticals | 8.3% | 16.7% |
| Food production | 9.1% | 36.4% |
| Retailers | 9.8% | 28.3% |
| Chemicals | 11.8% | 25.0% |
| Electric, gas, and sanitary services | 18.1% | 49.1% |
| Computer software | 20.0% | 30.0% |
| Airlines | 25.0% | 50.0% |
| All (includes financials) | 18.0% | 34.9% |
| All (excluding financials) | 13.8% | 33.6% |
In addition to subtracting the value of the disallowed interest, two other valuation techniques that do not use the WACC will properly account for the change in tax shields: APV (which is discussed in this chapter) and Free Cash Flow to Equity (which is discussed in Chapter 21).
How to Estimate a Project's Debt Rating and the Cost of Debt
If a potential project has an expected debt ratio far different from the rest of the firm, and if the project has not issued public debt under its own name/credit, it is sometimes difficult to estimate the cost of debt for the project. To explain, projects (and private firms) normally do not have publicly traded debt with observable market interest rates. When a project has a similar capital structure and risk level to its parent firm, the parent firm's interest rate can be used. When this is not the case, we must estimate the cost of debt to the project.
Since debt ratings reflect the risk of the debt to the investor, the cost of debt is highly correlated to its rating. Thus, if a market interest rate is not available to us directly, we can estimate one with a twin-firm technique using debt ratings. A twin-firm technique means determining the project's potential debt rating and then asking what interest rate the market charges for debt with that rating.
Now we ask the question: How are the ratings for a firm's debt determined? Rating agencies have guidelines for percentage of debt and coverage ratios. We can use these guidelines as a first pass: the ratings will be increased if the firm is large and has good management; the ratings will be decreased if the firm is small and management has not performed well. The age of the firm is also a factor, with older firms getting an upward bias and younger firms getting a downward bias. Your authors are not trying to explain how the ratios for different ratings are determined. Rather, we are explaining that if you know what ratios a firm is expected to have, you can estimate its debt rating.
Normally, debt ratings are obtained directly from one of the rating agencies or from a broker or other finance professional. When they are not publicly available, they can be predicted by using the firm's ratios from both its current and pro forma financials. As shown in Chapter 15, Sungreen's Kingsport plant and mill had an expected debt ratio of 22.5% in 2019. Additionally, Sungreen had an EBIT interest rate coverage ratio (EBIT/I) of about 8.4. Furthermore, it is a fairly stable business. Together, these three factors are consistent with firms that have a rating of A. Sungreen's debt rating depends on the size of the firm or project, the business risk (fairly stable cash flows with low risk), the debt ratio (22.5% is not high for the industry), and the coverage ratio (an EBIT/I of 8.4 provides a large margin of safety).
After estimating that Sungreen's debt rating is an A, we would now go to the market and see what interest rate corresponds to an A rating.
NUANCES ON CALCULATING THE COST OF EQUITY: LEVERING AND UNLEVERING BETA
Now, let's discuss different ways to unlever and relever a project's equity beta. There are several formulas to do this in finance. In Chapter 16, we used one of the simplest, listed below. (In footnote 7, we reference where you can look up other formulas.)
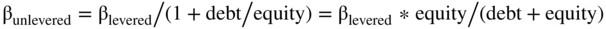
And then we relevered at our target debt ratio:
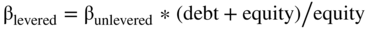
These formulas assume the betas are equity betas and that the beta of debt is zero.
To understand this formula and where it comes from, let's start with the beta for the entire project (or firm). The project's beta reflects the capital structure of the project as well as the beta of the debt and the beta of the equity. (There is an assumption that the tax rate is 0.)
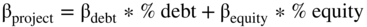
Does debt even have a beta? Yes, debt has a beta. What is its expected value? The beta of the debt reflects how the return on the debt correlates with the return on the market. Conceptually, it is identical to the beta of equity and is calculated the same way. The beta of riskless debt is zero, and the beta of corporate debt, which has risk, is greater than zero. (It is usually assumed that U.S. government debt is riskless.)
Using the CAPM formula on riskless debt, we get the following:
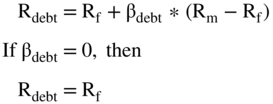
which is, of course, the same as saying that the return on government debt is the risk-free rate.
Let's now work through an example where the beta of the debt is not equal to zero. This is the case for all corporate debt. Using Apple as an example, if the overall market goes up, all else being equal, Apple's stock will also go up. (The beta of Apple stock is approximately 0.9.) When Apple's stock price increases, the price of Apple's outstanding debt will also probably increase. Why? With the market improving and the value of Apple's equity increasing, the likelihood of a default on the debt goes down. All else being equal, this will lower the required market return (discount rate) on Apple's debt, thereby increasing its value.6 Similarly, if the stock market and Apple stock price fall, the debt becomes riskier, the cost of debt rises, and the price of outstanding debt falls. The relationship between the return on Apple's debt and the market defines the beta for Apple's debt.
Note that these changes are not the same as a change in the value of a bond due to a change in the market interest rates. Bond prices go up and down inversely with interest rates, but this does not directly affect the beta of the bond. The beta of the bond is affected by the correlation between bond returns and market returns. Of course, market returns may also affect interest rates or vice versa. When calculating the beta for debt, we are not using the change in market interest rates; we are using changes in market returns.
In the last chapter, we noted that when discussing the risk-return spectrum, the beta of AAA debt is approximately 0.15. Assume a firm with AAA debt that has a beta of 0.15, an equity beta of 1.5, and a debt-to-total-capital ratio of 33.3% (which means the equity-to-total-capital is 66.7%).
From above, the beta of the project is:
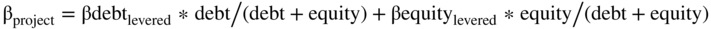
After plugging in the numbers, we get a project beta of 1.05 = 0.15 * 33.3% + 1.5 * 66.7%.
The project beta is also called an asset beta. An asset beta is equivalent to the unlevered equity beta in a firm with no debt.
In the last chapter, our formula for unlevering beta was:
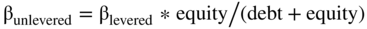
And our unlevered equity beta, using this formula, becomes 1.0 = 1.5 * 66.7%. This is close to the project beta of 1.05 derived from the full formula. Remember, the simplified formula we introduced earlier is obtained by taking the full formula and assuming the beta of the debt is zero.
In our example, the simplified formula gives an unlevered beta of 1.0 compared to an unlevered beta of 1.05 from the full-blown formula.
Now, let's relever our equity beta at a different target debt ratio, say 66.7% debt and 33.3% equity (instead of 33.3% debt and 66.7% equity), using both the full and the simplified formulas.
Our simplified formula is:
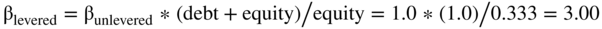
Our full formula is:
Again, the result from the full formula and the simplified formula are similar. Note that if the leverage of the firm doubles, we don't expect the beta on the debt to remain the same.
How much difference does it make using the full or simplified formulas when levering and unlevering beta? As long as the beta of your debt is fairly low (which it is for highly rated debt) and you have a low debt ratio (which is partly why you would have a low debt beta), then the beta calculated from the simpler model will be very close to the beta calculated with the full-blown model. Even with large changes in beta and the debt ratio, the difference between the models is not that large. Furthermore, it is generally pretty easy to find the beta of the equity, while the beta of the debt can be much more difficult to find. Hence, many analysts use the simplified approximation.
So, what are the important takeaways to remember regarding levering and unlevering beta? First, there are many different formulas (we covered just the two simplest and most common here).7 Second, realize that the simple model assumes that the beta of the project's debt equals zero.
What does this mean for the cost of capital used in valuations? Unlevering and levering beta are not exact. There are two large assumptions. One is that the beta of debt equals zero. We just showed that this assumption, although untrue, normally has little effect. However, a second assumption is that the beta increases linearly. We know this latter assumption is also not true.
In the example above, we assumed a huge increase in debt, a doubling from 33.3% to 66.7%. Our formulas, however, assume that the increase in debt causes a linear increase in the risk of the equity beta. When we discussed leverage and its effect on the cost of debt and equity in Chapters 5 and 6, we mentioned that as the percentage of debt increased, the cost of debt and equity at first increased slowly and then increased at a faster rate. That is, we assumed the relationship between leverage and risk was curvilinear.
The bottom line is that doing the full formula gives one approximation and doing the simpler formula gives a different approximation. They are both approximations, and now you can see the difference in their scale. On the street, almost everyone uses the simplified formula. Why? The difference in scale is normally not that large, and the real issue is that both formulas use assumptions. (After this section, if you ever see the full-blown formula, you now know what it is, how it is derived, and why it is not normally used.)
Another commonly used formula for levering and unlevering beta was developed by Bob Hamada at the University of Chicago and is as follows:
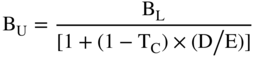
Where BU is the unlevered beta, BL is levered beta, TC is the corporate tax rate, and D/E is the debt-equity ratio.
Other Ways to Estimate the Cost of Equity: The Arbitrage Pricing Theory
So far, we have used the one-factor CAPM model to estimate Ke. The arbitrage pricing theory (APT) is another way to estimate the expected return to an asset such as equity. In its simplified form, it is a linear combination of a set of risk factors, with each factor having its own beta. The theory was developed by Steve Ross, who was a professor at MIT. The APT assumes the return to any asset can be written as a relationship with that asset's risk factors as follows:
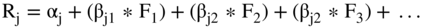
where:
- αj = a constant
- βjn= a beta specific to each factor
- Fn = a risk factor
The APT also states that the expected return to asset j can be written as:
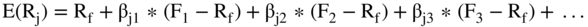
where:
- Rf = the risk-free rate
- βjn = a beta specific to each factor
- Fn = a risk factor
The betas are estimated from a regression (similar to the way it is done in the CAPM), with the return for the asset j (Rj) as the dependent variable and the risk factors as the independent variables. From our point of view, the important question is: What are the risk factors? The theory doesn't tell us which factors are important.8 In practice, we want to use risk factors that affect the security's return. The factors (Fn) can be macroeconomic (e.g., interest rates, oil prices), they can be related to the market (e.g., the market return is almost always used), they can be industry specific (e.g., a commodity index), or they can be firm characteristics (e.g., size).
Empirically, the APT regression, with its larger set of explanatory variables (one of which is usually the market return), generally provides a better fit than the CAPM. One way to view the CAPM is that it is a special one-factor case of the APT, with a beta derived by regressing the market returns on the asset's returns.
Fama and French (1993) empirically identify three factors related to equity returns. The factors are return to the market (Rm), return to size (Rs), and book-to-market.9 Fama and French find that equity returns are positively correlated with the return to the market, negatively correlated with firm size (smaller firms have higher returns than larger firms), and negatively correlated with the firm's book-to-market (high book-to-market firms have a lower return than low book-to-market firms). This Fama and French three-factor model can also be thought of as a special case of the APT.
Recently, some researchers have added a fourth factor to Fama and French's three-factor model: momentum. This factor captures whether if a stock is going up in price, it keeps going up, and if it is going down in price, it keeps going down.
Today, many/most investment management firms use multi-factor models. However, corporate finance practitioners still rely almost exclusively on the CAPM to estimate the cost of equity. Your authors believe that at some point in the future, the most commonly used valuation models will include variations of the APT to estimate the cost of equity. When they do, you will be ready.
SEPARATING CASH FLOWS AND TERMINAL VALUES
When we did valuation in the previous chapter, we added the present value of the cash flows and the present value of a terminal value and then compared them to a purchase price. (We will also do this for an acquisition in Chapter 18.) Does it matter how much of our total value is due to the cash flows versus the terminal value? Yes, as we showed in Chapter 16. Imagine the firm has two projects with different cash flows and different terminal values but the same total NPV. Suppose Project A has a present value of $10 million for the cash flows of the first three years of the project's life plus a present value of $2 million for the terminal value, which sums to a total present value of $12 million. If the total cost is $10 million, then it has a positive NPV of $2 million, and the firm will decide to proceed. By contrast, Project B has a present value of negative $20 million for the cash flows from the first three years of the project's life and a present value of $32 million for the terminal value, which sums to a total present value of $12 million. Assuming it has the same cost of $10 million, then it also has an NPV of $2 million.
Now, both Projects A and B have the same total present value. But are they really the same? Would management look at these two projects in the same way? Absolutely not. The two projects are very different. How so? Project A is much more likely to be adopted because most of its value is realized in the first few years of the project. Project B is less likely to be adopted because most of its value comes from the terminal value.
Although this is an extreme example, it illustrates why your authors believe it is important to separate out the value of the cash flows from the terminal value. In addition, if a project (or acquisition) has an initial investment outlay at time zero, we recommend keeping all three of the values separate: the investment outlay, the present value of the cash flows, and the terminal value. Because of the use of spreadsheet programs like Excel, most students and many analysts solve for and report the NPV as only one number. However, separating these three parts allows us to more clearly determine where the value comes from. This becomes particularly important when evaluating mergers, which we will discuss in the coming chapters. Technically, Project A and Project B have the same NPV; however, the timing of when the value is realized is sometimes an important nuance.
NUANCES OF TERMINAL VALUE METHODS
Having discussed the importance of separating out the terminal value, we next discuss differences in how they are calculated. It would be nice if we could simply compute cash flows out forever and ignore terminal value. Unfortunately, this is not possible. How many years of cash flows should we use before determining terminal value? As many as a firm provides, or what the firm is comfortable projecting. A five-year time horizon is quite common, but it can be as short as two years or as long as ten. The cash flow valuation can use any time period, after which a terminal value must be computed.
How do we compute terminal values? There are five principle methods:
- Cash flows using the perpetuity formula
- Book values or liquidation values
- Earnings or cash flow multiples
- Comparables
- Contingent claims
These methods of computing terminal values should look familiar since they are the same five techniques that are used to value a project. All the valuation methods your authors have ever seen in their careers can be classified into one of these five categories.
The first three methods are the most commonly used, and we will discuss them below.
We should note that valuation methods either value the entire firm or value the firm's debt and equity separately. This is also true for terminal values. Some terminal value techniques estimate the value of the entire firm; some only estimate the value of the debt or equity. We include examples of this in our discussion below.
Estimating Terminal Values Using the Perpetuity Formula
The perpetuity formula presented in Chapter 15 was:
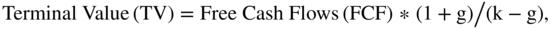
where:
- k = the cost of capital
- g = the growth rate of future cash flows
We noted in Chapter 15 that this formula is used in finance, but it is really driven by mathematics. We suggest readers return to that section if they need a review of how the formula is derived.
The nuance we would like to add here is the answer to the question: What growth rate should be used in the perpetuity formula for terminal value? The obvious answer is that it is the rate at which we expect the cash flows to grow. If a firm is at full capacity with a mature penetration of the market, the inflation rate is often used as the growth rate. However, a more common way to estimate the future growth of the cash flows is to look at how fast the cash flows are forecasted to grow in the pro formas. That is, with a five-year pro forma estimate, take the growth rate over the last four years and use that in the perpetuity formula. Unfortunately, doing this may result in an overestimation of the terminal value.
The overestimation occurs because pro formas, particularly for new firms or a new project, will often have a higher growth rate in the period covered by the pro formas than can be expected over the long term. Sometimes, in fact, the growth rate (g) may be higher than the cost of capital (k), which means the formula makes no sense. This is called “supernormal growth,” and it is not sustainable. As a general lesson, any “supernormal” growth rates should always be suspect in pro formas. Growth rates many times faster than the overall economy usually occur only for a short period, when a firm is starting and is either increasing market share at the expense of its competitors or creating a new industry.
For example, if our first five years of cash flows are growing at 30% per year and the cost of capital is 15%, we don't expect the situation to continue in perpetuity. If the situation were to continue, the firm would eventually grow to be worth more than the rest of the world's economy. In these cases, what we need to do is forecast out more years until the growth rate sufficiently slows to what we think can be sustained in perpetuity.
Note: As a reminder from Chapter 15, it is a very common mistake to calculate a terminal value using a growing perpetuity by taking the cash flow today (FCF) and dividing by (k – g) instead of the cash flow a year from today ((FCF) * (1 + g)). The perpetuity formula takes the cash flows one year in the future and brings it back to today. In order to get the value today, we must use the cash flow value one year in the future, not the value of the cash flow today.
Estimating Terminal Values Using Asset Values
A second way to determine terminal values is to estimate the value of the firm's assets: at what price a firm could sell or replace its assets. We used this concept when we considered the collateral value of PIPES' assets back in Chapter 3.
The starting point to estimate terminal asset values is book values. In fact, often the book value of the firm is used as one estimate of terminal value. However, the book value is a crude proxy since we know accounting values normally do not reflect market values. The question becomes: How to adjust accounting values to reflect market values?
The answer to this question is not straightforward. We can, however, usually determine whether the market value is above or below the accounting value. Let us explain this with an example:
Assume a firm has a book value for total assets of $100 million at the end of the estimated pro forma period. Now, let's compare the firm's book return on total capital with its required market return. That is, let's compare the firm's return on total capital (EBIT/total capital) with its market cost of capital (Ko). If the book return on assets is greater than the market-required return on assets, this means the market value of the firm's assets should be worth more than the book value. Alternatively, if the book return on assets is less than the required market return, it means the assets' market value should be less than their book value. Huh?
Let us explain. Imagine you start a bottled water company. You invest $1 million in net fixed assets, which are initially both the market and book value of the assets. Assume the expected free cash flows a year are $100,000 forever. The return on book assets is therefore 10% ($100,000/$1 million). Now, if we assume the market cost of capital (Ko) is also 10%, then the market value of this firm is (using the perpetuity formula discussed in Chapter 14) also $1 million ($100,000/10%). (We assume here that the cash flows are constant and forever so we can use the simple perpetuity formula.) Thus, when the market return on capital equals the book return on capital, the market value of assets equals the book value of assets.
Now, let's suppose we give our bottled water a fancy name and the firm starts advertising that its water is naturally effervescent (even though, in fact, the firm injects bubbles into the water). Consumers decide they like the product, and the cash flows increase to $200,000 a year forever. How much is the book return on assets now? It is 20% ($200,000/$1 million). Assume the market risk is the same, so the required market return remains at 10%. (Remember, market return is driven by the risk of the company or project.) This means the book return (at 20%) is now above the market-required return (of 10%).
If the firm was being sold, would it sell it for the book value of $1 million? No. How much would it sell for? A cash flow of $200,000 forever, discounted at 10%, has a market value of $2 million. In this instance, because the book return is above the market return, the market value of the assets is above the book value of the assets.
Once the firm is sold to new owners, the new owners write up the assets to $2 million, which becomes the new book value. The return on the book value of assets is now 10% ($200,000/$2 million), the same as the market rate. So, again the market value of the assets equals the book value.
Now suppose the public finds out the firm is injecting benzene into the water to create the bubbles and there is a worry that benzene may possibly be carcinogenic. Suddenly the sales of the firm plummet, and the cash flows are now expected to be $100,000 a year forever. The book return for the new owners is now 5% ($100,000/$2 million). If the market still requires a 10% return and if the assets are sold again, the new market price will be $1 million ($100,000/10%). Thus, when the book return is less than the market return, the market value of the assets is less than book value.
As nice as this example is, the actual relationship is not necessarily linear. That is, if book return is twice the required market return, the assets do not necessarily sell for double the book value. First, the cash flows are not necessarily perpetuities. Second, doubling the cash flows due to a change in the product market conditions may also change the market risk level. However, we know that if the market's required return is below (above) the book return, then the assets will probably sell above (below) book value. Thus, examining the book return on assets (ROA) versus the required market rate of return (Ko) provides a rule-of-thumb reality check for whether the terminal value is above or below book value.
A quick aside: An important question is whether to use the value of the assets before or after subtracting the liabilities. A more formal way of asking this question is: Should we use the terminal value of the firm or the terminal value of the equity? When using free cash flows to the firm, the terminal value used should be the terminal value of the firm. Subtracting off the terminal value of the debt provides the terminal value of equity. It is a common mistake for people to mix up the terminal values of equity and the terminal values of the firm (remember, the value of the firm equals the value of debt plus the value of equity).10
Estimating Terminal Value Using Multiples
So far, we've estimated the terminal value using the perpetuity formula and using asset values. A third approach to determine terminal values is by using multiples. The most common multiple used in finance is the P/E ratio (price per share/earnings per share). However, what kind of terminal value do you get when you use the P/E? You get the terminal value of equity. To get the terminal value of the firm requires adding the market value of debt (with the slight problem that you often have to use its book value as a proxy because the market value of debt is often unavailable) to the market value of equity (computed using the P/E).
There is another problem with using P/E multiples: different firms, even in the same industry, may have very different P/Es. Why are P/E ratios so different, even in the same industry? A common reason is the difference in the firms' leverage. From Chapter 7 (on Marriott), we can answer this question: As a firm increases its leverage, what happens to its P/E? In Chapter 7, we discussed the fact that as leverage increases, the P/E goes down and only down. The more debt a firm adds, the riskier the firm becomes and the lower the multiple.
So, can we unlever to get the right P/E? While there is no formula to unlever a P/E, the approach is to use a multiple that values the entire firm. The most commonly used multiples that value the entire firm are the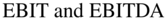 
multiples. They are calculated by dividing the value of the firm, which is the value of the debt plus the value of the equity, by 
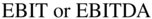. The value of the debt is usually assumed to be the book value, and the value of the equity is usually assumed to be the market capitalization (the price per share times the number of shares outstanding).
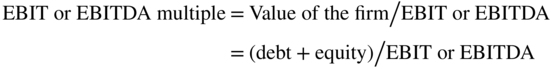
Generally,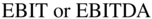 
multiples are much closer across firms in an industry than P/E multiples. Why? Using a multiple with the entire value of the firm negates the effect of leverage on just the P/E multiple. 
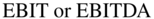multiples, when they first started to be used in the 1970s in LBOs, were initially called unlevered P/Es (though they are not technically unlevered).
To summarize: P/E multiples may be different across firms because of differing leverage ratios.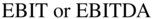 
numbers have both debt and equity included, so 
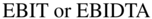multiples do not differ as much.
A Final Terminal Value Nuance
A useful approach when calculating terminal values is to consider the terminal value required to make a project break even (i.e., to get an NPV = 0 for the project). This is done by starting with the price of the project and subtracting the present value of the cash flow projections. That is, calculate the NPV without a terminal value. Normally this will result in a negative NPV. Next, evaluate the minimum terminal value required to bring the NPV to zero.
Then, depending on the terminal value technique used, determine the necessary assumptions to achieve that terminal value and see if these assumptions are likely to occur or not. If they cannot occur, then the firm will likely not be able to break even.
For example, using the perpetuity method of terminal value, what is the minimum growth rate required to get NPV = 0? When using the asset value method of terminal value, what percentage of book value would the assets have to be sold at to achieve NPV = 0? Finally, when using a multiple approach, such as EBIT, the question is: What is the EBIT multiple required to get NPV = 0?
The idea is to reverse engineer the assumptions necessary to achieve NPV = 0 under each terminal value method. In other words, determine what assumptions are required to break even. Then, compare these assumptions to the firm's past performance. If the assumptions are realistic and are likely to occur, then the terminal value will probably cause the firm to break even or have a positive NPV. If the assumptions are unlikely to occur given the firm's past performance, the terminal value will likely not be large enough for the firm to break even. For example, when using the perpetuity method, if the required break-even growth rate is 10% but the historic growth rate never exceeds 5%, the project is unlikely to have NPV = 0, let alone a positive NPV.
This demonstrates another reason why it is important to separate out the terminal value and not combine it into one number with the present value of the cash flows and the initial investment. Separating out the terminal value provides an added level of confidence when accepting or rejecting a project.
Bottom Line on Terminal Values
To repeat from above, we noted that there are five ways to value a project or investment: discounted cash flows, asset multiples, earnings multiples, comparables, and contingent claims. How are terminal values determined? Using the same five ways. The techniques used to value cash flows are exactly the same ones used for terminal values.
So, which method is the best one to use? Our recommendation is never to use just one technique to find the terminal value. Why not? Because understanding the differences between the techniques and their estimates increases confidence in the final valuation.
For example, if a project is near the end of its life (e.g., it is a plant with a 20-year life and is now at the end of year 18), it would not make sense to use the perpetuity formula or a sales multiple. This is probably a situation better suited for a liquidation value (which is a variant of the asset value technique). In contrast, if the firm is running in good shape and is expected to operate for another 100 years, then it makes no sense to use a liquidation value. This would be a situation to use a perpetuity formula, a sales multiple, or a P/E multiple. These examples show that finance requires us to use our judgment and discretion because the choice of valuation method requires understanding the context.
It is also important to warn that most people doing valuations concentrate on the cash flows and do the terminal values as an afterthought. But remember our result from Sungreen in the last chapter: the project had a negative present value before the terminal value was considered. After the terminal value was included the project had a positive NPV. Don't spend most of your effort in doing a valuation on cash flows and then tack on a quick perpetuity terminal value. Assumptions, such as which growth rate to use, can substantially alter the NPV of the project. Terminal value is important and often critical, so it should be considered carefully.
The Politics of Valuation
Another nuance, one not commonly considered in finance textbooks, is the importance of politics in valuation decisions. Politics or human nature (e.g., self-interest) will sometimes override the correct financial analysis. Managers may seek to maximize their bonus or their plant size, or they may try to avoid laying people off (which is painful). Political considerations may affect any part of the valuation, from what cash flow assumptions are made to how the cost of capital is calculated.
Back when we covered how to do pro formas in Chapters 2–4, we saw how important the assumptions about ratios and growth rates were in determining the pro forma numbers. Since discounted cash flow valuation uses pro forma cash flows as inputs, changing the assumptions in the pro formas (e.g., assuming sales growth is 8% a year instead of 6%, or assuming COGS is 20% instead of 22%) changes future cash flows and hence the valuation. This is important to keep in mind because politics can influence pro formas, at times substantially.
What causes a variation in the assumptions about ratios and growth rates used in pro formas? The reason listed in Chapters 2–4 was the uncertainty about what the true ratios and growth rates will be in the future. However, politics also has a role. Consider a manager who is advocating for plant modernization. The manager has an incentive to understate the true costs of the renovation and to overstate the benefits. A valuation is never about just the numbers. It is about the assumptions, and the assumptions are often about what people want subjectively, not necessarily about what is realistic.
Another example, one closer to home, is that many universities only allow construction on new buildings once a fixed percentage (e.g., 60%) of funding for the building has been collected from or at least pledged by donors. Imagine the building is expected to have a true total cost of $110 million and that $60 million has been collected. To begin construction, the dean might claim the building will cost only $100 million and then later argue the extra $10 million was a cost overrun. (This idea is summed up in an axiom: “It is easier to ask for forgiveness than it is to get permission.”)
Numerous project evaluations in many different settings are influenced by politics. A manager may make a modest proposal and expand it later after the organization has approved the initial proposal. Another option for the manager is to break a large project into smaller components (e.g., separate the building from the furnishings). Managers also manipulate project assumptions by changing the timing of cash flows.
It is not just projected cash flows that can be manipulated. Assumptions about the discount rate can also have a large effect on a project's valuation. For example, using a simple perpetuity formula, a true cash flow of $10 million a year has a present value of $100 million with a 10% discount rate and a present value of $111 million with a 9% discount rate. What is the correct discount rate to use is a recurring question in valuation.
A common example of this is the discount rate used in valuing a firm's pension liabilities, which determine its pension funding requirements. This can have a major impact. General Motors used a 3.73% discount rate to compute its 2014 U.S. pension plan benefit obligations. Ford, in contrast, used a 4.74% discount rate to compute its 2014 U.S. pension plan benefit. For a $100 million perpetuity this difference in discount rates changes the net present value by $570 million ($2.68 billion versus $2.11 billion).
Investment banks often formalize differences in cash flows and discount rate assumptions when they do valuations. When evaluating a project, an investment bank usually prepares a matrix (4 by 4 or 5 by 5) of the project's value with different cash flow growth and discount rate assumptions. While this may seem to remove politics, in fact a majority of the matrix cells will usually show the project has a positive NPV. That is, a majority of cells indicate the project should be done. Why would an investment bank's matrix mostly show the project should be done, regardless of the growth and discount rate assumptions used? Perhaps it is because the expected value is indeed positive. But perhaps it is because of the fee structure for how the investment banks are paid. Investment banks normally receive a base fee for the service of doing the valuation plus a contingency fee if the deal is consummated. This provides a powerful incentive for the investment bank to demonstrate that the deal should be done.
OTHER VALUATION TECHNIQUES: DCF VARIATIONS
Although we have mentioned several times that there are five main valuation methods, there are many variations within each method. The discounted cash flow (DCF) method is no exception, and we have already discussed two variations—IRR and Payback—in Chapter 14. In this chapter, we will add another variant: adjusted present value (APV).11 We have included it in this book because it is widely used by academics and in textbooks. However, at the end of the explanation below we will point out that it is rarely used in practice.
Adjusted Present Value (APV)
Adjusted present value (APV) separates the value of a firm or project into pieces. In its simplest form, it first values the firm or project as if it were financed entirely with equity (i.e., zero debt). It then values the tax shield of any debt financing and adds the two together to obtain the value of the levered firm or project.
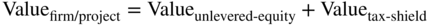
That is, APV is the value of the cash flows in an all-equity firm or project plus the tax shield to the debt. The cash flows are discounted at Ka, where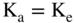 
using an unlevered beta. The tax shield is discounted at a rate between 
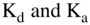, as discussed later.
So how does one value an all-equity firm? By using the free cash flows to equity (with zero debt) and discounting them with the cost of equity for an all-equity firm. When calculating APV, the free cash flows to an all-equity firm are the same as the free cash flows for a levered firm when using the WACC. How can FCF for an all-equity firm be the same as the FCF we got for a levered firm when calculating WACC? Because the free cash flows to the firm that we use with the WACC do not change with the percentage of debt used (0%, 10%, 20%, or more). Why? If you recall, there are no interest tax shields in the cash flows. (Remember, our discussion of the WACC showed that the interest tax shields were accounted for in the discount rate and not in the cash flows.) This means the free cash flows to the firm are the same at all levels of debt or without debt. (A proof will be provided in Chapter 20.)
So, if the cash flows are the same, what is the discount rate when there is no debt, which we call Ka? It is the discount rate for the cash flows from an unlevered firm (which are the cash flows from just the assets). Remember, the cash flows from the assets are the cash flows to the equity owners if there is no debt.
Finding the discount rate for the assets requires measuring the risk of the assets' cash flows. To do this, we have to calculate the cost of capital for an all-equity firm. We use the same CAPM formula we used in prior chapters, but the beta we use is for just the assets (without any debt).
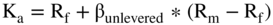
This is the unlevered or asset beta that we showed how to calculate with our unlevering formula.
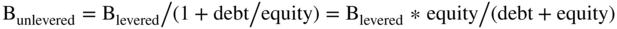
What about the risk-free rate and the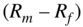 
term in the CAPM formula above? They are the same as before: Rf is the long-term government rate less 1%, and 
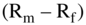is the market risk rate. In other words, when using APV, the value of the unlevered firm is calculated by discounting the cash flows using a WACC with 0% debt.
Now, as mentioned, we have to add the present value of the tax shields. How do we calculate this value? First, we have to assume how much debt the firm (or project) will use. One option is to assume that the face value of debt remains constant and thus the interest payments remain constant. That is, we would assume the firm issues a fixed amount of debt that does not vary over time. In this case, the correct discount rate for the interest payments is Kd (which is what the market charges the firm for the debt issue). That is, the tax shield is the tax rate times the interest payments 
to the debt discounted at the cost of capital Kd. Now, Kd represents the risk of the debt obtaining the tax shield. The equity cash flows are still discounted at Ka.
A second option is to assume the debt is a percentage of the value of the firm (and as such, the value of the debt goes up and down with the value of the firm). In this case, the value of the tax shields varies with the value of the firm. This means the risk on the tax shields is greater than the initial Kd. Since the amount of debt (and hence the amount of the tax shield) varies with the risk of the firm, the discount rate for the tax shield is close or equal to Ka.
Let's use an example. If a firm, let's say Sungreen, issues $50 million of debt, the tax shields are only as certain as its debt payments. The risk of the firm making its debt payments is Kd, so the correct discount rate for the debt and the tax shields is Kd. However, if the amount of debt the firm issues varies with the value of the firm, the tax shields also vary with the value of the firm. If the risk of the firm obtaining the tax shield varies exactly with the value of the firm going up and down, then the tax shields should be discounted at Ka.
Using the second option (the value of the debt varies with the value of the firm) introduces a complication. To obtain a value for the debt each year requires also estimating a value for the firm each year. That is, to get the value of the tax shield each year means it is first necessary to compute the value of the firm each year. Thus, valuing a firm or a project using the APV approach means first finding the value of the firm each year.
How is the value of the firm determined each year when using APV and assuming the percentage of debt changes with the value of the firm? Believe it or not, it is often done by using the free cash flows to the firm and discounting them with the WACC (which assumes the percentage of debt is constant). Really? Yes, really. Using the APV approach with the assumption that the percentage of debt goes up and down with the value of the firm requires knowing the amount of debt and the tax shield each year. This requires knowing the value of the firm each year, which is normally estimated using the free cash flows and the WACC each year. (If this appears circular, it is.)
Academics (and other textbooks) like the APV approach because it is a very elegant model. It shows that the value of the firm is the value of an all-equity firm plus the value of the tax shields. This is a nice way to think about firm valuation. It highlights that tax shields have a value that can be computed independently and emphasizes the impact of changing the leverage of the firm. In practice, however, the APV method has more computations (firm values and debt levels must be computed every year).
The APV approach can also be used to value more than just the equity cash flows and the tax shields from debt: APV can also include other valuation pieces such as the cost of financial distress or subsidized interest rates. In the case of the cost of financial distress, as a firm increases its debt and its tax shield, the firm also has a higher risk of financial distress and thus a higher cost of capital. One way to adjust the cost of capital for the increased risk of financial distress is to restate the APV formula as the present value of an all-equity firm plus the present value of the tax shield minus the present value of the additional cost of financial distress (the cost of financial distress is the probability of distress times the deadweight loss).
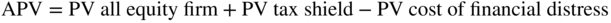
The above formula takes us back to an M&M (1963) world with taxes and financial distress.
APV would also easily handle the new 30%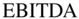 
cap on interest deductibility in the United States. The interest tax shield allowed would only be for the amount up to the 30% limit. Any interest over that amount would not be valued in the tax shield. Thus, the formula would be the same as above, but the tax shield would be limited to deductible interest.
APV is an elegant way to show that the value of a firm is the value of its equity plus the value of its tax shield (minus the cost of financial distress, if it is taken into account). However, estimating the APV is difficult in practice. Neither of your authors can think of any major bank that uses the APV as a primary method of valuation. Many don't use it at all, but its use may go up with the 2018 U.S. tax law. This is because of the difficulties introduced by the limits of interest deductibility, which makes the free cash flow to the firm evaluated at a WACC method incorrect (see the discussion above).
REAL OPTIONS (AKA STRATEGIC CHOICES)
Finally, let us briefly mention the topic of strategic choices, which finance professors call “real options.” A firm's strategic choices are, in fact, options. A firm's right to make future investments, switch investments, sell projects, liquidate projects, or abandon projects—these are all options. Imagine that a firm can choose to invest in Project A now with an option to invest in Project B later. If the firm does not invest in Project A now, it will not have the option to invest in Project B later. For example, a firm may want to gain entry to the Chinese market. Its first project into China, as a stand-alone, may have a negative NPV. However, if the firm does not undertake this first project, it may preclude the possibility to invest later. The value of the option to expand may make the first project a positive NPV. The question is how to determine the value of a strategic or real option.
Let us illustrate this concept using the U.S. movie industry. The median movie made in the United States loses money. This means 50% of all movies made in the United States each year lose money. If 50% of all movies made in the United States have negative NPVs (at least after the fact), why are movies made? One answer is that hit (profitable) movies are very profitable (so the average, or mean, is positive). Another answer is that profitable movies often have sequels that are also profitable.
When a movie is made, it is often unclear whether it will be profitable or not. If it becomes a blockbuster, however, it is almost certain that a sequel will be made and be profitable. The key is that the decision to make the sequel is not made until the results from the original movie are known. Thus, while determining whether to make the original movie is a difficult financial decision, determining whether to make a sequel is much clearer. If the original movie is not a hit, there is no sequel. If the original movie is a blockbuster, a sequel is forthcoming. The option value of the sequel increases the present value of the original movie.
This option value has other implications to the movie industry. For example, it is why the villain in a film like Star Wars is rarely killed off. Killing the villain reduces the probability of the sequel. Another implication of sequels is that viewers expect the same actors as the original. Moviegoers for Terminator 2 expect Arnie (Arnold Schwarzenegger, the star of The Terminator) to “be back.” This means Arnold Schwarzenegger has option value as well. If a sequel is made, Arnie can demand a higher remuneration to do the sequel. Knowing this, movie studios often have actors sign a contract for not only the current film but for sequels as well. It is also why all three Lord of the Rings films were filmed before any of them were released. The producers expected Lord of the Rings to be a blockbuster, and if they were correct, they wanted to ensure they would get Frodo for the sequels without him holding them up for more money (or without him taking the ring and disappearing).
This also explains which movies are more likely to be made. Consider the choice between making a film about the Flintstones or a movie based on Ernest Hemmingway's book The Old Man and the Sea. The Flintstones, if successful, can easily have a sequel. By contrast, a movie based on The Old Man and the Sea is unlikely to have a sequel (spoiler alert: the old man dies at the end). This type of choice is affected not only by the artistic merits of the movies but also by basic finance.
We do not cover real options in detail in this book, but we wanted to introduce the concept because a part of the value of any project is the value of its real options. Thus, the NPV of a project equals the value of the project plus the value of its real options. There might be cases when a firm is willing to undertake a project (e.g., build a soft drink plant in China, drill an exploratory well, etc.) without expecting the initial venture to have a positive NPV. Instead, the project is done because of the value of its real options.
Once the Numbers Are Done: Strategic Considerations
Running the numbers (i.e., determining whether the NPV is positive or negative and how much of the value comes from the cash flows versus the terminal value) is only one step in evaluating a project or acquisition. While we have treated it as the first step in this book (after all, it is a finance book), it should really be the second step. Strategic issues should come first.
The numbers alone don't tell a manager what to do. They only provide information regarding the cost or benefit of doing something. For example, all else being equal, a project with a positive NPV should be undertaken and a project with a negative NPV should not. However, there may be other factors not included in the valuation. For one thing, strategic and economic issues indicate whether the pro formas can even be achieved.
Pro formas are relatively easy to generate but hard to get correct. You should remember that if a project or firm earns a competitive return, it has a zero NPV. A positive NPV is only possible due to higher cash flows (brought about by higher prices or lower costs than competitors) or due to a lower cost of capital. Strategic considerations incorporate the economic analysis that determines whether the cash flows and/or cost of capital can actually be achieved. Remember, the economics drive the numbers; the numbers do not drive the economics. Your authors have a rule of thumb when faced with a positive NPV project: explain why the NPV of the project is positive in five sentences or less. If you can't, we don't believe it.
For example: What is the key strategic element for why Sungreen is building a new mill and plant? Some of the issues Sungreen must consider include what its competitors are doing, if there are any potential new entrants into the market, the price of raw materials, and the outlook for the final product (price and quantity). If the firm is using new technology, then the firm has to worry about whether it will work properly. In Sungreen's case, this may include new technology, including printing presses. Assume Sungreen is going to pay $205 million for the mill and $50 million for a new state-of-the-art printer. What happens to the firm's investment if the new printer does not work? Not only is the $50 million investment in the printer in jeopardy, but some or all of the $205 million investment in the mill is as well. (If the mill produces paper that Sungreen cannot use, the paper can be sold to others so that the plant and mill are not a total loss. However, this reduces the value of the mill and plant to Sungreen, which had included in its valuation the ability to use the paper itself.)
Thus, for Sungreen, a major concern of the project is whether the new printer will work—the printer is a key strategic element. Assume that if the printer works, then the project has a positive NPV. But what if the new technology fails? How should the project be valued? It is possible to estimate probabilities of success, but in the real world this valuation problem would probably be managed with a contingency contract. That is, the supplier would receive a partial upfront payment and then an additional payment if and when the new technology works.
This type of contracting is a large part of courses in entrepreneurial finance or venture capital. The valuation piece is done exactly as above: the methodology is exactly the same. The difference is contracting for all the contingencies. Often, if a firm pays for something up front, the selling party no longer feels any responsibility to ensure it works. However, if there is still a large outstanding payment based on a contingent result, the seller is motivated to ensure that the expected result is achieved. The seller has the same incentive as the buyer to ensure the project works as promised.
As an aside, in practice, without contingency contracts, lawyers get involved when something doesn't work. To avoid that, in finance, a side contingency contract can be set up to help resolve the issue. Regardless, the basic valuation is done the same as it is in the previous chapters.
An Additional Nuance
There are all sorts of additional valuation issues beyond the scope of this book. For example, imagine a firm approaching the end of its life that has unfunded pension liabilities. What discount rate is applied to the unfunded pension liabilities (or health benefits, for that matter)? They may be part of a union contract, and the firm is obligated to pay them but has not fully funded them. Are the unfunded pension liabilities paid off before or after the debt holders? If these liabilities are paid off before the debt holders, they have less risk and thus a lower discount than the debt. If they are paid off after the debt holders, they have more risk and a higher discount rate.12
This book has introduced the concepts and methods of valuation, but there remain many additional issues that must be dealt with in practice.
SUMMARY
We noted earlier in the book that valuation has three pieces: strategic, valuation, and execution. So far in this book, we have emphasized the valuation piece and have primarily used NPV to do valuation. We have used free cash flows to the firm and a WACC discount rate to calculate the NPV.
For free cash flows to the firm we used the formula:
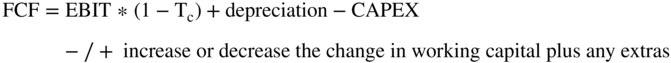
As we noted, it is a formula that has elements that do not appear in the financial statements and may not seem to initially make sense. However, as we worked through the formula, we saw how it results from various assumptions and modifications. For example,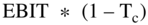 
is used instead of net income because the tax shield is accounted for in the WACC.
For the WACC discount rates, we started by computing the percentage of debt and equity, and then we determined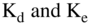 
.
It is important to remember, as we have mentioned before, that there is always a price so high that it will make a project's NPV negative, and there is usually a price that will make a project's NPV positive.
Key Points to Remember
- Cash is king. Valuation is all about the amount and timing of cash flows.
- A project's cash flows must include the cash flows, whether they are positive or negative, from anywhere and everywhere. Include any cash flows where the project changes their amount or timing.
- Overhead and accounting charges don't matter since they are not cash flows.
- Sunk costs are not considered.
- Inflation must be properly adjusted for. You should use either nominal cash flows and nominal discount rates or real cash flows and real discount rates.
- Terminal values should be separately determined. Furthermore, terminal values must match the valuation being done (i.e., the terminal value of equity is used when valuing equity, while the terminal value of the firm is used when valuing the firm).
- Changes in working capital (receivables plus inventory less payables) and the terminal value of working capital must be accounted for.
- CAPEX often matters a lot.
- Real options should be included but are difficult to value.
Coming Attractions
In the next chapter, we cover the case of Congoleum. This was the first major leveraged buyout (LBO). The issue emphasized in the chapter is not how to value an LBO, but rather where (or how) the value is created. The case also demonstrates how and why the private equity market works as it does.