CHAPTER 20
Valuing an Acquisition: Free Cash Flows to the Firm (The Dollar Stores)
In the previous chapter, we examined the strategic fit between Family Dollar and Dollar General or Dollar Tree. In this chapter, we will estimate the value of Family Dollar.
We introduced valuation in Chapters 15 and 16, using the Sungreen case. Chapter 17 extended the discussion on valuation by looking at a number of nuances. This chapter will do another valuation in more depth to help readers better understand the formulas, as opposed to merely memorizing them. As we did with Sungreen, we start with the free-cash-flows-to-the-firm (FCFf) technique. Then in the next chapter we will introduce the free-cash-flow-to-equity (FCFe) technique and compare it to the free-cash-flows-to-the-firm technique.
We begin with Dollar Tree's bid for Family Dollar. To obtain the pro formas used to generate the cash flows and to estimate the cost of capital for Family Dollar, we will rely upon Family Dollar's proxy statement, which includes the estimates done by Morgan Stanley (Family Dollar's investment banker). Where necessary, we will reverse engineer the valuation elements not explicitly provided in the proxy statement. We will then calculate the terminal value using the multiple and perpetuity approaches. We then put the three pieces of a valuation together (i.e., the purchase price, the discounted cash flows, and the terminal value) to value Family Dollar.
Note, the pro formas for Family Dollar were done prior to the Tax Cuts and Jobs Act of 2018. Thus, there was no cap on interest deductibility. In fact, the interest expenses were more than 30% of EBITDA prior to 2018 but less than 30% of EBITDA after. As such, the calculations done by Morgan Stanley and your authors would not change. However, as will be seen in the next chapter, the free cash flow to equity approach does not need an adjustment for the cap on interest deductibility.
THE BID FOR FAMILY DOLLAR
Dollar Tree's bid for Family Dollar on July 24, 2014, was for $8.52 billion or $74.50 per share (composed of $59.60 in cash plus 0.2665 shares of Dollar Tree, with each portion of Dollar Tree shares estimated to be worth $14.90 on the date of the offer). The bid was for all 114.3 million shares outstanding and offered a premium of roughly 22.9% above the firm's current market capitalization of $6.93 billion or $60.66 per share just prior to the bid.1
That is, the bid for Family Dollar was comprised of:
| Cash | $6.81 billion |
| 30.5 million newly issued shares of Dollar Tree | $1.71 billion |
| Total purchase price | $8.52 billion |
The bid offered a substantial premium to both the Family Dollar's market capitalization of $6.93 billion and book equity of $1.67 billion (as shown in Table 20.1). First, why is there such a large difference between market capitalization and book equity? The net book value from the Balance Sheet is an accounting number that has no necessary relation to economic reality, as discussed in Appendix 3A (“Accounting Is Not Economic Reality”) and to which we have alluded several times. The market capitalization is a finance number and reflects the market's value of equity.
TABLE 20.1 Family Dollar's Balance Sheet as of 8/30/2014 Pre-Acquisition2
| ($ millions) | |||
| Current assets | 2,102.0 | Current liabilities excluding debt | 1,112.8 |
| Property, plant, and equipment, | 1,688.2 | Debt | 500.4 |
| Goodwill | 0.0 | Other liabilities | 578.3 |
| Trade name and other intangibles | 0.0 | Total liabilities | 2,191.5 |
| Other long-term assets | 67.0 | Equity | 1,665.7 |
| Total assets | 3,857.2 | Total liabilities and equity | 3,857.2 |
Second, why is Dollar Tree offering a $1.59 billion premium over Family Dollar's current market capitalization? The reason is the hoped-for synergies discussed in Chapter 19.
The difference between the bid and the book (accounting) values are corrected for at the time of the merger by restating the Balance Sheet. That is, a merger provides an opportunity to restate (adjust) the accounting numbers so they are closer to economic reality. In the case of Family Dollar, this is done by allocating the $6.85 billion difference between the $8.52 billion purchase price and the $1.67 billion net book value. According to its proxy, Family Dollar estimated the differences as follows:
| Goodwill | $5.19 billion |
| Intangible assets | $2.42 billion |
| Other noncurrent liabilities (mostly deferred taxes) | −$0.76 billion |
| Total fair market value adjustments | $6.85 billion |
What is goodwill? It is an accounting adjustment for the amount paid by an acquiring company in excess of the net asset value of the acquired company. As noted above, the Dollar Tree bid is for much more than the accounting value of Family Dollar's net assets (assets less liabilities). When consolidating (combining) Family Dollar's financial statements into its own, Dollar Tree first revalues all the assets and liabilities to their “fair” or market values (including any intangible assets like patents and copyrights). Any remaining difference is listed as “goodwill” on the Balance Sheet. Thus, goodwill is the purchase price less the fair value of assets and liabilities at the date of acquisition.
What are intangible assets? They are the firm's trademarks, trade names, patents, copyrights, and any other asset that does not have a physical (tangible) form. In this case, $2.42 billion was the estimated value of the trade name “Family Dollar.”
Table 20.2 presents what Family Dollar's Balance Sheet would have looked like on September 1, 2014, had the firm's assets and liabilities been written up with the adjustments above.
TABLE 20.2 Family Dollar's Restated Balance Sheet as at 9/1/2014 Post-Acquisition
| ($ millions) | |||
| Current assets | 2,102.0 | Current liabilities excluding debt | 1,112.8 |
| Property, plant, and equipment | 1,688.2 | Debt (+6,810) | 7,310.4 |
| Goodwill (+5,190) | 5,190.0 | Other liabilities (+760) | 1,338.3 |
| Tradename and other intangibles (+2,420) | 2,420.0 | Total liabilities | 9,761.5 |
| Other long-term assets | 67.0 | Equity (–1,665.7 + 1,705.7) | 1,705.7 |
| Total assets (+7,610) | 11,467.2 | Total liabilities and equity (+7,610) | 11,467.2 |
Note that it is assumed the old equity is repurchased and retired with a cash payment of $6.81 billion (funded by a new debt issue by Dollar Tree) and a new equity issue of $1.71 billion for a total purchase price of $8.52 billion. The goodwill, trade name, and liabilities are increased to the fair values as noted above.
We are now ready to start our valuation. We start by creating pro forma Income Statements and Balance Sheets. These are used to generate the free cash flows to the firm. Next, we estimate the WACC for the firm. This involves estimating the capital structure of the firm going forward as well as the cost of debt and the cost of equity. The cash flows are then discounted by the WACC. Finally, a terminal value is estimated using several techniques. The sum of the purchase price, the discounted cash flows, and the discounted terminal value provide an estimate of the value added to Dollar Tree from the merger.3
FREE CASH FLOWS TO THE FIRM
We are now ready to calculate Family Dollar's cash flows. Table 20.3 provides Family Dollar's actual Income Statements and Balance Sheets for fiscal years from 2010 through 2014, the five years prior to the acquisition.4
TABLE 20.3 Family Dollar's Pre-Acquisition Financial Statements 2010–2014
| Income Statements ($000s) | 8/28/2010 | 8/27/2011 | 8/25/2012 | 8/31/2013 | 8/30/2014 |
| Sales | 7,866,971 | 8,547,835 | 9,331,005 | 10,391,457 | 10,489,330 |
| Cost of sales | 5,058,971 | 5,515,540 | 6,071,058 | 6,836,712 | 6,958,045 |
| Gross profit | 2,808,000 | 3,032,295 | 3,259,947 | 3,554,745 | 3,531,285 |
| SG&A | 2,060,365 | 2,211,768 | 2,381,899 | 2,627,303 | 2,844,372 |
| Depreciation and amortization | 172,037 | 182,455 | 213,835 | 239,485 | 265,461 |
| Operating profit | 575,598 | 638,072 | 664,213 | 687,957 | 421,452 |
| Interest income | 1,597 | 1,532 | 927 | 422 | 190 |
| Other income | — | — | 23,888 | 28,206 | 31,150 |
| Interest expense | 13,337 | 22,446 | 25,090 | 25,888 | 30,038 |
| Income before tax | 563,858 | 617,158 | 663,938 | 690,697 | 422,754 |
| Income tax | 205,723 | 228,713 | 241,698 | 247,122 | 138,251 |
| Net income | 358,135 | 388,445 | 422,240 | 443,575 | 284,503 |
| Balance Sheets ($000s) | 8/28/2010 | 8/27/2011 | 8/25/2012 | 8/31/2013 | 8/30/2014 |
| Current assets | 1,660,208 | 1,533,844 | 1,768,170 | 1,857,005 | 2,102,046 |
| Current liabilities | 1,054,487 | 1,000,855 | 1,034,457 | 1,064,022 | 1,112,830 |
| Net working capital | 605,721 | 532,989 | 733,713 | 792,983 | 989,216 |
| PP&E | 1,111,966 | 1,280,589 | 1,496,360 | 1,732,544 | 1,688,213 |
| Other | 209,883 | 181,772 | 108,535 | 120,312 | 67,036 |
| Total assets | 1,927,570 | 1,995,350 | 2,338,608 | 2,645,839 | 2,744,465 |
| Short-term debt | — | 16,200 | 31,200 | 16,200 | 16,200 |
| Long-term debt | 250,000 | 532,370 | 516,320 | 500,275 | 484,226 |
| Other | 256,016 | 359,706 | 493,461 | 530,309 | 578,314 |
| Total liabilities | 506,016 | 908,276 | 1,040,981 | 1,046,784 | 1,078,740 |
| Total equity | 1,421,554 | 1,087,074 | 1,297,627 | 1,599,055 | 1,665,725 |
| Total liabilities and equity | 1,927,570 | 1,995,350 | 2,338,608 | 2,645,839 | 2,744,465 |
| Debt ratio | 15.0% | 33.5% | 29.7% | 24.4% | 23.1% |
Table 20.4 provides Family Dollar's pro forma Income Statements and Balance Sheets for 2015–2019, the five years after the acquisition, adjusting for the fair market values (in this case, to goodwill, trade name, and debt) from the acquisition (as shown in Table 20.2).
TABLE 20.4 Pro Forma Family Dollar Post-Acquisition Financial Statements Adjusted for the Acquisition, 2015–2019
| Income Statements ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Sales | 11,207,000 | 12,355,000 | 13,523,000 | 14,537,225 | 15,627,517 |
| Cost of sales | 7,306,964 | 8,055,460 | 8,816,996 | 9,478,271 | 10,189,141 |
| Gross profit | 3,900,036 | 4,299,540 | 4,706,004 | 5,058,954 | 5,438,376 |
| SG&A | 2,942,014 | 3,081,623 | 3,267,248 | 3,512,193 | 3,775,608 |
| Depreciation | 310,000 | 307,000 | 306,000 | 305,000 | 304,000 |
| Operating profit | 648,022 | 910,917 | 1,132,756 | 1,241,761 | 1,358,768 |
| Interest expense | 381,702 | 377,284 | 388,580 | 400,060 | 410,153 |
| Income before tax | 266,320 | 533,633 | 744,176 | 841,701 | 948,615 |
| Income tax | 95,343 | 191,041 | 266,415 | 301,329 | 339,604 |
| Net income | 170,977 | 342,592 | 477,761 | 540,372 | 609,011 |
| Balance Sheets ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Current assets | 2,151,744 | 2,372,160 | 2,596,416 | 2,791,147 | 3,000,483 |
| Current liabilities | 1,277,598 | 1,408,470 | 1,541,622 | 1,657,244 | 1,781,537 |
| Net working capital | 874,146 | 963,690 | 1,054,794 | 1,133,904 | 1,218,946 |
| PP&E | 1,748,292 | 1,927,380 | 2,109,588 | 2,267,807 | 2,437,893 |
| Goodwill | 5,190,000 | 5,190,000 | 5,190,000 | 5,190,000 | 5,190,000 |
| Intangibles: trade name | 2,420,000 | 2,420,000 | 2,420,000 | 2,420,000 | 2,420,000 |
| Other | 67,036 | 67,036 | 67,036 | 67,036 | 67,036 |
| Total assets | 10,299,474 | 10,568,106 | 10,841,418 | 11,078,747 | 11,333,875 |
| Short-term debt | 16,200 | 16,200 | 16,200 | 16,200 | 16,200 |
| Long-term debt | 7,239,260 | 7,456,503 | 7,677,261 | 7,871,360 | 8,077,768 |
| Other | 1,338,314 | 1,338,314 | 1,338,314 | 1,338,314 | 1,338,314 |
| Total liabilities | 8,593,774 | 8,811,017 | 9,031,775 | 9,225,874 | 9,432,282 |
| Contributed capital | 1,705,700 | 1,705,700 | 1,705,700 | 1,705,700 | 1,705,700 |
| Retained earnings | 0 | 51,389 | 103,943 | 147,173 | 195,893 |
| Total equity | 1,705,700 | 1,757,089 | 1,809,643 | 1,852,873 | 1,901,593 |
| Total liabilities and equity | 10,299,474 | 10,568,106 | 10,841,418 | 11,078,747 | 11,333,875 |
| Debt ratio | 81.0% | 81.0% | 81.0% | 81.0% | 81.0% |
Table 20.5 provides the underlying assumptions for Table 20.4. These are largely from the Family Dollar proxy statement. However, as noted above, the proxy statement did not explicitly provide all of the assumptions required to generate the pro formas. Details of how the authors reverse engineered the proxy are also included.
TABLE 20.5 Pro Forma Family Dollar Assumptions (for Table 20.4)
|
|
From earlier chapters, we know free cash flows to the firm (or FCFf) equals 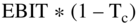 plus deprecation minus CAPEX minus the increase in working capital plus deferred taxes plus any extras.5
plus deprecation minus CAPEX minus the increase in working capital plus deferred taxes plus any extras.5
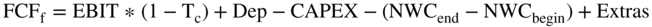
where:
- FCFf = free cash flows to the firm
- EBIT = earnings before interest and taxes
- Tc= the average tax rate to the firm
- Dep = depreciation and amortization
- CAPEX = capital expenditures
- NWCend/begin= net working capital at the end/start of the year (net working capital is required cash plus receivables plus inventory minus payables)
- Extras = items such as subsidies (which do not arise in all cases)
EBIT 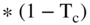
Let's stop for a second. We promised more depth in this chapter, so let us now provide some. An income statement includes the line items net income and taxes. It does not include 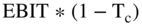 . You don't see this term because firms don't pay taxes on EBIT. Firms pay taxes on
. You don't see this term because firms don't pay taxes on EBIT. Firms pay taxes on 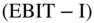 , which stands for earnings minus interest payments (since they are tax deductible) and is shown on the Income Statement as earnings before taxes. In other words, you have to subtract interest payments from EBIT before calculating how much is owed in taxes.
, which stands for earnings minus interest payments (since they are tax deductible) and is shown on the Income Statement as earnings before taxes. In other words, you have to subtract interest payments from EBIT before calculating how much is owed in taxes.
So why does the technique of free cash flows to the firm use 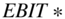 (1 − Tc) when firms that have interest deductions only pay taxes on (
(1 − Tc) when firms that have interest deductions only pay taxes on (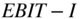 )? The reason is how the technique picks up the value of the tax shields. In the FCFf approach, the value of the tax shields is incorporated in the WACC (i.e., the discount rate). This means you don't need to account for tax shields in the cash flows because you do so later when you discount the cash flows.
)? The reason is how the technique picks up the value of the tax shields. In the FCFf approach, the value of the tax shields is incorporated in the WACC (i.e., the discount rate). This means you don't need to account for tax shields in the cash flows because you do so later when you discount the cash flows.
Remember, our formula for WACC is:
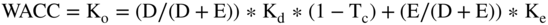
where:
- D = interest-bearing debt
- E = equity
- (D/(D + E)) = the percentage of debt in the capital structure
- (E/(D + E)) = the percentage of equity in the capital structure
- Kd= cost of debt
- Tc= the marginal tax rate
- Ke= cost of equity
WACC uses the after-tax cost of debt, 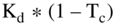 , which means it subtracts out the tax shield of interest on debt in the discount rate. To prevent the tax shield of interest from being double counted (both in the cash flows and in the discount rate), we don't take the interest deduction on earnings before we calculate the taxes paid.
, which means it subtracts out the tax shield of interest on debt in the discount rate. To prevent the tax shield of interest from being double counted (both in the cash flows and in the discount rate), we don't take the interest deduction on earnings before we calculate the taxes paid.
Let us restate the term 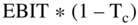 :
:
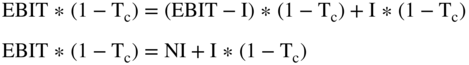
The two formulas above are merely algebraic reformulations and have no additional accounting or finance content, but we will use them later to substitute into the free cash flows formula.
WACC and Different Capital Structures
As noted in Chapter 17, “Valuation Nuances,” using the free cash flow to the firm approach with the WACC has some strong assumptions. One of the strongest is that the capital structure does not change (i.e., the debt/equity ratio remains constant). Another is that the value of the tax shield is picked up in the WACC formula by using 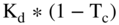 . Importantly, when using the FCFf approach, changing the capital structure does not change the cash flows.
. Importantly, when using the FCFf approach, changing the capital structure does not change the cash flows. 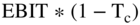 does not change with the amount of debt (or interest paid). Neither do any of the other elements of cash flow. Thus, cash flows (as opposed to net income and interest expense) remain constant.
does not change with the amount of debt (or interest paid). Neither do any of the other elements of cash flow. Thus, cash flows (as opposed to net income and interest expense) remain constant.
Using different amounts of debt affects firm value by changing the WACC, not the cash flows. A change in capital structure changes the WACC in several ways. The percentage of debt and the percentage of equity obviously change. In addition, the Kd and Ke will change with different risk levels (we explained earlier in Chapter 7 how a change in debt changes a firm's Kd, as well as the firm's beta and Ke, and, ultimately, its Ko).
In Table 20.4 we have assumed that the new capital structure of Family Dollar contains all of the debt used to acquire the firm. We will relax this assumption shortly, but note, as shown in Appendix 20A, that it will not change the free cash flows to the firm when we do. That is, Appendix 20A uses a capital structure of 35.7% debt (the authors' estimate), yet has the same free cash flows to the firm as Table 20.4, which uses a capital structure of 81.0% debt.
Depreciation and Amortization, Extras, CAPEX, and Working Capital
The next term in our FCFf formula is Dep, which represents the accounting charge for depreciation and amortization. It is not actually a cash flow. Depreciation affects the cash flows through the tax shields. For example, if you add $100 of new depreciation, how much does that add to the firm's free cash flows? The formula makes it seems that the cash flows increase by $100. But what is the actual cash flow effect of $100 in depreciation expense? It should be $100 * Tc. That is, if the tax rate is 35%, $100 of depreciation reduces the taxes paid to the government by $35. This is the amount of increased cash flow to the firm.
In fact, the free cash flow to the firm formula gives you exactly this effect. How? It works through several terms of the formula as follows: if depreciation goes up by $100, EBIT goes down by $100. As a consequence, EBIT minus taxes goes down by 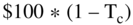 . So what is the extra cash flow? Adding back the $100 of depreciation gives an effect of
. So what is the extra cash flow? Adding back the $100 of depreciation gives an effect of 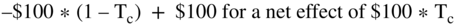 .
.
Working through the example again:
- If depreciation increases by $100, then
- EBIT ↓ $100, and
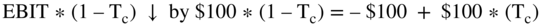 .
.- Adding the $100 of depreciation back (as in the formula) gives
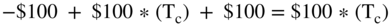 , which is the net cash effect.
, which is the net cash effect.
Thus, while it looks like adding $100 in depreciation (due to the formula) increases the firm's cash flow by $100, the actual impact is $100 million * Tc.6
Although not applicable in this case, the same logic applies to amortizing goodwill and intangibles if they are both deductible for reporting and tax purposes. However, today goodwill and many intangibles are not amortized for reporting purposes and are only deductible for tax purposes in special circumstances. In those circumstances where goodwill or intangibles can be amortized for tax purposes, the net cash impact (Tc * amortization) would be included as an “extra” (rather than as done for depreciation, where the full noncash amount is inserted into the formula).7
Other examples of extras include below-market financing costs and governmental subsidies, including tax credits. The thought process of how these should be treated is the same as for intangibles that are not deducted for accounting purposes but are tax deductible. That is, the net after-tax effect on the cash flows that the firm is generating is included as a separate item in the cash flows item. There were no such additional noncash items noted in the Family Dollar proxy, so they can be ignored in this case.
We now have two items left in our free-cash-flows-to-the-firm formula: CAPEX and Working Capital. How do we find CAPEX? We know that the change in net PP&E is the same as CAPEX minus depreciation. The intuition behind this is the grocery example we keep giving you (see Chapter 3 and 15). What is the change in the amount of food in the pantry? It's how much you had in the beginning plus what you purchased minus what you ate. CAPEX is what you purchased, depreciation is what you ate, and the net is the change in PP&E. We find the change in PP&E as the difference in the opening and closing Balance Sheet numbers and the depreciation expense is given on the Income Statement, which allows us to then calculate CAPEX.
Last, we have change in net working capital (current assets minus current liabilities excluding interest-bearing debt). This is simply the change in net working capital over the year, or the end-of-the-year amount less the beginning-of-the-year amount.
On to the Cash Flows
We are now ready to calculate Family Dollar's free cash flows to the firm, which are shown in Table 20.6:
TABLE 20.6 Family Dollar's Pro Forma Free Cash Flows to the Firm
| ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Net income | 170,977 | 342,592 | 477,761 | 540,372 | 609,011 |
| Interest * (1 − Tc) | 245,053 | 242,216 | 249,469 | 256,839 | 263,318 |
| Depreciation | 310,000 | 307,000 | 306,000 | 305,000 | 304,000 |
| CAPEX | 370,079 | 486,088 | 488,208 | 463,219 | 474,086 |
| Δ in net working capital | 115,070 | (89,544) | (91,104) | (79,110) | (85,043) |
| Free cash flow | 471,021 | 316,176 | 453,918 | 559,882 | 617,200 |
Remember, the formula from earlier is:
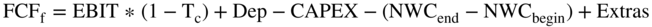
Since 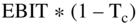 does not appear on our Income Statement, we must construct it by taking net income from Table 20.4 and adding the after-tax interest. Remember our reformulation was:
does not appear on our Income Statement, we must construct it by taking net income from Table 20.4 and adding the after-tax interest. Remember our reformulation was:
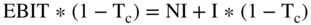
Then we add the depreciation, subtract the CAPEX, and adjust for the change in working capital.
Let's walk through the numbers for 2015 in detail. In Table 20.4, net income for 2015 is $171.0 million.
Then we add back the after-tax interest. So, how do we compute the after-tax interest? Table 20.4 gives the before-tax interest on the debt of $381.7 million. The after-tax interest on the debt is not given, so we have to calculate it. Since the tax rate at the time (and used in the table) is 35.8%, the after-tax interest will be 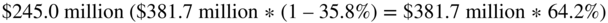 .
.
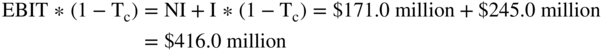
Next, from Table 20.4, we have depreciation of $310.0 million.
Using the depreciation and the opening and closing PP&E, we can compute CAPEX. Table 20.3 gives the opening PP&E for 2015 (which is the same as the ending PP&E for 2014) of $1,688.2 million. Table 20.4 gives the ending PP&E for 2015 of $1,748.3 million. Combining this with our depreciation of $310.0 million, we solve for CAPEX using the following formula:
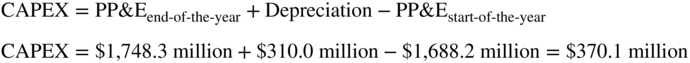
Last, we must compute the change in net working capital. Net working capital started the 2015 year at $989.2 million and ended the year at $874.1 million. This means working capital went down, and the change is a positive cash flow of $115.1 million for 2015.
Combining all the elements gives us:
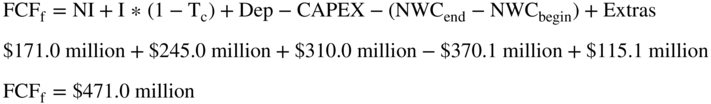
Years 2016 to 2019 follow similarly and are shown in Table 20.6.
ESTIMATING THE COST OF CAPITAL
Now that we have the free cash flows to the firm, we need to calculate the appropriate discount rates, which for free cash flows to the firm is the WACC (Ko). We will do two estimates, one from the Dollar Tree proxy prepared by Morgan Stanley and one by your authors.8 The main reason we are doing two is to show you some of the nuances and to prove that finance truly is an “art,” not a science.
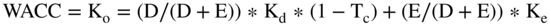
Let's start with the Ke first. The formula used for Ke is the one-factor CAPM:9
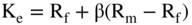
where:
- Rm = the market rate
- Rf = the risk-free rate
- β = a measure of risk
We begin with the risk-free rate, Rf, which as discussed in Chapter 15, is taken from U.S. Treasury rates. Morgan Stanley used a rate of 2.5% based on the 2.48% interest rate of 10-year U.S. Treasury note as of July 25, 2014.
By contrast, for long-term projects, your authors believe in using the longest-term U.S. Treasury rate minus a 1% liquidity premium to get an estimate of the T-bill rate over the long term. The 30-year U.S. T-bond rate was 3.24% on July 25, 2014. So your authors would have used a rate of 2.24% (3.24% less the 1% liquidity premium).
Morgan Stanley provides an estimated beta of 1.05 for Family Dollar, which they obtained from Barra Inc. as an average for the industry.10 By so doing, Morgan Stanley is effectively saying it doesn't believe there will be any significant difference in the beta of Family Dollar and the beta of the average firm in the industry.
However, as noted in Chapter 17 (on the nuances of valuation), the “theoretically correct” way to compute beta if a firm's leverage will change after the acquisition (as it will in this case) involves unlevering the beta (using the current capital structure) and then relevering the beta (using the expected future capital structure). In other words, you take the beta, remove the effect that the current debt ratio has on the beta, then apply to the unlevered beta the level of debt that the firm will have after acquisition. As we noted in Chapter 17, there are many different formulas to unlever and relever a firm's beta. Here, we will use the ones recommended in that chapter:11
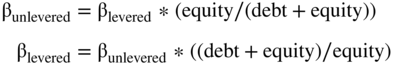
The three key elements for these calculations are: (1) the firm's current beta, (2) the firm's current capital structure, and (3) the firm's planned capital structure.
We begin with Family Dollar's beta at the time of the deal, which your authors estimated was 0.77. (We took the actual returns to Family Dollar and regressed it against the market returns for the year prior to the merger.)
Next, what was Family Dollar's capital structure, that is, the one that was used when the beta of 0.77 was calculated? First, we need to find Family Dollar's debt. At the time of the acquisition, Family Dollar had debt of $500.4 million. We would then reduce this by any excess cash to get net debt, but in this case Family Dollar did not appear to have any, so the $500.4 million is our net debt.12
Second, we need to find the value of Family Dollar's equity. According to the accountants, the equity value of Family Dollar was $1.67 billion. This is the book value, but we want to use the market value. How do we get the market value of Family Dollar's equity? There were 114 million Family Dollar shares on August 31, 2014, when Dollar Tree's bid of $74.50 per share was accepted. However, we don't use the $74.50 per share. Why don't we use the share price Dollar Tree included in its bid when we calculate the equity's market value? We are going to unlever the beta using the debt ratio pre-acquisition and then relever the beta using the debt ratio post-acquisition. The pre-acquisition stock price was $60.66 per share, giving an equity value of $6.9 billion prior to the acquisition ($60.66 * 114 million shares). Also remember that the beta of 0.77 was the result of a regression of the stock returns on the market's returns. Thus, the beta (one of the inputs) used the pre-acquisition stock prices, not the $74.50 bid.
So we've found that before the acquisition (and thus at the time the 0.77 beta was calculated), the debt to total capital was 6.8%, or $0.5 billion/($0.5 billion + $6.9 billion). We use this to unlever the pre-acquisition beta:
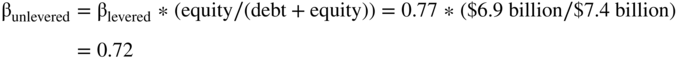
Now, to relever the unlevered beta, we need to know the debt level at which Family Dollar will operate after the merger. From our pro formas above in Table 20.2, we have total debt of $7.3 billion and accounting equity of $1.7 billion for a debt ratio of 81%. However, this is not necessarily how Dollar Tree will run Family Dollar.
The 81% debt ratio represents the “execution financing” of the acquisition, not necessarily the way the firm will be financed in the future (if you recall this was discussed in Chapter 17 on nuances). Our immediate problem is to determine at what capital structure the firm will be run. If we're doing an internal valuation of the firm, that is, we are an insider, we will know the new capital structure. Likewise, if we are the firm's investment banker, we can ask what capital structure to use for our estimates. As an outside analyst, we can go to the analyst meetings or merger road show and ask the question as well. Since we are none of these, we will use another way to estimate the capital structure of Family Dollar and then compare it with the Morgan Stanley estimate (which we impute to be 15% debt).
As of October 21, 2015, the capital structure of the major competing firms in this industry is as follows:
| Debt | Market Capitalization | Debt Ratio | Beta13 | |
| Walmart | $49.7 billion | $188.4 billion | 20.9% | 0.83 |
| Dollar Tree | $ 8.4 billion | $ 15.1 billion | 35.7% | 1.03 |
| Dollar General | $ 2.9 billion | $ 19.8 billion | 12.7% | 1.30 |
The Dollar Tree debt ratio above is postmerger and represents the combination of Dollar Tree and Family Dollar. From above, we know that $7.3 billion of the debt is from the Family Dollar acquisition. Your authors believe it is unlikely that Dollar Tree would run the premerger part of the business at one capital structure with very little debt and the newly acquired part of the business at a different capital structure with high debt. One of the major strategic reasons for the merger is the synergies between the two firms, since they were in the same business with similar risk. Therefore, your authors assume that both parts of Dollar Tree (the old and the acquired) will be run at the same capital structure of 35.7% debt (as we will see, it is somewhat different from Morgan Stanley's, an insider to the process, but not that much).
That is, it appears that Dollar Tree is using Family Dollar to leverage up its own Balance Sheet. Since Family Dollar is no longer traded, and since we assume Dollar Tree is effectively using the Family Dollar acquisition to leverage up its own Balance Sheet, we will use Dollar Tree's postacquisition numbers to relever Family Dollar as follows:
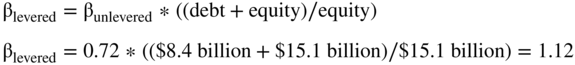
Thus, your authors compute a levered beta of 1.12 (as opposed to the 1.05 used by Morgan Stanley).
We then use the one-factor CAPM formula (copied below) to find Ke. We already have the estimates of Rf = 2.24% and β = 1.12.
Next, we need an estimate of 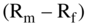 . As discussed in Chapter 16, there is disagreement about how to compute the market premium. Ibbotson Associates provides estimates of
. As discussed in Chapter 16, there is disagreement about how to compute the market premium. Ibbotson Associates provides estimates of 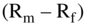 over different time periods, the longest being 1926 to present.14 These estimates vary with different time periods.15 In 2013, a survey of finance professionals found the average market premium used in valuation formulas in the United States was 5.00% (this is the mean market premium used; the median was 5.24%).16 Morgan Stanley, as revealed in the Dollar Tree proxy, used a rate of 6.00% for 2014, which was estimated using the firm's “professional judgment and experience.” This rate is in line with the Ibbotson and Associates estimates and seems reasonable and conservative to your authors. It is also the rate that we currently use in teaching our classes, and we will use it here.
over different time periods, the longest being 1926 to present.14 These estimates vary with different time periods.15 In 2013, a survey of finance professionals found the average market premium used in valuation formulas in the United States was 5.00% (this is the mean market premium used; the median was 5.24%).16 Morgan Stanley, as revealed in the Dollar Tree proxy, used a rate of 6.00% for 2014, which was estimated using the firm's “professional judgment and experience.” This rate is in line with the Ibbotson and Associates estimates and seems reasonable and conservative to your authors. It is also the rate that we currently use in teaching our classes, and we will use it here.
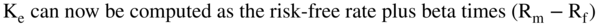
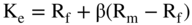
Using Morgan Stanley's numbers, we have:
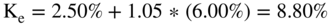
Using your authors' estimates, we have:
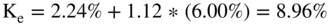
Thus, with slightly different assumptions, your authors and Morgan Stanley calculate very similar cost of equity.
To complete our estimation of the WACC (see formula below), however, we need to estimate the cost of debt and the tax rate.
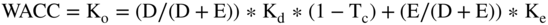
Morgan Stanley assumes a pretax cost of debt of 5.2%, a tax rate of 35.8%, and a leverage ratio of 15% to compute a 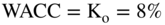 .17
.17
Your authors now have estimates of the cost of equity, the tax rate, and the leverage ratio. The final item before we compute the WACC is to determine whether we want to use Morgan Stanley's assumed pretax cost of debt—in the pro formas that Morgan Stanley created, the firm estimated that Family Dollar's borrowing interest rate would be 5.2%. If we accept Morgan Stanley's estimate of 5.2% (even though our debt level is slightly higher), we calculate 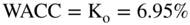 .
.
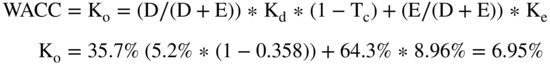
Thus, the cost of capital estimated by Morgan Stanley is 8.0% and the cost of capital estimated by your authors is 7.0%. These numbers are actually quite close, and if we were actually determining whether to pull the trigger on a $8.5 billion acquisition, we would be doing a lot of sensitivity analysis both on the cash flows and the discount rate. Thus, we would probably use both.
Remember, we used a capital structure of 35.7% debt versus the 15% used by Morgan Stanley. As the debt level changes, so will the Ko. We know from Chapters 6 and 7 that Ko will fall at first and then rise.
Let's stop and review. First, we examined the cash-flow-to-the-firm formula in detail. In earlier chapters, we gave you the standard formula and asked you to trust us. In this chapter, we explained the formula in more detail including why it uses 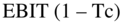 and why total depreciation is added to the formula even though the tax shield is only Tc * Dep. In the next chapter, when we do the free-cash-flow-to-equity as well, we will further show how the free-cash-flow-to-the-firm formula is derived. Next, we showed how the pro formas were estimated and used them to compute the free-cash-flows-to-the-firm. In the Appendix, we show that the free cash flows to the firm are the same regardless of the capital structure. Finally, we showed two calculations, Morgan Stanley's and our own, for the WACC and all of its components.
and why total depreciation is added to the formula even though the tax shield is only Tc * Dep. In the next chapter, when we do the free-cash-flow-to-equity as well, we will further show how the free-cash-flow-to-the-firm formula is derived. Next, we showed how the pro formas were estimated and used them to compute the free-cash-flows-to-the-firm. In the Appendix, we show that the free cash flows to the firm are the same regardless of the capital structure. Finally, we showed two calculations, Morgan Stanley's and our own, for the WACC and all of its components.
DISCOUNTED CASH FLOWS
The next step is to discount our projected free-cash-flows-to-the-firm for the next five years. That is, we discount Family Dollar's free cash flows for 2015–2019, using Family Dollar's WACC as the discount rate. For simplicity of exposition, we will show the results using Morgan Stanley's Ko = 8.0%. (We didn't want to load up an already number-heavy chapter with yet more numbers.) Table 20.7 shows the net present value of the five years free cash flows to the firm is $1.93 billion.
TABLE 20.7 Present Value of Family Dollar's Pro Forma Cash Flows
| ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Cash flow to the firm | 471,021 | 316,177 | 453,918 | 599,882 | 617,199 |
| Discount at 8.00% | 1.0800 | 1.1664 | 1.2597 | 1.3605 | 1.4693 |
| Present values | 436,131 | 271,071 | 360,338 | 440,928 | 420,063 |
| Net present value | 1,928,531 |
TERMINAL VALUES
If you recall from the discussion of Sungreen (Chapters 15 and 16), once we have the discounted cash flows, the last piece of a discounted-cash-flow valuation is the computation of the terminal value. While it would be ideal to be able to discount the cash flow stream forever, this is not possible.
In practice, firms forecast cash flows for the period with which they are comfortable (we used five years; in the Family Dollar proxy statement Morgan Stanley presents three years), and then they compute a terminal value. There are a number of methods to compute the terminal value. They are the same five methods we outlined to value the firm (as discussed in Chapter 15). As noted previously, it is important to compute the terminal value using more than one method in order to validate the terminal value figure you will end up using in your valuation.
Normally your authors start with the perpetuity formula, but for Dollar Tree we will use a multiple first. Why? Because Morgan Stanley used a multiple to calculate the terminal value it included in its proxy statement, and we would like to analyze it. Morgan Stanley uses an EBITDA multiple of 7.0 to 8.0. Since Morgan Stanley only did cash flows for three years and we did them for five, this means we take the EBITDA for 2019, and then multiply it by 7.5 (the average of 7.0 to 8.0) to get the terminal value at the end of 2019 (i.e., this is the terminal value for all cash flows after 2019, brought back to 2019).18 This number then must be discounted back to the start of fiscal 2015 at the WACC of 8.0%.
Our EBITDA at the end of 2019 (from Table 20.4) is $1.66 billion.
| Net income | $ 609.0 million |
| Interest | $ 410.2 million |
| Taxes | $ 339.6 million |
| Depreciation | $ 304.0 million |
| EBITDA | $1,662.8 million |
Taking the EBITDA of $1.66 billion and multiplying it by 7.5 gives a terminal value of $12.47 billion at the end of 2019. Discounting the $12.47 billion back five years at 8% gives a present value of $8.49 billion ($12.47 billion / 1.085).
Does the EBITDA multiple technique give us the terminal value of the firm or the terminal value of equity? The firm. Why? EBIT and EBITDA multiples are calculated as EBIT (or EBITDA) divided by the market value of the firm (i.e., the value of the debt and the value of the equity). Thus, when using the multiple, it gives a value of the debt and the equity together. In contrast, a P/E multiple is calculated by taking the stock price divided by the earnings per share. As such, when it is used on EPS or net income, it only gives the value of the stock or the equity. (If we use a P/E multiple with net income, it is an estimate of the market capitalization of the stock since net income is just EPS * the number of shares outstanding.) This is an important point. You must be careful not to mix the types of cash flows and the types of terminal values (i.e., cash flows to the firm and the terminal value of the equity or vice versa).19
Now, let's calculate the terminal value using a second technique and compare the two results. In this second case, we use the perpetuity formula, which is:
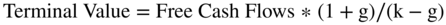
where:
- k = the discount rate
- g = the growth rate
Which free cash flows are used? The free cash flows to the firm, discounted at the WACC (adjusted for growth), are used to compute the terminal value of the firm.
Free cash flows to the firm in the last year of our forecast are $617.2 million (Table 20.6). However, as you may recall, the perpetuity formula brings the present value back one year. That is, if you use the perpetuity formula on the cash flows from the end of year 5, it gives you a value at the end of year 4. (We discussed this earlier in Chapter 16 and remarked that this is math, not finance.) What it means for finance is that the cash flow in the last year must be taken one year out, presumably at some growth rate.
What is the growth rate we should use, and where do we get it? We estimate it either from the past, if we think it will continue, or at the general growth rate of the economy, if we feel the firm's or project's cash flows will grow in line with the general economy, just as we do when we generate pro formas. The growth in the pro forma cash flow declines from 23.3% in 2018 to 10.2% in 2019. We don't expect that type of growth in perpetuity, so we will be conservative and assume a future growth rate of 3%. (Recall we discussed this issue in our chapter on nuances.) Again, this is an art, not a science, and your artists are academics, who are a conservative bunch. It is also important to recognize at some point that the firm can't grow faster than the economy as a whole.
This gives a numerator of $635.7 million ($617.2 * 1.03).
Using our Ko of 8.0% from earlier and our conservative g of 3.0%, the terminal value is:
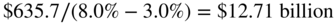
Discounting the $12.71 billion back from the end of 2019 to the start of fiscal 2015 at 8.0% gives a present value of $8.65 billion ($12.71 billion/1.085). This is very close to the $8.49 billion from the EBITDA multiple above.
Terminal Value Validation
Now, let's use our trick from the section on terminal value nuances in Chapter 17. It involves setting the terminal value to a break-even number (i.e., the amount required to have a net present value of zero). After determining the break-even number, we next determine the assumptions in the terminal value method necessary to achieve that number. Let's determine the implied growth rate in the perpetuity terminal value that is necessary to get our required value for the deal to work. The deal was priced at $8.52 billion. The NPV of the free cash flows to the firm is $1.93 billion. This means the break-even terminal value for the deal is $6.59 billion. This is at the time of the offer. Moving this amount forward five years to the end of fiscal 2019 at the 8.0% discount rate works out to $9.68 billion.
We can now solve for the required growth rate to break even by solving the following equation:

Thus, the NPV will be positive as long as the growth after 2019 is greater than 1.4%.
Alternatively, the EBITDA multiple required to break even is 5.83 (with the break-even terminal value of $9.68 billion and an EBITDA of $1.66 billion). We would then compare this multiple (5.83) with the industry EBITDA multiple of 7.0 to 8.0 provided by Morgan Stanley. Since it was lower, we would have confidence that the terminal value was achievable.
THE THREE PIECES
Finally, as always, we break our valuation down into the three pieces: the purchase price, the present value of the cash flows, and the present value of the terminal value.
Valuing the firm, we again start with the purchase price of $8.52 billion. Note: This was the purchase price for the equity of Family Dollar. When we bought the equity, we also assumed the liabilities of Family Dollar. Thus, the purchase price of the firm (the value of the debt and the equity) is $8.52 billion plus $0.50 billion in debt or $9.02 billion.
One way to think about this is imagine you buy a house for $500,000 cash. Normally, for this price you get the house mortgage free. (You may use a mortgage to buy the house, but the seller usually transfers you the house mortgage free.) However, imagine you buy a house for $500,000 cash but have to assume the seller's mortgage of $300,000. How much would you have paid for the house? $800,000 ($500,000 + $300,000). Buying a firm is no different. How much are you willing to pay for a firm? When you purchase all of the equity in a firm, you are also assuming the debt and other liabilities. We have to compare the price we pay for the entire firm to the present value of the cash flows and terminal value if we are using free cash flows to the firm.
Next, we add the present value of the free cash flows to the firm of $1.93 billion. Finally, we add the present value of the terminal value using our perpetuity formula of $8.65 billion.
| Purchase price | –$9.02 billion |
| PV cash flows to the firm | +$1.93 billion |
| PV terminal value (perpetuity formula) | +$8.65 billion |
| Net present value | +$1.56 billion |
One last point, as we noted in Chapter 17, when using an NPV it is important to look at where most of the value comes from: the cash flows in the next few years or the terminal value. As can be clearly seen above, most of Family Dollar's value comes from the terminal value, not the next five years' cash flows. This may indicate that the acquisition has considerable extra risk for Dollar Tree. That is one of the reasons we did our break-even reality checks to see if our terminal values were reasonable. At the same time, the NPV of roughly $1.56 billion is quite large and may be adequate to compensate for any extra risk.
Caveat: As we noted in Chapter 17, your authors have a rule of thumb when faced with a positive NPV project: explain why the NPV of the project is positive in five sentences or less. If you can't, we don't believe it. So, can we explain it here? Yes. As discussed in Chapter 19, Dollar Tree assumed they could improve the operations of Family Dollar by increasing the sales per square foot as well as reducing the costs by $300 million (in our pro formas the savings are reflected in SG&A). If true, this explains the positive NPV (and is done in less than 5 sentences).
SUMMARY
In this chapter we valued a firm, Family Dollar, using the technique of free cash flows to the firm. We used the numbers from Family Tree's proxy and discussed all the assumptions embedded there. We calculated the cash flows and the discount rate. We then calculated the terminal value using the multiple and perpetuity approaches and verified the terminal value's veracity. We then put the three pieces together—purchase price, discounted cash flows, and terminal value—to get the net present value.
The purpose of the chapter was not only to review the free cash flows to the firm, but also to dig deeper into the free-cash-flow approach and to understand the formulas and methodology rather than just memorizing them.
Taken together, this chapter and the next, Chapters 15 and 16 on Sungreen, and Chapter 17 on valuation nuances constitute this book's attempt to teach corporate valuation. If you were new to this topic, it might be useful to reread these chapters from the beginning.
Coming Attractions
The next chapter introduces free cash flows to equity. We will also spend some more time explaining how the free-cash-flow-to-the-firm and the free-cash-flow-to-equity formulas are derived. Then Chapter 22 finishes Family Dollar's valuation/takeover story and tells how this particular takeover happened.
APPENDIX 20A: FAMILY DOLLAR PRO FORMA FINANCIAL STATEMENTS WITH AUTHORS' CONSTANT DEBT RATIO
TABLE 20A.1 Income Statements with Constant Debt Ratio
| ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Sales | 11,207,000 | 12,355,000 | 13,523,000 | 14,537,225 | 15,627,517 |
| Cost of sales | 7,306,964 | 8,055,460 | 8,816,996 | 9,478,271 | 10,189,141 |
| Gross profit | 3,900,036 | 4,299,540 | 4,706,004 | 5,058,954 | 5,438,376 |
| SG&A | 2,942,014 | 3,081,623 | 3,267,248 | 3,512,194 | 3,775,608 |
| Depreciation | 310,000 | 307,000 | 306,000 | 305,000 | 304,000 |
| Operating profit | 648,022 | 910,917 | 1,132,756 | 1,241,760 | 1,358,768 |
| Interest expense | 167,203 | 164,344 | 171,334 | 176,559 | 180,722 |
| Income before tax | 480,819 | 746,573 | 961,422 | 1,065,201 | 1,178,046 |
| Income tax | 172,133 | 267,273 | 344,189 | 381,342 | 421,740 |
| Net income | 308,686 | 479,300 | 617,233 | 683,859 | 756,306 |
TABLE 20A.2 Balance Sheets with Constant Debt Ratio
| ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Current assets | 2,151,744 | 2,372,160 | 2,596,416 | 2,791,147 | 3,000,483 |
| Current liabilities | 1,277,598 | 1,408,470 | 1,541,622 | 1,657,243 | 1,781,537 |
| Net working capital | 874,146 | 963,690 | 1,054,794 | 1,133,904 | 1,218,946 |
| PP&E | 1,748,292 | 1,927,380 | 2,109,588 | 2,267,807 | 2,437,893 |
| Goodwill | 5,190,000 | 5,190,000 | 5,190,000 | 5,190,000 | 5,190,000 |
| Intangibles: trade name | 2,420,000 | 2,420,000 | 2,420,000 | 2,420,000 | 2,420,000 |
| Other | 67,036 | 67,036 | 67,036 | 67,036 | 67,036 |
| Total assets | 10,299,474 | 10,568,106 | 10,841,418 | 11,078,747 | 11,333,875 |
| Short-term debt | 16,200 | 16,200 | 16,200 | 16,200 | 16,200 |
| Long-term debt | 3,144,260 | 3,278,688 | 3,379,175 | 3,459,216 | 3,555,520 |
| Other | 1,338,314 | 1,338,314 | 1,338,314 | 1,338,314 | 1,338,314 |
| Total liabilities | 4,498,774 | 4,633,202 | 4,733,689 | 4,813,730 | 4,910,034 |
| Contributed capital | 5,800,700 | 5,800,700 | 5,800,700 | 5,800,700 | 5,800,700 |
| Retained earnings | 0 | 134,204 | 307,029 | 464,317 | 623,141 |
| Total equity | 5,870,700 | 5,934,904 | 6,107,729 | 6,256,017 | 6,423,841 |
| Total liabilities and equity | 10,299,474 | 10,568,106 | 10,841,418 | 11,078,747 | 11,333,875 |
| Debt ratio | 35.0% | 35.7% | 35.7% | 35.7% | 35.7% |
| Dividend payout ratio | 100.0% | 72.0% | 72.0% | 77.0% | 79.0% |
| Dividends | 308,686 | 345,096 | 444,408 | 463,219 | 617,201 |
TABLE 20A.3 Pro Forma Family Dollar Assumptions (for Tables 20A.1 and 20A.2)
|
|
TABLE 20A.4 Free Cash Flows to the Firm (using Tables 20A.1 and 20A.2)
| ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Net income | 308,686 | 479,300 | 617,233 | 683,859 | 756,306 |
| Interest * (1 – Tc) | 107,345 | 105,509 | 109,997 | 113,351 | 116,023 |
| Depreciation | 310,000 | 307,000 | 306,000 | 305,000 | 304,000 |
| CAPEX | 370,079 | 486,088 | 488,208 | 463,219 | 474,086 |
| Δ in net working capital | 115,070 | (89,544) | (91,104) | (79,110) | (85,043) |
| Free cash flow | 471,022 | 316,177 | 453,918 | 559,881 | 617,200 |