CHAPTER 21
Understanding Free Cash Flows (The Dollar Stores)
The previous chapter used the technique of free-cash flows to the firm (FCFf) to value Family Dollar. That approach used the WACC to discount the cash flows. In this chapter, we will explore more deeply how the free cash flow formulas are derived. We will do this while introducing the free cash flows to equity (FCFe) technique. The FCFe has several advantages over the FCFf approach. In particular, FCFe allows the debt ratio to vary, which is useful when evaluating LBOs and restructurings where the debt level may change dramatically over time. It can also handle subsidized interest rates and the new cap on interest deductibility in U.S. tax law. This approach is now a standard at almost all investment banks (and is usually called an LBO valuation) and is used in combination with the free-cash-flows-to-the-firm approach. The FCFf approach still dominates in corporations, although more corporations are using both FCFf and FCFe.
COMPARING THE FREE-CASH-FLOWS FORMULAS
As described in Chapter 15 and 20, the formula for free cash flows to the firm is: EBIT after tax plus depreciation minus CAPEX minus the change in working capital plus any extras.
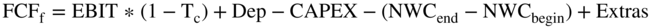
where:
- FCFf = free cash flows to the firm
- EBIT = earnings before interest and taxes
- Tc = the average tax rate to the firm
- Dep = depreciation and amortization
- CAPEX = capital expenditures
- NWCend/begin = net working capital at the end/start of the year (net working capital is cash required to maintain operations plus receivables plus inventory minus payables)
- Extras = items such as subsidies (extras do not arise in all cases)
The formula for free cash flows to equity is different. It is net income plus depreciation minus CAPEX minus the change in working capital plus any extras plus the change in debt.
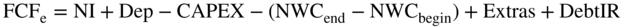
where:
- FCFe= free cash flow to equity
- NI = net income
- Dep = depreciation and amortization
- CAPEX = capital expenditures
- NWCend/begin= net working capital at the end or start of the year (net working capital is required cash plus receivables plus inventory minus payables)
- Extras = items such as subsidies (extras do not arise in all cases)
- DebtIR = new debt issues less the repayments of principal (Debtend-of-the-year – Debtstart-of-the-year)
These two formulas look very similar. A number of terms are identical: depreciation, CAPEX, change in working capital, and extras. The differences are that free cash flows to the firm uses 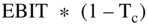 and does not include changes in debt, while the free cash flows to equity uses net income and does include changes in debt.
and does not include changes in debt, while the free cash flows to equity uses net income and does include changes in debt.
You may recall from the previous chapter, 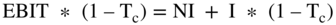 . Making this substitution in our FCFf formula we have:
. Making this substitution in our FCFf formula we have:
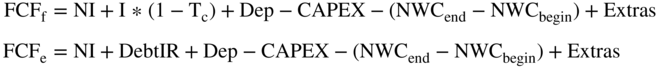
The difference between free cash flows to the firm and free cash flows to equity is thus:
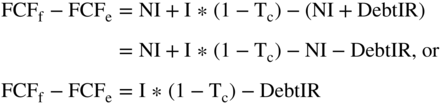
All the above may seem a little complicated, but it is basically algebra. So the difference in the two formulas is simply the after-tax cost of interest minus the net change in debt.
Now let's also examine the free cash flows to debt. The free cash flows to debt equals interest payments plus debt repayments (i.e., the principal) less new issues of debt. To compute the present value of a bond, you take the interest payments (also called the coupon payments) plus the principal repayments and discount them back at the appropriate discount rate (which for debt repayments is the market interest rate on debt with the same risk profile). We can state the formula as:
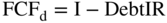
If we line up all three formulas, we get the following:
Why FCFf ≠ FCFd + FCFe
Notice that the free cash flows to the firm (FCFf) is almost equal to the free cash flows to equity (FCFe) plus the free cash flows to debt (FCFd). The difference is that FCFf includes the term 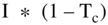 , whereas the sum of
, whereas the sum of 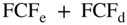 has only the term of I. Let's look at the algebra:
has only the term of I. Let's look at the algebra:

Since 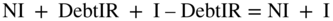 , then:
, then:
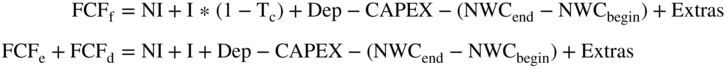
Thus, FCFf is almost equal to 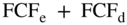 . The difference is
. The difference is 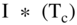 .
.
WHOA! Shouldn't the free cash flows from the firm equal the free cash flows to equity plus the free cash flow to debt (i.e., shouldn't the cash flows from the assets equal the cash flows to capital)? More on this soon.
BACK TO DISCOUNT RATES
Now let us discuss what discount rate to use with the different free-cash-flows techniques. We know the free cash flows to the firm, discounted at the WACC, equals the value of the firm. Not surprisingly, the free cash flows to equity, discounted at the cost of equity, equals the value of equity. Finally, as noted above, the free cash flows to debt, discounted at the cost of debt, equals the value of the debt.
The value of the firm can also be computed as the sum of the value of the debt plus the value of the equity.
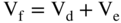
However, as noted, the free cash flows to the firm is almost but not quite equal to the free cash flows to the debt plus the free cash flows to the equity. Why is it not exactly equal? The reason is that the WACC (Ko) used to discount the free cash flows to the firm is not equal to the percentage of debt times the cost of debt plus the percentage of equity times the cost of equity. Ko is equal to the percentage of the debt times the after-tax cost of debt plus the percentage of equity time the cost of equity.
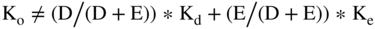
rather
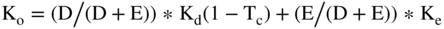
This is the reason the free cash flows formulas are not additive.
Stating this in a different way, since the WACC is not the weighted average of the cost of debt plus the cost of equity, the cash flows to the firm are not the sum of the cash flows to debt plus the cash flows to equity. Remember, the WACC formula uses the after-tax cost of debt to pick up the value of the tax shields. This is why we must use 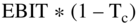 in the free-cash-flows-to-the-firm technique. This is also why the free cash flows to the firm is not equal to the free cash flows to debt plus the free cash flows to equity.
in the free-cash-flows-to-the-firm technique. This is also why the free cash flows to the firm is not equal to the free cash flows to debt plus the free cash flows to equity.
Now, it would be nice if the free cash flows to the firm were equal to the free cash flows to equity plus the free cash flows of debt. You might think WACC should therefore be defined differently to make the two sides equal. But WACC was defined a long time ago, before finance professors got involved with free-cash-flow formulas, and it is a well-established term. So, we are forced to accept the WACC definition as given.
Let us now discuss two additional caveats with WACC:
First, WACC assumes a constant debt ratio 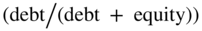 . That is, WACC assumes the debt remains at a constant percentage to the value of the firm. As the value of the firm goes up, so does the debt. If the debt starts out at 20.0% and the value of the firm doubles, then the amount of debt doubles (the percentage or debt ratio remains the same). This is a very strong assumption and results from the WACC valuing the tax shield from debt as a perpetuity.
. That is, WACC assumes the debt remains at a constant percentage to the value of the firm. As the value of the firm goes up, so does the debt. If the debt starts out at 20.0% and the value of the firm doubles, then the amount of debt doubles (the percentage or debt ratio remains the same). This is a very strong assumption and results from the WACC valuing the tax shield from debt as a perpetuity.
Why is it important to realize that WACC assumes a constant debt ratio? Consider the valuation of an LBO. In LBOs and private equity deals (which we covered in detail in Chapter 18), the firm is levered way up at first (to a very high debt ratio), and then the debt is paid down over time. So, as the value of the firm is (hopefully) increasing over time, the amount of debt is falling. Thus, the percentage of debt is not constant as a function of the value of the firm but instead decreases (and then the firm is perhaps taken public again and relevered up). In this situation, the valuation can't be done using a WACC because it would ignore the changing debt ratio. Instead, the valuation should use the free cash flows to equity discounted at Ke.
The second caveat is that WACC assumes the cost of debt is always the market rate. This means there are no subsidies and all interest is tax deductible (e.g., no industrial revenue bonds, as discussed in Chapter 7 or cap on interest tax deductibility). This assumption is easily adjusted for (as shown in Chapter 17): the benefit from any subsidy or loss from the cap on interest tax deductibility has to be calculated separately and added to or subtracted from the value of the project.2 It is already adjusted for in the FCFe formula, since taxes are calculated after the actual interest (even if it is subsidized) is subtracted.
There are also advantages to the WACC formulation. The most important is that with the technique of using FCFf and WACC, the cash flows of the firm don't change with changes in leverage. What changes when you change the leverage? The discount rate. In other words, if a firm changes its debt level, it changes its Ko. However, the free cash flows to the firm does not change with changes in leverage. The free cash flows to the firm formula gives you the same cash flows regardless of the amount of leverage. This makes it easy to apply different capital structures to a firm and see their impact on valuation.
ON TO FREE CASH FLOWS TO EQUITY
Let's now compute the free cash flows to equity for Family Dollar using our formula:
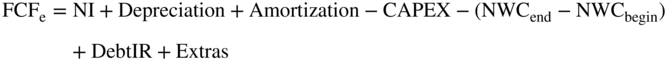
From Table 20.4 (using 81% debt), the pro forma net income in 2015 is $171.0 million. Do we have to add back the after-tax interest in order to calculate FCFe? No, after-tax interest is not in the formula for free cash flows to equity. Why not? Because interest is a cash flow to debt, and we are now calculating cash flows to equity. Furthermore, the impact of debt in reducing taxes is already calculated in net income. (When calculating net income, only the portion of interest that is deductible is subtracted before taxes. Thus, the 30% cap on interest deductibility is accounted for.)
Next, we have to add back depreciation and subtract CAPEX. These numbers are the same as in the FCFf discussion: $310.0 million for depreciation and $370.1 million for CAPEX.3
Note, in the FCFe approach, the entire amount of depreciation is added back to the cash flows. Just as in the FCFf technique, any increase in depreciation is subtracted from EBIT, the tax is computed after this deduction, so the net impact of adding back the full depreciation amount in the cash flow formula is Dep * Tc.
Next, the change in working capital is the same as in Chapter 20, $115.1 million. Finally, as before, there are no extras. Plugging these numbers into the FCFe formula, we get:
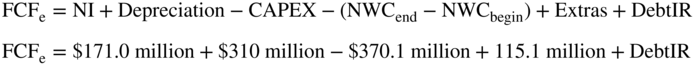
The last term in our FCFe formula is the net change in debt. That is, any proceeds from new debt financing less the payments to principal. Now, you might think that proceeds from debt or principal repayments would be included in the cash flows to debt and not in equity cash flows. In fact, these two items are part of both free cash flows to debt and free cash flows to equity.
How can financing from debt and principal repayments be included in both FCFe and FCFd? They are both added and subtracted to the financing (right) side of the Balance Sheet, which consists of debt and equity. Any new debt financing is added to the free cash flows to equity and subtracted from the free cash flows to debt. Likewise, any debt repayments are subtracted from the free cash flows to equity and added to the free cash flows to debt. This is how they are included in both cash flows (just in opposite directions).
Consider an example: If a firm issues $100 million of debt, this is $100 million of cash from debt that is now available to equity. Thus, free cash flows to equity are increased by $100 million and free cash flows to debt are decreased by $100 million. Note that this cash flow is not just one-way: when the debt is eventually repaid, the free cash flows to equity will be reduced by the same amount. If a firm repays $100 million of debt, this is $100 million that is no longer available to the equity holders. The free cash flows to equity are therefore reduced by the $100 million, and the free cash flows to debt are increased by $100 million.
An aside: Can a firm ever borrow (issue debt) to pay dividends? Yes, AT&T used to do it all the time, as did Apple. Apple has the cash needed to pay its dividends, but the cash is held overseas, and the firm would have to pay U.S. taxes if it repatriated the cash. It is cheaper for Apple to borrow funds to pay dividends rather than bring the overseas cash to the United States and pay taxes. Firms can borrow to pay equity holders today—doing so just changes the timing of the cash flows. The debt will eventually be repaid, and less will be paid to the equity holders in the future.
Returning now to Family Dollar's free cash flows to equity, how much is Family Dollar's change in net debt? From Table 20.4 we see that Family Dollar has total debt (short-term debt plus long-term debt) of $7,255.5 million at the end of 2015. From Table 20.2, we see that Family Dollar has total debt at the start of 2015 (the end of 2014) of $7,310.5 million. This is a decrease, or a net repayment, of $55.0 million. (Note that if your debt repayments are higher than your new debt issues, the last term in the free cash flow to equity formula will be negative, whereas if your debt repayments are lower than your new debt issues, the last term will be positive.) Including this $55.0 million in our formula gives us free cash flows to equity of $171.0 million in 2015.

Returning to our theme of understanding versus memorizing, remember the formula is:
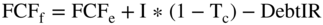
Thus, if we start with the free cash flows to equity of $171.0 million and add back the after-tax cost of interest of $245.0 million and then add back the net debt repayment of $55.0 million (or subtract the net debt issued), we are left with $471.0 million. That is exactly the free cash flows to the firm we calculated in Chapter 20.
Table 21.1 presents the free cash flows to equity from Table 20.4 (which assumed an 81% debt ratio) and the adjustments to get free cash flows to the firm for 2015–2019. (Appendix 21A shows the free cash flows to equity using the constant debt ratio of 35.7% assumed in Appendix 20A. Note that the free cash flows to equity change, as will the discount rate, but the free cash flows to the firm remain the same.)
TABLE 21.1 Family Dollar's Pro Forma Free Cash Flows to Equity (from Table 20.4)
| Postacquisition Adjusted | |||||
| ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Net income | 170,977 | 342,592 | 477,761 | 540,372 | 609,011 |
| Depreciation | 310,000 | 307,000 | 306,000 | 305,000 | 304,000 |
| CAPEX | 370,079 | 486,088 | 488,208 | 463,219 | 474,086 |
| Δ in net working capital | 115,070 | (89,544) | (91,104) | (79,110) | (85,043) |
| Δ in debt | (54,966) | 217,243 | 220,758 | 194,099 | 206,407 |
| Free cash flows to equity | 171,002 | 291,203 | 425,207 | 497,142 | 560,289 |
| Free cash flows to equity | 171,002 | 291,203 | 432,207 | 497,142 | 560,289 |
| Interest * (1 − Tc) | 245,053 | 242,216 | 249,469 | 256,839 | 263,318 |
| Δ in debt | 54,966 | (217,243) | (220,758) | (194,099) | (206,407) |
| Free cash flows firm | 471,021 | 316,176 | 460,918 | 559,882 | 617,200 |
Understanding the Cash Flow Formulas
Let's do another take on the free cash flows to equity. To repeat, the formula is:
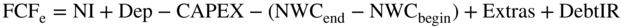
Another way to think of this formula is that it is the net income minus an increase in net fixed assets  minus an increase in working capital
minus an increase in working capital 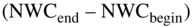 plus any extras plus an increase in debt
plus any extras plus an increase in debt 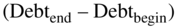 .4 Ignoring the extras we have:
.4 Ignoring the extras we have:
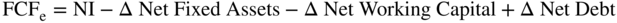
Now, consider for a moment the Balance Sheet as illustrated by our T diagram below:
| Balance Sheet | |
|
Spontaneous net working capital5 |
Debt |
| Fixed assets | Net worth |
The left-hand side, assets, is equal to the right-hand side, debt and net worth. Also, any change in one element necessitates a change in another to maintain the balance. Thus:
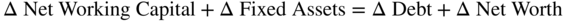
Restating this we get:
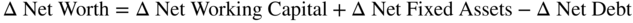
Note, net worth is increased by net income and reduced by dividends. Which can be written as:
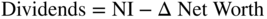
Substituting from above, therefore:
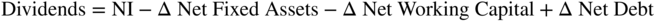
Surprise! The right-hand part of the formula above is the formula for free cash flows to equity. Let this sink in for a minute. This means that:
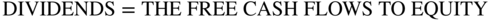
Stated differently, dividends are the amount of net income that remains after investing in net fixed assets or increases in net working capital, or paying down debt.
Now, since the value of the equity is the present value of the free cash flows to equity discounted at Ke and since the dividends are equal to the free cash flows to equity, the present value of a dividend stream discounted at Ke (the cost of equity) is the value of the equity.
Is this new? Actually, no, it is in Miller and Modigliani (1961), which we discussed in Chapter 11. M&M (1961) noted that the value of the equity of a firm is equal to the present value of the future dividend cash flows.
So we have come full circle. We have shown how the free cash flows to the firm relate to the free cash flows to debt and equity. We have also shown that the free cash flows to equity is equal to the dividend stream.
Now, the free cash flows to debt plus the free cash flows to equity are the cash flows to the financing side of the Balance Sheet. Not surprisingly, these are the cash flows from assets (i.e., from the firm's earnings after its investments in fixed assets and working capital). The algebra behind all these cash flows is covered above.
DISCOUNTING THE FREE CASH FLOWS TO EQUITY
The projected free cash flows to equity are then discounted at the cost of equity. The question is: Which cost of equity? If we keep capital structure constant (as done in Chapter 20), then it is the same cost of equity as used in the WACC. However, if the capital structure is different each year, then so will be the cost of equity. For example, if we use the 81% execution financing as the capital structure, the cost of equity will change due to the increased leverage and risk. More importantly, as in an LBO, if the capital structure changes each year, then the free cash flow to equity approach requires a change in the cost of equity each year.
We know from Chapter 6 that additional leverage adds value to the firm through the increased tax shields but subtracts value through the increased risk. The tax shields are picked up in the free cash flows, the additional risk is picked up in the Ke. As explained in Chapter 18 with LBOs and private equity, increased leverage does not increase the risk as much as non-LBO structures because of the joint debt-equity ownership. (This is because either equity is classified as debt or the agency costs of managing the firm are reduced.)
If we keep the same capital structure and the same risk as our WACC model, then the free cash flows to equity approach will give us the same valuation as the free cash flows to the firm approach. If an LBO can increase the tax shields without substantially increasing the risk, then an LBO will be a higher value than a stand-alone firm due to the higher tax shields.
The terminal value in the free cash flow to equity approach is handled in a similar way to the free cash flow to the firm approach. We use one of our five valuation techniques, being careful to use the terminal value of equity and not of the firm. For example:
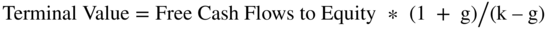
where:
- k = the discount rate
- g = the growth rate
Finally, as in the free cash flows to the firm approach, we must include the purchase price. Is the purchase price the same $9.02 billion computed with the free cash flows to the firm approach? No. When valuing the free cash flows to the firm, we are valuing the cash flows to the assets and include both the debt and equity used to purchase them. However, when valuing the free cash flows to equity we exclude any debt issued in the purchase price because we are looking for the equity investment.
Extending the discussion for LBOs is a topic beyond the scope of this text (perhaps in our next book).
SUMMARY
In this chapter, we focused on understanding the free cash flows used in valuation. In particular, we compared the free cash flows to the firm (i.e., the cash flows from the assets side of the Balance Sheet) to the free cash flows to the equity and the free cash flows to debt (i.e., the cash flows from the financing side). We explained further why the free cash flows to the firm use  and not NI and the nuances of using it (it assumes a constant debt ratio, a market interest rate, and no change in the cash flows with changes in debt levels). In addition, we showed that the free cash flows to equity is the same as the dividend stream available to equity holders. Finally, we stated that if the risk levels stay the same (which may not be true with LBOs and private equity), the value using the FCFf and the FCFe is the same.
and not NI and the nuances of using it (it assumes a constant debt ratio, a market interest rate, and no change in the cash flows with changes in debt levels). In addition, we showed that the free cash flows to equity is the same as the dividend stream available to equity holders. Finally, we stated that if the risk levels stay the same (which may not be true with LBOs and private equity), the value using the FCFf and the FCFe is the same.
Coming Attractions
The next chapter will explain the execution of this particularly interesting multiple-bidder takeover battle. The nature of who bids, how, and when are all explored.
APPENDIX 21A: FAMILY DOLLAR PRO FORMA FREE CASH FLOWS TO EQUITY WITH CONSTANT DEBT RATIO
TABLE 21A.1 Family Dollar's Pro Forma Free Cash Flows to Equity at a Constant 35.7% Debt Ratio
| ($000s) | 2015 | 2016 | 2017 | 2018 | 2019 |
| Net income | 308,686 | 479,300 | 617,233 | 683,859 | 756,306 |
| Depreciation | 310,000 | 307,000 | 306,000 | 305,000 | 304,000 |
| CAPEX | 370,079 | 486,088 | 488,208 | 463,219 | 474,086 |
| Δ in net working capital | 115,070 | (89,544) | (91,104) | (79,110) | (85,043) |
| Δ in debt | (54,991) | 134,428 | 100,487 | 80,041 | 96,304 |
| Free cash flows to equity | 308,686 | 345,096 | 444,408 | 526,572 | 597,481 |
| Free cash flows to equity | 308,686 | 345,096 | 444,408 | 526,572 | 597,481 |
| Interest * (1 − Tc) | 107,345 | 105,509 | 109,997 | 113,351 | 116,023 |
| Δ in debt | 54,991 | (134,428) | (100,487) | (80,041) | (96,304) |
| Free cash flows firm | 471,021 | 316,176 | 453,918 | 559,882 | 617,200 |