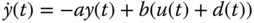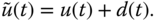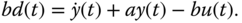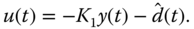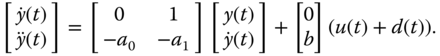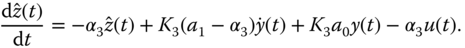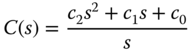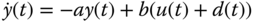5
Disturbance Observer- Based PID and Resonant Controller
5.1 Introduction
In Chapter 1 to Chapter 4, we discussed PID control systems with explicit functions of proportional control, integral control, and derivative control. Because integral control embeds a marginally stable mode in the controller structure, which could cause the problem of integrator windup when the control signal reaches its saturation limits, the PID control system implementation requires modification to overcome this problem. Similar implementation problems to a worse degree are faced by the resonant controllers.
This chapter examines the PID controller design and resonant controller design from a different angle to the previous chapters. It introduces the integral mode and resonant modes through disturbance estimation. By doing so, the design becomes simpler, and more importantly, the implementations of the PID and resonant controllers flow naturally from the designs with anti-windup mechanisms. This development is particularly significant for resonant controllers because simplicity in the implementation with anti-windup mechanisms is paramount for practical applications.
5.2 Disturbance observer-Based PI Controller
This section introduces the idea of disturbance estimation that leads to an equivalent PI control system. The mathematical model used in this section is a first order model. For systems with higher order transfer functions, approximation is required.
5.2.1 Estimation of Disturbance with Control
We assume that there is a constant input disturbance  , which is unknown. So the differential equation used to describe a first order system is given by
, which is unknown. So the differential equation used to describe a first order system is given by
where  and
and  are model coefficients, and
are model coefficients, and 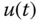 and
and 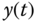 are the input and output variables. Figure 5.1 illustrates the mathematical model to be used for the estimator based PI controller design.
are the input and output variables. Figure 5.1 illustrates the mathematical model to be used for the estimator based PI controller design.
Because of the assumption that  is a constant, we have
is a constant, we have


Figure 5.1 Block diagram of the system for a disturbance observer-based PI controller.
We would like to specify two desired closed-loop poles  and
and 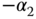 where
where  . In the proposed design, the choice of
. In the proposed design, the choice of  influences predominantly the proportional gain
influences predominantly the proportional gain 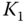 and
and  predominantly the integral gain
predominantly the integral gain  .
.
5.2.1.1 Choice of Proportional Controller 
The choice of  is straightforward. Firstly, we define:
is straightforward. Firstly, we define:
Then (5.1) becomes

Together with proportional control

we obtain the closed-loop system:
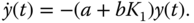
Equating the actual closed-loop pole 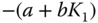 to the desired closed-loop pole
to the desired closed-loop pole  , we find the proportional gain
, we find the proportional gain 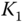 as
as

5.2.1.2 Compensation of Steady-state Error
We know that proportional control will lead to a closed-loop system with steady-state error for a constant reference signal or a disturbance signal. For overcoming the steady-state error, we need integral action incorporated into the control system. Here, we will estimate the steady-state error and then compensate it in the control signal. For this purpose, we extract the disturbance information from (5.1) leading to
One might attempt to directly calculate the unknown disturbance  using (5.7) and compensate for it in the control signal. However, it can be easily verified that such an approach fails to produce the control signal required because of uncertainties in the model parameters and other imperfections in practical applications. We will estimate the disturbance signal
using (5.7) and compensate for it in the control signal. However, it can be easily verified that such an approach fails to produce the control signal required because of uncertainties in the model parameters and other imperfections in practical applications. We will estimate the disturbance signal  with compensation on the error.
with compensation on the error.
Let 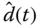 denote the estimated disturbance signal. The error, between what is given and what is to be estimated, is described by,
denote the estimated disturbance signal. The error, between what is given and what is to be estimated, is described by,

With the gain  weighted on the error
weighted on the error  , together with the assumption
, together with the assumption  , we construct the estimation
, we construct the estimation 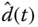 as
as
This is the so-called observer-equation. We will choose the gain  such that the error
such that the error  converges to zero.
converges to zero.
Note that

then, the parameter  is chosen such that
is chosen such that  . This then leads to
. This then leads to

Hence,
For any given initial condition  and
and  , the estimation error
, the estimation error 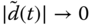 as
as  . The convergence rate is dependent on the parameter
. The convergence rate is dependent on the parameter  . The larger
. The larger  is, the faster the error will converge to zero.
is, the faster the error will converge to zero.
Now, to calculate the control signal with compensation on the steady-state error, the unknown disturbance  in (5.3) is replaced by the estimated
in (5.3) is replaced by the estimated  from (5.9), leading to the control signal calculated as
from (5.9), leading to the control signal calculated as
5.2.1.3 The closed-loop poles
To verify indeed that the closed-loop poles for the control system are  and
and 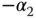 , substituting (5.12) into (5.1) gives
, substituting (5.12) into (5.1) gives

where  . Together with (5.11), the closed-loop system equation is written as
. Together with (5.11), the closed-loop system equation is written as

Because  is an upper triangular matrix, the closed-loop poles (or eigenvalues) are simply calculated as the solution of the characteristic equation:
is an upper triangular matrix, the closed-loop poles (or eigenvalues) are simply calculated as the solution of the characteristic equation:

where 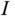 is the identity matrix with dimensions
is the identity matrix with dimensions  , equal to
, equal to  and
and 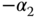 .
.
5.2.1.4 Implementation procedure
Because the estimation equation 5.9 contains the derivative of the output signal 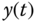 , direct discretization requires information of
, direct discretization requires information of  at sampling time
at sampling time 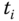 , which is not available to us.
, which is not available to us.
Let us define a variable  as
as
Then, substituting this variable into the estimation equation 5.9 yields
If the reference signal  , then both (5.15) and (5.16) are modified by replacing
, then both (5.15) and (5.16) are modified by replacing  with
with  . Furthermore, if the control signal
. Furthermore, if the control signal  reaches its saturation limit, this saturation information is updated in the estimation of the disturbance
reaches its saturation limit, this saturation information is updated in the estimation of the disturbance  via (5.16). Figure 5.2 illustrates the block diagram of the control system using disturbance observer. For discretizaton, at sampling time
via (5.16). Figure 5.2 illustrates the block diagram of the control system using disturbance observer. For discretizaton, at sampling time  , the derivative
, the derivative  is approximated using the first order approximation as
is approximated using the first order approximation as

Then, it follows that

The calculation procedure for control signal is summarized as follows. Choose initial condition for  at the beginning of the closed-loop operation. This could be selected to be zero if no other information is available. With the reference signal
at the beginning of the closed-loop operation. This could be selected to be zero if no other information is available. With the reference signal  and output signal
and output signal  available at sampling time
available at sampling time  , the control signal
, the control signal 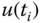 is calculated recursively. The control signal is limited between
is calculated recursively. The control signal is limited between  and
and  .
.
- Calculate the estimated disturbance signal at sample
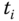 as
as

- Calculate the control signal using the following equation


Figure 5.2 Block diagram of the control system using a disturbance observer.
- Implement the control signal saturation:

- Update the estimation of disturbance
 for the next sampling instant as
for the next sampling instant as
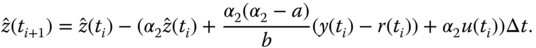
- Send the control signal
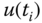 for implementation. When the next sampling period arrives, the new measurement of the output is taken and the computation is repeated from step 1.
for implementation. When the next sampling period arrives, the new measurement of the output is taken and the computation is repeated from step 1.
5.2.2 Equivalence to PI controller
In order to calculate the equivalent PI controller, the Laplace transform of  is expressed as
is expressed as

where  , and the Laplace transform
, and the Laplace transform 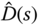 is
is
The Laplace transform of the control signal  becomes
becomes

which is

Thus, the equivalent PI controller is revealed as

The PI controller parameters are


where 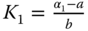 and
and  . We can verify that the closed-loop poles are at
. We can verify that the closed-loop poles are at  and
and 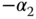 , which was the design specification.
, which was the design specification.

Figure 5.3 Transfer function realization of the estimator based PI controller and  is the saturation limiter.
is the saturation limiter.
Defining the coefficients  and
and  and the saturation limiter
and the saturation limiter  , Figure 5.3 shows the transfer function realization of the PI controller with anti-windup mechanism, which calculates the control signal
, Figure 5.3 shows the transfer function realization of the PI controller with anti-windup mechanism, which calculates the control signal  based on the reference signal
based on the reference signal 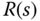 and the output signal
and the output signal  .
.
5.2.3 MATLAB Tutorial for Implementation of a PI Controller via Estimation
The embedded PI controller via estimation will be used in the simulation studies with the Simulink environment.
5.2.4 Examples for Estimator based PI Controllers
It is apparent that much larger control amplitude is required when  is used for the estimator based PI controller design. In practice, this much larger control amplitude may not be realizable due to the physical limitations of the actuators. An interesting question arises as how the closed-loop response speed will change if the control signal amplitude is limited. The following example illustrates the comparative studies.
is used for the estimator based PI controller design. In practice, this much larger control amplitude may not be realizable due to the physical limitations of the actuators. An interesting question arises as how the closed-loop response speed will change if the control signal amplitude is limited. The following example illustrates the comparative studies.
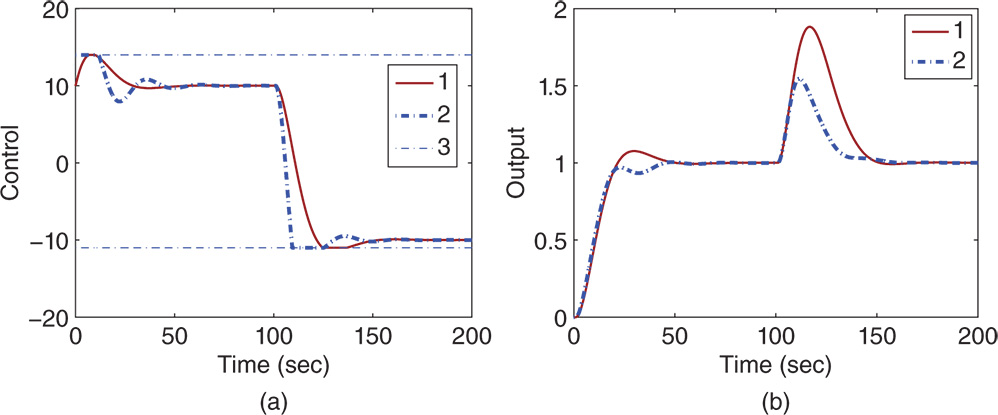
Figure 5.5 Comparison of closed-loop control performance using an estimator based PI controller with different  values (Example 5.2). (a) Control signal. (b) Output. Key: line (1)
values (Example 5.2). (a) Control signal. (b) Output. Key: line (1)  ; line (2)
; line (2)  ; and line (3) the limits of the control signal.
; and line (3) the limits of the control signal.

Figure 5.6 Comparison of closed-loop control performance between the PI controller in velocity form and the disturbance observer-based PI controller (Example 5.3). (a) Control signal. (b) Output. Key: line (1) the PI controller in velocity form; line (2) the disturbance observer-based PI controller.
The above two examples indicate that with the estimator based PI control system, the closed-loop performance limitation is limited by the model uncertainties due to unmodeled dynamics in the system. The performance limitation is reflected by the value of  . The control signal limits can be incorporated into the implementation of the control system with a naturally occurred anti-windup mechanism.
. The control signal limits can be incorporated into the implementation of the control system with a naturally occurred anti-windup mechanism.
From Section 5.2.2 it is clear that there is an equivalent PI controller with parameters  and
and  to this estimation based PI controller. The implementation of a PI controller using the velocity form was discussed with anti-windup mechanisms in Section 4.6. Naturally we wonder if these two implementations would lead to different outcomes. The following example compares the outcomes of these two PI controller with anti-windup mechanisms.
to this estimation based PI controller. The implementation of a PI controller using the velocity form was discussed with anti-windup mechanisms in Section 4.6. Naturally we wonder if these two implementations would lead to different outcomes. The following example compares the outcomes of these two PI controller with anti-windup mechanisms.
5.2.5 Food for Thought
- In the design of a disturbance observer-based PI controller, what effect will the desired closed-loop poles
 and
and  have on the closed-loop performance?
have on the closed-loop performance? - If the system has a large modelling error, would you decrease
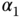 and
and  ?
? - If the steady-state values of the control signal and output signal are not zero at the initial time, how would you enter these steady-state values in the disturbance observer-based PI controller implementation?
- Is it possible to estimate the disturbance
 without compensating it in the control system?
without compensating it in the control system? - Is the implementation of integrator based on a stable system?
5.3 Disturbance observer-Based PID Controller
To design a PID controller using the estimation based approach, we consider a second order transfer function:
where  and
and  are the Laplace transforms of the input and output signals. We assume that
are the Laplace transforms of the input and output signals. We assume that  . By assuming zero initial conditions, the corresponding differential equation is expressed as
. By assuming zero initial conditions, the corresponding differential equation is expressed as

In matrix form, it is expressed as
5.3.1 Proportional Plus Derivative Control
We will first design a proportional plus derivative controller. For this purpose, the feedback control signal 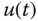 is
is
Substituting (5.25) into (5.24) leads to the closed-loop equation:

The closed-loop characteristic polynomial is then calculated as

This is clearly a second order polynomial. We can specify a damping coefficient  and choose the parameter
and choose the parameter 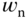 as the closed-loop performance parameter. Alternatively, we could also choose two desired closed-loop poles as
as the closed-loop performance parameter. Alternatively, we could also choose two desired closed-loop poles as  and
and  where
where  and
and  . In any case, to determine the proportional and the derivative controller gain, the actual closed-loop characteristic polynomial is made equal to the desired one, leading to
. In any case, to determine the proportional and the derivative controller gain, the actual closed-loop characteristic polynomial is made equal to the desired one, leading to

The solution of this polynomial equation gives the proportional control gain:

and the derivative control gain:
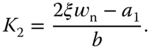
Since it is necessary to use a filter for the derivative action because of measurement noise, a quick way to calculate a first order filter time constant is to find the corresponding gain  , which is
, which is

based on (5.25). With this parameter, the derivative filter constant is

where  is often selected. The filtered derivative output signal is expressed as
is often selected. The filtered derivative output signal is expressed as

For many applications, it is preferable to design the PD controller together with derivative filter  to avoid the extra errors introduced from the approximation. A PD controller with filter design is discussed in detail in Section 3.4.1 with the filter constant calculated through the desired closed-loop performance specification.
to avoid the extra errors introduced from the approximation. A PD controller with filter design is discussed in detail in Section 3.4.1 with the filter constant calculated through the desired closed-loop performance specification.
5.3.2 Adding Integral Action
To add integral action to the PD controller, we assume that there is a constant input disturbance 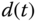 so we have
so we have  . The differential equation model (5.24) is modified to become:
. The differential equation model (5.24) is modified to become:
Similar to the PI controller design via estimation, we will write the unknown disturbance term as

Together with the assumption that  , the estimation of
, the estimation of  is constructed as
is constructed as
We choose  and determine the estimator's gain
and determine the estimator's gain  using
using
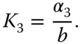
Because Equation 5.31 has double derivative and derivative of output signal  , it is not suitable for computational purposes. To this end, we define a new variable
, it is not suitable for computational purposes. To this end, we define a new variable

and rewrite Equation 5.31 as function of  :
:
Assuming that the reference signal is  at the sampling time
at the sampling time  and the output signal and its derivative are measured as
and the output signal and its derivative are measured as  ,
,  , with the sampling interval
, with the sampling interval  , with saturation limits
, with saturation limits  and
and  , the control signal is calculated using the following steps.
, the control signal is calculated using the following steps.
- Update the estimated disturbance signal. An initial condition on
 will be given as the start up of the control algorithm.
will be given as the start up of the control algorithm.

- Calculate the control signal
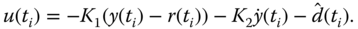
- Implement control signal saturation:

- Update the disturbance estimator for
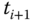 :
:

- When the next sample period arrives, repeat the computation at step 1.
Note that in the implementation of the PID controller, the derivative control is on the output only, avoiding producing a spike on the control signal when the reference signal signal  makes a step change. When a filter is used for the derivative signal
makes a step change. When a filter is used for the derivative signal  , the signal
, the signal  is replaced by
is replaced by  , which is illustrated in Tutorial 5.2.
, which is illustrated in Tutorial 5.2.
5.3.3 Equivalence to a PID Controller
To find the equivalence of the proposed estimation based PID controller to the PID controller expressed in transfer function form, we examine the Laplace transform of the estimation equation 5.31, which is,

where  . Solving for
. Solving for  gives
gives
Note that the Laplace transform of the control signal is expressed as
By substituting (5.34) into (5.35), the Laplace transform of the control signal 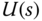 is found as
is found as

With the negative feedback, the equivalent controller transfer function  is obtained as
is obtained as

Now, it can be verified that the closed-loop polynomial is indeed
where  and
and  are the numerator and denominator of the transfer function model as given by (5.23). Additionally, it can be verified that the controller transfer function can be written in an equivalent form to a PID controller:
are the numerator and denominator of the transfer function model as given by (5.23). Additionally, it can be verified that the controller transfer function can be written in an equivalent form to a PID controller:
where the parameters 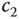 ,
,  , and
, and  are calculated as
are calculated as



Figure 5.7 shows the transfer function realization of the disturbance observer-based PID controller where  is the saturation limiter.
is the saturation limiter.
There are several comments related. Firstly, the relationship presented in (5.38) shows that there are three desired closed-loop poles for the PID controller designed. The pair of complex poles located at  with
with  or 1 is used to determine the parameters
or 1 is used to determine the parameters  and
and  , and the pole located at
, and the pole located at  is used to determine the parameter
is used to determine the parameter  . Secondly, the PID controller can be implemented using the estimation of the input disturbance, providing a stable implementation for the integrator. Thirdly, the controller transfer function shown in (5.39) can readily be used for frequency response analysis so that the gain margin, phase margin, and delay margin can be calculated for the controller designed.
. Secondly, the PID controller can be implemented using the estimation of the input disturbance, providing a stable implementation for the integrator. Thirdly, the controller transfer function shown in (5.39) can readily be used for frequency response analysis so that the gain margin, phase margin, and delay margin can be calculated for the controller designed.

Figure 5.7 Transfer function realization of the disturbance observer-based PID controller.
5.3.4 MATLAB Tutorial on the Implementation of a disturbance observer-based PID Controller
This section presents the MATLAB tutorial for the implementation of disturbance observer-based PID controller. This implementation will contain the anti-windup mechanism when the control signal reaches its maximum or minimum values. The embedded PID controller via estimation will be used in the simulation studies within the Simulink environment.
5.3.5 Examples for Disturbance observer-based PID Controller
5.3.6 Food for Thought
- In the design of disturbance observer-based PID controller, how would you modify Equations 5.29–(5.32) to include the derivative filter?
- Can you list three physical systems that have second order transfer functions and are suitable for a PD controller application?
- How would you propose to include the steady-state values of control signal and output signal in the implementation of the disturbance observer-based PID controller?
- Would you consider the possibility of adding the integral action after the PD controller has stabilize the system, which can be achieved subsequently by subtracting the disturbance term?
5.4 Disturbance observer-Based Resonant Controller
This section will investigate resonant controller design and implementation with anti-windup mechanism using the disturbance estimation approach.
5.4.1 Resonant Controller Design
Assume that a dynamic system is described by the differential equation:
where  and
and 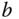 are the coefficients;
are the coefficients;  and
and  are the input and output signals;
are the input and output signals;  is the input disturbance signal. In particular, we assume that
is the input disturbance signal. In particular, we assume that  is a sinusoidal signal with known frequency
is a sinusoidal signal with known frequency  , but unknown amplitude
, but unknown amplitude 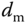 and phase angle
and phase angle  , which is expressed as
, which is expressed as
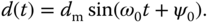
The resonant control law is expressed as
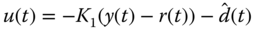
where  is an estimate of the unknown disturbance
is an estimate of the unknown disturbance  .
.
By choosing the desired closed-loop pole at 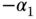 and
and  , the proportional feedback control gain
, the proportional feedback control gain  is calculated as
is calculated as

Now, the next question is how to compute the estimated input sinusoidal disturbance signal  . The derivative of this disturbance signal is
. The derivative of this disturbance signal is
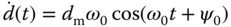
and its second derivative is
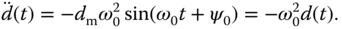
Now, we choose 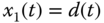 and
and 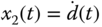 . With these choices, the following differential equations are used to describe the sinusoidal disturbance signal:
. With these choices, the following differential equations are used to describe the sinusoidal disturbance signal:

In order to estimate the disturbance signal  , from (5.44), we obtain
, from (5.44), we obtain

which is the output equation for the estimation. Thus, the estimated variables  and
and  are constructed as
are constructed as
where  and
and  are the estimator gains chosen for the design.
are the estimator gains chosen for the design.
The next question is how to choose 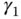 and
and  such that the errors between the estimated and true disturbance signals are ensured to converge to zero as
such that the errors between the estimated and true disturbance signals are ensured to converge to zero as  . For this purpose, we define
. For this purpose, we define  and
and  . It can be verified as an exercise that we have the following error system:
. It can be verified as an exercise that we have the following error system:

where we have used the following relationship:

Clearly, we can choose the parameters  and
and 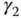 such that the poles (or eigenvalues) of the error system are on the left half of the complex plane, which ensures its stability. The characteristic polynomial for the error system is calculated as
such that the poles (or eigenvalues) of the error system are on the left half of the complex plane, which ensures its stability. The characteristic polynomial for the error system is calculated as

Now, we choose a desired characteristic polynomial for performance specification as 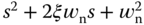 . Then, to make the characteristic polynomial for the error system equal to the desired characteristic polynomial, the coefficients
. Then, to make the characteristic polynomial for the error system equal to the desired characteristic polynomial, the coefficients  and
and 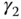 are found as,
are found as,

In the applications, the damping parameter  is chosen to be 0.707 and the parameter
is chosen to be 0.707 and the parameter  is adjusted for how fast we would like to see the errors converge to zero.
is adjusted for how fast we would like to see the errors converge to zero.
5.4.2 Resonant Controller Implementation
The calculation of the estimated input disturbance using (5.46) requires the derivative of the output signal  , which is not desirable in the implementation. To overcome the problem, we define a pair of new variables:
, which is not desirable in the implementation. To overcome the problem, we define a pair of new variables:

Then, from (5.46), the following two equations are obtained:
The control law presented above is a combination of proportional feedback and a disturbance observer. This section will present how this control law can be implemented in a discrete time environment with anti-windup mechanism.
The derivatives in the observer equations 5.49 and (5.50) are first discretized with a sampling interval 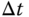 leading to their approximations at the sampling time
leading to their approximations at the sampling time  :
:

The following algorithm summarizes the computational procedure for the implementation of the resonant controller with anti-windup mechanism.
Assume that the control signal  is limited to
is limited to  and
and  , that is
, that is
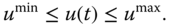
Choosing the initial conditions for 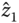 and
and  , the control signal is calculated iteratively according to the following steps, where
, the control signal is calculated iteratively according to the following steps, where 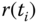 is the reference signal at sampling time
is the reference signal at sampling time  .
.
- Calculate the estimated sinusoidal disturbance
 as
as

- Calculate the control signal
 as
as

- Implement the saturations on the control signal using

- Update the estimated disturbance signals using the following equations:

- When the next sampling period arrives, repeat the computation from step 1.
5.4.3 Equivalence to a Resonant Controller
To find the Laplace transfer function of the resonant controller designed using disturbance estimation, we note that the Laplace transform of the control signal has the following expression:
where  is the Laplace transform of the estimated sinusoidal disturbance. It can be verified that the Laplace transform of (5.46) gives
is the Laplace transform of the estimated sinusoidal disturbance. It can be verified that the Laplace transform of (5.46) gives

Calculating the matrix inversion and multiplication gives
To find the Laplace transform of the control signal, we will substitute (5.53) into (5.51) and move the term containing 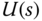 from the left-hand side to the right-hand side of the equation, which gives the expression of the control signal
from the left-hand side to the right-hand side of the equation, which gives the expression of the control signal
where  and
and  .
.
From (5.54), we find the Laplace transfer function of the resonant controller as
This controller has a pair of complex poles at  .
.
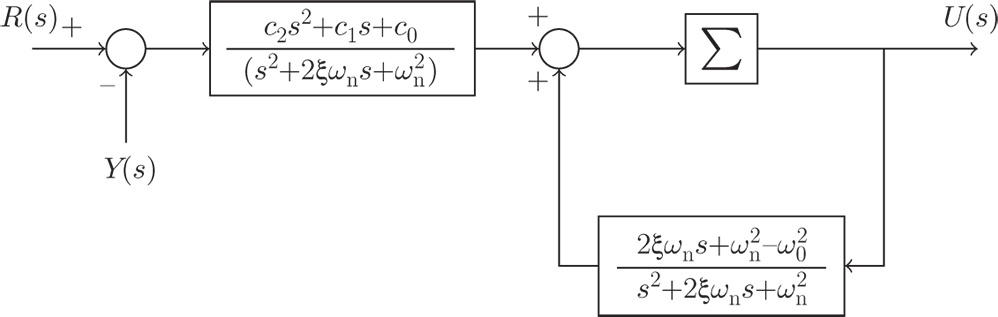
Figure 5.9 Transfer function realization of a resonant controller with saturation limits.
To verify if the closed-loop poles are indeed at the locations of  and
and 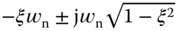 (
( or 0.707), we calculate the closed-loop characteristic polynomial as
or 0.707), we calculate the closed-loop characteristic polynomial as
where  ,
,  , and
, and  . The closed-loop characteristic polynomial (5.56) leads to the conclusion that the closed-loop poles are at the locations as we specified.
. The closed-loop characteristic polynomial (5.56) leads to the conclusion that the closed-loop poles are at the locations as we specified.
Figure 5.9 shows the transfer function realization of the resonant controller with anti-windup mechanism.
5.4.4 MATLAB Tutorial on Disturbance observer-Based Resonant Controller Implementation
This section presents the MATLAB tutorial for implementation of the disturbance observer-based resonant controller together with the anti-windup mechanism when the control signal reaches its maximum or minimum values. The embedded resonant controller via estimation will be used in the simulation studies within the Simulink environment.
5.4.5 Examples for Disturbance observer-Based Resonant Controllers
The following example is to illustrate the disturbance observer-based resonant controller design.
It is clear that these two approaches in selecting the parameters  and
and 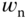 produced quite different controller parameters although the responses to the reference signal are similar. The question arises as how these two resonant controllers will behave in the presence of periodic disturbances. Clearly, if the disturbance has exactly the same frequency
produced quite different controller parameters although the responses to the reference signal are similar. The question arises as how these two resonant controllers will behave in the presence of periodic disturbances. Clearly, if the disturbance has exactly the same frequency  , then both resonant controllers will achieve the same disturbance rejection at the steady-state operation from the sensitivity analysis in Section 2.5. However, when the actual disturbance frequency is different from
, then both resonant controllers will achieve the same disturbance rejection at the steady-state operation from the sensitivity analysis in Section 2.5. However, when the actual disturbance frequency is different from  , there is a difference in the control system performance. The next example will compare the closed-loop performance of the two resonant controllers for the purpose of disturbance rejection.
, there is a difference in the control system performance. The next example will compare the closed-loop performance of the two resonant controllers for the purpose of disturbance rejection.
The next example is to illustrate the effectiveness of the anti-windup mechanism contained in the resonant controller.
5.4.6 Food for Thought
- Can you list three systems that have first order dynamics and require a resonant control system for disturbance rejection or reference following of a sinusoidal signal?
- Is it correct that with the disturbance observer-based resonant controller, the complementary sensitivity function has a magnitude of one at the frequency
 where
where  is the frequency of the sinusoidal reference signal or the disturbance signal?
is the frequency of the sinusoidal reference signal or the disturbance signal? - What do the closed-loop performance parameters
 and
and  represent in the design of disturbance observer-based resonant controller? If there are neglected dynamics in the system, how would you choose them?
represent in the design of disturbance observer-based resonant controller? If there are neglected dynamics in the system, how would you choose them? - What are the key components in the disturbance observer-based-resonant controller that lead to the anti-windup mechanism in its implementation?
- Would you say that it is quite straightforward to implement the resonant controller with anti-windup mechanism?
5.5 Multi-frequency Resonant Controller
In many applications, the resonant controller containing a single frequency introduced in Section 5.4 may not be adequate to track the reference signal or reject the disturbance signal that contains multiple frequencies. The framework we used in the single frequency case can be extended to multiple frequencies.
5.5.1 Adding Integral Action to the Resonant Controller
We consider the following first order differential equation as in Section 5.4
where  and
and 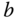 are the coefficients;
are the coefficients;  and
and  are the input and output signals;
are the input and output signals; 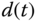 is the input disturbance signal. Different from the resonant controller design, we assume that
is the input disturbance signal. Different from the resonant controller design, we assume that  is a combination of a sinusoidal signal with a constant. For this purpose,
is a combination of a sinusoidal signal with a constant. For this purpose,  is expressed as
is expressed as

where  and
and  is an unknown constant. The feedback control law is determined as
is an unknown constant. The feedback control law is determined as

where  is an estimate of the unknown disturbance
is an estimate of the unknown disturbance  .
.
With the desired closed-loop pole specified at  and
and  , the proportional feedback control gain
, the proportional feedback control gain  is given as
is given as
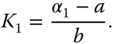
Now, we will extend the estimation algorithm presented in Section 5.4 to include the estimation of an unknown constant. Let us choose 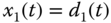 and
and  and
and  . Note that
. Note that  as
as  is a constant. The following differential equations will be used to describe the unknown disturbance
is a constant. The following differential equations will be used to describe the unknown disturbance 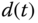 with the additional state
with the additional state  :
:

In order to estimate the disturbance signal  , from (5.58), we obtain
, from (5.58), we obtain
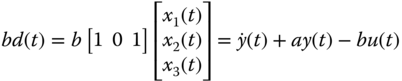
which is the output equation for the estimation. Thus, the estimated variables  ,
,  ,
, 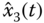 are expressed as
are expressed as

where  ,
,  and
and  are the estimator gains chosen for the design.
are the estimator gains chosen for the design.
As in Section 5.4, we will choose the parameters  ,
,  and
and  such that the poles of the error system are on the left half of the complex plane to ensure the convergence of the estimation errors. Here, the characteristic polynomial for the error system is computed as
such that the poles of the error system are on the left half of the complex plane to ensure the convergence of the estimation errors. Here, the characteristic polynomial for the error system is computed as
where 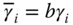 ,
,  for simplicity in the computation.
for simplicity in the computation.
There is an analytical expression for the determinant given by (5.61), which leads to analytical solutions for the parameters 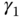 ,
,  , and
, and  . We firstly partition the
. We firstly partition the 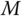 matrix into a block matrix as
matrix into a block matrix as

where
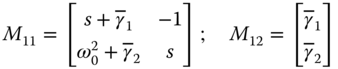

With this partition, the determinant of the block matrix becomes
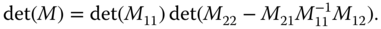
Note that  is exactly the same as the determinant described in the estimation of the sinusoidal signal in Section 5.4, which is
is exactly the same as the determinant described in the estimation of the sinusoidal signal in Section 5.4, which is

and the second determinant is

The characteristic polynomial for the closed-loop error system becomes

With the choice of desired characteristic polynomial for the performance specification that consists of a pair of complex poles and a real pole having the following form:  , we find the the coefficients
, we find the the coefficients  ,
, 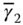 , and
, and  as
as

The actual gains used in the estimation are then scaled to yield:  for
for  .
.
Defining 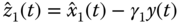 ,
,  , and
, and  , it can be verified that the implementation equation for the estimated disturbance becomes
, it can be verified that the implementation equation for the estimated disturbance becomes
where  is the system matrix defined as
is the system matrix defined as
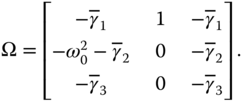
 has eigenvalues as the solutions of the characteristic equation:
has eigenvalues as the solutions of the characteristic equation:

Hence, the implementation of the estimator using (5.64) is a stable realization.
From the estimated 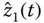 and
and  , we obtain
, we obtain

and  .
.
5.5.2 Adding More Periodic Components
If the system's disturbance or reference signal has more than one pair of periodic components, the disturbance estimator needs to be designed so to include those components.
We assume that the system is described by the differential equation 5.58. As before,  is the input disturbance signal and it is a combination of sinusoidal signals with a constant. For this purpose,
is the input disturbance signal and it is a combination of sinusoidal signals with a constant. For this purpose,  is expressed as
is expressed as

where  ,
,  (
( ) and
) and  is an unknown constant.
is an unknown constant.
Continuing from the design in Section 5.5.1, we choose  ,
,  ,
,  ,
,  , and
, and  . With the two additional states, the following differential equation is used to describe the input disturbance
. With the two additional states, the following differential equation is used to describe the input disturbance  :
:

To estimate the disturbance signal  from the dynamic system (5.58), the disturbance term is written as
from the dynamic system (5.58), the disturbance term is written as
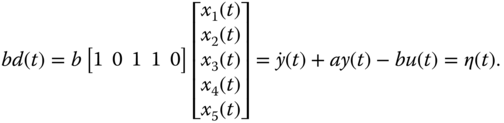
The estimated variables 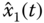 ,
,  ,
,  ,
, 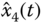 , and
, and  are written as
are written as
where  ,
, 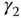 ,
,  ,
,  , and
, and  are the estimator gains chosen for the design.
are the estimator gains chosen for the design.
To find the estimator gains, we will consider the pair of matrices,  and
and  . Because of their higher dimensions, it is no longer easy to work out the analytical solutions of the estimator gains. Instead, we can use MATLAB programs for finding the estimator's gain matrix. For this purpose, we define the
. Because of their higher dimensions, it is no longer easy to work out the analytical solutions of the estimator gains. Instead, we can use MATLAB programs for finding the estimator's gain matrix. For this purpose, we define the  and
and  matrices as illustrated in (5.66), and we choose five desired closed-loop poles for the error system to ensure the convergence of the estimated variables. The MATLAB program place.m is used to compute the
matrices as illustrated in (5.66), and we choose five desired closed-loop poles for the error system to ensure the convergence of the estimated variables. The MATLAB program place.m is used to compute the  ,
,  , illustrated as below:
, illustrated as below:
Gamma=place(A',C',P)' where  contains the five desired closed-loop poles for the error system and gamma is the vector that contains
contains the five desired closed-loop poles for the error system and gamma is the vector that contains 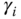 ,
,  .
.
5.5.3 Food for Thought
- Is it correct that in the design of disturbance observer-based resonant controller for the multi-frequency signal, the complexity of the estimator has increased in order to estimate the multi-frequency disturbance signal?
- Would you say that in general a higher accuracy of the model is required for estimating more frequency components?
- Can you devise a resonant controller scheme for the multi-frequency control so that you can sequentially enter the periodic component one at a time?
5.6 Summary
We have discussed the PID and resonant controller design from the angle of disturbance estimation. Using the disturbance observer-based approaches, the integral control or the resonant control is introduced through the estimation of an input disturbance with the assumption that the disturbance is a constant for the integral mode or the disturbance is a sinusoidal signal for the resonant mode. The advantages of the proposed approaches include the simplified design for the controller, and perhaps even more importantly a stable controller structure suitable for direct implementation with an anti-windup mechanism in the event of control signal saturation. The other important aspects of the chapter are summarized as follows.
- For a first order system with constant disturbance, the controller is a proportional control and the estimator is based on a first order model. This is equivalent to a PI controller with proportional and integral gains. The controller gain and estimator gains are selected with independent performance specifications.
- For a second order system with constant disturbance, the controller has the functions of proportional and derivative control, and the estimator is based on a first order model. This is equivalent to a PID controller with proportional, integral and derivative gains. The closed-loop performance for the controller and the estimator is specified separately through the locations of their closed-loop poles.
- For the resonant controller design, the system is assumed to have a first order model with input sinusoidal disturbance. The sinusoidal disturbance includes those with a single frequency or a multi-frequency. A proportional controller is used for the control function, and an estimator that embeds the sinusoidal modes is used to estimate the disturbance. This is equivalent to the resonant controller discussed in the previous chapters. Because the disturbance estimation is based on a stable system, the implementation of the proposed approach is numerically sound with a naturally embedded anti-windup mechanism if the control signal reaches its saturation limits.
For systems that have higher order dynamics, to use the design approaches proposed in this chapter, model order reduction is required.
5.7 Further Reading
- A book is devoted to disturbance observer-based linear and nonlinear control systems (Li et al. (2014)). A survey is presented in Chen et al. (2016). The same research group has also worked on various topics of disturbance observer in control systems (Li et al. (2012), Yang et al. (2012)).
- The early work on motion control using disturbance observer includes Komada et al. (1991). Disturbance observer is used for rigid mechanical systems in Schrijver and van Dijk (2002) and for robotic manipulator in Chen et al. (2000). Controller design for disturbance rejection is proposed using disturbance observer with estimation of frequency in Jia (2009). Stability and robust performance of motion control using disturbance observer is analyzed in Sariyildiz and Ohnishi (2015).
- PID control and active disturbance rejection are introduced in Han (2009).
 control is compared with disturbance observer-based control methods in Mita et al. (1998).
control is compared with disturbance observer-based control methods in Mita et al. (1998).- Disturbance rejection in dual-stage feed drive control system is discussed in She et al. (2011).
- A recent survey is presented for disturbance estimation and attenuation in PMSM drives (Yang et al. (2017)) using the framework of disturbance observer.
- The disturbance observer-based resonant controller is used to control a single phase voltage converter with experimental validation in McNabb et al. (2017).
Problems
- 5.1 Use the disturbance observer-based approach to design and implement a PI controller for the following systems:

- Find the approximate first order model
 by neglecting the relatively small time constant(s) and small time delay while maintaining the same steady-state gain.
by neglecting the relatively small time constant(s) and small time delay while maintaining the same steady-state gain. - Choose the desired closed-loop pole for the proportional controller
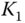 as
as  where
where  is the dominant pole for the system while the pole for the estimator is
is the dominant pole for the system while the pole for the estimator is  to obtain the estimator gain
to obtain the estimator gain  .
. - Compute the frequency responses of the controller
 , the sensitivity function
, the sensitivity function  , the input disturbance sensitivity function
, the input disturbance sensitivity function  and the complementary sensitivity function
and the complementary sensitivity function  . You can adjust the desired closed-loop poles for the controller and estimator, and observe their effects on the sensitivity functions.
. You can adjust the desired closed-loop poles for the controller and estimator, and observe their effects on the sensitivity functions. - Evaluate the closed-loop stability by using Nyquist diagram. If the closed-loop system is unstable, adjust the controller pole and the estimator pole to achieve stable closed-loop system.
- Evaluate the robust stability condition for all
 :
:

- What are your observations from the Nyquist diagram and robust stability condition? What can we do to improve the robustness of the closed-loop system?
- Build the MATLAB real-time function PIEstim.slx by following Tutorial 5.1 and simulate the closed-loop step response and input disturbance rejection. We choose sampling interval
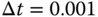 and set the constraints on the control amplitude to be sufficiently large. A unit step reference signal is used in the simulation studies where a step input disturbance with amplitude of
and set the constraints on the control amplitude to be sufficiently large. A unit step reference signal is used in the simulation studies where a step input disturbance with amplitude of  enters the simulation at half of the simulation time.
enters the simulation at half of the simulation time. - Evaluate the effect of constraints on the control signal where the constraint parameters
 and
and  are chosen to be 85 percent of the control signal's maximum amplitude from the previous step.
are chosen to be 85 percent of the control signal's maximum amplitude from the previous step. - What are your observations from the constrained control simulations?
- Find the approximate first order model
- 5.2 Use the disturbance observer-based approach to design a PID controller for the following systems:

- Choose the desired closed-loop characteristic polynomial for the proportional plus derivative controller as
 where
where  and
and  , while the pole for the estimator is
, while the pole for the estimator is  to obtain the estimator gain
to obtain the estimator gain  .
. - Build the MATLAB real-time function PIDEstim.slx by following Tutorial 5.2 and simulate the closed-loop step response and input disturbance rejection with the sampling interval
 where the constraints on the control amplitude are set to be sufficiently large. In the simulations, the derivative filter time constant
where the constraints on the control amplitude are set to be sufficiently large. In the simulations, the derivative filter time constant  . The reference signal is a unit step signal and the input disturbance signal has amplitude of
. The reference signal is a unit step signal and the input disturbance signal has amplitude of  that enters the simulation at half of the simulation time.
that enters the simulation at half of the simulation time. - Evaluate the effect of constraints on the control signal where the constraint parameters
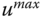 and
and 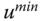 are chosen to be 85 percent of the control signal's maximum amplitude from the previous step.
are chosen to be 85 percent of the control signal's maximum amplitude from the previous step. - What are your observations from the constrained control simulations?
- Choose the desired closed-loop characteristic polynomial for the proportional plus derivative controller as
- 5.3 Consider the disturbance observer-based PID controller design for the three systems introduced in Problem 5.2. All the other conditions remain the same except designing the Proportional and Derivative controller with filter (see Section 3.4.1), where the filter time constant is considered in the process. The additional pole for the PD controller is chosen to be
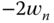 .
.
- 5.4 It is ideal to incorporate the derivative filter in the PID controller design and analysis. From Section 5.3, inclusion of the derivative filter
 will change the transfer function of the PID controller presented in (5.39). Find the PID controller transfer function
will change the transfer function of the PID controller presented in (5.39). Find the PID controller transfer function

that is equivalent to the disturbance observer-based PID controller.
- 5.5 Equation 5.18 reveals that the disturbance observer-based PI control is equivalent to computing the disturbance transfer function using the input and output signal:
which is, in essence, the inversion of the plant model together with a first order stable filter with unity steady-state gain for implementation, which is the essential component for disturbance observer-based approach (Li et al. (2014)).
- Propose a discretization scheme for the disturbance estimation based on (5.67).
- Draw a closed-loop feedback diagram with limits on the control signal amplitude. Does this implementation incorporate the anti-windup mechanism?
- 5.6 Equation 5.34 shows that the disturbance observer-based PID controller is equivalent to accessing the disturbance information with the following transfer function form:
which is the inversion of the plant model with first order filter that has a unity steady-state gain.
- Propose a discretization scheme for computing the estimated disturbance based on the transfer function (5.68) with an additional first order filter so to make it realizable.
- Draw the closed-loop diagram with control signal constraints.
- 5.7 From Problem 5.6, if the plant model has the following transfer function

where
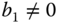 ,
,  and
and 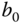 have the same sign, meaning a stable zero.
have the same sign, meaning a stable zero.- Express the
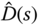 in terms of the inversion of the new plant model.
in terms of the inversion of the new plant model. - Will this stable zero result in slow disturbance rejection if
 or if
or if  ?
? - Verify your answer by examining the input disturbance sensitivity function
 for both cases.
for both cases.
- Express the
- 5.8 Consider the following systems with the given frequency
 for a resonant controller design:
for a resonant controller design:

- Design the resonant controller based on a first order model
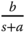 by neglecting either the small time delay or small time constant (s), where the proportional controller pole is selected as
by neglecting either the small time delay or small time constant (s), where the proportional controller pole is selected as  and the desired closed-loop characteristic polynomial for the estimator as
and the desired closed-loop characteristic polynomial for the estimator as 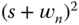 with
with  .
. - Calculate the frequency response of the complementary sensitivity function
 and the multiplicative modelling error
and the multiplicative modelling error  and check if the robust stability condition, for all
and check if the robust stability condition, for all  :
:

is satisfied. If not, reduce the parameter
 until it is satisfied.
until it is satisfied. - Build the MATLAB real-time function ResEstim.slx by following Tutorial 5.3 and simulate the closed-loop response to a sinusoidal reference signal
 , where
, where  .
. - Add a sinusoidal input disturbance
 at half of the simulation time and simulate the disturbance rejection of the closed-loop system.
at half of the simulation time and simulate the disturbance rejection of the closed-loop system. - In order to evaluate the anti-windup mechanism, you may choose the control signal limits
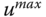 and
and  based on 85 percent of the maximum and minimum of the control signal in transient response.
based on 85 percent of the maximum and minimum of the control signal in transient response.
- Design the resonant controller based on a first order model
- 5.9 In many applications, tracking of a ramp reference signal is required. The disturbance observer-based resonant controller introduced in Section 5.4 can be modified to track a ramp reference signal by assuming the frequency
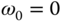 . Assume that a given first order system is described by the following transfer function model:
. Assume that a given first order system is described by the following transfer function model:

- Modify the disturbance observer-based resonant controller to track a ramp input signal;
- Find the proportional controller gain
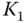 by positioning the desired closed-loop pole at
by positioning the desired closed-loop pole at  , and find the estimator gains
, and find the estimator gains  and
and  by choosing the desired closed-loop characteristic polynomial as
by choosing the desired closed-loop characteristic polynomial as  , where
, where  and
and  .
. - Use final value theorem to show that indeed this disturbance observer-based control system will track a ramp reference signal without steady-state error.
- With the reference signal as
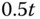 , simulate the closed-loop response using the MATLAB real-time function ResEstim.slx where the sampling interval
, simulate the closed-loop response using the MATLAB real-time function ResEstim.slx where the sampling interval  .
.
- 5.10 Consider the following first order system:
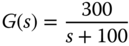
Design a resonant controller that will follow a reference signal
 , and reject an input disturbance
, and reject an input disturbance  , where all desired closed-loop poles for both the controller and the estimator are positioned at
, where all desired closed-loop poles for both the controller and the estimator are positioned at  .
. - 5.11 One application for the resonant controller is in the area of a single phase AC current regulator. The objective is to accurately track a sinusoidal reference signal with a frequency that matches the power grid.
The dynamic model for a single phase Voltage Source Inverter (VSI) coupled to a back electromotive force with an inductive-resistive filter network is expressed as
(5.69)
where
 is the output current from the inverter,
is the output current from the inverter,  is the input variable that is the pulse width modulated (PWM) switched voltage from the VSI, and
is the input variable that is the pulse width modulated (PWM) switched voltage from the VSI, and  is the back EMF voltage that is naturally a sinusoid with a nominal frequency
is the back EMF voltage that is naturally a sinusoid with a nominal frequency  . The parameter
. The parameter  is the resistance and
is the resistance and  is the inductance, associated with the inductive-resistive filter network.
is the inductance, associated with the inductive-resistive filter network.The control signal
 equals to the multiplication of a modulation signal
equals to the multiplication of a modulation signal 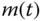 with the inverter DC link voltage
with the inverter DC link voltage  :(5.70)
:(5.70)
In the mathematical model of a single phase Voltage Source Inverter as in McNabb et al. (2017), the physical parameters are
 ,
,  ,
,  . The back EMF voltage is described by
. The back EMF voltage is described by 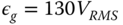 and
and  (
( ).
).- Design a resonant controller for the single phase Voltage source inverter, where
 . The closed-loop performance specifications are considered for the following two cases.
. The closed-loop performance specifications are considered for the following two cases.
- The feedback controller gain
 is selected such that the closed-loop control system pole is equal to the open-loop system pole. The parameters for the estimator are
is selected such that the closed-loop control system pole is equal to the open-loop system pole. The parameters for the estimator are 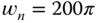 and
and  .
. - The feedback controller gain
 is selected such that the closed-loop control system pole is twice of the open-loop system pole in magnitude. The parameters for the estimator are
is selected such that the closed-loop control system pole is twice of the open-loop system pole in magnitude. The parameters for the estimator are  and
and  .
.
- The feedback controller gain
- Compare the sensitivity function
 and the complementary sensitivity function
and the complementary sensitivity function 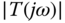 for the two cases. Determine the maximum time delay that the resonant control systems can tolerate. What are our observations? (Hint: the multiplicative modelling error is
for the two cases. Determine the maximum time delay that the resonant control systems can tolerate. What are our observations? (Hint: the multiplicative modelling error is  for neglected time delay
for neglected time delay  ).
). - Choosing sampling interval
 (sec), simulate the closed-loop response to reference following and disturbance rejection, in which the reference signal is
(sec), simulate the closed-loop response to reference following and disturbance rejection, in which the reference signal is  and the disturbance is
and the disturbance is  . In the simulation model, the control signal is
. In the simulation model, the control signal is  for simplification.
for simplification. - Impose the constraints on the amplitude of
 , where the maximum and minimum of the control signal are chosen to be 85 percent of the unconstrained control cases in transient responses.
, where the maximum and minimum of the control signal are chosen to be 85 percent of the unconstrained control cases in transient responses. - Discuss the closed-loop control performances with respect to the two desired closed-loop performance specifications.
- Design a resonant controller for the single phase Voltage source inverter, where