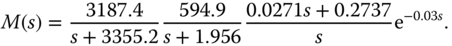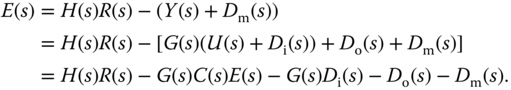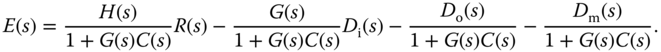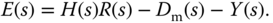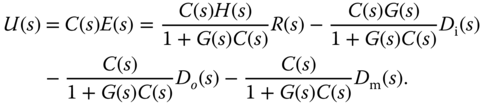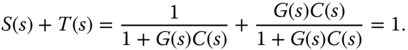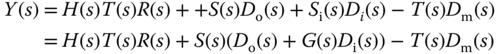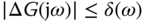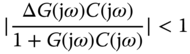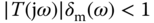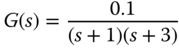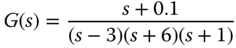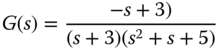2
Closed-loop Performance and Stability
2.1 Introduction
Because feedback control can cause a closed-loop system to become unstable, ensuring closed-loop stability is paramount in control system design. In Section 2.2, we will discuss closed-loop stability by examining the locations of closed-loop poles and the applications of the Routh–Hurwitz stability criterion. In Section 2.3, the Nyquist stability criterion is presented based on a frequency response analysis, which leads to conclusions of closed-loop stability by examining the frequency response of the loop transfer functions, particularly convenient for analysis of systems with time delay.
To understand the roles of external signals playing in a feedback control system, Section 2.4 introduces control system structures with different degrees of freedom, which are related to the topic of reducing overshoot in reference response discussed in Chapter 1. Also in this section, the sensitivity functions are introduced in relation to various external signals in the closed-loop system. In Sections 2.5 and 2.6, we will examine the key issues existed in a feedback control system that are related to reference following, disturbance rejection, and noise attenuation from the angles of sensitivity analysis. The final section of this chapter will discuss the robust stability using frequency response analysis. Many examples presented in this chapter use PID controllers designed with the tuning rules given in Chapter 1.
2.2 Routh–Hurwitz Stability Criterion
Feedback control can cause a system to become unstable. Ensuring closed-loop stability is the most important aspect in control system design. Therefore, for every control system designed, its closed-loop stability is required to be checked as the top priority.
For linear time invariant systems, there are two main categories of methods that have been widely used to check closed-loop stability. The first type is based on the direct computation of the poles of the closed-loop transfer function. We call them the closed-loop poles. If all the closed-loop poles have negative real parts, namely with all poles strictly on the left half of the complex plane, then the closed-loop system is stable. If there are one or more poles on the right half of the complex plane, having a positive real component, then the closed-loop system is unstable. If there are one or more poles with real part equal to zero, namely on the imaginary axis of the complex plane, we call this type of system marginally stable. The second type is based on the open-loop transfer function that includes the plant transfer function, sensor and actuator transfer functions, and the controller transfer function. The Nyquist stability criterion is one of the most widely used methods that is based on the open-loop frequency response analysis.
2.2.1 Determining Closed-loop Poles
The first step in the computation of closed-loop poles is to calculate the closed-loop transfer function. Once the closed-loop transfer function is determined, then the MATLAB function roots.m is used to find the zeros of the denominator of the closed-loop transfer function, which are the poles of the closed-loop transfer function.
Note that in the computation of the closed-loop transfer function, the sensor and actuator dynamics will be considered in addition to the controller transfer function.
2.2.2 Routh–Hurwitz Stability Criterion
It would not be a straightforward task if we had to calculate the closed-loop poles using pencil and paper for a third order system and above. The Routh–Hurwitz stability criterion was introduced in the development of control systems early on so that their closed-loop stability could be determined using pencil and paper. Without involving complex computation, using the Routh–Hurwitz stability criterion enables us to determine whether there are any closed-loop poles on the right half of the complex plane and how many of them there are. This simple calculation is performed using the coefficients of the denominator of the closed-loop transfer function.
Table 2.1 Routh–Hurwitz table.
 |
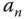 |
 |
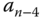 |
… |
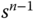 |
 |
 |
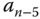 |
… |
| sn−2 | r2,1 | r2,2 | r2,3 | … |
| sn−3 | r3,1 | r3,2 | r3,3 | … |
| ⋮ | ⋮ | |||
| s2 | rn−2,1 | rn−2,2 | ||
| s | rn−1,1 | |||
| s0 | rn,1 |
In general, for the denominator of the closed-loop transfer function with the polynomial

we use its coefficients to form the first two rows of the Routh–Hurwitz table (see Table 2.1), and based on the first two rows complete the rest of the elements in the table. The first element in the third row is
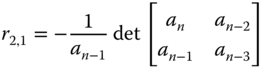
where it is seen that we used the nearest two previous rows to form the determinant scaled by the factor 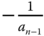 . The second element in the third row is
. The second element in the third row is
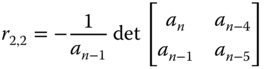
which is the same scaling but with the replacement of the next column in the determinant. With the same pattern,
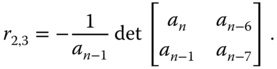
For the fourth row, we will use the elements in the nearest two rows (second and third rows) with the same pattern, where
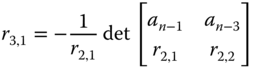
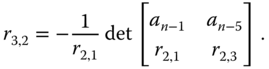
The remainder of the elements are expressed in a general form as
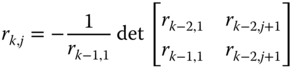
where  .
.
The elements in the first column of the Routh–Hurwitz table will determine whether the closed-loop system is stable. The number of roots of the polynomial  with real part greater than zero is equal to the number of sign changes in the first column of the Routh–Hurwitz table. Simply, if the first coefficient
with real part greater than zero is equal to the number of sign changes in the first column of the Routh–Hurwitz table. Simply, if the first coefficient 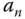 in
in 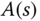 is positive, then closed-loop stability will follow if all elements in the first column are positive.
is positive, then closed-loop stability will follow if all elements in the first column are positive.
Note that, in the calculation of the table, if an element in the first column becomes zero, then the calculation continues by replacing the zero element with a variable  . The remainder of the elements will be expressed in the function of
. The remainder of the elements will be expressed in the function of 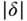 . Closed-loop stability will be determined by examining the coefficients in the first row using
. Closed-loop stability will be determined by examining the coefficients in the first row using 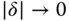 .
.
If the coefficients of the closed-loop transfer function are constant and known, the closed-loop poles are simply calculated using the MATLAB function roots.m, as illustrated in Example 2.1. However, the Routh–Hurwitz stability criterion is very effective in determining closed-loop stability when some of the controller or process parameters have uncertainties.
2.2.3 Food for Thought
- For a given system, when the closed-loop poles are found to be
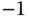 ,
, 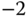 and
and 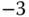 , what kind of behavior do you expect the closed-loop output response to be?
, what kind of behavior do you expect the closed-loop output response to be? - When the closed-loop poles are found to be
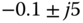 , what kind of output response do you expect?
, what kind of output response do you expect? - Why do the complex poles always appear in a complex conjugate form?
- Can we determine closed-loop stability if one of the coefficients in the leading column of Routh-Hurwitz stability criterion is zero?
- Can we apply Routh-Hurwitz stability criterion to systems with time delay?
2.3 Nyquist Stability Criterion
The Nyquist stability criterion is one of the most widely used tools in analyzing closed-loop stability. Using MATLAB graphic tools, the Nyquist diagram is very easy to produce by calculating the frequency response of the loop transfer function. The gain margin, phase margin and delay margin provide valuable insight into closed-loop stability with respect to parameter variations.
2.3.1 Nyquist Diagram
The Nyquist stability criterion uses the frequency response of an open-loop system, including the plant, the sensors and the actuator, to determine closed-loop stability. Here, the open-loop system  is expressed as
is expressed as
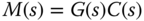
where 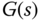 represents the system dynamics including the plant dynamics, the actuator dynamics, and the sensor dynamics, and
represents the system dynamics including the plant dynamics, the actuator dynamics, and the sensor dynamics, and 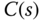 represents the controller transfer function. More specifically, it is a graphic approach using real and imaginary values of the frequency response
represents the controller transfer function. More specifically, it is a graphic approach using real and imaginary values of the frequency response 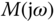 where
where  is that of the loop transfer function. The benefit of being a graphic approach lies in the intuition as well as both quantitative and qualitative measures.
is that of the loop transfer function. The benefit of being a graphic approach lies in the intuition as well as both quantitative and qualitative measures.
As an illustration, the Nyquist loci of a PI controlled system that has a stable open-loop transfer function with time delay is shown in Figure 2.2, where the following loop transfer function is used:
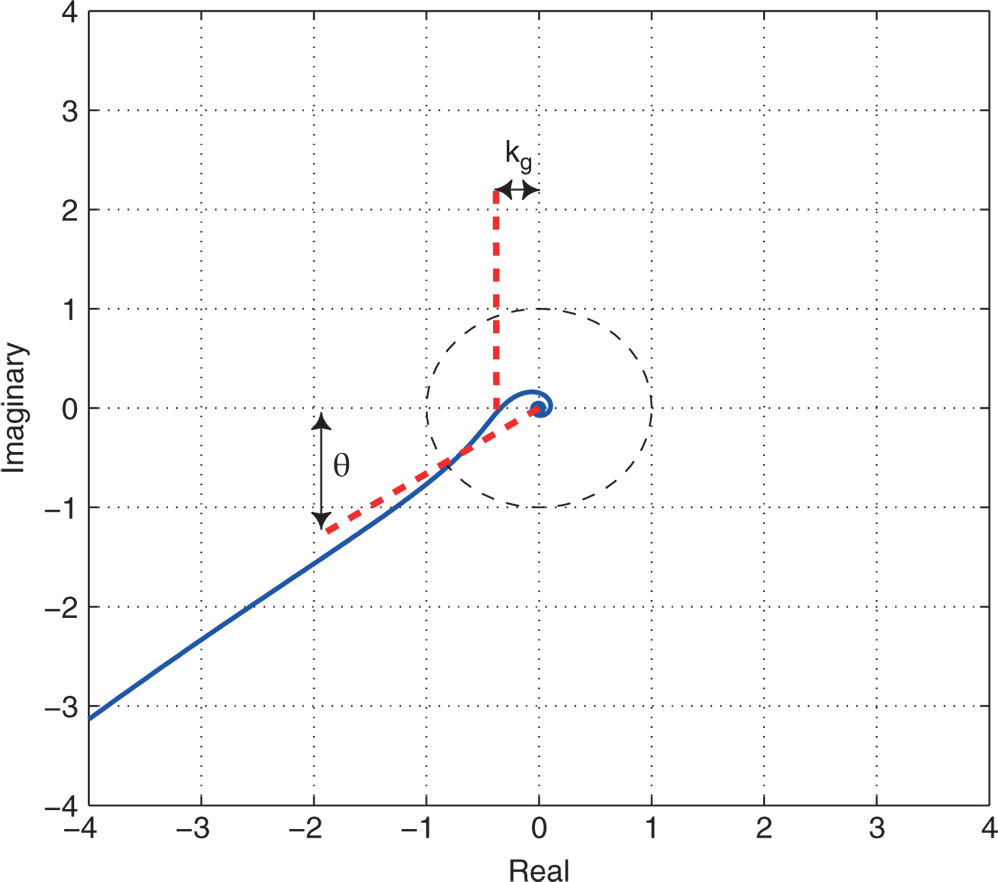
Figure 2.2 Nyquist plot with a unit circle for illustration of gain margin and phase margin. Solid line: Nyquist loci; dashed lines: pointers for the gain margin and phase margin.
We can specify the frequency vector 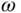 and use the MATLAB function freqs.m to calculate the frequency response of the open-loop transfer function. The time delay component
and use the MATLAB function freqs.m to calculate the frequency response of the open-loop transfer function. The time delay component 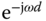 is computed first using the MATLAB exponential function and multiplied by the frequency response of the rest of the open-loop transfer functions. Tutorial 2.1 shows the MATLAB program for the Nyquist plot.
is computed first using the MATLAB exponential function and multiplied by the frequency response of the rest of the open-loop transfer functions. Tutorial 2.1 shows the MATLAB program for the Nyquist plot.
The Nyquist criterion states that a feedback control system with single input and single output is stable if and only if, for the frequency response of the loop transfer function  , number of counter clockwise encirclements of the
, number of counter clockwise encirclements of the 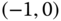 point is equal to the number of poles of this loop transfer function with positive real parts. Note that this criterion presents both necessary and sufficient conditions for closed-loop stability using its open-loop transfer function. There are two comments related as below.
point is equal to the number of poles of this loop transfer function with positive real parts. Note that this criterion presents both necessary and sufficient conditions for closed-loop stability using its open-loop transfer function. There are two comments related as below.
- For the majority of PID controlled systems, this loop transfer function does not contain any poles that have positive real parts. Thus, for closed-loop stability of these classes of systems, the Nyquist stability criterion simply becomes that the frequency response should not encircle the
 point on the complex plane.
point on the complex plane. - Because it uses the frequency response, closed-loop stability for systems with time delay will be examined without approximation. This is one of the most important advantages for using Nyquist loci to analyze control systems.
There are several quantitative, yet intuitive measurements that can be derived from the Nyquist loci. These quantities, termed gain margin, phase margin, and delay margin, are frequently used to assess the performance of the designed control system using the frequency information and safe-guard the closed-loop system against future model uncertainties.
2.3.1.1 Gain Margin
Gain margin is a quantity that is used to measure how much variation in gain the feedback control system could sustain before it became unstable. As illustrated in Figure 2.2, the gain margin is defined as  , where
, where 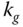 is the distance between the origin of the complex plane and the point that
is the distance between the origin of the complex plane and the point that 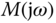 intersects the real axis (see the vertical dashed line in Figure 2.2). This means that if the loop gain were to exceed
intersects the real axis (see the vertical dashed line in Figure 2.2). This means that if the loop gain were to exceed  , then the closed-loop system would become unstable. The parameter
, then the closed-loop system would become unstable. The parameter  can be easily determined from the Nyquist loci. Using the following MATLAB command:
can be easily determined from the Nyquist loci. Using the following MATLAB command:
[x,y]=ginput(1) a cross hair appears on the Nyquist plot. By overlaying the center of the cross hair on the point that the Nyquist curve intersects the real axis, we obtain the coordinates as 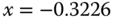 and
and 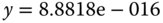 . The distance is
. The distance is 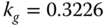 . Therefore, the gain margin is determined as
. Therefore, the gain margin is determined as 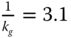 . This means that if we were to increase the loop gain to three times the original value, then the closed-loop system would become unstable. We can associate this gain margin with the variations in the steady-state gain of the plant, the sensor, the actuator, or the controller gain
. This means that if we were to increase the loop gain to three times the original value, then the closed-loop system would become unstable. We can associate this gain margin with the variations in the steady-state gain of the plant, the sensor, the actuator, or the controller gain 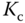 . It is the net effect of all the combined variations of gains.
. It is the net effect of all the combined variations of gains.
2.3.1.2 Phase Margin
To identify the phase margin, we first draw a unit circle with its origin located at the origin of the complex plane, as shown in Figure 2.2, and a straight dashed line that connects the point when the circle intersects the Nyquist loci with the origin of the complex plane. The phase margin 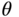 is the angle between the negative real axis and the dashed line. Clearly, it is the additional phase lag that could be associated with
is the angle between the negative real axis and the dashed line. Clearly, it is the additional phase lag that could be associated with 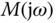 before the closed-loop system became unstable. The phase margin
before the closed-loop system became unstable. The phase margin 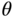 can be calculated using the following MATLAB function ginput.m. When using the following MATLAB function:
can be calculated using the following MATLAB function ginput.m. When using the following MATLAB function:
[x,y]=ginput(1) a cross hair appears. Overlaying the center of the cross hair on the point that the unit circle intersects the Nyquist loci, we obtain the coordinates of 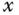 and
and  for that point. From Figure 2.2, the coordinates are
for that point. From Figure 2.2, the coordinates are 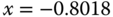 and
and 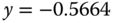 . Then the phase margin
. Then the phase margin 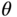 is computed as
is computed as
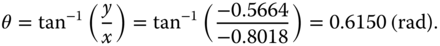
2.3.1.3 Delay Margin
Although the phase margin 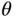 represents how much additional phase lag can be added to the feedback control system before it becomes unstable, it does not directly convey the size of maximum time delay that can be added to the system. To determine the maximum time delay that can be tolerated, we let
represents how much additional phase lag can be added to the feedback control system before it becomes unstable, it does not directly convey the size of maximum time delay that can be added to the system. To determine the maximum time delay that can be tolerated, we let
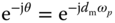
where  is the delay margin or the maximum delay to be tolerated and
is the delay margin or the maximum delay to be tolerated and 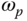 is the frequency when the unit circle intersects with the Nyquist loci. This yields
is the frequency when the unit circle intersects with the Nyquist loci. This yields

Clearly, a larger 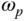 would lead to a smaller delay margin given the same phase margin
would lead to a smaller delay margin given the same phase margin 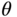 . Thus, the frequency
. Thus, the frequency 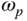 is an important parameter. To determine the frequency
is an important parameter. To determine the frequency 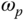 , we will plot
, we will plot 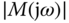 , as shown in Figure 2.3. Using the function ginput.m, we identify the intersecting point of the dashed line with the solid line in Figure 2.3 that has the coordinates
, as shown in Figure 2.3. Using the function ginput.m, we identify the intersecting point of the dashed line with the solid line in Figure 2.3 that has the coordinates 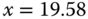 and
and 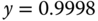 . Thus,
. Thus, 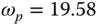
 . From the parameter
. From the parameter  and the phase margin
and the phase margin 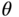 , we calculate the delay margin as
, we calculate the delay margin as
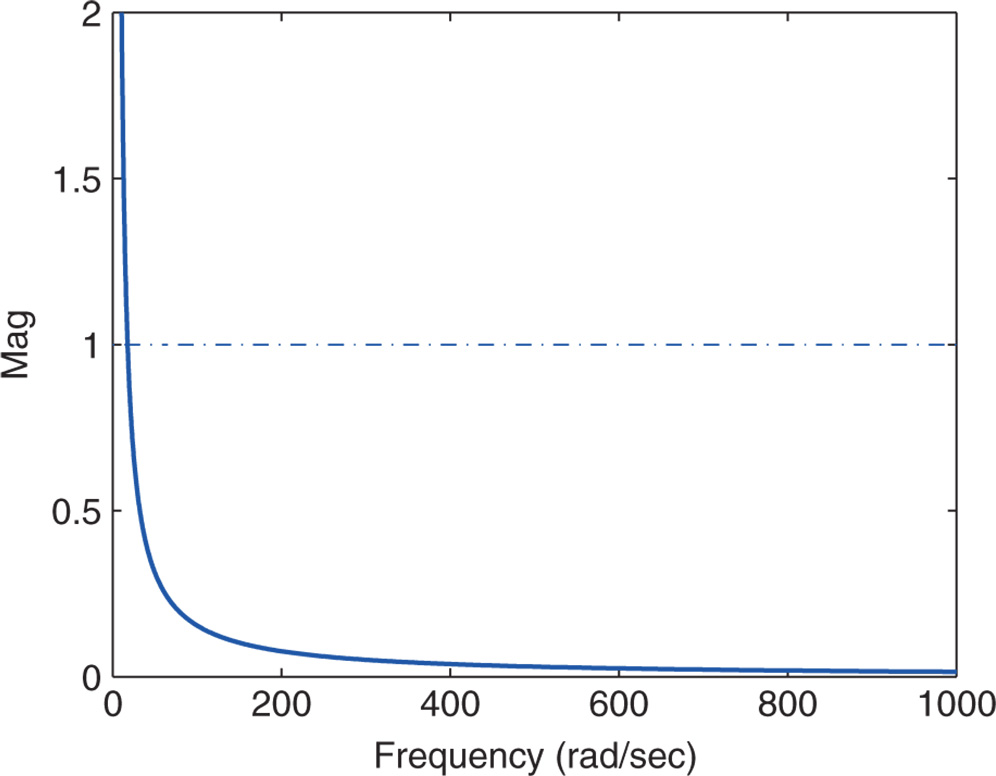
Figure 2.3 Magnitude of  (solid line) together with dashed line to determine
(solid line) together with dashed line to determine 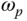 .
.
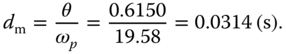
This means that the associated delay, which can be added to the system before it becomes unstable, is 0.0314 s.
2.3.2 Rework of Tuning Rules based PID Controllers
2.3.3 Food for Thought
- What would happen to a closed-loop system if its gain margin is equal to 1?
- Would you say that the Nyquist diagram is an effective means to check the performance of the PID controller designed when using the tuning rules?
- What would you do if the gain margin of the control system designed is too small?
- How would you be able to increase the phase margin of a control system?
2.4 Control System Structures and Sensitivity Functions
This section introduces control system structures with one and two degrees of freedom, which are related to the PID controller realization to reduce the overshoot in reference response discussed in Chapter 1. The external signals such as reference signal, disturbance signals and measurement noise are important in the analysis of control system performance. This section discusses these signals in relationships with the sensitivity functions.
2.4.1 One Degree of Freedom Control System Structure
A feedback control system of a one degree of freedom structure is represented by the block diagram, shown in Figure 2.8, where 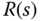 is the reference signal,
is the reference signal, 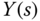 is the output, and
is the output, and 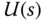 is the control signal. There is also an output disturbance in the system, denoted as
is the control signal. There is also an output disturbance in the system, denoted as 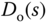 . For simplicity, the transfer function
. For simplicity, the transfer function  includes the plant dynamics, actuator dynamics, and sensor dynamics.
includes the plant dynamics, actuator dynamics, and sensor dynamics.
The Laplace transform of the error signal 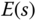 is expressed as
is expressed as
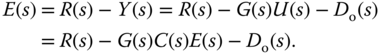
Therefore, the error signal is expressed as

Then, the output of the control system is

and the control signal is

Assuming that 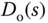 is zero, the transfer function between the reference signal and the plant output is
is zero, the transfer function between the reference signal and the plant output is

and the transfer function between the reference signal and the control signal is
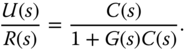
Figure 2.8 One degree of freedom control system structure.
Similarly, by assuming  , we derive the transfer functions between the output disturbance and the output, and the output disturbance and the control signal:
, we derive the transfer functions between the output disturbance and the output, and the output disturbance and the control signal:
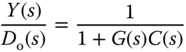
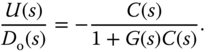
The properties of these closed-loop transfer functions are directly related to the closed-loop performance, determining the behavior of the output signal and the control signal in relation to reference signal 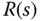 and the output disturbance
and the output disturbance  . In this controller structure, once the controller
. In this controller structure, once the controller 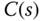 is selected, all four closed-loop transfer functions are fixed; only one degree of freedom is available to influence the output response
is selected, all four closed-loop transfer functions are fixed; only one degree of freedom is available to influence the output response 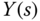 to the reference signal
to the reference signal 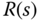 and to the disturbance
and to the disturbance 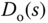 . This is called one degree of freedom design.
. This is called one degree of freedom design.
2.4.2 Two Degrees of Freedom Design
A two degrees of freedom control system is shown in Figure 2.9. In this structure, an extra component 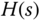 is placed after the reference signal
is placed after the reference signal 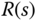 , which will be used in the design.
, which will be used in the design. 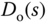 denotes the output disturbance,
denotes the output disturbance, 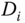 denotes the input disturbance,
denotes the input disturbance, 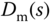 denotes the measurement noise. How does this structure offer two degrees of freedom in the design? For this, with the assumption that
denotes the measurement noise. How does this structure offer two degrees of freedom in the design? For this, with the assumption that 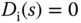 and
and  , we calculate the output response
, we calculate the output response 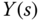 in relation to the reference signal
in relation to the reference signal 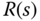 and the output disturbance
and the output disturbance 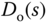 ,
,
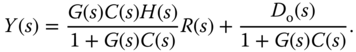
From this, we have the two transfer functions
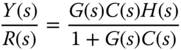

Transfer function  provides one more degree of freedom to shape the output response to the reference signal
provides one more degree of freedom to shape the output response to the reference signal 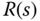 . This extra degree of freedom plus the original one degree of freedom gives the two degrees of freedom in the design. If the control system is configured as a, then we can shape, independently, the output response to the reference signal and to the disturbance.
. This extra degree of freedom plus the original one degree of freedom gives the two degrees of freedom in the design. If the control system is configured as a, then we can shape, independently, the output response to the reference signal and to the disturbance.
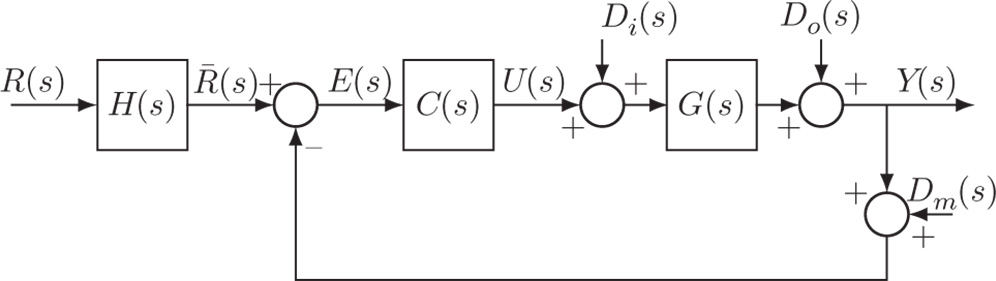
Figure 2.9 Two degrees of freedom control system structure.

Figure 2.10 Two degrees of freedom PI control system structure, where 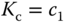 and
and 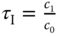 .
.
2.4.2.1 Two degrees of freedom implementation of PI controllers
From Example 1.3, the IP controller structure illustrated in Figure 1.7 is in fact a two degrees of freedom implementation of a PI controller with a reference filter  , where the reference filter is
, where the reference filter is 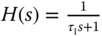 , which is illustrated in Figure 2.10. One may argue that the choices of proportional controller gain
, which is illustrated in Figure 2.10. One may argue that the choices of proportional controller gain 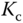 and the integral time constant
and the integral time constant 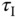 have cemented the characteristics of disturbance rejection; however, the value of
have cemented the characteristics of disturbance rejection; however, the value of 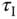 has provided an extra degree of freedom to influence reference response. The advantage of using the IP controller is that the implementation procedure is simpler, because there is no need for the implementation of reference signal filter. In the general framework of two degrees of freedom controller implementation,
has provided an extra degree of freedom to influence reference response. The advantage of using the IP controller is that the implementation procedure is simpler, because there is no need for the implementation of reference signal filter. In the general framework of two degrees of freedom controller implementation, 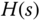 may also be designed carefully to achieve desired effect of reference response.
may also be designed carefully to achieve desired effect of reference response.
2.4.3 Sensitivity Functions in Feedback Control
To understand the sensitivity functions and their roles in feedback control, we examine the block diagram of a closed-loop feedback control system illustrated in Figure 2.9.
Based on the block diagram, we calculate the feedback error of the closed-loop system firstly as
By re-arranging (2.19), the closed-loop feedback error is
Note that the feedback error is relation to the output via,
By substituting (2.21) into (2.20), we obtain the expression of the closed-loop output 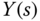 as
as
Also, from the feedback error (2.20), we calculate the closed-loop control signal as
Based on these relationships, the following sensitivity functions are defined.
- Sensitivity function:
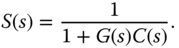
- Complementary sensitivity function:
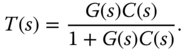
- Input disturbance sensitivity function:
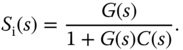
- Control sensitivity function:

The sensitivity functions are related to each other in the following ways.
- The sensitivity plus complementary sensitivity is equal to one:
- The input disturbance sensitivity is related to sensitivity:
(2.25)
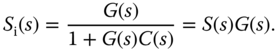
- The control sensitivity is related to sensitivity:
(2.26)

With the sensitivity functions, we re-write the output of the closed-loop system (2.22) as
and the control signal (2.23) as
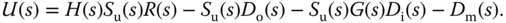
From these relationships, we can see that:
- The complementary sensitivity function
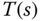 represents the effect of both reference signal and measurement noise on the output.
represents the effect of both reference signal and measurement noise on the output. - The sensitivity
 represents the effect of output disturbance on the output.
represents the effect of output disturbance on the output. - The input sensitivity
 represents the effect of input disturbance on the output.
represents the effect of input disturbance on the output.
2.4.4 Food for Thought
- In the two-degrees-of-freedom control system structure, must the reference filter
 be stable?
be stable? - In many applications, instead of designing the reference filter, it is simpler to design the reference signal by deploying a ramp signal between two constant references. Assuming that at time
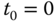 , the reference signal
, the reference signal 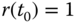 , we would like the reference signal to be increased to 3 in a duration of 10 seconds. What does this reference signal look on a piece of paper? If you would like to duplicate this signal using the reference filter
, we would like the reference signal to be increased to 3 in a duration of 10 seconds. What does this reference signal look on a piece of paper? If you would like to duplicate this signal using the reference filter 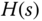 , what would you do?
, what would you do? - Can you think of a reason why we would use the IP controller instead of using the two-degrees-of- freedom approach when we need to overcome the reference overshoot problem in PID control systems?
- If the IP controller you designed still resulted in overshoot in reference response, what would you do?
- With respect to PID control, by examining the closed-loop transfer function (1.40) in Example 1.4, which reference filter would you use to reduce the overshoot in the closed-loop step response caused by the derivation control?
2.5 Reference Following and Disturbance Rejection
Aside from stabilization of unstable systems, the two most important purposes that a feedback control system serves are reference following and disturbance rejection. In this section, we will discuss these two topics in relation to the complementary sensitivity 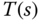 and the sensitivity function
and the sensitivity function 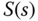 . Their effects on the output will be measured and analyzed in the frequency domain. One caution is that closed-loop stability is a pre-requisite for the sensitivity analysis to be valid.
. Their effects on the output will be measured and analyzed in the frequency domain. One caution is that closed-loop stability is a pre-requisite for the sensitivity analysis to be valid.
2.5.1 Closed-loop Bandwidth
For simplicity, we assume that 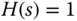 to begin the discussion. From (2.27), the complementary sensitivity
to begin the discussion. From (2.27), the complementary sensitivity  represents the effect of reference following on the output and the sensitivity
represents the effect of reference following on the output and the sensitivity 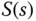 represents the effect of disturbance rejection. Intuitively, for a control system designed with good reference following properties, we would like to see the complementary sensitivity
represents the effect of disturbance rejection. Intuitively, for a control system designed with good reference following properties, we would like to see the complementary sensitivity 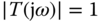 so that the output
so that the output 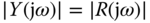 for some designated frequencies, where
for some designated frequencies, where 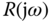 is the frequency response of the reference signal. On the contrary, for disturbance rejection, intuitively, we would like the magnitude of the sensitivity function
is the frequency response of the reference signal. On the contrary, for disturbance rejection, intuitively, we would like the magnitude of the sensitivity function  so that the output
so that the output  for some frequencies contained in the output disturbance signal
for some frequencies contained in the output disturbance signal  or the input disturbance signal
or the input disturbance signal 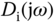 . As from (2.24), the sum of
. As from (2.24), the sum of  and
and 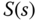 is equal to one. Two observations follow immediately.
is equal to one. Two observations follow immediately.
- If at a given frequency
 , then
, then 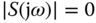 .
. - Similarly, if
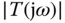 is large, then
is large, then  is small.
is small.
This basically says that the control objectives for reference tracking or disturbance rejection using feedback can be achieved using the same qualitative and quantitative measure of either complementary sensitivity function  or sensitivity function
or sensitivity function 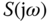 because
because  . The implication is that if a feedback control system has a good tracking performance for a reference signal, then it will also have a good disturbance rejection for the disturbance signals that have the identical frequency characteristics. In other words, the reference following and disturbance rejection in feedback control share the same goals in the design without conflicting.
. The implication is that if a feedback control system has a good tracking performance for a reference signal, then it will also have a good disturbance rejection for the disturbance signals that have the identical frequency characteristics. In other words, the reference following and disturbance rejection in feedback control share the same goals in the design without conflicting.
We can also examine the reference tracking from feedback error analysis to reach the same conclusions as above. Consider a unit negative feedback control system with the reference pre-compensation 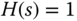 . The feedback error signal
. The feedback error signal 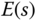 is simply computed as
is simply computed as

It is seen here that, for the reference tracking, the feedback error is directly related to the sensitivity function 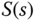 . Therefore, if
. Therefore, if 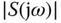 is small over some frequency band, then the feedback control system will yield, on the same frequency band, better reference tracking as well as disturbance rejection performance. This re-iterates that the control system design objectives for reference following and disturbance rejection share the same characteristics over either the complementary sensitivity or the sensitivity function.
is small over some frequency band, then the feedback control system will yield, on the same frequency band, better reference tracking as well as disturbance rejection performance. This re-iterates that the control system design objectives for reference following and disturbance rejection share the same characteristics over either the complementary sensitivity or the sensitivity function.
One of the qualitative measures in sensitivity analysis is the characterization of closed-loop bandwidth 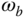 . The parameter bandwidth
. The parameter bandwidth  is a frequency parameter either in the unit of Hertz (Hz) or
is a frequency parameter either in the unit of Hertz (Hz) or 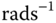 , which corresponds to the frequency when the complementary sensitivity function has the following value:
, which corresponds to the frequency when the complementary sensitivity function has the following value:

As illustrated in Figure 2.11, the magnitude of a complementary sensitivity function 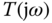 is intersected with a dash-dotted horizontal line with a value of
is intersected with a dash-dotted horizontal line with a value of 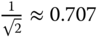 , where the vertical dash-dotted line leads to the bandwidth of
, where the vertical dash-dotted line leads to the bandwidth of 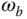 . As demonstrated in Section 2.3, one can easily use the MATLAB ginput.m function to identify the bandwidth from the plot of the complementary sensitivity function by putting the hair cross line at the point when the dash-dotted line intersects the magnitude of complementary sensitivity. For reference following, the bandwidth
. As demonstrated in Section 2.3, one can easily use the MATLAB ginput.m function to identify the bandwidth from the plot of the complementary sensitivity function by putting the hair cross line at the point when the dash-dotted line intersects the magnitude of complementary sensitivity. For reference following, the bandwidth 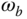 is interpreted as if the frequencies of the reference signal fall between 0 and
is interpreted as if the frequencies of the reference signal fall between 0 and  , then the output signal will have the capacity to closely duplicate this reference signal. For disturbance rejection, because
, then the output signal will have the capacity to closely duplicate this reference signal. For disturbance rejection, because 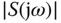 is small between 0 and
is small between 0 and 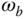 , if the frequencies of a disturbance signal fall into this range, then the output will have the capacity to suppress the disturbance.
, if the frequencies of a disturbance signal fall into this range, then the output will have the capacity to suppress the disturbance.
Having said that minimization of the effect of disturbance will certainly lead to maximizing tracking performance of the same type of reference signals, in engineering applications there might be additional constraints on the reference tracking such as output overshoot of the reference signal. The two degrees of freedom control system implementation provides an additional means in an open-loop manner to shape the reference tracking properties by selecting the stable reference filter 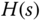 .
.
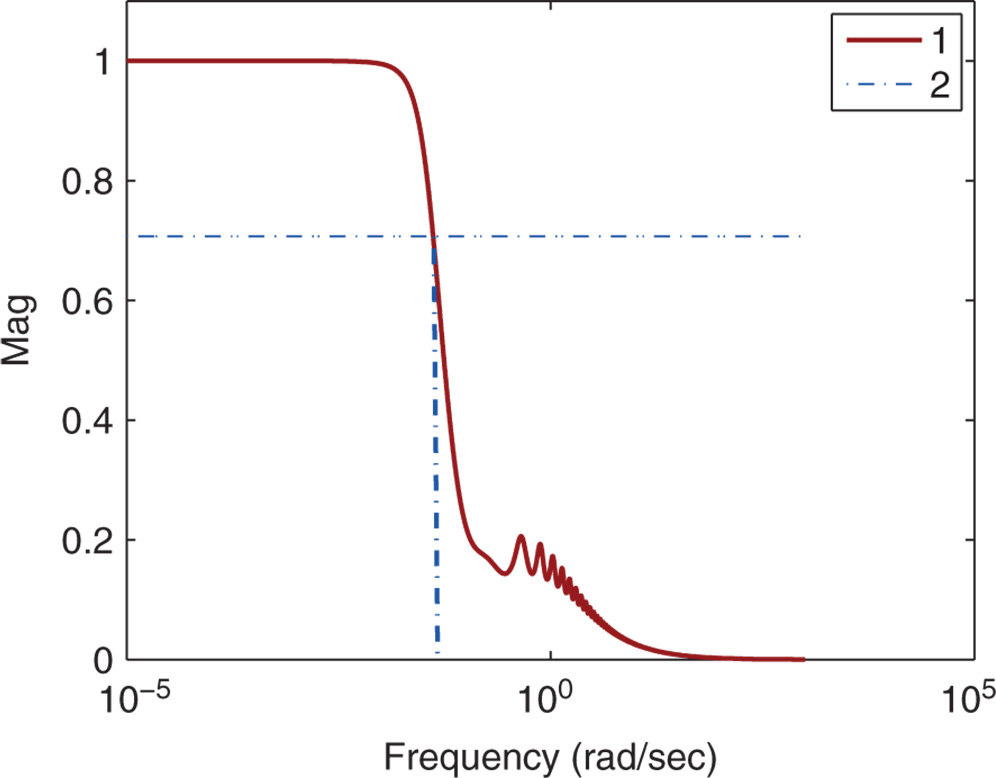
Figure 2.11 Complementary sensitivity function with bandwidth illustration. Key: solid line: 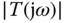 ; dash-dotted lines: illustration of bandwidth.
; dash-dotted lines: illustration of bandwidth.
One exception to the shared common ground of disturbance rejection and reference following is the scenario when there is pole-zero cancellation in the controller structure. Pole-zero cancellation is a commonly used technique for control system design because it simplifies the controller parameter solutions. Assuming that the controller transfer function is  and the model transfer function is
and the model transfer function is 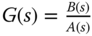 from Figure 2.9, with
from Figure 2.9, with 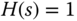 , the output response to the reference signal is
, the output response to the reference signal is

and to the input disturbance is
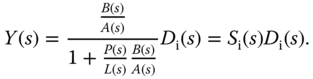
Note that in the complementary sensitivity function 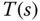 ,
,  and
and 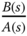 appear in pairs. Therefore, the poles or zeros that have been canceled in the design will disappear from the complementary sensitivity function, meaning that they will not affect the closed-loop performance of reference tracking. However, in the input disturbance sensitivity function
appear in pairs. Therefore, the poles or zeros that have been canceled in the design will disappear from the complementary sensitivity function, meaning that they will not affect the closed-loop performance of reference tracking. However, in the input disturbance sensitivity function 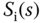 ,
, 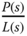 and
and 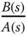 appear in pairs only for the denominator. Thus, if a pole from the system transfer function
appear in pairs only for the denominator. Thus, if a pole from the system transfer function  is canceled in the controller design, it will re-appear as the same pole in the input disturbance sensitivity function because
is canceled in the controller design, it will re-appear as the same pole in the input disturbance sensitivity function because 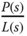 does not appear in the numerator. This means that if a system pole is canceled in the controller structure, a fast reference following response does not automatically imply a fast input disturbance rejection, depending on the location of the canceled pole. A detailed study of pole-zero cancellation on the effect of disturbance rejection is given in Example 3.7.
does not appear in the numerator. This means that if a system pole is canceled in the controller structure, a fast reference following response does not automatically imply a fast input disturbance rejection, depending on the location of the canceled pole. A detailed study of pole-zero cancellation on the effect of disturbance rejection is given in Example 3.7.
2.5.2 Reference Following and Disturbance Rejection with PID Controllers
PID controllers are the most widely used controllers in engineering applications. Their successful applications are aligned with the most commonly encountered reference signals and disturbance signals. The reference signals for PID controller applications are a step signal or a series of step signals. For instance, if we want to regulate a room temperature to 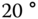 C from the current temperature of
C from the current temperature of 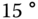 C, then the reference signal is a step signal with amplitude of
C, then the reference signal is a step signal with amplitude of 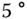 C. In other words, the output of a PID control system is regulated to a constant value. Note that the Laplace transform of a unit step signal is
C. In other words, the output of a PID control system is regulated to a constant value. Note that the Laplace transform of a unit step signal is 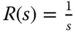 with the magnitude of frequency response
with the magnitude of frequency response 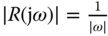 , which is infinity at
, which is infinity at  . Hence, for the output to follow a step reference signal perfectly, the complementary sensitivity function
. Hence, for the output to follow a step reference signal perfectly, the complementary sensitivity function 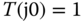 at the zero frequency. This automatically implies that the sensitivity function
at the zero frequency. This automatically implies that the sensitivity function 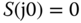 , which is required for tracking the step reference signal and rejecting a disturbance with its frequency contents concentrated at the zero frequency.
, which is required for tracking the step reference signal and rejecting a disturbance with its frequency contents concentrated at the zero frequency.
Now, on a back envelope calculation, if the plant model does not contain a zero at 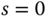 , the integrator contained in a PID controller will simultaneously yield
, the integrator contained in a PID controller will simultaneously yield  and
and  because the integrator in the controller creates an infinite gain for the loop transfer function
because the integrator in the controller creates an infinite gain for the loop transfer function 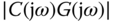 at
at  . The sensitivity function
. The sensitivity function 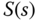 contains a zero at
contains a zero at 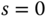 as long as the plant model
as long as the plant model 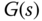 does not contain a zero at
does not contain a zero at  .
.
Because the majority of the control systems are designed to track a constant reference signal or regulate the output to a constant value, additionally, the most disturbances occurred in the process control applications are rich in the low frequency region, the PID controllers are adequate for the commonly encountered applications.
2.5.3 Reference Following and Disturbance Rejection with Resonant Controllers
In the applications of control systems to power electronics, aerospace, and mechanical engineering, it is often required for the output of the closed-loop control system to track sinusoidal reference signal or to reject a sinusoidal disturbance. In these applications, we assume that the sinusoidal reference signal is  with known parameters. However, for disturbance rejection, the disturbance signal is expressed as
with known parameters. However, for disturbance rejection, the disturbance signal is expressed as 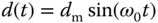 , where the frequency
, where the frequency 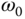 is known but the amplitude of the disturbance
is known but the amplitude of the disturbance 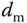 is unknown.
is unknown.
Note that the Laplace transform of the reference sinusoidal signal with frequency 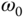 is
is
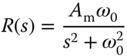
with frequency response
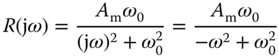
Thus, as 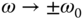 ,
, 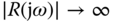 .
.
From the sensitivity analysis, in order for the feedback control system to have a good tracking performance for the sinusoidal reference signal, we need the complementary sensitivity function 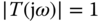 at
at 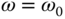 . Similarly, to reject the sinusoidal disturbance signal with unknown amplitude, we need to have the sensitivity function
. Similarly, to reject the sinusoidal disturbance signal with unknown amplitude, we need to have the sensitivity function  at
at 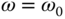 . In order to achieve these characteristics for the feedback control system, a quick calculation indicates that the feedback controller is required to embed the mode
. In order to achieve these characteristics for the feedback control system, a quick calculation indicates that the feedback controller is required to embed the mode 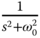 into its structure, assuming that the plant does not contain a pair of complex zeros at
into its structure, assuming that the plant does not contain a pair of complex zeros at 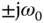 . In the literature, this type of controller is called either resonant controller or repetitive controller because of the periodic nature of the external signals.
. In the literature, this type of controller is called either resonant controller or repetitive controller because of the periodic nature of the external signals.
We consider the case that  is a multi-frequency periodic signal, defined as
is a multi-frequency periodic signal, defined as 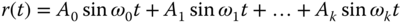 where the frequencies
where the frequencies 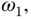

 , and
, and  are given. In order to track this multi-frequency periodic signal using a feedback controller, the complementary sensitivity function is required to satisfy
are given. In order to track this multi-frequency periodic signal using a feedback controller, the complementary sensitivity function is required to satisfy 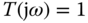 at the frequencies
at the frequencies 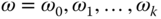 . As a result, the sensitivity function automatically satisfies
. As a result, the sensitivity function automatically satisfies 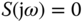 at the frequencies
at the frequencies 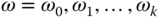 . Therefore, the controller designed for following the multi-frequency periodic reference signal will also reject a periodic disturbance with the same frequencies. The controller is required to embed the following components
. Therefore, the controller designed for following the multi-frequency periodic reference signal will also reject a periodic disturbance with the same frequencies. The controller is required to embed the following components
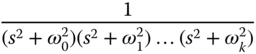
into its structure in order to achieve  or
or 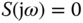 at the frequencies
at the frequencies 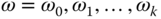 . Here we need to assume that the plant does not have complex zeros at the corresponding frequencies.
. Here we need to assume that the plant does not have complex zeros at the corresponding frequencies.
In Section 3.5, pole-assignment controller design techniques will be introduced for the design of resonant controller. In Section 5.4, a resonant controller will be designed using a disturbance estimation technique together with anti-windup implementation. This disturbance estimation based design technique is extended to a multi-frequency sinusoidal reference/disturbance signal in Section 5.5.
2.5.4 Food for Thought
- If the disturbance rejection is too slow, taking a long time for the output response to recover, would you decrease the closed-loop bandwidth?
- For a PID controlled system with
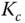 ,
, 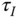 and
and 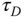 , if the bandwidth
, if the bandwidth 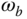 were too small, would you increase
were too small, would you increase 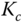 ?
? - For the IMC-PID tuning rules (see Section 1.4.1), the original tuning-rules (Equation (1.47)) will lead to a slow response to input disturbance. Can you explain this using the characteristics of the input sensitivity function?
- Why is the two-degrees-of-freedom PID controller implementation important in the context of reference following and disturbance rejection?
- In many applications, rejecting load disturbance is the primary objective of the control systems. Load disturbance is often modelled as a constant input disturbance. To avoid a large disruption to the system when switching on a load is paramount. How can we design such a load profile so that it can be switched gradually?
2.6 Disturbance Rejection and Noise Attenuation
Both noise and disturbance co-exist in a physical system. A good closed-loop performance requires minimization of the effects of both disturbance and noise.
2.6.1 Conflict between Disturbance Rejection and Noise Attenuation
For minimization of the effects of both input and output disturbances, we make the magnitude of the output in frequency response

as small as possible. For minimization of the measurement noise, we make the magnitude of the output in frequency response

as small as possible, indicating that there is a conflict between disturbance rejection and noise attenuation.
We cannot alter the disturbances and noise because they already existed in the system. Thus, what we do is to make:
- the magnitude of sensitivity
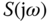 (
(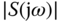 ) small for disturbance rejection;
) small for disturbance rejection; - the magnitude of complementary sensitivity
 (
( ) small for noise attenuation.
) small for noise attenuation.
These are the basic design principles for control systems. However, noting that the relationship between the sensitivity and complementary sensitivity is constrained by

which says that we cannot make both 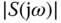 and
and 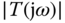 small over the same frequency bands. In other words, if the disturbance is minimized in a given frequency region where
small over the same frequency bands. In other words, if the disturbance is minimized in a given frequency region where  is small, then inevitably the measurement noise is not attenuated in the same frequency region where
is small, then inevitably the measurement noise is not attenuated in the same frequency region where 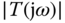 is large. So how are we going to design a closed-loop control system that will minimize the effects of disturbance and the measurement noise?
is large. So how are we going to design a closed-loop control system that will minimize the effects of disturbance and the measurement noise?
Note that the disturbances existing in the system correspond to slow movement of the variables or slow changes, therefore the frequency contents of the disturbance term 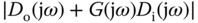 are concentrated in the low frequency region. In contrast, the measurement noise corresponds to fast movement of the variables or fast and frequent changes of the variables, therefore the frequency contents of the measurement noise
are concentrated in the low frequency region. In contrast, the measurement noise corresponds to fast movement of the variables or fast and frequent changes of the variables, therefore the frequency contents of the measurement noise  are concentrated in the higher frequency region. This means that we can achieve disturbance rejection by choosing the sensitivity function
are concentrated in the higher frequency region. This means that we can achieve disturbance rejection by choosing the sensitivity function 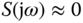 at the low frequency region, which implies
at the low frequency region, which implies 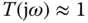 at the low frequency region, because
at the low frequency region, because  . This is not too bad for noise attenuation because
. This is not too bad for noise attenuation because 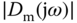 is small in the low frequency region. At the high frequency region, to avoid the amplification of measurement noise, we choose
is small in the low frequency region. At the high frequency region, to avoid the amplification of measurement noise, we choose 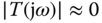 , which implies
, which implies  . This is not too bad for disturbance rejection because
. This is not too bad for disturbance rejection because 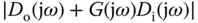 is small in the high frequency region. In short, to achieve a trade-off relationship between disturbance rejection and noise attenuation, a closed-loop bandwidth
is small in the high frequency region. In short, to achieve a trade-off relationship between disturbance rejection and noise attenuation, a closed-loop bandwidth 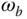 should be carefully selected.
should be carefully selected.
2.6.2 PID Controller for Disturbance Rejection and Noise Attenuation
Two examples are given in this section to illustrate the relationship between disturbance rejection and noise attenuation when using a PID controller.
A derivative filter plays an important role in noise attenuation for a PID controlled system because the derivative action will amplify the measurement noise. The following example is used to show its significance in the presence of measurement noise in conjunction with the choice of sampling interval in the implementation.
2.6.3 Food for Thought
- Would you increase the bandwidth of the closed-loop control system if a low quality sensor is used in the measurement device and the measurement noise is severe?
- When using a resonant controller, if the frequency
 embedded into the controller is large, would you expect that the measurement noise will be amplified more than that with a PID controller?
embedded into the controller is large, would you expect that the measurement noise will be amplified more than that with a PID controller? - In the implementation of PID controller, if the measurement noise is severe, would you decrease the derivative filter time constant?
- Would you prefer to use a PI controller instead of a PID controller if the noise is severe?
2.7 Robust Stability and Robust Performance
Robust stability and robust performance are two important issues for a control engineer to consider when a feedback control system is designed and to be implemented. The phrase “robust control” is used to imply that the control system designed can withstand the uncertainties caused by the discrepancies between the model used for the controller design and the actual plant model.
2.7.1 Modeling Errors
Many of us, as a control engineers, have experienced a feedback control system designed using the correct methodologies and the closed-loop simulation has yielded satisfactory performance; however, the control system failed to produce stable closed-loop operation when it was implemented. More than often, the key reason behind the discrepancy between what is desired and what is reality is the existence of modeling errors between the model used for the control system design and the behavior of the actual system at specific operation conditions.
There are a few factors causing the existence of modeling errors in control system design depending on how the mathematical model is derived. In electrical engineering applications, such as electrical machine control and power converter control, the mathematical models are derived from physical laws using current and voltage (see Wang et al. (2015)). Similarly physical laws are used to derive the mathematical models for electro-mechanical systems such as unmanned aerial vehicles (see Chapter 10), and ball and plate balancing systems (see Chapter 6). The mathematical models derived using physical laws are referred mechanistical models, which are often in the form of nonlinear differential equations (see Chapter 6). The modeling errors for the electrical systems and the electro-mechanical systems are often caused by an inaccurate measurement of the physical parameters and the variations of the operating conditions.
In chemical process control applications, due to the lack of clearly defined physical laws or the complexities of the physical systems, the mathematical models are commonly obtained by directly conducting identification experiments on the plant and estimating a transfer function model based on the input and output measurement data (see the fired heater system (Ralhan and Badgwell (2000)) in Section 1.5.2). The mathematical models derived using the identification experiments (see Chapter 9) are referred empirical models. The modeling errors for the chemical process control applications are often caused by restricted identification experimental conditions including small input signal amplitude, corruptions of large measurement noise and disturbances, model estimation errors, as well as variations of operating conditions.
Furthermore, when using a restricted controller structure such as a PID controller, the mathematical models could be too complex for the design of a simple controller. Thus, model order reduction is required, which leads to another source of modeling errors. In the context of control system design, there is an unknown transfer function denoted by 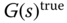 , which accurately describes the linear time invariant system at a given operating condition. However, for the various reasons discussed above, this
, which accurately describes the linear time invariant system at a given operating condition. However, for the various reasons discussed above, this 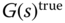 is seldom available to us. Instead, a transfer function model
is seldom available to us. Instead, a transfer function model  is obtained from linearization (see Chapter 6) or from identification experiments and used in the control system design. This leads to the conceptual description of modeling errors that consist of the following forms in the literature:
is obtained from linearization (see Chapter 6) or from identification experiments and used in the control system design. This leads to the conceptual description of modeling errors that consist of the following forms in the literature:
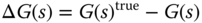

where 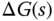 is called the additive modeling error and
is called the additive modeling error and 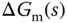 is called the multiplicative modeling error. We assume that the modeling errors are stable.
is called the multiplicative modeling error. We assume that the modeling errors are stable.
Except that in the case of model order reduction for PID controller design, 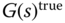 is assumed unknown, thus the exact descriptions of
is assumed unknown, thus the exact descriptions of 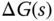 and
and 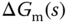 may not be available. However, in robust control, it is often that the bounds on the frequency responses are used to quantify the impact of the modeling errors, for
may not be available. However, in robust control, it is often that the bounds on the frequency responses are used to quantify the impact of the modeling errors, for 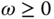 ,
,
In a simplified case, the modeling error bound may be chosen as a constant, which produces a conservative measure for the modeling errors.
2.7.2 Robust Stability
Robust stability for a control system is quantified and analyzed in the frequency domain in terms of the additive and multiplicative modeling errors defined, with its origin from the Nyquist stability criterion introduced in Section 2.3. The purpose is to assess closed-loop stability when the controller 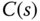 is applied to the unknown system
is applied to the unknown system  .
.
To start, we consider that the open-loop system 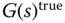 is stable and assume the following conditions are satisfied.
is stable and assume the following conditions are satisfied.
- The controller
 is designed to stabilize the model
is designed to stabilize the model 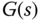 with all closed-loop poles strictly on the left half of the complex plane.
with all closed-loop poles strictly on the left half of the complex plane. - The modeling errors, either additive or multiplicative, are stable.
Then, from the Nyquist stability criterion, the necessary and sufficient condition for closed-loop stability when the controller 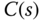 is applied to the unknown system
is applied to the unknown system 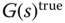 is that the frequency response of the loop transfer function
is that the frequency response of the loop transfer function  will not encircle the
will not encircle the  point on the complex plane. This is translated into the following inequality:
point on the complex plane. This is translated into the following inequality:
for all 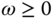 . Because
. Because 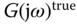 is unknown, in Equation 2.41 it is replaced by the model
is unknown, in Equation 2.41 it is replaced by the model  and the additive modeling error
and the additive modeling error 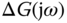 , leading to
, leading to

which is

Now, since the controller 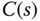 is designed to stabilize the model
is designed to stabilize the model 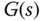 , the Nyquist loci of
, the Nyquist loci of 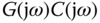 will not encircle the
will not encircle the  point, it ensures that
point, it ensures that
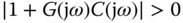
for all 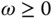 .
.
Therefore, the inequality (2.41) is satisfied if
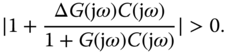
Or, more conservatively, for all 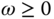 ,
,
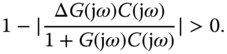
This leads to the robust stability condition in the frequency domain as
for all 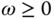 . This robust stability condition is a sufficient condition, which ensures the Nyquist loci of the
. This robust stability condition is a sufficient condition, which ensures the Nyquist loci of the 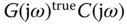 not to encircle the
not to encircle the 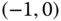 point through the representation of additive modeling error.
point through the representation of additive modeling error.
The robust stability condition (2.44) can also be written in terms of the multiplicative modeling error 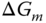 by noting that
by noting that
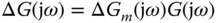
leading to

With the multiplicative modeling error, the robust stability condition is expressed in relation to the complementary sensitivity function  .
.
With the frequency response bound defined as  in (2.39), the robust stability condition becomes:
in (2.39), the robust stability condition becomes:
for all 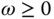 . Alternatively, with the multiplicative modeling error bound
. Alternatively, with the multiplicative modeling error bound 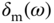 defined in (2.40), it has the following representation:
defined in (2.40), it has the following representation:
for all 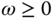 .
.
The first robust stability condition (2.46) is expressed in terms of the control sensitivity function whilst the second stability condition (2.47) is expressed in terms of the complementary sensitivity function, which is directly related to the closed-loop control performance specifications.
The robust stability condition (2.47) says that if the multiplicative modeling error 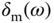 is larger than 1 at a given frequency
is larger than 1 at a given frequency  , then
, then  needs to be less than 1 to ensure closed-loop stability. Conversely, if
needs to be less than 1 to ensure closed-loop stability. Conversely, if  is large at a certain frequency region, then a small modeling error is required in the same region to ensure closed-loop stability. Clearly, if the controller contains an integrator, then
is large at a certain frequency region, then a small modeling error is required in the same region to ensure closed-loop stability. Clearly, if the controller contains an integrator, then 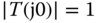 , which indicates that
, which indicates that 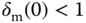 in order to guarantee closed-loop stability. Similarly, for the resonant controller that has embedded a sinusoidal mode at
in order to guarantee closed-loop stability. Similarly, for the resonant controller that has embedded a sinusoidal mode at  ,
, 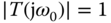 , leading to the condition that
, leading to the condition that  in order to guarantee robust closed-loop stability.
in order to guarantee robust closed-loop stability.
In summary, the existence of modeling error gives an additional constraint on the complementary sensitivity function. This constraint is translated into the selection of the desired closed-loop bandwidth as demonstrated in the following case study.
2.7.3 Case Study: Robust Control of Polymer Reactor
Note that many of the empirical tuning rules for PID controllers do not have a performance tuning parameter to adjust the desired closed-loop performance in order to account for the modeling errors. This is the biggest limitation for the empirical PID controller tuning rules. For the IMC-PID controller, the desired closed-loop bandwidth is selected by adjusting the desired closed-loop time constant  .
.
2.7.4 Food for Thought
- If we neglected a time delay
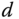 in the design, what would be the multiplicative modelling error?
in the design, what would be the multiplicative modelling error? - If the Padula and Visioli PID controller tuning rules produced an unstable closed-loop system, would you try to reduce the proportional control gain
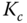 or increase the integral time constant
or increase the integral time constant 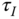 ?
? - Is it correct to say that the modelling error limits the closed-loop bandwidth?
- Is it correct to say that in general we need a model with higher accuracy for a higher demand in the closed-loop performance for disturbance rejection and reference following?
2.8 Summary
In this chapter, we have presented the commonly used tools for closed-loop stability and performance analysis. Understanding the relationships between the closed-loop poles, closed-loop stability, and performance is crucial in control system design and analysis. In the later chapters, we will discuss model based controller design methods that specifically use the locations of the desired closed-loop poles as performance specification. The important aspects discussed in this chapter are:
- If the closed-loop transfer function is known with constant coefficients, then the closed-loop poles can be simply determined by finding the solutions of the characteristic equation. Numerically, this is achieved using MATLAB function root.m for the denominator of the transfer function.
- The Routh-Hurwitz stability criterion explicitly determines whether a closed-loop system is stable by examining the coefficients of the closed-loop characteristic polynomial. This is particularly useful when we need to determine the effect of the variation of a parameter on the closed-loop system.
- Nyquist stability criterion is based on the frequency response of the open-loop transfer function that includes the system, the controller, the actuator and the sensor. It involves the presentation of the frequency response graphically with real and imaginary parts (a two dimensional plot), revealing the important quantities such as gain margin, phase margin and delay margin. Because it is based on the frequency domain, time delay in the system can be easily captured.
- Sensitivity analysis based on the frequency domain is fundamental to the understanding of the characteristics of closed-loop control systems. In the context of sensitivity analysis, the parameter called closed-loop bandwidth is defined.
- Understanding the closed-loop performance in terms of disturbance rejection and reference following is based on the frequency response of the sensitivity function and complementary sensitivity function. Because the relationship between the complementary sensitivity function and sensitivity function is captured by:
the performance requirements are consistent in the sense that a closed-loop system that has a fast reference following will also have a fast disturbance rejection.

- Understanding the closed-loop performance in terms of disturbance rejection (or reference following) and measurement noise attenuation is also based on the frequency response of the sensitivity function and complementary sensitivity function. However, the relationship
captures the fundamental trade-off between disturbance rejection and measurement noise attenuation. There is a conflict between the two requirements, meaning that a fast disturbance rejection in a closed-loop control system will inevitably lead to the amplification of measurement noise. The existence of measurement noise limits the closed-loop control performance in terms of disturbance rejection and reference following.
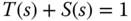
- Modelling errors are often present in the PID control system design. Because of their existence, there is a difference in the closed-loop performance between what is desired and what is actually achieved. Their effects on the closed-loop performance are analyzed and quantified in the frequency domain using the errors and the complementary sensitivity function. Furthermore, the Nyquist stability criterion provides an effective means to access the information about gain margin, phase margin and delay margin, which are important to assess the impact of modelling errors on closed-loop stability.
2.9 Further Reading
- Text books in control engineering include, Franklin et al. (1998), Franklin et al. (1991), Ogata (2002), Golnaraghi and Kuo (2010), Goodwin et al. (2000) and Astrom and Murray (2008).
- Disturbance rejection, reference following and robustness are discussed in Garpinger et al. (2014), in Alcántara et al. (2013). Two-degrees-of-freedom PID controller design is proposed in Gorez (2003) and Yukitomo et al. (2004), Araki and Taguchi (2003). Load disturbance rejection with consideration on robustness of closed-loop system is proposed in Panagopoulos et al. (2002). Effect of noise for tuning the controller parameters is discussed in Fertik (1975).
- The Ziegler-Nichols step response method is revisited from the point of view of robust loop shaping in Åström and Hägglund (2004).
- Tuning of PID controllers based on gain and phase margin specifications was proposed in Ho et al. (1995), Ho and Xu (1998), Ho et al. (2000). The Ziegler-Nichols, and Cohen-Coon tuning formulas that optimize for load disturbance response are analyzed in Ho et al. (1996) for gain margin and phase margin. Gain and phase margins are used in selecting PID controller parameters with consideration of robustness and closed-loop performance in Ho et al. (1998).
- Disturbance rejection for the modified IMC tuning rules is specifically addressed in Skogestad (2006). Robustness of IMC is discussed in Morari and Zafiriou (1989). Further discussions of tuning guidelines and robustness for IMC can be found in Vilanova (2008).
Problems
- 2.1 In Example 2.3, three PI controllers (see Table 2.3) were found using tuning-rules together with analysis of Nyquist diagram for the following continuous-time system:
(2.51)
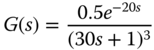
- Evaluate the closed-loop step response of the three PI control systems in one-degree-of-freedom using a Simulink simulation.
- Evaluate the closed-loop step response of the PI control systems in two-degrees-of-freedom where the reference filter is selected as
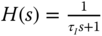 , and compare the output responses with the simulation results presented in Figure 2.7.
, and compare the output responses with the simulation results presented in Figure 2.7.
- 2.2 In Example 1.8, Padula and Visioli tuning rules were used to find PID controller for the following system
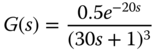
where
 ,
, 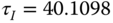 ,
, 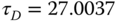 .
.- Find the closed-loop transfer function between
 and
and  with the control signal
with the control signal 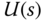 defined as
defined as

Simulate the closed-loop unit step response for this one-degree-of-freedom control system with sampling interval
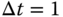 (sec).
(sec). - Find the closed-loop transfer function between
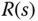 and
and 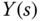 with the control signal
with the control signal 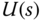 defined as
defined as
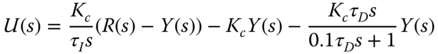
Simulate the closed-loop step response for this IPD control system and compare the results with the ones from the one-degree-of-freedom controller structure.
- Observing from the closed-loop transfer functions, what reference filter should be chosen if the remainder of the overshoot from the IPD implementation were to be eliminated? Verify the results using the selected reference filter.
- Find the closed-loop transfer function between
- 2.3 Use Routh-Hurwitz stability criterion to determine the range of the proportional controller
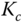 that will stabilize the systems with the following transfer functions.
that will stabilize the systems with the following transfer functions.
- 2.4 Use Routh-Hurwitz criterion to determine the range of the integral time constant
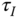 that will produce a stable closed-loop system for the plant with transfer function
that will produce a stable closed-loop system for the plant with transfer function 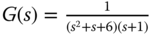 . Here we assume that the proportional gain
. Here we assume that the proportional gain  .
. - 2.5 Consider a system with the following transfer function:

- Assuming that the integral time constant
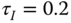 , form the closed-loop characteristic equation in terms of the proportional control
, form the closed-loop characteristic equation in terms of the proportional control 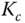 , and numerically determine the variations of closed-loop poles with respect to
, and numerically determine the variations of closed-loop poles with respect to  (
(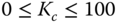 ). This numerical procedure leads to root-locus analysis of the PI control system with respect to the variations of
). This numerical procedure leads to root-locus analysis of the PI control system with respect to the variations of 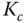 .
. - Alternatively, we can use MATLAB function ‘rlocus.m’ for the root-locus analysis with the loop transfer function:
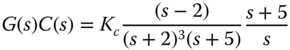
- From the root-locus analysis, determine the range of the proportional gain
 that will produce a stable closed-loop system.
that will produce a stable closed-loop system. - What are your observations on the closed-loop pole variations with respect to the proportional gain
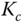 from the root-locus analysis?
from the root-locus analysis?
- Assuming that the integral time constant
- 2.6 This Problem is an extension to Example 2.7. Because the reactor's transfer function model has 8 stable zeros, it is difficult to design a PID controller using the PID tuning rules without desired closed-loop performance adjustment.
- Use Padula and Visioli PID controller tuning rules based on the first order plus delay model shown in (2.49) to find two sets of PID controller parameters for
 and
and 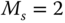 (see Table 1.5).
(see Table 1.5). - Plot the Nyquist diagrams for both PID controlled systems using the original reactor model (2.48) and verify if the closed-loop systems are stable.
- Based on the Nyquist diagrams, propose what we would do to improve the gain margin and phase margin for the two PID controlled systems, and modify the PID controller parameters accordingly.
- Simulate the closed-loop step response for both systems based on the original reactor model (2.48) using the modified PID controllers.
- Use Padula and Visioli PID controller tuning rules based on the first order plus delay model shown in (2.49) to find two sets of PID controller parameters for
- 2.7 One of the simple and yet effective approaches to model order reduction is to neglect the small time constant
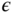 in the transfer function model:
in the transfer function model:
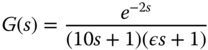
in order to obtain a first order plus delay model.
- Determine the multiplicative modelling error
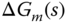 when the approximate model is taken as
when the approximate model is taken as 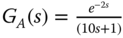 .
. - Calculate
 for
for  and compare their magnitudes in a diagram. What are your observations?
and compare their magnitudes in a diagram. What are your observations? - Use Padula and Visioli PID controller tuning rules (
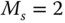 ) based on the first order plus delay model to find two sets of PID controller parameters.
) based on the first order plus delay model to find two sets of PID controller parameters. - Calculate the complementary sensitivity function
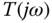 for the PID controller.
for the PID controller. - Determine the closed-loop robust stability using the relationship
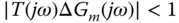
for all
 . Is the closed-loop system stable for
. Is the closed-loop system stable for 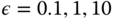 ?
? - Compare the closed-loop step responses, which are simulated based on the original second order plus delay model for
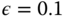 and
and 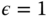 with sampling interval
with sampling interval 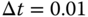 and derivative filter time constant equal to
and derivative filter time constant equal to 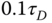 . What are your observations?
. What are your observations?
- Determine the multiplicative modelling error
- 2.8 The original IMC-PI tuning rules are given for a first order plus delay system:
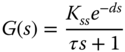
where
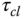 is the desired closed-loop time constant and(2.52)
is the desired closed-loop time constant and(2.52)
- Find the complementary sensitivity function
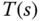 , the input disturbance sensitivity function
, the input disturbance sensitivity function  for the IMC-PI controlled system. What are your observations in terms of the poles of the sensitivity functions?
for the IMC-PI controlled system. What are your observations in terms of the poles of the sensitivity functions? - For a system with
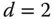 ,
, 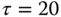 ,
, 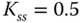 , calculate
, calculate 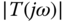 and
and 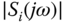 for
for  . Will
. Will 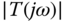 change with respect to
change with respect to  ? If so, what are the bandwidth parameters? Will
? If so, what are the bandwidth parameters? Will  change with respect to
change with respect to 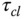 ?
? - Simulate the closed-loop step response for the two PI controlled systems with sampling interval
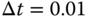 . Does
. Does 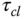 affect the closed-loop step response speed?
affect the closed-loop step response speed? - Simulate the closed-loop input disturbance response for the two PI controlled systems, where the disturbance is a constant with magnitude of 3. Does
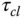 affect the closed-loop disturbance rejection?
affect the closed-loop disturbance rejection? - What if the disturbance occurred at the output, would
 make a difference on the disturbance rejection? Verify your intuition with the closed-loop simulation of output disturbance.
make a difference on the disturbance rejection? Verify your intuition with the closed-loop simulation of output disturbance.
- Find the complementary sensitivity function