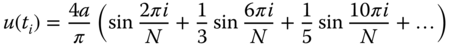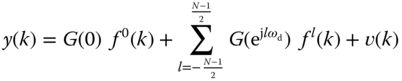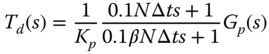9
Automatic Tuning of PID Controllers
9.1 Introduction
Relay feedback control has been one of the key instruments used in the automatic tuning of PID controllers. Its application is associated with the identification of process frequency response information via the self-generated excitation signals in a closed-loop operation. Because it is in a closed-loop operation, the feedback control effect maintains the system around its operating condition while conducting the experiment.
This chapter will discuss the automatic tuning of PID controllers where the process frequency response information is obtained from relay feedback experiments and the PID controllers are designed using the design methods introduced in Chapter 8.
9.2 Relay Feedback Control
This section will discuss relay feedback control systems in combination with hysteresis or with an integrator. Simulink tutorials are presented for both cases, which is convenient for simulation studies and experimental validations.
9.2.1 Relay Control with Hysteresis
In applications, because of measurement noise, a hysteresis element is incorporated within the relay feedback control mechanism to avoid possible random switches due to the effect of noise. Figure 9.1 illustrates a block diagram of relay feedback control.
For the purpose of relay feedback control, there are a few parameters that need to be defined.
- A plant steady-state operating condition with input signal
 and output signal
and output signal  is chosen based on which relay control experiment will be carried out. For some applications, the steady-state input and output signals are zero.
is chosen based on which relay control experiment will be carried out. For some applications, the steady-state input and output signals are zero. - The amplitude of the relay control signal is chosen as parameter
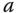 , which represents the variations of the input signal at the steady-state operating condition.
, which represents the variations of the input signal at the steady-state operating condition. - The hysteresis parameter is chosen to be
 , which is used to prevent the triggering of relay switching from random noise. If the standard deviation of the measurement noise is
, which is used to prevent the triggering of relay switching from random noise. If the standard deviation of the measurement noise is  , then approximately the hysteresis parameter
, then approximately the hysteresis parameter  is chosen to be
is chosen to be  .
.
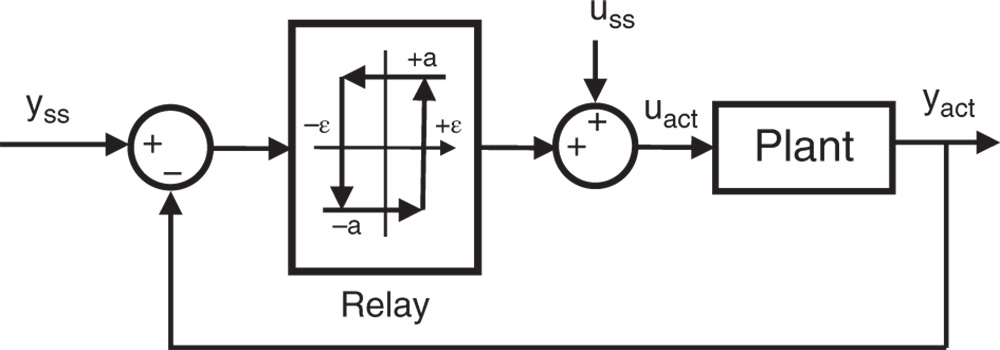
Figure 9.1 Block diagram of relay feedback control.
We define the deviation variable of the control signal as
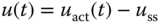
and the initial condition of the deviation control signal as  . We assume that the system is already operating at the steady state. With the actual measurement of the output
. We assume that the system is already operating at the steady state. With the actual measurement of the output  at the sampling time
at the sampling time 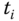 , the closed-loop control signal
, the closed-loop control signal  is calculated using the following relay switching rules:
is calculated using the following relay switching rules:
and

where 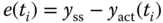 is the feedback error at the sampling time
is the feedback error at the sampling time  .
.
It is worthwhile emphasizing that the relay switching rule given in (9.1) is for the systems that have a positive steady-state gain. For the systems having a negative steady-state gain, the deviation variable  is calculated as
is calculated as


Clearly, the relay feedback control is a nonlinear control law with a small amount of a priori information required and it is very easy to implement.
It is known (Astrom and Hagglund (1984), Astrom and Hagglund (1988)) that this relay controlled system will generate a sustained periodic oscillation that contains the fundamental frequency 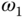 at the point of the Nyquist curve of the process, which approximately has the imaginary part as
at the point of the Nyquist curve of the process, which approximately has the imaginary part as 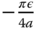 , as shown in Figure 9.2. One immediately pays attention to the location of the frequency
, as shown in Figure 9.2. One immediately pays attention to the location of the frequency  on the Nyquist curve. If the hysteresis value
on the Nyquist curve. If the hysteresis value  is chosen to be zero, then the frequency
is chosen to be zero, then the frequency 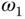 becomes the cross-over frequency on the Nyquist curve if a proportional controller is used. This was indeed the key link between the classical Ziegler–Nichols tuning rules and the first generation of auto-tuners (Astrom and Hagglund (1984), Astrom and Hagglund (1988)). The second point is that if the hysteresis
becomes the cross-over frequency on the Nyquist curve if a proportional controller is used. This was indeed the key link between the classical Ziegler–Nichols tuning rules and the first generation of auto-tuners (Astrom and Hagglund (1984), Astrom and Hagglund (1988)). The second point is that if the hysteresis  is increased, while maintaining the same amplitude
is increased, while maintaining the same amplitude  , the frequency
, the frequency 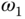 is reduced, meaning that the oscillation period
is reduced, meaning that the oscillation period  is increased.
is increased.
Under relay feedback control, there are several classes of systems that will have a sustained periodic oscillation. In general, these systems should be stable to ensure safety of the operation during experiments. They include the first order plus delay systems, systems with higher order dynamics, systems with non-minimum phase behavior and higher order under-damped systems. The common feature of these systems is that their Nyquist curve will expand to the second and third quadratures on the complex plane, as shown in Figure 9.2. For a first order system, relay feedback control will not generate sustained periodic oscillation unless there are additional dynamics from actuation and measurement involved leading to a higher order system as a result.
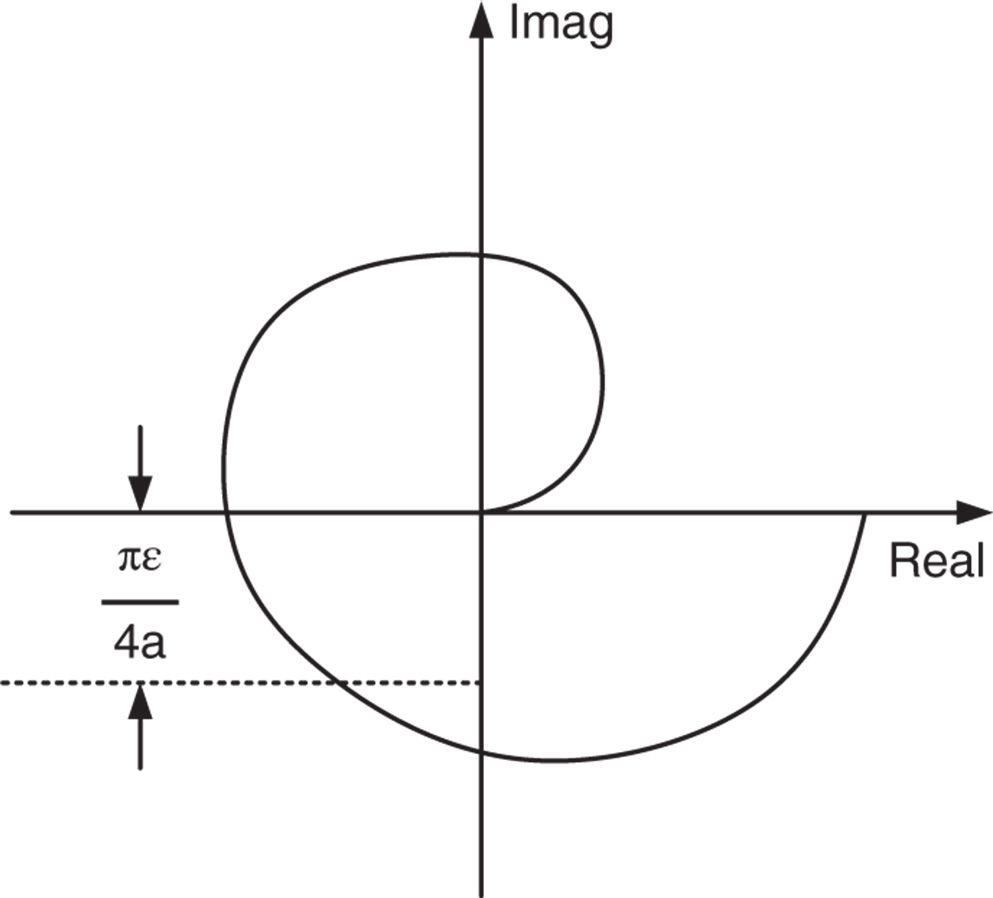
Figure 9.2 Location of  on a Nyquist curve.
on a Nyquist curve.
The following tutorial is written to produce a MATLAB function that can be used for Simulink simulations and for real-time implementations.
9.2.2 Relay Control with Integrator
Assuming that the plant is stable with all poles on the left half of the complex plane, the relay feedback controller incorporates an integrator in the closed-loop system, as illustrated in Figure 9.5. It is known (Astrom and Hagglund (1984), Astrom and Hagglund (1988)) that this relay controlled system will generate a sustained periodic oscillation that contains the fundamental frequency  at the point where the Nyquist curve of the process intersects the imaginary axis as shown in Figure 9.6.
at the point where the Nyquist curve of the process intersects the imaginary axis as shown in Figure 9.6.
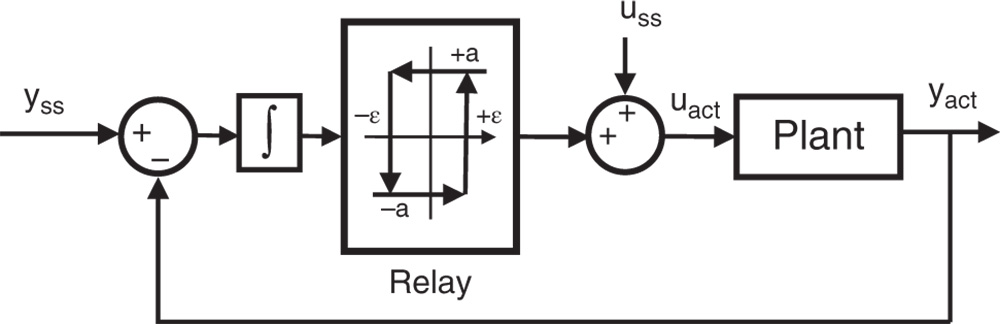
Figure 9.5 Block diagram of integrated relay feedback control.
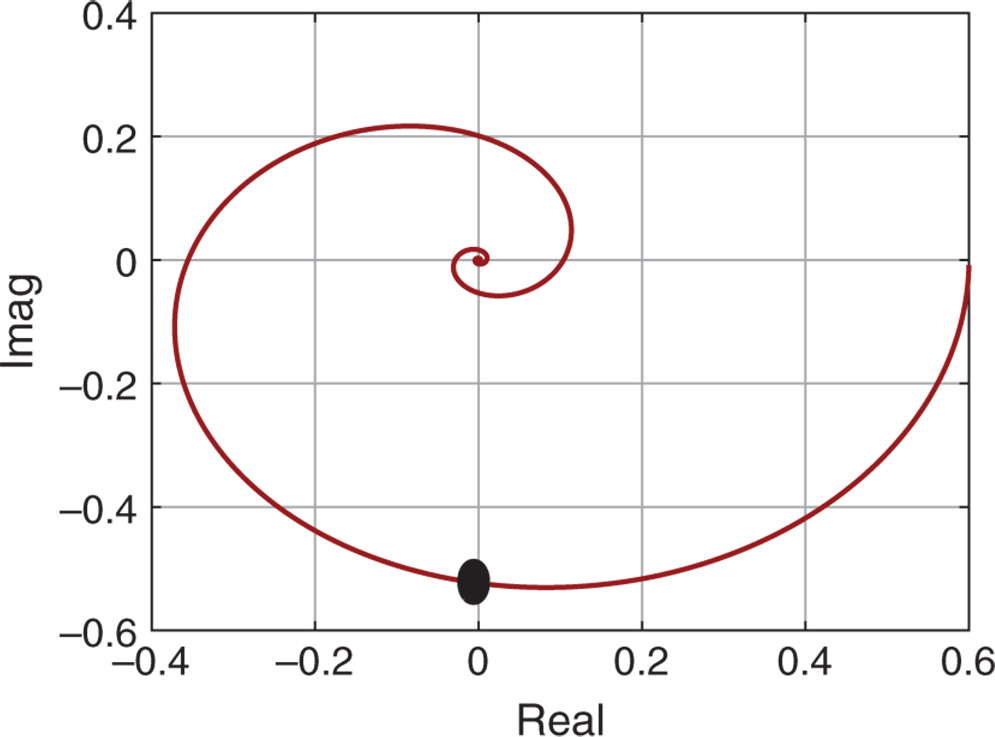
Figure 9.6 Location of  on a Nyquist curve when using an integrator with relay.
on a Nyquist curve when using an integrator with relay.
With the integrator incorporated in the relay feedback control, the frequency  is smaller than the case without the integrator, meaning that the oscillation period
is smaller than the case without the integrator, meaning that the oscillation period 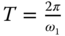 is larger. The main purpose of choosing this configuration instead of the basic relay feedback control is to ensure that the plant information obtained is contained at the lower and medium frequency range, as illustrated in Figure 9.6. Additionally, because of the integrator, the effect of high frequency measurement noise is minimized, and the need to use a hysteresis for the noise is reduced. It will be shown in Section 9.6 that the proposed configuration is essential in providing the key information of steady-state gain and dominant time constant in the auto-tuner design.
is larger. The main purpose of choosing this configuration instead of the basic relay feedback control is to ensure that the plant information obtained is contained at the lower and medium frequency range, as illustrated in Figure 9.6. Additionally, because of the integrator, the effect of high frequency measurement noise is minimized, and the need to use a hysteresis for the noise is reduced. It will be shown in Section 9.6 that the proposed configuration is essential in providing the key information of steady-state gain and dominant time constant in the auto-tuner design.
The relay feedback control with integrator is easy to implement. We assume that the system is operating at the steady state with given values of  and
and  . The integral error
. The integral error  is defined as
is defined as

With the first order approximation of the derivative  , we obtain at the sampling time
, we obtain at the sampling time 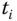 ,
,
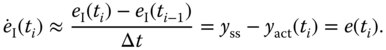
Thus, the integral error is calculated recursively with

The control law for the relay with integrator is summarized as follows. Here, we assume that the steady-state gain of the system is positive.



The following Tutorial is to present a Simulink function for the relay with integrator control law. It is very similar to Tutorial 9.1. With these real time functions, one can convert them into C-code for the real time implementation of the relay feedback control systems.
9.2.3 Food for Thought
- How do you determine the noise level in the system in order to choose the hysteresis level
 ?
? - If the noise is severe and you are not sure about the noise level, would you try to use the relay with integrator approach?
- If the system is first order, relay feedback control will not generate sustained oscillation. Would you consider to incorporate a delay element to the relay feedback control in order to generate a sustained oscillation? How will you define the input and output data in this situation?
- Instead of using an integrator, will you be able to use a stable transfer function to achieve the same effect? In comparison, what is the key advantage of using an integrator?
- Is it possible to use relay feedback control to stabilize an unstable system?
9.3 Estimation of Frequency Response using the Fast Fourier Transform (FFT)
It is well known that under a stable relay feedback control, both control input and process output signals are periodic in nature (Astrom and Hagglund (1984), Astrom and Hagglund (1988), Astrom and Hagglund (1995), Astrom and Hagglund (2006), Hagglund and Astrom (1985)). If a single relay experiment is conducted, a standard Fourier analysis (Kreyszig (2006)) shows that the periodic signals contain the frequencies in multiples of the fundamental frequency  as
as  ,
,  ,
,  ,
,  ,
,  , where
, where  is an odd number. Because of this, many approaches have been proposed to extract meaningful process information from the set of relay feedback control data, including the describing function analysis (Atherton (1975), Astrom and Hagglund (1984)) and fast Fourier analysis (Wang et al. (2001)).
is an odd number. Because of this, many approaches have been proposed to extract meaningful process information from the set of relay feedback control data, including the describing function analysis (Atherton (1975), Astrom and Hagglund (1984)) and fast Fourier analysis (Wang et al. (2001)).
9.3.1 FFT Estimation
For a period  , the Fourier series expansion of the periodic input signal
, the Fourier series expansion of the periodic input signal  , is expressed as (see Kreyszig (2006)),
, is expressed as (see Kreyszig (2006)),
Here, we emphasize that the continuous time fundamental frequency is 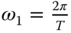 . From (9.9), it is seen that the construction of the periodic signal
. From (9.9), it is seen that the construction of the periodic signal  using the sinusoidal components is predominantly dependent on the first few terms because their contributions decay as the frequency increases.
using the sinusoidal components is predominantly dependent on the first few terms because their contributions decay as the frequency increases.
By choosing sampling interval  , the discretized input signal
, the discretized input signal  at sampling instant
at sampling instant  becomes
becomes
where  is the number of samples within one period. The expression of the discrete time signal
is the number of samples within one period. The expression of the discrete time signal  reveals the discrete time fundamental frequency as
reveals the discrete time fundamental frequency as  when we compare (9.10) with (9.9). Therefore, the relationship between the continuous time and discrete time frequencies exists as,
when we compare (9.10) with (9.9). Therefore, the relationship between the continuous time and discrete time frequencies exists as,

The simplest way to estimate the frequency response of the system under relay feedback is to use the FFT. Assuming that the data length is  , the Fourier transform of an input signal
, the Fourier transform of an input signal  ,
, 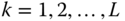 , is
, is
and the corresponding Fourier transform of the output is
where  . With the computation of the Fourier transformation of both input and output signals, the estimation of the frequency response of the plant
. With the computation of the Fourier transformation of both input and output signals, the estimation of the frequency response of the plant 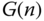 is simply (Ljung (1999))
is simply (Ljung (1999))
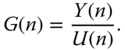
From both (9.12) and (9.13), with the definition of the Fourier transform, it is seen that the corresponding discrete frequency is defined from 0 to  with an incremental of
with an incremental of  , where
, where  is the data length.
is the data length.
The remaining tasks are to find which index  corresponds to the fundamental frequency
corresponds to the fundamental frequency  in discrete time, followed by converting the discrete time frequency to the continuous time frequency
in discrete time, followed by converting the discrete time frequency to the continuous time frequency  .
.
An intuitive way to find the fundamental frequency  is to find the averaged number of samples of the input signal
is to find the averaged number of samples of the input signal  within one period [see Figures 9.7(b)–(c)]. However, this could potentially lead to an inaccurate result because of the possible random switches in the input signal due to the measurement noise [see Figure 9.7(d)].
within one period [see Figures 9.7(b)–(c)]. However, this could potentially lead to an inaccurate result because of the possible random switches in the input signal due to the measurement noise [see Figure 9.7(d)].
Since the input signal exhibits the feature of a periodic signal, the amplitude of the discrete time Fourier transform of the input signal will yield a maximum value at the fundamental frequency 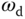 . Thus, we will use the maximum value of the amplitude of the Fourier transform as the signature to identify the discrete time fundamental frequency
. Thus, we will use the maximum value of the amplitude of the Fourier transform as the signature to identify the discrete time fundamental frequency  while taking into account of the incremental frequency
while taking into account of the incremental frequency  in a general Fourier transformation.
in a general Fourier transformation.
9.3.2 MATLAB Tutorial using the FFT for Estimation
The following MATLAB tutorial shows how to estimate  ,
, 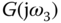 ,
,  and
and  through Fourier analysis.
through Fourier analysis.
9.3.3 Monte-Carlo Simulation Studies
In the Monte-Carlo simulation, the measurement noise is generated with a random initial seed that changes with each simulation to reflect the randomness of the noise and its effect on the estimation results. It means that the measurement noise sequence is unique for each simulation and different from others. Consequently, the estimated parameters for each simulation are unique due to the noise. From the total number of simulations, the mean and variance of the estimated parameters are assessed. This assessment can be performed graphically by plotting the estimated parameters for each run against the original parameters or by calculating the mean and variance of the parameters from the total number of simulations. We choose to use a graphic display of the Monte-Carlo simulation results.
Two examples are presented in this section to show the estimation of frequency response of the system using the FFT with relay feedback control data in a noisy environment. The first case is to investigate the estimation when a relay is used with hysteresis to control the system and the second case is to show the estimation when a relay with an integrator is used to control the system.
The system under study has the transfer function
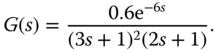
The noise used in the simulation is band limited noise with sampling interval 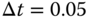 (s) and power strength 1 together with a gain 0.1. The simulation time is 800 s. The initial seed used to generate the noise sequence varies from 0 to 68 to form the Monte-Carlo simulation studies. In total, we will conduct 69 simulation studies for the estimation.
(s) and power strength 1 together with a gain 0.1. The simulation time is 800 s. The initial seed used to generate the noise sequence varies from 0 to 68 to form the Monte-Carlo simulation studies. In total, we will conduct 69 simulation studies for the estimation.
9.3.4 Food for Thought
- Is it correct to say that the periodicity of the input and output signals with relay feedback control plays the key role at obtaining accurate estimated frequency response parameters?
- Will you still get estimated frequency parameters if the estimated period
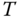 is wrong?
is wrong? - Why do we use the peak amplitude of the Fourier transform of input signal to identify the period of the oscillation?
- Why can not we reliably estimate the steady-state gain of the system from the periodic input and output data generated by the relay control?
- If the input and output data are not zero mean, will you be able to correctly obtain the frequency response estimation using the Fourier analysis?
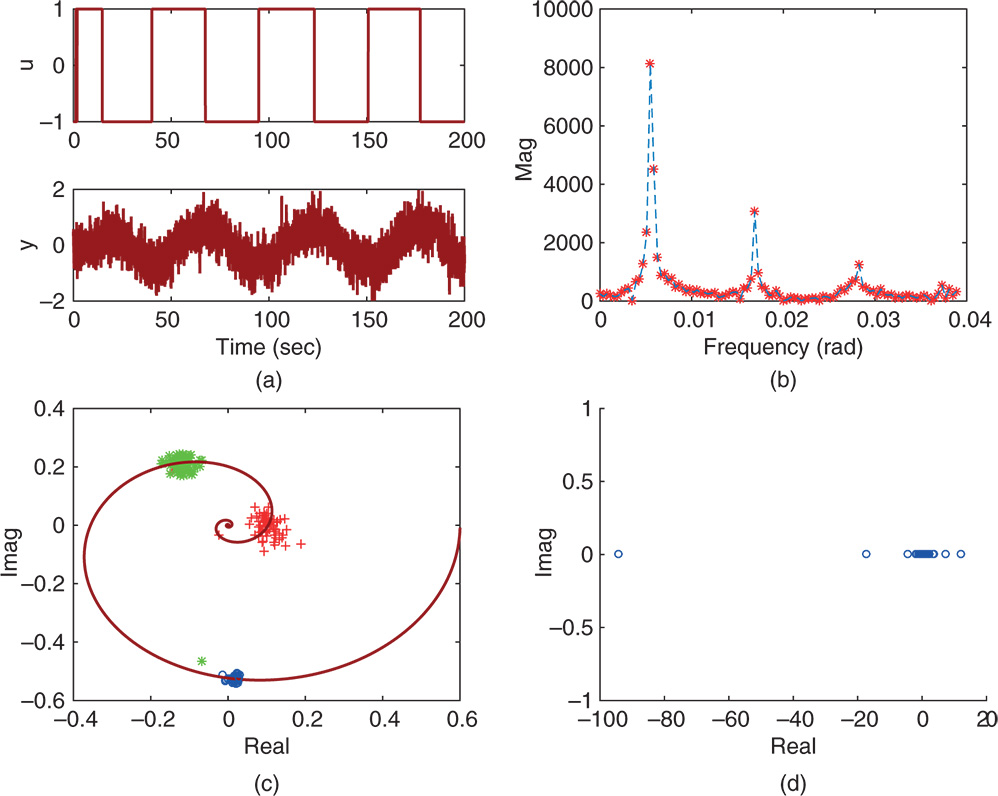
Figure 9.9 Frequency response estimation using FFT (Example 9.4). (a) Input and output data using seed  . (b) Fourier transform of the input data. (c) Estimated frequency responses (
. (b) Fourier transform of the input data. (c) Estimated frequency responses (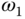 ,
,  ,
,  ). (d) Estimated steady-state gain.
). (d) Estimated steady-state gain.
9.4 Estimation of Frequency Response Using the frequency sampling filter (FSF)
This section introduces a model based approach for the estimation of process frequency response based on the input and output data collected from relay feedback control. The model is called the FSF model (Bitmead and Anderson (1981),Wang and Cluett (2000)). The advantages of using such a model based approach in comparison with the FFT analysis include that the computation can be performed recursively in real time and the estimated frequency responses have better accuracy because of the model optimization.
9.4.1 Frequency Sampling Filter Model
Assuming that a relay experiment is performed, a set of input and output signals  and
and  is obtained. Because the input and output signals are periodic signals, the period in number of samples, denoted by
is obtained. Because the input and output signals are periodic signals, the period in number of samples, denoted by  , is calculated and the fundamental discrete frequency is denoted by
, is calculated and the fundamental discrete frequency is denoted by  , where
, where  . Also, the backward shift operator
. Also, the backward shift operator  is defined as
is defined as  where
where  is a discrete time signal.
is a discrete time signal.
Then, associated with the plant frequency response,  and
and  , where
, where  , the output
, the output 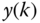 is expressed using the frequency sampling filter model in the relationship to the input signal
is expressed using the frequency sampling filter model in the relationship to the input signal  as (Bitmead and Anderson (1981),Wang and Cluett (2000)),
as (Bitmead and Anderson (1981),Wang and Cluett (2000)),
where 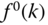 is the FSF output for the zero frequency, defined as
is the FSF output for the zero frequency, defined as
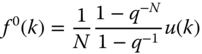
and  is the
is the  th FSF filter output defined as
th FSF filter output defined as

and  is the output measurement noise assumed to be Gaussian distributed with zero mean and variance
is the output measurement noise assumed to be Gaussian distributed with zero mean and variance  . If the input signal
. If the input signal  is a perfect period signal with period
is a perfect period signal with period  , then, from Fourier analysis (Kreyszig (2006)), it only contains the odd number of frequencies and the magnitude decays as the number increases (see (9.10)). As a result, the outputs from the frequency sampling filters with even numbers are zero in response to the relay feedback control signal
, then, from Fourier analysis (Kreyszig (2006)), it only contains the odd number of frequencies and the magnitude decays as the number increases (see (9.10)). As a result, the outputs from the frequency sampling filters with even numbers are zero in response to the relay feedback control signal  , and they could be removed from the sum in (9.15). Figure 9.10 shows a block diagram of the frequency sampling filter model with a reduced number of filters. In practice, because of nonlinearities and other imperfect conditions, the relay control signals may not be perfectly periodic signals. The outputs of the zero frequency sampling filter and the even number of frequency filters may have signals with small magnitudes. To avoid bias errors in estimation, the expression of the output signal will take into consideration the effect of the near zero terms, which yields,
, and they could be removed from the sum in (9.15). Figure 9.10 shows a block diagram of the frequency sampling filter model with a reduced number of filters. In practice, because of nonlinearities and other imperfect conditions, the relay control signals may not be perfectly periodic signals. The outputs of the zero frequency sampling filter and the even number of frequency filters may have signals with small magnitudes. To avoid bias errors in estimation, the expression of the output signal will take into consideration the effect of the near zero terms, which yields,
The model in (9.16) with seven complex parameters proves to be adequate for the majority of the applications even in the situation when the relay control does not produce perfect periodic signals.

Figure 9.10 Block diagram of the frequency sampling filter model with reduced order.
With the description of the output signal in terms of the frequency parameters, the next step is to estimate these parameters using the relay feedback control data. Define the complex parameter vector to be estimated as

and its corresponding regressor vector as
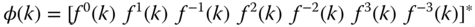
where  denotes the complex conjugate transpose of
denotes the complex conjugate transpose of  .
.
Assuming that the number of data samples is  , then the least squares estimation of
, then the least squares estimation of  has the following analytical solution (Soderstrom and Stoica (1989), Ljung (1999), Soderstrom (2018), Young (2012), Goodwin and Sin (1984)):
has the following analytical solution (Soderstrom and Stoica (1989), Ljung (1999), Soderstrom (2018), Young (2012), Goodwin and Sin (1984)):
For real-time computation, we can use a recursive least squares algorithm to compute the frequency parameter vector  at sampling instant
at sampling instant  (see Goodwin and Sin (1984),Young (2012),Ljung (1999)). Here, a standard recursive least squares algorithm is written in the following steps, where the initial conditions of
(see Goodwin and Sin (1984),Young (2012),Ljung (1999)). Here, a standard recursive least squares algorithm is written in the following steps, where the initial conditions of  and
and 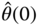 are selected by the user or they can also be calculated using the relay testing data based on the least squares algorithm (Wang and Cluett (2000)). The following computation steps are repeated in real time, beginning with the sampling instant
are selected by the user or they can also be calculated using the relay testing data based on the least squares algorithm (Wang and Cluett (2000)). The following computation steps are repeated in real time, beginning with the sampling instant  .
.
- Calculate the estimated parameter vector
 (9.18)
(9.18)
- Update the covariance matrix
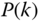 using
(9.19)where
using
(9.19)where
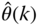 contains the estimated frequency response parameters at the sampling instant
contains the estimated frequency response parameters at the sampling instant 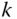 .
. - Go back to step one as the next sampling period arrives.
There are two comments given below.
- It is worthwhile emphasizing that the estimated zero frequency and even frequency parameters are not reliable due to the near zero magnitudes of their filter outputs due to the periodicity of the input signal. This is illustrated by the Monte-Carlo simulation in the examples.
- It is important to note that in an ideal situation, the parameter
 can be determined from the averaged period of the relay control signal. However, this calculation is no longer correct when the relay feedback control does not produce perfectly periodic oscillations. An effective way to calculate
can be determined from the averaged period of the relay control signal. However, this calculation is no longer correct when the relay feedback control does not produce perfectly periodic oscillations. An effective way to calculate  is to find the first maximum magnitude of the Fourier transformation of the input signal and the corresponding frequency
is to find the first maximum magnitude of the Fourier transformation of the input signal and the corresponding frequency  from which
from which 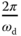 is rounded to the nearest integer to yield the parameter
is rounded to the nearest integer to yield the parameter  .
.
9.4.2 MATLAB Tutorial on Estimation Using the FSF Model
9.4.3 Monte-Carlo Simulation using the FSF Estimation
In this section, we will illustrate the estimation of frequency response using the frequency sampling filter model based on a relay with integrator control. The same Monte-Carlo simulation studies as in Example 9.4 will be used to generate the input and output data under relay feedback control.
In general, the frequency sampling filter model based estimation leads to an improved estimation compared with FFT based approaches when using the relay feedback control data because it is a model based approach that uses the principle of optimization in the parameter solutions. Additionally, the FSF model based approach can be implemented using a recursive method, as shown in Tutorial 9.4, which is suitable for real time computation on a micro-controller. If necessary, a noise model can be incorporated in the estimation (Wang and Cluett (2000)). The main advantage of using the FFT for the estimation is its simplicity of implementation, as shown in Tutorial 9.3.
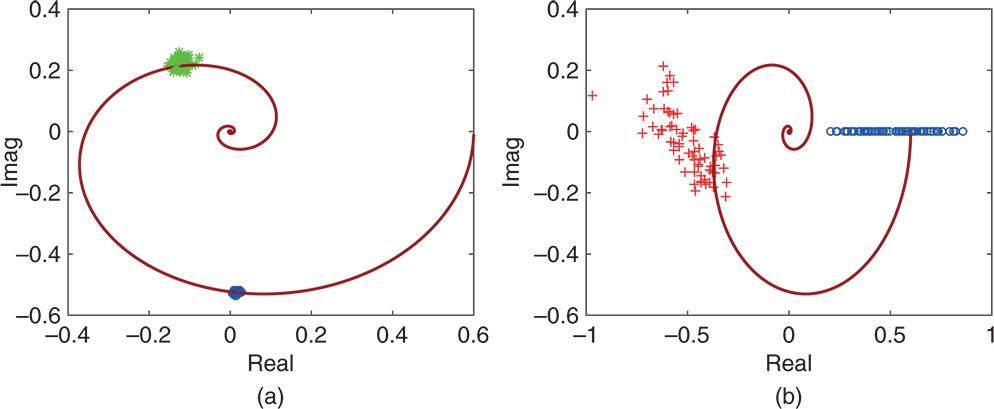
Figure 9.11 Frequency response estimation using FSF (Example 9.5).
9.4.4 Food for Thought
- In the frequency estimation when using the FSF model and the relay feedback control data, we need to estimate the period in number of samples,
 . Why do you think that we identify the parameter
. Why do you think that we identify the parameter  using the maximum peak value of the FFT of the input signal? Can you propose an alternative approach to identify the parameter
using the maximum peak value of the FFT of the input signal? Can you propose an alternative approach to identify the parameter  ?
? - What would happen to the frequency response estimation using FSF if the estimated parameter
 is wrong? Even so, would you still be able to get some estimation results?
is wrong? Even so, would you still be able to get some estimation results? - Where are the poles of the frequency sampling filters? Can you express the frequency sampling filter model in terms of real coefficients instead of the complex coefficients?
- Do you think that the estimated results from the recursive least squares estimation are identical to those obtained from the least squares estimation (see 9.17) with appropriately selected initial conditions?
- What are the advantages when using the recursive least squares estimation?
9.5 Monte-Carlo Simulation Studies
In this section, we will further evaluate the estimation of the plant frequency response using the frequency sampling filter model in comparison with the estimation using Fourier analysis, where Monte-Carlo simulation studies are used.
The transfer function used in the Monte-Carlo simulation is
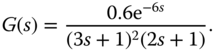
The relay amplitude is selected to be 1 and the sampling interval 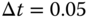 (s). The relay testing time is selected to be 800 (s). The noise used in the simulation is band limited noise with sampling interval
(s). The relay testing time is selected to be 800 (s). The noise used in the simulation is band limited noise with sampling interval 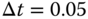 (s) and power strength 1 together with a gain 0.02. In the Monte-Carlo simulation, the measurement noise is generated with a random seed that changes with each simulation to reflect the randomness of noise and its effect on the estimation results. The seeds used in the simulations are 0, 2,
(s) and power strength 1 together with a gain 0.02. In the Monte-Carlo simulation, the measurement noise is generated with a random seed that changes with each simulation to reflect the randomness of noise and its effect on the estimation results. The seeds used in the simulations are 0, 2, ,60. Thus, there are 31 random seeds used in the Monte-Carlo simulation to generate the measurement noise. There is a small hysteresis in the proposed relay feedback control because the integral action acting as a low-pass filter has reduced the possible random switches caused by the noise.
,60. Thus, there are 31 random seeds used in the Monte-Carlo simulation to generate the measurement noise. There is a small hysteresis in the proposed relay feedback control because the integral action acting as a low-pass filter has reduced the possible random switches caused by the noise.
9.5.1 Effect of Unknown Constant Disturbance
In many applications, during the relay experiments, there is an unknown constant disturbance. This type of disturbance often enters the system at the input variable, which is called the input disturbance. A typical example is the electrical load in an AC motor (Wang et al. (2015)). This type of disturbances will cause periodic oscillations in the relay feedback control to become unbalanced.
A constant input disturbance with magnitude of 0.3 is added to the relay feedback control experiments. Figure 9.12(a) shows the closed-loop relay feedback control responses in the presence of measurement noise and the input disturbance. From this figure it is seen that with the disturbance the oscillations are no longer in symmetry. Fourier analysis reveals [see Figure 9.12(b)] that the input signal has the fundamental frequency  (rad), where
(rad), where 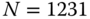 and the next significant frequency in the periodic signal is
and the next significant frequency in the periodic signal is  followed by
followed by 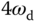 . By choosing the nine frequency parameters (
. By choosing the nine frequency parameters ( ) and
) and  in the frequency sampling filter model, we obtain the estimated frequency parameters as shown in Figure 9.12(c). It is seen that the estimated parameters are unbiased with small variances, as shown through the Monte-Carlo simulations. In comparison, Figure 9.12(d) shows the estimated parameters using Fourier analysis, which are seen to have larger variances. The estimation results for frequency parameters at 0 and
in the frequency sampling filter model, we obtain the estimated frequency parameters as shown in Figure 9.12(c). It is seen that the estimated parameters are unbiased with small variances, as shown through the Monte-Carlo simulations. In comparison, Figure 9.12(d) shows the estimated parameters using Fourier analysis, which are seen to have larger variances. The estimation results for frequency parameters at 0 and  are not consistent when the oscillations are not symmetric caused by the constant disturbance.
are not consistent when the oscillations are not symmetric caused by the constant disturbance.
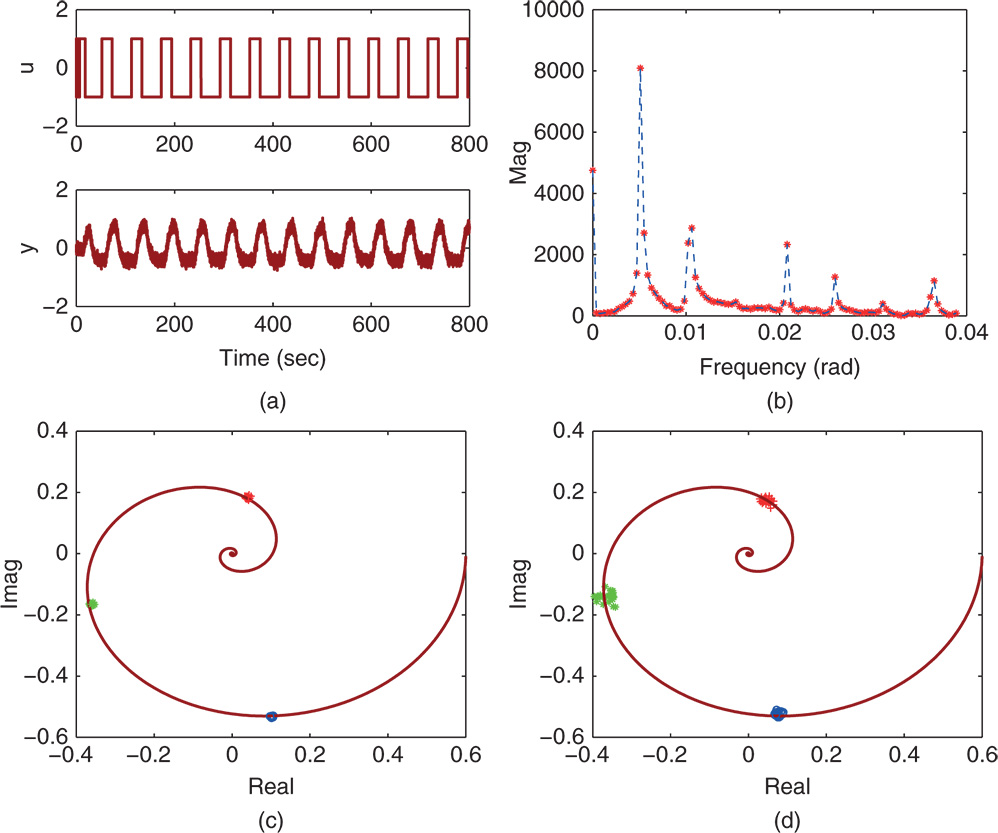
Figure 9.12 Monte-Carlo simulation results with  random seeds in the presence of constant load disturbance. (a) Input and output signal. (b) Magnitude of DFT. (c) FSF estimation. (d) FFT estimation. Key:
random seeds in the presence of constant load disturbance. (a) Input and output signal. (b) Magnitude of DFT. (c) FSF estimation. (d) FFT estimation. Key:  (solid line), o is the estimated values at
(solid line), o is the estimated values at  ,
,  is the estimated values at
is the estimated values at  ,
,  is the estimated values at
is the estimated values at  .
.
9.5.2 Effect of Unknown Low Frequency Disturbance
In the application of process control, low frequency disturbances are frequently encountered. This group of studies will investigate what would happen to the relay feedback control and to the frequency response estimation in the presence of unknown low frequency disturbance.
In the Monte-Carlo simulation studies, the low frequency disturbance, entering into the system via the input signal, is generated by passing the same band limited measurement noise through a first order filter with transfer function:

which is then sampled using the same sampling interval  (s). Note that the disturbance model has a time constant of 20 (s), which is much larger than the time constants of the system. Figure 9.13(a) shows the input and output data generated by the relay feedback control system. From this figure, it is interesting to see that the relay feedback control system no longer generates periodic oscillations in the presence of low frequency disturbances. This is confirmed through the Fourier analysis [see Figure 9.13(b)], from which only one spike in the magnitude of the Fourier transformation is observed. It is important to note that the relay feedback control system produces the oscillations that have the largest amplitude at
(s). Note that the disturbance model has a time constant of 20 (s), which is much larger than the time constants of the system. Figure 9.13(a) shows the input and output data generated by the relay feedback control system. From this figure, it is interesting to see that the relay feedback control system no longer generates periodic oscillations in the presence of low frequency disturbances. This is confirmed through the Fourier analysis [see Figure 9.13(b)], from which only one spike in the magnitude of the Fourier transformation is observed. It is important to note that the relay feedback control system produces the oscillations that have the largest amplitude at  , where
, where 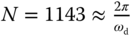 . Figures 9.13(c) and (d) compare the estimation results obtained using the frequency sampling filter model and the Fourier analysis of the input and output data. It is seen from Figure 9.13(c) that the variances of the estimated parameters using the frequency sampling filter model are relatively small; however, there are small biases in the estimated parameters. In contrast, because the input signal is not periodic, the frequency response estimation using Fourier analysis produces poor results except the estimated parameters at
. Figures 9.13(c) and (d) compare the estimation results obtained using the frequency sampling filter model and the Fourier analysis of the input and output data. It is seen from Figure 9.13(c) that the variances of the estimated parameters using the frequency sampling filter model are relatively small; however, there are small biases in the estimated parameters. In contrast, because the input signal is not periodic, the frequency response estimation using Fourier analysis produces poor results except the estimated parameters at  , as shown in Monte-Carlo simulation studies, which is evident by the scatters on the complex plane [see Figure 9.13(d)].
, as shown in Monte-Carlo simulation studies, which is evident by the scatters on the complex plane [see Figure 9.13(d)].

Figure 9.13 Monte-Carlo simulation results with 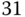 random seeds in the presence of unknown low frequency disturbance. (a) Input and output signal. (b) Magnitude of DFT. (c) FSF estimation. (d) FFT estimation. Key:
random seeds in the presence of unknown low frequency disturbance. (a) Input and output signal. (b) Magnitude of DFT. (c) FSF estimation. (d) FFT estimation. Key: 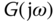 (solid line), o is the estimated values at
(solid line), o is the estimated values at 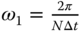 ,
,  is the estimated values at
is the estimated values at  ,
,  is the estimated values at
is the estimated values at 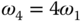 .
.
9.5.3 Estimation of the Steady-state Value
The final question to be answered in the Monte-Carlo simulation studies is whether the steady-state estimation will be valid using the frequency sampling filter model. Figure 9.14 shows that the estimation of steady-state information is not reliable when using relay feedback control. Depending on the particular seed of the noise generator, all the estimated steady-state gains vary significantly from the true value (0.6). The worst case is shown in Figure 9.14(b), where with the constant disturbance the steady-state gain estimated is 0.
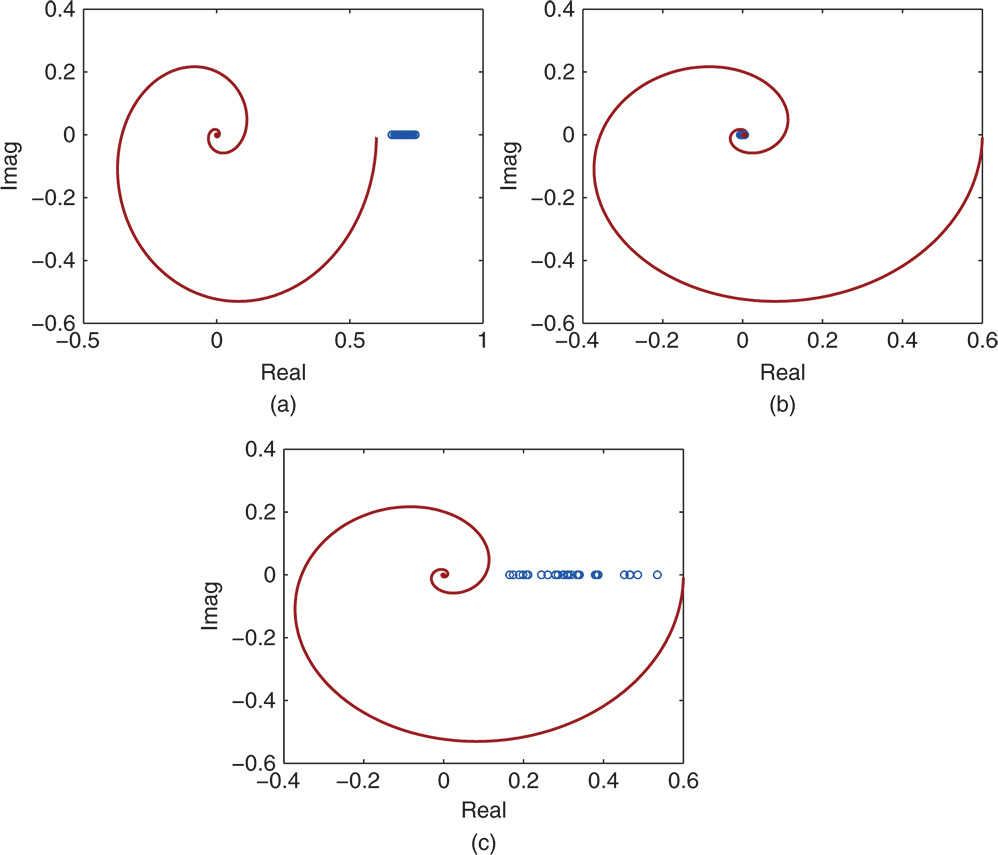
Figure 9.14 Monte-Carlo simulation results for estimation of steady-state gain with  random seeds. (a) Steady-state estimation (measurement noise). (b) Steady-state estimation (constant disturbance). (c) Steady-state estimation (low frequency disturbance). Key:
random seeds. (a) Steady-state estimation (measurement noise). (b) Steady-state estimation (constant disturbance). (c) Steady-state estimation (low frequency disturbance). Key:  (solid line), o is the estimated values at
(solid line), o is the estimated values at  .
.
9.5.4 Food for Thought
- The Monte-Carlo simulation studies presented in this section are based on integrator with relay feedback control. In the presence of constant disturbance, what is the role of the integrator played in the relay feedback control system? What are your observations in terms of the behavior of input and output signals?
- In the presence of low frequency disturbance, has the integrator with relay feedback control tried to compensate the disturbance? Does this cause the breakdown of the periodicity of the input and output signals?
- When there is a constant disturbance in the system, what kind of behavior would you expect from the input and output data for a relay with hysteresis? Do you expect accurate estimation results for this case when using FFT and FSF algorithms?
- Why can not we consistently estimate the steady-state gain of the system using the data generated from the relay feedback control? Even for the case with low frequency disturbance?
9.6 Auto-tuner Design for Stable Plant
To design the auto-tuner for a stable plant, the integrator with relay feedback control is used to generate the input and output data for the frequency response identification because this configuration handles the measurement noise and disturbances well and also provides the valuable low frequency information for the PID controller design. We assume that the two estimated frequency response points from the relay testing data are the fundamental frequency  ,
,  and
and  , where
, where 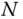 is the number of samples within one period. Because of noise, the oscillation generated from the relay feedback control may not be perfectly periodic. Thus, the parameter
is the number of samples within one period. Because of noise, the oscillation generated from the relay feedback control may not be perfectly periodic. Thus, the parameter 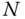 is estimated using FFT analysis as illustrated in the previous sections (see Section 9.4). In the majority of the cases, the second frequency
is estimated using FFT analysis as illustrated in the previous sections (see Section 9.4). In the majority of the cases, the second frequency 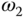 is selected as
is selected as  .
.
We assume that the plant transfer function  is stable with all poles strictly on the left-half complex plane. Recall the desired closed-loop performance for the PID controller design using frequency response data in Chapter 8, which is specified through the control sensitivity function (see (8.18)), as
is stable with all poles strictly on the left-half complex plane. Recall the desired closed-loop performance for the PID controller design using frequency response data in Chapter 8, which is specified through the control sensitivity function (see (8.18)), as
where  is the desired closed-loop time constant, the parameter
is the desired closed-loop time constant, the parameter  is selected so that
is selected so that 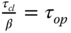 is approximately equal to the dominant time constant of the system,
is approximately equal to the dominant time constant of the system,  is the steady-state gain of the system.
is the steady-state gain of the system.
To link the PID controller design method to the auto-tuner, the question remains as how to choose the design parameters in (9.20). One possibility that works well is to derive the approximate dominant time constant of the system using the period of relay control,  . For the majority of the system, it can be readily verified through simulation studies that the settling time of the system is roughly
. For the majority of the system, it can be readily verified through simulation studies that the settling time of the system is roughly  , namely half of the period under integrated relay control. With this knowledge, the dominant time constant of the process is selected about one-fifth of the settling time as
, namely half of the period under integrated relay control. With this knowledge, the dominant time constant of the process is selected about one-fifth of the settling time as
Now, one can choose the desired closed-loop time constant  in relation to the dominant time constant of the process via the scaling parameter
in relation to the dominant time constant of the process via the scaling parameter  by defining
by defining
Substituting (9.21) and (9.22) into (9.20) leads to the desired control sensitivity function as,

hence, the desired closed-loop transfer function as
Note that in (9.24) the parameters  and
and  are known from the relay experiment and the user selected performance parameter is
are known from the relay experiment and the user selected performance parameter is 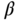 , which is the scaling factor between the estimated open-loop and the desired closed-loop time constants. This modification of the closed-loop performance specification leads to the automatic calculation of the PID controller parameters with minimum effort from the user.
, which is the scaling factor between the estimated open-loop and the desired closed-loop time constants. This modification of the closed-loop performance specification leads to the automatic calculation of the PID controller parameters with minimum effort from the user.
Because the direct estimation of the steady-state gain is not consistent using the relay control experiment, an approximation is taken to yield a rough estimation of the gain as

where  is the unknown steady-state gain of the system.
is the unknown steady-state gain of the system.
9.6.1 MATLAB Tutorial on Auto-tuner for Stable Plant
9.6.2 Evaluation of the Auto-tuner for a Stable Plant
In this section, we will firstly evaluate the closed-loop PID control performance of the proposed auto-tuner using four classes of systems commonly encountered in process control, and secondly perform comparative studies. For simplicity of the presentations, only measurement noise is added to the relay experiments. It has been verified that the auto-tuner will provide similar closed-loop performance when the constant disturbance or the low frequency disturbance are introduced during the relay experiments as long as we make an adjustment on the choice of the second frequency estimate for the PID controller design (see Sections 9.5.1 and 9.5.2).
There are four classes of systems used to evaluate the auto-tuner. Time delays are added for all testing cases to reflect the cases in process control. The same steady-state gain is used in all four cases for consistency in signal-to-noise ratio and the scaling of disturbance rejection in the closed-loop simulation. The sampling interval is  , the relay amplitude is selected to be 1, and a measurement noise with standard deviation
, the relay amplitude is selected to be 1, and a measurement noise with standard deviation  was added to the output. After the relay experiment, the number of samples for the period of the relay signal is calculated automatically to give the parameter
was added to the output. After the relay experiment, the number of samples for the period of the relay signal is calculated automatically to give the parameter  , and the frequency responses at
, and the frequency responses at  and
and  are estimated. Then, by choosing
are estimated. Then, by choosing  , 1, and 2, three sets of PID controller parameters are calculated using the program FR4PID.m.
, 1, and 2, three sets of PID controller parameters are calculated using the program FR4PID.m.
Case A. This is a testing case for high order systems. The transfer function of this system is given as

Case B. This is the testing case for systems with non-minimum phase behavior. The transfer function is given by

Case C. This is the testing case for systems with dominant time delay. The transfer function is given as
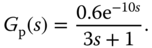
Case D. The final testing case uses an underdamped system, which has the transfer function

This transfer function has the damping coefficient  . Thus, the system has oscillatory response in open-loop operation.
. Thus, the system has oscillatory response in open-loop operation.
Relay feedback control is used to generate the input and output data for all four processes in the presence of measurement noise. Because of the integral action used in the relay feedback control, the measurement noise has not affected the input signal without using hysteresis in the design, and there is no correlation between the measurement noise and the input signal. This adds to the benefit of using an integrator in series with a relay control. The estimation of the frequency responses at  and
and  is performed using the frequency sampling filter model and the estimated frequency responses are accurate for all four cases.
is performed using the frequency sampling filter model and the estimated frequency responses are accurate for all four cases.
9.6.2.1 PID Controller Parameters
By choosing 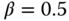 , 1, and 2, three sets of PID controller parameters are calculated, which corresponds to the selection of three different desired closed-loop response speed. For instance, when
, 1, and 2, three sets of PID controller parameters are calculated, which corresponds to the selection of three different desired closed-loop response speed. For instance, when 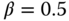 , the desired closed-loop time constant is selected equivalent to half of the estimated dominant open-loop time constant. Table 9.1 shows the PID controller parameters of the four cases for the three
, the desired closed-loop time constant is selected equivalent to half of the estimated dominant open-loop time constant. Table 9.1 shows the PID controller parameters of the four cases for the three 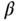 values together with the mean squared errors, where the mean squared error is defined as
values together with the mean squared errors, where the mean squared error is defined as  ,
,  being the number of samples and
being the number of samples and  being the error between the reference and output signals.
being the error between the reference and output signals.
It is noticed that as  increases, the proportional controller gain
increases, the proportional controller gain  reduces, and the derivative gain reduces. In contrast, the variation of integral gain is smaller when
reduces, and the derivative gain reduces. In contrast, the variation of integral gain is smaller when  changes.
changes.
9.6.2.2 Nyquist Plots
Figures 9.16(a)–(d) show the Nyquist plots of the four cases for the three control systems designed using 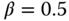 , 1 and 2, where the frequency response of the system,
, 1 and 2, where the frequency response of the system,  , is used in the computation. It is seen from the Nyquist plots that the PID controllers with all three choices of
, is used in the computation. It is seen from the Nyquist plots that the PID controllers with all three choices of  lead to stable closed-loop systems. However, for
lead to stable closed-loop systems. However, for  , the closed-loop control systems for case B to case D had gain margins less than 2. As
, the closed-loop control systems for case B to case D had gain margins less than 2. As  increases, both gain and phase margins for all four systems have increased. In particular, for the default choice of
increases, both gain and phase margins for all four systems have increased. In particular, for the default choice of 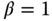 , the gain margins for all four case are greater than 2 and phase margins are greater than
, the gain margins for all four case are greater than 2 and phase margins are greater than  .
.
Table 9.1 PID controller parameters for different  values.
values.
| Case |  |
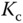 |
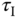 |
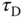 |
 |
| A | 0.5 | 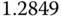 |
9.0098 | 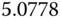 |
0.0894 |
| 1 |  |
 |
 |
 |
|
| 2 |  |
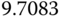 |
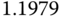 |
 |
|
| B | 0.5 |  |
6.2732 |  |
 |
| 1 |  |
 |
 |
 |
|
| 2 |  |
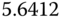 |
 |
0.1072 | |
| C | 0.5 |  |
 |
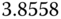 |
 |
| 1 |  |
 |
 |
 |
|
| 2 | 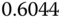 |
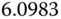 |
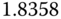 |
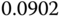 |
|
| D | 0.5 |  |
 |
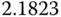 |
 |
| 1 |  |
 |
 |
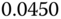 |
|
| 2 | 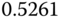 |
 |
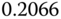 |
0.0543 |
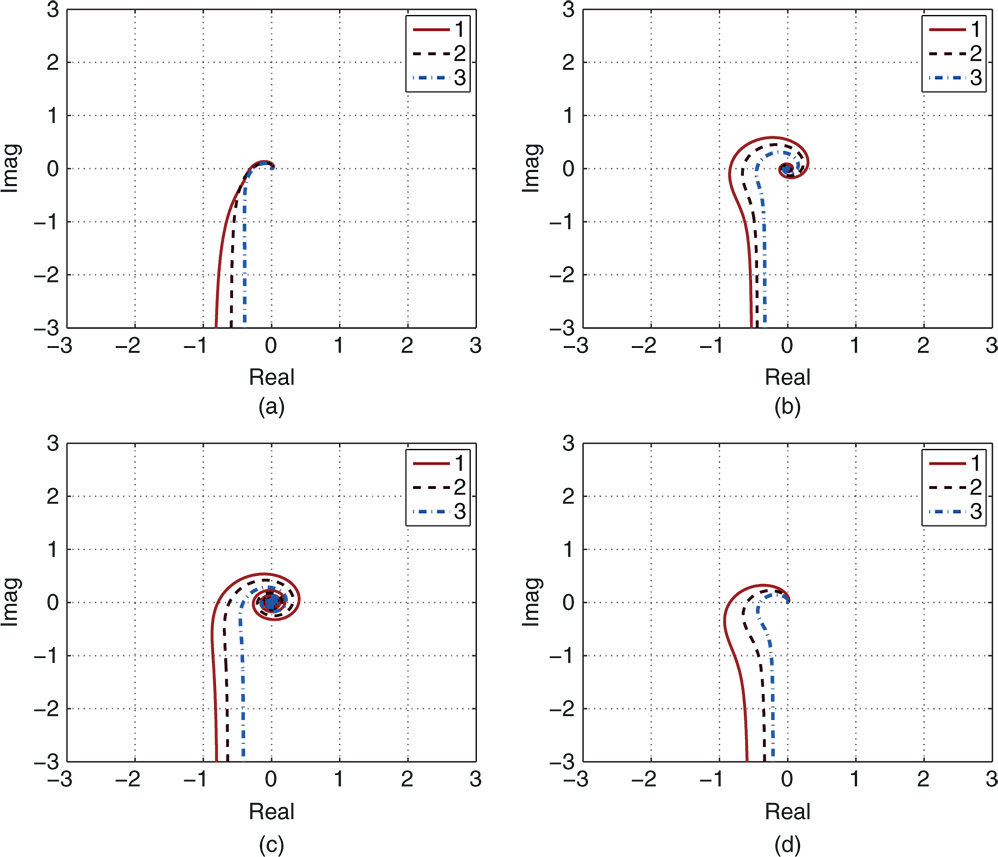
Figure 9.16 Nyquist plots using the PID controller parameters in Table 9.1. (a) Case A. (b) Case B. (c) Case C. (d) Case D. Key: line (1)  ; line (2)
; line (2)  ; line (3)
; line (3)  .
.
9.6.2.3 Closed-loop Simulation Results
Closed-loop simulation is conducted for all four cases with  , 1, and 2. In the closed-loop simulation, the derivative term is implemented on the output only and a derivative filter with time constant
, 1, and 2. In the closed-loop simulation, the derivative term is implemented on the output only and a derivative filter with time constant  is used. A unit step signal is used as the reference signal at
is used. A unit step signal is used as the reference signal at  (s), and a unit step input disturbance enters at time
(s), and a unit step input disturbance enters at time  (s). Figures 9.17(a)–(d) show the closed-loop simulation results for reference following and disturbance rejection. It is seen that all closed-loop systems are stable. The simulation results demonstrate that for a faster response to the reference signal, the PID control system will also have a faster response to disturbance rejection. The user can select the scaling parameter
(s). Figures 9.17(a)–(d) show the closed-loop simulation results for reference following and disturbance rejection. It is seen that all closed-loop systems are stable. The simulation results demonstrate that for a faster response to the reference signal, the PID control system will also have a faster response to disturbance rejection. The user can select the scaling parameter  to achieve the desired closed-loop response as required. As
to achieve the desired closed-loop response as required. As  increases, the closed-loop response speed reduces to both reference following and disturbance rejection. The overshoot in the reference response when
increases, the closed-loop response speed reduces to both reference following and disturbance rejection. The overshoot in the reference response when  is small could be overcome by using a two degree of freedom PID controller implementation as shown in Chapters 1 and 2.
is small could be overcome by using a two degree of freedom PID controller implementation as shown in Chapters 1 and 2.

Figure 9.17 Closed-loop simulation results using the PID controller parameters in Table 9.1. (a) Case A. (b) Case B. (c) Case C. (d) Case D. Key: line (1)  ; line (2)
; line (2)  ; line (3)
; line (3)  .
.
9.6.3 Comparative Studies
In this section, we will benchmark the closed-loop performance of the PID controller found by the auto-tuner against the performance of the several other well known PID controllers. We will consider the following first order plus time delay model,
In the comparative studies, we will calculate the PID controller parameters using the IMC-PID controller design proposed by Rivera et al. (1986) (see Section 1.4.1), and the PID controller design by Padula and Visioli (2011) (see Section 1.4.2).
As in Chapter 1, the PID controller parameters using IMC-PID controller and Padula and Visioli tuning rules are calculated using the transfer function model (9.25). The PID controller parameters from the auto-tuner are calculated from the relay experiment where measurement noise with standard deviation of 0.02 was added.
In Table 9.2, we will choose two  parameters to yield two sets of PID controller parameters from the auto-tuner. With this selection, it seems that all three PID controllers have a similar gain for the proportional control. However, the integral time constant varies between 26 and 35, and the derivative gain varies between 7 and 17. Figures 9.18(a)–(b) compare the three control signals and output signals in both reference following and disturbance rejection, which show that all three control systems have similar closed-loop performances in reference following and disturbance rejection.
parameters to yield two sets of PID controller parameters from the auto-tuner. With this selection, it seems that all three PID controllers have a similar gain for the proportional control. However, the integral time constant varies between 26 and 35, and the derivative gain varies between 7 and 17. Figures 9.18(a)–(b) compare the three control signals and output signals in both reference following and disturbance rejection, which show that all three control systems have similar closed-loop performances in reference following and disturbance rejection.
Table 9.2 PID controller parameters and mean squared errors from the control simulation studies. Cases A and B use an auto-tuner, case C uses IMC-PID, cases D and E use Padula and Visioli PID.
| Case | Spec. |  |
 |
 |
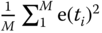 |
| A |  |
 |
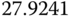 |
 |
0.1326 |
| B |  |
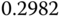 |
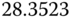 |
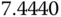 |
 |
| C | 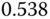 |
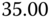 |
 |
 |
|
| D |  |
 |
17.2991 |  |
0.1923 |
| E | 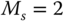 |
0.3205 | 22.5160 | 13.5770 | 0.1504 |
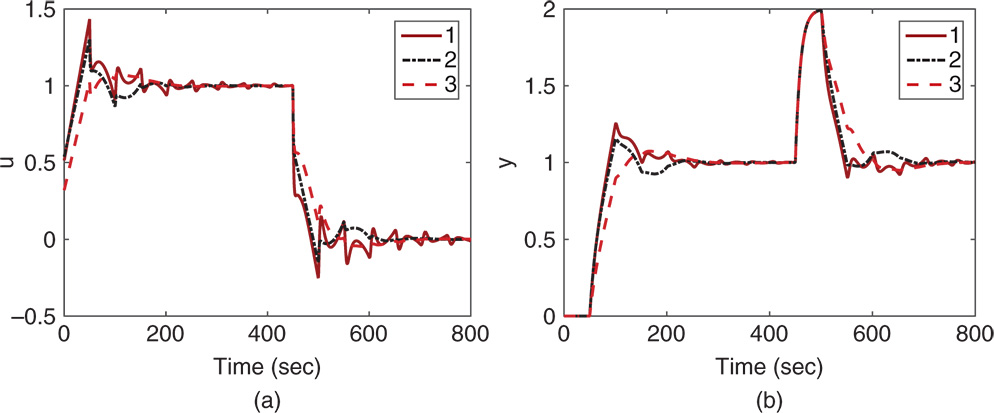
Figure 9.18 Closed-loop simulation results using the PID controller parameters in Table 9.2. (a) Control signal. (b) Output signal. Key: line (1) auto-tuner ( ); line (2) IMC-PID controller; line (3) Padula–Visioli design (
); line (2) IMC-PID controller; line (3) Padula–Visioli design ( ).
).
9.6.4 Food for Thought
- What are the key advantages when using the estimated frequency information directly for the auto-tuner design?
- Can you propose an approach to convert the estimated frequency points to first order plus delay model, then design PID controller using the Padula and Visioli tuning rules given in Chapter 1?
- If you wish to have a faster closed-loop response speed for disturbance rejection and reference following, should you increase or decrease the parameter
 ?
? - If the system has a large measurement noise, and you wish not to amplify it, should you increase or decrease the parameter
 ?
? - If the auto-tuner finds the derivative time constant to be negative, should we simply neglect the derivative term and implement the PI controller?

Figure 9.19 Block diagram of relay feedback control for an integrating system.
9.7 Auto-tuner Design for a Plant with an Integrator
For systems containing an integrator, in the design of auto-tuner for PID controllers, a proportional controller  is first used to stabilize the plant. A relay with hysteresis element is utilized to generate the sustained oscillation for the closed-loop control system. The block diagram of the relay feedback control for an integrating system is illustrated in Figure 9.19.
is first used to stabilize the plant. A relay with hysteresis element is utilized to generate the sustained oscillation for the closed-loop control system. The block diagram of the relay feedback control for an integrating system is illustrated in Figure 9.19.
9.7.1 Estimation of an Integrating Plus Delay Model
The approximate model of an integrating system is assumed to be of the following form:
For most physical systems, there are more or less approximations involved in obtaining the integrating plus time delay model. For an integrating plus time delay system, a single frequency is sufficient to determine its gain  and time delay
and time delay 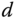 . Therefore, it is exceedingly simple to obtain an integrating plus delay model using the relay feedback control experimental data.
. Therefore, it is exceedingly simple to obtain an integrating plus delay model using the relay feedback control experimental data.
As shown in Section 9.4, the estimation of the closed-loop frequency response using either FFT analysis or an FSF model will yield the information  where
where 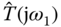 is the estimated closed-loop frequency response and
is the estimated closed-loop frequency response and 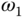 is the fundamental frequency of the relay feedback control.
is the fundamental frequency of the relay feedback control.
With the knowledge of the proportional controller  , the frequency response of the plant
, the frequency response of the plant  is calculated from the closed-loop frequency response relationship,
is calculated from the closed-loop frequency response relationship,

leading to
Now, letting the frequency response of the integrating plus delay model (9.26) be equal to the estimated  leads to
leads to
Equating the magnitudes on both side of (9.28) gives
where  . Additionally, from (9.28), the following relationship holds:
. Additionally, from (9.28), the following relationship holds:

This gives the estimate of time delay as
In the event that parameter  is negative, its absolute value is taken as the estimated time delay.
is negative, its absolute value is taken as the estimated time delay.
It is seen here that if the system is approximated by integrating with the time delay, the plant information at a single frequency is sufficient to determine the plant gain and time delay.
9.7.2 Auto-tuner for Integrating Systems
On obtaining the estimated integrating plus time delay model (9.26), one can find the PID controller using the empirical rules such as the modified IMC-PI controller in Skogestad (2003), which was discussed in Section 1.4.1, or tuning rules in Tyreus and Luyben (1992). We will use the empirical rules presented in Section 8.4.3, which gives the flexibility of PI, PID and PD controllers together with the gain margin and phase margin for the selection of performance parameter 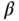 .
.
One is encouraged to follow Tutorial 9.1 for the relay feedback control and Tutorial 9.4 for the estimation of the frequency response using an FSF so as to validate the following simulation example.
The following example is to show the behaviour of the auto-tuner when it is applied to a complex integrating system.
Although it is derived for an integrator plus delay system, the auto-tuner provides satisfactory closed-loop performance for many classes of systems. This is illustrated by the following example.
This auto-tuner will be used for finding the PID controllers for the unmanned aerial vehicles in Chapter 10.
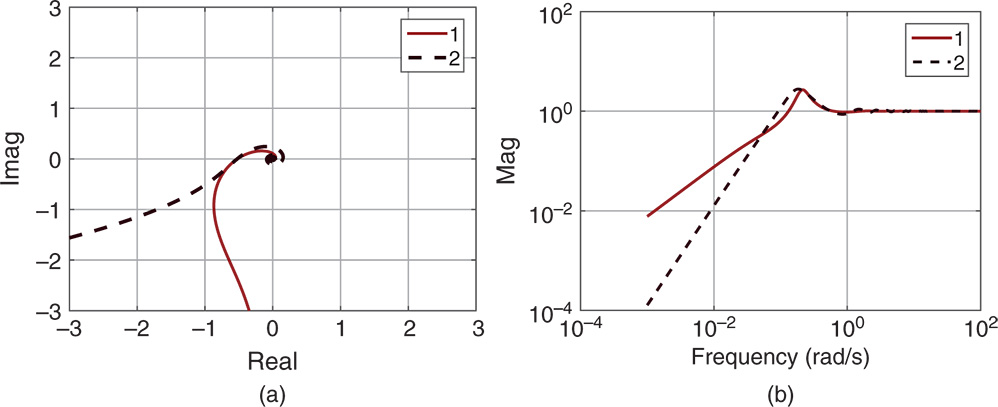
Figure 9.27 Frequency response comparison (Example 9.7). (a) Nyquist diagram. (b) Sensitivity function. Key: line (1) frequency response calculated with integrating plus delay model; line (2) frequency response calculated with the actual plant.
9.7.3 Auto-tuning of Cascade Control Systems
Auto-tuners are very convenient for tuning cascade control systems. The inner-loop control system will be auto-tuned first to find the appropriate controller, followed by the implementation of this secondary controller. An outer-loop control system will be auto-tuned with the closed-loop secondary system considered. As an illustration, we consider the following example.
9.7.4 Food for Thought
- Why do you think that the auto-tuner designed for integrating system can be applied to a stable system?
- Do you expect that this class of auto-tuners would produce a faster disturbance rejection based on the observation of the sensitivity function in Example 9.7?
- We use relay with hysteresis in the identification experiments. Do you think that it would work better if we use the integrator with relay control apparatus in the identification experiment? Why?
- If you wish to have a faster closed-loop response for disturbance rejection, should you increase or decrease the parameter
 ?
? - If you wish to reduce the effect of measurement noise, should you increase or decrease the parameter
 ?
?
9.8 Summary
We have discussed automatic tuning of PID controllers in this chapter. The auto-tuners are designed for stable systems and integrating systems. Both involve relay feedback control to generate the input and output data for estimation of plant frequency response. Then, the PID controller design methods discussed in Chapter 8 are used to automatically find the controller parameters.
The other important aspects of the chapter are summarized as follows.
- Relay feedback control is utilized in generating the input and output data for estimation of process frequency response. Following the MATLAB tutorials, we can create our own Simulink functions for simulations of relay feedback control system and those programs can also be translated into C-program for micro-controller implementation.
- The input and output data collected from the relay feedback control experiments in simulation or in real-time implementation are used for the estimation either using Fourier analysis or using the frequency sampling filter model. The frequency sampling filter based estimation is performed in a recursive least squares algorithm with the feature for real-time applications.
- Monte-Carlo simulation studies have been used to investigate the accuracy of the estimated models in the presence of measurement noise and low frequency disturbances.
- Once the process frequency response is estimated, the PID controller design methods either using two frequency points or using an integrating with delay model are applied to obtain the PID controller parameters.
9.9 Further Reading
- Relay feedback control has been one of the key instruments used in the automatic tuning of PID controllers (Astrom and Hagglund (1984), Astrom and Hagglund (1988), Astrom and Hagglund (1995), Astrom and Hagglund (2006), Hagglund and Astrom (1985), Yu (2006), Johnson and Moradi (2005)).
- The auto-tuner for stable systems was originally presented in Wang (2017).
- Auto-tuners are experimentally compared in laboratory test beds (Berner et al. (2018)).
- Books for automatic tuning of PID controllers include Yu (2006), Sung et al. (2009)
- Software package introduced for tuning of PID controllers is discussed in Oviedo et al. (2006). Use of phase-locked-loop idea is used to auto-tune PID controllers in Crowe and Johnson (2002).
- Auto-tuners in closed-loop operations include Lee et al. (1990), Schei (1992), Tan et al. (2000). Automatic tuning of cascade PID control system was discussed in Jeng and Lee (2012) and Jeng (2014). Automatic tuning of PID controller for nonlinear systems was presented in Cetin and Iplikci (2015). Multi-loop PID controller tuning was proposed using an optimization based approach (Dittmar et al. (2012)). A simplified approach to auto-tuner design with respect to disturbance rejection was proposed in Romero et al. (2011). An auto-tuner was designed for fractional order plus delay model in Jin.
- Estimation of transfer function model by changing between two relay feedback controllers to obtain multi-frequency signals (Schei (1994)), and estimation of step response model (Wang and Cluett (1997a)).
- Frequency sampling filters was introduced in Bitmead and Anderson (1981) and Wang and Cluett (2000).
- The auto-tuning algorithm presented in this chapter has been successfully used to attitude control of fixed-wing unmanned aerial vehicle with experimental validations (Poksawat et al. (2016), Poksawat et al. (2017) and Poksawat (2018)). It has been used to find a PID control system for an electro-mechanical system with two inputs and two outputs (see Wang et al. (2017)). In Chen (2017), the auto-tuning algorithm has been successfully used to find flight controllers for quadrotor UAVs.
- There are many books for the topics of system identification (see Ljung (1999), Soderstrom and Stoica (1989), Goodwin and Sin (1984), Young (2012), Soderstrom (2018)).
Problems
- 9.1 Consider the systems with the following transfer functions:
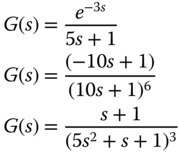
- Suppose that the measurement is corrupted by a noise source that has zero mean with variance 0.1. Following Tutorial 9.1, write the RelayH.slx real-time function and build a Simulink relay feedback control simulation program. Sampling interval
 .
. - Choose the relay amplitude to be
 and adjust the hysteresis level
and adjust the hysteresis level  to prevent the random switches caused by the noise. Apply the relay feedback control program to the above systems. What are your observations on the choice of
to prevent the random switches caused by the noise. Apply the relay feedback control program to the above systems. What are your observations on the choice of  with regard to relay amplitude and the magnitude of the measurement noise? If you use Simulink noise generator in the continuous-time, will the sampling interval
with regard to relay amplitude and the magnitude of the measurement noise? If you use Simulink noise generator in the continuous-time, will the sampling interval  affect the choice of
affect the choice of  ?
? - Add a constant input disturbance with amplitude of
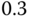 to the relay feedback control. What are the effects of this disturbance on the relay with hysteresis control system?
to the relay feedback control. What are the effects of this disturbance on the relay with hysteresis control system?
- Suppose that the measurement is corrupted by a noise source that has zero mean with variance 0.1. Following Tutorial 9.1, write the RelayH.slx real-time function and build a Simulink relay feedback control simulation program. Sampling interval
- 9.2 Consider the three systems given in Problem 9.1.
- Following Tutorial 9.2, write the MATLAB real-time function RelayI.slx for relay with integrator control. Choose the same relay amplitude with very small hysteresis (
 ).
). - Apply the relay with integrator control to the three systems given in Problem 9.2. What are your observations on the effect of noise with this type of relay feedback control system?
- Add a constant input disturbance with amplitude of
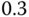 to the relay feedback control. What are the effects of this disturbance on the relay with integrator control system?
to the relay feedback control. What are the effects of this disturbance on the relay with integrator control system? - Will the sampling interval
 affect the relay with integrator control system?
affect the relay with integrator control system?
- Following Tutorial 9.2, write the MATLAB real-time function RelayI.slx for relay with integrator control. Choose the same relay amplitude with very small hysteresis (
- 9.3 Assume that we have generated relay feedback control data by solving Problem 9.1.
- Following Tutorial 9.3, write the MATLAB program FFTRelay.m for estimation of frequency response using relay feedback data.
- Apply the program to the six sets of data generated from Problem 9.1.
- Evaluate the estimation results against the Nyquist curves obtained from the transfer functions.
- What are your observations on the effect of measurement noise on the accuracy? The effect of constant input disturbance?
- Alternatively, following Tutorial 9.4, write the MATLAB program FSFRelay.m for the estimation of frequency response using relay feedback data and repeat the exercises outlined in the previous steps.
- 9.4 Apply the MATLAB program FFTRelay.m (or FSFRelay.m) to the six sets of data generated from Problem 9.2, where relay with integrator control has been used. What are your observations on the effect of measurement noise and disturbance on the accuracy of the estimation?
- 9.5 Consider the systems with the following transfer functions:

- Following Tutorial 9.5, write the auto-tuner for stable systems.
- Apply the auto-tuner to the above systems with appropriate sampling interval
 , where the performance parameter
, where the performance parameter 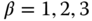 .
. - Evaluate the closed-loop performance with a unit step reference signal and a step input disturbance with magnitude of
 .
. - What are your observations on the closed-loop responses to reference following and disturbance rejection in terms of the parameter
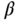 ?
? - Add measurement noise and the input disturbance in the relay with integrator control system. Will the noise and disturbance significantly affect the performance of the closed-loop control system produced by the auto-tuner?
- 9.6 Consider the integrating systems with the following transfer functions:

- Following the computational steps outlined in Section 9.7, write the auto-tuner for integrating systems where the relay with hysteresis is applied to a proportionally controlled system (see Figure 9.19).
- Choose a proportional controller
 that will produce a stable closed-loop system and apply the auto-tuner to the above systems, where sampling interval
that will produce a stable closed-loop system and apply the auto-tuner to the above systems, where sampling interval 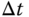 , relay amplitude and hysteresis are selected appropriately.
, relay amplitude and hysteresis are selected appropriately. - Evaluate the closed-loop control system performance with unit step reference signal and a step input disturbance with amplitude
 for the performance parameter
for the performance parameter  .
.
- 9.7 The auto-tuner derived for integrating system can also be applied to stable systems in a closed-loop controlled environment. Considering the systems with the following transfer functions

Use the auto-tuner with integrator model to find the PID controller parameters for these systems. In the relay control experiments, feedback control gain
 , and relay amplitude of
, and relay amplitude of 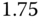 and hysteresis of
and hysteresis of  are used. Sampling interval
are used. Sampling interval  is selected. The performance parameters
is selected. The performance parameters 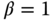 and
and  are selected for fast disturbance rejection. Evaluate the closed-loop control system performance for step input disturbance rejection with a disturbance amplitude of
are selected for fast disturbance rejection. Evaluate the closed-loop control system performance for step input disturbance rejection with a disturbance amplitude of  .
. - 9.8 The auto-tuners are very convenient for tuning cascade control systems. Consider that a cascade control system has the inner-loop transfer function

and the outer-loop transfer function

- Construct an auto-tuner for this cascade control system from tuning the inner-loop control system first followed by tuning the outer-loop control system.
- By choosing the closed-loop performance parameter
 , the closed-loop response speed can be specified for the inner-loop and outer-loop control systems. In order for the cascade control system to work properly, the inner-loop response speed needs to be much faster than the outer-loop's response speed. How do you choose
, the closed-loop response speed can be specified for the inner-loop and outer-loop control systems. In order for the cascade control system to work properly, the inner-loop response speed needs to be much faster than the outer-loop's response speed. How do you choose  for this auto-tuned cascade control system?
for this auto-tuned cascade control system?
- 9.9 We can design an auto-tuner for integrating systems using the modified IMC-PI controller introduced in Skogestad (2003), which was discussed in Section 1.4.1. For the estimated integrating with delay model,
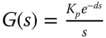 , the PI controller parameters are calculated using the following expressions:
, the PI controller parameters are calculated using the following expressions:
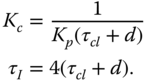
Repeat the exercises given in Problem 9.7 with the closed-loop performance parameter
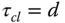 . What are your observations when you compare these two PI control systems?
. What are your observations when you compare these two PI control systems?