in which the author seeks insight
into physical laws by asking:
can highly advanced civilizations
build wormholes through hyperspace
for rapid interstellar travel
and machines for traveling backward in time?
Wormholes and Exotic Material
I had just taught my last class of the 1984–85 academic year and was sinking into my office chair to let the adrenaline subside, when the telephone rang. It was Carl Sagan, the Cornell University astrophysicist and a personal friend from way back. “Sorry to bother you, Kip,” he said. “But I’m just finishing a novel about the human race’s first contact with an extraterrestrial civilization, and I’m worried. I want the science to be as accurate as possible, and I’m afraid I may have got some of the gravitational physics wrong. Would you look at it and give me advice?” Of course I would. It would be interesting, since Carl is a clever guy. It might even be fun. Besides, how could I turn down this kind of request from a friend?
The novel arrived a couple of weeks later, a three-and-a-half-inch-thick stack of double-spaced typescript.
I slipped the stack into an overnight bag and threw the bag into the back seat of Linda’s Bronco, when she picked me up for the long drive from Pasadena to Santa Cruz. Linda is my ex-wife; she, I, and our son Bret were on our way to see our daughter Kares graduate from college.
As Linda and Bret took turns driving, I read and thought. (Linda and Bret were accustomed to such introversion; they had lived with me for many years.) The novel was fun, but Carl, indeed, was in trouble. He had his heroine, Eleanor Arroway, plunge into a black hole near Earth, travel through hyperspace in the manner of Figure 13.4, and emerge an hour later near the star Vega, 26 light-years away. Carl, not being a relativity expert, was unfamiliar with the message of perturbation calculations2: It is impossible to travel through hyperspace from a black hole’s core to another part of our Universe. Any black hole is continually being bombarded by tiny electromagnetic vacuum fluctuations and by tiny amounts of radiation. As these fluctuations and radiation fall into the hole, they get accelerated by the hole’s gravity to enormous energy, and they then rain down explosively on any “little closed universe” or “tunnel” or other vehicle by which one might try to launch the trip through hyperspace. The calculations were unequivocal; any vehicle for hyperspace travel gets destroyed by the explosive “rain” before the trip can be launched. Carl’s novel had to be changed.
During the return drive from Santa Cruz, somewhere west of Fresno on Interstate 5, a glimmer of an idea came to me. Maybe Carl could replace his black hole by a wormhole through hyperspace.
A wormhole is a hypothetical shortcut for travel between distant points in the Universe. The wormhole has two entrances called “mouths,” one (for example) near Earth, and the other (for example) in orbit around Vega, 26 light-years away. The mouths are connected to each other by a tunnel through hyperspace (the wormhole) that might be only a kilometer long. If we enter the near-Earth mouth, we find ourselves in the tunnel. By traveling just one kilometer down the tunnel we reach the other mouth and emerge near Vega, 26 light-years away as measured in the external Universe.
Figure 14.1 depicts such a wormhole in an embedding diagram. This diagram, as is usual for embedding diagrams, idealizes our Universe as having only two spatial dimensions rather than three (see Figures 3.2 and 3.3). In the diagram the space of our Universe is depicted as a two-dimensional sheet. Just as an ant crawling over a sheet of paper is oblivious to whether the paper is lying flat or is gently folded, so we in our Universe are oblivious to whether our Universe is lying flat in hyperspace or is gently folded, as in the diagram. However, the gentle fold is important; it permits the Earth and Vega to be near each other in hyperspace so they can be connected by the short wormhole. With the wormhole in place, we, like an ant or worm crawling over the embedding diagram’s surface, have two possible routes from Earth to Vega: the long, 26-light-year route through the external Universe, and the short, 1-kilometer route through the wormhole.
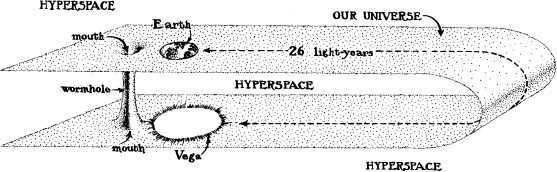
14.1 A1-kilometer-Iong wormhole through hyperspace linking the Earth to the neighborhood of Vega, 26 light-years away. (Not drawn to scale.)
What would the wormhole’s mouth look like, if it were on Earth, in front of us? In the diagram’s two-dimensional universe the wormhole’s mouth is drawn as a circle; therefore, in our three-dimensional Universe it would be the three-dimensional analogue of a circle; it would be a sphere. In fact, the mouth would look something like the spherical horizon of a nonrotating black hole, with one key exception: The horizon is a “one-way” surface; anything can go in, but nothing can come out. By contrast, the wormhole mouth is a “two-way” surface; we can cross it in both directions, inward into the wormhole, and back outward to the external Universe. Looking into the spherical mouth, we can see light from Vega; the light has entered the other mouth near Vega and has traveled through the wormhole, as though the wormhole were a light pipe or optical fiber, to the near-Earth mouth, where it now emerges and strikes us in the eyes.
Wormholes are not mere figments of a science fiction writer’s imagination. They were discovered by Ludwig Flamm mathematically, as a solution to Einstein’s field equation, in 1916, just a few months after Einstein formulated his equation; Einstein and Nathan Rosen explored them in the 1930s; and John Wheeler and his research group studied them extensively, by a variety of mathematical calculations, in the 1950s. However, none of the wormholes that had been found as solutions of Einstein’s equation, prior to my trip down Interstate 5 in 1985, was suitable for Carl Sagan’s novel, because none of them could be traversed safely. Each and everyone of them was predicted to evolve with time in a very peculiar way: The wormhole is created at some moment of time, opens up briefly, and then pinches off and disappears—and its total life span from creation to pinch-off is so short that nothing whatsoever (no person, no radiation, no signal of any sort) can travel through it, from one mouth to the other. Anything that tries will get caught and destroyed in the pinch-off. Figure 14.2 shows a simple example.
Like most of my physicist colleagues, I have been skeptical of wormholes for decades. Not only does Einstein’s field equation predict that wormholes live short lives if left to their own devices; their lives are made even shorter by random infalling bits of radiation: The radiation (according to calculations by Doug Eardley and Ian Redmount) gets accelerated to ultra-high energy by the wormhole’s gravity, and as the energized radiation bombards the wormhole’s throat, it triggers the throat to recontract and pinch off far faster than it would otherwise—so fast, in fact, that the wormhole has hardly any life at all.
There is another reason for skepticism. Whereas black holes are an inevitable consequence of stellar evolution (massive, slowly spinning stars, of just the sort that astronomers see in profusion in our galaxy, will implode to form black holes when they die), there is no analogous, natural way for a wormhole to be created. In fact, there is no reason at all to think that our Universe contains today any singularities of the sort that give birth to wormholes (Figure 14.2); and even if such singularities did exist, it is hard to understand how two of them could find each other in the vast reaches of hyperspace, so as to create a wormhole in the manner of Figure 14.2.
When one’s friend needs help, one is willing to turn most anywhere that help might be found. Wormholes—despite my skepticism about them—seemed to be the only help in sight. Perhaps, it occurred to me on Interstate 5 somewhere west of Fresno, there is some way that an infinitely advanced civilization could hold a wormhole open, that is, prevent it from pinching off, so that Eleanor Arroway could travel through it from Earth to Vega and back. I pulled out pen and paper and began to calculate. (Fortunately, Interstate 5 is very straight; I could calculate without getting carsick.)
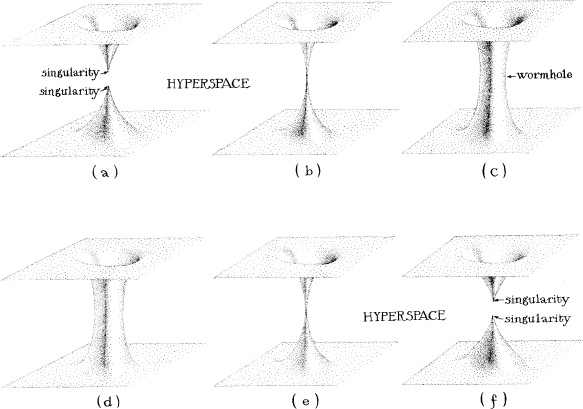
14.2 The evolution of a precisely spherical wormhole that has no material in its interior. (This evolution was discovered as a solution of Einstein’s field equation in the mid-1950s by Martin Kruskal, a young associate of Wheeler’s at Princeton University.) Initially (a) there is no wormhole; instead there is a singularity near Earth and one near Vega. Then, at some moment of time (b), the two singularities reach out through hyperspace, find each other, annihilate each other, and in the annihilation they create the wormhole. The wormhole grows in circumference (c), then begins to recontract (d), and pinches off (e), creating two singularities (f) similar to those in which the wormhole was born—but with one crucial exception. Each initial singularity (a) is like that of the big bang; time flows out of it, so it can give birth to something: the Universe in the case of the big bang, and the wormhole in this case. Each final singularity (f), by contrast, is like that of the big crunch (Chapter 13); time flows into it, so things get destroyed in it: the Universe in the case of the big crunch, and the wormhole in this case. Anything that tries to cross through the wormhole during its brief life gets caught in the pinch-off and, along with the wormhole itself, gets destroyed in the final singularities (f).
To make the calculations easy, I idealized the wormhole as precisely spherical (so in Figure 14.1, where one of our Universe’s three dimensions is suppressed, it is precisely circular in cross section). Then, by two pages of calculations based on the Einstein field equation, I discovered three things:
First, the only way to hold the wormhole open is to thread the wormhole with some sort of material that pushes the wormhole’s walls apart, gravitationally. I shall call such material exotic because, as we shall see, it is quite different from any material that any human has ever yet met.
Second, I discovered that, just as the required exotic material must push the wormhole’s walls outward, so also, whenever a beam of light passes through the material, the material will gravitationally push outward on the beam’s light rays, prying them apart from each other. In other words, the exotic material will behave like a “defocusing lens”; it will gravitationally defocus the light beam. See Box 14.1.
Third, I learned from the Einstein field equation that, in order to gravitationally defocus light beams and gravitationally push the wormhole’s walls apart, the exotic material threading the wormhole must have a negative average energy density, as seen by a light beam traveling through it. This requires a bit of explanation. Recall that gravity (spacetime curvature) is produced by mass (Box 2.6) and that mass and energy are equivalent (Box 5.2, where the equivalence is embodied in Einstein’s famous equation E = Mc2). This means that gravity can be thought of as produced by energy. Now, take the energy density of the material inside the wormhole (its energy per cubic centimeter), as measured by a light beam—that is, as measured by someone who travels through the wormhole at (nearly) the speed of light—and average that energy density along the light beam’s trajectory. The resulting averaged energy density must be negative in order for the material to be able to defocus the light beam and hold the wormhole open-that is, in order for the wormhole’s material to be “exotic.”3
This does not necessarily mean that the exotic material has a negative energy as measured by someone at rest inside the wormhole. Energy density is a relative concept, not absolute; in one reference frame it may be negative, in another positive. The exotic material can have a negative energy density as measured in the reference frame of a light beam that travels through it, but a positive energy density as measured in the wormhole’s reference frame. Nevertheless, because almost all forms of matter that we humans have ever encountered have positive average energy densities in everyone’s reference frame, physicists have long suspected that exotic material cannot exist. Presumably the laws of physics forbid exotic material, we physicists have conjectured, but just how the laws of physics might do so was not at all clear.
Holding a Wormhole Open: Exotic Material
Any spherical wormhole through which a beam of light can travel will gravitationally defocus the light beam. To see that this is so, imagine (as drawn below) that the beam is sent through a converging lens before it enters the wormhole, thereby making all its rays converge radially toward the wormhole’s center. Then the rays will always continue to travel radially (how else could they possibly move?), which means that when they emerge from the other mouth, they are diverging radially outward, away from the wormhole’s center, as shown. The beam has been defocused.
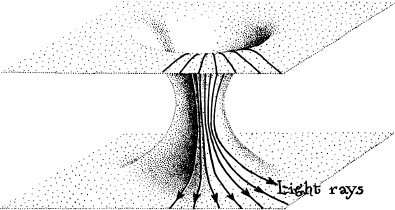
The wormhole’s spacetime curvature, which causes the defocusing, is produced by the “exotic” material that threads through the wormhole and holds the wormhole open. Since spacetime curvature is equivalent to gravity, it, in fact is the exotic material’s gravity that defocuses the light beam. In other words, the exotic material gravitationally repels the beam’s light rays, pushing them away from itself and hence away from each other, and thereby defocuses them.
This is precisely the opposite to what happens in a gravitational lens (Figure 8.2). There light from a distant star is focused by the gravitational pull of an intervening star or galaxy or black hole; here the light is defocused.
Perhaps our prejudice against the existence of exotic material is wrong, I thought to myself as I rode down Interstate 5. Perhaps exotic material can exist. This was the only way I could see to help Carl. So upon reaching Pasadena, I wrote Carl a long letter, explaining why his heroine could not use black holes for rapid interstellar travel, and suggesting that she use wormholes instead, and that somebody in the novel discover that exotic material can really exist and can be used to hold the wormholes open. Carl accepted my suggestion with pleasure and incorporated it into the final version of his novel, Contact.4
It occurred to me, after offering Carl Sagan my comments, that his novel could serve as a pedagogical tool for students studying general relativity. As an aid for such students, during the autumn of 1985 Mike Morris (one of my own students) and I began to write a paper on the general relativistic equations for wormholes supported by exotic material, and those equations’ connection to Sagan’s novel.
We wrote slowly. Other projects were more urgent and got higher priority. By the winter of 1987–88, we had submitted our paper to the American Journal of Physics, but it was not yet published; and Morris, nearing the end of his Ph.D. training, was applying for postdoctoral positions. With his applications, Morris enclosed the manuscript of our paper. Don Page (a professor at Pennsylvania State University and a former student of mine and Hawking’s) received the application, read our manuscript, and fired off a letter to Morris.
“Dear Mike, . . . it follows immediately from Proposition 9.2.8 of the book by Hawking- & Ellis, plus the Einstein field equations, that any wormhole [requires exotic material to hold it open] . . . Sincerely, Don N. Page.”
How stupid I felt. I had never studied global methods5 (the topic of the Hawking and Ellis book) in any depth, and I was now paying the price. I had deduced on Interstate 5, with modest labor, that to hold a precisely spherical wormhole open one must thread it with exotic material. However, now, using global methods and with even less labor, Page had deduced that to hold any wormhole open (a spherical wormhole, a cubical wormhole, a wormhole with random deformations), one must thread it with exotic material. I later learned that Dennis Gannon and C. W. Lee reached almost the same conclusion in 1975.
This discovery, that all wormholes require exotic material to hold them open, triggered much theoretical research during 1988–92. “Do the laws of physics permit exotic material to exist, and if so, under what circumstances?” This was the central issue.
A key to the answer had already been provided in the 1970s by Stephen Hawking. In 1970, when proving that the surface areas of black holes always increase (Chapter 12), Hawking had to assume that there is no exotic material near any black hole’s horizon. If exotic material were in the horizon’s vicinity, then Hawking’s proof would fail, his theorem would fail, and the horizon’s surface area could shrink. Hawking didn’t worry much about this possibility, however; it seemed in 1970 a rather safe bet that exotic material cannot exist.
Then, in 1974, came a great surprise: Hawking inferred as a by-product of his discovery of black-hole evaporation (Chapter 12) that vacuum fluctuations near a hole’s horizon are exotic: They have negative average energy density as seen by outgoing light beams near the hole’s horizon. In fact, it is this exotic property of the vacuum fluctuations that permits the hole’s horizon to shrink as the hole evaporates, in violation of Hawking’s area-increase theorem. Because exotic material is so important for physics, I shall explain this in greater detail:
Recall the origin and nature of vacuum fluctuations, as discussed in Box 12.4: When one tries to remove all electric and magnetic fields from some region of space, that is, when one tries to create a perfect vacuum, there always remain a plethora of random, unpredictable electromagnetic oscillations-oscillations caused by a tug-of-war between the fields in adjacent regions of space. The fields “here” borrow energy from the fields “there,” leaving the fields there with a deficit of energy, that is, leaving them momentarily with negative energy. The fields there then quickly grab the energy back and with it a little excess, driving their energy momentarily positive, and so it goes, onward and onward.
Under normal circumstances on Earth, the average energy of these vacuum fluctuations is zero. They spend equal amounts of time with energy deficits and energy excesses, and the average of deficit and excess vanishes. Not so near the horizon of an evaporating black hole, Hawking’s 1974 calculations suggested. Near a horizon the average energy must be negative, at least as measured by light beams, which means that the vacuum fluctuations are exotic.
How this comes about was not deduced in detail until the early 1980s, when Don Page at Pennsylvania State University, Philip Candelas at Oxford, and many other physicists used the laws of quantum fields in curved spacetime to explore in great detail the influence of a hole’s horizon on the vacuum fluctuations. They found that the horizon’s influence is key. The horizon distorts the vacuum fluctuations away from the shapes they would have on Earth, and by this distortion it makes their average energy density negative, that is, it makes the fluctuations exotic.
Under what other circumstances will vacuum fluctuations be exotic? Can they ever be exotic inside a wormhole, and thereby hold the wormhole open? This was the central thrust of the research effort triggered by Page’s noticing that the only way to hold any wormhole open is with exotic material.
The answer has not come easily, and is not entirely in hand. Gunnar Klinkhammer (a student of mine) has proved that in flat spacetime, that is, far from all gravitating objects, vacuum fluctuations can never be exotic—they can never have a negative average energy density as measured by light beams. On the other hand, Robert Wald (a former student of Wheeler’s) and Ulvi Yurtsever (a former student of mine) have proved that in curved spacetime, under a very wide variety of circumstances, the curvature distorts the vacuum fluctuations and thereby makes them exotic.
Is a wormhole that is trying to pinch off such a circumstance? Can the curvature of the wormhole, by distorting the vacuum fluctuations, make them exotic and enable them to hold the wormhole open? We still do not know, as this book goes to press.
In early 1988, as theoretical studies of exotic material were getting under way, I began to recognize the power of the kind of research that Carl Sagan’s phone call had triggered. Just as among all real physics experiments that an experimenter might do the ones most likely to yield deep new insights into the laws of physics are those that push on the laws the hardest, then similarly, among all thought experiments that a theorist might study, when probing laws that are beyond the reaches of modern technology, the ones most likely to yield deep new insights are those that push the hardest. And no type of thought experiment pushes the laws of physics harder than the type triggered by Carl Sagan’s phone call to me—thought experiments that ask, “What things do the laws of physics permit an infinitely advanced civilization to do, and what things do the laws forbid?” (By an “infinitely advanced civilization,” I mean one whose activities are limited only by the laws of physics, and not at all by ineptness, lack of know-how, or anything else.)
We physicists, I believe, have tended to avoid such questions because they are so close to science fiction. While many of us may enjoy reading science fiction or may even write some, we fear ridicule from our colleagues for working on research close to the science fiction fringe. We therefore have tended to focus on two other, less radical, types of questions: “What kinds of things occur naturally in the Universe?” (for example, do black holes occur naturally? and do wormholes occur naturally?). And “What kinds of things can we as humans, with our present or near-future technology, do?” (for example, can we produce new elements such as plutonium and use them to make atomic bombs? and can we produce high-temperature superconductors and use them to lower the power bills for levitated trains and Superconducting Supercollider magnets?).
By 1988 it seemed clear to me that we physicists had been much too conservative in our questions. Already, one Sagan-type question (as I shall call them) was beginning to bring a payoff. By asking, “Can an infinitely advanced civilization maintain wormholes for rapid interstellar travel?” Morris and I had identified exotic material as the key to wormhole maintenance, and we had triggered a somewhat fruitful effort to understand the circumstances under which the laws of physics do and do not permit exotic material to exist.
Suppose that our Universe was created (in the big bang) with no wormholes at all. Then eons later, when intelligent life has evolved and has produced a (hypothetical) infinitely advanced civilization, can that infinitely advanced civilization construct wormholes for rapid interstellar travel? Do the laws of physics permit wormholes to be constructed where previously there were none? Do the laws permit this type of change in the topology of our Universe’s space?
These questions are the second half of Carl Sagan’s interstellar transport problem. The first half, maintaining a wormhole once it has been constructed, Sagan solved with the help of exotic matter. The second half he finessed. In his novel, he describes the wormhole through which Eleanor Arroway traveled as now being maintained by exotic matter, but as having been created in the distant past by some infinitely advanced civilization, from which all records have been lost.
We physicists, of course, are not happy to relegate wormhole creation to prehistory. We want to know whether and how the Universe’s topology can be changed now, within the confines of physical law.
We can imagine two strategies for constructing a wormhole where before there was none: a quantum strategy, and a classical strategy.
The quantum strategy relies on gravitational vacuum fluctuations (Box 12.4), that is, the gravitational analogue of the electromagnetic vacuum fluctuations discussed above: random, probabilistic fluctuations in the curvature of space caused by a tug-of-war in which adjacent regions of space are continually stealing energy from each other and then giving it back. Gravitational vacuum fluctuations are thought to be everywhere, but under ordinary circumstances they are so tiny that no experimenter has ever detected them.
Just as an electron’s random degeneracy motions become more vigorous when one confines the electron to a smaller and smaller region (Chapter 4), so also gravitational vacuum fluctuations are more vigorous in small regions than in large, that is, for small wavelengths rather than for large. In 1955, John Wheeler, by combining the laws of quantum mechanics and the laws of general relativity in a tentative and crude way, deduced that in a region the size of the Planck–Wheeler length,6 1.62 × 10–33 centimeter or smaller, the vacuum fluctuations are so huge that space as we know it “boils” and becomes a froth of quantum foam—the same sort of quantum foam as makes up the core of a spacetime singularity (Chapter 13; Figure 14.3).
Quantum foam, therefore, is everywhere: inside black holes, in interstellar space, in the room where you sit, in your brain. But to see the quantum foam, one would have to zoom in with a (hypothetical) supermicroscope, looking at space and its contents on smaller and smaller scales. One would have to zoom in from the scale of you and me (hundreds of centimeters) to the scale of an atom (10−8 centimeter), to the scale of an atomic nucleus (10−13 centimeter), and then on downward by twenty factors of 10 more, to 10−33 centimeter. At all the early, “large” scales, space would look completely smooth, with a very definite (but tiny) amount of curvature. As the microscopic zoom nears, then passes 10−32 centimeter, however, one would see space begin to writhe, ever so slightly at first, and then more and more strongly until, when a region just 10−33 centimeter in size fills the supermicroscope’s entire eyepiece, space has become a froth of probabilistic quantum foam.
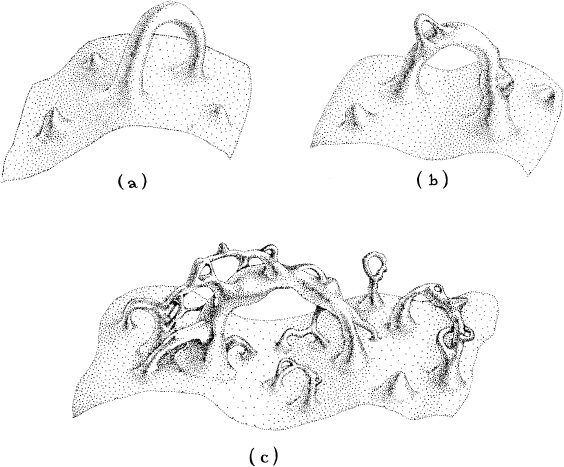
14.3 (Same as Figure 13.7.) Embedding diagrams illustrating quantum foam. The geometry and topology of space are not definite; instead, they are probabilistic. They might have, for example, a 0.1 percent probability for the form shown in (a), a 0.4 percent probability for (b), a 0.02 percent probability for (c), and so on.
Since the quantum foam is everywhere, it is tempting to imagine an infinitely advanced civilization reaching down into the quantum foam, finding in it a wormhole (say, the “big” one in Figure 14.3b with its 0.4 percent probability), and trying to grab that wormhole and enlarge it to classical size. In 0.4 percent of such attempts, if the civilization were truly infinitely advanced, they might succeed. Or would they?
We do not yet understand the laws of quantum gravity well enough to know. One reason for our ignorance is that we do not understand the quantum foam itself very well. We aren’t even 100 percent sure it exists. However, the challenge of this Sagan—type thought experiment—an advanced civilization pulling wormholes out of the quantum foam—might be of some conceptual help in the coming years, in efforts to firm up our understanding of quantum foam and quantum gravity.
So much for the quantum strategy of wormhole creation. What is the classical strategy?
In the classical strategy, our infinitely advanced civilization would try to warp and twist space on macroscopic scales (normal, human scales) so as to make a wormhole where previously none existed. It seems fairly obvious that, in order for such a strategy to succeed, one must tear two holes in space and sew them together. Figure 14.4 shows an example.
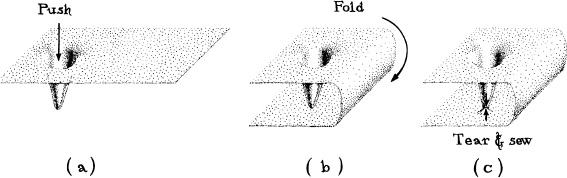
14.4 One strategy for making a wormhole. (a) A “sock” is created in the curvature of space. (b) Space outside the sock is gently folded in hyperspace. (c) A small hole is torn in the toe of the sock, a hole is torn in space just below the hole, and the edges of the holes are “sewn” together. This strategy looks classical (macroscopic) at first sight. However, the tearing produces, at least momentarily, a spacetime singularity which is governed by the laws of quantum gravity, so this strategy is really a quantum one.
Now, any such tearing of space produces, momentarily, at the point of the tear, a singularity of spacetime, that is, a sharp boundary at which spacetime ends; and since singularities are governed by the laws of quantum gravity, such a strategy for making wormholes is actually quantum mechanical, not classical. We will not know whether it is permitted until we understand the laws of quantum gravity.
Is there no way out? Is there no way to make a wormhole without getting entangled with the ill-understood laws of quantum gravity—no perfectly classical way?
Somewhat surprisingly, there is—but only if one pays a severe price. In 1966, Robert Geroch (a student of Wheeler’s at Princeton) used global methods to show that one can construct a wormhole by a smooth, singularity-free warping and twisting of spacetime, but one can do so only if, during the construction, time also becomes twisted up as seell in all reference frames.7 More specifically, while the construction is going on, it must be possible to travel backward in time, as well as forward; the “machinery” that does the construction, whatever it might be, must function briefly as a time machine that carries things from late moments of the construction back to early moments (but not back to moments before the construction began).
The universal reaction to Geroch’s theorem, in 1967, was “Surely the laws of physics forbid time machines, and thereby they will prevent a wormhole from ever being constructed classically, that is, without tearing holes in space.”
In the decades since 1967, some things we thought were sure have been proved wrong. (For example, we would never have believed in 1967 that a black hole can evaporate.) This has taught us caution. As part of our caution, and triggered by Sagan-type questions, we began asking in the late 1980s, “Do the laws of physics really forbid time machines, and if so, how? How might the laws enforce such a prohibition?” To this question I shall return below.
Let us now pause and take stock. In 1993 our best understanding of wormholes is this:
If no wormholes were made in the big bang, then an infinitely advanced civilization might try to construct one by two methods, quantum (pulling it out of the quantum foam) or classical (twisting spacetime without tearing it). We do not understand the laws of quantum gravity well enough to deduce, in 1993, whether the quantum construction of wormholes is possible. We do understand the laws of classical gravity (general relativity) well enough to know that the classical construction of wormholes is permitted only if the construction machinery, whatever it might be, twists time up so strongly, as seen in all reference frames, that it produces, at least briefly, a time machine.
We also know that, if an infinitely advanced civilization somehow acquires a wormhole, then the only way to hold the wormhole open (so it can be used for interstellar travel) is by threading it with exotic material. We know that vacuum fluctuations of the electromagnetic field are a promising form of exotic material: They can be exotic (have a negative average energy density as measured by a light beam) in curved spacetime under a wide variety of circumstances. However, we do not yet know whether they can be exotic inside a wormhole and thereby hold the wormhole open.
In the pages to come, I shall assume that an infinitely advanced civilization has somehow acquired a wormhole and is holding it open by means of some sort of exotic material; and I shall ask what other uses, besides interstellar travel, the civilization might find for its wormhole.
Time Machines
In December 1986, the fourteenth semi-annual Texas Symposium on Relativistic Astrophysics was held in Chicago, Illinois. These “Texas” symposia, patterned after the 1963 one in Dallas, Texas, where the mystery of quasars was first discussed (Chapters 7 and 9), had by now become a firmly established institution. I went to the symposium and lectured on dreams and plans for LIGO (Chapter 10). Mike Morris (my “wormhole” student) also went, to get his first full-blown exposure to the international community of relativity physicists and astrophysicists.
In the corridors between lectures, Morris became acquainted with Tom Roman, a young assistant professor from Central Connecticut State University who, several years earlier, had produced deep insights about exotic matter. Their conversation quickly turned to wormholes. “If a wormhole can really be held open, then it will permit one to travel over interstellar distances far faster than light,” Roman noted.
“Doesn’t this mean that one can also use a wormhole to travel backward in time?”
How stupid Mike and 1 felt! Of course; Roman was right. We, in fact, had learned about such time travel in our childhoods from a famous limerick:
There once was a lady named Bright
who traveled much faster than light.
She departed one day in a relative way
and came home the previous night.
With Roman’s comment and the famous limerick to goad us, we easily figured out how to construct a time machine using two wormholes that move at high speeds relative to each other.8 (I shall not describe that time machine here, because it is a bit complicated and there is a simpler, more easily described time machine to which I shall come shortly.)
I am a loner; I like to retreat to the mountains or an isolated seacoast, or even just into an attic, and think. New ideas come slowly and require large blocks of quiet, undisturbed time to gestate; and most worthwhile calculations require days or weeks of intense, steady concentration. A phone call at the wrong moment can knock my concentration off balance, setting me back by hours. So I hide from the world.
But hiding for too long is dangerous. I need, from time to time, the needle-pricking stimulus of conversations with people whose viewpoints and expertise are different from mine.
In this chapter thus far I have described three examples. Without Carl Sagan’s phone call and the challenge to make his novel scientifically correct, I would never have ventured into research on wormholes and time machines. Without Don Page’s letter, Mike Morris and I would not have known that all wormholes, regardless of their shape, require exotic material to keep them open. And without Tom Roman’s remark, Morris and I might have gone on blithely unaware that from wormholes an advanced civilization can easily make a time machine.
In the pages to come, I will describe other examples of the crucial role of needle-pricking interactions. However, not all ideas arise that way. Some arise from introspection. June 1987 was a case in point.
In early June 1987, emerging from several months of frenetic class-room teaching and interactions with my research group and the LIGO team, I retreated, exhausted, into isolation.
All spring long something had been gnawing at me, and I had been trying to ignore it, waiting for some days of quiet, to ponder. Those days, at last, had come. In isolation, I let the gnawing emerge from my subconscious and began to examine it: “How does time decide how to hook itself up through a wormhole?” That was the nub of the gnaw.
To make this question more concrete, I thought about an example: Suppose that I have a very short wormhole, one whose tunnel through hyperspace is only 30 centimeters long, and suppose that both mouths of the wormhole—two spheres, each 2 meters in diameter—are sitting in my Pasadena living room. And suppose that I climb through the wormhole, head first. From my viewpoint, I must emerge from the second mouth immediately after I enter the first, with no delay at all; in fact, my head is coming out of the second mouth while my feet are still entering the first. Does this mean that my wife, Carolee, sitting there on the living room sofa, will also see my head emerging from the second mouth while my feet are still climbing into the first, as in Figure 14.5? If so, then time “hooks up through the wormhole” in the same manner as it hooks up outside the wormhole.
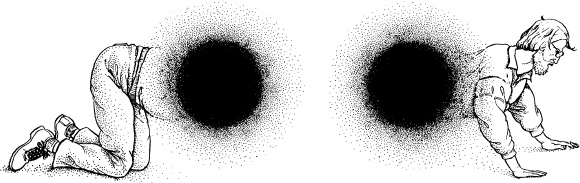
14.5 A picture of me crawling through a hypothetical, very short wormhole.
On the other hand, I asked myself, isn’t it possible that, although the trip through the wormhole takes almost no time as seen by me, Carolee must wait an hour before she sees me emerge from the second mouth; and isn’t it also possible that she sees me emerge an hour before I entered? If so, then time would be hooked up through the wormhole in a different manner than it hooks up outside the wormhole.
What could possibly make time behave so weirdly? I asked myself. On the other hand, why shouldn’t it behave in this way? Only the laws of physics know the answer, I reasoned. Somehow, I ought to be able to deduce from the laws of physics just how time will behave.
As an aid to understanding how the laws of physics control time’s hookup, I thought about a more complicated situation. Suppose that one mouth of the wormhole is at rest in my living room and the other is in interstellar space, traveling away from Earth at nearly the speed of light. And suppose that, despite this relative motion of its two mouths, the wormhole’s length (the length of its tunnel through hyperspace) remains always fixed at 30 centimeters. (Figure 14.6 explains how it is possible for the length of the wormhole to remain fixed while its mouths, as seen in the external Universe, move relative to each other.) Then, as seen in the external Universe, the two mouths are in different reference frames, frames that move at a high speed relative to each other; and the mouths therefore must experience different flows of time. On the other hand, as seen through the wormhole’s interior, the mouths are at rest with respect to each other, so they share a common reference frame, which means that the mouths must experience the same flow of time. From the external viewpoint they experience different time flows, and from the internal viewpoint, the same time flow; how confusing!
14.6 Explanation of how the mouths of a wormhole can move relative to each other as seen in the external Universe, while the length of the wormhole remains fixed. Each of the diagrams is an embedding diagram like that in Figure 14.1, seen in profile. The diagrams are a sequence of snapshots that depict motion of the Universe and the wormhole relative to hyperspace. (Recall, however, that hyperspace is just a useful figment of our imaginations; there is no way that we as humans can ever see or experience it in reality; see Figures 3.2 and 3.3.) Relative to hyperspace, the bottom part of our Universe is sliding rightward in the diagrams, while the wormhole and the top part of our Universe remain at rest. Correspondingly, as seen in our Universe, the mouths of the wormhole are moving relative to each other (they are getting farther apart), but as seen through the wormhole they are at rest with respect to each other; the wormhole’s length does not change.
Gradually, in my quiet isolation, the confusion subsided and all became clear. The laws of general relativity predict, unequivocally, the flow of time at the two mouths, and they predict, unequivocally, that the two time flows will be the same when compared through the wormhole, but will be different when compared outside the wormhole. Time, in this sense, hooks up to itself differently through the wormhole than through the external Universe, when the two mouths are moving relative to each other.
And this difference of hookup, I then realized, implies that from a single wormhole, an infinitely advanced civilization can make a time machine. There is no need for two wormholes. How? Easy, if you are infinitely advanced.
To explain how, I shall describe a thought experiment in which we humans are infinitely advanced beings. Carolee and I find a very short wormhole, and put one of its mouths in the living room of our home and the other in our family spacecraft, outside on the front lawn.
Now, as this thought experiment will show, the manner in which time is hooked up through any wormhole actually depends on the wormhole’s past history. For simplicity, I shall assume that when Carolee and I first acquire the wormhole, it has the simplest possible hookup of time: the same hookup through the wormhole’s interior as througll the exterior Universe. In other words, if I climb through the wormhole, Carolee, I, and everyone on Earth will agree that I emerge from the mouth in the spacecraft at essentially the same moment as I entered the mouth in the living room.
Having checked that time is, indeed, hooked up through the wormhole in this way, Carolee and I then make a plan: I will stay at home in our living room with the one mouth, while Carolee in our spacecraft takes the other mouth on a verv high speed trip out into the Universe and back. Throughout the trip, we will hold hands through the wormhole; see Figure 14.7.
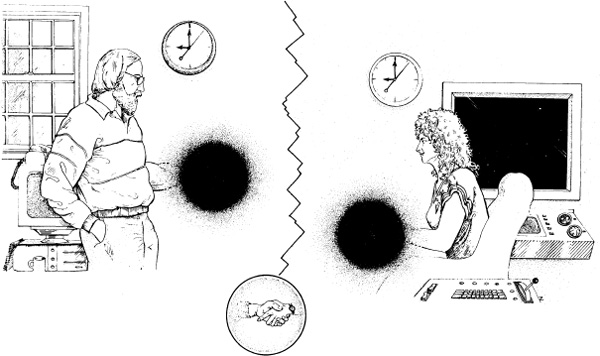
14.7 Carolee and I construct a time machine from a wormhole. Left: I stay at home in Pasadena with one mouth of the wormhole and hold hands with Carolee through the wormhole. Right: Carolee carries the other mouth on a high-speed trip through the Universe. Inset: Our hands inside the wormhole.
Carolee departs at 9:00 A.M. on 1 January 2000, as measured by herself, by me, and by everybody else on Earth. Carolee zooms away from Earth at nearly the speed of light for 6 hours as measured by her own time; then she reverses course and zooms back, arriving on the front lawn 12 hours after her departure as measured by her own time.9 I hold hands with her and watch her through the wormhole throughout the trip, so obviously I agree, while looking through the wormhole, that she has returned after just 12 hours, at 9:00 P.M. on 1 January 2000. Looking through the wormhole at 9:00 P.M., I can see not only Carolee; I can also see, behind her, our front lawn and our house.
Then, at 9:01 P.M., I turn and look out the window—and there I see an empty front lawn. The spaceship is not there; Carolee and the other wormhole mouth are not there. Instead, if I had a good enough telescope pointed out the window, I would see Carolee’s spaceship flying away from Earth on its outbound journey, a journey that as measured on Earth, looking through the external Universe, will require 10 years. [This is the standard “twins paradox”; the high-speed “twin” who goes out and comes back (Carolee) measures a time lapse of only 12 hours, while the “twin” who stays behind on Earth (me) must wait 10 years for the trip to be completed.]
I then go about my daily routine of life. For day after day, month after month, year after year, I carry on with life, waiting—until finally, on 1 January 2010, Carolee returns from her journey and lands on the front lawn. I go out to meet her, and find, as expected, that she has aged just 12 hours, not 10 years. She is sitting there in the spaceship, her hand thrust into the wormhole mouth, holding hands with somebody. I stand behind her, look into the mouth, and see that the person whose hand she holds is myself, 10 years younger, sitting in our living room on 1 January 2000. The wormhole has become a time machine. If I now (on 1 January 2010) climb into the wormhole mouth in the spaceship, I will emerge through the other mouth in our living room on 1 January 2000, and there I will meet my younger self. Similarly, if my younger self climbs into the mouth in the living room on 1 January 2000, he will emerge from the mouth in the spaceship on 1 January 2010. Travel through the wormhole in one direction takes me backward 10 years in time; travel in the other direction takes me 10 years forward.
Neither I nor anyone else, however, can use the wormhole to travel back in time beyond 9:00 P.M., 1 January 2000. It is impossible to travel to a time earlier than when the wormhole first became a time machine.
The laws of general relativity are unequivocal. If wormholes can be held open by exotic material, then these are general relativity’s predictions.
In summer 1987, a month or so after I arrived at these predictions, Richard Price telephoned Carolee. Richard—a close friend of mine and the man who sixteen years earlier had shown that a black hole radiates away all its “hair” (Chapter 7)—was worried about me. He had heard that I was working on the theory of time machines, and he feared I had gone a little crazy or senile or. . . Carolee tried to reassure him.
Richard’s call shook me up a bit. Not because I doubted my own sanity; I had few doubts. However, if even my closest friends were worried, then (at least as a protection for Mike Morris and my other students, if not for myself) I would have to be careful about how we presented our research to the community of physicists and to the general public.
During the winter of 1987–88, as part of my caution, I decided to move slowly on publishing anything about time machines. Together with two students, Mike Morris and Ulvi Yurtsever, I focused on trying to understand everything I could about wormholes and time. Only after all issues were crystal clear did I want to publish.
Morris, Yurtsever, and I worked together by computer link and telephone, since I was hiding in isolation. Carolee had taken a two-year postdoctoral appointment in Madison, Wisconsin, and I had gone along as her “house husband” for the first seven months (January–July 1988). I had set up my computer and working tables in the attic of the house we rented in Madison; and I was spending most of my waking hours there in the attic, thinking, calculating, and writing—largely on other projects, but partly on wormholes and time.
For stimulus and to test my ideas against skilled “opponents,” every few weeks I drove over to Milwaukee to talk with a superb group of relativity researchers led by John Friedman and Leonard Parker, and occasionally I drove down to Chicago to talk with another superb group led by Subrahmanyan Chandrasekhar, Robert Geroch, and Robert Wald.
On a March visit to Chicago, I got a jolt. I gave a seminar describing everything I understood about wormholes and time machines; and after the seminar, Geroch and Wald asked me (in effect), “Won’t a wormhole be automatically destroyed whenever an advanced civilization tries to convert it into a time machine?”
Why? How? I wanted to know. They explained. Translated into the language of the Carolee-and-me story, their explanation was the following: Imagine that Carolee is zooming back to Earth with one wormhole mouth in her spacecraft and I am sitting at home on Earth with the other. Shortly after she turns around and begins zooming home, it suddenly becomes possible for radiation (electromagnetic waves) to use the wormhole for time travel: Any random bit of radiation that leaves our home in Pasadena traveling at the speed of light toward her spacecraft can arrive at the spacecraft after 5 years’ time (as seen on Earth), enter the wormhole mouth there, travel back in time by 5 years (as seen on Earth), and emerge from the mouth on Earth at precisely the same moment as it started its trip. The radiation piles right on top of its previous self, not just in space but in spacetime, doubling its strength. What’s more, during the trip each quantum of radiation (each photon) got boosted in energy due to the relative motion of the wormhole mouths (a “Doppler-shift” boost).
After the radiation’s next trip out to the spacecraft then back through the wormhole, it again returns at the same time as it left and again piles up on itself, again with a Doppler-boosted energy. Again and again this happens, making the beam of radiation infinitely strong (Figure 14.8a).
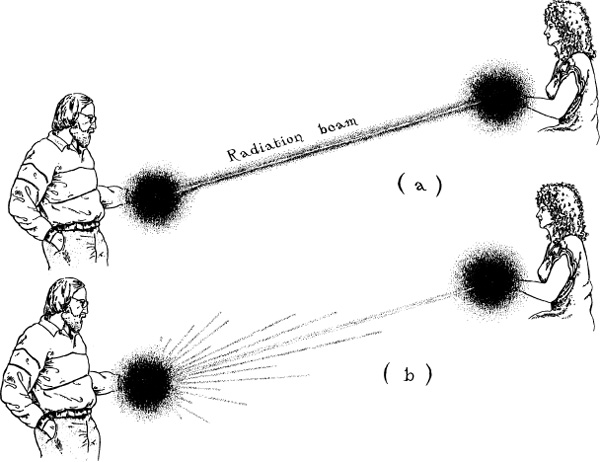
14.8 (a) The Geroch-Wald suggestion for how a wormhole might get destroyed when one tries to make it into a time machine. An intense beam of radiation zooms between the two mouths and through the wormhole, piling up on and reinforcing itself. The beam becomes infinitely energetic and destroys the wormhole. (b) What actually happens. The wormhole defocuses the beam, reducing the amount of pileup. The beam remains weak; the wormhole is not destroyed.
In this way, beginning with an arbitrarily tiny amount of radiation, a beam of infinite energy is created, coursing through space between the two wormhole mouths. As the beam passes through the wormhole, Geroch and Wald argued, it will produce infinite spacetime curvature and probably destroy the wormhole, thereby preventing the wormhole from becoming a time machine.
I drove away from Chicago and up Interstate 90 toward Madison in a daze. My mind was filled with geometric pictures of radiation beams shooting from one wormhole mouth to the other, as the mouths move toward each other. I was trying to compute, pictorially, just what would happen. I was trying to understand whether Geroch and Wald were right or wrong.
Gradually, as I neared the Wisconsin border, the pictures in my mind became clear. The wormhole would not be destroyed. Geroch and Wald had overlooked a crucial fact: Every time the beam of radiation passes through the wormhole, the wormhole defocuses it in the manner of Box 14.1 above. After the defocusing, the beam emerges from the mouth on Earth and spreads out over a wide swath of space, so that only a tiny fraction of it can get caught by the mouth on the spacecraft and transported through the wormhole back to Earth to “pile up” on itself (Figure 14.8b).
I could do the sum visually in my head, as I drove. By adding up all the radiation from all the trips through the wormhole (a tinier and tinier amount after each defocusing trip), I computed that the final beam would be weak; far too weak to destroy the wormhole.
My calculation turned out to be right; but, as I shall explain later, I should have been more cautious. This brush with wormhole destruction should have warned me that unexpected dangers await any maker of time machines.
When graduate students reach the final year of their research, they often give me great pleasure. They produce major insights on their own; they argue with me and win; they teach me unexpected things. Such was the case with Morris and Yurtsever as we gradually moved toward finalizing our manuscript for Physical Review Letters. Large portions of the manuscript’s technical details and technical ideas were theirs.
As our work neared completion, I oscillated between worrying about tarnishing Morris’s and Yurtsever’s budding scientific reputations with a label of “crazy science fiction physicists” and waxing enthusiastic about the things we had learned and about our realization that Sagan-type questions can be powerful in physics research. At the last minute, as we finalized the paper, I suppressed my caution (which Morris and Yurtsever seemed not to share), and agreed with them to give our paper the title “Wormholes, Time Machines, and the Weak Energy Condition” (“weak energy condition” being the technical term associated with “exotic matter”).
Despite the “time machines” in the title, our paper was accepted for publication without question. The two anonymous referees seemed to be sympathetic; I heaved a sigh of relief.
With the publication date nearing, caution took hold of me again; I asked the staff of the Caltech Public Relations Office to avoid and, indeed, try to suppress any and all publicity about our time machine research. A sensational splash in the press might brand our research as crazy in the eyes of many physicists, and I wanted our paper to be studied seriously by the physics community. The public relations staff acquiesced.
Our paper was published, and all went well. As I had hoped, the press missed it, but among physicists it generated interest and controversy. Letters trickled in, asking questions and challenging our claims; but we had done our homework. We had answers.
My friends’ reactions were mixed. Richard Price continued to worry; he had decided I wasn’t crazy or senile, but he feared I would sully my reputation. My Russian friend Igor Novikov, by contrast, was ecstatic. Telephoning from Santa Cruz, California, where he was visiting, Novikov said, “I’m so happy, Kip! You have broken the barrier. If you can publish research on time machines, then so can I!” And he proceeded to do so, forthwith.
The Matricide Paradox
Among the controversies stirred up by our paper, the most vigorous was over what I like to call the matricide paradox10: If I have a time machine (wormhole-based or otherwise), I should be able to use it to go back in time and kill my mother before I was conceived, thereby preventing myself from being born and killing my mother.11
Central to the matricide paradox is the issue of free will: Do I, or do I not, as a human being, have the power to determine my own fate? Can I really kill my mother, after going backward in time, or (as in so many science fiction stories) will something inevitably stay my hand as I try to stab her in her sleep?
Now, even in a universe without time machines, free will is a terribly difficult thing for physicists to deal with. We usually try to avoid it. It just confuses issues that otherwise might be lucid. With time machines, all the more so. Accordingly, before publishing our paper (but after long discussions with our Milwaukee colleagues), Morris, Yurtsever, and I decided to avoid entirely the issue of free will. We insisted on not discussing at all, in print, human beings who go through a wormhole-based time machine. Instead, we dealt only with simple, inanimate time-traveling things, such as electromagnetic waves.
Before publishing, we thought a lot about waves that travel backward in time through a wormhole; we searched hard for unresolvable paradoxes in the waves’ evolution. Ultimately (and with crucial proddings from John Friedman), we convinced ourselves that there probably will be no unresolvable paradoxes, and we conjectured so in our paper.12 We even broadened our conjecture to suggest that there would never be unresolvable paradoxes for any inanimate object that passes through the wormhole. It was this conjecture that created the most controversy.
Of the letters we received, the most interesting was from Joe Polchinski, a professor of physics at the University of Texas in Austin. Polchinski wrote, “Dear Kip, . . . If I understand correctly, you are conjecturing that in your [wormhole-based time machine there will be no unresolvable paradoxes]. It seems to me that . . . this is not the case.” He then posed an elegant and simple variant of the matricide paradox—a variant that is not entangled with free will and that we therefore felt competent to analyze:
Take a wormhole that has been made into a time machine, and place its two mouths at rest near each other, out in interplanetary space (Figure 14.9). Then, if a billiard ball is launched toward the right mouth from an appropriate initial location and with an appropriate initial velocity, the ball will enter the right mouth, travel backward in time, and fly out of the left mouth before it entered the right (as seen by you and me outside the wormhole), and it will then hit its younger self, thereby preventing itself from ever entering the right mouth and hitting itself.
This situation, like the matricide paradox, entails going back in time and changing history. In the matricide paradox, I go back in time and, by killing my mother, prevent myself from being born. In Polchinski’s paradox, the billiard ball goes back in time and, by hitting itself, prevents itself from ever going back in time.
Both situations are nonsensical. Just as the laws of physics must be logically consistent with each other, so also the evolution of the Universe, as governed by the laws of physics, must be fully consistent with itself—or at least it must be so when the Universe is behaving classically (non–quantum mechanically); the quantum mechanical realm is a little more subtle. Since both I and a billiard ball are highly classical objects (that is, we can exhibit quantum mechanical behavior only when one makes exceedingly accurate measurements on us; see Chapter 10), there is no way that either I or the billiard ball can go back in time and change our own histories.
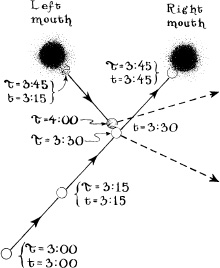
14.9 Polchinski’s billiard ball version of the matricide paradox. The wormhole is very short and has been made into a time machine, so that anything that enters the right mouth emerges, as measured on the outside, 30 minutes before it went in. The flow of time outside the mouth is denoted by the symbol t; the flow of time as experienced by the billiard ball itself is denoted by τ. The billiard ball is launched at t = 3:00 P.M. from the indicated location and with just the right velocity to enter the right mouth at t = 3:45. The ball emerges from the left mouth 30 minutes earlier, at t = 3:15, and then hits its younger self at t = 3:30 P.M., knocking itself off track so it cannot enter the right mouth and hit itself.
So what happens to the billiard ball? To find out, Morris, Yurtsever, and I focused our attention on the ball’s initial conditions, that is, its initial location and velocity. We asked ourselves, “For the same initial conditions as led to Polchinski’s paradox, is there any other billiard ball trajectory that, unlike the one in Figure 14.9, is a logically self-consistent solution to the physical laws that govern classical billiard balls?” After much discussion, we agreed that the answer was probably “yes,” but we were not absolutely sure—and there was no time for us to figure it out. Morris and Yurtsever had completed their Ph.D.s and were leaving Caltech to take up postdoctoral appointments in Milwaukee and Trieste.
Fortunately, Caltech continually draws great students. There were two new ones waiting in the wings: Fernando Echeverria and Gunnar Klinkhammer. Echeverria and Klinkhammer took Polchinski’s paradox and ran with it: After some months of on-and-off mathematical struggle, they proved that there indeed is a fully self-consistent billiard ball trajectory that begins with Polchinski’s initial data and satisfies all the laws of physics that govern classical billiard balls. In fact, there are two such trajectories. They are shown in Figure 14.10. I shall describe each of these trajectories in turn, from the viewpoint of the ball itself.
On trajectory (a) (left half of Figure 14.10), the ball, young, clean, and pristine, starts out at time t = 3:00 P.M., moving along precisely the same route as in Polchinski’s paradox (Figure 14.9), a route taking it toward the wormhole’s right mouth. A half hour later, at t = 3:30, the young, pristine ball gets hit on its left, rear side, by an older-looking, cracked ball (which will turn out to be its older self). The collision is gentle enough to deflect the young ball only slightly from its original course, but hard enough to crack it. The young ball, now cracked, continues onward along its slightly altered trajectory and enters the wormhole mouth at t = 3:45, travels backward in time by 30 minutes, and exits from the other mouth at t = 3:15. Because its trajectory has been altered slightly by comparison with Polchinski’s paradoxical trajectory (Figure 14.9), the ball, now old and cracked, hits its younger self a gentle, glancing blow on the left, rear side at t = 3:30, instead of the vigorous, highly deflecting blow of Figure 14.9. The evolution thereby is made fully self-consistent.
Trajectory (b), the right half of Figure 14.10, is the same as (a), except that the geometry of the collision is slightly different, and correspondingly the trajectory between collisions is slightly different. In particular, the old, cracked ball emerges from the left mouth on a different trajectory than in (a), a trajectory that takes it in front of the young, pristine ball (instead of behind it), and produces a glancing blow on the young ball’s front, right side (instead of left rear side).
Echeverria and Klinkhammer showed that both trajectories, (a) and (b), satisfy all the physical laws that govern classical billiard balls, so both are possible candidates to occur in the real Universe (if the real Universe can have wormhole-based time machines).
This is most disquieting. Such a situation can never occur in a universe without time machines. Without time machines, each set of initial conditions for a billiard ball gives rise to one and only one trajectory that satisfies all the classical laws of physics. There is a unique prediction for the ball’s motion. The time machine has ruined this. There now are two, equally good predictions for the ball’s motion.
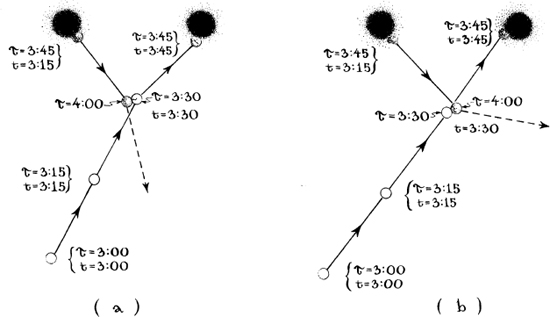
14.10 The resolution of Polchinski’s version of the matricide paradox (Figure 14.9): A billiard ball, starting out at 3:00 P.M. with the same initial conditions (same location and velocity) as in Polchinski’s paradox, can move along either of the two trajectories shown here. Each of these trajectories is fully self-consistent and satisfies the classical laws of physics everywhere along the trajectory.
Actually, the situation is even worse than it looks at first sight: The time machine makes possible an infinite number of equally good predictions for the ball’s motion, not just two. Box 14.2 shows a simple example.
Box 14.2
The Billiard Ball Crisis: An Infinity of Trajectories
One day, while sitting in San Francisco Airport waiting for a plane, it occurred to me that, if a billiard ball is fired between the two mouths of a wormhole-based time machine, there are two trajectories on which it can travel. On one (a), it hurtles between the mouths unscathed. On the other (b), as it is passing between the two mouths, it gets hit and knocked rightward, toward the right mouth; it then goes down the wormhole, emerges from the left mouth before it went down, hits itself, and flies away.
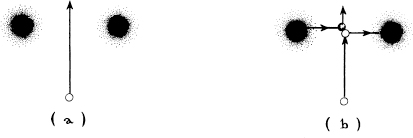
Some months later, Robert Forward [one of the pioneers of laser interferometer gravitational-wave detectors (Chapter 10) and also a science fiction writer] discovered a third trajectory that satisfies all the laws of physics, the trajectory (c) below: The collision, instead of occurring between the mouths, occurs before the ball reaches the mouths’ vicinity. I then realized that the collision could be made to occur earlier and earlier, as in (d) and (e), if the ball travels through the wormhole several times between its two visits to the collision event. For example, in (e), the ball travels up route α, gets hit by its older self and knocked along β and into the right mouth; it then travels through the wormhole (and backward in time), emerging from the left mouth on γ, which takes it through the wormhole again (and still farther back in time), emerging along δ, which takes it through the wormhole yet again (and even farther back in time), emerging along ε, which takes it to the collision event, from which it is deflected down ζ.
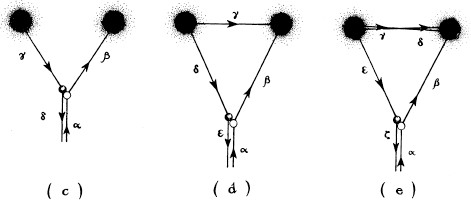
Evidently, there are an infinite number of trajectories (each with a different number of wormhole traversals) that all satisfy the classical (non-quantum) laws of physics, and all begin with identically the same initial conditions (the same initial billiard ball location and velocity). One is left wondering whether physics has gone crazy, or whether, instead, the laws of physics can somehow tell us which trajectory the ball ought to take.
Do time machines make physics go crazy? Do they make it impossible to predict how things evolve? If not, then how do the laws of physics choose which trajectory, out of the infinite allowed set, a billiard ball will follow?
In search of an answer, Gunnar Klinkhammer and I in 1989 turned from the classical laws of physics to the quantum laws. Why the quantum laws? Because they are the Ultimate Rulers of our Universe.
For example, the laws of quantum gravity have ultimate control over gravitation and the structure of space and time. Einstein’s classical, general relativistic laws of gravity are mere approximations to the quantum gravity laws—approximations with excellent accuracy when one is far from all singularities and looks at spacetime on scales far larger than 10−33 centimeter, but approximations nevertheless (Chapter 13).
Similarly, the classical laws of billiard ball physics, which my students and I had used in studying Polchinski’s paradox, are mere approximations to the quantum mechanical laws. Since the classical laws seem to predict “nonsense” (an infinity of possible billiard ball trajectories), Klinkhammer and I turned to the quantum mechanical laws for deeper understanding.
The “rules of the game” are very different in quantum physics than in classical physics. When one provides the classical laws with initial conditions, they predict what will happen afterward (for example, what trajectory a ball will follow); and, if there are no time machines, their predictions are unique. The quantum laws, by contrast, predict only probabilities for what will happen, not certainties (for example, the probability that a ball will travel through this, that, or another region of space).
In light of these rules of the quantum mechanical game, the answer that Klinkhammer and I got from the quantum mechanical laws is not surprising. We learned that, if the ball starts out moving along Polchinski’s paradoxical trajectory (Figures 14.9 and 14.10 at time t = 3:00 P.M.), then there will be a certain quantum mechanical probability—say, 48 percent—for it subsequently to follow trajectory Ca) in Figure 14.10, and a certain probability-say, also 48 percent—for trajectory (b), and a certain (far smaller) probability for each of the infinity of other classically allowed trajectories. In anyone “experiment,” the ball will follow just one of the trajectories that the classical laws allow; but if we perform a huge number of identical billiard ball experiments, in 48 percent of them the ball will follow trajectory (a), in 48 percent trajectory (b), and so forth.
This conclusion is somewhat satisfying. It suggests that the laws of physics might accommodate themselves to time machines fairly nicely. There are surprises, but there seem not to be any outrageous predictions, and there is no sign of any unresolvable paradox. Indeed, the National Enquirer, hearing of this, could easily display a banner headline: PHYSICISTS PROVE TIME MACHINES EXIST. (That kind of outrageous distortion, of course, has been my recurrent fear.)
In the autumn of 1988, three months after the publication of our paper “Wormholes, Time Machines, and the Weak Energy Condition,” Keay Davidson, a reporter for the San Francisco Examiner, discovered it in Physical Review Letters and broke the story.
It could have been worse. At least the physics community had had three months of quiet in which to absorb our ideas without the blare of sensational headlines.
But the blare was unstoppable. PHYSICISTS INVENT TIME MACHINES, read a typical headline. California magazine, in an article on “The Man Who Invented Time Travel,” even ran a photograph of me doing physics in the nude on Palomar Mountain. I was mortified—not by the photo, but by the totally outrageous claims that I had invented time machines and time travel. If time machines are, in fact, allowed by the laws of physics (and, as will become clear at the end of the chapter, I doubt that they are), then they are probably much farther beyond the human race’s present technological capabilities than space travel was beyond the capabilities of cavemen.
After talking with two reporters, I abandoned all efforts to stem the tide and get the story told accurately, and went into hiding. My besieged administrative assistant, Pat Lyon, had to fend off the press with a firm “Professor Thorne believes it is too early in this research effort to communicate results to the general public. When he feels he has a better understanding of whether or not time machines are forbidden by the laws of physics, he will write an article for the public, explaining.”
With this chapter of this book, I am making good on that promise.
Chronology Protection?
In February 1989, as the hoopla in the press was beginning to subside, and while Echeverria, Klinkhammer, and I were struggling with Polchinski’s paradox, I flew to Bozeman, Montana, to give a lecture. There I ran into Bill Hiscock, a former student of Charles Misner’s. As I have with so many colleagues, I pressed Hiscock for his views on wormholes and time machines. I was searching for cogent criticisms, new ideas, new viewpoints.
“Maybe you should study electromagnetic vacuum fluctuations,” Hiscock told me. “Maybe they will destroy the wormhole when infinitely advanced beings try to turn it into a time machine.” Hiscock had in mind the thought experiment in which my wife Carolee (assumed to be infinitely advanced) is flying back to Earth in the family spacecraft with one wormhole mouth, while I sit on Earth with the other mouth, and the wormhole is on the verge of becoming a time machine (Figures 14.7 and 14.8 above). Hiscock was speculating that electromagnetic vacuum fluctuations might circulate through the wormhole in the same manner as did bits of radiation in Figure 14.8; and, piling up on themselves, the fluctuations might become infinitely violent and destroy the wormhole.
I was skeptical. A year earlier, on my drive home from Chicago, I had convinced myself that bits of radiation, circulating through the wormhole, will not pile up on themselves, create an infinitely energetic beam, and destroy the wormhole. By defocusing the radiation, the wormhole saves itself. Surely, I thought, the wormhole will also defocus a circulating beam of electromagnetic vacuum fluctuations and thereby save itself.
On the other hand, I thought to myself, time machines are such a radical concept in physics that we must investigate anything which has any chance at all of destroying them. So, despite my skepticism, I set out with a postdoc in my group, Sung-Won Kim, to compute the behavior of circulating vacuum fluctuations.
Though we were helped greatly by mathematical tools and ideas that Hiscock and Deborah Konkowski had developed a few years earlier, Kim and I were hampered by our own ineptness. Neither of us was an expert on the laws that govern the circulating vacuum fluctuations: the laws of quantum fields in curved spacetime (Chapter 13). Finally, however, in February 1990, after a full year of false starts and mistakes, our calculations coalesced and gave an answer.
I was surprised and shocked. Despite the wormhole’s attempt to defocus them, the vacuum fluctuations tended to refocus of their own accord (Figure 14.11). Defocused by the wormhole, they splayed out from the mouth on Earth as though they were going to miss the spacecraft; then of their own accord, as though being attracted by some mysterious force, they zeroed in on the wormhole mouth in Carolee’s spacecraft. Returning to Earth through the wormhole, they then splayed out from the mouth on Earth again, and zeroed in once again on the mouth in the spacecraft. Over and over again they repeated this motion, building up an intense beam of fluctuational energy.
Will this beam of electromagnetic vacuum fluctuations be intense enough to destroy the wormhole? Kim and I asked ourselves. For eight months, February to September 1990, we struggled with this question. Finally, after several flip-flops, we concluded (incorrectly) “probably not.” Our reasoning seemed compelling to us and to the several colleagues we ran it past, so we laid it out in a manuscript and submitted it to the Physical Review.
Our reasoning was this: Our calculations had shown that the circulating electromagnetic vacuum fluctuations are infinitely intense only for a vanishingly short period of time. They rise to their peak at precisely the instant when it is first possible to use the wormhole for backward time travel (that is, at the moment when the wormhole first becomes a time machine), and then they immediately start to die out; see Figure 14.12.
Now, the (ill-understood) laws of quantum gravity seem to insist that there is no such thing as a “vanishingly short period of time.” Rather, just as fluctuations of spacetime curvature make the concept of length meaningless on scales smaller than the Planck–Wheeler length, 10−33 centimeter (Figure 14.3 and associated discussion), so also the curvature fluctuations should make the concept of time meaningless on scales smaller than 10−43 second (the “Planck-Wheeler time,” which is equal to the Planck–Wheeler length divided by the speed of light). Time intervals shorter than this cannot exist, the laws of quantum gravity seem to insist. The concepts of before and after and evolution with time make no sense during intervals so small.
14.11 As Carolee and I try to convert a wormhole into a time machine by the method of Figure 14.7, electromagnetic vacuum fluctuations zoom between the two mouths and through the wormhole, piling up on themselves and creating a beam of huge fluctuational energy.
Therefore, Kim and I reasoned, the circulating electromagnetic vacuum fluctuations must stop evolving with time, that is, must stop growing, 10−43 second before the wormhole becomes a time machine; the laws of quantum gravity must cut off the fluctuations’ growth. And the quantum gravity laws will let the fluctuations continue their evolution again only 10−43 second after the time machine is born, which means after they have begun to die out. In between these times, there is no time and there is no evolution (Figure 14.12). The crucial issue, then, was just how intense has the beam of circulating fluctuations become when quantum gravity cuts off their growth? Our calculations were clear and unequivocal: The beam, when it stops growing, is far too weak to damage the wormhole, and therefore, in the words of our manuscript, it seemed likely that “vacuum fluctuations cannot prevent the formation of or existence of closed time-like curves.” (Closed time-like curves is physicists’ jargon for “time machines”; having been burned by the press, I had stopped using the phrase “time machines” in my papers; and the press, unfamiliar with physicists’ jargon, was now unaware of the new time machine results I was publishing.)
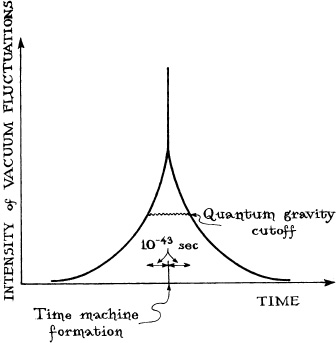
14.12 Evolution of the intensity of the electromagnetic vacuum fluctuations that circulate through a wormhole just before and just after the wormhole becomes a time machine.
In September 1990, when we submitted our manuscript to the Physical Review, Kim and I sent copies to a number of colleagues, including Stephen Hawking. Hawking read our manuscript with interest—and disagreed. Hawking had no quarrel with our calculation of the beam of circulating vacuum fluctuations (and, in fact, a similar calculation by Valery Frolov in Moscow had by then verified our results). Hawking’s quarrel was with our analysis of quantum gravity’s effects.
Hawking agreed that quantum gravity was likely to cut off the growth of the vacuum fluctuations 10−43 second before the time machine is created, that is, 10−43 second before they otherwise would become infinitely strong. “But 10−43 second as measured by whom? In whose reference frame?” he asked. Time is “relative,” not absolute, Hawking reminded us; it depends on one’s reference frame. Kim and I had assumed that the appropriate reference frame was that of somebody at rest in the wormhole throat. Hawking argued, instead (in effect), for a different choice of reference frame: that of the fluctuations themselves—or, stated more precisely, the reference frame of an observer who circulates, along with the fluctuations, from Earth to spacecraft and through the wormhole so rapidly that he sees the Earth—spacecraft distance contracted from 10 light-years (1019 centimeters) down to the Planck—Wheeler length (10−33 centimeter). The laws of quantum gravity can take over and stop the growth of the beam only 10−43 second before the wormhole becomes a time machine, as seen by such a circulating observer, Hawking conjectured.
Translating back to the viewpoint of an observer at rest in the wormhole (the observer that Kim and I had relied on), Hawking’s conjecture meant that the quantum gravity cutoff occurs 10−95 second before the wormhole becomes a time machine, not 10−43 second—and by then, according to our calculations, the vacuum fluctuational beam is strong enough, but just barely so, that it might indeed destroy the wormhole.
Hawking’s conjecture about the location of the quantum gravity cutoff was cogent. He might well be right, Kim and I concluded after much contemplation; and we managed to change our paper to say so before it got published.
The bottom line, however, was equivocal. Even if Hawking was right, it was far from clear whether the beam of vacuum fluctuations would destroy the wormhole or not—and to find out for certain would require understanding what quantum gravity does, when it takes hold in the 10−95-second interval around the moment of time machine formation.
To put it succinctly, the laws if quantum gravity are hiding from us the answer to whether wormholes can be converted successfully into time machines. To learn the answer, we humans must first become experts on quantum gravity’s laws.
Hawking has a firm opinion on time machines. He thinks that nature abhors them, and he has embodied that abhorence in a conjecture, the chronology protection conjecture, which says that the laws if physics do not allow time machines. (Hawking, in his characteristic off-the-wall humor, describes this as a conjecture that will “keep the world safe for historians.”)
Hawking suspects that the growing beam of vacuum fluctuations is nature’s way of enforcing chronology protection: Whenever one tries to make a time machine, and no matter what kind of device one uses in one’s attempt (a wormhole, a spinning cylinder,13 a “cosmic string”14 or whatever), just before one’s device becomes a time machine, a beam of vacuum fluctuations will circulate through the device and destroy it Hawking seems ready to bet heavily on this outcome.
I am not willing to take the other side in such a bet. I do enjoy making bets with Hawking, but only bets that I have a reasonable chance of winning. My strong gut feeling is that I would lose this one. My own calculations with Kim, and unpublished calculations that Eanna Flanagan (a student of mine) has done more recently, suggest to me that Hawking is likely to be right. Every time machine is likely to self destruct (by means of circulating vacuum fluctuations) at the moment one tries to activate it. However, we cannot know for sure until physicists have fathomed in depth the laws of quantum gravity.
1. I have chosen to write this chapter solely from my own personal viewpoint. It therefore is much less objective than the rest of the book, and represents other people’s research much less fairly and less completely than it does my own.
2. See the “Best Guesses” section of Chapter 13.
3. In technical language, we say that the exotic material “violates the averaged weak energy condition.”
4. See especially pages 347, 348, and 406 of Contact by Carl Sagan. There the exotic condition (negative average energy density as seen by light beams traveling through the wormhole) is expressed in a different, but equivalent way: As seen by someone at rest inside the wormhole, the material must have a large tension, along the radial direction, a tension that is bigger than the material’s energy density.
6. The Planck–Wheeler length is the square root of the Planck–Wheeler area (which entered into the formula for the entropy of a black hole, Chapter 12); it is given by the formula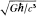 
, where G = 6.670 × 10−8 dyne-centimeter2/gram2 is Newton’s gravitation constant, ħ= 1.055 × 10−27 erg-second is Planck’s quantum mechanical constant, and c = 2.998 × 1010 centimeter/second is the speed of light.
7. I wish that I could draw a simple, clear picture to show how this smooth creation of a wormhole is accomplished; unfortunately, I cannot.
8. This time machine and others described later in this chapter are by no means the first time machine—type solutions to the Einstein field equation that people have found. In 1937, W. J. van Stockum in Edinburgh discovered a solution in which an infinitely long, rapidly spinning cylinder functions as a time machine. Physicists have long objected that nothing in the Universe can be infinitely long, and they have suspected (but nobody has proved) that, if the length of the cylinder were made finite, it would cease to be a time machine. In 1949, Kurt Godel, at the Institute for Advanced Study in Princeton, New Jersey, found a solution to Einstein’s equation that describes a whole universe which spins but does not expand or contract, and in which one can travel backward in time by simply going out to great distances from Earth and then returning. Physicists object, of course, that our real Universe does not at all resemble Godel’s solution: It is not spinning, at least not much, and it is expanding. In 1976 Frank Tipler used the Einstein field equation to prove that, in order to create a time machine in a finite-sized region of space, one must use exotic material as part of the machine. (Since any traversable wormhole must be threaded by exotic material, the wormhole-based time machines described in this chapter satisfy Tipler’s requirement.)
9. In reality, if Carolee were to accelerate up to the speed of light and then back down so quickly, the acceleration would be so great that it would kill her and mutilate her body. However, in the spirit of a physicist’s thought experiment, I shall pretend that her body is made of such strong stuff that she can survive the acceleration comfortably.
10. In most science fiction literature, the term “grandfather paradox” is used rather than “matricide paradox.” Presumably, the chivalrous men who dominate the science fiction writing profession feel more comfortable pushing the murder back a generation and onto a male.
11. I and my four siblings are very respectful and obedient toward our mother; see, for example, Footnote 2 in Chapter 7. Accordingly, I have sought and received permission from my mother to use this example.
12. Three years later, John Friedman and Mike Morris together managed to prove rigorously that, when waves travel backward in time through a wormhole, there indeed are no unresolvable paradoxes—provided the waves superimpose linearly on themselves in the manner of Box 10.3.
13. See Footnote 8 on page 499.
14. Recently Richard Gott of Princeton University has discovered that one can make a time machine by taking two infinitely long cosmic strings (hypothetical objects that might or might not exist in the real Universe) and moving them past each other at very high speed.