‘Freedom,’ wrote Winston Smith, ‘is the freedom to say that two and two make four. If that is granted, all else follows.’ But under torture, he says: ‘Five! Five! Five!’ George Orwell, like G. H. Hardy, held on to mathematics as a paragon of objective truth. That two and two make four was his version of 317 being prime, because it is so, whatever anyone tells you to say.
Like Hardy, Orwell was sceptical about the practical role of science, Hardy’s gloomy verdict on radio being that it had resulted in menacing propaganda, Orwell foreseeing that the main aims of science would be ‘to discover, against his will, what another human being is thinking, and … how to kill several hundred million people in a few seconds…’ Orwell’s language of Newspeak might well have been influenced by the functional and nuance-eliminating artificial language Interglossa, devised and published by none other than Lancelot Hogben in 1943.
I wonder what Hardy and Orwell would have made of the voyeuristic reality show Big Brother showing that, in fact, people will do and say anything merely to attain celebrity—all amidst rolling news info-tainment so readily absorbing the torture of unpersons, with language like ‘rendition’ surpassing Orwell’s cynical ingenuity. Five is the new four, no problem! Actually Nineteen Eighty-Four does show the author’s grumpy old man aspect, despairing of those who would not take the world seriously enough. Perhaps Orwell also took an unrealistically high-minded attitude—Hardy’s attitude—towards objectivity, for fiction and faith are generally valued more highly.
Science is less popular than reality shows, and magic has more mileage. Five is the traditional number of magic, which has just the same inquisitive roots as science, but is more comfortable with putting two and two together and making—well, 575. Unfortunately the very things people want most from science may prove the hardest to tackle. The success of classical astronomy, with its wonderful predictions of eclipses, gave a misleading picture because they involve spaces of so few dimensions. Even Newton, having explained the motions of the solar system, got nowhere with the complexities of chemistry. Scientific medicine is very recent, and with epidemics and earthquakes science still disappoints with its inability to give exact predictions. Climate prediction has only just arrived inside the borderline, thanks to the possibility of huge computer-based trials.
What’s more, a magically inspired guess, based on very little data, is sometimes right; this was true with Fermat’s conjecture, with general relativity, and the colour force. Popper’s famous criterion of falsifiability is not the story of how science actually arrives at new ideas: personal, cultural and aesthetic criteria come into it. String theory and twistor theory are remote from experimental test even though ultimately that is how they will live or die. Mathematics and mathematical physics (often to the annoyance of experimental scientists) are especially influenced by aesthetic criteria of elegance, and there may be little agreement on when those criteria are met. The actual business of research is a very subtle relationship between fact and imagination.
With this in mind, I take the number Five more positively than Orwell did: not as an image of falsity, but as the number of imagination, guided by aesthetics as well as by contact with reality. This reflects the ancient idea of four earthly elements and a fifth, ‘quintessence’, for the celestial regions. G. H. Hardy in 1940, at a time of crisis when everyone was supposed to be practical and pulling together, asserted a fifth freedom: not just the freedom to say that two and two make four, but to roam in pure mathematics, not knowing where it might lead. President Roosevelt proclaimed four freedoms a little later, and the ‘fifth freedom’ has been evoked by others to express more challenging aspirations. Asserting mind over matter, as do disabled people (including the President himself, though secretly), is perhaps the most genuine magic of human life. Stephen Hawking has shown the power of the inner eye, exploring space-time despite intense physical limitations. It is the eye of mathematics, seeing with insight.
Some squares are actually called magic, and were known in ancient Chinese, Egyptian and Indian mysticism. The magic consists of having the rows and columns all adding to the same total, and the diagonals as well. The 3 × 3 magic square, using the numbers One to Nine, is:
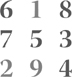
You can easily show by Sudoku methods that there is essentially only one such square—that is, you can obtain all the others by permuting the rows and columns. There is no 2 × 2 magic square. There are 880 different 4 × 4 squares and 275305224 5 × 5 squares. The general problem of counting them is not solved.
In 1776, Euler showed a way of generating magic squares from two Latin squares. In the 3 × 3 case, this amounts to writing down
then combining them into
and interpreting the entries as numbers written in base 3. Add 1 to each cell to make the numbers run from 1 to 9 rather than 0 to 8. This results in the magic square above: the addition of all rows and columns to 15 comes out automatically through this construction.
Euler’s idea does not solve the problem as there are many magic squares which do not arise from two Latin squares in this way. But it illustrates a very general mathematical strategy of finding a way to break a structure down into a multiplication of simpler things. The splitting of on-beat primes into complex pairs, the understanding of the proton as three quarks, and the description of light rays with complex numbers, are successful examples of this kind of generalised factorisation.
Magic squares will probably not lead to any more serious discovery. Yet Euler’s observation is a model of other explorations which at the time might have seemed self-indulgent play with useless abstractions. The quaternions discovered by Hamilton, like his development of Newton’s laws of motion, only came to life many decades later when they became vital in quantum mechanics. The geometry of many-dimensional curved spaces came out of Riemann’s work in the 1850s, which was not driven by any practical need, but now through general relativity keeps satellites in place. In this spirit we step ahead from four to five by starting on the magic pentagon.
A pentagon has a natural way of growing new pentagons. Drawing the interior diagonals and exterior extensions turns it into a star, as found in ancient magic formulas:
The five points of the star form a new large pentagon, of which the star gives the diagonals. A new smaller pentagon emerges at the centre, for which new diagonals could be drawn, and so the whole process be repeated indefinitely.
A natural question to ask is how large the new pentagons are, compared with the original one. We can also ask about the lengths of the diagonals. Both questions can be answered together by starting with a simple observation. There are only two triangular shapes in the picture: fit and fat. That is, they have the same shape, although they come in different sizes.
Inside every fat one there’s a fit one, struggling to get out, leaving a smaller fat one.
Less well known is that inside every fit one there’s a fat one, leaving a smaller fit one.
Take the sides of the original pentagon to be 1 unit. We shall use the Greek letter Φ (phi) for the lengths of its diagonals Extract these two triangles from the star:
The first figure has the fat shape, with lengths greater by a factor of Φ than those of the fat triangle which is inside it. Thus its base must be of length Φ2. Yet its base is also 1 + Φ. So Φ must have the special property that
1 + Φ = Φ2.
The second figure, with the fit shape, tells the same story, which is also equivalent to
Φ − 1 = Φ−1.
The ratio 1: Φ is the same as the ratio Φ—1: 1, and it is the ratio of every two consecutive line segments in the five-star picture. You could now look for Φ using a calculator: it is a number which differs from its reciprocal (and from its square) by exactly 1. If you have ever noticed that the conversion factors for miles to kilometres and vice versa are close to this (being 1.609 and 0.621 respectively), then you have a start. By experimenting with a calculator, you can find the approximate values:
We can do better than this by finding a connection of Φ with 5—not entirely surprising, since it comes from a pentagon:
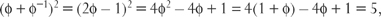
and so
This deconstructs the secret: the magic comes from the irrationality of square roots. But there is more to it.
The ratio Φ is called the golden ratio, mean, section or number. A rectangle with this ratio for its sides has the property that if you remove a square from one end, the remaining rectangle is also golden. By continuing the process, it gives a spiral of squares:
A rectangle of this shape has been held to be the most pleasing: not obtrusively long, not boringly squat. Plato thought it was just perfect. I am a sceptic about such a classical ideal, not because I consider A4, portrait, landscape or widescreen rectangles to be better shapes, but because such a fixed aesthetic seems incompatible with the ever-changing development of human vision and expression. The romantic ideal was quite different: Hogarth taught an S-shaped line of beauty. Current conceptual art abandons beauty and all authority, the only rule apparently being to do something new, however trivial.
There is a three-dimensional analogue of the golden number. Whilst the golden ratio is the number which is squared by adding one to it, the plastic number P is cubed by adding one to it: i.e. P3 = P + 1. Instead of being based on 5, it is based on 23, the exact value being
Numerically the plastic number is 1.324718…, nearly 4/3. (Approximating it by 4/3 is the same approximation as is made in music by taking the seventh harmonic to be equal to two fourths.) The 23 arises as 33—22, parallel to 5 = 22 +1. Does this give the number 23 some aesthetic property? David Beckham, who took this number, is beautiful, but the mystical cult of 23 finds sinister characteristics in it.
The exact formula for P, with its cube roots, tells another important story about Five. It is obtained by solving the cubic equation exactly, not an easy business, and the greatest advance in European mathematics before the scientific revolution. The quartic equation x4 = x + 1 can also be solved in a similar way, but the quintic equation x5 = x + 1 cannot be solved by a method which needs only adding, subtracting, multiplying, dividing and the taking of roots. The non-existence of such a classical method was established by Abel and Galois, both very young, in the 1820s. As so often, proving the impossibility of something led to completely new advances. Quintic equations, ugly customers to the eighteenth century, became a gateway of enlightenment.
Aesthetic criteria change: the fifth harmonic gives the major third, a paragon of concord in the common chord, but now for art-music almost unbearably—well, common. Beethoven’s Fifth Symphony resolves into a triumphant major C-E-G, but when Vaughan Williams opens the last movement of his 1935 Fourth Symphony with three major chords, it speaks of horrible irony. Many suspect the same of Shostakovich’s Fifth. The blue notes of jazz likewise do everything to avoid asserting that fifth harmonic. Only genius can still make a major third sound new and cool: Messiaen, Pärt, even Glass now and then, and of course the Beatles. Nothing can stop the ear from hearing the resonance of the fifth harmonic, but it does not supply a static standard of perfection, only a stimulus to ever-new forms of expression.
We return to the shapes with the Plato-rated ratio, and use them to extract a sequence of numbers. First, we arrange the shapes into a sequence, beginning as follows and extending indefinitely from small to medium, large, XL, XXL…
Each fit and fat pair combine to make the next triangle in the sequence, or equivalently, each triangle breaks apart into the preceding fit and fat. Note that there are two ways of making the breakdown.
Each triangle has an area exactly Φ times that of the preceding one, so we have another example of exponential growth. The A paper series simply gives the power of 2 arising from one shape, but something more subtle emerges from counting these two different shapes.
Suppose we break all the triangles down into the smallest-size fit and fat triangles. This can be done in many ways, but if we are only counting the number of shapes this makes no difference to the answer. So, for instance,
shows that the fit/fat count is, respectively: (0, 1), (1, 0), (1, 1), (2, 1), (3, 2). Each one comes from putting together the previous two shapes, so the sequence will continue (5, 3), (8, 5), (13, 8), (21, 13), (34, 21)…
From now on we will concentrate on the properties of these integers, which are very famous in mathematics. They define the Fibonacci number sequence
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
in which each number is the sum of the previous two. It was the same Fibonacci who appeared in Chapter 1, introducing the base-10 Eurabian numerals. This sequence of numbers had been known and studied in classical Indian rhythms, but Fibonacci described them in a more down-to-earth way, in terms of rabbit propagation. I will refrain from drawing a family tree of the inbreeding bunnies, leaving these activities to the reader’s imagination. My fit-and-fat pictures are intended to be more tasteful than Fibonacci’s cunnilinguistics, although of course lines of beauty are in the eye of the beholder, and one man’s meat is another man’s bottom line. The noughth Fibonacci number is 0, and the next 25 are:
At first sight they look completely random, but a second look shows a hidden connection with the primes.
The number Five makes this connection most transparent. The fifth Fibonacci number is 5. Then every fifth Fibonacci number thereafter is divisible by 5. Why is this, and how can one be sure that the pattern will continue forever?
One way is just to look at the last figure in the Fibonacci numbers. These run
(1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4, 1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7, 9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7, 2, 9, 1, 0)
and that sequence of 60 will then repeat. Every fifth number is either 5 or 0. However, it is more systematic to use the language of congruence and modular arithmetic introduced in Chapter 4.
First, look modulo 2: i.e. at evenness or oddness. The sequence runs: odd, odd, even, odd, odd, even … which we can write as (1, 1, 0, 1, 1, 0, 1, 1, 0…) in a repeating cycle of three. Modulo 3, the repeating cycle turns out to be of length 8: (1, 1, 2, 0, 2, 2, 1, 0). Modulo 4, it is of length 6: (1, 1, 2, 3, 1, 0).
Modulo 5, the repeating sequence is (1, 1, 2, 3, 0, 3, 3, 1, 4, 0, 4, 4, 3, 2, 0, 2, 2, 4, 1, 0) of length 20, and this is the simplest way to see that every fifth Fibonacci number must be divisible by 5.
The same applies to any modulus. Extending this argument a little, you can see that because the seventh Fibonacci number is 13, every seventh number is divisible by 13. In general, the nth Fibonacci number Fn must divide exactly into all of F2n, F3n … If m and n have a common factor p, then Fm and Fn share Fp as a common factor.
These more challenging problems can be solved by extending these counting arguments. They reveal more of the way that the prime numbers are hidden inside the Fibonacci numbers.
TRICKY: Show that every prime is the factor of some Fibonacci number. Suppose a prime p first occurs as a factor of Fs, then s ≤ p2 − 1. (Hint: consider how many pairs of numbers there are which could be consecutive integers in the Fibonacci sequence modulo p.)
FIENDISH: In fact s ≤ p + 1.
SUPER-FIENDISH: In fact s is a factor of p + 1 if p ends in 3 or 7; s is a factor of p − 1 if p ends in 1 or 9. (Hint: the question turns on whether there exists a discrete Φ modulo p, i.e. a number f such that f2 is congruent to f + 1 modulo p. This can be solved by using Gauss’s Law of Quadratic Reciprocity.) Five is special, as F5 is 5.
Neighbouring Fibonacci numbers, or those two apart, have no common factor. Those three apart can at most share a factor of two. You might compare the walk the sequence takes from 3 to 55 with the route that the triangular numbers take—3, 6, 10, 15, 21, 28, 36, 45, 55—which has common factors as intertwined as the residents of Wisteria Lane. The Fibonacci numbers are like spoddy webcammers, chatting globally, but unaware of their local neighbours. (There is a sense in which the Fibonacci neighbours are as lacking in common factors as they could possibly be, which will be explained in Chapter 9.) Far from exemplifying classical harmony, they are more like a lumpy installation at the Tate Modern.
The Fibonacci sequence has unique properties which makes it pop up throughout mathematics. But it does not stand alone. There is one obvious thing setting the sequence in a larger context: it grows exponentially. The ratio between neighbouring numbers gets closer and closer to Φ, as you can see from their origin in the sequence of triangles where the growth ratio is exactly Φ. It is not true to say that this sequence is the only way to arrive at Φ. You can start with any two numbers you like and use the same addition rule for generating a sequence: the golden ratio will appear as the limiting growth factor. However, the Fibonacci sequence has an extra symmetry, and a graph of the odd Fibonacci numbers lies on exactly the same exponentially growing shape as the soap film of Chapter 2. This symmetry and the exponential dependence on Φ are shown by the formula
which is useful, but does not make it obvious that each Fn is an integer! This is typical in the aesthetics of mathematics: a formula or picture illuminates one aspect of a structure, yet disguises another one. The mind needs many different pictures to build up understanding, piecing them together into a manifold of insight.
As integers, the Fn have Diophantine relationships similar to those of the numbers used to calculate 
in Chapter 4. The square of Fn differs by 1 from the product of its neighbours. F2n-1 is the sum of the squares of Fn and Fn-1, and F2n = Fn × (Fn-1 + Fn+1); these are analogous to the jumping-ahead rule for approximations to . In fact the fractions (Fn-1 + Fn+1)/Fn give better and better approximations to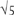 
, and satisfy
There is a duller dual sequence (0, 1,—1, 0, 1,—1, 0…) in which each number is the negative of the sum of the preceding two. You would be right to suspect that its repetitive cycle is an aspect of the duality of growth and oscillation. In fact any recursive rule of this type can be reduced to such growth and oscillation: this is an aspect of the fundamental theorem of algebra for complex numbers. The plastic number comes into another very special example of this. It is the limiting growth ratio of the sequence
0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90, 119, 158, 209, 277, 367, 486, 644…
You are invited to find the rule that is being applied to generate this sequence, and to spot a magical connection with the prime numbers.
Artists, architects, musicians, not to mention fiction-writers, like to bring Fibonacci numbers into their work, and such borrowing is generally admired. But I doubt whether the numbers in themselves lend any aesthetic character to artistic work. Copying them is no more worthwhile than chanting a multiplication table. The value and beauty, if any, lies in the understanding of the sequence, with its roots in five-fold symmetry, the interlocking with primes, the connection with growth and rotation, and the infinitude of all these and many other properties.
The broken-down triangles suggest that there is a further story to be found. Is there some systematic way of doing this breakdown in a way that respects the self-similarity and fivefold symmetry of the original pentagram? The Penrose tilings of the plane achieve something very closely related to this. These were discovered in the 1970s by Roger Penrose, the originator of twistor geometry.
In the best-known form of the construction, the fat and fit triangles are doubled up into kites and darts, thus:
The arrows indicate a constraint: that two tiles can adjoin only if the arrows agree. A very rich body of theory then shows that with this constraint the entire infinite plane can be completely covered with the kites and darts in such a way that the tiling is aperiodic. Wallpaper is periodic: there is always a way of moving across the wall and up the wall by certain fixed lengths, so as to arrive at another point where the pattern is exactly repeated. There is no such symmetry in a Penrose tiling. The reason for this rests on self-similarity and the golden ratio, the concepts found in the pentagram.
A very small piece of tiling looks like this:
You can check that the arrows are consistent with these shapes. This fragment also illustrates a very important property: the freedom in creating a pattern. Starting from the central star of five darts, a choice could have been made to keep the five-fold symmetry going. Instead, by choosing two kites rather than two darts, the symmetry is broken. In covering the whole plane, infinitely many choices must be made, and there are indeed infinitely many different coverings of the plane. In placing the tiles consecutively, however, it is very far from obvious where there is a freedom to make a choice and where there is not. This problem of choice and rules is in fact the main point of the Penrose tiling.
In early 2007, a paper in Science by the physicists Peter Lu and Paul Steinhardt analysed medieval Islamic mosaics where pentagonal symmetry plays a stunning role in the design. Of one particular work, the 1453 Darb-i Imam shrine at Isfahan, Iran, they wrote that the designs ‘were nearly perfect’ Penrose tilings, although ‘the underlying mathematics were not understood for another five centuries in the West’. This claim was taken up enthusiastically in the media. But according to the analysis itself, the designers were placing tiles without respecting the ‘matching rule’ of the arrows. And this rule is not just an ‘approach’ to creating patterns as these writers suggest: it is the definition of the pattern, just as having every number from one to nine in every row, column and subsquare is the definition of Sudoku. Although it is conceivable, as they suggest, that workmen made errors in placing the tiles, it seems to me virtually impossible that the designers had the modern theory.
The mathematics behind the Penrose tiling, which took another five centuries, is not really about pentagons. Fiveness is the medium for a deeper mathematical message about infinity and about unity, a message which comes from modern work starting from Gödel. Penrose tilings give a way to embody the logic of aperiodicity which is, as so far known, the simplest possible. But the logical message can be conveyed equally well by shapes which have nothing to do with pentagons.
This does not make the medieval tilings any less marvellous. As images of inspiration, as well as meticulous constructions, they come as a shock to modern European eyes, and a reminder that al-Khwarizmi’s mathematical culture was so far ahead.
Another shock, and a parallel question about rules, arises in asking whether Penrose tilings can appear in physical reality. So far we have had various deep levels in which integers play a role: symmetries of space, the quarks, the nuclear numbers, the electrons and their bondings. There is another level on a scale higher than that of atoms: crystals. For very good reasons, five-based structures had never been expected in crystallography. Four or six, yes: five no. Yet in 1984—as it happened—solid-state physicists were in for a big surprise. Pentagonal patterns had been discovered in certain metal alloys. To some it was like hearing that two and two made five, and the news was much resisted.
These aperiodic solids are called ‘quasi-crystals’ and do seem to be three-dimensional forms of Penrose tilings. As always, quantum mechanics is involved. Penrose’s question about the rules for constructing the tilings leads to the question of how the atoms in a growing quasi-crystal can possibly manage to situate themselves so as to create a globally consistent pattern. Much more is now known about electronic structure in quasi-crystals—but there does not yet seem to be a clear answer to this question, which relates to the most fundamental questions about quantum mechanics.
Kurt Vonnegut’s story Cat’s Cradle was a warning about the scientific imagination. Vonnegut challenges the Hardy-like claim that the beautiful and true demands to be followed regardless of consequences. Quasi-crystals, as surprising in reality as the ‘ice-nine’ of Vonnegut’s fiction, make a test case So far, they have only been used for creating slippery surfaces, and I am unaware of any danger posed by their discovery. But if there were some malign use, it is hard to see how it could have been anticipated and averted. Where and when was the place to draw a line on a slippery slope? Was it in Plato’s aesthetics, Euclid’s pentagons, Fibonacci’s rabbits, or in the inspiration of Islamic art and its parallels in Kepler? Was it in Gödel or in Wang, the pure logician who started the link from logic to tilings? Did it happen when Penrose refined the aperiodic tilings to kites and darts, or when another mathematician, Robert Amman, found similar patterns independently? Nor is there a simple way to draw a line between mathematical theory and physical discovery, because interpretation of the X-ray pictures needs considerable mathematical understanding.
There is a yet higher level where the integers play a role: life.
The Fibonacci numbers appear quite conspicuously as integers in the leaf and flower patterns of certain plants. They have been known for centuries, and for this reason, have turned up relentlessly like C-list chat-show guests in books about numbers and science, not making a very good advertisement for mathematics because they have only been observed and not fully understood. Life is the hardest area for mathematics to exercise explanatory power, and there is much danger of jumping to wrong conclusions. Many more people now know of Fibonacci numbers, because of the Da Vinci Code fiction. But this has exaggerated their significance in a magical direction: Fibonacci numbers are not the key to all Nature; they just occur in certain particular physiological processes.
Sunflowers make for the clearest examples of Fibonacci numbers in the spiral patterns of their gigantic seed-heads. They can have up to 89, 144, 233 in their patterns. In Tony Robinson’s most recent archaeological series he debunked The DaVinci Code. He had a scientist pooh-poohing everything about the golden ratio in biology. But Fibonacci leaf and bud arrangements have been meticulously measured and documented. This programme missed an opportunity to explain a genuine puzzle of numbers of the kind that hooks people on science, as opposed to the Dan Brown principle of adding two and two to make a profitable five. In 1995 some first good explanations were given of why Fibonacci numbers would occur. Their stand-offish, repulsive, unneighbourly characteristics are the key.
There is an evolutionary factor favouring Fibonacci numbers in plants. Their unneighbourly property is highly suitable for leaves which must sprout with equal weight and light catchment in all directions. But the number 233 as against 234 in giant sunflowers is far too specific to be from evolutionary selection alone: it must be the outcome of an actual physical aspect of the growth process. Evolution can only exploit the pathways made available by physical reality. It seems that Fibonacci development is, in some processes, a physical constraint. But that actual physiological mechanism is still lacking. Generally speaking, there is no complete explanation of the whole process from coded genes to proteins via chemical reactions to the growing shapes of organisms.
There are broader questions prompted by the inelegant, gangly sunflowers, which are also famous because of Vincent van Gogh’s almost painfully unpretty paintings. Did Vincent notice the Fibonacci patterns? It appears not: he seems to have ignored them in a broad-brush treatment. Detailed representation of physical appearance was not his purpose. As photography made three-into-two art redundant, fin de siècle Europe was bursting with new vision. The very idea of symbolism and representation took on new life, and so it did in mathematics. It was during this same period that mathematics finally separated abstract number from physical space. It was also at this time that physics reached beyond the immediately visible and measurable to the abstractions in relativity, radioactivity and the quantum. Proust loved to be compared with Einstein, both upsetting received views, not clinging to ancient standards of perfection. Van Gogh’s harsh goldenness anticipated the coming twentieth century. The five-four waltz in Tchaikovsky’s last symphony signals an end to classical rhythm, and Holst’s ‘Mars, the bringer of war’, so prophetic in its ugliness for 1914, is also in five-four time.
The sunflower tells a story about quantum mechanics. It is striking that green leaves and yellow flowers, by virtue of their colour, are rejecting light from the centre of the Sun’s spectrum—apparently as ungrateful as young humans spurning nutritious food with disgust and insisting on a diet of fat, sugar and salt. A matt-black plant, like a solar panel, could absorb much more energy. Sunflowers, turning towards the Sun yet throwing away its most brilliant light, seem to exhibit evolutionary fatness, not fitness! But green is cool: if plants were black they could not use the energy effectively. For this they depend on the quantum magic of electrons in the chlorophyll molecule—as indeed the molecules of the retina by which we see ‘green’ also depend on quantum mechanics.
Biologists tend to be suspicious of grand mathematical arguments and physical principles, given the incredible complexity of detail connecting the genes, chemistry and environment of an organism. But possibly there are mathematical constraints on physical form which cut through the complexity and favour—for instance—the five-fingeredness which goes far back in evolution. If so, your present location just halfway through One to Nine is not just a consequence of an arbitary convention to write numbers in a scale of ten digits, but goes much deeper into the very nature of physical embodiment. Alan Turing, already quoted as talking about conjectures, started a ground-breaking investigation of such ideas in 1950. (It was literally ground-breaking as he ran round collecting plants, and Turing was literally running round, as he was a champion marathon athlete.) Few knew of his strong interest in Fibonacci numbers in plants, because he left this work unpublished at his death in 1954. What he did publish was a much broader theory of how biochemistry could give rise to the shapes and patterns of biology, based on the mathematical properties of equations which became accessible to study through the then new electronic computer—essentially his own invention.
Since then, Roger Penrose has contributed a quite different argument that there is a physical grounding in quantum mechanics to the brain, on which consciousness depends. He has suggested a crucial role for structures called microtubules. One striking feature of the microtubules is that they have a pattern as definite as that of the sunflower heads, based on the Fibonacci numbers 5, 8 and 13. If Penrose is right, Five is at the root of consciousness.
This is not at all the prevailing view of scientists in neurology, neural networks and Artificial Intelligence, and has gained no general acceptance. But it is still unclear what the physical basis of memory actually is. When learning that two and two make four, not five, what is actually happening in the brain? Coming back to Nineteen Eighty-Four, what is it that makes seeing the truth of 2 + 2 = 4 so different from rote-learning 2 + 2 = 4, a sequence of syllables that might just as well have been 2 + 2 = 5? This is Penrose’s central question. In his book Shadows of the Mind he has suggested a new view of the connection between the mental and the physical, much more subtle than the false choice between Hardy-ish idealism and Hogben-ish practicality.
There has recently been a dramatic development. Late in 2006, a group of European molecular biologists reported a first example of where Turing’s theory could be verified with actual chemicals reacting in just the way he had suggested. It was found in patterns for mouse hairs. So there is at least one place where his conjecture seems right—and there is no reason to suppose it a unique case. Some 54 years have passed since Turing saw this principle of morphogenesis and worked out the theoretical framework. There is plenty of scope for more discovery by the mathematical eye. Meanwhile there is a lot of life in the number—
