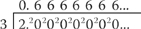
The number Nine completes the Sudoku square. Ninth is last: ninth symphonies spell doom. Beethoven had just started on his tenth when he died; Bruckner didn’t finish his ninth; and perhaps fearing the same, Mahler didn’t call Das Lied von der Erde his ninth symphony, with the result that the one he called his ninth, beginning with his failing heartbeat, was indeed the last he completed. But parting has a secret sweetness in its sadness. The Indo-European word for 9 is the new number: novem/novus, neun/neu and neuf/neuf. Nine is not the end: it opens the door to the Eurabian decimals.
Nine is the gateway to the continuous world of measurement, and the mathematics of functions rather than numbers. Nine opens the way to the serious work of differential equations, and hence calculating climate, quarks, cosmology, space probes, protein shapes and everything else. Unfortunately, the music of Nine does not always resound as stirringly as this vision suggests. Nine is haunted by a tasteless in-store muzak, full of glitches and fudges, with prices like £12.99 trying to look less than they are. Nine, for most people, is not a radiant gateway but a dark door with a lock where the key doesn’t work. Nine means sums with decimals, fractions and percentages filling school hours with fidgeting, clock-watching, gloom and anxiety.
G. H. Hardy wrote off school mathematics as useful but boring, adding contemptuously that it was all Hogben understood. This was unfair on Hogben, who must have taken many readers far beyond the scope of school lessons. Constance Reid prudently steered clear of the subject altogether. But her illustration of Zero, that it counts the number of elephants in the room, provokes the thought that this number is actually One. The elephant in the room is the dismal experience of school examinations.
In the English system, the ‘GCSE’ consists of a streamlined form of the Indian-Arab arithmetic introduced to Europe by Fibonacci, plus the decimals introduced in the sixteenth century, together with some snippets of algebra and geometry. It is tested at fifteen or sixteen. The ‘A-level’ is a simplified and selective version of important seventeenth-century advances, with some extra bits of statistics, and sat at seventeen or eighteen. This pattern continues at degree level, where students start on a more logical basis with topics sorted out in the eighteenth and nineteenth centuries. After three years they reach a selection of twentieth-century advances, and can better appreciate Hardy’s planet. By about twenty, it is possible to catch up with current knowledge in one small area—for instance in that heartland of mystery and discovery to which the elliptic functions are the doorway. After that, it is no longer possible to squeeze a century into a year, and you are doing well to discover something new with a doctorate at twenty-four.
It’s tough trying to find out new things, for the very few who get to that stage, but I am more concerned here with those first steps which everyone is supposed to have covered. In reality, the sums of medieval Europe are still stumbling blocks for bored teen youth, despite the most dedicated efforts. Perhaps one problem is the very word ‘mathematics’, and the implied aspiration of embarking on centuries of mind-bending difficulties. It might be better to abandon the concept of teaching ‘mathematics’, and to concentrate on arithmetic purely as a survival skill. Anyone is at a great disadvantage without numbers for counting, telling the time and date, wages, shopping, credit cards, sharing bills equitably, keeping track of the miserable trail of debts, tax and benefit forms. A reasonable criterion for mass, compulsory schooling is that it should cover enough to understand articles, advertisements and graphs in the mass-circulation press. People certainly desperately need this numeracy when faced with baffling bureaucracy, mendacious commerce and ‘financial advisers’ pushing worthless pension funds and pointless insurance policies.
Whether it is even essential to memorise the base-10 multiplication table, I doubt. It is more important to have a good general sense of what people call ballpark estimates; to know motes from beams, gnats from elephants, sledgehammers from nuts. Such good sense does not have a handy name, cannot easily be tested, and so is not fetishised like ‘times tables’. But understanding what is vital and what is not, making good approximations and good models, and arranging in orders of magnitude, are central ideas in the most serious mathematics, as well as in ordinary life.
After that basic element of force-feeding, I doubt whether any more mathematics should be made compulsory. Notable, successful people say that they see no point to the morsels of algebra and geometry they had to do in school, and that they have never needed them once in their lives. It is nonsense to say that in a technology-based culture, it is necessary to understand science. The broadcast media are dependent on the enormous engineering practice built on the mathematics of Maxwell’s equations for electromagnetism, the quantum mechanics of the electron and the concept of the universal machine. But you need know nothing whatever of these to be a star.
In the case of the universal machine, the discussion in Chapter 8 showed how its very user-friendliness makes technical understanding unnecessary. The computer makes an extreme example of what Gauss said about the role of mathematics as both Queen and Servant. The rather aristocratic world of mathematical logic has become the language of—well, servers. In large measure, all the high-level achievements of mathematical understanding likewise carry on as the world’s invisible infra-structure. Sometimes it seems too invisible. Square roots were understood in ancient Babylon, but if some economic or statistical formula needs them, it meets ridicule in the press. This gives me pause, if only because the climate change question needs some mathematical appreciation, if it is to be put in the right perspective.
Even so, pushing the unwilling and unmotivated towards this hidden structure is an unappealing aspect of education. Like their brattish offspring, the computer, the numbers are needed to keep the human party going, but they are not good company for everyone. It’s not surprising if young people prefer to embark on a more direct exploration of the huge spaces of possibilities in sport, music, alcohol, gang warfare, etc. etc. Brains have evolved to do just that. In contrast, mathematicians have banged their heads on the wall for centuries trying to figure out questions about just a few dimensions.
To limit the compulsory element in education to the most basic number skills needed for everyday use, would be considered a surrender to the ‘lowest common denominator’. But that expression itself tells a story. It is wrongly used to suggest something small and cheap, and this misuse illustrates just how little was actually learned in school in bygone days when more formal arithmetic was supposed to be imparted. A lowest common denominator is generally a rather grand number! The term arises in the context of fractions p/q, where p is called a numerator and q a denominator. To add 1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9, the trick is to find the lowest common denominator from 1, 2, 3, 4, 5, 6, 7, 8, 9. That is the smallest number which can be divided exactly by all of 1, 2, 3, 4, 5, 6, 7, 8, 9—which turns out to be 2520. You are supposed to use it to write 1/2 as 1260/2520, 1/3 as 840/2520 … 1/9 as 280/2520 and so add them up.
In practice, few people add up fractions much more complicated than 1/2 hour + 1/4 hour, and I am not surprised that this complicated theory has left little trace on the collective mind. Probably the misuse of the metaphor has arisen by confusing it with the highest common factor of a set of numbers. This is typically something modest, like my proposal for more realism in compulsory schooling.
Asking for realism about schooling is to open up several cans of unwelcome worms. In adult talk, education seems mostly to be dominated by questions about social class, national identity, religious indoctrination, racial groupings and dressing up in uniforms. Further fetish elements, humiliation and punishment, are not far under the surface of ‘adult’ images of education. For the young it is mainly about finding peer-groups, gaining popularity, coping with bullying and above all—the explosion of sexual desire and everything to do with it. Every novel, film, and soap opera ever made has told a story of hopeless mismatch between official design and actual experience. In 2007 the British Education Secretary, already busy pushing ‘times tables’ (and Jane Austen) on reluctant teenagers, found a new priority in stopping them from putting rude videos on YouTube. Another mammoth in the class-room lies in the fact that intellectual achievements may attract the most relentless aggression, with the word ‘gay’ increasingly used as the damning verdict on such aspirations.
In this context, the word ‘mathematics’ should not be invoked as if it implied a world of unchanging, traditional standards. The question of whether school students should do arithmetic without calculators is very telling. It is perfectly true that you must understand what you are asking the calculator to do, and be able to interpret what it says. You must know what numbers are all about. If you don’t, you end up writing down answers a hundred times too big, or upside down. For this reason it is essential to learn about adding and multiplying without using a calculator. On the other hand, calculators are now available worldwide, as software working on the computers called mobile phones. This marvellous resource should be used to good effect. Gauss enjoyed doing arithmetic in his head, being generally rather unbearable, but other mathematicians of the past would gladly have had a calculator to cut short their long labours on numerical work. There is no virtue in being made to do repetitive arithmetic in an old-fashioned way, like soldiers drilling on the parade ground for the sake of it.
Submitting to discipline has its attractions. Channel Four television has a good line in bossy gurus for diets and decorating, and running bad-lads boot camps with a back-to-1950s theme. People pay good money to be ordered around by personal trainers, sport trainers, and life coaches. But involuntary servitude is soul-destroying and in mathematics it is the kiss of death, leaving a derelict corpus of half-remembered routines.
There are several mixed-up strands in ‘mathematics’ education, elements once with sense but now virtually obsolete. One line is that it is vital for trade and industry: roughly Hogben’s approach, but now seen through the eye of nothing-can-stop-me-now capitalism. A hundred years ago, even forty years ago, training in commercial arithmetic was needed for an army of accounting clerks in shops, offices and banks. They were supposed to be machine-like calculators—although in reality, little books called ‘ready reckoners’ were in heavy use. All such mechanical work is now done by calculators or spreadsheet software.
More elevated than these Gradgrind objectives is the proposition that a modern state needs a scientifically trained population to compete successfully. Past panics about Germany and Russia are now recurring with China in mind. There is sense to this aspiration, but science stretches over a gigantic field, of which only a few snippets can get attention in schools. Much of science rests on intense and deep mathematics. It is unrealistically ambitious as the basis of mass education.
Another strand is the element corresponding to Hardy: that of mathematics studied for its own truth and beauty. A hundred years ago, this meant following Euclid’s superb logical scheme. This ideal had some sense to it, and Sudoku shows what fascination pure logic has. But in those days Euclid benefited from association with the literary classics of antiquity, then a common culture to the ruling élite, but virtually unknown today. And Euclid’s model of logical deduction is anyway now obsolete. In the late nineteenth century mathematicians found deeper foundations in the logic of numbers. While this work has flowered—with the modern computer as one of its offshoots—school geometry has degenerated into pointless applications of a few formulas concerning circles and triangles.
Yet if the dead hand of compulsion were removed, mathematical thinking could become a lively option for those school students who are heading for something scientific or technical. It would suit those who enjoy puzzles and logic games, stimulate those with an eye for the geometry behind music and art, and offer something to those who just want to be different, even extreme. But to make it lively I would cut loose from the teenage GCSE syllabus, and in particular, place a new emphasis on using computers.
This does not mean using a computer screen as a medium for delivering maths-book text with cartoon characters, posing multi-choice quiz questions with beeps and honks, pasting slabs of on-line documents into projects, or buying on-line essays. Nor do I have the content of ‘information technology’ courses in mind. What I suggest is not dumbing down but wising up: students can take charge of the amazing computer power now available so cheaply, and make it do the donkey work while they think for themselves.
What happened to the kind of logical rigour which used to be taught through Euclid’s geometry? It flowed into the logic of numbers, and then through Russell, Gödel and Turing into computer languages. Computers do exactly what you tell them, not what you mean, and writing programs for them reignites the extreme rigour and mind-game challenge that used to go into Euclid. Usually this is thought too hard for school students, and ‘information technology’ students seem to be trained to parrot waffle about programs (though this may be unfair on parrots). I don’t believe it is too hard. The skill of computer gaming is a good step towards programming.
In fact, I suggest going back to the constructivist can-do hands-on philosophy of Diophantus and Al-Khwarizmi. Students don’t have to act like machine-slaves, nor pretend to be an above-it-all Athenian aristocracy, but could instead act as the intelligent multi-tasking craftsperson using the staggering resources of a universal machine. The computer can be used for that old-school discipline of logic, and for exploring the patterns of number and geometry for their own sake, and for acquiring an up-to-date technical and scientific expertise for text, music, photography, graphics and animation. It can be the platform for creativity. Fermat was inspired to a good idea in the margins of a constructivist book, and others may also take off from recipes to cook up new thoughts.
This chapter will look at an old-fashioned school topic: Victorian long division and those ancient HCFs. By actually doing it, and not just talking about it, we will create the number patterns which lie behind the brilliance of the RSA cipher. On the way, we will also ponder on something that goes beyond what computers do: the idea of infinity. For an aural image of this final chapter, hear the Pet Shop Boys end their Introspective, suggesting how the music will go on and on and on and on … They end with a huge fading tone-cluster of all the integers, a musical rendition of the ellipsis of the ad infinitum. That originality in sound design is also an echo of what mathematics could be like for willing, energetic school students using Alan Turing’s wonderful invention.
The Independent newspaper recently offered a column about the number 23, to coincide with a film of that name. It didn’t mention the plastic number, nor that 23 is a third of soixante-neuf, but it did reveal a perfect example of how not to use a calculator:
…More freaky numerical coincidences: Charles Darwin’s Origin of Species was published in 1859—1+8+5+9 = 23. Two divided by three makes 0.666 recurring (allegedly—actually it makes 0.6666666667). The Hiroshima bomb was dropped at 8.15am—8+15 = 23…
Allegedly 0.666 recurring? Actually 0.6666666667? The Independent writer has put 2/3 into a calculator, pressed the buttons and thoughtlessly copied the display.
It is not difficult to do the division by hand. The raised index figures indicate the remainders which arise at each stage.
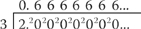
3 doesn’t go into 2, so write 0 and carry 2; 3 goes into 20 six times, remainder 2, so write 6 and carry 2 … and so on, always carrying two and never ending. This is what ‘recurring’ means, and 2/3 is, as correctly alleged by the film, 0.666 recurring. The Independent’s calculator only stopped at ten decimal places because a calculator is programmed to stop there and display, with the last 6 ‘rounded up’ to 7.
Here are some other results of performing divisions, all recurring decimals:
1/9 = .111111111…
2/9 = .222222222…
3/9 = 1/3 = .333333333 … and so on to
8/9 = .888888888…
EASY: Rewrite 1/9 as 1/10 + 1/102 + 1/103…
TRICKY: This suggests another way of looking at recurring decimals, using a little algebra. The infinite geometric progession r + r2 + r3 + r4 … can be summed to r/(1 − r). Show why this is true by multiplying both sides by (1 − r). Then apply it in the case of r = 1/10 and show it agrees with the result of the division sum.
The interesting thing about this pattern is that it suggests that 9/9 = 1 = .999999999 … Is this a contradiction? If you put a price tag of ‘£9.999 recurring’ on a £10 item, would you be breaking the law? We have come full circle, back to the question of the integrity of One. If we turn a microscope on all the fudge and fiddle of Nine, all that seems awkward and doesn’t work properly, we can find something new and exact.
There is no contradiction. It is true that 1 = 0.999999999… recurring. These are different decimal representations of the same number, and this gives us a useful way of looking at the ad infinitum.
When running on the treadmill, if you get bored with thinking about relativity, you can think about fractions and infinity instead. There is nothing like an unwelcome duty as a spur to concentrating the mind on rational numbers. When 1/3 is done, you know that only half as much again is needed to get half way; when 2/3 is done, only one eighth as much again to get 3/4 through. As the counter heads towards 10000 metres, the glow of achievement, on seeing 3/4, 5/6, 7/8, and 9/10 done, burns more and more often. At last, when 99/100 and 999/1000 and 9999/10000 have been done, you experience infinitely many achievements in a flash. That’s the problem of ‘0.9999 recurrring’: it seems to mean that infinitely many achievements are needed to express the simple idea of One.
This is a form of ‘Zeno’s paradox’: to run 10000 metres, or indeed one metre, it seems that you have to achieve infinitely many things. This classical problem was addressed by the sorting-out process, which in the nineteenth century made sense of the concept of ‘limit’, and so of the calculus of continuous curves. Instead of ‘going to infinity’, and so actually taking infinitely many steps, it is possible to define why.999999 … = 1 by making precise the sense in which a finite number of steps gets as close to 1 as you choose.
This logic still leaves a potential infinity in the concept of ‘as close to 1 as you choose’, and the infinite sequence of numbers.9,.99,.999,.9999,.99999 … still must be considered as existing in some Platonic sense. How this relates to physical measurements, and the world in which we actually take those treadmill steps, is quite unclear. It depends on the truth about the fundamental level of space and matter, the level perhaps defined by strings or twistors. The standard answer, a stopgap reflecting the unfinished business of Chapter 7, is that distances below the Planck distance are not meaningful. But we can leave open this question about how.99999 … relates to the physical world, while continuing to explore the inner life of numbers.
The first really strange-looking decimal is for 1/7—seven being the awkward customer again. It has an ugly-looking answer. You could get it on a calculator, but that won’t show the inner logic which a division sum reveals.
Thus, 7 goes 0 times into 1, with remainder 1; carry it forward; 7 goes once into 10, with remainder 3, carry it forward; 7 goes 4 times into 30, remainder 2, and so on. At the last stage, we have 7 going 7 times into 50, with a remainder 1. After this we can write ‘…’ because we are back to where we started: the decimal recurs. So
1/7 = 0.142857142857142857142857…
has a recurring cycle of six digits.
To calculate the decimal for 2/7, it is enough to notice that it starts off with a remainder 2. After that, we have already done the work in the division sum for 1/7: we just pick up the calculation where the remainder 2 occurs, and read off the answer as 0.285714 … recurring. I will call this the carousel property, thinking of the baggage circling after it has emerged from the chute in the airport arrivals hall. Wherever you stand, the same items pass by. To find the decimal for 3/7, just stand at the point where the remainder 3 occurs, and then watch the cycle thereafter appear as 0.428571…
There are only six possible remainders: 1, 2, 3, 4, 5, 6, and and each of them arises just once. This means that the number 142857 has the carousel property
142857 × 1 = 142857,
142857 × 2 = 285714,
142857 × 3 = 428571,
142857 × 4 = 571428,
142857 × 5 = 714285,
142857 × 6 = 857142.
Now a connection with nines emerges:
142857 × 7 = 999999.
The remainder is 1 when six figures of 1/7 have been found. So 7 divides into 1000000 with remainder 1, so 7 divides exactly into 999999, 142857 times. Alternatively, you can start with 7/7 = 0.999999 … and divide both sides by 7; you will get exactly the same answer for 1/7, but this time getting a remainder 0 after six 9’s, instead of remainder 1 after six 0’s.
Either way, the fraction 1/7 and its decimal tell a story about integers: seven divides exactly into the number written as six nines.
EASY: The decimal expression is equivalent to the geometric progression 1/7 = 142857 × (10−6 + 10−12 + 10−18…).
From now on we will leave aside the infinite addition, and concentrate on the finite numbers like 142857 which emerge on the carousel. Is there a pattern which extends to other fractions?
We shall find that there is indeed a simple common pattern for 1/p, if p is a prime. But if p is greater than 10, knowing the multiplication table is not enough to do the division sum for 1/p. For 1/17, you need to pre-compute an extra table of information: 1 × 17 = 17, 2 × 17 = 34 … 9 × 17 = 153. You then use this to execute the same logic as for 1/7, but with the remainders worked out by subtraction sums.
This is long division. It has been dropped from school maths as unnecessary. My attention was drawn to this by a letter in the Guardian to the effect that the kind of people clever enough to do long division are the kind of people who build weapons of mass destruction. This is a valid criticism of mathematics, which Hardy might well have agreed with. Maybe a wise old Babylonian foresaw the trouble that long division would bring in its train. Alas, the Second Law prevents the unspilling of milk. Perhaps more fundamentally, the invention of agriculture was the disaster; since then it has been downhill all the way as the long division of land into property started the cycle of tribal war and mutual destruction. If humanity had remained as tropical hunter-gatherers, like the Pirahã with their blissful ignorance of abstractions, then none of these problems would have arisen, and there would be no letters to the Guardian either.
You can ask a calculator for 1/17 but it probably won’t display enough digits to show the pattern. So it’s still useful to be old-fashioned and do 1/17 with a strict, firm hand:
The steps begin: 17 goes 0 times into 1, remainder 1; 17 goes 0 times into 10, remainder 10; 17 goes 5 times into 100, using 17 × 5 = 85, and working out the remainder 15 by subtraction. 17 goes 8 times into 150, using 17 × 8 = 136…
After a while, you find yourself working like a machine to carry out these steps. There is little virtue in doing this once you have got the idea. To learn about the real life of numbers, it would be much more valuable to program a computer to perform the routine and so discover the repeating cycle.
The remainders run in a repeating cycle of 16: (1, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12) and 1/17 = 0.0588235294117647 … has a recurring cycle of length 16. The sixteen-digit number 0588235294117647 also has the carousel property, and without any more work:
2/17 = 0.1176470588235294…,
3/17 = 0.1764705882352941…,
4/17 = 0.2352941176470588 … and so on.
Equivalently, 17 divides exactly into 9999999999999999 = 1016 − 1. A pattern emerges: 16 is just one less than 17, just as 6 was one less than 7. Does this hold for every prime? For example, does 13 divide exactly into 1012 − 1?
The situation with 1/13 = 0.076923076923 … is actually a little different. The number 076923 has the rotating property when it is multiplied by 3, 4, 9, 10 or 12; but when multiplied by 2, 5, 6, 7, 8 or 11 it gives a different sequence: 153846. This is because the remainders break down into two separate cycles: 1-10-9-12-3-4 and 2-7-5-11-6-8. But none of this affects the main feature. Both cycles are of length 6. and this is just half of 12. So the decimal for 1/13 does repeat after 12 digits, and it is likewise true that 13 divides exactly into 999999999999 = 1012 − 1.
This pattern will always hold. The decimal for 1/p will always return to its starting point in (p − 1) steps, though it will not always return for the first time in (p − 1) steps. It is worth experimenting with numbers and then seeing why the decimals logically must show the patterns that emerge.
EASY: 1/11 has cycles of length 2; 1/37 has cycles of length 3, 1/101 has cycles of length 4, 1/41 has cycles of length 5. Check these fit the rule.
HARD: In working out the decimals for any 1/p, every remainder has a unique successor and also a unique predecessor. HARD: Each cycle of remainders must be of the same length, and that length divides (p −1).
We draw the conclusion that if p is a prime other than 2 or 5, p divides into 10p-1 − 1. Equivalently, 10p-1 is congruent to 1 (modulo p).
But there is nothing special about the number base 10. It is equally true that if p is a prime and m is any number greater than 1, not a multiple of p, then p divides exactly into mp-1 − 1.
This fact is known as Fermat’s Little Theorem, because Fermat stated it in 1640, though without a proof. Euler published a proof 100 years later, considerably extending it. There are quicker proofs, but exploring decimals gives a picture of Fermat’s discovery as a pattern of interweaving numbers.
The RSA property needs just a little beyond Fermat’s Little Theorem: not going as far as Euler’s contribution, but just enough to double it up. We need the fact that if p and q are both primes, and m a number which is not a multiple of p or q, then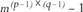 
is divisible by p × q. This is equivalent to saying that the decimal for 1/(p × q) repeats at the period length (p − 1) × (q − 1). This can be seen by the following argument.
First, we need the fact that if m is congruent to 1 modulo n, then so is any power of m. (This is like seeing why all the powers of 11 end in a 1.) Next take two primes, p and q and a number m which is not divisible by p or by q.
Then Fermat tells us that mp−1 is congruent to 1 (modulo p). So its power m(p−1) × (q−1) is also congruent to 1 (modulo p).
Also m(p−1) × (q−1) is congruent to 1 (modulo q) by the same argument.
So m(p−1) × (q−1) − 1 is divisible by p and divisible by q, so by p × q. If k is any integer, mk × (p−1) × (q−1) − 1 is also divisible by p × q.
The RSA cipher rests on this fact. Suppose we have two numbers d and e such that d × e is congruent to 1 modulo (p − 1) × (q − 1).
Then d × e = k × (p − 1) × (q − 1) + 1 for some integer k.
Then md × e−1 − 1 is divisible by p × q.
Multiplying by m shows that md x e − m is divisible by p × q, i.e. md x e = m (modulo p × q).
This final statement is still true even if m is a multiple of p or q, so we can forget the tiresome restriction on m.
Now think of the number m as the message number M, e as the enciphering number E, d as the deciphering number D, and n as the public-key number N.
We have MD x E = M (modulo N). This means that taking the Dth power always undoes the effect of taking the Eth power.
So if ME = C (modulo N), CD = M (modulo N), just as required for the RSA cryptosystem.
There is one thing left. The number E is the enciphering number, made public; and D is the secret deciphering number. But given E, P and Q, how do we find a D such that D × E = k × (P − 1) × (Q- 1) + 1?
This does not need advanced modern mathematics. It does not even need Fermat’s insights. It needs something from Euclid: the ancient Greek algorithm for finding the highest common factor (HCF) of two numbers. Our technical exploration of numbers can end in some constructivist mathematics from the heart of classical antiquity.
The construction can be shown by example. Take N = 77, so P = 11, Q = 7, and (P − 1) × (Q − 1) = 60. Given an enciphering number E, we need to find a number D such that D × E is one more than a multiple of 60.
There is no hope of finding such a D if E has a common factor with 60. For instance, if E is even then any D × E must be even, and so cannot possibly be 1 more than a multiple of 60. The HCF of E and 60 must be 1. This is a necessary condition, but it turns out also to be sufficient. Given an E, we use Euclid’s algorithm to check that the highest common factor it shares with 60 is 1. Then, if it is, we can run the algorithm backwards to find what D is.
As an example, take E = 43, so that we must examine the pair of numbers (60, 43) for common factors. One way of doing this would be to find all the factors of both numbers and then check them against each other. But Euclid’s method is much simpler and smarter. It works by repeated division and taking remainders. Each time, it reduces the pair to a smaller pair of numbers which have the same highest common factor. Eventually it must reduce to zero, and then the HCF is found.
Start with (60, 43) then write:
60 = 1 × 43 + remainder 17. This reduces the pair to (43, 17).
43 = 2 × 17 + remainder 9, reducing the pair to (17, 9).
17 = 1 × 9 + remainder 8, reducing the pair to (9, 8).
9 = 1 × 8 + remainder 1, reducing the pair to (8, 1).
Now 8 and 1 have highest common factor 1 and that’s the end.
To find D, we work backwards through this logic, turning each line into a statement about 1:
1 = 9 − 8.
1 = 9 − (17 − 9) = 2 × 9 − 17.
1 = 2 × (43 − 2 × 17) − 17 = 2 × 43 − 5 × 17.
1 = 2 × 43 − 5 × (60 − 43) = 7 × 43 − 5 × 60. So 7 × 43 = 1 (modulo 60), so D = 7.
Provided that the HCF is indeed 1, this will always result in a unique deciphering number D. It is an EASY algorithm which computers can perform in a flash even for 100-digit numbers. There is a connection with Fibonacci numbers: two neighbouring Fibonacci numbers are the very slowest to reduce and confess their lack of any common factor but 1. That is the sense in which they are the most unneighbourly numbers of all, the property mentioned in Chapter 5.
Actually working out an RSA encipherment makes a TRICKY puzzle. Again, take N = 77 and E = 43. You can encipher the message M = 51 as follows. Use a calculator to show that modulo 77, M2 = 60, M4 = 58, M8 = 53, M16 = 37, M32 = 60. Use 43 = 32 + 8 +2 + 1 to show M43 = 2, so C = 2. Check that D = 7 does indeed effect the decipherment because C7 = 51 = M.
These calculations only illustrate the principle of how the D is found, and how the D undoes the E. They are of no use whatever as a practical cipher, since the prime factors of 77 are obvious. The whole point of RSA is to use a huge N which cannot in practice be factorised. For actual encipherment using such numbers an ordinary calculator is useless: you need software such as Maple or Mathematica which can handle large numbers. Even better, you can learn a lot from writing a program yourself to handle such large numbers. It is then quite magical to see it reproduce the original message M.
With a public-key cipher, you cannot decipher something you have yourself enciphered. Suppose, for instance, that you were an industrial spy transmitting data to China, and had your computer encode it by RSA without even seeing it yourself. Then you would not be able to decipher the messages that you yourself had sent. If you were caught by the British government and ordered to decipher your messages, in accordance with its Regulation of Investigatory Powers Act, you would not be able to obey.
As with many other computer applications, this is probably not quite what Lancelot Hogben had in mind when promoting the usefulness of Mathematics for the Million. Nor is it what Hardy expected. In 1940 he wrote that ‘no one has yet discovered any warlike purpose to be served by the theory of numbers or relativity, and it seems unlikely that anyone will do for many years’. By 1945 everyone knew that E = mc2 had an application; in 1946 Turing reported on the military importance of combinatorial problems, as an aspect of future computer power. The RSA cipher is just the tip of an iceberg of crypto-mathematics, and the superpowers have armed themselves with the theory of numbers. One key development, which neither Hardy nor Hogben foresaw, is the speed and cheapness of electronic computing.
The relation between theoretical and practical has changed so much in the past 60 years, that it is unwise to predict how the picture may change in the future. There is certainly a possibility of more efficient factorisation methods being found, and so of the whole system being rendered useless. Current methods are mostly still based on refining an observation of Fermat, that the difference between two squares always factorises. This is a point where very advanced developments in the theory of numbers can combine with the fantastic power of computing. A new Euler or Gauss, Riemann or Ramanujan may find something completely new.
Another possibility is that quantum computing will make factorisation into an EASY problem to solve. Theory already shows that this is true: there is a way of exploiting the Two-ness of quantum mechanics to find factors more quickly than by any computer method so far known. It is an odd fact that the problem which shows the greatest theoretical promise for quantum computing is also the one of most commercial relevance. It is not yet feasible to build quantum computers with enough storage to factorise seriously large numbers. But there have never been so many new minds at work with new ideas.
The RSA algorithm requires rather intensive calculation and in practice it is not used for the entire communication of, for instance, a secure webpage. It is used only to solve the key distribution problem: i.e. to transmit the secret key for a conventional cipher system on which the bulk of the message is sent. But that could still be broken by a cryptanalyst able to search through all the possible keys for that system. A special lock on your front door is of no use if anyone can open a window instead.
Another important limitation of RSA is that anyone who guesses the exact message M can verify it simply by encoding M with the public E and N, and checking that it does indeed agree with C. A computer could do this checking process for a million, or a billion guesses. So for true security it is not enough to encode a message M: a ‘padded’ M must be created by adding random material that cannot be guessed. But ensuring that this padding is truly random is itself a serious cryptographic problem.
In practice it may be more important that the secret deciphering number has to be kept on a hard disk, vulnerable to spyware smuggled in by cookies, hidden cams and burglary. An even more down-to-earth point regarding e-commerce on the Internet is that there is little point to elaborate mathematical encryption when the data may be collected and sold by people working in remote call centres. Or when, indeed, people are so easily taken in by scams that they cheerfully divulge their secret data to complete strangers.
These considerations are salutary reminders of the place of mathematics in the world. Human minds can mess everything up. But first, a little more about what human minds have realised.
Long division reveals a lot about the fractions, or rational numbers. Written as decimals, they are exactly those that, after a certain point, repeat in a cycle forever. What about the other, irrational, numbers? We have met 
, 
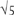, e and π, amongst others. It is quite common to hear it said that π ‘can’t be found exactly’.
This is true in the obvious sense that π needs an infinite decimal. But then, so does the decimal for 1/7 = 0.142857142857 … The symbols or ‘recurring’ are actually rules. In this sense, , , 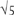e and π are no different, or are different only in degree, from 1/7: there are rules for finding the entire decimal which are more complicated than saying ‘repeat the cycle for ever’, but are still finite rules, expressible as computer programs. This makes them computable numbers: the title of Turing’s 1936 paper was ‘On computable numbers, with an application to the Entscheidungsproblem’. Computability answers the question of what π is, exactly. Its decimal, as everyone who studies it remarks, looks competely random and patternless. But actually it is pseudo-random, generated by rules which go as deep as Ramanujan into the structure of number.
How many numbers are there in the continuum? Obviously there are infinitely many. Not so obviously, this infinity is infinitely greater than the infinity of the integers! This comparison can be made exact. It comes from seeing that a real number is equivalent to a set of integers. For instance, the fractional part of the number π, written in base 2, is:.00100100 00111111 01101010 10001000 10000101 10100011 00001000 11010011 … Knowing this is equivalent to knowing the infinite set of numbers (3, 6, 11, 12, 13, 14, 15, 16, 18, 19, 21, 23, 25, 29, 33, 38, 40, 41, 43, 47, 48, 53, 57, 58, 60, 63, 64…) which mark where a 1 appears. Conversely, any set of integers, finite or infinite, defines a number between 0 and 1. We are using the either/or logic of the number Two to do this.
TRICKY: Which numbers are represented by two sets of integers? How many such numbers are there?
Given a set of N things, how many subsets does it have? The subsets can be counted like this: the first element may be in or out, giving two choices, the second element likewise, giving two choices, and so on to the Nth element, giving N choices altogether and so 2N possibilities. Thus there are 264 choices for the subsets of 64 items, corresponding to the 264 different possibilities for a 64-bit register in a computer chip. This fact gives a more primitive picture of what a ‘power’ is: a counting of subsets. And it can be extended to infinite sets, for instance the set of integers. If we say there are ∞ integers, we can say that there are 2∞ sets of integers. This is the step that Georg Cantor took in the 1870s and it lit a long fuse which did not explode until the twentieth century. Cantor’s proof that 2∞ is definitely a greater infinity than the ∞ of the integers, turned into the argument which shows there is no set of all sets. It led on to Russell’s efforts to repair the problem and thence to Gödel and to Turing. This, the basic idea of set theory, is where we came in with Chapter 1! Incidentally, the well-intentioned efforts to bring ‘modern maths’ into the school syllabus with ‘Venn diagrams’ for sets are not, in fact, addressing the serious content of modernity at all. Those diagrams simply sharpen appreciation of AND and OR. It is only in the study of infinity that set theory matters.
In contrast, there are no more rational numbers than there are integers. This is because the rationals can be put in a kind of alphabetical order, starting with the simplest numerators and denominators. The same applies to computable numbers, given Turing’s clear definition. This is because each computable number comes from a program, and like recipes in a cookery book, programs can be put into alphabetical order.
There are infinitely more real numbers, defined as decimals with infinitely many digits, than computable numbers. In fact the computable numbers are infinitely sparse: a random real number has a zero probability of being rational and a zero probability even of being computable. Almost all real numbers are uncomputable; all the thickness and solidity of the continuum comes from numbers which have no effective definition. So in what sense do they exist? At this point mathematicians can take different views, and explore different levels of logical axioms about what to assume, a topic that is meat and drink to logicians. There are quite marvellous discoveries about ways of looking at the continuum: ‘ p-adic numbers’ as a completely different picture of how the real numbers fit together, and ‘hyper-real numbers’, allowing for infinitely large and small numbers. From Chapter 8 you will guess that exponentiation of sets can go on to really really large sets of size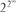 
—and far beyond. Rudy Rucker’s book Infinity and the Mind takes up the challenge of explaining what happens.
Coming down nearer to earth, a vivid picture of the infinite inner life of the integers has become accessible in the spectacular computer-generated images of the famous Mandelbrot set. It sums up much that has happened since Constance Reid’s 1956. It is a two-dimensional space of complex numbers, made tantalisingly visual. In fact it brings alive the idea of a space of possibilities, leading to a picture of chaos.
Although the basic features were understood in the late nineteenth century, they could never have been found in such extraordinary detail without computer power. Your own computer experiment can find out how its solid blobs correspond to integers and how their meeting expresses multiplicative structure. (The biggest blob, the heart-shaped cardioid, corresponds to 1. The circular disc to its left corresponds to 2.) But its infinite intricacy poses other questions which cannot be answered by computers, and still defeat mathematical minds.
It is worth thinking about why algorithms are so central. The reason is to do with large numbers: an algorithm is needed when there are more possibilities to deal with than could ever be listed as a table. Politicians always say they won’t answer hypothetical questions, although they pass laws to deal with hypothetical situations. Programs have no such luxury of choice; they must deal with input that has never been foreseen. The number of potential images, or text files, or webpages, which a program must be able to cope with, is far more than a googol, far more than astronomical. Typically, a program embodies a definite principle, or finite set of principles, applicable to an effectively infinite number of possible cases.
Can the brain do any better? While working on the first computers after 1945, Turing became very keen on the idea that everything the brain does must be an algorithm, from which it follows that the computer could do it too. Turing devised his famous Test to put this comparison of computer and brain on a reasonably objective footing. This is where Roger Penrose, in The Emperor’s New Mind and Shadows of the Mind, takes issue. He makes an argument from Turing’s original 1936 work to the effect that human minds can see the truth of something that no program can show. This is because we know what numbers are, but the computer only has symbols. A program that prints out.999999 … for ever knows nothing about why that number is the same as One, or indeed what One is. It is like a cook that doesn’t know what food is, but obediently prepares it in accordance with orders. Penrose’s argument is central to the question of human consciousness, freewill and responsibility—and of course it agrees with what everyone feels: ‘I think, therefore I am not a machine.’
Turing was highly alive to these objections, even though he considered that they should be overruled, and it is a paradox that he of all people had an acute sense of individuality and freedom. I have said that he was affected by the climate of thought about mathematics and logic in the 1930s, but he was also driven by an intense and emotional interest in the nature of the mind. This becomes clear from his personal writing in about 1932, which I was able to bring out in Alan Turing: the Enigma. The human factor, at that stage, led him to think that consciousness must have something quite definite to do with quantum mechanics. Penrose’s conclusions are remarkably similar. Turing himself went back to physics in 1953, with a particular interest in the mysterious process of measurement that turns complex wave-functions into real probabilities.
Logic and physics were each transformed in the revolutionary period of a century ago. But science and mathematics tend to divide into non-communicating sectors, and the explosion of knowledge in the last 100 years has created almost impossible barriers. Thus the question of what ‘one photon’ means seems to attract little interest from logicians, although quantum information, quantum computing, the quantum Zeno effect, interaction-free measurement, and teleporting pose this question with new acuteness. It is hard to believe that another 100 years will pass without a major rethink of the integrity of One, the continuity of Nine, maybe the supersymmetry of Two and the space-time reality of Four.
But as ever, a question mark surrounds that word ‘will’.
The sequence 1-4-9 is the Star Gate in Arthur C. Clarke’s 2001, but the events of the real 2001 came as quite a surprise. The human factor is unpredictable. The Intergovernmental Panel on Climate Change makes this unpredictability strikingly vivid. There is a wide spread of outcomes for anthropic climate change depending on what the anthropos, or at least its rulers, chooses to do with the Anthropocene geological era it has started. As New Scientist comment puts it, there are tipping points in political choices as well as in physical evolution. And as scientists know, doing the computation itself affects those choices. They may express caution in predictions, sensing the danger of crying wolf through premature announcements. But they may actually have been overcautious: revisions to the model so far have included more slippery ice-sheets and glaciers, greater methane release, less oceanic absorption of CO2, and more trouble from uncontrolled logging, than expected. There seems to be a Gödelian impossibility about finding the correct balance, one which encourages neither complacency nor fatalistic pessimism.
Mathematical prediction comes up against the mystery of human consciousness. There is a parallel in cryptology. Turing and Shannon created the theory of mathematical information as a development of probability and statistics, by using letter frequencies as a start. Such frequencies can be turned into numbers. But letters join into words, and words shade into meaning, sense and truth. Information slides into the human purpose of the messages; this cannot be quantified, and depends on knowledge and understanding. This is not an abstract philosophical distinction. The strength of the British code-breaking work (after a classic Two Cultures mis-match in 1940) lay in the synthesis of mathematical theory and human understanding. There may be parallel questions now. The sophisticated mathematical work at NSA/GCHQ is of little use if no one can understand deciphered messages because all the Arabic linguists have been sacked for being gay, or if their content goes to a faith-based circle in which the ‘reality community’ is denigrated.
Alan Turing was himself a serious loss to Anglospheric intelligence-gathering. On a notable day, 6 June 1944, he reported on his Delilah speech encipherment, decades ahead of GSM, but never used. His computer plans were stalled, his software plans never used. When he was revealed as a gay man, his work for the state was finished; on 7 June 1954 he was dead. Oppenheimer was widely denounced as disloyal that same week. Once people find themselves swimming against the human tide, molehills of dispute become mountains of contentiousness and even great scientists become as welcome as moles. Discovering black holes, inventing the computer, count for nothing. And like Cold War science in the 1950s, climate predictions have had to face a cool reception—notably in the United States, but more generally against a global tide of commitment to unstoppable growth requiring minimal state regulation of economic activity.
Reason is a back-seat driver, with responsibility and no power, unwelcome on board, unable to strike, and too often sniped at by other, weightier passengers for being a mere materialist. Nor is reason a single voice, but a dialectic, an argument taking centuries and never really finished. Is it cool to do serious mathematics? I am—well, cool about it, as cool as Cordelia was to Lear. It is an enormous privilege to be detached from the torture and slavery under which most of the world labours. But it does not have much to do with optimising personal profit or pleasure as commonly understood. Mathematics needs a stoicism—a G. H. Hardiness, and a Thomas Hardiness too—which runs at odds with noughth-impression, have-it-now, sound-bite culture. Hardy did not like Hogben describing serious mathematics as having a ‘coldly impersonal attraction’, but cold and impersonal it is, though some like it cold.
Turing’s own summary in 1948 of a mathematician’s life was that ‘he may perhaps do a little research of his own, and make a very few discoveries which are passed on to other men’. Though a supreme individualist, he cast his role as being in a long process of collective advance. As individuals, some come out on top, but many more must lose, and do so gracefully. And mathematics can be cruel rather than cool to those individuals. Gödel’s 1931 work made a point of showing that Russell’s program had missed the point; while Russell himself had dropped a similar bombshell on an earlier logician, Frege.
Mathematics sometimes tries to re-brand itself and court popularity by advertising fame and fortune, Botoxing those lines that betray hard thinking. But if fame and fortune are the priorities then there are far more enjoyable ways of achieving them. The PSB get it right about Opportunities: ‘Doctored in mathematics, I could have been a don, I can program a computer …’—but sensibly, they took the opportunity to make music. Few make the journey in the other direction. Brian May has shown it is possible, finishing a doctorate in astronomy after 30 years, but perhaps only someone capable of performing with Freddie Mercury could rise to that challenge.
Numbers are cool only in the sense that the coolest people can ignore fashion. Numbers are cool in being adult, and showing naked reality. Numbers have the icy-cool taste of eternity, the four-dimensional view. Writing this book, and so being taken back to Constance Reid’s book of 50 years ago, has refreshed that timelessness. Perhaps the sweetest thing about One is the glorious first step. As we reach the ending, Nine can remember the music of primal vision, even though it bears a weary experience of the world.
The anthropos is faced with the outcome of its own dissipated youth, now suddenly having to grow up while keeping cool. It looks like Mission Impossible, but the RSA crypto-system is a model of how cool heads can overcome an apparent impossibility. That apparently deadly either/or can be transcended—by using mathematics to analyse its own hardness. Having solved one problem, new questions open up. The entropy crisis may have solutions using new methods: they will need new mathematics, and will lead to new problems. Adult mathematics is the only hope, even if it increases the creases in the human face.
Why does the planet work in operating system Ten? Mathematicians usually disparage base-ten notation, with its tiresome over-large, over-complicated multiplication table. It seems an arbitrary choice driven by the ten biological digits. But that product of primes, two and five, is a good reminder of our complexity. The Two has the basic broken symmetries of time and space. Doubling and redoubling to calculate with fours and eights would have been highly utilitarian, but the Five has an added and magic aesthetic of imagination. An ever-growing sphere of very faint radio waves, with the radius of a hundred light years, now surrounds the planet. It carries those human two-times-fives. If alien life is curious, or hungry, it can figure them out for itself.
Yet Ten has a life of its own, nothing to do with sticky human fingers grabbing quick fixes. It is connected with the four-squareness of the physical world. Ten is 1 + 2 + 3 + 4, and that triangular number counts Einstein’s equations for four-dimensional curved space-time. Those equations, according to present and imperfect understanding, don’t seem to care whether anthropos is around to think about them or not. The future, on its grandest scale, is determined by the properties of—
