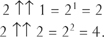
Computers work with zeroes and ones. Digital art installations regularly show the inhuman reductionist nature of science, etc. etc., with images rendered in chilly zeroes and frigid ones. Sadie Plant wrote on Zeroes and Ones: Digital Women and the New Technoculture. Back in the 1950s, zeroes and ones were still cutting-edge news and Constance Reid explained them in Chapter 2 of From Zero to Infinity. Now everyone knows that binary digits, or bits for short, underpin electronic computing. And yet:—
As Constance Reid pointed out, you might also say that computers use numbers in base 4, 8, or 16. Use of these bases only amounts to employing slightly different names for the binary numbers. Take the number we usually write as 2885, which is 2048 + 512 + 256 + 64 + 4 + 1 and so represented in binary as 101101000101.
Writing it as 10 11 01 00 01 01 is completely equivalent to using base-4 representation, with 00, 01, 10, 11 as numerals instead of 0, 1, 2, 3.
Writing it as 101 101 000 101 is completely equivalent to using base-8 representation, using 000, 001, 010 … 111 as numerals instead of the usual octal 0, 1, 2 … 7.
Writing it as 1011 0100 0101 is completely equivalent to using the base-16 representation, using 0000, 0001, 0010 … 1110, 1111 instead of the hexadecimal 0, 1, 2, 3 … E, F.
The same argument applies to any other power of 2. Some early computers used teleprinters for input and output, and so used 5-bit sequences for alphanumerical symbols; they were effectively using base 32. Bases of 8 and 16 became more popular, and base 16 became standard for microprocessors. But the number Eight has made a comeback, not as the octal representation but through the fact that 256 = 28. This means that a sequence of eight binary digits is effectively a numeral in base 256. By the 1970s it was standard to work in such 8-bit units, called bytes. A byte can be written as a pair of hexadecimal symbols.
Another aspect of computing, increasingly important with the global development of the Internet, is that the coding of alphanumeric symbols has evolved from those original 5-bit teleprinter symbols into ASCII (American Standard Code for Information Interchange) and now includes all world writing systems, including Chinese ideograms, in the Unicode system. This expansion also uses a base of 256. Meanwhile the internal processing chips themselves have come to use 64-bit registers, consisting of eight bytes each of eight bits.
So Eight is the number of computing. It was prefigured by Archimedes’ organisation by myriad-myriads, and also by the 8 × 8 chessboard for well-calculated strategy. Readers of my earlier book Alan Turing: the Enigma will know the drama of the Eighth Square, borrowed from Lewis Carroll.
The hugeness of possibilities within a computer is even greater than the number of possible bridge hands. Just one 64-bit register, a microscopic component of a computer, can hold any one of 264 different numbers. At a thousand trillion operations a second (the fastest in 2006) it would take five hours to work through them all. There are 2128 possible states of two such registers, and even using ten billion chips in parallel, it would take a million years to work through them. Therefore most simple additions of two 64-bit registers have never been performed.
That super-eight number 264 was used at least twice in pre-computer days to illustrate the enormous scale of combinatorial numbers arising even from simple pictures. A legend tells of the inventor of chess, who asked for a reward consisting of a grain of rice, redoubled for each square of the chessboard, a request to which the Indian king rashly agreed. A nineteenth-century French mathematician, Edouard Lucas, devised a puzzle called the Tower of Hanoi, looking innocuous enough, but soluble only in 264 − 1 moves. But the formidable power of modern computing comes not from the zeroes and ones of binary numbers, nor even from the huge number of ways of combining them.
Fact: You need to understand binary numbers to know how computers work.
Deeper fact: You don’t need to understand binary numbers to know how computers work.
The power of computers comes from the potential to run programs.
Although Eight has thus played a practical part in computing, something much deeper comes from thinking about the way that eight arises as the cube of two. In Chapter 4, we saw cubing as a function, pictured as a graph. This holds the idea of cubing as a platonic relationship: the function is defined to exist. The cube and its inverse, the cube root, are both simply there. But there is quite another way of thinking of cubing, in which the symmetry of doing and undoing is completely broken. In writing 23 = 8, that 3 can be thought of as an instruction: start with 1 and multiply by 2 three times.
Think of this as a cookery recipe. It is no more difficult to write a recipe for 2n, where n is any natural number. But doubling three times comes close to the limit of what you can do without keeping a careful note of how many doublings you have done. So a wise cook will do something like this to keep a count of the doublings:
POWER BREAKFAST RECIPE
Step 1: Put 1 into the pot, put n in the pan.
Step 2: Double the number in the pot, decrease the number in the pan by 1.
Step 3: If the number in the pan is not 0, go back to step 2; otherwise take the number out of the pot.
The number that emerges is just 2 to the power of n. Now there is no problem if the phone rings in the middle. This flexibility imposes a price: the cook must apply a test and go to a step which depends on the outcome. But this is natural for cookery: it embodies the idea of ‘bring to the boil’. It is simple for numbers as well.
It is no harder to write a recipe for mn, by changing ‘doubling’ to ‘multiplying by m’. So the operation of working out a power, or exponentiation, can be reduced to a sequence of easier multiplications, augmented by the business of testing and jumping. Is this the end of the story? No, because multiplication is not really a single step. It also needs a recipe to reduce it to a sequence of even easier additions. In turn addition can also be reduced to the repeating of the very basic operation of incrementing by one. Putting these recipes together, the business of working out mn can be reduced to a succession of primitive add-on-one operations, but with constant testing and jumping required.
To put these recipes together, another principle is needed. It is that of ‘here’s one I made yesterday’, as tirelessly used in cookery demonstrations. Imagine that the recipe for addition has been written out and is available on demand. Then the recipe for multiplication goes ahead by instructing the cook at various points to ‘look up the recipe for addition, and follow it’. The recipe for exponentiation similarly contains instructions for getting and using the multiplication recipe.
This is, basically, just how computer programs break everything down into very simple operations, each to be implemented electronically in a trillionth of a second. Yet it was conceived before computers existed.
We have already seen something of the background to this in Chapter 1. The meticulous logic, such as Russell pursued, set the stage. It put mathematicians into the mind-set of deriving conclusions from axioms mechanically, completely without imagination. Indeed Hardy actually used the word ‘machine’, rather pejoratively, to describe this attempt to make mathematics into a complete set of formal rules. Gödel’s work in 1931 had introduced the idea of coding, and mathematics thereafter was edging towards the kind of logic needed for computers, the logic of actually performing operations, not just asserting truths.
Yet this recipe-book tradition had always been present in mathematics. An older, mathematical word for method is ‘algorithm’. The word is nothing to do with Al Gore, but comes from al-Khwarizmi in medieval Iran, long before cando America was thought of. He in turn drew on the Greek mathematicians Archimedes and Diophantus who expressed their discoveries as methods for solving problems. Some of Euclid’s statements were also put in this way. Fermat’s famous ‘last theorem’ conjecture, written in the margin of his copy of Diophantus, is usually given in the form of a ‘non-existence’ statement, but actually what he wrote was that ‘it is impossible to separate a cube into two cubes …’ using the Diophantine language of performing an operation. Galois and Abel drew on this tradition in showing that the methods for solving quadratic, cubic and quartic equations could not be extended to quintic equations. In the twentieth century, the ‘constructivist’ philosophy, as a development of intuition-ism, had already challenged the Platonic ideal of pure ‘existence’ and was all part of the shake-up of logic.
Nevertheless, it needed someone quite new to crystallise this. If you are a believer in genetic connections, you will find it significant that George Stoney’s second cousin’s granddaughter Sara Stoney had a son who turned out to be just this person. Alan Turing, when just turning 23, had the idea soon called Turing machines—essentially like the recipes described above, reducing everything to the simplest possible components, but showing a potential for encompassing enormous tasks.
Turing’s work was published in 1936. It was stimulated by what Gödel had done in 1931. It had nothing to do with IBM, and was not done for profit. Nor was it motivated by current needs for computing in science. The early 1930s marked a point when enormous calculations for quantum chemistry were put on the agenda. Turing certainly knew of such problems, but his new cuisine was not devised to solve them. An interesting question is whether Turing was guided by the Marxist Zeitgeist which emerged in Lancelot Hogben’s writing at just this period. I think not: certainly he had a hands-on approach to mathematics, but this was a distinctively individualistic passion rather than something drawn from an ideology about workers by hand and brain. Once that passion had emerged in the form of Turing machines, it inspired others who were alive to its potential.
In 1938, as war approached, two mathematicians, Janos von Neumann from Hungary and Stanislaw Ulam from Poland, were crossing the Atlantic on the Georgic liner. Ulam wrote later that von Neumann ‘proposed a game to me … writing down on a piece of paper as big a number as we could, defining it by a method which indeed has something to do with some schemata of Turing’s … Von Neumann mentioned to me Turing’s name several times in 1939 in conversations concerning mechanical ways to develop formal mathematical systems.’
To write down big numbers on a piece of paper, using Turing machines, they very likely started with the following idea. It illustrates the power of programs by getting some really really large numbers from just a few lines. We simply go in the opposite direction, and treat the exponentiation recipe as the ‘one I made yesterday’, to be read and followed as part of a much more ambitious recipe:
Step 1: Put 1 in the pot, put n in the pan.
Step 2: Get the Power Breakfast recipe. Use it to replace the number in the pot by 2 to the power of the number in the pot. Then subtract 1 from the pan.
Step 3: If the number in the pan is not 0, go back to step 2; otherwise take the number out of the pot.
What kind of numbers come out of the pot? They rapidly become so large that new notation is necessary even to describe them. First, we introduce a single arrow ↑ for exponentiation, writing m ↑ n instead of mn. Next, we define the double arrow ↑↑ by the rules: 2 ↑↑ 0 = 1, and then 2 ↑↑ n = 2 ↑ (2 ↑↑ (n − 1)). Then following this rule:
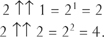
This gives a new way in which two and two make four!
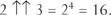
Now the repeated exponentiation begins to get serious:
After this we cannot even write out the exponent and have to leave it as:
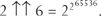
Without the use of the double arrow notation, any further numbers have to be written as towers of powers. 2 ↑↑ n is a tower of twos of height n, like this:
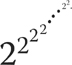
But even this needs a forest of brackets to make it clear that the evaluation must start at the top and work downwards. This is why the arrow notation is valuable.
The number 65536 can be visualised: a town, a big crowd, or the number of bits in a small image. The next number, 2 ↑↑ 5, is about 20000 digits long in decimal notation, far greater than astronomical numbers. It is comparable with the number of possible images that the eye and brain must be able to cope with. 2 ↑↑ 5 is not as great as Archimedes’ largest number, but 2 ↑↑ 6 leaps ahead, far beyond any mental picture.
DEADLY: Arrange in order of size the following numbers:
(A) Archimedes’ largest number,
(B) Eddington’s guess for the number of particles in the universe, 2 × 136 × 2256,
(C) a googol,
(D) a googolplex, defined as 10 to the power of a googol,
(E) the largest number you can make with four fours,
(F) Penrose’s number measuring the specialness of the Big Bang,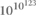 
,
(G) 2 ↑↑ 5, (H) 2 ↑↑ 6.
But this is only the beginning of what can be done with the arrows, or equivalently, what can be done with a few lines of programming. Taking this just one stage further, you can go on to write a simple recipe for really really really large numbers. Its outputs cannot be expressed with conventional mathematical notation, even allowing for towers of powers. The recipe is equivalent to the rules: 2 ↑↑↑ 0 = 1 and 2 ↑↑↑ n = 2 ↑↑ (2 ↑↑↑ (n − 1)).
Then 2 ↑↑↑ 1 = 2 and 2 ↑↑↑ 2 = 4 again. Next,
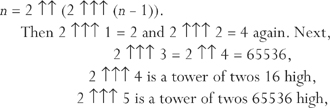
and after that you can’t even imagine the size of the tower of twos.
The arrow notation can be extended without limit. 2 ↑↑ … ↑↑ 2 is always 4. 2 ↑↑↑↑ 3 is 2 ↑↑↑ 4, on the edge of comprehensibility, but 2 ↑↑↑↑ 4 = 2 ↑↑↑↑↑ 3 and all further numbers of this kind defy imagination.
If he had been sharing that voyage in 1938, and had overheard this pair of mitteleuropäische professors excitedly scribbling Turing machines in their deckchairs, Lancelot Hogben might have considered their competition a frivolous exercise in abstract mathematics. Yet the principle of programs calling other programs has turned out useful for even more millions of people than have ever read Hogben’s book, and has changed the very nature of work by hand and brain. That is because it is the principle on which modern computers work. Underlying it is the fundamental discovery that Turing made in 1936, the concept of a universal machine. The modern computer (more strictly defined as a computer with ‘modifiable internally stored program’) is an embodiment of that concept.
It is easiest to appreciate it with the advantage of hindsight. A computer stores everything in zeroes and ones. The numbers it works with are all in zeroes and ones—but so are the programs. If one program needs to call on another, it needs to fetch and read a sequence of zeroes and ones. This is no different from fetching a number. The technology for storing and communicating the programs can be exactly the same as that for numbers. The cookery demonstration imagined numbers in pots and pans, and recipes in a book, but you could keep the recipes in pots as well. In a word, computers are not kosher. For modern PC users all this is familiar. A click on the mouse may run a program, and so use it as a recipe, but you may just as well download, install, store, copy or compile the program, thus treating it as a file of 0-and-1 data.
In 1936, the idea of encoding operations on numbers as numbers, which Turing announced, was revolutionary. But it was strongly connected with Gödel’s 1931 work, which had encoded statements about numbers, by numbers. This in turn derived from the logical problems of Russell’s sets which are members of themselves. So the power of modern computing does in fact derive from the most rarified of intellectual efforts to find consistency and unity in mathematics.
The upshot of Turing’s work was that however complicated the task, it could be reduced to simple operations like adding-on-one, and performed by a single machine. The complexity of the task would go entirely into the logic of the instructions. This is the concept of the modern computer, which, as we would say now, only needs new software in order to switch from one task to a new and completely different one.
Often the word ‘digital’ is used as if it expressed the one and only essential principle of computer technology. It is indeed true that the digitalisation of information is necessary for it. But that is not sufficient. A universal machine, reading programs and carrying them out, needs a certain level of organisational complexity, and this took over two thousand years of logic to develop. Charles Babbage, often claimed to be the inventor of the computer, developed some first ideas about programming in the 1840s. Ada Lovelace gave a famous account of his most advanced application—the calculation of Bernoulli numbers, as mentioned in Chapter 6. But her explanation shows that their ideas about how to take output and feed it back as input were vague and confused. They never had the central idea that instructions and numbers can be stored and manipulated alike. I would compare the Analytical Engine plans with the tiles of Darb-i Imam: they are amazing and seem to jump out of their time-frame but cannot be said to express the content of modern understanding.
The aristocratic Ada Lovelace, Byron’s daughter, gives a particularly vivid example of a woman who seems out of her time-frame. But it is not clear how much she actually contributed to the Analytical Engine. Other women, such as her teacher Mary Somerville, and the later Sofia Kovalevskaya and Emmy Noether, are less celebrated but arguably greater mathematical pioneers.
Turing, in contrast, saw the whole thing. It is not clear whether in 1936 he surveyed the possibilities of constructing a universal machine. The price of universality is that a great many logical operations have to be performed to follow the instructions, and this is not worthwhile unless millions of them can be performed in a second. The speed of electronic components, necessary for this, was not available in 1936. But once Turing learnt electronics from the new technology developed for code-breaking at Bletchley Park, he realised it could be applied to his concept of the universal machine. After emerging from the war against Nazi Germany, which he probably did as much as any individual to win, the first thing Alan Turing did was to draw up a plan.
He was beaten to it. Von Neumann’s first design of an electronic computer appeared some months before Turing’s own detailed scheme, and von Neumann has largely gained the credit for initiating the post-war computer revolution. (His first program bore the iconic date 8 May 1945.) Von Neumann was a more organised and powerful proponent, but Turing had the sharper and deeper picture of universality. This still took a long time to sink in after 1945, even though the power of von Neumann’s and Turing’s designs rapidly swept the field. Martin Davis, one of the leading logicians of the past half-century, has written a history of Turing’s concept as The Universal Computer. He quotes Howard Aiken, the computing chief of the of US Navy, and the person who did most to bring Babbage’s ideas to fruition. As late as 1956 Aiken wrote that ‘If it should turn out that the basic logic of a machine designed for the numerical solution of differential equations coincide with the logics of a machine intended to make bills for a department store, I would regard this as the most amazing coincidence that I have ever encountered.’ This amazing coincidence—a very good statement of the power of the universal machine—is now completely taken for granted.
At first, department stores—and capitalist enterprises generally—were little interested, leaving government and advanced scientific research to realise its potential. As with the Eurabian zero, realisation is just the right word. The internally stored program has conquered though being realised in electronics, and now there is no going back. With enormous advances in scale and speed and reliability, a mass market has been created such as no one dreamt of in early days. Programs for gaming and webcamming, linking a global network of teenage bedrooms, are not exactly what progressive thinkers of the 1930s planned for future society, nor what technocrats of the 1940s and 1950s envisaged as the economic role of computing. Indeed, they go far beyond what Bill Gates saw in 1993. But they follow from the power of the universal machine, and its internally stored programs all calling each other.
Hardware is ephemeral, as Turing saw. Today’s personal computer may disappear, and the word ‘computer’ itself may be overtaken by new developments. Already, mobile phones are (rightly) advertised as showing where computers are going. They may become too small to see, they may be implanted in brains, but universal machines will retain their logical power.
The huge success of the personal computer market has not been because of the public wising up to binary numbers. Computer users are quite right not to know or care about them. As Turing also explained very clearly in 1947, any conversion between decimal and binary numbers could be done by the machine itself, simply by writing appropriate software. This is just another aspect of universality, and it makes the computer essentially user-friendly.
This is why you don’t need to know about binary numbers to use a computer. You do not need to cater to its way of working: it can be instructed to cater to yours. As long as you can tell it exactly what you want, the computer can do it. You could call this the ‘Hot Pink’ principle. In Chapter 3 I explained how that name is given to the mixture of red, green and blue expressed by the hexadecimal symbols FF69B4, which web-browsers read. But if you want to create a webpage with Hot Pink background, there is no need to remember or look up those symbols yourself. The computer itself can translate the more user-friendly words ‘Hot Pink’ into hexadecimal form. As Turing put it in 1946, ‘The process of constructing instruction tables should be very fascinating. There need be no real danger of it ever becoming a drudge, for any processes that are quite mechanical may be turned over to the machine itself.’ From this perception flows the idea of computer languages, which Turing himself started with instructions written in what he called a ‘Popular Form’.
Turing wrote in 1946 that ‘Every known process has got to be translated into instruction tables.’ Turing was far ahead of von Neumann in seeing the importance of software, and this is indeed how it has gone, though with applications that would have surprised the 1940s pioneers. Turing also saw that computer experts would resist user-friendliness and use ‘well-chosen gibberish’ to explain why things could not be done. Maddening error messages, incompatible files, crashes and connection failures bear out his words. ‘Computer says no’ is a running joke in the BBC’s Little Britain. But these are not faults of the underlying concept. If anything, the problem lies in the other direction: the computer can’t say no to anyone, in any language. The universal machine is a shameless slut worthy of Little Britain, just as friendly to abusers as to users. If instructed, it sends out a million spam emails with spoofing and phishing, or injects Trojan-horse viruses into millions of other computers. It can create firewalls or hack into firewalls, censor the Web or defeat the censorship. It follows instructions.
One of the climate-change-sceptic arguments is that the predicted increase in global temperature is ‘only a computer model’. This is not a strong argument: successful landings of spacecraft on Mars, and the prediction of protein shapes from DNA sequences, are the results of computer models. The fact that a prediction is run on a computer is not of primary significance. The validity of the model comes from the correctness of its mathematics and physics. Making predictions is the business of science, and computers simply extend the scope of human mental faculties for doing that business. To reject computer models per se is to reject science. On the other hand, there are serious questions about how the continuous world of physics can be modelled on the discrete states of computers, and for climate questions—as for the proton model—much hangs on the fineness of the grid, or lattice, of space-time points. Treatment of this question needs its own sophisticated mathematical theory, that of numerical analysis.
Conversely, if a theory is wrong then running it on a computer won’t make it come right. Astrology does not become scientific by being computer-based. In view of the fact that many people take leave of their senses when computers are involved, there is a good place for scepticism about computer outputs unsupported by reason. The tendency of people to believe in machines is not new: the wartime German authorities could not believe the Enigma was at fault, and preferred to distrust their own U-boat crews. With gigantic software contracts, identity register systems, medical records, on-line voting—computers are quite capable of generating a stream of crime and folly to enhance all the others.
Computers do algorithms. Whether the results are true or false, elegant or ugly, fraudulent or frightening, tedious or puerile, illegal or totally ridiculous, they carry them out. But specifying an algorithm means giving a completely definite, finitely expressed set of instructions. For many tasks it is doubtful whether complete rules can ever be given. An example which causes frequent hilarity in the press is the application of software to filter messages for rude words. But even if we stick to the safety of pure numbers, we encounter tasks which cannot be performed by algorithms and so cannot be done by computers.
Just as the idea of the universal machine predated electronic machines, so did the discovery of the uncomputable. It was there right at the beginning in Turing’s 1936 work, and it had roots in the logical antecedents: Russell’s sets which are members of themselves, and Gödel’s mathematical statements which refer to themselves. Turing had followed these by considering programs operating on themselves. This led to the very positive idea of the universal machine. But it also established the negative fact that some problems are, in a strict sense, unsolvable.
A program will involve much testing and jumping back and forth between instructions, and it is hard to tell by looking at it that it will not go into a loop of operations from which it will never escape. Define ‘debugging’ a program to mean checking it to ensure that it will actually terminate, rather than go into such an unending loop—the effect seen with faulty software as a computer ‘crash’. Can debugging of programs itself be done by a program? It turns out that this is impossible. Turing’s principal result in 1936 can be thought of as showing the non-existence of any completely general program for debugging. It can also be seen as showing that there is no general algorithm for settling mathematical questions.
Why can the apparently technical business of ‘debugging’ be equated to a problem of pure mathematics? The underlying idea can be seen from our simple cookery recipes. These used a single pot, or register, for a number acting as a counter ticking down to zero. The recipe relied on the fact that we know the properties of numbers, and therefore know that however large the starting value n, it will, if decreased each time, eventually reach zero and so stop the computation. But a slightly more complicated program might have not one but several counters ticking away. At each stage they could be tested not for whether they have reached zero, but for some more complicated mathematical property. Four counters a, b, c, n could be tested for the truth of an + bn = cn. To know whether a program depending on this test would go into an unending loop, you would have to know the truth of Fermat’s conjecture. As it happens we do now know this truth, but there are infinitely more statements whose truth is unknown. Having a complete debugging program would be equivalent to being able to decide all of them.
But Turing’s theory made it easy to see that no such debugging program could exist. If it did, it could be applied to itself, and would produce a self-contradictory tangle. Putting these ideas together, Turing showed that mathematical methods cannot be exhausted by a finite instruction book: creativity will always be required.
Twenty years later, the theory of computation was re-entering the serious heartland of Number by extending Turing’s discovery. Although Constance Reid’s 1956 book gave a rather low-level picture of computers doing binary arithmetic, she actually knew better than that. She was connected with another American mathematician, Julia Robinson, a pioneer in this high-level appreciation of computing. Julia Robinson, like Martin Davis, did important work in a long series of discoveries which culminated in 1970 when a young Russian, Yuri Matyesevich, finally showed that there is no algorithm for solving all Diophantine equations. In this way, computing got back to Diophantus, the proponent of the constructive method.
The proof required extraordinary new algebra, in which Fibonacci numbers played a vital part. It led to the discovery of hitherto unsuspected aspects of the theory of numbers. A polynomial is a formula using only addition and multiplication: as a result of this work it was found that there is a polynomial in 26 integer variables whose positive values are precisely the prime numbers. There are analogous polynomials for any series of numbers that can be produced by a computer program. As a more vivid picture of this line of research, the Penrose tilings arose from studying an uncomputable problem. This is yet another example of how a proof that something can’t be done leads to completely new ideas.
Practical work with computers has also shed a little new light on those powers and primes of the classical mathematicians.
The world’s first universal machine was working in Manchester in 1948. It only had a store of 1024 bits. But this was enough to launch a search for Mersenne primes, named after Martin Mersenne, another seventeenth-century figure from Fermat’s France. Mersenne primes are those which are just one less than a power of two, and so appear as 111111 … 1111 in binary notation; they have particularly interesting properties. One is that they are connected with perfect numbers. A perfect number is equal to the sum of its divisors. The first example is 6 = 1 + 2 + 3 and the next is 28 = 1 + 2 + 4 + 7 + 14.
DIFFICULT: The number expressed in binary notation as 1111 … 111000… 000, with n 1’s and (n −1) 0’s, is perfect if 1111 … 111 is prime.
Only numbers of form 2p − 1, where p is prime, can be Mersenne primes. The first of these occur for p = 2, 3, 5, 7, 13, 17, 19, 31, as Euler found. These give the primes 3, 7, 31, 127, 8191, 131071, 524387, 2147483647.
DIFFICULT: Constance Reid left this as a ‘challenge’ to her readers: If n is not prime, then 2n − 1 is not prime. (Hint: Express 2n − 1 in binary notation.)
Beyond p = 31, the question becomes decidedly TRICKY. It is solved by using a special test for the primality of numbers of this particular form. This test was found by the same Edouard Lucas who devised the Tower of Hanoi puzzle. It involves an extension of Fibonacci numbers. Using it, Lucas showed 2127 − 1 to be prime, and this number remained the largest known prime for many decades, until the record fell to the computer. The Lucas test, a little refined, is particularly suitable for the zeroes and ones of computers, and this is why it could be run as virtually the first program on that tiny Manchester prototype. Even though Turing was involved, it didn’t find any more, but in 1952 a new prime, 2521 − 1, was found at Cambridge, and a few more followed. The new results were impressive enough to inspire Chapter 6 of Constance Reid’s From Zero to Infinity.
The subsequent story of Mersenne numbers marks the complete change from the days when the world’s few computers were reserved for a tiny élite. Personal computers far more powerful than any computer of the 1950s, and linked through the Internet, allow anyone to join in. In September 2006, the 44th known Mersenne prime was found and 232582657 − 1 became the largest known prime. The organisation of ‘distributed computing’ for amateur participation, like the SETI search for messages from outer space, fightaidsathome.net and climateprediction.net, shows the power of universal user-friendliness. But whether there are infinitely many Mersenne primes, and numerous other such questions, cannot be resolved by computing, however vast the scale.
Those really really large numbers give a sense of how strong a statement it is to say that something is true for all numbers. Never, never, never, even for those unimaginably large numbers defined by the repeated ↑↑↑, can it be true that an + bn = cn for n > 2. That truth, proved at last by Andrew Wiles in 1995, could not have been established by computers. Computers could have disproved Fermat if his conjecture had been wrong. They have disposed of less lucky conjectures. Euler, for instance, guessed a generalisation, that just as there is no cube which is the sum of two cubes, there is no fourth power that is the sum of three fourth powers, no fifth power that is the sum of four fifth powers. But he was wrong, because computer search has revealed that 1445 = 275 + 845 + 1105 + 1335 and 4224814 = 958004 + 2175194 + 4145604.
The Riemann hypothesis, which is about the behaviour of all prime numbers, however large, is another statement that cannot be shown to be true by computing. But if untrue, it could be shown to be so by numerical calculation. In 1950, when the Manchester computer had more storage capacity, this was the first question to which Turing turned. This was probably the first time that the power of the universal machine was seriously used to probe the inner life of the numbers.
Fermat had another conjecture—a simpler one—about primes. He studied the numbers which are one more than a power of 2. Now, it is (fairly) easy to check that 2r + 1 cannot be prime if r has any odd factor. So the only possible candidates for primes are numbers of the form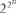 
+ 1. The first examples are 
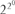257, and 
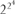. These are prime. Fermat guessed that all numbers of the form 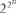+ 1 would turn out to be prime.
Constance Reid devoted Chapter 7 of From Zero to Infinity to this question. She told the story of how in this case Fermat was proved wrong, because 100 years later Euler showed the next Fermat number, 232 + 1, could be divided by 641. By 1954 a few further Fermat numbers were known not to be prime. No more Fermat primes have been found, but there is no proof that there are none to be found. In this case, computing has not made much difference.
Fermat did not know that this question was connected with Euclid’s classical constructions with straight-edge and compasses. In Chapter 5, we found that drawing a pentagon was tantamount to constructing a line of length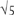 
. In Chapter 7, I mentioned the annoying fact that being able to draw a length of 
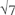is not enough to draw a heptagon. The Greek mathematicians knew this, but did not know the whole story. In fact, a regular polygon with seventeen sides can indeed be constructed, though in a more complicated way, based on lines of length 
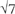. This was shown by Gauss, but even he lacked the complete picture. Only in 1837 was it proved that an n-agon is constructible by Euclid’s methods if and only if n has very particular factors. These can include any number of 2’s, but at most one of each of the numbers 3, 5, 17, 257, 65537—and any other Fermat primes, if they exist.
MODERATE: Explain why this means that (in principle) you can construct a 65535 × 65536 × 65537-gon with straight-edge and compasses.
If 65537 is the last Fermat prime, there must be some as yet unknown reason why the remaining infinite number of Fermat numbers are all composite. Or else, there are finitely or infinitely many gigantic Fermat primes. In either case there is something to be found out. The connection of Fermat primes with polygons can be expressed entirely in terms of square roots and squares, so mathematicians certainly don’t know everything, even about squaring.
Fermat numbers are probably not of great significance, but this question gives a model, in the way it links numbers, algebra and geometry with other surprising features of advanced mathematics. Certain things do not work, do not fit, except for certain huge and unexpected numbers. The numbers 196883 and 196884 have turned out to give extraordinary connections between string theory, complex numbers and the structures mentioned in Chapter 6 as the ‘finite simple groups’. This is where modern research is following Fermat and Gauss and Ramanujan today. These structures involve astronomical numbers, and some people conjecture that they have to do with why the universe has to be so big, and so may restore a pure mathematical basis to it after all. This is certainly an example of how string theory has energised every part of mathematics, including pure number theory—even if it is not, in the end, the key to physical reality. Maybe computers will play a vital role in grasping these connections.
Computers certainly play a central part in breaking the code of the universe: both in cosmology and in particle physics the demands of science constantly push at the boundaries of computing power. (The World Wide Web emerged as a sort of spin-off from CERN, the European centre for fundamental research in physics.) But now we will turn to the breaking of more down-to-earth ciphers.
Codes and code-breaking were, behind the scenes, a major factor in encouraging governments to build computers after 1945. The Anglo-American government code-breaking establishments have, ever since, been major employers of mathematicians. Fermat’s last prime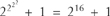 
65537 gives a point of departure for illustrating the kind of mathematics that is involved.
I will first use the smaller Fermat number 17 instead of 65537, as a miniature version suitable for a book page. The resulting patterns can then be seen without using a computer. Consider this recipe, short but sweet:
Step 1: Choose any number from 1 to 16.
Step 2: Multiply it by 10.
Step 3: If the result is bigger than 16, subtract 17
Continue subtracting 17 until the result is 16 or less.
Step 4: Write down this result, then go back to step 2.
It produces a sequence of numbers from the following repeating cycle:
…1, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12, 1…
where the sixteen numbers from 1 to 16 each appear once. The interesting thing about this pattern is that it seems devoid of pattern.
The apparently patternless sequence is not random, since each number depends on the previous one in a specific and simple way. The non-randomness shows up on closer inspection: take the first eight values (1, 10, 15, 14, 4, 6, 9, 5), subtract them from 17, and you will find the remaining values in order (16, 7, 2, 3, 13, 11, 8, 12).
In fact a super-intelligent being might say immediately: ‘Random? What’s random about that sequence? They are obviously the powers of 10 modulo 17!’ From this point of view it is no more random than is the sequence 2, 4, 6, 2, 4, 6, 2, 4, 6 … which lists the remainders when the powers of 2 are divided by 10 (i.e. the last digits of 2, 4, 8, 16, 32, 64 …). It is useful to think in terms of an argument or contest with a higher intelligence, because this brings out the similarity to the problem of breaking a code by spotting a pattern in the apparently patternless.
Despite the objection of the higher being, there is a good reason for calling the sequence ‘random-looking’. Coding these numbers as binary digits (using 0000 for 16) gives a sequence of 64 bits with very special properties which resemble those of a genuinely random stream, as produced by tossing coins or throwing dice:
00011010111111100100011010010101000001110010001 11101101101001100.
EASY: Check that there are equal numbers of zeroes and ones, that zeroes and ones are equally likely to be followed by a zero or a one, and that the sequences 000, 001, 010, etc. are also equally frequent. The frequencies of the various possible sequences of four and five symbols are also close to equality.
MODERATE: Show that powers of 3, 5, 6, 7, 11, 12, 14, also generate random-looking sequences of sixteen numbers, but the remaining numbers do not.
DIFFICULT: The numbers 3, 5, 6, 7, 10, 11, 12, 14, are those which do not appear in the diagonal of the base-17 multiplication table.
So this apparently abstruse investigation of diagonals, the subject of Gauss’s Law of Quadratic Reciprocity, leads to something useful: pseudo-random streams.
When Fermat’s number 65537 is substituted for 17, a longer pseudo-random stream of 65536 × 16 = 1048576 bits, or 128k bytes, is produced. It would take more than the length of this book to write out the bits, which is why the number seventeen is useful to give a miniature illustration of it. Nowadays, a 128k file is typical for a single picture, a mere detail of spam in an ephemeral inbox, but in the early 1980s it was seriously large—the first Macintosh was launched in 1984 with RAM of only 128k. When the first mass-marketed microprocessors became available, a random stream of this length was perfectly adequate for game-playing purposes.
The ‘random number’ function in the Sinclair Spectrum microcomputer was a program that generated the powers of 75 modulo 65537 as a pseudo-random sequence. The number 75 is suitable because its powers run through all 65536 possibilities, modulo 65537. It is a particularly neat choice because 75 = 20 + 20+1 + 20+1+2 + 20+1+2+3. This means that only the simplest operations on zeroes and ones are needed to multiply by 75 modulo 65537. (But, as a footnote to the history of computing, I may remark that Sinclair’s inefficient code did not even exploit the fact that 65537 is simple in binary representation. Sinclair Research soon vanished from the page of history.)
The well-hidden nature of a pseudo-random pattern makes it suitable for use in ciphers. To see how ciphers are made and broken, however, we should first look at what can be done with truly random streams.
The problem of defining a truly random stream revisits the problem of defining probabilities, as we met in Chapter 6. A puzzling fact is that if you create a random sequence, and then publish it in a book, it is no longer random but very special! One modern idea is that a random stream can be defined as one that can’t be produced by a Turing machine any more efficiently than by listing it bit by bit. So pseudo-random streams are definitely not random.
Despite this difficulty of theoretical definition, it is not hard to generate a stream which is random for all practical purposes, by using an electronic equivalent of dice-throwing. You can then use such a stream to encipher a message with true security, so that it can only be read by its intended recipient. To do this you use the random stream as a one-time pad. First, make just two copies of it; keep one secure and somehow convey the other to your partner in such a way that it cannot be intercepted. Later, you can use this stream of bits —just once—to send a secure message to your partner. To illustrate how it works, suppose that the message to be sent consists of the four symbols of ‘Yes?’. Coding these in standard ASCII, these symbols become 5965733F in hexadecimal, or 01011001011001010111001100111111 in binary digits. Suppose that the one-time pad, as agreed in advance between sender and receiver, consists of the stream 01100010101001001001101001011011. Call these M for message, K for key, respectively. Then the ciphertext C is obtained by combining M and K by addition modulo 2:
This operation needs only the rules 0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 0. It is equivalent to applying the logical XOR operation from Chapter 2. The ciphertext C can then be safely transmitted and if the recipient of the message applies exactly the same operation with the same pre-agreed key K, the message M will emerge. XOR has the elegant property of being self-inverse: doing and undoing are the same.
This kind of cipher has a counter-intuitive aspect which has been known to scare military minds: half the binary digits of the message are transmitted undisguised. This might be compared with the famous problem of advertising, that half the budget is always wasted. But the total uncertainty about which half is unenciphered gives a proof of security which runs like this: assume that the keys really are generated randomly, so that all key-streams are equally likely. Then a cryptanalyst might indeed guess, from the ciphertext as above, that the message is ‘Yes!’. But if a rival cryptanalyst guesses that it is ‘No!!”, there is absolutely no evidence to favour either of these guesses—nor, indeed, to prefer any four-symbol guess over any other.
A truly random key-stream must be as long as the message to be enciphered. This makes it long and inflexible in operation. It also carries the danger of a false sense of security if the pad is used more than once by mistake. This is exactly what happened with certain Soviet messages of the period 1942-1945, which were subsequently broken and became a key element in the Cold War. That said, one-time pads are still perfectly viable for one-to-one systems, and modern personal computers make it easier than ever to manufacture one.
For ciphers used on an industrial scale—as for mobile phone wireless links—you cannot arrange for the physical transfer of CD’s. You might therefore be tempted to use a pseudo-random sequence instead. Such a sequence has the virtue of being generated by a program and so not needing secure physical transport of huge keys. But its use in encipherment must be quite different. Anyone using a system based on pseudo-randomness must assume the worst-case scenario: that the enemy will find out that it is not random at all. The enemy then only has to find the key, which is generally much shorter than the length of the stream. For the 17-sequence, for instance, the key is just the starting point in the sequence. There are only 64 possibilities, each specified by just 6 bits. For the Spectrum 65537 sequence, similarly, there are only 1048576 keys, each defined by only 20 bits.
The number of possible keys is generally called the strength of encryption, but such a stated ‘strength’ can be highly misleading. As an analogy, a safe may have a PIN combination lock of four decimal digits. This means it has 10000 possible keys, formidable if all combinations must be tried in turn. But a safe-cracker who can detect internal motions in the lock, and so discover one digit at a time, will need only four operations to crack the PIN. Just such a shortcut exists if the Spectrum stream is used. Suppose that you can guess a few letters of plaintext (as was so successfully achieved with the Enigma). A XOR with the ciphertext then produces a segment of the key sequence. This immediately shows the times-75 pattern, identifying the place in the sequence, and so the whole stream. Something a little like this, but much more complicated, happened with the cipher used for Hitler’s messages, which was not Enigma-based but used an XOR with a pseudo-random stream. A single fatal message of 30 August 1941 revealed the pseudo-randomness to sharp British eyes.
Even if no plaintext can be guessed, the task of trying out a mere million possibilities (which is what so-called 20-bit security means) would be small beer for a computer now. A trillion keys, 40-bit security, is about the lowest serious number for privacy. This is essentially the basis of the GSM system for mobile phones, which has 54-bit security. It enciphers the handset-to-mast signal with a shift register algebra which is an extension and complication of the times-75 idea. When you use a GSM phone you hope that its extended, complicated pseudo-randomness means there is no clever method of eliminating many keys at once—so that there is nothing better than trying out all possible keys, which would take a very long time. The reason why an element of hope is involved is that it is very hard to be certain that there is no clever shortcut—for reasons which seem to go deep into the nature of numbers, as we shall see. And in fact, in 2006 it was shown by Israeli analysts that there is such a shortcut. The weakness of GSM is that it employs error correction before encryption, and this introduces a redundancy—a guessability—into the transmitted message. Of course, as people often make their mobile phone calls very loudly in public, the attempt at secure encipherment is largely redundant anyway.
Nowadays there is intense, open, international scientific discussion of all such questions, completely different from the 1930s era when Turing took on the Enigma. Cryptology in the scientific sense has little to do with treasure-hunt puzzles popular in fiction and in the media, which require informed guessing of one-off texts using culture-based clues.
Like the computer, scientific cryptology is the outcome of a revolution of the 1940s, in which Turing was a major figure, along with Claude Shannon, the founder of the mathematical theory of communication. In 1944 Turing devised a precursor of GSM: it was a compact speech scrambler using a pseudo-random key, which he called Delilah after the bewitching lady of the Old Testament. It was never used, and like much of Turing’s cryptological theory was probably 30 years ahead of its time. The Allied powers-that-were of the Second World War had the advantage of a kind of time travel, as they did also with the enlistment of the world’s leading physicists to build the nuclear weapon of 1945. To them, the productions of science were as magical as the powers of Delilah, although they were in fact the exercise of pure reason. But Turing’s logical revolution had much further to go.
Computers and ciphers, discussed in an open, international scientific forum, have spurred a development that in the 1940s was hardly a dot on the horizon. This is the theory of computational complexity. It discusses not whether it is possible or impossible to solve a problem, but how hard it is to solve. This question is rather different from the classification of individual Sudoku problems as EASY, DEADLY, or FIENDISH. It measures the complexity of Sudoku as a whole by considering how much more difficult Sudoku becomes in going from 3 × 3 to 4 × 4 and on to n × n puzzles.
The guiding idea is that the difficulty of the problem should be measured by the time taken to solve it by the best possible method. But it is usually far from obvious what the best possible method is. We have touched on this question in Chapter 4 with the finding of a square root, and then in Chapter 6 with the calculation of π based on Ramanujan’s out-of-this-world insight. Code-breaking dramatises the seriousness of the question. The story in Chapter 6 of how Enigma messages could be broken in hours, using Turing’s Sudoku-like logic, gives an example of where the existence of a non-obvious fast method was of immense significance to world events.
Just as Constance Reid was explaining binary numbers to the public in 1956, Gödel made a remark addressing this much higher-level question of complexity. Papers began to appear in the 1960s, but only took off after 1970. By that time, computers had made complexity an essential and practical issue in software engineering. Sometimes the provision of faster hardware makes scarcely any difference, compared with the benefits of brilliant software. To measure these benefits independently of the brand of computer, the 1936 concept of the Turing machine became essential. As in other ways, it was only in the 1970s that Turing’s work was really appreciated.
As an example of an EASY problem, that of searching, or finding needles in a haystack, is one that computers can solve with laid-back unconcern. Not so obvious is that sorting files into order is almost as quick as reading them, although the brilliance of search engine software makes this feat vivid on computer screens. With the best method, a million items can be sorted in roughly twenty times the time taken to read them.
In contrast, the problem of finding how best to get from A to B in a network is definitely HARD. (Sending information over the Internet is an example of where this problem would arise.) The London transport system has offered a striking picture of how difficult this is. Until recently, London bus stops had a map showing all the bus routes, and an instruction for planning a bus journey from A to B. You were told to study the routes of the buses passing through A, and those passing through B, and to find a point where they crossed. For the small number of lines on the London underground train system, where the eye is assisted by colour-coding, such a search is feasible. With hundreds of snaking bus routes on a large map, it was generally impossible to perform. It could be done with a pencil, carefully tracing the routes and checking all the possibilities in turn. But it could not be achieved in a single step (let alone in the conditions of a bus stop on a dark night). This impractical bus-map instruction gives a good picture of what is called a non-deterministic algorithm. It is something that could be done, but only with an unlimited number of testing and checking operations.
Some people have amazing gifts of visualisation and memory, and it is a tricky question as to what connection such mental powers have with mathematical thought. Often it is said that autistic people, who like following rules and procedures in a literal-minded way, have an affinity with mathematics and science. But that characterisation overlooks the imaginative aspects of mathematical thought, seeing only its precision and rule-following, the things that can be left for computers to do. The charming autobiography of Daniel Tammet, Born on a Blue Day, brings out something rather different from this, namely a deep and immediate sensation of the numbers going far beyond One to Nine, and an ability to combine them in extraordinary calculations without consciously worked out steps.
Inspired by his magical picture of the colour and texture of numbers, I want now to imagine an Autistic Angel with the power of being able to perform such a ‘non-deterministic algorithm’, such as solving the bus-map puzzle in a flash. An Autistic Angel would likewise be able to solve SUPER-FIENDISH Sudoku puzzles in one go, just by seeing the solution and checking its correctness. A third example comes from the problem of primes and factorisation. An Autistic Angel could see in one go whether a number is prime, and find its factors if it is not. As with the bus-map problem, there does exist a method for doing this, if only by trying out all possible factors, but it takes ordinary humans and ordinary computers a long time.
Complexity theorists have defined a class of problems called P which consists, roughly speaking, of those that are as quick and easy as searching. The class NP then consists of problems which would be quick for an Autistic Angel. It might seem that NP is obviously a bigger class than P. But no one has yet been able to prove that this is the case. It turns out to be FIENDISHLY difficult to prove the non-existence of an EASY method for an apparently HARD problem. This question is very similar to the problem of ensuring that there isn’t a quick clever method for breaking a cipher system.
Resolving this question is another Millennium Prize problem, and so another (HARD!) way to win a million dollars. Nowadays this subject has a vast literature detailing subtle variations and distinctions. Everything suggests that this is a deep problem involving the very nature of symbolic representation. It appears that the apparently abstruse and impractical Gödel theorem described in Chapter 1 has this extension of great practical significance for everything computers do.
Within NP there is a class of NP-complete problems, comprising what are in a sense the hardest nuts to crack: if any of these have easy solutions then all NP problems do. Sudoku is claimed as an example of a NP-complete problem. The problem of factorising integers is a more important case of an NP problem. It is not known to be NP-complete, and is thought probably not to be so. But if anyone found a P method for factorisation, it would make large waves in the theory of numbers, and also in the practical world. This is because the RSA (Rivest-Shamir-Adelman) system of public-key cryptography rests entirely on the apparent DEADLY difficulty of finding factors of large numbers. If factorisation turns out to be EASY after all, the whole system will collapse.
The motivation for public-key cryptography must first be explained. Chapter 6 described some basic features of the Enigma cipher machine which made it vulnerable to attack. But a more subtle problem, the key distribution problem, is also important. For the Enigma, the key consisted of the starting position of the rotors, plus the plugboard choice: this was the information that the British code-breakers were trying to get, and which had to be kept completely secret. But how would the German sender and receiver themselves know the correct key for a message? Typically, one would be a U-boat out in the Atlantic for months, the other a shore station. There are basically two possibilities: (1) to agree the keys in advance, each participant keeping a secure copy, or (2) to communicate the key for the message at the time of the message itself.
As an extreme form of the first option, each could have a physical copy of a one-time pad. GSM mobile phones also rely on the first option, as they depend on a secret key of 54 bits. However, they send, unenciphered, an extra 22 bits which determine the starting point in the key-stream. This is no protection against an enemy who knows the secret key, but makes it very unlikely that the same sequence of key-stream will be used twice. The Enigma systems, in contrast, made extensive and vital use of the second option. The Polish break into Enigma messages before the war was possible because the Luftwaffe used a foolish method for enciphering that part of the key which was made up and transmitted at the time of the message. (The folly lay in repeating a triplet of letters before enciphering them: this primitive approach to error correction added a fatal redundancy which the Polish mathematicians brilliantly exploited. Apparently GSM design has repeated this mistake in a more subtle form.)
E-commerce demands enciphered communication of credit-card details. But the key distribution problem appears to pose an insuperable barrier. Both methods (1) and (2) demand prior contact and agreement between sender and receiver. Retailing is a service to the public, not to a private clientele, so the retailer can never know who will be buying, nor when. Nothing secret can be pre-arranged.
This problem had been foreseen in the 1970s, a time when the US government was torn between conflicting interests. It was under pressure to underwrite a standard for confidential communication in commercial business. For this, the Data Encryption Standard, as an enormously improved sort of Enigma, was developed. On the other hand, the National Security Agency wanted to keep cryptology completely out of public discussion. Although the conflict continued for decades, the genie got out of the bottle for good. The critical point probably came in 1977 when Martin Gardner published a description of the RSA system in Scientific American. A fascinated public then learnt that there is a form of cryptography where the sender and receiver need have no prior contact. It solved the e-commerce problem, twenty years before e-commerce started.
RSA brings out and exploits the difference between the ‘it is so’ of Platonic existence, and the ‘how to do it’ approach of Diophantus. The situation could be compared with Sudoku. When a newspaper publishes the puzzle, then ‘in principle’ it has also defined the solution, which is logically deduced from the information given in the Sudoku square. Yet obtaining that solution is difficult—indeed, the whole point of Sudoku lies in the challenge. In the same way, you can publish a public key. This ‘in principle’ defines the decipherment method, but in practice, for anyone other than an Autistic Angel, it is a hard, virtually impossible problem. So the idea of public-key cryptography rests on breaking the symmetry of doing and undoing, in fact making it as asymmetric as possible.
The problem of factorising a number with hundreds of digits gives a classic example of such asymmetry. It is easy to multiply, hard to factorise. This problem can also be exploited in a very elegant fashion to give a practical cipher scheme. It makes a recipe based on the tastiest properties of numbers—the powers and primes that have been peppering these pages.
The retailer needs to have two large prime numbers P and Q, and to keep their identity a secret. Their product N = P × Q, however, is made public. Multiplying P and Q is EASY, but factorising N is HARD. Everything depends on this broken symmetry: it means that N can be announced publicly and yet P and Q remain effectively secret.
Two other numbers are involved: E and D. The enciphering number E (often 65537) is advertised to the public. But D is the retailer’s deadly secret: it is the deciphering number. D is easy to find if you possess the secret P and Q: but otherwise it is as difficult to find as it is to factorise N.
The customer has a message, which we will take to be a large number M. Thinking of a message as a number is natural: any message, written out in ASCII bits, is a long number in binary notation. But M must be less than N. If the message is larger than N, it must be divided into N-sized segments and the following procedure applied as many times as necessary.
The procedure uses modular arithmetic. It runs as follows. Using the publicly available N and E, the customer has her computer work out the number C = ME modulo N. She transmits C, the enciphered message, to the retailer. Then the retailer, using her secret number D, works out CD modulo N. The result of this should astonish you, like a mind-reading magician announcing the chosen number that was supposed to be a secret. It will always be equal to the original M.
The customer and retailer each need a computer—one to work out C and one to work out M—but the calculation is not as difficult as it looks from the formulas. There is no need to find the gigantic number ME, for the work can be arranged so that no numbers bigger than N ever appear. No one but the retailer can get M from C unless they have managed to steal, guess or work out the secret number D.
There are plenty of primes, as already noted in Chapter 6, so there is no danger of running out of suitable P and Q from which to form a public number N, and virtually no chance of two different people choosing the same N. It is also easy to find primes, because it is far easier to test a number for primality than it is to factorise it. The reason for this is that the public-key system itself is very unlikely to work if P and Q are not prime, so trying out a few enciphering and deciphering operations will serve as a good test of primality. This idea can be refined to give a more economical test and causes no practical difficulty at all.
But why does this magic trick work? Why should there exist a deciphering number D which neatly and completely undoes the effect of the enciphering number E? The proof rests on a theory of numbers which goes back to Fermat. It can be considered as an aspect of—