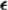 , and a probability measure P(·) defined for each event E ∈
, and a probability measure P(·) defined for each event E ∈ 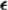 .
.The concept of a random variable has been introduced as a mathematical device for representing a physical quantity whose value is characterized by a quality of “randomness,” in the sense that there is uncertainty as to which of the possible values will be observed. The concept is essentially static in nature, for it does not take account of the fact that, in real-life situations, phenomena are usually dependent upon the passage of time. Most of the problems to which probability concepts are applied involve a discrete sequence of observations in time or a continuous process of observing the behavior of a dynamic system. At any one instant of time, the outcome has the quality of “randomness.” Knowledge of the outcomes at previous times may or may not reduce the uncertainty. The quantity under observation may be the fluctuating magnitude of a signal from a communication system, the quotations on the stock market, the incidence of particles from a radiation source, a critical parameter of a manufactured item, or any one of a large number of other items that one can readily call to mind. There are, of course, situations in which the outcome to be observed may depend upon a parameter other than (or in addition to) time. The random quantity to be observed may depend in some manner upon such parameters as position, temperature, age of a patient, etc. Mathematically, these dependences are not essentially different from the dependence upon time, and it is helpful to think in terms of a time variable and to develop our notation as if the parameter indicated time.
The problem is to find a generalization of the notion of random variable which allows the extension of probability models to dynamic systems. We have, in fact, already moved in this direction in considering vector-valued random variables or, equivalently, finite families of random variables considered jointly. The components of the vector or the members of the family can be conceived to represent observed values of a physical quantity at successive instants of time. The full generalization of these ideas leads naturally to the concept of a random, or stochastic, process.
The treatment of random processes in this chapter must of necessity be introductory and incomplete. Full-sized treatises on the subject usually have an introductory or prefatory remark to the effect that only selected topics can be treated therein. We introduce the general concept and discuss its meaning as a mathematical model of actual processes. Then we consider briefly some special processes and classes of processes which are often encountered in practice and which illustrate concepts, relationships, and properties that play an important role in the theory.
The general concept of a random process is a simple extension of the idea of a random variable. We suppose there is defined a suitable probability space, consisting of a basic space S, a class of events 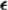 , and a probability measure P(·) defined for each event E ∈
, and a probability measure P(·) defined for each event E ∈ 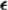 .
.
Definition 7-1a
Let T be an infinite set of real numbers (countable or uncountable). A random process X is a family of random variables {X(·, t): t ∈ T}. T is called the index set, or the parameter set, for the process.
The terms stochastic process and random function are used by various authors instead of the term random process. Some authors include finite families of random variables in the category of random processes, but they then point out that the term is usually reserved for the infinite case. For most of the processes discussed in this chapter, T is either the set of positive integers, the set of positive integers and zero, the set of all integers, or an interval on the real line (possibly the whole real line). In the case of a countable index set, the term random, sequence is sometimes employed. We shall use the term random process to designate either the countable or uncountable case.
A random process X may be considered from three points of view, each of which is natural for certain considerations.
1. As a function X·,·) on S × T.

To know the value of a random process as defined above, it is necessary to determine the parameter t and the choice variable  . Thus, from a mathematical point of view, it is entirely natural to view the process as a function. Mathematically, the manner in which
. Thus, from a mathematical point of view, it is entirely natural to view the process as a function. Mathematically, the manner in which  and t are determined is of no consequence.
and t are determined is of no consequence.
2. As a family of random variables {X(·, t): t ∈ T}. It is in these terms that the definition is framed. For each choice of t ∈ T, a random variable is chosen. It is usual to think of the choice of t as somehow deterministic. If t represents the time of observation, the choice of this time is taken to be deliberate and premeditated. The choice of  is, however, in some sense “random.” This means that there is some uncertainty before the choice as to which of the possible
is, however, in some sense “random.” This means that there is some uncertainty before the choice as to which of the possible  will be chosen. It is this choice which is the mathematical counterpart of selection from a jar, sampling from a population, or otherwise selecting by a trial or experiment. For this reason, it is helpful to think of
will be chosen. It is this choice which is the mathematical counterpart of selection from a jar, sampling from a population, or otherwise selecting by a trial or experiment. For this reason, it is helpful to think of  as the random choice variable, or simply the choice variable. Selection of subsets (finite or infinite) of the index set T amounts to selection of subfamilies of the process. One important way to study random processes is to study the joint distributions of finite subfamilies of the process.
as the random choice variable, or simply the choice variable. Selection of subsets (finite or infinite) of the index set T amounts to selection of subfamilies of the process. One important way to study random processes is to study the joint distributions of finite subfamilies of the process.
3. As a family of functions on T, {X( ,·):
,·): ∈S). For each choice of
∈S). For each choice of  , a function X(
, a function X( ,·) is determined. The domain of this function is T. Should T be countable, the function so defined is a sequence. Each such function is called a sample function, or a realization of the process, or a member of the process.
,·) is determined. The domain of this function is T. Should T be countable, the function so defined is a sequence. Each such function is called a sample function, or a realization of the process, or a member of the process.
It is the sample function which is observed in practice. The random process can serve as a model of a physical process only if, in observing the behavior of the physical process, one can take the point of view that the function observed is one of a family of possible realizations of the process. The concept of randomness is associated precisely with the uncertainty of the choice of one of the sample functions in the family of such functions. The mechanism of this choice is represented in the choice of  from the basic space. The concept of randomness has nothing to do with the character of the function chosen. This sample function may be quite smooth and regular, or it may have the wild fluctuations popularly and naively associated with “random” phenomena. One can conceive of a simple generator of a specific curve which has this “random” character; each time the generator is set in motion, the same curve is produced. There is nothing random about the function represented by the curve. The outcome of the operation is completely determined.
from the basic space. The concept of randomness has nothing to do with the character of the function chosen. This sample function may be quite smooth and regular, or it may have the wild fluctuations popularly and naively associated with “random” phenomena. One can conceive of a simple generator of a specific curve which has this “random” character; each time the generator is set in motion, the same curve is produced. There is nothing random about the function represented by the curve. The outcome of the operation is completely determined.
As an example of a simple random process whose sample functions have quite regular characteristics, consider the following
Example 7-1-1 Random Sinusoid
Let A(·), ω(·), and  (·) be random variables. Define the process X by the relation
(·) be random variables. Define the process X by the relation
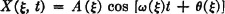
For each choice of  a choice of amplitude A(
a choice of amplitude A( ), angular frequency ω(
), angular frequency ω( ), and phase angle
), and phase angle  (
( ) is made. Once this choice is made, a perfectly regular sinusoidal function of time is determined. The uncertainty preceding the choice is the uncertainty as to which of the possible functions in the family is to be chosen. On the other hand, if a value of t is determined, each choice of
) is made. Once this choice is made, a perfectly regular sinusoidal function of time is determined. The uncertainty preceding the choice is the uncertainty as to which of the possible functions in the family is to be chosen. On the other hand, if a value of t is determined, each choice of  determines a value of X(·, t). As a Borel function of three random variables, X(·, t) is itself a random variable.
determines a value of X(·, t). As a Borel function of three random variables, X(·, t) is itself a random variable. 
Before continuing to further examples, we take note of some common variations of notation used in the literature. Most authors suppress the choice variable, since it plays no role in practical computations. They write Xt or X(t) where we have used X(·, t), above. Since there are distinct conceptual advantages in thinking of  as the choice variable, we shall commonly use the notation X(·, t) to emphasize that, for any given determination of the parameter t, we have a function of
as the choice variable, we shall commonly use the notation X(·, t) to emphasize that, for any given determination of the parameter t, we have a function of  (i.e., a random variable). In some situations, however, particularly in the writing of expectations, we find it notationally convenient to suppress the choice variable. In designating mathematical expectations we shall usually write E[X(t)].
(i.e., a random variable). In some situations, however, particularly in the writing of expectations, we find it notationally convenient to suppress the choice variable. In designating mathematical expectations we shall usually write E[X(t)].
The following examples indicate some ways in which random processes may arise in practice and how certain analytical or stochastic assumptions give character to the process.
Example 7-1-2 A Coin-flipping Sequence
A coin is flipped at regular time intervals t = k, k = 0, 1, 2, …. If a head appears at t = k, the sample function has the value 1 for k ≤ t < k + 1. The value during this interval is 0 if a tail is thrown at t = k.
SOLUTION Each sample function is a step function having values 0 or 1, with steps occurring only at integral values of time. If the sequence of 0’s or 1’s resulting from a sequence of trials is written down in succession after the binary point, the result is a number in binary form in the interval [0, 1]. To each element  there corresponds a point on the unit interval and a sample function X(
there corresponds a point on the unit interval and a sample function X( , ·). We may conveniently take the unit interval to be the basic space S and let
, ·). We may conveniently take the unit interval to be the basic space S and let  be the number whose binary equivalent describes the sample function X(
be the number whose binary equivalent describes the sample function X( ,·). If we let An = {
,·). If we let An = { : X(
: X( , t) = 1, n ≤ t < n + 1}, we have, under the usual assumptions, P(An) =
, t) = 1, n ≤ t < n + 1}, we have, under the usual assumptions, P(An) =  for any n. It may be shown that the probability mass is distributed uniformly on the unit interval, so that the probability measure coincides with the Lebesgue measure, which assigns to each interval a mass equal to the length of that interval.
for any n. It may be shown that the probability mass is distributed uniformly on the unit interval, so that the probability measure coincides with the Lebesgue measure, which assigns to each interval a mass equal to the length of that interval. 
Example 7-1-3 Shot Effect in a Vacuum Tube
Suppose a vacuum tube is connected to a linear circuit. Let the response of the system to a single electron striking the plate at t = 0 be given at any time by the value g(t), where g(·) is a suitable response function. Then the resulting current in the tube is

where {τK(·): − ∞ < k <∞} is a random sequence which describes the arrival times of the electrons. A choice of  amounts to a choice of the sequence of arrival times. Once these are determined, the value of the sample function (representing the current in the tube) is determined for each t. Ways of describing in probability terms the arrival times in terms of counting processes are considered in Sec. 7-3.
amounts to a choice of the sequence of arrival times. Once these are determined, the value of the sample function (representing the current in the tube) is determined for each t. Ways of describing in probability terms the arrival times in terms of counting processes are considered in Sec. 7-3. 
Example 7-1-4 Signal from a Communication System
An important branch of modern communication theory applies the theory of random processes to the analysis and design of communication systems. To use this approach, one must take the point of view that the signal under observation is one of the set of signals that are conceptually possible from such a system; that is, the signal is a sample signal from the process. Signals from communication systems can usually be characterized in terms of a variety of analytical properties. The transmitted signal may be taken from a known class of signals, as in the case of certain types of pulse-code modulation schemes. The dynamics of the transmission system place certain restrictions on the character of the signals. Certainly they must be bounded. The “frequency spectrum” of the signals is limited in specified ways. The mechanism producing unwanted “noise” can often be described in probabilistic terms. Utilization of these analytical properties enables the communication theorist to develop and study various processes as models of communication systems. 
This simple list of examples does not begin to indicate the extent of the applications of random processes to physical and statistical problems. For a more adequate picture of the scope of the theory and its applications, one should examine such works as those by Parzen [1962], Rosenblatt [1962], Bharucha-Reid [1960], Wax [1954], and Middleton [1960]. Examples included in these works, as well as the voluminous literature cited therein, should serve to convey an impression of the extent and importance of the field.
The simplest kind of a random process is a sequence of discrete random variables. The simplest sequences to deal with are those in which the random variables form an independent family. Much of the early work on sequences of trials has dealt with the case of independent random variables. There are many systems, however, for which the independence assumption is not satisfactory. In a sequence of trials, the outcome of any trial may be influenced by the outcome for one or more previous trials in the sequence. Early in this century, A, A. Markov (1856–1922) considered an important case of such dependence in which the outcome of any trial in a sequence is conditioned by the outcome of the trial immediately preceding, but by no earlier ones. Such dependence has come to be known as chain dependence.
Such a chain of dependences is common in many important practical situations. The result of one choice affects the next. This is true in many games of chance, when a sequence of moves is considered rather than a single, isolated play. Many physical, psychological, biological, and economic phenomena exhibit such a chain dependence. Even when the dependence extends further back than one step, a reasonable approximation may result from considering only one-step dependence. Some simple examples are given later in this section.
The systems to be studied are described in terms of the results of a sequence of trials. Each trial in the sequence is performed at a given transition time. During the period between two transition times, the system is in one of a discrete set of states, corresponding to one of the possible outcomes of any trial in the sequence. This set of states is called the state space  . We thus have a random process {X(·, n):0 ≤ n < ∞}, in which the value of the random variable X(·, n) is the state of the system (or a number corresponding to that state) in the period following the nth trial in the sequence. We take the zeroth period to be the initial period, and the value of X(·,0) is the initial state of the system. The process may be characterized by giving the probabilities of the various states in the initial period [i.e., the distribution of X(·, 0)] and the appropriate conditional probabilities of the various states in each succeeding period, given the states of the previous periods. The precise manner in which this is done is formulated below.
. We thus have a random process {X(·, n):0 ≤ n < ∞}, in which the value of the random variable X(·, n) is the state of the system (or a number corresponding to that state) in the period following the nth trial in the sequence. We take the zeroth period to be the initial period, and the value of X(·,0) is the initial state of the system. The process may be characterized by giving the probabilities of the various states in the initial period [i.e., the distribution of X(·, 0)] and the appropriate conditional probabilities of the various states in each succeeding period, given the states of the previous periods. The precise manner in which this is done is formulated below.
Suppose the state space  is the set {si: i ∈ J}, where J is a finite or countably infinite index set. The elements si of the state space represent possible states of the system and appear in the model as possible values of the various X(·, n); that is,
is the set {si: i ∈ J}, where J is a finite or countably infinite index set. The elements si of the state space represent possible states of the system and appear in the model as possible values of the various X(·, n); that is,  is the range set for each of the random variables in the process. We may take the si to be real numbers without loss of generality. The random variables may be written
is the range set for each of the random variables in the process. We may take the si to be real numbers without loss of generality. The random variables may be written
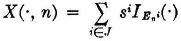
where 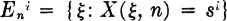 . In words,
. In words,  is the event that the system is in the ith state during the nth period or interval. The probability distributions for the X(·, n) are determined by specifying (1) the initial probabilities P(E0i) for each i ∈ J and (2) the conditional probabilities
is the event that the system is in the ith state during the nth period or interval. The probability distributions for the X(·, n) are determined by specifying (1) the initial probabilities P(E0i) for each i ∈ J and (2) the conditional probabilities  for all the possible combinations of the indices.
for all the possible combinations of the indices.
A wide variety of dependency arrangements is possible, according to the nature of the conditional probabilities. We shall limit consideration to processes in which the probabilities for the state after a transition are conditioned only by the state immediately before the transition. This may be stated precisely as follows:
(MCI) Markov property. 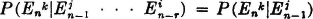 for each permissible n, r, k, and j.
for each permissible n, r, k, and j.
Definition 7-2a
The conditional probabilities in property (MCI) are called the transition probabilities for the process.
In most of the processes studied, it is assumed further that the transition probabilities do not depend upon n; that is, we have the
(MC2) Constancy property.  for each permissible n, r, k, and j.
for each permissible n, r, k, and j.
It is convenient, in the case of constant transition probabilities, to designate them by the shorter notation
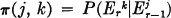
In a similar manner, the total probability for any state i in the rth period is designated by

These probabilities define the probability distribution for the random variable X(·, r).
Definition 7-2b
A random process {X(·, n): 0 ≤ n < ∞} with finite or countably infinite state space  = {si: i ∈ j} and which has the Markov property (MCI) and the constancy property (MC2) is called a Markov chain with constant transition probabilities (or more briefly, a constant Markov chain). If the state space
= {si: i ∈ j} and which has the Markov property (MCI) and the constancy property (MC2) is called a Markov chain with constant transition probabilities (or more briefly, a constant Markov chain). If the state space  is finite, the process is called a finite Markov chain. The set of probabilities {π0(i):i ∈ J} is called the set of initial state probabilities. The matrix
is finite, the process is called a finite Markov chain. The set of probabilities {π0(i):i ∈ J} is called the set of initial state probabilities. The matrix  = [π(j, k)] is called the transition matrix.
= [π(j, k)] is called the transition matrix.
Constant Markov chains are also called homogeneous chains, or stationary chains. Most often the reference is simply to Markov chains, the constancy property being tacitly assumed.
A very extensive literature has developed on the subject of constant Markov chains. We can touch upon only a few basic ideas and results in a manner intended to introduce the subject and to facilitate further reference to the pertinent literature.
Since a conditional probability measure, given a fixed event, is itself a probability measure, and since the events  form a partition for each r, we must have, for each i,
form a partition for each r, we must have, for each i,

The last equation means that the elements on each row of the transition matrix  sum to 1, and hence form a probability vector. Such matrices are of sufficient importance to be given a name as follows:
sum to 1, and hence form a probability vector. Such matrices are of sufficient importance to be given a name as follows:
Definition 7-2c
A square matrix (finite or infinite) whose elements are nonnegative and whose sum along any row is unity is called a stochastic matrix. If, in addition, the sum of the elements along any column is unity, the matrix is called doubly stochastic.
The transition matrix for a constant Markov chain is a stochastic matrix. In special cases, it may be doubly stochastic.
We now note that a constant Markov process is characterized by the initial probabilities and the transition matrix. As a direct consequence of properties (CP1), (MC1), and (MC2), we have

If we put r = 0, we see that specification of the initial state probabilities and of the matrix of transition probabilities serves to specify the joint probability mass distribution for any finite subfamily of random variables in the process. In particular, we may use property (P6) to derive the following expression for the stats probabilities in the nth period:
(MC4) State probabilities

PROOF This follows from (MC3) and the fundamental relation

Before developing further the theoretical apparatus, we consider some simple examples of Markov processes and their characteristic probabilities. To simplify writing, we shall consider finite chains.
Example 7-2-1 Urn Model
Feller [1957] has shown that a constant Markov chain is equivalent to the following urn model. There is an urn for each state of the system. Each urn has balls marked with numbers corresponding to the states. The probability of drawing a ball marked k from urn j is π (j, k). Sampling is with replacement, so that the distribution in any given urn is not disturbed by the sampling. The process consists in making a sequence of samplings according to the following procedure. The first sampling, to start the process, consists of making a choice of an urn according to some prescribed set of probabilities. Call this the zeroth choice, and let  be the event that the jth urn is chosen on this initial step. The choice of urn j is made with probability π0(J) so that
be the event that the jth urn is chosen on this initial step. The choice of urn j is made with probability π0(J) so that 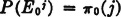 . From this urn make the first choice of a ball. A ball numbered k is chosen, on a random basis, from urn j with probability π (j, k). The next choice is made from urn k. A ball numbered h is chosen with probability π (k, h). The process, once started, continues indefinitely. If we let
. From this urn make the first choice of a ball. A ball numbered k is chosen, on a random basis, from urn j with probability π (j, k). The next choice is made from urn k. A ball numbered h is chosen with probability π (k, h). The process, once started, continues indefinitely. If we let  be the event that a ball numbered k is chosen at the nth trial, then because of the independence of the successive samples, we have
be the event that a ball numbered k is chosen at the nth trial, then because of the independence of the successive samples, we have

This is exactly the Markov property with constant transition probabilities. 
Example 7-2-2
Any square stochastic matrix plus a set of initial probabilities defines a constant Markov chain. Consider a finite chain with three states. Let

SOLUTION The set of initial probabilities is chosen so that, with probability 1, the system starts in state 3. Thus, in the first period, it is sure that the system is in state 3. At the first transition time, the system remains in state 3 with probability 0.4, moves into state 1 with probability 0.3, or into state 2 with probability 0.3. Once in state 1 or state 2, the probability of returning to state 3 is zero. Thus, once the system leaves the state 3, into which it is forced initially, it oscillates between states 1 and 2. If it is in state 1, it remains there with probability 0.5 and changes to state 2 with probability 0.5. When in state 2, it remains there with probability 0.2 or changes to state 1 with probability 0.8. The probability of being in states 3, 3, 1, 2, 2, 1 in that order is π0(3) π (3, 3)π(3, 1)π(1, 2)π(2, 2)π(2, 1) = 1 × 0.4 × 0.3 × 0.5 × 0.2 × 0.8. 
For the next example, we consider a simple problem of the “random-walk” type, which is important in the analysis of many physical problems. The example is quite simple and schematic, but it illustrates a number of important ideas and suggests possibilities for processes.
Example 7-2-3
A particle is positioned on the grid shown in Fig. 7-2-1 in a “random manner” as follows. If it is in position 1 or position 9, it remains there with probability 1. If it is in any other position, at the next transition time it moves with equal probability to one of its adjacent neighbors along one of the grid lines (but not diagonally). In position 5 there are four possible moves, each with probability  . In positions 2, 4, 6, or 8 there are three possible moves, each with probability
. In positions 2, 4, 6, or 8 there are three possible moves, each with probability  . In positions 3 and 7 there are two possible moves, each with probability
. In positions 3 and 7 there are two possible moves, each with probability  .
.
Fig. 7-2-1 Grid for the random-walk problem of Example 7-2-3.

The numbers outside the matrix are simply an aid to identifying the rows and columns. To formulate (or to read) such a matrix, the following procedure is helpful. Go to a position on the main diagonal, say, in the jth row and column. Enter (or read) π(j, j), the conditional probability of remaining in that position once in it. For the present example, this is zero except in positions 1, 1 and 9, 9 on the matrix, corresponding to positions 1 and 9 on the grid. Then consider various possible positions to be reached from position j. Suppose position k is such a position; this corresponds to the matrix element in the kth column but on the same (i.e., the jth) row. Enter π(j, k), the conditional probability of moving to position k, given that the present position is j. For example, in the fifth row of the transition matrix above (corresponding to present position 5), π(5, 5) is zero; but π(5, 2), π(5, 4), π(5, 6), and π(5, 8) each has the same value  . Thus the number a is entered into the positions in columns 2, 4, 6, and 8 on the fifth row. In the third row there are only two nonzero entries, each of value
. Thus the number a is entered into the positions in columns 2, 4, 6, and 8 on the fifth row. In the third row there are only two nonzero entries, each of value 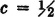 , corresponding to the fact that from position 3 only two moves are possible. The matrix should be examined to see that the other entries correspond to the physical system assumed.
, corresponding to the fact that from position 3 only two moves are possible. The matrix should be examined to see that the other entries correspond to the physical system assumed.
Once the initial state probabilities are specified, the Markov chain is determined. 
Higher-order transition probabilities
By the use of elementary probability relations, we may develop formulas for conditional probabilities which span several periods.
The mth-order transition probability from state si to state sq is the quantity
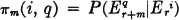
It is apparent that, for constant chains, the higher-order transition probabilities are independent of the beginning period and depend only upon m and the two states involved. For m = 1, the first-order transition probability is just the ordinary transition probability; that is, π(i, q) = π(i, q). A number of basic relations are easily derived.
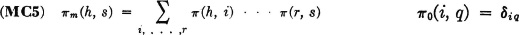
This property can be derived easily by applying properties (CP1), (MC1), and (P6). In a similar way, the following result can be developed.
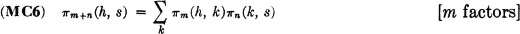
This equation is a special case of the Chapman-Kolmogorov equation. The state probabilities in the (n + m)th period can be derived from those for the mth period by the following formula:
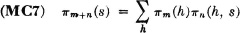
Use of the definitions and application of fundamental probability theorems suffices to demonstrate the validity of this expression.
In the case of finite Markov processes, in which the state space index set J = {1, 2, …, N}, several of the properties for Markov processes can be expressed compactly in terms of the matrix of transition probabilities.
Let 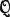 r be the row matrix of state probabilities in the rth period, and let
r be the row matrix of state probabilities in the rth period, and let  be the matrix of transition probabilities. Since the latter matrix is square, the nth power
be the matrix of transition probabilities. Since the latter matrix is square, the nth power  =
=  ×
×  × · · · ×
× · · · ×  (n factors) is defined. We may then write in matrix form
(n factors) is defined. We may then write in matrix form

Because of this matrix formulation, it has been possible to exploit properties of matrix algebra to develop a very general theory of finite chains. Also, a major tool for analysis is a type of generating function which is identical with the z transform, much used in the theory of sampled-data control systems. We shall not attempt to describe or exploit these special techniques, although we shall assume familiarity with the simple rules of matrix multiplication. For theoretical developments and applications employing these techniques, see Feller [1957], Kemeny and Snell [1960], and Howard [1960].
Example 7-2-4 The Success-Failure Model
The model is characterized by two states: state 1 may correspond to “success,” and state 2 to “failure.” This may be used as a somewhat crude model of marketing success. A manufacturer features a specific product in each marketing period. If he is successful in sales during one period, he has a reasonable probability of being successful in the succeeding period; if he is unsuccessful, he may have a high probability of remaining unsuccessful. For example, if he is successful, he may have a 50-50 chance of remaining successful; if he is unsuccessful in a given period, his probability of being successful in the next period may only be 1 in 4. Under these assumptions, suppose he is successful in a given sales period. What are the probabilities of success and lack of it in the first, second, and third subsequent sales periods?
SOLUTION Under the assumptions stated above, π(1, 1) = π(1, 2) =  , π(2, 1) =
, π(2, 1) = 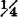 π, and π(2, 2) =
π, and π(2, 2) =  . The matrix of transition probabilities is thus
. The matrix of transition probabilities is thus

Direct matrix multiplication shows that

As a check, we note that  2 and
2 and  3 are stochastic matrices. The assumption that the system is initially in state 1 is equivalent to the assumption π0(1) = 1 and π0(2) = 0. Thus
3 are stochastic matrices. The assumption that the system is initially in state 1 is equivalent to the assumption π0(1) = 1 and π0(2) = 0. Thus 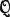 0 = [1 0], so that
0 = [1 0], so that

In the first period (after the initial one) the system is equally likely to be in either state. In the second and third periods, state 2 becomes the more likely. The probabilities for subsequent periods may be calculated similarly. 
Example 7-2-5 Alternative Routing in Communication Networks
A communication system has trunk lines connecting five cities, which we designate by numbers. There are central-office switching facilities in each city. If it is desired to establish a line from city 1 to city 5, the switching facilities make a search for a line. Three possibilities exist: (1) a direct line is available, (2) a line to an intermediate city is found, or (3) no line is available. In the first case, the line is established. In the second alternative, a new search procedure is set up in the intermediate city to find a line to city 5 or to another intermediate city. In the third alternative, the system begins a new search after a prescribed delay (which may be quite short in a modern, high-capacity system). A fundamental problem is to design the system so that the waiting time (in terms of numbers of searching operations) is below some prescribed level. Searching operations mean not only delay in establishing communication, but also use of extensive switching equipment in the central offices. Traffic conditions and the number of trunk lines available determine probabilities that various connections will be made on any search operation. We may set up a Markov-chain model by assuming that the state of the system corresponds to the connection established. Consider the network shown in Fig. 7-2-2. The system is in state 1 if no line has been found at the originating city. The system is in state 5 if a connecting link—either direct or through intermediate cities—is established with city 5. The system is in state 4 if a connecting link is established to city 4, etc. Suppose the probabilities of establishing connections are those indicated in the transition matrix
Fig. 7-2-2 Possible trunk-line connections for establishing communication from city 1 to city 5.

Since it is determined that the call originates in city 1, the initial probability matrix is [1 0 0 0 0]. The transition matrix reflects the fact that in city 1 and in each intermediate city the probability is 0.1 of not finding a line on any search operation. Cities 3 and 4 are assumed to be closer to city 5 and to have more connecting lines, so that the probabilities of establishing connection to that city are higher than for cities 1 and 2. The connection network is such as to provide connections to higher-numbered cities. The probability of establishing connection in n or fewer search operations is πn(5). Since π0(1) = 1, we must have πn(5) = πn(1, 5). Using the fundamental relations, we may calculate the following values:
Thus only about 1 call in 19 takes more than three search operations; and only about 1 percent of the calls take more than 4 search operations. About 1 call in 5 (0.192 = 0.942 – 0.750) takes three search operations. Other probabilities may be determined similarly. 
Closed state sets and irreducible chains
In the analysis of constant Markov chains, it is convenient to classify the various states of the system in a variety of ways. We introduce some terminology to facilitate discussion and then consider the concept of closure.
Definition 7-2e
We say that state sk is accessible from state si (indicated si → sk) iffi there is a positive integer n such that πn(i, k) > 0. States si and sk are said to communicate iffi both si → sk and sk → si. We designate this condition by writing si ↔ sk.
It should be noted that the case i = k is included in the definition above. From the basic Markov relation (MC6) it is easy to derive the following facts:
Theorem 7-2A
1. si → sj and sj→ sk implies si → sk.
2. si ↔ sj and sj ↔ sk implies si ↔ sk.
3. si ↔ sj for some j implies si ↔ si.
In the case of finite chains (or even some special infinite chains), these relations can often be visualized with the aid of a transition diagram.
Definition 7-2f
A transition diagram for a finite chain is a linear graph with one node for each state and one directed branch for each one-step transition with positive probability. It is customary to indicate the transition probability along the branch.
Figure 7-2-3 shows a transition diagram corresponding to the three-state process described in Example 7-2-2. The nodes are numbered to correspond to the number of the state represented. The probability π(i, j) is placed along the branch directed from node i to node j. If for any i and j the transition probability π(i, j) = 0, the branch directed from node i to node j is omitted.
Fig. 7-2-3 The transition diagram for the process of Example 7-2-2.
With such a diagram, the relation si→ sk is equivalent to the existence of at least one path through the diagram (traced in the direction of the arrows) which leads from node i to node k. It is apparent in Fig. 7-2-3 that nodes 1 and 2 communicate and that each node can be reached from node 3; but node 3 cannot be reached from node 1 or from node 2.
Definition 7-2g
A set C of states is said to be closed if no state outside C may be reached from any state in C. If a closed set C consists of only one member state si, that state is called an absorbing state, or a trapping state. A chain is called irreducible (or indecomposable) iffi there are no closed sets of states other than the entire state space.
In the chain represented in Fig. 7-2-3, the set of states {s1, s2} is a closed set, since the only other state in the state space cannot be reached from either member. The chain is thus reducible. It has no absorbing states, however. In order to be absorbing, a state sk must be characterized by π(k, k) = 1. In terms of the transition diagram, this means that the only branch leaving node k must be a self-loop branch beginning and ending on node k. The transition probability associated with this branch is unity.
We note that a set of states C is closed iffi si ∈ C and sk  C implies πn(i, k) = 0 for all positive integers n. In this case we must have π(i, k) = 0. This means that the nonzero entries in row i of a transition matrix of any order must lie in columns corresponding to states in C. This statement is true for every row corresponding to a state in C. If from each
C implies πn(i, k) = 0 for all positive integers n. In this case we must have π(i, k) = 0. This means that the nonzero entries in row i of a transition matrix of any order must lie in columns corresponding to states in C. This statement is true for every row corresponding to a state in C. If from each  n we form the submatrix
n we form the submatrix  cn containing only rows and columns corresponding to states in C, this submatrix is a stochastic matrix. In fact, from the basic properties it follows that:
cn containing only rows and columns corresponding to states in C, this submatrix is a stochastic matrix. In fact, from the basic properties it follows that:
Theorem 7-2B
If C is a closed set, a stochastic matrix  cn may be derived from each matrix
cn may be derived from each matrix  n by taking the rows and columns corresponding to the states in C. The elements of
n by taking the rows and columns corresponding to the states in C. The elements of  c and
c and  cn satisfy the fundamental relations (MC1) through (MC7).
cn satisfy the fundamental relations (MC1) through (MC7).
This theorem implies that a Markov chain is defined on any closed state set. Once the closed set is entered, it is never left. The behavior of the system, once this closed set of states is entered, can be studied in isolation, as a separate problem.
It is easy to show that the set Ri of all states which can be reached from a given state si is closed. From this fact, the following theorem is an immediate consequence.
Theorem 7-2C
A constant Markov chain is irreducible iffi all states communicate.
For finite chains (i.e., finite state spaces) a systematic check for irreducibility can be made to discover if every state can be reached from each given state. This may be done either with the transition matrix or with the aid of the transition diagram for the chain. If the chain is reducible, it is usually desirable to identify the closed subsets of the state space.
Waiting-time distributions
Suppose the system starts in state si at the rth period and reaches state sj for the first time in the (r + n)th period. For each n, i, and j we can designate a conditional probability which we define as follows:
Definition 7-2h
The waiting-time distribution function is given by
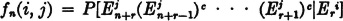
In words, fn(i, j) is the conditional probability that, starting with the system in state si, it will reach state si for the first time n steps later. It is apparent that for constant Markov processes these conditional probabilities are independent of the choice of r. The waiting-time distribution is determined by the following recursion relations:

The first expression is obvious. The second expression can be derived by recognizing that the system moves from state si to state sj in n steps by reaching sj for the first time in n steps; or by reaching sj for the first time in n − 1 steps and returning to sj in one more step; or by reaching sj for the first time in n − 2 steps and then returning in exactly two more steps; etc. The product relation in each of the terms of the final sum can be derived by considering carefully the events involved and using the fundamental Markov properties.
Let f(i, j) be the conditional probability that, starting from state si the system ever reaches state sj. It is apparent that

If the initial state and final state are the same, it is customary to call the waiting times recurrence times. We shall define some quantities which serve as the basis of useful classifications of states.
Definition 7-2i
The quantity f(i, i) is referred to as the recurrence probability for si The mean recurrence time τ(i) for a state si is given by
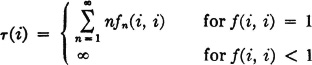
If state si communicates with itself, the periodicity parameter ω(i) is the greatest integer such that πn(i, i) can differ from zero only for n = kω(i), k an integer; if si does not communicate with itself, ω(i) = 0.
In terms of the quantities just derived, we may classify the states of a Markov process as follows:
Definition 7-2j
A state is said to be
1. Transient iffi f(i, i) < 1.
2. Persistent iffi f(i, i) = 1.
3. Periodic with period ω(i) iffi ω(i) > 1.
4. A periodic iffi ω(i) ≤ 1.
5. Null iffi f(i, i) = 1, τ(i) = ∞.
6. Positive iffi f(i, i) = 1, τ(i) < ∞.
7. Ergodic iffi f(i, i) = 1, τ(i) < ∞, ω(i) = 1.
Classify the states in the process described in Example 7-2-2 and Fig. 7-2-3.
SOLUTION We may use the transition diagram as an aid to classification and in calculating waiting-time distributions.
State 3. This state is obviously transient, for once the system leaves this state, it does not return. We thus have

From this it follows that  . It is obvious that ω(3) = 1, so that the state is aperiodic. By definition, the mean recurrence time τ(3) = ∞.
. It is obvious that ω(3) = 1, so that the state is aperiodic. By definition, the mean recurrence time τ(3) = ∞.
State 1. It would appear that this state is persistent and aperiodic. For one thing, it is obvious that ω(1) = 1. We also note that the possibility of a return for the first time to state 1 after starting in that state must follow a simple pattern. There is either (1) a return in one step, (2) a transition to state 2, then back on the second step, or (3) a transition to state 2, one or more returns to state 2, and an eventual return to state 1. We thus have

Now 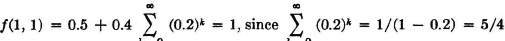 . The mean recurrence time τ(1) is given by
. The mean recurrence time τ(1) is given by 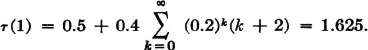
In obtaining this result, we put k + 2 = (k + 1) + 1 = n + 1, and write
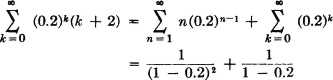
The other state has similar properties, and the numerical results for that state may be obtained by similar computations. The return probability f(2, 2) = 1, and the mean recurrence time τ(2) = 2.6. 
Two fundamental theorems
Next we state two fundamental theorems which give important characterizations of constant Markov chains. These are stated without proof; for proofs based on certain analytical, nonprobabilistic properties of the so-called renewal equation, see Feller [1957].
Theorem 7-2D
In an irreducible, constant Markov chain, all states belong to the same class: they are either all transient, all null, or all positive. If any state is periodic, all states are periodic with the same period.
In every constant Markov chain, the persistent states can be partitioned uniquely into closed sets C1 C2, …, such that, from any state in a given set Ck, all other states in that set can be reached. All states belonging to a given closed set Ck belong to the same class.
In addition to the states in the closed sets, the chain may have transient states from which the states of one or more of the closed sets may be reached.
According to Theorem 7-2B, each of the closed sets Ck described in the theorem just stated may be studied as a subchain. The behavior of the entire chain may be studied by examining the behavior of each of the subchains, once its set of states is entered, and by studying the ways in which the subchains may be entered from the transient states.
Before stating the next theorem, we make the following
Definition 7-2k
A set of probabilities {πi: i ∈ J}, where J is the index set for the state space  , is called a stationary distribution for the process iffi
, is called a stationary distribution for the process iffi
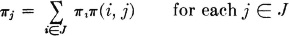
The significance of this set of probabilities and the justification for the terminology may be seen by noting that if πr(j) = πj for some r and all j ∈ J, then
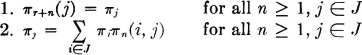
Theorem 7-2E
An irreducible, aperiodic, constant Markov chain is characterized by one of two conditions: either
1. All states are transient or null, in which case 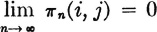 for any pair i, j and there is no stationary distribution for the process, or
for any pair i, j and there is no stationary distribution for the process, or
2. All states are ergodic, in which case
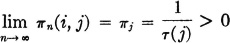
for all pairs i, j, and {πj: j ∈ J} is a stationary distribution for the chain.
In the ergodic case, we have  regardless of the choice of initial probabilities π0(i), i ∈ J.
regardless of the choice of initial probabilities π0(i), i ∈ J.
The validity of the last statement, assuming condition 2, may be seen from the following argument:

If, for some n, all |πn(i, j) − πj| <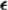 , then
, then

since the π0(i) sum to unity.
To determine whether or not an irreducible, aperiodic chain is ergodic, the problem is to determine whether there is a set of πj to satisfy the equation in Definition 7-2k. In the case of finite chains, this may be approached algebraically.
Example 7-2-7
Consider once more the two-state process described in Example 7-2-4. This process is characterized by the transition matrix
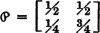
The equation in the definition for stationary distributions can be written

where 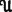 is the unit matrix. In addition, we have the condition π1+π2 = 1. Writing out the matrix equation, we get
is the unit matrix. In addition, we have the condition π1+π2 = 1. Writing out the matrix equation, we get

From this we get π1 = π2/2, so that 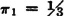 and
and  . A check shows that this set is in fact a stationary distribution. It is interesting to compare these stationary probabilities with those in
. A check shows that this set is in fact a stationary distribution. It is interesting to compare these stationary probabilities with those in  2,
2, 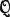 3,
3,  2, and
2, and  3 in Example 7-2-4. It appears that the convergence to the limiting values is quite rapid. After a relatively few periods, the probability of being in state 2 (the failure state) during any given period approaches
3 in Example 7-2-4. It appears that the convergence to the limiting values is quite rapid. After a relatively few periods, the probability of being in state 2 (the failure state) during any given period approaches 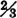 . This condition prevails regardless of the initial probabilities.
. This condition prevails regardless of the initial probabilities. 
As a final example, we consider a classical application which has been widely studied (cf. Feller [1957, pp. 343 and 358f] or Kemeny and Snell [1960, chap. 7, sec. 3]).
Example 7-2-8 The Ehrenfest Diffusion Model
This model assumes N + 1 states, s0, s1, …, sN. The transition probabilities are π(i, i) = 0 for all i, π(i, j) = 0 for |i − j| > 1, π(i, i −1) = i/N, and π(i, i + 1) = 1πi/N. This model was presented in a paper on statistical mechanics (1907) as a representation of a conceptual experiment in which N molecules are distributed in two containers labeled A and B. At any given transition time, a molecule is chosen at random from the total set and moved from its container to the other. The state of the system is taken to be the number of molecules in container A. If the system is in state i, the molecule chosen is taken from A and put into B, with probability i/N, or is taken from B and put into A, with probability 1 − i/N. The first case changes the state from si to si−1; the second case results in moving to state si+1.
SOLUTION The defining equations for the stationary distributions become

Solving recursively, we can obtain expressions for each of the πj in terms of π0. We have immediately

The basic equation may be rewritten in the form
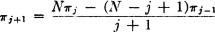
so that

It may be noted that this is of the form  . If πr =
. If πr =  for 0 ≤ r ≤ j, the same formula must hold for r = j + 1. We have
for 0 ≤ r ≤ j, the same formula must hold for r = j + 1. We have

Use of the definitions and some easy algebraic manipulations show that the expression on the right reduces to the desired form. Hence, by induction,  for all j = 1. 2, …, N. Now
for all j = 1. 2, …, N. Now

so that the stationary distribution is the binomial distribution with  The mean value of a random variable with this distribution is thus N/2 (Example 5-2-2).
The mean value of a random variable with this distribution is thus N/2 (Example 5-2-2). 
Feller [1957] has given an alternative physical interpretation of this random process. For a detailed study of the characteristics of the probabilities, waiting times, etc., the work by Kemeny and Snell [1960], cited above, may be referred to.
A wide variety of physical and economic problems have been studied with Markov-chain models. The present treatment has sketched some of the fundamental ideas and results. For more details of both application and theory, the references cited in this section and at the end of the chapter may be consulted. Extensive bibliographies are included in several of these works, notably that by Bharucha-Reid [1960].
In some applications it is natural to consider the differences between values taken on by a sample function at specific instants of time. For such purposes, it is natural to make the following
Definition 7-3a
If X is a random process and t1 and t2 are any two distinct values of the parameter set T, then the random variable X(·, t2) − X(·, t1) is called an increment of the process.
Increments of random processes are frequently assumed to have one or both of two properties, which we consider briefly.
Definition 7-3b
A random process X is said to have independent increments iffi, for any n and any t1 < t2 < · · · < tn, with each ti ∈ T, it is true that the increments X(·, t2) − X(·, t1), X(·, t3) − X(·, t2), …, X(·, tn) − X(·, tn−1) form an independent class of random variables.
One may construct a simple example of a process with independent increments as follows. Begin with any sequence of independent random variables {Yi(·): 1 ≤ i < ∞ } and an arbitrary random variable X0(·). Put
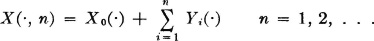
The resulting process {X(·, n): 1 ≤ n < ∞} has independent increments.
Definition 7-3c
A random process X is said to have stationary increments iffi, for each t1 < t2 and h > 0 such that t1, t2, t1 + h, t2 + h all belong to T, the increments X(·, t2) − X(·, t1) and X(·, t2 + h) − X(·, h + h) have the same distribution.
The Poisson process considered below has increments that are both independent and stationary.
Counting processes
A counting process N is one in which the value N( , t) of a sample function “counts” the number of occurrences of a specified phenomenon in an interval [0, t). For each choice of
, t) of a sample function “counts” the number of occurrences of a specified phenomenon in an interval [0, t). For each choice of  , a particular sequence of occurrences of this phenomenon results. The sample function N(
, a particular sequence of occurrences of this phenomenon results. The sample function N( ,·) for the process is the counting function corresponding to this particular sequence. The number of occurrences in the interval [t1, t2) is given by the increment N(
,·) for the process is the counting function corresponding to this particular sequence. The number of occurrences in the interval [t1, t2) is given by the increment N( , t2) − N(
, t2) − N( , t1) of that particular sample function. Obviously, a counting process has values which are integers. Counting processes have been derived which count a wide variety of phenomena, e.g., the number of telephone calls in a given time interval, the number of errors in decoding a message from a communication channel in a given time period, the number of particles from a radioactive source striking a target in a given time, etc.
, t1) of that particular sample function. Obviously, a counting process has values which are integers. Counting processes have been derived which count a wide variety of phenomena, e.g., the number of telephone calls in a given time interval, the number of errors in decoding a message from a communication channel in a given time period, the number of particles from a radioactive source striking a target in a given time, etc.
The Poisson process
One of the most common of the counting processes is the Poisson process, so named because of the nature of the distributions for its random variables. Since it is a counting process, it has integer values. Its parameter or index set T is usually taken to be the nonnegative real numbers [0, ∞). The process appears in situations for which the following assumptions are valid.
1. N(·, 0) = 0 [P]; that is, P[N(·, 0) = 0] = 1.
2. The increments of the process are independent.
3. The increments of the process are stationary.
4. P[N(·, t) > 0] > 0 for all t > 0
5. 
We have thus described a counting process with stationary and independent increments which has unit probability of zero count in an interval of length zero. The probability of a positive count in an interval of positive length is positive, and the probability of more than one count in a very short interval is of smaller order than the probability of a single count.
With the aid of a standard theorem from analysis, it may be shown that assumptions 4 and 5 may be replaced with the following:

In order to see this, consider
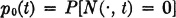
Then
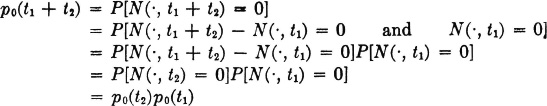
If we consider g(t) = − loge p0(t), for t ≥ 0, we must have

This linear functional equation is known to have the solution

Putting g(1) = λ, a positive constant, we have

This being the case,

which implies

Assumption 5 then requires
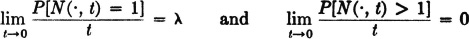
It is also apparent that conditions 1, 2, 3, 4′, and 5′ imply the original set.
We now wish to determine the probabilities

We begin by noting that we may have i occurrences in an interval of length t + Δt by having
i occurrences in the first interval of length t and
0 occurrences in the second interval of length Δt,
or i − 1 in the first interval and 1 in the second,
or i − 2 in the first interval and 2 in the second,
etc., to the case
0 in the first interval and i in the second.
These events are mutually exclusive, so that their probabilities add. Thus

We have used conditions 2 and 3 to obtain the last expression. Conditions 4′ and 5′ imply

where o(Δt) indicates a quantity which goes to zero faster than Δt as the latter goes to zero. Substituting these expressions into the sum for p(i, t + Δt) and rearranging, we obtain

or
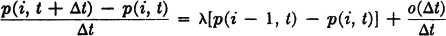
Taking the limit as Δt goes to zero, we obtain the right-hand derivatives. A slightly more complicated argument holds for Δt < 0, so that we have the differential equations

Condition 1 implies the boundary conditions

The solution of the set of differential equations under the boundary conditions imposed is readily found to be

which means that, for each positive t, the random variable N(·, t) has the Poisson distribution with  = λt (Example 3-4-7). Since the mean value for the Poisson distribution is
= λt (Example 3-4-7). Since the mean value for the Poisson distribution is  , we have
, we have
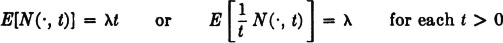
so that λ is the expected frequency, or mean rate, of occurrence of the phenomenon counted by the process.
The Poisson process has served as a model for a surprising number of physical and other phenomena. Some of these which are commonly found in the literature are
Radiation phenomena: the number of particles emitted in a given time t
Accidents, traffic counts, misprints
Demands for service, maintenance, sales of units of merchandise, admissions, etc.
Counts of particles suspended in liquids
Shot noise in vacuum tubes
A fortunate feature of the Poisson process is the fact that it is governed by a single parameter which has a simple interpretation, as noted above.
A number of generalizations and modifications of the Poisson process have been studied and applied in a variety of situations. For a discussion of some of these, one may refer to Parzen [1962, chap. 4] or Bharucha-Reid [1960, sec. 2.4] and to references cited in these works.
In Sec. 7-1 it was pointed out that one way of describing and studying random processes is by using joint distributions for finite subfamilies of random variables in the process. Analytically, this description is made in terms of distribution functions, just as in the case of several random variables considered jointly.
Definition 7-4a
The first-order distribution function F(·,·) for a random process X is the function defined by
 for every real x and every t ∈ T
for every real x and every t ∈ T
The second-order distribution function for the process is the function defined by
F(x, t; y, s) = P[X(·, t) ≤ x, X(·, s) ≤ y] for every pair of real x and y and every pair of numbers t and s from the index set T.
Distribution functions of any order n are defined similarly.
The first-order distribution function for any fixed t is the ordinary distribution function for the random variable X(·, t) selected from the family that makes up the process. The second-order distribution is the ordinary joint distribution function for the pair of random variables X(·, t) and X(·, s) selected from the process. These distribution functions have the properties generally possessed by joint distribution functions, as discussed in Sees. 3-5 and 3-6.
The following schematic example may be of some help in grasping the significance of the distribution functions for the process.
A process has four sample functions (hence the basic space may be considered to have four elementary events). The functions are shown in Fig. 7-4-1. We let

SOLUTION Examination of the figure shows that none of the sample functions lies below the value a at t = t1, so that F (a, t1) = 0. Only the function X( 1,·) lies below b at t = t1 so that F(b, t1) = p1. Examination of the other cases indicated shows that
1,·) lies below b at t = t1 so that F(b, t1) = p1. Examination of the other cases indicated shows that

For the second-order distribution, some values are
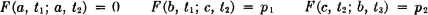
In the first case, none of the sample functions lies below a at both t1 and t2; in the second case, only X( 1,·) lies below b at t1 and c at t2; in the third case, only X(
1,·) lies below b at t1 and c at t2; in the third case, only X( 2,·) lies below c at t2 and below b at t3. Other cases may be evaluated similarly.
2,·) lies below c at t2 and below b at t3. Other cases may be evaluated similarly. 
That this process is not realistic is obvious; almost any process in which the sample functions are continuous will have an infinity of such sample functions.
It is apparent that if a process is defined, the distribution functions of all finite orders are defined. Kolmogorov [1933, 1956] has shown that if a family of such distribution functions is defined, there exists a process for which they are in fact the distribution functions. The events involved in the definition are of the form
Fig. 7-4-1 A simple schematic random process with four sample functions
The distribution functions of finite order assign probabilities to these events for any finite subset T0 of the parameter set. Fundamental measure theory shows that the probability measure so defined ensures the unique definition of probability for all such sets when T0 is countably infinite. Serious technical mathematical problems arise when T0 is uncountably infinite. It usually occurs in practice, however, that analytic conditions upon the sample functions are such that they are determined by values at a countable number of points t in the index set T. A discussion of these conditions is well beyond the scope of the present treatment. For a careful development of these mathematical conditions, the treatise by Doob [1953, chap. 2] may be consulted. Fortunately, in practice it is rarely necessary to be concerned with these problems, so that we can forgo a discussion of them in an introductory treatment.
In this section we consider a random process (actually a class of processes) whose sample functions have a step-function character; i.e., the graph of a member function has jumps in value at discrete instants of time and remains constant between these transition times. The distribution of amplitudes in the various time intervals and the distribution of transition, or jump, times at which the sample function changes value is described in rather general terms, so that a class of processes is thus included.
Such a step process is commonly assumed in practice, e.g., in the theory of control systems with “randomly varying” inputs. The derivation of the first and second distribution functions illustrates a number of interesting points of theory. These processes are used in later sections to illustrate a number of concepts and ideas developed there.
Description of the process
Consider the step-function process
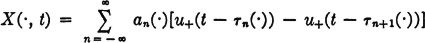
where u+(t) = 0 for t < 0 and = 1 for t ≥ 0. For any choice of  , a step function is defined. The steps occur at times t = τn(
, a step function is defined. The steps occur at times t = τn( ). The value of the function in the nth interval [τn(
). The value of the function in the nth interval [τn( ), τn+1(
), τn+1( )) is an(
)) is an( ). We make the following assumptions about the random sequences which characterize the process.
). We make the following assumptions about the random sequences which characterize the process.
1. {an(·): − ∞ < n < ∞} is a random process whose members form an independent class; each of these random variables has the same distribution, described by the distribution function FA(·).
2. {τn(·): − ∞ < n <∞} is a random process satisfying the following conditions:
a. For every  and every n, τn(
and every n, τn( ) < τn+1(
) < τn+1( ).
).
b. The distribution of the jump points τn( ) is described by a counting process N(·, t). For any pair of real numbers t1, t2 we put N(
) is described by a counting process N(·, t). For any pair of real numbers t1, t2 we put N( , t1, t2) = |N(
, t1, t2) = |N( , t2) −N(
, t2) −N( , t1)| and suppose
, t1)| and suppose
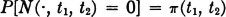
is a known function of t1 t2. For example, if the counting process is Poisson,  . We must also have
. We must also have

3. The an(·) process and the τn(·) process must be independent in an appropriate sense. We may state the independence conditions precisely in terms of certain events defined as follows. Let t1, t2 be any two arbitrarily chosen real numbers (t1 ≠ t2). Let
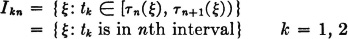
If x1, x2 are any two real numbers, let

Then {A1m, A2n, I1pI2q} is an independent class for each choice of the indices m, n, p, q, provided m ≠ n. The significance of the independence assumption in this particular form will appear in the subsequent analysis.
Determination of the distribution functions
We wish to determine the first and second distribution functions for the process X. In order to state the arguments with precision, it is expedient to define some events. Let


We shall use the relation

Under the assumed independence conditions, it seems intuitively likely that P[X(·, t1) ≤ X1] = FA(x1). A problem arises, however, from the fact that, for each  , the point t1 may be in a different interval. To validate the expected result, we establish a series of propositions.
, the point t1 may be in a different interval. To validate the expected result, we establish a series of propositions.
1. For fixed k, {Ikn: −∞ < n < ∞} is a partition, since, for each  , tk belongs to one and only one interval. We may then assert that for each k, j, n, fixed, {IknIjm: − ∞ < m < ∞ } is a partition of Ikn
, tk belongs to one and only one interval. We may then assert that for each k, j, n, fixed, {IknIjm: − ∞ < m < ∞ } is a partition of Ikn
2. 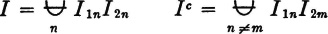
This follows from the fact that t1 and t2 belong to the same interval iffi, for some n, I1n and I2n both occur. The disjointedness follows from property 1.
3. Use of Theorem 2-6G shows that for each permissible j, k, m, n, each class {Ajm, Ikn}, {Ajm, I}, and {A1mA2n, I} is an independent class.
4. 
5. F(xk, tk) = FA(xk). We may argue as follows:
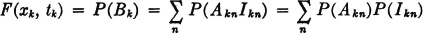
Now P(Akn) = FA(xk) for any n; hence
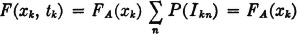
We have thus established the first assertion to be proved. A somewhat more complicated argument, along the same lines, is used to develop an expression for the second distribution. We shall argue in terms of the conditional probabilities in expression (C), above.
6. Bk and I are independent for k = 1 or 2.

from which the result follows as in the previous arguments. An exactly similar argument follows for B2I.

We note that I1nI2nIc = 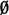 and I1nI2n ⊂ Ic for n ≠ m; hence
and I1nI2n ⊂ Ic for n ≠ m; hence
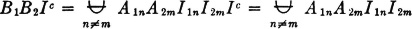
By the independence assumptions
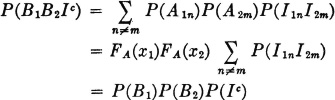
Thus

For the last assertion we have used the independence of Bk and Ic, which follows from the independence of Bk and I.

If I occurs, 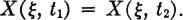
For x1 ≤ x2, B1I ⊂ B2I and B1B2I = B1I; similarly, for x2 ≤ x1, B2I ⊂ B1I and B1B2I = B2I. Because of the independence shown earlier, if x1 ≤ x2, P(B1B2I) = P(B1I) = P(B1)P(I) = FA(x1)P(I). For x2 ≤ x1, interchange subscripts 1 and 2 in the previous statements. Thus

from which the asserted relation follows immediately.
We thus may assert

When the counting process describing the distribution of jump points is known, the probabilities P(I) = π(t1 t2) and P(Ic) = 1 − π(t1, t2) are known. If the distribution of jump points is Poisson, we have

It is of interest to note that the first distribution function is independent of t and the second depends upon the difference between the two values t1 and t2 of the parameter. The significance of this fact is discussed in Sec. 7-8.
The following special case represents a situation found in many pulse-code transmission systems and computer systems. We deal with it as a special case, although it could be dealt with directly by simple arguments based on fundamentals.
Example 7-5-1
Suppose each member of the random process consists of a voltage wave whose value in any interval is either ±a volts. Switching may occur at any of the prescribed instants τn = nT, where T is a positive constant. The values ±a are taken on with probability ½ each. Values in different intervals are independent. This process may be considered a special case of the general step process. The τ process consists of the constants τn(·) = nT. The process  is an independent class with
is an independent class with
Since constant random variables are independent of any combination of other random variables, the required independence conditions follow. For any t1 t2 P[N(·, t1 t2) = 0] = π(t1, t2) is either 0 or 1 and is a known function of t1 t2. Thus

π(t, u) = 1, whenever t, u are in the same interval, and has the value 0 whenever t, u are in different intervals. Note that in this case we do not have π(t, u) a function of the difference t − u alone, as in the case of a Poisson distribution of the transition times. 
In many control situations, say, an on-off control, the value of the control signal may be limited to two values, as in the pulse-code example above, but the transition times are not known in advance. In this case, it is necessary to assume (usually on the basis of experience) a counting-function distribution. When the expected number of occurrences in any interval is a constant, the assumptions leading to the Poisson counting function are often valid.
Example 7-5-2
The first stage of an electronic binary counter produces a voltage wave which takes on one of two values. Each time a “count” occurs, the stage switches from one of its two states to the other. The output is a constant voltage corresponding to the state. The state, and hence the voltage, is maintained until the next count. If the counter should be counting cars passing a given point, the output wave would have the character of a two-value step function with a Poisson distribution of the transition times. 
It should not be surprising that the important role of mathematical expectations in the study of random variables should extend to random processes, since the latter are infinite families of random variables. In this section, we shall consider briefly some special expectations which are important in the analytical treatment of many random processes. In particular, we shall be concerned with the covariance function and with the closely related correlation functions. These functions play a central role in the celebrated theory of extrapolation and smoothing of “time series” developed somewhat independently in Russia by A. N. Kolmogorov and in the United States by Norbert Wiener, about 1940. The first applications of this theory were to wartime problems of “fire control” of radar and antiaircraft guns and to related problems of communicating in the presence of noise. Through his teaching and writing on the subject, Y. W. Lee pioneered in the task of making this abstruse theory available to engineers. In this country the work is often referred to as the Wiener-Lee statistical theory of communication. The original theoretical development laid the groundwork for further intensive development of the theory, as well as for applications of the theory to a wide range of real-world problems. Unfortunately, to develop this theory to the point that significant applications could be made would require the development of topics outside the scope of this book. Technique becomes difficult, even for simple problems. The complete theory requires the use of spectral methods based on the Fourier, Laplace, and other related transforms. We shall limit our discussion to an introduction of the probability concepts which underlie the theory. Examples must therefore be limited essentially to simple illustrations of the concept. For applications, one may consult any of a number of books in the field of statistical theory of communication and control (e.g., Laning and Battin [1956] or Davenport and Root [1958]).
We proceed to define and discuss several concepts.
Definition 7-6a
A process X is said to be of order  if, for each
if, for each 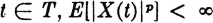 (
( is a positive integer).
is a positive integer).
From an elementary property of random variables it follows that if the process X is of order  , it is of order k for all positive integers k <
, it is of order k for all positive integers k <  .
.
Definition 7-6b
The mean-value function for a process is the first moment  X(t) = E[X(t)]
X(t) = E[X(t)]
The mean-value function for a process X exists if the process is of first order (or higher).
In the consideration of any two real-valued random variables of order 2, a convenient measure of their relatedness is provided by the covariance factor, defined as follows:
Definition 7-6c
The covariance factor cov [X, Y] for two random variables is given by 
Simple manipulations show cov [X, Y] = E[X Y] −  X
X Y. If the random variables are independent, cov [X, Y] = 0; if one of the random variables is a linear function of the other—say, Y(·) = aX(·) + b—then
Y. If the random variables are independent, cov [X, Y] = 0; if one of the random variables is a linear function of the other—say, Y(·) = aX(·) + b—then

The covariance factor may be normalized in a useful way to give the correlation coefficient, defined as follows:
Definition 7-6d
The correlation coefficient for two random variables is given by 
Use of the Schwarz inequality (E5) shows that

so that − 1 ≤ 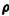 [X, Y] ≤ 1. When
[X, Y] ≤ 1. When 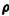 [X, Y] = 0, we say the random variables are uncorrelated. Independent random variables are always uncorrelated; however, if two random variables are uncorrelated, it does not follow that they are independent, as may be shown by simple examples. By the use of properties (V2) and (V4), one may show that
[X, Y] = 0, we say the random variables are uncorrelated. Independent random variables are always uncorrelated; however, if two random variables are uncorrelated, it does not follow that they are independent, as may be shown by simple examples. By the use of properties (V2) and (V4), one may show that

Equality can occur iffi  , where c is an appropriate constant. This means that
, where c is an appropriate constant. This means that

The plus sign corresponds to 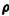 =
= 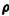 [X, Y] = 1, and the minus sign corresponds to
[X, Y] = 1, and the minus sign corresponds to 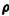 = − 1.
= − 1.
Let us look further at the significance of the correlation coefficient by considering the joint probability mass distribution. If 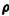 = +1, the probability mass must all lie on the straight line
= +1, the probability mass must all lie on the straight line
Fig. 7-6-1 Geometric relations for interpreting the correlation coefficient 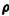 .
.

This line is shown in Fig. 7-6-1. Now suppose 0 < 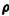 < 1. Image points for the mapping, and hence probability mass, may lie at points off the straight line. Consider the image point t1 u1 shown in Fig. 7-6-1. The distance of the point from the line is proportional to the vertical distance |υ1|, where
< 1. Image points for the mapping, and hence probability mass, may lie at points off the straight line. Consider the image point t1 u1 shown in Fig. 7-6-1. The distance of the point from the line is proportional to the vertical distance |υ1|, where
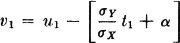
It is convenient, in fact, to consider the quantity w1 proportional to υ1, determined by the relation

An examination of the argument above shows that we must have

so that

Since t1 and u1 are supposed to be simultaneous observations of the random variables X(·) and Y(·), respectively, w1 must be a corresponding observation of the random variable

This is the difference between the standardized random variables X′(·) and Y′(·). The mean value  w = 0, and the variance σW2 = 2(1 −
w = 0, and the variance σW2 = 2(1 − 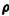 ). Thus
). Thus 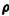 serves to measure the tendency of the standardized random variables X′(·) and Y′(·) to take on different values. The expression for σW2 holds for negative as well as positive values of
serves to measure the tendency of the standardized random variables X′(·) and Y′(·) to take on different values. The expression for σW2 holds for negative as well as positive values of 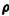 .
.
As an illustration of these ideas, consider two random variables distributed uniformly on the interval [−a, a]. Several joint distributions are shown in Fig. 7-6-2. For 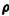 = 1, the mass is concentrated along the line u = t. For
= 1, the mass is concentrated along the line u = t. For 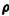 = − 1, the mass is concentrated along the line u = −t. For uniform distribution of the mass over the square, the random variables are independent and
= − 1, the mass is concentrated along the line u = −t. For uniform distribution of the mass over the square, the random variables are independent and 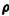 = 0. For the case shown in Fig. 7-6-2d, the probability mass is distributed uniformly over the portions of the square in the first and third quadrants. For this distribution,
= 0. For the case shown in Fig. 7-6-2d, the probability mass is distributed uniformly over the portions of the square in the first and third quadrants. For this distribution, 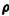 =
=  .
.
Fig. 7-6-2 Joint mass distributions for two uniformly distributed random variables X(·), Y(·).
Fig. 7-6-3 Probability mass distribution for uncorrelated random variables which are not independent.
The joint distribution in Fig. 7-6-3 shows that 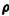 = 0 does not imply independence. Both X(·) and Y(·) are uniformly distributed on the interval [−a, a] and
= 0 does not imply independence. Both X(·) and Y(·) are uniformly distributed on the interval [−a, a] and 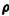 = 0. But the test for independence discussed in Sec. 3-7 (Example 3-7-3) shows that the variables cannot be independent. Note the symmetry of the mass distribution which gives rise to the uncorrelated condition.
= 0. But the test for independence discussed in Sec. 3-7 (Example 3-7-3) shows that the variables cannot be independent. Note the symmetry of the mass distribution which gives rise to the uncorrelated condition.
These concepts may be extended to pairs of random variables X(·, s) and X(·, t), which are members of a random process. In this case, the covariance is a function of the pair of parameters s, t. In order to allow for complex-valued processes, we modify the definition slightly by using the complex conjugate of the second factor. Also, we modify the use of the term correlation, somewhat, in deference to widespread practice in the literature.
Definition 7-6e
The covariance function KX(·, ·) of a process X, if it exists, is the function defined by
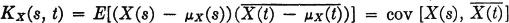
The bar denotes the complex conjugate. The autocorrelation function  XX(·, ·) of a process, if it exists, is the function defined by
XX(·, ·) of a process, if it exists, is the function defined by

It is apparent from the definition that the covariance function and the autocorrelation function coincide if the mean-value function is identically zero. Use of the linearity property for expectations shows that these two functions are related by

If the autocorrelation function exists, the process must be of second order, since on setting s = t we have

On the other hand, if the process is of second order, the mean-value function, the autocorrelation function, and the covariance function, all exist. The existence of the mean-value function has already been noted. By the Schwarz inequality

so that the finiteness of the expectations on the right-hand side, ensured by the second-order condition, implies the finiteness of the autocorrelation function. The existence of the covariance function follows immediately.
The above discussion of the correlation coefficient as a measure of the similarity of two random variables may be extended to pairs of random variables from a random process. In order to simplify discussion, we restrict our attention to real-valued processes. It is convenient to introduce the notation

and

We may therefore write
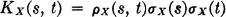
We wish to relate the behavior of the covariance function to the character of the sample functions X( , ·) from the process. This can be done in a qualitative way, which gives some valuable insight. First, suppose all the sample functions are constant over a given interval. This requires X(·, s) = X(·, t) for each s and t in the interval. In this case
, ·) from the process. This can be done in a qualitative way, which gives some valuable insight. First, suppose all the sample functions are constant over a given interval. This requires X(·, s) = X(·, t) for each s and t in the interval. In this case  X(s, t) = 1 and KX(s, t) = KX(s, s). Now suppose, for some pair of values s and t, the correlation coefficient is near zero. The two random variables X(·, s) and X(·, t) would show little tendency to take on the same values. If this situation occurs for s and t quite close together, the sample functions of the process might well be expected to fluctuate quite rapidly in value from point to point, even though the mean-value function
X(s, t) = 1 and KX(s, t) = KX(s, s). Now suppose, for some pair of values s and t, the correlation coefficient is near zero. The two random variables X(·, s) and X(·, t) would show little tendency to take on the same values. If this situation occurs for s and t quite close together, the sample functions of the process might well be expected to fluctuate quite rapidly in value from point to point, even though the mean-value function  X(·) and the variance σX2(·) may not change much. If
X(·) and the variance σX2(·) may not change much. If 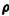 X(s, t) should be negative, there would be a tendency for the sample functions to take on values of opposite sign.
X(s, t) should be negative, there would be a tendency for the sample functions to take on values of opposite sign.
In many processes, one would expect the random variables X(·, s) and X(· t) to become uncorrelated for s and t at great distances from one another. If the process represents an actual physical process, there are many situations in which the value taken on by the process at one time s would have little influence on the value taken on at some very much later time t. Suppose we start with a process whose random variables are X(·, t) and whose covariance function has the property that 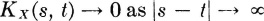 . Now consider a new process whose random variables are
. Now consider a new process whose random variables are  , with λ > 1. Then
, with λ > 1. Then  In the Y process, any sample function Y(
In the Y process, any sample function Y( , ·) will fluctuate more rapidly with time than does the corresponding function X(
, ·) will fluctuate more rapidly with time than does the corresponding function X( , ·) in the X process. Associated with this is the fact that KY(s, t) → 0 more rapidly than does
, ·) in the X process. Associated with this is the fact that KY(s, t) → 0 more rapidly than does 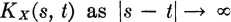 . This suggests that processes whose member functions fluctuate rapidly are likely to have a rapid drop-off of correlation between random variables X(·, s) and X(·, t) as s and t become separated. Experience—supported by some mathematics outside the scope of this treatment—shows that this is frequently the case.
. This suggests that processes whose member functions fluctuate rapidly are likely to have a rapid drop-off of correlation between random variables X(·, s) and X(·, t) as s and t become separated. Experience—supported by some mathematics outside the scope of this treatment—shows that this is frequently the case.
Example 7-6-1
A step process X has jumps at integral values of t. In each interval k ≤ t < k + 1, the process X has the value zero or one, each with probability ½. Values in different intervals are independent.
DISCUSSION The mean-value function 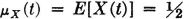 for all t.
for all t.
For s, t in the same interval: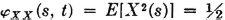
For s, t in different intervals: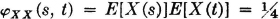
Fig. 7-6-4 shows values of  XX(·, ·) in the appropriate regions in the plane. The covariance function is given by
XX(·, ·) in the appropriate regions in the plane. The covariance function is given by
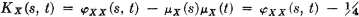
Note that KX(s, t) = 0 for |s − t| > 1. This condition ensures that s and t are in different intervals, so that, by assumption. X(· s) and X(·, t) are independent. 
Example 7-6-2
Consider the general step process of Sec. 7-5. The autocorrelation function may be determined by using conditional expectations.
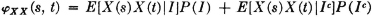
Now

where A(·) is a random variable having the common distribution of the an(·). To evaluate the first conditional expectation, we must approach the problem in a somewhat more fundamental manner. We note that, for any Borel function g(·, ·),
Fig. 7-6-4 Values of  XX(s, t) for the process in Example 7-6-1 in various regions of the plane.
XX(s, t) for the process in Example 7-6-1 in various regions of the plane.
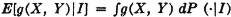
It is a property of the conditional probability that P(C|I) = 0 for any event C contained in Ic or for any event C such that P(CI) = 0. This implies that the values of g[X(·), Y(·)] for any  ∈ Ic do not affect the value of the integral. Hence we may replace g(X, Y) by any convenient function which has the same values for
∈ Ic do not affect the value of the integral. Hence we may replace g(X, Y) by any convenient function which has the same values for  ∈ I; the values for
∈ I; the values for  ∈ I, may be assigned in any desired fashion. Now for
∈ I, may be assigned in any desired fashion. Now for  ∈ I,
∈ I,  . We may thus assert that
. We may thus assert that

We may therefore write
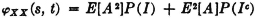
Since  X (t) = E[A] for all t, we have
X (t) = E[A] for all t, we have

For a Poisson distribution of the jump points, we have

Several things may be noted about this process. For one thing, KX(s, t) → 0 as |s − t| → ∞. The rapidity with which this occurs increases with increasing values of the parameter λ. Because of the nature of the Poisson counting function, the average number of jumps in any interval of time (hence the rapidity of fluctuation of the sample functions) increases proportionally with λ. The process is also characterized by the fact that the mean-value function does not vary with t, and the covariance (or the autocorrelation) function depends only upon the difference s − t of the parameters s and t. The importance of the last two conditions is discussed in the next section. 
Example 7-6-3
Suppose the outputs of several generators of sinusoidal signals of the same frequency are added together. Although the frequencies are the same, the phases are selected at random. We may represent the resulting signal by the random process whose value is given by

where ω is 2π times the frequency in cycles per second, and the class  is an independent class of random variables, each of which is uniformly distributed on the interval [0, 2π]. The mean-value function is given by
is an independent class of random variables, each of which is uniformly distributed on the interval [0, 2π]. The mean-value function is given by

Applying the results of Prob. 5-11 to each term, we find that  X (t) = 0 for all t. To obtain the autocorrelation function, we utilize the linearity of the expectation function to write
X (t) = 0 for all t. To obtain the autocorrelation function, we utilize the linearity of the expectation function to write

By the results of Prob. 5-11 and the independence of the random variables  k (·) and
k (·) and  i(·) for k ≠ j, the only terms which survive are those for k = j. For this case, we use the trigonometric identity cos x cos
i(·) for k ≠ j, the only terms which survive are those for k = j. For this case, we use the trigonometric identity cos x cos  . The kth term becomes
. The kth term becomes

Hence, using the result of Prob. 5-11 once more, we have

For s = t
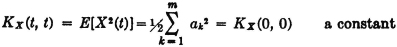
Thus
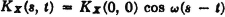
Again we have a constant mean-value function (with value zero) and a covariance or autocorrelation function which depends only on the difference s − t. In this case, however, we do not have the condition  . For fixed t, KX(s, t) is periodic in s. This is a reflection of the fact that each sample function has period 2π/ω (Prob. 7-20). The average power, in time, in the kth-component sine wave is proportional to ak2. The probability average of the instantaneous power in the members of the process at any time t is proportional to E[X2(t)]; we have seen that this is the sum of the ak2. This suggests a certain interchangeability of time averages on sample functions and probability averages among the various sample functions. We shall discuss these matters more fully in Sec. 7-8.
. For fixed t, KX(s, t) is periodic in s. This is a reflection of the fact that each sample function has period 2π/ω (Prob. 7-20). The average power, in time, in the kth-component sine wave is proportional to ak2. The probability average of the instantaneous power in the members of the process at any time t is proportional to E[X2(t)]; we have seen that this is the sum of the ak2. This suggests a certain interchangeability of time averages on sample functions and probability averages among the various sample functions. We shall discuss these matters more fully in Sec. 7-8. 
Joint processes
The ideas introduced above for a single process may be extended to a joint consideration of two random processes. Each process is a family of random variables. The two processes, considered jointly, constitute a new family of random variables. Joint distribution functions of various orders may be defined. Mixed moments of various kinds may be described. One of the most natural is described in the following
Definition 7-6f
The cross-correlation functions for two random processes X and Y are defined by

Note the order in which the parameters and the conjugated random variables are listed. Other orders could be used; in fact, when reading an article, one must check to see which of the possible orders is used.
The following simple argument based on the Schwarz inequality shows that if the processes X and Y are of second order, the correlation functions exist.

A parallel argument holds for the other case.
Properties of correlation functions
We may list a number of properties of correlation functions which have been found useful in the study of random processes. As a direct consequence of the definition, we may assert

The argument above, based on the Schwarz inequality, shows that

These two properties imply (among other things) that  XX(s, s) is real-valued and that, if X is real,
XX(s, s) is real-valued and that, if X is real,  XX(s, t) =
XX(s, t) =  XX(t, s).
XX(t, s).
Before introducing the next property, we define a class of functions as follows:
Definition 7-6g
A function g(·, ·) defined on T × T is positive semidefinite (or non-negative definite) iffi, for every finite subset Tn contained in T and every function h(·) defined on Tn, it follows that

( 3) The autocorrelation function
3) The autocorrelation function  XX(·, ·) is positive semidefinite.
XX(·, ·) is positive semidefinite.
PROOF Suppose Tn = {t1, t2, …, tn} Then
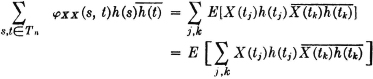
The sum in the last expression is of the form
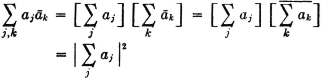
Hence the last expression in the previous development becomes
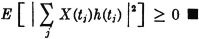
The concept of continuity in analysis is tied to the concept of a limit. In Sec. 6-3, several types of convergence to limits are considered. So long as the ordinary properties of limits hold for these types of convergence, it is possible to define corresponding concepts of continuity. One of the most useful in the theory of random processes is given in the following
Definition 7-6h
A random process X is said to be continuous [mean2] at t iffi t ∈ T and

The assertion concerning the limit is equivalent to the assertion

The following property gives an important characterization of processes which are continuous [mean2].
( 4) The random process X is continuous [mean2] at t iffi the autocorrelation function
4) The random process X is continuous [mean2] at t iffi the autocorrelation function  XX(·, ·) is continuous at the point t, t.
XX(·, ·) is continuous at the point t, t.
PROOF Suppose X is continuous [mean2] at t. Then
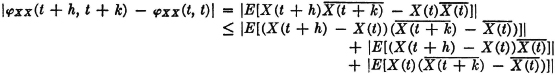
We may apply the Schwarz inequality to the first term in the last expression to assert

Because of the continuity, the factors in the last expression go to zero as h goes to zero and k goes to zero. A similar argument holds for the other two terms in the previous inequality, so that the continuity of the autocorrelation function is established. If the autocorrelation is continuous, we may use the following identity to show the continuity [mean2] of the process.
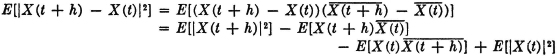
In the limit as h goes to zero, each term approaches (or remains at) the value  XX(t, t) so that the sum goes to zero.
XX(t, t) so that the sum goes to zero. 
An argument very similar to that used for the first part of the proof above,-using  rather than
rather than 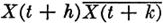 , etc., leads to the following property.
, etc., leads to the following property.
( 5) If
5) If  XX(s, t) is continuous at all points t, t, it is continuous for all s, t.
XX(s, t) is continuous at all points t, t, it is continuous for all s, t.
In establishing this theorem, one uses the fact that continuity at t, t guarantees continuity [mean2] of the process X.
Mean-square calculus
For second-order processes, it is possible to develop a calculus in which the limits are taken in the mean-square sense. For example, we may make the following
Definition 7-6i
A second-order process X has a derivative [mean2] at t, denoted by X′(·, t) iffi
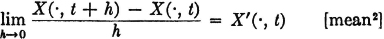
One may use continuity arguments similar in character to those carried out above (although more complicated in detail) to derive the following properties of the autocorrelation function.
( 6) If
6) If  exists for all points t, t, then X′ (·, t) exists for all t.
exists for all points t, t, then X′ (·, t) exists for all t.
( 7) If X′ (·, s) exists for all s and Y′ (·, t) exists for all t, then the following correlation functions and partial derivatives exist and the equalities indicated hold.
7) If X′ (·, s) exists for all s and Y′ (·, t) exists for all t, then the following correlation functions and partial derivatives exist and the equalities indicated hold.
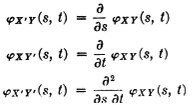
Properties ( 6) and (
6) and ( 7) may be specialized to the case X = Y and combined to give a number of corollary statements.
7) may be specialized to the case X = Y and combined to give a number of corollary statements.
Riemann and Riemann-Stieltjes integrals of random processes may also be defined, using mean-square limits. Approximating sums are defined as in the case of ordinary functions, except that, in dealing with random processes, the choice of a parameter determines a random variable rather than a value of the function. The approximating sum for a definite integral is thus a random variable. The integral [mean2] is the limit [mean2] of the approximating sums. Thus the “value” of the integral is a random variable. For a detailed development of this calculus, see Loève [1963, secs. 34.2 through 34.4].
The importance of the autocorrelation function rests in part on its close connection with gaussian processes, which are encountered in many physical applications. A brief discussion of these processes and of the role of the autocorrelation function is presented in the last section of this chapter.
In many applications it is possible to assume that the process under study has the property that its statistics do not change with time. Equivalently, these processes have the property that a shift in time origin does not affect the behavior to be expected in observing the process. The following definition gives a precise formulation of the manner in which this invariance with change of time origin is assumed to hold.
Definition 7-7a
A random process X is said to be stationary iffi, for every choice of any finite number n of elements t1 t2, …, tn form the parameter set T and of any h such that t1 + h, t2 + h, …, tn + h all belong to T, we have the shift property
In order to simplify discussion, we shall suppose that T is the entire real line, so that we do not have to be concerned about which values of the parameters are actually in the index set T. We note from the definition that if we take h = −t1, we have

That is, the distribution really depends upon the differences of the parameters from any one taken as reference (or origin on the time scale).
For a stationary process of second order, we have a simplification of the mean-value function and the autocorrelation function. For all t ∈ T,

In a similar fashion, for the autocorrelation function we have, for all permissible s, t,
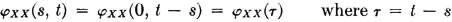
We have used here the same functional notation  XX(·) for two different functions, one a function of two variables and the other a function of a single variable. If the fact is kept in mind, no confusion need result. It should be noted that a second notational possibility exists as follows:
XX(·) for two different functions, one a function of two variables and the other a function of a single variable. If the fact is kept in mind, no confusion need result. It should be noted that a second notational possibility exists as follows:

This form is employed by some writers, and the particular choice should be checked when reading any given article.
The results may be extended to a pair of stationary processes X and Y. In the stationary case

The same alternative exists with respect to  XY (S − t, 0) as for the autocorrelation function. The properties of the correlation functions [(
XY (S − t, 0) as for the autocorrelation function. The properties of the correlation functions [( 1) through (
1) through ( 7)], derived in the previous section, may be specialized to the stationary case. In reformulating these properties one should note that the point t, t corresponds to τ = 0 and if the point s, t corresponds to τ, the point t, s corresponds to − τ.
7)], derived in the previous section, may be specialized to the stationary case. In reformulating these properties one should note that the point t, t corresponds to τ = 0 and if the point s, t corresponds to τ, the point t, s corresponds to − τ.
In investigations involving only the mean-value function and the correlation function, the definition of stationarity is much more restrictive than necessary. The definition given above requires the shift property for distribution functions of all orders. Only the first and second distributions enter into an analysis based on the mean-value function and the correlation function. Hence it is natural to make the following
Definition 7-7b
A random process X is said to be second-order stationary if it is of second order and if its first and second distribution functions have the shift property

If the process is of second order and  XX(t, t + τ) =
XX(t, t + τ) =  XX(0, τ) for all t, τ, the process is said to be stationary in the wide sense (Doob [1953]).
XX(0, τ) for all t, τ, the process is said to be stationary in the wide sense (Doob [1953]).
It is easy to show that if a process is second-order stationary it is also wide-sense stationary. The converse is not necessarily true.
Example 7-7-1
Consider once more the step process derived in Sec. 7-5. In the case that the jump points have a Poisson counting process, we have
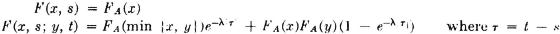
The process is thus second-order stationary (stationary in the wide sense). As noted in Example 7-6-2, the mean-value function is constant and the autocorrelation function is a function of τ = t − s. 
Example 7-7-2
Consider a process of the form

We wish to consider the possibility that 
DISCUSSION First we note that E[X(t)] = f(t)E[A], so that E[A] = 0 except for the trivial case f(t) = 0. In order for the process to be of second order, we must have  . Now
. Now  . To make the autocorrelation function independent of t, we must have
. To make the autocorrelation function independent of t, we must have  invariant with t. Let
invariant with t. Let 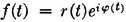 with r(t) ≥ 0. Then we must have
with r(t) ≥ 0. Then we must have
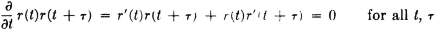
For τ = 0, r′(t)r(t) ≡ 0, which implies r′(t) ≡ 0, which in turn implies r(t) ≡ r, a positive constant. Since

we must have

This is satisfied only by  ′(t) = λ, a constant, so that
′(t) = λ, a constant, so that  (t) = λt +
(t) = λt +  , with
, with  an arbitrary constant.
an arbitrary constant.
If we put 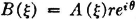 , we have,
, we have,  . In this case we have
. In this case we have

Example 7-7-3
A more general process for which  XX(t, t + τ) =
XX(t, t + τ) =  XX(τ) may be formed by taking a linear combination of processes of the type in the previous example. Consider
XX(τ) may be formed by taking a linear combination of processes of the type in the previous example. Consider

DISCUSSION
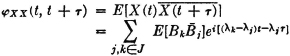
In order for the autocorrelation function to be independent of t, we must have 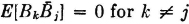 . In this case
. In this case

Now  . If the index set J is infinite, it is necessary that the sum of the bk converge.
. If the index set J is infinite, it is necessary that the sum of the bk converge.
If the process is real-valued, so also is  XX(·). In this case, the complex terms must appear in conjugate pairs. Suppose
XX(·). In this case, the complex terms must appear in conjugate pairs. Suppose 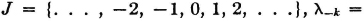
 , and
, and  . If we let Bk(·) = Ck(·) − iDk(·), we may write
. If we let Bk(·) = Ck(·) − iDk(·), we may write

B0(·) must be real-valued, and  k(·) is the phase angle for the sinusoid with angular frequency λk.
k(·) is the phase angle for the sinusoid with angular frequency λk.
The autocorrelation function must be given by

It is of interest that the autocorrelation function does not depend in any way on the phases of the sinusoidal components of the process; it depends only upon the amplitudes and frequencies of these components. This fact is important in certain problems of statistical communication theory. 
Processes of the type considered in the last example are important in the spectral analysis of random processes (cf. Doob [1953] or Yaglom [1962]). Further investigation of this important topic would require a knowledge of harmonic analysis and would take us far beyond the scope of the present work.
In the introduction and the first section of this chapter it is pointed out that the “randomness” of a random process is a matter of the uncertainty about which sample function has been selected rather than the “random” character of the shape of the graph of the function. Yet in both popular thought and in actual experimental practice the notion of randomness is associated in an important way with the fluctuating characteristic of the graph of the sample function.
The situation that usually exists is that one obtains experimentally a record of successive values of the physical quantity represented by the values of the random process. The record so obtained is a graph over some finite interval of one of the sample functions. It is sometimes possible, because several devices or systems are available, to obtain partial records of several sample functions. When several recordings are made from one device or system, these must be viewed as graphs of the same sample function over the various finite intervals. With partial information on one or a few sample functions, how is one to characterize a random process which has an infinity of sample functions?
What one assumes in practice is that the sample function available is typical of the process in some appropriate sense. One seeks to determine from the record of this function information on the statistics of the process—probability distributions, expectations, etc. In order to do this, one has to suppose that the time sequence of observed values corresponds in some way to the distribution of the set of values of the whole ensemble of sample functions.
The practical approach is to take whatever sample functions are available and determine various time averages. These time averages are then assumed to give at least approximate values of corresponding probability averages (expectations). For one thing, this assumes that the probability distributions are stationary—at least over the period in which the time averaging is carried out. In this section we shall assume the processes are stationary to whatever degree is needed for the problem at hand.
To facilitate discussion of the problem, we need to make precise the notion of time average.
Definition 7-8a
The time average (or time mean) of a function f (·) over the interval (a, b) is given by

If either limit of the interval is infinite, we take the limit of the average over finite intervals as a, or b, or both, become infinite.
If f (·) is defined only for discrete values of t, we replace the integral by the sum and divide by the number of terms.
To simplify discussion, we shall suppose the interval of averaging is the whole real line and shall shorten the notation to A[f],
Time averages have a number of properties which we may list for convenience. Since time averaging involves an integration process, it should be apparent that the operation of time averaging has properties in common with the property of taking mathematical expectations (probability averaging).
The following properties hold for complex-valued functions, except in the cases in which inequalities demand real-valued functions. We state these properties without proof, since most of them are readily derivable from properties of integrals and may be visualized in terms of the intuitive idea of averaging the values of a function. These properties are stated and numbered so that the first five properties correspond to the first five properties listed for mathematical expectation. The first five properties hold for averaging over any interval.
(A1) If c is any constant, A[c] = c.
(A2) Linearity. If a and b are real or complex constants,

(A3) Positivity. If f (·) ≥ 0, then A[f] ≥ 0. If f(·) ≥ 0 and the interval of averaging is finite, A[f] = 0 iffi f(t) = 0 for almost all t in the interval. If f(·) ≥ g(·), then A[f] ≥ A[g].
(A4) A[f] exists iffi A[|f|] does, and |A[f]| ≤ A[|f|].
(A5) Schwarz inequality. |A [fg]|2 ≤ A[|f|2]A[|g|2]. In the real case, equality holds for finite intervals of averaging iffi there is a real constant λ such that λf(t) + g(t) = 0 for almost all t in the interval.
The following properties hold for infinite intervals of averaging.
(A∞6) If  dt exists, then A [f] = 0.
dt exists, then A [f] = 0.
(A∞7) If A[|f|] exists, then A[f(t + a)] = A[f(t)], where a is any real constant.
(A∞8) If f(·) is periodic with period T,

It should be noted that the time average is defined for any suitable function of time, whether the function is a member of a random process or not. If the time function is a sample function from a random process, the average will, in general, depend upon which choice variable  is selected. In most cases of interest, we are safe in assuming that this average, as a function of
is selected. In most cases of interest, we are safe in assuming that this average, as a function of  , is a random variable.
, is a random variable.
In many investigations, one is interested in the relationship between time averages for a given sample function from a random process and the mathematical expectation for the process. One of the first things that may be noted is that under very general conditions we may interchange the order of taking time averages and taking the mathematical expectation. Thus

This follows from the fact that both operations are integration processes. The expression above represents the following integral expression:

The very general theorem of Fubini allows the interchange of order of integration under most practical conditions. This result may be extended to averages and expectations of functions of the members of the process and to functions of members of more than one process.
Among the most useful time averages in the study of stationary random processes are the time correlation functions defined as follows:
Definition 7-8b
Suppose f(·) and g(·) are real or complex-valued functions defined on the whole real line. The time autocorrelation function Rff(·) for the function f(·) is given by

The time cross-correlation function for f(·) and g(·) is given by

As we shall see, these are closely associated, in the theory of stationary random processes, with the corresponding correlation functions defined in Sec. 7-6 as mathematical expectations. To distinguish the two kinds of correlation, we shall speak of time correlation and stochastic correlation.
The time autocorrelation is a very simple operation, which may be viewed graphically in the case of real-valued functions. The graph of f(t + τ) is obtained from the graph of f(t) by shifting the latter τ units to the left for τ > 0 or |τ| units to the right for τ < 0. The product of the function f(·) and the shifted function f(· + τ) is a new function of time, which is then averaged. The process may be illustrated by the following simple example.
Fig. 7-8-1 Time autocorrelation function Rff(·) for a rectangular wave function.
Example 7-8-1 Time Autocorrelation of a Rectangular Wave
We consider the real-valued function whose graph is a periodic succession of rectangular waves, as shown in Fig. 7-8-1. In dealing with a periodic wave, we need deal with only one period and extend the result periodically. Figure 7-8-1a shows one period of the graph of f(·). Figure 7-8-1b shows one period of the graph of f(· + τ), in the case 0 < τ. Figure 7-8-1c shows one period of the product function f(·)f(· + τ). The time average, which is the time average over one period by property  is given by
is given by
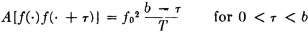
Other cases may be argued similarly, to give the function Rff(·) shown in Fig. 7-8-1d. 
If the value f(t) of the function fluctuates rapidly in a “random” manner as t varies, in such a way that A[f] = 0, it is to be expected that, after a suitable shift τ, the product function will be positive as much as it is negative, so that the average Rff(τ) becomes small for large shift τ. The more rapidly the function fluctuates, the more rapidly Rff(τ) might be expected to drop off from its maximum value of Rff(0) = A[f2] at τ = 0. If, however, the function contains a periodic component hidden in the fluctuations, this periodic component will line up when the shift is a multiple of the period. This value will show up in the time correlation function as a periodic term. It is properties such as these, plus some important theorems in harmonic analysis, which direct attention to the time correlation functions. We cannot deal in any complete way with this topic. For a careful and extensive treatment, one may consult the important book by Lee [1960, chap. 2].
Suppose X(·, ·) is a stationary second-order process. We have considered two operations which are designated by the term correlation.
Stochastic correlation:

Time correlation:

In most cases, RXX(·, ·) will be a random process; that is, for each τ, we have a random variable. Intuition and experience indicate the possibility that  XX(τ) and RXX(
XX(τ) and RXX( , τ) should be the same, at least for some functions which are typical of the process, in the sense that they reflect in their time variations the statistics of the process.
, τ) should be the same, at least for some functions which are typical of the process, in the sense that they reflect in their time variations the statistics of the process.
Let us examine the concept of a typical function more closely. Suppose we have such a function X( , ·) from the process, or at least a graph of the function as observed over a finite period of time. In what sense can the analytical character of this sample function give meaningful information about the statistical or probabilistic character of the process? For one thing, we should suppose that the time average of the sample function should agree with the mean-value function (which is constant for stationary processes). That is,
, ·) from the process, or at least a graph of the function as observed over a finite period of time. In what sense can the analytical character of this sample function give meaningful information about the statistical or probabilistic character of the process? For one thing, we should suppose that the time average of the sample function should agree with the mean-value function (which is constant for stationary processes). That is,

We should suppose further that
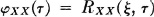
That is, the stochastic autocorrelation function for the process should coincide with the time autocorrelation function for the typical function. In order to emphasize the importance of the idea, we formalize it in the following
Definition 7-8c
A sample function X( , ·) from a stationary random process is said to be typical (in the wide sense) iffi
, ·) from a stationary random process is said to be typical (in the wide sense) iffi

When other expectations are under consideration, the concept of a typical function may be modified in an appropriate way. Also, it may be that a sample function is typical over certain finite intervals, in which case we say it is locally typical. This is the sort of thing that occurs in experimental work. A record is taken of the behavior of some physical system. At times, “something is wrong”—perhaps the equipment is not working in the proper manner. At these times, the record is not typical. When the record is locally typical over a sufficiently long interval, the time averages over that interval may provide reasonable approximations to the time average of a typical function over the whole real line.
The key to empirical work with random processes is in finding a function which is typical over an interval of sufficient length so that the time averages provide suitable approximations to the corresponding probability averages. When one has only a few short records—either of various intervals on the same sample function or of intervals for a few different sample functions—he has to assume the records are typical. From these he must draw conclusions about the entire process which serve as the basis for analysis of the system under study. In order to test for the condition of being locally typical, one may perform the time averaging over various subintervals of the records available and compare the results with the average over the entire record or set of records. If sufficient record is available, one may be able to check the tendency of the various averages to approximate the same function. If they do approximate the same function, one must then proceed on the assumption that this function is the desired function for the process.
There are processes for which no sample function is typical. As a trivial example, consider the case in which every sample function is a constant. This means that every random variable in the process is identical (as a function of the choice variable  ) with every other. There are no variations in any sample function to provide information about the ensemble variations in the process.
) with every other. There are no variations in any sample function to provide information about the ensemble variations in the process.
On the other hand, there are important processes for which the probability of selecting a typical function is quite high. Processes which have this property have been singled out and given a special name.
Definition 7-8d
A random process X is said to be ergodic (in the wide sense) iffi it is stationary in the wide sense and
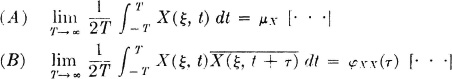
The symbol [· · ·] is intended to indicate that the limit may be taken in any one of the senses which are common in probability theory (Sec. 6-3). Thus we may have convergence [mean2], which implies convergence [in prob]; or we may have convergence [P], which is ordinary convergence for all but possibly a set of sample functions with zero probability of occurrence.
In the case of random sequences, the integral in expression (A) becomes a sum. If the convergence is [in prob], we then have a form of the weak law of large numbers discussed in Sec. 6-1. If the convergence is [P], we have a form of the strong law of large numbers, examined briefly in Sec. 6-4. The ergodic property (B) may thus be viewed as an extension of the law of large numbers—weak or strong, depending upon the kind of convergence assumed.
The strong form (convergence [P]) is highly desirable. With this condition, if we choose a sample function “at random,” the probability is 1 that the time averages for the sample function chosen will give the mathematical expectations corresponding to expressions (A) and (B). We are quite free to operate, in this case, with whatever sample function is available. The weak forms of convergence are not quite so desirable. In the case of convergence [in prob], we are assured that for sufficiently large T we have a high probability of choosing a sample function for which the integral differs from the limiting value by an arbitrarily small number. The weak convergence does not, however, assure us that if we are successful in choosing such a desirable function for a given T, the value of the integral for this sample function will continue to approach the desired limit as T is increased.
A variety of conditions have been studied which ensure ergodicity, either in the strong or the weak sense. The difficulty with these conditions is that they are necessarily expressed in terms of probability distributions or mathematical expectations (such as the autocorrelation function). It is precisely this probability information which is missing when one has only a single sample function or a small number of sample functions available for study. The mathematical problem is to express the conditions in such a manner that one can tell from physical considerations or past experience whether or not the assumptions are likely to lead to a useful probability model. For a readable discussion of the conditions which ensure convergence [mean2], see Yaglom [1962, Sec. 4].
In spite of the theoretical limitations, the practice of utilizing various time averages to obtain estimates of mathematical expectations has proved successful in many practical situations. The success of this approach depends upon success in obtaining a function which is typical of the process in the sense that its time variations exhibit the properties of the “ensemble variations” characteristic of the process. Here, as in all applications of theoretical models to physical situations, the final appeal must be to experience, to determine the adequacy of the model.
These remarks should not be interpreted as detracting from the importance of theoretical developments. Very often, assumptions based on physical experience can be used to derive important characteristics of the underlying probability model. This is the case for the Poisson counting process discussed in Sec. 7-3. A careful theoretical study of the process so derived often leads to the identification of parameters or characteristics, which may then be checked experimentally. On the basis of experience, the model is postulated. Conclusions are drawn which are checked experimentally, to test the hypothesis. If the “fit” is satisfactory, one uses the model as an aid to analysis and further experimentation.
The class of random processes known as gaussian processes (or normal processes) plays a strategic role in both mathematical theory and in the application of the theory to real-world problems. This is notably true in the study of electrical “noise” and related phenomena in other physical systems. Because of the central limit theorem, one might expect to encounter the gaussian distribution in random processes whose member functions are the result of the superposition of many component functions. The “shot noise” in thermionic vacuum tubes, which places limitations on their use as amplifiers of electrical signals, is the result of the superposition of a large number of very small current pulses. Each pulse is due to the emission from the cathode of single electrons and their passage across the interelectrode space to the anode. Since these electrons are emitted “randomly”—in many situations the emission times are described by a Poisson counting function—and the current pulses produced in the associated circuit overlap and add up, the instantaneous current has a gaussian distribution at any time t. Under certain natural assumptions, the random variables of the process are jointly gaussian, so that the resulting current is a sample function from a gaussian process. In a similar manner, the “thermal noise,” which consists of the voltage fluctuations produced by thermal agitation of ions in a resistive material, is represented by a gaussian process.
Gaussian processes are characteristic of electrical noise and other noise phenomena resulting from the superposition of many component effects in another respect. Gaussian signals have the property that when a signal is passed through a linear filter, the waveform of the response signal is also a member of a gaussian process. This is not true for most nongaussian processes; there is no simple (and often no known) relation between the nongaussian input to a linear filter and the output from the filter in response to this input. The gaussian process is thus in many ways “natural” to the important topic of electrical noise, since many transmission or control systems behave approximately as linear filters. Analogous situations hold in many other types of physical systems.
In addition to the widespread occurrence in nature of physical processes which are gaussian or very nearly gaussian, the mathematics of the gaussian process is much more completely developed than for most other processes of similar complexity and generality. In part, this is because the gaussian process is completely described in terms of second-order effects: the mean-value function and the autocorrelation function determine completely the character of the gaussian process. In this section we shall give a very brief outline of some of the more important mathematical characteristics of gaussian processes. For more detailed treatments, see any of the references listed at the end of the chapter.
Before turning to general processes, we consider finite families of random variables. An extension of the uniqueness property (M1) on moment-generating functions (Sec. 5-7) asserts that a joint distribution function for a finite number of random variables is uniquely determined by the moment-generating function
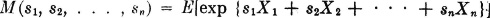
or, equivalently, by the characteristic function
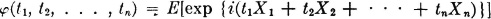
For each Xk(·) we denote the mean value by  k = E[Xk], and for each pair Xj(·) and Xk(·), we indicate the covariance by
k = E[Xk], and for each pair Xj(·) and Xk(·), we indicate the covariance by

Using an argument exactly parallel to that for property ( 3) for the autocorrelation function, we find that the quadratic form
3) for the autocorrelation function, we find that the quadratic form
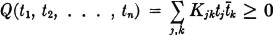
so that it is positive semidefinite. If the stronger condition holds that the value is zero only when all tk are zero (in which case the form is said to be positive definite), then the inverse form exists as follows:

The numbers  are obtained by inverting the matrix [Kjk] of the covariance factors.
are obtained by inverting the matrix [Kjk] of the covariance factors. 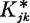 is the element of the jth row and kth column of the inverse matrix.
is the element of the jth row and kth column of the inverse matrix.
Definition 7-9a
The class of random variables {Xk(·): 1 ≤ k ≤ n} is said to have a joint gaussian distribution (or to be normally distributed) iffi the characteristic function

If the quadratic form is positive definite, so that the inverse exists, it can be shown (cf. Cramér [1946]) that the joint density function is given by
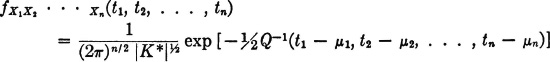
where |K*| is the determinant of the matrix  . If the quadratic form is only positive semidefinite, special arguments must be carried out. The distribution in this case is said to be singular. The quadratic form Q, and hence the matrix [Kjk], have rank r < n. Cramér has shown that in this case the probability mass distribution induced by the random variables is limited to a linear subspace Rr of dimension r, rather than being distributed in n-dimensional space Rn.
. If the quadratic form is only positive semidefinite, special arguments must be carried out. The distribution in this case is said to be singular. The quadratic form Q, and hence the matrix [Kjk], have rank r < n. Cramér has shown that in this case the probability mass distribution induced by the random variables is limited to a linear subspace Rr of dimension r, rather than being distributed in n-dimensional space Rn.
Using properties of the characteristic function and properties of convergence [mean2], one may prove the following theorems:
Theorem 7-9A
If the class {Xk(·): 1 ≤ k ≤ n} is normally distributed and if a class {Yi(·): 1 ≤ i ≤ m} is obtained by a linear transformation,
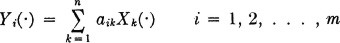
then the new class is also normally distributed.
Theorem 7-9B
Suppose  is a sequence of random variables, each of which is normally distributed. If Xn(·) → X(·) [mean2] as n becomes infinite, then X(·) is also normally distributed.
is a sequence of random variables, each of which is normally distributed. If Xn(·) → X(·) [mean2] as n becomes infinite, then X(·) is also normally distributed.
Proof of the second theorem utilizes the continuity property of the characteristic function and the Schwarz inequality.
We are now in a position to state a definition of a gaussian random process.
Definition 7-9b
A random process X is said to be gaussian (or normal) iffi every finite subfamily of random variables from the process is normally distributed.
A random process is strongly normal iffi it is normal and either (1) all X(·, t) are real-valued or (2) E[X(·, s)X(·, t)] = 0 for s ≠ t.
Theorems 7-9A and 7-9B imply that derivatives and integrals (in the mean-square calculus discussed briefly in Sec. 7-6) of gaussian processes are also gaussian. A specific value KX(s, t) of the covariance function (Definition 7-6e) is the covariance of the pair of random variables X(·, s) and X(·, t) from the process. The characteristic function, hence the density or distribution function, for any finite subclass {X(·, t1), X(·, t2), …, X(·, tn)} from the process is determined by the values  (tk) of the mean-value function and the values KX(tj, tk) of the covariance function, or equivalently, by the
(tk) of the mean-value function and the values KX(tj, tk) of the covariance function, or equivalently, by the  (tk) and the values
(tk) and the values  XX(tj, tk) of the autocorrelation function. It follows immediately that if a normal process is second-order stationary (i.e., stationary in the wide sense), it is also stationary in the strict sense, since distribution functions of all orders are determined by the autocorrelation function.
XX(tj, tk) of the autocorrelation function. It follows immediately that if a normal process is second-order stationary (i.e., stationary in the wide sense), it is also stationary in the strict sense, since distribution functions of all orders are determined by the autocorrelation function.
The following theorem, which we state without proof (cf. Loève [1963, p. 466]), further characterizes the role of the gaussian process.
Theorem 7-9C
A function g(·, ·) defined on T × T is an autocorrelation function (or a covariance function) iffi it is positive semidefinite.
Every autocorrelation function is the autocorrelation function of a strongly normal process. If the autocorrelation function is real-valued, the process may be chosen to be real-valued.
In particular, any second-order stationary process can be represented by a gaussian stationary process having the same mean-value function and autocorrelation function. Such processes play a central role in investigations in which mean-square approximations are used. Even a cursory survey of the literature on random signals and noise in communication theory will provide convincing evidence of the importance of this topic.
7-1. The transition matrix for a constant Markov chain is

Initial probabilities are  . Determine the matrix of second-order transition probabilities and determine
. Determine the matrix of second-order transition probabilities and determine 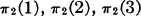 .
.
ANSWER: 
7-2. An electronic computer operates in the binary number system; i.e., it uses the digits 0 and 1. In the process of computation, numbers are transferred from one part of the machine to another. Suppose that at each transfer there is a small probability  that the digit transferred will be changed into its opposite. Let the digits 0 and 1 correspond to states of the system, and let each stage in the chain of transfer operations correspond to one period.
that the digit transferred will be changed into its opposite. Let the digits 0 and 1 correspond to states of the system, and let each stage in the chain of transfer operations correspond to one period.
(a) Write the transition matrix for the Markov chain describing the probabilities of the states.
(b) Draw a transition diagram for the process.
(c) Determine the second-order and third-order transition matrices.
(d) If the initial probabilities for the two states are 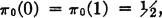 show that the probabilities after n transitions are
show that the probabilities after n transitions are  Interpret this result.
Interpret this result.
7-3. Construct a transition diagram for the chain described in Example 7-2-3. Identify the closed sets, including the absorbing states, if any.
ANSWER: States 1 and 9 are absorbing
7-4. Consider a finite chain with N states. Show that if sj → sk, then state k can be reached in not more than N transitions from the initial state j. (Suggestion: Consider the transition diagram.)
7-5. Draw the transition diagram for the chain described in Prob. 7-1. Show that the chain is irreducible and aperiodic.
7-6. Consider a finite, constant Markov chain having N states. Show that if the transition matrix is doubly stochastic, the chain has stationary distribution πi = 1/N, i = 1, 2, …, N.
7-7. Show that the “success-failure” process (Example 7-2-4) is always ergodic if none of the π(i, j) is zero. Determine the values of the stationary probabilities.
ANSWER: 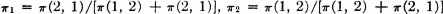
7-8. Assume the validity of Theorem 7-2E. Show that if a finite, constant Markov chain is irreducible and aperiodic, then it must be ergodic (i.e., all states are ergodic). In this case  for all pairs i, j.
for all pairs i, j.
7-9. Obtain the stationary distribution for the chain described in Prob. 7-1, and obtain the mean recurrence times for the various states.
ANSWER: 
7-10. Modify the chain described in Example 7-2-3 and Fig. 7-2-1 by making the behavior in positions 1 and 9 the same as that in other positions.
(a) Show that the resulting chain is irreducible and that every state is periodic with period 2.
(b) Show that the chain has a stationary distribution in which the stationary probability for any position is proportional to the number of ways of reaching that position. Determine these probabilities.
7-11. A random process X consists of four sample functions X( , t), 0 ≤ t ≤ 6. The sample functions may be described as follows:
, t), 0 ≤ t ≤ 6. The sample functions may be described as follows:
X( 1, t) rises linearly from X(
1, t) rises linearly from X( 1, 0) = 1 to X(
1, 0) = 1 to X( 1, 6) = 5.
1, 6) = 5.
X( 2, t) is a step function, having value 4 for 0 ≤ t < 2.5, value 1 for 2.5 ≤ t < 4.5, and value 2 for 4.5 ≤ t ≤ 6.
2, t) is a step function, having value 4 for 0 ≤ t < 2.5, value 1 for 2.5 ≤ t < 4.5, and value 2 for 4.5 ≤ t ≤ 6.
X( 3, t) is a triangular function, rising linearly from X(
3, t) is a triangular function, rising linearly from X( 3, 0) = 0 to X(
3, 0) = 0 to X( 3, 3) = 4.5 and then decreasing linearly to X(
3, 3) = 4.5 and then decreasing linearly to X( 3, 6) = 0.
3, 6) = 0.
X ( 4, t) is a linear function, decreasing from X(
4, t) is a linear function, decreasing from X( 4, 0) = 5 to X(
4, 0) = 5 to X( 4, 6) = 2.
4, 6) = 2.
Probabilities pk = P({ k}) are p1, = 0.2, p2 = 0.4, p3 = 0.3, and p4 = 0.1.
k}) are p1, = 0.2, p2 = 0.4, p3 = 0.3, and p4 = 0.1.
(a) Plot F(·, 1) and F(·, 3).
ANSWER: F(·, 1) has jumps of 0.3, 0.2, 0.4, 0.1 at k = 1.5, 1.67, 4.0, 4.5, respectively.
(b) Determine F(x, t1; y, t2) for
(1) (x, t1, y, t2) = (2, 1, 3, 5)
(2) (x, t1 y, t2) = (4, 2, 4, 3)
(3) (x, t1, y, t2) = (4, 1, 3, 4)
ANSWER: 0.3, 0.7, 0.7
7-12. Radioactive particles obey a Poisson probability law (i.e., the Poisson process is the counting process for the number of arrivals in a given time t). The average rate λ for a radioactive source is known to be 0.25 particle per second. The number of arrivals in each of five nonoverlapping intervals of 8 seconds duration each is noted. What is the probability of one or more observations of exactly two arrival times in 8 seconds?
ANSWER: 1 − (1 − 2e−2)5
7-13. Let N be the Poisson process.
(a) Evaluate  [N(·, t)/t) and σ2[N(·, t)/t] for t < 0.
[N(·, t)/t) and σ2[N(·, t)/t] for t < 0.
ANSWER: λ, λ/t
(b) Discuss with the aid of the Chebyshev inequality (or other suitable relation) the problem of determining the parameter λ for the process.
7-14. Let N be the Poisson process, and for a fixed T > 0, define the increment process X by the relation X( , t) = N(
, t) = N( , t + T) − N(
, t + T) − N( , t).
, t).
(a) Show that E[X(·, t)) = λT.
(b) Show that the autocorrelation function is given by
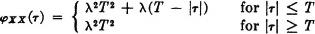
[Suggestion: Use the results of Examples 5-3-3 and 5-4-4 and the fact that the increments of the Poisson process are independent and stationary. Use the device 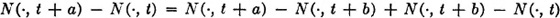 for suitable choices of b.]
for suitable choices of b.]
7-15. Suppose Z = X + Y, where X and Y are random processes. Determine the autocorrelation function for Z in terms of autocorrelation functions and cross-correlation functions for X and Y.
7-16. Suppose X and Y are second-order stationary random processes. Consider 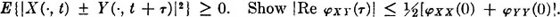
7-17. Let X be a real-valued, stationary random process. It is desired to estimate X( , t3) when X(
, t3) when X( , t1) and X(
, t1) and X( , t2) are known (t1, < t2 < t3). One type of estimate is provided by the so-called linear predictor. As an estimate, one takes
, t2) are known (t1, < t2 < t3). One type of estimate is provided by the so-called linear predictor. As an estimate, one takes  , where a and b are suitable constants. Let
, where a and b are suitable constants. Let 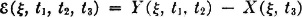 . As a measure of goodness of the predictor, we take the mean-square error
. As a measure of goodness of the predictor, we take the mean-square error  .
.
(a) Let t2 = t1 + α and t3 = t2 + τ. Obtain an expression for the mean-square error in terms of the autocorrelation function for the process X.
ANSWER: 
(b) Determine values of the constants a and b to minimize the mean-square error.
Instructions for probs. 7-18 through 7-27
Assume that the random variables and the random processes are real-valued, unless stated otherwise. In working any problem in the sequence, assume the results of previous problems in the sequence; also assume the results of Probs. 5-10 through 5-12.
7-18. Consider the random sinusoid (cf. Example 7-1-1) given by X( , t) = A(
, t) = A( ) cos [ωt +
) cos [ωt +  (
( )], where ω is a constant, A (·) and
)], where ω is a constant, A (·) and  (·) are independent random variables, and
(·) are independent random variables, and  (·) is distributed uniformly on the interval [0, 2π]. Use the results of Prob. 5-11.
(·) is distributed uniformly on the interval [0, 2π]. Use the results of Prob. 5-11.
(a) Show that the mean-value function is identically zero.
(b) Determine the autocorrelation function for the process, and show that  XX(t, t + τ) does not depend upon t.
XX(t, t + τ) does not depend upon t.
[Suggestion: Use the formula cos x cos y = ½ cos (x + y) + ½ cos (x − y)].
7-19. Repeat Prob. 7-18 for the case in which ω(·) is a random variable such that {A(·), ω(·),  (·)} is an independent class and
(·)} is an independent class and  (·) is uniformly distributed on the interval [0, 2π]. (Suggestion: Use the results of Prob. 5-12.)
(·) is uniformly distributed on the interval [0, 2π]. (Suggestion: Use the results of Prob. 5-12.)
7-20. Suppose X is a random process (real or complex) such that, with probability 1, each sample function X( ,·) is periodic with period T [i.e., for each
,·) is periodic with period T [i.e., for each  , except possibly for a set of probability 0, X(
, except possibly for a set of probability 0, X( , t) = X(
, t) = X( , t + T) for all t]. Show that
, t + T) for all t]. Show that
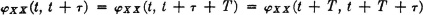
[Suggestion: Use the general definition of mathematical expectation and property (15) for the abstract integral.]
7-21. Show that if X is a second-order stationary random process and g(·, ·) is a Borel function, then E{g[X(·, t), X(·, t + τ)]} is a function of τ but does not depend upon t. (Suggestion: Use the Stieltjes integral form of the expectation.)
7-22. Consider the real-valued random process Y defined by

where (1) X is a second-order stationary process and (2) A(·),  (·), and X are independent in the sense that, for any Borel function g(·, ·), the class {A(·),
(·), and X are independent in the sense that, for any Borel function g(·, ·), the class {A(·),  (·), g[X(·. t), X(·, t + τ)]} is an independent class for each t and τ. The parameter ω is a constant.
(·), g[X(·. t), X(·, t + τ)]} is an independent class for each t and τ. The parameter ω is a constant.  (·) is uniformly distributed [0, 2π].
(·) is uniformly distributed [0, 2π].
(a) Show that the mean-value function for Y is identically zero.
(b) Show that 
(Suggestion: Use the results of Probs. 5-12 and 7-21.)
7-23. Let {Xi: 1 ≤ i ≤ n } be a class of second-order stationary random processes. Suppose that, for any pair of these processes and any choice of the pair of parameters s, t, the random variables Xi(·, s) and Xj(·, t) are independent. Let the mean-value function for Xi be  i, a constant, and the autocorrelation function for Xi be
i, a constant, and the autocorrelation function for Xi be  ii(·). Derive the mean-value function and the autocorrelation function for the process
ii(·). Derive the mean-value function and the autocorrelation function for the process , and show that
, and show that  Y(t) =
Y(t) =  Y and
Y and  YY(t, t + τ) =
YY(t, t + τ) =  YY(τ).
YY(τ).
7-24. Suppose X is the random process defined by
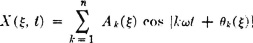
where ω is a constant and the class {Ak(·),  (·): 1 ≤ k ≤ n, 1 ≤ j ≤ n} is an independent class of random variables, with the further property that each
(·): 1 ≤ k ≤ n, 1 ≤ j ≤ n} is an independent class of random variables, with the further property that each  j(·) is uniformly distributed on the interval [0, 2π]. Determine the mean-value function and the autocorrelation function, and show that
j(·) is uniformly distributed on the interval [0, 2π]. Determine the mean-value function and the autocorrelation function, and show that  X(t) =
X(t) =  X and
X and  XX{t, t + τ) =
XX{t, t + τ) =  XX (τ)-Show that the autocorrelation function is periodic, with period 2π/ω. (Suggestion: Use the results of Prob. 7-23.)
XX (τ)-Show that the autocorrelation function is periodic, with period 2π/ω. (Suggestion: Use the results of Prob. 7-23.)
7-25. Repeat Prob. 7-24 in the case that ω is also a random variable, with the condition that the class 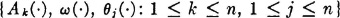 is an independent class. In this case the autocorrelation function may not be periodic. Note, also, that the results of Prob. 7-23 do not apply.
is an independent class. In this case the autocorrelation function may not be periodic. Note, also, that the results of Prob. 7-23 do not apply.
7-26. Suppose W is a real-valued, second-order stationary random process; suppose  (·) and
(·) and 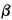 (·) are uniformly distributed on [0, 2π]; and suppose that, for each Borel function g(·, ·) and each pair of real numbers s, t, the class {g[W(·, s), W(·, t)],
(·) are uniformly distributed on [0, 2π]; and suppose that, for each Borel function g(·, ·) and each pair of real numbers s, t, the class {g[W(·, s), W(·, t)],  (·),
(·), 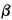 (·)} is an independent class. Let ω and a be constants. Consider the processes
(·)} is an independent class. Let ω and a be constants. Consider the processes
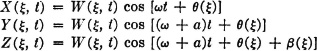
(a) Show that X, Y, and Z are second-order stationary random processes with respect to mean value and autocorrelation functions.
(b) Show that  XY(t, t + τ) depends upon t, but that
XY(t, t + τ) depends upon t, but that  XZ(t, t + τ) does not.
XZ(t, t + τ) does not.
(c) Use the results of part b to show that the process X + Z is second-order stationary with respect to mean value and autocorrelation functions but that the process X + Y is not.
7-27. Suppose the real-valued process X is denned by X( , t) = g[t −
, t) = g[t −  (
( )], with g(·) a periodic Borel function, with period T, and
)], with g(·) a periodic Borel function, with period T, and  (·) a random variable distributed uniformly on the interval [0, T]. We suppose further that
(·) a random variable distributed uniformly on the interval [0, T]. We suppose further that

(a) Show that the process X is second-order stationary with respect to mean value and autocorrelation functions.
(b) Show that, for every  , the time correlation function must be the same as the probability correlation function, i.e., that
, the time correlation function must be the same as the probability correlation function, i.e., that
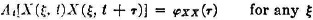
[Suggestion: Note that if f(t) = f(t + T) for all t, we must have  for every a and
for every a and  .]
.]
7-28. A random process X has sample functions which are step functions described as follows. For any given  the sample function has value An(
the sample function has value An( ) for
) for  , where (1)
, where (1)  is an independent class, (2) all An(·) have the same distribution with
is an independent class, (2) all An(·) have the same distribution with  [An] =
[An] =  and σ2[An] = σ2, and (3) α(·) is uniformly distributed on the interval (0, T). Obtain the autocorrelation function. (Suggestion: Show that the appropriate independence conditions are met so that the results of Sec. 7-5 and of Example 7-6-2 may be used.)
and σ2[An] = σ2, and (3) α(·) is uniformly distributed on the interval (0, T). Obtain the autocorrelation function. (Suggestion: Show that the appropriate independence conditions are met so that the results of Sec. 7-5 and of Example 7-6-2 may be used.)
ANSWER: 
General references
DOOB [1953]: “Stochastic Processes.” A treatise written for the mature mathematician. This, however, is one of the standard works on random processes and is an indispensable source for those prepared to read it.
GNEDENKO [1962]: cited at the end of our Chap. 3.
LOÈVE [1963]: cited at the end of our Chap. 4.
PARZEN [1962]: “Stochastic Processes.” A readable treatment of the subject, which demands less mathematical preparation than the works of Loève or Doob, yet presents a generally sound development. Considerable attention to applications.
ROSENBLATT [1962]: “Random Processes.” An exposition of the fundamental ideas of random processes, which is mathematically sound but not so complete or advanced as the work of Loève or of Doob. A good companion to the work of Parzen [1962].
Markov chains
BHARUCHA-REID [I960]: “Elements of the Theory of Markov Processes and Their Applications.” A treatise which considers much more general Markov processes than the simple case of constant chains. Develops fundamental theory and gives considerable attention to applications in a variety of fields.
FELLER [1957], chaps. 15, 16. Cited at the end of our Chap. 1. Has an excellent treatment of the fundamental theory of constant chains, with some attention to applications.
HOWARD [1960]: “Dynamic Programming and Markov Processes.” Uses the z transform (a type of generating function) to deal with finite chains. Provides some interesting applications to economic problems.
KEMENY, MIRKIL, SNELL, AND THOMPSON [1959]: “Finite Mathematical Structures” A lucid exposition of a wide range of topics coming under the general heading of “finite mathematics.” Chapter 6 has a readable treatment of finite, constant chains.
KEMENY AND SNELL [1960]: “Finite Markov Chains.” A detailed treatment of the finite chains, with considerable attention to applications.
Poisson processes
GNEDENKO [1962], sec. 51. Provides a derivation similar to that given in our Sec. 7-4. Cited at the end of our Chap. 3.
PARZEN [1962], chap. 4. Provides an extensive discussion of the Poisson and related processes, with axiomatic derivations. Cited above.
Correlation functions, covariance functions
DOOB [1953]: cited above.
LANING AND BATTIN [1956]: “Random Processes in Automatic Control.” One of several books dealing with the application of the theory of random processes to problems in filtering and control. Although much of the mathematics is developed heuristically, the work presents major ideas in an important field of application.
LEE [1960]: “Statistical Theory of Communication,” chap. 2. An extensive text by one of the pioneer teachers in the field. Chapter 2 gives a very detailed discussion of time correlation functions and their role in signal analysis.
LOÈVE [1963], chap. 10, on second-order properties. Contains a detailed discussion of the covariance function and develops the mean-square calculus. The work is written for graduate-level mathematical courses. Cited at the end of our Chap. 4.
MIDDLETON [1960]: “An Introduction to Statistical Communication Theory.” An extensive treatise on the application of random processes to communication theory.
TAGLOM [1962]: “An Introduction to the Theory of Stationary Random Functions.” A revision and translation of a well-known work in Russian. Provides a readable treatment of topics in random processes important in statistical communication theory, with more attention to mathematical foundation than is customary in engineering literature.
Gaussian processes
CRAMÉR [1946]: chap. 24. Gives a careful development of the joint gaussian distribution. This famous work is written for the mathematician but is widely consulted by others. Cited at the end of our Chap. 5.
DAVENPORT AND ROOT [1958]: “Introduction to Random Signals and Noise,” chaps. 7, 8. Discusses physically and mathematically some common types of noise processes and gives a good account of the central features of the gaussian process important for applications.
DOOB [1953], chap. 2, sec. 3. Provides a discussion of wide-sense and strict-sense stationary properties in gaussian processes. Cited above.
PARZEN [1962]. “Stochastic Processes,” chap. 3. Gives a readable discussion of the topic. Cited above.