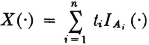
The concept of mathematical expectation seems to have been introduced first in connection with the development of probability theory in the early study of games of chance. It also arose in a more general form in the applications of probability theory to statistical studies, where the idea of a probability-weighted average appears quite naturally. The concept of a probability-weighted average finds general expression in terms of the abstract integrals studied in Chap. 4. Use of the theorems on the transformation of integrals, developed in Sec. 4-6, makes it possible to derive from a single basic expression a variety of special forms of mathematical expectation employed in practice; the topic is thus given unity and coherence. The abstract integral provides the underlying basic concept; the various forms derived therefrom provide the tools for actual formulation and analysis of various problems. Direct application of certain basic properties of abstract integrals yields corresponding properties of mathematical expectation. These properties are expressed as rules for a calculus of expectations. In many arguments and manipulations it is not necessary to deal directly with the abstract integral or with the detailed special forms.
The clear identification of the character of a mathematical expectation as a probability-weighted average makes it possible to give concrete interpretations, in terms of probability mass distributions, to some of the more commonly employed expectations.
Brief attention is given to the concept of random sampling, which is fundamental to statistical applications. Some of the basic ideas of information theory are presented in terms of random variables and mathematical expectations. Moment-generating functions and the closely related characteristic functions for random variables are examined briefly.
The concept of mathematical expectation arose early in the history of the theory of probability. It seems to have been introduced first in connection with problems in gambling, which served as a spur to much of the early effort. Suppose a game has a number of mutually exclusive ways of being realized. Each way has its probability of occurring, and each way results in a certain return (or loss, which may be considered a negative return) to the gambler. If one sums the various possible returns multiplied by their respective probabilities, one obtains a number which, by intuition and a certain kind of experience, may be called the expected return. In terms of our modern model, this situation could be represented by introducing a simple random variable X(·) whose value is the return realized by the gambler. Suppose X(·) is expressed in canonical form as follows:
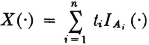
The values ti are the possible returns, and the corresponding Ai are the events which result in these values of return. The expected return for the game described by this random variable is the sum
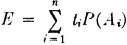
This is a probability-weighted average of the possible values of X(·).
The concept of a weighted average plays a significant role in sampling statistics. A sample of size n is taken. The members of the sample are characterized by numbers. Either these values are from a discrete set of possible values or they are classified in groups, by placing all values in a given interval into a single classification. Each of these classifications is represented by a single number in the interval. Suppose the value assigned to the ith classification is ti and the number of members of the sample in this classification is ni. The average value is given by
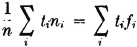
where fi = ni/n is the relative frequency of occurrence of the ith classification in the sample.
To apply probability theory to the sampling problem, we may suppose that we are dealing with a random variable X(·) whose range T is the set of ti. To a first approximation, at least, we suppose P(X = ti) = fi. In that case, the sum becomes
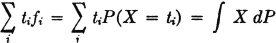
In a similar way, if we deal with a function g(·) of the values of the sample, the weighted average becomes
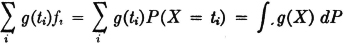
The notion of mathematical expectation arose out of such considerations as these. Because of the manner in which integrals are defined in Chap. 4, it seems natural to make the following definition in the general case.
Definition 5-1a
If X(·) is a real-valued random variable and g(·) a Borel function, the mathematical expectation E[g(X)] = E[Z] of the random variable Z(·) = g[X(·)] is given by
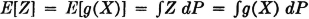
Similarly, if X(·) and Y(·) are two real-valued random variables and h(·) is a Borel function of two real variables, the mathematical expectation E[h(X, Y)] = E[Z] of the random variable Z(·) = h[X(·), Y(·)] is given by
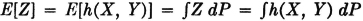
The terms ensemble average (ensemble being a synonym for set) and probability average are sometimes used. The term expectation is frequently suggestive and useful in attempting to visualize or anticipate results. But as in the case of names for other concepts, such as independence, the name may tempt one to bypass a mathematical argument in favor of some intuitively or experientially based idea of “what may be expected.” It is probably most satisfactory to think in terms of probability-weighted averages, in the manner discussed after the definitions of the integral in Secs. 4-2 and 4-4.
By virtue of the theoretical development of Chap. 4, we may proceed to state immediately a number of equivalent expressions and relations for mathematical expectations. These are summarized below:
Single real-valued random variable X(·): Mapping t = X(
) from S to R1
Probability measure PX(·) induced on Borel sets of R1
Probability distribution function FX(·) on R1
Probability density function fX(·) in the absolutely continuous case Mapping υ = g(t) from R1 to R2 produces mapping υ = Z() = g[X()] from S to R2
Probability measure PZ(·) induced on the Borel sets of R2
Probability distribution function FZ(·) on R2
Probability density function fZ(·) in the absolutely continuous case
In dealing with continuous distributions and mixed distributions, we shall assume throughout this chapter that there is no singular continuous part (Sec. 4-5). Thus the continuous part is the absolutely continuous part, for which a density function exists.
General case:
Discrete case:
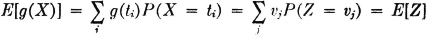
Absolutely continuous case:
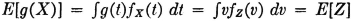
Mixed case: Consider the probability measure PX(·) on R1. We may express PX(·) = mXd(·) + mXc(·). The measure mXd(·) describes the discrete mass distribution on R1, and the measure mXc(·) describes the (absolutely) continuous mass distribution on R1. Corresponding to the first, there is a distribution function FXd(·), and corresponding to the second, there is a distribution function FXc(·) and a density function fXc(·). We may then write
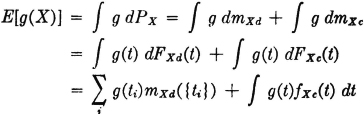
We note that mXd({ti}) = PX({ti}) = P(X = ti).
A similar development may be made for the mass distribution on the line R2 corresponding to PZ(·).
We have adopted the notational convention that integrals over the whole real line (or over the whole euclidean space in the case of several random variables) are written without the infinite limits, in order to simplify the writing of expressions. Integrals over subsets are to be designated as before.
Let us illustrate the ideas presented above with some simple examples.
Example 5-1-1
Determine E[X] when X(·) has the geometric distribution (Example 3-4-6). The range is {k: 0 ≤ k < ∞}, with pk = P(X = k) = pqk, where q = 1 − p.
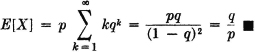
As an example of the absolutely continuous case, consider
Example 5-1-2
Let g(t) = tn, and let X(·) have the exponential distribution with fX(t) = αe−αtu(t), α > 0.
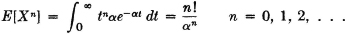
The lower limit of the integral is set to zero because the integrand is zero for negative t. 
In the mixed case, each part is handled as if it were the expectation for a discrete or a continuous random variable, with the exception that the probabilities, distribution functions, and density functions are modified according to the total probability mass which is discretely or continuously distributed. As the next example shows, it is usually easier to calculate the expectation as E[g(X)] rather than as E[Z], since it is then not necessary to derive the mass distribution for Z(·) from that given for X(·).
Example 5-1-3
Suppose g(t) = t2 and suppose X(·) produces a mass distribution PX(·) on R1 which may be described as follows. A mass of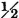 
is uniformly distributed in the interval [−2, 2]. A point mass of 
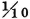is located at each of the points t = −2, −1, 0, 1, 2.
DISCUSSION The density function for the continuous part of the distribution for X(·) is given by
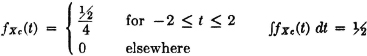
The probability masses for the discrete part of the distribution for X(·) are described by
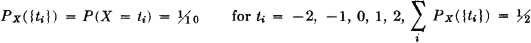
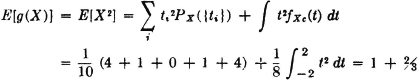
We may make an alternative calculation by dealing with the mass distribution induced on R2 by Z(·) = g[X(·)], as follows. Using the result of Example 3-9-1 for the continuous part, we have
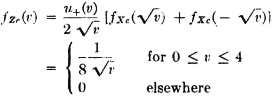
For the discrete part, we have range υk = 0, 1, 4, with probabilities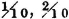 
, and 
respectively.
The situation outlined above for a single random variable may be extended to two or more random variables. We write out the case for two random variables. As in the case of real-valued random variables, we shall assume that there is no continuous singular part, so that continuous distributions or continuous parts of distributions are absolutely continuous and have appropriate density functions.
Two random variables X(·) and Y(·) considered jointly:
Mapping (t, u) = [X, Y]() from S to the plane R1 × R2 Probability measure PXY(·) induced on the Borel sets of R1 × R2
Joint probability distribution function FXY(·, ·) on R1 × R2
Joint probability density function fXY(·, ·) in the continuous case Mapping υ = h(t, u) from R1 × R2 to R3 produces the mapping υ = Z() = h[X(), Y()] from S to R3
Probability measure PZ(·) induced on the Borel sets of R3
Probability distribution function FZ(·) on R3
Probability density function fZ(·) in the continuous case
General case:
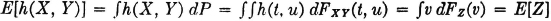
Discrete case:
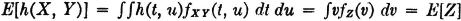
Mixed cases for point masses and continuous masses may be handled in a manner analogous to that for the single variable. Suitable joint distributions must be described by the appropriate functions. We illustrate with a simple mixed case.
Example 5-1-4
Let h(t, u) = tu so that Z(·) = X(·)Y(·). The random variables are those in Example 3-9-8 (Fig. 3-9-5). A mass of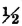 
is continuously and uniformly distributed over the square, which has corners at (t, u) = (·1, −1), (−1, 1), (1, 1), (1, −1). A point mass of 
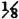is located at each of these corners.
DISCUSSION The discrete distribution is characterized by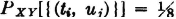 
for each pair (ti, uj) corresponding to a corner of the square. The continuous distribution can be described by a joint density function
Thus
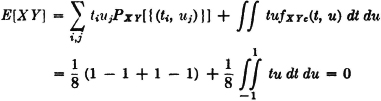
Calculations for E[Z] are somewhat more complicated because of the more complicated expressions for the mass distribution on R2.
Before considering further examples, we develop some general properties of mathematical expectation which make possible a considerable calculus of mathematical expectation, without direct use of the integral and summation formulas. This is the topic of the next section.
A wide variety of mathematical expectations are encountered in practice. Two very important ones, known as the mean value and the standard deviation, are studied in the next two sections. Before examining these, however, we discuss in this section some general properties of mathematical expectation which do not depend upon the nature of any given probability distribution. These properties are, for the most part, direct consequences of the properties of integrals developed in Chap. 4. These properties provide the basis for a calculus of expectations which makes it unnecessary in many arguments and manipulations to deal directly with the abstract integral or with the detailed special forms derived therefrom.
Unless special conditions—particularly the use of inequalities—indicate otherwise, the properties developed below hold for complex-valued random variables as well as for real-valued ones. For a brief discussion of the complex-valued case, see Appendix E. The statements of the properties given below tacitly assume the existence of the indicated expectations. This is equivalent to assuming the integrability of the random variables.
We first obtain a list of basic properties and then give some very simple examples to illustrate their use in analytical arguments. As a first property, we utilize the definition of the integral of a simple function to obtain
(E1) E[aIA] = aP(A) where a is a real or complex constant
A constant may be considered to be a random variable whose value is the same for all . If the random variable is almost surely equal to a constant, then for most purposes in probability theory it is indistinguishable from that constant. As an expression of the linearity property of the integral, we have
(E2) Linearity. If a and b are real or complex constants,
E[aX + BY] = aE[X] + bE[Y]
By a simple process of mathematical induction, the linearity property may be extended to linear combinations of any finite number of random variables. The mathematical expectation thus belongs to the class of linear operators and hence shares the properties common to this important class of operators.
Members of the class of linear operators which have the positivity property share a number of important properties. If X(·) and Y(·) are real-valued or complex-valued random variables, the mathematical expectation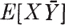 
has the character of an inner product, which plays an important role in the theory of linear metric spaces. Note that the bar over Y indicates the complex conjugate.
A restatement of property (I4) for integrals (as extended to the complex case in Appendix E) yields the important result
(E4) E[X] exists iffi E[|X|] does, and [E|X|] ≤ E[|X|].
The importance of this inequality in analysis is well known.
Another inequality of classical importance is the Schwarz inequality, characteristic of linear operators with the positivity property.
(E5) Schwarz inequality. |E[XY)|2 ≤ E|[X|2]E[|Y|2]. In the real case, equality holds iffi there is a real constant λ such that λX(·) + Y(·) = 0 [P].
PROOF We first prove the theorem in the real case and then extend it to the complex case. By the positivity property (E3), for any real λ, E[(λX + Y)2] ≥ 0, with equality iffi λX(·) + Y(·) = 0 [P], Expanding the squared term and using linearity, we get
This is of the form Aλ2 + Bλ + C ≥ 0. The strict inequality holds iffi there is no real zero for the quadratic in λ. Equality holds iffi there is a second-order zero for the quadratic, which makes it a perfect square. Use of the quadratic formula for the zeros shows there is no real zero iffi B2 − 4AC < 0 and a pair of real zeros iffi B2 = 4AC. Examination shows these statements are equivalent to the Schwarz inequality. To extend to the complex case, we use property (E4) and the result for the real case as follows:
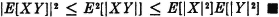
The product rule for integrals of independent random variables may be restated to give the
(E6) Product rule for independent random variables. If X(·) and Y(·) are independent, integrable random variables, then E[XY] = E[X]E[Y].
By a process of mathematical induction, this may be extended to any finite, independent class of random variables.
The next property is not a direct consequence of the properties of integrals, but may be derived with the aid of property (E3), above. It is so frequently useful in analytical arguments that we list it among the basic properties of mathematical expectation.
(E7) If g(·) is a nonnegative Borel function and if A = {: g(X) ≥ σ}, then E[g(X)] ≥ aP(A).
PROOF If we show g[X()] ≥ aIA() for all , the statement follows from property (E3). For ∈ A, g[X()] ≥ a while aIA() = a; for ∈ Ac, g[X()] ≥ 0 while aIA() = 0. Thus the inequality holds for all .
This elementary inequality is useful in deriving certain classical inequalities, such as the celebrated Chebyshev inequality in Theorem 5-4B.
A somewhat similar inequality is an extension of an inequality attributed to A. A. Markov.
(E8) If g(·) is a nonnegative, strictly increasing, Borel function of a single real variable and c is a nonnegative constant, then
PROOF |X| ≥ c iffi g(|X|) ≥ g(c). In property (E7), replace the constant a by the constant g(c).
For the special case g(t) = tk, we have the so-called Markov inequality.
The next inequality deals with convex functions, which are defined as follows:
Definition 5-2a
A Borel function g(·) defined on a finite or infinite open interval I on the real line is said to be convex (on I) iffi for every pair of real numbers a, b belonging to I we have
It is known that a convex function must be continuous on I in order to be a Borel function. If g(·) is continuous, it is convex on I iffi to every t0 in I there is a number λ(t0) such that for all t in I
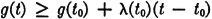
In terms of the graph of the function, this means that the graph of g(·) lies above a line passing through the point (t0, g(t0)). Using this inequality, we may extend a celebrated inequality for sums and integrals to mathematical expectation.
(E9) Jensen’s inequality. If g(·) is a convex Borel function and X(·) is a random variable whose expectation exists, then
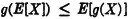
PROOF In the inequality above, let t0 = E[X] and t = X(·); then take expectations of both sides, utilizing property (E3).
We now consider some simple examples designed to illustrate how the basic properties may be used in analytical arguments. The significance of mathematical expectation for real-world problems will appear more explicitly in later sections.
Example 5-2-1 Discrete Random Variables
Let 
. By the linearity property (E2) and property (E1), we have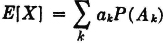 
, whether or not the expression is in canonical form. In general, 
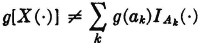if the Ak do not form a partition (Example 3-8-1); therefore, in general, 
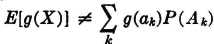. By virtue of the formulas in Sec. 3-8 for the canonical form, equality does hold if the Ak form a partition.
Example 5-2-2 Sequences of n Repeated Trials
Let Ek be the event of a success on the kth trial. Then
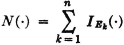
is the number of successes in a sequence of n trials. According to the result in Example 5-2-1,
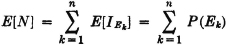
If P(Ek) = p for all k, this reduces to E[N] = np. No condition of independence is required. If, however, the Ek form an independent class, we have the case of Bernoulli trials studied in Examples 2-8-3 and 3-1-4. In that case, if we let Arn be the event of exactly r successes in the sequence of n trials, we know that the Arn form a partition and P(Arn) = Crnpr(1 − p)n−r. Hence
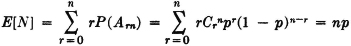
The series is summed in Example 2-8-10, in another connection, to give the same result. For purposes of computing the mathematical expectation, the first form for N(·) given above is the more convenient.
Example 5-2-3
Two real-valued random variables X(·) and Y(·) have a joint probability mass distribution which is continuous and uniform over the rectangle a ≤ t ≤ b and c ≤ u ≤ d. Find the mathematical expectation E[XY].
SOLUTION The marginal mass distributions are uniform over the intervals a ≤ t ≤ b and c ≤ u ≤ d, respectively. The induced measures have the product property, which ensures independence of the two random variables. Hence, by property (E6), we have
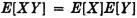
Now
Similarly, E[Y] = (c + d)/2, so that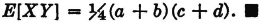 
The next example is of interest in studying the variance and standard deviation, to be introduced in Sec. 5-4.
Suppose X(·) and X2(·) are integrable and E[X] = 
. Then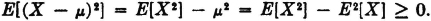 
SOLUTION
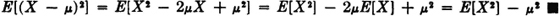
Another result which is sometimes useful is the following:
Example 5-2-5
For any two random variables X(·) and Y(·) whose squares are integrable, |E[XY]| ≤ max {E[|X|2], E[|Y|2]}.
SOLUTION By the Schwarz inequality, |E[XY]|2 ≤ E[|X|2]E[|Y|2]. The inequality is strengthened by replacing the smaller of the factors on the right-hand side by the larger. Hence |E[XY]|2 ≤ max {E2[|X|2], E2[|Y|2]). The asserted inequality follows immediately from elementary properties of inequalities for real numbers.
We turn, in the next two sections, to a study of two special expectations which are useful in describing the probability distributions induced by random variables.
Discussions in earlier sections show that a real-valued random variable is essentially described for many purposes, if the mass distribution which it induces on the real line is properly described. Complete analytical descriptions are provided by the probability distribution function. In many cases, a complete description of the distribution is not possible and may not be needed. Certain parameters provide a partial description, which may be satisfactory for many investigations. In this and the succeeding section, we consider two of the most common and useful parameters of the probability distribution induced by a random variable.
The simplest of the parameters is described in the following
Definition 5-3a
If X(·) is a real-valued random variable, its mean value, denoted by one of the following symbols , X, or [X], is denned by [X] = E[X].
We shall use PX(·) to denote the probability measure induced on the real line R, as in the previous sections. The mean value can be given a very simple geometrical interpretation in terms of the mass distribution. According to the fundamental forms for expectations, we may write
If {ti: i ∈ J} is the set of values of a simple random variable which approximates X(·) and if Mi = [ti, ti+1), then the approximating integral is
As the subdivisions become finer and finer, this approaches the first moment of the mass distribution on the real line about the origin. Since the total mass is unity, this moment is also the coordinate of the center of mass. Thus the mean value is the coordinate of the center of mass of the probability mass distribution. This mechanical picture is an aid in visualizing the location of the possible values of the random variable. As an example of the use of this interpretation, consider first the uniform distribution over an interval.
Example 5-3-1
Suppose X(·) is uniformly distributed over the interval [a, b]. This means that probability mass is uniformly distributed along the real line between the points t = a and t = b. The center of mass, and hence the mean value, should be given by X = (a + b)/2. This fact may be checked analytically as follows:
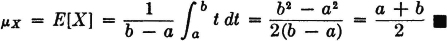
As a second example, we may consider the gaussian, or normal, distribution.
Example 5-3-2 The Normal Distribution
A real-valued random variable X(·) is said to have the normal, or gaussian, distribution if it is continuously distributed with probability density function
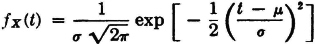
where is a constant and σ is a positive constant. A graph of the density function is shown in Fig. 3-4-4. This is seen to be a curve symmetrical about the point t = , as can be checked easily from the analytical expression. This means that the probability mass is distributed symmetrically about t = and hence has its center of mass at that point. The mean value of a random variable with the normal distribution is therefore the parameter . Again, we may check these results by straightforward analytical evaluation. We have
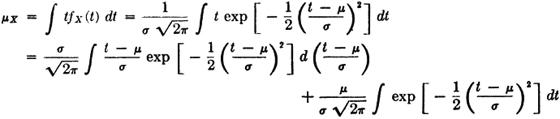
The integrand in the first integral in the last expression is an odd function of t − ; since the integral exists, its value must be zero. The second term in this expression is times the area under the graph for the density function and therefore must have the value .
It is not always possible to use the center-of-mass interpretation so easily. Since [X] is a mathematical expectation, the various forms of expression for and properties of the mean value are obtained directly from the expressions and properties of the mathematical expectation. Some of the examples in Sec. 5-2 are examples of calculation of the mean value. Example 5-2-1 gives a general formula for the mean value of a simple random variable. Example 5-2-2 gives the mean value for the number of successes in a sequence of n trials. In the Bernoulli case, in which the random variable has the binomial distribution (Example 3-4-5), the mean value is np. The constant in Example 5-2-4 is the mean value for the random variable considered in that example.
Example 5-3-3 Poisson’s Distribution
A random variable having the Poisson distribution is described in Example 3-4-7. This random variable has values 0, 1, 2, …, with probabilities
The mean value is thus
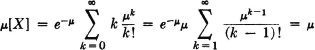
since the last series expression converges to e. Again, the choice of the symbol for the parameter in the formulas is based on the fact that this is a traditional symbol for the mean value.
Example 5-3-4
A man plays a game in which he wins an amount t1 with probability p or loses an amount t2 with probability q = 1 − p. The net winnings may be expressed as a random variable W(·) = t1IA(·) − t2IAc(·), where A is the event that the man wins and Ac is the event that he loses. The game is considered a “fair game” if the mathematical expectation, or mean value, of the random variable is zero. Determine p in terms of the amounts t1 and t2 in order that the game be fair.
SOLUTION We set [W] = t1p − t2q = 0. Thus p/q = t2/t1 = r, from which we obtain, by a little algebra, p = r/(1 + r) = t2/(t1 + t2).
Example 5-3-5
The sales demand in a given period for an item of merchandise may be represented by a random variable X(·) whose distribution is exponential (Example 3-4-8). The density function is given by
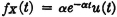
Suppose 1/α = 1,500 units of merchandise. What amount must be stocked at the beginning of the period so that the probability is 0.99 that the sales demand will not exceed the supply? What is the “expected number” of sales in the period?
SOLUTION The first question amounts to asking what value of t makes FX(t) = u(t)[1 − e−αt] = 0.99. This is equivalent to making e−αt = 0.01. Use of a table of exponentials shows that this requires a value αt = 4.6. Thus t = 4.6/α = 6,900 units. The expected number of sales is interpreted as the mathematical expectation, or mean value
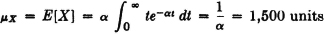
Note that this expectation may be obtained from the result of Example 5-1-2, with n = 1. The result above may be expressed in a general formula for the exponential distribution. If it is desired to make the probability of meeting sales demand equal to 1 − p, then e−αt = p or αt = −loge p, so that
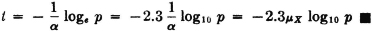
The next example involves some assumptions that may not be realistic in many situations, but it points to the role of probability theory in decision making. Even such an oversimplified model may often give insight into the alternatives offered in a decision process.
Example 5-3-6
A government agency has m research and development problems it would like to have solved in a given period of time and n contracts to offer n equally qualified laboratories that will work essentially independently on the problems assigned to them. Each laboratory has a probability p of solving any one of the problems which may be assigned to it. The agency is faced with the decision whether to assign contracts with a uniform number n/m (assumed to be an integer) of laboratories working on each problem or to let the laboratories choose (presumably in a manner that is essentially random) the problem that it will attack. Which policy offers the greater prospect of success in the sense that it will result in the solution of the larger number of problems?
SOLUTION AND DISCUSSION We shall approach this problem by defining the random variable N(·) whose value is the number of problems solved and determine E[N] under each of the assignment schemes. If we let Aj be the event that the jth problem is solved, then
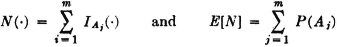
The problem reduces to finding the P(Aj). Consider the events
Bij = event ith laboratory works on jth problem
Ci = event ith laboratory is successful
We suppose P(Ci) = p and P(Bij) depends upon the method of assignment. We suppose further that {Ci, Bij: 1 ≤ i ≤ n, 1 ≤ j ≤ m} is an independent class of events. Now
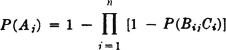
Uniform assignment: P(Bij) = 1 for n/m of the i for any j and 0 for the others; this means that 1 − P(BijCi) = 1 − p for n/m factors and = 1 for the others in the expression for P(Aj). Thus
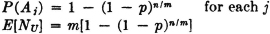
Random assignment: P(Bij) = 1/m for each i and j. P(Bij Ci) = p/m. Therefore P(Aj) = 1 − (1 − p/m)n, and
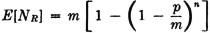
The following numerical values may be of some interest.
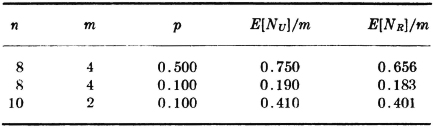
It would appear that for small p there is little advantage in a uniform assignment. When one allows for the fact that the probability of success is likely to increase if the laboratory chooses its problem, one would suspect that for difficult problems with low probability of success it might be better to allow the laboratories to choose. On the other hand, one problem might be attractive to all laboratories and the others unattractive to them all, resulting in several solutions to one problem and no attempt to solve the others. A variety of assumptions as to probabilities and corresponding methods of assignments must be tested before a sound decision can be made.
We turn next to a second parameter which is important in characterizing most probability distributions encountered in practice.
The mean value, introduced in the preceding section, determines the location of the center of mass of the probability distribution induced by a real-valued random variable. As such, it gives a measure of the central tendency of the values of the random variable. We next introduce a parameter which gives an indication of the spread, or dispersion, of values of the random variable about the mean value.
Consider a real-valued random variable X(·) whose square is integrable. The variance of X(·), denoted σ2[X], is given by
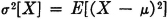
where = [X] is the mean value of X(·).
The standard deviation for X(·), denoted σ[X], is the positive square root of the variance.
We sometimes employ symbols σ or σX, to simplify writing.
A mechanical interpretation
As in the case of the mean value, we may give a simple mechanical interpretation of the variance in terms of the mass distribution induced by X(·). In integral form
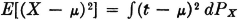
To form an approximating integral, we divide the t axis into small intervals; the mass located in each interval is multiplied by the square of the distance from the center of mass to a point in the interval; the sum is taken over all the intervals. The integral is thus the second moment about the center of mass; this is the moment of inertia of the mass about its center of mass. Since the total mass is unity, this is equal to the square of the radius of gyration of the mass distribution. The standard deviation is thus equal to the radius of gyration, and the variance to its square. As the mass is scattered more widely about the mean, the values of these parameters increase. Small variance, or standard deviation, indicates that the mass is located near its center of mass; in this case the probability that the random variable will take on values in a small interval about the mean value tends to be large.
Some basic properties
Utilizing properties of mathematical expectation, we may derive a number of properties of the variance which are useful. We suppose the variances indicated in the following expressions exist; this means that the squares of the random variables are integrable.
A restatement of the result obtained in Example 5-2-4 shows that
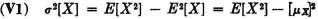
Multiplication by a constant produces the following effect on the variance.
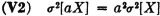
PROOF
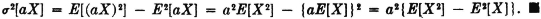
This property may be visualized in terms of the mass distribution. If |a| > 1, the variable aX(·) spreads the probability mass more widely about the mean than does X(·), with a consequent increase of the moment of inertia. For |a| < 1, the opposite condition is true. A change in sign produced by a negative value of a does not alter the spread of the probability mass about the center of mass.
Adding a constant to a random variable does not change the variance. That is,
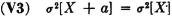
PROOF
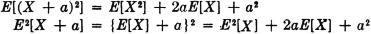
The difference is equal to σ2[X] by (V1).
In terms of the mass distributions, the random variable X(·) + a induces a probability mass distribution which differs from that for X(·) only in being shifted by an amount a. This shifts the center of mass by an amount a. The spread about the center of mass is the same in both cases.
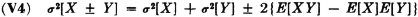
PROOF
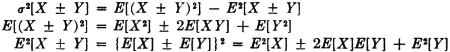
Taking the difference and using (V1) gives the desired result.
An important simplification of the formula (V4) results if the random variables are independent, so that E[XY] = E[X]E[Y]. More generally, we have
(V5) If {Xi(·): 1 ≤ i ≤ n} is a class of random variables and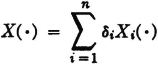 
, where each δi has one of the values +1 or −1, then
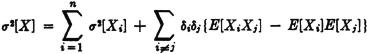
PROOF
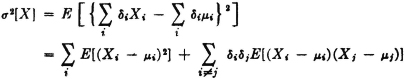
If the product rule E[XiXj] = E[Xi]E[Xj] holds for all i ≠ j, then each of the terms in the final summation in (V5) is zero. In particular, this is the case if the class is independent. Random variables satisfying this product law for expectations are said to be uncorrelated.
SOLUTION In Example 5-3-3 it is shown that E[X] = .
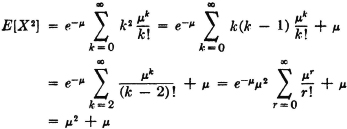
From this it follows that
The normal distribution
We next obtain the variance for the normal, or gaussian, distribution and obtain some properties of this important distribution.
Example 5-4-5 The Normal Distribution
Find σ2[X] if X(·) has the normal distribution, as defined in Example 5-3-2.
SOLUTION
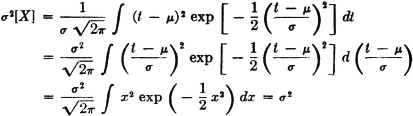
as may be verified from a table of integrals.
Definition 5-4b
A random variable X(·) is said to be normal (, σ) iffi it is continuous and has the normal density function
If X(·) is normal (, σ), we may standardize it in the manner indicated in (V6). It is of considerable interest and importance that the standardized variable is also normal.
Theorem 5-4A
If X(·) is normal (, σ), the standardized random variable
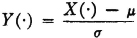
is normal (0, 1).
Let X(·) be a simple random variable given in canonical form by the expression
Let pi = P(Ai) and qi = 1 − pi. Determine σ2[X].
SOLUTION
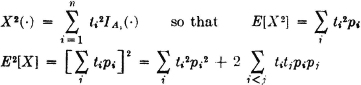
Using (V1), we get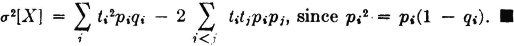 
In the last summation, the index notation i < j is intended to indicate the sum of all distinct pairs of integers, with the pair (i, j) considered the same as the pair (j, i). The factor 2 takes account of the two possible ways any pair can appear.
Example 5-4-3
Suppose {Ai: 1 ≤ i ≤ n} is a class of pairwise independent events. Let 
. Put P(Ai) = pi and qi.= 1 − pi. Determine σ2[X].
SOLUTION Since by Example 3-7-1, we may assert {aiIAi,(·): 1 ≤ i ≤ n} is a class of pairwise independent random variables, we may apply (V5), (V2), and the result of Example 5-4-1 to give
For the random variable giving the number of successes in Bernoulli trials (Example 5-2-2), Ai = Ei, ai = 1, and pi = p. Hence the random variable N(·) with the Binomial distribution has σ2[N] = npq.
Example 5-4-4 Poisson Distribution
The random variable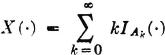 
, with the Ak forming a disjoint class and with 
, has the Poisson distribution. Determine σ2[X].
It is frequently convenient to make a transformation from a random variable X(·) having a specified mean and variance to a related random variable having zero mean and unit variance. This may be done as indicated in the following:
(V6) Consider the random variable X(·) with mean [X] = and standard deviation σ[X] = σ. Then the random variable
has mean [Y] = 0 and standard deviation σ[Y] = 1.
PROOF
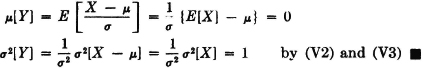
Some examples
We now consider a number of simple but important examples.
Example 5-4-1 The Indicator Function IA (·)
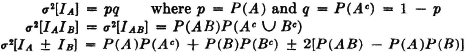
PROOF AND DISCUSSION σ2[IA] = E[IA2] − E2[IA]. Since IA(·) has values only zero or one, IA2(·) = IA(·). Using the fact that E[IA] = P(A) = p, we have σ2[IA] = p − p2 = p(1 − p) = pq. This problem may also be viewed in terms of the mass distribution with the aid of Fig. 5-4-1. Mass p = P(A) is located at t = 1, and mass q is located at t = 0. The center of mass is at t = p. Summing the products of the mass times the square of its distance from the center of mass yields
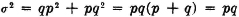
The second case follows from the first and the fact that (AB)c = Ac ∪ Bc.
The third relation comes from a direct application of (V4).
Fig. 5-4-1 Variance for the indicator function IA(·).
PROOF This result may be obtained easily from the result of Example 3-9-4. Putting a = 1/σ, which is positive, and b = −/σ, we have
Substituting συ + for t in the expression for fX(t) gives
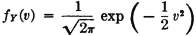
which is the condition required.
It is customary to use special symbols for the distribution and density functions for a random variable X(·) which is normal (0, 1). In this case it is customary to designate FX(·) by Φ(·) and fX(·) by 
(·). Extensive tables of these functions are found in many places. The general shape of the graphs for these functions is given in Fig. 3-4-4. By letting = 0 and adjusting the scale for σ = 1, these become curves for Φ(t) and (t) as shown in Fig. 5-4-2.
Fig. 5-4-2 (a) Distribution function Φ(·) and (b) density function (·) for a random variable normal (0, 1).
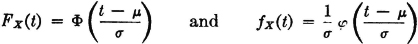
so that tables of Φ(·) and (·) suffice for any normally distributed random variable. As an illustration of this fact, consider the following
Example 5-4-6
A random variable X(·) is normal (, σ). What is the probability that it does not differ from its mean value by more than k standard deviations?
SOLUTION 
. Since (X − )/σ is normal (0, 1), the desired probability is Φ(k) − Φ (−k). This may be put into another form which requires only values of Φ(·) for positive k, by utilizing the symmetries of the distribution or density function. From the curves in Fig. 5-4-2, it is apparent that Φ(−k) = 1 − Φ(k), so that Φ(k) − Φ(−k) = 2Φ(k) − 1.
This example merely serves to illustrate how the symmetries of the normal distribution and density functions may be exploited to simplify or otherwise modify expressions for probabilities of normally distributed random variables. Once these symmetries are carefully noted, the manner in which they may be utilized becomes apparent in a variety of situations. Extensive tables of Φ(·), (·), and related functions are to be found in most handbooks, as well as in books on statistics or applied probability. The table below provides some typical values which are helpful in making estimates.
The inequality of Chebyshev
We have seen that the standard deviation gives an indication of the spread of possible values of a random variable about the mean. This fact has been given analytical expression in the following inequality of Chebyshev (spelled variously in the literature as Tchebycheff or Tshebysheff).
Theorem 5-4B Chebyshev Inequality
Let X(·) be any random variable whose mean and standard deviation σ exist. Then
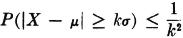
or, equivalently,
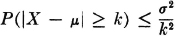
PROOF Since |X − | ≥ k iffi (X − )2 ≥ k2, we may use property (E7) with g(X) = (X − )2 to assert
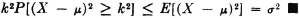
The first form of the inequality is interesting in that it shows the effective spread of probability mass to be measured in multiples of σ. Thus the standard deviation provides an important unit of measure in evaluating the spread of probability mass. This fact is also illustrated in Example 5-4-6. It should be noted that the Chebyshev inequality is quite general in its application. It has played a significant role in providing the estimates needed to prove various limit theorems (Chap. 6). Numerical examples show, however, that it does not provide the best possible estimate of the probability in special cases. For example, in the case of the normal distribution, Chebyshev’s estimate for k = 2 is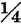 
, whereas from the table above for the normal distribution, it is apparent that
Another comparison is made for an important special case in Sec. 6-2. The general inequality is useful, however, for estimates in situations where detailed information concerning the distribution of the random variable is not available.
A number of other special mathematical expectations are used extensively in mathematical statistics to describe important characteristics of a probability mass distribution. For a careful treatment of some of the more important of these, one may consult any of a number of works in mathematical statistics (e.g., Brunk [1964], Cramér [1946], or Fisz [1963]).
It may be well at this point to make a new comparison of the situation in the real world, in the mathematical model, and in the auxiliary model, as we have done previously.
The process of sampling is fundamental in statistics. In Examples 2-8-9 and 2-8-10, the idea of random sampling is touched upon briefly. In this section, we examine the idea in terms of random variables.
Suppose a physical quantity is under observation in some sort of experiment. A sequence of n observations (t1, t2, …, tn) is recorded. Under appropriate conditions, these observations may be considered to be n observations, or “samples,” of a single random variable X(·), having a given probability distribution. A more natural way to consider these observations, from the viewpoint of our mathematical model, is to think of them as a single observation of the values of a class of random variables {X1(·), X2(·), …, Xn(·)}, where t1 = X1(), t2 = X2(), etc.
Definition 5-5a
If the conditions of the physical sampling or observation process described above are such that
1. The class {X1(·), X2(·), …, Xn(·)} is an independent class, and
2. Each random variable Xi(·) has the same distribution as does X(·), the set of observations is called a random sample of size n of the variable X(·).
This model seems to be a satisfactory one in many physical sampling processes. The concept of stochastic independence is the mathematical counterpart of an assumed “physical independence” between the various members of the sample. The condition that the Xi(·) have the same distribution seems to be met when the sampling is from an infinite population (that is, one so large that the removal of a unit does not appreciably affect the distribution in the population) or from a finite population with replacement.
When a sample is taken, it is often desirable to average the set of values observed. The significance of this operation from the point of view of the probability model may be obtained as follows. First we make the
The random variable A(·) given by the expression
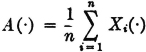
is known as the sample mean.
Each choice of an elementary outcome corresponds to the choice of a set of values (t1, t2, …, tn). But this also corresponds to the choice of the number
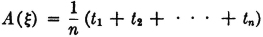
which is the sample mean. The following simple but important theorem shows the significance of the sample mean in statistical analysis.
Theorem 5-5A
If A(·) is the sample mean for a sample of size n of the random variable X(·), then
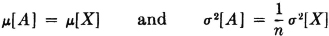
provided [X] and σ2[X] exist
PROOF The first relation is a direct result of the linearity property for expectations, and the second is a direct result of the additivity property (V5) for variances of independent random variables. Thus
This theorem says that the mean of the sample mean is the same as the mean of the random variable being sampled. The variance of the sample mean, however, is only 1/n times the variance of the random variable being sampled. In view of the role of the variance in measuring the spread of possible values of the random variable about its mean, this indicates that the values of the sample mean can be concentrated about the mean by taking large enough samples. This may be given analytical formulation with the help of the Chebyshev inequality (Theorem 5-4B). If we put [X] = and σ2[X] = σ2, we have
For any given k we can make the probability that A(·) differs from by more than kσ as small as we please by making the sample size n sufficiently large.
In various situations of practical interest, much better estimates are available than that provided by Chebyshev inequality. One of the central problems of mathematical statistics is to study such estimates. For an introduction to such studies, one may refer to any of a number of standard works on statistics (e.g., Brunk [1964] or Fisz [1963]).
Probability ideas are being applied to problems of communication, control, and data processing in a variety of ways. One of the important aspects of this statistical communication theory is the so-called information theory, whose foundations were laid by Claude Shannon in a series of brilliant researches carried out in the 1940s at Bell Telephone Laboratories. In this section, we sketch briefly some of the central ideas of information theory and see how they may be given expression in terms of the concepts of probability theory.
We suppose the communication system under study transmits signals in terms of some known, finite set of symbols. These may be the symbols of an alphabet, words chosen from a given code-word list, or messages from a prescribed set of possible messages. For convenience, we refer to the unit of signal under consideration as a message. The situation assumed is this: when a signal conveying a message is received, it is known that one of the given set of possible messages has been sent. The usual communication channel is characterized by noise or disturbances of a “random” character which perturb the transmitted signal. The actual physical process may be quite complicated.
The behavior of such a system is characterized by uncertainties. The problem of communication is to remove these uncertainties. If there were no uncertainty about the message transmitted over a communication system, there would be no real reason for the system. All that is needed in this case is a device to generate the appropriate signal at the receiving station. There are two sources of uncertainty in the communication system:
1. The message source (whether a person or a physical device under observation). It is not known with certainty which of the possible messages will be sent at any given transmission time.
2. The transmission channel. Because of the effects of noise, it is not known with certainty which signal was transmitted even when the received signal is known.
This characterization of a communication system points to two fundamental ideas underlying the development of a model of information theory.
1. The signal transmitted (or received) is one of a set of conceptually possible signals. The signal actually sent (or received) is chosen from this set.
2. The receipt of information is equivalent to the removal of uncertainty.
The problem of establishing a model for information theory requires first the identification of a suitable measure of information or uncertainty.
Shannon, in a remarkable work [1948], identified such a concept and succeeded in establishing the foundations of a mathematical theory of information. In this theory, uncertainty is related to probabilities. Shannon showed that a reasonable model for a communication source describes the source in terms of probabilities assigned to the various messages and subsets of messages in the basic set. The effects of noise in the communication channel are characterized by conditional probabilities. A given signal is transmitted. The signal is perturbed in such a manner that one can assign, in principle at least, conditional probabilities to each of the possible received signals, given the particular signal transmitted.
In this theory, the receipt of information is equivalent to the removal of uncertainty about which of the possible signals is transmitted. The concept of information employed has nothing to do with the meaning of the message or with its value to the recipient. It simply deals with the problem of getting knowledge of the correct message to the person at the receiving end.
For a review of the ideas which led up to the formulation of the mathematical concepts, Shannon’s original papers are probably the best source available. We simply begin with some definitions, due principally to Shannon, but bearing the mark of considerable development by various workers, notably R. M. Fano and a group of associates at the Massachusetts Institute of Technology (Fano [1961] or Abramson [1963]). The importance of the concepts defined rests upon certain properties and the interpretation of these properties in terms of the communication problem.
Probability schemes and uncertainty
The output of an information source or of a communication channel at any given time can be considered to be a random variable. This may be a random variable whose “values” are nonnumerical, but this causes no difficulty. The random variable indicates in some way which of the possible messages is chosen (transmitted or received). We limit ourselves to the case where the number of possible messages is finite. Information theory depends upon the identification of which of the possible outcomes has been realized. Once this is known, it is assumed that the proper signal can be generated (i.e., that the “value” is known). If the random variable is
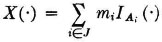
where mi represents the ith message, and Ai is the event that the message mi is sent, there is uncertainty about which message mi will be sent. This means that there is uncertainty about which event in the partition {Ai: i ∈ J} will occur. This uncertainty must be related in some manner to the set of probabilities {P(Ai): i ∈ J} for the events in the partition. For example, consider three possible partitions of the basic space into two events (corresponding to two possible messages):
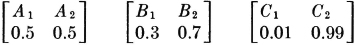
It is intuitively obvious that the first system, or scheme, indicates the greatest uncertainty as to the outcome; the next two schemes indicate decreasing amounts of uncertainty as to which event may be expected to occur. One may test his intuition by asking himself how he would bet on the outcome in each case. There is little doubt how one would bet in the third case; one would not bet with as much confidence in the second case; and in the first case the outcome would be so uncertain that he may reasonably bet either way. In evaluating more complicated schemes, or in comparing schemes with different numbers of events, the amounts of uncertainty may not be obvious. The problem is to find a measure which assigns a number to the uncertainty of the outcome. Actually, Shannon’s measure is a measure of the average uncertainty for the various events in the partition; and as the examples above suggest, this measure must be a function of the set of probabilities of the events in the partition. A number of intuitive and theoretical considerations led to the introduction of a measure of uncertainty which depends upon the logarithms of the probabilities. We shall not attempt to trace the development that led to this choice, but shall simply introduce the measure discovered by Shannon (and anticipated by others) and see that the properties of such a measure admit of an appropriate interpretation in terms of uncertainty.
Mutual and self-information of individual events
Shannon’s measure refers to probability schemes consisting of partitions and the associated set of probabilities. It is helpful, however, to begin with the idea of the mutual information in any two events; these events may or may not be given as members of a partition. At this point we simply make a mathematical definition. The justification of this definition must rest on its mathematical consequences and on the interpretations which can be made in terms of uncertainties among events in the real world.
Definition 5-6a
The mutual information in two events A and B is given by the expression
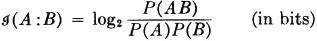
It should be noted that the logarithm in the definition is to the base 2. If any other base had been chosen, the result would be to multiply the expression above by an appropriate constant. This is equivalent to a scale change. Unless otherwise indicated, logarithms in this section are taken to base 2, in keeping with the custom in works on information theory. With this choice of base, the unit of information is the bit; the term was coined as a contraction of the term binary digit. Reasons for the choice of this term are discussed in practically all the introductions to information theory.
A number of facts about the properties of mutual information are easily derived. First we note a symmetry property which helps justify the term mutual.
The mutual information in events A and B is the same as the mutual information in events B and A. The order of considering or listing is not important. The function may also be written in a form which hides the symmetry but which leads to some relationships that are important in the development of the topic.
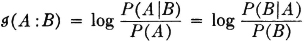
An examination of the possibilities shows that mutual information may take on any real value, positive, negative, or zero. That is,
The phenomenon of negative mutual information usually surprises the beginner. The following argument shows the significance of this condition. From the form above, which uses conditional probabilities, it is apparent that
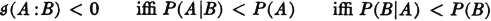
Use of elementary properties of conditional probabilities verifies the equivalence of the last two inequalities as well as the fact that
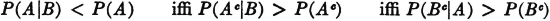
so that
We may thus say that the mutual information between A and B is negative under the condition that the occurrence of B makes the nonoccurrence of A more likely or the occurrence of A makes the nonoccurrence of B more likely. It is also easy to see from the definition that
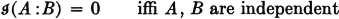
The mutual information is zero if the occurrence of one event does not influence (or condition) the probability of the occurrence of the other.
We may rewrite the expression, using conditional probabilities in the following manner to exhibit an important property.
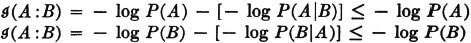
It is apparent that
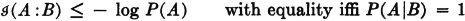
In particular,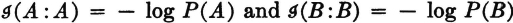 
. The mutual information of an event with itself is naturally interpreted as an information property of that event. It is thus natural to make the
Definition 5-6b
The self-information in an event A is given by
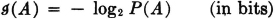
The self-information is nonnegative; it has value zero iffi P(A) = 1, which means there is no uncertainty about the occurrence of A. In this case, its occurrence removes no uncertainty, hence conveys no information.
Parallel definitions may be made when the probabilities involved are conditional probabilities.
The conditional mutual information in A and B, given C, is
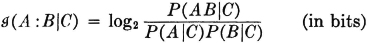
The conditional self-information in A, given C, is
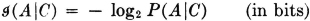
Properties of the conditional-information measures are similar to those for the information, since conditional probability is a probability measure. Some interpretations are of interest. The conditional self-information is nonnegative.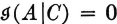 
iffi P(A|C) = 1. This means that there is no uncertainty about the occurrence of A, given that C is known to have occurred. 
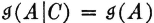iffi A and C are independent. Independence of the events A and C implies that knowledge of the occurrence of C gives no knowledge of the occurrence of A.
Some simple but important relations between the concepts defined above are of interest.
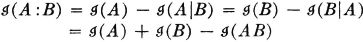
The last relation may be rewritten
These relations may be given interpretations in terms of uncertainties. We suppose 
is the uncertainty about the occurrence of event A (i.e., the information received when event A occurs). If event B occurs, it may or may not change the uncertainty about event A. We suppose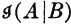 
is the residual uncertainty about A when one has knowledge of the occurrence of B. We may interpret 
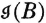and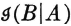 
similarly. Then, according to the first relation, 
is the information about A provided by the occurrence of the event B; similarly, the mutual information is the information about B provided by the occurrence of A. The last relation above may then be interpreted to mean that the information in the joint occurrence of events A and B is the information in the occurrence of A plus that in the occurrence of B minus the mutual information. Since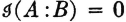 
iffi A and B are independent, the information in the joint occurrence AB is the sum of the information in A and in B iffi the two events are independent.
We turn next to the problem of measuring the average uncertainties in systems or schemes in which any one of several outcomes is possible. In order to be able to speak with precision and economy of statement, we formalize some notions and introduce some terminology.
The concept of a partition has played an important role in the development of the theory of probability. For a given probability measure defined on a suitable class of events, there is associated with each partition a corresponding set of probabilities. If the partition is
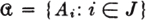
there is a corresponding set of probabilities {pi = P(Ai): i ∈ J} with the properties
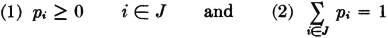
It should be apparent that, if we were given any set of numbers pi satisfying these two conditions, we could define a probability space and a partition such that these are the probabilities of the members of the partition. It is frequently convenient to use the following terminology in dealing with such a set of numbers:
Definition 5-6d
If {pi: i ∈ J} is a finite or countably infinite set of nonnegative numbers whose sum is 1, we refer to this indexed or ordered set as a probability vector. If there is a finite number n of elements, it is sometimes useful to refer to the set as a probability n-vector.
The combination of a partition and its associated probability vector we refer to according to the following
Definition 5-6e
If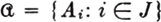 
is a finite or countably infinite partition with associated probability vector {P(Ai): i ∈ J}, we speak of the collection 
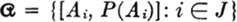as a probability scheme. If the partition has a finite number of members, we speak of a finite (probability) scheme.
The simple schemes used earlier in this section to illustrate the uncertainty associated with such schemes are special cases having two member events each. It is easy to extend this idea to joint probability schemes in which the partition is a joint partition 
of the type discussed in Sec. 2-7.
If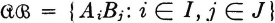 
is a joint partition, the collection 
is called a joint probability scheme.
This concept may be extended in an obvious way to the joint scheme for three or more schemes. In the case of the joint scheme 
, we must have the following relationships between probability vectors. We let
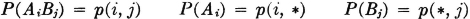
Then (p(i, j): i ∈ I, j ∈ J}, {p(i, *): i ∈ I}, and {p(*, j):j ∈ J} are all probability vectors. They are related by the fact that
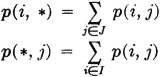
Definition 5-6g
Two schemes 
and 
are said to be independent iffi
P(AiBj) = P(Ai)P(Bj)
for all i ∈ I and j ∈ J.
Average uncertainty for probability schemes
We have already illustrated the fact that the uncertainty as to the outcome of a probability scheme is dependent in some manner on the probability vector for the scheme. Also, we have noted that in a communication system the probability scheme of interest is that determined by the choice of a message from among a set of possible messages. Shannon developed his very powerful mathematical theory of information upon the following basic measure for the average uncertainty of the scheme associated with the choice of a message.
Definition 5-6h
For schemes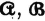 
, and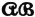 
, described above, we define the entropies
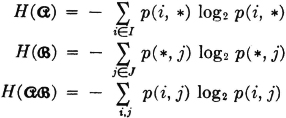
The term entropy is used because the mathematical functions are the same as the entropy functions which play a central role in statistical mechanics. Numerous attempts have been made to relate the entropy concept in communication theory to the entropy concept in statistical mechanics. For an interesting discussion written for the nonspecialist, one may consult Pierce [1961, chaps. 1 and 10]. For our purposes, we shall be concerned only to see that the functions introduced do have the properties that one would reasonably demand of a measure of uncertainty or information.
Since the partitions of interest in the probability schemes are related to random variables X(·) and Y(·) whose values are messages (or numbers representing the messages), the corresponding entropies are often designated H(X), H(Y), and H(XY). The random variables rather than the schemes are displayed by this notation. For our purposes, it seems desirable to continue with the notation designating the scheme.
We have alluded to the fact that the value of the entropy in some sense measures the average uncertainty for the scheme. We wish to see that this is the case, provided the self- and mutual-information concepts introduced earlier measure the uncertainty associated with any single event or pair of events.
First let us note that if we have a sum of the form
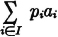
where the pi are components of the probability vector for a scheme, this sum is in fact the mathematical expectation of a random variable. We suppose {Ai: i ∈ I} is a partition and that pi = P(Ai) for each i. Then if we form the random variable (in canonical form)
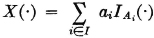
it follows immediately from the definition of mathematical expectation that
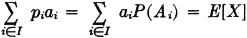
Now suppose we let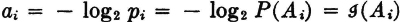 
. That is, ai is the self-information of the event Ai. We define the random variable 
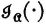by
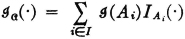
This is the random variable whose value for any is the self-information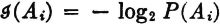 
for the event Ai which occurs when this is chosen. The mathematical expectation or probability-weighted average for this random variable is
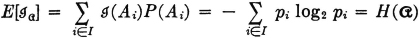
We may define similar random variables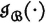 
and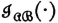 
for the schemes 
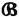and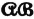 
and have as a result
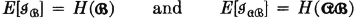
We may also define the random variable 
whose value for any ∈ AiBj is the conditional self-information in Ai, given Bj. That is,
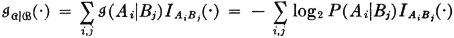
In a similar manner the variable 
may be defined. It is also convenient to define the random variable
Conditions for independence of the schemes 
and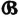 
show that the following relations hold iffi 
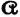and 
are independent:
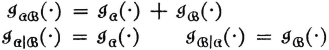
In terms of these functions we may define two further entropies:
These entropies may be expanded in terms of the probabilities as follows:
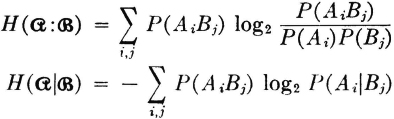
Linearity properties of the mathematical expectation show that various relations developed between information expressions for events can be extended to the entropies. Thus
Interpretations for these expressions parallel those for the information expressions, with the addition of the term average.
The following very simple example deals with a system studied extensively in information theory. It shows how the entropy concepts appear in this theory.
Example 5-6-1 Binary Symmetric Channel
In information theory, a binary channel is one which transmits a succession of binary symbols, which may be represented by 0 and 1 (see also Example 2-5-7). We suppose the system deals independently with each successive symbol, so that we may study the behavior in terms of one symbol at a time. Let S0 be the event a 0 is sent and S1 be the event a 1 is sent; let R0 and R1 be the events of receiving a 0 or a 1, respectively. If the probabilities of the two input events are P(S0) = π and P(S1) =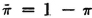 
, then the input scheme (which characterizes the message source) consists of the collection 
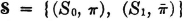. The channel is characterized by the conditional probabilities of the outputs, given the inputs. The channel is referred to as a binary symmetric channel (BSC) if P(R1|S0) = P(R0|S1) = p and P(R0|S0) = P(R1|S1) = q, where q = 1 − p; that is, the probability that an input digit is changed into its opposite is p and the probability that an input digit is transmitted unchanged is q. These probability relations are frequently represented schematically as in Fig. 5-6-1.
The binary entropy function H(p) = −p log2 p − q log2 q plays an important role in the theory of binary systems. [Note that we have used H(·) in a different sense here. This is in keeping with a custom that need cause no real difficulty]. A sketch of this function against the value of the transition probability p is shown in Fig. 5-6-2. Two characteristics important for our purposes in this example are evident in that figure. These are easily checked analytically.
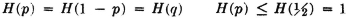
If we let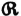 
be the output scheme consisting of the partition {R0, R1} and the associated probability vector, we may calculate the average mutual information between the input and output schemes and show it to be
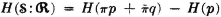
To see this, we write
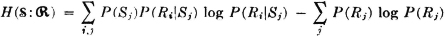
Fig. 5-6-1 Schematic representation of the binary symmetric channel.
Fig. 5-6-2 The binary entropy function
Substituting and recognizing the form for the binary entropy function, we obtain
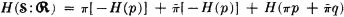
from which the desired result follows because 
. This function gives the average information about the input provided by the receipt of symbols at the output. If we set the input probabilities equal to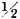 
, so that either input symbol is equally likely, the resulting value is
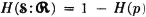
which is a maximum, since the maximum value of H(·) is 1 and it occurs when the argument is 
.
The entropy for an input-message scheme plays a central role in the theory of information. If a source produces one of n messages {mi: 1 ≤ i ≤ n} with corresponding probabilities {pi: 1 ≤ i ≤ n}, the source entropy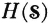 
is given by
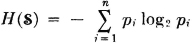
A basic coding theorem shows that these messages may be represented by a binary code in which the probability-weighted average L of the word lengths satisfies
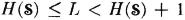
By considering coding schemes in which several messages are coded in groups, it is possible to make the average code-word length as close to the source entropy as desired. This is done at the expense of complications in coding, of course. Roughly speaking, then, the source entropy in bits (i.e., when logarithms are to base 2) measures the minimum number of binary digits per code word required to encode the source. It is interesting to note that the codes which achieve this minimum length do so by assigning to each message mi a binary code word whose length is the integer next larger than the self-information −log2 pi for that message. In the more sophisticated theory of coding for efficient transmission in the presence of noise, the source entropy and the mutual and conditional entropies for channel input and output play similar roles. It is outside the scope of this book to deal with these topics, although some groundwork has been laid. For a clear, concise, and easily readable treatment, one may consult the very fine work by Abramson [1963], who deals with simple cases in a way that illuminates the content and essential character of the theory.
We shall conclude this section by deriving several properties of the entropy functions which strengthen the interpretation in terms of uncertainty or information. In doing so, we shall find the following inequality and some inequalities derived from it very useful.
with equality iffi x = 1. This inequality follows from the fact that the curve y = loge x is tangent to the line y = x − 1 at x = 1 while the slope of y = loge x is a decreasing function of x.
In calculations with entropy expressions, we note that x log x is 0 when x has the value 1. Since x log x approaches 0 as x goes to 0, we define 0 log 0 to be 0.
Consider two probability vectors {pi: 1 ≤ i ≤ n} and {qi: 1 ≤ i ≤ n}. Then we show that
with equality iffi pi = qi for each i. To show this, we note
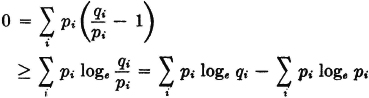
Equality holds iffi qi/pi = 1 for each i.
We now collect some properties and relations for entropies which are important in information theory. Some of these properties have already been considered above.
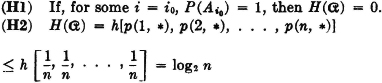
with equality iffi p(i, *) = 1/n for each i.
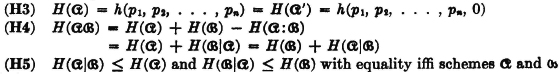
are independent schemes.
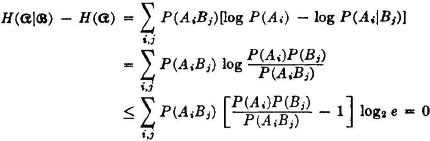
Equality holds iffi P(AiBj) = P(Ai)P(Bj) for each i, j.
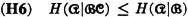
PROOF The proof is similar to that in (H5), but the details are somewhat more complicated. We omit the proof.
Property (H1) indicates that the average uncertainty in a scheme is zero if there is probability 1 that one of the events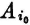 
will occur. Property (H2) says that the average uncertainty is a maximum iffi the events of the scheme are all equally likely. Property (H3) indicates that no change in the uncertainty of a scheme is made if an event of zero probability is split off as a separate event. Property (H4) has been discussed above. Property (H5) says that conditioning (i.e., giving information about one scheme) cannot increase the average uncertainty about the other. Property (H6) extends this result to conditioning by several schemes.
A number of investigators have shown that entropies defined as functions of the probabilities in schemes must have the functional form given in the definition, if the entropy function is to have the properties listed above. Shannon showed this in his original investigation [1948]. Investigators have differed in the list of properties taken as axiomatic, although they have usually taken an appropriate subset of the properties listed above. Their lists have been equivalent in the sense that any one implies the others. As Shannon has pointed out, however, the importance of the entropy concept lies not in its uniqueness, but in the fact that theorems of far-reaching consequence for communication systems may be proved about it. For a discussion of these developments, one may consult any of several references (cf. Fano [1961] or Abramson [1963]).
In the analytical theory of probability distributions, two special functions play a very powerful role. Although these two functions are usually treated somewhat independently, we shall emphasize the fundamental connection made evident in the following definition.
If X(·) is a random variable and s is a parameter, real or complex, the function of s defined by
is called the moment-generating function for X(·). If s = iu, where i is the imaginary unit having the formal properties of the square root of −1, the function X(·) defined by
is called the characteristic function for X(·)
Many works on probability theory limit the parameter s in the definition of the moment-generating function to real values. It seems desirable, however, to treat the more general case, in order to exploit an extensive theory developed in connection with classical integral transforms. Examination of the following integral expressions reveals the connection of the functions defined above with the classical theory.
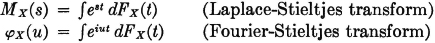
Absolutely continuous case:
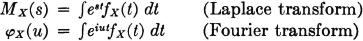
Discrete case:
The names in parentheses indicate that the functions in the various cases are well-known forms which have been studied intensively. The results of this nonprobabilistic theory are available for use in probability theory.
Before considering examples, we shall list some important properties of the moment-generating and characteristic functions. We shall state the results in terms of the moment-generating function. Where it is necessary to limit statements essentially to characteristic functions, this may be done by requiring that s = iu, with u real.
For a number of reasons, most probabilists prefer to use the characteristic function. One of these is the fact that the integral defining X(u) = MX(iu) exists for all real u. The integral for MX(s), where s is complex, may exist only for s in a particular region of the complex plane, the region of convergence. In general, the region of convergence is a vertical strip in the complex plane; in special cases this may be a half plane, the whole plane, or the degenerate strip consisting of the imaginary axis. Two cases are frequently encountered in practice: (1) the probability mass is all located in a finite interval on the real line, in which case the region of convergence for the moment-generating function is the whole complex plane; (2) the probability mass is distributed on the line in such a manner that there are positive numbers A and γ such that, for large t, P(|X| ≥ t) ≤ Ae−γi, in which case the region of convergence is the strip −γ < Re s < γ. When the region of convergence for the moment-generating function is a proper strip, the moment-generating function can be expanded in a Taylor’s series about the origin (i.e., it is an analytic function). The importance of this fact appears in the development below.
(M1) Consider two random variables X(·) and Y(·) with distribution functions FX(·) and FY(·), respectively. Let MX(·) and MY(·) be the corresponding moment-generating functions for the two variables. Then MX(iu) = MY(iu) for all real u iffi FX(t) = FY(t) for all real t.
In the case of a proper strip of convergence, the equality of the moment-generating functions extends (by analytic continuation) throughout the interior of the region of convergence. The property stated is a special case of a uniqueness theorem on the Laplace-Stieltjes transform or the Laplace-Fourier transform (cf. Widder [1941, p. 243, theorem 6A] or Loève [1963, sec. 12.1]).
(M2) If E[|X|n] exists, the nth-order derivative of the characteristic function exists and
In important special cases we can be assured that the derivatives and the nth-order moments exist, as indicated in the following property.
(M3) If the region of convergence for MX(·) is a proper strip in the s plane (which will include the imaginary axis), derivatives of all orders exist and
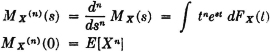
This theorem is based on the analytic property of the bilateral Laplace-Stieltjes integral (cf. Widder [1941]). Two important cases of mass distribution ensuring the condition of convergence in a proper strip are noted above—all probability mass in a finite interval or an exponential decay of the mass distribution.
Under the conditions of property (M3), the moment-generating function may be expanded in a power series in s about s = 0 to give
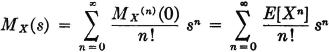
Thus, if the moment-generating function is known in explicit form and can be expanded in a power series, the various moments for the mass distribution can be determined from the coefficients of the expansion.
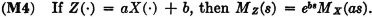
PROOF
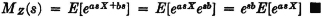
The moment-generating function is particularly useful in dealing with sums of independent random variables because of the following property.
(M5) If X(·) and Y(·) are independent random variables and if Z(·) = X(·) + Y(·), then MZ(s) = MX(s) MY(s) for all s.
PROOF It is known that g(t) = est is a Borel function. Hence the random variables esX(·) and esY(·) are independent when X(·) and Y(·) are. Now E[es(X + Y)] = E[esXesY] = E[esX]E[esY] by property (E6).
The result can be extended immediately by induction to any finite number of random variables.
We consider now several examples.
Example 5-7-1
Uniformly distributed random variable. Let X(·) be distributed uniformly on the interval a ≤ t ≤ b.
SOLUTION
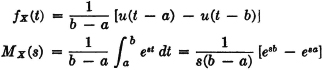
Using the well-known expansion of ebs and eas in a power series about s = 0, we obtain
Thus
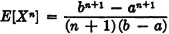
which may be checked by straightforward evaluation of the integral
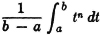
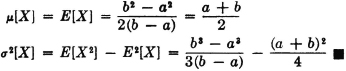
The next result is so important that we state it as a theorem.
Theorem 5-7A
The random variable X(·) is normal (, σ) iffi
PROOF First, consider the random variable Y(·), which is normal (0, 1).
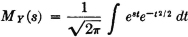
Evaluation can be carried out by noting that the combined exponent st − t2/2 = s2/2 − s2/2 + st − t2/2 = s2/2 − ½ (t − s)2. Thus
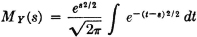
Making the change of variable x = t − s, we have, for each fixed s,
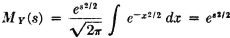
The random variable X(·) = σY(·) + is normal (, σ), as may be seen from Example 3-9-4. By properties (M4) and (M1) the theorem follows.
In many investigations, it is simpler to identify the moment-generating function or the characteristic function than to identify the density function directly.
Example 5-7-2
We may use the series expansion for the moment-generating function for a normally distributed random variable to obtain its mean and variance.
SOLUTION Using the first three terms of the expansion ez = 1 + z + z2/2 + · · ·, we obtain
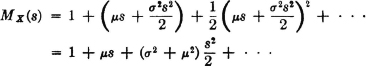
Hence
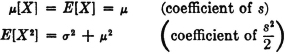
so that σ2[X] = σ2 + 2 − 2 = σ2.
Our next result, also stated as a theorem, displays an important property of normally distributed random variables.
Theorem 5-7B
The sum of a finite number of independent, normally distributed random variables is normally distributed.
PROOF Let Xi(·) be normal (i, σi), 1 ≤ i ≤ n. The Xi(·) form an independent class. Let Mi(·) be the moment-generating function for Xi, and let MX(·) be the moment-generating function for sum X(·). By property (M5),
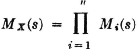
By Theorem 5-7A,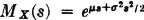 
, where 
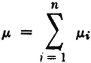and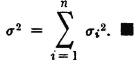 
One important consequence of this theorem for sampling theory is that, if the sampling is from a normal distribution, the sample average A(·) defined in Sec. 5-5 (Theorem 5-5A) is a normally distributed random variable. This is important in determining the probability that the sample average differs from the mean by any given amount.
The importance of the moment-generating function is greatly enhanced by certain limit theorems. We state, without proof, the following general theorem as one of the fundamental properties of the moment-generating function (Loève [1963, sec. 12.2]).
(M6) Suppose {Fn(·): 1 ≤ n < ∞} is a sequence of probability distribution functions and, for each n, Mn(·) is the moment-generating function corresponding to Fn(·).
(A) If F(·) is a probability distribution function such that Fn(t) → F(t) at every point of continuity of F(·), then
(B) If Mn(iu) → M(iu) for each real u and M(iu) is continuous at u = 0, then Fn(t) → F(t) at every point of continuity of F(·).
One of the historically important applications of this theorem has been its role in establishing the central limit theorem (discussed very briefly in Chap. 6). Its importance is not limited to this application, however, for the moment-generating function or the characteristic function is an important analytical tool in many phases of the development of probability theory. For the mathematical foundations of this theory, one should consult standard works such as Loève [1963, chap. 4], Cramér [1946, chap. 10], or Gnedenko [1962, chap. 7]. Applications are found in most books on statistics or on random processes.
5-1. A discrete random variable X(·) has values tk, k = 1, 2, 3, 4, 5, with corresponding probabilities pk = P(X = tk) given below:
(a) Calculate E[X] and E[X − 2.5].
ANSWER: 2.5, 0
(b) Calculate E[X − 2.5)2].
ANSWER: 8.25
5-2. A man stands in a certain position (which we may call the origin). He tosses a fair coin. If a head appears, he moves three units to the right (which we designate as plus three units); if a tail appears, he moves two units to the left (in the negative direction). Make the usual assumptions on coin flipping; i.e., let Ai be the event of a head on the ith throw. Assume the Ai form an independent class, with 
for each i. Let Xn(·) be the random variable whose value is the position of the man after n successive flips of the coin (the sequence of n flips is considered one composite trial).
(a) What are the possible values of X4(·), and what are the probabilities that each of these values is taken on? Determine from these numbers the mathematical expectation E[XA].
(b) Show that, for any n ≥ 1, Xn(·) may be written
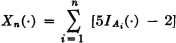
Determine E[Xn] from this expression, and compare the result for n = 4 with that obtained in part a.
5-3. A man bets on three horse races. He places a $2 bet on one horse in each race. Let H1, H2, and H3 be the events that the first, second, and third horses, respectively, win their races. Suppose the Hi form an independent class and that
(a) Let W(·) be the random variable which represents the man’s net winnings in dollars (a negative win is a loss). Express W(·) in terms of the indicator functions for H1, H2, and H3 and appropriate constants.
(b) Calculate the possible values for W(·) and the corresponding probabilities.
(c) What is the probability of coming out ahead on the betting (i.e., of having positive “winnings”)?
ANSWER: P(W > 0) = 0.344
(d) Determine the “expected” value of the winnings, E[W).
ANSWER: −0.7
5-4. A random variable X(·) has a distribution function FX(·) which rises linearly from zero at t = a to the value unity at t = b. Determine E[X], E[X2], and E[X3].
ANSWER: E[X) = (b + a)/2, E[X2] = (b3 − a3)/[3(b − a)]
5-5. A random variable X(·) produces a probability mass distribution which may be described as follows. A point mass of 0.2 is located at each of the points t = −1 and t = 2. The remaining mass is distributed smoothly between t = −2 and t = 2, with a density that begins with zero value at t = −2 and increases linearly to a maximum density at t = 2. Find E[X] and E[(X − 1)2].
ANSWER: 0.6, 1.6
5-6. The distribution function FX(·) for a random variable X(·) has jumps of 0.1 at t = −2 and t = 1; otherwise it increases linearly at the same rate between t = −3 and t = 2. Determine E[X] and 
.
ANSWER: −0.5, 2.99
5-7. Suppose the sales demand for a given item sold by a store is represented by a random variable X(·). The item is stocked to capacity at the beginning of the period. There are fixed costs associated with storage which are approximately proportional to the amount of storage N. A fixed gross profit is made on sales. If the demand exceeds the supply, however, certain losses (due to the decrease of sales of other items merchandised, etc.) occur; this loss may be approximated by a constant times the excess of the demand over the supply. We may thus express the profit or gain G(·) in terms of the demand X(·) as follows:
(a) If fX(t) = αe−αtu(t), determine the expected profit in terms of α, g, c, L, and N.
(b) For any given storage capacity N, what is the probability that demand will exceed the supply? Express E[G] in terms of X, P(X > N), g, c, L, and N.
5-8. A random variable X(·) has values ti = (i − 1)2, i = 1,2, 3, 4, and random variable Y(·) has range uj = 2j, j = 1, 2, 3. The values of p(i, j) = P(X = ti, Y = uj) are as follows:
Determine the mathematical expectations E[X], E[Y], and E[2X − 3Y].
ANSWER: 3.50, 4.40, −6.20
5-9. A random variable X(·) has range 
. A random variable Y(·) has range 
. The values of p(i, j) = P(X = ti, Y = uj) are as follows:
(a) Let the random variable Z(·) be defined by Z() = X() + Y(). Determine the distribution function FZ(·).
(b) Determine E[X], E[Y], and E[Z], and verify in this case that
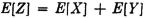
5-10. If g(·) is an odd Borel function and if the density function fX(·) for the random variable X(·) is an even function, show that E[g(X)] = 0.
5-11. Two real-valued functions g(·) and h(·) are said to be orthogonal on the interval (a, b) iffi
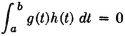
Two real-valued functions g(·) and h(·) are said to be orthogonal on the interval (a, b) with respect to the weighting function r(·) iffi
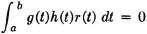
(a) If g(·) is a Borel function orthogonal to the density function fX(·) for the random variable X(·) on the interval (−∞, ∞), show that E[g(X)] = 0.
(b) If g(·) and h(·) are two Borel functions orthogonal on the interval (−∞, ∞) with respect to the density function fX(·), show that E[g(X)h(X)] = 0.
(c) If the random variable X(·) is uniformly distributed on the interval [0, 2π], if n and m are nonzero integers, and if a and b are arbitrary real constants, show that the following hold:
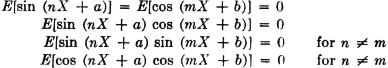
(Suggestion: Apply the well-known orthogonality relations on sinusoidal functions used in developing Fourier series.)
5-12. Suppose X(·) and 
(·) are independent random variables with (·) uniformly distributed on the interval [0, 2π]. Show that, for any nonzero integer n,
Note that this result includes the special case X(·) = c [P], in which case E[X] = c. [Suggestion: Use formulas for cos (x + y) and sin (x + y) and the results of Prob. 5-11.]
5-13. A discrete random variable has the following set of values and probabilities. Calculate the mean and standard deviation.
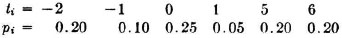
ANSWER: = 1.75, σ = 3.17
5-14. A random variable X(·) has range (−30, −10, 0, 20, 40) and corresponding probabilities (0.2, 0.1, 0.3, 0.3, 0.1); for example, P(X = −30) = 0.2, P(X = 40) = 0.1, etc. Determine the mean value [X] and the variance σ2[X].
ANSWER: 3, 461
5-15. A random variable X(·) is distributed according to the binomial distribution with n = 10, p = 0.1. Consider the random variable Y(·) = X2(·) − 1.
(a) Calculate the mean value of Y(·).
ANSWER: 0.9
(b) Calculate the standard deviation of Y(·). (Simplify as far as possible, and indicate how tables could be used to determine numerical results.)
5-16. A man stands in a certain position (which we may call the origin). He makes a sequence of n moves or steps. At each move, with probability p, he will move a units to the right, and with probability q = 1 − p, he will move b units to the left. The various moves are stochastically independent events. Let Xn(·) be the random variable which gives the distance moved after n steps (cf. Prob. 5-2).
(a) Obtain an expression for Xn(·) if Ai is the event of a move to the right at the ith step.
(b) Determine expressions for n = E[Xn] and σn2 = σ2[Xn].
ANSWER: n(ap − bq), n(a + b)2pq
(c) Determine numerical values for n = 4, p = 0.3, a = 2, and b = 1.
Aids to computation
From the geometric series
the following may be derived by differentiation and algebraic manipulation:
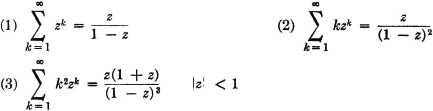
5-17. An experiment consists of a sequence of tosses of an honest coin (i.e., to each elementary event corresponds an infinite sequence of heads and tails). Let Ak be the event that a head appears for the first time at the kth toss in a sequence, and let Hk be the event of a head at the kth toss. Suppose the Hk form an independent class with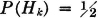 
for each k. For a given sequence corresponding to the elementary outcome , let X() be the number of the toss in the sequence for which the first head appears.
(a) Express X(·) in terms of indicator functions for the Ak.
(b) Determine [X] and σ2[X]. (Suggestion: Use the appropriate formulas above for summing the series.)
ANSWER: [X] = 2, σ2[X] = 2
5-18. Consider two random variables X(·) and Y(·) with joint probability distribution which is uniform over the triangular region having vertices at points (0, 0), (0, 1), and (1, 0). Let Z(·) = X(·) + Y(·).
(a) Determine the distribution functions FX(·) and FZ(·) and the density functions fX(·) and fZ(·).
(b) Calculate X, Y, Z, σX2, σY2, and σZ2.
ANSWER: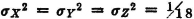 
5-19. Consider two random variables X(·) and Y(·) with joint probability distribution which is uniform over the triangular region having vertices at points (0, 0), (1, 0), and (0, -1). Let W(·) = X(·) − Y(·).
(a) Determine the distribution functions FX(·) and FW(·) and the density functions fX(·) and fW(·).
(b) Calculate X, Y, W, σX2, σY2, and σW2.
5-20. If X(·) and Y(·) are real-valued random variables whose variances exist, show that (σ[X] − σ[Y])2 ≤ σ2[X − Y]. (Suggestion: Use the Schwarz inequality and the fact that the variance does not depend upon an additive constant.)
5-21. Scores on college board examinations vary between 200 and 800. To a good approximation, these may be considered to be values of a random variable which is normally distributed with mean 500 and standard deviation 100. What is the probability of selecting a person at random with a score of 700 or more?
ANSWER: 0.023
5-22. Suppose that X(·) is normal (15, 2). Use the table of normal probability functions (Sec. 5-4) to determine:
(a) P(X < 13)
ANSWER: 0.1587
(b) P(X ≤ 15)
(c) P(|X − 15| ≤ 4)
ANSWER: 0.9545
5-23. A random variable X(·) is distributed normally (2, 0.25); that is, = 2, σ = 0.25
(a) Determine the mean and standard deviation for the variable
(b) What is the probability 1.5 ≤ X(·) ≤ 2.25?
ANSWER: 0.8185
(c) What is the probability |X(·) − 2| ≤ 0.5?
5-24. A lot of manufactured items have weights, when packaged, which are distributed approximately normally, with mean = 10 pounds and standard deviation σ = 0.25 pound. A load of 100 items is gathered randomly from the lot for shipment. What is the probability that the weight of the load is no greater than 1,005 pounds? State your assumptions.
5-25. Readings of a certain physical quantity may be considered to be values of a random variable which has the normal distribution with mean and standard deviation σ = 0.20 unit. A sequence of n independent readings may be represented by the respective values of n independent random variables, each with the same distribution.
(a) Determine the probability r that a single reading will lie within 0.1 unit of the mean value .
ANSWER: r = 0.383
(b) Determine, in terms of r as defined in part a, the probability that at least one reading in four lies within 0.1 unit of .
ANSWER: 1 − (1 − r)4
(c) Determine, in terms of r, the probability that exactly one reading in four lies within 0.1 unit of .
(d) Determine the probability that the average of four readings lies within 0.1 unit of .
ANSWER: 0.683
5-26. Suppose X(·) is a random variable and g(·) is a Borel function which may be expanded in a Taylor’s series about the point t = = [X]. Thus g(t) = g() + g′()(t − ) + r(t). If the remainder r(t) is negligible throughout the set of t on which most of the probability mass is located, determine expressions for [g(X)] and σ2[g(X)].
ANSWER: g(), [g′()]2σ2[X]
5-27. A sample of size n is taken (with or without replacement). From this sample, a single value is taken at random.
Let A be the event a certain result is achieved on the final choice from the sample of size n; Ai be the event of a success on the ith trial in taking the original sample; and Bk be the event of exactly k successes in the n trials making up the sample. Consider 
, the number of successes in the n trials.
(a) Write N(·) in terms of the indicator functions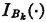 
.
(b) Assume P(A|Bk) = k/n. Show that P(A) can be expressed simply in terms of E[N]. Give the formula.
ANSWER: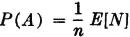 
(c) Use the results of parts a and b to express P(A) in terms of the P(Ai). What does this reduce to if P(Ai) = p for each i?
5-28. In information theory, frequent attention is given to binary schemes having two events (often designated by 0 and 1) with probabilities p and q = 1 − p. In this case, the entropy function is usually indicated by H(p) and is given by H(p) = − p log2 p − q log2 q.
(a) Show that the derivative H′(p) = log2 (q/p). (Note that, in differentiating the logarithm, it is desirable to convert to base e.)
(b) Show that the graph for H(p) versus p has a maximum at 
and is symmetrical about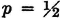 
(Fig. 5-6-2).
5-29. Consider a set of N boxes, each of which is occupied by an object with probability p and is empty with probability 1 − p. If Ai is the event the ith box is occupied, the Ai are assumed to form an independent class. What is the information about the occupancy of the ith box provided by the knowledge that k of the N boxes are occupied. Let Bk be the event k boxes are occupied.
ANSWER: log2 (k/Np)
5-30. Each of two objects, a and b, is to be put into one of N cells. Either a or b may occupy any cell with probability 1/N, but they cannot both occupy the same cell. Let Ai be the event that object a is in the cell numbered i, and Bj be the event that object b is in the cell numbered j. Let Oi = Ai 
Bi be the event that cell i is occupied, and let Dij = OiOj = AiBj AjBi be the event that cells i and j are occupied. Assume P(Ai) = P(Bj) = 1/N for each i and j, and P(Ai|Bj) = P(Bj|Ai) = 1/(N − 1) for i ≠ j. Find and interpret the following quantities:
(a)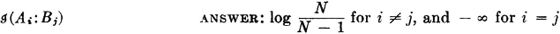 
(b)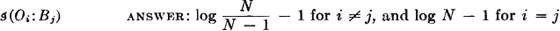 
(c) 
(d) 
(Note that the latter two quantities are meaningless for i = j.)
5-31. Show that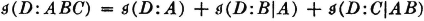 
. Interpret this expression.
5-32. Consider a set of messages m0, m1, m2, m3, m4, m5, m6, m7 which have probabilities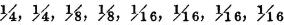 
and code words 000, 001, 010, 011, 100, 101, 110, 111, respectively. Message m5 is received digit by digit. What information is provided about the message m5 by each successive digit received? (Suggestion: Let Wi be the event the ith code word is sent. Let Ai be the event that the first letter in the code word received is the first letter in the ith code word. Similarly for Bi and Ci and the second and third letters of the code word received. Calculate the conditional probabilities needed to apply the results of Prob. 5-31.)
ANSWER: 2, 1, 1
5-33. A binary communication system is disturbed by noise in such a way that each input digit has a probability p of being changed by the channel noise. Eight messages may be transmitted with equal probabilities; they are represented by the following code words:
If the sequence of digits υ = 0100 is received, determine the amount of information provided about message u3 by each digit as it is received. (Suggestion: Let Ui be the event the code word ui is sent; A be the event the first letter received is a zero; B be the event the second letter received is a zero; etc. Calculate the conditional probabilities needed to use the results of Prob. 5-31, extended to the case of five events.)
ANSWER: 1 + log q, 1 + log q, 1 + log q, − log [4q(p2 + q2)]
5-34. Consider a scheme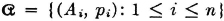 
.
(a) Suppose, for a given pair of integers r and s, it is possible to modify pr and ps but all other pi are to remain unchanged. Show that if the smaller of the two values pr, ps is increased and the larger is decreased accordingly, the value of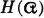 
is increased, with a maximum value occurring when the two probabilities are equal. (Suggestion: Let pr + ps = 2a, pr = a − δ, and ps = a + δ.)
(b) Suppose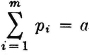 
. Show that 
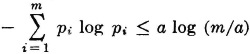with equality iffi pi = a/m for each i. What can be concluded about maximizing 
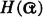if any subset of the probabilities may be modified while the others are held constant?
Aid to computation
5-35. Joint probabilities p(i, j) for a joint probability scheme 
are shown below:
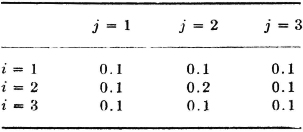
Calculate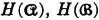 
, and 
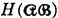, and show for this case that 
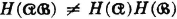and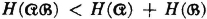 
.
5-36. Consider N schemes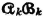 
with joint probabilities pk(i, j), 1 ≤ i ≤ n, 1 ≤ j ≤ m, 1 ≤ k ≤ N. Let λ1, λ2, …, λN be nonnegative numbers whose sum is unity, and put 
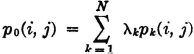. The p0(i, j) are joint probabilities of a scheme which we call 
.
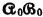(a) Show 
(b) It is possible to construct examples which show that, in general,
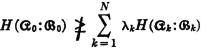
However, in the special case (of importance in information theory) that
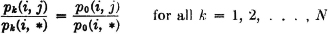
the inequality does hold. Show that this is so.
5-37. Show that the average probability discussed in Sec. 2-5, just prior to and in Example 2-5-5, may be expressed as the expectation of a random variable. Show that the result in Example 2-5-5 is then a consequence of property (E7).
5-38. For the binary symmetric channel, use the notation of Example 5-6-1. Show that
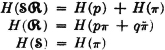
Obtain the result of Example 5-6-1 by use of the appropriate relationship between the entropy functions.
5-39. The simple random variable X(·) takes on values −2, −1, 0, 2, 4 with probabilities 0.1, 0.3, 0.2, 0.3, 0.1, respectively.
(a) Write an expression for the moment-generating function MX(·).
(b) Show by direct calculation that M′X(0) = E[X] and M″X(0) = E[X2].
5-40. If MX(·) is the moment-generating function for a random variable X(·), show that σ2[X] is the second derivative of e−s
MX(s) with respect to s, evaluated at s = 0. [Suggestion: Use properties (M3) and (M4).]
5-41. Simple random variables X(·) and Y(·) are independent. The variable X(·) takes on values −2, 0, 1, 2 with probabilities 0.2, 0.3, 0.3, 0.2, respectively. Random variable Y(·) takes on values 0, 1, 2 with probabilities 0.3, 0.4, 0.3, respectively.
(a) Write the moment-generating functions MX(·) and MY(·).
(b) Use the moment-generating functions to determine the range and the probabilities for each value of the random variable Z(·) = X(·) + Y(·).
5-42. Suppose X(·) is binomially distributed (Example 3-4-5), with basic probability p and range t = 0, 1, 2, …, n.
(a) Show that MX(s) = (pes + q)n.
(b) Use this expression to determine [X] and σ2[X].
5-43. An exponentially distributed random variable X(·) has probability density function fX(·) defined by
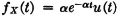
(a) Determine the moment-generating function MX(s).
(b) Determine X and σX2 with the aid of the moment-generating function.
General ideas about expectations
GNEDENKO [1962], chap. 5. Cited at the end of our Chap. 3.
PARZEN [1960], chap. 8. Cited at the end of our Chap. 2.
WADSWORTH AND BRYAN [1960], chap. 7. Cited at the end of our Chap. 3.
Normal distribution
ARLEY AND BUCH [1950]: “Introduction to the Theory of Probability and Statistics,” chap. 7 (transl. from the Danish). A very fine treatment of applications of probability theory, particularly to statistics. Does not emphasize the measure-theoretic foundation of probability theory, but is generally a sound, careful treatment, designed for the engineer and physicist.
CRAMERÉR [1946]: “Mathematical Methods of Statistics,” chap. 17. A standard reference for the serious worker in statistics. Lays the foundations of topics in probability theory necessary for statistical applications.
Random samples and random variables
BRUNK [1964], chap. 6. Cited at the end of our Chap. 2.
FISZ [1963]. Cited at the end of our Chap. 2.
Probability and information
SHANNON [1948]: A Mathematical Theory of Communication, Bell System Technical Journal. Original papers reporting the fundamental work in establishing the field now known as information theory. For insight into some of the central ideas, these papers are still unsurpassed.
ABRAMSON [1963]: “Information Theory and Coding,” chaps. 2, 5. A very readable yet precise account of fundamental concepts of information theory and their application to communication systems.
FANO [1961]: “Transmission of Information.” A book by one of the fundamental contributors to information theory. Although designed as a text, it has something of the character of a research monograph. For fundamental measures of information, see chap. 2.
Moment-generating and characteristic functions
BRUNK [1964], sec. 81. Cited at the end of our Chap. 2.
CRAMÉR, [1946], chap. 10. Cited above.
GNEDENKO [1962], chap. 7. Provides a succinct and readable development of the more commonly used properties of characteristic functions. Cited at the end of our Chap. 3.
LOÈVE [1963], chap. 4. Provides a thorough treatment of characteristic functions. Cited at the end of our Chap. 4.
WIDDER [1941]: “The Laplace Transform.” A thorough treatment of the Laplace-Stieltjes transform. Provides the basic theorems and properties of the moment-generating function for complex parameter s. See especially chap. 6, secs. 1 through 6.
